南航理论力学习题答案7(1)
南京航空航天大学 结构力学 课后习题答案 第7章
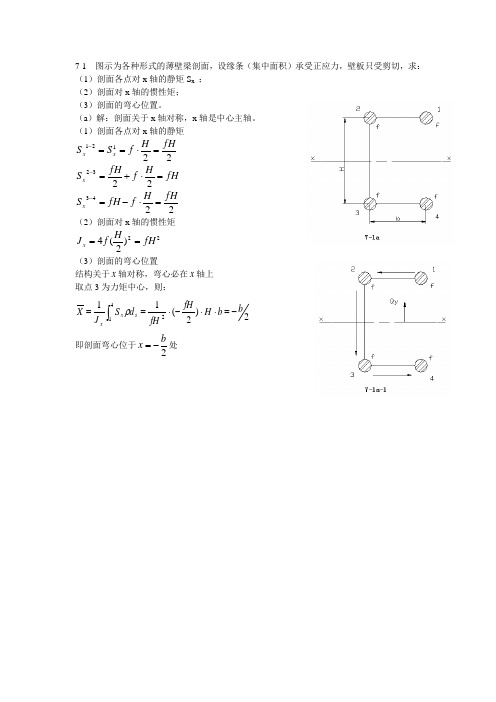
7-1 图示为各种形式的薄壁梁剖面,设缘条(集中面积)承受正应力,壁板只受剪切,求: (1)剖面各点对x 轴的静矩S x ; (2)剖面对x 轴的惯性矩; (3)剖面的弯心位置。
(a )解:剖面关于x 轴对称,x 轴是中心主轴。
(1)剖面各点对x 轴的静矩22121fHH f S S x x =⋅==- fH H f fH S x =⋅+=-2232 2243fHH f fH S x=⋅-=- (2)剖面对x 轴的惯性矩22)2(4fH H f J x == (3)剖面的弯心位置结构关于x 轴对称,弯心必在x 轴上 取点3为力矩中心,则:2)2(11241b b H fH fHd S J X s x x-=⋅⋅-⋅==⎰ρ 即剖面弯心位于2b x -=处(1)剖面各点对x 轴的静矩12233445563()28837828711828117()82873()828x x x x x H H S f fH H S fH f fH H S fH f fHH S fH f fH H S fH f fH -----=⋅-==+⋅==+⋅==+⋅-==+⋅-= 剪流沿1-2-3-4-5-6方向为正(2)剖面对x 轴的惯性矩2222412[()2()]28232x i i H H H J f y f f fH ==⋅-+⋅=∑ (3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上设弯心在3-4杆左侧,距3-4杆的距离为X ,由弯心的定义可知当弯心处作用有y Q 时,结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和3-4杆交点处取矩,则1223455608228y H H H HQ X q b q b q b q b ----⋅-⋅⋅-⋅⋅-⋅⋅-⋅⋅= (1) 又知y x y xQ q S J =则(1)式可化为12234556131()822841x x x x x bH bH bH bH X S S S S b J ----=⋅+⋅+⋅+⋅=即结构弯心在x 轴上3-4杆左侧3141b 处题7-1b 图(1)剖面各点对x 轴的静矩12322545651221221122221()221()22x x x x x H S f fH H S f fH H S fH fH f H S f fHH S f fH-----=⋅==⋅==++⋅=⋅-=-=⋅-=- 剪流方向如图(2)剖面对x 轴的惯性矩22224()22()222x i i H HJ f y f f fH ==⋅+⋅⋅=∑(3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上设弯心在2-5杆左侧,距2-5杆的距离为X ,由弯心的定义可知当弯心处作用有y Q 时,结构上的剪流和y Q 在结构上任意一点 的合力矩为零现对x 轴和2-5杆交点处取矩,则12234556022222222y b H b H b H b HQ X q q q q ----⋅+⋅⋅-⋅⋅+⋅⋅-⋅⋅= (1)又知y x y xQ q S J =则(1)式可化为122345561()04444x x x xx bH bH bH bH X S S S S J ----=-⋅+⋅-⋅+⋅= 即结构弯心在x 轴上与2-5杆相交处题7-1c 图(1)剖面各点对x 轴的静矩x S fR =(2)剖面对x 轴的惯性矩222x i i J f y fR ==∑(3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上11Rx x xs X S ds fR ds J J πρρ=⋅=⋅⎰⎰(1)其中ρ为承受剪流的面积到x 轴的距离,取极坐标θ,记上缘条处0θ=,逆时针方向为正,则cos R ρθ=,代入(1)式得11cos cos 0RxxX fR R ds fR R Rd J J ππθθθ=⋅=⋅⋅=⎰⎰即剖面弯心在两缘条中心连线与x 轴的交点处题7-1d 图(1)剖面各点对x 轴的静矩122343355667871099714452424144515244225722227522221()441()44152()424x x x x x x x x x H S f fH fH H S f fHH S f fHH S fH fH f fHH S fH f fHH S fH f fHH S f fHH S f fHH S fH f fH---------=⋅==+⋅==⋅==++⋅==+⋅==-⋅==⋅-=-=⋅-=-=-+⋅-=- 剪流方向如图(2)剖面对x 轴的惯性矩2222134()62()224x i i H H J f y f f fH ==⋅+⋅⋅=∑ (3)剖面的弯心结构关于x 轴对称,弯心必在x 轴上设弯心在5-6杆右侧,距5-6杆的距离为X ,由弯心的定义可知当弯心处作用有y Q 时,结构上的剪流和y Q 在结构上任意一点的合力矩为零 现对x 轴和5-6杆交点处取矩,则1223433567()42422y H H H H HQ X q a b q a q b q b q b -----⋅-⋅⋅+-⋅⋅-⋅⋅-⋅⋅-⋅⋅ 7879910()0424H H Hq b q a q a b ----⋅⋅-⋅⋅-⋅⋅+= (1) 又知y x y xQ q S J =代入(1)式可得11(2)26X a b =+ 即结构弯心在x 轴上5-6杆右侧11(2)26a b +处 题7-1e 图7-2 题7-2图所示薄壁梁剖面,缘条承受正应力,其截面积为22cm f =。
南京航空航天大学08年理论力学考研试题及答案

aBC = ae = 3ω R2 ( ← )
共 4 页 第2 页
va
vr
ve
A
ω
O
?
B
O1
C
(12 分)
R
t
ar
ae
(13 分)
aa
n
ar
第 4题 (25 分)
解:速度分析:
vA = OA ?ω= 1× 10 =10 (m/s)
取 AB 杆,在图示瞬时, C 为 AB 的速度瞬心,则
ω AB = vA / AC = 10/2 = 5(rad/s) ( 顺时针 ) vB = BC ?ω AB = 2× 5 = 10 (m/s) ω BC = vB /BC =10/2 = 5 (rad/s) (顺时针 )
(12 分)
加速度分析:
取 AB 杆,以 A 为基点,则
t
n
t
n
vA ω O
A
共 2 页 第2 页
B
O
A
C
ω
第 4 题图
A
30 D 第 5 题图
B C
第 6 题(20 分)
A
图示均质杆 AB 可绕轴 O 转动,质量为 m ,长度为 L ,且 OA =L 。 3
O
θ
若在图示位置时 θ= 30 D ,杆 AB的角速度为 ω。试用达朗贝尔原理求 该瞬时:(1)杆 AB 的角加速度; (2)O 处的约束反力。
试题编号: 415
共 2 页 第1 页
南京航空航天大学
二 OO 八年硕士研究生入学考试试题
考试科目: 理论力学 说 明:答案一律写在答题纸上,写在试卷上无效。
第 1 题 (25 分) 图示平面结构由 ABC、CD、BE 和 HED 四根杆件组成, 尺寸
理论力学习题及答案(全)

第一章静力学基础一、是非题1.力有两种作用效果,即力可以使物体的运动状态发生变化,也可以使物体发生变形。
()2.在理论力学中只研究力的外效应。
()3.两端用光滑铰链连接的构件是二力构件。
()4.作用在一个刚体上的任意两个力成平衡的必要与充分条件是:两个力的作用线相同,大小相等,方向相反。
()5.作用于刚体的力可沿其作用线移动而不改变其对刚体的运动效应。
()6.三力平衡定理指出:三力汇交于一点,则这三个力必然互相平衡。
()7.平面汇交力系平衡时,力多边形各力应首尾相接,但在作图时力的顺序可以不同。
()8.约束力的方向总是与约束所能阻止的被约束物体的运动方向一致的。
()二、选择题1.若作用在A点的两个大小不等的力F1和F2,沿同一直线但方向相反。
则其合力可以表示为。
①F1-F2;②F2-F1;③F1+F2;2.作用在一个刚体上的两个力F A、F B,满足F A=-F B的条件,则该二力可能是。
①作用力和反作用力或一对平衡的力;②一对平衡的力或一个力偶。
③一对平衡的力或一个力和一个力偶;④作用力和反作用力或一个力偶。
3.三力平衡定理是。
①共面不平行的三个力互相平衡必汇交于一点;②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
4.已知F1、F2、F3、F4为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
5.在下述原理、法则、定理中,只适用于刚体的有。
①二力平衡原理;②力的平行四边形法则;③加减平衡力系原理;④力的可传性原理;⑤作用与反作用定理。
三、填空题1.二力平衡和作用反作用定律中的两个力,都是等值、反向、共线的,所不同的是。
2.已知力F沿直线AB作用,其中一个分力的作用与AB成30°角,若欲使另一个分力的大小在所有分力中为最小,则此二分力间的夹角为度。
理论力学习题及答案1-7.doc

第1章静力分析习题1.是非题(对画√,错画×)1-1.凡在二力作用下的约束称为二力构件。
()1-2.在两个力作用下,使刚体处于平衡的必要条件与充分条件式这两个力等值、反向、共线。
()1-3.力的可传性只适用于一般物体。
()1-4.合力比分力大。
()1-5.凡矢量都可以用平行四边形法则合成。
()1-6.汇交的三个力是平衡力。
()1-7.约束力是与主动力有关的力。
()1-8.作用力与反作用力是平衡力。
()1-9.画受力图时,对一般的物体力的可沿作用现任以的滑动。
()1-10. 受力图中不应出现内力。
()2.填空题(把正确的答案写在横线上)1-11.均质杆在A、B两点分别于矩形光滑槽接触,并在如图所示情况下平衡。
A点的受力方向为,B点的受力方向为。
1-12.AB杆自重不计,在5个已知力作用下处于平衡,则作用于B点的四个力的合力F R的大小F R= ,方向沿。
题1-11图F3R题1-12图3. 简答题1-13.如图所示刚体A、B自重不计,在光滑斜面上接触。
其中分别作用两等值、反向、共线的力F1和F2,问A、B是否平衡?若能平衡斜面是光滑的吗?1-14.如图所示,已知A点作用力F,能否在B点加一力使AB杆平衡?若能平衡A点的力F的方向应如何?1-15.如图所示刚架AC和BC,在C 处用销钉连接,在A、B处分别用铰链支座支承构件形成一个三铰拱。
现将作用在杆BC上的力F沿着其作用线移至刚体AC上。
不计三铰刚架自重。
试问移动后对A、B、C约束反力有没有影响?为什么?1-16.在刚体上的加上任意个的平衡力系,能改变原来力系对刚体的作用吗?但对于变形体而言又是如何?1-17.为什么说二力平衡条件、加减平衡力系原理和力的可传性等只能适用于刚体?1-18.如何区分二力平衡力和作用力与反作用力?1-19.为什么受力图中不画内力?如何理解?1-20.如何判定二力体或者二力杆?(a)(c)(d) (e)(g)(h)题1-21图题1-13图题1-14图题1-15图4.受力分析题1-21.画出下列标注字母物体的受力图,未画重力的各物体其自重不计,所有接触面均为光滑接触。
南航理论力学习题答案17(1)

第十七章机械振动基础1.质量为m 的物体M ,置于光滑水平面上,在图示的连接情况下,系统的固有频率为( )。
① )(2121k k m k k + ② 2121)(k k k k m + ③m k k 21+ ④ 21k k m + 正确答案:①2.如图所示,在倾角为α的光滑斜面上,置一刚度系数为k 的弹簧,一质量为m 的物块沿斜面下滑s 距离与弹簧相碰,碰后弹簧与物块不分离并发生振动,则自由振动的固有频率为( )。
① mk ② ms k ③αsin m k ④ m k αsin 正确答案:①3.如图所示,单摆由无重刚杆OA 和质量为m 的小球A 构成。
小球上连接有两个刚度系数为k 的水平弹簧,则单摆微振动的固有频率为( )。
① mk ② m k 2 ③m k L g 2+ ④ m k L g + 正确答案:③4.图示的两个振动系统中,如果物块的质量和弹簧的刚度系数均相等,则此两种情况下系统的固有频率( )。
① 相同② 不同③ 由质量和刚度系数尚不能确定正确答案:①5.图示质量弹簧系统,已知物块的质量为m ,弹簧的刚度系数为k ,静伸长为δs ,原长是l 0 。
若以弹簧未伸长的下端点为坐标原点O ,则物块的运动微分方程为( )。
① 0=+x mk x ② 0)(=−+s x mk x δ ③ g x mk x s =−+)(δ ④ 0)(=++s x mk x δ 正确答案:②6.在图示中,当把弹簧原长的中点O 固定后,系统的固有频率与原来固有频率的比值为( )。
① 21 ② 2③ 2④ 4正确答案:③7.图示弹簧秤,秤盘重未知,当盘上放一重P 的物体时,测得振动周期为T 1;换一重Q 的物体时,其振动周期为T 2,则弹簧的刚度系数应为k =( )。
正确答案:)()(421222T T g P Q −−π8.图示为四根弹簧连接而成的振动装置,弹簧的刚度系数分别为k 1和k 2。
假设质量为m 的物块A 沿倾角为α的斜面作平动,则该振动装置的固有频率ω =( )。
理论力学第7章答案

x′
a
n A
sin
θ
−
aAτ
cosθ= NhomakorabeaaBx
cos
θ
−
aBy
sin
θ
aAτ
=
−aBx
+
(a
n A
+ aBy )tgθ
=
−1cm/s 2
α OA
=
a
τ A
/ OA
=
−(1/ 40)rad/s2
7.13 滚压机构的滚子沿水平面作纯滚动如图示 曲柄 OA 长 r 连杆 AB 长 l 滚子 半径为 R 若曲柄以匀角速度 ω 绕固定轴 O 转动 计算连杆 AB 和滚子的角加速度
向
v A
垂直于
OA
杆
因此瞬心为 C
不难看出 C 点相对
AB 杆和定系的位置可分别以 (2r, ϕ) 和 (r,2ϕ) 表示 则动 定瞬心迹线分别是半径为 2r 和 r 的圆
7.9 图示反平行四边形机构中 AB = CD = 2a AC = BD = 2c a > c 求杆 BD
的动瞬心轨迹和定瞬心轨迹
b
杆速度瞬心在 点 vC = 0
∴ ωBC = vB / a = ω ωCD = 0
基点
aCτ = aBn + aCτ B + aCnB
x′ acτ cos θ = −aBn − aCnB
Q cos θ = sin ϕ = 7 / 4
aBn = ω2a
aCnB = ω2a
∴ aCτ = −8ω2a / 7
上二式中消去 ψ 得 (ρsin ϕ)2 + (2c − ρ cos ϕ)2 = (2a − ρ)2
理论力学 陈立群 第7章习题解答

第七章 质点动力学 习题解答7-1 质量为40 g 的小球M 以初速度v =8 j (m/s)从点A (0, 0, 0.3m)抛出后,受到沿i 方向恒定的电磁力作用,其大小F = 0.8 kN ,如图所示。
求小球M 到达xy 平面点B 时,点B 的坐标和小球的速度。
解:取小球M 为研究对象,小球所受到的主动力为 k i F mg F R -=由质点运动微分方程R F m =r ,写出投影式F x m = ,0=ym ,mg z m -= 初始条件为000====t t y x ,3.00==t z ;000====t t z x,v y t ==0 解得质点的速度方程为t mFx= ,v y = ,gt z -= 质点的运动方程为 22t m F x =,vt y =,3.022+-=t gz 当0=z 时,小球到达xy 平面,由03.022=+-=t g z 解得s 247.01=t ,于是小球到达xy 平面时的各速度分量为m/s 7.494811===t mFxt t ,m/s 81===v y t t ,m/s 425.211-=-==gt z t t . 各坐标为m 2.6122211===t m F x t t ,m 979.111===vt y t t ,m 137.23.02211-=+-==t gz tt .7-2 图示A ,B 两物体的质量分别为m A 和m B ,二者用一细绳连接,此绳跨过一定滑轮,滑轮半径为r 。
运动开始时,两物体的高度差为h ,且m A > m B ,不计滑轮质量。
求由静止释放后,两物体达到相同高度时所需的时间。
解:分别取A 和B 物体为研究对象,受力图如图示,列出动力学方程TA A A A F W x m -= , TB B B B F W x m -= , 式中g m W A A =,g m W B B =,根据题意,有TB TA F F =,B A x x -=,B A xx -= 初始条件00==t A x ,h x t B ==0,00==t A x,00==t B x . 解以上初值问题,得题7-2图g m m m m xBA B A A +-= , ()22gt m m m m x B A BA A +-=g m m m m x B A B A B +--= , ()h gt m m m m x B A BA B ++--=22令B A x x =,即()()h gt m m m m gt m m m m B A BA B A B A ++--=+-2222解得当两物体达到相同高度时 ()()gm m h m m t B A B A -+=...7-3 质量为m 的质点M 受到引力F = -k 2m r 的作用,其中k 为常量,运动开始时,质点M在轴x 上,OM 0 = b ,初速度v 0与轴x 的夹角为β,如图所示。
理论力学 第六版部分习题答案 第七章
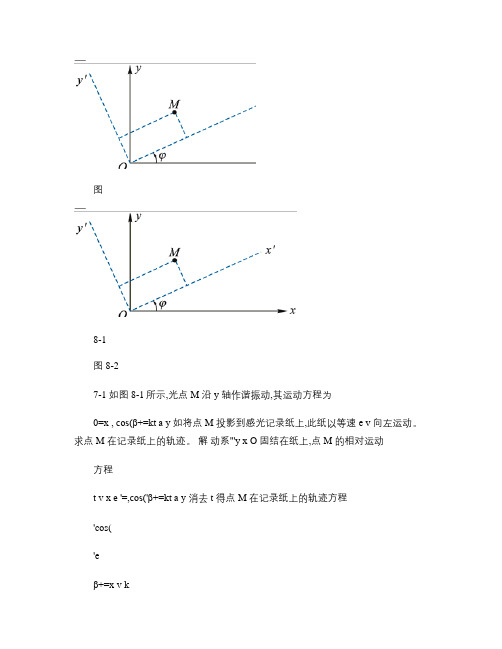
图8-1图8-27-1 如图8-1所示,光点M 沿y 轴作谐振动,其运动方程为0=x , cos(β+=kt a y 如将点M 投影到感光记录纸上,此纸以等速e v 向左运动。
求点M 在记录纸上的轨迹。
解动系'''y x O 固结在纸上,点M 的相对运动方程t v x e '=,cos('β+=kt a y 消去t 得点M 在记录纸上的轨迹方程'cos('eβ+=x v ka y 7-2 如图8-2所示,点M 在平面''y Ox 中运动,运动方程为cos 1(40't x −=,t y sin 40'= 式中t 以s 计,'x 和'y 以mm 计。
平面''y Ox 又绕垂直于该平面的轴O 转动,转动方程为rad t =ϕ,式中角ϕ为动系的'x 轴与定系的x 轴间的交角。
求点M 的相对轨迹和绝对轨迹。
解由点M 的相对运动方程可改写为t yt x sin 40cos 140''=−=⎟⎟⎠⎞⎜⎜⎝⎛−上2式两边平方后相加,得点M 的相对轨迹方程 1600'40'(22=+−y x 由题得点M 的坐标变换关系式ϕϕsin 'cos 'y x x −= ϕϕcos 'sin 'y x y +=将t =ϕ和相对运动方程代入,消去t 得点M 的绝对轨迹方程160040(22=++y x7-3 水流在水轮机工作轮入口处的绝对速度m/s 15a =v ,并与直径成°=60β角,如图8-3a 所示,工作轮的半径m 2=R ,转速r/min 30=n 。
为避免水流与工作轮叶片相冲击,叶片应恰当地安装,以使水流对工作轮的相对速度与叶片相切。
求在工作轮外缘处水流对工作轮的相对速度的大小方向。
′′v(a (b图8-3解水轮机工作轮入口处的1滴水为动点M ,动系固结于工作轮,定系固结于机架/地面(一般定系可不别说明,默认为固结于机架,下同;牵连运动为定轴转动,相对运动与叶片曲面相切,速度分析如图8-3b 所示,设θ为r v 与'x 轴的夹角。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章
刚体的简单运动
1.刚体作平动时,刚体内各点的轨迹()。
①一定是直线
②一定是曲线
③可以是直线,也可以是曲线
④可以是直线,也可以是不同半径的圆
正确答案:③
2.某瞬时,刚体上任意两点A、B的速度分别为v A、v B,则下述结论正确的是()。
①当v A = v B时,刚体必平动
②当刚体作平动时,必有|v A| = |v B|,但v A与v B的方向有可能不同
③当刚体作平动时,必有v A = v B
④当刚体作平动时,v A与v B的方向必然相同,但可能|v A| ≠|v B|
正确答案:③
3.一对外啮合或内啮合的定轴传动齿轮,若啮合处不打滑,则任一瞬时两轮啮合点处的速度和加速度所满足的关系为()。
①速度矢量和加速度矢量均相等
②速度大小与加速度大小均相等
③速度矢量和加速度矢量均不相等
④速度矢量和切向加速度矢量均相等
正确答案:④
4.如图所示的平面机构中,三角板ABC与杆O1A、O2B铰接,
若O1A = O2B = r,O2O1 = AB,则顶点C的运动轨迹为()。
①以CO1长为半径,以O1点为圆心的圆
②以CH长为半径,以H点为圆心的圆
③以CD长(CD // AO1)为半径,以D点为圆心的圆
④以CO = r长(CO // AO1)为半径,以O点为圆心的圆
正确答案:④
5.刚体绕定轴转动,()。
①当转角ϕ>0时,角速度ω为正
②当角速度ω>0时,角加速度α为正
③当ω与α同号时为加速转动,当ω与α异号时为减速转动
④当α>0时为加速转动,当α<0时为减速转动
正确答案:③
6.汽车左转弯时,已知车身作定轴转动,汽车左前灯A的速度大小为v A,汽车右前灯B的速度大小为v B。
A、B之间的距离为b,则汽车定轴转动的角速度大小为()。
① b v A ② b v B ③ b v v B A )(+ ④ b
v v B A )(− 正确答案:④
7.每段长度相等的直角折杆在图示的平面内绕O 轴转动,角速度ω为顺时针转向,则M 点的速度
方向如图中的( )所示。
① ② ③ ④
正确答案:①
8.圆盘作定轴转动,若某瞬时其边缘上A 、B 、C 三点的速度
和加速度如图所示,则( )的运动是不可能的。
① 点A 、B
② 点A 、C
③ 点B 、C
④ 点A 、B 、C
正确答案:①
9.刚体运动时,其上有两条相交直线始终与各自初始位置保持平行,则刚体一定作( )。
正确答案:平动
10.直角曲杆OBC 可绕O 轴转动,如图所示。
已知:
OB =10cm 。
图示位置ϕ=60°,曲杆的角速度ω=
0.2rad/s ,角加速度α= 0.2rad/s 2,则曲杆上M 点的法
向加速度的大小为( ),方向为( );
切向加速度的大小为( ),方向为( )。
正确答案:0.8cm/s 2 水平向左 4cm/s 2 垂直向下
11.如图所示的皮带轮传动机构中,Ⅰ轮的半径为r ,
Ⅱ轮的半径为R = 2r ,Ⅰ轮以匀角速度ω1绕O 1轴
转动。
若皮带与轮间无相对滑动,则皮带上A 、B 、
C 、
D 四点中,加速度最大的是( )点,其加
速度大小a max = ( )。
正确答案:A r ω12
12.已知正方形板ABCD 作定轴转动,转轴垂直于板面,A 点的
速度大小v A = 5cm/s ,加速度大小a A = 52cm/s 2,方向如图
所示。
则该板转动轴到A 点的距离OA 为( )cm 。
正确答案:5。
