复变函数一复数的乘幂与方根
合集下载
复变函数入门 1ppt课件
3. 两复数的商:
z1 z2
x1 x2 x22
y1 y2 y22
i
x2 y1 x22
x1 y2 y22
ቤተ መጻሕፍቲ ባይዱ
.
注解：
➢ 复数的减法运算是加法运算的逆运算
➢ 复数的除法运算是乘法运算的逆运算
➢ 复数的四则运算与实数的四则运算保持一致
7
定理: 全体复数关于上述运算做成一个数域.
称为复数域，用C表示.即
复数的四则运算满足以下运算律 ①加法交换律 z1 z2 z2 z1 ②加法结合律 z1 (z2 z3) (z1 z2 ) z3 ③乘法交换律 z1 z2 z2 z1 ④乘法结合律 z1 (z2 z3) (z1 z2 ) z3 ⑤乘法对加法的分配律
面上的点向量oz 表示.
o
x
x
18
结论:
两个复数的加减法运算与相应的向量的 加减法运算一致.
y
z2
z1 z2
y
z2
z1
o
z1
x
o
x
z1 z2
z2
19
附录： 向Hamilton 学习
Hamilton.William Rowan（威廉.罗万.哈 密儿顿，1805——1865）爵士，无 疑是使爱尔兰人在数学领域中享有 盛益的最伟大的人物，同时也是有 名望的物理学家和天文学家。他 1805年生于都柏林，除了短时间外 出访问外，一生都是在这里度过 的。他才一岁时，被委托给一位叔 叔教育，这位叔叔的热心在于给他 侧重语言上的教育，不久之后，他 就成了孤儿。Hamilton是个神童，3 岁时能阅读英文，5岁时能阅读、
以上各式证明略.
10
例3 将下列复数表示为 x iy 的形式.
复变函数(全)解析
1
2
1
2
1
2
乘法
z z (x x y y ) i(x y x y ),
12
12
12
21
12
商
z 1
xx 12
yy 12
i
xy 21
xy 12
z
x2 y2
x2 y2
2
2
2
2
2
第一节 复数及其代数运算
(2)性质
z z z z , zz zz;
1
2
2
1
12
21
z (z z ) (z z ) z ,z (z z ) (z z )z
1
2
3
1
2
3 1 23
12 3
z (z z ) z z z z
12
3
12
13
第二节 复数的几何表示
1.复平面 （ 1 ） 定 义 复 数 z x iy 与 有 序 实 数
(x, y) 一一对应，对于平面上给定的直角 坐标系，复数的全体与该平面上的点的全
体成一一对应关系，从而复数 z x iy 可
对复平面内任一点z ,用一条直线将N 与z 连结起来,该直线与球面交于异于N 的 唯一点P ,这样除了N 之外,复平面内点与 球面上的点存在一一对应的关系.这样的 球面称为复球面.
第三节 复数的乘幂与方根
1. 乘积与商
设有两个复数
（1）乘积
z1
r1 (cos 1
sin1 )
r e i1 1
,
z2
r2 (cos2
z2 r2
第二节 复数的几何表示
2.幂与根 (1) 幂 n个相同复数z 的乘积称为z 的n次幂,记作zn ,即
第一章3复数的乘幂与方根
复变函数与积分变换
第二节
复数的运算
一、复数的代数运算及共轭复数的运算法则
二、复数的代数运算的几何表示
三、复数的乘幂与方根
三、复数的乘幂与方根
1. 乘幂
设复数 ≠ 0, = (cos+sin),
则 = (cosn+sinn) ，为正整数．
规定 z
−n
1
= n.
z
), w3 = 2 (cos
+ i sin
),
16
16
16
16
1
8
1
8
这四个根是内接于以原点为圆心，半径为 2的圆的正方形的顶点
8
谢谢观看！
当 = , + 1, ⋯ 时，这些根又重复出现.
=
=
1
[cos
2 在几何上，
+ 2
+ 2
+ sin
], = 0,1,2, ⋯ , − 1
1
的个值是以原点为圆心， 为
半径的圆的内接正边形的个顶点.
例3．求 1 + .
4
解： 1 + = 2(cos + sin )
特别地，当 = 1时，得到棣莫弗公式
(cos+sin) = cosn+sinn.
2. 方根
z 称为的次方根.
设 z = r (cos + i sin ), w = (cos + i sin )
方程 wn = z 的根 w ，即 w =
n
n
有 (cos n + i sin n ) = r (cos + i sin )
第二节
复数的运算
一、复数的代数运算及共轭复数的运算法则
二、复数的代数运算的几何表示
三、复数的乘幂与方根
三、复数的乘幂与方根
1. 乘幂
设复数 ≠ 0, = (cos+sin),
则 = (cosn+sinn) ，为正整数．
规定 z
−n
1
= n.
z
), w3 = 2 (cos
+ i sin
),
16
16
16
16
1
8
1
8
这四个根是内接于以原点为圆心，半径为 2的圆的正方形的顶点
8
谢谢观看！
当 = , + 1, ⋯ 时，这些根又重复出现.
=
=
1
[cos
2 在几何上，
+ 2
+ 2
+ sin
], = 0,1,2, ⋯ , − 1
1
的个值是以原点为圆心， 为
半径的圆的内接正边形的个顶点.
例3．求 1 + .
4
解： 1 + = 2(cos + sin )
特别地，当 = 1时，得到棣莫弗公式
(cos+sin) = cosn+sinn.
2. 方根
z 称为的次方根.
设 z = r (cos + i sin ), w = (cos + i sin )
方程 wn = z 的根 w ，即 w =
n
n
有 (cos n + i sin n ) = r (cos + i sin )
复变函数1-3
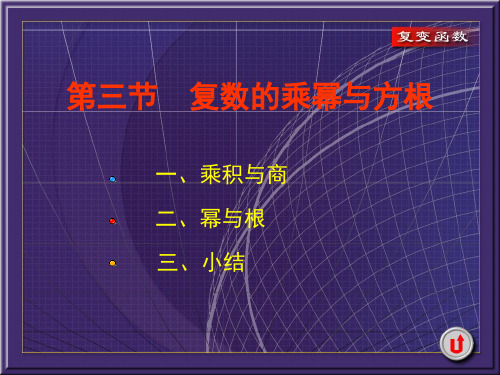
i,
z1 z2
cos
3
6
i
sin
3
6
3 1i. 22
7
二、幂与根
1. n次幂: n 个相同复数 z 的乘积称为z 的 n 次幂,
记作 zn , zn z z z .
n个
对于任何正整数n, 有 zn rn(cosn i sin n ).
如果我们定义
zn
1 zn
,
那么当
幂为负整数时,
求出z的幂.
8
2.棣莫佛公式
当 z 的模 r 1,即 z cos i sin ,
(cos i sin )n cosn i sin n .
棣莫佛公式
3. 方程 wn z 的根 w, 其中 z 为已知复数.
w
n
z
r
1 n
cos
2kπ n
i sin
2kπ n
(k 0,1,2, ,n 1)
w2
o
w0 x
w3
15
三、小结
应熟练掌握复数乘积与商，幂与根的运算. 在各种形式中以三角形式、指数形式最为方便:
z1
z2
r1
r ei(12 ) 2
z2 r e2 i(2 1 )
z1 r1
对于任何正整数n, 有 zn rn(cosn i sin n ).
w
n
z
r
1 n
cos
2kπ
i sin
2kπ
n
n
(k 0,1,2, ,n 1)
放映结束，按Esc退出.
16
i sin(1 2 n )]
r1 r2 rnei(12 n ) .
5
定理二 两个复数的商的模等于它们的模的商; 两 个复数的商的辐角等于被除数与除数的辐角之差.
复数的乘幂与方根
复数的乘幂与方根教学目的：掌握复数的乘幂与方根的计算方法，了解乘幂、方根的几何意义教学重点：掌握利用复数的三角表示式求解复数的乘幂与方根教学难点：理解乘幂与方根的几何解释，方根的计算方法教学类型：板书教学时数：1学时教学过程：1、乘幂的计算定义1 n 个相同的复数 z 的乘积称为 z 的 n 次幂，记为 z n.显然由定理1 及其推广可知,|z n|=|z|n; Arg z n=nArg z,即若 z=r(cosθ+i sinθ),则有z n=r n(cos nθ+i sin nθ).思考：若是用代数形式 z=x+iy 计算 z n难度有多大？例：计算 (1+i)100.,解：|1+i|=2+12=√2,θ=π4因此，(1+i)100=(√2)100(cos25π+i sin25π)=250(−1+i∙0)=−250.2、方根的计算n.定义2 若 w=z n,称 z 为 w 的 n 次方根,记为 z=√w分析：已知复数 w =r (cos θ+i sin θ)，求复数z =ρ(cos φ+i sin φ),使得 w =z n 成立，即有r (cos θ+i sin θ)= ρn (cos nφ+i sin nφ).从上式中可以得到r = ρn ,θ+2kπ=nφ,k ∈Z .因此，ρ= r 1n , φ=θ+2kπn ⁄, k ∈Z ,z =√w n =r 1n (cos θ+2kπ+i sin θ+2kπ) 究竟有几个？k =0,1,2,⋯,n −1时，得到 n 个互异的值z 0=r 1n (cos θn +i sin θn )； z 1=r 1n (cos θ+2πn +i sin θ+2πn)； ⋯⋯z n−1=r 1n (cos θ+2(n −1)πn +i sin θ+2(n −1)πn) 由三角函数的周期性，可知当 k 取其他整数值时，方根的值重复出现，因此可知 n 次方根有且仅有 n 个！综上所述，n 次方根的计算方法为（1） 将复数w =x +iy 表示成三角表示式w =r (cos θ+i sin θ)（2） √w n =r 1n (cos θ+2kπn +i sin θ+2kπn )（3） k =0,1,2,⋯,n −1例：计算√i 3.解：（1）r =|i |=1,θ=π2, w =i =r (cos θ+i sin θ);（2）√w 3=r 1(cosθ+2kπ3+i sin θ+2kπ3) =cos (1+4k)π6+i sin (1+4k)π6;（3）k =0,1,2.即√i 3 分别为z 0=cos π6+i sin π6；z 1=cos 5π+i sin 5π; z 2=cos 9π6+i sin 9π6. 注解 n 次方根的几何解释上述例子中的3个3次方根正好是以原点为中心以1为半径的圆的内接正三角形的三个顶点。
1.3 复数的乘幂与方根
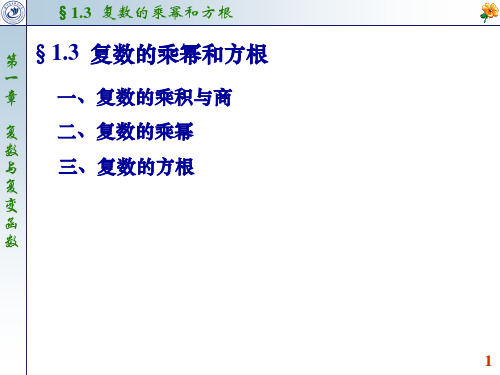
)3
eπi
1.
变
2 2
函
数
此外，显然有 (1)3 1.
由此引出方根的概念。
8
§1.3 复数的乘幂与方根
§1.3 复数的乘幂与方根
第 一 三、 复数的方根 P15
章
复数求方根是复数乘幂的逆运算。
复 数
定义
设 z 是给定的复数，n 是正整数，求所有满足wn z 的
与 复
复数 w ，称为把复数 z 开 n 次方，或者称为求复数 z 的
2e 3 .
1
12
§1.2 复数的几种表示
附：关于 Arg (z1 z2 ) Arg z1 Arg z2(在集合意义下)
第
一
所谓“在集合意义下”是指：
章 分别从集合 Arg z1 中与集合 Arg z2 中任取一个
复 数
元素(即辐角)，相加后，得到集合Arg (z1 z2 ) 中的
与
一个元素(即辐角)。
2e 6
有
复 数
πi
5π i
( π 5π )i
(1 3 i)( 3 i) 2e 3 2e 6 4e 3 6
与
复
πi
变
4e 2 4 i .
函 数
1 3i 3i
πi
2e 3
5π i
( π 5π )i
7π i
e 3 6 e 6
2e 6
cos 7π i sin 7π 3 1 i .
章 复
wk
n
z
n
r
i(
en
2k n
)
,
(k 0,1, , n 1) .
数 与
描述 在复平面上， 这 n 个根均匀地
复变函数课件
10
2.棣莫佛公式
当 z 的模 r 1, 即 z cos i sin ,
棣莫佛介绍
(cos i sin )n cos n i sin n . 棣莫佛公式
3. 方程 w n z 的根 w , 其中 z 为已知复数.
2kπ 2kπ w z r cos i sin n n ( k 0,1,2,, n 1)
r 为半径的圆的内接正n 边形的 n 个顶点.
14
例3
解
化简 (1 i )n (1 i )n .
1 1 1 i 2 i 2 2 2 cos i sin 4 4 1 1 1 i 2 i 2 2
因为复数 e 的模为1, 转角为 , 3
8
i 3
z3 z1 e ( z2 z1 )
i 3
3 1 i (1 i ) 2 2 3 1 3 1 i 2 2 2 2
o
y
z3
z2 2 i
3
z1 1
4
设复数z1和z2的指数形式分别为
z1 r1e ,
i 1
z2 r2e i 2 , 则 z1 z2 r1 r2e i (1 2 ) .
由此可将结论推广到 n 个复数相乘的情况:
设 zk rk (cos k i sin k ) rk e
i k
, ( k 1,2,, n)
4 i 5
,
,
w4 e
21
w 1 e i 1 cos i sin 1 因为 z i w 1 e 1 cos i sin 1
2.棣莫佛公式
当 z 的模 r 1, 即 z cos i sin ,
棣莫佛介绍
(cos i sin )n cos n i sin n . 棣莫佛公式
3. 方程 w n z 的根 w , 其中 z 为已知复数.
2kπ 2kπ w z r cos i sin n n ( k 0,1,2,, n 1)
r 为半径的圆的内接正n 边形的 n 个顶点.
14
例3
解
化简 (1 i )n (1 i )n .
1 1 1 i 2 i 2 2 2 cos i sin 4 4 1 1 1 i 2 i 2 2
因为复数 e 的模为1, 转角为 , 3
8
i 3
z3 z1 e ( z2 z1 )
i 3
3 1 i (1 i ) 2 2 3 1 3 1 i 2 2 2 2
o
y
z3
z2 2 i
3
z1 1
4
设复数z1和z2的指数形式分别为
z1 r1e ,
i 1
z2 r2e i 2 , 则 z1 z2 r1 r2e i (1 2 ) .
由此可将结论推广到 n 个复数相乘的情况:
设 zk rk (cos k i sin k ) rk e
i k
, ( k 1,2,, n)
4 i 5
,
,
w4 e
21
w 1 e i 1 cos i sin 1 因为 z i w 1 e 1 cos i sin 1
复变函数论
arg
z
arctg
3 1
3
2 3
，
Argz arg z 2k 2 2k ,
3
(k 0,1,2,3)
z
2(cos(
2
)
sin(
2
))
i(
2e
2 3
)
3
3
二、复数的运算：
1．相等： x1 iy1 x2 iy2 x1 x2, y1 y2 2.四则运算：运算规律
复数形式的方程表示时更简明。
2
2i
实数形式复数形式
z xiy
例 6: 连接 z1及 z2两点的线段的参数方程为：
z z1 t(z2 z1) (o t 1)
过 z1及z2两点直线的参数方程为：
z z1 t(z2 z1) ( t )
例 7: 求下列方程所表示的曲线
2
2
当 x 0, y 0 时，
x 0, y 0, arg z 0
x
0,
y
0, arg
z
当 x 0 时，
一象限 二象限
arg z( (0, )) arctan y ( (0, ))
2
x
2
arg
z (
(
,
))
arctan
y
(
(
,0))
(x 2)2 y2 9 .
2）几何上，该方程表示到复平面上点 2 和点 4
距离相等的点的轨迹，所以方程表示的曲线就是连接
2023年大学_《高等数学》第四册(数学物理方法)课后习题答案下载
2023年《高等数学》第四册(数学物理方法)课后习题答案下载《高等数学》第四册内容简介第一篇复变函数论第一章复数与复变函数第一节复数1.1.1. 复数域1.1.2. 复平面1.1.3. 复数的模与幅角1.1.4. 复数的乘幂与方根第二节复变函数的基本概念1.2.1. 区域与约当曲线1.2.2. 复变函数的概念1.2.3. 复变函数的极限与连续性第三节复球面与无穷远点1.3.1. 复球面1.3.2. 闭平面上的几个概念习题第二章解析函数第一节解析函数的概念及哥西一黎曼条件 2.1.1. 导数的定义2.1.2. 哥西一黎曼条件2.1.3. 解析函数的定义第二节解析函数与调和函数的关系2.2.1. 共轭调和函数的求法2.2.2. 共轭调和函数的几何意义第三节初等解析函数2.3.1. 初等单值函数2.3.2. 初等多值函数习题第三章哥西定理哥西积分第一节复变积分的概念及其简单性质3.1.1. 复变积分的定义及其计算方法3.1.2. 复变积分的简单性质第二节哥西积分定理及其推广3.2.1. 哥西积分定理3.2.2. 不定积分3.2.3. 哥西积分定理推广到复围线的情形第三节哥西积分公式及其推广3.3.1. 哥西积分公式3.3.2. 解析函数的无限次可微性3.3.3. 模的最大值原理哥西不等式刘维尔定理摩勒纳定理第四节解析函数在平面场中的应用3.4.1. 什么叫平面场3.4.2. 复位势3.4.3. 举例习题第四章解析函数的幂级数表示第一节函数项级数的基本性质4.1.1. 数项级数4.1.2. 一致收敛的函数项级数第二节幂级数与解析函数4.2.1. 幂级数的敛散性4.2.2. 解析函数的幂级数表示第三节罗朗级数4.3.1. 双边幂级数的收敛圆环4.3.2. 解析函数的罗朗展式4.3.3. 罗朗展式举例第四节单值函数的孤立奇点4.4.1. 孤立奇点的`三种类型4.4.2. 可去奇点……习题第五章残数及其应用第六章保角变换第二篇数学物理方程第七章一维波动方程的付氏解第八章热传导方程的付氏解第九章拉普拉斯方程的圆的狄利克雷问题的付氏解第十章波动方程的达朗贝尔解第十一章数学物理方程的解的积分方式第十二章定解问题的适定性第十三章付里叶变换第十四章拉普拉斯变换第三篇特殊函数第十五章勒让德多项式球函数第十六章贝塞耳函数柱函数第十七章厄密多项式和拉盖尔多项式附录《高等数学》第四册目录本书内容为数学物理方法，包括复变函数论、数学物理方程、积分变换和特殊函数等部分，可供综合大学和师范学院物理类专业作为教材。
复变函数的可导与解析
zz0
z z0
定义3
设复变函数 w f (z)在N (z0 )内有定义， 如 果 存 在 与 z无 关 的 复 常 数 L, 使 得 对 z z0 z N ( z0 ), 总有
w f ( z0 z) f ( z0 ) Lz o(| z |), 则称w f (z)在点z0处可微，并称 Lz为函数f (z)在点z0处的微分，记作
f(z)在 复 平 面 上 处 处处 处 解可 析导 ，， 且 f(z)ux ivx ex(coysisiny)f(z)
（ 2 ）f(z)xyixy
解 u(x, y) x y,v(x, y) xy，而
ux 1,uy 1, vx y,vy x ux,uy,vx,vy在复平面上处处但 连仅 续在 ， x1, y 1时满足 CR条件
(7) f z 1w,其中与为两个互为反 数的单值函,且数w 0.
需要注意的是，复变数函的导数定义与一元 实函数的导数定义，然虽形式上一样，但在 本质上有很大的不同因。为一元实函数导数 定义中的极限是一元函实数的极限，而复变 函数导数定义中的极对限应于二元实函数的 极限。
设f(z)在z0可 导 ， 即 极 限
f(z)在z 1i 处可导，在复平面上 处处不解析 .
（ 3）f(z)x2iy
解 u(x, y) x2 ,v(x, y) y，而
ux 2x, uy 0, vx 0,vy 1 ux ,uy ,vx ,vy在复平面上处处连续， 但仅在直线x 1 上满足C R条件
f(z)在 直 线 x21上可 导 ， 在 复 平 面 2
y
x y
y x
z在第一象限 z在第二象限 z在第三象限
x
arctan
y x
z在第四象限
复变函数第2讲
w = ρ (cosnϕ + i sinnϕ) = z = r(cos + i sinθ ) θ
n n
比较， 比较，得
ρ n = r, ⇒ ρ =
nϕ = θ + 2 k π ,
n
r;
⇒ϕ =
θ + 2kπ
n
Hale Waihona Puke 由此得到方根公式n (k = 0, 1, 2, L, n − 1)
w = z = r (cos
结论： 结论： 两个复数乘积的模等于各自模的乘积， 两个复数乘积的模等于各自模的乘积，乘积的幅 角等于各自幅角之和； 角等于各自幅角之和； 两个复数商的模等于各自模的商， 两个复数商的模等于各自模的商，商的幅角等于 被除数与除数的幅角之差。 被除数与除数的幅角之差。 Arg(z1z2)=Argz1+Argz2，Arg(z1/z2)= Argz1-Argz2，
3
0 + 2 kπ 0 + 2 kπ 1 = cos + i sin 3 3 ( k = 0 ,1, 2 ).
1 3 1 3 i, w2 = - i. 即 w 0 = 1, w1 = - + 2 2 2 2
练习： 求下列根式的值. (1) 1+ i ; (2)
3
-2 + 2i .
§4
复平面上的点集
13. 单连通、多连通区域：复平面上的一个区域 如果在其 单连通、多连通区域：复平面上的一个区域D,如果在其 中任作一条简单闭曲线,而曲线的内部仍属于 而曲线的内部仍属于D，则称D 中任作一条简单闭曲线 而曲线的内部仍属于 ，则称 为单连通域，不是单连通域的都叫多连通域。 为单连通域，不是单连通域的都叫多连通域。 多连通区域的一个显著特点：内部含有洞或裂缝。 注：1. 多连通区域的一个显著特点：内部含有洞或裂缝。 2. 任一简单闭曲线将复平面分为内、外两部分，内部 任一简单闭曲线将复平面分为内、外两部分， 单连通，外部多连通。 单连通，外部多连通。 3. 属于单连通域 内的任何一条简单闭曲线，在D内可 属于单连通域D内的任何一条简单闭曲线 内的任何一条简单闭曲线， 内可 以经过连续的变形而缩成一点， 以经过连续的变形而缩成一点，多联通区域不具备 这个特征。 这个特征。
n n
比较， 比较，得
ρ n = r, ⇒ ρ =
nϕ = θ + 2 k π ,
n
r;
⇒ϕ =
θ + 2kπ
n
Hale Waihona Puke 由此得到方根公式n (k = 0, 1, 2, L, n − 1)
w = z = r (cos
结论： 结论： 两个复数乘积的模等于各自模的乘积， 两个复数乘积的模等于各自模的乘积，乘积的幅 角等于各自幅角之和； 角等于各自幅角之和； 两个复数商的模等于各自模的商， 两个复数商的模等于各自模的商，商的幅角等于 被除数与除数的幅角之差。 被除数与除数的幅角之差。 Arg(z1z2)=Argz1+Argz2，Arg(z1/z2)= Argz1-Argz2，
3
0 + 2 kπ 0 + 2 kπ 1 = cos + i sin 3 3 ( k = 0 ,1, 2 ).
1 3 1 3 i, w2 = - i. 即 w 0 = 1, w1 = - + 2 2 2 2
练习： 求下列根式的值. (1) 1+ i ; (2)
3
-2 + 2i .
§4
复平面上的点集
13. 单连通、多连通区域：复平面上的一个区域 如果在其 单连通、多连通区域：复平面上的一个区域D,如果在其 中任作一条简单闭曲线,而曲线的内部仍属于 而曲线的内部仍属于D，则称D 中任作一条简单闭曲线 而曲线的内部仍属于 ，则称 为单连通域，不是单连通域的都叫多连通域。 为单连通域，不是单连通域的都叫多连通域。 多连通区域的一个显著特点：内部含有洞或裂缝。 注：1. 多连通区域的一个显著特点：内部含有洞或裂缝。 2. 任一简单闭曲线将复平面分为内、外两部分，内部 任一简单闭曲线将复平面分为内、外两部分， 单连通，外部多连通。 单连通，外部多连通。 3. 属于单连通域 内的任何一条简单闭曲线，在D内可 属于单连通域D内的任何一条简单闭曲线 内的任何一条简单闭曲线， 内可 以经过连续的变形而缩成一点， 以经过连续的变形而缩成一点，多联通区域不具备 这个特征。 这个特征。
第一章 复变函数
3
第二节 复变函数
§1.2.1区域与约当曲线
1. 区域的概念 2. 简单曲线（或Jordan曲线) 3. 单连通域与复连通域
1. 区域的概念
设G是一平面上点集 内点 对任意z0属于G，若存在Ｕ(z 0 ,δ)， 使该邻 域内的所有点都属于G，则称z 0是G的内点。 开集 若G内的每一点都是 外点 内点，则称G是开集。 z •区域 设 D是一个开集， 且D是连通的，称 D是一个区域。
sin 3 3cos 2 sin 3 3sin 4sin 3
例: 求
3in0
3
1 3 1 3 即0 1, 1 i , 2 i. 2 2 2 2
0 2k 0 2k 1 cos i sin , ( k 0,1,2). 3 3
§1.1.2 复数的表示方法
1. 点的表示
2. 向量表示法 3. 三角表示法
4. 指数表示法
1. 点的表示
易见， x iy 一对有序实数x, y ), z (
在 平 面 上 取 定 直 角 坐系 ， 则 标 任 意 点 ( x , y ) 一 对 有 序 实 数x , y ) P ( z x iy 平 面 上 的 点 ( x , y ) P
例5. 将z sin i cos 化 为 三 角 形 式 与 指 数 式. 形 5 5
两个复数乘积的模等于它们的模相乘， 两个复数乘积的辐角等于它们的辐角相加。 证明 设 z1=r1(cosθ1+isinθ1)=r1eiθ1 z2=r2(cosθ2+isinθ2)=r2eiθ2 则 z1z2=r1r2(cosθ1+isinθ1)( cosθ2+isinθ2) = r1r2[cos (θ1+θ2)+isin(θ1+θ2)] =r1r2e i(θ1+θ2) 因此 |z1z2|=r1r2，Arg(z1z2)=Argz1+Argz2
复变函数第2讲
z 例如讨论当 z 0 时 f ( z ) 的极限. z 令y kx，于是 x kxi 1 ki f (z) , x kxi 1 ki 故此极限也不存在.
24
相关性质
定理 1 令 f ( z) u( x, y) iv( x, y), A u0 iv0 , z0 x0 iy0 ,
令z(t)=x(t)+i y(t) a≤t≤b ; 则曲线方程可记为：z=z(t)， a≤t≤b
若x' (t )、y' ( t ) C[a, b]且[ x' (t )]2 [ y' ( t )]2 0 则称该曲线为光滑的 .
有限条光滑曲线相连接构成一条分段光滑曲线.
11
2.2 重点 设连续曲线C：z=z(t)，a≤t≤b， 对于t1∈(a，b), t2 ∈[a, b],当t1≠t2时，若z(t1)=z(t2)， 称z(t1)为曲线C的重点. 2.3定义 称没有重点的连续曲线C为简单曲线或 Jordan曲线;若简单曲线C 满足z(a)=z(b)时，则称此曲线C 是简单闭曲线或Jordan闭曲线. z(a)=z(b)
外部 边界
13
例 |z|<1是单连通区域；而|z|>1是多连通区域. 注：1. 多连通区域的一个显著特点：内部含有洞或 裂缝. 2. 任一简单闭曲线将复平面分为内、外两部分，内部 单连通，外部多连通. 3. 属于单连通区域D内的任何一条简单闭曲线，在D内 可以经过连续的变形而缩成一点.
单连通区域
多连通区域
因此 |z1z2|=r1r2， Arg(z1z2)=Argz1+Argz2. 注意其几何意义.
1
则
z1 r1 (cos1 i si n1 )(cos 2 i si n 2 ) z 2 r2 r1 [cos( 1 2 ) i si n ( 1 2 )], r2 r1 i (1 2 ) e r2 ( r2 0).
24
相关性质
定理 1 令 f ( z) u( x, y) iv( x, y), A u0 iv0 , z0 x0 iy0 ,
令z(t)=x(t)+i y(t) a≤t≤b ; 则曲线方程可记为：z=z(t)， a≤t≤b
若x' (t )、y' ( t ) C[a, b]且[ x' (t )]2 [ y' ( t )]2 0 则称该曲线为光滑的 .
有限条光滑曲线相连接构成一条分段光滑曲线.
11
2.2 重点 设连续曲线C：z=z(t)，a≤t≤b， 对于t1∈(a，b), t2 ∈[a, b],当t1≠t2时，若z(t1)=z(t2)， 称z(t1)为曲线C的重点. 2.3定义 称没有重点的连续曲线C为简单曲线或 Jordan曲线;若简单曲线C 满足z(a)=z(b)时，则称此曲线C 是简单闭曲线或Jordan闭曲线. z(a)=z(b)
外部 边界
13
例 |z|<1是单连通区域；而|z|>1是多连通区域. 注：1. 多连通区域的一个显著特点：内部含有洞或 裂缝. 2. 任一简单闭曲线将复平面分为内、外两部分，内部 单连通，外部多连通. 3. 属于单连通区域D内的任何一条简单闭曲线，在D内 可以经过连续的变形而缩成一点.
单连通区域
多连通区域
因此 |z1z2|=r1r2， Arg(z1z2)=Argz1+Argz2. 注意其几何意义.
1
则
z1 r1 (cos1 i si n1 )(cos 2 i si n 2 ) z 2 r2 r1 [cos( 1 2 ) i si n ( 1 2 )], r2 r1 i (1 2 ) e r2 ( r2 0).
复变函数第一章
1.1.4.复数四则运算的几何意义 .1.4.复数四则运算的几何意义 , θ θ 设有两个复数 z1 = r1(cos 1 + i sinθ1） z2 = r2 (cos 2 + i sinθ2）
则，z1 z 2 = r1 (cos θ 1 + i sin θ 1 )r2 (cos θ 2 + i sin θ 2 )
例1：下列复数化为三角表示式与指数表示式
2i ( 1 ) z = − 12 − 2i, ( 2 ) z = , ( 3 ) z = −3 + 4i −1+ i
例3：求下列方程所表示的曲线
(1) |z + i| = 2, ( 2) |z − 2i| = |z + 2|, ( 3 ) Im(i + z) = 4
________
7 1 z1 ∴ ( )=− + i z2 5 5
__ 1 3i 例2： z = - − 求 Re (z),Im (z)与z z i 1-i
− ( 1 − i) − 3i(i) − 1 + i + 3 2 + i （ 2 + i)( 1 − i) = = 解： z = = i( 1 − i) i +1 1+ i 2
x
(3)幅角主值的求法 (3)幅角主值的求法 y arctan x , ( x > 0 , y > 0 ) arctan y + π （ x < 0 , y > 0 ) , x arg z = arctan y − π , ( x < 0 , y < 0 ) x y arctan , ( x > 0, y < 0) x
复变函数第一章
区域:
连通的开集称为区域.
闭区域 区域D与它的边界一起构成闭区域,
记为D.
有界区域 如果一个区域可以被包含在一个以原点
为中心的圆里面,则称D为有界的. 即存在正数M, 使区域D的每个点z都满足|z|<M.
r r1 2 z0
如果在圆环域内去掉一个(或几个)点, 它仍然构成区域, 只是区域的边界由 两个圆周和一个(或几个)孤立的点所 构成
-n
r n cos(n ) i sin(n )
四 复数的方根
定义 如果 n z, 则称为z的n次根, 记作 = n z.
n 当z 0时，z有n个不同的根:
2k 2k k = z r cos i sin , n n k 0,1, 2,, n 1.
1) 集合G称为f (z)的定义集合(定义域);
2) G中所有z对应的全体值所组成的集合G , 称为函数值集合(值域).
3)
如果对z G，它仅有一个值与之
对应,则称函数f ( z )是单值函数;
如果z0 G，它有多个值与之对应, 则称函数f ( z )是多值函数.
2 复变函数与二元实函数的关系
n in
(n为整数)
1 定义 z,当 | z |n.则当n为负整数时上i式仍然成立. 特别地 r 1时,即z cos sin , 有: z 1n cos 0 i sin 0 n z (cos i sin n) (cos n i sin n ) 棣莫弗公式 z r n (cos n i sin n )
y
2z
2z相当与将z伸长2倍.
z 2 2i
x
o
复变函数(1.1.2)--复数概念与运算
�7 � �
(
2)
1
i -
i
+
1
i
i
解
(
1)
�1 � �1 +
i i
�7 � �
=
(
1
(
+
1 - i ) 14 i) 7 ( 1-
i
)
7
=
� �( 1 - i )
27
2 � �7
( -2i ) 7
= 27
= i.
(
2)
i 1-
i
+
1i
i
=
i( 1+ i) (1-i) (1+
i)
+
(
1-i)
i ﾹi
i
zn = r n (cos nq + i sin nq ). r=1,De Movie 公式
复数的
n
次 方 根对 给 定 的 复 数 1
z,
方程 wn=z 的解 w 称为 z
次方根 记作 n z or z n
z = r(cosq + i sinq ), w = r (cos + i sin ),
1.3 复数的乘幂与方根
复数乘积和商的模与幅角
z1 = r1 (cosq1 + i sinq1 ) = r1e iq1 z2 = r2 (cosq2 + i sinq2）= r2e iq2
z1 �z2 = r1 �r2[cos(q1 + q2 ) + i sin(q1 + q2 )].
z1z2 = r1 �r2 = z1 �z2
r n (cos n + i sin n ) = r(cosq + i sinq ).
复变函数复习要点
轴
轴 轴 轴
4
2.复变函数——映射
w f ( z ) u( x , y ) iv ( x , y )
u u( x , y ) v v ( x , y )
例3 求下列方程所表示的曲线: (1) z i 2; i z ) 4.
复变函数与积分变换 复习概要
1.复数的运算
加减乘除 共轭 乘幂 方根
zz z
2
复数的三角表示式： 1）模和幅角的定义 z x iy 习惯上把表示式 称为复数的直角坐标表 三 示式或代数形式，利用直角坐标系和极坐标之间的 角 x r cos y r sin 表 联系 则 示
0
7.由调和函数确定解析函数
已知一个调和函数 u (v), 求调和函数 v( u), 使得u+vi是一个解析函数. 偏积分法 凑微分法 曲线积分法
dv v x dx v y dy u y dx ux dy .
不定积分法
f ( z ) ux iu y U ( z ) f ( z ) U ( z )dz ,
10
如果将 Lnz ln z iArgz 中 Argz 取主值arg z ,
那末 Lnz 为一单值函数， 记为 ln z， 称为 Lnz 的主值.
ln z ln z i arg z .
其余各值为 Lnz ln z 2ki ( k 1,2,),
对于每一个固定的k , 上式确定一个单值函数 , 称为 Lnz 的一个分支.
C2 Cn
常用参数方程形式
z (1 t )z1 tz2
0 t 1
(b)圆周
z z0 re
i
0 2
复变函数总结可修改文字
(6) sin z , cos z can be greater than 1
tan z sin z , cot z cos z ,
cos z
sin z
sec z 1 , csc z 1 ,
cos z
sin z
4. 双曲函数
ez ez
ez ez
sinhz
, cosh z
,
2
2
tanh z sinh z , coth z cosh z ,
k 0
称为以 b 为展开中心的幂级数。其中 ak 为复常数。
幂级数的收敛圆及其收敛半径
k
对于幂级数 ak (z b)k ，必定存在一以 b 为圆心，R 为
k 0
半径的圆，在圆内该级数绝对收敛（而且在较小的圆内 一致收敛），而在圆外发散。这个圆称为该幂级数的收敛 圆，R 称为它的收敛半径。
确定幂级数的收敛半径
z rei
(1.2.14)
复数的乘幂与方根
zn z z z
zn rn (cos n i sin n )
wk
n
i 2kπ
re n
n
r [cos(
2kπ ) i sin(
n
2kπ )], n
(k 0,1, 2,, n 1)
区域
z0的去心邻域 : 点集 z 0 z z0
复变函数总结
复数的表示
1.2.1 复数的几何表示
y
P y
r
x
o
图 1.1
x
y
0
x
2kπ 0
图 1.2
复数的指数表示
定义 1.2.6 复数的指数表示 利用欧拉(Euler)公式
ei cos i sin
tan z sin z , cot z cos z ,
cos z
sin z
sec z 1 , csc z 1 ,
cos z
sin z
4. 双曲函数
ez ez
ez ez
sinhz
, cosh z
,
2
2
tanh z sinh z , coth z cosh z ,
k 0
称为以 b 为展开中心的幂级数。其中 ak 为复常数。
幂级数的收敛圆及其收敛半径
k
对于幂级数 ak (z b)k ，必定存在一以 b 为圆心，R 为
k 0
半径的圆，在圆内该级数绝对收敛（而且在较小的圆内 一致收敛），而在圆外发散。这个圆称为该幂级数的收敛 圆，R 称为它的收敛半径。
确定幂级数的收敛半径
z rei
(1.2.14)
复数的乘幂与方根
zn z z z
zn rn (cos n i sin n )
wk
n
i 2kπ
re n
n
r [cos(
2kπ ) i sin(
n
2kπ )], n
(k 0,1, 2,, n 1)
区域
z0的去心邻域 : 点集 z 0 z z0
复变函数总结
复数的表示
1.2.1 复数的几何表示
y
P y
r
x
o
图 1.1
x
y
0
x
2kπ 0
图 1.2
复数的指数表示
定义 1.2.6 复数的指数表示 利用欧拉(Euler)公式
ei cos i sin
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
单连通域 (一个整体)
多连通域 (带有裂痕,漏洞)
9 )
16
w2
8
17
2 (c os 16
i sin 17
16
)
w2
w3
8
2 (c os 25
16
i sin
25
16
)
四个根是内接于中心在原点,半 径为21/8的圆的正方形的四个 顶点.
y
w1
1i
8 2 w0
x
w3
1.3 平面点集
1.3.1 区域
平面上以 z0为中心, d (任意的正数)为半径的圆: |zz0|<d 内部的点的集合称为z0的邻域, 而称由不等式 0<|zz0|<d
1.2 复数的乘幂与方根
1.2.1 复数的乘幂
复数乘积的指数表达式
z1
z2
r r ei(1 2 ) 12
z1 r1ei1 , z2 r2ei2
特殊情况：z1 z2 z rei ,则z 2 z1 z2 r 2ei2
推广(幂运算）：若z rei ,则zn r nein
注: (1)此公式对于任意整数n都成立。
由几段光滑曲线衔接而成的曲线称为分段光滑曲线.
假设x'(t), y'(t)同时为零，则
导数（斜率）dy y' (t) 不存在 dx x' (t)
1.3.3 单连通区域,多连通区域
定义：设D是平面上一区域，若在D内任作一条简单 闭曲线，而曲线所围成的部分总属于D，则称区域 D为单连通区域；
不是单连通的区域称为多连通区域（复连通区域）。
(c
os
)k
(i
sin
)3
k
cos3 3 cos sin2 i(3 cos2 sin sin3 )
cos3 cos3 3cos sin2
例2： 计算（1 i）5
( 3 i)6
解: 1 i 2 Arg(1 i) 2k
i
1 i 2e 4
4
(1 i)5 (
2)5
i 5
e4
3 i 2 Arg( 3 i) 2k
i
3 i 2e 6
(3ຫໍສະໝຸດ 6i)626
i
e
6
6
（1 i）5
(
2
)5
i
e
5 4
( 3 i)6
26
e
i
6 6
( 2)5 26
ei( 5 6 )
4 6
1
i
e4
82
1.2.3 复数的方根(乘幂的逆运算)
称满足方程 wn z (w 0, n 2)的复数w为z的n次方根， 1
记作n z 或 z n。
设z rcos i sin , w cos i sin
则 wn n (cos n i sin n)
n cos n r cos , n sin n r sin
n r , cos n cos , sin n sin
n 2k , k 0,1,2,
n r为半径的圆内接正n边形的n个顶点。
例3：计算4 1 i
解:
因为
1i
2(cos i sin )
4
4
2k
2k
所以 4 1 i 8 2 (cos 4
i sin 4
)
4
4
(k 0,1,2,3)
即
w0
8
2(cos i sin )
16
16
w1
8
2 (c os 9
16
i sin
(2)特别地，当r 1时， (ei )n ein
cos i sin n cos n i sin n 棣莫弗公式.
例1：将cos 3利用cos ,sin表示
解: cos3 Re[cos3 i sin 3 ]
cos 3 i sin 3 (cos i sin )3
3 k0
c3k
所确定的点集为z0的去心邻域.
设G为一平面点集, z0为G中任意一点. 如果存在z0的一 个邻域, 该邻域内的所有点都属于G, 则称z0为G的内点.
如果G内的每个点都是它的内点, 则称G为开集
平面点集D称为一个区域, 如果它满足下列两个条件: 1) D是一个开集; 2) D是连通的。就是说D中任何两点都可以用完全属于D
z=z(t) (atb) 来代表. 这就是平面曲线的复数表示式.
设C: z=z(t) (atb)为一条连续曲线, z(a)与z(b)分别为C
的起点与终点. 对于满足 a<t1<b, at2b 的 t1与 t2, 当 t1t2 而有 z(t1)=z(t2) 时, 点 z(t1)称为曲线 C的重点. 没有重点的 连续曲线 C, 称为简单曲线或若尔当(Jardan)曲线. 如果简
k
n
1,
wn1
n
r (cos
2(n 1)
n
i sin
2(n 1)
n
)
k n,
wn
n
r (cos
2n
n
i sin
2n
n
)
w0
n z n r (cos 2k i sin 2k ), k o,1, , n 1
n
n
注: （1）复数z的n次方根共有n个。
(2)几何意义：n z的n个值就在以原点为圆心，
的一条折线连接起来.
例4: 圆环：r1 z z0 r2
r
z0
z z0 r
不是区域 (不是开集)
z1
点集S {z | z 1}{z | z 2 1}
不是区域(不连通)
r2 z0 r1
区域
z2
如果一个区域可以被包含在一个以原点为中心的圆里面, 即存在正数 M,使区域 D的每个点z都满足 |z|<M, 则称 D为 有界的, 否则称为无界的.
|z|>M M
0
1.3.2 曲线
1.简单曲线,简单闭曲线
在数学上, 经常用参数方程来表示各种平面曲线. 如果 x(t)和y(t)是两个连续的实变函数, 则方程组
x=x(t), y=y(t), (atb) 代表一条平面曲线, 称为连续曲线. 如果令
z(t)=x(t)+iy(t) 则此曲线可用一个方程
2k , k 0,1,
n
w
n
z
n
r (cos
2k
i sin
2k
)
n
n
k 0
k 1,
w0
w1 n
n r (cos
n
r (cos 2 n
i sin )
n
isin 2 ) n
w1 wn1
(cos 2
n
(cos 2
n
2
i sin n )w0
2
i sin n )wn2
单曲线 C的起点与终点闭合, 即 z(a)=z(b) , 则曲线 C 称为
简单闭曲线.
z(b)
z(b)
z(a) z(b)
简单,闭
z(a)
简单,不闭
z(a)
非简单,不闭
z(a) z(b)
非简单,闭
2.光滑曲线,逐段光滑曲线
设曲线C的方程为
z(t) x(t) iy(t), (a t b)
若在区间[a,b]上，x'(t), y'(t)连续且不全为零，则称 曲线C为光滑曲线。