复变函数论课第五章后题答案_(第三版_钟玉泉)完整版
复变函数论_钟玉泉_第三版_高教_答案_清晰版

n 1
z z 0 nM n1 , 故对 0 ,
n
只需取
nM
n 1
,于是当 z z 0 时,就有 z n z 0 .
(2)由连续函数运算法则,两连续函数相除,在分母不为零时,仍连续.因此 f ( z ) 在
z 平面上除使分母为零点外都连续.
arg z, z 0 13.证明:令 f ( z ) arg z 0, z 0
2
2
z 3 z1 为实数. z 2 z1
10.解:(1)令 z x yi t (1 i) ,得 x y ,即曲线为一,三象限的角平分线. (2)令 z x yi a cos t ib sin t , 得 x a cos t , y b sin t ,则有
2
.
因而对任何自然数 p ,也有 z n p z 0
2
.
利用三角不等式及上面两不等式, 当 n N 时,有
z n p z n z n p z 0 z n z 0
充分性 :设对 0, N ( ) 0 ,当 n, n p N 时,有 z n p z 0 ,由定义 得
12.证明:(1)首先考虑函数 f ( z ) z n 在 z 平面上的连续性. 对复平面上任意一点 z 0 ,来证明 lim z n z 0
z z0 n
不妨在圆 z M z 0 1 内考虑. 因为 z n z 0 z z 0 ( z
n n 1
z
n2
z0 z0
3
2k
(k 0,1,2,)
1 i 2
复变函数论第三版课后习题答案解析

第一章习题解答(一)1.设z ,求z 及Arcz 。
解:由于3i z e π-== 所以1z =,2,0,1,3Arcz k k ππ=-+=±L 。
2.设121z z =,试用指数形式表示12z z 及12z z 。
解:由于6412,2i i z e z i e ππ-==== 所以()64641212222i i iiz z e eee πππππ--===54()146122611222ii i i z e e e z e πππππ+-===。
3.解二项方程440,(0)z a a +=>。
解:12444(),0,1,2,3k ii za e aek πππ+====。
4.证明2221212122()z z z z z z ++-=+,并说明其几何意义。
证明:由于2221212122Re()z z z z z z +=++2221212122Re()z z z z z z -=+-所以2221212122()z z z z z z ++-=+其几何意义是:平行四边形对角线长平方和等于于两边长的和的平方。
5.设z 1,z 2,z 3三点适合条件:0321=++z z z ,1321===z z z 。
证明z 1,z 2,z 3是内接于单位圆1=z 的一个正三角形的顶点。
证 由于1321===z z z,知321z z z ∆的三个顶点均在单位圆上。
因为33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+-+-=21212z z z z ++=所以, 12121-=+z z z z ,又)())((122122112121221z z z z z z z z z z z z z z +-+=--=-()322121=+-=z z z z故 321=-z z ,同理33231=-=-z z z z ,知321z z z ∆是内接于单位圆1=z 的一个正三角形。
复变函数四五六七章总复习钟玉泉

若a为f (z)的孤立奇点,则在K {a}内可展成Laurent级数
f (z) cn (z a)n cn (z a)n
cn (z a)n
n
n1
n0
f (z)在a的主要部分 f (z)在a的正则部分
f (z)在点a的奇点性质体现在K内收敛于一解析函数
定义5.3 设a为f (z)孤立奇点
(1) fn (z)(n 1, 2,...)在区域D内解析;
(2) fn (z)在D内内闭一致收敛于函数f (z)
n1
f (z) fn(z).
n1
则 (1) 函数f (z)在区域D内解析;
(2) f ( p) (z)
f
( n
p)
(
z),
(
z
D,
p
1,
2,
).
n1
第二节 幂级数
1. 幂级数的敛散性 阿贝尔(Abel)定理
i z
1,
z 1. 2
f
(z)
(z
1 i)(z
2)
1 2
i
z
1
i
2
1
z
1 2i
1 z1
i z
1 21
2z
1 2
i
(i)n zn1
n0
n0
zn 2n1
1 2
i
n0
( i )n z n1
1 2
i
n0
zn 2n1 .
(2) 在 2 z 内,
i 1, 2 1
1ezຫໍສະໝຸດ n01 n!zn ,
所以
1
z2e z
z21
1 z
1 2! z 2
1 n! z n
复变函数答案 钟玉泉 第五章习题全解
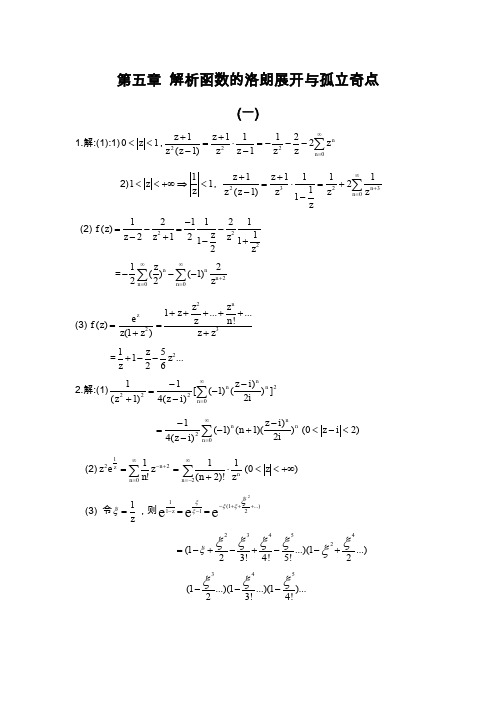
(z 2 1)2 4(z i)2 n0
2i
1 4(z i)2
(1)n (n 1)( z i)n )n
n0
2i
(0
z i
2)
1
(2) z 2e z
1 z n2
1 1 (0 z )
n0 n!
n2(n 2)! z n
e e e (3) 令 1 ,则 z
1
1z
1
2
(1 ...) 2
f (z) w0 解 析 , 即 为整函数 . 又 因 f (z) 非 常 数 , 所 以 g(z) 非常 数 , 其值全 含于一圆
g(z) 1 之内,与刘维尔定理矛盾. 0
11.证明:由题意, f (z) 在 z0 的去心邻域内的洛朗展开式可设为
f (z)
c1 z z0
cn (z z0 )n
(a)
0
6.证明:令 g(z) (z a)k f (z) 。由题设, g(z) 在 k {a}: 0 | z a | R 内有界。由
定理 5.3(3),a 为 g(z) 的可去奇点,则 a 为 g(z) 的解析点。又由定理 5.4(2),
若
a
为
f
(z) 的
m
级极点,则在点
a
的某去心邻域内能表成
正好是以 1 为中心的无穷远点的去心领域。所以根据题中的洛朗展式,只能判
定 z 是 f (z) 的可去奇点。
3.证明:由孤立奇点的定义,又有 f (z) 在点 a 解析,故知 a 为 g(z) 的孤立奇点,
且 lim g(z) lim f (z) f (a) f (a) g(a) ,故 a 为 g(z) 的可去奇点。故在 a 业
(充分性) 若
复变函数论第三版课后习题答案

第一章习题解答(一)1.设z ,求z 及Arcz 。
解:由于3i z e π-== 所以1z =,2,0,1,3Arcz k k ππ=-+=±。
2.设121z z =,试用指数形式表示12z z 及12z z 。
解:由于6412,2i i z e z i e ππ-==== 所以()64641212222i i iiz z e eee πππππ--===54()146122611222ii i i z e e e z e πππππ+-===。
3.解二项方程440,(0)z a a +=>。
解:12444(),0,1,2,3k ii za e aek πππ+====。
4.证明2221212122()z z z z z z ++-=+,并说明其几何意义。
证明:由于2221212122Re()z z z z z z +=++2221212122Re()z z z z z z -=+-所以2221212122()z z z z z z ++-=+其几何意义是:平行四边形对角线长平方和等于于两边长的和的平方。
5.设z 1,z 2,z 3三点适合条件:0321=++z z z ,1321===z z z 。
证明z 1,z 2,z 3是内接于单位圆1=z 的一个正三角形的顶点。
证 由于1321===z z z,知321z z z ∆的三个顶点均在单位圆上。
因为33331z z z ==()[]()[]212322112121z z z z z z z z z z z z +++=+-+-=21212z z z z ++=所以, 12121-=+z z z z ,又)())((122122112121221z z z z z z z z z z z z z z +-+=--=-()322121=+-=z z z z故 321=-z z ,同理33231=-=-z z z z ,知321z z z ∆是内接于单位圆1=z 的一个正三角形。
复变函数论习题及答案

第一章习题1.设12z -=,求||z 及Arg z .2.设12z z i ==,试用指数形式表 z 1 z 2及12z z .3.解二项方程440(0).z a a +=> 4.证明2222121212||||2(||||)z z z z z z ++-=+,并说明其几何意义。
5.设z 1、z 2、z 3三点适合条件: 1231230 |z ||||| 1.z z z z z ++=++=及试证明z 1、z 2、z 3是一个内接于单位圆周||1z =的正三角形的顶点。
6.下列关系表示的点z 的轨迹的图形是什么?它是不是区域? (1)1|212|||,()z z z z z z -=-≠;(2)|||4|z z ≤-;(3)111z z -<+;(4)0arg(1) 2Re 34z z π<-<≤≤且;(5)|| 2 z >且|3|1z ->; (6)Im 1 ||2z z ><且;(7)||2 0arg 4z z π<<<且;(8)131 2222i i z z ->->且.7.证明:z 平面上的直线方程可以写成 .az az c += (a 是非零复常数,c 是实常数)8.证明:z 平面上的圆周可以写成0Azz z z C ββ+++=.其中A 、C 为实数,0,A β≠为复数,且2||.AC β> 9.试证:复平面上的三点1,0,a bi a bi +-+共直线。
10.求下列方程(t 是实参数)给出的曲线: (1)(1)z i t =+; (2)cos sin z a t ib t =+;(3)i z t t =+; (4)22i z t t =+.11.函数1w z =将z 平面上的下列曲线变成w 平面上的什么曲线(,z x iy w u iv =+=+)?(1)224;x y +=(2)y x =;(3)x = 1; (4)( x -1)2+y 2=1. 12.试证:(1)多项式1010()(0)n n n p z a z a z a a -=+++≠在z 平面上连续;(2)有理分式函数101101()n n nm m m a z a z a f z b z b z b --+++=+++(000,0a b ≠≠)在z 平面上除分母为的点外都连续。
复变函数论第三版钟玉泉ppt 3 shu-PPT精品文档79页

第一节 复积分的概念及其简单性质
29.09.2019
1
1.有向曲线:
简单曲线(Jordan曲线): 无重点的连续曲线
光滑曲线:处处有切线,且切线随切点的移动而 连续转动的曲线
逐段光滑曲线:有限条光滑曲线衔接而成的连 续曲线
重点
重点
29.09.2019
重点
2
在讨论复变函数积分时,将要用到有向曲线的概 念,如果一条光滑或逐段光滑曲线规定了其起点 和终点,则称该曲线为有向曲线,曲线的方向是 这样规定的:
(1) 曲线C是开口弧段,
若规定它的端点P为起点,Q为终点,则
沿曲线 C 从 P 到Q 的方向为曲线C的正方向
把正向曲线记为C或C+.
y
BQ
而由Q到P的方向称为C的负方向, AP
负向曲线记为 C.
o
x
29.09.2019
3
(2) 如果 是简单闭曲线,规定人沿着曲线边 界行走时C ,区域内部总保持在人的左侧为正方 向,因此,逆时针方向为正方向,顺时针方向 为负方向.
o
1
19
(1)连接由点O到点1i的直线段的参数方程是
z (1i)t (0 t 1)
故CRezdz 01Re(1i)t(1i)dt
(1i)
1
tdt
1
i
0
2
29.09.2019
20
(2)先沿着正实轴从 O到1,再沿着平行于
虚轴的方向从 1到1 i
先沿着正实轴从 O到1,连接 0与1的直线段的参数方程为
5, 93
25
故
从而 1 dz C z i
1 dz 25.
复变函数课后习题答案(全)

习题一答案1. 求下列复数的实部、虚部、模、幅角主值及共轭复数:(1)132i+(2)(1)(2)i i i --(3)131i i i--(4)8214i i i -+-解:(1)1323213iz i -==+, 因此:32Re , Im 1313z z ==-,(2)3(1)(2)1310i i iz i i i -+===---,因此,31Re , Im 1010z z =-=,(3)133335122i i iz i i i --=-=-+=-, 因此,35Re , Im 32z z ==-,(4)82141413z i i i i i i =-+-=-+-=-+ 因此,Re 1, Im 3z z =-=,2. 将下列复数化为三角表达式和指数表达式: (1)i (2)1-+(3)(sin cos )r i θθ+(4)(cos sin )r i θθ-(5)1cos sin (02)i θθθπ-+≤≤解:(1)2cossin22iii e πππ=+=(2)1-+23222(cos sin )233i i e πππ=+=(3)(sin cos )r i θθ+()2[cos()sin()]22ir i reπθππθθ-=-+-=(4)(cos sin )r i θθ-[cos()sin()]i r i re θθθ-=-+-=(5)21cos sin 2sin 2sin cos 222i i θθθθθ-+=+ 3. 求下列各式的值: (1)5)i -(2)100100(1)(1)i i ++-(3)(1)(cos sin )(1)(cos sin )i i i θθθθ-+--(4)23(cos5sin 5)(cos3sin 3)i i ϕϕϕϕ+-(56解:(1)5)i -5[2(cos()sin())]66i ππ=-+- (2)100100(1)(1)i i ++-50505051(2)(2)2(2)2i i =+-=-=-(3)(1)(cos sin )(1)(cos sin )i i i θθθθ-+--(4)23(cos5sin 5)(cos3sin 3)i i ϕϕϕϕ+- (5=(6=4.设12 ,z z i ==-试用三角形式表示12z z 与12z z 解:12cossin, 2[cos()sin()]4466z i z i ππππ=+=-+-,所以12z z 2[cos()sin()]2(cos sin )46461212i i ππππππ=-+-=+,5. 解下列方程: (1)5()1z i +=(2)440 (0)z a a +=>解:(1)z i +=由此25k iz i e iπ=-=-,(0,1,2,3,4)k=(2)z==11[cos(2)sin(2)]44a k i kππππ=+++,当0,1,2,3k=时,对应的4(1),1),1),)i i i i+-+---6.证明下列各题:(1)设,z x iy=+z x y≤≤+证明:首先,显然有z x y=≤+;其次,因222,x y x y+≥固此有2222()(),x y x y+≥+从而z=≥。
