一.数形结合谈数轴
七年级数学思维探究(1)数形结合话数轴(含答案)

七年级数学思维探究数与代数刘徽(生于公元250年左右),是中国数学史上伟大的数学家,在世界数学史上也占有杰出的地位,他的杰作《九章算术注》和《海岛算经》是我国最宝贵的数学遗产.刘徽钻研学术严谨、求实,讲究“析理以辞,解体用图”,他善于启发,主张“告往而知来,举一隅而三隅反”. 1.数形结合话数轴 解读课标1.数形结合话数轴数学是研究“数”和“形”的一门学科,从古希腊时期起,人们就已试图把它们统一起来.在日常生活中我们通常对有形的东西认识比较快,而对抽象的东西认识比较慢,这正是现阶段数学学习的特点,以形助数是数学学习的一个重要方法. 运用数形结合思想解题的关键是建立数与形之间的联系,现阶段数轴是数形联系的有力工具,主要反映在: 1.利用数轴形象地表示有理数; 2.利用数轴直观地解释相反数;3.利用数轴解决与绝对值有关的问题; 4.利用数轴比较有理数的大小. 问题例1(1)已知a 、b 为有理数,且0a >,0b <,0a b +<,将四个数a 、b 、a -、b -按由小到大的顺序排列是_________.(2)已知数轴上有A 、B 两点,A 、B 之间的距离为1,点A 与原点O 的距离为3,那么点B 对应的数是__________. 试一试 对于(1),赋值或借助数轴比较大小;对于(2)确定A 、B 两点在数轴上的位置,充分考虑A 、B 两点的多种位置关系.例2 如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且210d a -=,那么数轴的原点应是( ) A .A 点 B .B 点 C .C 点 D .D 点试一试从寻找d 与a 的另一关系式入手.例3 已知两数a 、b ,如果a 比b 大,试判断a 与b 的大小.试一试 因a 、b 符号未定,故a 比b 大有多种情形,借助数轴可直观全面比较a 与b 的大小.例4 电子跳蚤落在数轴上的某点0K ,第一步从0K 向左跳1个单位到1K ,第一步由1K 向右跳2个单位到2K ,第三步由2K 向左跳3个单位到3K ,第四步由3K 向右跳4个单位到4K ,……,按以上规律跳了100步时,电子跳蚤落在数轴上的点100K 所表示的数恰是19.94,试求电子跳蚤的初始位置0K 点所表示的数.DCBA试一试 设0K 点表示的数为x ,把1K 、2K 、…、100K 点所表示的数用x 的式子表示.例5 已知数轴上的点A 和点B 之间的距离为28个单位长度,点A 在原点的左边,距离原点8个单位长度,点B 在原点的右边. (1)求A 、B 两点所对应的数.(2)数轴上点A 以每秒1个单位长度出发向左运动,同时点B 以每秒3个单位长度的速度向左运动,在点C 处追上了点A ,求C 点对应的数.(3)已知在数轴上点M 从点A 出发向右运动,速度为每秒1个单位长度,同时点N 从点B 出发向右运动,速度为每秒2个单位长度,设线段NO 的中点为P (O 为原点),在运动的过程中线段PO AM -的值是否变化?若不变,求其值;若变化,请说明理由. 分析与解 对于(3),设M 点运动时间为t 秒,把PO AM -用t 的式子表示. (1)A 、B 两点所对应的数分别为8-,20; (2)C 点对应的数为22-; (3)AM t =,202102tOP t +==+(为什么?),则1010PO AM t t -=+-=,即PO AM -的值不变. 生活启示例6 李老师从油条的制作中受到启发,设计了一个数学问题.如图,在数轴上截取从原点到1的对应点的线段AB ,对折后(点A 与点B 重合),固定左端向右均匀地拉成1个单位长度的线段,这一过程称为一次操作(例如,在第一次操作后,原线段AB 上的14,34均变成12;12变成1;等等).那么在线段AB上(除点A 、点B 外)的点中,在第二次操作后,求恰好被拉到与1重合的点所对应的数字之和.分析 捕捉问题所蕴含的信息,阅读理解“一次操作”的意义:将线段沿中点翻折,中点左侧的点不动,中点右侧的点翻折到左侧的对应位置上,由原来的一个等分点变为两个等分点.解:原图B A 78348123814181BA对折后拉长后对折后拉长后故在第二次操作后,恰好被拉到与1重合的点所对应的数字之和是13144+=. 数学冲浪 知识技能广场1.数轴上有A 、B 两点,若点A 对应的数是2-,且A 、B 两点的距离为3,则点B 对应的数是______.2.电影《哈利·波特》中,小哈利·波特穿墙进入“394站台”的镜头(如示意图中的M 站台),构思奇妙,能给观众留下深刻的印象,若A 、B 站台分别位于2-,1-处,2AN NB =,则N 站台用类似电影中的方法可称为“_________站台”.3.已知点A 、B 、P 在数轴上,点B 表示的数为6,8AB =,5AP =,那么点P 表示的数是_______.4.如图所示,按下列方法将数轴的正半轴绕在一个圆(该圆周长为3个单位长,且在圆周的三等分点处分别标上了数字0、1、2)上:先让原点与圆周上数字0所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1所对应的点重合.这样,正半轴上的整数就与圆周上的数字建立了一种对应关系. (1)圆周上的数字a 与数轴上的数5对应,则a =________;(2)数轴上的一个整数点刚刚绕过圆周n 圈(n 为正整数)后,并落在圆周123858()1434()1878()0(1)38418121878()1434()3858()0(1)34121120141434()1878,38,58()01,12()1401201,12()1878,38,58()1434()121M109-1-2上数字1所对应的位置,这个整数是________(用含n 的代数式表示).5.有理数a 、b 在数轴上的位置如图所示:,则下列各式正确的是()A .0a b +>B .0ab >C .0a b +<D .0a b ->6.文具店、书店、玩具店依次坐落在一条东西走向的大街上,文具店在书店西20米,玩具店位于书店东100米处,小明以书店沿街向东走了40米,接着又向东走了60-米,此时小明的位置在( )A .文具店B .玩具店C .文具店西边40米D .玩具店东60-米 7.将一刻度尺如图所示放在数轴上(数轴的单位长度是1cm ),刻度尺上的“0cm ”、“15cm ”分别对应数轴上的 3.6-和x ,则( )A .910x <<B .1011x <<C .1112x <<D .1213x <<8.在数轴上任取一条长度为119999的线段,则此线段在这条数轴上最多能盖住的整数点的个数是( )A . 1998B .1999C .2000D .20019.一个跳蚤在一条直线上,从O 点开始,第1次向右跳1个单位,紧接着第2次向左跳2个单位,第3次向右跳3个单位,第4次向左跳4个单位……依此规律跳下去,当它跳第100次落下时,求落点处离O 点的距离(用单位表示). 10.已知数轴上有A 、B 两点,A 、B 之间的距离为1,点A 与原点O 的距离为3,求所有满足条件的点B 与原点O 的距离的和. 思维方法天地11.在数轴上,点A 、B 分别表示13-和15,则线段AB 的中点所表示的数是______. 12.在数轴上,表示数22a ⎛⎫+ ⎪⎝⎭的点M 与表示数33a ⎛⎫+ ⎪⎝⎭的点N 关于原点对称,则a 的值为_______. 13.数形相伴 (1)如图所示,点A 、B 所代表的数分别为1-,2,在数轴上画出与A 、B 两点的距离和为5的点(并标上字母).1ba 210-1-2x-3.6A B 043215-3-2-1(2)若数轴上点A 、B 所代表的数分别为a 、b ,则A 、B 两点之间的距离可表示为AB a b =-,那么,当127x x ++-=时,x =________;当125x x ++->时,数x 所对应的点在数轴上的位置是在________.14.点A 、B 分别是数3-、12-在数轴上对应的点,使线段AB 沿数轴向右移动为''A B ,且线段''A B 的中点对应的数是3,则点'A 对应的数是_______,点A 移动的距离是________.15.点1A 、2A 、3A 、…、n A (n 为正整数)都在数轴上,点1A 在原点O 的左边,且11AO =,点2A 在点1A 的右边,且212A A =;点3A 在点2A 的左边,且323A A =,点4A 在点3A 的右边,且434A A =,……,依照上述规律,点2008A 、2009A 所表示的数分别为( )A .2008,2009-B .2008-,2009C .1004,1005-D .1004,1004- 16.如图:,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a 、b 、c 、d ,且29b a -=,那么数轴的原点对应点是( )A .A 点B .B 点C .C 点D .D 点17.有理数a 、b 、c 在数轴上的位置如图,式子a b a b b c ++++-化简结果为( )A .23a b c +-B .3b c -C .b c +D .c b -18.不相等的有理数a 、b 、c 在数轴上对应点分别为A 、B 、C ,若a b b c a c -+-=-,那么点B ( )A .在A 、C 点右边B .在A 、C 点左边 C .在A 、C 点之间D .以上均有可能19.在数轴上,N 点与O 点的距离是N 点与30所对应点之间的距离的4倍,那么N 点表示的数是多少?20.已知数轴上有A 、B 、C 三点,分别代表24-、10-、10,两只电子蚂蚁甲、乙分别从A 、C 两点同时相向而行,甲的速度为4个单位/秒. (1)问多少秒后甲到A 、B 、C 的距离和为40个单位?(2)若乙的速度为6个单位/秒,两只电子蚂蚁甲、乙分别从A 、C 两点同时相向而行,问甲、乙在数轴上的哪个点相遇? (3)在(1)、(2)的条件下,当甲到A 、B 、C 的距离和为40个单位时,甲调头返回,问甲、乙还能在数轴上相遇吗?若能,求出相遇点;若不能,请说明理由. 应用探究乐园 21.操作与探究对数轴上的点P 进行如下操作:先把点P 表示的数乘以13,再把所得数对应的DCBAcb a点向右平移1个单位,得到点P 的对应点'P .点A ,B 在数轴上,对线段AB 上的每个点进行上述操作后得到线段''A B ,其中,点A ,B 的对应点分别为'A ,'B .如图所示,若点A 表示的数是3-,则点'A 表示的数是_______;若点'B 表示的数是2,则点B 表示的数是________;已知线段AB 上的点E 经过上述操作后得到的对应点'E 与点E 重合,则点E 表示的数是__________.22.一动点P 从数轴上的原点出发,沿数轴的正方向以每前进5个单位、后退3个单位的程序运动,已知点P 每秒前进或后退1个单位,设n x 表示第n 秒点P 在数轴上的位置所对应的数(如44x =,55x =,64x =),求2011x 所对应的数.B'A -1-2-3-412341.数形结合话数轴 问题解决例1 (1)b a a b <-<<- (2)4或2或2-或4- 例2 B 由图知7d a -=,又210d a -=,得3a =-.例3 当点B 在原点的右边时,0b a <<,则a b >;当点A 在原点的左边时,0b a <<,则a b <;当点A 、B 分别在原点的右、左两侧时,0b a <<,这时无法比较a 与b 的大小关系;当点A 正好在原点位置时,0b a <=,则b a >;当点B 正好在原点位置时,0b a =<,则a b >.例4 30.06- 设0K 点表示的有理数为x ,则1K 、2K 、…、100K 点所表示的有理数分别为1x -,12x -+,123x -+-,…,123499100x -+-+-+,由题意得12349910019.94x -+-+-+=. 数学冲浪1.5-或1 2.113- 3.3或7-4.(1)2;(2)31n + 5.A 6.A 7.C 8.C 9.12349910050-+-++-=-,落点处与O 点距离为50个单位长. 10.12 11.115-AB 中点所表示的数是11123515⎛⎫-+÷=- ⎪⎝⎭12.6-13.(1)如图所示,点C 、D 两点即为所求. (2)3x =-或4;点C 的左边或点D 的右边.14.74;194 AB 长为()15322⎛⎫---= ⎪⎝⎭,'A 对应数为1573224-⨯=,点A 移动的距离为()719344--=. 15.C 16.C 17.C 18.C19. 24与40 20.(1)设x 秒后甲到A 、B 、C 距离和为40 ()102414---= ()101020--=.①当甲在A 、B 之间时 ()()41441442040x x x +-+-+=,得2x =. ②当甲在B 、C 之间时 ()()44142041440x x x +-+-+=,得5x =,即2秒或5秒后. (2)设x 秒后相遇()()461024x +=-- 1034x = 3.4x =.24 3.4410.4-+⨯=-,即在10.4-处相遇.(3)①设甲向C 走2秒后掉头返回x 秒与乙相遇 2442410266x x -+⨯-=+-⨯-,解得7x =. ∴()102661062106944x x -⨯-=-+=-⨯=-.D C B A 4321-1-2-3②设甲向C走5秒后掉头返回y秒与乙相遇2445410566y y-+⨯-=-⨯-,解得8y=-.∴不合题意,舍去.即甲、乙能在44-所表示的点处相遇.21.0;3;32.设E点表示的数为x,则'E点表示的数为113x+,由113x x=+得32x=.22.因201182513=⨯+,22513505⨯+=,故2011x所对应的数为505.。
七年级数学竞赛题:数形结合谈数轴

七年级数学竞赛题:数形结合谈数轴数学是研究数和形的学科,在数学里数和形是有密切联系的.我们常用代数的方法来处理几何问题;反过来,也借助于几何图形来处理代数问题,寻找解题思路,这种数与形之间的相互作用叫数形结合,是-种重要的数学思想.运用数形结合思想解题的关键是建立数与形之间的联系,现阶段数轴是数形结合的有力工具,主要体现在以下几个方面:1.利用数轴能形象地表示有理数;2.利用数轴能直观地解释相反数;3.利用数轴比较有理数的大小;4.利用数轴解决与绝对值相关的问题.例1 已知数轴上有A 、B 两点,A 、B 之间的距离为l ,点A 与原点0的距离为3,那么所有满足条件的点B 与原点0的距离之和等于 . (北京市“迎春杯”竞赛题) 解题思路 确定A 、B 在数轴上的位置,求出A 、B 两点所表示的有理数.例2已知有理数a 、b 、c 在数轴上的对应位置如下图:则1-c +c a -+b a -化简后的结果是( ).(湖北省初中数学竞赛选拔赛试题)(A)b -l (B)2a -6—1(C)l+2a -b -2c (D)1—2c+b解题思路 从数轴上获取关于a 、b 、c 的相关信息,判断代数式c —l ,a -c ,a -b 的正负性.例3 a 、b 、c 在数轴上的位置如图所示:试判定b a b a +-,b a b a -+,cba cb a -+之间的大小关系. 解题思路 推断各分数分子、分母的正负性及大小关系。
……….例4(1)阅读下面材料:点A 、B 在数轴上分别表示实数a 、b ,A 、B两点之间的距离表示为|AB|.当A 、B 两点中有一点在原点时,不妨设点A 在原点,如图1,|AB|=|OB|=|b|=|a-b|;当A 、B 两点都不在原点时,①如图2,点A 、B 都在原点的右边|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|;②如图3,点A、B都在原点的左边,|AB|=|OB|—|OA|=|b|—|a|=-b-(-a)=|a-b|;③如图4,点A、B在原点的两边,|AB|=|OA|+|OB|=|a|+|b|=a+(-b)=|a-b|.综上,数轴上A、B两点之间的距离|AB|=|a-b|.(2)回答下列问题:.①数轴上表示2和5的两点之间的距离是______,数轴上表示一2和一5的两点之间的距离是_______,数轴上表示1和一3的两点之间的距离是_______;②数轴上表示x和-1的两点A和B之间的距离是_____,如果∣AB∣=2,那么x为______;③当代数式∣x+1∣+∣x-2∣取最小值时,相应的x的取值范围是______;④求∣x-1∣+∣x-2∣+∣x-3∣+…+∣x-1997∣的最小值..(2002年南京市中考题)解题思路通过观察图形,阅读理解代数∣a-b∣所表示的意义,来回答所提出的具体问题.例5某城镇沿环形路有五所小学,依次为-小、二小、三小、四小、五小,它们分别有电脑15、7、1l、3、14台,现在为使各校电脑台数相等,各调几台给邻校:-小给二小,二小给三小,三小给四小,四小给五小,五小给-小,若甲小给乙小-3台,即为乙小给甲小3台,要使电脑移动的总台数最小,应作怎样安排?(湖北省荆州市竞赛题) 解题思路通过设未知数,把调动的电脑总台数用相关代数式表示,解题的关键是,如何将实际问题转化为类似“例4”的问题加以解决..1.已知数轴上表示负有理数Ⅲ的点是点M,那么在数轴上与点M相距∣m∣个单位的点中,与原点距离较远的点对应的数是_______.(第十五届江苏省竞赛题)2.如果数轴上点A到原点的距离为3,点B到原点的距离为5,那么A、B两点的距离为______.3.在数轴上表示数a的点到原点的距离为3,则以a-3=______.4.已知a>0,b<O且以a+b<O,那么有理数a,b,-a,∣b∣的大小关系是_____________.(用“<”号连接)(北京市“迎春杯”竞赛题)5.已知有理数以在数轴上原点的右方,有理数b在原点的左方,那么( ).(A)ab<b (B)ab>b (C)a+b>0 (D)a-b>O6.如图,a、b为数轴上的两点表示的有理数,在a+b,b—2a,∣a-b∣,∣b∣-∣a∣中,负数的个数有( ).(“祖冲之杯”邀请赛试题)(A)1 (B)2 (C)3 (D))47.有理数a 、b 、c 在数轴上的位置如图所示,式子|a|+|b|+|a+b||b-c|化简结果为( ).(A)2a+3b -c (B)3b -c (C)b+c (D)c -b8.如图所示,在数轴上有六个点,且AB=BC=CD=DE=EF ,则与点C 所表示的数最接近的整数是( ).(A)-l (B)0 (C)1 (D)2(第十二届“希望杯”邀请赛试题)9.已知a 、b 、c 、d 为有理数,在数轴上的位置如图所示:且6∣a ∣=6∣b ∣=3∣c ∣=4∣d ∣=6,求∣3a -2d ∣—∣3b —2a ∣+∣2b -c ∣的值.10.电子跳蚤落在数轴上的某点K 0,第-步从K 。
数轴中的数形结合思想

数轴中的数形结合思想 Company number:【WTUT-WT88Y-W8BBGB-BWYTT-19998】第1讲数轴中的数形结合思想【链接方法】数学一开始就是研究“数”和“形”的,从古希腊时期起,人们就已试图把它们统一起来.数与形有着密切的联系,我们常用代数的方法研究图形问题;另一方面,也利用图形来处理代数问题,这种数与形相互作用,是一种重要的数学思想──数形结合思想.华罗庚说:“数缺形时少直观,形缺数时难入微”.利用数形结合思想解题的关键是建立数与形之间的联系,现阶段,数轴是联系数与形的桥梁,主要体现在:1.运用数轴直观地表示有理数(rationalnumber);2.运用数轴形象地解释相反数(oppositenumber);3.运用数轴准确地比较有理数的大小;4.运用数轴恰当地解决与绝对值有关联的问题.【挑战例题】【例1】(1)(第17届江苏省竞赛题)数轴上有A、B两点,如果点A对应的数是-2,且A、B两点的距离为3,•那么点B对应的数是________.(2)(第15届江苏省竞赛题)在数轴上,点A、B分别表示-13和15,则线段AB的中点所表示的数是________.【例2】(第12届“希望杯”邀请赛试题)如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则与点C•所表示的数最接近的整数是().【例3】比较a与1a的大小.【例4】(1)工作流水线上顺次排列5个工作台A、B、C、D、E,一只工具箱应该放在何处,才能使工作台上操作机器的人取工具所走的路程最短(2)如果工作台由5个改为6个,那么工具箱应如何放置能使6•个操作机器的人取工具所走的路程之和最短(3)当流水线上有n个工作台时,怎样放置工具箱最适宜【提升能力】1.(2003年河南省竞赛题)如图,A、B、C、D、E为数轴上的五个点,且AB=BC=CD=DE,则图中与P•点表示的数比较接近的一个数是().(2013年山东省菏泽市中考题)如图,数轴上的A、B、C三点所表示的数分别是a、b、c,其中AB=BC,如果|a|>|b|>|c|,那么该数轴的原点O的位置应该在()A.点A的左边B.点A与点B之间C.点B与点C之间D.点B与点C之间或点C的右边3.(第15届江苏省竞赛题)如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、B、C、D对应的数分别是整数a,b,c,d,且d-2a=10,那么数轴的原点应是().点点点点4.(第18届江苏省竞赛题)数a、b、c、d所对应的点A、B、C、D在数轴上的位置如图所示,那么a+c与b+d的大小关系是().+c<b++c=b++c>b+dD.不确定的(第3题)(第4题)5.(2007年江苏省镇江市中考题)一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动,设该机器人每秒钟前进或后退1步,并且每步的距离为1个单位长,n x 表示第n 秒时机器人在数轴上的位置所对应的数,给出下列结论:①33=x ;②15=x ;③108104x x <;④20082007x x <.其中,正确的结论的序号是()A .①、③B .②、③C .①、②、③D .①、②、④6.在数轴上表示数a 的点到原点的距离为3,则a-3=________.、b 、c 在数轴上的位置如图所示,则1a b -、1c b -、1a c -中最大的是________.(第7题)(第8题)8.如图,工作流程线上A 、B 、C 、D 处各有1名工人,且AB=BC=CD=1,现在工作流程线上安放一个工具箱,使4个人到工具箱的距离之和为最短,•则工具箱的安放位置是__________.9.已知a 、b 为有理数,且a >0,0<b ,0<+b a ,将四个数a ,b ,a -,b -按由小到大的顺序排列是________________________.10.(山东省竞赛题)已知数轴上表示负有理数m 的点是点M,那么在数轴上与点M 相距│m │个单位的点中,与原点距离较远的点对应的数是________.11.(2005年江西省中考题)如图所示,按下列方法将数轴的正半轴绕在一个圆(该圆周长为3个单位长,且在圆周的三等分点处分别标上了数字0、1、2)上:先让原点与圆周上的数字0所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合.这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.(1)圆周上的数字a 与数轴上的数5对应,则a =______;(2)数轴上的一个整数点刚刚绕过圆周为正整数)n n (圈后,并落在圆周上数字1所对应的位置,这个整数是______(用含n 的代数式表示).12.(北京市“迎春杯”竞赛题)已知数轴上有A 、B 两点,A 、B 之间的距离为1,点A与原点O 的距离为3,求所有满足条件的点B 与原点O 的距离的和.13.已知两数a 、b,如果a 比b 大,试判断│a │与│b │的大小.14.电子跳蚤落在数轴上的某点K 0,第一步从K 0向左跳1个单位到K 1,第二步由K 1向右跳2个单位到K 2,第三步由K 2向左跳3个单位到K 3,第四步由K 3向右跳4个单位到K 4…,•按以上规律跳了100步时,电子跳蚤落在数轴上的点K 100所表示的数恰是,•试求电子跳蚤的初始位置K 0点所表示的数.15.动点A 从原点出发向数轴负方向运动,同时,动点B 也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A 、B 的速度比是1:4.(速度单位:单位长度/秒)(1)求出两个动点运动的速度,并在数轴上标出A 、B 两点从原点出发运动3秒时的位置;(2)若A 、B 两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;(3)在(2)中A 、B 两点继续同时向数轴负方向运动时,另一动点C 同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度.。
几何直观—与数轴相关的数形结合问题 教学设计

几何直观—与数轴相关的数形结合问题教学设计几何直观—与数轴相关的数形结合问题教学设计一、引言在数学教学中,几何直观的理解对学生的数学学习至关重要。
数轴作为数学中的重要工具,是帮助学生理解数学概念的重要手段之一。
本文将围绕几何直观与数轴的关系展开讨论,结合数形结合问题的教学设计,帮助学生更好地理解和应用数学知识。
二、数轴的基本概念1. 数轴的定义数轴是一条直线上按照一定的单位长度刻度的线段,通常用于表示实数。
数轴上将实数与坐标一一对应,帮助我们直观地理解数的大小和大小之间的关系。
2. 数轴的特点数轴上的任意一点都可以与实数一一对应,数轴上距离原点越远的点对应的实数值也越大。
通过数轴,我们可以直观地比较不同实数的大小,并且进行加减乘除运算。
三、数形结合的教学设计在教学中,我们可以结合数轴的几何直观,帮助学生更好地理解数学概念。
以下是针对数形结合问题的教学设计:1. 引入实际问题引入一个与学生生活相关的实际问题,例如买菜花了多少钱、走路花费了多少时间等等。
2. 绘制数轴让学生自己绘制数轴,并在数轴上标出相关的数值。
通过绘制数轴,让学生更直观地理解数值之间的大小关系。
3. 解决问题让学生通过数轴来解决实际问题,比如计算买菜花了多少钱、走路花费了多少时间等等。
通过解决问题,让学生对数轴的应用有更深刻的理解。
四、个人观点和理解数轴作为一种几何直观的工具,在数学教学中有着重要的作用。
通过数轴,学生可以更直观地理解数值之间的大小关系,并且解决实际问题。
在教学中,我们应该注重培养学生对几何直观的理解和应用能力,让他们在数学学习中更加自信和熟练。
五、总结通过本文的讨论,我们可以看到几何直观与数轴的关系对于数学教学的重要性,并且结合数形结合问题的教学设计,帮助学生更好地理解和应用数学知识。
在今后的教学中,我们应该注重培养学生的几何直观,让他们在数学学习中更加得心应手。
六、参考资料- 张三, 《数学教学研究》,2008年。
数形结合之数轴上的动点问题

数形结合之数轴上的动点问题数形结合是数学中一种重要的解题思想,它通过将抽象的数学语言与直观的图形相结合,使复杂的问题变得简单易懂。
数轴上的动点问题是一个典型的数形结合问题,通过将数轴上的点与代数式相结合,可以解决一系列与距离、速度、加速度等有关的实际问题。
数轴上的动点问题通常涉及以下几个步骤:1. 建立数轴:根据题意,在数轴上标出已知的点,并确定动点的初始位置。
2. 确定动点运动规律:根据题意,确定动点的运动方式(如匀速、匀加速等)和运动规律(如时间、速度、加速度等)。
3. 计算动点位置:根据动点的运动规律,计算出动点在任意时刻的位置。
4. 求解问题:根据题目要求的问题,利用数轴上的距离、速度、加速度等概念进行求解。
下面是一个具体的数轴上的动点问题的例子:题目:在数轴上,一动点A从原点出发,沿数轴向右以每秒3个单位长度的速度移动,同时动点B也从原点出发,沿数轴向左以每秒2个单位长度的速度移动。
设动点A、B的运动时间为t秒。
(1)求出点A、B运动的路程;(2)求出点A、B运动的速度;(3)当A、B两点相距的路程不超过3个单位长度时,求t的取值范围。
解:(1)由题意可知,点A、B运动的路程分别为3t和2t。
(2)由题意可知,点A、B运动的速度分别为每秒3个单位长度和每秒2个单位长度。
(3)当A、B两点相距的路程不超过3个单位长度时,有两种情况:一是A、B两点相遇前相距的路程不超过3个单位长度;二是A、B两点相遇后继续运动一段时间,相距的路程不超过3个单位长度。
①当A、B两点相遇前相距的路程不超过3个单位长度时,有(3t - 2t) ≤ 3,解得t ≤ 3;②当A、B两点相遇后继续运动一段时间,相距的路程不超过3个单位长度时,有(3t + 2t) - 3 ≤ 3,解得t ≤ 2。
综上所述,当A、B两点相距的路程不超过3个单位长度时,t的取值范围为t ≤ 3或t ≤ 2。
数形结合话数轴

数形结合话数轴例1.已知b a 、为有理数。
且0>a ,0<b ,0<+b a ,将b a b a --、、、,按由小到大的顺序排列是_____________________________________________练习:已知b a 、为有理数。
且0>a ,0<b ,0>+b a ,将b a b a --、、、,按由小到大的顺序排列是_____________________________________________例2.已知数轴上有A 、B 两点,A 、B 之间的距离为1,点A 与原点O 的距离为3,那么点B 对应的数是________________练习:1.已知数轴上有A 、B 两点,A 、B 之间的距离为5,点A 与原点O 的距离为2,那么点B 对应的数是________________2.数轴上有A 、B 两点,若点A 对应的数是2-,且A 、B 两点的距离为3,则点B 对应的数是__________________3.已知点A 、B 、P 在数轴上,点B 表示的数是6,AB=8,AP=5,那么点P 表示的数是____4.已知数轴上有A 、B 两点,A 、B 之间的距离为1,点A 与原点O 的距离为3,求所有满足条件的点B 与原点O 的距离的和。
例3.在数轴上,点A 、B 分别表示4-和6,则线段AB 的中点所表示的数是____________练习:1.在数轴上,点A 、B 分别表示31-和51,则线段AB 的中点所表示的数是____________2.在数轴上,点A 、B 分别表示10-和2-,则线段AB 的中点所表示的数是____________例4.在数轴上,点A 、B 分别表示4-和6,则线段AB 的距离为_________________练习1.在数轴上,点A 、B 分别表示6-和1-,则线段AB 的距离为_________________2在数轴上,点A 、B 分别表示10-和6,则线段AB 的距离为_________________例5.点A 、B 分别是数3-、1-在数轴上对应的点,使线段AB 沿数轴向右移动为''B A ,且线段''B A 的中点对应的数是3,则点'A 对应的数是_________,点A 移动的距离是_____练习:点A 、B 分别是数6-、21-在数轴上对应的点,使线段AB 沿数轴向右移动为''B A ,且线段''B A 的中点对应的数是3,则点'A 对应的数是_________,点A 移动的距离是_____例6.在数轴上,N 点与O 点的距离是N 点与30所对应点之间的距离的4倍,那么N 点表示的数是__________________练习:在数轴上,N 点与O 点的距离是N 点与20所对应点之间的距离的3倍,那么N 点表示的数是__________________聚焦绝对值例1.已知0423=-+-y x ,求y x 32-的相反数练习:已知0938=-+-b a ,求b a 43-的相反数例2.已知5=x ,2=y ,且)(y x y x +-=+,求y x -的值练习:1.已知6=x ,1=y ,且y x y x +=+,求y x -的值2.已知3=x ,4=y ,且y x y x -=-,求y x +的值例3.已知5=x ,2=y ,求y x y x +--的值练习1.已知5=x ,2=y ,求y x y x +--的值2.已知9=x ,3=y ,求y x y x ++-的值例3.已知1=x ,2=y ,3=z ,且z y x >>,那么=++z y x ____________练习:1.已知3=x ,6=y ,8=z ,且z y x >>,那么=--z y x ____________2.已知2=a ,5=b ,8=c ,且c b a <<,那么=+-c b a ____________(二 ) 聚焦绝对值例1..已知2020--+-+-=b x x b x y ,其中200≤<b ,20≤≤x b ,那么y 的最小值为____________练习:已知88--+-+-=b x x b x y ,其中80≤<b ,8≤≤x b ,那么y 的最小值为____________例2.a 、b 都不为零,式子ab ab b b a a ++的所有可能的值有________________________练习:a 、b 、c 都不为零,式子acac bc bc ab ab c c b b a a +++++的所有可能的值有________________________例3.已知:022=-+-a ab , 求)2014)(2013(1)2)(2(1)1)(1(11+++∙∙∙+++++++b a b a b a ab练习:计算201420121861641421⨯+∙∙∙+⨯+⨯+⨯例4 .如图:化简:c b a c b a ---+-如图:化简: d c a c b c a b a --++--++例5.阅读下列材料并解决有关问题: 我们知道⎪⎩⎪⎨⎧<-=>=)0()0(0)0(x x x x x x 现在我们可以用这一结论来化简含有绝对值的代数式,如化简代数式21-++x x 时,可令01=+x 和02=-x ,分别求出1-=x ,2=x (称1-,2分别是1+x 和2-x 的零点值)在有理数范围内,零点值1-=x 和2=x 可将有理数分成不重复且不遗漏的如下3种情况:(1)1-<x ;21≤≤-x ;(3)2>x ,从而化简代数式 21-++x x 可分以下3种情况:(1)当1-<x 时,原式=1221)2()1(+-=+---=--+-x x x x x(2)当21≤≤-x 时,原式=321)2(1=+-+=--+x x x x(3)当2>x 时,原式=1221-=-++x x x通过以上阅读,请你解决以下问题:(1)分别求出2+x 和4-x 的零点值;(2)化简代数式42-++x x练习:(1)化简:23++-x x (2)化简:51+--x x例6.(1)当x 取何值时,3-x 有最小值?这个最小值是多少?(2)当x 取何值时,25+-x 有最大值?这个最大值时多少?(3)求87-+-x x 的最小值。
初中数学复习,数形结合谈数轴_

初中数学复习,数形结合谈数轴_数形结合谈数轴一、阅读与思考数学是研究数和形的学科,在数学里数和形是有密切联系的。
我们常用代数的方法来处理几何问题;反过来,也借助于几何图形来处理代数问题,寻找解题思路,这种数与形之间的相互作用叫数形结合,是一种重要的数学思想。
运用数形结合思想解题的关键是建立数与形之间的联系,现阶段数轴是数形结合的有力工具,主要体现在以下几个方面:1、利用数轴能形象地表示有理数;2、利用数轴能直观地解释相反数;3、利用数轴比较有理数的大小;4、利用数轴解决与绝对值相关的问题。
二、知识点反馈1、利用数轴能形象地表示有理数;例1:已知有理数在数轴上原点的右方,有理数在原点的左方,那么()A.B.C.D.拓广训练:1、如图为数轴上的两点表示的有理数,在中,负数的个数有()(“祖冲之杯”邀请赛试题)A.1 B.2 C.3 D.4 3、把满足中的整数表示在数轴上,并用不等号连接。
2、利用数轴能直观地解释相反数;例2:如果数轴上点A到原点的距离为3,点B到原点的距离为5,那么A、B两点的距离为。
拓广训练:1、在数轴上表示数的点到原点的距离为3,则2、已知数轴上有A、B两点,A、B之间的距离为1,点A与原点O的距离为3,那么所有满足条件的点B与原点O的距离之和等于。
(北京市“迎春杯”竞赛题)3、利用数轴比较有理数的大小;例3:已知且,那么有理数的大小关系是。
(用“”号连接)(北京市“迎春杯”竞赛题)拓广训练:1、若且,比较的大小,并用“”号连接。
例4:已知比较与4的大小拓广训练:1、已知,试讨论与3的大小2、已知两数,如果比大,试判断与的大小4、利用数轴解决与绝对值相关的问题。
例5:有理数在数轴上的位置如图所示,式子化简结果为()A.B.C.D.拓广训练:1、有理数在数轴上的位置如图所示,则化简的结果为。
2、已知,在数轴上给出关于的四种情况如图所示,则成立的是。
① ② ③ ④ 3、已知有理数在数轴上的对应的位置如下图:则化简后的结果是()(湖北省初中数学竞赛选拨赛试题)A.B.C.D.三、培优训练1、已知是有理数,且,那以的值是()A.B.C.或D.或1 0 A 2 B 5 C 2、(07乐山)如图,数轴上一动点向左移动2个单位长度到达点,再向右移动5个单位长度到达点.若点表示的数为1,则点表示的数为()A.B.C.D.3、如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、B、C、D对应的数分别是整数且,那么数轴的原点应是()A.A点B.B点C.C点D.D点4、数所对应的点A,B,C,D在数轴上的位置如图所示,那么与的大小关系是()A.B.C.D.不确定的5、不相等的有理数在数轴上对应点分别为A,B,C,若,那么点B()A.在A、C点右边B.在A、C点左边C.在A、C点之间D.以上均有可能6、设,则下面四个结论中正确的是()(全国初中数学联赛题)A.没有最小值B.只一个使取最小值C.有限个(不止一个)使取最小值D.有无穷多个使取最小值7、在数轴上,点A,B分别表示和,则线段AB的中点所表示的数是。
七年级数学思维探究(一)数形结合话数轴(含答案).doc

数与代数刘徽(生于公元250年左右),是中国数学史上伟大的数学家,在世界数学史上也占有杰出的地位,他的杰作《九章算术注》和《海胡算经》是我国最宝贵的数学遗产.刘徽钻研学术严谨、求实,讲究“析理以辞,解体用图”,他善于启发,主张“告往而知来,举一隅而三隅反”.1.数形结合话数轴解读课标1.数形结合话数轴数学是研究“数”和“形”的一门学科,从古希腊时期起,人们就已试图把它们统一起來.在日常生活中我们通常对有形的东西认识比较快,而对抽象的东西认识比较慢,这正是现阶段数学学习的特点,以形助数是数学学习的一个重要方法.运用数形结合思想解题的关键是建立数与形之间的联系,现阶段数轴是数形联系的有力工具,主要反映在:1.利用数轴形象地表示有理数;2.利用数轴直观地解释相反数;3.利用数轴解决与绝对值有关的问题;4.利用数轴比较有理数的大小.问题例1 (1)己知b为有理数,且a>0, , a + b<0 f将四个数b、-Q、-b按由小到大的顺序排列是_________ .(2)已知数轴上有A、B两点,A、B之I'可的距离为1,点A与原点O的距离为3,那么点B对应的数是.试一试对于(1),赋值或借助数轴比较大小;对于(2)确定4、3两点在数轴上的位置,充分考虑A、B两点的多种位置关系.例2如图,数轴上标出若干个点,每相邻两点相距1个单位,点A、B、C、D对应的数分别是整数a、b、c、〃,且〃-2° = 10,那么数轴的原点应是()A. A点B. B点C. C点D. D点-A 13 c IT试一试从寻找d与0的另一关系式入手.例3已知两数0、b,如果。
比b大,试判断问与问的大小.试一试因b符号未定,故。
比b大有多种情形,借助数轴可直观全面比较问与问的大小.例4电子跳蚤落在数轴上的某点K。
,第一步从K。
向左跳1个单位到龟,第一步由人向右跳2个单位到心,第三步由心向左跳3个单位到心,第四步由心向右跳4个单位到心,……,按以上规律跳了100步时,电子跳蚤落在数轴上的点心。
数轴的数形结合及分类讨论

的距离.|x |也可写成|x -0|,指的是 x 所表示的点到原点的距离.【例 1】|x -1|是数轴上 x 所表示的点到 1 的距离.那么|x -5|是练习 1:(1)|x +2|是的距离,(2)|x +5.5|是的距离.例2:|x -3|=4可理解为x 到3的距离等于4,利用数轴可得x =.练习2:(1)已知|x -2|=5,则x =.为什么?(仿照例2解释)(2)已知|x +3|=2,则x =.(3)已知|x +2.5|=4,则x =.(4)|x +2|=|x -1|的解是.(5)已知|a -6|=2,|b -2|=1,且数a ,b 在数轴上表示的点分别是A 、B ,求AB 的最大距离和最小距离.【例3】当|x +1|+|x -2|取最小值时,求x 的取值范围.练习3:(1)当|x -1|+|x +2|取最小值时,求x 的取值范围.(2)当|x +1|+|x +4|取最小值时,求x 的取值范围.(3)当|x -5|-|x -2|取最大值时,求x 的取值范围.(4)当|x +5|-|x -1|取最大值时,求x 的取值范围.数轴的数形结合及分类讨论(5)已知|x-3|+|x+2|的最小值为a,|x-3|-|x+2|的最大值为b,求a+b的值.(6)已知A=|a-2|-3|a|+|a+5|,且-5≤a≤2,求A的最大值.【例4】已知数轴上有A、B两点,A、B之间的距离为1,点A与原点O的距离为3,那么点B对应的数是.练习4:(1)已知数轴上有A、B两点,点A对应的数是-2,A、B之间的距离为3,那么点B对应的数是.(2)已知数轴上有A、B两点,点A与原点O的距离为3,B点到原点的距离为4,则A、B之间的距离为.(3)数轴上,点A表示-3,点B与点A到原点的距离相等,且A、B不重合,点C与点B之间的距离是2,则点C表示的数是.(4)使得|x+5|+|x-2|=7的整数x为.【例5】已知a<5,比较|a|与4的大小.练习5:已知a>-3,比较|a|与3的大小.【例6】拓展:(利用数轴分析)(1)当x为时,|x-1|+|x-2|+|x-3|有最小值,最小值是.(2)当x为时,|x-1|+|x-2|+|x-3|+|x-4|有最小值,最小值是.(3)当x为时,|x-1|+|x-2|+|x-3|+|x-4|+|x-5|有最小值,最小值是.(4)当x为时,|x-1|+|x-2|+|x-3|+…+|x-2002|有最小值,最小值是.(5)当x为时,|x-1|+|x-2|+|x-3|+…+|x-2025|有最小值,最小值是.。
数形结合-利用数轴表示有理数,有理数比较大小

数形结合-利用数轴表示有理数,有理数比较大小我们先看一下数轴的基本定义(注意三要素:原点、正方向、长度单位,经常出现在判断题中):数轴是一条规定了原点,正方向,单位长度的直线。
(规定原点向右为正方向,向左为负方向)学习了有理数和数轴的基本概念后,我们知道任意一个有理数都可以用数轴上的一个点来表示。
数轴可以直观的表示有理数的正负性,与原点的距离,以及点与点间的距离。
两个有理数的大小由它们在数轴上对应点的位置来确定,右边的点对应的数大于左边的点对应的数。
所以很自然的就可以想到利用数轴来比较有理数的大小。
今天主要介绍利用数轴表示有理数与比较有理数的大小,进一步熟悉有理数,以及逐步理解数形结合的思想。
(一)利用数轴表示有理数任意一个有理数都可以用数轴上的一个点来表示,最常用的就是表示相反数。
例如1与-1就可以形象的表示在数轴上。
1在原点右侧,-1在原点左侧,它俩到原点的距离相等(都是1)!1与-1间的距离就是1+1=2实际上这个数对应的点到原点的距离就是这个数的绝对值,所以可知1与-1的绝对值都是1。
利用正负性与点间距离我们可以计算或估计点的大概位置。
例题:在数轴上的点P与原点的距离是它与-10对应点距离的3倍,那么P点表示的数是多少。
我们利用数轴先画出点-10,根据条件所求点可以在-10与原点之间(点P1),也可以在-10的左侧(点P2),在原点右侧不存在这样的点。
分别计算一下,可以得到答案-7.5(点P1)或-15(点P2)。
(二)有理数比较大小有理数比较大小的基本性质①a>b ⇔ a-b>0②a=b ⇔ a-b=0③a<b ⇔ a-b<0④a>b ⇔ b<a⑤a>b,b>c ⇒ a>c根据基本性质利用数轴,运用数形结合的思想,把抽象的问题具体化,有助于我们的理解。
例题:已知a,b是有理数,a>0,b<0,a+b<0。
那么a,b,-a,-b四个数从小到大的顺序是。
苏教版初一数学数轴中的数形结合思想

数轴中的数形结合思想【链接方法】数学一开始就是研究“数”和“形”的,从古希腊时期起,人们就已试图把它们统一起来.数与形有着密切的联系,我们常用代数的方法研究图形问题;另一方面,也利用图形来处理代数问题,这种数与形相互作用,是一种重要的数学思想──数形结合思想.华罗庚说:“数缺形时少直观,形缺数时难入微”.利用数形结合思想解题的关键是建立数与形之间的联系,现阶段,数轴是联系数与形的桥梁,主要体现在:1.运用数轴直观地表示有理数(rational number);2.运用数轴形象地解释相反数(opposite number);3.运用数轴准确地比较有理数的大小;4.运用数轴恰当地解决与绝对值有关联的问题.【挑战例题】【例1】(1) (第17届江苏省竞赛题)数轴上有A 、B 两点,如果点A 对应的数是-2,且A 、B 两点的距离为3,•那么点B 对应的数是________.(2) (第15届江苏省竞赛题)在数轴上,点A 、B 分别表示-13和15,则线段AB 的中点所表示的数是________.【例2】(第12届“希望杯”邀请赛试题)如图,在数轴上有六个点,且AB=BC=CD=DE=EF,则与点C•所表示的数最接近的整数是( ). F E D C AA.-1B.0C.1D.2【例3】比较a 与1a的大小.【例4】(1)工作流水线上顺次排列5个工作台A 、B 、C 、D 、E ,一只工具箱应该放在何处,才能使工作台上操作机器的人取工具所走的路程最短?(2)如果工作台由5个改为6个,那么工具箱应如何放置能使6•个操作机器的人取工具所走的路程之和最短?(3)当流水线上有n 个工作台时,怎样放置工具箱最适宜?【提升能力】1. (2003年河南省竞赛题)如图,A 、B 、C 、D 、E 为数轴上的五个点,且AB=BC=CD=DE,则图中与P•点表示的数比较接近的一个数是( ).A.-1B.1C.3D.52.(2013年山东省菏泽市中考题)如图,数轴上的A 、B 、C 三点所表示的数分别是a 、b 、c ,其中AB=BC ,如果|a|>|b|>|c|,那么该数轴的原点O 的位置应该在( )A .点A 的左边B .点A 与点B 之间C .点B 与点C 之间D .点B 与点C 之间或点C 的右边3. (第15届江苏省竞赛题)如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数a,b,c,d,且d-2a=10,那么数轴的原点应是( ).A.A 点B.B 点C.C 点D.D 点4. (第18届江苏省竞赛题)数a 、b 、c 、d 所对应的点A 、B 、C 、D 在数轴上的位置如图所示,那么a+c 与b+d 的大小关系是( ).A.a+c<b+dB.a+c=b+dC.a+c>b+dD.不确定的 D C B A O(第3题) (第4题)5.(2007年江苏省镇江市中考题)一个机器人从数轴原点出发,沿数轴正方向,以每前进3步后退2步的程序运动,设该机器人每秒钟前进或后退1步,并且每步的距离为1个单位长,n x 表示第n 秒时机器人在数轴上的位置所对应的数,给出下列结论:①33=x ;②15=x ;③108104x x <;④20082007x x <.其中,正确的结论的序号是( )A .①、③B .②、③C .①、②、③D .①、②、④6.在数轴上表示数a 的点到原点的距离为3,则a-3=________.7.a 、b 、c 在数轴上的位置如图所示,则1a b -、1c b -、1a c-中最大的是________. c a b 0 (第7题) (第8题)8.如图,工作流程线上A 、B 、C 、D 处各有1名工人,且AB=BC=CD=1,现在工作流程线上 安放一个工具箱,使4个人到工具箱的距离之和为最短,•则工具箱的安放位置是__________.9. 已知a 、b 为有理数,且a >0,0<b ,0<+b a ,将四个数a ,b ,a -,b -按由小到大的顺序排列是________________________.10. (山东省竞赛题)已知数轴上表示负有理数m 的点是点M,那么在数轴上与点M 相距│m │个单位的点中,与原点距离较远的点对应的数是________.11.(2005年江西省中考题)如图所示,按下列方法将数轴的正半轴绕在一个圆(该 圆周长为3个单位长,且在圆周的三等分点处分别标上了数字0、1、2)上:先让原点与圆周上的数字0所对应的点重合,再将正半轴按顺时针方向绕在该圆周上,使数轴上1、2、3、4、…所对应的点分别与圆周上1、2、0、1、…所对应的点重合.这样,正半轴上的整数就与圆周上的数字建立了一种对应关系.(1)圆周上的数字a 与数轴上的数5对应,则a =______;(2)数轴上的一个整数点刚刚绕过圆周为正整数)n n (圈后,并落在圆周上数字1所对应的位置,这个整数是______(用含n 的代数式表示).12. (北京市“迎春杯”竞赛题)已知数轴上有A 、B 两点,A 、B 之间的距离为1,点A 与原点O 的距离为3,求所有满足条件的点B 与原点O 的距离的和.310513.已知两数a、b,如果a比b大,试判断│a│与│b│的大小.14.电子跳蚤落在数轴上的某点K0,第一步从K0向左跳1个单位到K1,第二步由K1向右跳2个单位到K2,第三步由K2向左跳3个单位到K3,第四步由K3向右跳4个单位到K4…,•按以上规律跳了100步时,电子跳蚤落在数轴上的点K100所表示的数恰是19.94,•试求电子跳蚤的初始位置K0点所表示的数.15.动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后,两点相距15个单位长度.已知动点A、B的速度比是1:4.(速度单位:单位长度/秒)(1)求出两个动点运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;(2)若A、B两点从(1)中的位置同时向数轴负方向运动,几秒后原点恰好处在两个动点正中间;(3)在(2)中A、B两点继续同时向数轴负方向运动时,另一动点C同时从B点位置出发向A运动,当遇到A后,立即返回向B点运动,遇到B点后立即返回向A点运动,如此往返,直到B追上A时,C立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始到停止运动,运动的路程是多少单位长度.。
七年级上册数学-数形结合——数轴压轴题

第6讲数形结合——数轴压轴题【板块一】数轴上的行程问题方法技巧此类问题一般已知起点、路程(距离)、速度,在运动后满足一定距离条件,求点运动后所表示的数.一般较为简单的问题可用算术方法先求运动时间,再求运动路程,从而得点表示的数,此类问题一般有多种情况,注意分类讨论,但这里建议采用设未知数,用绝对值表示数轴上两点间的距离的方法列式计算,一来比较简洁通用,二来不易掉解,这类问题也可能交换部分题设和结论反过来求,方法反之亦然.【例1】如图,数轴上A,B两点所对应的数分别为-8,4,A,B两点各自以一定的速度同时运动,且点A运动速度为2个单位/秒.(1)若A,B两点相向而行,在原点处相遇,求点B运动的速度(2)若A,B两点从开始位置上同时按照(1)中的速度向数轴正方向运动,多少秒钟后,A,B与原点距离相等?【例2】如图,A,B分别为数轴上的两点,点A对应的数为-10,点B对应的数90.现有一电子蚂蚁P 从A出发,以3个单位/秒的速度向右运动,同时另一只电子妈蚁Q恰好从B点出发,以5个单位/秒的速度向左运动,求经过多长时间两只电子妈蚁在数轴上相距20个单位?针对练习11.已知,在一条东西向的双轨铁路上理面驶来一快一慢两列火车,快车长AB=2(单位长度),慢车长CD =4(单位长度),设正在行驶途中的某一时刻,如图,以两车之间的某点O为原点,取向东方向为正方向面数轴,此时快车头A在数轴上表示的数是a,慢车头C在数轴上表示的数是b.若快车AB以6个单位长度/秒的速度向右匀速维续行驶,同时慢车CD以2个单位长度/秒的速度向左匀速继续行驶,且│a+8│与(b-16)2互为相反数.(1)求此时刻快车头A与慢车头C之间相距多少单位长度?(2)从此时刻开始算起,同再行驶多少秒钟,两列火车的车头A,C相距8个单位长度?(3)此时在快车AB上有一位爱动脑筋的七年级学生乘客P,他发现行驶中有一段时间t秒钟内,他的位置P到两列火车头A,C的距离和加上到两列火车超B,D的距离和是一个不变的值(即P A+PB+PC+PD为定值).你认为学生P发现的这一结论是否正确?若正确,求出这个时间及定值:若不正确,请说明理由.【板块二】数轴上的和差倍分问题方法技巧此类问题一般由一些已知点和未知点(或者已知点运动形成未知点)构成,它们的距离满足一定数量关系,如和差倍分等,根据条件计算未知点表示的数,此类问题一般可采用设未知数,用绝对值表示出数轴上两点间的距离,再根据距离之间的数量关系列方程计算的方法.【例3】如图,数轴上点A,B表示的数分别为-10和10,C为数轴上一点(1)若AC+BC=28,求C点表示的数;(2)若2AC=3BC,求C点表示的数.【例4】如图,在数轴上A点表示数a,B点表示数b,AB表示A点和B点之间的距离,且a、b满足|a+3|+(b+3a)2=0,设P从A点出发以3个单位每秒向右运动,点Q同时从B点出发以2个单位每秒向左运动,当AP+BQ=2PQ时,求运动时间.OA【分析】设时间为t秒,由绝对值和平方的非负性先求出A、B两点表示的数,然后用含t的式子表示出P、Q两点表示的数,进而表示出AP、BQ、和PQ,根据AP+BQ=2PQ建立方程求解.针对练习21.数轴上,A 、B 两点表示的数分别为-4和3.(1)点C 在数轴上,点C 到A 、B 两点的距离之和为11,求点C 在数轴上所对应的数;(2)若A 点、B 点同时沿数轴向正方向运动,A 点的速度是B 点速度的2倍,且3秒后,2OA =OB ,求点B 的速度.【板块三】数轴上的动点定值问题方法技巧 设参计算法设动点表示的数(若是行程问题一般设运动时间),从而表示出线段长(两点间的距离),计算可解. 【例5】如图,在数轴上A 、B 、C 三点表示的数分别为-10、10、50,A 、B 、C 三点同时运动,点A 以1个单位每秒的速度向左运动,点B 、C 分别以2个单位、5个单位每秒的速度向右运动,请问:BC -AB 的值是否随时间t 的变化而变化?若变化,请说明理由;若不变,请求其值.CBA例6 如图,数轴上A 、B 两点所对应的数分别为-8、4, A 、B 两点分别以2个单位/秒和1个单位/秒的速度同时出发,向数轴负方向运动,与此同时,C 点从原点出发也向数轴负方向运动,且 C 点总在A 、B 两点之间,并在运动过程中始终有BC AC =12,设运动t 秒钟后,点A 、B 、C 运动后的对应点分别为A 1、B 1、C 1 下列两个结论:①AA 1+BB 1的值不变;②CC 1AA 1的值不变 ,请选择正确的结论,并求其值.例7 如图,点A 在数轴上表示的数为-10,C 、D 为数轴上两个动点,点D 在点C 的右边,且CD =16,M 为AD 中点,N 为AC 的中点,当C 、D 运动时, M 、N 两点的距离即M N 的长是否改变?若不变求出其值;若变化说明理由.DMN﹣10A C针对练习31. 如图,已知数轴上有A 、B 、C 三个点,他们表示的数分别为是18,8,-10 (1)填空:AB = ,BC =A CB 188﹣10(2)若点A 以每秒1个单位长度的速度向右运动,同时,点B 和点C 分别以每秒2个单位长度和5个单位长度的速度向左运动,试探索:BC -AB 的值是否随着时间t 的变化而变化?请说明理由;(3)现有动点P ,Q 都从A 点出发,点P ,以每秒1个单位长度的速度向终点C 移动;当点P 移动到B 点时,点Q 才从A 出发,并以每秒3个单位的速度向左移动,且当点P 到达C 点时,点Q 就停止移动,设点P ,移动的时间为t 秒,试用含t 的代数式表示P ,Q 两点间的距离。
数形结合思想与数轴
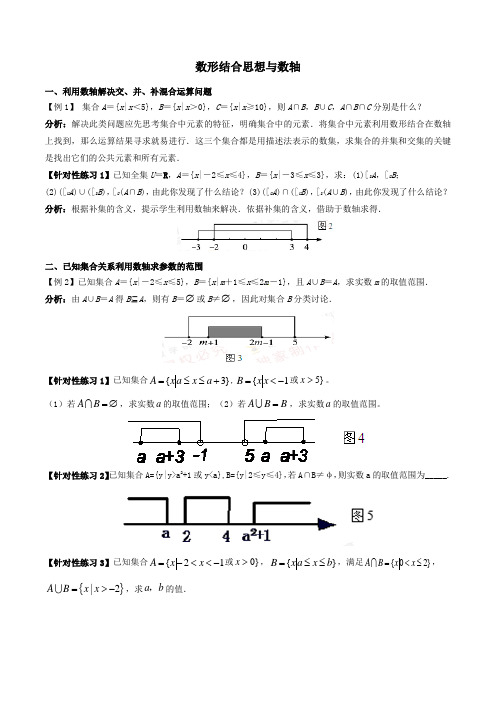
数形结合思想与数轴一、利用数轴解决交、并、补混合运算问题【例1】 集合A ={x |x <5},B ={x |x >0},C ={x |x ≥10},则A ∩B ,B ∪C ,A ∩B ∩C 分别是什么? 分析:解决此类问题应先思考集合中元素的特征,明确集合中的元素.将集合中元素利用数形结合在数轴上找到,那么运算结果寻求就易进行.这三个集合都是用描述法表示的数集,求集合的并集和交集的关键是找出它们的公共元素和所有元素.【针对性练习1】已知全集U =R ,A ={x |-2≤x ≤4},B ={x |-3≤x ≤3},求:(1)∁U A ,∁U B ;(2)(∁U A )∪(∁U B ),∁U (A ∩B ),由此你发现了什么结论?(3)(∁U A )∩(∁U B ),∁U (A ∪B ),由此你发现了什么结论? 分析:根据补集的含义,提示学生利用数轴来解决.依据补集的含义,借助于数轴求得.二、已知集合关系利用数轴求参数的范围【例2】已知集合A ={x |-2≤x ≤5},B ={x |m +1≤x ≤2m -1},且A ∪B =A ,求实数m 的取值范围. 分析:由A ∪B =A 得B ⊆A ,则有B =∅或B ≠∅,因此对集合B 分类讨论.【针对性练习1】已知集合}3{+≤≤=a x a x A ,1{-<=x x B 或}5>x 。
(1)若∅=B A ,求实数a 的取值范围;(2)若B B A = ,求实数a 的取值范围。
【针对性练习2】已知集合A={y|y>a 2+1或y<a},B={y|2≤y≤4},若A∩B≠φ,则实数a 的取值范围为_____.【针对性练习3】已知集合12{-<<-=x x A 或}0>x ,}{b x a x B ≤≤=,满足}20{≤<=x x B A , {}|2A B x x =>-,求a b ,的值.。
数形结合思想在数轴教学中的体现

数形结合思想在数轴教学中的体现
《数学课程标准》中明确指出:“通过义务教育阶段的数学学习,学生能够获得适应未来社会生活和进一步发展所必需的重要数学知识(包括数学事实、数学活动经验)以及基本的数学思想方法和必要的应用技能。
”
数形结合思想是重要的数学思想。
数轴是数形结合的产物,它是一个重要概念,后续的直角坐标系也是以它为基础的。
借助数轴可以加深对正数、0、负数的认识,利用数轴这个工具,从数形结合观点出发,可以研究相反数和绝对值、有理数大小比较以及有理数的运算等内容。
数轴 平面直角坐标系 数形结合

数轴平面直角坐标系数形结合
在数学学习中,数轴和平面直角坐标系是两个常见的工具。
除了在数学中使用外,它们还可以与几何形状相结合,帮助我们更好地理解数学概念。
数轴是一条直线,用于表示数字和它们的关系。
它可以帮助我们理解正数和负数之间的关系,以及数字的大小和位置。
例如,我们可以使用数轴来解决一些基本的数学问题,如加减法和绝对值问题。
平面直角坐标系是一个二维平面,由水平和竖直轴组成,分别称为x轴和y轴。
它们交叉于原点(0,0),它们的正方向是向右和向上。
平面直角坐标系可以帮助我们更好地理解几何形状和物体的位置。
例如,我们可以使用平面直角坐标系来解决几何问题,如计算三角形的面积和寻找两个点之间的距离。
当数轴和平面直角坐标系相结合时,我们可以更好地理解数学概念和几何形状。
例如,我们可以使用平面直角坐标系和数轴来计算平面上两个点之间的距离。
我们可以通过将两个点绘制在平面直角坐标系上,然后使用勾股定理来计算它们之间的距离。
我们还可以使用数轴来解决简单的方程,如求解x的值使得|x-3| = 5。
在数学学习中,数轴和平面直角坐标系是非常有用的工具,因为它们可以帮助我们更好地理解数学概念和几何形状。
通过使用数轴和平面直角坐标系,我们可以更轻松地解决数学问题,更好地理解几何形状,从而更好地掌握数学知识。
- 1 -。
第1课时 实数及数形结合—数轴的应用

第1课时 实数及数形结合——数轴的应用【考纲要求】1.理解有理数、无理数和实数的概念,会用数轴上的点表示有理数.2.借助数轴理解相反数和绝对值的意义,会求一个数的相反数、倒数与绝对值.3.理解平方根、算术平方根、立方根的概念,会求一个数的算术平方根、平方根、立方根.4.理解科学记数法、近似数与有效数字的概念,能按要求用四舍五入法求一个数的近似值,能正确识别一个数的有效数字的个数,会用科学记数法表示一个数.5.熟练掌握实数的运算,会用各种方法比较两个实数的大小.【自主测试】1.-2的倒数是( )A .-12B ..12C .-2D .2 2.-2的绝对值等于( )A .2B .-2C .12D .-123.下列运算正确的是( )A .-|-3|=3B .⎝⎛⎭⎫13-1=-3 C .9=±3 D .3-27=-3 4.2012年世界水日主题是“水与粮食安全”.若每人每天浪费水0.32 L ,那么100万人每天浪费的水,用科学记数法表示为( )A .3.2×107 LB .3.2×106 LC .3.2×105 LD .3.2×104 L5.已知实数m ,n 在数轴上的对应点的位置如图所示,则下列判断正确的是( )A .m >0B .n <0C .mn <0D .m -n >06.计算:|-5|+16-32【考点分析】考点1 实数的分类例1 四个数-5,-0.1 ,12, 3 中为无理数的是( ) A .-5 B .-0.1 C .12D . 3 触类旁通1 在实数5,37,2,4中,无理数是( ) A .5 B .37C . 2D . 4考点2 相反数、倒数、绝对值与数轴例2 (1)-15的倒数是__________; (2)(-3)2的相反数是( )A .6B .-6C .9D .-9(3)实数a ,b 在数轴上的位置如图所示,化简|a +b |+b -a 2=__________.触类旁通2 下列各数中,相反数等于5的数是( )A .-5B .5C .-15D .15 考点3 平方根、算术平方根与立方根例3 (1)(-2)2的算术平方根是( )A .2B .±2C .-2D . 2(2)实数27的立方根是__________.触类旁通3 4的平方根是( )A .2B .±2C .16D .±16考点4 科学记数法与近似数例4 无锡是全国重点旅游城市,2018年实现旅游总收入约为26 000 000万元,数据26 000 000 用科学计数法可表示为( )A. 0.26×108B. 2.6×108C. 26×106D. 2.6×107触类旁通4 某种细胞的直径是5×10-4毫米,这个数是( )A .0.05毫米B .0.005毫米C .0.000 5毫米D .0.000 05毫米考点5 非负数性质的应用例5 若实数x ,y 满足x -2+(3-y )2=0,则代数式xy -x 2的值为__________.触类旁通5 若|m -3|+(n +2)2=0,则m +2n 的值为 ( )A .-4B .-1C .0D .4考点6 实数的运算例6 计算:(1) 2-1+3cos 30°+|-5|-(π-2 011)0.(2) (-1)2 011-⎝⎛⎭⎫12-3+⎝⎛⎭⎫cos 68°+5π0+|33-8sin 60°|.考点7 实数的大小比较例7 比较2.5,-3,7的大小,正确的是( ) A .-3<2.5<7 B .2.5<-3<7 C .-3<7<2.5 D .7<2.5<-3触类旁通6 在-6,0,3,8这四个数中,最小的数是( )A .-6B .0C .3D .8考点8 数形结合思想——数轴的应用例8 (1)实数a ,b ,c 在数轴上位置如图,则代数式2a a b c a b c +++---的值等于____.(2)如图,在数轴上,点A 、B 分别表示数1、-2x +3.①求x 的取值范围;②数轴上表示数-x +2的点应落在 .A .点A 的左边B .线段AB 上C .点B 的右边【经典考题】1.5的相反数是( )A . 15B . -15C .5D .-5 2.在下列四个实数中,最大的数是( )A . 3-B . 0C . 32D . 343.地球与月球之间的平均距离大约为384 000 km ,384 000用科学记数法可表示为( )xA .33.8410⨯B .43.8410⨯C .53.8410⨯D .63.8410⨯4. ()217-÷的结果是( )A .3B .3-C .13D .13- 5.一个罐头的质量为2.026kg ,用四舍五入法将2.026精确到0.01的近似值为( )A .2B .2.0C .2.02D .2.036.计算 (1): 20(3)2(2)π+--- (2): 2129()22-+- (3): ()0143π-+--【预测试题】1.下列各数中,最小的数是( )A .0B .1C .-1D .- 22.若|a |=3,则a 的值是( )A .-3B .3C .13D .±3 3.下列计算正确的是( )A .(-8)-8=0B .⎝⎛⎭⎫-12×(-2)=1C .-(-1)0=1D .|-2|=-24.如图,数轴上A ,B 两点对应的实数分别为1和3,若点A 关于点B 的对称点为C ,则点C 所表示的实数是( )A .23-1B .1+ 3C .2+ 3D .23+15. (1)实数12的倒数是____. (2)写出一个比-4大的负无理数__________.6.若将三个数-3,7,11表示在数轴上,其中能被如图所示的墨迹覆盖的数是__________.7.定义一种运算☆,其规则为a ☆b =1a +1b,根据这个规则,计算2☆3的值是__________. 8.如图,物体从点A 出发,按照A →B (第1步)→C (第2步)→D →A →E →F →G →A →B →…的顺序循环运动,则第2 012步到达点________处.9.计算:|-2|+(-1)2 012-(π-4)0.。
数轴 平面直角坐标系 数形结合

数轴平面直角坐标系数形结合
数轴
数轴是数学中一个重要的概念,它是指一个一维空间中的直线,该直线上的点都对应
着一个实数。
通常来说,数轴上选取一个点作为0点,然后向左右两侧分别用正数和负数
来表示实数。
数轴可以帮助我们更好地理解数学概念,比如说绝对值、正负数、数的大小关系等
等。
平面直角坐标系是指在平面上建立起了一个直角坐标系,任意一个点都可以用其横纵
坐标的数值来唯一地表示。
在平面直角坐标系中,横坐标通常表示横向位移,纵坐标表示
纵向位移。
平面直角坐标系具有广泛的应用,比如说在几何学中,它被用于表示图形的位置和大
小等信息;在物理学中,它被用于表示物体在空间中的位置,速度和加速度等信息。
数形结合
数形结合是指将数学的抽象概念与生动形象的图形相结合,以便更好地理解数学概念,从而更好地解决数学问题。
数形结合具有很多实际应用,比如说在几何学中,数形结合被广泛应用,可以帮助我
们更好地理解图形的性质和定理;在物理学中,数形结合被用来解决各种物理问题,比如
说运动学和力学问题。
总结
数轴、平面直角坐标系和数形结合都是数学中非常重要的概念和工具,它们在解决数
学问题和实际应用中都起到了重要的作用。
学好这些概念不仅可以帮助我们更好地理解数
学知识,而且可以帮助我们在实际应用中更好地解决问题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
一.数形结合谈数轴
一、详解知识点
数学是研究数和形的学科,在数学里数和形是有密切联系的。
我们常用代数的方法来处理几何问题;反过来,也借助于几何图形来处理代数问题,寻找解题思路,这种数与形之间的相互作用叫数形结合,是一种重要的数学思想。
运用数形结合思想解题的关键是建立数与形之间的联系,现阶段数轴是数形结合的有力工具,主要体现在以下几个方面: 1、利用数轴能形象地表示有理数; 2、利用数轴能直观地解释相反数; 3、利用数轴比较有理数的大小;
4、利用数轴解决与绝对值相关的问题。
二、知识点反馈
1、利用数轴能形象地表示有理数;
例1:已知有理数a 在数轴上原点的右方,有理数b 在原点的左方,那么( ) A .b ab < B .b ab > C .0>+b a D .0>-b a 拓广训练:
1、如图b a ,为数轴上的两点表示的有理数,在a b b a a b b a ---+,,2,中,负数的个数有( )
A .1
B .2
C .3
D .4
2、把满足52≤<a 中的整数a 表示在数轴上,并用不等号连接。
2、利用数轴能直观地解释相反数;
例2:如果数轴上点A 到原点的距离为3,点B 到原点的距离为5,那么A 、B 两点的距离为 。
拓广训练:
1、在数轴上表示数a 的点到原点的距离为3,则._________3=-a
2、已知数轴上有A 、B 两点,A 、B 之间的距离为1,点A 与原点O 的距离为3,那么所有满足条件的点B 与原点O 的距离之和等于 。
3、利用数轴比较有理数的大小;
例3:已知0,0<>b a 且0<+b a ,那么有理数b a b a ,,,-的大小关系是 。
(用“<”号连接) 拓广训练:
若0,0><n m 且n m >,比较m n n m n m n m --+--,,,,的大小,并用“>”号连接。
例4:已知5<a ,比较a 与4的大小
拓广训练:
已知3->a ,试讨论a 与3的大小 。
4、利用数轴解决与绝对值相关的问题。
例5: 有理数c b a ,,在数轴上的位置如图所示,式子c b b a b a -++++化简结果为( )
A .c b a -+32
B .c b -3
C .c b +
D .b c - 拓广训练:
1、有理数c b a ,,在数轴上的位置如图所示,则化简c c a b b a ------+11的结果为 。
2、已知有理数c b a ,,在数轴上的对应的位置如下图:则b a c a
c -+-+-1化简后的结果是( )
A .1-b
B .12--b a
C .c b a 221--+
D .b c +-21 三、培优训练
1、已知是有理数,且()()
012
12
2
=++-y x ,那以y x +的值是( )
A .
21 B .23 C .21或23- D .1-或2
3 2、如图,数轴上一动点A 向左移动2个单位长度到达点B ,再向右移动5个单位长度到达
点C .若点C 表示的数为1,则点A 表示的数为( )
A.7 B.3 C.3- D.2-
3、如图,数轴上标出若干个点,每相邻两点相距1个单位,点A 、B 、C 、D 对应的数分别是整数d c b a ,,,且102=-a d ,那么数轴的原点应是( ) A .A 点 B .B 点 C .C 点 D .D 点
4、数d c b a ,,,所对应的点A ,B ,C ,D 在数轴上的位置如图所示,那么c a +与d b +的大小关系是( )
A .d b c a +<+
B .d b c a +=+
C .d b c a +>+
D .不确定的 5、设11++-=x x y ,则下面四个结论中正确的是( )
A .y 没有最小值
B .只一个x 使y 取最小值
C .有限个x (不止一个)使y 取最小值
D .有无穷多个x 使y 取最小值 6、在数轴上,点A ,B 分别表示31-
和5
1
,则线段AB 的中点所表示的数是 。
7、已知d c b a ,,,为有理数,在数轴上的位置如图所示:且,64366====d c b a 求
c b a b
d a -+---22323的值。
8、(南京市中考题)(1)阅读下面材料:
点A 、B 在数轴上分别表示实数b a ,,A 、B 两点这间的距离表示为AB ,当A 、B 两点中有一点在原点时,不妨设点A 在原点,如图1,b a b OB AB -===;当A 、B 两点都不在原点时,
①如图2,点A 、B 都在原点的右边
a b a b OA OB AB =-=-=-=②如图3,点A 、B 都在原点的左边()b
a a
b a b OA OB AB -=---=-=-=;
③如图4,点A 、B 在原点的两边()b a b a b a OB OA AB -=-+=+=+=。
综上,数轴上A 、B 两点之间的距离b a AB -=。
(2)回答下列问题:
①数轴上表示2和5两点之间的距离是 ,数轴上表示-2和-5的两点之间的距离是 ,数轴上表示1和-3的两点之间的距离是 ;
②数轴上表示x 和-1的两点A 和B 之间的距离是 ,如果2=AB ,那么x 为 ;
③当代数式21-++x x 取最小值时,相应的x 的取值范围是 ; ④求1997321-+⋅⋅⋅+-+-+-x x x x 的最小值。
B
A
O
B
(A)
O o a B
A
O
o。
