微积分三大中值定理详解共54页
微分中值定理【高等数学PPT课件】

可导,且
证:设辅助函数
显然 在 因此至少存在
上满足罗尔定理条件, 使得
推广: 存在
使
例3. 若
可导, 试证在其两个零点间一定有 的零点.
的零点. 的零点.
(2) 提示: 欲证:
使
只要证
亦即
二、拉格朗日中值定理
满足: (1) 在区间 [ a , b ] 上连续
(2) 在区间 ( a , b ) 内可导
证: 在 I 上任取两点
日中值公式 , 得
由 的任意性知, 在 I 上为常数 .
例1. 证明等式 证: 设
由推论可知
(常数)
令x=0,得
又 经验: 欲证
故所证等式在定义域
上成立.
时
只需证在 I 上
自证:
例2. 证明不等式 证: 设 中值定理条件, 因此应有
即 因为
故 推论2: 若函数f 和g 均在区间上可导,且
证: M 和最小值 m .
若M=m,则 因此
故在[ a , b ]上取得最大值
若 M > m , 则 M 和 m 中至少有一个与端点值不等,
不妨设
则至少存在一点
使
则由费马引理得
注意: 1) 定理条件条件不全具备, 结论不一定成立. 例如,
2) 定理条件只是充分的. 本定理可推广为 在 ( a , b ) 内可导, 且
至少存在一点
使
证: 问题转化为证
作辅助函数
显然 ,
在 [ a , b ] 上连续 , 在 ( a , b ) 内可导, 且 由罗尔定理知至少存在一点
思路: 利用逆向思维找即出定一理个结满论足成罗立尔.定证理毕条件的函数
拉格朗日中值定理的有限增量形式:
微分中值定理PPT课件

f (1) f (0) 10
f () 2
f ( x) ( x 2 )
x .
设 g(x) x2 ,
则 f ( x), g( x) 在[0,1]上满足柯西中值定理的条件,
在(0,1)内至少存在一点, 有
f (1) f (0) f ()
10
2
即 f () 2[ f (1) f (0)].
第23页/共42页
0
由
的任意性知,
在 I 上为常数 .
经验: 欲证 x I 时 f (x) C0, 只需证在 I 上 f (x) 0,
且 x0 I , 使 f (x0 ) C0.
第16页/共42页
例5 证明 arcsin x arccos x (1 x 1). 2
证 设 f ( x) arcsin x arccos x, x [1,1]
f (b) f (a) f ' ()(b a) 成立.
注意 : 与罗尔定理相比条件中去掉了 f (a) f (b).
结论亦可写成 f (b) f (a) f (). ba
第12页/共42页
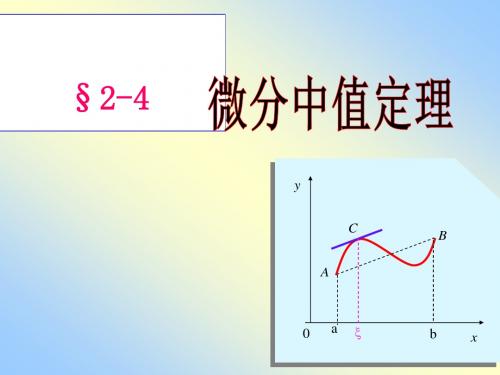
y 几何解释:
在曲线弧 AB 上至少有
一点 C ,在该点处的切
A
C
y f (x)
M
B
N
D
线平行于弦 AB.
第14页/共42页
注意:
1. Lagrange定理是罗尔定理的推广.
2.等价形式 f (b) f (a) f ( ).
ba 3.设 f ( x)在 (a, b)内可导, x0 , x0 x (a, b), 则有
f ( x0 x) f ( x0 ) f ( x0 x) x (0 1).
即 f '() 0
中值定理的三个公式

中值定理的三个公式中值定理是微积分中的一个重要定理,用于研究函数的性质和推导函数的一些特征。
中值定理有三个不同的形式,罗尔(Rolle)定理、拉格朗日(Lagrange)中值定理和柯西(Cauchy)中值定理。
下面我将详细介绍这三个公式。
1.罗尔定理:罗尔定理是拉格朗日中值定理的一种特殊情况。
设函数$f(x)$在区间$[a,b]$上连续,在开区间$(a,b)$上可导,且满足$f(a)=f(b)$,则在开区间$(a,b)$内,存在至少一点$c$,使得$f'(c)=0$。
简而言之,如果一个函数在两个端点的函数值相等且在区间内可导,那么在该区间内一定存在至少一个导数为零的点。
2.拉格朗日中值定理:拉格朗日中值定理是微积分中的一个重要定理,它给出了一个函数在一个闭区间上存在一个导数与函数在区间两个端点的斜率相等的点的位置。
设函数$f(x)$在闭区间$[a, b]$上连续,在开区间$(a, b)$上可导,那么在$[a, b]$之间有一个点$c$,使得$f'(c) = \frac{f(b)-f(a)}{b-a}$。
换句话说,如果一个函数在闭区间内连续且在开区间内可导,那么在这个闭区间内至少存在一个点,其导数等于函数在这个区间两个端点的函数值斜率。
3.柯西中值定理:柯西中值定理是微积分中的一个重要定理,它给出了两个函数在一个闭区间上存在一个导数与函数在区间两个端点的函数值斜率之差的商相等的点的位置。
设函数$f(x)$和$g(x)$在闭区间$[a, b]$上连续,在开区间$(a, b)$上可导,且$g'(x)\neq 0$ ,那么在$[a, b]$之间有一个点$c$,使得$\frac{f'(c)}{g'(c)}=\frac{f(b)-f(a)}{g(b)-g(a)}$。
总结一下,如果两个函数在闭区间内连续且在开区间内可导,且其中一个函数的导数不为零,那么在这个闭区间内至少存在一个点,其导数与两个函数的函数值斜率之差的商相等。
微分的中值定理

微分的中值定理
微分的中值定理是微积分中的一个重要定理,它是研究函数变化的基础。
在微分学中,中值定理有三种形式:罗尔定理、拉格朗日中值定理和柯西中值定理。
罗尔定理是指,如果一个函数在区间的两个端点处取同样的值,那么在这个区间内至少存在一个点,使得该点的导数为0。
这个定理常常被用于证明函数在某个区间内存在极值点。
拉格朗日中值定理是指,如果一个函数在区间内是可导的,那么在这个区间内至少存在一个点,使得该点的导数等于区间两个端点的函数值之差除以区间长度。
这个定理常被用于证明某些函数的性质,如可凸性和上凸性等。
柯西中值定理是指,如果两个函数在某个区间内是可导的且其中一个函数在某个点的导数不为0,那么在这个区间内至少存在一个点,使得两个函数在该点的导数之比等于两个函数在该点的函数值之比。
这个定理常被用于证明函数的单调性。
这些中值定理不仅仅是微积分理论的重要基础,也是许多实际问题的解决方法。
在物理、经济学和工程学等领域中,中值定理经常被用于分析和解决实际问题。
- 1 -。
微积分x02-4中值定理
f (x)在 x 处于可微:
△ydy=f
(x )· △x
f (x)在 [a, b] 上满足 拉格朗日定理条件:
△y=
要求:| △x |很小,
且f (x)0
f ( x+ △x )· △x
要求: △x有限.
拉格朗日中值公式又称有限增量公式.
注:拉氏公式的几种形式
f (b) f (a) f ( ) ba
而 (x) f ( x) f (b) f (a) , ba 所以 ( ) f ( ) f (b) f (a) =0 由此得 f ( )
f (b) f (a) . ba
ba
即 f (b)f (a)=f ( )(ba).
证法二
证 设F ( x) [ f (b) f (a)]x f ( x)(b a)
f ( x) a1 x a2 x an x ,
2 n
则 f(0)=f(1)=0,从而存在0<<1,使得
f ( ) 0.
'
f ( ) a1 2a2 nan
'
n1
0.
2. 拉格朗日
(Lagrange) 中值定理.
y
拉格朗日中值定理 (微分中值定理): 若函数 f (x)满足
f ( x ) f (0) f ( )( x 0), (0 x )
x ln(1 x ) , 1 x x x, 1 x 1
x 即 ln(1 x ) x . 1 x
• 例3 试证 |sin x -sin y| | x - y |
所以 f ( x)
2
2
第三章微分中值定理资料

当 F ( x) x, F (b) F (a) b a, F ( x) 1,
f (b) f (a) f () F (b) F (a) F ()
f (b) f (a) f (). ba
例4 设函数f ( x)在[0,1]上连续, 在(0,1)内可导, 证明 :
F ( x) 满足罗尔定理的条件,
则在(a, b)内至少存在一点, 使得 F () 0.
即 f () f (b) f (a) 0 ba
或 f (b) f (a) f ()(b a).
拉格朗日中值公式
注意:拉氏公式精确地表达了函数在一个区间上的 增量与函数在这区间内某点处的导数之间的关系.
)成立. )
几何解释:
y
在曲线弧AB上至少有 一点C(F (), f ()),在 该点处的切线平行于 A
X F(x)
C
Y
f (x)
M
B
N
D
弦AB.
o F(a) F(1) F(x)
F (2 )F (b)
x
证 作辅助函数
( x) f ( x) f (a) f (b) f (a) [F ( x) F (a)]. F(b) F(a)
即 f '() 0
例如, f ( x) x2 2x 3 ( x 3)(x 1).
在[1,3]上连续, 在(1,3)上可导, 且 f (1) f (3) 0,
f ( x) 2( x 1), 取 1, (1 (1,3)) f () 0.
以上两个都可说明问题.
练习题
一、填空题: 1、函数 f ( x) x 4 在区间[1,2]上满足拉格朗日中值 定理,则ξ =_______. 2、设 f ( x) ( x 1)( x 2)( x 3)( x 4) , 方 程 f ( x) 0 有____________个根,它们分别在区间 _____________上. 3、罗 尔 定 理 与 拉 格 朗 日 定 理 之 间 的 关 系 是 _________________. 4 、微 分中 值定 理精 确地 表 达 函 数 在 一 个区 间上 的 _______与函数在这区间内某点处的_______之间 的关系. 5、如果函数 f ( x)在区间I 上的导数__________,那 么 f ( x)在区间I 上是一个常数.
中值定理详细讲解

则 (a,b),使等式
f '() g'()
f (b) g(b)
f (a) g(a)
成立.
例7 设f(x)在[a,b]连续,在(a,b)可导,证 (a,b) 使eab[ f (b) f (a)] (eb ea )e f ( )
四、小结
罗尔定理、拉格朗日中值定理及柯西中值定理 之间的关系;
函数的极大值与极小值统称为极值,使函数取得 极值的点称为极值点.
例:
若
lim
xa
f
(x) f (a) (x a)2
1 ,则f (x)在x 2
a处取的( A
)
(A)极大值; (B)极小值;
定理 4.1 (费马定理) 设f(x)在x0取得极值,若f (x)在x0可导,则f (x0 ) 0
定义 : 满足f(x0 ) 0的点x0称为驻点
证 f (x) arcsin x arcsin 1 x2在[0,1]连续
f (x)
1 ( 1 x2
1 x2
2
2x 1 x2
)
0.
x (0,1)
f (x) C, x [0,1]
又f (0) arcsin 0 arcsin 1 0 , 22
即C . 2
arcsin x arccos x . 2
二、试证明对函数 y px 2 qx r 应用拉氏中值定理
时所求得的点 总是位于区间的正中间 . 三、证明等式arcsin 1 x2 arctan x
1 x2 2 ( x (0,1) ) . 四、设a b 0 ,n 1 ,证明
nb n1 (a b) a n bn na n1 (a b) .
证:作辅助函数
F(x) f (x) f (a) f (b) f (a) (x a). ba
微积分三大中值定理详解共54页文档

6
、
露
凝
无
游
氛
,
天
高
风
景
澈
。
7、翩翩新 来燕,双双入我庐 ,先巢故尚在,相 将还旧居。
8
、
吁
嗟
身
后
名
,
于
我
若
浮
烟
。
9、 陶渊 明( 约 365年 —427年 ),字 元亮, (又 一说名 潜,字 渊明 )号五 柳先生 ,私 谥“靖 节”, 东晋 末期南 朝宋初 期诗 人、文 学家、 辞赋 家、散
拉
60、生活的道路一旦选定,就要勇敢地 走到底 ,决不 回头。 ——左
1
0
、
倚
南
窗
以
寄
傲
,
审
容
膝
之
易
安
。
56、书不仅是生活,而且是现在、过 去和未 来文化 生活的 源泉。 ——库 法耶夫 57、生命不可能有两次,但许多人连一 次也不 善于度 过。— —吕凯 特 58、问渠哪得清如许,为有源头活水来 。—— 朱熹 59、我的努力求学没有得到别的好处, 只不过 是愈来 愈发觉 自己的 无知。 ——笛 卡儿
文 家 。汉 族 ,东 晋 浔阳 柴桑 人 (今 江西 九江 ) 。曾 做过 几 年小 官, 后辞 官 回家 ,从 此 隐居 ,田 园生 活 是陶 渊明 诗 的主 要题 材, 相 关作 品有 《饮 酒 》 、 《 归 园 田 居 》 、 《 桃花 源 记 》 、 《 五 柳先 生 传 》 、 《 归 去来 兮 辞 》 等 。
中值定理_精品文档

中值定理1. 简介中值定理是微积分中的一个重要定理,它与函数的导数和函数在一个闭区间上的平均值有关。
中值定理包括了拉格朗日中值定理和柯西中值定理。
2. 拉格朗日中值定理拉格朗日中值定理是中值定理中的一种形式,描述了函数导数的性质。
定理的表述如下:定理1(拉格朗日中值定理): 设函数f(x)在闭区间[a,b]上连续,在开区间(a,b)上可导。
则在(a,b)内存在一个点c,使得f(b)−f(a)=f′(c)(b−a)。
定理1的几何意义是:在闭区间[a,b]上,存在一个点c,使得函数的切线斜率等于函数在闭区间上的平均改变率。
从图像上看,这相当于函数曲线上的某一点,其切线与函数曲线与线段AB的斜率相等。
拉格朗日中值定理的一个重要推论是费马定理,其表述如下:定理2(费马定理):设函数f(x)在点x=c处取得了极值,并且在x=c处可导,那么f′(c)= 0。
也就是说,在一个连续且可导的函数f(x)的局部极值点上,函数的导数等于零。
3. 柯西中值定理柯西中值定理也是中值定理中的一种形式,它是拉格朗日中值定理的推广形式。
柯西中值定理的表述如下:定理3(柯西中值定理):设函数f(x)和g(x)在闭区间[a,b]上连续,并且在开区间(a,b)上可导,且g′(x)eq0。
那么,存在一个点c,使得$\\frac{f(b)-f(a)}{g(b)-g(a)} = \\frac{f'(c)}{g'(c)}$。
定理3的几何意义是:在闭区间[a,b]上,存在一个点c,使得函数曲线上的切线与函数曲线的斜率的比值等于两个函数之间的平均改变率的比值。
4. 应用中值定理在微积分中有广泛的应用。
下面介绍几个常见的应用场景:4.1 判断函数在某个区间上的增减性通过中值定理,可以判断函数在某个区间上的增减性。
如果函数在某个区间上的导数恒为正,则函数在该区间上单调递增;如果导数恒为负,则函数在该区间上单调递减。
4.2 寻找函数极值点利用拉格朗日中值定理的推论——费马定理,可以寻找函数的极值点。
微积分中的积分中值定理

微积分中的积分中值定理积分中值定理是微积分中的一个重要定理,指在一个函数在区间[a,b]上积分的平均值等于这个函数在区间[a,b]上的某一点的函数值。
积分中值定理起源于求平均速度的问题,随着时间的推移,它逐渐成为微积分学中的一个重要定理,被广泛应用于各种物理问题和工程问题中。
定理描述积分中值定理主要有三种形式,分别为第一型,第二型和第三型。
这些形式的积分中值定理都是基于微积分的基本定理的。
第一型:如果f(x)是在[a,b]上可积的函数,且b>a,则至少存在一个数字c∈[a,b],使得$$\int_{a}^{b}f(x)dx=f(c)\cdot(b-a)$$第二型:如果f(x)和g(x)是在[a,b]上可积的函数,且g(x)不等于0,则至少存在一个数字c∈[a,b],使得$$\int_{a}^{b}f(x)g(x)dx=f(c)\cdot\int_{a}^{b}g(x)dx$$第三型:如果f(x)是在[a,b]上连续的函数,且存在一个数字k,使得对于区间[a,b]上的任意一点x,都有|f(x)|<=k,则至少存在一个数字c∈[a,b],使得$$\int_{a}^{b}f(x)dx=f(c)\cdot(b-a)$$其中,第一型积分中值定理是积分学中最基本的积分中值定理,第二型积分中值定理可以用于证明微积分基本定理,第三型积分中值定理则是积分中值定理的一个推论。
理解积分中值定理的物理意义积分中值定理的物理意义可以通过一个具体的例子来说明。
我们知道,物体在垂直下落的过程中,其速度可以用时间t的函数v(t)表示。
假设物体下落的高度为h,则其速度v(t)可以表示为$$v(t)=\frac{dh}{dt}$$因此,物体下落的时间t和高度h之间的关系可以表示为$$h=\int_{0}^{t}v(t)dt$$由积分中值定理,我们知道存在一个时刻t0,使得$$h=v(t_0)\cdot t_0$$即物体下落的平均高度等于某一时刻的高度,这也说明了物体下落的速度在不同时间段内是不同的。
微分中值定理

中值定理
罗尔中值定理
推广
拉格朗日中值定理
泰勒公式
柯西中值定理
(第三节)
研究函数性质及曲线性态 应用
利用导数解决实际问题
第一节
第三章
中值定理
一、罗尔( Rolle )定理
二、拉格朗日( Lagrange )中值定理 三、柯西(Cauchy)中值定理
本章将讨论导数的更多应用, 需要先介绍一些理论基础: 微分中值定理
v拉格朗日中值定理 如果函数f(x)在闭区间[a b]上连续 在开区间(a b)内
可导 那么在(a b)内至少有一点 使得 f(b)f(a)f ()(ba)
•有限增量公式
f(xx)f(x)f (xqx)x (0<q <1)
yf (xqx)x (0<q <1)
注: dyf (x)x是函数增量y的近似表达式
1.费马引理
y f (x)
且 f (x0 ) 存在,若 x U (x0 ) 有 f (x) f (x0 ) , ( f (x) f (x0 ))
y f (x1) 0
f (x2 ) 0
极大值
极小值
( )( )
O
x1
x2
x
证: 设
则
负的 y
f(x0)
lim
x0
f (x0 x) x
f (x0) 0 ,
ba
作辅助函数
( x)
f((x))
f
(b) f (a) ba
x
显然 , (x) 在[a, b] 上连续, 在(a, b)内可导, 且
(a) b f (a) a f (b) (b), 由罗尔定理知至少存在一点 思路(a:,利b),用使逆b向a(思) 维0找, 即出定一理个结满论足成罗立尔定. 证理毕条件的函数
微分中值定理

17
几何解释:
在曲线弧AB上至少有 一点C,在该点处的切 线平行于弦AB.
物理解释:
y
C
yf(x)
M
B
A
N
D
o a 1 x
2 b
x
拉格朗日中值定理告诉我们, 在 t=a 到 t=b 的时间段内, 连续运动的物体至少会在 某一时刻达到它的平均速度.
究竟等于什么数, 只要知道 存在即可.
9
例 证明方x5程 5x10有且仅有一1个 的正实 . 根
证 (1) 存在性
设 f(x )x 5 5 x 1 ,则f(x)在 [0,1]连,续 且f(0)1, f(1)3. 零点定理 x0(0,1),使f(x0)0.
即为方程的小于1的正实根.
(2)|f(x)|M . ? |f( x ) f( x 0 ) | M |x x 0 |.
(3 )f(x ) 0( 0 ). ?
f(x)()
还有什么?
21
推论 1 若 f ( x ) 0 , x I , 则 f ( x ) C , x I .
推论 2
18
例 证明不等式
arx c 2 t aarn x c 1 tx 2 a x 1 n ,(x1 x2).
如果f(x)在某区间上可导,要分析函数 在该区间上任意两点的函数值有何关系, 通常就想到微分中值定理.
证 记 f(x)arctax,n在[x1,x2]上,
利用微分中值定理, 得
1
arcx2 t a an rcx1 t a 1 n 2(x2x1)
20
由拉格朗日 以中 得值 出定 其理 它 ? 可 的
《微分中值定理》课件

目录
• 微分中值定理的概述 • 罗尔定理 • 拉格朗日中值定理 • 柯西中值定理 • 泰勒中值定理
01
微分中值定理的概述
微分中值定理的定义
微分中值定理
若函数$f(x)$在闭区间$[a, b]$上连续,在开区间$(a, b)$上可导, 则存在$c in (a, b)$,使得$f'(c) = frac{f(b) - f(a)}{b - a}$。
罗尔定理
若函数$f(x)$在闭区间$[a, b]$上连续,在开区间$(a, b)$上可 导,且$f(a) = f(b)$,则存在$c in (a, b)$,使得$f'(c) = 0$。
拉格朗日中值定理
若函数$f(x)$在闭区间$[a, b]$上连续,在开区间$(a, b)$上可导, 则存在$c in (a, b)$,使得$f'(c) = frac{f(b) - f(a)}{b - a}$。
详细描述
如果函数f(x)在闭区间[a, b]上连续,开区间(a, b)上可导,那么在开区间(a, b)内 至少存在一点ξ,使得f'(ξ)=(f(b)-f(a))/(b-a)。
拉格朗日中值定理的证明
总结词
详细介绍了拉格朗日中值定理的证明 过程。
详细描述
通过构造辅助函数g(x)=f(x)-f(a)[f(b)-f(a)]*(x-a)/(b-a),利用罗尔定 理证明存在ξ属于(a, b),使得g'(ξ)=0 ,从而得到拉格朗日中值定理的结论 。
应用三
研究极值问题。柯西中值定理可以用于研究函数的极值问题,通过分 析导数的符号变化,可以判断函数在某点是否存在极值。
05
泰勒中值定理
泰勒中值定理的表述
微积分三大中值定理详解

第十一页,共51页。
例 2已 知 f(x) (x 2 )(x 1 )(x 1 )(x 3 ),不 求 导 数 , 试 确 定 f(x) 0 有 几 个 实 根 及 其 所 在 范 围 . 解 f (x), f (x)都是多项式
若满足,求出定理中使f()0的.
解 f (x) 2x3 5x2 2x 5 f (x) 6x2 10x 2都是多项式;
f (x)在[1,1]上连续,在(1,1)内可导 且f (1) f (1) 0.
f (x)满足Rolle定理的三个条件.
第十页,共51页。
而 f ( ) 6 2 10 2 0 (1 1) 得 1 5 6 37 (1,1),
f (x)在闭区间[-2,-1], [-1, 1], [1,3]上连续, f (x)在开区间(-2,-1),(-1, 1),(1,3)上可导;
且f (2) f (1) f (1) f (3) 0, f (x)在[-2,-1], [-1, 1], [1,3]上均满足RTh条件.
第十二页,共51页。
注:本例中,应用定理的关键是主动找区间。
第十三页,共51页。
例3 设f (x)在[a,b](0ab)上连续,在(a,b) 内可导,且f(a)b, f(b)a,证明在(a,b)内至
少存在一点,使得f()f().
分析 f (x) f (x) xf (x) f (x) 0 x
(xf (x)) 0;若令F (x) xf (x) 则问题的结论就转化为证明F(x) 0 构造辅助函数F (x) xf (x),就可以用 罗尔定理来证明。
至少存 (在 x 在 0,x1之 一 )使 间 ,个得 f()0.
微积分12-微分中值定理

第五节微分中值定理一. 费马定理二. 罗尔中值定理三. 拉格朗日中值定理费马定理罗尔中值定理拉格朗日中值定理微分中值定理我们常常需要从函数的导数所给出的局部的或“小范围”性质, 推出函数本身整体的或“大范围”性质. 为此, 我们需要建立函数的差商与函数的导数间的基本关系式, 这些关系式称为“微分学中值定理”.这些中值定理的创建要归功于费马、拉格朗日等数学家.首先, 从直观上来看看是怎么一回事.极值的定义若内有定义在设 , )(U )( 0x x f , )(Uˆ )()(00x x x f x f ∈≤, )( )( 0的极大值为则称x f x f , )(Uˆ )()(00x x x f x f ∈≥, )( )( 0的极小值为则称x f x f .0为函数的极大点x .0为函数的极小点xI , I )( 内某点且在内有定义在区间设x f 则必有存在若处取极大(小)值 , )( . ξξf '. 0)(='ξf 一. 费马定理可微函数在区间内部取极值的必要条件是函数在该点的导数值为零.定理O x y )(x f y =a b ξP 费马定理的几何解释 如何证明如何证明, I )( 内有定义在区间设x f 处且在 ξ=x ),( ξf 取极大值则有)(Uˆ )()(ξξ∈≤x f x f 则存在若 , )( ξf ' , 0)()(lim )(0≤∆-∆+='+→∆+xf x f f x ξξξ , 0)()(lim )(0≥∆-∆+='-→∆-xf x f f x ξξξ于是. 0)(='ξf (极小值类似可证)证如何保证函数在区间内部取极值?O xy a b )(x f y 但是……不保证在内部!O xy)(x f y =ξPa b 0)(='ξf 水平的可保证在内部一点取到极值二. 罗尔中值定理设;]) ,([)( )1(b a C x f ∈;) ,( )( )2(内可导在b a x f ,)()( )3(b f a f =则至少存在一点.0)( , ) ,(='∈ξξf b a 使得定理O xy)(x f y =ξa b A B实际上, 切线与弦线 AB 平行. 实际上, 切线与弦线 AB 平行.]) ,([)( b a C x f ∈ 上取到它的最大值、必在 ] ,[ )( b a x f ∴最小值至少各一次.)(min , )(max ],[] ,[x f m x f M b a x b a x ∈∈==令mM = )1(若],[ )( b a x M x f m ∈∀≤≤ ],[ )( b a x m x f ∈=∴.0)( , ) ,( ='∈∀ξξf b a 均有故证)( )2(m M M m ≠<即若]) ,([)( b a C x f ∈ 上取到它的最大值、必在 ] ,[ )( b a x f ∴最小值至少各一次., )()( b f a f =又 . )( m M b x a x x f 和处分别取到和不能同时在故==使得即至少存在一点 ,) ,( b a ∈ξ.)( )(m f M f ==ξξ或由费马定理可知:.) ,( 0)(b a f ∈='ξξ, , ,,, d c b a d c b a <<<皆为实数设,))()()(()(d x c x b x a x x f ----= . , 0)( 并指出根所在区间仅有三个实根证明方程='x f , ) ] ,[], ,[], ,[()(d c c b b a C x f ∈,0)()()()( ====d f c f b f a f 又,),( , )(内可微在是四次多项式+∞-∞x f 得上运用罗尔中值定理在 , ] ,[, ] ,[, ] ,[ d c c b b a. 0)()()(321='='='ξξξf f f 例1证其中,. ) ,( , ) ,( , ) ,(321d c c b b a ∈∈∈ξξξ.0)( 至少有三个实根即='x f, )( 是四次多项式x f, )( 是三次多项式x f '∴.0)(至多有三个实根='x f 综上所述,,0)(仅有三个实根='x f .) ,( ), ,( ), ,(中分别在d c c b b a证明内可导在设 , ) ,( , ]) ,([)( b a b a C x f ∈)()())()(( 222x f a b a f b f x '-=- . ) ,( 内至少有一根在b a 例2分析1)目的:证明至少存在),(b a ∈ξ使)()())()(( 222='---ξξf a b a f b f 0)()())()(( 2)(22='---='=ξξξf a b a f b f x F x )()())()(( 2)(22x f a b a f b f x x F '---='即2)找辅助函数:得)()())()(( )(222x f a b a f b f x x F ---=由证明内可导在设 , ) ,( , ]) ,([)( b a b a C x f ∈)()())()(( 222x f a b a f b f x '-=-. ) ,( 内至少有一根在b a 例2证)()())()(()( 222x f a b a f b f x x F ---=令, )( 得的连续性和可导性则由x f , ) ,( )( , ]) ,([)(内可导在b a x F b a C x F ∈)()()()( 22a f b b f a b F a F -==又由罗尔定理, 至少存在一点使得 ) ,(b a ∈ξ0)()())()(( 2)(22='---='ξξξf a b a f b f F . ) ,( 内至少有一根方程在即b a满足其中实数 , , 1n a a 012)1(3121=--++--n a a a n n证明方程0)12cos(3cos cos 21=-+++x n a x a x a n , 2 ,0 内至少有一根在)(πx n n a x a x a x F n )12sin(123sin 3sin )( 21--+++= 令, )(02)0( ==πF F 则且满足罗尔定理其它条件,使故 2,0 )(πξ∈∃0)12cos(3cos cos )()(21=-+++='='=ξξξξξn a a a x F F n x 例3证. 2 ,0 内至少有一根即方程在)(π, ) ,( , ]) ,([)( )( 内可导在、设b a b a C x g x f ∈ . 0)( 0)( 的一个根的两各根之间至少有==x g x f 2))(()()()()( )()(x g x g x f x g x f x g x f '-'='⎪⎪⎭⎫ ⎝⎛则的两个根是如果 , 0)( , 21=x f x x 0)()()()(2211==x g x f x g x f . ) 0)( (≠x g 这时必须想想, 看能不能找到证明的方法.例4分析证明方程且 . 0)()()()( ), ,(≠'-'∈∀x g x f x g x f b a x, ) ,( , ]) ,([)( )( 内可导在、设b a b a C x g x f ∈证明方程且 . 0)()()()( ), ,(≠'-'∈∀x g x f x g x f b a x . 0)( 0)( 的一个根的两各根之间至少有==x g x f 例4证. 0)( ) ,( , 21的两个根是设=∈x f b a x x. 0)( 21及其之间没有根与在并设方程x x x g =, )()()( x g x f x F =令.21x x <不妨假设 . 0)( )(此时≠x g ,] ,[ )(21上满足罗尔定理条件在x x x F 则由已知条件可知:使得故至少存在一点 , ) ,( 21x x ∈ξ0)()()()()()(2='-'='ξξξξξξg g f g f F . , 0)()()()( 与已知矛盾从而='-'ξξξξg f g f 该矛盾说明命题为真 .如果使用一次罗尔定理后,能否再一次使用罗尔定理?如果需要, 当然可以使用.例5证, ),( ]), ,([)(),( 内二阶可导在设b a b a C x g x f ∈ ),,( ),()( ),()( ),()( b a c b g b f c g c f a g a f ∈===且).()( ),,( :ξξξg f b a ''=''∈使得至少存在一点证明 ,)()( ),()()( 0==-=c a x g x f x ϕϕϕ则令 .0)( ),,( ,11='∈ξϕξ使得至少存在一点由罗尔中值定理c a0.)( ),,( ,22='∈ξϕξ使得至少存在一点同理b c , )( ],[ 21则再运用罗尔中值定理上对函数在x ϕξξ'),,(),( 21使得至少存在一点b a ⊂∈ξξξ,0)())((=''=''=ξϕϕξx x).()( ξξg f ''=''即例6证,0)( , )( ),( =a f I x g x f 且有上可微在区间设 0)()()( , , ,0)(='+'∈=x g x f x f I b a b f 证明方程).,( 0b a x ∈至少存在一根, ),,( 0 ,)( 令所以由于+∞-∞∈>='x e e e x x x,)()()(x f ex F x g = .0)()()())(()(0)(0)(0)(0000='+'='='=x g e x f e x f x f ex F x g x g x x x g ,0)()( , ),( ]),,([)(==∈b F a F b a b a C x F 且内可导在 :则由已知条件可知 ),( :0使得至少存在一点故由罗尔中值定理b a x ∈. ,0)()()( ,0 000)(0即得所证故有因为='+'>x g x f x f e x g例6+设)(x f 在],[b a 上连续,),(b a 内可导,且1)()(==b f a f ,试证存在),(b a ∈ξ,使1)()(='+ξξf f 注:))()((])([x f x f e x f e x x '+='))(1)((])1)(([x f x f e x f e x x '+-='--三. 拉格朗日中值定理设;]) ,([)( )1(b a C x f ∈,) ,( )( )2(内可导在b a x f 则至少存在一点, ) ,(使得b a ∈ξab a f b f f --=')()()(ξ))(()()( a b f a f b f -'=-ξ即定理O x y)(x f y =ξa b A B切线与弦线 AB 平行 切线与弦线 AB 平行)()()()( a x a b a f b f a f y AB ---+=的方程:弦如何利用罗尔定理来证明?如何利用罗尔定理来证明?)()()()()()( a x ab a f b f a f x f x -----=ϕ令则由已知条件可得:, ]) ,([)(b a C x ∈ϕ. ) ,( )(内可导在b a x ϕ,0)()( ==b a ϕϕ且故由罗尔定理, 至少存在一点使得, ) ,(b a ∈ξ0)()()()(=---'='ab a f b f f ξξϕ))(()()( a b f a f b f -'=-ξ即证定理的证明方法很多, 例如, 可作辅助函数)()())()(()(x f a b x a f b f x F ---=定理中的公式均可写成还是不论 b a b a ><) , ( ))(()()(之间在b a a b f a f b f ξξ-'=-拉格朗日有限增量公式1)(0 )()()(<<∆∆+'=-∆+θθx x x f x f x x f )( )(之间与在x x x x f y ∆+∆'=∆ξξ式可写成拉格朗日中值定理的公), ( |||)(| |)()(|之间在b a a b f a f b f ξξ-'=-拉格朗日中值定理告诉我们, 在t=a 到t=b 的时间段内, 连续运动的物体至少会在某一时刻达到它的平均速度.?以得出其它的什么结论由拉格朗日中值定理可)( )()()(a b f a f b f -'=-ξ)( )()()(1212x x f x f x f -'=-ξ).,( 0)( )1(b a x x f ∈='.)(常数=x f .|)(| )2(M x f ≤'.|| |)()(|00x x M x f x f -≤-).0( 0)( )3(≤≥'x f )( )(↓↑x f 还有什么?, I , . I , 0)( 21有则若∈∀∈='x x x x f, 0))(()()(2121=-'=-x x f x f x f ξ推论 1.I , )( , I , 0)( ∈=∈∀='x C x f x x f 则若. )()(21x f x f =推论 2)()())()((x g x f x g x f '-'='-, I )()( ∈'='x x g x f 若 , I , 0))()(()( ∈='-='x x g x f x F 则.I )()( , I )()( ∈+=∈'='x C x g x f x x g x f 则若( C 为常数 ). I , )()()(∈=-=x C x g x f x F推论 3, ) )( ( |)(| 有界即若x f M x f '≤' . || |||)(| |)()(| a b M a b f a f b f -≤-'=-ξ则则且条件 ), ,( , |)(| ,b a x M x f ∈≤'|||)()(|a b M a f b f -≤-理上满足拉格朗日中值定在若 ] ,[ )( b a x f 用来证明一些重要的不等式用来证明一些重要的不等式推论 4. , I ,1221x x x x >∈∀不妨设 )( ))(()()(211212x x x x f x f x f <<-'=-ξξ,)()( , I 0)( 12x f x f x x f >∈>'则若,)()( , I 0)( 12x f x f x x f <∈<'则若, )0)(( 0)( , I )( ≤'≥'x f x f x f 且可导在区间若.减少上单调增加在区间则)( I )( x f 用来判断函数的单调性用来判断函数的单调性(在后面讲)该推论可以用来证明不等式., 0 时当证明:b a <<.ln a a b a b b a b -<<-)(1ln ln )(1 a b aa b a b b -<-<-即要证,]b ,[ , ln )( a x x x f ∈=令, ] ,[ )( 理条件上满足拉格朗日中值定在则b a x f 故, )(1ln ln b a a b a b <<-=-ξξ从而 .ln aa b a b b a b -<<-例8证. , 1 x e e x x>>时当证明:)1( ln 1 >>-x x x 即要证))(()()( a b f a f b f -'=-ξ比较有上运用在 , 01ln ] ,1[ =x .1ln ln 1->-x x ], ,1[ ln )( 则由拉格朗日中值定理令x t t t f ∈=).1( , 1)1(11ln ln x x x x <<-<-=-ξξ得 . , 1 ex e x x>>时故当例9证. ]1 ,1[ , 2arccos arcsin -∈≡+x x x π证明: , 0)11(11)arccos (arcsin 22=--+-='+x x x x , 1) ,1( 时当-∈x )1 ,1( arccos arcsin -∈≡+x C x x 故从而计算得取 ,2 0 π==C x . )1 ,1( 2arccos arcsin -∈≡+x x x π例10证, ) ]1 ,1[ ()arccos (arcsin 可得由-∈+C x x . ]1 ,1[ 2arccos arcsin -∈≡+x x x π延拓!内满足关系式在若证明: ) ,( )( ∞+-∞x f .)( , )()( , 1)0(xe xf x f x f f =='=则. ) ,( , 1)( ∞+-∞∈≡x e x f x 即要证), ,( ,)()( ∞+-∞∈=x ex f x x ϕ令x x x ee xf e x f x 2)()()( -'='ϕ ), ,( ,0∞+-∞∈=x 例11证). ,( ,)( ∞+-∞∈=∴x C x ϕ,1)0( =f 又 )()( C e x f x x ==ϕ1)0()0( 0==e f ϕ故 . 1=C 从而.) ,( ,)(∞+-∞∈=x e x f x] ,[ )( , 523)( 2b a x f x x x f 在求设++= . 值理的上满足拉格朗日中值定ξ ] ,[ )( 满足拉格朗日中值在易验证b a x f .定理的条件 , )2)((6)52(35)2(3 22a b a a b b -+=++-++ξ由, 6)(3 ξ=+a b 得 . 2 a b +=ξ从而所求为例12解, ) ,( , ] ,[ )( 内可导在上连续在如果b a b a x f )( , )0)(( 0)( ] ,[b a x f x f x f ↑≤'≥'则可推出且.))((] ,[b a x f ↓ )( , )0)(( 0)( x f x f x f I 则上如果在区间<'>').( 严格单调减少上严格单调增加在区间I 由推论4知:. ) ,( , 3的单调性讨论∞+-∞∈=x x y O xy 3x y =, 03)(23≥='='x x y , 0 时且仅当=x , 0='y . ) ,(3∞+-∞↑x 故, ) ,(时∞+-∞∈x 解例7. ]2 ,0[ sin 上的单调性在讨论πx x y -=,) ]2 ,0[ (sin πC x x y ∈-= , )2 ,0( , 0cos 1π∈>-='x x y .sin ]2 ,0[π↑-=∴x x y 例13解. )1ln( , 0 x x x +>>时:证明,) ,0[ , )1ln()( ∞+∈+-=x x x x f 令, ) ) ,0[ ()( ∞+∈C x f 则,0)0(=f 又 , ) 0( , 0111)(时>>+-='x xx f 故, )() ,0[∞+↑x f 从而 , )0( , 0)0()(>=>x f x f 即. )1ln( , 0x x x +>>时例14证。
