理论力学第六章 点的合成运动 [同济大学]
点的合成运动教学与思维方式问题的分析

点的合成运动教学与思维方式问题的分析培养创新型人才是新世纪高等教育发展的趋势。
创新性,表现在富有研究能力和科学精神,善于钻研、勤于思考。
培养研究意识,积累研究能力,是培养创新人才的根本。
课堂教学是大学教育中的重要环节,仅仅以讲授知识为目的的教学过程,不能够改变当前教育中人才培养的狭窄化、技术化的倾向。
而经过严格训练的思维方式对学生能力的影响,可能大于知识本身。
如何以教学为载体,在传授知识的同时,训练和培养学生的研究型和创新型思维方式,是每个大学教师应当思考的问题。
特别在力学类课程的教学中,由于知识具有基础与技术的双重属性,且几何和物理意义清晰,最适宜于进行研究型思维方式的训练。
理论力学属于力学类基础课,所要讲授的内容多,而且学时相对较少,并不适宜进行全面的讨论式、实践式教学。
如何在“教”中引导学生发现问题、主动思考是基础课教学中应当考虑的。
根据对几届学生的教学经验,尝试在各个章节的教学设计中融汇研究型思维方式的讲授方法和能力训练。
下面,以笔者在理论力学中点的合成运动一章的教学设计谈谈研究型思维方式的培养。
1 点的合成运动教学设计点的合成运动一章是理论力学中运动学的重点和难点,其概念抽象,速度合成定理与加速度合成定理推导也有一定难度。
如果仅从讲授知识和应用的角度出发,可以在建立基本概念基础上,弱化定理的推导过程,而着重于大量应用练习,学生也完全可以掌握这部分知识。
但是,由于对定理理解不深,很多学生只会比着葫芦画瓢,知其然而不知其所以然,当碰到复杂问题或概念性强的问题时无从下手,更不用说去主动思考和解决实际问题了。
所以,在教学内容上,知识的讲授应该要逻辑清晰,有理有据;在教学设计中,要发挥学生的主观能动性,与学生积极互动,通过问题加强思维方式的训练。
下面将笔者采用的教学方案进行如下阐述。
1.1 问题的引出与探索未知领域一样,符合认知规律的教学过程可使学生形成清晰的知识脉络和解决问题的思路。
因此,知识点讲授前应该有问题引出的过程。
《理论力学》点的合成运动(课件二)

■*ira川釦点的合成运动(二)5.2速度合成定理5.2.2速度合成定理Ar =2加+ Ar'\7^a=叫+人X上述结果表明,无论牵连运动为平动还是定轴转动,动点的绝对速度均等于其相对速度与牵连速度的矢量和。
即"a二人+上这一结论称为点的速度合成定理。
注意事项:1.上述结论适用于任何形式的相对运动和牵连运动。
2.注意公式的矢量性和瞬时性。
3.在定理的应用中常用几何法,作速度合成图,最后归结为解三角形。
X例卜正弦平动机构如图示,已知u,OM = R o 用合成法求©二45°时0M的角速度。
A匚解:动点:滑块M,定系:地面,动系:AB O速度合成图如图示,v e = U,故v a = v e / cos(p = ^2uA co=v a/R= ^2u/R,© = % ;求 © = 90' 解:动点:滑块M,定系: 地面,动系:OAo速度合成图如图示, V^=r (p= rco^ 故v e = v a sin^= r690sin 0 OM = r/sin 0 =69 = v e /OM =例2.己知 O C=h,CM = 时^ 04杆转动的角速度。
r2690/(r2+/z2)rB 例3.己知g 0C = r刁在图示位置4B丄CO,CD = OD。
求此时顶杆的速度。
解:动点:顶杆上的4点,定系:地面,动系:园盘。
速度合成图如图示。
=> v a = v e=ra例4・己知AB、CD平动,夹角为丄AB,V2 丄CD。
引」2为已知。
求交点M的速度。
"2解:此题用常规的办法来求解会有些问题。
设动点为交点胚分别取和CQ为动系。
#1.动系v el = Vj, v rl沿BA> % =儿+人1#2.动系CD"2人2二"2,片2沿CD> +叫2"1 +人1 =卩2 +人2上式沿丄仞方向投影得cos a + v rl sin a=v2v rl = (v2— Vj cos a)/ sin a+ —2V1V9COS a sin a5.3加速度合成定理绝对加速度(偽):动点相对于定系的加速度a. = dv a / dt = d 2r / dr 2相对加速度(舛):动点相对于动系的加速度,即动 点的相对速度对时间的相对导数牵连加速度(假):牵连点相对于定系的加速度。
工程力学Ⅱ智慧树知到答案章节测试2023年同济大学

第一章测试1.用自然法表示动点的加速度时,加速度等于切向加速度和法向加速度的矢量和。
其中切向加速度反映__________________________;法向加速度反映________________________________。
()A:中点曲线;速度方向变化;速度大小变化。
B:矢端曲线;速度大小变化;速度方向变化。
C:矢端曲线;速度方向变化;速度大小变化。
D:中点曲线;速度大小变化;速度方向变化。
答案:B2.点做曲线运动如图所示。
若点在不同位置时的加速度是一个恒矢量,则该点做。
()A:匀减速运动B:匀速运动C:变速运动D:匀加速运动答案:C3.在图示曲柄滑块机构中,曲柄OC绕O轴转动,j=wt(w为常量)。
滑块A,B可分别沿通过O点且相互垂直的两直槽滑动,若AC=CB=OC=L,则A、B点速度的大小分别为()A:Lwcosj;LwsinjB:Lwsinj;LwcosjC:2Lwsinj;2LwcosjD:2Lwcosj;2Lwsinj答案:D4.点沿半径R=500mm的圆周运动,已知点的运动规律为s=10Rt3(mm),则当t=1s时,该点的加速度的大小为()m/s2A:3.000B:4.500C:7.508D:5.408答案:D第二章测试1.刚体作平移时,某瞬时体内各点不但有相同的速度,而且有相同的加速度。
()A:错B:对答案:B2.平面机构如图所示。
已知AB//O1O2,且AB=O1O2=L,AO1=BO2=r,ABCD是矩形板,AD=BC=b,AO1杆以匀角速度w绕O1轴转动,则矩形板重心点的速度和加速度的大小分别为()答案:C3.若刚体运动时,其上两点的轨迹相同,则该刚体一定作平行移动。
()A:对B:错答案:B4.在图示平面机构中,杆_____作平面运动,则该瞬时此杆的速度瞬心在____。
()A:OA;A点B:AB;B点C:OA;B点D:AB;A点答案:B5.图示机构中,已知O1A=O2B。
理论力学《点的合成运动》答案

4
动系:固连于CBDE上的坐标系。 动系平动, v A = v CBDE = v BC 静系:固连于地面的坐标系。 绝对速度:A相对于地面的速度。 相对速度:A相对于DE的速度。 牵连速度:CBDE相对于地面的速度。
→ → →
vr
900 − ϕ A
120 0
va
ϕ
ve = vBC
ϕ O
5
相对速度:C相对于OC杆的速度。 牵连速度:OC杆相对于地面的速度。
ve = OC ⋅ ω =
→ → →
0.4 × 0.5 = 0.231( m / s ) cos 30 0
va = ve + vr va = ve 0.2 = = 0.267( m / s ) 0 cos 30 cos 2 30 0
BC作平动,故
v BC = v a = 1.155lω 0
[习题7-9] 一外形为半圆弧的凸轮A,半径r=300mm,沿水平方向向右作匀加速运动, 其加速度aA=800mm/s 。凸轮推动直杆BC沿铅直导槽上下运动。设在图所示瞬时, vA=600mm/s,求杆BC的速度及加速度。 解: 动点:B。 动系:固连于凸轮A上的坐标系。 静系:固连于地面的坐标系。 绝对速度:B相对于地面的速度。 相对速度:B相对于凸轮的速度。 牵连速度:B相对于凸轮的速度。
θ = 40.930
→ →
即 v 与 v1 之间的夹角为 θ = 40.93 。 种子走过的水平距离为:
0
s = v x t = v cos θ ⋅ t h = vyt +
1 2 gt 2 1 2 gt 2
h = v sin θt +
0.25 = 2.65 sin 40.930 t + 0.5 × 9.8t 2
理论力学 第6章 点的合成运动

牵连速度ve:ve为所要求的未知量,方向垂直于O1B 。
va
ve
vr
作出速度矢量图
因为
所以
设摇杆在此瞬时的角速度为ω1,则
其中
所以可得
va
ve
vr
例题3
如图所示,半径为R,偏心距为e的凸轮,以匀角速度ω绕O轴转动,杆AB能在滑槽中上下平动,杆的端点A始终与凸轮接触,且OAB成一直线。求在图示位置时,杆AB的速度。
把固定在地球上的坐标系称为定参考坐标系Oxyz。
定系
动系
6.1.2 三种运动
*
6.1.3 三种速度和加速度
动点在相对运动中的速度和加速度 称为:相对速度和相对加速度 记作:vr 和 ar (Relative Motion)
动点在绝对运动中的速度和加速度 称为:绝对速度和绝对加速度 记作:va 和 aa (Absolute Motion)
组坐标系
1
个动点
明确求解的那一点(或对求解最有帮助的一点),选这一点为动点。
选择ቤተ መጻሕፍቲ ባይዱ
1
2
3
区分
搞清绝对运动、相对运动和牵连运动
种运动
3
绝对运动 相对运动 牵连运动
区分三种运动应注意:
站在什么地方看物体的运动; 看什么物体的运动
动点与定参考系的运动为绝对运动;
绝对运动
动点与动参考系的运动为相对运动;
3
动点的绝对运动和相对运动都是指点的运动, 直线运动, 曲线运动。
还有什么?
三种速度和加速度
*
动参考系中,与动点重合的那一点的速度和加速度 称为:牵连速度和牵连加速度 记作:ve 和 ae (Carrier Motion)
理论力学06点的合成运动

第六章 点的合成运动
§6–1 点的合成运动的概念 §6–2.1 点的速度合成定理 §6–2.2 牵连运动为平动时点的加速度合成定理 §6–3 牵连运动为转动时点的加速度合成定理 习题课
2
前两章中我们研究点和刚体的运动,一般都是以地面为参考 体的。然而在实际问题中,还常常要在相对于地面运动着的参 考系上观察和研究物体的运动。例如,从行驶的汽车上观看飞 机的运动等,坐在行驶的火车内看下雨的雨点是向后斜落的等。
9
若动点A在偏心轮上时
动点:A(在AB杆上)
A(在偏心轮上)
动系:偏心轮
AB杆
静系:地面
地面
绝对运动:直线
圆周(红色虚线)
相对运动:圆周(曲线) 曲线(未知)
牵连运动:定轴转动
平动
[注] 要指明动点应在哪个 物体上, 但不能选在 动系上。
10
§6-2点的速度、加速度合成定理
绝对、相对和牵连速度之间的关系就是速度合成定理,它表明: 三个速度矢量的任何一个可以由其余两个叠加得到,表达式为:
牵连加速度: aeτ 0 , ae aen 2r , 方向指向轴心O ;
科氏加速度:ak 2vr 2 2r/cos ,
方向//n, 指向与n 相反。
29
由牵连运动为转动时的加速度合成定 理
aa
ae
at r
an r
ak
作出加速度矢量图如图示
向 n 轴投影: aa cos ae cos arn ak
3.动参考系:把固结于相对于地面运动物体上的坐标系,
称为动坐标系,简称动系。例如在行驶的汽车。
3
二.三种运动及三种速度与三种加速度。
1.绝对运动:动点对静系的运动。 2.相对运动:动点对动系的运动。
理论力学_同济大学中国大学mooc课后章节答案期末考试题库2023年

理论力学_同济大学中国大学mooc课后章节答案期末考试题库2023年1.只要平面力偶的力偶矩保持不变,可将力偶的力和力偶臂作相应的改变,而不影响其对刚体的效应。
参考答案:正确2.力可以沿着作用线移动而不改变它对物体的运动效应。
参考答案:错误3.一空间力系,若各力作用线垂直某一固定平面,则其独立的平衡方程最多有3个。
参考答案:正确4.一空间力系,若各力作用线与某一固定直线相交,则其独立的平衡方程最多有5个。
参考答案:正确5.由n个力组成的空间平衡力系,若其中(n-1)个力相交于A点,则另一个力___________________。
参考答案:也一定通过A点;6.在合成运动问题中,静坐标系是被认为固定不动的坐标系,而动坐标系是相对于该静坐标系有运动的坐标系。
参考答案:正确7.系统在某一运动过程中,作用于系统的所有外力的冲量和的方向与系统在此运动过程中______________的方向相同。
参考答案:动量的改变量8.某一平面力系,如其力多边形不封闭,则该力系对任意一点的主矩都不可能为零。
参考答案:错误9.人重P1,车重P2,置于光滑水平地面上,人可在车上运动,系统开始时静止。
则不论人采用何种方式(走,跑)从车头运动到车尾,车的______________________。
参考答案:位移是不变的10.质点系动能的变化等于作用在质点系上全部外力所作的功。
参考答案:错误11.滚阻力偶的转向与物体滚动的转向相反。
参考答案:正确12.质心的加速度只与质点系所受外力的大小和方向有关,而与这些外力是否作用在质心上无关。
参考答案:正确13.在任何情况下,摩擦力的大小总等于摩擦因数与正压力的乘积。
参考答案:错误14.一个力不可能分解为一个力偶;一个力偶也不可能合成为一个力。
参考答案:正确15.若质点系的动量在x方向的分量守恒,则该质点系的质心的速度在x轴上的投影保持为常量。
参考答案:正确16.已知均质滑轮重P0=200N,物块A重P1=200N,B重P2=100N,拉力F2=100N,系统从静止开始运动,任一瞬时图(a)系统的物块A有加速度a1,图(b)系统的物块A有加速度a2,则_________。
理论力学:第6章 点的合成运动

·1·第6章 点的合成运动6.1 主要内容6.1.1 点的绝对运动、相对运动和牵连运动1.定系和动系若存在两个有相对运动的坐标系,则可指定其中一个为定系,另一个即为动系。
但工程上一般以固定在地面上的坐标系为定系,相对于定系运动着的坐标系称为动系。
2.动点和牵连点动点为研究的对象,牵连点是动点在动系上的重合点,随动点的相对运动而变,是动系上的点,不同瞬时,有不同的牵连点。
3.三种运动的关系动点相对于定系的运动定义为绝对运动;动点相对于动系的运动定义为相对运动;动系相对于定系的运动定义为牵连运动。
本章的主要任务就是建立这三者之间的定量关系,从而用来解决工程实际某些运动分析问题。
6.1.2 点的速度合成定理动点的绝对速度等于它的牵连速度与相对速度的矢量和。
这就是点的速度合成定理。
a e r =+v v v6.1.3 牵连运动为平移时,点的加速度合成定理当牵连运动为平移时,动点的绝对加速度等于牵连加速度与相对加速度的矢量和。
a e r =+a a a6.1.4 牵连运动为转动时,点的加速度合成定理当牵连运动为转动时,动点的绝对加速度等于牵连加速度、相对加速度与科氏加速度的矢量和,这就是牵连运动为转动时点的加速度合成定理。
a e r C =++a a a a其中r C v a ⨯=ω2。
当取平动动系时0=e ω;0=C a 。
6.2 基本要求1.掌握运动合成与分解的基本概念和方法,准确理解本章阐述的若干概念。
2.明确动点与动系的选择原则,能在具体问题中恰当地选择动点与动系,并正确地分析三种运动。
3.熟练掌握点的速度合成定理和牵连运动为平动时的加速度合成定理及其应用。
4.掌握科氏加速度的概念和计算,准确应用牵连运动为转动时的加速度合成定理及其应用。
6.3 重点讨论应用点的合成运动理论解决实际问题时,其关键是正确地选择动点和动系。
选择原则因具体情况不同而略有区别。
常见的问题有三种题型。
1.两个独立运动的物体,研究两者的相对运动。
理论力学-点地合成运动

6.已知半径为R的圆盘平面与铅直轴成30°角,以匀角速度ω转动。轮缘上有一点M,以相对于盘的速度 r沿圆盘边缘运动。则M点经过水平直径AB的端点A时的科氏加速度为(方向在图上表示)。
8.在图示平面机构中,已知:AD=BE=L,且AD平行BE,OF与CE杆垂直。当=60°时,BE杆的角速度为ω、角加速度为。试求止瞬时OF杆的速度与加速度。
9.具有半长R=0.2m的半圆形槽的滑块,以速度u0=1m/s,加速度0=2m/s2水平向右运动,推动杆AB沿铅垂方向运动。试求在图示=60°时,AB杆的速度和加速度。
15.半径r的圆环以匀角速度ω绕垂直于纸面的O轴转动,OA杆固定于水平方向,小环M套在大圆环及杆上。试用点的合成运动方法求当OC垂直于CM时,小环M的速度和加速度。
16.已知:OA杆以匀角速度ω0=2rad/s绕O轴转动,半径r=2cm的小轮沿OA杆作无滑动的滚动,轮心相对OA杆的运用规律b=4t2(式中b以cm计,t以s计)。当t=1s时,=60°,试求该瞬时轮心O1的绝对速度和绝对加速度。
3.杆CD可沿水平槽移动,并推动杆AB绕轴A转动,L为常数。试用点的合成运动方法求图示位置θ=30°时,CD杆的绝对速度u。
4.沿铅直轨道运动的T字杆AB,其上的销钉C插在半径为R的圆槽内,带动物块D沿水平方向运动。在图示位置,AB杆的速度为 ,方向如图示,=30°。试求此瞬时物块D的速度。
5.联合收获机的平行四边形机械在铅垂面内运动。已知:曲柄OA=O1B=500mm,OA转速n=36r/min,收获机的水平速度u=2km/h。试求在图示位置=30°时,AB杆的端点M的水平速度和铅垂直速度。
第6章 点的合成运动理论力学

33
例 题 6-5
已知:凸轮半径R ,v0 , a0 ,试求:j =60o时, 顶杆AB的加速度。
解:取杆AB上的点A为 动点,动系与凸轮 固连。
理论力学电子教案
点的运动合成
34
例 题 6-5
绝对速度va = ? , 方向∥AB ; 相对速度vr = ? , 方向CA; 牵连速度ve=v0 , 方向 → ; 由速度合成定理
上面的推导过程中,动参考系并未限制作何运动, 因此点的速度合成定理对任意的牵连运动都适用。
点的速度合成定理是瞬时矢量式,每一速度包 括大小‚方向两个元素,总共六个元素,已知任意四 个元素,就能求出其余两个。
理论力学电子教案
点的运动合成
15
例 题 6-1
凸轮顶杆机构中半径 为 R 的半圆形凸轮以等速 度 v0沿水平轨道向右运动, 带 动 顶 杆 AB 沿 铅 垂 方 向 运动,如图所示,试求 j = 60º 时,顶杆 AB 的速 度。
va ve vr
v0 cot 60 0.577v0 v AB va
此瞬时杆AB的速度方向 向上。
理论力学电子教案
点的运动合成
19
例 题 6-2
军舰以速度 v=37.04 km/h 的速度前进,直
升 飞 机 以 每 小 时 18
km/h 的速度垂直降落。
点的运动合成
21
3. 速度分析 绝对速度 va:大小已知,方 向沿铅垂方向向下。 牵连速度 ve :大小已知,方 向水平向右。 相对速度 vr :大小方向均 未知,为所要求的量。 应用速度合成定理 va ve vr
2 vr ve va 41.18 km / h , 2
点的合成运动理论力学课件

根据速度和加速度的合成定理,一个点的速度和加速度可以由其相对于不同参考系的速度和加速度进行合成。具体来说,点的速度可以由绝对速度、相对速度和牵连速度进行合成,点的加速度可以由绝对加速度、相对加速度和牵连加速度进行合成。
详细描述
速度和加速度的合成定理在解决实际运动问题中具有广泛的应用。
总结词
通过应用速度和加速度的合成定理,可以解决各种复杂的运动问题,例如行星运动、卫星轨道、机械运动等。该定理可以帮助我们更好地理解点的运动规律,并预测其在不同参考系下的运动轨迹。
03
点的合成运动的应用
刚体的平面运动是指刚体在平面内的运动,包括平移和旋转。点的合成运动理论力学在刚体的平面运动中有着广泛的应用,如分析刚体的速度和加速度、计算刚体的动能和势能等。
刚体的平移运动是指刚体在平面内沿直线或曲线移动,其速度和加速度可以通过点的合成运动理论力学中的速度和加速度合成定理进行分析。
概念
物体在平面内运动,点在该平面内跟随物体一起运动。
平面运动
空间运动
刚体运动
物体在三维空间中运动,点在该空间内跟随物体一起运动。
物体的各部分之间没有相对运动,点跟随整个物体一起做刚体运动。
03
02
01
02
点的合成运动的基本定理
速系的定理。
该理论广泛应用于航天、航海、车辆工程等领域。通过理解和应用点的合成运动理论,工程师们能够更准确地预测和控制物体的运动轨迹。
尽管点的合成运动理论在许多情况下非常有效,但它也有局限性。例如,在处理高速或微观尺度的运动时,该理论可能会出现误差。
点的合成运动理论与经典力学、相对论、量子力学等其他理论有密切的联系。深入理解这些联系有助于推动物理学的发展。
详细描述
理论力学-点的合成运动

第 页1 教学目标知识目标:定系和动系,三种运动的速度与加速度,点的速度合成定理,牵连运动为平移时点的加速度合成定理,牵连运动为转动时点的加速度合成定理·科氏加速度。
能力目标: 掌握点的速度合成定理素质目标:沟通、协作能力;观察、信息收集能力;分析总结能力。
良好的职业道德和严谨的工作作风理论力学-点的合成运动〖理论学习〗8.1点的合成运动的概念 8.1.1定系和动系当选取两个不同的参考系来研究同一动点的运动时,通常把固定于地面的参考系称之为定参考系(简称定系);而将固定在其他相对于地面运动的参考体上的参考系称为动参考系(简称动系)。
动点相对于定系与相对于动系运动之间的关系,显然要取决于动系相对于定系的运动情况。
相对于不同的参考系,点的运动轨迹不同,速度、加速度也不相同。
8.1.2三种运动图8-1绝对运动:动点相对于定系的运动,即站在定系中观察动点的运动。
相对运动:动点相对于动系的运动,即站在动系中观察动点的运动。
牵连运动:动系相对于定系的运动,即站在定系中观察动系的运动。
点的绝对运动可以看成是相对运动与牵连运动的合成运动(或复合运动)。
8.1.3三种运动的速度与加速度速度和加速度是描述动点相对参考系运动特征的物理量。
把动点相对定系运动的速度和加速度分别称为动点的绝对速度与绝对加速度,用va 和aa 表示;把动点相对动系运动的速度和加速度分别称为动点的相对速度与相对加速度,用vr 和ar 表示。
动系上与动点相重合的点为该瞬时动点的牵连点。
牵连点相对于定系的速度和加速度分别称为动点的牵连速度和牵连加速度,用ve 和ae 表示。
8.2点的速度合成定理设动点M 沿固连于动坐标系的曲线AB 运动,而曲线AB 又随动系相对地面做某种运动。
则动点M 沿曲线AB 的运动是相对运动,曲线AB 相对地面的运动是牵连运动,动点M 相对地面的运动是绝对运动。
点的速度合成定理:动点在某一瞬时的绝对速度等于该瞬时的牵连速度与相对速度的矢量和。
同济继续教育理论力学-答案
一、受力分析作业(1)一、受力分析作业(2)姓名学号交批日期9月10日批阅日期月日二、平面力系作业(1)姓名学号交批日期9月10 日批阅日期月日姓名学号交批日期9月17 日批阅日期月日二、平面力系作业(2)姓名学号交批日期9月17日批阅日期月日姓名学号交批日期9月24 日批阅日期月姓名学号交批日期9月24 日批阅日期月日三、空间力系作业姓名学号交批日期10月1 日批阅日期月日姓名学号交批日期10月1日批阅日期月日姓名学号交批日期10月8日批阅日期月日四、摩擦作业姓名学号交批日期10月8日批阅日期月日姓名学号交批日期10月15 日批阅日期月日五、点的运动和刚体的基本运动作业姓名学号交批日期10月15日批阅日期月日姓名学号交批日期10月22日批阅日期月日六、点的合成运动作业(1)姓名学号交批日期10月22日批阅日期月日六、点的合成运动作业(2)姓名学号交批日期10月29日批阅日期月日七、刚体平面运动作业(1)姓名学号交批日期10月29日批阅日期月日七、刚体平面运动作业(2)姓名学号交批日期11月5日批阅日期月日姓名学号交批日期11月5日批阅日期月日八、动力学基本方程作业姓名学号交批日期11月12日批阅日期月日姓名学号交批日期11月12日批阅日期月日九、动量定理作业姓名学号交批日期11月19日批阅日期月日姓名学号交批日期11月19日批阅日期月日十、动量矩定理作业姓名学号交批日期11月26日批阅日期月日姓名学号交批日期11月26日批阅日期月日姓名学号交批日期12月3 日批阅日期月日十一、动能定理作业姓名学号交批日期12月3日批阅日期月日姓名学号交批日期12月10日批阅日期月日姓名学号交批日期12月10日批阅日期月日十二、达朗贝尔原理作业姓名学号交批日期12月17日批阅日期月日学号尾数 1 2 3 4 5 6 7 8 9 0第1次作业交批日期9.3 9.10 9.17 9.24 10.1 9.3 9.10 9.17 9.24 10.8 第2次作业交批日期10.15 10.22 10.29 10.15 10.22 10.29 10.15 10.22 10.29 11.5 第3次作业交批日期11.12 11.19 11.26 12.3 12.10 11.12 11.19 11.26 12.3 12.10理论力学练习册(网络专用)同济大学航空航天与力学学院基础力学教学研究部王斌耀编。
理论力学6—点的合成运动3
rO xi y j z k
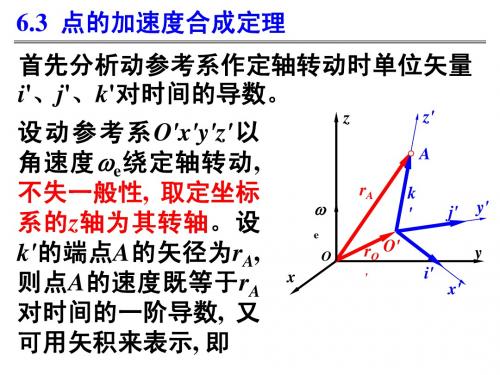
6.3 点的加速度合成定理
rM rO xi yj zk
va
解 : 在本题中应选取滑块 A 作为研究的动点, 把动参考 系固定在摇杆O1B上。 点A的绝对运动是以点 O 为圆心的圆周运动 , 相对 运动是沿O1B方向的直线运 动, 而牵连运动则是摇杆绕 轴O1的摆动。
w ve
O
B vr
A
j
O1
w1
ve va sin j rw sin j
O1 A l r
ve2 va2 cos30 325 mm/s
即滑枕的运动速度是325 mm/s, 方向向左。
650
va2 ve2
O1 w1 A
j
vr2
B
w2
O2
二、加速度分析, 动点和动系的选择分别同前。 1 ) A 点的加速度分析如图所示 , 由于动参考系 O2B作定轴转动, 有科氏加速度, 其方向可由相对 速度 vr顺着摇杆 O2B的转动方向转过 90º 得到 , 是 C D 垂直于O2B斜向上方, 大小为 aC 2w2vr1 200 3 mm/s2 y B n 2 2 ar1 aa1 O1 A w1 800 mm/s aC
650
O1
O2
相对速度
vr1 va1 sin60 200 3 mm/s
2)取套筒B为动点, 动参考系与滑枕CD固连。相 对运动是套筒 B沿滑杆的竖直直线运动 , 牵连运 动是滑枕CD的水平平动, 绝对运动是套筒B绕O2 的圆周运动。
D C
理论力学第六章点的合成运动

PDF 文件使用 "pdfFactory Pro" 试用版本创建
例6-6:三角楔块可在光滑地面滑动,现在楔块上放一物块可
沿光滑斜面滑下,当t=0,x=0,y=h,v2=0,a1=10cm/s2 , a2=10 2cm/s2,试求:物块轨迹方程。
解: aax= a1+ a2 cos450 =20cm/s2;
υϖa = υϖe +υϖr
绝对速度
相对速度
牵连速度
速度合成定理 —— 动点的绝对速度等于其牵连速 度与相对速度的的矢量和。
22
PDF 文件使用 "pdfFactory Pro" 试用版本创建
例6-1:雨铅垂下落,客车以匀速v行驶,在无风时下雨打在 窗玻璃上 的夹角为θ,试求:雨的速度。
10
PDF 文件使用 "pdfFactory Pro" 试用版本创建
运动的分解:动点动系的选择
11
PDF 文件使用 "pdfFactory Pro" 试用版本创建
若选杆为动系,圆上一点为动点
12
PDF 文件使用 "pdfFactory Pro" 试用版本创建
例6-5:曲柄滑道机构,OA=O1A=r=10cm, θ= ϕ , ω=4π, 试求:ϕ 转到300时直杆的加速度a。
解:动点取A; 绝对:圆周;
va
vr
相对:圆周;牵连:平动;
ve
ω
[速度]
y: vacos300=vrcos300;
va= ω r=40 π; vr= va= ω r=40 π ,
选法2 Х
19
PDF 文件使用 "pdfFactory Pro" 试用版本创建
理论力学-点的合成运动

第六章点的合成运动一、是非题1、不论牵连运动的何种运动,点的速度合成定理a=e+r皆成立。
()2、在点的合成运动中,动点的绝对加速度总是等于牵连加速度与相对加速度的矢量和。
()3、当牵连运动为平动时,相对加速度等于相对速度对时间的一阶导数。
()4、用合成运动的方法分析点的运动时,若牵连角速度ωe≠0,相对速度υr≠0,则一定有不为零的科氏加速度。
()5、若将动坐标取在作定轴转动的刚体上,则刚体内沿平行于转动轴的直线运动的动点,其加速度一定等于牵连加速度和相对加速度的矢量和。
()6、刚体作定轴转动,动点M在刚体内沿平行于转动轴的直线运动,若取刚体为动坐标系,则任一瞬时动点的牵连加速度都是相等的。
()7、当牵连运动定轴转动时一定有科氏加速度。
()8、如果考虑地球自转,则在地球上的任何地方运动的物体(视为质点),都有科氏加速度。
()二、选择题1、长L的直杆OA,以角速度ω绕O轴转动,杆的A端铰接一个半径为r的圆盘,圆盘相对于直杆以角速度ωr,绕A轴转动。
今以圆盘边缘上的一点M为动点,OA为动坐标,当AM垂直OA时,点M的相对速度为。
①υr=Lωr,方向沿AM;②υr=r(ωr-ω),方向垂直AM,指向左下方;③υr=r(L2+r2)1/2ωr,方向垂直OM,指向右下方;④υr=rωr,方向垂直AM,指向在左下方。
2、直角三角形板ABC,一边长L,以匀角速度ω绕B轴转动,点M以S=Lt的规律自A向C运动,当t=1秒时,点M的相对加速度的大小αr= ;牵连加速度的大小αe = ;科氏加速度的大小αk = 。
方向均需在图中画出。
①Lω2;②0;③3Lω2;④23 L ω2。
3.圆盘以匀角速度ω0绕O 轴转动,其上一动点M 相对于圆盘以匀速u 在直槽内运动。
若以圆盘为动系,则当M 运动到A 、B 、C 各点时,动点的牵连加速度的大小 ,科氏加速度的大小 。
①相等;②不相等;③处于A ,B 位置时相等。
4.一动点在圆盘内运动,同时圆盘又绕直径轴x以角速度ω转动,若AB ∥OX ,CD ⊥OX ,则当动点沿 运动时,可使科氏加速度恒等于零。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
解: 从例6-2已知得: 1 =
vr r 3 , 2
ω 4
O
解: 从上例已知得: 1 =
r
M
ω 4
va
A
aaτ =0 ,
3 , 4
aan=2r aen=
ωr 8
x’
2
ac 21vr 2 r
va
30°
3 1 1/ s2 8
2
动点取A,
va v A
ar
dvr d 2 x ' ' d 2 y ' ' d 2 z ' ' 2 r 2 j 2 k dt dt dt dt
dx ' di ' dy ' dj' dz ' dk ' dt dt dt dt dt dt
ar ω vr
a a ae a r ac; ac= 2vr
ve
a n a ae a rn a rτ
矢量
1.瞬时状态; 2.可解两个未知量 (大小,方向)。
例6-5 曲柄滑道机构,OA=01A=r=10cm, =30°,=4, 求: 转到30°时直杆的加速度a。 va vr 动点取A; 绝对:圆周; ve 解:相对:圆周;牵连:直线。 [速度] =
a a ae a r ac; aa a an ae aen ar arn ac;
例6-8 曲柄绕O转动,並通过滑块M带动滑槽绕O′摆动, ’ y 求摆动到30°时的角加速度1。
例6-9 将例6-8滑槽改变为图示牛头刨床机构,MA=2r, 求:刨床刨刀的速度,加速度。
vr
dv e dω dr r ω dt dt dt α r ω v e ω v r ae ω v r
vr
vr′ ac
1. vr , ac =0; 2. =0, ac =0; 3. vr =0, ac =0;
dx ' ' dy ' ' dz ' ' i j k; dt dt dt
例6-6 三角楔块可在光滑地面滑动,现在楔块上放一物块可 沿光滑斜面滑下,当t=0时,x=0,y=h,v2=0,a1=10cm/s2 ,a2=10 2 cm/s2,求物块轨迹方程。 解: aax= a1+ a2 cos45°=20cm/s2 aay = –a2 sin45° = – 10cm/s2
2 2 aa aax aay 10 5;tan = aax/ aay=0.5x来自A M b vy
v
M
A b v
y
vA= 3b = 3v/4, vr v
3 2
O
30°
O
30°
aacos60°=0= aeτ–ac
ae 2vr ae 3 v2 ; 2b 8 b 2 v a A (3b ) 2 (3b 2 ) 2 0.676 b 3 v2 , 4 b
车
y x
vr
v sin α
1
例6-2 军舰以20节(1节=1.852 km⁄h)的速度前进,直升飞机以每 小时18 km的速度垂直降落。求直升飞机相对于军舰的速度 的速度垂直降落。求直升飞机相对于军舰的速度。 ` 解:动点:直升飞机。 y' 动系: :O'x'y',固连于军舰。 M
定系:固连于海岸。 定系 :固连于海岸。
ve=14r= r O
r
M
: aancos30°= ac–aeτ
aeτ 2 r 3 4
3 1/ s2 8 a e O 'M
1 1
O′
r 2 r cos30 3 va r vr 2 3
1
2
: aacos30°= ac+aeτ=2 1vr+ 1×4r
如动点为圆盘上一点, 动系在直杆上。
y
x
南
例6-12 直角杆水平匀速推动直杆绕O转动,已知:v=2cm/s, OA=L,b=L/3,求直杆转到30°时直杆A点的速度,加速度。 解: ve= vcos60° = v/2
ω ve v OM 4b
x
如动点M选在OA杆上结果如何? 速度求解尚可,但求加 速度时因轨迹变化复杂, 故向心加速度无法求解, 因此动点选取时应选该 动点不变的点,如直角 端点为动点。 va
y’
O′
vr′ vr
z
北
: aacos30°= ac –aencos60°–arn
ac 2vr ,
arn=vr2/R , aen 3e
aa
e
x′
Fc mv r sin哥氏惯性力
西
e
2
Fc vr
ac
ac
vr
东
M
水流
3
va
千百年的河流冲刷造成右岸高 于左岸(顺水流方向)。 同样火车行驶对钢轨的作用力 也有哥氏惯性力问题。
哥氏加速度
波桑公式
di dj dk ωk' ωi' , ω j'; dt dt dt
'
'
'
例6-7 空心直管绕O摆动,一个小球沿管作直线运动,试推导 加速度关系。 x ve’– ve” ' ' ” t : v a v e v r , t t : v a ve v r'; ve ve’ ' ' va ve ve va vr' v r lim a lim lim ” ve t t t t 0 t 0 t 0
A M O
a a aan ae aen a r a rn ac;
例6-13 两根T形直角杆如图组合,水平T形直角杆以匀 速v1推动,斜T形直角杆以匀速v2拉动,求滑块M的速度。 解:
y2 y1
例6-14 机构如图,销钉M能在DBE杆的竖直槽内滑动,又能在OA杆槽内 滑动,现DBE以匀速度v =20cm/s向右平动。OA杆以匀角速度ω= 2 rad/s转动。当θ=45°时,M点运动到图示位置,L=30cm。试求此瞬时 销钉M的绝对速度。 A D 解 : 以销钉M 为动点,OA为动系 从图中有:
A′ A x
B
lim
t 0
MM ' M "M ' MM " lim lim t t t t 0 t 0
vr
M”
ve y
动点绝对速度=相对速度+牵连速度 z
通过一个动点、 两种坐标,将复杂 运动分解成简单运动。
va vr ve
va
矢量
vr
x
1.瞬时状态; 2.可解两个未知量 (大小,方向)。
v M v1e v1r v 2 e v 2 r
v1= v1e, v2= v2e 投影方程求得vr1,vr2,再求得vM。
v M v1e v1r
再以销钉M为动点,DBE为动系 v1 速度有:
v M v 2e v 2r
M
L
v M v1e v1r v 2 e v 2 r
' ve v' v" v" v ve lim e e lim e e a1 ae lim t t t t 0 t 0 t 0
va vr ve
ve va vr
[速度矢量图] aC
ve vr vr vr” vr’– vr”
’
aen
aeτ aa τ
ve’ vr’
aa a A 2 r 2 3
30°
1 1
O′
3
例6-10 偏心园盘绕O转动,并推动直杆上、下运动, 求转到60°时直杆的速度a。
例6-11
河流由北朝南流动,求哥氏加速度的方向。
解: 从例6-3得: vr = R
aa
M R O
vr′= vrsin
c v r sin
第六章 点的合成运动
雨点 车 v
月 火箭
地球
运动学
韋林教授
v
两个水手决斗
§6-1 概念
AB AA A B
' '
y′
x′
y′
x′
§6-2 速度合成定理
绝对运动=相对运动+牵连运动 x'
z′
y′ vr va
M
M′
静系:固结在地面
动系:相对于地面运动 y 动点:对于动系、静系 运动 绝对运动=相对运动+牵连运动
v vr2 vr1 M B
O
M
E 在Mx轴投影,得 ve2=ve1cos45°-vr1cos45° 有:vr1=10cm/s
arn= arn= 2r =160 2
aan
x: –aan cos30°= arncos30° –ae
a n a ae a rn a r
ae 2 160 π 2
3 3 160 π 2 2
ae =a
dx 20t , dt dy 10t , vy dt vx
α
例6-3 曲柄绕O转动,並通过滑块M带动滑槽绕O′摆动, y′ 求摆动到30°时的角速度1。
ve
解:
动点取M,
绝对:转动; O
绝对速度va:大小已知,方向 大小已知,方向沿 沿 铅垂方向向下。 牵连速度ve:大小已知,方向水 平向右。 平向右 。 相对速度vr:大小方向均未知,为 所要求的量。 所要求的量 。
