恒定电场
恒定电场和交变电场的作用和应用

恒定电场和交变电场的作用和应用1. 恒定电场1.1 定义恒定电场是指电场强度和方向不随时间变化的电场。
在理想情况下,恒定电场的电场线是直线,且电场强度在空间和时间上都是恒定的。
1.2 作用1.电荷分离:在恒定电场的作用下,正负电荷会分别移向电场的相反方向,从而实现电荷的分离。
2.电荷加速:带电粒子在恒定电场中会受到电场力的作用,从而产生加速度,实现电荷的加速。
3.电势差:恒定电场中,电场线与等势面垂直,因此可以通过电场线来确定电势差,进而计算电能。
1.3 应用1.静电场计算:在工程和物理问题中,经常需要计算在恒定电场中的电势、电场强度等物理量。
2.静电平衡:在静电场中,带电体的电荷分布会受到恒定电场的影响,从而达到静电平衡状态。
3.电容器设计:电容器是存储电能的装置,其工作原理就是基于恒定电场下的电荷存储。
2. 交变电场2.1 定义交变电场是指电场强度和方向随时间变化的电场。
交变电场的特点是电场强度和方向周期性变化,形成电场矢量在空间中的旋转。
2.2 作用1.电荷周期性运动:在交变电场中,带电粒子受到周期性变化的电场力,从而产生周期性运动。
2.电磁感应:交变电场可以通过电磁感应现象产生磁场,或者通过变化的磁场产生交变电场。
3.能量传输:交变电场是交流电信号传输的基础,可以有效地传输电能和信息。
2.3 应用1.交流电装置:交变电场是交流电灯、交流电动机、交流发电机等设备工作的基础。
2.信号传输:在无线电通信、有线通信等领域,交变电场是信号传输的重要手段。
3.电磁兼容性:交变电场的存在可能导致电磁干扰,因此在电子设备设计中需要考虑电磁兼容性。
3. 恒定电场和交变电场的比较恒定电场和交变电场在作用和应用上有很大的不同。
恒定电场主要涉及电荷的分离和加速,适用于静电场计算和电容器设计等领域。
而交变电场涉及电荷的周期性运动和能量传输,适用于交流电装置和信号传输等领域。
4. 结论恒定电场和交变电场是电磁学中的基础概念,它们在日常生活和工业应用中扮演着重要的角色。
恒定电场的源

恒定电场的源
一个恒定电场是由一个永久性电荷分布所产生的,这个分布是恒定的,也就是说它不会改变。
因此,恒定电场的源必须是一个永久性的电荷分布。
电荷的永久性分布可以来自自然界中被发现的各种材料。
例如,氢原子具有一个稳定的电荷分布,它的原子核包含一个正电荷和单位质量的电子,因此形成了一个恒定的电荷分布。
其他元素也具有稳定的电荷分布,有些具有正电荷,有些具有负电荷,但它们总体上为电荷分布提供了恒定的状态。
另一个恒定电场源是人工制造的电荷分布,如电容器中的电荷分布。
电容器是由一个金属片和一个绝缘物料构成的一个简单的装置,金属片负责吸收正电荷,绝缘物料负责吸收负电荷。
当给电容器通电时,电荷会被向内积累,形成一个恒定的电场,而当断开电容器时,电荷会慢慢散发,这种电场会渐渐减弱。
有时候,电荷的永久性分布可以从无电荷开始通过一系列过程慢慢发展。
比如,当静电场在两个金属片之间引起电容器的充电时,由此产生的电荷分布就会变成恒定的电场,这种慢慢发展的电荷分布也能产生恒定的电场。
恒定的电场也可以通过磁场来产生。
例如,当一个磁体放入空气中,会在磁体周围产生电场,这个电场是恒定的,不会随着时间的改变而改变。
总的来说,电荷分布是恒定电场的源,无论这种电荷分布是自然
界中被发现的还是人工制造的,或者来自磁场,都能形成恒定的电场。
恒定电场的特点

恒定电场的特点
1. 嘿,你知道吗,恒定电场那可是相当稳定啊!就好比你走在一条直直的路上,不用担心突然有什么大的波动。
比如说电池提供的电场,那可一直稳稳的呢,这多可靠啊!
2. 哎呀呀,恒定电场还有个特点呢,它的电场强度是恒定的呀!这就好像是你的好朋友,一直那么靠谱,始终保持一个样。
比如在一个稳定运行的电路中,电场强度就是不变的哟,厉害吧?
3. 恒定电场还有一点很牛哦,电流密度是均匀分布的呢!想想看,就像把糖果平均分给小朋友们一样,多公平呀。
就像在一个均匀的导体中,电流就是这样均匀分布的,是不是很神奇?
4. 嘿哟,恒定电场里电荷的分布也是很有规律的呀!这简直就像是士兵排队一样整齐。
比如在一个电容器中,电荷就会有规律地分布呢,这简直太妙啦!
5. 哇塞,恒定电场可是一直持续不间断的哟!简直就像是永不停歇的小火车。
就比如家里一直通电的电线,那电场可是一直都在呀,是不是很厉害?
6. 还有啊,恒定电场基本不受时间影响哦!这就好似时间在它面前都没啥作用。
好比一个古老的钟表,自顾自地走着,一直保持稳定。
你说说,恒定电场是不是很特别呀?
结论:恒定电场有着诸多独特又稳定的特点,这些特点让其在各种电学现象和应用中发挥着重要作用,真的是很了不起呢!。
恒定电场

S
R1 r
R1
电导
G I h ln R2 U R1
3.4.2 多电极系统的部分电导
三个及以上良导体电极组成的系统,任意两个电极之间的
电流不仅要受到它们自身间电压的影响,还要受到其他电极 间电压的影响。电压与电流的关系,不能再仅用一个电导来 表示,需要引入部分电导的概念。
第三章恒定电场
分界面可近似地看作等位面。
例3-3 铁1=5×106S/m,土壤2=102S/m,已知铁中电流J1
与法线的夹角1=895950,求土壤中电流J2与法线夹角。
解:根据
tan1 tan 2
1 2
5 10 6 10 2
5 10 8
当1=895950时,可得 2=8
第三章恒定电场
12
3.2.4 载流导体与理想介质
载流导体外的理想介质中,没有电流 J2=0 ,存在电场E2
D2 = 0
E2 = 0
22 = 0
由分界面衔接条件 J1n=J2n=0。 可知,载流导线内电流和场强 只有切线分量
J1 = Jt E1= E1t = J1t / 1
也就是说,无论导线如何弯曲,电流线和电力线同样弯曲。
6.091020 (C
/ m)2
第三章恒定电场
11
3.2.3 从良导体进入不良导体
设两种导电媒质的电导率12
tan1 1 tan 2 2
J1
1900
J2
20
可见,只要 190,tan1∞,
12
则 tan 20,20 。
电流从良导体进入不良导体时可看为与分界面垂直,
第三章恒定电场
20
恒定电场与恒定磁场

A
于是跨步电压为
r d
E dr
I 2 (r d )
U A B
1 1 ) 2 r d r I d 20 0.8 3.9(V ) 1 2 r d 2 10 3 2.2 (
l H dl I
s B ds 0
安培环路定律
磁通连续性原理
7
§4.2 恒定磁场的基本方程和边界条件
二、恒定磁场的边界条件
两种不同媒质的分界面上恒定磁场的边界条件为: n (4.2 6) ˆ ( H1 H 2 ) J s ( B1 B2 ) 0 (4.2 7) 在不同媒质的分界面上,磁通密度的法向分量永远是连续的,而磁场强 度的切向分量仅当分界面上不存在面电流时才是连续的。 在分界面上不存在面电流时,恒定磁场的边界条件化为: H1t H 2t (4.2 8) B1n B2 n (4.2 7) 若媒质的磁导率,→∞称为理想导磁体。 某些边界可近似为理想导磁体边界,称为磁壁, 该壁上切向磁场为0;
E
的关系是欧姆定律的微分形式 J E
l s
E dl 0, J ds 0,
引入电位函数 E
得到无源区电位函数方程(拉普拉斯方程)
2 0
1
§4.1 恒定电场
二、恒定电场的边界条件
在具有不同电导率1和2的两种导体的分界面上
E1t E2t , J1n J 2n
§4.1 恒定电场
Steady Electric Field
一、恒定电场基本方程
恒定电场是电磁场的特例, 满足条件
F 0 t
恒定电场
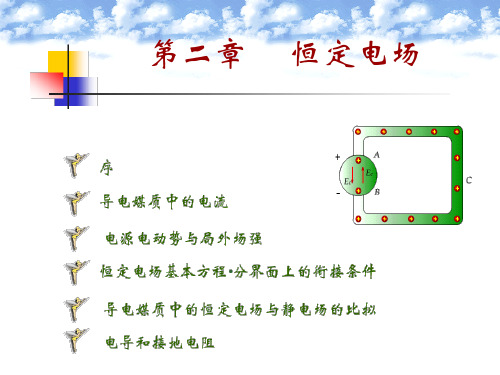
图2.5.1
同轴电缆横截面
绝缘电阻
1 1 ln R2 R G 2l R1
I dI J lim n n S 0 S dS
单位: 安培/米2 (A/m2)
电流密度
可以从电流密度J求出流过任意面积S的电流强度。一
般情况下,电流密度J和面积元dS的方向并不相同。
此时,通过面积S的电流就等于电流密度J在S上的通
量,即
I J dS JdScosθ
R2
1
U 0 e
电流 电导
I J dS
U 0 U h R (e ) hd (e ) 0 ln 2 S R R1 I h R2 G ln ( S m) U 0 R1
2.5.2
接地电阻
安全接地与工作接地的概念
接地器电阻
接地电阻 接地器与土壤之间的接触电阻 土壤电阻(接地电阻以此电阻为主) 1. 深埋球形接地器
•
• •
两种场的电极形状、尺寸与相对位置相同(相拟);
相应电极的电压相同; 若两种场中媒质分片均匀,只要分界面具有相似
r1 1 r2 2
的几何形状,且满足条件
时,则这两种场
在分界面处折射情况仍然一样,相拟关系仍成立。
2.4.3
静电比拟的应用
1. 静电场便于计算—— 用静电比拟方法计算 恒定电场
2 0
D1n D2n
I J dS
S
2 0
S
q D dS
E1t E2t
3-恒定电场

γ2
=
γ1 γ1
+
I’
γ2 γ2
镜像法
γ1 −γ 2 I′ = I γ1 +γ 2
2γ 2 I ′′ = I γ1 +γ 2
实验——用恒定电场实验模拟静电场 用恒定电场实验模拟静电场
模拟法就是应用一种具有中等导电率的媒质代替静电场所 在空间的介质或真空; 在空间的介质或真空;另外一种具有高导电率的导体制成电极 使其形状与形成静电场的导体电极相同。 使其形状与形成静电场的导体电极相同。在模拟电极上加上与 原静电场中电极上电位成比例的电位, 原静电场中电极上电位成比例的电位,于是在导电媒质中形成 恒定电流场。 恒定电流场。 v v 完全相同。 这个恒定电场的 E 与静电场中的 E 完全相同。电位分布也 必然与被模拟的静电场的电位分布完全相同。 必然与被模拟的静电场的电位分布完全相同。 实际的模拟装置有电阻纸、电解槽、电阻网络等。 实际的模拟装置有电阻纸、电解槽、电阻网络等。
第3章 恒定电场 章
导体内电场如何求解? 导体内电场如何求解? 1. 2. 3. 4.
恒定电场的特点
导体电位差? 导体电位差?
电荷处于动态平衡状态。 电荷处于动态平衡状态。 导体内电场不为零,表面不是等位面。 导体内电场不为零,表面不是等位面。 外电源供给的能量用于电荷克服阻力运动——转化为热能。 转化为热能。 外电源供给的能量用于电荷克服阻力运动 转化为热能 对导电媒质以外而言场相对稳定----与静电场相似 相似, 对导电媒质以外而言场相对稳定 与静电场相似,可用静电场 方法求解。 方法求解。 恒定电场周围还有恒定磁场,二者互不激发,均可分别讨论。 恒定电场周围还有恒定磁场,二者互不激发,均可分别讨论。
J 2n
恒定电场

Fk 反抗 Fe
断路:
作用机理: 做功,
将其他形式能转变为电能
Fe
K
U
Fk Fe
Fe
Fk Fe
时平衡
R
外电路: Fe 作用,将 q由正极 负极
通路
内电路: Fk Fe 将 q 由负极 正极
Fk , Fe 共同作用形成持续电流 .
空间电荷分布不变(流入 = 流出),电场分布不变
一.
电流密度矢量
自由电子、正负离子、 载流子:
1. 电流的形成 传导电流 电流
电子—空穴对…
电场
位移电流
金属导电的经典解释: 电场中,自由电子除热运动外, 叠加定向加速运动.
频繁碰撞使加速运动间断进行, 其平均效果为定向匀速运动——漂移运动.
漂移速率 u: 比较
1)静电力所做总功为零; 2)非静电力所做总功为零; 3)静电力和非静电力做功代数和为零; 4)在电源内只有非静电力做功, 在外电路只有静电力做功。
三.
欧姆定律与焦耳定律的微分形式 欧姆定律 焦耳定律
积分形式 微分形式
U I R
电流密度
Q I 2 Rt;
热功率密度
P I 2R
j E
Fe
K
Fk Fe
Fe
R
试比较电源路端电压和电源电动势这两个概念
电源路端电压 电源电动势
比较
U
E e dl
E k dl
(经外电路)
(经内电路)
练习:
单位正电荷从电源正极出发,沿闭合回路一周, 又回到电源正极时,下列哪种说法正确?
第四章 恒定电场和恒定磁场

E , 2 0
E1t E2t
1 2 , 1
J E
D1n D2n
1 2 2 n n
J1n J 2n
1 2 2 n n
静电场
对应物理量
12
恒定电场
E E
D
q
I
J
C G
电磁场与波
和夹角为 0的两半径割出的一段环形导电媒质,如图所示。计算 沿方向的两电极之间的电阻。设导电媒质的电导率为σ。 解: 设在沿方向的两电极之间外加电压U0,则电流沿 方
向流动,而且电流密度是随变化的。但容易判定电位Ψ 只是变
量 的函数,因此电位函数Ψ 满足一维拉普拉斯方程
2 1 0 2 2 , z不变,变量
此时,良导体表面可近似地看作为 等位面; 若媒质1为理想介质,即1=0,则 J1=0,故J2n=0 且 E2n=0,即导体中
媒质1
E1
媒质2
E2 2
( 2 1 )
1 2
媒质1 1 0 媒质2
ˆ n E1
的电流和电场与分界面平行。
9
E2
2
( 1 0)
2
2u 1 u 1 2u 2u 2 2 2 z
方程通解为
C1 C2
0
r2
代入边界条件 可以得到
20
U0 ,
0
0
0
J σ
h r1
C1 U 0 / 0 , C2 U 0
流密度的切向分量并不连续。
理想导体与另一导体的分界面处,将只可能存在法向的恒定电 场和恒定电流。
恒定电场形成的机制

恒定电场形成的机制众所周知,恒定电场是指电场强度不变的特殊情况,即电子耦合不变。
恒定电场在电子设备、光学仪器、医疗器械和高精度仪器仪表等领域都有着广泛的应用。
因此,了解恒定电场形成机制及原理,对于优化这些装置的工作环境,提高设备的精度和可靠性,都急需研究和解决。
首先,恒定电场的形成是基本现象,由多个空间上的相互作用的原子构成的。
这些原子的形成一定会影响其控制对象的电和磁恒定场,最终形成恒定场。
从物理机理上来讲,在电恒定场中,具有四种类型:单原子恒定电场、空间恒定电场、局部恒定电场和全部恒定电场。
其中,单原子恒定电场是由原子的电子孤子耦合形成的,这些电子孤子均具有相同的势能,这将会影响其力学行为,最终形成恒定电场;空间恒定电场是由连续的晶体中电子的相互耦合作用形成的,通过电子的耦合作用,整体的电子系统的能量也将恒定。
局部恒定电场是由多个相互作用的电子组成的,当电场的强度与介质形成恒定状态时,它就会形成一个局部恒定电场。
而全部恒定电场,则依赖于对晶体中受控制元素的电磁耦合作用,从而产生恒定的结果。
此外,另一重要的影响因素是材料本身,材料可分为导体、介质、超导体等,每种材料都有不同的特性,因此也会影响恒定电场的形成。
对于导体材料,其电子的耦合作用极强,它的电性和热性特性也极强,从而影响恒定电场的形成;对于介质材料,由于其较弱的电子耦合作用,它可以产生恒定的电场,因为每个电子的活动会在介质中起到抵消作用,最终形成恒定电场;超导体由于其特殊的电子耦合作用,当电子耦合力强时,其特性会发生改变,而在一定温度下,其特性会发生变化,由此形成恒定的电场。
此外,电子耦合作用也会影响恒定电场的形成,电子耦合作用具有相互作用的特点,也就是说电子不断的相互作用,最终能形成恒定的电场。
电子耦合还可以和材料相结合,当材料具有良好的电子耦合作用和电磁耦合作用时,其原子形成恒定场,电子耦合作用可以保持这种恒定场状态稳定不变。
由以上分析可知,恒定电场的形成包括了电子耦合作用、材料本身和多个空间上的相互作用的原子构成等,电子耦合作用最终可以稳定恒定电场的强度,材料本身也可以影响电场的强度及其耦合作用,而由于多个空间上的相互作用的原子构成的的影响,可以使电场的强度保持恒定状态。
静电场和恒定电场的异同

静电场和恒定电场的异同
静电场和恒定电场是电场的两种特殊情况,它们之间有一些异同之处。
一、相同点:
1. 都是电场:静电场和恒定电场都是指电荷周围的电场,都是由电荷所产生的电场。
2. 都是稳定的:静电场和恒定电场都是稳定的,即它们的电场强度和分布不会随时间变化。
3. 都符合库仑定律:静电场和恒定电场都符合库仑定律,即电荷之间的相互作用力与它们之间的距离的平方成反比。
二、不同点:
1. 定义不同:静电场是指电荷周围的电场,其中的电荷是静止的;而恒定电场是指电荷周围的电场,其中的电荷在运动,但是速度不变。
2. 电场强度的变化:静电场中,电荷周围的电场强度是由静止电荷所产生的,因此电场强度不会随时间变化;而恒定电场中,电荷在运动,因此电场强度会随
时间变化。
3. 电荷的运动:静电场中,电荷是静止的,不会发生运动;而恒定电场中,电荷在运动,但是速度不变。
4. 电场的形状:静电场中,电荷周围的电场呈球对称分布;而恒定电场中,电荷周围的电场呈线对称分布。
5. 应用不同:静电场主要应用于静电学中,如电荷的积累、电荷的移动等;而恒定电场主要应用于电路中,如电流的流动、电势差等。
综上所述,静电场和恒定电场在定义、电场强度的变化、电荷的运动、电场的形状、应用等方面存在一些异同之处。
了解它们的异同,可以更好地理解电场的性质和应用。
恒定电场

什么是恒定电场?
处于静电场中的导体,其内部的电场强度为零。 如果将导体与电源的两极相连,则导体内部就会 有电流产生。而想要维持电流的存在,则导体内 部的电场强度就不为零。那么这个维持电流的电 场就是恒定电场。 电流的描述 电流强度 I 就是单位时间流过导线某一截面的电 荷量
dq I dt
的电位要满足拉普拉斯方程。
2 0
边界条件
E1t E2 t J 1n J 2 n
7
第四章 恒定电场
对于电位,则有
1 2 1 2 1 n 2 n
8
第四章 恒定电场
恒定电场与静电场的比拟 均匀导电媒质中的恒 均匀电介质中的静电 定电场(电源外部) 场( 0 的区域)
J 0 微分形式 E 0 本构方程 J E
6
第四章 恒定电场
同静电场一样,由于 E 0 ,所以我们可以 引入一个标量函数电位 ,有 E 。 将其带入 J 0 ,我们同样可以得到恒定电场
第四章 恒定电场
电流密度 J 就是在垂直于电荷流动方向的截面上, 某点处单位面积内的电流总量,那么通过面元 dS 的电流为
dI J d S
I
流过任意截面 S 的电流强度为
S
J dS
2
第四章 恒定电场
图 4.1 电流与电流密度
(a) 体电流;(b) 面电流;(c) 线电流
基本方程
S J d S 0 l E dl 0 J 0 E 0
S D d S 0 l E dl 0 D 0 E 0
第三章 恒定电场

11
单位长度上所消耗的功率
P = ∫ P0 dV = ∫ γE dV = γ ∫
2 V V
R2
R1
U0 R ln (R R ) 2πRdR 2 1
2
2πγU 02 = ln (R2 R1 )
单位长度上的绝缘电阻
U 0 ln R2 R1 R0 = = I 2πγ
(3-10) 10)
2
6
§3-3
1 电流连续性方程
恒定电场的基本定理
在任意恒定电场中, 在任意恒定电场中,作任意闭合曲 面S,由电荷守恒定律得 ,
v ∂q 11) ∫S δ ⋅ dS = I = − ∂t (3-11) v
在恒定电流场中, 在恒定电流场中,
∂q ∂t = 0
(3-12) 12)
v ∴ ∫ δ ⋅ dS = 0
ϕ
用拉普拉斯方程来求解。 解 用拉普拉斯方程来求解。选 ϕ 用圆柱坐标系, 有关, 用圆柱坐标系, 仅与坐标α 有关, 而与r、 坐标无关 坐标无关, 而与 、z坐标无关,拉普拉斯方 程简化为
∇ 2ϕ 1 ∂ ∂ϕ 1 d 2ϕ d 2ϕ = + 2 r + 2 2 r ∂r ∂r r dα dz 1 d 2ϕ ∴ 2 =0 2 r dα
2U 0
通过薄钢片截面的电流
v R2 2γU 2γU 0 h R2 0 I = ∫ δ ⋅ dS = ∫ hdr = ln S R1 πr π R1 v
15
因此电极之间的电阻
U0 π R= = R2 I 2γh ln R1
最后, 最后,代入已知数据
60 ×10 −3 2 × 5 ×106 × 4 ×10 −3 × ln 30 ×10 −3 = 1.13 ×10 − 4 Ω
恒定电场ppt课件
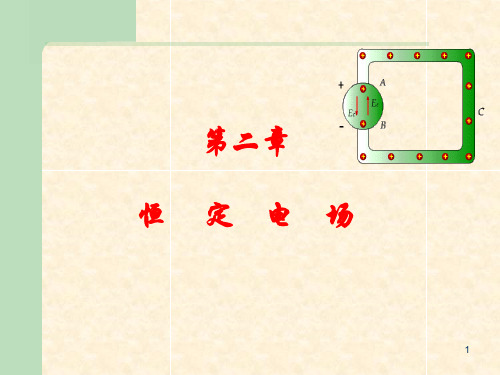
即:
E • d l E • d S 0 导电媒质(电源外)的恒定电场
l
S
为无旋场、保守场
微分形式: E0
18
§2.3.3 恒定电场的基本方程
一、基本方程:
导电媒质(电源外)的恒定电场:
SJ•dS0
积分形式:
lE•dl 0
微分形式:
JE
•J0
E0
JE
二、导电媒质(电源外)的恒定电场的性质:
或: 2=1
2
2
n
1
1
n
J2t
J1n
P
2
1
J1t
J1
J2 J2n
20
§2.3.4 分界面上的衔接条件
二、良导体1与不良导体2的分界面: 1 >> 2
由折射定律: tg 1 /tg 2 = 1 / 2
tg2 2 0 tg1 1
若1≠900
结论:
2 很小
钢 5106 S m
P
1
J1
土壤 10-2 S m
1. 无源场,电流线总是连续的(无头无尾的闭合曲线);
2. 无旋场,保守场(电位存在的前提)
19
§2.3.4 分界面上的衔接条件
一、媒质1与媒质2的分界面:
1 2
若分界面上无局外场的存在:
lE•dl 0
E1t = E2t
SJ•dS0
J1n = J2n
JE tg 1 /tg 2 = 1 / 2
折射定律
电荷守恒定律:由任一闭合面流出的传导电流,
应等于该面内自由电荷的减少率。
积分形式: 微分形式:
q
SJ•dSt
•J
t
S J•dSV •Jd V Vtd V
第二章恒定电场
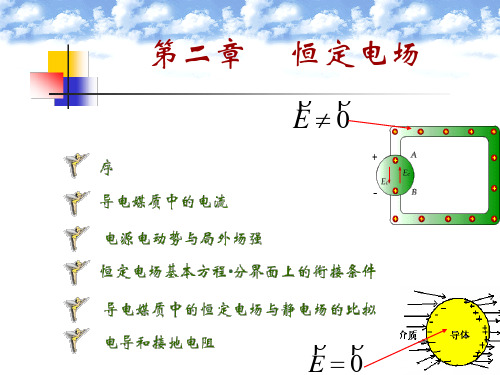
τ 分布的线电荷沿着导线以速度 v 运动形成的电流I = τv 。
图2.1.4
媒质的磁化电流
图2-3 电流元示意
r r 注意: 电流密度的符号通常用 的符号通常用: 注意:1) 电流密度的符号通常用:J , K , I 2) 电荷密度的符号通常用: , σ , τ 电荷密度的符号通常用 ρ 的符号通常用:
γ 1 >> γ 2
α1 ≠ 90 o
α 2 ≈ 0o
J2 n°
例如,钢的电导率 γ1 = 5×106 S/m,周围土壤的电 例如 导率γ2 = 10-2 S/m,α1 = 89°,可知,α2 ≈ 8″。 良导体表面可近似看作为等位面 (3) 导体与理想介质分界面上的边界条件
J 2n = 0
γ2 γ1
γ 1 E1n = γ 2 E 2 n
J2
ε2E2n −ε1E1n =σ
γ2, ε2
P
σ
ε 2γ 1 − ε 1γ 2 σ= J 2n γ 1γ 2
γ1, ε1
J1
1-3-1 有恒定电流通过两种不同的导体媒质 介电常数和 有恒定电流通过两种不同的导体媒质(介电常数和 的分界面. 电导率分别是 ε1, γ 1和ε 2 , γ 2)的分界面 问若要使两种电解 的分界面 质分界面处的电荷面密度为零, 则应该满足何条件. 质分界面处的电荷面密度为零 则应该满足何条件
包括良导体和不良导体). 中(包括良导体和不良导体 包括良导体和不良导体 2) 前者场强处处为零并且为等位体;后者 库仑 场强 前者场强处处为零并且为等位体;后者(库仑 库仑)场强 一般不为零并且为非等位体. 一般不为零并且为非等位体 3) 电场为恒定电场的条件为任何闭合面电流量对 时间导数为零。 时间导数为零。
第四章 恒定电场

= q ∫ E ′ ⋅ dl = q ∫ E ′ ⋅ dl
C1 C
= qξ
在引入外部电动势的情况下, 欧姆定律可写为 在引入外部电动势的情况下,
∇ ⋅ J = ∇ ⋅ [σ ( E + E ′)] = 0 ⇒ ∇ ⋅ (σE ) = −∇ ⋅ (σE ′)
11
J = σ ( E + E ′) ⇒
∇⋅B = 0 ∇ × H = J
J =σE
and
D = εE
4
可知: 由 ∇⋅ J = 0可知:
D ∇ ⋅ J = 0 ⇒ ∇ ⋅ (σ E ) = 0 ⇒ ∇ ⋅ σ = 0 ε
σ ⇒ ρ = 0 ⇒ ρ = 0 ε
∴选择 J 代替 D ,则方程变成
∇ ⋅ D = ρ and ∇ × E = 0
9
三、电流稳定分布的必要条件
恒定电流体系最为重要的特点是内部会不断产 焦耳热,即电磁能将不断损耗。因而, 生焦耳热,即电磁能将不断损耗。因而,体系 保证电流稳定流动 必要条件 必须有 电流稳定流动的 条件是 要保证电流稳定流动的必要条件是必须有外来 电动力, 外来电动 电动势 的电动力,即外来电动势。
I = ∫ J ⋅ dS 为一常数,此种情况称为恒定电流。 为一常数,
S
恒定电流可分为 导电媒质 中的自由电子运动所形成的 传导电流和真空中电子或离子运动所形成的运流电流。
2
电流密度可表示为: 电流密度可表示为:ห้องสมุดไป่ตู้
J = ρυ 或 J = ∑ J i = ∑ ρυ
由电荷守恒定律可知
由于 ∇ ⋅ J = 0 ,则体电荷密度 ρ
dQ ∂ρ ∫SJ ⋅ dS = − dt ⇒ ∫V∇ ⋅ JdV = −∫V ∂t dV ∂ρ ⇒ ∇⋅ J = − ∂t
恒定电场知识点总结

恒定电场知识点总结首先,我们需要了解什么是电场。
电场是一种物理场,描述了电荷之间相互作用的力。
在空间中的任意一点,如果放置一个试验电荷,它会受到电场力的作用。
电场可以由其他电荷所产生,也可以通过外部装置如电容器、电偶极子等来产生。
在典型的静电学问题中,我们经常研究恒定电场,也就是描述电场中的电荷分布是不随时间变化的。
在恒定电场中,我们能够推导出一些重要的规律和定律来描述电场中电荷的受力和运动。
下面,我们将在本文中详细探讨恒定电场的知识点,并且总结其重要的概念和定律。
1. 电场强度电场强度是描述某一点上电场强度大小和方向的物理量。
在恒定电场中,电场强度是一个常矢量,表示了电场在该点上对单位正电荷的力。
当我们插入一个试验电荷到电场中,该电荷所受到的电场力就是电场强度的矢量乘以电荷的大小。
电场强度的方向指向电场力的方向,大小则表示了单位正电荷所受到的电场力。
电场强度可以用数学公式来表示,在恒定电场中,它通常可以由电场势能的梯度来描述。
在直角坐标系中,电场强度的三个分量可以表示为:\[ \vec{E} = -\nabla V \]其中,E是电场强度的矢量,V是电场的电势。
这个公式用数学上的梯度运算符$\nabla$来表示,表明了电场强度和电势之间的关系。
通过计算电场势能在某点上的梯度,我们可以得到该点上的电场强度。
2. 超定定电场在超定定电场中,电场强度不仅与电场势能有关,而且还与场中存在的其他电荷分布有关。
在这种情况下,电场强度的计算要考虑到所有的电荷对于某一点上的贡献。
一般来说,我们会利用库仑定律来描述这种超定定电场下的电场强度。
库仑定律给出了两个电荷之间的电场强度与它们之间距离平方的关系:\[ \vec{E} = \dfrac{1}{4\pi\epsilon_0} \dfrac{q}{r^2} \hat{r} \]其中,$\vec{E}$是电场强度,q是电荷大小,r是电荷之间的距离,$\epsilon_0$是真空中的介电常数(8.85×10^-12 F/m)。
chapter3-恒定电场(zhang)

恒定电场
什么是恒定电场?
静电场:静止电荷产生的电场—静态平衡 恒定电流:
电荷的流动不随时间改变—动态平衡
恒定电场: 维持恒定电流的电场为恒定电场 传导电流—导电煤质中
传导电流是指大量排列在一起的电荷在受到外电场力的作用之下,朝着一个 固定的方向移动,因而实现电能的传导的。 每一个电荷位移十分微小的,仅仅在平衡位置附近运动。但由于电荷排列的 紧密,受力电荷通过与相邻电荷的碰撞,将能量传导给下一个电荷,瞬时传 到很远的地方。
解法二
U
I J dS J 2πrl
r
R2
R1
E
I E J 2πrl I
2π Rl
l
R2 dr I R2 U E dr ln R1 2π lr 2π l R1
I,J,E,P
2
恒定电场的基本性质
2.1 电流连续性方程:
从任一闭合面流出的总电流
(2)电流强度与电流密度的关系: I
S J dS
(3)运动电荷的体电流:已知运动电荷的体密
度v及运动速度v,如果在电流区域某点取一面
元dS垂直于电流方向,则在dt时间内,穿过dS的 电荷为:
dq v vdtdS
则:
J
dI dq / dt v v dS dS
J v v
J E
•
欧姆定律的积分形式只适用于稳恒情况,而欧姆定律的微分形式不仅对
稳恒情况,而且对非稳恒情况也适用。
例3-1:运用欧姆定理的微分形式推导图中均匀导电材料(长度为L,导电率为, 横截面为S)中的电压与电流关系式。 L 解:在导电材料内部,有:J=E,J与E的方向均与电流方向一致。在导体两 端点之间有:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
恒定电场
恒定电场的基本方程与电路的基本定律
J dS 0
s
l1
应用到电 路的结点
I 0
应用到电 路的回路
l E dl E dl E dl
l2
U 1 U 2 U 0
恒定电场的基本方程是基尔霍夫定律的场的表示。
上 页
下 页
第 二 章
1. 基本方程 (Basic Equations)
① E的闭合线积分及旋度
l E dl
l( Ec Ee ) dl l Ec dl l Ee dl e
斯托克斯定理
若所取积分路径不经过电源区,则
l E dl 0
得
s ( E ) dS 0
恒定电场
2. 分界面上的衔接条件(Boundary Conditions)
采用与静电场类比的方式可以方便的得 到恒定电场中不同媒质分界面的衔接条件。
静电场(=0) 恒定电场(无源区)
E dl 0
l
E1t E2t
l E dl 0
D dS 0
s
D1n D2 n
上 页 下 页
第 二 章
恒定电场
通解
1 A B ,
2 C D
4 2U 0 ( 1 2 )U 0 电位 1 ( 1 2 ) 1 2
4 1U 0 2 ( 1 2 )
氢氧燃料电池示意图
上 页 下 页
第 二 章
恒定电场
3. 太阳能电池(光能电源)
一块太阳能电池电动势0.6V。太阳光照射到P-N结上, 形成一个从N区流向P区的电流。约 11%的光能转变为电 能,故常用太阳能电池板。 一个50cm2太阳能电池的电动势0.6V,电流0.1A
太阳能电池示意图
上 页 下 页
+
U -
Et
静电场
恒定电场
上 页 下 页
第 二 章
恒定电场
+ + + 导线端面电荷 引起的电场
-
+ + + 导线侧面电荷 引起的电场
-
+ + + 所有电荷引起 的电场叠加
-
③ 导体不是等位体; ④ 导体媒质内外伴随有磁场和温度场。
3.导电媒质周围介质中的恒定电场 介质中的恒定电场是导电媒质中动态平衡电荷 所产生的恒定场,与静电场的分布相同。
恒定电场 是无旋场
上 页 下 页
E 0
第 二 章
恒定电场
② J 的闭合面积分及散度 电荷守恒原理
0 在恒定电场中 t
q s J dS t
s
故
J dS 0
散度定理
v JdV 0
恒定电场 是无源场
J 0
上式亦称电流连续性方程,即流进的电流等于流 出的电流,电流线是闭合曲线。
上 页 下 页
第 二 章
恒定电场
4. 焦尔定律的微分形式 导体有电流时,必伴随功率损耗,其功率为
P UI
设小块导体
W
dP ( J dS ) ( E dl ) J EdV
功率密度
J 与 E 之关系
J p J E γE γ
2
2
W/m
3
Joule’s Law微分形式
1 2 1 1 E1n 2 E1n 1 E1n 2 1 2
表明
一般情况下介质交界面上总有净自由电荷存在
上 页
下 页
第 二 章
恒定电场
折射定律
tan1 J1t J1n J1t tan 2 J 2 t J 2 n J 2 t
1 E1t 1 2 E2 t 2
分界面上电位 的衔接条件 由
电流线的折射
E1t E2t J1n J 2n
1 2
1 2 1 2 n n
上 页 下 页
第 二 章
恒定电场
讨论 ① 良导体与不良导体的交界面。
1 2
tan1 1 tan 2 2 tan α1 2 tan 2 0 1
上 页 下 页
第 二 章
恒定电场
注意
本章主要讨论导电媒质中的恒定电场。
4.研究恒定电场的意义
① 进一步理解直流电路中的有关规律; ② 解决绝缘电阻、接地电阻的计算等实际问题; ③ 为实验方法研究场的问题提供理论依据。
上 页
下 页
第 二 章
恒定电场
2.1 导电媒质中的电流
Current in Conductive Media 1. 电流 (Current) 定义:单位时间内通过某一横截面的电量。
电流线密度及其通量
上 页 下 页
第 二 章
恒定电场
面电流的实例
媒质磁化后的表面磁化电流; 同轴电缆的外导体视为电流线密度分布; 高频时,因集肤效应,电流趋于导体表面分布。 ③ 元电流的概念 线电荷 在曲线上以速度 v 运动形成的电流
dI v
媒质的磁化电流
上 页
下 页
第 二 章
恒定电场
上 页 下 页
第 二 章
恒定电场
③ 恒定电场(电源外)的基本方程 积分形式 微分形式
s J dS 0
E dl 0
l
J 0
E 0
J E
说明
J E
恒定电场是无源无旋场,在无源区是守恒场。
上 页 下 页
第 二 章
恒定电场
④ 电位方程 由基本方程出发 =常数
上 页
下 页
第 二 章
恒定电场
2.2
1. 电源 (Source)
电源电势与局外场强
Source EMF and 0ther Field Intensity
提供非静电力将其它形式的 能转为电能的装置称为电源。 2. 电源电动势 (Source EMF)
恒定电流的形成
电源电动势是电源本身的特征量,与外电路无关。
J1n J 2n
s J dS 0
说明分界面上 E 切向分量连续,J 的法向分量连续。
上 页 下 页
第 二 章
恒定电场
在不同媒质分界面上
J 1n J 2 n
D1n D2 n
注意
1 E1n 2 E2 n
1 E1n 2 E2 n
有关静电场的定律适用于恒定电场, 因静电场是恒页 下 页
第 二 章
恒定电场
恒定电场与静电场不同之处
① 有推动自由电荷运动的电场存在,说明E不仅存在于 介质中而且存在于导体中;
② 电流恒定说明流走的自由电子被新的自由电子补充,空 间电荷密度处于动态平衡,因而场分布不同于静电场; En + U -
1
2
α1
α2
2 0
表 明
0
E1t E2t 0
1)不良导体中电流线与良导体界面几乎垂直。
2)良导体可以近似认为是等位体。
3)可以用电流场模拟静电场。
上 页 下 页
第 二 章
恒定电场
讨论 ② 导体与理想介质的分界面 在理想介质中
J 1n J 2 n 0
导体与理想介质分界面
2 0, J 2 0
0 空气中 E2n = 0 2 0
J 2n
导体中
E1n 0
D2n D1n 2 E 2n
E1t E2t J1t / 1 0
表 明
1)分界面导体侧的电流一定与导体表面平行。 2)导体与理想介质分界面上必有面电荷。 3)电场切向分量不为零,导体非等位体,导体表 面非等位面
上 页 下 页
第 二 章
恒定电场
讨论 ③ 理想导体与理想介质的分界面。
1
E1 0
J1 1 E1 有限值
1
2 0
E 2 E2 n
E1t E2 t
E 2 E2 n
表 明
1)理想导体中电场为零,沿电流方向没有压降 2)理想介质中的E垂直于导体表面。
上 页
下 页
第 二 章
恒定电场
实际电源
1. 干电池和钮扣电池(化学电源)
干电池电动势1.5V,仅取决于(糊状)化学材料,其大 小决定储存的能量,化学反应不可逆。 钮扣电池电动势1.35V,用固体化学材料,化学反应不可逆。
钮扣电池
干电池
上 页 下 页
第 二 章
恒定电场
2. 燃料电池(化学电源)
电池电动势1.23V。以氢、氧作为燃料。约40-45%的化学能 转变为电能。实验阶段加燃料可继续工作。
第 二 章
恒定电场
第二章 恒定电场
Steady Electric Field
重点: 1. 电流密度的概念 2. 恒定电场的基本方程、边界条件
3. 恒定电场的基本计算方法 4. 电导和接地电阻
下 页
第 二 章
恒定电场
2.0 引言
Introduction 1.恒定电场 自由电荷在电场作用下做宏观定向运动形成电 流,通有电流的导电媒质中的场称为电流场,当空 间各点的电流密度不随时间而变时就是恒定电流场 ,简称恒定电场。 超导体或 理想导体 2.导电媒质中的恒定电场 导电媒质
第 二 章
恒定电场
4. 蓄电池(化学电源)
电池电动势2V。使用时,电池放电,当电解液浓度小 于一定值时,电动势低于2V,常要充电,化学反应可逆。
蓄电池示意图
上 页 上 页
第 二 章
恒定电场
总场强
