无穷级数
高等数学第七章无穷级数.ppt
推论 (比较审敛法) 设
是两个正项级数,
且存在
对一切
有
则有
(1) 若强级数 收敛 , 则弱级数
(常数 k > 0 ), 也收敛 ;
(2) 若弱级数 发散 , 则强级数 也发散 .
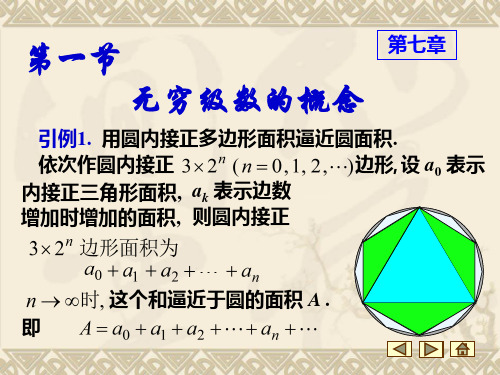
例1.
讨论
p
级数1
1 2p
1 3p
1 np
(常数
p
>
0)
的敛散性.
解: 1) 若 p 1, 因为对一切
1 n
而调和级数
知存在 N Z , 当n N 时, un1 1
un
收敛 , 由比较审敛法可知 un 收敛.
(2) 当 1 或 时,必存在 N Z , uN 0,当n N
时
从而
un1 un un1 uN
因此
lim
n
un
uN
0,
所以级数发散.
说明: 当 lim un1 1 时,级数可能收敛也可能发散.
不存在 , 因此级数发散.
由定义, 讨论 级数敛散性的方法 1. 先求部分和; 2. 求部分和的极限.
综合 1)、2)可知, q 1 时, 等比级数收敛 ;
q 1 时, 等比级数发散 .
利用此结论,可以直接判别某此级数的敛散性。例如:
例如:
公比 q 1 ,
2
q 1,
n1
(1) n1 2n1
3.按基本性质.
第三节 正项级数
第七章
一、正项级数收敛的基本定理 二、比较审敛法 三、比值审敛法 四、根值审敛法
一、正项级数收敛的基本定理
若 un 0, 则称 un 为正项级数 . n1
分析特点:部分和序列 单调递增。
当
无穷级数

第十章 无穷级数一、本章结构图⎪⎪⎪⎪⎪⎪⎩⎪⎪⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧→⎪⎪⎪⎪⎩⎪⎪⎪⎪⎨⎧⎪⎩⎪⎨⎧→⎪⎩⎪⎨⎧→函数的幂级数展开收敛半径、收敛区间和函数求解幂级数函数项级数发散条件收敛绝对收敛敛散性判定交错级数根值审敛法比值审敛法比较审敛法敛散性判定正项级数常数项级数无穷级数二、基本概念1.无穷级数:设给定一个数列1u ,2u ,, n u ,,则由这数列构成的表达式12n u u u ++++称为无穷级数,简称级数,记为1nn u∞=∑,即121nn n uu u u ∞==++++∑其中n u 称为级数的一般项(或通项),2.级数1n n u ∞=∑前n 项的部分和:级数1n n u ∞=∑的前n 项的和,记作n S3.级数的和:若级数1n n u ∞=∑的部分和数列{}n S 的极限存在,即lim n n S S →∞=,则称级数1nn u∞=∑收敛,S 为级数1nn u∞=∑的和,记为121nn n uu u u S ∞==++++=∑如果lim n n S →∞不存在,则称级数1nn u∞=∑发散4.正项级数:如果级数1nn u∞=∑的每一项都是非负数,即0(1,2,)n u n ≥=,则称此级数为正项级数5.交错级数:如果各项是正负交错的级数,可以写成下面的形式1234u u u u -+-+-或 1234u u u u -+-+其中1u ,2u ,都是正数,则称此级数为交错级数6.绝对收敛:如果级数1nn u∞=∑各项的绝对值所构成的正项级数1nn u∞=∑收敛,则称级数1nn u∞=∑绝对收敛7.条件收敛:如果级数1nn u∞=∑收敛,而级数1nn u∞=∑发散,则称级数1nn u∞=∑条件收敛8.函数项级数:如果给定一个定义在区间I 上的函数列12(),(),,(),n u x u x u x ,则称有这个函数列构成的表达式121()()()nn n uu x u x u x ∞==++++∑ (1)为定义在区间I 上的函数项无穷级数,简称函数项级数9.收敛点:对于任意的0x I ∈,函数项级数就成为常数项级数1()nn u x ∞=∑,若此常数项级数收敛,则称点0x 是函数项级数的收敛点;若常数项级数发散,则称点0x 是函数项级数的发散点10.收敛域:函数项级数的所有收敛点的全体称为它的收敛域;所有发散点的全体称为它的发散域11.和函数:在收敛域上,函数项级数的和是x 的函数()S x ,称()S x 为函数项级数的和函数,这个函数的定义域就是级数的收敛域,即12()()()()n S x u x u x u x =++++12.幂级数:形如2012nn a a x a x a x +++++的级数称为幂级数,记作nn n a x∞=∑,其中012,,,,,n a a a a 都是常数,称为幂级数的系数13.幂级数收敛半径:对于幂级数nn n a x∞=∑,若存在正数R ,使得当x R <时,幂级数绝对收敛;使得当x R >时,幂级数发散;当x R =与x R =-时,幂级数可能收敛也可能发散,这个正数R 称为幂级数nn n a x∞=∑的收敛半径,收敛域内的最大开区间),R R -(称为幂级数nn n a x∞=∑的收敛区间14.泰勒级数:如果函数)(x f 在点0x 的某邻域内具有任意阶导数,有泰勒公式可知,函数)(x f 将展成幂级数+-++-''+-'+n n x x n x f x x x f x x x f x f )(!)()(!2)())(()(00)(200000称以上幂级数为函数)(x f 在点0x 处的泰勒级数,其系数称为函数)(x f 在点0x 处的泰勒系数三、基本定理1.收敛级数的基本性质:(1)如果级数1n n u ∞=∑收敛于S ,则它的各项同乘以一个常数k 所得的级数1n n ku ∞=∑也收敛,且级数1nn ku∞=∑收敛于kS(2)如果级数1n n u ∞=∑,1n n v ∞=∑分别收敛于1S 和2S ,则级数1()n n n u v ∞=±∑也收敛,且级数1()nn n uv ∞=±∑收敛于12S S ±(3)在级数1n n u ∞=∑中任意去掉、增加或改变有限项,级数的敛散性不会改变,但对于收敛级数,其和将受到影响(4)如果级数1n n u ∞=∑收敛,则任意加括号后得到的级数1121111()()()k k n n n n n u u u u u u -++++++++++++仍收敛,其和不变(5)如果加括号后所得的级数发散,则原来级数也发散 (6)级数收敛的必要条件:若级数1nn u∞=∑收敛,则它的一般项n u 趋于零,即lim 0n n u →∞=(7)lim 0n n u →∞≠(包括极限不存在),则级数1nn u∞=∑必发散2、正项级数审敛法(1)正项级数1nn u∞=∑收敛的成分必要条件是它的部分和数列有界(2)比较审敛法:设级数1nn u∞=∑和1nn v∞=∑都是正项级数,且(1,2,)n n u v n ≤=,若级数1nn v∞=∑收敛,则级数1nn u∞=∑收敛;反之,若级数1nn u∞=∑发散,则级数1nn v∞=∑发散(3)设级数1nn u∞=∑和1nn v∞=∑都是正项级数,如果级数1nn v∞=∑收敛,且存在自然数N ,使当n N ≥时,有(0)k n u kv k ≤>成立,则级数1nn u∞=∑收敛;若级数1nn v∞=∑发散,且当n N≥时,有(0)k n u kv k ≥>成立,则级数1nn u∞=∑发散(4)设级数1n n u ∞=∑是正项级数,如果有1p >,使1(1,2,)n p u n n ≤=,则级数1nn u ∞=∑收敛;如果1(1,2,)n u n n≥=,则级数1n n u ∞=∑发散(5)比较审敛法的极限形式:设级数1nn u∞=∑和1nn v∞=∑都是正项级数,如果lim (0)nn nu l l v →∞=<<+∞,则级数1n n u ∞=∑和1n n v ∞=∑有相同的敛散性 (6)比值审敛法:若正项级数1n n u ∞=∑的后项与前项的比的极限等于ρ,即1lim n n nu u ρ+→∞=,则当1ρ<时级数收敛;当1ρ>(或1lim n n nu u +→∞=∞)时级数发散;当1ρ=时级数可能收敛也可能发散,要用其他方法判定(7)根值审敛法:设级数1nn u∞=∑是正项级数,如果它的一般项n u 的n 次根的极限等于ρ,即n ρ=,则当1ρ<时级数收敛;当1ρ>(或n =∞)时级数发散;当1ρ=时级数可能收敛也可能发散 3、交错级数审敛法莱布尼茨定理:如果交错级数11(1)n n n u ∞-=-∑满足条件1(1,2,)n n u u n +≥=及lim 0n n u →∞=,则级数收敛,且其和1S u ≤,其余项n r 的绝对值1n n r u +≤4、绝对收敛与条件收敛的关系如果级数1nn u∞=∑绝对收敛,则级数1nn u∞=∑一定收敛 (逆定理不成立)5、幂级数收敛域的定理(1)阿贝尔定理:如果幂级数nn n a x∞=∑,当00(0)x x x =≠时收敛,则适合不等式0x x <的一切x 使次幂级数绝对收敛。
无穷级数的概念与性质

无穷级数的概念与性质无穷级数(Infinite series)是数学中一个非常重要的概念,它是由无限多个数相加或相减得到的数列。
在数学中,我们经常会遇到各种各样的无穷级数,它们具有丰富的性质和应用。
本文将介绍无穷级数的基本概念,并探讨其性质及应用。
一、无穷级数的概念无穷级数指的是无限多个数按照一定的规律连加(或连减)得到的数列。
一般可以表示为下面的形式:S = a₁ + a₂ + a₃ + ...其中,a₁、a₂、a₃是无穷级数的通项,S是无穷级数的和。
无穷级数的和并不一定存在,它可能是一个有限数值,也可能是无穷大或不存在。
二、常见的无穷级数1.等差数列等差数列是最简单的无穷级数之一。
它的通项公式为:aₙ = a₁ + (n-1)d其中,a₁是首项,d是公差,n表示项数。
等差数列的无穷级数可以通过求和公式来计算:S = a₁ + (a₁+d) + (a₁+2d) + ...通过对等差数列求和,我们可以得到如下公式:S = (a₁ + aₙ) * n / 22.等比数列等比数列也是常见的无穷级数之一,它的通项公式为:aₙ = a₁ * q^(n-1)其中,a₁为首项,q为公比,n表示项数。
等比数列的无穷级数可以通过求和公式来计算:S = a₁ / (1-q)其中,当0<q<1时,S存在且为有限值,当q≥1时,S不存在。
3.调和级数调和级数是指无穷级数的通项是倒数的情况,它的通项公式为:aₙ = 1/n调和级数可以表示为:S = 1/1 + 1/2 + 1/3 + ...调和级数是一个特殊的无穷级数,它的和可以无限增大。
例如,前n项和可以表示为:Sₙ = 1/1 + 1/2 + ... + 1/n当n趋向于无穷大时,Sₙ趋向于无穷大。
三、无穷级数的性质1.收敛与发散无穷级数的和可能是有限的,也可能是无穷大,也有可能不存在。
如果一个无穷级数的和存在并且有限,我们称该级数是收敛的;反之,如果一个无穷级数的和不存在或者无穷大,我们称该级数是发散的。
高等数学-无穷级数ppt

根据级数项的性质,无穷级数可分为正项级数、交错级数和任意 项级数。
收敛与发散性质பைடு நூலகம்
收敛性质
如果无穷级数的部分和数列有极限, 则称该无穷级数收敛,此时极限值称 为级数的和。
发散性质
如果无穷级数的部分和数列没有极限 ,或者极限为无穷大,则称该无穷级 数发散。
绝对收敛与条件收敛
绝对收敛
如果无穷级数的每一项的绝对值所构 成的级数收敛,则称原级数为绝对收 敛。
在量子力学中,波函数通常表示为无穷级数形式,用于 描述微观粒子的状态和行为。
电磁学中的场强计算
通过无穷级数的展开,可以计算电磁场中各点的场强分 布,进而分析电磁现象。
在工程学中的应用,如信号处理、控制系统设计等
信号处理中的滤波
在信号处理领域,利用无穷级数设计的滤波器可以对 信号进行平滑处理、降噪等操作。
要点二
洛朗级数展开
将函数f(z)在圆环域D内展开成双边幂级数形式,即f(z) = ... + a-2/z^2 + a-1/z + a0 + a1z + a2z^2 + ...,其中an是 洛朗系数,可通过计算f(z)在D内的各阶导数求得。
泰勒级数与洛朗级数的比较
适用范围不同
泰勒级数适用于在一点处展开 的情况,而洛朗级数适用于在 圆环域内展开的情况。
控制系统设计中的稳定性分析
在控制系统设计中,通过无穷级数的稳定性分析方法 ,可以判断控制系统的稳定性并进行相应的优化设计 。
THANK YOU
感谢聆听
幂级数展开
幂级数是指形如$sum_{n=0}^{infty} a_n x^n$的级数,其 中$a_n$为常数。幂级数在收敛域内可以逐项求导和逐项积 分,具有连续性和可微性。
微积分 无穷级数

i 1
级数敛散性定义:
如果级数 un 的部分和数列 {sn} 有极限 s,即
n 1
则称无穷级数 un 收敛,这时极限 s 叫做这级数的和,并写成
n 1
n
lim sn s ,
s un u1 u2 u3 un
n
lim [(u1 u2 un ) (v1 v2 vn )]
n
lim (sn n ) s .
n
微积分
第八章
无穷级数
上页
下页
返回
无穷级数的基本性质
性质1 性质 1 如果 un s ,则 kun ks .
n
(3)当q-1时,因为sn当n为奇数时等于a ;当n为偶数 时等于零。
所以 snn 的极限不存在,从而这时级数 aqn 也发散. 所以 s 的极限不存在,从而这时级数 aqn 也发散.
n 0 n 0
n 0
微积分
第八章
无穷级数
上页
下页
返回
a 因此, 仅当|q|1 时, 几何级数 aq n (a0)收敛, 其和为 .
等比级数 aqn a aq n-1 2 aqn aq aq 几何级数 n 0 1 1 1 1 1 1 p 1 1p n p 2 p 3 p 2 p—级数 p n 3p n 1 n 1 n 1 1 1 1 11 n(n 1) 1 n(21) 12 n(n 1) 2 23 n 1 n 1 n 3
级数举例:
级数的展开形式 简写形式
一般项
第七章-无穷级数

11
(1 ) ( ) L ( )
2 23
n n1
1
lim
n
Sn
lim(1
n
n
) 1
1
1 1 n1
故级数收敛,其和为1. (例2解法称为连锁相销法)
例3 讨论几何级数(等比级数)
aqn1 a aq aq2 L aqn1 L
n1
的敛散性.若收敛,则求出其和.u(n 参 aq见n1书P272例1)
其中的一种各项正负相间的特殊情形 ——交错级数,
它是一种常见而有实用价值的特殊级数.
(二) 交错级数的莱布尼兹判别法
设un>0,(n=1,2,…),则称
(1)n1 un u1 u2 u3 u4 L
n1
为交错级数。例如
(1)n1 1
n1
n
等等。
(7.7)
对于交错级数,判定其敛散性,有如下使用方便的莱
a n n
a0 1
.
由上面的性质5,级数
un
发散。
n1
例2 若级数 un 收敛,则下列级数不收敛的是( B ) 1
A. 2un 1
B. (un 2) 1
C. 2 un
1
D. un nk
分析与解:注意到已知
un
收敛,由性质2知
1
2un
是收敛的;
1
由性质3 知,C、D 所示级数也是收敛的;
n1
aun收敛到aS ;若级数 un 发散,则 aun
n1
n1
n1
也发散。
性质3. 将级数 un 的前面加上(或去掉)有限项, n1
级数的敛散性不变。(当然,收敛时,和一般要变)
性质4. 收敛级数加括号后得到的级数仍收敛,且和不 变。
高数课件28无穷级数

任意项级数审敛法总结
绝对收敛判别法
对于任意项级数,首先尝试判断其是否绝对收敛。若绝对收敛,则原级数一定收敛。
交错级数审敛法
对于交错级数,可以利用交错级数审敛法进行判断。若满足条件,则交错级数收敛。
其他审敛法
除了绝对收敛和交错级数审敛法外,还有其他一些审敛法可用于判断任意项级数的敛散性 ,如比较审敛法、比值审敛法等。在实际应用中,可以根据级数的具体形式选择合适的审 敛法进行判断。
泰勒级数是用无限项连加式——级数来表示一个函数,这些相加的项由函数在某一点的导数求得。
原理介绍
泰勒级数的基本思想是将复杂的函数用多项式来逼近,通过逐次求导并代入展开点的值,得到各阶导 数在该点的值,进而构造出相应的多项式。
常见函数泰勒展开式举例
要点一
常见函数泰勒展开式
如$e^x$、$sin x$、$cos x$、$ln(1+x)$等函数的泰勒展 开式。
电力系统
在电力系统中,傅里叶级数被用于 分析周期性电气信号的谐波成分, 为电力系统的稳定运行提供支持。
傅里叶变换与离散时间信号处理关系
傅里叶变换与傅里叶级数关系
傅里叶变换是傅里叶级数的推广,可以将非周期函数表 示为连续频谱的形式。
离散时间信号处理中的傅里叶变 换
在离散时间信号处理中,傅里叶变换被广泛应用于频域分 析和滤波器设计等方面,为数字信号处理提供了重要工具。 同时,离散傅里叶变换(DFT)及其快速算法(FFT)也在 实际应用中发挥着重要作用。
判断原级数的收敛性。
适用范围
02
适用于通项可以表示为某个函数的级数,且该函数在相应区间
内单调、可积。
应用举例
03
如对于形如$sum_{n=1}^{infty}frac{1}{n^p}$的$p$级数,可
无穷级数总结

无穷级数总结无穷级数是数学中的重要概念,常出现在分析学、代数学、数论等领域。
它的形式为一列数相加的无穷和。
无穷级数的研究对于了解数学的发展历程和数学的基本思想方法具有重要意义。
本文将对无穷级数的定义、性质、收敛与发散的判定方法以及一些典型的无穷级数进行介绍和总结。
无穷级数的定义意味着\[S_n=a_1+a_2+...+a_n\]\[S=a_1+a_2+a_3+...\]其中,$S_n$表示级数的前n项和,S表示整个级数的和,$a_n$表示级数的第n项。
我们称一个无穷级数收敛或发散取决于它的部分和序列。
具体来说,如果存在一个有限的实数 S,使得对于任意给定的正数 $\varepsilon $,当 n 大于一些自然数 N 时,总有\[ ,S-S_n,< \varepsilon \]那么我们说该级数是收敛的,并把这个实数S叫做级数的和,记做\[ S=\sum_{n=1}^{+ \infty } a_n\]如果上述性质不成立,即对于任意给定的正数S,当n大于一些自然数N时,总存在\[ ,S-S_n, \geq \varepsilon \]那么我们说该级数是发散的。
在判断无穷级数是否收敛时,可以运用收敛的充分条件。
其中,比较判别法、比值判别法、根值判别法是最常用的方法之一1.比较判别法:如果存在一个收敛的级数 $\sum b_n$,使得对于所有的正整数 n,有 $,a_n, \leq b_n$,那么级数 $\sum a_n$ 收敛。
反之,如果级数$\sum a_n$ 发散,那么对于所有的正整数 n,必有 $,a_n, \geqb_n$ 对一些发散的正项级数 $\sum b_n$ 成立。
2.比值判别法:对于正项级数 $\sum a_n$,如果存在一个常数 L,使得当 n 大于一些正整数 N 时,总有 $\frac{a_{n+1}}{a_n} \leq L < 1$,那么级数$\sum a_n$ 收敛。
无穷级数知识点总结

无穷级数知识点总结一、无穷级数的定义无穷级数是指由无限个实数或复数项组成的数列之和。
一般地,我们用数列 {a_n} 来表示无穷级数的各项,那么无穷级数就可以表示为:S = a_1 + a_2 + a_3 + ...其中 S 代表无穷级数的和,而 a_1, a_2, a_3, ... 分别代表无穷级数的各项。
无穷级数通常可以用极限的概念来进行定义,即无穷级数的和就是数列的极限。
如果数列 {S_n} 的部分和数列收敛到某个数 L,那么无穷级数 S 的和便为 L,即:S = lim (n->∞) S_n = L这里的 S_n 代表无穷级数的部分和数列,它可以写成:S_n = a_1 + a_2 + ... + a_n无穷级数的定义是无穷数列极限的推广,它引入了无穷个数的概念,因此无穷级数的性质和收敛性等问题相对于有限级数来说更加复杂和多样。
二、无穷级数的性质无穷级数在数学中有着许多重要的性质,这些性质对于研究无穷级数的收敛性、计算方法以及应用等方面都有着重要的作用。
下面我们将详细介绍无穷级数的一些重要性质。
1. 无穷级数的有限项相加结果相同如果无穷级数的有限项相加的结果相同,那么这个无穷级数的和也相同。
即如果无穷级数S = a_1 + a_2 + a_3 + ... 的前 n 项之和等于 S_n,而无穷级数 T = b_1 + b_2 + b_3 + ... 的前 n 项之和等于 T_n,并且 S_n = T_n,那么这两个无穷级数的和也相等,即 S = T。
2. 无穷级数的倒序相加结果相同如果无穷级数的倒序相加的结果与原来的无穷级数相同,那么这个无穷级数的和同样相同,即如果无穷级数 S = a_1 + a_2 + a_3 + ... 的倒序相加的结果也等于 S,那么这个无穷级数的和就等于 S。
3. 无穷级数的部分和数列的有界性如果无穷级数的部分和数列 {S_n} 是有界的,即存在一个正数 M,使得对于所有的正整数n,都有 |S_n| <= M,那么这个无穷级数是收敛的。
无穷级数基本概念

无穷级数基本概念在数学中,无穷级数是一种由无限多个项组成的数列求和形式。
它是数学分析的重要概念之一,有着广泛的应用和研究。
本文将介绍无穷级数的基本概念和相关定义,帮助读者更好地理解和掌握这一概念。
一、无穷级数的定义与形式无穷级数的定义如下:设给定一个实数序列{a_n},则称S_n=a_1+a_2+...+a_n为该序列的部分和,如果该部分和的极限存在,即lim(n→∞)S_n=S,那么S就是该无穷级数的和,记作∑(n=1→∞)a_n=S。
其中∑表示求和符号,n=1表示从n=1开始求和,∞表示求和到无穷大。
无穷级数的一般形式为∑(n=1→∞)a_n,其中a_n表示该序列的第n个项。
例如,∑(n=1→∞)2^n就是一个以2为公比的等比数列的无穷级数。
二、收敛和发散对于无穷级数,我们可以将其分为两类:收敛和发散。
如果一个无穷级数的部分和S_n在n趋于无穷大时存在有限极限S,即lim(n→∞)S_n=S,那么该无穷级数称为收敛的;反之,如果该无穷级数的部分和S_n在n趋于无穷大时不存在有限极限,那么该无穷级数称为发散的。
例如,无穷级数∑(n=1→∞)1/n是一个著名的调和级数。
经过数学推导可知,该级数是发散的,即部分和S_n在n趋于无穷大时趋于正无穷。
三、收敛性的判定对于给定的无穷级数,判断其收敛性是数学中的一个重要问题。
有许多判定条件可以用来判断无穷级数的收敛性,常见的有比较判别法、比值判别法、根值判别法等。
下面简要介绍两个常用的判定法。
1. 比较判别法比较判别法是判断无穷级数收敛性的常用方法之一。
设有两个数列{a_n}和{b_n},满足当n趋于无穷大时,对于所有的n,有0 ≤ a_n ≤b_n。
若级数∑(n=1→∞)b_n收敛,则级数∑(n=1→∞)a_n也收敛;若级数∑(n=1→∞)a_n发散,则级数∑(n=1→∞)b_n也发散。
2. 比值判别法比值判别法也是常用的判断无穷级数收敛性的方法之一。
设给定一个无穷级数∑(n=1→∞)a_n,如果存在一个正数q,使得当n趋于无穷大时,有|(a_(n+1))/a_n| ≤ q,那么该级数收敛;如果对于所有的n,都有|(a_(n+1))/a_n| > 1,那么该级数发散。
无穷级数知识点总结简短

无穷级数知识点总结简短
1. 无穷级数的定义
无穷级数是指由无限个数相加而成的级数,通常表示为:
S = a1 + a2 + a3 + ...
其中,a1, a2, a3...表示级数的每一项。
2. 无穷级数的收敛与发散
无穷级数可能收敛也可能发散。
如果无穷级数的部分和S_n在n趋向无穷时收敛于某一有
限数,即lim(S_n) = S,则称该无穷级数收敛;如果无穷级数的部分和S_n在n趋向无穷
时发散至无穷大或者发散至负无穷大,即lim(S_n) = ±∞,则称该无穷级数发散。
3. 无穷级数的收敛性判别法
无穷级数的收敛性判别法有很多种,包括比较判别法、比值判别法、根值判别法、积分判
别法等。
这些判别法可以用来判断无穷级数的收敛性,并且在实际问题中有很多应用。
4. 无穷级数的性质
无穷级数有许多重要的性质,包括级数的线性性质、级数的绝对收敛性、级数的收敛域等。
这些性质在研究无穷级数的收敛性和计算级数的和时非常重要。
5. 无穷级数的应用
无穷级数在物理、工程、计算机科学等领域都有重要的应用。
例如,在物理学中,泰勒级
数可用于近似计算非线性函数的值;在工程学中,级数可以用来描述振动、波动等现象;
在计算机科学中,级数在算法复杂性分析和数值计算中也有广泛的应用。
总之,无穷级数是数学中一个重要的概念,它涉及到收敛与发散、收敛性判别法、性质和
应用等方面,对于理解和应用级数有着重要的意义。
无穷极数知识点总结

无穷极数知识点总结1. 无穷级数的定义无穷级数是指由无穷多个项组成的级数,通常表示为a1 + a2 + a3 + ... + an + ...,其中每一项an是一个实数或复数。
无穷级数可以是收敛的,即其和是一个有限的值,也可以是发散的,即其和不存在或为无穷大。
2. 无穷级数的收敛无穷级数收敛的概念是指无穷级数的和在某个范围内趋于一个有限的值。
收敛的无穷级数在数学分析和实际应用中有着广泛的应用,例如在泰勒级数展开、微积分中的积分计算等方面。
无穷级数的收敛有多种判别法,如比较判别法、根值判别法、积分判别法等。
3. 无穷级数的发散无穷级数发散的概念是指无穷级数的和无法趋向于一个有限的值,而是趋向于无穷大或者根本无法定义。
无穷级数的发散也有多种判别法,例如奇偶项判别法、柯西收敛准则等。
4. 绝对收敛与条件收敛无穷级数的收敛有两种情况,一种是绝对收敛,即该级数每一项的绝对值级数收敛;另一种是条件收敛,即该级数每一项的绝对值级数发散,但级数本身却收敛。
绝对收敛级数在某种程度上更容易处理和计算,而条件收敛级数的性质相对更为复杂,也更有意思。
5. 级数收敛的充分条件对于实数级数来说,级数部分和序列的收敛性与级数本身的收敛性之间是十分紧密的,因此研究级数部分和序列的收敛性可以得到级数收敛的充分条件。
比如级数收敛的柯西准则、级数收敛的柯西——施瓦茨准则、莱布尼茨级数收敛准则等。
6. 无穷级数的运算无穷级数也可以进行加减乘除等运算,不过进行这些运算时需要满足一定的条件,比如级数收敛、级数部分和序列的收敛性等。
无穷级数的运算规则也有许多特殊的性质,如级数的收敛性与绝对收敛性的性质、级数的乘法运算性质、级数的幂级数展开等。
7. 级数收敛的应用无穷级数的研究在数学中有着广泛的应用,比如在分析学中的泰勒级数展开、微积分中的求和、微分方程的求解、数论中的级数和等方面都有不同程度的应用。
无穷级数也在物理学、工程学、经济学等应用领域中有着很多重要的应用。
无穷级数知识点总结公式

无穷级数知识点总结公式无穷级数的定义:无穷级数的一般形式可以表示为:\[ \sum_{n=1}^{\infty} a_n = a_1 + a_2 + a_3 + \ldots + a_n + \ldots \]其中,\( a_n \) 是级数的第 n 个项。
级数的和通常记为 \( S \),即\[ S = a_1 + a_2 + a_3 + \ldots + a_n + \ldots \]当级数的和存在有限值时,称级数收敛;当级数的和不存在有限值时,称级数发散。
无穷级数的性质:1. 无穷级数的和与项的次序无关级数的项次序可以进行重新排列,其和仍然相同。
2. 收敛级数的任意项的和都趋于零对于收敛级数,其各项的和对应的部分和序列的极限为级数的和。
3. 收敛级数的每一项都可以表示为部分和序列的差对于收敛级数,其每一项都可以表示为相邻两个部分和之差。
无穷级数的收敛性:在讨论无穷级数时,我们关心的一个重要问题是该级数是否收敛。
无穷级数的收敛性可以通过不同的收敛判别法来进行判断。
1. 正项级数收敛判别法对于正项级数 \(\sum_{n=1}^{\infty} a_n\):- 若 \( \lim_{n \to \infty} a_n = 0 \) 且 \( a_n \) 单调递减(即 \( a_{n+1} \leq a_n \)),则级数收敛;- 若 \( a_n \) 单调递减且有界,则级数收敛;- 若 \( \lim_{n \to \infty} a_n \) 不存在或 \( \lim_{n \to \infty} a_n \neq 0 \) ,则级数发散。
2. 比较判别法设 \( \sum_{n=1}^{\infty} a_n \) 和 \( \sum_{n=1}^{\infty} b_n \) 为两个级数,若存在正常数 \( C \),当 \( n \) 充分大时有 \( 0 \leq a_n \leq Cb_n \),则级数\( \sum_{n=1}^{\infty} b_n \) 收敛时级数 \( \sum_{n=1}^{\infty} a_n \) 收敛,级数\( \sum_{n=1}^{\infty} b_n \) 发散时级数 \( \sum_{n=1}^{\infty} a_n \) 发散。
无穷级数(全)

无穷级数1、无穷级数:表达式 +++++n u u u u 321 称为无穷级数,简称级数.记作∑∞=1n nu, 其中n u 称为级数的一般项.2、部分和: 级数∑∞=1n nu的前n 项和 ∑==nk kn uS 1称为级数∑∞=1n nu的部分和.3、收敛的定义: 如果级数∑∞=1n nu的部分和数列}{n S 有极限S ,即S S n n =∞→lim ,则称级数∑∞=1n nu收敛.S 称为级数∑∞=1n nu的和, 并写成: ++++=321u u u S ∑∞==1n nu.如果}{n S 没有极限, 则称级数∑∞=1n nu发散.4、常数项级数收敛的必要条件:若级数∑∞=1n nu收敛,则必有0lim =∞→n n u ,反之若0lim ≠∞→n n u ,则级数一定发散5常用级数敛散性判定方法: ①等比级数:∑∞=0n n aq ,当 1q < 收敛,且级数收敛于qa -111q ≥ 发散当然等比级数的敛散性也可以由等比级数的部分和数列来判断:若S 存在则收敛,反之则发散. ②P-级数:∑∞=1n P n 11p >收敛,1p ≤发散(p=1时为调和级数);③常数级数:∑∞=0n C 当0≠C 时级数发散,0=C 时,级数收敛.6、级数收敛的性质 以下假设∑∞=1n nu与∑∞=1n nv收敛于S 与T , 则①∑∑∞=∞==11n n n nu u λλ, (λ为常数). ②∑∑∑∞=∞=∞=±=±111)(n n n n n n nv u v u.③∑∞=1n nu收敛⇔对任意的非负整数m ,有∑∞+=1m n nu收敛.即: 在级数前面去掉或加上有限项不影响级数的敛散性. ④若S un n=∑∞=1,则将级数的项任意加括号后所成的级数S n n=∑∞=1σ. 反之不然.7、正项级数敛散性的判定方法: ①充要条件:部分和数列有界②比较法:对级数的缩放,利用已知的级数来判断未知级数的敛散性;适用于含有P(型)-级数、、多项式和正余弦的级数.其中P(型)-级数、对数、多项式主要是删减低次项和常数项,而正余弦主要是利用其小于1的性质.③比阶法:找到一个已知敛散性的级数,通过其与需求级数作商曲极限,来判断需求级数的敛散性.适用于P(型)-级数,等比级数、多项式等.定义如下:设∑∞=1n n u 与∑∞=1n n v 均为正项级数,若L v u nnn =∞→lim,则(1)当L=0时,若∑∞=1n nv收敛,则∑∞=1n nu也收敛;(2)当L=+∞时,若∑∞=1n nv发散,则∑∞=1n nu也发散.(3)当0<L<+∞时,∑∞=1n nv与∑∞=1n nu有相同敛散性.④比值法:通过对级数通向第n+1项与第n 项作商取极限来判断级数敛散性.不适用含有对数、多项式和正余弦的级数.定义如下:设∑∞=1n n u 为正项级数,若ρ=+∞→nn n u u 1lim,则(1)1<ρ时, 级数∑∞=1n nu收敛;(2) 1>ρ或+∞=ρ时, 级数∑∞=1n nu发散;(3)1=ρ时, 级数∑∞=1n nu可能收敛也可能发散.⑤其他常用方法(1)关于级数中带有多项式的分式方程的:ⅰ分子最高次≥分母最高次则级数一定发散; ⅱ分子最高次<分母最高次,则用比阶法来判断. 设sn n V 1=(s 为分子最高项-分母最高项的差值) (2)关于级数中带有对数的:用比阶法题目中()c n U tn +=ln ,就设tn n V 1=作商取极限,需要用L ,hospital 定理8、交错级数的审敛法:(莱布尼茨定理) 设∑∞=--11)1(n n n u 为交错级数, 若满足(1) n n u u ≤+1, ,2,1=n ; (2) 0lim =∞→n n u , 则 ∑∞=--11)1(n n n u 收敛,9、任意项级数的绝对收敛和条件收敛 ①绝对收敛的级数∑∞=1n nu :∑∞=1||n nu 收敛;②条件收敛的级数∑∞=1n n u:∑∞=1||n nu发散, 但∑∞=1n n u 收敛.③∑∞=1||n nu收敛 ⇒ ∑∞=1n n u 收敛. 反之不然.④此类级数多用比值法来判断绝对值级数是否发散 ⑤若任意项级数∑∞=1n nu条件收敛,则其所有正项或者负项构成的级数均为发散的.10、函数项级数①定义: 设 ),(,),(),(21x u x u x u n 是定义在I 上的函数,则++++=∑∞=)()()()(211x u x u x u x u nn n称为定义在区间I 上的(函数项)无穷级数.②收敛域(1) 收敛点I x ∈0—— ∑∞=10)(n nx u 收敛;(2) 发散点I x ∈0——∑∞=10)(n nx u 发散;(3) 收敛域D —— ∑∞=1)(n nx u 的所有收敛点的全体D ;(4) 发散域G ——∑∞=1)(n n x u 的所有发散点的全体G .(5)解题方法:已知级数∑∞=1)(n nx u,求其收敛域.ⅰ用比值法算出大致收敛域:)(的式子关于x 1Q x lim==+∞→nn n u u ρ,令)(x Q <1,算出x 收敛大范围(a ,b ),收敛半径R=2b-a (()∞++∞∞-∈可以为R R ,,) ⅱ将端点值带入级数∑∞=1)(n nx u中,算出∑∞=1)(n n a u 与∑∞=1)(n n b u 的敛散性,判断端点值是否可以取到,过程可以略过. ⅲ综上所述,写出级数∑∞=1)(n nx u的收敛域③和函数)(x S —— ∑∞==1)()(n nx u x S , D x ∈.解题方法:已知级数∑∞=1)(n nx u,求其和函数.ⅰ求出其收敛域;ⅱ将级数经过求导或者积分,得到一个等比级数 ⅲ用等比级数收敛公式qa -11算出和函数的导数或者原函数的表达式;ⅳ将求出的表达式积分或求导,写成)(x S 的形式,并注明收敛域.【注】已知级数∑∞=1)(n nx u,求∑∞=1n n V 的和ⅰ-ⅳ步骤同上ⅴ将n n V x u 与)(建立起联系,想当x 为何值时n n V x u =)(,然后将x 带入)(x S 中.11、函数项级数的展开式.(1) f (x ) = e x= ∑∞=0!n nn x , x ∈(-∞, +∞);(2) f (x ) = sin x = ∑∞=++-012!)12()1(n n n xn ,x ∈(-∞, + ∞);(3) f (x ) = cos x = ∑∞=-02!)2()1(n nn x n ,x ∈(-∞, + ∞);(4) 11()1n n f x x x ∞===-∑ ,x ∈(-1, 1);(5) 11()()1n n f x x x ∞===-+∑ ,x ∈(-1, 1);(6) f (x ) = ln (1 + x ) = ∑∞=+-11)1(n nn x n , x ∈(-1, 1]。
无穷级数的定义及应用

无穷级数的定义及应用无穷级数是数学领域中一个重要的概念,它在多个领域中都有着广泛的应用。
本文将从定义、性质和应用三个方面来介绍无穷级数,并探讨其在实际问题中的应用。
一、无穷级数的定义无穷级数是由一列实数(或复数)按照一定的规律相加得到的。
它的一般形式可以表示为S=a_1+a_2+a_3+...+a_n+...,其中a_n表示级数的第n项。
当级数中的各项a_n的和S存在有限的极限时,称该级数收敛;当级数的和S不存在有限的极限时,称该级数发散。
二、无穷级数的性质1. 收敛性:无穷级数的收敛性是判断其是否有意义的重要性质。
常见的判别方法有比较判别法、比值判别法、根值判别法等。
2. 绝对收敛性:如果一个级数的所有项都是正数,并且这个级数收敛,那么称该级数是绝对收敛的。
绝对收敛的级数一定是收敛的,但反之不成立。
3. 条件收敛性:如果一个级数是收敛的,但不是绝对收敛的,那么称该级数是条件收敛的。
条件收敛的级数可以通过重新排列项的顺序得到不同的和。
4. 收敛级数的和与项的排列顺序无关:对于收敛级数,改变它的项的顺序并不会改变其和。
5. 级数的运算:对于两个级数,可以进行加法、减法、乘法和除法等运算。
三、无穷级数的应用无穷级数在数学中具有广泛的应用,下面将介绍几个常见的应用领域。
1. 数学分析中的级数:无穷级数在数学分析中有着重要的地位,它可以用来研究函数的性质,如连续性、可导性、积分等。
级数的收敛性和和函数的性质之间有着紧密的联系。
2. 物理学中的级数:无穷级数在物理学中也有着广泛的应用。
例如,在力学中,泰勒级数可以用来近似表示一个函数,从而简化复杂的计算。
在电磁学中,无穷级数可以用来求解电场、磁场等问题。
3. 统计学中的级数:无穷级数在统计学中也有一定的应用。
例如,在概率论中,无穷级数可以用来表示事件发生的概率。
在统计学中,级数可以用来计算样本的累计百分比。
4. 经济学中的级数:无穷级数在经济学中也有一定的应用。
无穷级数的常用公式

无穷级数是一种数学表达式,用来表示一个无限序列的和。
它可以用来表示一个函数的极限,或者用来求解一些复杂的数学问题。
无穷级数的一般形式为:
∑a_n = a_1 + a_2 + a_3 + ... + a_n + ...
其中,a_n是第n项的系数,n是一个正整数,表示第n项。
无穷级数的求和可以用以下公式:
1. 如果系数a_n是一个常数,则无穷级数的和为:
∑a_n = a_1 + a_2 + a_3 + ... + a_n + ... = a_1 + a_1 + a_1 + ... = a_1 * n
2. 如果系数a_n是一个等比数列,则无穷级数的和为:
∑a_n = a_1 + a_2 + a_3 + ... + a_n + ... = a_1 + a_1 * q + a_1 * q^2 + ... = a_1 * (1 - q^n) / (1 - q)
其中,q是等比数列的公比。
3. 如果系数a_n是一个等差数列,则无穷级数的和为:
∑a_n = a_1 + a_2 + a_3 + ... + a_n + ... = a_1 + a_1 + d + a_1 + 2d + ... = a_1 * n + d * (n * (n - 1)) / 2
其中,d是等差数列的公差。
4. 如果系数a_n是一个指数数列,则无穷级数的和为:
∑a_n = a_1 + a_2 + a_3 + ... + a_n + ... = a_1 + a_1 * r + a_1 * r^2 + ... = a_1 * (1 - r^n) / (1 - r)
其中,r是指数数列的公比。
以上就是无穷级数的常用公式。
高数大一知识点无穷级数

高数大一知识点无穷级数高数大一知识点:无穷级数无穷级数是数学分析中一个重要的概念,指的是一个由无穷多个数相加或相乘而得到的数列或数列的和。
在大一的高等数学课程中,无穷级数是一个重要的知识点,本文将介绍无穷级数的定义、性质以及一些常见的无穷级数。
1. 无穷级数的定义在数学中,无穷级数的定义如下:设给定一个数列{an},则称S = a1 + a2 + a3 + ... + an + ...为该数列的无穷级数。
其中,ai为无穷级数的通项。
2. 无穷级数的性质无穷级数具有以下几个性质:2.1 收敛性:如果无穷级数的部分和数列{Sn}存在有限极限s,即lim(n→∞)Sn = s,则称该无穷级数收敛,s为该无穷级数的和。
2.2 敛散性:如果无穷级数的部分和数列{Sn}不存在有限极限,即lim(n→∞)Sn不存在或为无穷大,则称该无穷级数发散。
2.3 绝对收敛性:如果无穷级数的绝对值级数收敛,则称该无穷级数绝对收敛。
2.4 条件收敛性:如果无穷级数收敛但绝对值级数发散,则称该无穷级数条件收敛。
3. 常见的无穷级数3.1 等差数列的无穷级数等差数列的无穷级数是一类常见的无穷级数。
它的通项可以表示为an = a + (n-1)d,其中a为首项,d为公差。
等差数列的无穷级数可以用以下公式进行求和:Sn = n(a + a + (n-1)d)/23.2 等比数列的无穷级数等比数列的无穷级数也是常见的无穷级数类型。
它的通项可以表示为an = ar^(n-1),其中a为首项,r为公比(不等于0)。
等比数列的无穷级数可以用以下公式进行求和:S = a/(1-r),当|r|<1时3.3 调和级数调和级数是一类极其重要的无穷级数,它的通项可以表示为an = 1/n。
调和级数的部分和数列可以用以下公式表示:Sn = 1 + 1/2 + 1/3 + ... + 1/n4. 无穷级数的应用无穷级数在数学及其他领域中有广泛的应用。
第七章 无穷级数

故所给级数也收敛 且其和小于 2
1 1 2 n n n
22
(二)正项级数的比较判别法
例4 判定级数
n 1
1 3n 2 n 1
的敛散性
解: 因
1 3n 2 n
1 ( n 1,2,), 3 n 2 n 2 2n
1 级数 发散, n 1 2n
故级数
这表明级数 aun 收敛 且和为 aS
n1
n n
n n
11
第二节
无穷级数的基本性质
1 2 例1. 判定级数 ( n n ) 的敛散性. 5 n 1 3
1 2 解: 因级数 n 和级数 n 都收敛, n 1 3 n 1 5 1 2 故级数 ( n n ) 收敛. 5 n 1 3
无穷级数的概念
1 1 1 1 1 例2. 判定级数 1 2 2 3 3 4 n( n 1) n 1 n( n 1)
的敛散性.若级数收敛,求此级数的和.
解:
所以这级数收敛 它的和是1
7
第一节
无穷级数的概念
n1 2 3 4 n1 ln ln ln 例3. 判定级数 ln n 1 2 3 n n 1
无穷级数的基本性质
Sn、Wn、Tn 则
n
lim Tn lim [(u1 v1) (u2 v2) (un vn )]
lim[(u1 u2 un ) (v1 v2 vn )]
n
n
lim (Sn Wn ) S W
3
的敛散性
1 3n 2 n 1 1 3 n
无穷级数的概念和性质

无穷级数的概念和性质无穷级数是数学中一个非常重要且有趣的概念。
在本文中,我们将介绍无穷级数的定义、收敛性、发散性以及一些相关的性质。
一、无穷级数的定义无穷级数是由无限个数相加(或相减)得到的一种数列。
一般的无穷级数可以写成以下的形式:S = a₁ + a₂ + a₃ + ...其中,a₁, a₂, a₃, ... 是数列的项。
二、收敛性和发散性无穷级数可以分为收敛和发散两种情况。
1. 收敛:如果一个无穷级数的部分和数列有极限L,即当n趋向于无穷时,Sₙ(前n项的和)趋向于L,则称该无穷级数收敛,记作S = L。
2. 发散:如果无穷级数不收敛,则称该无穷级数发散。
三、收敛级数的性质1. 加法性:如果两个收敛级数S₁和S₂都收敛,并且它们的和数列分别为S₁₀和S₂₀,则它们的和级数S = S₁ + S₂也收敛,且其和数列为S₁₀ + S₂₀。
2. 数乘性:对于一个收敛级数S,如果乘以一个常数c,则所得到的级数cS也收敛,并且其和数列为cS₀,其中S₀是级数S的和数列。
3. 子序列收敛性:如果一个级数S收敛,则它的任意子序列也收敛,且收敛于相同的极限。
四、底达到性底达到性是指对于一个收敛级数S,无论收敛级数前面有多少项被去掉,剩下的级数仍然收敛,并且收敛于相同的极限。
五、绝对收敛和条件收敛1. 绝对收敛:如果级数的所有项的绝对值的和收敛,那么该级数称为绝对收敛。
2. 条件收敛:如果级数本身是收敛的,但是它的绝对值级数却是发散的,那么这个级数称为条件收敛。
六、收敛判定方法1. 正项级数判别法:如果级数的所有项都是非负数,并且后一项总是比前一项大或相等,那么该级数收敛当且仅当它的部分和数列有界。
2. 比值判别法:对于一个级数S,计算相邻两项的比值aₙ₊₁/aₙ的极限值L,如果L小于1,则级数绝对收敛;如果L大于1,则级数发散;如果L等于1,比值判别法失效。
3. 根值判别法:对于一个级数S,计算相邻两项的n次方根∛ₙ(aₙ)的极限值L,如果L小于1,则级数绝对收敛;如果L大于1,则级数发散;如果L等于1,根值判别法失效。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
教学目的:1.理解常数项级数收敛、发散以及收敛级数的和的概念,掌握级数的基本性质及收敛的必要条件。
2.掌握几何级数与P 级数的收敛与发散的条件。
3.掌握正项级数收敛性的比较判别法和比值判别法,会用根值判别法。
4.掌握交错级数的莱布尼茨判别法。
5.了解任意项级数绝对收敛与条件收敛的概念,以及绝对收敛与条件收敛的关系。
6.了解函数项级数的收敛域及和函数的概念。
7.理解幂级数收敛半径的概念,并掌握幂级数的收敛半径、收敛区间及收敛域的求法。
8.了解幂级数在其收敛区间内的一些基本性质(和函数的连续性、逐项微分和逐项积分),会求一些幂级数在收敛区间内的和函数,并会由此求出某些常数项级数的和。
9.了解函数展开为泰勒级数的充分必要条件。
10.掌握,sin ,cos x e x x ,ln(1)x +和(1)x α+的麦克劳林展开式,会用它们将一些简单函数间接展开成幂级数。
11. 了解傅里叶级数的概念和函数展开为傅里叶级数的狄利克雷定理,会将定义在[-l ,l]上的函数展开为傅里叶级数,会将定义在[0,l]上的函数展开为正弦级数与余弦级数,会写出傅里叶级数的和的表达式。
教学难点:1、 比较判别法的极限形式;2、 莱布尼茨判别法;3、 任意项级数的绝对收敛与条件收敛;4、 函数项级数的收敛域及和函数;5、 泰勒级数;6、傅里叶级数的狄利克雷定理。
第一节 常数项级数的概念和性质 一、 概念常数项级数: 给定一个数列 u 1, u 2, u 3, ⋅ ⋅ ⋅, u n , ⋅ ⋅ ⋅, 则由这数列构成的表达式u 1 + u 2 + u 3 + ⋅ ⋅ ⋅+ u n + ⋅ ⋅叫做常数项)无穷级数, 简称常数项)级数, 记为∑∞=1n n u , 即3211⋅⋅⋅++⋅⋅⋅+++=∑∞=n n n u u u u u , 其中第n 项u n 叫做级数的一般项.级数的部分和: 作级数∑∞=1n n u 的前n 项和n n i i n u u u u u s +⋅⋅⋅+++==∑= 3211称为级数∑∞=1n n u 的部分和.级数敛散性定义: 如果级数∑∞=1n n u 的部分和数列}{n s 有极限s , 即s s n n =∞→lim , 则称无穷级数∑∞=1n n u 收敛, 这时极限s 叫做这级数的和, 并写成 3211⋅⋅⋅++⋅⋅⋅+++==∑∞=n n n u u u u u s 如果}{n s 没有极限, 则称无穷级数∑∞=1n n u 发散.定义 若部分和数列{}n S 有极限S ,即S S n n =∞→lim ,则称级数∑∞=1n n u 收敛,S 称为级数∑∞=1n nu的和,记为∑∞==1n n u S 。
若{}n S 无极限,则称级数∑∞=1n n u 发散。
++=-=++21n n n n u u S S r 称为级数的余项,n r 称为误差。
二、 两个重要级数① 几何级数或等比级数)0(0≠++++=∑∞=a aq aq a aq n n n 1<q 时收敛,1≥q 时发散。
② 和级数 +++++=∑∞=n nn 13121111发散三、 性质1、 若S u n n =∑∞=1,则kS u k ku n n n n ==∑∑∞=∞=112、 若11S u n n =∑∞=,21S v n n =∑∞=,则()∑∞=±1n n n v u 也收敛,且()211S S v u n n n ±=±∑∞=3、 在级数中去掉或添加有限项不影响其敛散性。
4、 如果级数收敛,则它的一般项趋于0,反之如果一般项不趋于0,则级数必定发散。
注意:级数一般项趋于0不是级数收敛的充分条件,调和级数一般项趋于0却是发散的第二节 常数项级数审敛法一、 正项级数及其审敛法正项级数: 各项都是正数或零的级数称为正项级数.定理1 正项级数∑∞=1n n u 收敛的充分必要条件它的部分和数列{s n }有界.定理2(比较审敛法)设∑∞=1n n u 和∑∞=1n n v 都是正项级数, 且u n ≤v n (n =1, 2, ⋅ ⋅ ⋅ ). 若级数∑∞=1n n v 收敛, 则级数∑∞=1n n u 收敛; 反之, 若级数∑∞=1n n u 发散, 则级数∑∞=1n n v 发散.定理3(比较审敛法的极限形式) 设∑u n 和∑v n 都是正项级数, (1)如果lim(u n /v n )=l (0≤l <+∞), 且∑v n 收敛, 则∑u n 收敛; (2)如果lim(u n /v n )=l (0<l ≤+∞), 且∑v n 发散, 则∑u n 发散. 定理4(比值审敛法, 达朗贝尔判别法) 若正项级数∑∞=1n n u 满足ρ=+∞→nn n u u 1lim, 则当ρ<1时级数收敛; 当ρ>1(或∞=+∞→n n n u u 1lim )时级数发散. 当ρ =1时级数可能收敛也可能发散.定理5(根值审敛法, 柯西判别法)设∑∞=1n n u 是正项级数, 如果它的一般项u n 的n 次根的极限等于ρ:ρ=∞→n n n u lim , 则当ρ<1时级数收敛; 当ρ>1(或+∞=∞→n n n u lim )时级数发散; 当ρ=1时级数可能收敛也可能发散.定理6(极限审敛法) 设∑∞=1n n u 为正项级数,(1)如果)lim (0lim +∞=>=∞→∞→n n n n nu l nu 或, 则级数∑∞=1n n u 发散;(2)如果p >1, 而)0( lim +∞<≤=∞→l l u n n p n , 则级数∑∞=1n n u 收敛.二、交错级数及其审敛法交错级数: 交错级数是这样的级数, 它的各项是正负交错的. 交错级数的一般形式为∑∞=--11)1(n n n u , 其中0>n u .定理6(莱布尼茨定理) 如果交错级数∑∞=--11)1(n n n u 满足条件:(1)u n ≥u n +1 (n =1, 2, 3, ⋅ ⋅ ⋅); (2)0lim =∞→n n u , 则级数收敛, 且其和s ≤u 1, 其余项r n 的绝对值|r n |≤u n +1.三、绝对收敛与条件收敛若级数∑∞=1||n n u 收敛, 则称级数∑∞=1n n u 绝对收敛; 若级数∑∞=1n n u 收敛, 而级数∑∞=1||n n u 发散, 则称级∑∞=1n n u 条件收敛.定理7 如果级数∑∞=1n n u 绝对收敛, 则级数∑∞=1n n u 必定收敛. 值得注意的问题: 如果级数∑∞=1||n n u 发散, 我们不能断定级数∑∞=1n n u 也发散. 但是, 如果我们用比值法或根值法判定级数∑∞=1||n n u 发散,则我们可以断定级数∑∞=1n n u 必定发散. 这是因为, 此时|u n |不趋向于零, 从而u n 也不趋向于零, 因此级数∑∞=1n n u 也是发散的.第三节 幂级数一、 函数项级数的概念函数项级数: 给定一个定义在区间I 上的函数列{u n (x )}, 由这函数列构成的表达式 u 1(x )+u 2(x )+u 3(x )+ ⋅ ⋅ ⋅ +u n (x )+ ⋅ ⋅ ⋅称为定义在区间I 上的(函数项)级数, 记为∑∞=1)(n n x u .收敛点与发散点:对于区间I 内的一定点x 0, 若常数项级数∑∞=10)(n n x u 收敛, 则称点x 0是级数∑∞=1)(n n x u 的收敛点. 若常数项级数∑∞=10)(n n x u 发散, 则称点x 0是级数∑∞=1)(n n x u 的发散点.收敛域与发散域: 函数项级数∑∞=1)(n n x u 的所有收敛点的全体称为它的收敛域, 所有发散点的全体称为它的发散域.和函数: 在收敛域上, 函数项级数∑∞=1)(n n x u 的和是x 的函数s (x ,)s (x )称为函数项级数∑∞=1)(n n x u 的和函数,并写成∑∞==1)()(n n x u x s .部分和: 函数项级数∑∞=1)(n n x u 的前n 项的部分和记作s n (x ), 函数项级数∑u n (x )的前n 项的部分和记作s n (x ), 即 s n (x )= u 1(x )+u 2(x )+u 3(x )+ ⋅ ⋅ ⋅ +u n (x ). 在收敛域上有)()(lim x s x s n n =∞→或s n (x )→s (x )(n →∞) .余项: 函数项级数∑∞=1)(n n x u 的和函数s (x )与部分和s n (x )的差 r n (x )=s (x )-s n (x )叫做函数项级数∑∞=1)(n n x u 的余项. 函数项级数∑u n (x )的余项记为r n (x ), 它是和函数s (x )与部分和s n (x )的差 r n (x )=s (x )-s n (x ). 在收敛域上有0)(lim =∞→x r n n .二、幂级数及其收敛性幂级数: 函数项级数中简单而常见的一类级数就是各项都幂函数的函数项级数, 这种形式的级数称为幂级数, 它的形式是a 0+a 1x +a 2x 2+ ⋅ ⋅ ⋅ +a n x n + ⋅ ⋅ ⋅ , 其中常数a 0, a 1, a 2, ⋅ ⋅ ⋅ , a n , ⋅ ⋅ ⋅叫做幂级数的系数. 定理1 (阿贝尔定理) 如果级数∑∞=0n n n x a 当x =x 0 (x 0≠0)时收敛, 则适合不等式|x |<|x 0|的一切x 使这幂级数绝对收敛. 反之, 如果级数∑∞=0n n n x a 当x =x 0时发散, 则适合不等式|x |>|x 0|的一切x 使这幂级数发散.定理2 如果幂级数∑∞=0n n n x a 系数满足ρ=+∞→||lim 1nn n a a , 则这幂级数的收敛半径⎪⎪⎩⎪⎪⎨⎧+∞=≠=∞+=ρρρρ 00 10 R .三、幂级数的运算设幂级数∑∞=0n nn x a 及∑∞=0n n n x b 分别在区间(-R , R )及(-R ', R ')内收敛, 则在(-R , R )与(-R ', R ')中较小的区间内有 加法:∑∑∑∞=∞=∞=+=+000)(n n n n n nn n n n x b a x b x a ,减法:∑∑∑∞=∞=∞=-=-0)(n n n n n nn n n n x b a x b x a ,乘法: )()(0∑∑∞=∞=⋅n n n n nn x b x a =a 0b 0+(a 0b 1+a 1b 0)x +(a 0b 2+a 1b 1+a 2b 0)x 2+ ⋅ ⋅ ⋅ +(a 0b n +a 1b n -1+ ⋅ ⋅ ⋅ +a n b 0)x n + ⋅ ⋅ ⋅性质1 幂级数∑∞=0n n n x a 的和函数s (x )在其收敛域I 上连续.如果幂级数在x =R (或x =-R )也收敛, 则和函数s (x )在(-R , R ](或[-R , R ))连续.性质2 幂级数∑∞=0n n n x a 的和函数s (x )在其收敛域I 上可积, 并且有逐项积分公式∑∑⎰⎰∑⎰∞=+∞=∞=+===0100001)()(n n n n xnn xn nn x x n a dx x a dx x a dx x s (x ∈I ), 逐项积分后所得到的幂级数和原级数有相同的收敛半径.性质3 幂级数∑∞=0n n n x a 的和函数s (x )在其收敛区间(-R , R )内可导, 并且有逐项求导公式∑∑∑∞=-∞=∞=='='='110)()()(n n n n n n n n n x na x a x a x s (|x |<R ), 逐项求导后所得到的幂级数和原级数有相同的收敛半径.第四节 函数展开成幂级数一、 泰勒级数泰勒级数: 如果f (x )在点x 0的某邻域内具有各阶导数f '(x ), f ''(x ), ⋅ ⋅ ⋅ , f (n )(x ), ⋅ ⋅ ⋅ , 则当n →∞时, f (x )在点x 0的泰勒多项式n n n x x n x f x x x f x x x f x f x p )(!)( )(!2)())(()()(00)(200000-+⋅⋅⋅+-''+-'+= 定理 设函数f (x )在点x 0的某一邻域U (x 0)内具有各阶导数, 则f (x )在该邻域内能展开成泰勒级数的充分必要条件是f (x )的泰勒公式中的余项R n (x )当n →0时的极限为零, 即))(( 0)(lim 0x U x x R n n ∈=∞→麦克劳林级数: 在泰勒级数中取x 0=0, 得⋅⋅⋅++⋅⋅⋅+''+'+ !)0( !2)0()0()0()(2nn x n f x f x f f , 此级数称为f (x )的麦克劳林级数.展开式的唯一性: 若f (x )能展开成x 的幂级数, 那么这种展式是唯一的, 一定与f (x )的麦克劳林级数一致.因为, 若f (x )在点x 0=0的某邻域(-R , R )内能展开成x 的幂级数, 即 f (x )=a 0+a 1x +a 2x 2+ ⋅ ⋅ ⋅ +a n x n + ⋅ ⋅ ⋅ ,二、函数展开成幂级数第一步 求出f (x )的各阶导数: f '(x ), f ''(x ), ⋅ ⋅ ⋅ , f (n )(x ), ⋅ ⋅ ⋅ .第二步 求函数及其各阶导数在x =0 处的值: f (0), f '(0), f ''(0), ⋅ ⋅ ⋅ , f (n )( 0), ⋅ ⋅ ⋅ .第三步 写出幂级数 !)0( !2)0()0()0()(2⋅⋅⋅++⋅⋅⋅+''+'+nn x n f x f x f f , 并求出收敛半径R . 第四步 考察在区间(-R , R )内时是否R n (x )→0(n →∞).1)1()!1()(lim )(lim ++∞→∞→+=n n n n n x n f x R ξ是否为零. 如果R n (x )→0(n →∞), 则f (x )在(-R , R )内有展开式!)0( !2)0()0()0()()(2⋅⋅⋅++⋅⋅⋅+''+'+=nn x n f x f x f f x f (-R <x <R ). 展开式小结:)11( 1112<<-⋅⋅⋅++⋅⋅⋅+++=-x x x x xn ,)( !1 !2112+∞<<-∞⋅⋅⋅+⋅⋅⋅+++=x x n x x e n x ,)( )!12()1( !5!3sin 12153+∞<<-∞⋅⋅⋅+--+⋅⋅⋅-+-=--x n x x x x x n n ,)( )!2()1( !4!21cos 242+∞<<-∞⋅⋅⋅+-+⋅⋅⋅-+-=x n x x x x n n , )11( 1)1( 432)1ln(1432≤<-⋅⋅⋅++-+⋅⋅⋅+-+-=++x n x x x x x x n n , !2)1(1)1(2⋅⋅⋅+-++=+x m m mx x m )11( !)1( )1(<<-⋅⋅⋅++-⋅⋅⋅-+x x n n m m m n第五节 函数的幂级数展开式的应用一、近似计算例1 计算5240的近似值, 要求误差不超过0.0001.解 因为5/1455)311(33243240-=-=, 所以在二项展开式中取51=m , 431-=x , 即得) 31!3594131!254131511(32401238245⋅⋅⋅-⋅⋅⋅⋅-⋅⋅⋅-⋅-=. 这个级数收敛很快. 取前两项的和作为5240的近似值, 其误差(也叫做截断误差)为) 31!451494131!3594131!2541(3||164123822⋅⋅⋅+⋅⋅⋅⋅⋅+⋅⋅⋅⋅+⋅⋅⋅=r ] )811(8111[31!25413282⋅⋅⋅+++⋅⋅⋅<200001402725181111312568<⋅⋅=-⋅⋅=. 于是取近似式为)31511(324045⋅-≈, 为了使“四舍五入”引起的误差(叫做舍入误差)与截断误差之和不超过10-4, 计算时应取五位小数, 然后四舍五入. 因此最后得 9926.22405≈.例2 计算ln 2的近似值, 要求误差不超过0.0001.解 x =1可得 1)1( 312112ln 1⋅⋅⋅+-+⋅⋅⋅-+-=-nn .如果取这级数前n 项和作为ln2的近似值, 其误差为 11||+≤n r n .为了保证误差不超过410-, 就需要取级数的前10000项进行计算. 这样做计算量太大了, 我们必需用收敛较快的级数来代替它.把展开式)11( 1)1( 432)1ln(1432≤<-⋅⋅⋅++-+⋅⋅⋅+-+-=++x n x x x x x x n n 中的x 换成-x , 得 )11( 432)1ln(432<≤⋅⋅⋅-----=-x x x x x x ,两式相减, 得到不含有偶次幂的展开式:)1ln()1ln(11ln x x x x --+=-+)11( ) 5131(253<<-⋅⋅⋅+++=x x x x . 令211=-+xx , 解出31=x . 以31=x 代入最后一个展开式, 得 ) 31713151313131(22ln 753⋅⋅⋅+⋅+⋅+⋅+=. 如果取前四项作为ln2的近似值, 则误差为) 31131311113191(2||131194⋅⋅⋅+⋅++=r ] 91(911[32211⋅⋅⋅+++<7000001341911132<⋅=-⋅=.于是取 )31713151313131(22ln 753⋅+⋅+⋅+≈.同样地, 考虑到舍入误差, 计算时应取五位小数:33333.031≈, 01235.031313≈⋅, 00082.031515≈⋅, 00007.031717≈⋅.因此得 ln 2≈0.6931例3 求积分dx e x ⎰-2122π的近似值(误差不超过10-4).解 将e x 的幂级数展开式中的x 换成-x 2, 得到被积函数的幂级数展开式!3)(!2)(!1)(1322222⋅⋅⋅+-+-+-+=-x x x ex )( !)1(20+∞<<-∞-=∑∞=x n x n n n .根据幂级数收敛区间内逐项可积,dx x n dx n x dx e n n n n n n x ⎰∑⎰∑⎰∞=∞=--=-=102010201!)1(2]!)1(222πππ) !3721!25213211(1642⋅⋅⋅+⋅⋅-⋅⋅+⋅-=π.前四项的和作为近似值, 其误差为 900001!49211||84<⋅⋅≤πr ,所以5295.0)!3721!25213211(12642212≈⋅⋅-⋅⋅+⋅-≈⎰-ππdx e x .二、欧拉公式复数项级数: 设有复数项级数 (u 1+iv 1)+(u 2+iv 2)+ ⋅ ⋅ ⋅+(u n +iv n )+ ⋅ ⋅ ⋅其中u n , v n (n =1, 2, 3, ⋅ ⋅ ⋅)为实常数或实函数. 如果实部所成的级数 u 1+u 2 + ⋅ ⋅ ⋅ +u n + ⋅ ⋅ ⋅收敛于和u , 并且虚部所成的级数. v 1+v 2+ ⋅ ⋅ ⋅ +v n + ⋅ ⋅ ⋅ 收敛于和v , 就说复数项级数收敛且和为u +iv . 绝对收敛: 若级∑∞=+1)(n n n iv u 的各项模所构成的级数∑∞=+122n nn v u 收敛,则称级数∑∞=+1)(n n n iv u 绝对收敛. 复变量指数函数: 考察复数项级数 !1 !2112⋅⋅⋅++⋅⋅⋅+++n z n z z . 可以证明此级数在复平面上是绝对收敛的, 在x 轴上它表示指数函数e x , 在复平面上我们用它来定义复变量指数函数, 记为e z . 即 !1 !2112⋅⋅⋅++⋅⋅⋅+++=n z z n z z e .欧拉公式: 当x =0时, z =iy , 于是 )(!1 )(!2112⋅⋅⋅++⋅⋅⋅+++=n iy iy n iy iy e⋅⋅⋅-++--+= !51!41!31!2115432y i y y i y iy ) !51!31() !41!211(5342⋅⋅⋅-+-+⋅⋅⋅-+-=y y y i y y =cos y +i sin y .把y 定成x 得 e ix =cos x +i sin x , 这就是欧拉公式. 复数的指数形式: 复数z 可以表示为 z =r (cos θ +i sin θ)=re i θ , 其中r =|z |是z 的模, θ =arg z 是z 的辐角.三角函数与复变量指数函数之间的联系: 因为e ix =cos x +i sin x , e -ix =cos x -i sin x , 所以 e ix +e -ix =2cos x , e x -e -ix =2i sin x .)(21cos ix ix e e x -+=, )(21sin ix ix e e ix --=. 这两个式子也叫做欧拉公式. 复变量指数函数的性质: 2121z z z z e e e ⋅=+.特殊地, 有e x +iy =e x e i y =e x (cos y + i sin y ).第六节 傅里叶级数一、三角级数 三角函数系的正交性三角级数: 级数)sin cos (2110nx b nx a a n n n ++∑∞=称为三角级数, 其中a 0, a n , b n (n = 1, 2, ⋅ ⋅ ⋅)都是常数. 三角函数系: 1, cos x , sin x , cos 2x , sin 2x , ⋅ ⋅ ⋅, cos nx , sin nx , ⋅ ⋅ 三角函数系的正交性: 三角函数系中任何两个不同的函数的乘积在区间[-π, π]上的积分等于零.⎰-=ππ0cos nxdx (n =1, 2, ⋅ ⋅ ⋅),⎰-=ππ0sin nxdx (n =1, 2, ⋅ ⋅ ⋅),⎰-=ππ0cos sin nxdx kx (k , n =1, 2, ⋅ ⋅ ⋅),⎰-=ππ0sin sin nxdx kx (k , n =1, 2, ⋅ ⋅ ⋅, k ≠n ), ⎰-=ππ0cos cos nxdx kx (k , n =1, 2, ⋅ ⋅ ⋅, k ≠n ).三角函数系中任何两个相同的函数的乘积在区间[-π,π]上的积分不等于零,⎰-=πππ212dx ,⎰-=πππnxdx 2cos (n =1, 2, ⋅ ⋅ ⋅),⎰-=πππnxdx 2sin (n =1, 2, ⋅ ⋅ ⋅).二、函数展开成傅里叶级数傅里叶系数: ⎰-=πππdx x f a )(10 ⎰-=πππn x d x x f a n c o s )(1, (n =1, 2, ⋅ ⋅ ⋅),⎰-=πππnxdx x f b n sin )(1, (n =1, 2, ⋅ ⋅ ⋅). 系数a 0, a 1, b 1, ⋅ ⋅ ⋅ 叫做函数f (x )的傅里叶系数.傅里叶级数: 三角级数∑∞=++10)sin cos (2n n n nx b nx a a 称傅里叶级数, 其中a 0, a 1, b 1, ⋅ ⋅ ⋅是傅里叶系数.定理(收敛定理, 狄利克雷充分条件) 设f (x )是周期为2π的周期函数, 如果它满足: 在一个周期内连续或只有有限个第一类间断点, 在一个周期内至多只有有限个极值点, 则f (x )的傅里叶级数收敛, 并且 当x 是f (x )的连续点时, 级数收敛于f (x );当x 是f (x )的间断点时, 级数收敛于)]0()0(21++-x f x f .四、 正弦级数和余弦级数当f (x )为奇函数时, f (x )cos nx 是奇函数, f (x )sin nx 是偶函数, 故傅里叶系数为 a n =0 (n =0, 1, 2, ⋅ ⋅ ⋅),⎰=ππsin )(2nxdx x f b n (n =1, 2, 3, ⋅ ⋅ ⋅). 因此奇数函数的傅里叶级数是只含有正弦项的正弦级数∑∞=1sin n n nx b . 当f (x )为偶函数时, f (x )cos nx 是偶函数, f (x )sin nx 是奇函数, 故傅里叶系数为 ⎰=ππcos )(2nxdx x f a n (n =0, 1, 2, 3, ⋅ ⋅ ⋅), b n =0 (n =1, 2, ⋅ ⋅ ⋅). 因此偶数函数的傅里叶级数是只含有余弦项的余弦级数 nx a a n n cos 210∑∞=+.奇延拓与偶延拓: 设函数f (x )定义在区间[0, π]上并且满足收敛定理的条件, 我们在开区间(-π, 0)内补充函数f (x )的定义, 得到定义在(-π, π]上的函数F (x ), 使它在(-π, π)上成为奇函数(偶函数). 按这种方式拓广函数定义域的过程称为奇延拓(偶延拓). 限制在(0, π]上, 有F (x )=f (x ).。
