统计学之时间序列分析在经济预测中的应用(doc 17页)
统计学在社会经济研究中的应用

统计学在社会经济研究中的应用在当今社会,社会经济研究对于理解和解决各种经济问题、制定政策以及推动社会发展至关重要。
而统计学作为一门研究数据收集、整理、分析和解释的学科,在社会经济研究中发挥着不可或缺的作用。
它犹如一把神奇的钥匙,为我们打开了深入了解社会经济现象的大门,帮助我们揭示隐藏在数据背后的规律和趋势。
首先,统计学在经济数据的收集和整理方面具有重要意义。
在社会经济研究中,我们需要获取大量关于经济活动、市场状况、消费者行为等方面的数据。
统计学提供了科学的抽样方法和数据收集技术,确保所收集的数据具有代表性和可靠性。
例如,在进行居民消费调查时,通过随机抽样的方法选择一定数量的家庭进行调查,可以在有限的资源下获取到能够反映整体居民消费情况的数据。
同时,统计学还能帮助我们对收集到的数据进行整理和分类,使其更加清晰和易于分析。
比如,将企业的财务数据按照不同的指标和时间段进行分类汇总,为后续的分析提供了便利。
其次,统计学在描述经济现象方面发挥着关键作用。
通过各种统计指标和图表,我们可以对经济数据进行简洁而直观的描述。
均值、中位数、众数等统计量能够反映数据的集中趋势,让我们了解到某个经济变量的一般水平。
方差、标准差等则能体现数据的离散程度,帮助我们判断经济现象的波动情况。
例如,通过计算某地区居民收入的均值和标准差,我们可以了解到该地区居民收入的平均水平以及收入差距的大小。
此外,柱状图、折线图、饼图等统计图表能够将复杂的数据以形象的方式呈现出来,使人们更容易理解和比较不同的经济现象。
比如,用柱状图展示不同行业的产值增长情况,用折线图反映物价的变化趋势,用饼图展示消费结构的构成等。
再者,统计学在经济现象的分析和推断中也具有不可替代的地位。
通过建立统计模型,我们可以对经济变量之间的关系进行深入研究,并进行预测和推断。
回归分析是其中一种常用的方法,它可以帮助我们确定一个或多个自变量对因变量的影响程度。
例如,研究消费者收入对消费支出的影响,或者分析广告投入与销售额之间的关系。
统计学时间序列分析

统计学时间序列分析时间序列是经济学、金融学和其他社会科学领域中的一个重要分析对象。
通过对时间序列数据的分析,我们可以揭示数据之间的关系、趋势和周期性,从而为决策提供有力的支持和预测。
统计学时间序列分析是一种应用数学方法的工具,用于对时间序列数据进行建模和预测。
一、时间序列的基本概念时间序列是按时间顺序排列的一系列观测值的集合。
在时间序列分析中,我们关注数据之间的内在关系,而忽略其他因素的影响。
时间序列数据通常具有以下特征:1. 趋势性:时间序列数据的长期变化趋势。
2. 季节性:时间序列数据在一年内固定时间段内的重复模式。
3. 循环性:时间序列数据中存在的多重周期性波动。
4. 随机性:时间序列数据中的不规则、无法预测的波动。
二、时间序列分析的方法在进行时间序列分析时,我们可以采用以下方法来揭示数据的内在规律:1. 描述性统计分析:通过计算数据的均值、方差、相关系数等指标,对数据的整体特征进行描述。
2. 图表分析:通过绘制折线图、柱状图等图表,展示时间序列数据的变化趋势和周期性。
3. 分解模型:将时间序列数据分解为趋势项、季节性项和残差项,以揭示数据的内在结构。
4. 平滑法:通过移动平均法、指数平滑法等方法,消除时间序列数据的随机波动,从而揭示趋势和季节性成分。
5. 自回归移动平均模型(ARIMA):ARIMA模型是一种常用的时间序列分析方法,可以对数据进行预测和建模。
它综合考虑了自回归、移动平均和差分的影响因素。
三、时间序列分析的应用领域时间序列分析广泛应用于经济学、金融学、市场调研等领域,具体应用包括:1. 经济预测:通过对经济数据进行时间序列分析,可以预测未来的经济发展趋势,为政府决策提供参考。
2. 股票市场分析:时间序列分析可以帮助分析师预测股票市场的走势,制定投资策略。
3. 需求预测:通过对销售数据进行时间序列分析,可以预测产品的需求量,为企业的生产和供应链管理提供指导。
4. 天气预测:通过对气象数据进行时间序列分析,可以预测未来的天气状况,为农业、旅游等行业提供参考。
统计学-第十章 时间序列分析

1
38(a1)
2
42(a2)
3
39(a3)
4
37(a4)
5
41(a5)
解: a 38 42 39 37 41 39.(4 台/天) 11111
三、平均发展水平
3.由绝对数时间序列计算的序时平均数
(2)由时点序列计算序时平均数
②间隔不相等的连续的时点数列
a af
季度在某地区销售量的走势 250 200
图。
150
100
那么,如何预测该品牌 50
空调2018年各个季度在该地 0
区的销售量呢?
单位:销售量(百台)
3
第一节 时间序列概述
一、时间序列概述
1.定义:将表明社会经济现象在不同时间发展 变化的某同一指标数值,按时间先后顺序排列所形 成的序列。(规模和水平)
③序列中每个指标的数值,通 常通过连续不断的登记取得。
由反映某种现象在一定 时点(瞬间)上发展状况的总量 指标所构成的绝对数动态序列所 处的数量水平。其中时点序列无 时点长度;两个相邻时点间的时 间距离称为时点间隔。也可为 日、周、旬、季、年等。
①序列中各个指标的 数值不可以直接相加;
②序列中指标数值的大小与其 时间间隔长短没有直接联系;
表9.3 我国普通高校毕业生数(时期序列)
年份 1912-1948 1978 1995 2000 2004 2014 2016
毕业生数(万人) 21.08 16.5 80.5 95 239.1 669.4 756
10
第二节 时间序列分析的基本原 理 一、时间序列分析的意义
:以时间序列为依据,对影响动态序列变 动过程的主要因素及其相互关系进行分解与综合, 以认识社会经济现象发展变量的规律性,借以鉴别 过去、预测未来的分析研究工作。
统计学文档时间序列分析

第5章时间序列分析5.1时间序列的基本问题5.1.1时间序列的概念时间序列是指反映客观现象的同一指标在不同时间上的数值,按时间先后顺序排列而形成的序列,它由两个基本要素组成:一个是现象的所属时间;另一个是反映该现象的同一指标在不同时间条件下的具体数值。
也称为时间数列,或动态数列。
时间序列的一般形式是:例如,表5.1是一个国内生产总值及其部分构成统计表。
表时间序列可以描述客观现象发展变化的状况、过程和规律,利用时间序列资料可以计算一系列动态分析指标,通过时间序列分析,可以揭示客观现象发展变化的趋势,为预测、决策提供依据。
5.1.2时间序列的分类时间序列可以分为绝对数时间序列、相对数时间序列和平均数时间序列三种。
其中绝对数时间序列是最基本的时间序列,其余两种是在其基础上派生的。
1、绝对数时间序列,简称绝对序列:它是把同一总量指标在不同时间上的数值按时间先后顺序排列而形成的时间序列。
绝对序列反映现象在不同时间上所达到的总量及其增减变化的过程。
绝对序列有时期序列和时点序列两种。
时期序列是由时期绝对数数据所构成的时间序列,其中的每个数值反映现象在一段时间内发展过程的总量。
时点序列是由时点绝对数数据所构成的时间序列,其中的每个数值反映现象在某一时点上所达到的水平。
时期序列中的各个数数值可以相加,各个数数值的和表示了在所对应的时期之内事物及其现象的发展总量。
而时点序列中各个数数值相加通常没有明确的意义;时期序列中各项数值的大小与所包括的时期长短有直接关系,时点序列中各数数值与其时点间隔长短没有直接关系。
2、相对数时间序列:它是把一系列同类的统计相对数按照时间先后顺序排列起来而形成的时间序列,反映事物之间对比关系的变化情况。
3、平均数时间序列:它是把一系列同类的统计平均数按照时间先后顺序排列起来而形成的时间序列,表现事物一般水平的变化过程的发展趋势。
参看上表格。
5.1.3编制时间序列的原则编制时间序列的目的是要通过对序列中各个时期指标值进行比较,以达到研究客观现象的发展变化状况、过程及其规律。
应用统计学时间数列分析

应用统计学时间数列分析时间数列分析是统计学中的一项重要内容,通过对时间序列数据进行分析,可以揭示数据之间的内在关联和规律。
本文将探讨时间数列分析在实际应用中的重要性和方法。
什么是时间数列分析时间数列(Time Series)指的是按时间顺序排列的一系列数据观测值。
时间数列分析是指根据时间数列数据进行的统计分析方法,旨在发现数据中存在的趋势、季节性、周期性等规律,以便进行预测和决策。
时间数列分析的重要性时间数列分析在许多领域都有广泛的应用,包括经济学、金融、医学、气象等。
通过时间数列分析,我们可以:•发现数据中的趋势和规律•预测未来数据走势•制定决策和策略•检验模型的有效性•揭示不同变量之间的关联时间数列分析方法1. 平稳性检验平稳性是时间数列分析的前提条件之一,可以通过单位根检验、ADF检验等方法来判断时间数列是否平稳。
如果时间数列不平稳,需要进行差分处理或其他转换方法使其平稳化。
2. 自相关性分析自相关性分析是检验数据是否存在自相关性(即相邻数据之间的相关性)的方法,可以通过自相关图和偏自相关图来判断数据中的自相关性程度。
3. 移动平均法移动平均法是一种基本的时间数列预测方法,通过计算一定窗口内的数据均值来平滑数据曲线,以便更好地观察数据走势和预测未来走向。
4. 季节性调整在时间数列分析中,常常需要对数据进行季节性调整,以消除季节性影响,使预测结果更为准确。
应用实例1. 股票价格预测时间数列分析在金融领域有着广泛的应用。
通过分析股票价格的时间数列数据,可以预测股价的未来走势,指导投资决策。
2. 气象预测气象数据也是时间数列数据的一种,通过对气象数据进行时间数列分析,可以预测未来的气候变化和天气情况,为灾害预警和农业生产提供依据。
3. 经济指标分析经济数据的时间数列分析可以揭示经济增长趋势、波动周期等信息,帮助政府和企业做出相应决策。
结语时间数列分析是统计学中一个重要的分析方法,通过对时间序列数据进行分析,可以揭示数据之间的规律、趋势和关联。
时间序列分析案例

时间序列分析案例时间序列分析是指对一系列按照时间顺序排列的数据进行分析和预测的统计方法。
在实际生活中,时间序列分析可以应用于经济预测、股票价格预测、气象预测等多个领域。
本文将以一个实际案例来介绍时间序列分析的基本步骤和方法。
首先,我们选取了某公司过去五年的月销售额数据作为研究对象。
我们首先对数据进行可视化分析,绘制出销售额随时间变化的折线图。
通过观察折线图,我们可以初步判断销售额是否存在趋势、季节性和周期性等特点。
接下来,我们对销售额数据进行平稳性检验。
平稳性是时间序列分析的基本假设之一,如果数据不是平稳的,就需要对数据进行差分处理。
我们使用单位根检验(ADF检验)来判断销售额数据是否平稳。
如果数据不是平稳的,我们将对数据进行一阶差分处理,直到数据变得平稳为止。
在确认数据平稳后,我们将对销售额数据进行自相关性和偏自相关性分析。
自相关性分析可以帮助我们确定时间序列的阶数,偏自相关性分析可以帮助我们确定ARIMA模型的参数。
通过自相关性和偏自相关性图,我们可以初步确定ARIMA 模型的参数p和q的取值。
接下来,我们将建立ARIMA模型并进行参数估计。
ARIMA模型是一种常用的时间序列预测模型,它可以很好地捕捉时间序列的趋势、季节性和周期性。
我们使用最大似然估计方法对ARIMA模型的参数进行估计,并对模型的拟合效果进行检验。
最后,我们将使用建立好的ARIMA模型对未来几个月的销售额进行预测。
我们将绘制出销售额的预测图,并计算出预测误差的均方根误差(RMSE)。
通过对预测结果的分析,我们可以评估ARIMA模型的预测效果,并对未来的销售额进行合理的预测。
通过以上案例,我们可以看到时间序列分析在实际中的应用。
通过对销售额数据的分析和预测,我们可以为公司的经营决策提供重要的参考依据。
同时,时间序列分析也可以应用于其他领域,帮助我们更好地理解数据的规律和特点,为未来的预测和决策提供支持。
计量经济学中的时间序列分析

计量经济学中的时间序列分析时间序列分析是计量经济学中的重要内容之一,它主要研究特定变量随时间变化的规律性和趋势。
通过时间序列分析,我们可以更好地理解经济现象,预测未来变化趋势,制定合适的政策和策略。
本文将从时间序列的概念入手,介绍时间序列分析的基本原理、方法和应用。
一、时间序列的概念时间序列是按照时间顺序排列的一系列数据观测值的集合。
在计量经济学中,时间序列通常用来观察和研究某一经济变量在不同时间点上的变化情况。
时间序列数据可以是连续的,也可以是间断的,常见的时间单位包括年、季、月、周等。
通过对时间序列数据的分析,我们可以揭示出其中的规律性和特征。
二、时间序列分析的基本原理时间序列分析的基本原理是利用过去的数据来预测未来的发展趋势。
在时间序列分析中,常用的方法包括趋势分析、周期性分析、季节性分析和不规则波动分析。
趋势分析主要用来观察时间序列数据的长期变化趋势,周期性分析则是研究数据是否存在固定长度的周期性波动,季节性分析则是研究数据是否呈现出固定的季节性变化规律,而不规则波动分析则是研究一些随机因素对数据的影响。
三、时间序列分析的方法时间序列分析的方法有很多种,其中常用的包括移动平均法、指数平滑法、回归分析法、ARIMA模型等。
移动平均法通过计算连续几个期间的平均值来平滑数据,达到去除数据波动的目的;指数平滑法则是通过计算加权平均来对数据进行平滑处理,使得预测值更加准确;回归分析法则是通过建立经济模型来研究时间序列数据之间的关系,进行预测和分析;ARIMA模型则是一种时间序列的自回归与移动平均模型,可以对时间序列数据进行拟合和预测。
四、时间序列分析的应用时间序列分析在经济学、金融学、管理学等领域有着广泛的应用。
在经济学中,时间序列分析可以用来研究经济增长、通货膨胀、失业等经济现象的发展趋势;在金融学中,时间序列分析可以用来预测股票价格、汇率、利率等金融变量的变化情况;在管理学中,时间序列分析可以用来制定企业的生产计划和销售策略,提高企业的运营效率。
统计学原理第5章:时间序列分析

a a
n 118729 129034 132616 132410 124000 5
127357.8
②时点序列
若是连续时点序列: 计算方法与时期序列一样; 若是间断时点序列: 则必须先假设两个条件,分别是 假设上期期末水平等于本期期初水平; 假设现象在间隔期内数量变化是均匀的。 间隔期相等的时点序列 采用一般首尾折半法计算。 例如:数列 a i , i 0,1,2, n 有 n 1 个数据,计算 期内的平均水平 a n a n 1 a 0 a1 a1 a 2
(3)联系
环比发展速度的乘积等于相应的定基发展速度,
n n i 0 i 1 i 1
相邻两期的定基发展速度之商等于后期的环比发展速度
i i 1 i 0 0 i 1
(二)增减速度
1、定义:增长量与基期水平之比 2、反映内容:现象的增长程度 3、公式:增长速度
0.55
二、时间序列的速度分析指标
(一)发展速度 (二)增长速度 (三)平均发展水平
(四)平均增长速度
(一)发展速度
1、定义:现象两个不同发展水平的比值 2、反映内容:反映社会经济现象发展变化快慢相对程度 3、公式:v 报告期水平 100%
基期水平
(1)定基发展速度
是时间数列中报告期期发展水平与固定基期发展水平对比所 得到的相对数,说明某种社会经济现象在较长时期内总的发 展方向和速度,故亦称为总速度。 (2)环比发展速度 是时间数列中报告期发展水平与前期发展水平之比,说明某 种社会经济现象的逐期发展方向和速度。
c
a
b
均为时期或时点数列,一个时期数列一个时点数列,注意平均的时间长度 ,比如计算季度的月平均数,时点数据需要四个月的数据,而时期数据则 只需要三个月的数据。
时间序列分析

时间序列分析时间序列分析是一种重要的统计学方法,用于研究随时间变化的数据。
它可以帮助我们了解数据的趋势、周期性和季节性,预测未来的变化趋势,并做出相应的决策。
本文将介绍时间序列分析的基本概念、常见的方法和应用领域。
一、时间序列的基本概念时间序列是按时间先后顺序排列的一组观察数据。
它可以是连续的,例如每天的股票价格;也可以是离散的,例如每月的销售量。
时间序列的分析要求数据点之间存在一定的相关性和规律性。
二、时间序列的组成部分时间序列通常由三个主要组成部分构成:趋势、季节性和随机性。
趋势是时间序列在长期内呈现的整体变化趋势;季节性是时间序列在较短的时间内出现的重复周期性变化;随机性是时间序列中无法解释的随机波动。
三、时间序列分析的方法1. 描述性分析描述性分析是对时间序列数据进行可视化和概括的方法。
常用的方法包括绘制折线图、直方图和自相关图等,以帮助我们了解数据的分布和相关性。
2. 平稳性检验平稳性是时间序列分析的基本假设。
平稳序列的统计特性在时间上是不随时间变化的,包括均值、方差和自相关性等。
常见的平稳性检验方法有单位根检验和ADF检验。
3. 建立模型建立时间序列模型是对数据进行预测和分析的关键步骤。
常用的时间序列模型有ARIMA模型、AR模型和MA模型等。
通过对历史数据的拟合,我们可以得到模型的参数,从而进行未来值的预测。
4. 模型诊断与改进在建立模型之后,需要对其进行诊断和改进。
常见的诊断方法包括残差检验、模型稳定性检验和模型比较等。
根据诊断结果,我们可以对模型进行改进,提高预测的准确性。
四、时间序列分析的应用领域时间序列分析在许多领域都有广泛的应用,例如经济学、金融学、气象学和市场营销等。
在经济学中,时间序列分析可以用于预测经济增长趋势和通货膨胀率。
在金融学中,它可以帮助我们预测股票价格和利率走势。
在气象学中,时间序列分析可以用于预测天气变化和自然灾害。
在市场营销中,它可以帮助我们预测销售量和用户行为。
统计学第八章 时间序列分析

季节指数
乘法模型中的季节成分通过季节指数来反映。 季节指数(季节比率):反映季节变动的相
对数。 1、月(或季)的指数之和等于1200%(或
400%) 。 2、季节指数离100%越远,季节变动程度
越大,数据越远离其趋势值。
用移动平均趋势剔除法计算季节指数
1、计算移动平均值(TC),移动期数为4或 12,注意需要进行移正操作。
移动平均的结果 4000 3500 3000 2500 2000 1500 1000 500 0
Example 2
移动平均法可以作为测定长期趋势的一种 较为简单的方法,在股市技术分析中有广 泛的应用。比如对某只股票的日收盘价格 序列分别求一次5日、10日、一个月的移动 平均就可以得到其5日、10日、一个月的移 动平均股价序列,进而得到5日线、10日线、 月线,用以反映股价变动的长期趋势。
1987 1800 1992 1980 1997 2880
1988 1620 1993 2520 1998 3060
1989 1440 1994 2559 1999 2700
4000
3500
销售收入
3000
2500
2000
1500
1000
500
0
年份
2000 2001 2002 2003 2004
销售 收入 3240 3420 3240 3060 3600
部分数据
销售 收入
t
1985 1080
1
1986 1260
2
1987 1800
3
1988 1620
4
1989 1440
5
……
…
2003 3060
19
统计学预测方法

统计学预测方法统计学预测方法是统计学中的一个重要分支,它主要研究如何利用已有的数据和统计模型来进行未来事件的预测。
统计学预测方法在各个领域都有着广泛的应用,比如经济学、金融学、医学、环境科学等。
本文将介绍一些常见的统计学预测方法,包括时间序列分析、回归分析、贝叶斯统计等,并且分析它们的优缺点及适用范围。
时间序列分析是一种常见的统计学预测方法,它主要用于分析时间序列数据,即按照时间顺序排列的数据。
时间序列分析可以帮助我们发现数据中的趋势、周期性和规律性,从而进行未来事件的预测。
常见的时间序列分析方法包括移动平均法、指数平滑法、ARIMA模型等。
这些方法在预测经济指标、股票价格、气温变化等方面有着广泛的应用。
回归分析是另一种常见的统计学预测方法,它主要用于分析自变量和因变量之间的关系,并建立预测模型。
回归分析可以帮助我们理解变量之间的因果关系,并进行未来事件的预测。
常见的回归分析方法包括线性回归、逻辑回归、岭回归等。
这些方法在预测销售额、市场份额、疾病发生率等方面有着广泛的应用。
贝叶斯统计是一种基于贝叶斯定理的统计学预测方法,它主要用于更新先验概率,得出后验概率,并进行未来事件的预测。
贝叶斯统计可以帮助我们在不断获得新数据的情况下,不断修正对未来事件的预测。
贝叶斯统计在医学诊断、风险评估、网络安全等领域有着广泛的应用。
除了上述方法,还有很多其他的统计学预测方法,比如神经网络、支持向量机、决策树等。
这些方法各有特点,适用于不同的预测场景。
在选择预测方法时,我们需要根据具体的问题和数据特点来进行综合考虑,选择最合适的方法进行预测。
总之,统计学预测方法在实际应用中有着广泛的意义和价值,它可以帮助我们理解数据背后的规律,预测未来的趋势,为决策提供科学依据。
在未来的发展中,统计学预测方法将继续发挥重要作用,为各个领域的发展和进步提供有力支持。
时间序列分析在经济预测中的应用

时间序列分析在经济预测中的应用时间序列分析是一种经济学和统计学中常用的方法,用于研究随时间变化的数据。
在经济学领域,时间序列分析被广泛应用于经济预测,帮助政府、企业和个人做出更准确的决策。
本文将探讨时间序列分析在经济预测中的应用,介绍其基本概念、方法和实际案例。
### 1. 时间序列分析基本概念时间序列是按照时间顺序排列的一系列数据点。
时间序列分析旨在揭示数据随时间变化的规律性,以便进行预测和决策。
在经济学中,时间序列可以是股票价格、GDP增长率、通货膨胀率等经济指标,通过对这些数据进行分析,可以帮助我们了解经济的发展趋势和周期性变化。
时间序列分析的基本概念包括趋势、季节性和周期性。
趋势是数据长期变化的方向,可以是增长趋势、下降趋势或平稳趋势。
季节性是数据在特定时间段内重复出现的规律性波动,如节假日销售额增加、冬季用电量增加等。
周期性是数据在较长时间跨度内呈现的波动,通常周期为数年或数十年。
### 2. 时间序列分析方法时间序列分析的方法主要包括描述统计、平稳性检验、自相关性检验、建立模型和预测。
描述统计是对时间序列数据的基本特征进行总结和分析,包括均值、方差、标准差等。
平稳性检验是检验时间序列数据是否具有稳定的统计特性,如果数据不稳定,需要进行差分处理。
自相关性检验是检验时间序列数据是否存在自相关性,即相邻观测值之间的相关性。
建立模型是根据时间序列数据的特点选择合适的模型,常用的模型包括ARIMA模型、ARCH模型等。
预测是利用建立的模型对未来数据进行预测,帮助做出决策。
### 3. 时间序列分析在经济预测中的应用时间序列分析在经济预测中有着广泛的应用,可以帮助政府、企业和个人做出更准确的决策。
以下是时间序列分析在经济预测中的几个典型应用场景:#### 3.1 GDP增长预测GDP(国内生产总值)是衡量一个国家经济总量的重要指标,对于政府制定经济政策和企业投资决策具有重要意义。
通过时间序列分析,可以对GDP增长趋势进行预测,帮助政府和企业做出相应调整。
经济数据时间序列分析

经济数据时间序列分析经济数据是衡量一个国家或地区经济发展水平的重要指标,而时间序列分析是经济数据分析的重要方法之一。
时间序列分析是一种将一系列时间上连续的数据按时间顺序排列,然后利用统计学方法进行分析和预测的方法。
时间序列分析的目标是研究在某一时间间隔内经济数据的变化规律和趋势,借此来预测未来的发展趋势和可能出现的风险。
时间序列分析可以从多个角度分析经济数据,例如总量、结构、动态等多个方面,并且可以通过预测模型实现对未来的预测。
在时间序列分析中,首先需要对经济数据进行整理和处理。
经济数据的来源非常广泛,包括政府统计数据、商业数据、金融数据等等。
这些数据往往存在着噪声和异常值,需要经过数据清理和处理来进行分析。
对于一些长期存在的经济指标,例如国内生产总值、物价指数、居民消费价格指数等,需要对数据进行季节性和趋势性的拟合和分解,以便更好地分析和预测。
时间序列分析主要包括基本分析方法和高级分析方法两种。
基本分析方法主要包括建立时间序列模型、计算趋势指数、计算季节性指数等等。
而高级分析方法则包括自回归模型、移动平均模型、自回归移动平均模型等等。
这些模型都可以通过统计学的方法来评估预测结果的可靠性和精确度,帮助分析师对未来的经济趋势和风险做出更好的预测和决策。
除了时间序列分析以外,趋势分析、对比分析、比率分析等方法也是经济数据分析的重要手段。
与时间序列分析不同的是,这些方法更侧重于经济数据不同时间点之间的比较,从中分析出个别和整体数据的变化及其存在的问题和趋势。
在经济数据分析的过程中,统计学方法具有重要的作用。
统计学方法可以通过各种统计指标和模型来分析和解释经济数据,例如平均数、标准差、相关系数、回归分析等等。
这些方法可以帮助分析师更准确地识别经济数据中的变化、趋势和周期,以便更好地预测和制定经济政策。
总之,经济数据时间序列分析是一种重要的经济数据分析方法,可以帮助分析师更好地理解经济数据、预测经济趋势和风险,并且制定相应的经济政策和决策。
统计学_第八章__时间序列分析
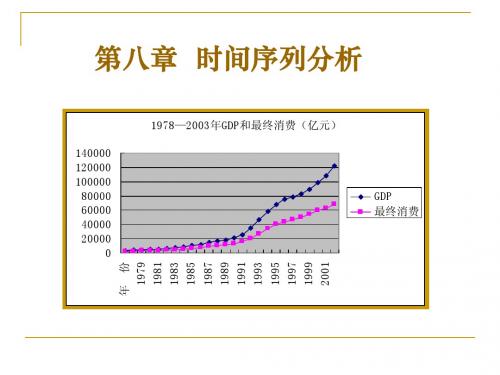
1978—2003年GDP和最终消费(亿元) 140000 120000 100000 80000 60000 40000 20000 0
年 份 1979 1981 1983 1985 1987 1989 1991 1993 1995 1997 1999 2001
GDP 最终消费
4、二者关系 (1)各逐期增长量之和等于相应的累计增长量
an a0 (a1 a0 ) (a2 a1 ) (a3 a2 ) (an an1 )
(2)相邻两期的逐期增长量之和等于相应的 累计增长量;相邻两期的累计增长量之差等于 相应的逐期增长量
(二)平均增长量 1、概念 一段时期内平均每期增加或者减少的绝 对数量。或者说是逐期增长量的序时平均数。 2、计算公式
a0 a1 a 2 a n 或 a n 1
af a f
B、如果是间断时点数列,计算方法为: 『两个假设条件: 一是假设上期期末水平等于本期期初水平; 二是假设现象在间隔期内数量变化是均匀的。』 Ⅰ、间隔期相等的时点数列,采用“首尾(首末)折半 法”计算。 先计算各间隔期的平均数;然后再将这些平均数进行 简单算术平均。例如:
第一节
时间序列分析概述
一、时间序列的概念和作用
(一)、概念: 1、时间序列:将不同时间的某一统计指标数据按照 时间的先后顺序排列起来而形成的统计序列,也称时间 数列或动态数列。 2、基本构成要素(从形式上看): 一是时间顺序(现象所属的时间)。可以是年份、季 度、月份或其他任何时间,称时间要素(常用t表示); 二是不同时间的统计数据(现象在不同时间上的观察 值)。可以是绝对数、相对数、平均数,称数据要素 (常用小写的英文字母a、b、c表示)。
统计学 时间序列分析

7
商品流转次数(c)
1.9 65 75 2.41 2.22 2.4 80.7
2 2.0 2.4
4 2.27
72
120 145+185+190+200+250
c
a(平均销售额) b(平均库存额)
60
6 65 75 78 80 100 105
2.27次
2
2
6
3. 增长量和平均增长量
增长量说明社会经济现象在一定时期内所增长的绝对数量, 它是报告期水平与基期水平之差。 由于采用的基期不同,增长量分为逐期增长量和累积增长量
某企业1996-2000年产量增长速度
年份
1996 1997 1998 1999 2000
环比增长速度(%) 20 (2) 25 15 (5)
定基增长速度(%) (1) 50 (3) (4) 132.5
解: 1996年定基增长速度=20%
1997年环比增长速度=
1+50% 1+20%
1
25%
1998年定基增长速度
535 552 562 676
a 2
2 573人
4 1
例.某地区2008年城乡居民储蓄余款额资料如下
日期
1月1日 3月1日 7月1日 8月1日 12月31日
储蓄余款额
38
42
54
56
60
(亿元)
38 42 2 42 54 4 54 56 1 56 60 5
a 2
2
2
2
53.29万元
定基发展速度: 环比发展ቤተ መጻሕፍቲ ባይዱ度:
x1 , x2 , , xn
x0 x0
x0
应用统计学之时间序列分析

励志人生 好好学习
9 . 4 季节变动分析
一、季节变动分析的原始资料平均法 二、季节变动分析的趋势-循环剔除法 三、季节变动的调整
励志人生 好好学习
季节变动分析的原理与方法
什么是季节变动?
4. 移动平均会使原序列失去部分信息,平均项数越 大,失去的信息越多。
励志人生 好好学习
二、测定长期趋势的线性趋势模型
法
线性趋势的模型法
利用线性回归的方法对原时间序列拟合线性 方程
其中
励志人生 好好学习
三、测定长期趋势的非线性趋势模型
法
(1)抛物线型
(2)指数曲线型
长期趋势模型的拟合比较困难,可参考以下做法 :
●揭示循环变动规律性 ●研究循环波动的原因 ●对循环规律作科学预测
励志人生 好好学习
二、循环变动的测定方 法
直接法:
计算序列的年距发展速度或年距增长速度, 以消除或减弱趋势变动和季节变动
年距发展速度序列
年距增长速度序列
励志人生 好好学习
ቤተ መጻሕፍቲ ባይዱ
剩余法
思想:
先从序列中分别分解出长期趋势和季 节变动,然后再消除不规则变动成分, 剩余的变动则揭示出序列的循环变动特 征
间隔:在一个时间序列中,两个相邻指标数 值所在时间间隔。有等间隔和不等间隔时 间序列。
2、时点序列:排列在绝对数时间序列中的 每个指标数值,都反映现象在某一时点上 的总量。(时点序列没有时期,只有间隔 )
励志人生
好好学习 时期序列与时点序列的区别
• 前者中的每个指标数值都是反映现象在一定时期内发 展过程的总量;后者中的每个指标数值都是反映现象 在某一时点上的总量。
时间序列分析案例

时间序列分析案例(总17页) -CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除《时间序列分析》案例案例名时间序列分析在经济预测中的应用称:内容要确定性与随机性时间序列之比较求:设计作者:许启发,王艳明设计时间:2003年8月案例四:时间序列分析在经济预测中的应用一、案例简介为了配合《统计学》课程时间序列分析部分的课堂教学,提高学生运用统计分析方法解决实际问题的能力,我们组织了一次案例教学,其内容是:对烟台市的未来经济发展状况作一预测分析,数据取烟台市1949—1998年国内生产总值(GDP)的年度数据,并以此为依据建立预测模型,对1999年和2000年的国内生产总值作出预测并检验其预测效果。
国内生产总值是指一个国家或地区所有常住单位在一定时期内生产活动的最终成果,是反映国民经济活动最重要的经济指标之一,科学地预测该指标,对制定经济发展目标以及与之相配套的方针政策具有重要的理论与实际意义。
在组织实施时,我们首先将数据资料印发给学生,并讲清本案例的教学目的与要求,明确案例所涉及的教学内容;然后给学生一段时间,由学生根据资料,运用不同的方法进行预测分析,并确定具体的讨论日期;在课堂讨论时让学生自由发言,阐述自己的观点;最后,由主持教师作点评发言,取得了良好的教学效果。
经济预测是研究客观经济过程未来一定时期的发展变化趋势,其目的在于通过对客观经济现象历史规律的探讨和现状的研究,求得对未来经济活动的了解,以确定社会经济活动的发展水平,为决策提供依据。
时间序列分析预测法,首先将预测目标的历史数据按照时间的先后顺序排列,然后分析它随时间的变化趋势及自身的统计规律,外推得到预测目标的未来取值。
它与回归分析预测法的最大区别在于:该方法可以根据单个变量的取值对其自身的变动进行预测,无须添加任何的辅助信息。
本案例的最大特色在于:它汇集了统计学原理中的时间序列分析这一章节的所有知识点,通过本案例的教学,可以把不同的时间序列分析方法进行综合的比较,便于学生更好地掌握本章的内容。
时间序列分析在金融市场中的应用

时间序列分析在金融市场中的应用在金融市场中,时间序列分析是一个非常重要的分析方法。
时间序列分析是指对某一现象在时间上的变化进行观察和分析,并运用统计学方法,找出其中的规律和趋势。
在金融市场中,时间序列分析可以用来预测股票价格、利率变化等重要指标。
首先,时间序列分析的数据源是金融市场中的历史数据。
历史数据包括股票价格、交易量、宏观经济指标等,并随着时间的推移形成时间序列。
时间序列分析的目的是找到这些时间序列的规律和趋势,并通过这些规律和趋势来进行预测和决策。
其次,时间序列分析可以进行时间序列分解。
时间序列分解是指将一个时间序列分解为趋势、季节性和随机性三个部分的过程。
趋势是指时间序列的长期变化趋势,季节性是指时间序列在特定时间段内的周期性波动,而随机性则是指时间序列的非系统性波动。
通过时间序列分解,我们可以更加深入地了解时间序列的规律和特征,更加准确地预测其未来走势。
时间序列分析还可以用来进行数据拟合和预测。
时间序列分析可以利用历史数据,通过一定的算法建立时间序列模型,然后利用这个模型来预测未来的走势。
常用的时间序列模型有AR、MA、ARMA等模型。
这些模型可以用来捕捉时间序列中的基本特征,比如自相关性、平稳性等,并将这些特征用于预测未来的走势。
最后,时间序列分析还可以用来进行风险管理和投资策略决策。
在金融市场中,风险是一个永恒的话题。
时间序列分析可以用来预测未来的走势,并根据预测的信息来进行风险管理。
在投资策略决策方面,时间序列分析可以用来为投资者提供股票买卖的建议,包括长期投资、短期投机、穿越交易等多种投资策略。
这些策略不仅可以为投资者带来收益,同时也可以降低投资风险。
总之,时间序列分析在金融市场中的应用非常广泛。
它可以用来预测股票价格、利率变化等指标,可以进行时间序列分解并找到规律和趋势,可以进行数据拟合和预测,并可以用来进行风险管理和投资策略决策。
这些应用使得时间序列分析成为金融市场中不可或缺的分析工具。
时间序列分析在经济预测中的应用

时间序列分析在经济预测中的应用时间序列分析是一种经济预测中常用的工具,它通过对过去的数据进行分析,从中找出随时间变动的模式和规律,进而预测未来的情况。
本文将围绕时间序列分析在经济预测中的应用展开讨论。
首先,时间序列分析在经济领域中有着广泛的应用。
经济是一个动态的系统,受到多种因素的影响,如季节变化、经济政策调整、市场需求变化等等。
而时间序列分析可以帮助我们理解这些影响因素对经济变化的影响程度以及变化趋势。
其次,时间序列分析可以用于短期经济预测。
在政府制定经济政策和企业制定经营策略时,对未来经济的预测是非常重要的。
通过对历史数据的时间序列分析,可以建立模型,进而预测未来一段时间内的经济走势。
这对于企业合理安排生产、销售计划,以及政府制定经济政策都有着重要的指导意义。
此外,时间序列分析也可以应用于长期经济预测。
经济是一个复杂的系统,受到多种因素的综合作用,如人口变动、技术进步、经济结构调整等。
通过对长期统计数据的时间序列分析,可以找到经济发展的潜在规律和趋势。
这对于制定长期发展战略、推动经济结构升级具有重要意义。
另外,时间序列分析在金融领域也有广泛的应用。
金融市场的波动受到多种因素的影响,如政策利率变动、贸易战、资本流动等。
通过对金融市场的时间序列数据进行分析,可以帮助投资者制定投资策略,降低风险,并获取更好的收益。
时间序列分析方法有很多,其中包括传统的统计方法,如移动平均、指数平滑、ARIMA模型等,以及机器学习方法,如神经网络、支持向量机、随机森林等。
不同的方法适用于不同的数据特征和预测需求。
选择合适的方法对于准确预测经济走势至关重要。
然而,时间序列分析也存在一些挑战和限制。
首先,经济领域的数据通常是非常复杂的,受到多种因素的影响,如季节性、趋势性、周期性和随机性等。
对于这种复杂数据的分析和建模是十分困难的。
其次,经济变量之间常常存在相互关联和共同演化的关系,这也给时间序列分析带来了一定的挑战。
时间序列分析在经济预测中的应用

时间序列分析在经济预测中的应用在当今复杂多变的经济环境中,准确预测经济走势对于企业决策、政府规划以及个人投资都具有至关重要的意义。
时间序列分析作为一种强大的数据分析工具,在经济预测领域发挥着不可或缺的作用。
时间序列,简单来说,就是按照时间顺序排列的数据点序列。
这些数据点可以是股票价格、销售额、国内生产总值(GDP)等经济指标。
时间序列分析的核心目标是通过研究这些数据的历史模式和趋势,来预测未来的可能值。
时间序列分析之所以能够在经济预测中发挥作用,主要基于以下几个关键特点。
首先,它能够捕捉数据中的趋势性。
经济数据往往呈现出一定的长期趋势,例如经济的增长或衰退。
通过时间序列分析,可以识别并量化这种趋势,从而为预测未来的发展方向提供依据。
其次,它可以揭示周期性。
许多经济现象都具有周期性特征,如季节性波动或商业周期。
时间序列分析能够帮助我们发现这些周期规律,并据此对未来的周期阶段进行预估。
再者,它能够考虑到随机性因素。
经济活动受到众多不确定因素的影响,导致数据中存在随机波动。
时间序列模型可以对这种随机性进行建模和处理,从而提高预测的准确性。
在实际应用中,常用的时间序列分析方法包括移动平均法、指数平滑法和自回归移动平均(ARMA)模型等。
移动平均法是一种简单而直观的方法。
它通过计算一定时间段内数据的平均值来平滑数据,从而减少随机波动的影响。
例如,我们可以计算过去几个月的平均销售额来预测下一个月的销售额。
然而,移动平均法的缺点是它对历史数据的权重相同,可能无法充分反映近期数据的重要性。
指数平滑法则对移动平均法进行了改进。
它给予近期数据更高的权重,使得预测更能及时反映数据的最新变化。
这种方法在处理具有一定稳定性的数据时表现较好。
ARMA 模型则更加复杂和精确。
它将时间序列看作是过去值和随机误差项的线性组合。
通过对模型参数的估计,可以预测未来的值。
但ARMA 模型的应用需要一定的前提假设和数据特征满足,否则可能导致不准确的预测。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
统计学之时间序列分析在经济预测中的应用(doc 17页)《时间序列分析》案例案例名称:时间序列分析在经济预测中的应用内容要求:确定性与随机性时间序列之比较设计作者:许启发,王艳明设计时间:2003年8月案例四:时间序列分析在经济预测中的应用一、案例简介为了配合《统计学》课程时间序列分析部分的课堂教学,提高学生运用统计分析方法解决实际问题的能力,我们组织了一次案例教学,其内容是:对烟台市的未来经济发展状况作一预测分析,数据取烟台市1949—1998年国内生产总值(GDP)的年度数据,并以此为依据建立预测模型,对1999年和2000年的国内生产总值作出预测并检验其预测效果。
国内生产总值是指一个国家或地区所有常住单位在一定时期内生产活动的最终成果,是反映国民经济活动最重要的经济指标之一,科学地预测该指标,对制定经济发展目标以及与之相配套的方针政策具有重要的理论与实际意义。
在组织实施时,我们首先将数据资料印发给学生,并讲清本案例的教学目的与要求,明确案例所涉及的教学内容;然后给学生一段时间,由学生根据资料,运用不同的方法进行预测分析,并确定具体的讨论日期;在课堂讨论时让学生自由发言,阐述自己的观点;最后,由主持教师作点评发言,取得了良好的教学效果。
经济预测是研究客观经济过程未来一定时期的发展变化趋势,其目的在于通过对客观经济现象历史规律的探讨和现状的研究,求得对未来经济活动的了解,以确定社会经济活动的发展水平,为决策提供依据。
时间序列分析预测法,首先将预测目标的历史数据按照时间的先后顺序排列,然后分析它随时间的变化趋势及自身的统计规律,外推得到预测目标的未来取值。
它与回归分析预测法的最大区别在于:该方法可以根据单个变量的取值对其自身的变动进行预测,无须添加任何的辅助信息。
本案例的最大特色在于:它汇集了统计学原理中的时间序列分析这一章节的所有知识点,通过本案例的教学,可以把不同的时间序列分析方法进行综合的比较,便于学生更好地掌握本章的内容。
二、案例的目的与要求(一)教学目的1.通过本案例的教学,使学生认识到时间序列分析方法在实际工作中应用的必要性和可能性;2.本案例将时间序列分析中的水平指标、速度指标、长期趋势的测定等内容有机的结合在一起,以巩固学生所学的课本知识,深化学生对课本知识的理解;3.本案例是对烟台市的国内生产总值数据进行预测,通过对实证结果的比较和分析,使学生认识到对同一问题的解决,可以采取不同的方法,根据约束条件,从中选择一种合适的预测方法;4.通过本案例的教学,让学生掌握EXCEL 软件在时间序列分析中的应用,对统计、计量分析软件SPSS或Eviews等有一个初步的了解;5.通过本案例的教学,有助于提高学生运用所学知识和方法分析解决问题的能力、合作共事的能力和沟通交流的能力。
(二)教学要求1.学生必须具备相应的时间序列分析的基本理论知识;2.学生必须熟悉相应的预测方法和具备一定的数据处理能力;3.学生以主角身份积极地参与到案例分析中来,主动地分析和解决案例中的问题;4.在提出解决问题的方案之前,学生可以根据提供的样本数据,自己选择不同的统计分析方法,对这一案例进行预测,比较不同预测方法的异同,提出若干可供选择的方案;5.学生必须提交完整的分析报告。
分析报告的内容应包括:选题的目的及意义、使用数据的特征及其说明、采用的预测方法及其优劣、预测结果及其评价、有待于进一步改进的思路或需要进一步研究的问题。
三、数据搜集与处理时间序列数据按照不同的分类标准可以划分为不同的类型,最常见的有:年度数据、季度数据、月度数据。
本案例主要讨论对年度数据如何进行预测分析。
考虑到案例设计时的侧重点,本案例只是对烟台市国内生产总值进行预测,故数据的搜集与处理过程相对简单。
我们通过查阅《烟台统计年鉴》、《烟台五十年》等有关的资料获得烟台市1949—2000年共52年的国内生产总值资料数据(原始数据详见表3)。
该指标是反映国民经济发展情况最重要的指标之一,我们选择该指标进行预测具有较强的实用价值。
此外,预测的方法具有普遍的适用性,使用者也可以将其应用于其它的研究领域。
资料数据是预测的依据和基础,一般是根据确定的预测目标及影响因素搜集有关的资料和数据,并结合初步拟定的预测模型,对所搜集的数据进行分析和处理,然后再选取适当的预测模型。
我们可以将整个数据处理过程概括如下,见图1。
明确预确定预收集和选择预结果是计算预推荐预测进行综精度的时间的资金的YN图1 经济预测流程图四、建议使用的预测分析方法(一)确定性时间序列分析法1.指标法:平均增长量法、平均发展速度法;2.趋势预测法:移动平均法、指数平滑法、曲线拟合法。
(二)随机性时间序列分析法1.ARIMA模型预测;2.组合模型预测。
五、案例分析过程(一)确定性时间序列分析法1.平均增长量法该方法是利用历史资料计算出它的平均增长量,然后再假定在以后各期当中,它仍按这样一个平均增长量去增长,从而得出在未来一段时期内的预测值。
根据烟台市的国内生产总值1949年—1998年的观察值,我们计算出GDP 的平均增长量为150647.69万元(水平法)和38437.81万元(总和法),利用其对烟台市1999年和2000年的GDP 值进行预测并与实际GDP 值[1]比较,结果见表1。
表1 平均增长量法预测结果1999年2000年GDP 预测值(万元)预测相对误差(%)GDP 预测值(万元)预测相对误差(%)水平法 7550647.7 5.69 7701295.4 12.44 累计法7438437.87.107476875.615.00教师点评:①平均增长量法不仅得到了烟台市1999年、2000年GDP 数据的预测值,而且还让学生认识到平均增长量预测法中水平法与总和法的区别所在,图1较明显地反映出平均增长量水平法与累计法计算的区别,即水平法仅考虑首尾年份的数值,而不考虑中间年份的数值变化,因而有na n a=∆-+)1(0;②而总和法则考虑了整个样本区间上的总体变化情况,有∑==∆+++∆++∆+ni ia n a a a 100)()2()( ,图2中A 的面积和B 的面积应该相等。
[1] 1999年为8006600万元,2000年为8795900万元。
1000000200000030000004000000500000060000007000000800000019491952195519581961196419671970197319761979198219851988199119941997年份万元原始GDP 水平法GDP 总和法GDPA B图2 由平均增长量推算出的时间序列变化图2.平均发展速度法该方法就是利用时间序列资料计算出它的平均发展速度,然后再假定在以后各期当中,它仍按这样一个平均发展速度去变化,从而得出时间序列的预测值。
我们计算出GDP在1949年—1998年间的平均发展速度为113.036%(几何法)和112.248%(方程法)[2],利用其对烟台市1999年和2000年的GDP 进行预测得到结果见表2。
表2 平均发展速度法预测结果1999年2000年GDP预测值(万元)预测相对误差(%)GDP预测值(万元)预测相对误差(%)几何法8364664 -4.47 9455081.6 -7.49方程法8306352 -3.74 9323713.9 -6.00教师点评:①同平均增长量的计算方法一样,平均发展速度的计算方法也有两种,其中几何法也只是[2]在该问题中几何法与方程法计算出的平均发展速度差别不大。
考虑起始年份的取值,有nnX a a 0=,而方程式法则要考虑到整个年份取值的变化,有∑==+++ni ina X a X a X a 120 ,方程式法的内插预测曲线与原始曲线所夹的面积A 和面积B 也相等;②在方程式法计算中,计算平均增长速度可以采取试错法(让学生尝试着编写小的循环程序求解)或插值法;③同平均增长量的计算一样,平均发展速度的计算方法也有两种,其中几何法也只是考虑起始年份的取值,而方程法则要考虑到整个年份取值的变化;④由预测的结果可以看出,无论是平均增长量法还是平均发展速度法只适于作短期预测,否则预测相对误差会显著提高。
0.001000000.002000000.003000000.004000000.005000000.006000000.007000000.008000000.001949195119531955195719591961196319651967196919711973197519771979198119831985198719891991199319951997年份万元原始GDP 几何法GDP 方程法GDP3. 移动平均法移动平均法是根据时间序列资料,采取逐项移动平均的办法,计算一定项数的序时平均数,以反映长期趋势的方法。
移动平均法主要有简单移动平均法、加权移动平均法、趋势移动平均法等。
这里主要介绍简单移动平均法。
图3 由平均发展速度推算出的时间序列变AB记11,t t t N ty y y Mt NN--++++=≥为t 期移动平均数;N 为移动平均项数。
由于移动平均可以平滑数据,消除周期变动和不规则变动的影响,使长期趋势显示出来,可以利用其进行外推预测。
预测公式为:1ˆt tyM +=,即以第t 期移动平均数作为第t +1期的预测值。
表3 移动平均预测结果年份序号t原始GDP三期移动平均值(T=3)五期移动平均值(T=5)194918263 —— —— 1950 1 25639 —— —— 1951 2 29327 —— —— 1952 3 34993 24409.67 —— 1953 4 36725 29986.33 —— 1954 5 40796 33681.67 28989.40 1955 6 41752 37504.67 33496.00 1956 7 48204 39757.67 36718.60 1957 8 46608 43584.00 40494.00 1958 9 51759 45521.33 42817.00 1959 10 58699 48857.00 45823.80 1960 11 59348 52355.33 49404.40 1961 12 52275 56602.00 52923.60 1962 13 53408 56774.00 53737.80 1963 14 62012 55010.33 55097.80 1964 15 65407 55898.33 57148.40 1965 16 76014 60275.67 58490.00 1966 17 88388 67811.00 61823.20 1967 18 91758 76603.00 69045.80 1968 19 82229 85386.67 76715.80 1969 20 92063 87458.33 80759.20 1970 21 105603 88683.33 86090.40 1971 22 122584 93298.33 92008.20 1972 23 131998 106750.00 98847.40 1973 24 141524 120061.67 106895.40 1974 25 145245 132035.33 118754.40 1975 26 177917 139589.00 129390.80 1976 27 191185 154895.33 143853.60 1977 28 218721 171449.00 157573.80 197829257782195941.00174918.401979 30 276146 222562.67 198170.00 1980 31 304923 250883.00 224350.20 1981 32 311590 279617.00 249751.40 1982 33 340400 297553.00 273832.40 1983 34 407773 318971.00 298168.20 1984 35 470404 353254.33 328166.40 1985 36 572569 406192.33 367018.00 1986 37 660180 483582.00 420547.20 1987 38 847263 567717.67 490265.20 1988 39 1150970 693337.33 591637.80 1989 40 1258556 886137.67 740277.20 1990 41 1485282 1085596.33 897907.60 1991 42 1721637 1298269.33 1080450.20 1992 43 2296046 1488491.67 1292741.60 1993 44 3254235 1834321.67 1582498.20 1994 45 4278600 2423972.67 2003151.20 1995 46 5394000 3276293.67 2607160.00 1996 47 6152400 4308945.00 3388903.60 1997 48 6750000 5275000.00 4275056.20 1998 49 7400000 6098800.00 5165847.00 19995080066006767466.675995000.001000000200000030000004000000500000060000007000000800000019491951195319551957195919611963196519671969197119731975197719791981198319851987198919911993199519971999年份万元原始GDP 三期移动平均值五期移动平均值由图4,我们可以得出这样的结论:移动平均法图4 烟台市GDP 的移动平均预测曲线对原始序列产生了一个修匀作用,并且移动平均所使用的间隔期越长,即N越大,修匀的程度也越大,但对原始数据的反应越不灵敏;反之,则反是。
