双曲线的简单几何性质导学案
双曲线的简单几何性质(学案)

学案2.3.2双曲线的简单几何性质(第一课时)一、教学目标1、了解双曲线的范围、对称性、顶点、离心率。
2、理解双曲线的渐近线。
二、教学重点难点双曲线的渐近线既是重点也是难点。
三、 教学过程 (一)复习1、椭圆标准方程及其几何性质:2、双曲线及其标准方程方程:参数关系:请同学们对比椭圆的几何性质的推导方法,推导出双曲线的几何性质。
(二)双曲线的性质1、范围:推导:把双曲线方程12222=-by a x 变形为:结论 范围:2、对称性推导:结论3、顶点:结论 顶点:等轴双曲线:4、离心率定义:双曲线的 与 的比 ,叫做双曲线的离心率。
结论 双曲线的离心率1>e 且e 越大双曲线的开口就越开阔。
5、渐近线结论 双曲线)0,0(12222>>=-b a b y a x 的渐近线方程双曲线)0,0(12222>>=-b a bx a y 的渐近线方程练习:求下列双曲线的渐近线方程(写成直线的一般式)。
(1)369422=-y x 的渐近线方程是: ; (2)369422-=-y x 的渐近线方程是: ; (3)10042522=-y x 的渐近线方程是: ; (4)10042522-=-y x 的渐近线方程是: 。
结论:把双曲线标准方程中等号右边的 改成 ,然后变形,即可得其渐近线方程。
例1、 求双曲线14416922=-x y 的半实轴长和半虚轴长、焦点坐标、离心率、渐近线方程。
解:把方程14416922=-x y 化为标准方程1342222=-x y由此可知,半实轴长4=a ,半虚轴长3=b ;5342222=+=+=b a c焦点坐标是)5,0(),5,0(-;离心率45==a c e ;渐近线方程为x y 34±=。
【变式练习】1、求双曲线14416922-=-x y 的半实轴长和半虚轴长、焦点坐标、离心率、渐近线方程。
例2、 求适合下列条件的双曲线标准方程(1) 顶点在x 轴上,虚轴长为12,离心率为45; (2) 顶点间距离为6,渐近线方程为x y 23±=;解:(1)设双曲线的标准方程为12222=-b y a x 或)0,0(>>b a 。
《2.2.2双曲线的简单几何性质》导学案1

2.2.2《双曲线的简单几何性质》导学案【学习目标】1.了解双曲线的范围、对称性、顶点、离心率、渐近线等几何性质;2.能解决一些简单的双曲线问题.【重点难点】双曲线的简单几何性质及其简单应用,对离心率的理解.【学习过程】一、问题情景导入1.前面我们研究了椭圆的哪些几何性质?2.类比椭圆几何性质的研究方法,怎样根据双曲线的标准方程()0,012222>>=-b a by a x 研究它的几何性质? 二、自学探究:(阅读课本第49-51页,完成下面知识点的梳理)1.双曲线的范围:2.双曲线的对称性:3.双曲线的顶点与实轴、虚轴:4.双曲线的离心率:5.双曲线渐近线:思考:双曲线()0,012222>>=-b a bx a y 的几何性质是怎样的? 三、例题演练:例1.求双曲线14416922=-x y 的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.变式:求下列双曲线的实轴、虚轴的长,顶点、焦点的坐标、离心率和渐近线方程: ⑴32822=-y x ; ⑵81922=-y x ;⑶422-=-y x ; ⑷1254922-=-y x例2.根据以下条件,分别求出双曲线的标准方程: ⑴过点()2,3-P ,离心率25=e ; ⑵与双曲线116922=-y x 有共同的渐近线,且过点()32,3-.变式:根据下列条件,求双曲线的标准方程: ⑴过点⎪⎭⎫ ⎝⎛-⎪⎭⎫ ⎝⎛5,316,415,3Q P ,且焦点在坐标轴上; ⑵过点()2,5-, 6=c ,焦点在x 轴上; ⑶与双曲线141622=-y x 有相同焦点,且经过点()2,23; ⑷与双曲线116922=-y x 有共同的渐近线,且过点()32,3-.【课堂小结与反思】【课后作业与练习】1.下列方程中,以x ±2y =0为渐近线的双曲线方程是().12)(12)(1164)(1416)(22222222=-=-=-=-y x D y x C y x B y x A2.中心在原点,一个焦点为(3,0),一条渐近线方程2x -3y =0的双曲线方程是(A )138********x y -= (B )13361381122x y -= (C )536554122x y -= (D )554536122x y -=。
双曲线的简单几何性质(一)导学案
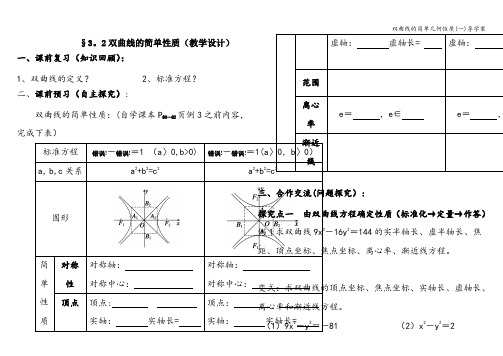
1标准方程 错误!-错误!=1 (a 〉0,b>0) 错误!-错误!=1(a 〉0,b 〉0) a ,b,c 关系 a 2+b 2=c 2 a 2+b 2=c 2
渐近
线
探究点二由性质求标准方程(定型→设方程→定量→作答)
例2 求满足下列条件的双曲线的标准方程:
(1)双曲线的焦点为(2,0),右顶点为(错误!,0); (2)实半轴长为8,离心率为错误!;
变式:求满足下列条件的双曲线方程
(1)双曲线C的焦点为(0,5),虚轴长为4; (2)实轴长为2,离心率为2;
四、巩固提高(链接高考):
1、(2013陕西卷)双曲线x2
16
-错误!=1的离心率为______,两条渐近线的方程为_____.
2、(2011年高考安徽卷)双曲线2x2-y2=8的实轴长是
3、(2011年高考江西卷)若双曲线错误!-错误!=1的离心率e=2,则m=__ __.
4、思考:若a=b,则渐近线的方程为_____,离心率e=
五、小结(方法总结):
(1)双曲线的简单性质(2)应用:①方程→性质②性质→方程
六、作业:1、P835 2、补充:求适合下列条件的双曲线的标准方程:
(1)焦点分别为F1(-3,0),F2(3,0),离心率e= 3
(2)虚轴长为12,离心率为4
5
;。
高中数学《双曲线的简单几何性质》导学案

2.2.2双曲线的简单几何性质1.双曲线的简单几何性质2.等轴双曲线(1)□14实轴和虚轴等长的双曲线叫做等轴双曲线.(2)等轴双曲线具有以下性质:①方程形式为□15x-y=λ(λ≠0);②渐近线方程为□16y=±x,它们互相垂直,并且平分双曲线实轴和虚轴所成的角;③实轴长和虚轴长都等于□172a,离心率e=□18 2.对双曲线的简单几何性质的四点认识(1)双曲线的焦点决定双曲线的位置;(2)双曲线的范围决定了双曲线的开放性和无限延展性,由双曲线的方程x2 a2-y2b2=1(a>0,b>0),得x2a2=1+y2b2≥1,∴x2≥a2,∴|x|≥a,即x≤-a或x≥a;(3)双曲线的离心率和渐近线刻画了双曲线的开口大小,离心率越大,双曲线的开口越大,反之亦然;(4)对称性:由双曲线的方程x2a2-y2b2=1(a>0,b>0),若P(x,y)是双曲线上任意一点,则P1(-x,y),P2(x,-y)均在双曲线上,故P与P1,P2分别关于y轴、x轴对称,因此双曲线分别关于y轴、x轴对称,只不过双曲线的顶点只有两个,而椭圆有四个.1.判一判(正确的打“√”,错误的打“×”)(1)等轴双曲线的离心率为 2.()(2)方程y2a2-x2b2=1(a>0,b>0)的渐近线方程为y=±ba x.()(3)与双曲线渐近线平行的直线与此双曲线有且只有一个公共点.() 答案(1)√(2)×(3)√2.做一做(请把正确的答案写在横线上)(1)双曲线x2-y23=1的渐近线方程为________,离心率e=________.(2)双曲线x2-16y2=1的实半轴长为________,虚半轴长为________.(3)焦点在x轴上,且焦距为4的等轴双曲线方程为________.答案(1)y=±3x2(2)114(3)x22-y22=1探究1双曲线的简单几何性质例1求双曲线9y2-4x2=-36的顶点坐标、焦点坐标、实轴长、虚轴长、离心率和渐近线方程,并作出草图.[解]将9y2-4x2=-36变形为x29-y24=1,即x232-y222=1,∴a=3,b=2,c=13,因此顶点为A1(-3,0),A2(3,0),焦点坐标F1(-13,0),F2(13,0),实轴长是2a=6,虚轴长是2b=4,离心率e=ca =133,渐近线方程y=±ba x=±23x.作草图:拓展提升(1)由双曲线的标准方程求几何性质的四个步骤(2)双曲线共有两个焦点、两个顶点、两个虚轴端点六个特殊点,注意双曲线的焦点一定在双曲线的实轴所在的直线上.(3)直线x=±a,y=±b或x=±b,y=±a围成的矩形中,双曲线的渐近线即两条对角线所在的直线.依据(2)(3)两点,可画出双曲线的大致图形.【跟踪训练1】(1)已知0<θ<π4,则双曲线C1:x2cos2θ-y2sin2θ=1与C2:y2sin2θ-x 2sin 2θtan 2θ=1的( )A .实轴长相等B .虚轴长相等C .离心率相等D .焦距相等 答案 C解析 因为0<θ<π4,所以sin θ>0,cos θ>0,所以双曲线C 1的实轴长为2cos θ,虚轴长为2sin θ,焦距为2,离心率e 1=1cos θ,双曲线C 2的实轴长为2sin θ,虚轴长为2sin θtan θ=2sin 2θcos θ,焦距2sin 2θ+sin 2θtan 2θ=2sin θcos θ,离心率e 2=1cos θ,所以两个双曲线的离心率相等.(2)设双曲线x 2a 2-y 29=1(a >0)的渐近线方程为3x ±2y =0,则a 的值为( ) A .4 B .3 C .2 D .1 答案 C解析 令x 2a 2-y 29=0,得x a =±y 3,所以双曲线x 2a 2-y 29=1的渐近线方程为3x ±ay=0,与已知方程比较系数得a =2.探究2 双曲线的离心率问题例2 (1)已知双曲线x 2a 2-y 2b 2=1(a >0,b >0),若过右焦点F 且倾斜角为30°的直线与双曲线的右支有两个交点,则此双曲线离心率的取值范围是( )A .(1,2) B.⎝⎛⎭⎪⎫1,233 C .[2,+∞)D.⎣⎢⎡⎭⎪⎫233,+∞(2)我们把离心率e =5+12的双曲线x 2a 2-y 2b 2=1(a >0,b >0)称为黄金双曲线.如图是双曲线x 2a 2-y 2b 2=1(a >0,b >0,c =a 2+b 2)的图象,给出以下几个说法:①若b 2=ac ,则该双曲线是黄金双曲线;②若F 1,F 2为左右焦点,A 1,A 2为左右顶点,B 1(0,b ),B 2(0,-b )且∠F 1B 1A 2=90°,则该双曲线是黄金双曲线;③若MN 经过右焦点F 2且MN ⊥F 1F 2,∠MON =90°,则该双曲线是黄金双曲线.其中正确命题的序号为________.[解析] (1)由题意知,过右焦点F 且倾斜角为30°的直线与双曲线右支有两个交点,需满足b a <tan30°,即b <33a .∴3b 2<a 2,∴3(c 2-a 2)<a 2,c 2<43a 2,∴e 2<43,∴-233<e <233.又e >1,∴1<e <233.(2)①正确.由⎩⎨⎧b 2=ac ,c 2=a 2+b 2得c 2-ac -a 2=0,所以e 2-e -1=0,解得e =5+12或e =1-52(舍去),该双曲线是黄金双曲线. ②正确.F 1B 1→=(c ,b ),A 2B 1→=(-a ,b ). 因为∠F 1B 1A 2=90°,所以F 1B 1→·A 2B 1→=0.所以-ac +b 2=0,即b 2=ac ,由①可知该双曲线是黄金双曲线. ③正确.由⎩⎪⎨⎪⎧x =c ,x 2a 2-y 2b 2=1解得M ,N 的坐标分别为⎝ ⎛⎭⎪⎫c ,-b 2a ,⎝ ⎛⎭⎪⎫c ,b 2a ,所以OM→=⎝ ⎛⎭⎪⎫c ,-b 2a , ON →=⎝ ⎛⎭⎪⎫c ,b 2a . 因为∠MON =90°,所以OM →·ON →=c 2-b 4a 2=0,即b 2=ac ,由①知该双曲线是黄金双曲线.[答案] (1)B (2)①②③[条件探究] 若把例2(1)的条件“30°”改为“60°”,“有两个”改为“有且只有一个”,其他条件不变,应如何解答?解 由题可得直线的斜率为3,要使直线l 与双曲线的右支有且只有一个交点,只要b a ≥ 3,∴e 2=1+⎝ ⎛⎭⎪⎫b a 2≥4.∴e ≥2,离心率取值范围为[2,+∞).拓展提升1.求双曲线离心率的两种方法(1)直接法:若已知a ,c 可直接利用e =ca 求解,若已知a ,b ,可利用e =1+⎝ ⎛⎭⎪⎫b a 2求解. (2)方程法:若无法求出a ,b ,c 的具体值,但根据条件可确定a ,b ,c 之间的关系,可通过b 2=c 2-a 2,将关系式转化为关于a ,c 的齐次方程,借助于e =ca ,转化为关于e 的n 次方程求解.2.求双曲线离心率范围的思路求双曲线离心率的范围,关键是根据题目条件得到不等关系,并想办法转化为关于a ,b ,c 的不等关系,结合c 2=a 2+b 2和ca =e 得到关于e 的不等式,然后求解.在建立不等式求e 时,经常用到结论:双曲线上一点到相应焦点距离的最小值为c -a .双曲线的离心率常以双曲线的渐近线为载体进行命题,注意二者参数之间的转化.【跟踪训练2】 (1)若双曲线x 2a 2-y 2b 2=1与x 2a 2-y 2b 2=-1(a >0,b >0)的离心率分别为e 1,e 2,则必有( )A.e1=e2B.e1e2=1C.1e1+1e2=1 D.1e21+1e22=1答案 D解析依题意,知e21=a2+b2a2,e22=a2+b2b2,所以1e21+1e22=a2+b2a2+b2=1.故选D.(2)已知F1,F2是双曲线x2a2-y2b2=1(a>0,b>0)的两焦点,以线段F1F2为边作正三角形MF1F2,若边MF1的中点在双曲线上,则双曲线的离心率是() A.4+2 3 B.3+1C.3-1D.3+1 2答案 B解析设边MF1的中点为P,由题意知,MF1⊥PF2,在Rt△PF1F2中,|PF1|=|F1F2|cos60°=2c×12=c,|PF2|=|F1F2|sin60°=2c×32=3c,根据双曲线的意义可知2a=|PF2|-|PF1|=3c-c,所以e=ca =23-1=3+1.探究3由双曲线的几何性质求标准方程例3求与双曲线x216-y29=1共渐近线且过点A(23,-3)的双曲线的方程及其离心率.[解]解法一:双曲线x216-y29=1的渐近线方程为y=±34x.(1)设所求双曲线方程为x2a2-y2b2=1(a>0,b>0).因为ba=34,所以b=34a①.因为点A(23,-3)在所求的双曲线上,所以12a2-9b2=1②.联立①②所得的方程组无解.(2)设所求的双曲线方程为y2a2-x2b2=1(a>0,b>0).因为ab=34,所以a=34b③.因为点A(23,-3)在所求的双曲线上,所以9a2-12b2=1④,联立③④得a2=94,b2=4.所以所求双曲线方程为y294-x24=1且离心率e=53.解法二:设与双曲线x216-y29=1共渐近线的双曲线的方程为x216-y29=λ(λ≠0).因为点A (23,-3)在所求的双曲线上,所以λ=1216-99=-14,所以所求双曲线方程为x 216-y 29=-14,即y 294-x 24=1.从而可求得离心率e =53.拓展提升巧设双曲线方程的六种常用方法(1)焦点在x 轴上的双曲线的标准方程可设为x 2a 2-y 2b 2=1(a >0,b >0). (2)焦点在y 轴上的双曲线的标准方程可设为y 2a 2-x 2b 2=1(a >0,b >0). (3)与双曲线x 2a 2-y 2b 2=1共焦点的方程可设为x 2a 2-λ-y 2b 2+λ=1(λ≠0,-b 2<λ<a 2).(4)与双曲线x 2a 2-y 2b 2=1具有相同渐近线的方程可设为x 2a 2-y 2b 2=λ(λ≠0). (5)渐近线为y =kx 的双曲线方程可设为k 2x 2-y 2=λ(λ≠0). (6)渐近线为ax ±by =0的双曲线方程可设为a 2x 2-b 2y 2=λ(λ≠0).【跟踪训练3】 根据以下条件,求双曲线的标准方程.(1)以圆C :x 2+y 2-6x -4y +8=0与坐标轴的交点分别作为双曲线的一个焦点和一个顶点;(2)焦点在x 轴上,渐近线方程为y =±33x ,且顶点到渐近线的距离为1. (3)中心在原点,焦点F 1,F 2在坐标轴上,离心率为2,且过点P (4,-10). 解 (1)对圆C 的方程,令y =0,得x 2-6x +8=0,解得x 1=2,x 2=4,即圆C 与x 轴的两个交点分别为(2,0),(4,0). 令x =0,得y 2-4y +8=0,此方程无解,即圆C 与y 轴没有交点. 因此点(2,0)为双曲线的右顶点,点(4,0)为双曲线的右焦点. 设双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0), 则a =2,c =4,所以b 2=c 2-a 2=12, 从而双曲线的标准方程为x 24-y 212=1.(2)由焦点在x轴上,可设双曲线的标准方程为x2a2-y2b2=1(a>0,b>0),渐近线方程为y=±ba x=±33x,则a=3b.由顶点(a,0)到渐近线y=33x的距离为1,得|a|2=1,得a=2,b=33a=233.从而双曲线的标准方程为x24-y243=1.(3)因为离心率e=2,所以可设双曲线的方程为x2-y2=λ(λ≠0).由双曲线过点P(4,-10),得16-10=λ,即λ=6,所以双曲线的标准方程为x26-y26=1.探究4直线与双曲线的位置关系例4双曲线C与椭圆x28+y24=1有相同的焦点,直线y=3x为C的一条渐近线.(1)求双曲线C的方程;(2)如右图,过点P(0,4)的直线l交双曲线C于A,B两点,交x轴于Q点(Q 点与C的顶点不重合).当PQ→=λ1QA→=λ2QB→,且λ1+λ2=-83时,求Q点的坐标.[解](1)设双曲线的方程为x2a2-y2b2=1(a>0,b>0).由椭圆x28+y24=1求得两焦点为(-2,0),(2,0),∴对于双曲线C:c=2,焦点在x轴上.又y=3x为双曲线C的一条渐近线,∴ba=3,解得a2=1,b2=3,∴双曲线C的方程为x2-y23=1.(2)解法一:由题意知直线l 的斜率k 存在且不等于零. 设l 的方程:y =kx +4,A (x 1,y 1),B (x 2,y 2), 则Q ⎝ ⎛⎭⎪⎫-4k ,0,∵PQ →=λ1QA →,∴⎝ ⎛⎭⎪⎫-4k ,-4=λ1⎝ ⎛⎭⎪⎫x 1+4k ,y 1, ∴⎩⎪⎨⎪⎧-4k=λ1⎝ ⎛⎭⎪⎫x 1+4k ,-4=λ1y 1⇒⎩⎪⎨⎪⎧x 1=-4kλ1-4k ,y 1=-4λ1,∵A (x 1,y 1)在双曲线C 上, ∴16k 2⎝⎛⎭⎪⎫1+λ1λ12-163λ21-1=0, ∴16+32λ1+16λ21-163k 2-k 2λ21=0, ∴(16-k 2)λ21+32λ1+16-163k 2=0. 同理有(16-k 2)λ22+32λ2+16-163k 2=0. 若16-k 2=0,则直线l 过顶点,不符合题意,∴16-k 2≠0,∴λ1,λ2是一元二次方程(16-k 2)x 2+32x +16-163k 2=0的两根,∴λ1+λ2=32k 2-16=-83,∴k 2=4,此时Δ>0,∴k =±2,所求Q 的坐标为(±2,0). 解法二:由题意知直线l 的斜率k 存在且不等于零. 设l 的方程y =kx +4,A (x 1,y 1),B (x 2,y 2), 则Q ⎝ ⎛⎭⎪⎫-4k ,0,∵PQ →=λ1QA →=λ2QB →,∴⎝ ⎛⎭⎪⎫-4k ,-4=λ1⎝ ⎛⎭⎪⎫x 1+4k ,y 1=λ2⎝ ⎛⎭⎪⎫x 2+4k ,y 2, ∴-4=λ1y 1=λ2y 2,∴λ1=-4y 1,λ2=-4y 2.又λ1+λ2=-83,∴1y 1+1y 2=23,即3(y 1+y 2)=2y 1y 2.将y =kx +4代入x 2-y 23=1得(3-k 2)y 2-24y +48-3k 2=0.∵3-k 2≠0,否则l 与渐近线平行, ∴y 1+y 2=243-k 2,y 1y 2=48-3k 23-k 2, ∴3×243-k 2=2×48-3k 23-k 2, ∴k =±2,∴Q (±2,0). 拓展提升(1)判断直线与双曲线的位置关系时,通常是将直线方程与双曲线方程联立方程组,方程组解的个数就是直线与双曲线交点的个数,联立方程消去x 或y 中的一个后,得到的形如一元二次方程的式子中,要注意x 2项或y 2项系数是否为零的情况,否则容易漏解.(2)直线y =kx +b 与双曲线相交所得的弦长d = 1+k 2·|x 1-x 2|=1+1k 2|y 1-y 2|.【跟踪训练4】 已知双曲线x 2-y 22=1,问:过点A (1,1)能否作直线l ,使l与双曲线交于P ,Q 两点,并且A 为线段PQ 的中点?若能,求出直线l 的方程;若不能,请说明理由.解 假设符合题意的直线l 存在,并设P (x 1,y 1),Q (x 2,y 2),则⎩⎪⎨⎪⎧x 21-y 212=1,x 22-y 222=1.两式相减,得(x 1-x 2)(x 1+x 2)=12(y 1-y 2)(y 1+y 2).① 又A (1,1)为线段PQ 的中点,所以⎩⎪⎨⎪⎧x 1+x 2=2,②y 1+y 2=2.③将②③代入①,得x 1-x 2=12(y 1-y 2), 由题意,知直线l 的斜率存在,则x 1≠x 2, 则直线l 的斜率k =y 1-y 2x 1-x 2=2,所以直线l 的方程为2x -y -1=0.而由⎩⎨⎧2x -y -1=0,x 2-y22=1,得2x 2-4x +3=0,根据Δ=(-4)2-4×2×3=-8<0,说明所求直线不存在.1.双曲线的几何性质主要包括“六点”——实轴端点、虚轴端点、焦点;“四线”——对称轴、渐近线;“两比率”——离心率、渐近线的斜率.双曲线的实轴长、虚轴长、焦距、离心率只与双曲线的形状和大小有关而与双曲线的位置无关.双曲线的顶点坐标、实轴端点坐标、虚轴端点坐标、焦点坐标、渐近线方程不仅与双曲线的形状和大小有关,而且与双曲线的实轴位置有关.2.已知双曲线的几何性质确定双曲线的标准方程,常用待定系数法,首先要依据焦点的位置设出方程的形式,再由题设条件确定参数的值;当双曲线焦点位置不确定时,方程可能有两种形式,此时应注意分类讨论,以防止遗漏.3.求双曲线离心率的常用方法 (1)依据条件求出a ,c ,计算e =c a ;(2)依据条件建立a ,b ,c 的关系式,一种方法是消去b 转化成离心率e 的方程求解,另一种方法是消去c 转化成含b a 的方程,求出ba 后利用e =1+b 2a 2求解.4.渐近线是双曲线特有的性质,两方程联系密切,把双曲线的标准方程x 2a 2-y 2b 2=1(a >0,b >0)右边的常数1换为0,就是渐近线方程,反之由渐近线方程ax ±by =0变为a 2x 2-b 2y 2=λ(λ≠0),再结合其他条件求得λ就可得双曲线方程.5.直线与双曲线有一个公共点的两种情况 (1)直线与双曲线相切; (2)直线与双曲线的渐近线平行.1.双曲线x 216-y 29=1的一个焦点到它的一条渐近线的距离等于( ) A .4 B .8 C .3 D .6 答案 C解析 双曲线x 216-y 29=1的焦点坐标为(-5,0),(5,0),渐近线方程为x 4±y3=0,即3x ±4y =0,根据双曲线的对称性,不妨求(5,0)到直线3x -4y =0的距离,d =|3×5-4×0|32+(-4)2=3.2.已知双曲线x 2a 2-y 23=1(a >0)的离心率为2,则a =( )A .2 B.62 C.52 D .1 答案 D解析 因为双曲线的方程为x 2a 2-y 23=1,所以e 2=1+3a 2=4,因此a 2=1,a =1.选D.3.等轴双曲线的一个焦点是F 1(-6,0),则其标准方程为( ) A.x 29-y 29=1 B.y 29-x 29=1 C.y 218-x 218=1 D.x 218-y 218=1 答案 D解析 由题意知双曲线焦点在x 轴上,设所求双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0),则由已知得⎩⎪⎨⎪⎧a =b ,a 2+b 2=36,解得a 2=b 2=18,所以所求双曲线的标准方程为x 218-y 218=1. 4.双曲线x 25-y 24=1的实轴长等于________,虚轴长等于________,焦点坐标是________,离心率是________,渐近线方程是________.答案 25 4 (-3,0)和(3,0) 355 y =±255x解析 由题意知a =5,b =2,c =3,∴实轴长2a =25,虚轴长2b =4,焦点坐标为(-3,0),(3,0),离心率e =c a =35=355,渐近线方程y =±b a x =±255x . 5.已知双曲线两顶点间距离为6,渐近线方程为y =±32x ,求双曲线的标准方程.解 设以y =±32x 为渐近线的双曲线方程为x 24-y 29=λ(λ≠0), 当λ>0时,a 2=4λ, ∴2a =24λ=6⇒λ=94. 当λ<0时,a 2=-9λ, ∴2a =2-9λ=6⇒λ=-1.∴双曲线的标准方程为x 29-y 2814=1和y 29-x 24=1.A 级:基础巩固练一、选择题1.双曲线mx 2+y 2=1的虚轴长是实轴长的2倍,则实数m 的值为( ) A .-14 B .-4 C .4 D.14 答案 A解析 双曲线的标准方程为y 2-x 2-1m=1,∴a 2=1,b 2=-1m .由题意,得b 2=4a 2,∴-1m =4,∴m =-14.2.过双曲线x 2-y 23=1的右焦点且与x 轴垂直的直线,交该双曲线的两条渐近线于A ,B 两点,则|AB |=( )A.433 B .2 3 C .6 D .4 3 答案 D解析 由双曲线的标准方程x 2-y23=1得,右焦点F (2,0),两条渐近线方程为y =±3x ,直线AB :x =2,所以不妨取A (2,23),B (2,-23),则|AB |=43,选D.3.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的焦距为25,且双曲线的一条渐近线与直线2x +y =0垂直,则双曲线的方程为( )A.x 24-y 2=1 B .x 2-y 24=1C.3x 220-3y 25=1 D.3x 25-3y 220=1答案 A解析 由题意得c =5,b a =12,则a =2,b =1,所以双曲线的方程为x 24-y 2=1.4.过原点作直线,与双曲线x 2-y 2=1恰有一个交点的直线有( ) A .0条 B .1条 C .2条 D .4条 答案 A解析 设l 的方程为y =kx .由⎩⎪⎨⎪⎧y =kx ,x 2-y 2=1,得(1-k 2)x 2=1.显然方程不可能只有一个解.故过原点与双曲线x 2-y 2=1恰有一个交点的直线有0条.5.已知直线y =12x 与双曲线x 29-y 24=1交于A ,B 两点,P 为双曲线上不同于A ,B 的点,当直线P A ,PB 的斜率k P A ,k PB 存在时,k P A ·k PB =( )A.49B.12C.23 D .与P 点位置有关 答案 A解析 设A (x 0,y 0),B (-x 0,-y 0),P (x ,y ),∴k P A ·k PB =y -y 0x -x 0·y +y 0x +x 0=y 2-y 2x 2-x 2= 4⎝ ⎛⎭⎪⎫x 29-1-4⎝ ⎛⎭⎪⎫x 209-1x 2-x 20=49(x 2-x 20)x 2-x 20=49.故选A. 6.若双曲线x 2a 2-y 2b 2=1与椭圆x 2m 2+y 2b 2=1(m >b >0)的离心率之积等于1,则以a ,b ,m 为边长的三角形一定是( )A .等腰三角形B .钝角三角形C .锐角三角形D .直角三角形 答案 D解析 双曲线的离心率e 1=a 2+b 2a,椭圆的离心率e 2=m 2-b 2m,由e 1e 2=1得(a 2+b 2)(m 2-b 2)=a 2m 2,故a 2+b 2=m 2,因此三角形为直角三角形.二、填空题7.已知双曲线过点(4,3),且渐近线方程为y =±12x ,则该双曲线的标准方程为________.答案 x 24-y 2=1解析 根据渐近线方程为x ±2y =0,可设双曲线方程为x 2-4y 2=λ(λ≠0).因为双曲线过点(4,3),所以42-4×(3)2=λ,即λ=4.故双曲线的标准方程为x 24-y 2=1.8.已知F 1,F 2是椭圆和双曲线的公共焦点,P 是它们的一个公共点,且∠F 1PF 2=π3,椭圆和双曲线的离心率分别为e 1,e 2,则1e 21+3e 22=________.答案 4解析 如图,设椭圆的长半轴长为a 1,双曲线的实半轴长为a 2,则根据椭圆及双曲线的定义:⎩⎪⎨⎪⎧|PF 1|+|PF 2|=2a 1,|PF 1|-|PF 2|=2a 2,∴|PF 1|=a 1+a 2,|PF 2|=a 1-a 2,设|F 1F 2|=2c ,∠F 1PF 2=π3,则在△PF 1F 2中,由余弦定理得4c 2=(a 1+a 2)2+(a 1-a 2)2-2(a 1+a 2)(a 1-a 2)·cos π3,化简得a 21+3a 22=4c 2,该式可变形为a 21c 2+3a 22c 2=4,∴1e 21+3e 22=4.9.已知双曲线E 的中心为原点,F (3,0)是E 的焦点,过F 的直线l 与E 相交于A ,B 两点,且AB 的中点为N (-12,-15),则E 的方程为________.答案 x 24-y 25=1解析 设双曲线的标准方程为x 2a 2-y 2b 2=1(a >0,b >0), 由题意知c =3,a 2+b 2=9,设A (x 1,y 1),B (x 2,y 2),则有:⎩⎪⎨⎪⎧x 21a 2-y 21b2=1,x 22a 2-y 22b 2=1,两式作差得,y 1-y 2x 1-x 2=b 2(x 1+x 2)a 2(y 1+y 2)=-12b 2-15a 2=4b 25a 2, 又AB 的斜率是-15-0-12-3=1,所以4b 2=5a 2,代入a 2+b 2=9得a 2=4,b 2=5, 所以双曲线标准方程是x 24-y 25=1. 三、解答题10.已知双曲线E 与双曲线x 22-y 2=1共渐近线,且过点(2,-2),若双曲线M 以双曲线E 的实轴为虚轴,虚轴为实轴,试求双曲线M 的标准方程.解 由题意,设E 的方程为x 22-y 2=t (t ≠0). ∵点(2,-2)在E 上,∴222-(-2)21=t ,∴t =-2, ∴双曲线E 的标准方程为y 22-x 24=1,又双曲线M 与E 为共轭双曲线,则双曲线M 的标准方程为x 24-y 22=1.B 级:能力提升练1.求两条渐近线为x ±2y =0且截直线x -y -3=0所得弦长为833的双曲线方程.解 设双曲线方程为x 2-4y 2=λ(λ≠0).联立方程组得:⎩⎪⎨⎪⎧x 2-4y 2=λ,x -y -3=0,消去y 得,3x 2-24x +(36+λ)=0.设直线被双曲线截得的弦为AB , 且A (x 1,y 1),B (x 2,y 2),那么⎩⎪⎨⎪⎧x 1+x 2=8,x 1x 2=36+λ3,Δ=242-12(36+λ)>0.那么|AB |=(1+k 2)[(x 1+x 2)2-4x 1x 2]=(1+1)⎝ ⎛⎭⎪⎫82-4×36+λ3 =8(12-λ)3=833. 解得λ=4,所以,所求双曲线方程是x 24-y 2=1.2.已知双曲线x 2a 2-y 2b 2=1(a >0,b >0)的离心率e =233,直线l 过A (a,0),B (0,-b )两点,原点O 到l 的距离是32.(1)求双曲线的方程;(2)过点B 作直线m 交双曲线于M ,N 两点,若OM →·ON →=-23,求直线m 的方程.解 (1)依题意,直线l 的方程为:x a +y -b =1,即bx -ay -ab =0.由原点O 到l 的距离是32,得aba 2+b 2=abc =32, 又e =c a =233,所以b =1,a = 3. 故所求双曲线方程为x 23-y 2=1.(2)显然直线m 不与x 轴垂直,设m 方程为y =kx -1,设点M ,N 坐标分别为(x 1,y 1),(x 2,y 2),联立方程⎩⎨⎧y =kx -1,x 23-y 2=1消去y ,得(1-3k 2)x 2+6kx -6=0.(*)依题意知1-3k 2≠0,由根与系数的关系知x 1+x 2=6k 3k 2-1,x 1x 2=63k 2-1.OM →·ON →=x 1x 2+y 1y 2=x 1x 2+(kx 1-1)(kx 2-1)=(1+k 2)x 1x 2-k (x 1+x 2)+1=6(1+k 2)3k 2-1-6k 23k 2-1+1=-23,解得k =±12,当k =±12时,判别式Δ=15>0,方程(*)有两个不等的实数根,满足条件. 故直线m 方程为y =12x -1或y =-12x -1.。
高中数学《双曲线的简单几何性质》导学案

授课教师:姓名:班级:2.3.2 双曲线的简单几何性质复习回顾:椭圆的图像与性质类比椭圆,探讨双曲线 的几何性质:范围;对称性;顶点;离心率;渐近线一、探究双曲线 的简单几何性质1、范围:2、对称性:3、顶点(与对称轴的交点):4、顶点(1)双曲线与对称轴的交点,叫做双曲线的顶点(2)线段 叫做双曲线的实轴,它的长为2a,a 叫做实半轴长;线段 叫做双曲线的虚轴,它的长为2b,b 叫做双曲线的虚半轴长. (3)实轴与虚轴等长的双曲线叫等轴双曲线 4.渐近线思考(1)双曲线 的渐近线方程是? (2)等轴双曲线的渐近线方程是什么?(3)利用渐近线可以较准确的画出双曲线的草图5.离心率二、根据双曲线的几何性质求标准方程例2. 根据下列条件,求双曲线的标准方程.(1)双曲线的渐近线的方程为2x ±3y =0且经过P (6,2);(2)经过点P (3,-2),离心率e =52.22221(0,0)x y a b a b -=>>22221(0,0)x y a b a b-=>> xyo -b 1B2Bb1A 2A-aa 722-.图1A 2A O1F 2F 2B 1B xy22221(0,0)x y a b a b -=>>变式2. 求适合下列条件的双曲线的标准方程: (1)一个焦点为(0,13),且离心率为135; (2)渐近线方程为y =±12x ,且经过点A (2,-3).例3:1、双曲线 9x 2-16y 2=144的实半轴长等于 ;虚半轴长等于 ; 顶点坐标是 ;渐近线方是 . 离心率e= 。
2、离心率e=2是双曲线为等轴双曲线的 条件 。
(用“充分条件”“必要条件”“充要条件”填空。
)例4:如图所示,过双曲线 的右焦点F 2,倾斜角为30°的直线交双曲线于A ,B 两点,求|AB|.22136x y -=。
高中数学《2.2.1双曲线简单的几何性质》导学案 新人教A版选修1-1

§2.2.1双曲线简单的几何性质 ( 第1课时)[自学目标]:掌握双曲线的范围、对称性及对称轴,对称中心、离心率、顶点、渐近线的概念。
[重点]:双曲线几何性质[难点]:双曲线几何性质的应用,双曲线第二定义。
教学过程一、课前准备:复习 1:写出满足下列条件的双曲线的标准方程:①a = 3,b = 4 ,焦点在x轴上;②焦点在y 轴上,焦距为 8,a = 2 .复习 2:前面我们学习了椭圆的哪些几何性质?二、新课导学:学习探究?问题 2:实轴与虚轴等长的双曲线叫___________ 双曲线.等轴双曲线a=b,渐近线方程为________,离心率=_________.[预习自测] 1.双曲线x 24-y 29=1的渐近线方程是( ) A .y =±32x B .y =±23x C .y =±94x D .y =±49x 2.中心在原点,实轴长为10,虚轴长为6的双曲线的标准方程是( )A 、192522=-y xB 、192522=-y x 或192522=-x y C 、13610022=-y x D 、13610022=-y x 或13610022=-x y 3.下列曲线的离心率为26的是( ) A 、14222=-y x B 、12422=-y x C 、16422=-y x D 、110422=-y x 4.双曲线204522-=-x y 的实轴长为 ,虚轴长为 ,渐近线方程为 ,离心率为 。
请你将预习中未能解决的问题和有疑惑的问题写下来,待课堂上与老师和同学探究解决。
[合作探究 展示点评]探究一:双曲线简单几何性质例1:求双曲线14491622=-y x 的实轴长和虚轴长、焦点的坐标、离心率、渐近线方程。
探究二:由性质求方程 例2:求双曲线的标准方程: (1)实轴的长是10,虚轴长是8,焦点在x 轴上;(2)焦距是10,虚轴长是8,焦点在y 轴上;例3: 点 M (x , y ) 到定点 F (5,0) 的距离和它到定直线l :516x 的距离的比是常数45,求点M 的轨迹。
双曲线的简单几何性质教导学案

x2 y2 = 1 的离心率为 5 , 2、 (2012· 江苏) 在平面直角坐标系 xoy 中, 若双曲线 - 2 m m +4
则 m 的值为 。 。 3、双曲线 x 2-y 2 = 1 的顶点到其渐近线的距离等于
①
②
4、如图(1) ,火力发电厂的冷却塔的外形是由双曲线绕其虚轴旋转所成的
以焦点在 x 轴为双曲线为例,根据其的图像及标准方程 ,研究它的几何性质。
知识与技能 教 学 目 标 过程与方法 情感态度 与价值观 重点 难点 教学 方法 学生 自学 反馈
①能运用双曲线的标准方程讨论双曲线的范围、对称点、顶点、离心 率、渐近线等几何性质。 ②掌握双曲线标准方程中 a、b、c 的几何意义,理解双曲线的渐近线的 概念及证明,能运用双曲线的几何性质解决双曲线的一些基本问题。 ③使学生进一步掌握利用方程研究曲线方程的基本方法,加深对直角 坐标系中曲线与方程的概念的理解。 通过对问题的类比探究活动,让学生类比已知的知识,通过观察、推 导、形成新知识,进一步理解坐标系中根据曲线的方程研究曲线的几 何性质的一般方法,领悟其中所蕴涵的数学思想。 通过类比探究体验挫折的艰辛与成功的快乐,激发学习热情,逐步培 养正确的数学观、创新艺术与科学精神。
寺前中学高二数学教(学)案
年级: 高 课题 班级 二 编写人: 郝贵川 审核人:__________ 编制时间: 双曲线的简单几何性质 授课(完成)时间 教师(学生)
解类” C“应 问题 2:我们研究过椭圆的哪些性质?我们是用什么思想方法研究的?双曲 用类” D“能 线是否也有类似性质?又该怎样研究? 力提 对称性: 范围: 升类” 顶点: 【探索新知】
离心率:
双曲线及简单几何性质导学案

§2.3.2双曲线的简单几何性质(1)1.理解并掌握双曲线的几何性质. 学习过程 一课前准备:复习1:写出满足下列条件的双曲线的标准方程: ①3,4a b ==,焦点在x 轴上;②焦点在y 轴上,焦距为8,2a =.复习2:前面我们学习了椭圆的哪些几何性质?二、新课导学: 学习探究问题1:由椭圆的哪些几何性质出发,类比探究双曲线22221x y a b-=的几何性质?范围:x : y :对称性:双曲线关于轴、轴及都对称. 顶点:( ),( ).实轴,其长为;虚轴,其长为.离心率:1ce a=>.渐近线:双曲线22221x y a b-=的渐近线方程为:0x ya b ±=.问题2:双曲线22221y x a b-=的几何性质?图形:范围:x : y :对称性:双曲线关于轴、轴及都对称.顶点:( ),( )实轴,其长为;虚轴,其长为.离心率:1ce a =>.渐近线: 双曲线22221y x a b-=的渐近线方程为:.新知:实轴与虚轴等长的双曲线叫 双曲线.典型例题例1求双曲线2214925x y -=的实半轴长、虚半轴的长、焦点坐标、离心率及渐近线的方程.变式:求双曲线22916144y x -=的实半轴长和虚半轴长、焦点坐标、离心率、渐近线方程.例2求双曲线的标准方程:⑴实轴的长是10,虚轴长是8,焦点在x轴上;⑵离心率2e=,经过点(5,3)M-;⑶渐近线方程为23y x=±,经过点9(,1)2M-.练一练练1.求以椭圆22185x y+=的焦点为顶点,以椭圆的顶点为焦点的双曲线的方程.练2.对称轴都在坐标轴上的等到轴双曲线的一个焦点是1(6,0)F-,求它的标准方程和渐近线方程.三、总结提升:学习小结1、双曲线的图形、范围、顶点、对称性、离心率、渐近线.2、与双曲线22221x ya b-=有相同的渐近线的双曲线系方程式为2222x ya bλ-=(0)λ≠当堂检测1.双曲线221168x y-=实轴和虚轴长分别是().A.8、42 B.8、22C.4、42 D.4、222.双曲线224x y-=-的顶点坐标是().A.(0,1)± B.(0,2)± C.(1,0)± D.(2,0±)3.双曲线22148x y-=的离心率为().A.1 B .2 C .3 D.24.双曲线2241x y-=的渐近线方程是.5.经过点(3,1)A-,并且对称轴都在坐标轴上的等轴双曲线的方程是.6.求焦点在y轴上,焦距是16,43e=的双曲线的标准方程.7.求与椭圆2214924x y+=有公共焦点,且离心率54e=的双曲线的方程.§2.3.2双曲线的简单几何性质(2)学习目标1.从具体情境中抽象出椭圆的模型;2.掌握椭圆的定义; 3.掌握椭圆的标准方程. 学习过程 一、课前准备复习1:说出双曲线的几何性质?复习2:双曲线的方程为221914x y -=,其顶点坐标是( ),( );渐近线方程.二、新课导学 学习探究探究1:椭圆22464x y +=的焦点是?探究2:双曲线的一条渐近线方程是30x y +=,则可设双曲线方程为?问题:若双曲线与22464x y +=有相同的焦点,它的一条渐近线方程是30x y +=,则双曲线的方程是?典型例题例1双曲线型冷却塔的外形,是双曲线的一部分绕其虚轴旋转所成的曲面,它的最小半径为12m ,上口半径为13m ,下口半径为25m ,高为55m ,试选择适当的坐标系,求出此双曲线的方程.例2点(,)M x y 到定点(5,0)F 的距离和它到定直线l :165x =的距离的比是常数54,求点M 的轨迹.例3过双曲线22136x y -=的右焦点,倾斜角为30的直线交双曲线于,A B 两点,求,A B 两点的坐标.变式:求AB ?思考:1AF B ∆的周长?练一练练1.若椭圆22214x y a +=与双曲线2212x y a -=的焦点相同,则a =____.练2 .若双曲线2214x y m -=的渐近线方程为32y x =±,求双曲线的焦点坐标.三、总结提升 ※学习小结1.双曲线的综合应用:与椭圆知识对比,结合; 2.双曲线的另一定义;3.直线与双曲线的位置关系.4、双曲线的第二定义:到定点的距离与到定直线的距离之比大于1的点的轨迹是双曲线. 当堂检测1.若椭圆2212516x y +=和双曲线22145x y -=的共同焦点为F 1,F 2,P 是两曲线的一个交点,则12PF PF ∙的值为( ).A .212B .84C .3D .212.以椭圆2212516x y +=的焦点为顶点,离心率为2的双曲线的方程( ). A. 2211648x y -= B. 221927x y -= C. 2211648x y -=或221927x y -= D. 以上都不对3.过双曲线的一个焦点2F 作垂直于实轴的直线,交双曲线于P 、Q ,1F 是另一焦点,若∠12PFQ π=,则双曲线的离心率e 等于( ).A.21-B. 2C. 21+D. 22+4.双曲线的渐近线方程为20x y ±=,焦距为10,这双曲线的方程为_______________.5.方程22141x y k k+=--表示焦点在x 轴上的双曲线,则k 的取值范围.6.已知双曲线的焦点在x 轴上,方程为22221x y a b-=,两顶点的距离为8,一渐近线上有点(8,6)A ,试求此双曲线的方程.。
2.3.2双曲线的几何性质导学案

2.3.2双曲线的几何性质一、 知识目标:1.掌握双曲线的简单几何性质2.了解双曲线的渐近性及渐近线的概念3.能区别椭圆与双曲线的性质二、 自主学习:2.等轴双曲线:实轴与虚轴________的双曲线叫等轴双曲线,它的渐近线方程是___________三、课堂检测:1、写出下列双曲线的实轴长和虚轴长、顶点坐标、焦点坐标和渐近线方程。
(1)221259x y -= (2)14491622=-y x (3)22981x y -+=2.已知双曲线的焦点在x 轴上,中心在原点,如果焦距为8,实轴长为6,求此双曲线的标准方程及其离心率。
3.根据下列条件求双曲线的标准方程。
(1)已知双曲线一焦点坐标为(5,0),一渐近线方程为04-3=y x 。
(2)与双曲线221169x y -=有公共的渐近线,且经过点3)A -。
(3)焦点在x 轴上,12||12F F =,顶点12,A A 是线段12F F 的三等分点四.课堂小结: 我的收获:__________________________________________________________________ __________________________________________________________________________ 我的疑惑:________________________________________________________________ __________________________________________________________________________ 五.课后练习:1.双曲线2228x y -=的实轴长是_______,渐近线方程是:_____________.2.双曲线221412x y -=的焦点到渐近线的距离为___________.3.双曲线221mx y +=的虚轴长是实轴长的2倍,则m =_______.4.已知双曲线的一条渐近线为0x =,且与椭圆22464x y +=有相同的焦点,求双曲线的标准方程.5.双曲线22221(0,0)x y a b a b-=>>的左、右焦点分别是12F F 、,过1F 做倾斜角为30°的直线,交双曲线右支于M 点,若2MF 垂直于x 轴,求双曲线的离心率.6. 已知双曲线22221(0,0)x y a b a b -=>>的两条渐近线方程为y =,若顶点到渐近线的距离为1,求双曲线的标准方程.7.已知双曲线22221(0,0)x y a b a b-=>>的两条渐近线均和圆22:650C x y x +-+=相切,且双曲线的右焦点为圆C 的圆心,求双曲线的标准方程.。
双曲线简单几何性质导学案

《双曲线的简单几何性质》导学案编写人:熊富丽 审核人:邓晖 编写时间:2014.1.9班级:_________ 组别:_____ 组名:________________ 姓名:________【学习目标】(1)通过对双曲线标准方程的讨论,掌握双曲线的范围、对称性、极点、渐近线和离心率等几何性质。
(2)了解双曲线中心、实轴、虚轴、渐近线等概念,和它们的关系及其几何意义。
(3)通过探讨,明确双曲线性质的研究进程和研究方式,培育咱们类比、分析、归纳、猜想、归纳、论证等逻辑思维能力。
(4)通过类比旧知识,探索新知识,培育咱们学习数学的兴趣,探索新知识的能力及勇于创新的精神。
【学习重难点】学习重点:双曲线的简单几何性质。
学习难点:双曲线的离心率和渐近线。
【学习方式】:自主探讨 合作交流 【学习思路】:通过类比椭圆的几何性质,然后利用双曲线的图象探讨它的几何性质,再利用几何性质解决实际问题。
【知识链接】温习1:双曲线的概念和标准方程是什么?温习2:椭圆有哪些简单几何性质?以核心在x 轴上的椭圆 为例,并画出草图。
【学习进程】以方程12222=-by a x 为例研究双曲线的简单几何性质(一)范围问题1:看图可知其范围是什么?问题2:类比椭圆,从双曲线方程如何研究其范围? (二)对称性问题3:看图可知其有如何的对称性?问题4:类比椭圆,可否证明其对称性?(三)极点问题5:双曲线的极点有几个?坐标是什么?新知:双曲线的实轴:线段12A A ,长为2a ,半实轴长a ;双曲线的虚轴:线段12B B ,长为2b ,半虚轴长b .实轴与虚轴等长的双曲线叫等轴双曲线,22-y =x m(m =0) 反思:与椭圆比较,为何),0(),,0(21b B b B -不叫双曲线的极点?(四)渐近线新知: 练习:(1) ___________________________(2) ___________________________反思:(1)等轴双曲线的渐近线是什么?(2)能不能从双曲线的方程直接推出渐近线方程?(五)离心率:ace =问题6:双曲线的离心率范围?问题7: 椭圆的离心率刻画了椭圆的圆扁程度,双曲线的离心率刻画了双曲线的什么几何特性呢?(将a c e =与abk =的联系起来)反思:等轴双曲线的离心率等于多少?展示单元一:双曲线的性质 2222+=1(>>0)x y a b a bby x a 直线叫做双曲线的渐近线.=±22-=143x y的渐近线为:22-=122x y 的渐近线为:A1求双曲线116922=-x y 的半实轴长和半虚轴长、核心坐标、离心率、渐近方程。
双曲线的简单几何性质+导学案- 高二上学期数学人教A版(2019)选择性必修第一册
3.2.2 双曲线的简单几何性质导学案课时目标:1.掌握双曲线的简单几何性质,了解双曲线的渐近线及渐近线的求法;2理解离心率的几何意义.活动一、复习回顾1.双曲线的定义:一般地,把平面内与两个定点F 1,F 2的距离的______________ 等于非零常数(小于|F 1F 2|)的点的轨迹叫做_________ .这两个定点叫做双曲线的________,两焦点间的距离叫做双曲线的_______ .2. 焦点位置 焦点在x轴上 焦点在y 轴上图形标准方程 焦点坐标a, b, c 的关系活动二:类比探究1.思考:我们前面在学习椭圆的几何性质时,主要从哪几方面学习了椭圆的几何性质?2.类比探究双曲线的几何性质 (1焦点位置焦点在x 轴上焦点在y 轴上图形标准方程x 2a 2-y 2b 2=1 (a>0,b>0)y 2a 2-x 2b 2=1 (a>0,b>0)性质范围对称性顶点轴及轴长 实轴长=____,虚轴长=____离心率渐近线(2)重、难点突破:双曲线的渐近线渐近线方程:____________________ 渐近线方程:____________________(3)思考归纳:结合双曲线的离心率与渐近线斜率的关系总结出离心率的几何意义.活动三:练习巩固例. 求双曲线 229-16=144y x 的顶点坐标、焦点坐标、实轴长、虚轴长、离心率及渐近线方程.活动四:课堂小结1.知识清单:双曲线的几何性质:范围、对称性、顶点、渐近线及离心率;结论1:渐近线方程为:y =±ba x (焦点在x 轴上)或y =±ab x (焦点在y 轴上). 结论2:离心率越大,双曲线开口越___ ;离心率越小,开口越___.2.数学思想方法归纳: 类比、数形结合等.3.常见误区:忽略焦点位置致错.活动五:作业布置课后思考:设双曲线方程为22(0)x y k k R k -=∈≠且,求该双曲线的渐近线方程与离心率,并观察该双曲线有什么特点?。
高中数学 3.3.2《双曲线的简单几何性质》导学案 北师大版选修2-1

2.3.2《双曲线的简单几何性质》导学案【学习目标】1.通过方程,研究曲线的性质.理解双曲线的范围、对称性及对称轴,对称中心、离心率、顶点、渐近线的概念;2.掌握双曲线的标准方程、会用双曲线的定义解决实际问题;3.掌握双曲线的渐近线的求法. 【导入新课】 复习导入1.复习椭圆的几何性质,重点复习它的范围、对称性、离心率、和有关量,类比得到双曲线的有关性质;2. 双曲线的标准方程及其推导过程. 新授课阶段双曲线的简单几何性质①范围:由双曲线的标准方程得,222210y x b a=-≥,进一步得:x a ≤-,或x a ≥.这说明双曲线在不等式 所表示的区域;②对称性:由以x -代x ,以y -代y 和x -代x ,且以y -代y 这三个方面来研究双曲线的标准方程发生变化没有,从而得到双曲线是以 为对称轴, 为对称中心;③顶点:圆锥曲线的顶点的统一定义,即圆锥曲线的对称轴与圆锥曲线的交点叫做圆锥曲线的顶点.因此双曲线有两个顶点,由于双曲线的对称轴有实虚之分,焦点所在的对称轴叫做 ,焦点不在的对称轴叫做 ;④渐近线:直线 叫做双曲线22221x y a b-=的渐近线;⑤离心率: 双曲线的焦距与实轴长的比 叫做双曲线的离心率(1e >). 例1双曲线方程为2221x y -=,则它的右焦点坐标为( )A.0⎫⎪⎪⎝⎭B.0⎫⎪⎪⎝⎭C.0⎫⎪⎪⎝⎭D.)【解析】例2求与双曲线221169x y -=共渐近线,且经过()3A -点的双曲线的标准方及离心率. 解:【点评】这个要进行分类讨论,但只有一种情形有解,事实上,可直接设所求的双曲线的方程为()22,0169x y m m R m -=∈≠. 例3 已知双曲线C :12222=-by a x (0,0)a b >>,B 是右顶点,F 是右焦点, 点A 在x 轴正半轴上,且满足 OA OB OF ||、||、||成等比数列,过F 作双曲线C 在第一、三象限的渐近线的垂线l ,垂足为P . (1)求证:⋅=⋅;(2)若l 与双曲线C 的左、右两支分别相交于点D 、E ,求双曲线C 的离心率e 的取值范围. 解:1.双曲线的几何性质的灵活运用;2.双曲线的渐近线的求法及其运用. 作业见同步练习部分 拓展提升1.双曲线1322=-y x 的渐近线中,斜率较小的一条渐近线的倾斜角是( ) A.060 B.090 C.0120 D.01502.如果221||21x y k k+=---表示焦点在y 轴上的双曲线,那么它的半焦距C 的取值范围是( ) A .(1,+∞) B .(0,2) C .(2,+∞) D .(1,2)3.已知对称轴为坐标轴的双曲线的一条渐近线为x -2y =0,则该双曲线的离心率为( )A 或 5B 或 3CD .54 或54.过点(-7,-6 2 )与(27 ,-3)的双曲线标准方程为 .5.已知F 1,F 2是双曲线22221x y a b-=(a >0,b >0)的左、右两个焦点,点P 在双曲线右支上,O 为坐标原点,若△POF 2是面积为1的正三角形,则b 的值是 .6. 设双曲线的一个焦点为F ,虚轴的一个端点为B ,如果直线FB 与该双曲线的一条渐近线垂直,那么此双曲线的离心率为( )A. 2B. 3C.3+12 D.5+127. 已知双曲线x 2-y 23=1的左顶点为A 1,右焦点为F 2,P 为双曲线右支上一点,则PA 1→·PF 2→的最小值为( )A .-2B .-8116C .1D .0 8. 双曲线x 216-y 29=1上到定点(5,0)的距离是9的点的个数是( )A .0B .2C .3D .49. 双曲线2x 2-3y 2=1的渐近线方程是________.10.在平面直角坐标系中,双曲线Γ的中心在原点,它的一个焦点坐标为(5,0),e 1=(2,1)、e 2=(2,-1)分别是两条渐近线的方向向量.任取双曲线Γ上的点P ,若OP →=a e 1+b e 2(a 、b ∈R ),则a 、b 满足的一个等式是________.11.双曲线的渐近线为y =±43x ,则双曲线的离心率为________.12.点M (x ,y )到定点F (5,0)距离和它到定直线l :x =95的距离的比是53,(1)求点M 的轨迹方程;(2)设(1)中所求方程为C ,在C 上求点P ,使|OP |=34(O 为坐标系原点).13.已知双曲线的中心在原点,离心率为2,一个焦点F (-2,0) .(1)求双曲线方程;(2)设Q 是双曲线上一点,且过点F 、Q 的直线l 与y 轴交于点M ,若|MQ →|=2|QF →|,求直线l 的方程.参考答案新授课阶段双曲线的简单几何性质x a ≤-,或x a ≥ x 轴和y 轴,原点 实轴,虚轴;b y x a =±ac e = 例1【解析】双曲线的222131,,,22a b c c ====.【答案】C 例2解:根据双曲线221169x y -=的渐近线方程为34y x =±. ① 焦点在x 轴上时,设所求的双曲线为22221169x y k k-=, ∵()3A -点在双曲线上,∴214k =-,无解; ② 焦点在y 轴上时,设所求的双曲线为22221169x y k k -+=, ∵()3A -点在双曲线上,∴214k =, 因此,所求双曲线的标准方程为221944y x -=,离心率53e =. 【点评】这个要进行分类讨论,但只有一种情形有解,事实上,可直接设所求的双曲线的方程为()22R,0169x y m m m -=∈≠. 例3 解:(1)法一.:()al y x c b=--, (),,a y x c bb y x a ⎧=--⎪⎪⎨⎪=⎪⎩解得2(,).a ab P c c |OA → |,|OB → |,|OF → |成等比数列,PA →=(0,-ab c)法二:同上得2(,).a ab P c c0.PA x PA OP PA FP PA OF PA OP PA FP ∴⊥⋅-⋅=⋅=∴⋅=⋅轴.. (2)222222(),,a y x c bb x a y a b ⎧=--⎪⎨⎪-=⎩422222244422222222422221242244222222)2()0,()0,.,.2a b x x c a b b a a a c b x cx a b b b b a c a b b x x a b bb a b ac a a e e ∴--=-+-+=-+⋅=<-∴>>->∴>>().即(即.即 拓展提升1.C 【解析】求出倾斜角的正切值. 2.A 【解析】解不等式组.3.A 【解析】由a,b 之间的关系转化成a,c 之间的关系.4.2212575x y -=【解析】待定系数法. 5. 2 【解析】数形结合.6.D 【解析】设双曲线的方程为x 2a 2-y 2b 2=1,设F (c,0),B (0,b ),直线FB 的斜率为-bc ,与其垂直的渐近线的斜率为b a ,所以有-b 2ac =-1,即b 2=ac ,所以c 2-a 2=ac ,两边同时除以a 2可得e 2-e -1=0,解得e =1+52. 22222222(,),(,),,..a ab b ab OP FP c c c ca b a b PA OP PA FP c cPA OP PA FP ==-∴⋅=-⋅=-∴⋅=⋅7.A [解析] 由已知可得A 1(-1,0),F 2(2,0),设点P 的坐标为(x ,y ),则PA 1→·PF 2→=(-1-x ,-y )·(2-x ,-y )=x 2-x -2+y 2,因为x 2-y 23=1 (x ≥1),所以PA 1→·PF 2→=4x 2-x -5,当x =1时,PA 1→·PF 2→有最小值-2.故选A.8.C [解析] (5,0)是双曲线的右焦点,它到双曲线左顶点的距离为9,所以以(5,0)为圆心,以9为半径作圆,该圆与双曲线的右支有两个交点,所以共有3个这样的点. 9.y =±63x [解析] 双曲线2x 2-3y 2=1的渐近线方程为2x ±3y =0,即y =±63x . 10.4ab =1 [解析] 易知双曲线Γ的方程为x 24-y 2=1,设P (x 0,y 0),又e 1=(2,1),e 2=(2,-1),由OP →=a e 1+b e 2,得(x 0,y 0)=a (2,1)+b (2,-1),即(x 0,y 0)=(2a +2b ,a -b ), ∴x 0=2a +2b ,y 0=a -b , 代入x 24-y 2=1整理得4ab =1.11.53或54 [解析] 当焦点在y 轴上时,a b =43,即9a 2=16b 2=16(c 2-a 2),解得e =54;当焦点在x 轴上时,b a =43,即16a 2=9b 2=9(c 2-a 2),解得e =53.12.[解答] (1)|MF |=x -2+y 2,点M 到直线l 的距离d =⎪⎪⎪⎪⎪⎪x -95,依题意,有x -2+y2⎪⎪⎪⎪⎪⎪x -95=53, 去分母,得3x -2+y 2=|5x -9|,平方整理得x 29-y 216=1,即为点M 的轨迹方程.(2)设点P 坐标为P (x ,y ), 由|OP |=34得x 2+y 2=34,解方程组⎩⎪⎨⎪⎧x 29-y 216=1,x 2+y 2=34,得⎩⎨⎧x =32,y =4或⎩⎨⎧x =-32,y =-4或⎩⎨⎧x =-32,y =4或⎩⎨⎧x =32,y =-4,∴点P 为(32,4)或(-32,-4)或(-32,4)或(32,-4).13.解:(1)由题意可设所求的双曲线方程为x 2a 2-y 2b 2=1(a >0,b >0),则有e =ca=2,c =2,所以a =1,则b =3,所以所求的双曲线方程为x 2-y 23=1 .(2)因为直线l 与y 轴相交于M 且过焦点F (-2,0),所以l 的斜率一定存在,设为k ,则l :y =k (x +2), 令x =0,得M (0,2k ),因为|MQ →|=2|QF →|且M 、Q 、F 共线于l , 所以MQ →=2QF →或MQ →=-2QF →. 当MQ →=2QF →时,x Q =-43,y Q =23k ,所以Q 的坐标为⎝ ⎛⎭⎪⎫-43,23k , 因为Q 在双曲线x 2-y 23=1上,所以169-4k 227=1,所以k =±212,所以直线l 的方程为y =±212(x +2),当MQ →=-2QF →时,同理求得Q (-4,-2k )代入双曲线方程得, 16-4k 23=1,所以k =±352,所以直线l 的方程为y =±352(x +2) . 综上:所求的直线l 的方程为y =±212(x +2)或y =±352(x +2).。
高中数学《双曲线的简单几何性质第二课时》(导学案)

第二章 圆锥曲线与方程2.2.2 双曲线的简单几何性质(第二课时)一、学习目标1.掌握双曲线的简单的几何性质.2.掌握直线与双曲线的位置关系.【重点、难点】1.了解双曲线的几何性质,并会应用于实际问题之中.(重点)2.会利用双曲线的定义、标准方程、几何性质及图形四者之间的内在联系,分析和解决实际问题.(难点)二、学习过程【复习引入】复习 1:直线与椭圆有哪些位置关系:复习2: 判断直线与椭圆位置关系的方法:【导入新课】直线与双曲线的位置关系(1)一般地,设直线l :y =kx +m ,①双曲线C :x 2a 2-y 2b2=1(a>0,b>0).② 把①代入②得(b 2-a 2k 2)x 2-2a 2mkx -a 2m 2-a 2b 2=0.①当b 2-a 2k 2=0时,直线l 与双曲线的渐近线平行,直线与双曲线C 相交于一点.②当b 2-a 2k 2≠0时,Δ>0⇒直线与双曲线有两个公共点,此时称直线与双曲线相交;Δ=0⇒直线与双曲线有一个公共点,此时称直线与双曲线相切;Δ<0⇒直线与双曲线没有公共点,此时称直线与双曲线相离.注意:直线和双曲线只有一个公共点时,直线不一定与双曲线相切,当直线与双曲线的渐近线平行时,直线与双曲线相交,只有一个交点.(2)弦长公式:斜率为k 的直线l 与双曲线相交于A(x 1,y 1),B(x 2,y 2),则|AB|=1+k 2|x 1-x 2|=1+k 2x 1+x 22-4x 1x 2.【典型例题】例1.若直线y=kx-1与双曲线122=-y x 有且只有一个交点,则k 的值为__________ .例2.过点(0,1)且斜率为1的直线交双曲线x 2-错误!未找到引用源。
=1于A,B 两点,则|AB|= .例3.过点P(8,1)的直线与双曲线x 2-4y 2=4相交于A,B 两点,且P 是线段AB 的中点,求直线AB 的方程.【变式拓展】1 直线2x-y-10=0与双曲线152022=-y x 的交点是 ____________ .2.双曲线的两条渐近线的方程为y =±2x ,且经过点(3,-23).(1)求双曲线的方程;(2)过双曲线的右焦点F 且倾斜角为60°的直线交双曲线于A 、B 两点,求|AB|.3.双曲线中心在原点,一个焦点坐标为F(7,0),直线y =x -1与其相交于M ,N 两点,MN 中点的横坐标为-23,则双曲线的方程为________.三、总结反思1.求弦长的两种方法(1)距离公式法:当弦的两端点坐标易求时,可直接求出交点坐标,再利用两点间距离公式求弦长.(2)弦长公式法:当弦的两端点坐标不易求时,可利用弦长公式求解,即若直线l:y=kx+b(k ≠0)与双曲线C:12222=-b y a x (a>0,b>0)交于A(11,y x ),B(22,y x )两点,则|AB|= ||1||1211212y y x x k k -+=-+ 提醒:若直线方程涉及斜率,要注意讨论斜率不存在的情况.2.中点弦问题与弦中点有关的问题主要用点差法,根与系数的关系解决.另外,要注意灵活转化,如垂直、相等等问题也可以转化成中点、弦长等问题解决.四、随堂检测1.已知双曲线方程为x 2-y 24=1,过P(1,0)的直线l 与双曲线只有一个公共点,则l 的条数为( ) A .4 B .3C .2D .12.若直线x =a 与双曲线x 24-y 2=1有两个交点,则a 的值可以是( ) A .4 B .2 C .1 D .-23.直线y=x+4与双曲线x 2-y 2=1的交点坐标为 .4.过点(0,1)且斜率为1的直线交双曲线x 2-错误!未找到引用源。
2022年《导学案双曲线的几何性质》优秀教案

双曲线的几何性质一、教学目标1、知识与技能理解双曲线的几何性质,能根据几何性质解决一些简单问题,从而培养分析、归纳、推理等能力;2、过程与方法在与椭圆的几何性质类比中获得双曲线的性质,进一步体会数形结合的思想,掌握利用方程研究曲线性质的根本方法;3、情感、态度与价值观通过本节课的学习,进一步的体会曲线与方程的对应关系,感受圆锥曲线在刻画现实世界和解决实际问题中的作用教学重点及难点二、教学重难点:重点:双曲线的几何性质及其初步应用;难点:双曲线的渐近线、离心率的应用三、复习回忆问题1、双曲线的两种标准方程是什么?a,b,c三个量之间的关系是怎样的?问题2、根据椭圆的几何性质,试完成下表四、新知探索类比椭圆的几何性质及其研究方法,我们根据双曲线的标准方程〔以焦点在轴上的为例〕来研究双曲线的性质思考:想一想椭圆的几何性质,你认为应该研究双曲线的哪些几何性质?环节一、双曲线几何性质的探究1、类比椭圆的几何性质,填写下表:说明:1、双曲线的对称中心叫做双曲线的中心2、双曲线与它的对称轴的交点即为双曲线的顶点双曲线仅有两个顶点:线段叫做双曲线的实轴,实轴长是,叫实半轴长,线段叫做双曲线的虚轴,虚轴长是,叫虚半轴长拓展:实轴和虚轴等长的双曲线叫等轴双曲线2、渐近线〔性质4〕直线叫做双曲线〔〕的渐近线探究:中心在原点,焦点在轴上的双曲线的渐近线方程是什么呢?归纳:3、离心率〔性质5〕双曲线的焦距与实轴长的比值叫做双曲线的离心率,即,因为,所以思考:椭圆的离心率刻画椭圆的扁平程度,那么双曲线的离心率能够刻画什么几何特征呢因为,所以,越大,说明e越〔填大、小〕,说明双曲线的开口越〔填大、小〕4、自主整理:归纳双曲线的几何性质:环节二、双曲线的几何性质的简单应用例1、双曲线的焦点在轴上,中心在原点,如果焦距为8,实轴长为6,求此双曲线的标准方程及其渐近线的方程,并画出其草图例2、求双曲线的实半轴长,虚半轴长,顶点坐标、焦点坐标、渐近线方程环节三、课堂练习1、求以下双曲线的实轴长和虚轴长,焦点坐标和渐近线方程(1)〔2〕(3)〔4〕2、一双曲线的焦点坐标为〔5,0〕,渐近线的方程为,求此双曲线的标准方程和离心率3、求双曲线的渐近线方程,并画出草图课堂小结:学完本节课,你有什么收获,试着自己总结一下吧!作业:55习题2-2A 第1,3题。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
)0(12
2
22>>=+b a b y a x 学案:2.3.2双曲线的简单几何性质
【学习目标】
1、通过对双曲线标准方程的讨论,掌握双曲线的范围,对称性,顶点,渐近线和离心率等几何性质与双曲线的中心,实轴,虚轴,渐进线,等轴双曲线的概念,加深对a 、b 、c 、e 的关系及其几何意义的理解。
2、能利用双曲线的简单几何性质及标准方程解决相关的基本问题。
【学习重点】双曲线的简单几何性质及其应用。
【学习难点】渐近线方程的导出。
知识回顾
1、双曲线的定义:
》
2、双曲线的标准方程:
3、回想我们是怎样利用椭圆的标准方程探究椭圆性质的
】
{
一、学习探究
(一)试一试
类比探究椭圆的简单几何性质的方法,根据双曲线的标准方程
)0,0(,12
2
22>>=-b a b y a x ,研究它的几何性质。
①范围 :由双曲线的标准方程可得:=22
b
y 从
而得x 的范围: ;即双曲线在不等式 和
所表示的区域内。
22
a
x = 从而得y 的
范围为 。
"
过程方法
性质
过程
-
范围
对称性
顶点 .
离心率
②对称性:以x -代x ,方程不变,这说明
所以双曲线关于 对称。
同理,以y -代y ,方程不变
得双曲线关于 对称,以x -代x ,且以y -代y ,方程也不变,得双曲线关于 对称。
③顶点:即双曲线与对称轴的交点。
在方程122
22=-b
y a x 里,令y=0,得x= 得到
双曲线的顶点坐标为1A ( )2A ( ) ;我们把1B ( )2B ( )也画在y 轴上(如图)。
线段 分别叫做双曲线的实轴和虚轴,它们的长分别为 。
④离心率:双曲线的离心率e= ,范围为 。
思考:离心率可以刻画椭圆的扁平程度,双曲线的离心率刻画双曲线的什么几何特征
○
5双曲线特有性质-----渐近线: 《
双曲线22
221x y a b
-=的渐近线方程为 ,双曲线各支向外延伸时,与它的
渐近线 , 。
(二)想一想
1、根据上述五个性质,画出椭圆 191622=+y x 与双曲线19
162
2=-y x 的图象。
)
二、学生展示
1)整合前面的探究结果,类比出双曲线焦点在y 轴时的几何性质,完成下表。
标准方程
122
22=-b y a x (a>0,b>0) 122
22=-b
x a y (a>0,b>0) 图 象
%
范围
对称轴
对称中心
[
2)等轴双曲线定义及性质是什么
(
3)探究共渐近线的双曲线系
三.学生点评:
优点: 缺点
,
四、总结延伸
(一)已知双曲线方程研究几何性质
例1:求双曲线 22
916144y x -= 的实半轴长和虚半轴长、焦点坐标、顶点坐标、离心率、
渐进线方程。
练习(1) :22
832x y -=的实轴长 虚轴长 ,顶点坐标 焦点坐标 离心率
|
(2)2
2
4x y -=-的实轴长为 虚轴长 顶点坐标
焦点坐标 离心率 渐近线方程
拓展提升
1y -4x 22
=的渐近线方程为: 2244x y -=的渐近线方程为: 2
214
x
y -=-的渐近线方程为:
2244
x y -=-的渐近线方程
为: 。
思考:共渐近线的双曲线方程有什么特点
、
(二)由双曲线方程性质求双曲线方程
例2:求中心在原点,对称轴为坐标轴,过点A (-5,3),且离心率e=2的双曲线的标准方程。
练习:求顶点在x 轴上,两顶点间距离为8,离心率e=
4
5
的双曲线的标准方程。
(
五、巩固训练
1求与椭圆
1244922=+y x 有公共焦点,且离心率4
5=e 的双曲线方程。
2求经过点A (3,-1),并且对称轴都在坐标轴上的等轴双曲线的方程。
3求离心率为2,经过点M (-5,-3)的双曲线标准方程。
'
4若双曲线的渐近线方程为x 4
3
y ±=求双曲线的离心率
5若双曲线1k
-42
2=y x 的离心率)(2,1e ∈,求k 的范围
6设双曲线19-a
222=y x (a>0)的渐近线方程为x 23
y ±=,求a 的值
7双曲线与椭圆
124
492
2=+y x 有公共焦点,它的一条渐近线方程为y=x ,求双曲线方程。
8设p 是双曲线19-a
2
22=y x (a>0)上的一点,双曲线的一条渐近线方程为3x-2y=0,F 1,,F 2是双曲线的左右焦点,若)(pF 3p 21==,求F
9、双曲线12
2
=-y x 的左支上一点P (a ,b )到直线y=x 的距离为2,求a+b 的值
10、椭圆和双曲线
1m
-162
2=y x (m>0)有相同的焦点,P (3,4)是椭圆和双曲线渐近线的一个交点,求m 的值及椭圆方程
六、课时小结。
