矩形的判定课件PPT
合集下载
矩形的判定公开课ppt课件

1
B
E C
又∵AE,BG分别平分∠BAD,∠ABC
∴∠1+∠2=90°
∴∠AFB=180°-∠1-∠2=90°
∴∠GFE=90°
同理:∠GHE=∠E=∠F=90°
∴四边形EFGH是矩形。
一木工师傅拿尺子要检测一个窗户是否是矩形应 该如何操作?
通过测量四个角是否为直角
除度量角度之外,师傅还可以度量什么 也能进行检测?
已知: 四边形ABCD是平行四边形,AC=BD
判别二 对角线相等的平行四边形是矩形。
求证: 四边形ABCD是矩形
A
D
证明:在
ABCD中,AB
∥
=
CD
在△BAD和△CDA
O
AB=DC, BD=CA,
B
C
AD=DAΒιβλιοθήκη ∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
∵AB∥CD
∴∠BAD +∠CDA=180° ∴∠BAD=90°
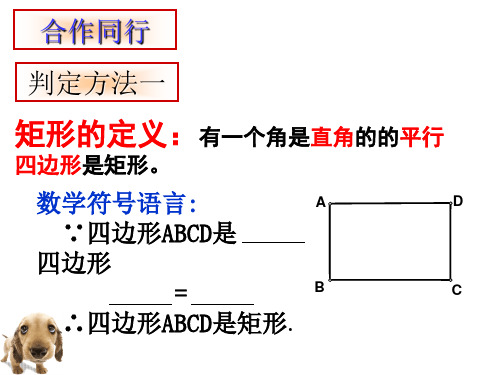
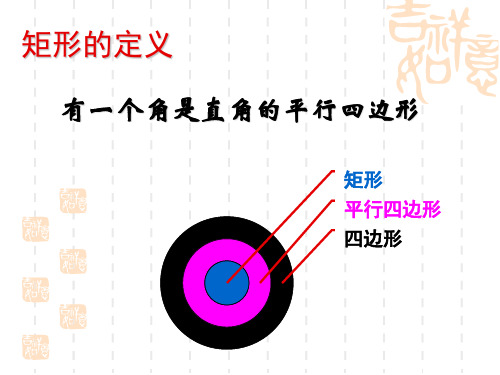
1.矩形的定义 有一个角是直角的平行四边形叫做矩形。
质矩 形 的 性
边
矩形的对边平行且相等
角
矩形的四个角都是直角
对角线 矩形的两条对角线相等且互相平分
2.判定平行四边形的方法
寻找平行四边形的判定方法时,我们从 它的定义和性质入手:
从边的角度:(1)两组对边分别平行 (2)两组对边分别相等 (3)一组对边平行且相等
三.选择题
(1)下列命题中错误的是( C )
(A)有三A 个角是直角的四D 边形是矩形
(B)两条对角线互O相平分且相等的四边形是矩形( C)对角线相等的四边形是矩形 (D)对角B 线互相平分且有C 一个角是直角的四边形是
矩形的判定(优质课件)PPT

题目3
一个四边形的对角线相等且互 相平分,这个四边形是矩形吗
?为什么?
题目4
一个四边形的对角线互相垂直 且相等,这个四边形是矩形吗
?为什么?
解答及解析
• 解答1:是的,如果一个平行四边形的一个角是直角,那么它的对角线相等,并 且其他两个角也是直角。因此,这个条件是充分必要条件。
• 解答2:根据矩形的判定条件,我们可以逐一检查每个四边形的对角线是否相等 且互相平分。如果有一个四边形的对角线满足这个条件,那么它就是矩形。
PART 04
矩形的应用
REPORTING
WENKU DESIGN
建筑学中的应用
建筑设计
矩形在建筑设计中广泛应 用,如窗户、门、墙等, 其规则、对称的特性使建 筑更加稳定、美观。
空间规划
矩形的空间布局有助于实 现合理的空间利用,提高 建筑的使用效率。
结构设计
矩形的结构特性使其在建 筑承重、支撑等方面具有 优势,能够保证建筑的稳 固性。
PART 03
矩形的判定方法
REPORTING
WENKU DESIGN
判定定理一:所有角都是直角的四边形是矩形
解释
如果一个四边形的所有角都是直角,则这个四边形一定是矩 形。
证明
假设一个四边形ABCD的所有角都是直角,那么有∠A=90°, ∠B=90°,∠C=90°,∠D=90°。根据四边形的内角和性质, ∠A+∠B+∠C+∠D=360°,由于四个角都是直角,所以每个角都 等于90°,因此四边形ABCD是矩形。
THANKS
感谢观看
REPORTING
https://
优质课件:矩形的判 定
https://
矩形的判定1 PPT课件

线AC、BD相交于点O, 且E、F、G、H分别是AO、BO、CO、DO的中点,求证 四边形EFGH是矩形.
例 如果平行四边形四个内角的平分线能够围成一个四边形,那么 这个四边形是矩形.
已知:如图, ABCD的四个内角的平 分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
矩形判定定理2
有三个角是直角的四边形是矩形。
矩形的判定口诀:
任意一个四边形, 三个直角定矩形。 对于平行四边形, 一个直角即可定, 对线相等也矩形。
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形; (2)对角线互相平分且相等的四边形是矩形; (3)有一个角是直角的四边形是矩形; (4)有三个角都相等的四边形是矩形; (5)有三个角是直角的四边形是矩形; (6)四个角都相等的四边形是矩形; (7)对角线相等,且有一个角是直角 的四边形是矩形; (8)一组对角互补的平行四边形是矩形; (9)对角线相等且互相垂直的四边形是矩形; (10)一组邻边垂直,一组对边平行且相等 的四边形是矩形;
例2已知 ABCD的对角线AC和BD相交于点O,△AOB 是等边三角形,AB= 4 cm.求这个平行四边形的面积.
分析一: 由△AOB是等边三角形,易得 ABCD 是矩形.又AB=4cm,只要求出 BC的长 即可.
分析二: 由于平行四边形的两条对角线把平行四边 形分成四个面积相等的三角形,因此本题 只要求出 △AOB的面积即可获解.
证明:∵AB∥CD ∴∠ABC+∠BCD=180° ∵BG平分∠ABC,CG平分∠BCD
∴∠BGC=90° 同理可证∠AFB=∠AED=90° ∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
小结
作业:P104,1,2,3,
例 如果平行四边形四个内角的平分线能够围成一个四边形,那么 这个四边形是矩形.
已知:如图, ABCD的四个内角的平 分线分别相交于E、F、G、H,
求证:四边形 EFGH为矩形.
矩形判定定理2
有三个角是直角的四边形是矩形。
矩形的判定口诀:
任意一个四边形, 三个直角定矩形。 对于平行四边形, 一个直角即可定, 对线相等也矩形。
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形; (2)对角线互相平分且相等的四边形是矩形; (3)有一个角是直角的四边形是矩形; (4)有三个角都相等的四边形是矩形; (5)有三个角是直角的四边形是矩形; (6)四个角都相等的四边形是矩形; (7)对角线相等,且有一个角是直角 的四边形是矩形; (8)一组对角互补的平行四边形是矩形; (9)对角线相等且互相垂直的四边形是矩形; (10)一组邻边垂直,一组对边平行且相等 的四边形是矩形;
例2已知 ABCD的对角线AC和BD相交于点O,△AOB 是等边三角形,AB= 4 cm.求这个平行四边形的面积.
分析一: 由△AOB是等边三角形,易得 ABCD 是矩形.又AB=4cm,只要求出 BC的长 即可.
分析二: 由于平行四边形的两条对角线把平行四边 形分成四个面积相等的三角形,因此本题 只要求出 △AOB的面积即可获解.
证明:∵AB∥CD ∴∠ABC+∠BCD=180° ∵BG平分∠ABC,CG平分∠BCD
∴∠BGC=90° 同理可证∠AFB=∠AED=90° ∴四边形EFGH是矩形.(有三个角是直角的四边形是矩形)
小结
作业:P104,1,2,3,
八年级数学下册-矩形的判定-ppt课件新人教版
随堂练习
p 136(1)(2)
1、下面说法中正确的是 ( D )
A 有一个角是直角的四边形是矩形 B 两条对角线相等的四边形是矩形 C 两条对角线互相垂直的四边形是矩形 D 四个角都是直角的四边形是矩形
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
生活中的数学
给你一根足够长的绳子,你能检查教 室的门窗或你的桌子是不是矩形吗?你 怎样检查?你现在能解释其中的道理吗?
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
随堂练习 (1)已知:如图,在平行四边 形ABCD中,AC、BD 相交于点 O,△ AOB是等腰三角形。求: ∠BAD的度数
解:∵ △AOB是等腰三角形 ∴OA=OB
∵四边形ABCD是平行四边形
∴AC=2OA,BD=2BO
A
∴AC=BD
∴平行四边形ABCD是矩形
∴∠BAD=90°
B
D O
C
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
随堂练习
3、能够判断一个四边形是矩形的条件是(A)
A 对角线相等
矩形的判定精选教学PPT课件
他们总是爱你这样或者那样 绝不仅仅 单纯的爱你
这样一个女人 所以
如果一个男人不爱你的钱 只爱你的身体 那么
你已经可以为自己的幸运 烧香拜佛了
还有什么是真爱呢 真正的爱情
年少时站在校园里期待的那种爱情 早已
在尘世中消失离别的时候 每一句话都是那么重
缓缓地扣击着我们的心灵 窗被敲开了
我们诉说着回忆中的快乐 回想著一张张可爱的笑脸
把每种都印刻在记忆里
望著他们远去的背影,我知道,我们 离别了 我们带著共同的回忆和永远的祝福 各自奔向远方…… 轻轻哼一首离别的歌~ 眼里噙满了泪……
重逢
重逢的时候 那是心情的又一次触动
惊喜的表情 熟悉的面庞 回忆中的甜蜜 一瞬间在脑海中隐现 于是,永远成为了所谓的缘分的代表 重逢…惊喜… 重逢的时候 那是思念的又一次宣泄 深情的一个拥抱 紧紧的一个握手 彼此的心轻鬆了许多 才发现思念是一种病 重逢…思念…… 重逢的时候 那是记忆的又一次翻新 彼此回忆著孩提时的美好 诉说着自己的苦恼 谈论着朋友的生活 讲述着自己无奈的过往 重逢…记忆… 重逢的时候 那是时间的又一次停滞 那一刻,时间终于停了 自己终于可以放假 感动的身体一时瘫在那里 重逢时的感动告诉了时光老人 时间不能改变的东西…… 重逢…感动… 重逢的时候,那是一阵欣喜,一阵感 动 欣喜之余还有一丝的忧伤 因为我们毕竟还要赶路 那么多线终有相交的一点 可是相交以后注定还要分别 但是,至少我明白 暂时的离别是为了再次相聚时的感动 ……
院子里,操场上 充满了甜甜的空气
离别的时候 每一句话都是那么轻 轻轻地说着离别时的感言 轻轻的拉着彼此的手 轻轻地在耳际说声对不起
或永远祝福你
离别的时候 每一句话都显得那么悲伤 离别时的感动在顷刻间爆发
这样一个女人 所以
如果一个男人不爱你的钱 只爱你的身体 那么
你已经可以为自己的幸运 烧香拜佛了
还有什么是真爱呢 真正的爱情
年少时站在校园里期待的那种爱情 早已
在尘世中消失离别的时候 每一句话都是那么重
缓缓地扣击着我们的心灵 窗被敲开了
我们诉说着回忆中的快乐 回想著一张张可爱的笑脸
把每种都印刻在记忆里
望著他们远去的背影,我知道,我们 离别了 我们带著共同的回忆和永远的祝福 各自奔向远方…… 轻轻哼一首离别的歌~ 眼里噙满了泪……
重逢
重逢的时候 那是心情的又一次触动
惊喜的表情 熟悉的面庞 回忆中的甜蜜 一瞬间在脑海中隐现 于是,永远成为了所谓的缘分的代表 重逢…惊喜… 重逢的时候 那是思念的又一次宣泄 深情的一个拥抱 紧紧的一个握手 彼此的心轻鬆了许多 才发现思念是一种病 重逢…思念…… 重逢的时候 那是记忆的又一次翻新 彼此回忆著孩提时的美好 诉说着自己的苦恼 谈论着朋友的生活 讲述着自己无奈的过往 重逢…记忆… 重逢的时候 那是时间的又一次停滞 那一刻,时间终于停了 自己终于可以放假 感动的身体一时瘫在那里 重逢时的感动告诉了时光老人 时间不能改变的东西…… 重逢…感动… 重逢的时候,那是一阵欣喜,一阵感 动 欣喜之余还有一丝的忧伤 因为我们毕竟还要赶路 那么多线终有相交的一点 可是相交以后注定还要分别 但是,至少我明白 暂时的离别是为了再次相聚时的感动 ……
院子里,操场上 充满了甜甜的空气
离别的时候 每一句话都是那么轻 轻轻地说着离别时的感言 轻轻的拉着彼此的手 轻轻地在耳际说声对不起
或永远祝福你
离别的时候 每一句话都显得那么悲伤 离别时的感动在顷刻间爆发
矩形的判定ppt课件

矩形的定义
有一个角是直角的平行四边形
矩形 平行四边形 四边形
回顾与联想: (1)AB∥CD, BC∥AD
(2) AB=CD,BC=AD (3) AB∥CD,AB=CD (4) ∠A= ∠C , ∠ B=∠ D
(5) AO=OC, BO=OD
□ ABCD A
D
O
B
C
师傅是怎样知道窗户是矩形的呢?
(8)一组对角互补的平行四边形是矩形; (9)对角线相等且互相垂直的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是 矩形;
下列各句判定矩形的说法是否正确?
(1)对角线相相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
X
(4)有三个角都相等的四边形是矩形;
已知:如图, ABCD的四个内角的平 分线分别相交于E、F、G、H, 求证:四边形 EFGH为矩形.
已知:如图.矩形ABCD的对角线AC、 BD相交于点O,且E、F、G、H分别是 AO、BO、CO、DO的中点,求证四边 形EFGH是矩形.
例 已知 ABCD的对角线AC和BD相 交于点O,△AOB是等边三角形,AB= 4 cm.求这个平行四边形的面积.
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
X
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
X
(4)有三个角都相等的四边形是矩形;
X
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形X;
X
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
有一个角是直角的平行四边形
矩形 平行四边形 四边形
回顾与联想: (1)AB∥CD, BC∥AD
(2) AB=CD,BC=AD (3) AB∥CD,AB=CD (4) ∠A= ∠C , ∠ B=∠ D
(5) AO=OC, BO=OD
□ ABCD A
D
O
B
C
师傅是怎样知道窗户是矩形的呢?
(8)一组对角互补的平行四边形是矩形; (9)对角线相等且互相垂直的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形是 矩形;
下列各句判定矩形的说法是否正确?
(1)对角线相相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
X
(4)有三个角都相等的四边形是矩形;
已知:如图, ABCD的四个内角的平 分线分别相交于E、F、G、H, 求证:四边形 EFGH为矩形.
已知:如图.矩形ABCD的对角线AC、 BD相交于点O,且E、F、G、H分别是 AO、BO、CO、DO的中点,求证四边 形EFGH是矩形.
例 已知 ABCD的对角线AC和BD相 交于点O,△AOB是等边三角形,AB= 4 cm.求这个平行四边形的面积.
下列各句判定矩形的说法是否正确?
(1)对角线相等的四边形是矩形;
X
(2)对角线互相平分且相等的四边形是矩形;
(3)有一个角是直角的四边形是矩形;
X
(4)有三个角都相等的四边形是矩形;
X
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
(7)对角线相等,且有一个角是直角的四边形是矩形X;
X
(5)有三个角是直角的四边形是矩形;
(6)四个角都相等的四边形是矩形;
《矩形的判定》课件

详细描述
首先,我们知道平行四边形的对角线互相平分且相等,且对角线将平行四边形分成两个 全等的三角形。如果平行四边形有一个角是直角,那么这个角所对的对角线将被这个直 角平分,从而使得其他两个角均为45度。由此,我们可以推断出平行四边形的其他两
个角均为直角,从而证明了有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形的证明
总结词
此判定方法基于矩形的性质,如果一个平行四边形的对角线长度相等,则它是 矩形。
详细描述
矩形的对角线不仅相等,而且还互相平分。因此,如果一个平行四边形的对角 线长度相等,那么它必然是一个矩形。
三个角都是直角的四边形是矩形
总结词
此判定方法基于四边形的内角和性质,如果一个四边形有三个直角,则第四个角 也必然是直角,从而它是矩形。
在证明多边形是矩形的题目中,可以 通过应用判定定理来证明。
证明平行四边形是矩形
在证明平行四边形是矩形的题目中, 可以通过应用判定定理来证明。
06
总结与回顾
本章重点回顾
01
02
03
矩形的定义
矩形是一个四边形,其中 相对边相等且相对角相等 。
矩形的判定方法
根据矩形的定义,可以通 过测量四边形的边和角来 判断是否为矩形。
总结词
通过三个直角的性质和四边形的内角和 性质,证明三个角都是直角的四边形是 矩形。
VS
详细描述
首先,我们知道任何四边形的内角和为 360度。如果一个四边形有三个直角,那 么它的内角和为270度。由此,我们可以 推断出第四个角也为直角,从而证明了三 个角都是直角的四边形是矩形。
05
判定定理的应用
判定实际问题中的矩形
矩形的性质
矩形具有平行四边形的所 有性质,此外,它还是轴 对称图形。
首先,我们知道平行四边形的对角线互相平分且相等,且对角线将平行四边形分成两个 全等的三角形。如果平行四边形有一个角是直角,那么这个角所对的对角线将被这个直 角平分,从而使得其他两个角均为45度。由此,我们可以推断出平行四边形的其他两
个角均为直角,从而证明了有一个角是直角的平行四边形是矩形。
对角线相等的平行四边形是矩形的证明
总结词
此判定方法基于矩形的性质,如果一个平行四边形的对角线长度相等,则它是 矩形。
详细描述
矩形的对角线不仅相等,而且还互相平分。因此,如果一个平行四边形的对角 线长度相等,那么它必然是一个矩形。
三个角都是直角的四边形是矩形
总结词
此判定方法基于四边形的内角和性质,如果一个四边形有三个直角,则第四个角 也必然是直角,从而它是矩形。
在证明多边形是矩形的题目中,可以 通过应用判定定理来证明。
证明平行四边形是矩形
在证明平行四边形是矩形的题目中, 可以通过应用判定定理来证明。
06
总结与回顾
本章重点回顾
01
02
03
矩形的定义
矩形是一个四边形,其中 相对边相等且相对角相等 。
矩形的判定方法
根据矩形的定义,可以通 过测量四边形的边和角来 判断是否为矩形。
总结词
通过三个直角的性质和四边形的内角和 性质,证明三个角都是直角的四边形是 矩形。
VS
详细描述
首先,我们知道任何四边形的内角和为 360度。如果一个四边形有三个直角,那 么它的内角和为270度。由此,我们可以 推断出第四个角也为直角,从而证明了三 个角都是直角的四边形是矩形。
05
判定定理的应用
判定实际问题中的矩形
矩形的性质
矩形具有平行四边形的所 有性质,此外,它还是轴 对称图形。
矩形的判定ppt课件

(1)猜想AC和BD间的关系是_A_C_=_B_D_; (2)试用理由说明你的猜想.
1
2
例5:如图,在△ABC中,点0是AC边上的一个动 点,过点0作直线MN∥BC,若MN交∠BCA的平分 线于点E,交∠BCA的外角平分线于点F. (1)求证: 0E=0F
(2)当0运动到何处时, 四边形AECF为矩形?
(8)一组对角互补的平行四边形是矩形; (9)对角线相等且互相垂直的四边形是矩形;
(10)一组邻边垂直,一组对边平行且相等的四边形 是矩形;
方法1:
有一个角是直角的平行四边形是矩形。
方法2:
对角线相等的平行四边形是矩形 。
(对角线相等且互相平分的四边形是矩形。)
方法3:
有三个角是直角的四边形是矩形 。
求证:四边形ABCD是矩形。
A
M
D
B
C
例2:已知:如图,AC与BD相交于点O, AB CD ,且∠1=∠2 。
求证:四边形ABCD是矩形
3
例3:已知:如图,四边形ABCD的对角线AC与BD相交
于点O,且AC⊥BD。E、F、G、H分别是AB、 BC、CD、AD的中点。 求证:四边形EFGH是矩形
例4:已知MN∥PQ,同旁内角的平分线 AB、CB和AD、CD分别相交于点B、D.
有三个角是直角的四边形是矩形 。
A
D
几何语言:
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形 B
C
你能归纳矩形的几种判定方法吗?
方法1:
有一个角是直角的平行四边形是矩形
方法2:
对角线相等的平行四边形是矩形 (对角线相等且互相平分的四边形是矩形)
方法3:
有三个角是直角的四边形是矩形
矩形的定义及性质课件

主题和情感。
矩形可以用于设计画布、画框 和展示板,提供稳定的支撑。
在平面设计和排版中,矩形常 被用于布局和组织内容。
在平面设计和排版中,矩形常 被用于布局和组织内容,提高
视觉效果。
其他应用场景
在包装和运输中,矩形纸箱和托 盘被广泛使用,便于堆叠和搬运
。
在科学实验中,矩形玻璃器皿常 被用于盛放液体或气体。
近代的矩形研究
近代数学家对矩形的深入 研究
随着数学的发展,人们对矩形的研究更加深 入。例如,矩形的一些重要性质被发现,如 矩形的对角线相等、矩形的面积等于长乘以 宽等。
近代的应用
在工业生产和建筑设计等领域中,矩形的应 用更加广泛。例如,在制造机器时,人们会 使用矩形的零件来确保机器的稳定性和精度
。
特殊情况下矩形的判定
总结词
在特殊情况下,如矩形的一条对角线被另一条对角线平分,则该四边形为矩形。
详细描述
如果一个四边形的一条对角线被另一条对角线平分,则该四边形的两条对角线长度相等,因此该四边 形为矩形。此外,如果一个四边形的两条对角线互相平分且相等,则该四边形也一定是矩形。
04
矩形在实际生活中的 应用
详细描述
轴对称性意味着矩形沿一条垂直或水平的直线对折后两部分能够完全重合,而中 心对称性则意味着矩形关于其中心点对称。这两种对称性在建筑设计、图案设计 等领域有着广泛的应用,使得矩形成为一种非常受欢迎的几何图形。
03
矩形的判定
根据定义判定矩形
总结词
根据矩形定义,矩形是四个角都是直 角的平行四边形。
总结词
矩形的对角线长度相等,这是由矩形的基本性质推导出的一 个重要结论。
详细描述
由于矩形的两组相对边分别平行且等长,根据勾股定理,矩 形的两条对角线长度相等。这一性质在解决几何问题时非常 有用,特别是在证明和计算与矩形相关的定理和公式时。
矩形可以用于设计画布、画框 和展示板,提供稳定的支撑。
在平面设计和排版中,矩形常 被用于布局和组织内容。
在平面设计和排版中,矩形常 被用于布局和组织内容,提高
视觉效果。
其他应用场景
在包装和运输中,矩形纸箱和托 盘被广泛使用,便于堆叠和搬运
。
在科学实验中,矩形玻璃器皿常 被用于盛放液体或气体。
近代的矩形研究
近代数学家对矩形的深入 研究
随着数学的发展,人们对矩形的研究更加深 入。例如,矩形的一些重要性质被发现,如 矩形的对角线相等、矩形的面积等于长乘以 宽等。
近代的应用
在工业生产和建筑设计等领域中,矩形的应 用更加广泛。例如,在制造机器时,人们会 使用矩形的零件来确保机器的稳定性和精度
。
特殊情况下矩形的判定
总结词
在特殊情况下,如矩形的一条对角线被另一条对角线平分,则该四边形为矩形。
详细描述
如果一个四边形的一条对角线被另一条对角线平分,则该四边形的两条对角线长度相等,因此该四边 形为矩形。此外,如果一个四边形的两条对角线互相平分且相等,则该四边形也一定是矩形。
04
矩形在实际生活中的 应用
详细描述
轴对称性意味着矩形沿一条垂直或水平的直线对折后两部分能够完全重合,而中 心对称性则意味着矩形关于其中心点对称。这两种对称性在建筑设计、图案设计 等领域有着广泛的应用,使得矩形成为一种非常受欢迎的几何图形。
03
矩形的判定
根据定义判定矩形
总结词
根据矩形定义,矩形是四个角都是直 角的平行四边形。
总结词
矩形的对角线长度相等,这是由矩形的基本性质推导出的一 个重要结论。
详细描述
由于矩形的两组相对边分别平行且等长,根据勾股定理,矩 形的两条对角线长度相等。这一性质在解决几何问题时非常 有用,特别是在证明和计算与矩形相关的定理和公式时。
1.2.2矩形的判定 课件(共19张PPT)

1.请同学们阅读课本14-16页.
2.动手操作,拿一个活动的平行四边形教具,轻轻拉动一对不相邻的顶点(如图).
思考:①随着∠α的变化,两条对角线的长度是否发生变化? (发生了变化)
②当两条对角线的长度相等时,平行四边形有什么特征?
(对角线相等的平行四边形是矩形)
③矩形的四个角都是直角,反过来,一个四边形至少有几个角是直角时,这个
框符不符合我的要求?”王子听后,找来一把三角尺,用三角尺量了量
门框的三个角,然后对国王说:“父王,我量了门框的三个角,它们都
是90度,因此,这个门框是矩形.”
(1)问:你认为王子说得对吗?请同学们分组讨论并给出老师答案.(让其中的
一组来讲)
(2)有三个角是直角的四边形是矩形吗?
自主探究 (10min)
中点, ∴ = =
,
∥ .
∴四边形 DECF 是平行四边形.
∵∠ACB=90°,∴四边形 DECF 是矩形,∴EF=CD=6cm.
典例精讲
例 6: 如图,在四边形 ABCD 中,AC,BD 相交于点 O,O 是 AC 的中点,AD∥BC.
(1)求证:四边形 ABCD是平行四边形;
四边形就是矩形?
(一个四边形至少有三个角是直角时,这个四边形就是矩形)
小组讨论(4min)
①如果仅有一根足够长的绳子,如何判定一个四边形是平行四边形?
(两组对边分别相等为平行四边形)
②如果仅有一根足够长的绳子,如何判定一个四边形是菱形?
(四边相等为菱形)
③如果仅有一根足够长的绳子,如何判定一个四边形是矩形?
测量…?
李芳同学用“边——直角、边——直角、边——直角、边”
这样四步,画出了一个四边形,她说这就是一个矩形,她的判断
2.动手操作,拿一个活动的平行四边形教具,轻轻拉动一对不相邻的顶点(如图).
思考:①随着∠α的变化,两条对角线的长度是否发生变化? (发生了变化)
②当两条对角线的长度相等时,平行四边形有什么特征?
(对角线相等的平行四边形是矩形)
③矩形的四个角都是直角,反过来,一个四边形至少有几个角是直角时,这个
框符不符合我的要求?”王子听后,找来一把三角尺,用三角尺量了量
门框的三个角,然后对国王说:“父王,我量了门框的三个角,它们都
是90度,因此,这个门框是矩形.”
(1)问:你认为王子说得对吗?请同学们分组讨论并给出老师答案.(让其中的
一组来讲)
(2)有三个角是直角的四边形是矩形吗?
自主探究 (10min)
中点, ∴ = =
,
∥ .
∴四边形 DECF 是平行四边形.
∵∠ACB=90°,∴四边形 DECF 是矩形,∴EF=CD=6cm.
典例精讲
例 6: 如图,在四边形 ABCD 中,AC,BD 相交于点 O,O 是 AC 的中点,AD∥BC.
(1)求证:四边形 ABCD是平行四边形;
四边形就是矩形?
(一个四边形至少有三个角是直角时,这个四边形就是矩形)
小组讨论(4min)
①如果仅有一根足够长的绳子,如何判定一个四边形是平行四边形?
(两组对边分别相等为平行四边形)
②如果仅有一根足够长的绳子,如何判定一个四边形是菱形?
(四边相等为菱形)
③如果仅有一根足够长的绳子,如何判定一个四边形是矩形?
测量…?
李芳同学用“边——直角、边——直角、边——直角、边”
这样四步,画出了一个四边形,她说这就是一个矩形,她的判断
矩形的判定课件.pptx

④∠ABC=90°;⑤OA=OC;⑥OB=O D.
下列组合中,不能使四边形 ABCD 成为矩形的是( )
A. ①②③
B. ②③④ C. ②⑤⑥ D. ④⑤⑥
分层抢答
3 4. 如图,已知四边形 ABCD,E,F,G,H 分别是四边的中点,只要四边形 ABCD 的对角线 AC,BD 再满足条件________,则四边形 EFGH 一 定是矩形.
分层抢答
1/2
5. 如图 1-2-30,在△ABC 中,O 是边 AC 上的一个动点,过点 O 作直 线 MN∥B C. 设 MN 交∠ACB 的平分线于点 E,交△ACB 的外角 ∠ACD 的平分线于点 F. (1)求证:OE=OF; (2)若 CE=12,CF=5,求 OC 的长; (3)当点 O 在边 AC 上运动到什么位置 时,四边形 AECF 是矩形?并说明理由.
(1)当 AC________(填“等于”或“不等于”)BD 时,门框符合要求; (2)这种做法的根据是_______________________________.
分层抢答
4 3. 如图,四边形 ABCD 的对角线 AC,BD 相交于点 O,已知下列 6 个条 件:
①AB∥DC;②AB=DC;③AC=BD;
分层抢答
1
2
行
3
能
4
我
6
5
试
一
试
分层抢答
6 1. 如图,平行四边形 ABCD 的对角线 AC 与 BD 相交于点 O,要使它成为矩形,需再添加的条件是( ) A. AO=OC B. AC=BD C. AC⊥BD D. BD 平分∠ABC
分层抢答
5 2. 如图,工人师傅砌门时,要想检验门框 ABCD 是否符合设计要求(即 门框是不是矩形),在确保两组对边分别平行的前提下,只要测量 出对角线 AC,BD 的长度,然后看它们是否相等就可以判断了.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
B C
∴四边形ABCD是平行四边形. ∴四边形ABCD是矩形.
矩形判定1:有三个角是直角的四边形是矩形
∠A= ∠B= ∠C=90°
四边形ABCD 是矩形
A
D
B
C
除度量角度之外,她们需要度量什么也 能知道做好的相框是矩形呢?
能证明它的正确等的平行四边形是矩形吗?
已知: 四边形ABCD是平行四边形,AC=BD
A O B C D
求证: 四边形ABCD是矩形 证明: 在 ABCD中 AB=DC,BD=CA,AD=DA ∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA ∵AB∥CD ∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形(有一个内角是直角的平行四边形 是矩形)
青岛版数学教材八年级上
矩形的判定
矩形的定义
有一个角是直角的平行四边形叫做矩形 一个角是直角
平行四边形
矩形
边
矩形的对边平行且相等
矩 形 的 性 质
角
矩形的四个角都是直角
对角线
矩形的 两条对角线相等且互相平分
思考与探究
一天,小丽和吴娟到一个商店准备给今天要过生日 的肖华买生日礼物,选了半天,她们俩最后决定买相框 送给她,在里面摆放她们三个好朋友的相片,为了保证 相框摆放的美观性,她们选择了矩形的相框,那么她们 是用什么方法可以知道她们拿的就是矩形相框呢?
∴四边形EFGH是矩形(对角线相等的 平行四边形是矩形)。
变式一: 已知:如图,矩形ABCD的对角线AC、BD相 交于点O,E、F、G 、 H分别是AO 、BO 、 CO 、 DO上的一点 ,且AE=BF=CG=DH. 求证:四边形EFGH是矩形
A E H D
O F B G C
课堂小结 这节课你有什么收获?
例 1 已知:如图.矩形ABCD的对角线AC、BD 相交于点O,且E、F、G、H分别是AO、BO、 CO、DO的中点,求证四边形EFGH是矩形.
证明: ∵四边形ABCD是矩形 ∴AC=BD(矩形的对角线相等) AO=BO=CO=DO(矩形的对角线互相平分) ∵ E、F、G、H分别是AO、BO、 CO、DO的中点 ∴OE=OF=OG=OH ∴四边形EFGH是平行四边形(对角 线互相平分的四边形是平行四边形) ∵EO+OG=FO+OH 即EG=FH
A D O B C
ABCD AC = BD
∠A= ∠B= ∠C=90°
ABCD 是矩形
四边形ABCD 是矩形
小丽和吴娟是怎样知道所买的相框是矩形的呢?
通过测量四个角是直角
八年级 数学
猜想加证明
有三个角是直角的四边形是矩形吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°. 求证:四边形ABCD是矩形. 证明: ∵ ∠A=∠B=∠C=90°, ∴AD∥BC,AB∥CD.
A D
∴∠A+∠B=180°,∠B+∠C=180°.
课堂练习:
一.选择题
(1)矩形具有而平行四边形不具有的性质( D ) (A)内角和是360度(B)对角相等(C)对边平行且相 等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( D )
(A)对角线相等(B)四个角相等(C)是轴对称图形 (D)对角线垂直
• • • • • • •
二.判断题 对角线相等的四边形是矩形。 对角线互相平分且相等的四边形是矩形。 有一个角是直角的四边形是矩形。 四个角都是直角的四边形是矩形。 四个角都相等的四边形是矩形。 对角线相等且有一个角是直角的四边形是 矩形。 对角线相等且互相垂直的四边形是矩形。
矩形判定2:对角线相等的平行四边形是矩形
A D O B C
ABCD AC = BD
ABCD 是矩形
推论:对角线互相平分且相等的四边形是矩形
AO CO, BO DO AC BD
四边形ABCD 是矩形
活动二:
1、为了庆祝十一国庆节,八年级(3)班同学 要在广场上布置一个矩形的花坛。计划用“串 红”摆成两条对角线。如果一条对角线用了37 盆“串红”,还 需要从花房运来多少盆“串 红”?为什么?如果一条对角线用了48盆呢? 为什么?
∴四边形ABCD是平行四边形. ∴四边形ABCD是矩形.
矩形判定1:有三个角是直角的四边形是矩形
∠A= ∠B= ∠C=90°
四边形ABCD 是矩形
A
D
B
C
除度量角度之外,她们需要度量什么也 能知道做好的相框是矩形呢?
能证明它的正确等的平行四边形是矩形吗?
已知: 四边形ABCD是平行四边形,AC=BD
A O B C D
求证: 四边形ABCD是矩形 证明: 在 ABCD中 AB=DC,BD=CA,AD=DA ∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA ∵AB∥CD ∴∠BAD +∠CDA=180°
∴∠BAD=90°
∴四边形ABCD是矩形(有一个内角是直角的平行四边形 是矩形)
青岛版数学教材八年级上
矩形的判定
矩形的定义
有一个角是直角的平行四边形叫做矩形 一个角是直角
平行四边形
矩形
边
矩形的对边平行且相等
矩 形 的 性 质
角
矩形的四个角都是直角
对角线
矩形的 两条对角线相等且互相平分
思考与探究
一天,小丽和吴娟到一个商店准备给今天要过生日 的肖华买生日礼物,选了半天,她们俩最后决定买相框 送给她,在里面摆放她们三个好朋友的相片,为了保证 相框摆放的美观性,她们选择了矩形的相框,那么她们 是用什么方法可以知道她们拿的就是矩形相框呢?
∴四边形EFGH是矩形(对角线相等的 平行四边形是矩形)。
变式一: 已知:如图,矩形ABCD的对角线AC、BD相 交于点O,E、F、G 、 H分别是AO 、BO 、 CO 、 DO上的一点 ,且AE=BF=CG=DH. 求证:四边形EFGH是矩形
A E H D
O F B G C
课堂小结 这节课你有什么收获?
例 1 已知:如图.矩形ABCD的对角线AC、BD 相交于点O,且E、F、G、H分别是AO、BO、 CO、DO的中点,求证四边形EFGH是矩形.
证明: ∵四边形ABCD是矩形 ∴AC=BD(矩形的对角线相等) AO=BO=CO=DO(矩形的对角线互相平分) ∵ E、F、G、H分别是AO、BO、 CO、DO的中点 ∴OE=OF=OG=OH ∴四边形EFGH是平行四边形(对角 线互相平分的四边形是平行四边形) ∵EO+OG=FO+OH 即EG=FH
A D O B C
ABCD AC = BD
∠A= ∠B= ∠C=90°
ABCD 是矩形
四边形ABCD 是矩形
小丽和吴娟是怎样知道所买的相框是矩形的呢?
通过测量四个角是直角
八年级 数学
猜想加证明
有三个角是直角的四边形是矩形吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°. 求证:四边形ABCD是矩形. 证明: ∵ ∠A=∠B=∠C=90°, ∴AD∥BC,AB∥CD.
A D
∴∠A+∠B=180°,∠B+∠C=180°.
课堂练习:
一.选择题
(1)矩形具有而平行四边形不具有的性质( D ) (A)内角和是360度(B)对角相等(C)对边平行且相 等(D)对角线相等 (2)下面性质中,矩形不一定具有的是( D )
(A)对角线相等(B)四个角相等(C)是轴对称图形 (D)对角线垂直
• • • • • • •
二.判断题 对角线相等的四边形是矩形。 对角线互相平分且相等的四边形是矩形。 有一个角是直角的四边形是矩形。 四个角都是直角的四边形是矩形。 四个角都相等的四边形是矩形。 对角线相等且有一个角是直角的四边形是 矩形。 对角线相等且互相垂直的四边形是矩形。
矩形判定2:对角线相等的平行四边形是矩形
A D O B C
ABCD AC = BD
ABCD 是矩形
推论:对角线互相平分且相等的四边形是矩形
AO CO, BO DO AC BD
四边形ABCD 是矩形
活动二:
1、为了庆祝十一国庆节,八年级(3)班同学 要在广场上布置一个矩形的花坛。计划用“串 红”摆成两条对角线。如果一条对角线用了37 盆“串红”,还 需要从花房运来多少盆“串 红”?为什么?如果一条对角线用了48盆呢? 为什么?
