矩形的判定(优质课件)PPTPPT课件
合集下载
矩形的性质与判定知识点总结ppt课件.pptx

直角三角形斜边上的中线等于斜边的一半
如果一个三角形一边上的中线等于这边的一半,那么这个三角形会是直角三角形
知识延伸
(1)“直角三角形斜边中线定理”与“含30°角的直角三角形性质” 及“三角形中位线性质”是解决线段倍分问题的重要依据;
(2)①“三角形中位线性质”适用于任何三角形; ②“直角三角形斜边上的中线性质”适用于任何直角三角形; ③“含30°角的直角三角形性质”仅适用于含30°角的特殊 直角三角形;
(3)直角三角形还具有以下性质: ①两锐角互余;②两直角边的平方和等于斜边平方.
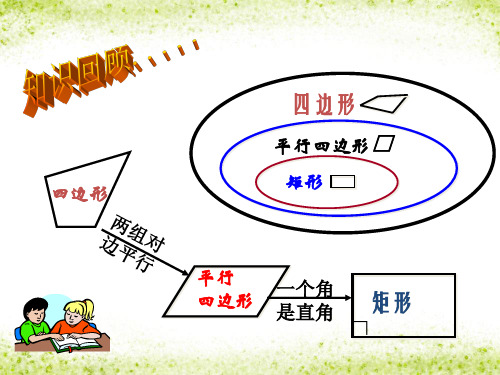
知识点 2 矩形的判定
两组对边分别平行 两组对边分别相等 一组对边平行且相等 两组对角分别相等 对角线互相平分
有一个角是直角 对角线相等
有三个角是直角
知识点 3 矩形的性质与判定的综合运用
本小节知识点常结合上学期《平行四边形》《三角形的 证明》《图形的平移与旋转》等相关内容进行考查。
知识点 1 矩形的定义、性质、推论
矩 形
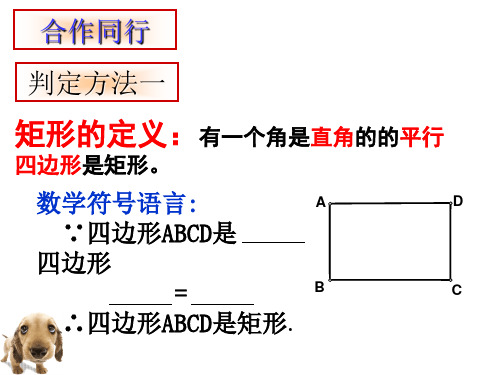
定义 有一个角是直角的平行四边形叫做矩形
性质 推论
边 矩形的对边平行且相对称性
矩形的对角线平分且相等;
矩形被两条对角线分成四个面积相等的小等腰三角形
矩形既是中心对称图形, 又是轴对称图形
邻边不相等的矩形有两条对称轴,对称轴在各边的中垂线上
考查角度较广,如线段关系(位置与数量)、角度问题、 确定图形形状、面积问题、坐标点问题、动点问题、折 叠问题等,注意数形结合、分析推理以及转化思想。
上学期知识点若不熟悉请及时复习准备课课件,此节注 意和菱形的性质与判定相区分,相关定理切勿混用
矩形的判定课件市公开课一等奖省优质课获奖课件.pptx

二、判断正误
1、有一个角是直角四边形是矩形( ×)
a
2、对角线相等四边形是矩形( × )
3、有三个角都相等四边形是矩形( ×)
4、对角线相互平分且相等四边形是矩形( √ ) Nhomakorabeab
b
5、对角互补平行四边形是矩形 ( √ )
三、生活中数学
a
1、农村家庭建房打地基时,不像大城市盖大楼用专门仪器测量,而是经常 采取“土”方法,先用绳子拉成一个四边形,分别量出房基长a和宽b,但 还要有一道主要工序才能确保房基是矩形,你能说出这道工序吗?请说明 理由。
第12页
已知:如图.矩形ABCD对角线AC、BD相交于点 O,且E、F、G、H分别是AO、BO、CO、DO中 点,求证四边形EFGH是矩形.
第13页
猜测加证实
有三个角是直角四边形是矩形
已知: 四边形ABCD中,
求证: ∠四A边=形∠BA=B∠CCD=是9矩0°
证实:
形
第14页
已知:如图,平行四边形ABCD A 中,∠OAB=∠OBA
矩形。
( √)
3、邻角相等平行四边形是矩形。 ( √)
4、平行四边形 ABCD中,AB=6,BC=8,
AC=10, 则四边形ABCD是矩形 。(√ )
A
D
B
C
第8页
活动一:
第9页
猜测加证实
对角线相等平行四边形是矩形
已知: 四边形ABCD是平行四边形,AC=BD
求证: 四边形ABCD是矩形
证实:∵四边形ABCD是平行四边形
第2页
第3页
第4页
矩形性质
边 矩形对边平行且相等 角 矩形四个角都是直角 对角线 矩形两条对角线相等且相互平分
矩形的判定(优质课件)PPT

题目3
一个四边形的对角线相等且互 相平分,这个四边形是矩形吗
?为什么?
题目4
一个四边形的对角线互相垂直 且相等,这个四边形是矩形吗
?为什么?
解答及解析
• 解答1:是的,如果一个平行四边形的一个角是直角,那么它的对角线相等,并 且其他两个角也是直角。因此,这个条件是充分必要条件。
• 解答2:根据矩形的判定条件,我们可以逐一检查每个四边形的对角线是否相等 且互相平分。如果有一个四边形的对角线满足这个条件,那么它就是矩形。
PART 04
矩形的应用
REPORTING
WENKU DESIGN
建筑学中的应用
建筑设计
矩形在建筑设计中广泛应 用,如窗户、门、墙等, 其规则、对称的特性使建 筑更加稳定、美观。
空间规划
矩形的空间布局有助于实 现合理的空间利用,提高 建筑的使用效率。
结构设计
矩形的结构特性使其在建 筑承重、支撑等方面具有 优势,能够保证建筑的稳 固性。
PART 03
矩形的判定方法
REPORTING
WENKU DESIGN
判定定理一:所有角都是直角的四边形是矩形
解释
如果一个四边形的所有角都是直角,则这个四边形一定是矩 形。
证明
假设一个四边形ABCD的所有角都是直角,那么有∠A=90°, ∠B=90°,∠C=90°,∠D=90°。根据四边形的内角和性质, ∠A+∠B+∠C+∠D=360°,由于四个角都是直角,所以每个角都 等于90°,因此四边形ABCD是矩形。
THANKS
感谢观看
REPORTING
https://
优质课件:矩形的判 定
https://
八年级数学下册-矩形的判定-ppt课件新人教版
随堂练习
p 136(1)(2)
1、下面说法中正确的是 ( D )
A 有一个角是直角的四边形是矩形 B 两条对角线相等的四边形是矩形 C 两条对角线互相垂直的四边形是矩形 D 四个角都是直角的四边形是矩形
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
生活中的数学
给你一根足够长的绳子,你能检查教 室的门窗或你的桌子是不是矩形吗?你 怎样检查?你现在能解释其中的道理吗?
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
随堂练习 (1)已知:如图,在平行四边 形ABCD中,AC、BD 相交于点 O,△ AOB是等腰三角形。求: ∠BAD的度数
解:∵ △AOB是等腰三角形 ∴OA=OB
∵四边形ABCD是平行四边形
∴AC=2OA,BD=2BO
A
∴AC=BD
∴平行四边形ABCD是矩形
∴∠BAD=90°
B
D O
C
“ 雪 亮 工 程 "是以区 (县) 、乡( 镇)、 村(社 区)三 级综治 中心为 指挥平 台、以 综治信 息化为 支撑、 以网格 化管理 为基础 、以公 共安全 视频监 控联网 应用为 重点的 “群众 性治安 防控工 程”。
随堂练习
3、能够判断一个四边形是矩形的条件是(A)
A 对角线相等
矩形的性质ppt课件

矩形的对称性可以用来解决一些几何问题。
05
矩形的面积和周长计算
矩形的面积计算公式
公式
如果矩形的长为a,宽为b,那么矩形的 面积S=a×b。
VS
解释
矩形的面积是其长和宽的乘积,这是因为 矩形的长和宽代表了平行四边形的底和高 。
矩形的周长计算公式
公式
如果矩形的长为a,宽为b,那么矩形的周 长P=2×(a+b)。
。如果四边形的对角线相等且互相平分,则该四边形为矩形。
02
三个角是直角的四边形是矩形
如果一个四边形的三个角都是直角,则该四边形为矩形。
03
对角线相等的平行四边形是矩形
如果一个平行四边形的对角线相等,则该四边形为矩形。
矩形的证明方法
综合法
利用综合法证明三角形全等、平 行线性质等基本定理,以及利用 这些基本定理推导出其他定理,
矩形的边长关系
总结词
矩形的两边长度相等,相对的两边长度也相等。
详细描述
矩形的定义决定了其具有两边长度相等的特点。相对的两边长度也相等,这是由 于矩形的对称性所决定的。这种边长关系在几何学中有着重要的应用和意义。
04
矩形的判定和证明方法
矩形的判定方法
01
定义法
根据矩形的定义,通过测量四条边的长度来判断一个四边形是否为矩形
解释
矩形的周长是矩形四条边的长度之和,两条 长边各为a,两条短边各为b,所以周长 P=2×(a+b)。
矩形面积和周长的关系
关系
矩形的面积和周长之间没有直接的关系,但是它们都与矩形 的长和宽有关。
解释
矩形的面积和周长是两个不同的属性,面积关注的是矩形的 占据的空间大小,而周长关注的是矩形四条边的长度之和。 虽然它们都受到矩形长和宽的影响,但它们之间并没有直接 的关系。
05
矩形的面积和周长计算
矩形的面积计算公式
公式
如果矩形的长为a,宽为b,那么矩形的 面积S=a×b。
VS
解释
矩形的面积是其长和宽的乘积,这是因为 矩形的长和宽代表了平行四边形的底和高 。
矩形的周长计算公式
公式
如果矩形的长为a,宽为b,那么矩形的周 长P=2×(a+b)。
。如果四边形的对角线相等且互相平分,则该四边形为矩形。
02
三个角是直角的四边形是矩形
如果一个四边形的三个角都是直角,则该四边形为矩形。
03
对角线相等的平行四边形是矩形
如果一个平行四边形的对角线相等,则该四边形为矩形。
矩形的证明方法
综合法
利用综合法证明三角形全等、平 行线性质等基本定理,以及利用 这些基本定理推导出其他定理,
矩形的边长关系
总结词
矩形的两边长度相等,相对的两边长度也相等。
详细描述
矩形的定义决定了其具有两边长度相等的特点。相对的两边长度也相等,这是由 于矩形的对称性所决定的。这种边长关系在几何学中有着重要的应用和意义。
04
矩形的判定和证明方法
矩形的判定方法
01
定义法
根据矩形的定义,通过测量四条边的长度来判断一个四边形是否为矩形
解释
矩形的周长是矩形四条边的长度之和,两条 长边各为a,两条短边各为b,所以周长 P=2×(a+b)。
矩形面积和周长的关系
关系
矩形的面积和周长之间没有直接的关系,但是它们都与矩形 的长和宽有关。
解释
矩形的面积和周长是两个不同的属性,面积关注的是矩形的 占据的空间大小,而周长关注的是矩形四条边的长度之和。 虽然它们都受到矩形长和宽的影响,但它们之间并没有直接 的关系。
矩形的判定课件ppt.ppt

八年级 数学 经营者提供商品或者服务有欺诈行为的,应当按照消费者的要求增加赔偿其受到的损失,增加赔偿的金额为消费者购买商品的价款或接受服务的费用
猜想加证明
对角线相等的平行四边形是矩形吗?
已知: 四边形ABCD是平行四边形,AC=BD
求证: 四边形ABCD是矩形
A
D
证明: 在 ABCD中
AB=DC,BD=CA,AD=DA
平行四边形是矩形)。
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
课后作业:
课本110页习题20.2第1、2题
矩形判定2:对角线相等的平行四边形是矩形
ABCD AC = BD
A
ABCD 是矩形
B
D O
C
推论:对角线互相平分且相等的四边形是矩形
AOCO,BODO
ACBD
四边形ABCD 是矩形
经营者提供商品或者服务有欺诈行为 的,应 当按照 消费者 的要求 增加赔 偿其受 到的损 失,增 加赔偿 的金额 为消费 者购买 商品的 价款或 接受服 务的费 用
证明:∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分) ∵ E、F、G、H分别是AO、BO、 CO、DO的中点 ∴OE=OF=OG=OH
∴四边形EFGH是平行四边形(对角 线互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH ∴四边形EFGH是矩形(对角线相等的
1、理解并掌握矩形的判定方法。 2、能应用矩形定义、判定等知识,
解决简单的证明题和计算题。
矩形的判定优质课ppt课件.ppt

锐角角是60 °, 则矩形的长是_______. 宽是_______.
1、必做题:P110练习1、2; 习 题1
2、选做题:P110习题2、3
3、用两种方法检验你的课桌面是否是矩 形。
思考:
问题:怎样检验木工做成的
门框是否是矩形?说说你的做法.
1.一个角是直角的平行四边形是矩形。 2.对角线相等的平行四边形是矩形。 3.三个角是直角的四边形是矩形。
回顾平行四边形、矩形的性质,完成表格.
性质 图形 分类
平行四边形 矩 形 (所特有)
边
对边平行且
相等
对边平行且相 等
角
对角相等
四个角都是直角
∠ABC=∠DCB
AB∥DC ∠ABC+∠DCB=180°
几何语言:在 ABCD中,
∠ABC=90°
∵ AC=BD
ABCD是矩形。
∴ ABCD是矩形。
探究三
有四个角是直角的 四边形是矩形吗? 有三个角是直角的 四边形是矩形吗? 有两个角是直角的 四边形是矩形吗?
方法三: 三个角都是直角的四边形是矩形。
问题
一位很有名望的木工师傅,招收了两名徒弟, 一天,师傅有事外出,两徒弟就自已在家练习用 两块四边形的废料各做了一扇矩形式的门,做完 之后,两人都说对方的门不是矩形,而自已 的是 矩形。
你能想一个办法确定 谁做的门是矩形吗?
。。
探究一:
某天邻居张大爷想为他家的厨房做扇 新窗,小强随做木匠的爸爸一起来到 邻居家,小强爸爸说:“我先测测这 个门窗是否变形。”这时小强抢着说: “这个我也会检测。”说完拿起身边 的皮尺量起了门窗的四边,再用角尺 放到门窗的一个角上测量了一下,然 后就说,这个门窗没有变形,还是矩 形形状。
1、必做题:P110练习1、2; 习 题1
2、选做题:P110习题2、3
3、用两种方法检验你的课桌面是否是矩 形。
思考:
问题:怎样检验木工做成的
门框是否是矩形?说说你的做法.
1.一个角是直角的平行四边形是矩形。 2.对角线相等的平行四边形是矩形。 3.三个角是直角的四边形是矩形。
回顾平行四边形、矩形的性质,完成表格.
性质 图形 分类
平行四边形 矩 形 (所特有)
边
对边平行且
相等
对边平行且相 等
角
对角相等
四个角都是直角
∠ABC=∠DCB
AB∥DC ∠ABC+∠DCB=180°
几何语言:在 ABCD中,
∠ABC=90°
∵ AC=BD
ABCD是矩形。
∴ ABCD是矩形。
探究三
有四个角是直角的 四边形是矩形吗? 有三个角是直角的 四边形是矩形吗? 有两个角是直角的 四边形是矩形吗?
方法三: 三个角都是直角的四边形是矩形。
问题
一位很有名望的木工师傅,招收了两名徒弟, 一天,师傅有事外出,两徒弟就自已在家练习用 两块四边形的废料各做了一扇矩形式的门,做完 之后,两人都说对方的门不是矩形,而自已 的是 矩形。
你能想一个办法确定 谁做的门是矩形吗?
。。
探究一:
某天邻居张大爷想为他家的厨房做扇 新窗,小强随做木匠的爸爸一起来到 邻居家,小强爸爸说:“我先测测这 个门窗是否变形。”这时小强抢着说: “这个我也会检测。”说完拿起身边 的皮尺量起了门窗的四边,再用角尺 放到门窗的一个角上测量了一下,然 后就说,这个门窗没有变形,还是矩 形形状。
矩形的判定ppt课件.ppt
先用一组对边平行且相等判定是平行四 边再用定义判定是矩形
方法1:
有一个角是直角的平行四边形是矩形。
方法2:
有三个角是直角的四边形是矩形 。
方法3:
对角线相等的平行四边形是矩形 。 (对角线互相平分且相等的四边形是矩形。)
1、下列各句判定矩形的说法是否正确?
(1)有一个角是直角的四边形是矩形;( )
∟
∟
同理可证:AB∥CD B
C
∴四边形ABCD是平行四边形
又∵ ∠A=90° ∴四边形ABCD是矩形
有三个角是直角的四边形是矩形
A
D
符号表达式:
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形 B
C
命题:对角线相等的平行四边形是矩形。
已知:在□ ABCD,AC=BD
求证:□ ABCD是矩形
A
D
EFGH,猜想四边形EFGH的形状,并说明理由
证明: ∵四边形ABCD是平行四边形
A
PQ D
∴∠ABC=∠ADC
H
E
G
又∵AN、DM是∠ABC、∠ADC的平分线
∴∠ABQ=∠QBC=∠ADM=∠CDM
B
F
MN
C
又∵AD∥BC ∴ ∠ AQB ∠ QBC= = ∠ ADM
∴BQ∥DM 同理:AN∥CP ∴四边形EFGH是平行四边形
C
边——直角、边——直角、边”
这样四步,画出了一个四边形,
她说这就是一个矩形。猜想她判
断的依据?
A
B
有三个角是直角的四边形是矩形
你能证明上述结论吗?
已知:在四边形ABCD中,
∠A=∠B=∠C=90° 求证证明::∵四∠边A形=∠ABB=C9D0是° 矩形。A
方法1:
有一个角是直角的平行四边形是矩形。
方法2:
有三个角是直角的四边形是矩形 。
方法3:
对角线相等的平行四边形是矩形 。 (对角线互相平分且相等的四边形是矩形。)
1、下列各句判定矩形的说法是否正确?
(1)有一个角是直角的四边形是矩形;( )
∟
∟
同理可证:AB∥CD B
C
∴四边形ABCD是平行四边形
又∵ ∠A=90° ∴四边形ABCD是矩形
有三个角是直角的四边形是矩形
A
D
符号表达式:
∵ ∠A=∠B=∠C=90°
∴四边形ABCD是矩形 B
C
命题:对角线相等的平行四边形是矩形。
已知:在□ ABCD,AC=BD
求证:□ ABCD是矩形
A
D
EFGH,猜想四边形EFGH的形状,并说明理由
证明: ∵四边形ABCD是平行四边形
A
PQ D
∴∠ABC=∠ADC
H
E
G
又∵AN、DM是∠ABC、∠ADC的平分线
∴∠ABQ=∠QBC=∠ADM=∠CDM
B
F
MN
C
又∵AD∥BC ∴ ∠ AQB ∠ QBC= = ∠ ADM
∴BQ∥DM 同理:AN∥CP ∴四边形EFGH是平行四边形
C
边——直角、边——直角、边”
这样四步,画出了一个四边形,
她说这就是一个矩形。猜想她判
断的依据?
A
B
有三个角是直角的四边形是矩形
你能证明上述结论吗?
已知:在四边形ABCD中,
∠A=∠B=∠C=90° 求证证明::∵四∠边A形=∠ABB=C9D0是° 矩形。A
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
12
课堂练习:
一.选择题
(1)矩形具有而平行四边形不具有的性质( D ) (A)内角和是360度(B)对角相等(C)对边平行且相 等(D)对角线相等
(2)下面性质中,矩形不一定具有的是( D ) (A)对角线相等(B)四个角相等(C)是轴对称图形 (D)对角线垂直
13
二.判断题 • 对角线相等的四边形是矩形。 • 对角线互相平分且相等的四边形是矩形。 • 有一个角是直角的四边形是矩形。 • 四个角都是直角的四边形是矩形。 • 四个角都相等的四边形是矩形。 • 对角线相等且有一个角是直角的四边形是
数学八年级下
20.2 矩形的判定
理科备课组05.4.15
1
2
矩形的定义 有一个角是直角的平行四边形叫做矩形
平行四边形
一个角是直角
矩形
质矩 形 的 性
边
矩形的对边平行且相等
角
矩形的四个角都是直角
对角线 矩形的 两条对角线相等且互相平分
3
思考与探究
一天,小丽和吴娟到一个商店准备给今天要过生日 的肖华买生日礼物,选了半天,她们俩最后决定买相框 送给她,在里面摆放她们三个好朋友的相片,为了保证 相框摆放的美观性,她们选择了矩形的相框,那么她们 是用什么方法可以知道她们拿的就是矩形相框呢?
已知: 四边形ABCD是平行四边形,AC=BD
求证: 四边形ABCD是矩形
A
D
证明: 在 ABCD中
AB=DC,BD=CA,AD=DA
O
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
B
C
∵AB∥CD
∴∠BAD +∠CDA=180° ∴∠BAD=90°
∴四边形ABCD是矩形(有一个内角是直角的平行四边形
4
小丽和吴娟是怎样知道所买的相框是矩形的呢?
通过测量四个角是直角
5
八年级 数学
猜想加证明
有三个角是直角的四边形是矩形吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明: ∵ ∠A=∠B=∠C=90°, NhomakorabeaA
D
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
CO 、 DO上的一点 ,且AE=BF=CG=DH.
求证:四边形EFGH是矩形
A E
D H
O
F B
G C
16
课堂小结
这节课你有什么收获?
ABCD AC = BD
∠A= ∠B= ∠C=90°
A
ABCD 是矩形
B
四边形ABCD 是矩形
D O
C
17
课后作业:
课本110页习题20.2第1、2题
18
B
C
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形. 6
矩形判定1:有三个角是直角的四边形是矩形
∠A= ∠B= ∠C=90°
四边形ABCD 是矩形
A
D
B
C
7
除度量角度之外,她们需要度量什么也 能知道做好的相框是矩形呢?
能证明它的正确 性吗?
8
活动一:
9
八年级 数学
猜想加证明
对角线相等的平行四边形是矩形吗?
矩形。 • 对角线相等且互相垂直的四边形是矩形。
14
例 1 已知:如图.矩形ABCD的对角线AC、BD相 交于点O,且E、F、G、H分别是AO、BO、CO、
DO的中点,求证四边形EFGH是矩形.
证明:∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ E、F、G、H分别是AO、BO、 CO、DO的中点
∴OE=OF=OG=OH ∴四边形EFGH是平行四边形(对角 线互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的
平行四边形是矩形)。
15
变式一:
已知:如图,矩形ABCD的对角线AC、BD相 交于点O,E、F、G 、 H分别是AO 、BO 、
是矩形)
10
矩形判定2:对角线相等的平行四边形是矩形
ABCD AC = BD
A
ABCD 是矩形
B
D O
C
推论:对角线互相平分且相等的四边形是矩形
AO CO, BO DO
AC BD
四边形ABCD 是矩形
11
活动二:
1、为了庆祝十一国庆节,八年级(3)班同学 要在广场上布置一个矩形的花坛。计划用“串 红”摆成两条对角线。如果一条对角线用了37 盆“串红”,还 需要从花房运来多少盆“串 红”?为什么?如果一条对角线用了48盆呢? 为什么?
课堂练习:
一.选择题
(1)矩形具有而平行四边形不具有的性质( D ) (A)内角和是360度(B)对角相等(C)对边平行且相 等(D)对角线相等
(2)下面性质中,矩形不一定具有的是( D ) (A)对角线相等(B)四个角相等(C)是轴对称图形 (D)对角线垂直
13
二.判断题 • 对角线相等的四边形是矩形。 • 对角线互相平分且相等的四边形是矩形。 • 有一个角是直角的四边形是矩形。 • 四个角都是直角的四边形是矩形。 • 四个角都相等的四边形是矩形。 • 对角线相等且有一个角是直角的四边形是
数学八年级下
20.2 矩形的判定
理科备课组05.4.15
1
2
矩形的定义 有一个角是直角的平行四边形叫做矩形
平行四边形
一个角是直角
矩形
质矩 形 的 性
边
矩形的对边平行且相等
角
矩形的四个角都是直角
对角线 矩形的 两条对角线相等且互相平分
3
思考与探究
一天,小丽和吴娟到一个商店准备给今天要过生日 的肖华买生日礼物,选了半天,她们俩最后决定买相框 送给她,在里面摆放她们三个好朋友的相片,为了保证 相框摆放的美观性,她们选择了矩形的相框,那么她们 是用什么方法可以知道她们拿的就是矩形相框呢?
已知: 四边形ABCD是平行四边形,AC=BD
求证: 四边形ABCD是矩形
A
D
证明: 在 ABCD中
AB=DC,BD=CA,AD=DA
O
∴△BAD≌△CDA(SSS)
∴∠BAD=∠CDA
B
C
∵AB∥CD
∴∠BAD +∠CDA=180° ∴∠BAD=90°
∴四边形ABCD是矩形(有一个内角是直角的平行四边形
4
小丽和吴娟是怎样知道所买的相框是矩形的呢?
通过测量四个角是直角
5
八年级 数学
猜想加证明
有三个角是直角的四边形是矩形吗?
已知:如图,在四边形ABCD中,∠A=∠B=∠C=90°.
求证:四边形ABCD是矩形.
证明: ∵ ∠A=∠B=∠C=90°, NhomakorabeaA
D
∴∠A+∠B=180°,∠B+∠C=180°.
∴AD∥BC,AB∥CD.
CO 、 DO上的一点 ,且AE=BF=CG=DH.
求证:四边形EFGH是矩形
A E
D H
O
F B
G C
16
课堂小结
这节课你有什么收获?
ABCD AC = BD
∠A= ∠B= ∠C=90°
A
ABCD 是矩形
B
四边形ABCD 是矩形
D O
C
17
课后作业:
课本110页习题20.2第1、2题
18
B
C
∴四边形ABCD是平行四边形.
∴四边形ABCD是矩形. 6
矩形判定1:有三个角是直角的四边形是矩形
∠A= ∠B= ∠C=90°
四边形ABCD 是矩形
A
D
B
C
7
除度量角度之外,她们需要度量什么也 能知道做好的相框是矩形呢?
能证明它的正确 性吗?
8
活动一:
9
八年级 数学
猜想加证明
对角线相等的平行四边形是矩形吗?
矩形。 • 对角线相等且互相垂直的四边形是矩形。
14
例 1 已知:如图.矩形ABCD的对角线AC、BD相 交于点O,且E、F、G、H分别是AO、BO、CO、
DO的中点,求证四边形EFGH是矩形.
证明:∵四边形ABCD是矩形
∴AC=BD(矩形的对角线相等)
AO=BO=CO=DO(矩形的对角线互相平分)
∵ E、F、G、H分别是AO、BO、 CO、DO的中点
∴OE=OF=OG=OH ∴四边形EFGH是平行四边形(对角 线互相平分的四边形是平行四边形)
∵EO+OG=FO+OH
即EG=FH
∴四边形EFGH是矩形(对角线相等的
平行四边形是矩形)。
15
变式一:
已知:如图,矩形ABCD的对角线AC、BD相 交于点O,E、F、G 、 H分别是AO 、BO 、
是矩形)
10
矩形判定2:对角线相等的平行四边形是矩形
ABCD AC = BD
A
ABCD 是矩形
B
D O
C
推论:对角线互相平分且相等的四边形是矩形
AO CO, BO DO
AC BD
四边形ABCD 是矩形
11
活动二:
1、为了庆祝十一国庆节,八年级(3)班同学 要在广场上布置一个矩形的花坛。计划用“串 红”摆成两条对角线。如果一条对角线用了37 盆“串红”,还 需要从花房运来多少盆“串 红”?为什么?如果一条对角线用了48盆呢? 为什么?
