正弦稳态电路分析和功率计算要点
07第七章正弦稳态电路的分析功率部分详解

1
ω
Z
Z R j(ωL 1 )
ωC
当 ω 0
1 即 ω0 L 0C
时
Im[ Z ( j )] 0
•
I
R
jL
•
•
•U I
U
U
Z RR
u
•
电压电流同相位。
U
1
jC
谐振:当满足一定条件(对RLC串联电路,使 ( L=1/ C), 电
路中电压、电流同相,电路的这种状态称为谐振。
串联谐振:
ω
0L
使功率因数提高到0.9 , 求并联电容C。
•
I
+
• P=20kW
U cos1=0.6
C
_
•
•
IL
IC
R
•
U
L 解:
并电容前: Q QL Ptg1
并电容后: Q QL QC
Q Ptg2
C
P U
2
( tgφ1
tgφ2 )
QC Q QL QC CU 2
cosφ1 0.6 得: φ1 53.13 cosφ2 0.9 得: φ2 25.84
有:
•
•
U ZI
•
(R jX ) I
或:
•
•
I YU
•
(G jB)U
复功率 或:
• •
SU I
• •
ZII
(R jX )I 2
• •
SU I
•
U (Y
•
U
)
(G
jB)U
2
R、L、C元件的复功率为:
•
•
SR UR I R
• •
华科电工技术第6章 正弦稳态电路分析 (2)
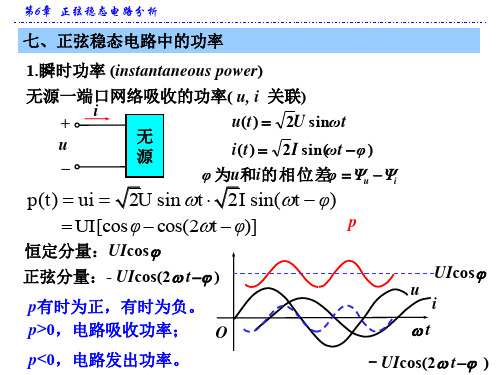
压、电流存在相位差。
cos 1,纯电阻
0,纯电抗
一般地,有 0cos1
X>0, >0,感性, 滞后功率因数 X<0, <0,容性, 超前功率因数
例: cos =0.5 (滞后), 则 =60o (电流滞后电压60o)。
u
C 对电容,i 超前 u 90°,QC<0,故电容发出无功
-
功率。
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率
电感、电容的无功补偿作用
iR
L
+
+ uL - +
u -
C
uC -
O
pL pC
i uC
uL t
当L发出功率时,C刚好吸收功率,则与外电路交换功率 为pL+pC。因此,L、C的无功具有互相补偿的作用。
30 12
30(Ω)
|Z| U / I 50(Ω) |Z| R2 (L)2
L 1
| Z |2 R2
1 314
502 302 0.127(H)
第6章 正弦稳态电路分析
七、正弦稳态电路中的功率 3.无功功率 (reactive power) Q
p(t) UI[cos φ cos(2t φ)] UI cos φ(1 cos 2t) UI sin sin 2t
第6章 正弦稳态电路分析
例:如图电路中,已知 is 5 2 sin 2(t A ),求电源提供的P、
Q,并计算电源的视在功率S和功率因素cos 。
2
解法一: 采用定义计算;
·IS
第6章 正弦稳态电路的功率

例 求图所示电路电源对电路提供的功率(有功功率)。
3 + 2H – 4 + 1F 8 • I 3 4
j4
– 10 0°
–j4
10 2 cos2tV
解 利用 P = UI cos z 计算,只要算得阻抗 Z 即可, j4(4–j4) Z = 3 + j4+4 –j4 = 3 + 4 + j4 = 7 + j4 = 8.0623 29.74° I = U = 10 = 1.2403 A 8.0623 |Z| P = UI cos z = 10×1.2403×cos 29.74° = 10.77W
+ I
10kW 0.8 (超前) 15kW 0.6 (滞后)
– = 10000 [0.8 – j 1 – 0.82 ] 2300V 0.8 = 10000 – j7500 V•A • S2 = S2[cosZ2+ jsinZ2] = 15000 [0.6 + j 1 – 0.62 ] 0.6 = 15000 + j20000 V•A • S = S1 + S2 = 25000 + j12500 = 27950.85 26.57° V•A
Us2 RL 由此可得 PL = ( Rs+RL)2 第二步,令以上关于RL的导数等于零,或直接引用第四章中的 结论,即: RL = Rs 时,负载上获得的功率最大。 Us2 RL Us2 此时 PLmax = = 2 (2RL) 4RL 总结:当 ZL = RL + jXL = Rs – jXs = Zs* 时(共轭匹配),负载获 得的功率最大。 如果阻抗模值可变而阻抗角不变,那么在满足什么条件下获 得最大功率?
电路分析基础正弦稳态电路的功率

电路分析基础
对指标点1-2的贡献: • 掌握正弦稳态功率的基本知识,能够应用基本理论分 析计算正弦稳态功率问题。 对指标点2-2的贡献: • 能够运用电路网络的基本定理,准确描述二端网络的 等效阻抗、阻抗匹配等工程问题。
返节目录
电路分析基础
10.1 二端网络的功率
1、瞬时功率
设端口电压、电流,且 u(t) Um cos(t u )V
S
显然 cos(u i ) 功率因数角:u i
有功功率、无功功率、视在功率的关系:
SQ
S2 P 2 Q2
P
功率三角形
返节目录
电路分析基础
S UI
P UI cos(u i ) Q UI sin(u i )
5、复功率
,
设:U Uu I Ii
定义: S~ UI 伏安(VA)
视在功率: S UI 复功率: S~ UI
返节目录
电路分析基础
测试题2 有功功率、无功功率、视在功率、复功率、 功率因素之间有何联系?
S~ P 2 Q2 S
P Re S
S~ P jQ
P
S
Q Im S
返节目录
电路分析基础
测试题3 填空题
返节目录
电路分析基础
例1 电路如图所示,已知 is (t) 20 cos100tmA 求三条支路的有功功率、视在功率和功率因数。
(2)电容
z 90o
Q UI CU 2 I 2 C
(3)电感 z 90 o
Q
UI
U2
LI 2
(4)若二端网络不含受控源,则 L
Q 网络内各电容和电感元件的无功功率之和。
返节目录
电路分析基础
第9章 正弦稳态电路的分析
§9.3 电路的相量图
例1: 应用相量图求图示电路的电压表的读数。
解:RC串联电路, I 设参考相量:= I 00 A I· + 8V + R 画相量图: + 1 · 先画参考相量: 如图(a)所示, U V jwC 11V I, 再画相量 UR , UR 与相量 I 同相, 再画相量 UC, UC 相量滞后 I90º 。 · UR 而 U=UR+UC ·I· 因此得直角三角形,所以 · UC U
1 | Y |= , φz = -φy |Z |
RL串联电路如图,求在w=106rad/s时的等效并 例 联电路。 50W 解 RL串联电路的阻抗为:
X L = w L = 106 0.06 10-3 = 60W
0.06mH
Z = R jX L = 50 j60 = 78.150.20 W
z
但有受控源时,可能会出现
| j z | 90
或
| j y | 90
其实部将为负值,其等效电路要设定受控 源来表示实部;
注意
③一端口N0的两种参数Z和Y具有同等效用,彼 此可以等效互换,其极坐标形式表示的互换 条件为
| Z || Y |= 1
jz j y = 0
6. 阻抗(导纳)的串联和并联 ①阻抗的串联
1 1 Y= = = 0.0128 - 50.20 W Z 78.150.20 = 0.0082 - j0.0098 S 1 1 R = = = 122 W G 0.0082 1 L = = 0.102 mH 0.0098w
R’
L’
注意
①一端口N0的阻抗或导纳是由其内部的参数、结 构和正弦电源的频率决定的,在一般情况下, 其每一部分都是频率的函数,随频率而变; ②一端口N0中如不含受控源,则有 | j y | 90 | j | 90 或
电路设计--正弦稳态电路的功率讲解
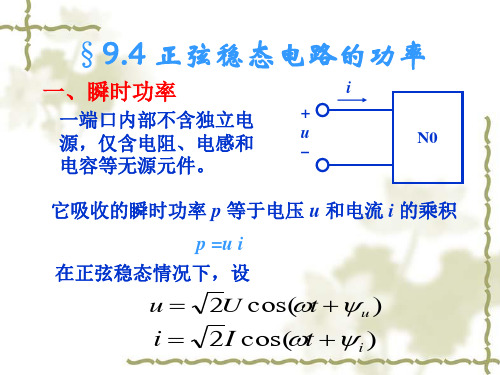
2I cos( t i )
UI cos( u i ) UI cos(2t u i )
u i
为电压和电流之间的相位差
p UI cos UI cos(2t u i )
瞬时功率有两个分量: 第一个为恒定分量,第二个为正弦分量。
§9.4 正弦稳态电路的功率
一、瞬时功率
一端口内部不含独立电 源,仅含电阻、电感和 电容等无源元件。
+ u i N0
它吸收的瞬时功率 p 等于电压 u 和电流 i 的乘积 p =u i 在正弦稳态情况下,设
u
2U cos( t u )
i
2I cos( t i )
瞬时功率 p= 令
另一种解法
而 R = 30 Ω I R 30 Z R 2 (L) 2
2
故可求得: L 502 302 = 40Ω 40 L = 127 mH
解:
u 10
i 50 2 sin(314t 45 )=50 2 cos(314t 45 )
i 45
故:P UI cos(u i )=300 50cos55 8610(W )
例9-17:测量电感线圈R、L的实验电路,已知电压 表的读数为50V,电流表的读数为1A,功率表读数为 30W,电源的频率f =50Hz。试求R、L之值。
PC=UIcos =UIcos(-90)=0
电容不消耗有功 且QC<0
1 2 QC UI I wCU 2 wC
* 电感、电容的无功功率具有互相补偿的作用
例9-16: 求平均功率P。 已知u, i关联取向,且: u 300 2 cos(314t 10 )(V) i 50 2 sin(314t 45 )(A)
正弦稳态的功率要点

其相量图如图(d)所示。单口网络吸收的平均功率为
P UI cos φ 10 2 cos(53.1 ) 12W
此时的功率因数=cos=0.6,功率的利用效率很低。
为了提高功率因数,可以在ab两端上并联一个电容, 如图(b)所示。为分析方便,先将电阻与电感串联等效变换 为电阻和电感的并联,如图(c)所示,其电导和电纳值由下 式确定
能量。
值得注意的是在用UIcos计算单口网络吸收的平均功 率时,一定要采用电压电流的关联参考方向,否则会影响 相位差的数值,从而影响到功率因数cos以及平均功率 的正负。
二、功率因数
从式(9-19)可见,在单口网络电压电流有效值的乘积 UI一定的情况下,单口网络吸收的平均功率P与cos的大 小密切相关,cos表示功率的利用程度,称为功率因数,
时,功率因数角=090以及功率因数cos<1,以致于 P<UI。为了提高电能的利用效率,电力部门采用各种措施 力求提高功率因数。
例9-15 图(a)表示电压源向一个电感性负载供电的电路模 型,试用并联电容的方法来提高负载的功率因数。
解:图(a)电路中的电流为
U 10 0 I S I 2 53 . 1 A 1 Z 3 j4
其波形如下图所示。
图9-24 电阻的瞬时功率和平均功率
瞬时功率p(t)在任何时刻均大于或等于零,电阻始终吸 收功率和消耗能量。此时平均功率的表达式为
U P UI I R R
2
2
(9 20)
p(t ) UI cos UI cos(2t 2 u ) (9 - 18)
下面我们讨论单口网络的几种特殊情况。 1. 单口网络是一个电阻,或其等效阻抗为一个电阻。 此时单口网络电压与电流相位相同,即=u-i=0, cos=1,式(9-18)变为
第九章 正弦稳态电路的分析

1 1 Y = = −53.13°S = (0.024 − j0.032)S (感 ) 性 eq Zeq 25
9-2
电路的相量图
分析阻抗(导纳) 分析阻抗(导纳)串、并联电路时,可以利用相关的 并联电路时, 电压和电流相量在复平面上组成的电路的相量图。 电压和电流相量在复平面上组成的电路的相量图。 1. 并联电路相量图的画法 并联电路相量图的画法 ① 参考电路并联部分的电压相量。 参考电路并联部分的电压相量。 根据支路的VCR确定各并联支路的电流相量与电压相 ② 根据支路的 确定各并联支路的电流相量与电压相 量之间的夹角。 量之间的夹角。 根据结点上的KCL方程,用相量平移求和法则,画出结点 方程, ③ 根据结点上的 方程 用相量平移求和法则, 上各支路电流相量组成的多边形。 上各支路电流相量组成的多边形。
R = G2GB2 , +
−B X = G2+B2
1 | Y |= , φZ = −φY |Z|
已知:R=15Ω, L=12mH, C=5µF, u =100 2cos(5000t) 例9-1 已知 试求:(1)电路中的电流 i, (瞬时表达式)和各元件的 电路中的电流 瞬时表达式) 试求 电压相量; 电路的等效导纳和并联等效电路 电路的等效导纳和并联等效电路。 电压相量;(2)电路的等效导纳和并联等效电路。 jω L R L R • + • - + UL + + uR - + uL - + + + uS C
第二种分解方法
第一种分解方法: p(t) =UI[cosϕ + cos(2ωt −ϕ)] 第一种分解方法: p UIcosϕ 恒定分量 恒定分量 u i
O
正弦稳态电路的功率公式

正弦稳态电路的功率公式在电路中,功率是电能转换的重要指标之一。
而对于正弦稳态电路,我们可以通过一条简单而有效的公式来计算其功率。
本文将详细介绍正弦稳态电路的功率公式,并解释其背后的原理和应用。
一、正弦稳态电路的功率公式正弦稳态电路是指电路中的电流和电压都是正弦波形式,并且其频率保持不变。
在这种情况下,我们可以使用以下功率公式来计算电路中的功率:P = Vrms * Irms * cos(θ)其中,P表示电路的功率,Vrms表示电压的有效值,Irms表示电流的有效值,θ表示电压和电流之间的相位差。
二、功率公式的原理解释为了更好地理解功率公式的原理,我们可以从电能转换的角度来解释。
在正弦稳态电路中,电流和电压都是周期性变化的,而功率则是电能转化的速率。
根据能量守恒定律,电路中产生的功率等于电能的消耗速率。
在公式中,Vrms和Irms分别表示电压和电流的有效值。
有效值是指在一个周期内,电压和电流的平方值的平均值的平方根。
有效值可以反映电压和电流的实际大小,而不受正弦波形式的影响。
而c os(θ)则表示电压和电流之间的相位差。
相位差是指电压和电流的波形之间的时间差,它可以是正值、负值或零值。
当相位差为零时,电压和电流完全同相,功率取得最大值。
当相位差为正值或负值时,电压和电流存在一定的错位,功率将减小。
因此,正弦稳态电路的功率公式可以通过电压和电流的有效值以及它们之间的相位差来计算电路的功率。
三、功率公式的应用功率公式在电路分析和设计中有着广泛的应用。
它可以帮助我们计算电路中的功率消耗,并进一步优化电路的设计。
功率公式可以用于计算电路中不同元件的功率消耗。
例如,我们可以通过测量电压和电流的有效值,并计算它们之间的相位差,来确定电阻、电容或电感元件的功率消耗。
功率公式可以用于分析电路中的功率传递和传输效率。
通过计算电路中不同节点的功率,我们可以了解能量在电路中的分布情况,找出能量损失的原因,并进一步改进电路的效率。
第09章正弦稳态电路的分析-2功率计算(丘关源)

cos
I
希望将cos 提高
2、提高线路功率因数的原则 必须保证原负载的工作状态不变。即: 负载上的电压、电流、功率、功率因数……不变。
3、提高线路功率因数的方法
并电容
. I . U
R. IRL
L
. IC
C
并联电容提高线路功率因数的原理
. I . U
R. IRL
L
. IC
C
IC
U
I 2
1
IRL
并联电容C以前:I IRL,U、I的夹角为 1
(P jQ) S 0
或:S总 S1 S2
注意:复功率守恒,不等于视在功率守恒。即∑S≠0 比如串联电路∵U≠U1+U2 +……
∴S≠S1+S2 +……
§9.6 交流电路中的最大功率传输
一、负载获得的有功功率?
I
有源 + 线性 U ZL 网络 -
用戴维南 定理等效
Zi +
US
-
I + U ZL -
设:Zi=Ri + jXi , ZL= RL + jXL
I US Zi ZL
US us (R i RL )2 ( X i XL )2 iL
I I
负载获有功功率: P RLI 2
( Ri
RL
RLU
2 S
)2 (Xi
XL
)2
P
(R i
RLU
2 S
RL )2 ( X
i
XL )2
二、最大功率传输的条件(什么情况下负载获P max?)
P
pdt
T0
1
T
T 0
[UI
cos
( u
简明电路分析基础_12正弦稳态功率和能量解析

简明电路分析基础_12正弦稳态功率和能量解析正弦稳态功率和能量解析是电路分析中的重要内容,能够为我们深入理解电路中电能的转化和传输提供帮助。
本文将介绍正弦稳态功率和能量解析的基础知识和分析方法。
一、正弦稳态功率正弦稳态功率是指在正弦信号作用下,电路所吸收或输出的功率。
在分析电路功率时,通常使用的是有效(均方)值,即RMS值。
正弦信号的均方值与其幅值的平方有关,对于电压为 V(t) 的正弦信号,其均方值为Vrms=Vm/√2,其中 Vm 为幅值。
在电路分析中,常用到的功率有以下三种:1.有功功率(P):表示电路吸收或输出的真实功率,单位为瓦特(W)。
2.无功功率(Q):表示电路吸收或输出的无用功率,单位为乏特(VAR)。
3.视在功率(S):表示电路吸收或输出的总功率,单位为伏安(VA)。
有功功率的公式为P = Vrms * Irms * cos(θ),其中 Vrms 和Irms 分别为电压和电流的均方值,θ 为电压和电流的相位差。
无功功率的公式为Q = Vrms * Irms * sin(θ),视在功率的公式为 S = Vrms * Irms。
可以看出,有功功率和视在功率与电压和电流的相位差有关,而无功功率则与相位差的正弦值有关。
相位差为正时,电流滞后于电压,此时电路吸收无功功率。
相位差为负时,电流超前于电压,此时电路输出无功功率。
二、正弦稳态能量正弦稳态能量是指电路在正弦信号作用下的能量转化和传输。
在电路中,能量主要以电压和电流的形式存在。
电压和电流可以通过以下关系计算能量:能量=电压或电流的平方×时间对于正弦信号V(t)来说,其能量可以表示为:E=(1/2)*Vm^2*T*f其中,Vm为信号幅值,T为信号周期,f为信号频率。
这个公式表示了正弦信号的能量与其幅值的平方、周期和频率之间的关系。
可以看出,能量与幅值的平方成正比,与周期和频率成正比。
正弦稳态能量在电路中有着重要的应用。
例如,在交流电路中,能量的传输通常是通过电路元件产生的电压和电流之间的相位差来实现的。
正弦稳态电路的分析

正弦稳态电路的分析1.复数法分析:a. 复数电压和电流表示:将正弦波电流和电压表示为复数形式,即I = Im * exp(jωt),V = Vm * exp(jωt),其中Im和Vm为幅值,ω为角频率,j为虚数单位。
b.使用欧姆定律和基尔霍夫定律来建立复数表达式。
c.找到电路中的频域参数,如电阻、电感和电容等,并使用复数法计算电路中的电流和电压。
d.计算电源电压和电流的相位差,这会决定电路中的功率因数。
2.相量法分析:a.相量表示:将电路中的电流和电压表示为相量形式,即以幅值和相位角表示,例如I=Im∠θ,V=Vm∠θ。
b.使用欧姆定律和基尔霍夫定律来建立相量表达式。
c.对电路中的频域参数应用相量法,计算电路中的电流和电压。
d.计算电源电压和电流的相位差,以确定电路中的功率因数。
无论是复数法还是相量法,分析正弦稳态电路的关键是计算电路中的电流和电压的幅值和相位。
在计算过程中,需要使用复数代数、欧姆定律、基尔霍夫定律以及频域的电路参数等相关知识。
在实际应用中,正弦稳态电路的分析主要包括以下几个方面:1.交流电路中的电阻:电阻对交流电流的影响与直流电路相同,即按欧姆定律计算。
复数法计算时,电流和电压与频率无关,可以直接使用欧姆定律计算。
2.交流电路中的电感:电感器对交流电流的响应取决于电流的频率。
复数法计算电感电压和电流时,需要将频率变量引入到电感的阻抗中。
3.交流电路中的电容:电容器对交流电压的响应取决于电压的频率。
复数法计算电容电压和电流时,需要将频率变量引入到电容的阻抗中。
4.交流电路中的复数阻抗:电路中的电感、电容和电阻组成复数阻抗。
复数阻抗可以用来计算电路中的电流和电压。
根据欧姆定律和基尔霍夫定律,可以建立复数电流和电压之间的关系。
5.交流电路中的功率因数:功率因数是电路中有功功率与视在功率之比。
在分析正弦稳态电路时,可以计算电路中电源电压和电流的相位差,从而确定功率因数。
总结起来,正弦稳态电路的分析步骤包括选择复数法或相量法、建立复数或相量表达式、计算电流和电压的幅值和相位、计算功率因数等。
第9章 正弦交流稳态电路分析

G 2R 2 , R X
B 2 X 2 R X
1 | Y | , φ y φz |Z|
注
一般情况 G1/R B1/X。若Z为感性, X>0,则B<0,即仍为感性。
同样,若由Y变为Z,则有:
R
Y
G
jB
Z
jX
Y G jB | Y | φ y ,
Z R jX | Z | φz
1 . U U R U L UC R I jL I j I C
.
.
.
.
.
.
U 1 Z R jL j R jX Z z I C
Z— 复阻抗;R—电阻(阻抗的实部);X—电抗(阻抗的虚部); |Z|—复阻抗的模;z —阻抗角。 转换关系:
例
L + + uR - + uL u C -
i
R
已知:R=15, L=0.3mH, C=0.2F,
u 5 2 cos(t 60 )
+ uC -
f 3 104 Hz . 求 i, uR , uL , uC .
.
解
其相量模型为:
I
R
.
j L
.
U 560 V
jL j2 3 104 0.3 103 j56.5Ω 1 1 j j j26.5Ω 4 6 C 2π 3 10 0.2 10 1 15 j56.5 j26.5 33.5463.4o Ω Z R j L j C
(1)C > 1/L ,B>0, y>0,电路为容性,电流超前电压 相量图:选电压为参考向量, u 0
正弦稳态电路的功率公式

正弦稳态电路的功率公式1.有功功率:有功功率表示电路中能转化为其他形式的功率,通常是用于实现有用功能的功率。
在正弦稳态电路中,有功功率可以通过电压和电流的乘积来计算。
对于单相电路,有功功率的公式如下:P = V × I × cos(θ)其中,P表示有功功率,V表示电流的有效值,I表示电压的有效值,θ表示电压和电流之间的相位差。
在三相电路中,有功功率的公式如下:P = √3 × V × I × cos(θ)其中,P表示有功功率,V表示电压的有效值,I表示电流的有效值,θ表示电压和电流之间的相位差。
2.无功功率:无功功率表示电路中产生的电能不能被转化为其他形式的功率,它主要是用来提供电路元件的无效功率。
在正弦稳态电路中,无功功率可以通过电压和电流的乘积来计算。
对于单相电路,无功功率的公式如下:Q = V × I × sin(θ)其中,Q表示无功功率,V表示电流的有效值,I表示电压的有效值,θ表示电压和电流之间的相位差。
在三相电路中,无功功率的公式如下:Q = √3 × V × I × sin(θ)其中,Q表示无功功率,V表示电压的有效值,I表示电流的有效值,θ表示电压和电流之间的相位差。
3.视在功率:视在功率表示电路中的总功率,它等于有功功率和无功功率的向量和。
在正弦稳态电路中,视在功率可以通过电压和电流的乘积来计算。
对于单相电路,视在功率的公式如下:S=V×I其中,S表示视在功率,V表示电流的有效值,I表示电压的有效值。
在三相电路中,视在功率的公式如下:S=√3×V×I其中,S表示视在功率,V表示电压的有效值,I表示电流的有效值。
4.功率因数:功率因数表示有功功率和视在功率之间的比率,它反映了电路中有效功率的利用率。
功率因数通常用cos(θ)表示,在正弦稳态电路中,功率因数可以通过有功功率和视在功率的比值来计算。
《电路基础》第23讲 正弦稳态电路的功率

Z
cos
Z 2 2 Zo Z [coso cos sino sin ]
U
2 oc
cos
Zo Z
2
Z
2 Zo
cos ( o
)
18
P
U
2 oc
cos
Zo Z
2
Z
2 Zo
cos(o
)
显然, 当 Zo 2 Z 最小时, P最大。
i
Zo
+
+u
Uoc - -
Z
Z
令
d
Zo
2
Z
0
d Z Z
即:
Z Zo
10
复功率守恒
b S~k 0
k 1
b
(Pk jQk ) 0
k 1
b • •*
UkIk 0
k 1
b
k 1 b
Pk
0
k
1
Qk
0
* 复功率守恒, 不等于视在功率守恒.
一般情况下:
b
S Sk
k 1
11
例. 已知如图,求各支路的复功率。
I2
10∠0o A
+ I1
U
_
10W j25W
5W -j15W
第23讲 正弦稳态电路的功率
学习重点: 1、基本概念: 2、各种功率的计算
1
一、 基本概念
无源一端口网络吸收的功率( u, i 关联)
i
+
u _
无 源
u(t) 2U cos(t u ) i(t) 2I cos(t φi )
2I cos(t φu )
u i 为电压u超前于电流 i 的相位差。
5-5 正弦稳态电路的功率

邹建龙,西安交通大学电气工程学院
正弦稳态电路的功率是电路的难点之一,下面我们给出正弦稳态电路不同类型功率的定 义及其分析。
1. 瞬时功率
正弦稳态电路的瞬时功率等于时域的电压乘以电流,即
p(t) = u(t)i(t)
(1)
对于电阻来说,
U = RI
可见,电阻的电压电流同相位。假定时域的电阻电压、电流为
=P UI cos (ϕu = − ϕi ) UI cosϕ
(14)
式中,ϕ= ϕu − ϕi ,即支路电压和电流的相位差。对于电阻来说ϕ = 0o ,对于电感来说ϕ = 90o ,
对于电容来说ϕ = −90o 。
3. 无功功率
由图 2 和图 3 的电感和电容瞬时功率波形可见,电感和电容在正半周期吸收功率,负半 周期发出功率,并且发出的功率等于吸收的功率,相当于功率在不停吞吐。
(12)
可见,电阻平均功率大于零,电阻做功,吸收功率;而电感和电容的平均功率都为零,因而 电容和电感不做功。
对于正弦稳态电路中任意一条支路,假定其时域电压、电流为
u(t=) 2U cos (ωt + ϕu ), i(t=) 2U cos (ωt + ϕi )
(13)
将式(13)先后代入式(1)和式(11),可得其平均功率为
复功率,就能同时得到有功功率和无功功率,这就是构造复功率的初衷。当然了,构造出复
功率不仅有以上好处,还有其他好处,在本节的问答环节,我们会给出解释。
由于计算复功率的目的是求出有功功率和无功功率,所以如果先求有功和无功,再得出
复功率,这就违背了复功率定义的初衷。因此,我们还需要找出复功率的计算公式。
将式(14)和式(16)代入式(18)可得
第6章(3)正弦稳态电路的功率

单位:瓦 (6.5-3)
在正弦稳态情况下,平均功率不仅与电压、电流的有 效值有关,而且与电压、电流的位相差有关。 式中 λ = cos ϕ 称为功率因数(power factor) ϕ = ϕu − ϕi 称功率因数角(power-factor angle) 通常所说的功率,都是指平均功率而言。平均功 率又叫有功功率(active power)。
Q = UI sin ϕ = UI sin ϕ Z
(6.5-27)
②Reactive Power in Terms of Z or Y : 对于不含 独立源的一端口,无功功率也可以 用阻抗或导纳计算。根据式(6.5-6)和(6.5-18), (6.5-18),即 2 * * (6.5-28a) Q = Im(UI ) = Im( ZII ) = I Im( Z ) = I 2 X (ω )
p (t ) = UI cos ϕ + UI cos(2ωt + 2ϕu − ϕ ) = UI cos ϕ + UI cos ϕ cos(2ωt + 2ϕu ) + UI sin ϕ sin(2ωt + 2ϕu )
(6.5-2) 上式中第一项始终大于(或小于、或等于零),它是 瞬时功率中的不可逆部分;第二项是瞬时功率中的 可逆部分,其值正负交替,说明能量在外施电源和 二端网络之间来回交换。
第六章 正弦电路的稳态分析
注: i) 如果一端口只由R、L、C等无源元件组成,则功率 因数角φ=阻抗角φZ,且|φZ|≤900,所以平均功率P≥0, 一端口吸收能量。根据能量守恒可知,P为一端口中电阻 元件所消耗的总功率(∵L、C元件不耗能)。 ii) 如果一端口除无源元件外尚有受控源(亦有功率因 数角φ=阻抗角φZ), |φZ|可能>900。其平均功率P为负 值,说明该一端口对外提供能量。 iii) 如果一端口内含有独立电源,则功率因数角φ为 端口电压与端口电流的位相差。P可能为正,也可能为负 值。即一端口可能吸收能量,也可能对外提供能量。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
其中: R — 电阻分量( ); X — 电抗分量()
1 — 容抗 XL = L — 感抗; X C C
U U (3) Z u i I I
Z R X
2
2
= R + jX = |Z| Z
第 九 章
正弦稳态电路的分析
9-1Байду номын сангаас
阻抗和导纳
一、阻抗 1. 元件的阻抗 元件在正弦稳态下,电压相量与电流相量(关联
U 参考方向)之比为元件的阻抗,记为 Z。即 Z 。 I
单位:欧姆(). 电阻
IR
电感 R
U R I L jL U L
电容
IC
1 j C
1 记为 Y。 即 Y I 。单位:西门子(S). Z U Y I YU I
元件
U
—— 欧姆定律的相量形式
一端口
+ U
I
N0
1 I U Y Z Z U I —— 输入阻抗 (导纳)
N 只含阻抗与受控源
3. 分析
I YU
称阻抗 Z 呈容性;
iii) X = 0 , Z = 0 , u – i = 0 , 电压与电流同相,
称阻抗 Z 呈阻性;
(5) 阻抗三角形
Z R X
2 2
|Z|
|Z|
|X| R
例 已知 R = 15 , L = 10mH , C = 100µ F , 求 uS(t)分别 为 120 2 cos 500 t V与 120 2 cos 3000 t V 时的稳态电 流 i(t),并画出相量图。
IC
j
1 C
U C
IR 1 YR U R R
IL 1 YL U L jL
IC YC jC U
C
二、导纳 1. 定义 阻抗的倒数 称为导纳。 元件 (一端口) 在正弦稳态下,电流相量与电压相 量(关联参考方向)之比为元件 (一端口) 的导纳,
I I (4) 导纳的性质 Y i u = G + jB = |Y| Y U U
i) B > 0 , Y > 0 , i – u > 0 , 电流超前于电压, 称导纳 Y 呈容性; ii) B < 0 , Y < 0 , i – u < 0 , 电流滞后于电压, 称导纳 Y 呈感性; iii) B = 0 , Y = 0 , i – u = 0 , 电流与电压同相, 称导纳 Y 呈阻性; 思考:感性的阻抗对应的导纳的性质如何?
二、导纳 1. 定义 阻抗的倒数 称为导纳。 元件 (一端口) 在正弦稳态下,电流相量与电压相 量(关联参考方向)之比为元件 (一端口) 的导纳,
1 记为 Y。 即 Y I 。单位:西门子(S). Z U
电阻
IR
电感
R
U R I L jL U L
电容
U C
U ZR R R IR
U Z L L jL IL
U 1 C ZC j IC C
9-1
阻抗和导纳
一、阻抗 1. 元件的阻抗 元件在正弦稳态下,电压相量与电流相量(关联
U 参考方向)之比为元件的阻抗,记为 Z。即 Z 。 I
单位:欧姆(). 元件
I
Z
U
Z U I
—— 欧姆定律的相量形式
2. 一端口的阻抗 对于不含独立源的一端口,在正弦稳态下其端口 电压相量与端口电流相量(关联参考方向)之比为 一端口的阻抗,记为 Z。单位:欧姆().
3. 分析
Z U I
(1) 元件与不含独立源的一端口的 VCR 统一表达为: Z U I ,不再表现为微积分的关系;
i(t)
iR
iL iC (1)
IC
+j IR
+1 U S
uS(t)
(2) +j
R
L
C
O 66
I
IC
I = 19.7 –66 A Z = 6.09 66
I = 33 76 A
I
76 IR
IL
Z = 3.64 –76
+1 U S
O IL
(6) 阻抗是频率的函数 Z(j) = R() + jX()
X = – Z arctg Z u i R
U Z I
(4) 阻抗的性质
U U Z u i = R + jX = |Z| Z I I
i) X > 0 , Z > 0 , u – i > 0 , 电压超前于电流,
称阻抗 Z 呈感性;
ii) X < 0 , Z < 0 , u – i < 0 , 电压滞后于电流,
(1) 元件与不含独立源的一端口的 VCR 统一表达为: ,不再表现为微积分的关系; I YU I (2) Y 为一复数,记为 Y = G + jB . U 其中: G — 电导分量 (S); B — 电纳分量 (S) 1 — 感纳 BC = C — 容纳; BL L I I I 2 2 (3) Y i u Y G B Y U U U B Y = i – u Y arctg = G + jB = |Y| Y G
i(t)
iR
iL iC (1)
IC
+j IR
+1 U S
uS(t)
(2) +j
R
L
C
O 66
I
IC
I = 19.7 –66 A Z = 6.09 66
I = 33 76 A
I
76 IR
IL
Z = 3.64 –76
+1 U S
Y = 0.164 –66 S
仍为感性。
(5) 导纳三角形
|Y|
2
Y G B
2
|Y|
|B| G
(6) 导纳是频率的函数
Y(j) = G() + jB()
例 已知 R = 15 , L = 10mH , C = 100µ F , 求 uS(t)分别 为 120 2 cos 500 t V与 120 2 cos 3000 t V 时的稳态电 流 i(t),并画出相量图。
