函数的连续性
函数的连续性

4、连续函数的局部保号性
定理3(局部保号性) 若函数 f 在点 x0 连续, 且 f ( x0 ) 0 ( 或 f ( x0 ) 0 ) , 则 0, x x x0
f ( x) 0
(或 f ( x) 0)
二、闭区间上连续函数的性质
一、最大(小)值的定义 定义 设 f ( x )为定义在数集 D上的一个函数 . 若 存在 x0 D , 使得对一切 x D, 均有
应的函数(在 y0 处)的增量
例1 证明 f ( x ) xD( x ) 在 x 0 处连续 , 其中 D( x )
为狄利克雷函数. 证 因为 f (0) 0, D( x ) 1, lim x 0, 所以
x 0
lim f ( x ) lim xD( x ) 0 f (0).
x 0
所以 f (x) 在 x 0 处右连续而不左连续,从而不 连续. 既然它的左、右极限都存在,那么这个间
断点是跳跃间断点.
1 例 试问 x 0 是函数 f ( x ) sin 的哪一类间断 x 点?
解 因为由归结原理可知,
1 1 lim sin 与 lim sin x 0 x 0 x x
在 x 0 处的连续性.
y
y xa a0
lim f ( x ) lim x 0 f (0),
x 0
y xa a0
y xa a0
所以 f 在 x 0 处左连续. 又因为
x 0
y x
o
x
lim f ( x ) lim ( x a ) a,
设 x x x0 , y y y0 f ( x ) f ( x0 ) f ( x0 x ) f ( x0 ).
函数的连续性

| f ( x) f ( x0 )| .
| x x0 | ,
在点 x0 连续之间的关系: (i) f 在点 x0 有极限是 f 在点 x0 连续的必要条件. (ii) “ f 在点 x0 连续”要求: f 在点 x0 有极限且其极限值 应等于 f 在点 x0 的函数值.
注4 由上述定义, 我们可得出函数 f 在点 x0 有极限与 f
f 在点 x0 连续
lim f ( x ) f ( x0 ) f ( lim x ) . x x x x
0 0
首页
×
例1 证明函数 f ( x ) xD( x ) 在点 x = 0 连续, 其中
D ( x ) 为狄利克雷函数. 证 由 f (0) = 0 及 |D(x)|1, 对任给的 > 0 , 为使
| f ( x ) f (0) | | x D ( x ) | | x | ,
只要取 = , 即可按 - 定义推得 f 在点 x = 0 连续. 注 函数在一点处连续是函数的局部性态,例1就是 一个仅在点 x = 0 连续的函数.
▌
首页
×
3. 左右连续 定义2 设函数 f 在某U+(x0) (或 U-(x0) )内有定义, 若
×
如何分析增量x, y,正是微积分的灵魂.
它只 实际上,不必把增量看成是一个新的数学概念, 是表示变量的一个新的记法. 用它来描述变量的变化是分 析函数的一个十分重要角度. 特别是在研究函数在一点附 近的变化时,增量的记法具有特殊的重要性和优越性.
例如,设变量 y — 某商品销售量,x — 该商品价格. 在一定条件下,x与 y 的关系可用价格——销售函数来描述 . 作为销售经理虽然关心价格销售函数,但更重要的问题是: 如果现在价格是x0,在 x0的基础上调整x时,市场的反应 (销售的增减量)如何? 他须要研究的是与增量 x 相应的增量 y 的关系.
函数的连续性

结论: 设(1)设函数 f (x) 在点x0连续,函数 g (x)在点x0不连续;(2)函数 f (x)和 g (x) 在点x0 都不连续. 问函数 f (x) + g (x), f (x) g (x) 分别在(1), (2)情况下,在点 x0是否连续? x4 e 1 补例3. 求 lim x 0 1 cos( x 1 cos x )
有函数的增量
函数连续性的等价定义 对自变量x0的增量 函数
在点 x0 连续有下列等价命题:
x x0
lim f ( x) f ( x0 )
x 0
lim y 0
左连续
lim f ( x0 x) f ( x0 ) x 0 y y f ( x)
y
f ( x0 0) f ( x0 ) f ( x0 0)
注意:对于非连续函数,极限符号与函数符号不 一定可以交换.
x 0 x 0
x x0
二、 函数的间断点
在点 的某空心邻域内有定义 , 则下列 设 情形之一函数 f (x) 在点 不连续 : (1) 函数 在 无定义 ; (2) 函数 在 虽有定义,但 不存在; (3) 函数 在 虽有定义 , 且 存在 , 但
若函数 f (x)在开区间(a, b)内每一点都连续 , 而且在 点 x =a 右连续,在点 x =b 左连续 , 则称函数 f (x)在闭 区间[a, b]上连续. 或称它为[a, b]上的连续函数 . 由 f ( x) 在 x0 连续知
f ( lim x)
这说明,对于连续函数,极限符号与函数符号可 以交换. 例如 lim cos x cos(lim x) cos 0 1
x t a 1, 则 x log a (1 t ) , 解: 令
函数的连续性(122)

一致连续性是指函数在定义域内的任何自变量变化都非常小,对应的函数值变化也非常小。也就是说,对 于任意给定的正数$epsilon$,存在一个正数$delta$,使得当$|x_1 - x_2| < delta$时,有$|f(x_1) f(x_2)| < epsilon$。
ห้องสมุดไป่ตู้
紧致性定理
总结词
紧致性定理是函数连续性的一种重要推 论,它表明如果一个函数在一个闭区间 上连续,则该函数在该区间上必有最大 值和最小值。
断。
03 函数连续性的应用
利用连续性求极限
极限定义
极限是描述函数在某点附近的行为的数学工具。如果函数在某点 的极限存在,则函数在该点连续。
单侧极限
单侧极限是研究函数在某点左侧或右侧的行为,通过单侧极限可以 判断函数在该点是否连续。
极限的四则运算
通过函数的连续性,可以推导出极限的四则运算性质,例如加减、 乘除等运算的极限。
有限覆盖定理是指如果一个闭区间被有限个 开子区间覆盖,则这些开子区间中至少有一 个是包含在另一个开子区间中的。这个定理 在实数理论中非常重要,它表明实数轴上的 任何开覆盖都可以被有限个开子区间所覆盖。
THANKS FOR WATCHING
感谢您的观看
函数在区间上的连续性
总结词
函数在区间上的连续性是指函数在区间内的任意一点都连续 。
详细描述
如果一个函数在其定义域的每一个子区间内都连续,则称该函 数在其定义域上连续。这意味着对于定义域内的任意两点$x_0$ 和$x_1$,当$x_0<x<x_1$时,函数$f(x)$都满足连续性的定义。
连续函数的基本性质
02 函数连续性的判定
函数在某点连续的判定
函数的连续性

函数的连续性
函数的连续性是指函数在定义域上的变化情况,其主要内容是有限性、连续性和可导性。
有限性的概念是指函数的解析可以是有限的,它可以用有限的表示法来描述。
例如,函数y = x^2 + 2x - 4的解析表示式就是一个有限的表达式。
有限性是理解函数特征的基础,而连续性是更进一步理解函数特征的手段。
连续性定义为:存在任意位置x0处,它的函数值y0(即
y=f(x0)=y0)与其附近的函数值的差别不会超过一定的正定值,当此附近的自变量值在x0处的改变量趋近于零时,此函数值
的改变量也趋近于零,我们就称该函数在x0处是连续的,写
成数学形式就是:lim (x→x0) f(x) = y0
可导性是连续性的强化,也就是说它综合考虑了函数的变化和变化量之间的关系,它是指函数在定义域上任意一点x处,只要自变量x存在可导的微分,就说明函数y有可导的前提。
可导性的表述方式就是不等式:|f(x1)-f(x2)| ≤ M|x1-x2|,即自变
量x1和x2之间的变化量应小于某个正常数M,函数值在x1
和x2之间的变化量应小于M |x1-x2|。
函数的连续性是数学分析中的基本概念,它与微积分的应用紧密相连。
它的概念很容易理解,但在实际应用中却要求解答者拥有较强的抽象意识和概括能力,因此学习和研究它的概念是非常重要的。
函数的连续性

第八讲 函数的连续性一、 函数的连续性客观世界许多现象都是连续变化的;比如时间的变化是连续的;所谓连续就是不间断;1、 函数连续的定义1引例:观察函数图像 y =x 2,y =1x ,y ={2x ,x ≤0x +1,x >0,y ={1,x ≠00,x =02 定义:设函数yfx 在点x 0 的某一个邻域内有定义若)()(lim 00x f x f x x =→ 则称函数yfx 在点x 0 处连续否则称函数fx 在点x 0不连续,点x 0为函数fx 的不连续点或间断点注 ① 0lim 0=∆→∆y x )()(lim 00x f x f x x =→ ②函数在点x 0连续的几何意义:函数的图形在x 0不断开;连续的实质是当自变量变化不大时,函数值变化也不大;2、左右连续性如果)()(lim 00x f x f x x =-→ 则称yfx 在点0x 处左连续 如果)()(lim 00x f x f x x =+→ 则称yfx 在点0x 处右连续 左右连续与连续的关系3、 函数在区间上的连续性在区间上每一点都连续的函数 叫做在该区间上的连续函数如果区间包括端点 那么函数在右端点连续是指左连续 在左端点连续是指右连续连续函数举例1 如果fx 是多项式函数 则函数fx 在区间 内是连续的2 函数y sin x 在区间 内是连续的二、函数的间断点的分类通常把间断点分成两类如果x 0是函数fx 的间断点左极限fx 00及右极限fx 00都存在 那么x 0称为函数fx 的第一类间断点其中左、右极限相等者称为可去间断点 不相等者称为跳跃间断点不是第一类间断点的任何间断点 称为第二类间断点例1 正切函数y tan x 在2 π=x 处没有定义 点2π=x 是函数tan x 的无穷间断点 例2 函数x y 1sin =在点x 0没有定义 所以点x 0是函数x1sin 的振荡间断点 例3 函数112--=x x y 在x 1没有定义点x 1是函数的可去间断点 例4 设函数⎪⎩⎪⎨⎧>+=<-=010 00 1)(x x x x x x f函数fx 的图形在x 0处产生跳跃现象 我们称x 0为函数fx 的跳跃间断点三、初等函数的连续性定理1 设函数fx 和gx 在点x 0连续 则函数 fxgx fxgx)()(x g x f 当0)(0≠x g 时在点x 0也连续 例1 sin x 和cos x 都在区间 内连续故tan x 和cot x 在它们的定义域内是连续的 定理2 设函数yfgx 由函数yfu 与函数ugx 复合而成 若函数ugx 在点x 0连续 函数yfu在点u 0gx 0连续 则复合函数yfx 在点x 0也连续例4 讨论函数xy 1sin =的连续性 解 函数x y 1sin =是由y sin u 及x u 1=复合而成的 sin u 当<u <时是连续的 x1当<x <0和0<x <时是连续的 函数x1sin 在无限区间 0和0 内是连续的 结论 基本初等函数在它们的定义域内都是连续的如果fx 是初等函数 且x 0是fx 的定义区间内的点则0lim x x →fxfx 0 例5 求201lim x x -→ 例6 求x x sin ln lim 2π→四、闭区间上连续函数的性质定理1最大值和最小值定理在闭区间上连续的函数在该区间上一定能取得它的最大值和最小值注意如果函数在开区间内连续或函数在闭区间上有间断点那么函数在该区间上就不一定有最大值或最小值定理2有界性定理在闭区间上连续的函数一定在该区间上有界零点如果x0使fx00 则x0称为函数fx的零点定理3零点定理设函数fx在闭区间a b上连续且fa与fb异号那么在开区间a b内至少有一点使f0例1 证明方程x 34x 210在区间0 1内至少有一个根定理4介值定理设函数fx在闭区间a b上连续且fafb那么对于fa与fb之间的任意一个数C在开区间a b内至少有一点使得fC推论在闭区间上连续的函数必取得介于最大值M与最小值m之间的任何值。
函数的连续性

二、初等函数的连续性
★ 三角函数及反三角函数在它们的定义域内是
连续的.
★ 指数函数 y a x
(a 0, a 1)
在( ,)内单调且连续;
★ 对数函数 y log a x
(a 0, a 1)
在(0,)内单调且连续 ;
14
★ y x
e
ln x
y e , u ln x.
证 f ( x )在x 0及其近旁有定义,且 f (0) 0,
1 0, 又 lim f ( x ) lim x sin x 0 x 0 x lim f ( x ) f (0) 0,
x 0
由定义1知,
函数 f ( x )在 x 0处连续.
6
3.单侧连续定义(定义2)
则复合函数 y f [ ( x )]在点 x x0也连续.
定理
若 lim ( x ) u0 , lim f ( u) A
x x0 u u0 x x0 u u0
则有 lim f [ ( x )] lim f ( u) A.
以上定理中的x x0换成x 等结论也成立
u
y x 在(0, )内连续;
讨论不同值, y x 均在其定义域内连续.
定理
定理
基本初等函数在定义域内是连续的.
一切初等函数在其定义区间内都是连续的.
注: 定义区间是指包含在定义域内的区间.
15
注意1. 初等函数仅在其定义区间内连续, 在其定义域内不一定连续; 例如,
y cos x 1,
显然这两个定义是等价的.讨论分段函数 在分界点处的连续性时,通常用定义1.
4
函数的连续性

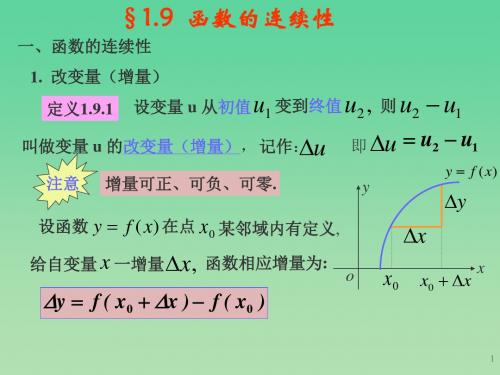
一、函数的连续性 对 y f x ,当自变量从 x0 变到 x ,称 x x x0 叫自变量 x 的增量,而
y f x x0 f x0 叫函数 y 的增量.
定义 设函数 y f x 在点 x0 的某一邻域内有定义, 如果当自变量的增量 x x x0 趋于零时, 对应的函数的增量 y f x x0 f x0 也趋于零, 那么就称函数 y f x 在 点 x0 连续. 它的另一等价定义是:设函数 y f x 在点 x0 的某一邻域内有定义,如果函数 f x 当
x x0 0
在点 x0 左连续.如果 lim f x f x0 0 存在且等于 f x0 ,即 f x0 0 f x0 ,
x x0 0
就说ቤተ መጻሕፍቲ ባይዱ数 f x 在点 x0 右连续. 在区间上每一点都连续的函数,叫做在该区间上的连续函数,或者说函数在该区间上连 续.如果区间包括端点,那么函数在右端点连续是指左连续,在左端点连续是指右连续. 连续函数的图形是一条连续而不间断的曲线.
������→������������
������������������ ������ ������ =f(������ ������ )
2、函数在点x0 处连续的充要条件是 f(x)在x0 处既左连续又右连续,且在x0 有定 义.即: ������������������−������ ������ = ������������������+ ������ ������ =f(������ ������ )
x x0 时的极限存在,且等于它在点 x0 处的函数值 f x0 ,即 lim f x f x0 ,那么就
函数的连续性

函数的连续性定义1 函数f 在点0x 的某邻域内有定义,若函数f 在点0x 有极限且此极限等于该点的函数值,即)()(lim 00x f x f x x =→,则称f 在点0x 连续 f 在点0x 连续必须满足三个条件:(1)在点0x 的一个邻域内有定义(2))(lim 0x f x x →存在 (3)上述极限值等于函数值)(0x f若上述条件有一个不满足,则点0x 就是函数f 的间断点。
等价定义1 函数f 在点0x 的某邻域内有定义,如果自变量的增量0x x x -=∆趋于零时,对应的函数增量也趋于零,即0)]()([lim lim 0000=-∆+=∆→∆→∆x f x x f y x x ,则称f 在点0x 是连续的在区间上每一点都连续的函数,称为在该区间上的连续函数,或说函数在该区间上连续,该区间也称为函数的连续区间。
若连续区间包括端点,那么函数在右端点连续是左连续,在左端点连续是右连续。
连续函数的图像是一条连续且不间断的曲线结论 f 在点0x 是连续当且仅当该点的函数值)(0x f 、左极限)0(0-x f 与右极限)0(0+x f 三者相等,即)0()()0(000+==-x f x f x f注 多项式函数,有理分式函数,正弦余弦函数在各自定义域连续间断点的分类设0x 是)(x f 的一个间断点,如果:(1))(x f 的左右极限都存在,称0x 为)(x f 第一类间断点,可分为可去型:)0()0(00+=-x f x f ,但)()(lim 00x f x f x x ≠→ 跳跃型:)0()0(00-≠+x f x f(2)左极限)0(0-x f 与右极限)0(0+x f 两者之中至少有一个不存在(无穷型间断点和振荡型间断点)例1 设⎩⎨⎧>+≤≤=1,110,)(2x x x x x f ,讨论)(x f 在1=x 处的连续性解 由于1)1(=f ,而-→1lim x )(x f =-→1lim x 2x =1,+→1lim x )(x f =+→1lim x (1+x )=2 因此1l i m →x )(x f 不存在,1=x 是第一类间断点,且为跳跃间断点。
函数的连续性

一、函数的连续性 二、函数的间断点
三、闭区间上连续函数的性质
首页
上页
返回
下页
结束
铃
一、函数的连续性
变量的增量
设函数y=f(x)在点x0的某一个邻域U(x0)内有定义 在邻域U(x0)内 若自变量x从初值x0变到终值x1 则称Dx=x1-x0为自变量x的增量 称Dy=f(x0+Dx)-f(x0)为函数y的增量
二、函数的间断点
y
y
f (x)在 x0 处无定义
O
x
0
x0
x
0
x0
y
f (x)在 x0 处无极限
O
x
0
x0
y
lim
xx0
f (x)
f
(x0 )
O
x
0
x0
二、函数的间断点
•间断点的定义
设函数 f(x)在点x0的某去心邻域内有定义 在此前提 下 如果函数 f(x)有下列三种情形之一
(1)在x0没有定义
这是因为 函数P(x)在(- +)内任意一点 x0处有定 义 并且
lim
x x0
P(
x)
=
P(x0
)
注: 如果区间包括端点 那么函数在右端点连续是指左连续
在左端点连续是指右连续
下页
连续函数
在区间上每一点都连续的函数 叫做在该区间上的 连续函数 或者说函数在该区间上连续
并且
f(0)=1>0 f(1)=-2<0
根据零点定理 在(0 1)内至少有一点x 使得 f(x)=0
即
x 3-4x 2+1=0
函数的连续性

x
定理6 一切初等函数在其定义区间内都是连续的.
定义区间是指包含在定义域内的区间.
注意 1. 初等函数仅在其定义区间内连续, 在 其定义域内不一定连续;
例如, y cos x 1, D {x | x 2k , k Z}
函数的连续性
一、函数的连续性 二、连续性原理 三、函数的间断点 四、闭区间上连续函数的性质
一、函数的连续性
1.函数的增量
设函数 f ( x)在U ( x0 )内有定义, x U ( x0 ), x x x0 , 称为自变量在点 x0的增量.
y f ( x) f ( x0 ),称为函数 f ( x)相应于x的增量.
又 f (0) 1 0, f (1) 2 0, 由零点定理,
3.第二类间断点
如果 f ( x) 在点 x0 处的左、右极限至 少有一个不存在, 则称点 x0 为函数 f ( x)的 第二类间断点.
例6
讨论函数
f
(x)
1 x
,
x 0,在x 0处的连续性.
x, x 0,
y
解 f (0 0) 0, f (0 0) ,
x 0为函数的第二类间断点.
上连续,且 f (a)与 f (b) 异号(即 f (a) f (b) 0 ),
那末在开区间a, b内至少有函数f ( x) 的一个零
点,即至少有一点 (a b),使 f () 0 .
即方程 f ( x) 0在(a, b)内至少存在一个实根 .
几何解释:
y
连续曲线弧 y f ( x)的两个 端点位于x轴的不同侧,则曲 a o
求 lim
函数的连续性
y y f x
a o
x b
17
例1.证明方程 x3 3x2 1 在(0,1)内至少有一个根. 证. 设 f (x) x3 3x2 1, f (x) C[0,1],
f (0) 1, f (1) 1, f (0) f (1) 0,
由零点定理知,在(0,1)内至少有一点 ,使得 f ( ) 0.
间断点的分类:
第一类间断点 ( 特点:左、右极限都存在 )
f f
( (
x0 x0
0) 0)
f ( x0 f ( x0
0 ), 0 ),
可去间断点; 跳跃间断点;
第二类间断点 (特点:左、右极限至少有一个不存在)
7
例4. 函数 f (x) 1 在x 0处无定义, 从而间断.
所以 f (x)在 x 0 处连续.
6
二、函数的间断点及其分类
f
(x) 在点x0
处连续.
12))..fli(mx0
) f
; (x)
;
3)
.
x x0
lim
x x0
f (x)
f ( x0 ).
以上三个条件只要有一条不满足,函数f (x) 在点 x0 处不连续. 即 f (x) 在点 x0 处间断, 并称 x0为函数f (x)的间断点.
10
定理1.9.2 (复合函数的连续性)
设函数 u g( x ) 在点 x x0 处连续, 函数 y f (u)在点u u0处连续, 则 函数 y f ( g( x )) 在点 x x0 处连续
g( x0 ) u0
lim f ( g( x )) f ( lim g( x ))
函数的连续性知识点及例题解析

函数的连续性知识点及例题解析1. 函数的连续性概念在数学中,函数的连续性指的是当自变量的值变化时,函数值的变化趋势和自变量的变化趋势相一致。
如果在某个区间内,函数在该区间的任意一点都存在极限,并且极限与该点的函数值相等,则称该函数在该区间内连续。
2. 函数的连续性条件函数f(x)在点x=a处连续的条件是:- 函数在点x=a处存在- 函数在点x=a处的左极限等于右极限- 函数在点x=a处的极限与函数在该点的函数值相等3. 函数的连续性的判定方法3.1 图像法:通过观察函数的图像来确定函数是否连续。
如果函数的图像没有跳跃、断裂或间断现象,那么该函数在相应区间内是连续的。
3.2 极限法:通过计算函数的极限来判定函数是否连续。
如果函数在某个点的极限存在并与函数在该点的函数值相等,则该函数在该点连续。
4. 函数的连续性例题解析例题1:考虑函数:\[ f(x) = \begin{cases} x+1, & \text{if } x \leq 0 \\ x-1, & \text{if } x > 0 \end{cases} \]问:函数f(x)在点x=0是否连续?解析:根据函数的定义可知,函数在x=0处存在极限,即\(\lim_{x\to0^-}f(x) = 0+1 = 1\)和\(\lim_{x\to0^+}f(x) = 0-1 = -1\)。
由于左极限和右极限不相等,所以函数在x=0处不连续。
例题2:考虑函数:\[ g(x) = \begin{cases} \sin(x), & \text{if } x \neq 0 \\ 1, & \text{if } x = 0 \end{cases} \]问:函数g(x)在点x=0是否连续?解析:根据函数的定义可知,函数在x=0处存在极限,即\(\lim_{x\to0}g(x) = \lim_{x\to0}\sin(x) = \sin(0) = 0\)。
函数的连续性

函数的连续性函数的连续性是数学中重要的一个概念,它描述了函数在某个点附近的表现。
连续性可以用来刻画函数的光滑程度和连贯性,对于分析和解决实际问题具有重要的意义。
本文将详细介绍函数的连续性以及相关的性质和定理。
1. 连续函数的定义与性质连续函数是指在定义域上的每一个点都具有连续性的函数。
具体而言,若函数f(x)在某一点x=a处的极限存在且与f(a)的函数值相等,那么函数f(x)在点x=a处连续。
连续函数具有以下重要性质:- 连续函数的和、差、积仍为连续函数;- 连续函数的复合函数仍为连续函数;- 有界闭区间上的连续函数一定存在最大值和最小值。
2. 初等函数的连续性初等函数是由常数函数、幂函数、指数函数、对数函数、三角函数、反三角函数等通过有限次的代数运算与函数复合得到的函数。
初等函数在其定义域上都是连续函数。
初等函数的连续性可以通过初等函数的定义和性质来证明。
以指数函数为例,指数函数f(x) = exp(x)在整个实数域上都是连续函数,因为它是由幂函数与以基数e为底的指数函数复合得到的。
3. 间断点与连续点函数可以在某些点上具有间断现象,这些点称为间断点。
间断点分为可去间断点、跳跃间断点和无穷间断点。
相应地,函数在某些点上具有连续性,这些点称为连续点。
可去间断点是指在该点处存在左极限和右极限,但极限值不相等。
通过修正函数在该点处的定义可以使其连续。
跳跃间断点是指在该点处左右极限存在且不相等,函数在该点处无法修正。
4. 连续函数的中值定理中值定理是连续函数的重要定理之一,它刻画了连续函数在某个区间上的平均增长率等于其两个端点处斜率之间某个值的关系。
根据中值定理,如果函数f(x)在闭区间[a,b]上连续,且可导于开区间(a,b)内,则存在一个点c∈(a,b),满足f(b)-f(a)=(b-a)f'(c)。
这个定理在微积分和实际问题的分析中有广泛的应用。
5. 连续函数的一致连续性一致连续性是连续函数的另一个重要性质,它描述了函数在整个定义域上的连续性。
函数的连续性

16
可 f ( x0 )无定义 去 lim lim 间 x x f ( x) x x f ( x) 第 0 0 断 f ( x0 )有定义,但 lim f ( x) f ( x0 ) 一 x x0 点 类 间 跳 断 跃 f ( x0 )有定义,但 lim f ( x) lim f ( x) 点 间 x x0 x x0 断 点 第 二 lim lim 类 x x0 f ( x)与 x x0 f ( x) 间 至少有一个不存在 断 点
无 穷 非 无 穷
x x0
lim f ( x)与 lim f ( x)
x x0
至少有一个为无穷
17
三、连续函数的性质
1、连续函数的四则运算 若函数 f (x), g (x) 在点 x0 连续,则
f ( x) f ( x)g ( x), f ( x) g ( x), ( g ( x0 ) 0) g ( x)
x 0
lim y 0
则称函数y f ( x)在 x0 点连续。
注:x x x0 , y f ( x) f ( x0 )或者y f ( x0 x) f ( x0 )
定义1 设函数y f ( x)在点 x0 的某领域内有定义, 若有
x x0
lim f ( x) f ( x0 )
8
解 (2)函数f(x)在x=1处有定义,且 f(1)=1
x 1
lim f ( x ) lim ( 2 x ) 1 ,
x 1
x 1
lim f ( x ) lim x 1 ,
x 1
因为当x→0时,f(x)的左﹑右极限存在且相等, 所以极限存在
lim f ( x ) 1 f (1)
函数的连续性(课件

函数在区间上的连续性
函数在区间上的连续性是指,对于该区间内的任意一点,函数在该点都连续。如 果一个函数在某个闭区间$[a, b]$内的每一点都连续,则称该函数在区间$[a, b]$ 上连续。
THANKS FOR WATCHING
感谢您的观看
闭区间上的连续函数满足中值定理, 即如果一个闭区间上的连续函数在两 端取值相等,则该函数在这个区间内 至少有一个不动点。
闭区间上的连续函数具有介值性质, 即如果一个闭区间上的连续函数在两 端取值异号,则该函数在这个区间内 至少有一个零点。
连续函数在无穷区间上的性质
连续函数在无穷区间上可以取到无穷大或无穷小 的值。
一致连续性
总结词
如果一个函数在其定义域内的任意两点x1 和x2,当x1趋近于x2时,函数值也趋近于 相同值,则称该函数一致连续。
VS
详细描述
一致连续性是连续函数的一个重要性质, 它表明函数在定义域内的任意两点之间的 变化都是均匀的。一致连续的函数在定义 域内不会出现剧烈的波动或间断,因此其 性质比较稳定。这个性质在解决一些数学 问题时也非常有用,例如求解函数的极限 等。
连续函数与不等式的关系
连续函数在定义域内的单调性可以用来证明不等 式。
3
利用连续函数证明不等式的方法
通过构造函数、利用函数的单调性、求导数等手 段,将不等式问题转化为连续函数的性质问题。
利用连续函数解决实际问题
实际问题的数学模型
实际问题通常需要建立数学模型进行描述和求解。
连续函数与实际问题的关系
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高等数学上册知识点一、 函数与极限 (一) 函数1、 函数定义及性质(有界性、单调性、奇偶性、周期性);2、 反函数、复合函数、函数的运算;3、 初等函数:幂函数、指数函数、对数函数、三角函数、反三角函数、双曲函数、反双曲函数; 4、 函数的连续性与间断点;函数)(x f 在0x 连续 )()(lim 00x f x f xx =→第一类:左右极限均存在.间断点 可去间断点、跳跃间断点 第二类:左右极限、至少有一个不存在. 无穷间断点、振荡间断点5、 闭区间上连续函数的性质:有界性与最大值最小值定理、零点定理、介值定理及其推论.(二) 极限 1、 定义 1) 数列极限εε<->∀N ∈∃>∀⇔=∞→a x N n N a x n n n , , ,0lim2) 函数极限εδδε<-<-<∀>∃>∀⇔=→A x f x x x A x f x x )( 0 , ,0 ,0)(lim 00时,当左极限:)(lim )(00x f x f x x -→-= 右极限:)(lim )(00x f x f xx +→+= )()( )(lim 000+-→=⇔=x f x f A x f x x 存在2、 极限存在准则 1) 夹逼准则: 1))(0n n z x y n n n ≥≤≤2)a z y n n n n ==→∞→∞lim lim a x n n =∞→lim2) 单调有界准则:单调有界数列必有极限. 3、 无穷小(大)量1) 定义:若0lim =α则称为无穷小量;若∞=αlim 则称为无穷大量. 2) 无穷小的阶:高阶无穷小、同阶无穷小、等价无穷小、k 阶无穷小 Th1)(~ααββαo +=⇔;Th2 αβαβαβββαα''=''''lim lim lim ,~,~存在,则(无穷小代换) 4、 求极限的方法 1) 单调有界准则; 2) 夹逼准则;3) 极限运算准则及函数连续性; 4) 两个重要极限:a) 1sin lim 0=→xx x b) e x x xx xx =+=++∞→→)11(lim )1(lim 10 5) 无穷小代换:(0→x ) a)x x x x x arctan ~arcsin ~tan ~sin ~b) 221~cos 1x x -c) x e x ~1- (a x a x ln ~1-) d) x x ~)1ln(+ (ax x a ln ~)1(log +)e) x x αα~1)1(-+二、 导数与微分 (一) 导数1、 定义:000)()(lim )(0x x x f x f x f x x --='→ 左导数:000)()(lim )(0x x x f x f x f x x --='-→-右导数:000)()(lim )(0x x x f x f x f x x --='+→+ 函数)(x f 在0x 点可导)()(00x f x f +-'='⇔2、 几何意义:)(0x f '为曲线)(x f y =在点())(,00x f x 处的切线的斜率.3、 可导与连续的关系:()f x 在0x 点可导 ⇒ ()f x 在0x 点连续4、 求导的方法1) 导数定义; 2) 基本公式; 3) 四则运算;4) 复合函数求导(链式法则); 5) 隐函数求导数; 6) 参数方程求导;7) 对数求导法. 5、 高阶导数1) 定义:⎪⎭⎫⎝⎛=dx dy dx d dx y d 22 2)Leibniz 公式:()∑=-=nk k n k k n n v u C uv 0)()()( (二) 微分1) 定义:)()()(00x o x A x f x x f y ∆+∆=-∆+=∆,其中A 与x ∆无关. 2) 可微与可导的关系:可微⇔可导,且dx x f x x f dy )()(00'=∆'=三、 微分中值定理与导数的应用 (一) 中值定理1、 Rolle 定理:若函数)(x f 满足:1)],[)(b a C x f ∈; 2)),()(b a D x f ∈; 3))()(b f a f =;则0)(),,(='∈∃ξξf b a 使.2、 Lagrange 中值定理:若函数)(x f 满足:1)],[)(b a C x f ∈; 2)),()(b a D x f ∈;则))(()()(),,(a b f a f b f b a -'=-∈∃ξξ使. 3、 Cauchy 中值定理:若函数)(),(x F x f 满足:1)],[)(),(b a C x F x f ∈; 2)),()(),(b a D x F x f ∈;3)),(,0)(b a x x F ∈≠' 则)()()()()()(),,(ξξξF f a F b F a f b f b a ''=--∈∃使(二) 洛必达法则1、尽量先化简(有理化、无穷小代换、分离非零因子)再用洛必达法则!:如:xxx x 420tan cos 1lim --→2、对于某些数列极限问题,可化为连续变量的极限,然后用洛必达法则!nnnn b a ⎪⎪⎭⎫⎝⎛+∞→2lim 如:(三) T aylor 公式n 阶Taylor 公式:10)1(00)(200000)()!1()()(!)( )(!2)())(()()(++-++-++-''+-'+=n n nn x x n f x x n x f x x x f x x x f x f x f ξξ在0x 与x 之间.当00=x 时,成为n 阶麦克劳林公式:1)1()(2)!1()(!)0(!2)0(!1)0()0()(++++++''+'+=n n n n x n f x n f x f x f f x f ξξ在0与x 之间.常见函数的麦克劳林公式:1)12)!1(!1!211+++++++=n n x x n e x n x x e ξξ在0与x 之间,+∞<<∞-x ;2)12121753)!12(2)12(sin )!12()1(!7!5!3sin +--+⎥⎦⎤⎢⎣⎡+++--++-+-=m m m x m m m x x x x x x πξξ在0与x 之间,+∞<<∞-x ;3)m m m x m m m x x x x x 2221642)!2(22cos )!22()1(!6!4!21cos ⎥⎦⎤⎢⎣⎡⋅++--++-+-=--πξ ξ在0与x 之间,+∞<<∞-x ;4)111432)1)(1()1()1(432)1ln(++-++-+-++-+-=+n n n n n n x n x x x x x x ξξ在0与x 之间,11<<-x5)nx n n x x x x !)1()1(!3)2)(1(!2)1(1)1(32+--++--+-++=+αααααααααα11)!1()1)(()1(+--++--+n n x n n αξααα ,ξ在0与x 之间,11<<-x .(四) 单调性及极值1、 单调性判别法:],[)(b a C x f ∈,),()(b a D x f ∈,则若0)(>'x f ,则)(x f单调增加;则若0)(<'x f ,则)(x f 单调减少.2、 极值及其判定定理:a) 必要条件:)(x f 在0x 可导,若0x 为)(x f 的极值点,则0)(0='x f . b) 第一充分条件:)(x f 在0x 的邻域内可导,且0)(0='x f ,则①若当0x x <时,0)(>'x f ,当0x x >时,0)(<'x f ,则0x 为极大值点;②若当0x x <时,0)(<'x f ,当0x x >时,0)(>'x f ,则0x 为极小值点;③若在0x 的两侧)(x f '不变号,则0x 不是极值点.c) 第二充分条件:)(x f 在0x 处二阶可导,且0)(0='x f ,0)(0≠''x f ,则①若0)(0<''x f ,则0x 为极大值点;②若0)(0>''x f ,则0x 为极小值点.3、 凹凸性及其判断,拐点1))(x f 在区间I 上连续,若2)()()2( ,,212121x f x f x x f I x x +<+∈∀,则称)(x f 在区间I 上的图形是凹的;若2)()()2( ,,212121x f x f x x f I x x +>+∈∀,则称)(x f 在区间I 上的图形是凸的.2)判定定理:)(x f 在],[b a 上连续,在),(b a 上有一阶、二阶导数,则 a) 若0)(),,(>''∈∀x f b a x ,则)(x f 在],[b a 上的图形是凹的; b) 若0)(),,(<''∈∀x f b a x ,则)(x f 在],[b a 上的图形是凸的.3)拐点:设)(x f y =在区间I 上连续,0x 是)(x f 的内点,如果曲线)(x f y =经过点))(,(00x f x 时,曲线的凹凸性改变了,则称点))(,(00x f x 为曲线的拐点. (五) 不等式证明1、 利用微分中值定理;2、 利用函数单调性;3、 利用极值(最值). (六) 方程根的讨论1、 连续函数的介值定理;2、 Rolle 定理;3、 函数的单调性;4、 极值、最值;5、 凹凸性. (七) 渐近线1、 铅直渐近线:∞=→)(lim x f ax ,则a x =为一条铅直渐近线; 2、 水平渐近线:b x f x =∞→)(lim ,则b y =为一条水平渐近线; 3、 斜渐近线:k xx f x =∞→)(lim b kx x f x =-∞→])([lim 存在,则b kx y +=为一条斜 渐近线.(八) 图形描绘 步骤 :1. 确定函数)(x f y =的定义域,并考察其对称性及周期性;2. 求)(),(x f x f '''并求出)(x f '及)(x f ''为零和不存在的点;3. 列表判别函数的增减及曲线的凹向 , 求出极值和拐点;4. 求渐近线;5. 确定某些特殊点, 描绘函数图形.四、 不定积分 (一) 概念和性质1、 原函数:在区间I 上,若函数)(x F 可导,且)()(x f x F =',则)(x F 称为)(x f 的一个原函数.2、 不定积分:在区间I 上,函数)(x f 的带有任意常数的原函数称为)(x f 在区间I 上的不定积分.3、 基本积分表(P188,13个公式);4、 性质(线性性).(二) 换元积分法1、 第一类换元法(凑微分):[])()(d )()]([x u du u f x x x f ϕϕϕ=⎰⎰='2、 第二类换元法(变量代换):[])(1d )()]([)(x t t t t f dx x f -='=⎰⎰ϕϕϕ(三) 分部积分法:⎰⎰-=vdu uv udv(四) 有理函数积分 1、“拆”;2、变量代换(三角代换、倒代换、根式代换等).五、 定积分 (一) 概念与性质:1、 定义:∑⎰=→∆=ni i i bax f dx x f 1)(lim )(ξλ2、 性质:(7条)性质7 (积分中值定理) 函数)(x f 在区间],[b a 上连续,则],[b a ∈∃ξ,使))(()(a b f dx x f ba-=⎰ξ (平均值:ab dx x f f ba-=⎰)()(ξ)(二) 微积分基本公式(N —L 公式) 1、 变上限积分:设⎰=Φxadt t f x )()(,则)()(x f x =Φ'推广:)()]([)()]([)()()(x x f x x f dt t f dx d x x ααβββα'-'=⎰ 2、 N —L 公式:若)(x F 为)(x f 的一个原函数,则)()()(a F b F dx x f ba-=⎰(三) 换元法和分部积分 1、 换元法:⎰⎰'=βαϕϕt t t f dx x f bad )()]([)(2、 分部积分法:[]⎰⎰-=babab a vdu uv udv (四) 反常积分 1、 无穷积分:⎰⎰+∞→+∞=tat a dx x f dx x f )(lim )( ⎰⎰-∞→∞-=btt bdx x f dx x f )(lim)(⎰⎰⎰+∞∞-+∞∞-+=0)()()(dx x f dx x f dx x f2、 瑕积分:⎰⎰+→=btat ba dx x f dx x f )(lim )((a 为瑕点)⎰⎰-→=tabt badx x f dx x f )(lim )((b 为瑕点)两个重要的反常积分:1) ⎪⎩⎪⎨⎧>-≤∞+=-∞+⎰1 ,11,d 1p p a p x x p a p 2) ⎪⎩⎪⎨⎧≥∞+<--=-=--⎰⎰1,1 ,1)()(d )(d 1q q q a b x b x a x x qb a q b a q六、 定积分的应用 (一) 平面图形的面积1、 直角坐标:⎰-=badx x f x fA )]()([122、 极坐标:⎰-=βαθθϕθϕd A )]()([212122(二) 体积1、 旋转体体积:a)曲边梯形x b x a x x f y ,,),(===轴,绕x 轴旋转而成的旋转体的体积:⎰=bax dx x f V )(2πb)曲边梯形x b x a x x f y ,,),(===轴,绕y 轴旋转而成的旋转体的体积:⎰=bay dx x xf V )(2π (柱壳法)2、 平行截面面积已知的立体:⎰=badx x A V )((三) 弧长1、 直角坐标:[]⎰'+=badx x f s 2)(12、 参数方程:[][]⎰'+'=βαφϕdt t t s 22)()( 3、 极坐标:[][]⎰'+=βαθθρθρd s 22)()(七、 微分方程 (一) 概念1、 微分方程:表示未知函数、未知函数的导数及自变量之间关系的方程. 阶:微分方程中所出现的未知函数的最高阶导数的阶数.2、 解:使微分方程成为恒等式的函数.通解:方程的解中含有任意的常数,且常数的个数与微分方程的阶数相同. 特解:确定了通解中的任意常数后得到的解.(二) 变量可分离的方程dx x f dy y g )()(=,两边积分⎰⎰=dx x f dy y g )()((三) 齐次型方程)(x y dx dy ϕ=,设x y u =,则dx dux u dx dy +=; 或)(y x dy dx φ=,设y x v =,则dydv y v dy dx += (四) 一阶线性微分方程)()(x Q y x P dxdy=+ 用常数变易法或用公式:⎥⎦⎤⎢⎣⎡+⎰⎰=⎰-C dx e x Q e y dx x P dxx P )()()((五) 可降阶的高阶微分方程1、)()(x f y n =,两边积分n 次; 2、),(y x f y '=''(不显含有y ),令p y =',则p y '='';3、),(y y f y '=''(不显含有x ),令p y =',则dy dpp y =''(六) 线性微分方程解的结构1、21,y y 是齐次线性方程的解,则2211y C y C +也是;2、21,y y 是齐次线性方程的线性无关的特解,则2211y C y C +是方程的通解;3、*2211y y C y C y ++=为非齐次方程的通解,其中21,y y 为对应齐次方程的线性无关的解,*y 非齐次方程的特解.(七) 常系数齐次线性微分方程二阶常系数齐次线性方程:0=+'+''qy y p y特征方程:02=++q pr r ,特征根: 21,r r(八) 常系数非齐次线性微分方程 )(x f qy y p y =+'+''1、)()(x P e x f m x λ=设特解)(*x Q e x y m x k λ=,其中⎪⎪⎩⎪⎪⎨⎧=是重根是一个单根不是特征根, λ, λ, λk 210 2、()x x P x x P e x f n l x ωωλsin )(cos )()(+=设特解[]xx R x x R e x y m m x k ωωλsin )(cos )()2()1(*+=,其中 } ,max{n l m =,⎪⎩⎪⎨⎧++=是特征根不是特征根i i k ωλωλ ,1 ,0。
