Excle做概率累计曲线粒度
excel粒径频率分布曲线

excel粒径频率分布曲线
Excel粒径频率分布曲线是一种用于展示颗粒物尺寸分布的统计图表。
它显示了粒径在不同范围内的颗粒物数量与其对应频率的关系。
创建Excel粒径频率分布曲线步骤如下:
1.准备数据表格,包含以下两列:粒径值和对应的颗粒物数量。
2.将数据表格按照粒径值从小到大排序。
3.计算每个粒径值对应的频率。
即,在表格中添加一列,计算每个粒
径值的数量占总数量的比例。
4.打开Excel并新建一个工作簿。
5.在工作簿中选择一个空白的单元格,并输入“粒径值”和“频率”
这两个文字标签。
6.将粒径值和对应频率的数据逐一输入到对应单元格中。
7.选中数据区域,包括“粒径值”和“频率”这两列,然后点击“插入”选项卡,并选择“散点图”(Scatter)。
选择“只有标记”(Markers Only)的样式。
8.将散点图中的水平轴替换成“粒径值”,并将垂直轴替换成“频率”。
9.在“设计”选项卡中,可以更改散点图的标题、轴标题和图例等元素。
10.最终,Excel粒径频率分布曲线就可以制成了。
您可以根据需要
对图表进行调整和美化,以使其更具有吸引力和可读性。
如何使用excel进行概率统计

数理统计实验1Excel基本操作1.1单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 和F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将2 乘以3(结果是6),然后再加上5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用5 加上2,再用其结果乘以3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从1 到65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列D 和行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮.C. 单击“函数”下拉列表框右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按ENTER 键.1.2几种常见的统计函数1.2.1均值Excel计算平均数使用AVERAGE函数,其格式如下:AVERAGE(参数1,参数2,…,参数30)范例:AVERAGE(12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用AVERAGE(A1:B20).1.2.2标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel计算样本标准差采用无偏估计式,STDEV函数格式如下:STDEV(参数1,参数2,…,参数30)范例:STDEV(3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP (参数1,参数2,…,参数30)范例:STDEVP (3,5,6,4,6,7,5)=1.251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用VAR 函数,格式如下:VAR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 VAR(A1:B20). 范例:VAR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用VARP 函数,格式如下:VARP (参数1,参数2,…,参数30)范例:VAR (3,5,6,4,6,7,5)=1.551.2.4 正态分布函数Excel 计算正态分布时,使用NORMDIST 函数,其格式如下:NORMDIST(变量,均值,标准差,累积)其中:变量(x):为分布要计算的x值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE,则为分布函数;若为FALSE,则为概率密度函数.范例:已知X服从正态分布,μ=600,σ=100,求P{X≤500}.输入公式=NORMDIST(500,600,100,TRUE)得到的结果为0.158655,即P{X≤500}=0.158655.1.2.5正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMINV函数,格式如下:NORMINV(下侧概率,均值,标准差)范例:已知概率P=0.841345,均值μ=360,标准差σ=40,求NORMINV函数的值.输入公式=NORMINV(0.841345,360,40)得到结果为400,即P{X≤400}=0.841345.注意:(1) NORMDIST函数的反函数NORMINV用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数NORMSDIST(x),及标准正态分布的反函数NORMSINV(概率).Φ=P{X<2}.输入公式范例:已知X~N(0,1), 计算(2)=NORMSDIST(2)Φ=0.97725.得到0.97725,即(2)范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值uα(n),则使用公式=NORMSINV(1-α).1.2.6t分布Excel计算t分布的值(查表值)采用TDIST函数,格式如下:TDIST(变量,自由度,侧数)其中:变量(t):为判断分布的数值;自由度(v):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T服从t(n-1)分布,样本数为25,求P(T>1.711).已知t=1.711,n=25,采用单侧,则T分布的值:=TDIST(1.711,24,1)得到0.05,即P(T>1.711)=0.05.若采用双侧,则T分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462.1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(2n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2αχ(n),则使用公式=CHIINV(α, n). 1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值.范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1 2已知时的置信区间 置信区间为22x u x u n n αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.131.15 1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.141.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米). 步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,=0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025). 2.1.2 2未知时的置信区间置信区间为 22((x t n x t n n n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) =average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5)) 计算结果为(1.133695, 1.172555).2.1.3未知时2的置信区间:置信区间为2222122(1)(1),(1)(1)n nn ns sααχχ-⎛⎫ ⎪--⎪--⎪⎝⎭.例3从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=VAR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当12 =22 =2但未知时1-2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭.例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.8 13.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=AVERAGE(A2:A6),在单元格B12中输入公式=AVERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=VAR(A2:A6),=VAR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限和上限.2.2.21和未知时方差比σ21/σ22的置信区间置信区间为22 112221221212211,(1,1)(1,1)s ss F n n s F n nαα-⎛⎫⎪⎪----⎪⎝⎭.例5有两个化验员A、B,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是SA=0.5419,SB=0.6065.设σ2A和σ2B分别是A、B所测量的数据总体(设为正态分布)的方差.求方差比σ2A/σ2B的0.95置信区间.操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A组和B组的方差比的置信区间上限和下限.2.3练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2, 23.3, 21.4,19.8, 18.3, 20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8, 27.1, 20.6, 25.0, 22.5,23.5, 23.9, 25.3, 23.5, 22.6, 21.5, 20.6, 25.8, 24.0, 23.5, 22.6, 21.8, 20.8, 19.5,20.9, 22.1, 22.7, 23.6, 24.5, 23.6, 21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8,21.7, 19.1, 20.3, 19.8试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区:62 57 65 60 63 58 57 60 60 58第二实验区:56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1单个正态总体均值μ的检验3.1.12已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:=800kg 有无显著变化.(1)若方差未变,本地平均产量μ与原产地的平均产量μ0(2)本地平均产量μ是否比原产地的平均产量μ=800kg高.0=800kg低.(3)本地平均产量μ是否比原产地的平均产量μ0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=AVERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U检验下侧的临界值=NORMSINV(0.05).3.1.22未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=AVERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1).欲检验假设H0:μ=250;H:μ>250.1已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t=2.093.由上面计算得025.0到t检验统计量的值1.06087落在接收域内,故接收原假设H0.3.2两个正态总体参数的假设检验3.2.1当12 =22 =2但未知时μ-μ的检验12在此情况下,采用t检验.例试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显著影响?欲检验假设H0:μ1=μ2;H:μ1>μ2.1操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组:91 88 76 98 94 92 90 87 100 69第2组:90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α =0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3两个正态总体的方差齐性的F检验例5羊毛在处理前与后分别抽样分析其含脂率如下:处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12问处理前后含脂率的标准差是否有显著差异?欲检验假设H0:σ21=σ22;H1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”.(4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显著水平“α”框,输入0.025. (8)在“输出区域”框输入D1. (9)选择“确定”,得到结果如图所示.计算出F 值2.35049小于“F 单尾临界”值5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i i n np np χ=-=∑, (11.1) i i n np k 其中为实测频数,为理论频数,为分组数。
excel累计曲线

excel累计曲线
Excel累计曲线是一种用于展示数据分布情况的图表,它将数据按照大小排序,并计算每个数据点所占的累积比例。
这种图表通常用于分析产品质量、客户满意度和市场份额等方面。
在Excel中绘制累计曲线需要进行以下步骤:
1. 将数据按照大小排序。
2. 计算每个数据点的累积比例。
3. 在数据表格中添加一个新的列,将每个数据点的累积比例填入该列。
4. 选中整个数据区域,点击“插入”菜单下的“图表”选项,选择“累计曲线图”,即可生成累计曲线图。
在生成的累计曲线图中,横坐标为数据的大小顺序,纵坐标为累积比例,曲线为根据数据计算出的累积比例曲线。
通过观察累计曲线图,可以直观地了解数据的分布情况,以及各个数据点在整体中所占的比例。
概率值累积粒度曲线流程

关于沉积相研究中粒度作图(石头)一、概率值累积粒度曲线流程:(X井为例)1、数据准备一般取到的数据是下面这种格式,首先将粒级中的<、>去掉,然后根据其值计算粒级Φ值,粒级Φ值=-log(粒级,2),得到粒级从负到正的一些列数据,然后根据小数取左值或右值。
然后整理成下面的格式保存成txt格式粒级Φ值 累积质量含量(%)-5 4.18-4 12.99-3 35.95-2 56.55-1 74.31-0.3 78.300 81.350.5 86.721 90.172 94.873 96.844 98.275 98.666 99.98然后就可以在grapher中作图了。
2、作图(1)准备数据体,X-粒度区间(左值或者是右值),Φ值;Y-累积重量百分比(2)打开Grapher,点击Graph→New Graph→Line/Simbol(3)Open worksheet,选定数据源,选定XY坐标(4)图形显示后,选定纵坐标,Scale→Probability(%Lable),Axis Limits→(0.0001,0.9999),Y轴即成为概率百分数标度。
(5)在成果图上如果想再加上另一条曲线,在刚才做出的曲线的整个图上点击,出现一个将坐标和数据点都包括其中的一个矩形,右键单击选择->Add plot,默认-》OK继续点ok,进入选择数据表对话框即可。
二、C-M图1、基础知识摘自(博研石油论坛)转帖][原创] 关于C-M图[转帖][原创] 关于C-M图C-M图是应用每个样品对C值和M值绘成的图形。
C值是积累曲线上颗粒含量1%处对应的粒径,M值是积累曲线使50%处对应的粒径。
C值与样品中最粗颗粒的粒径相当,代表了水动力搅动开始搬运的最大能量;M 值是中值,代表了水动力的平均能量。
为研究地层的沉积成因,需从该地层成因单元取得几十个样品,这些样品必须属于同一沉积环境的产物。
对于不同岩性要分别取样,而且样品要包括该单元由粗到细的全部粒度结构类型,几十个样品各按其C值、M值在图纸上投得一群点,按群点的分布绘出相应的图形,就是C-M图。
EXCEL2010制作颗粒级配曲线(图文说明)

Office制作颗粒级配曲线很方便:制作方法如下
1、随意选取一组数据如下:
粒径1006040201050.20.10.01
筛余%100897662524327197
2在excel2010中选中插入—散点图—带平滑线和数据标记点的散点图(第二个)
2、得到图形:
3、进行调整:
1调整纵坐标,鼠标双击纵坐标数字(或鼠标左键选中纵坐标数字右键—设置坐标轴格式)
修改“坐标轴选项”如下:
修改“线条颜色”改为:实线,颜色选择黑色;修改“线型”为0.25磅。
2调整横坐标,双击横坐标数字
修改坐标轴选项如下:
修改“线条颜色”改为:实线,颜色选择黑色;修改“线型”为0.25磅。
3修改曲线双击选中蓝色曲线依次修改如下:修改“数据标记选项”
修改数据标记填充:
修改“线条线条颜色”为实线黑色;修改“线型”宽度为1.25磅;
修改“标记颜色”为实线黑色;修改“标记线样式”为1磅。
得下图:
4修改图框,鼠标双击图框内部,菜单栏出现如下,在图表布局中选第三个;得到下图:
删除直线,鼠标选中改直线按delete键删除
修改线条,鼠标双击图框内中线条,“线型”全改为实线黑色
5修改坐标轴标题得下图:
完成!。
excel2010制作颗粒级配曲线(图文说明)

Office制作颗粒级配曲线很方便:制作方法如下
2、得到图形:
3、进行调整:
①调整纵坐标,鼠标双击纵坐标数字(或鼠标左键选中纵坐标数字右键—设置坐标轴格式)
修改“坐标轴选项”如下:
修改“线条颜色”改为:实线,颜色选择黑色;修改“线型”为0.25磅。
②调整横坐标,双击横坐标数字
修改坐标轴选项如下:
修改“线条颜色”改为:实线,颜色选择黑色;修改“线型”为0.25磅。
③修改曲线双击选中蓝色曲线依次修改如下:修改“数据标记选项”
修改数据标记填充:
修改“线条线条颜色”为实线黑色;修改“线型”宽度为1.25磅;
修改“标记颜色”为实线黑色;修改“标记线样式”为1磅。
得下图:
④修改图框,鼠标双击图框内部,菜单栏出现如下,在图表布局中选第三个;
得到下图:
删除直线,鼠标选中改直线按delete键删除
修改线条,鼠标双击图框内中线条,“线型”全改为实线黑色
⑤修改坐标轴标题得下图:
完成!。
excel中的概率统计(非常好的资料)

数理统计实验1Excel基本操作1.1 单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 和F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将 2 乘以3(结果是6),然后再加上5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用 5 加上2,再用其结果乘以3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从 1 到65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列D 和行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮 .C. 单击“函数”下拉列表框 右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按 ENTER 键.1.2 几种常见的统计函数1.2.1均值 Excel 计算平均数使用A VERAGE 函数,其格式如下:A VERAGE (参数1,参数2,…,参数30)范例:A VERAGE (12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用 A VERAGE(A1:B20).1.2.2 标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel 计算样本标准差采用无偏估计式,STDEV 函数格式如下:STDEV (参数1,参数2,…,参数30)范例:STDEV (3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用 STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP (参数1,参数2,…,参数30)范例:STDEVP (3,5,6,4,6,7,5)=1.251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用V AR 函数,格式如下:V AR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 V AR(A1:B20).范例:V AR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用V ARP 函数,格式如下:V ARP (参数1,参数2,…,参数30)范例:V AR (3,5,6,4,6,7,5)=1.551.2.4 正态分布函数Excel 计算正态分布时,使用NORMDIST 函数,其格式如下:NORMDIST (变量,均值,标准差,累积)其中:变量(x ):为分布要计算的x 值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE ,则为分布函数;若为FALSE ,则为概率密度函数.范例:已知X 服从正态分布,μ=600,σ=100,求P {X ≤500}.输入公式=NORMDIST (500,600,100,TRUE )得到的结果为0.158655,即P {X ≤500}=0.158655.1.2.5 正态分布函数的反函数Excel 计算正态分布函数的反函数使用NORMINV 函数,格式如下:NORMINV (下侧概率,均值,标准差)范例:已知概率P =0.841345,均值μ=360,标准差σ=40,求NORMINV 函数的值.输入公式=NORMINV (0.841345,360,40)得到结果为400,即P {X ≤400}=0.841345.注意:(1) NORMDIST 函数的反函数NORMINV 用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数 NORMSDIST(x),及标准正态分布的反函数 NORMSINV(概率).范例:已知X~N(0,1), 计算(2)Φ=P {X <2}.输入公式=NORMSDIST(2)得到0.97725,即(2)Φ=0.97725.范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值u α(n ),则使用公式=NORMSINV(1-α).1.2.6 t 分布Excel 计算t 分布的值(查表值)采用TDIST 函数,格式如下:TDIST (变量,自由度,侧数)其中:变量(t ):为判断分布的数值;自由度(v ):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T 服从t (n-1)分布,样本数为25,求P (T >1.711).已知t =1.711,n =25,采用单侧,则T 分布的值:=TDIST(1.711,24,1)得到0.05,即P (T >1.711)=0.05.若采用双侧,则T 分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462. 1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(2n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2αχ(n),则使用公式=CHIINV(α, n). 1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值. 范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1?2已知时?的置信区间 置信区间为22x u x u αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.131.15 1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.14 1.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米).步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显着性水平α和标准差σ是具体的数值而不是符号.本例中,? =0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025).2.1.2 ?2未知时?的置信区间置信区间为22((x t n x t n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))计算结果为(1.133695, 1.172555).2.1.3 ?未知时?2的置信区间:置信区间为 2222122(1)(1),(1)(1)n n n n s s ααχχ-⎛⎫ ⎪-- ⎪-- ⎪⎝⎭. 例3 从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间 (单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1当?12 =??22 =??2但未知时?1-?2的置信区间置信区间为()122(2) x y t n n Sα⎛-±+-⎝.例4在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.813.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=A VERAGE(A2:A6),在单元格B12中输入公式=A VERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=V AR(A2:A6),=V AR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显着性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限和上限.2.2.2 ?1和??未知时方差比σ21/σ22的置信区间置信区间为 22112221221212211,(1,1)(1,1)s s s F n n s F n n αα-⎛⎫ ⎪ ⎪---- ⎪⎝⎭ . 例5 有两个化验员A 、B ,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是S A =0.5419,S B =0.6065.设σ2A 和σ2B 分别是A 、B 所测量的数据总体(设为正态分布)的方差.求方差比σ2A /σ2B 的 0.95置信区间.操作步骤: (1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A 组和B 组的方差比的置信区间上限和下限.2.3 练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2, 23.3, 21.4, 19.8, 18.3,20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8, 27.1, 20.6, 25.0, 22.5, 23.5, 23.9, 25.3, 23.5,22.6, 21.5, 20.6, 25.8, 24.0, 23.5, 22.6, 21.8, 20.8, 19.5, 20.9, 22.1, 22.7, 23.6, 24.5, 23.6,21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8, 21.7, 19.1, 20.3, 19.8试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区:62 57 65 60 63 58 57 60 60 58第二实验区:56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1 单个正态总体均值μ的检验3.1.1 2已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:(1)若方差未变,本地平均产量μ与原产地的平均产量μ=800kg 有无显着变化.0=800kg高.(2)本地平均产量μ是否比原产地的平均产量μ0=800kg低.(3)本地平均产量μ是否比原产地的平均产量μ0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=A VERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显着差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U 检验下侧的临界值=NORMSINV(0.05).3.1.2?2未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显着性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=A VERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1).欲检验假设H0:μ=250;H:μ>250.1已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t=2.093.由上面计算得到t.0025检验统计量的值1.06087落在接收域内,故接收原假设H0.3.2 两个正态总体参数的假设检验μ-μ的检验3.2.1当?12 =??22 =??2但未知时12在此情况下,采用t检验.例试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显着影响?欲检验假设:μ1>μ2.H0:μ1=μ2;H1操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显着水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显着影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组:91 88 76 98 94 92 90 87 100 69第2组:90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α =0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显着水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3两个正态总体的方差齐性的F检验例5羊毛在处理前与后分别抽样分析其含脂率如下:处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12问处理前后含脂率的标准差是否有显着差异?欲检验假设H0:σ21=σ22;H1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”. (4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显着水平“α”框,输入0.025. (8)在“输出区域”框输入D1. (9)选择“确定”,得到结果如图所示.计算出F 值2.35049小于“F 单尾临界”值5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i i n np np χ=-=∑, (11.1) i i n np k 其中为实测频数,为理论频数,为分组数。
excel中的概率统计(非常好的资料)

数理统计实验1Excel基本操作1.1 单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 和F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将 2 乘以3(结果是6),然后再加上5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用 5 加上2,再用其结果乘以3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从1 到65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列D 和行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮 .C. 单击“函数”下拉列表框 右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按 ENTER 键.1.2 几种常见的统计函数1.2.1均值 Excel 计算平均数使用A VERAGE 函数,其格式如下:A VERAGE (参数1,参数2,…,参数30)范例:A VERAGE (12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用 A VERAGE(A1:B20).1.2.2 标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel 计算样本标准差采用无偏估计式,STDEV 函数格式如下:STDEV (参数1,参数2,…,参数30)范例:STDEV (3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用 STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP (参数1,参数2,…,参数30)范例:STDEVP (3,5,6,4,6,7,5)=1.251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用V AR 函数,格式如下:V AR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 V AR(A1:B20).范例:V AR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用V ARP 函数,格式如下:V ARP (参数1,参数2,…,参数30)范例:V AR (3,5,6,4,6,7,5)=1.551.2.4 正态分布函数Excel 计算正态分布时,使用NORMDIST 函数,其格式如下:NORMDIST (变量,均值,标准差,累积)其中:变量(x ):为分布要计算的x 值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE ,则为分布函数;若为FALSE ,则为概率密度函数.范例:已知X 服从正态分布,μ=600,σ=100,求P {X ≤500}.输入公式=NORMDIST (500,600,100,TRUE )得到的结果为0.158655,即P {X ≤500}=0.158655.1.2.5 正态分布函数的反函数Excel 计算正态分布函数的反函数使用NORMINV 函数,格式如下:NORMINV (下侧概率,均值,标准差)范例:已知概率P =0.841345,均值μ=360,标准差σ=40,求NORMINV 函数的值.输入公式=NORMINV (0.841345,360,40)得到结果为400,即P {X ≤400}=0.841345.注意:(1) NORMDIST 函数的反函数NORMINV 用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数 NORMSDIST(x),及标准正态分布的反函数 NORMSINV(概率).范例:已知X~N(0,1), 计算(2)Φ=P {X <2}.输入公式=NORMSDIST(2)得到0.97725,即(2)Φ=0.97725.范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值u α(n ),则使用公式=NORMSINV(1-α).1.2.6 t 分布Excel 计算t 分布的值(查表值)采用TDIST 函数,格式如下:TDIST (变量,自由度,侧数)其中:变量(t ):为判断分布的数值;自由度(v ):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T 服从t (n-1)分布,样本数为25,求P (T >1.711).已知t =1.711,n =25,采用单侧,则T 分布的值:=TDIST(1.711,24,1)得到0.05,即P (T >1.711)=0.05.若采用双侧,则T 分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462. 1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(2n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2αχ(n),则使用公式=CHIINV(α, n). 1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值. 范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1?2已知时?的置信区间 置信区间为22x u x u αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.131.15 1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.14 1.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米).步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显着性水平α和标准差σ是具体的数值而不是符号.本例中,? =0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025).2.1.2 ?2未知时?的置信区间置信区间为22((x t n x t n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))计算结果为(1.133695, 1.172555).2.1.3 ?未知时?2的置信区间:置信区间为 2222122(1)(1),(1)(1)n n n n s s ααχχ-⎛⎫ ⎪-- ⎪-- ⎪⎝⎭. 例3 从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间 (单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1当?12 =??22 =??2但未知时?1-?2的置信区间置信区间为()122(2) x y t n n Sα⎛-±+-⎝.例4在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.813.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=A VERAGE(A2:A6),在单元格B12中输入公式=A VERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=V AR(A2:A6),=V AR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显着性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限和上限.2.2.2 ?1和??未知时方差比σ21/σ22的置信区间置信区间为 22112221221212211,(1,1)(1,1)s s s F n n s F n n αα-⎛⎫ ⎪ ⎪---- ⎪⎝⎭ . 例5 有两个化验员A 、B ,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是S A =0.5419,S B =0.6065.设σ2A 和σ2B 分别是A 、B 所测量的数据总体(设为正态分布)的方差.求方差比σ2A /σ2B 的 0.95置信区间.操作步骤: (1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A 组和B 组的方差比的置信区间上限和下限.2.3 练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2, 23.3, 21.4, 19.8, 18.3,20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8, 27.1, 20.6, 25.0, 22.5, 23.5, 23.9, 25.3, 23.5,22.6, 21.5, 20.6, 25.8, 24.0, 23.5, 22.6, 21.8, 20.8, 19.5, 20.9, 22.1, 22.7, 23.6, 24.5, 23.6,21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8, 21.7, 19.1, 20.3, 19.8试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区:62 57 65 60 63 58 57 60 60 58第二实验区:56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1 单个正态总体均值μ的检验3.1.1 2已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:(1)若方差未变,本地平均产量μ与原产地的平均产量μ=800kg 有无显着变化.0=800kg高.(2)本地平均产量μ是否比原产地的平均产量μ0=800kg低.(3)本地平均产量μ是否比原产地的平均产量μ0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=A VERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显着差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U 检验下侧的临界值=NORMSINV(0.05).3.1.2?2未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显着性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=A VERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1).欲检验假设H0:μ=250;H:μ>250.1已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t=2.093.由上面计算得到t.0025检验统计量的值1.06087落在接收域内,故接收原假设H0.3.2 两个正态总体参数的假设检验μ-μ的检验3.2.1当?12 =??22 =??2但未知时12在此情况下,采用t检验.例试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显着影响?欲检验假设:μ1>μ2.H0:μ1=μ2;H1操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显着水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显着影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组:91 88 76 98 94 92 90 87 100 69第2组:90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α =0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显着水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3两个正态总体的方差齐性的F检验例5羊毛在处理前与后分别抽样分析其含脂率如下:处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12问处理前后含脂率的标准差是否有显着差异?欲检验假设H0:σ21=σ22;H1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”. (4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显着水平“α”框,输入0.025. (8)在“输出区域”框输入D1. (9)选择“确定”,得到结果如图所示.计算出F 值2.35049小于“F 单尾临界”值5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i i n np np χ=-=∑, (11.1) i i n np k 其中为实测频数,为理论频数,为分组数。
excel中的概率统计(非常好的资料).

数理统计实验1Excel基本操作1.1 单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 和F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将 2 乘以3(结果是6),然后再加上5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用 5 加上2,再用其结果乘以3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从 1 到65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列D 和行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮 .C. 单击“函数”下拉列表框 右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按 ENTER 键.1.2 几种常见的统计函数1.2.1均值 Excel 计算平均数使用A VERAGE 函数,其格式如下:A VERAGE (参数1,参数2,…,参数30)范例:A VERAGE (12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用 A VERAGE(A1:B20).1.2.2 标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel 计算样本标准差采用无偏估计式,STDEV 函数格式如下:STDEV (参数1,参数2,…,参数30)范例:STDEV (3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用 STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP (参数1,参数2,…,参数30)范例:STDEVP (3,5,6,4,6,7,5)=1.251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用V AR 函数,格式如下:V AR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 V AR(A1:B20).范例:V AR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用V ARP 函数,格式如下:V ARP (参数1,参数2,…,参数30)范例:V AR (3,5,6,4,6,7,5)=1.551.2.4 正态分布函数Excel 计算正态分布时,使用NORMDIST 函数,其格式如下:NORMDIST (变量,均值,标准差,累积)其中:变量(x ):为分布要计算的x 值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE ,则为分布函数;若为FALSE ,则为概率密度函数.范例:已知X 服从正态分布,μ=600,σ=100,求P {X ≤500}.输入公式=NORMDIST (500,600,100,TRUE )得到的结果为0.158655,即P {X ≤500}=0.158655.1.2.5 正态分布函数的反函数Excel 计算正态分布函数的反函数使用NORMINV 函数,格式如下:NORMINV (下侧概率,均值,标准差)范例:已知概率P =0.841345,均值μ=360,标准差σ=40,求NORMINV 函数的值.输入公式=NORMINV (0.841345,360,40)得到结果为400,即P {X ≤400}=0.841345.注意:(1) NORMDIST 函数的反函数NORMINV 用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数 NORMSDIST(x),及标准正态分布的反函数 NORMSINV(概率).范例:已知X~N(0,1), 计算(2)Φ=P {X <2}.输入公式=NORMSDIST(2)得到0.97725,即(2)Φ=0.97725.范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值u α(n ),则使用公式=NORMSINV(1-α).1.2.6 t 分布Excel 计算t 分布的值(查表值)采用TDIST 函数,格式如下:TDIST (变量,自由度,侧数)其中:变量(t ):为判断分布的数值;自由度(v ):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T 服从t (n-1)分布,样本数为25,求P (T >1.711).已知t =1.711,n =25,采用单侧,则T 分布的值:=TDIST(1.711,24,1)得到0.05,即P (T >1.711)=0.05.若采用双侧,则T 分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462.1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2χ(n),则使用公式=CHIINV(α, n).1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值. 范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1σ2已知时μ的置信区间 置信区间为22x u x u αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.131.15 1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.14 1.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米).步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,α =0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025).2.1.2 σ2未知时μ的置信区间置信区间为22((x t n x t n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))计算结果为(1.133695, 1.172555).2.1.3 μ未知时σ2的置信区间:置信区间为 2222122(1)(1),(1)(1)n n n n s s ααχχ-⎛⎫ ⎪-- ⎪-- ⎪⎝⎭. 例3 从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当σ12 = σ22 = σ2但未知时μ1-μ2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭. 例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.8 13.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=A VERAGE(A2:A6),在单元格B12中输入公式=A VERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=V AR(A2:A6),=V AR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7) 计算出置信区间的下限和上限.2.2.2μ1和μ2未知时方差比σ21/σ22的置信区间置信区间为22 112221221212211,(1,1)(1,1)s ss F n n s F n nαα-⎛⎫⎪⎪----⎪⎝⎭.例5有两个化验员A、B,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是SA=0.5419,SB=0.6065.设σ2A和σ2B分别是A、B所测量的数据总体(设为正态分布)的方差.求方差比σ2A/σ2B的0.95置信区间.操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A组和B组的方差比的置信区间上限和下限.2.3 练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2, 23.3, 21.4, 19.8, 18.3,20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8, 27.1, 20.6, 25.0, 22.5, 23.5, 23.9, 25.3, 23.5,22.6, 21.5, 20.6, 25.8, 24.0, 23.5, 22.6, 21.8, 20.8, 19.5, 20.9, 22.1, 22.7, 23.6, 24.5, 23.6,21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8, 21.7, 19.1, 20.3, 19.8试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区:62 57 65 60 63 58 57 60 60 58第二实验区:56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1 单个正态总体均值μ的检验3.1.1 2已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:=800kg 有无显著变化.(1)若方差未变,本地平均产量μ与原产地的平均产量μ0=800kg高.(2)本地平均产量μ是否比原产地的平均产量μ0=800kg低.(3)本地平均产量μ是否比原产地的平均产量μ0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=A VERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U 检验下侧的临界值=NORMSINV(0.05).3.1.2 2未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=A VERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1).欲检验假设:μ>250.H0:μ=250;H1已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t=2.093.由上面计算得到t025.0检验统计量的值1.06087落在接收域内,故接收原假设H0.3.2 两个正态总体参数的假设检验μ-μ的检验3.2.1当σ12 = σ22 = σ2但未知时12在此情况下,采用t检验.例试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显著影响?欲检验假设:μ1>μ2.H0:μ1=μ2;H1操作步骤:(1)(2)(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组:91 88 76 98 94 92 90 87 100 69第2组:90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α =0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3 两个正态总体的方差齐性的F检验例5 羊毛在处理前与后分别抽样分析其含脂率如下: 处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12 问处理前后含脂率的标准差是否有显著差异? 欲检验假设H 0:σ21=σ22; H 1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”. (4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显著水平“α”框,输入0.025. (8)在“输出区域”框输入D1. (9)选择“确定”,得到结果如图所示.计算出F 值2.35049小于“F 单尾临界”值5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i in np np χ=-=∑, (11.1) i i n np k 其中为实测频数,为理论频数,为分组数。
excel中的概率统计(非常好的资料)

excel中的概率统计(非常好的资料)数理统计实验1Excel基本操作1.1 单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.21.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后3在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 和F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为411,将 2 乘以3(结果是6),然后再加上5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用 5 加上2,再用其结果乘以3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从 A 到IV ,5共256 列),用数字标志行(从 1 到65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列 D 和行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.单元格引用范围引用符号在列 A 和行10 中的单元A10 格A10:A20 属于列 A 和行10 到行20中的单元格区域属于行15 和列 B 到列 EB15:E15 中的单元格区域A10:E20 从列 A 行10 到列E行20的矩形区域中的单元格行 5 中的所有单元格5:55:10 从行 5 到行10 中的所有单元格6列H 中的所有单元格H:HH:J 从列H 到列J 中的所有单元格1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编7辑栏中单击“编辑公式”按钮.C. 单击“函数”下拉列表框右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按ENTER 键.1.2 几种常见的统计函数1.2.1均值Excel计算平均数使用A VERAGE函数,其格式如下:A VERAGE(参数1,参数2,…,参数30)范例:A VERAGE (12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用A VERAGE(A1:B20).1.2.2标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称8作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel计算样本标准差采用无偏估计式,STDEV函数格式如下:STDEV(参数1,参数2,…,参数30)范例:STDEV(3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用STDEV(A1:B20).(2)总体标准差Excel计算总体标准差采用有偏估计式STDEVP函数,其格式如下:STDEVP(参数1,参数2,…,参数30)范例:STDEVP(3,5,6,4,6,7,5)=1.251.2.3方差方差为标准差的平方,在统计上亦分样本910 方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用V AR 函数,格式如下:V AR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 V AR(A1:B20).范例:V AR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用V ARP 函数,格式如下:V ARP (参数1,参数2,…,参数30)范例:V AR (3,5,6,4,6,7,5)=1.551.2.4正态分布函数Excel计算正态分布时,使用NORMDIST函数,其格式如下:NORMDIST(变量,均值,标准差,累积)其中:变量(x):为分布要计算的x值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE,则为分布函数;若为FALSE,则为概率密度函数.范例:已知X服从正态分布,μ=600,σ=100,求P{X≤500}.输入公式=NORMDIST(500,600,100,TRUE)得到的结果为0.158655,即P{X≤500}=0.158655.1.2.5正态分布函数的反函数Excel计算正态分布函数的反函数使用NORMINV函数,格式如下:NORMINV(下侧概率,均值,标准差)范例:已知概率P=0.841345,均值μ=360,标准差σ=40,求NORMINV函数的值.输入公式=NORMINV(0.841345,360,40)得到结果为400,即P{X≤400}=0.841345.注意:(1) NORMDIST函数的反函数NORMINV用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数NORMSDIST(x),及标准正态分布的反函数NORMSINV(概率).范例:已知X~N(0,1), 计算Φ=P{X<2}.输入公式(2)=NORMSDIST(2)得到0.97725,即(2)Φ=0.97725.范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值uα(n),则使用公式=NORMSINV(1-α).1.2.6t分布Excel计算t分布的值(查表值)采用TDIST函数,格式如下:TDIST(变量,自由度,侧数)其中:变量(t):为判断分布的数值;自由度(v):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T服从t(n-1)分布,样本数为25,求P(T>1.711).已知t=1.711,n=25,采用单侧,则T分布的值:=TDIST(1.711,24,1)得到0.05,即P(T>1.711)=0.05.若采用双侧,则T分布的值:=TDIST(1.711,24,2)得到0.1,即()P T>=.1.7110.11.2.7t分布的反函数Excel使用TINV函数得到t分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式 =TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462.1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度; 自由度2(2n ):代表第2个样本的自由度. 范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n ,格式为: FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897. 若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)=5.226.若求临界值2αχ(n),则使用公式=CHIINV(α, n).1.2.12泊松分布计算泊松分布使用POISSON函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE,为泊松分布函数值;若FALSE,则为泊松分布概率分布值.范例:设X服从参数为4的泊松分布,计算P{X=6}及P{X≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT,开平方函数SQRT,和函数SUM,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1σ2已知时μ的置信区间 置信区间为22x u x u n n αα⎛⎫-+ ⎝.例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.13 1.151.20 1.12 1.17 1.19 1.15 1.12 1.141.20 1.23 1.11 1.14 1.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米).步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,α =0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025).2.1.2 σ2未知时μ的置信区间置信区间为 22((x t n x t n n n αα⎛⎫--+- ⎝.例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))计算结果为(1.133695, 1.172555).2.1.3 μ未知时σ2的置信区间:置信区间为 2222122(1)(1),(1)(1)n n n n s s ααχχ-⎛⎫ ⎪-- ⎪-- ⎪⎝⎭.例3 从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.466.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2,count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2,count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1 当σ12 = σ22 = σ2但未知时μ1-μ2的置信区间置信区间为 ()1212211(2)w x y t n n S n n α⎛⎫-±+-+ ⎪ ⎪⎝⎭.例4 在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.8 13.0乙:13.1 13.4 12.8 13.5 13.3 12.712.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=A VERAGE(A2:A6),在单元格B12中输入公式=A VERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=V AR(A2:A6),=V AR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6* C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6* C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限和上限.2.2.2 μ1和μ2未知时方差比σ21/σ22的置信区间置信区间为 22112221221212211,(1,1)(1,1)s s s F n n s F n n αα-⎛⎫ ⎪ ⎪---- ⎪⎝⎭ .例5 有两个化验员A 、B ,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是S A=0.5419,S B =0.6065.设σ2A 和σ2B分别是A 、B 所测量的数据总体(设为正态分布)的方差.求方差比σ2A /σ2B的 0.95置信区间. 操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A组和B组的方差比的置信区间上限和下限.2.3 练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2, 23.3, 21.4, 19.8, 18.3, 20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8, 27.1, 20.6, 25.0, 22.5, 23.5, 23.9, 25.3, 23.5, 22.6, 21.5, 20.6, 25.8, 24.0, 23.5, 22.6, 21.8, 20.8, 19.5, 20.9, 22.1, 22.7, 23.6, 24.5, 23.6,21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8, 21.7, 19.1, 20.3, 19.8试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区:62 57 65 60 63 58 57 60 60 58第二实验区:56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1 单个正态总体均值μ的检验3.1.1 2已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:(1)若方差未变,本地平均产量μ与原产地的平均产量μ0=800kg 有无显著变化.(2)本地平均产量μ是否比原产地的平均产量μ0=800kg 高.(3)本地平均产量μ是否比原产地的平均产量μ0=800kg 低.操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=A VERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U 检验的下侧临界值,在单元格D11输入U检验下侧的临界值=NORMSINV(0.05).3.1.2 2未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255236 245 261254 256 246 242 247 256 258259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=A VERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1).欲检验假设H0:μ=250;H1:μ>250.已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t >t 025.0 =2.093.由上面计算得到t 检验统计量的值1.06087落在接收域内,故接收原假设H 0.3.2 两个正态总体参数的假设检验3.2.1当σ12 = σ22 = σ2但未知时12μ-μ的检验 在此情况下,采用t 检验.例 试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显著影响? 欲检验假设H 0:μ1=μ2;H 1:μ1>μ2. 操作步骤:(1) 建立如图所示工作表: 甲方乙方t-检验: 双样本等方差假设62565759甲方乙方6556平均60576057方差7.111111112.666666676358观测值10105857合并方差 4.888888895760假设平均差06055df 186057t Stat 3.033899385855P(T<=t) 单尾0.00356934t 单尾临界1.73406359P(T<=t) 双尾0.00713869t 双尾临界2.10092204(2)选取“工具”—“数据分析”;(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为 3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组:91 88 76 98 94 92 90 87 100 69第2组:90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α=0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3两个正态总体的方差齐性的F检验例5羊毛在处理前与后分别抽样分析其含脂率如下:处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12问处理前后含脂率的标准差是否有显著差异?欲检验假设H 0:σ21=σ22;H1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“F-检验双样本方差”.(4)选择“确定”,显示一个“F-检验:双样本方差”对话框;(5)在“变量1的区域”输入A2:A8.(6)在“变量2的区域”输入B2:B9.(7)在显著水平“α”框,输入0.025.(8)在“输出区域”框输入D1.(9)选择“确定”,得到结果如图所示.计算出F值2.35049小于“F单尾临界”值5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()k i i i i n np np χ=-=∑, (11.1)i i n np k 其中为实测频数,为理论频数,为分组数。
(完整版)用excel画颗粒级配曲线

exceI中颗粒级配曲线的画法首先,将粒径以及小于某粒径的土所占的分数填在excel然后将数据全部选中点击菜单栏的插入选项,在下拉菜单中选择图表,出现如图界面选XY 散点图,在右侧字表图类型中选择第三个,即无数据点平滑散点图回BlJ45LO1213 1438I*SM接下来点击下hi V 卜卜 \Sh^tl 12 /ihefi 1J_/ffl] W (I ) 謁sfi© 视雨灼 肉入⑴ 蒂式① 丁且⑴ 聃糕⑪ 同□吐1 稠创血口也90瓦丨爭島E - il il 營孕l (m0.002*壮典=aj'i&1栓径【irn :2水亍某粒径的土萨占分数(X 子 E^KSll?-比誌花用平亡统单忙 ]十咸叩|桜堆类型自电乂类里.E^K31<£:- 血柱廉閱 H 議孫图 克折犠51°馆闻L U R S I◎圆环期 歯r 窑低测 解曲肖甜色文肾Q 綁楊⑴ 視图电)殒入「格式Q)工貝① 数免迎窗口⑩ WQI)I》©I為吐治231 诞入.需要菸就的问盪粒包(nm)J2小丁莫粒径的土所占分数的)阿3q5679101112131516171819202122232425262728293031K > M \ Sixestl/Slice (2/ SLise 13/点克士艺我I—f I畠据区域系列飲拓凶域Q)糸列产生E•吨•貝JIL)0.25HL数字C6.5;°81 2」2K«/s * A审嚮LOssU KJ fl -35>1t EXC... UL-]闵I 塞J圭和=3蛙.的T靈宇在 标 题 中 输 入 图 表 标 题, X 轴 Y 轴 标 示 量, 选 中 网 格 线 选 项 卡A 弓 C D E FC HIJ KLNP1 粒症CirnL 20.2i C.l临0.02 <LU 】O(KJ> C.(K2 2 3 屮于某粒胫吃土听疔分数 0 1W75.7 6L5 413 2b.i1610>934 £/1 g CHF\I 刃"TB L ]| w 7 u =RT hE.'t ' f 仝 ;邑|丈件巴 骗槓② 训囚叩 ffiA© W IflO? wJT 丙口世 命防⑧■ J J ,. J . 且爺屯二F /|吟・卩・|靠乞”訂訂|・・10 11 12 13 iq 15 16 17 L819 20訂稼塞:坐彌]剛a 戦|酮 ]掘毎鈕 矍耒标範a谿a 忧料⑧ 梢罡(mm ) 過伯[Ylfttlf ]于于英粒垃的土所占的分澈go n■tta—K 上Ta/23劄25茨27h21 22 is§-T^28卜M \riicctL X jhicti! /Skt e -3/文杵① 編轲⑥ 探司密 陌入9 格式g 二辰① SS1)童口型 帮動③ 存工丢手秆汁曲訂•」弓3垮9 申IA 黔CI '召>»*“"• e 艺•斡列塑F 小曲 •前伽皿厘 < 105 < B / U 辜兰W 虽镇%,協鹦=Qi Dfl .fl 7^1TAB | 匚DEF~GHIJ厂L M W 0 P T |数字 ¥ 阴科 | 诅JflS h .■ - .ftExc.,tf 5 -na粒任jnri)<|叶其粒栓的土加占分數(>)7a J_ 1117.13 / 15 L& _7 IS为21 21 22 23 24 25 26 27 ?8 29 3U 31.I* « 卜 H \ Shes 11 / jkeelS/SliEe-tOy100 75.7 51.5 41.316 102grsM^qi:W 次要冋槪u : 空苗附诩 団主雯冋格蛭0.02I —站川r 坐纭擾0.)1CJO5,都打上对号,然后直接点完成,记得到大致曲线。
cm图绘制

请教大家,在excel中能否绘制粒度概率曲线和C-M图?如果能,具体怎么操作呢?这是某个材料中说的:概率累积曲线是在正态概率纸上绘制的,横座标代表粒径;纵座标为累积百分数,并以概率标度(以50%处为对称中心,上下两端相应地逐渐加大),将粗尾、细尾部放大,并清楚地表现出来。
感觉主要是累计百分数怎么求,y轴坐标如何画?如果excel做不到,有没有可以绘制这两种曲线的软件?[quote]引用第1楼guo87于2009-04-10 13:03发表的 :可以,在excel里面工具-数据分析-直方图,做直方图的时候把那个累计概率打勾就可以了。
[/quote]卡奔里面也可以做,建立一个离散数据道,把数据倒进去。
选中数据之后点右键有个数据统计excel就可以对数坐标 over[quote]引用第6楼雨人火舞冰峰于2008-08-05 15:44发表的 :GRAPHER可以做,第一步:数据准备,采集沉积层(一套同成因岩层)的C值(粒度概率累计曲线上1%累计含量的粒度。
)以及M值(粒度概率累计曲线上50%累计含量的粒度)。
第二步:把横纵坐标都设置成对数坐标,C值为纵坐标,上粗下细。
M值为横坐标,左粗右细。
其实不用GRAPHER,而用EXCEL照样可以做。
很简单,当粒径以微米为单位时,使用双对数坐标,而粒径以φ为单位时,使用普通的线性坐标就可以了。
另外,需要注意的是:1.样品数量要足够多,20-30个以上比较好。
2.对一套同成因岩层从粗到细依次采集一系列样品分析,不同岩性不能混合采样。
..[/quote][quote]引用第7楼diego于2009-03-04 19:31发表的 :楼上的说得很好!我再说几句吧!C-M图是应用每个样品对C值和M值绘成的图形。
C值是积累曲线上颗粒含量1%处对应的粒径,M值是积累曲线使50%处对应的粒径。
C值与样品中最粗颗粒的粒径相当,代表了水动力搅动开始搬运的最大能量;M值是中值,代表了水动力的平均能量。
excle做概率累计曲线粒度 (1)

excel做概率分布累积曲线步骤绝对详细的用excel做概率分布累积曲线的好东西,是我一步一步的摸索出来的,热的哦,有问题也可以发消息我解答的。
1. 建立模板建立模板. A. 新建EXCEL 文件, 在A1 : A17 单元格内输入数字“0”, 在B1 : B17 单元格内分别输入数字99. 99 , 99.9 ,99 ,95 ,90 ,80 ,70 ,60 ,50 ,40 ,30 ,20 ,10 ,5 ,1 ,0. 1 ,0. 01 。
前者作为横坐标, 代表将来纵轴与横轴的交叉位置, 其数值以后要根据实际情况调整。
后者代表纵轴以百分数表示的概率刻度值。
B. 选择C1 单元后击粘贴函数(见图1 中箭头所指位置) , 待出现粘贴函数菜单后选取统计类的NORMSINV 函数。
C. 出现新的对话框后, 在probability 后输入“B1/ 100”, 然后确定. D.这时C1 单元格内就有了一个函数值, 拖动C1单元格的填充柄(C1 单元格右下角的小黑块) 向下填充, 则C2 : C17 单元格内都自动生成了函数值。
E. 设置C1 : C17 单元格格式, 将其数值的小数位数定为“2”。
2.做草图 2.做草图选中A1 : A17 和C1 : C17 单元格后, 选择图表向导, 按照提示进行: A.在4 步骤之1 中, 选择X、Y 散点图类型中的第一子类型, 后单击下一步; B.在4 步骤之2 中, 确认系列产生在列(点中“列”前面的小圈) , 后单击下一步; C.在4 步骤之3 中, 可暂不做选择, 直接单击下一步; D.在4 步骤之4 , 根据喜好选图表位置, 本文中选“新工作表”, 单击“完成”后草图就算做成了. 3. 修图 A.首先先去掉图例框、绘图区背景色以及网格线,便于下面的修改; B. 选择数值( Y) 轴, 按鼠标右键弹出菜单后选“坐标轴格式”, 在“坐标轴格式” 菜单中做如下设置: ①在“图案” 项中将主、次刻度线类型及刻度线标志均选“无” ; ②在“刻度”项中,最小值选“-3. 72 ”, 最大值选“3. 72 ”,数值( X) 轴交叉于( C) : 选“-3. 72 ” ; C. 选择数据系列, 按鼠标右键弹出菜单后选“数据系列格式”, 在该菜单作如下设置: ①将图案中的“数据标记样式”选为短横线作为纵轴刻度线; ②在“数据标志”项中选“显示值”, 然后确定。
excel 累积概率曲线

在Excel中制作累积概率曲线,可以按照以下步骤进行:
1.建立数据表格:在Excel中创建一个新的工作表,并输入需要的数据。
假设数据在A列,从A1
单元格开始输入数据。
2.添加辅助列:在B列添加辅助列,用于计算累积概率。
在B1单元格中输入“累积概率”,然后在
B2单元格中输入公式“=SUM(A$1:A2)”。
3.复制公式:将B2单元格中的公式复制到B列的其他单元格中,以计算每个数据的累积概率。
4.添加图表:选择A列和B列的数据,然后选择“插入”菜单中的“图表”选项。
在图表类型中选择“线
图”,然后选择“累积概率曲线”。
5.调整图表格式:可以根据需要调整图表的格式,例如更改图表标题、坐标轴标签等。
完成以上步骤后,就可以在Excel中制作出累积概率曲线了。
利用EXCEL自动绘制颗粒级配曲线的方法
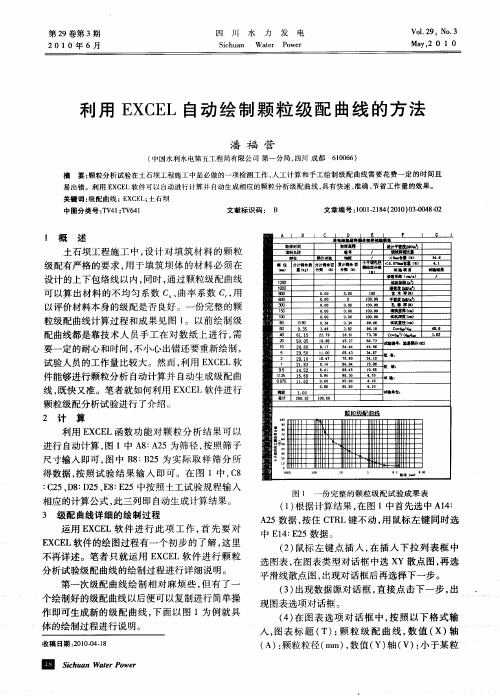
I
I
l
Iw .e rr ru  ̄
粒级 配曲线计 算过程 和成 果见 图 1 。以前 绘 制级
配曲线都是靠技术人员手工在对数纸上进行 , 需
要一定 的耐心 和时 间 , 不小心 出错还要 重新绘 制 ,
试验人员 的工作 量 比较 大 。然 而 , 利用 E C L软 XE 件能够进 行颗粒 分析 自动计算并 自动 生成级 配 曲 线, 既快 又准 。笔 者就如 何利用 E C L软件 进行 X E 颗粒级配 分析试 验进行 了介绍 。 2 计 算
1 概
述
#栅
土石 坝工程施 工 中 , 设计 对 填 筑材 料 的颗粒 级 配有严格 的要 求 , 于填 筑 坝体 的材料 必 须在 用 设计 的上 下包络线 以 内 , 同时 , 通过 颗粒级 配 曲线 可 以算 出材 料 的不均 匀 系数 C 、 曲率 系数 C , 用 以评 价材料本 身 的级 配是 否 良好 。一份完 整 的颗
10 0 主要刻 度单 位 设 置 为 1 次 要 刻 度单 位 设 0 , 0,
验结 果输 入数 值 , 面 就 会 自然 得 出相 应 的计 算 后
结果 , 然后 用 鼠标 左键 选 中级 配 曲线 , 数据 源 , 点
点 系列 , Y 值 , 中 E 4 E 5 点 确 定 , 图 中 点 选 l: 2 , 则
曲线 自动调 整成第 二 次 的试 验成 果 曲线 。几秒钟
即 可完成 。
4 结 语
置 为 1 数 值 ( 轴 交 叉设 置 为 100 将 底部 的 0, Y) 0 , 复选 框 : 对数 刻度 、 值 次 序 反 转 、 值 ( 轴 交 数 数 Y)
叉 于最 大值选 中。
累积概率分布函数在excel中的公式

累积概率分布函数在excel中的公式
在Excel中,累积概率分布函数可以使用NORM.DIST函数来计算。
NORM.DIST函数的一般语法如下:
NORM.DIST(x, mean, standard_dev, cumulative)
其中,
- x:要计算概率的值。
- mean:概率分布的平均值。
- standard_dev:概率分布的标准差。
- cumulative:一个逻辑值,确定是否计算累积概率分布函数。
如果为TRUE(默认),则计算累积概率分布函数;如果为FALSE,则
计算概率密度函数。
注意,在使用NORM.DIST函数之前,首先要启用“分析工具包”
插件,以便在函数库中使用此函数。
除了NORM.DIST函数,Excel还提供了其他一些用于计算累积概率分布函数的函数,如STANDARDIZE函数、T.DIST函数、T.DIST.RT函数等,可以根据具体需求来选择使用。
另外,如果需要拓展到其他分布的累积概率分布函数,可以通过Excel的插件或自定义函数来实现。
例如,可以使用R语言的插件来调用R中的分布函数,或者使用VBA编写自定义函数来计算其他分布的累积概率分布函数。
excel中的概率统计(非常好的资料)

数理统计实验1Excel基本操作1.1 单元格操作1.1.1单元格的选取Excel启动后首先将自动选取第A列第1行的单元格即A1(或a1)作为活动格,我们可以用键盘或鼠标来选取其它单元格.用鼠标选取时,只需将鼠标移至希望选取的单元格上并单击即可.被选取的单元格将以反色显示.1.1.2选取单元格范围(矩形区域)可以按如下两种方式选取单元格范围.(1) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后按住鼠标左键不放,拖动鼠标指针至终点(右下角)位置,然后放开鼠标即可.(2) 先选取范围的起始点(左上角),即用鼠标单击所需位置使其反色显示.然后将鼠标指针移到终点(右下角)位置,先按下Shift键不放,而后点击鼠标左键.1.1.3选取特殊单元格在实际中,有时要选取的单元格由若干不相连的单元格范围组成的.此类有两种情况.第一种情况是间断的单元格选取.选取方法是先选取第一个单元格,然后按住[Ctrl]键,再依次选取其它单元格即可.第二种情况是间断的单元格范围选取.选取方法是先选取第一个单元格范围,然后按住[Ctrl]键,用鼠标拖拉的方式选取第二个单元格范围即可.1.1.4公式中的数值计算要输入计算公式,可先单击待输入公式的单元格,而后键入=(等号),并接着键入公式,公式输入完毕后按Enter键即可确认..如果单击了“编辑公式”按钮或“粘贴函数”按钮,Excel将自动插入一个等号.提示:(1) 通过先选定一个区域,再键入公式,然后按CTRL+ENTER 组合键,可以在区域内的所有单元格中输入同一公式.(2) 可以通过另一单元格复制公式,然后在目标区域内输入同一公式.公式是在工作表中对数据进行分析的等式.它可以对工作表数值进行加法、减法和乘法等运算.公式可以引用同一工作表中的其它单元格、同一工作簿不同工作表中的单元格,或者其它工作簿的工作表中的单元格.下面的示例中将单元格B4 中的数值加上25,再除以单元格D5、E5 和F5 中数值的和.=(B4+25)/SUM(D5:F5)1.1.5公式中的语法公式语法也就是公式中元素的结构或顺序.Excel 中的公式遵守一个特定的语法:最前面是等号(=),后面是参与计算的元素(运算数)和运算符.每个运算数可以是不改变的数值(常量数值)、单元格或区域引用、标志、名称,或工作表函数.在默认状态下,Excel 从等号(=)开始,从左到右计算公式.可以通过修改公式语法来控制计算的顺序.例如,公式=5+2*3的结果为11,将 2 乘以3(结果是6),然后再加上5.因为Excel 先计算乘法再计算加法;可以使用圆括号来改变语法,圆括号内的内容将首先被计算.公式=(5+2)*3的结果为21,即先用 5 加上2,再用其结果乘以3.1.1.6单元格引用一个单元格中的数值或公式可以被另一个单元格引用.含有单元格引用公式的单元格称为从属单元格,它的值依赖于被引用单元格的值.只要被引用单元格做了修改,包含引用公式的单元格也就随之修改.例如,公式“=B15*5”将单元格B15 中的数值乘以5.每当单元格B15 中的值修改时,公式都将重新计算.公式可以引用单元格组或单元格区域,还可以引用代表单元格或单元格区域的名称或标志.在默认状态下,Excel 使用A1 引用类型.这种类型用字母标志列(从A 到IV ,共256 列),用数字标志行(从 1 到65536).如果要引用单元格,请顺序输入列字母和行数字.例如,D50 引用了列D 和行50 交叉处的单元格.如果要引用单元格区域,请输入区域左上角单元格的引用、冒号(:)和区域右下角单元格的引用.下面是引用的示例.1.1.7工作表函数Excel 包含许多预定义的,或称内置的公式,它们被叫做函数.函数可以进行简单的或复杂的计算.工作表中常用的函数是“SUM”函数,它被用来对单元格区域进行加法运算.虽然也可以通过创建公式来计算单元格中数值的总和,但是“SUM”工作表函数还可以方便地计算多个单元格区域.函数的语法以函数名称开始,后面是左圆括号、以逗号隔开的参数和右圆括号.如果函数以公式的形式出现,请在函数名称前面键入等号(=).当生成包含函数的公式时,公式选项板将会提供相关的帮助.使用公式的步骤:A. 单击需要输入公式的单元格.B. 如果公式以函数的形式出现,请在编辑栏中单击“编辑公式”按钮 .C. 单击“函数”下拉列表框 右端的下拉箭头.D. 单击选定需要添加到公式中的函数.如果函数没有出现在列表中,请单击“其它函数”查看其它函数列表.E. 输入参数.F. 完成输入公式后,请按 ENTER 键.1.2 几种常见的统计函数1.2.1均值 Excel 计算平均数使用A VERAGE 函数,其格式如下:A VERAGE (参数1,参数2,…,参数30)范例:A VERAGE (12.6,13.4,11.9,12.8,13.0)=12.74如果要计算单元格中A1到B20元素的平均数,可用 A VERAGE(A1:B20).1.2.2 标准差计算标准差可依据样本当作变量或总体当作变量来分别计算,根据样本计算的结果称作样本标准差,而依据总体计算的结果称作总体标准差.(1)样本标准差Excel 计算样本标准差采用无偏估计式,STDEV 函数格式如下:STDEV (参数1,参数2,…,参数30)范例:STDEV (3,5,6,4,6,7,5)=1.35如果要计算单元格中A1到B20元素的样本标准差,可用 STDEV(A1:B20).(2)总体标准差Excel 计算总体标准差采用有偏估计式STDEVP 函数,其格式如下:STDEVP (参数1,参数2,…,参数30)范例:STDEVP (3,5,6,4,6,7,5)=1.251.2.3 方差方差为标准差的平方,在统计上亦分样本方差与总体方差.(1)样本方差S 2=1)(2--∑n x x iExcel 计算样本方差使用V AR 函数,格式如下:V AR (参数1,参数2,…,参数30)如果要计算单元格中A1到B20元素的样本方差,可用 V AR(A1:B20).范例:V AR (3,5,6,4,6,7,5)=1.81(2)总体方差S 2=n x x i ∑-2)(Excel 计算总体方差使用V ARP 函数,格式如下:V ARP (参数1,参数2,…,参数30)范例:V AR (3,5,6,4,6,7,5)=1.551.2.4 正态分布函数Excel 计算正态分布时,使用NORMDIST 函数,其格式如下:NORMDIST (变量,均值,标准差,累积)其中:变量(x ):为分布要计算的x 值;均值(μ):分布的均值;标准差(σ):分布的标准差;累积:若为TRUE ,则为分布函数;若为FALSE ,则为概率密度函数.范例:已知X 服从正态分布,μ=600,σ=100,求P {X ≤500}.输入公式=NORMDIST (500,600,100,TRUE )得到的结果为0.158655,即P {X ≤500}=0.158655.1.2.5 正态分布函数的反函数Excel 计算正态分布函数的反函数使用NORMINV 函数,格式如下:NORMINV (下侧概率,均值,标准差)范例:已知概率P =0.841345,均值μ=360,标准差σ=40,求NORMINV 函数的值.输入公式=NORMINV (0.841345,360,40)得到结果为400,即P {X ≤400}=0.841345.注意:(1) NORMDIST 函数的反函数NORMINV 用于分布函数,而非概率密度函数,请务必注意;(2) Excel 提供了计算标准正态分布函数 NORMSDIST(x),及标准正态分布的反函数 NORMSINV(概率).范例:已知X~N(0,1), 计算(2)Φ=P {X <2}.输入公式=NORMSDIST(2)得到0.97725,即(2)Φ=0.97725.范例:输入公式=NORMSINV(0.97725) ,得到数值2.若求临界值u α(n ),则使用公式=NORMSINV(1-α).1.2.6 t 分布Excel 计算t 分布的值(查表值)采用TDIST 函数,格式如下:TDIST (变量,自由度,侧数)其中:变量(t ):为判断分布的数值;自由度(v ):以整数表明的自由度;侧数:指明分布为单侧或双侧:若为1,为单侧;若为2,为双侧.范例:设T 服从t (n-1)分布,样本数为25,求P (T >1.711).已知t =1.711,n =25,采用单侧,则T 分布的值:=TDIST(1.711,24,1)得到0.05,即P (T >1.711)=0.05.若采用双侧,则T 分布的值:=TDIST(1.711,24,2)得到0.1,即()1.7110.1P T >=. 1.2.7 t 分布的反函数Excel 使用TINV 函数得到t 分布的反函数,格式如下:TINV (双侧概率,自由度)范例:已知随机变量服从t (10)分布,置信度为0.05,求t 205.0(10).输入公式=TINV(0.05,10)得到2.2281,即()2.22810.05P T >=.若求临界值t α(n ),则使用公式=TINV(2*α, n ).范例:已知随机变量服从t (10)分布,置信度为0.05,求t 0.05 (10).输入公式=TINV(0.1,10)得到1.812462,即t 0.05 (10)= 1.812462.1.2.8 F 分布Excel 采用FDIST 函数计算F 分布的上侧概率1()F x -,格式如下:FDIST(变量,自由度1,自由度2)其中:变量(x ):判断函数的变量值;自由度1(1n ):代表第1个样本的自由度;自由度2(n ):代表第2个样本的自由度.范例:设X 服从自由度1n =5,2n =15的F 分布,求P (X >2.9)的值.输入公式=FDIST(2.9,5,15)得到值为0.05,相当于临界值α.1.2.9 F 分布的反函数Excel 使用FINV 函数得到F 分布的反函数,即临界值12(,)F n n α,格式为:FINV(上侧概率,自由度1,自由度2)范例:已知随机变量X 服从F (9,9)分布,临界值α=0.05,求其上侧0.05分位点F 0.05(9,9).输入公式=FINV(0.05,9,9)得到值为3.178897,即F 0.05(9,9)= 3.178897.若求单侧百分位点F 0.025(9,9),F 0.975(9,9).可使用公式=FINV(0.025,9,9)=FINV(0.975,9,9)得到两个临界值4.025992和0.248386.若求临界值F α(n 1,n 2),则使用公式=FINV(α, n 1,n 2).1.2.10 卡方分布Excel 使用CHIDIST 函数得到卡方分布的上侧概率1()F x -,其格式为:CHIDIST(数值,自由度)其中:数值(x ):要判断分布的数值;自由度(v ):指明自由度的数字.范例:若X 服从自由度v =12的卡方分布,求P (X >5.226)的值.输入公式=CHIDIST(5.226,12)得到0.95,即1(5.226)F -=0.95或(5.226)F =0.05.1.2.11 卡方分布的反函数Excel 使用CHIINV 函数得到卡方分布的反函数,即临界值2()n αχ.格式为:CHIINV (上侧概率值α,自由度n )范例:下面的公式计算卡方分布的反函数:=CHIINV(0.95,12)得到值为5.226,即20.95(12)χ=5.226.若求临界值2χ(n),则使用公式=CHIINV(α, n).1.2.12 泊松分布计算泊松分布使用POISSON 函数,格式如下:POISSON(变量,参数,累计)其中:变量:表示事件发生的次数;参数:泊松分布的参数值;累计:若TRUE ,为泊松分布函数值;若FALSE ,则为泊松分布概率分布值. 范例:设X服从参数为4的泊松分布,计算P {X =6}及P {X ≤6}.输入公式=POISSON(6,4,FALSE)=POISSON(6,4,TRUE)得到概率0.104196和0.889326.在下面的实验中,还将碰到一些其它函数,例如:计算样本容量的函数COUNT ,开平方函数SQRT ,和函数SUM ,等等.关于这些函数的具体用法,可以查看Excel 的关于函数的说明,不再赘述.2 区间估计实验计算置信区间的本质是输入两个公式,分别计算置信下限与置信上限.当熟悉了数据输入方法及常见统计函数后,变得十分简单.2.1 单个正态总体均值与方差的区间估计:2.1.1σ2已知时μ的置信区间 置信区间为22x u x u αα⎛⎫-+ ⎝. 例1 随机从一批苗木中抽取16株,测得其高度(单位:m )为:1.14 1.10 1.131.15 1.20 1.12 1.17 1.19 1.15 1.12 1.14 1.20 1.23 1.11 1.14 1.16.设苗高服从正态分布,求总体均值μ的0.95的置信区间.已知σ =0.01(米).步骤:(1)在一个矩形区域内输入观测数据,例如在矩形区域B3:G5内输入样本数据.(2)计算置信下限和置信上限.可以在数据区域B3:G5以外的任意两个单元格内分别输入如下两个表达式:=average(b3:g5)-normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))=average(b3:g5)+normsinv(1-0.5*α)*σ/sqrt(count(b3:g5))上述第一个表达式计算置信下限,第二个表达式计算置信上限.其中,显著性水平α和标准差σ是具体的数值而不是符号.本例中,α =0.05, 0.01σ=,上述两个公式应实际输入为=average(b3:g5)-normsinv(0.975)*0.01/sqrt(count(b3:g5))=average(b3:g5)+normsinv(0.975)*0.01/sqrt(count(b3:g5))计算结果为(1.148225, 1.158025).2.1.2 σ2未知时μ的置信区间置信区间为22((x t n x t n αα⎛⎫--+- ⎝. 例2 同例1,但σ未知.输入公式为:=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))=average(b3:g5)-tinv(0.05,count(b:3:g5)-1)*stdev(b3:g5)/sqrt(count(b3:g5))计算结果为(1.133695, 1.172555).2.1.3 μ未知时σ2的置信区间:置信区间为 2222122(1)(1),(1)(1)n n n n s s ααχχ-⎛⎫ ⎪-- ⎪-- ⎪⎝⎭. 例3 从一批火箭推力装置中随机抽取10个进行试验,它们的燃烧时间(单位:s)如下:50.7 54.9 54.3 44.8 42.2 69.8 53.4 66.1 48.1 34.5试求总体方差2σ的0.9的置信区间(设总体为正态).操作步骤:(1)在单元格B3:C7分别输入样本数据;(2)在单元格C9中输入样本数或输入公式=COUNT(B3:C7);(3)在单元格C10中输入置信水平0.1.(4)计算样本方差:在单元格C11中输入公式=V AR(B3:C7)(5)计算两个查表值:在单元格C12中输入公式=CHIINV(C10/2,C9-1),在单元格C13中输入公式=CHIINV(1-C10/2,C9-1)(6)计算置信区间下限:在单元格C14中输入公式=(C9-1)*C11/C12(7)计算置信区间上限:在单元格C15中输入公式=(C9-1)*C11/C13.当然,读者可以在输入数据后,直接输入如下两个表达式计算两个置信限:=(count(b3:c7)-1)*var(b3:c7)/chiinv(0.1/2, count(b3:c7)-1)=(count(b3:c7)-1)*var(b3:c7)/chiinv(1-0.1/2, count(b3:c7)-1)2.2 两正态总体均值差与方差比的区间估计2.2.1当σ12 = σ22 = σ2但未知时μ1-μ2的置信区间置信区间为()122(2) x y t n n Sα⎛-±+-⎝.例4在甲,乙两地随机抽取同一品种小麦籽粒的样本,其容量分别为5和7,分析其蛋白质含量为甲:12.6 13.4 11.9 12.813.0乙:13.1 13.4 12.8 13.5 13.3 12.7 12.4蛋白质含量符合正态等方差条件,试估计甲,乙两地小麦蛋白质含量差μ1-μ2所在的范围.(取α=0.05)实验步骤:(1)在A2:A6输入甲组数据,在B2:B8输入乙组数据;(2)在单元格B11输入公式=A VERAGE(A2:A6),在单元格B12中输入公式=A VERAGE(B2:B8),分别计算出甲组和乙组样本均值.(3)分别在单元格C11和C12分别输入公式=V AR(A2:A6),=V AR(B2:B8),计算出两组样本的方差.(4)在单元格D11和D12分别输入公式=COUNT(A2:A6),=COUNT(B2:B8),计算各样本的容量大小.(5)将显著性水平0.05输入到单元格E11中.(6)分别在单元格B13和B14输入=B11-B12-TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)和=B11-B12+TINV(0.025,10)*SQRT((4*C11+6*C12)/10)*SQRT(1/ 5+1/7)计算出置信区间的下限和上限.2.2.2 μ1和μ2未知时方差比σ21/σ22的置信区间置信区间为 22112221221212211,(1,1)(1,1)s s s F n n s F n n αα-⎛⎫ ⎪ ⎪---- ⎪⎝⎭ . 例5 有两个化验员A 、B ,他们独立地对某种聚合物的含氯量用相同的方法各作了10次测定.其测定值的方差分别是S A =0.5419,S B =0.6065.设σ2A 和σ2B 分别是A 、B 所测量的数据总体(设为正态分布)的方差.求方差比σ2A /σ2B 的 0.95置信区间.操作步骤:(1)在单元格B2,B3输入样本数,C2,C3输入样本方差,D2输入置信度.(2)在B4和B5利用公式输入=C2/(C3*FINV(1-D2/2,B2-1,B3-1))和=C2/(C3*FINV(D2/2,B2-1,B3-1))计算出A 组和B 组的方差比的置信区间上限和下限.2.3 练习题1. 已知某树种的树高服从正态分布,随机抽取了该树种的60株林木组成样本.样本中各林木的树高资料如下(单位:m)22.3, 21.2, 19.2, 16.6, 23.1, 23.9, 24.8, 26.4, 26.6, 24.8, 23.9, 23.2, 23.3, 21.4, 19.8, 18.3,20.0, 21.5, 18.7, 22.4, 26.6, 23.9, 24.8, 18.8, 27.1, 20.6, 25.0, 22.5, 23.5, 23.9, 25.3, 23.5,22.6, 21.5, 20.6, 25.8, 24.0, 23.5, 22.6, 21.8, 20.8, 19.5, 20.9, 22.1, 22.7, 23.6, 24.5, 23.6,21.0, 21.3, 22.4,18.7, 21.3, 15.4, 22.9, 17.8, 21.7, 19.1, 20.3, 19.8试以0.95的可靠性,对于该林地上全部林木的平均高进行估计.2. 从一批灯泡中随机抽取10个进行测试,测得它们的寿命(单位:100h)为:50.7,54.9,54.3,44.8,42.2,69.8,53.4,66.1,48.1,34.5.试求总体方差的0.9的置信区间(设总体为正态).3. 已知某种玉米的产量服从正态分布,现有种植该玉米的两个实验区,各分为10个小区,各小区的面积相同,在这两个实验区中,除第一实验区施以磷肥外,其它条件相同,两实验区的玉米产量(kg)如下:第一实验区:62 57 65 60 63 58 57 60 60 58第二实验区:56 59 56 57 60 58 57 55 57 55试求出施以磷肥的玉米产量均值和未施以磷肥的玉米产量均值之差的范围(α=0.05)3假设检验实验实验内容:单个总体均值的假设检验;两个总体均值差的假设检验;两个正态总体方差齐性的假设检验;拟合优度检验.实验目的与要求:(1)理解假设检验的统计思想,掌握假设检验的计算步骤;(2)掌握运用Excel进行假设检验的方法和操作步骤;(3)能够利用试验结果的信息,对所关心的事物作出合理的推断.3.1 单个正态总体均值μ的检验3.1.1 2已知时μ的U检验例1 外地一良种作物,其1000m2产量(单位:kg)服从N(800, 502),引入本地试种,收获时任取5块地,其1000m2产量分别是800,850,780,900,820(kg),假定引种后1000m2产量X也服从正态分布,试问:=800kg 有无显著变化.(1)若方差未变,本地平均产量μ与原产地的平均产量μ0=800kg高.(2)本地平均产量μ是否比原产地的平均产量μ0=800kg低.(3)本地平均产量μ是否比原产地的平均产量μ0操作步骤:(1)先建一个如下图所示的工作表:(2)计算样本均值(平均产量),在单元格D5输入公式=A VERAGE(A3:E3);(3)在单元格D6输入样本数5;(4)在单元格D8输入U检验值计算公式=(D5-800)/(50/SQRT(D6);(5)在单元格D9输入U检验的临界值=NORMSINV(0.975);(6)根据算出的数值作出推论.本例中,U的检验值1.341641小于临界值1.959961,故接受原假设,即平均产量与原产地无显著差异.(7)注:在例1中,问题(2)要计算U检验的右侧临界值:在单元格D10输入U检验的上侧临界值=NORMSINV(0.95).问题(3)要计算U检验的下侧临界值,在单元格D11输入U 检验下侧的临界值=NORMSINV(0.05).3.1.2 2未知时的t检验例2某一引擎制造商新生产某一种引擎,将生产的引擎装入汽车内进行速度测试,得到行驶速度如下:250 238 265 242 248 258 255 236 245 261254 256 246 242 247 256 258 259 262 263该引擎制造商宣称引擎的平均速度高于250 km/h,请问样本数据在显著性水平为0.025时,是否和他的声明抵触?操作步骤:(1)先建如图所示的工作表:(2)计算样本均值:在单元格D8输入公式=A VERAGE(A3:E6);(3)计算标准差:在单元格D9输入公式=STDEV(A3:E6);(4)在单元格D10输入样本数20.(5)在单元格D11输入t检验值计算公式=(D8-250)/(D9/(SQRT(D10)),得到结果1.06087;(6)在单元格D12输入t检验上侧临界值计算公式=TINV(0.05, D10-1).欲检验假设:μ>250.H0:μ=250;H1已知t统计量的自由度为(n-1)=20-1=19,拒绝域为t>t=2.093.由上面计算得到t025.0检验统计量的值1.06087落在接收域内,故接收原假设H0.3.2 两个正态总体参数的假设检验μ-μ的检验3.2.1当σ12 = σ22 = σ2但未知时12在此情况下,采用t检验.例试验及观测数据同11.2中的练习题3,试判别磷肥对玉米产量有无显著影响?欲检验假设:μ1>μ2.H0:μ1=μ2;H1操作步骤:(1)(2)选取“工具”—“数据分析”;(3)选定“t-检验:双样本等方差假设”.(4)选择“确定”.显示一个“t-检验:双样本等方差假设”对话框;(5)在“变量1的区域”输入A2:A11.(6)在“变量2的区域”输入B2:B11.(7)在“输出区域”输入D1,表示输出结果放置于D1向右方的单元格中.(8)在显著水平“α”框,输入0.05.(9)在“假设平均差”窗口输入0.(10)选择“确定”,计算结果如D1:F14显示.得到t值为3.03,“t单尾临界”值为1.734063.由于3.03>1.73,所以拒绝原假设,接收备择假设,即认为使用磷肥对提高玉米产量有显著影响.3.2.2σ21与σ22已知时12μ-μ的U检验例3 某班20人进行了数学测验,第1组和第2组测验结果如下:第1组:91 88 76 98 94 92 90 87 100 69第2组:90 91 80 92 92 94 98 78 86 91已知两组的总体方差分别是57与53,取α =0.05,可否认为两组学生的成绩有差异?操作步骤:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”;(3)选定“z-检验:双样本平均差检验”;(4)选择“确定”,显示一个“z-检验:双样本平均差检验”对话框;(5)在“变量1的区域”输入A2:A11;(6)在“变量2的区域”输入B2:B11;(7)在“输出区域”输入D1;(8)在显著水平“α”框,输入0.05;(9)在“假设平均差”窗口输入0;(10)在“变量1的方差”窗口输入57;(11)在“变量2的方差”窗口输入53;(12)选择“确定”,得到结果如图所示.计算结果得到z=-0.21106(即u统计量的值),其绝对值小于“z双尾临界”值1.959961,故接收原假设,表示无充分证据表明两组学生数学测验成绩有差异.3.2.3 两个正态总体的方差齐性的F检验例5 羊毛在处理前与后分别抽样分析其含脂率如下: 处理前:0.19 0.18 0.21 0.30 0.41 0.12 0.27处理后:0.15 0.13 0.07 0.24 0.19 0.06 0.08 0.12 问处理前后含脂率的标准差是否有显著差异? 欲检验假设H 0:σ21=σ22;H 1:σ21≠σ22.操作步骤如下:(1)建立如图所示工作表:(2)选取“工具”—“数据分析”; (3)选定“F-检验 双样本方差”. (4)选择“确定”,显示一个“F-检验:双样本方差”对话框; (5)在“变量1的区域”输入A2:A8. (6)在“变量2的区域”输入B2:B9. (7)在显著水平“α”框,输入0.025. (8)在“输出区域”框输入D1. (9)选择“确定”,得到结果如图所示.计算出F 值2.35049小于“F 单尾临界”值5.118579,且P(F<=f)=0.144119>0.025,故接收原假设,表示无理由怀疑两总体方差相等.4 拟合优度检验拟合优度检验使用统计量221()ki i i in np np χ=-=∑, (11.1) i i n np k 其中为实测频数,为理论频数,为分组数。
基于Excel VBA的图解粒度参数计算

基于Excel VBA的图解粒度参数计算
张永成;王洪辉;谭桂花
【期刊名称】《成都理工大学学报(自然科学版)》
【年(卷),期】2010(37)6
【摘要】计算粒度参数较常用的图解法一般要通过手工绘制粒度概率累积曲线,从中读取百分位数,不利于计算大量样品.作者利用Excel函数将正态概率坐标转化为线性坐标,再进行线性插值,通过Excel VBA直接调用Excel内置的丰富函数,编写了粒度参数计算程序.该程序可不通过作图,直接利用图解法的原理批量计算粒度参数.与手工绘图计算相比,该方法精度较高,极大地提高了工作效率.
【总页数】4页(P650-653)
【作者】张永成;王洪辉;谭桂花
【作者单位】成都理工大学能源学院,成都,610059;成都理工大学能源学院,成都,610059;四川文理学院,四川,达州,635000;大庆油田勘探开发研究院海塔开发研究室,黑龙江,大庆,163712
【正文语种】中文
【中图分类】TP391.13;TE122.23
【相关文献】
1.基于Excel VBA的无定向导线计算程序的编制及应用 [J], 陈军伟
2.基于Excel VBA的短路电流实用计算软件在太平湾电站的开发应用 [J], 苏有权
3.基于Excel VBA技术的货币时间价值计算模型设计 [J], 雷金东
4.基于Excel VBA的短路电流实用计算软件在太平湾电站的开发应用 [J], 苏有权
5.基于MATLAB的图解粒度参数计算 [J], 王为;吴正
因版权原因,仅展示原文概要,查看原文内容请购买。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
excel做概率分布累积曲线步骤绝对详细的用excel做概率分布累积曲线的好东西,是我一步一步的摸索出来的,热的哦,有问题也可以发消息我解答的。
1. 建立模板建立模板. A. 新建EXCEL 文件, 在A1 : A17 单元格内输入数字“0”, 在B1 : B17 单元格内分别输入数字99. 99 , 99.9 ,99 ,95 ,90 ,80 ,70 ,60 ,50 ,40 ,30 ,20 ,10 ,5 ,1 ,0. 1 ,0. 01 。
前者作为横坐标, 代表将来纵轴与横轴的交叉位置, 其数值以后要根据实际情况调整。
后者代表纵轴以百分数表示的概率刻度值。
B. 选择C1 单元后击粘贴函数(见图1 中箭头所指位置) , 待出现粘贴函数菜单后选取统计类的NORMSINV 函数。
C. 出现新的对话框后, 在probability 后输入“B1/ 100”, 然后确定. D.这时C1 单元格内就有了一个函数值, 拖动C1单元格的填充柄(C1 单元格右下角的小黑块) 向下填充, 则C2 : C17 单元格内都自动生成了函数值。
E. 设置C1 : C17 单元格格式, 将其数值的小数位数定为“2”。
2.做草图 2.做草图选中A1 : A17 和C1 : C17 单元格后, 选择图表向导, 按照提示进行: A.在4 步骤之1 中, 选择X、Y 散点图类型中的第一子类型, 后单击下一步; B.在4 步骤之2 中, 确认系列产生在列(点中“列”前面的小圈) , 后单击下一步; C.在4 步骤之3 中, 可暂不做选择, 直接单击下一步; D.在4 步骤之4 , 根据喜好选图表位置, 本文中选“新工作表”, 单击“完成”后草图就算做成了. 3. 修图 A.首先先去掉图例框、绘图区背景色以及网格线,便于下面的修改; B. 选择数值( Y) 轴, 按鼠标右键弹出菜单后选“坐标轴格式”, 在“坐标轴格式” 菜单中做如下设置: ①在“图案” 项中将主、次刻度线类型及刻度线标志均选“无” ; ②在“刻度”项中,最小值选“-3. 72 ”, 最大值选“3. 72 ”,数值( X) 轴交叉于( C) : 选“-3. 72 ” ; C. 选择数据系列, 按鼠标右键弹出菜单后选“数据系列格式”, 在该菜单作如下设置: ①将图案中的“数据标记样式”选为短横线作为纵轴刻度线; ②在“数据标志”项中选“显示值”, 然后确定。
D.选中数据系列点的“数据标志”,自上而下依次将各标志值改为99.99, 99.9…0.01 (即B1 :B17 的值) 作为刻度值; E 在“数据标志格式”菜单中将文本对齐方式选为水平“靠左”, 垂直“居中”, 标志位置选“靠左”,然后确定。
F 将绘图区框向右拉小一些使刻度值清楚可见。
G 至此, 概率坐标纸就做好了,可以将“sheet1”改名为“数据表”,“图表1”改名为“图表”后将文件以模板的形式保存起来. 4 实际应用例如根据某砂样的粒度资料得到以下孔隙半径φ与累积重量百分比值的数据表: Φ值累积百分比 -1 1.00 1.00 5.24 2.00 30.76 3.00 63.76 4.00 83.32 5.00 90.24 5.02 91.84 6.6 91.92 需要对以上数据做概率值累积曲线。
步骤:1.打开模板, 自A18 向下输入φ值, 自B18 向下输入累积重量百分比值, 在 C 列填充得到各百分比值对应的区间值, 2. 2 然后选中模板中的图表, 在“图表”菜单中选“添加数据”, 在出现对话框后选中要添加的数据区域(此处选A18 : A25和C18 : C25) , 在下一对话框中选添加单元格为“新系列”, 数值( Y) 轴在“列”, 并选中“首列为分类X 值”前面的方框, 然后确定, 对这些统计点所做的累积频率曲线草图就做好了。
3 调整坐标轴格式, 使图看起来直观些: 在坐标轴格式菜单中将横轴刻度值范围调整为-2~7 , 刻度间隔为1 , 并将A1~A17 内的数据改为“-2” , 这样就得到了一张直观的概率图(图102例2 砂样粒度概率累积曲线) , 地质人员可据此分析沉积成因等。
概率值累积粒度曲线流程如何做粒度概率曲线流程关于沉积相研究中粒度作图(石头)一、概率值累积粒度曲线流程:井为例)(X 1、数据准备一般取到的数据是下面这种格式,首先将粒级中的<、>去掉,然后根据其值计算粒级Φ值,粒级Φ值=-log(粒级,2),得到粒级从负到正的一些列数据,然后根据小数取左值或右值。
然后整理成下面的格式保存成txt 格式粒级Φ值累积质量含量(%) -5 4.18 -4 12.99 -3 -2 -1 -0.3 0 0.5 1 2 3 4 5 6 35.95 56.55 74.31 78.30 81.35 86.72 90.17 94.87 96.84 98.27 98.66 99.98 然后就可以在 grapher 中作图了。
2、作图(1)准备数据体,X -粒度区间(左值或者是右值),Φ值;Y-累积重量百分比(2)打开 Grapher,点击 Gr aph→New Graph→Line/Simbol (3)Open worksheet,选定数据源,选定 XY 坐标(4)图形显示后,选定纵坐标,Scale→Probability(%Lable),Axis Limits→(0.0001,0.9999),Y 轴即成为概率百分数标度。
(5)在成果图上如果想再加上另一条曲线,在刚才做出的曲线的整个图上点击,出现一个将坐标和数据点都包括其中的一个矩形,右键单击选择->Add plot,默认-》OK 继续点 ok,进入选择数据表对话框即可。
二、C-M 图 1、基础知识摘自(博研石油论坛)转帖][原创] 关于 C-M 图 [转帖][原创] 关于 C-M 图 C-M 图是应用每个样品对 C 值和 M 值绘成的图形。
C 值是积累曲线上颗粒含量 1%处对应的粒径,M 值是积累曲线使 50%处对应的粒径。
C 值与样品中最粗颗粒的粒径相当,代表了水动力搅动开始搬运的最大能量;M 值是中值,代表了水动力的平均能量。
为研究地层的沉积成因,需从该地层成因单元取得几十个样品,这些样品必须属于同一沉积环境的产物。
对于不同岩性要分别取样,而且样品要包括该单元由粗到细的全部粒度结构类型,几十个样品各按其 C 值、M 值在图纸上投得一群点,按群点的分布绘出相应的图形,就是 C-M 图。
根据所得图形的形态、分布范围以及图形与 C-M 基线的关系等特点,与已知沉积环境的典型C-M 图进行比较,再结合其他岩性特征,从而可以对该层沉积岩的沉积环境作出判断。
C-M 图是帕塞加(Passega,1957,1964)提出来的。
帕塞加将搬运沉积物的底流分为牵引流和浊流两种形式。
本文来自: 博研石油论坛详细出处参考/thread-17675-1-1.html C-M 图用 GRAPHER 可以做第一步:数据准备,采集沉积层(一套同成因岩层)的 C 值(粒度概率累计曲线上 1%累计含量的粒度。
)以及 M 值(粒度概率累计曲线上 50%累计含量的粒度)。
第二步:把横纵坐标都设置成对数坐标,C 值为纵坐标,上粗下细。
M 值为横坐标,左粗右细。
其实不用 GRAPHER,而用 EXCEL 照样可以做。
很简单,当粒径以微米为单位时,使用双对数坐标,而粒径以φ为单位时,使用普通的线性坐标就可以了。
另外,需要注意的是: 1.样品数量要足够多,20-30 个以上比较好。
2.对一套同成因岩层从粗到细依次采集一系列样品分析,不同岩性不能混合采样。
本文来自: 博研石油论坛详细出处参考/thread-17675-1-1.html 2、数据准备(1)将统计的每个深度点的数据中累积质量含量 1%、50%的粒级单独挑出,换算成粒级φ值,如下图数据(2)然后用 1000*power(2,-粒级φ值),可以求出 C、M 的值,单位为(um) 2、作图第二节岩石结构和粒度标志(摘自中国地质大学精品课程《沉积学与古地理》陈建强教授课件)一、岩石结构标志碎屑岩的结构包括三方面内容,即: 1、碎屑颗粒的特征:粒度、形状及颗粒表面结构。
2、填隙物的特征:包括杂基和胶结物。
3、碎屑颗粒与填隙物之间的关系:即支撑和胶结类型。
1.碎屑颗粒的特征碎屑颗粒特征包括磨圆度、球度、粒度、分选性以及颗粒的表面结构。
磨圆度:颗粒原始棱角被磨圆的程度。
影响因素:取决于粒度大小、物理性质及磨蚀历史。
在一定距离内:※较大的颗粒一般较小颗粒圆化得好;※硬度较小的颗粒比大的颗粒圆化好;※经长距离(或长时间)搬运的颗粒比短距离(或短时间)搬运的颗粒磨圆度好。
※另外, 搬运介质和搬运方式对颗粒圆度也有影响,如颗粒在风中搬运要比在水中更容易磨圆,而冰川的搬运则不易发生圆化作用。
球度: 颗粒近于球体的程度。
影响因素:取决于粒度大小、物理性质及磨蚀历史。
※石英: 无解理,故搬运愈远,球度愈大; ※云母: 虽经远距离搬运,其球度也可能较低。
颗粒表面结构: 是颗粒表面的形态特征。
※主要包括:颗粒表面磨光程度和刻蚀痕迹。
※作用:揭示侵蚀、搬运、沉积的细节。
※手段:肉眼、放大镜、显微镜、电子显微镜。
2.填隙物的特征填隙物(基质,与颗粒相应)包括杂基和胶结物。
杂基:与粗颗粒一起(同时)沉积下来的细粒(小于 0.03 mm ),不是沉积之后孔隙水化学沉淀物。
杂基反映:颗粒的分选性(结构成熟度的标志);介质的粘度、密度、水动力;高能条件:杂基少,纯净砂岩;低能条件:杂基多,复杂成分砂。
胶结物:与杂基不同,是沉积后,孔隙水化学沉淀物。
颗粒是上代产物,胶结物是相当于“自生矿物”或“准同生产物”,所以其是结晶结构。
结构有:非晶质及隐晶质结构、显晶质结构。
作用:反映粒间溶液的成分和成岩期的化学条件。
3.胶结类型和支撑结构 (1) 胶结类型① 基底胶结② 孔隙胶结③ 接触胶结④ 镶嵌结构 Which one it belong to? (2)支撑结构支撑类型分为:杂基支撑结构和颗粒支撑结构。
杂基(基质)支撑结构:杂基含量高,颗粒漂浮其中。
颗粒支撑结构:颗粒之间有接触(点、线、面、凹凸接触、缝合状接触)。
成因上:反映沉积和成岩中经受压实、压溶等强度,如缝合接触是成岩程度很深的特征。
二、粒度分布特征及其环境意义粒度分析的意义: (1)确定介质的类型;(2)判断介质的能量; (3)确定搬运方式; (4)确定沉积方式。
沉积物的颗粒大小称为粒度。
粒度特征反映沉积作用的流体力学性质,是判别沉积环境的重要标志。
粒度分析主要研究沉积物的结构特征(粒度大小和粒级分布)。
碎屑物质埋藏后除部分石英有生加大或溶解外,一般颗粒变化不大,因此,粒度特征直接反映水动力条件。
