初中数学《三角形》知识点总结及习题大全(附答案)

合集下载

三角形的证明详细知识点、例题、习题)

三角形的证明详细知识点、例题、习题)1.定义：全等三角形指的是能够完全相等的三角形。

2.性质：全等三角形的对应边和对应角都相等。

3.判定方法：XXX、SSS、ASA、AAS、HL。

需要注意的是，SSA和AAA不能作为判定三角形全等的方法，必须有边的参与。

若有两边一角相等时，角必须是两边的夹角。

4.证题思路：找夹角（SAS）已知两边，找直角（HL）找第三边（SSS）若边为角的对边，则找任意角（AAS）已知一边一角，边为角的邻边找已知边的对角（AAS）找已知角的另一边（SAS）找夹已知边的另一角（ASA）找两角的夹边（ASA）已知两角，找任意一边（AAS）1.等腰三角形的性质：两个底角相等（等边对等角）。

2.判定方法：有两个角相等的三角形是等腰三角形（等角对等边）。

推论：等腰三角形顶角的平分线、底边上的中线、底边上的高互相重合（即“三线合一”）。

3.等边三角形的性质：三个角都相等，并且每个角都等于60°；等边三角形是轴对称图形，有3条对称轴。

判定方法：有一个角是60°的等腰三角形是等边三角形；三个角都相等的三角形是等边三角形。

4.含30°的直角三角形的边的性质：在直角三角形中，如果一个锐角等于30°，那么它所对的直角边等于斜边的一半。

1.勾股定理及其逆定理：直角三角形的两条直角边的平方和等于斜边的平方。

逆定理：如果三角形两边的平方和等于第三边的平方，那么这个三角形是直角三角形。

2.命题与逆命题：命题包括题设和结论两部分；逆命题是将原命题的题设和结论交换位置得到的。

3.直角三角形全等的判定定理：斜边和一条直角边对应相等的两个直角三角形全等。

需要注意的是，勾股定理的逆定理在语言叙述的时候一定要注意，不能说成“两条边的平方和等于斜边的平方”，应该说成“三角形两边的平方和等于第三边的平方”。

1.线段垂直平分线的性质：线段垂直平分线上的点到这条线段两个端点的距离相等。

2.判定方法：到一条线段两个端点距离相等的点在这条线段的垂直平分线上。

初一数学三角形与全等三角形知识点大全-经典练习-含答案

初一数学三角形知识点归纳一、与三角形有关的线段1、不在同一条直线上的三条线段首尾顺次相接组成的图形叫做三角形2、等边三角形:三边都相等的三角形3、等腰三角形：有两条边相等的三角形4、不等边三角形：三边都不相等的三角形5、在等腰三角形中,相等的两边都叫腰,另一边叫底，两腰的夹角叫做顶角，腰和底边的夹角叫做底角6、三角形分类：不等边三角形等腰三角形：底边和腰不等的等腰三角形等边三角形7、三角形两边之和大于第三边，两边之差小于第三边注：1）在实际运用中,只需检验最短的两边之和大于第三边，则可说明能组成三角形 2）在实际运用中，已经两边，则第三边的取值范围为：两边之差〈第三边〈两边之和3）所有通过周长相加减求三角形的边，求出两个答案的，注意检查每个答案能否组成三角形8、三角形的高：从△ABC的顶点A向它所对的边BC所在的直线画垂线，垂足为D，所得线段AD叫做△ABC的边BC上的高9、三角形的中线：连接△ABC的顶点A和它所对的边BC的中点D，所得线段AD叫做△ABC的边BC上的中线注：两个三角形周长之差为x,则存在两种可能：即可能是第一个△周长大，也有可能是第一个△周长小10、三角形的角平分线：画∠A的平分线AD，交∠A所对的边BC于D，所得线段AD叫做△ABC的角平分线11、三角形的稳定性,四边形没有稳定性二、与三角形有关的角1、三角形内角和定理:三角形三个内角的和等于180度。

证明方法：利用平行线性质2、三角形的外角:三角形的一边与另一边的延长线组成的角，叫做三角形的外角3、三角形的一个外角等于与它不相邻的两个内角的和4、三角形的一个外角大于与它不相邻的任何一个内角5、三角形的外角和为360度6、等腰三角形两个底角相等三、多边形及其内角和1、多边形：在平面内，由一些线段首尾顺次相接组成的图形叫做多边形2、N边形：如果一个多边形由N条线段组成，那么这个多边形就叫做N边形。

3、内角:多边形相邻两边组成的角叫做它的内角4、外角:多边形的边与它的邻边的延长线组成的角叫做多边形的外角5、对角线：连接多边形不相邻的两个顶点的线段，叫做多边形的对角线6、正多边形：各个角都相等，各条边都相等的多边形叫做正多边形7、多边形的内角和：n边形内角和等于(n-2）＊1808、多边形的外角和：360度注：有些题，利用外角和,能提升解题速度9、从n边形的一个顶点出发，可以引n-3条对角线，它们将n边形分成n-2个△注：探索题型中，一定要注意是否是从N边形顶点出发，不要盲目背诵答案10、从n边形的一个顶点出发，可以引n—3条对角线,n边形共有对角线23)-n(n条。

(完整版)初中三角形知识点总结

图形的初步认识：三角形考点一、三角形1、三角形的三边关系定理及推论（1）三角形三边关系定理：三角形的两边之和大于第三边。

推论：三角形的两边之差小于第三边。

2、三角形的内角和定理及推论三角形的内角和定理：三角形三个内角和等于180°。

推论：①直角三角形的两个锐角互余。

②三角形的一个外角等于和它不相邻的来两个内角的和。

③三角形的一个外角大于任何一个和它不相邻的内角。

注：在同一个三角形中：等角平等边；等边平等角；大角对大边；大边对大角。

4、三角形的面积三角形的面积 = 1×底×高2考点二、全等三角形1、全等三角形的观点能够完整重合的两个三角形叫做全等三角形。

2、三角形全等的判断三角形全等的判断定理：（1）边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“ SAS”）（2）角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ ASA”）（3）边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“ SSS”）。

（4）角角边定理：有两角和一边对应相等的两个三角形全等（可简写成“角角边”或“ AAS”）。

直角三角形全等的判断：关于特别的直角三角形，判断它们全等时，还有 HL定理（斜边、直角边定理）：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“ HL”）3、全等变换只改变图形的地点，不改变其形状大小的图形变换叫做全等变换。

全等变换包含一下三种：（1）平移变换：把图形沿某条直线平行挪动的变换叫做平移变换。

（2）对称变换：将图形沿某直线翻折 180°，这类变换叫做对称变换。

（3）旋转变换：将图形绕某点旋转必定的角度到另一个地点，这类变换叫做旋转变换。

考点三、等腰三角形1、等腰三角形的性质（1）等腰三角形的性质定理及推论：定理：等腰三角形的两个底角相等（简称：等边平等角）推论 1：等腰三角形顶角均分线均分底边并且垂直于底边。

自学初中数学资料-三角形的定义与性质(资料附答案)

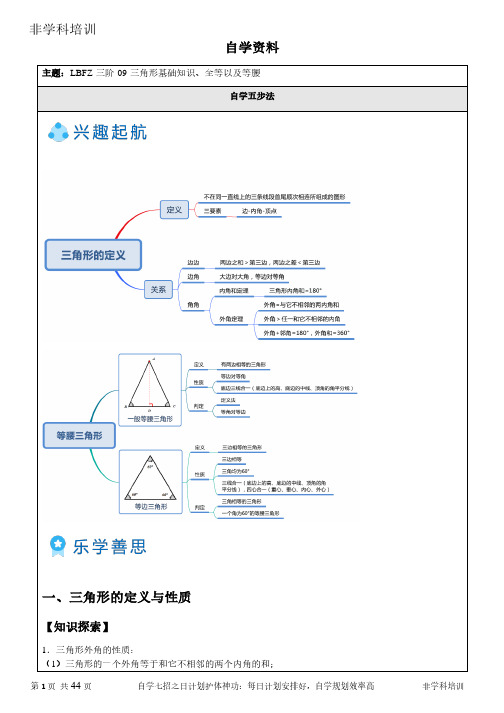
自学资料一、三角形的定义与性质【知识探索】1．三角形外角的性质：（1）三角形的一个外角等于和它不相邻的两个内角的和；第1页共44页自学七招之日计划护体神功：每日计划安排好，自学规划效率高非学科培训（2）三角形的一个外角大于任何一个与它不相邻的内角．2．三角形的三边关系：三角形任意两边的和大于第三边．【说明】三角形任意两边的差小于第三边．【错题精练】例1．如图，已知BE和CF是△ABC的两条高，∠ABC=42°，∠ACB=74°，则∠FDE=______．【解答】解：在△ABC中，∵∠A+∠ABC+∠ACB=180°∴∠A=180°-42°-74°=64°在四边形AFDE中，∵∠A+∠AFC+∠AEB+∠FDE=360°又∵∠AFC=∠AEB=90°，∠A=64°∴∠FDE=360°-90°-90°-64°=116°故答案为：116°【答案】116°例2．如图所示，在△ABC中，∠A=52°，若∠ABC与∠ACB的角平分线交于点D1，得到∠D1，∠ABD1与∠ACD1的角平分线交于点D2，得到∠D2；依此类推，∠ABD4与∠ACD4的角平分线交于点D5，得到∠D5，则∠D5的度数是______．【解答】解：∵∠A=52°，∴∠ABC+∠ACB=180°-52°=128°，又∠ABC与∠ACB的角平分线交于D1，∴∠ABD1=∠CBD1=12∠ABC，∠ACD1=∠BCD1=12∠ACB，∴∠CBD1+∠BCD1=12（∠ABC+∠ACB）=12×128°=64°，第2页共44页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训∴∠BD1C=180°-1（∠ABC+∠ACB）=180°-64°=116°，2（∠ABC+∠ACB）=180°-96°=84°，同理∠BD2C=180°-34（∠ABC+∠ACB）=180°-124°=56°．依此类推，∠BD5C=180°-3132故答案为：56°．【答案】56°例3．如图，在△ABC中，BD平分∠ABC，DE⊥AB于E，AB=3cm，BC=2.5cm，△ABD的面积为2cm2，求△ABC的面积．【答案】解：在△ABD中，∵S△ABD=12AB•DE，AB=3cm，S△ABD=2cm2，∴DE=43cm…（2分）过D作DF⊥BC于F．∵BD平分∠ABC，DE⊥AB，DF⊥BC，∴DE=DF，∴DF=43第3页共44页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训cm…（4分）在△BCD中，BC=2.5cm，DF=43cm∴S△BCD=12BC•DF=53(cm)2…（6分）∵S△ABC=S△ABD+S△BCD，∴S△ABC=2+53=113(cm)2…（8分）例4．已知：如图，在△ABC中，∠A=∠ABC，直线EF分别交△ABC 的边AB、AC和CB的延长线于D、E、F．求证：∠F+∠FEC=2∠A．【答案】证明：∵∠FEC=∠A+∠ADE，∠F+∠BDF=∠ABC，∴∠F+∠FEC=∠F+∠A+∠ADE，∵∠ADE=∠BDF，第4页共44页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训∴∠F+∠FEC=∠A+∠ABC，∵∠A=∠ABC，∴∠F+∠FEC=∠A+∠ABC=2∠A．例5．问题1如图①，一张三角形ABC纸片，点D、E分别是△ABC边上两点．研究（1）：如果沿直线DE折叠，使A点落在CE上，则∠BDA′与∠A的数量关系是______研究（2）：如果折成图②的形状，猜想∠BDA′、∠CEA′和∠A的数量关系是______研究（3）：如果折成图③的形状，猜想∠BDA′、∠CEA′和∠A的数量关系，并说明理由．猜想：______理由问题2研究（4）：将问题1推广，如图④，将四边形ABCD纸片沿EF折叠，使点A、B落在四边形EFCD的内部时，∠1+∠2与∠A、∠B之间的数量关系是______．【解答】解：（1）根据折叠的性质可知∠DA′E=∠A，∠DA′E+∠A=∠BDA′，故∠BDA′=2∠A；（2）由图形折叠的性质可知，∠CEA′=180°-2∠DEA′…①，∠BDA′=180°-2∠A′DE…②，①+②得，∠BDA′+∠CEA′=360°-2（∠DEA′+∠A′DE即∠BDA′+∠CEA′=360°-2（180°-∠A），故∠BDA′+∠CEA′=2∠A；（3）∠BDA′-∠CEA′=2∠A．证明如下：连接AA′构造等腰三角形，∠BDA′=2∠DA'A，∠CEA'=2∠EA'A，得∠BDA'-∠CEA'=2∠A，（4）如图④，由图形折叠的性质可知∠1=180°-2∠AEF，∠2=180°-2∠BFE，两式相加得，∠1+∠2=360°-2（∠AEF+∠BFE）即∠1+∠2=360°-2（360°-∠A-∠B），所以，∠1+∠2=2（∠A+∠B）-360°．第5页共44页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训【答案】∠BDA′=2∠A∠BDA′+∠CEA′=2∠A∠BDA′-∠CEA′=2∠A∠1+∠2=2（∠A+∠B）-360°例6．我们定义：在一个三角形中，如果一个角的度数是另一个角度数的3倍，那么这样的三角形我们称之为“和谐三角形”．如：三个内角分别为105°，40°，35°的三角形是“和谐三角形”概念理解：如图1，∠MON=60°，在射线OM上找一点A，过点A作AB⊥OM交ON于点B，以A为端点作射线AD，交线段OB于点C（点C不与O，B重合）（1）∠ABO的度数为______，△AOB______（填“是”或“不是”）“和谐三角形”；（2）若∠ACB=80°，求证：△AOC是“和谐三角形”．应用拓展：如图2，点D在△ABC的边AB上，连接DC，作∠ADC的平分线交AC于点E，在DC上取点F，使∠EFC+∠BDC=180°，∠DEF=∠B．若△BCD是“和谐三角形”，求∠B的度数．【解答】解：（1）∵AB⊥OM，∴∠OAB=90°，∴∠ABO=90°-∠MON=30°，∵∠OAB=3∠ABO，∴△AOB为“和谐三角形”，故答案为：30；是；（2）证明：∵∠MON=60°，∠ACB=80°，∵∠ACB=∠OAC+∠MON，∴∠OAC=80°-60°=20°，∵∠AOB=60°=3×20°=3∠OAC，∴△AOC是“和谐三角形”；应用拓展：∵∠EFC+∠BDC=180°，∠ADC+∠BDC=180°，∴∠EFC=∠ADC，∴AD∥EF，∴∠DEF=∠ADE，第6页共44页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训∵∠DEF=∠B，∴∠B=∠ADE，∴DE∥BC，∴∠CDE=∠BCD，∵AE平分∠ADC，∴∠ADE=∠CDE，∴∠B=∠BCD，∵△BCD是“和谐三角形”，∴∠BDC=3∠B，或∠B=3∠BDC，∵∠BDC+∠BCD+∠B=180°，∴∠B=36°或∠B=540°7．【答案】30°是【举一反三】1．如图所示，△ABC中，点D，E分别是AC，BD上的点，且∠A=65°，∠ABD=∠DCE=30°，则∠BEC的度数是______．【解答】解：∵∠BDC=∠A+∠ABD=65°+30°=95°，∠BEC=∠BDC+∠DCE=95°+30°=125°，故答案为125°．【答案】125°2．已知等腰三角形的周长为29，一边长为7，则此等腰三角形的腰长为______．【解答】解：若腰长为7，则底边=29-2×7=15，∵7+7＜15∴不能组成三角形第7页共44页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训若底边为7，则腰长=（29-7）÷2=11故答案为11【答案】113．在△ABC中，已知点D，E，F分别是BC、AD、CE的中点，且三角形ABC的面积等于4cm2，则三角形BEF的面积等于______cm2．【解答】解：如图，点F是CE的中点，∴△BEF的底是EF，△BEC的底是EC，即EF=12EC，高相等；∴S△BEF=12S△BEC，同理得，S△EBC=12S△ABC，∴S△BEF=14S△ABC，且S△ABC=4cm2，∴S△BEF=1cm2，即阴影部分的面积为1cm2．故答案为：1．【答案】1第8页共44页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训4．如图，将△ABC的三边AB，BC，CA分别延长至B′，C′，A′，且使BB′=AB，CC′=2BC，AA′=3AC．若S△ABC=1，那么S△A'B'C'是（）A. 15B. 16C. 17D. 18【解答】解：连接CB'，∵AB=BB'，∴S△BB'C=S△ABC=1，又CC'=2BC，∴S△B'CC'=2S△BB'C=2．∴S△BB'C'=3．同理可得S△A'CC'=8，S△A'B'A=6．∴S△A'B'C'=3+8+6+1=18．∴故选D．【答案】D5．如图1，在△ABC中，AD平分∠BAC，AE⊥BC，垂足为E．（1）若∠B=35°，∠C=75°，求∠DAE的度数；（2）若∠B=α，∠C=β，且0°＜α＜β＜90°，试探究下列问题：①∠DAE=______（用含α、β的代数式表示）；②若点P为射线AD上任意一点（除点A、点D外），过点P作PQ⊥BC，垂足为Q（请在图2、图3中将图形补充完整），请用含α、β的代数式表示∠DPQ并说明理由．【解答】解：（1）∵∠B=35°，∠C=75°，∴∠BAC=180°-∠B-∠C=70°，∵AD平分∠BAC，∠BAC=35°，∴∠DAC=12∵AE⊥BC，∴∠AEC=90°，∵∠C=75°，第9页共44页自学七招之以背代诵掌：高效记忆有妙招，以背代诵效果好非学科培训∴∠EAC=90°-75°=15°，∴∠DAE=∠DAC-∠EAC=35°-15°=20°；（2）①∵∠B=α，∠C=β，∴∠BAC=180°-∠B-∠C=（180-α-β）°，∵AD平分∠BAC，∴∠DAC=12∠BAC=12（180-α-β）°=90°-12α-12β，∵AE⊥BC，∴∠AEC=90°，∵∠C=β，∴∠EAC=90°-β，∴∠DAE=∠DAC-∠EAC=（90°-12α-12β）-（90°-β）=12β-12α，故答案为：12β-12α；②如图，∵∠B=α，∠C=β，∴∠BAC=180°-∠B-∠C=180°-α-β，∵AD平分∠BAC，∴∠DAC=12∠BAC=12×（180°-α-β）=90°-12α-12β，∵∠ADC=180°-∠C-∠DAC=180°-β-（90°-12α-12β）=90°-12β+12α，∴∠QDP=∠ADC=90°-12β+12α，∵PQ⊥BC，∴∠PQD=90°，∴∠DPQ=90°-∠PDQ=90°-（90°-12β+12α）=1 2β-12α，即∠DPQ=12β-12α．【答案】12β-12α第10页共44页自学七招之举一反三剑：总结归纳典型题，多种解法开脑洞非学科培训6．（1）如图1，在△ABC中，BD、CD分别是△ABC两个内角∠ABC、∠ACB的平分线．①若∠A=70°，求∠BDC的度数．②∠A=α，请用含有α的代数式表示∠BDC的度数．（2）如图2，BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线．若∠A=α，请用含有α的代数式表示∠BEC的度数．【答案】解：（1）①∵∠ABC，∠ACB的平分线相交于点D，∴∠ABD=∠CBD，∠BCD=∠ACD，∵∠DBC+∠BCD+∠BDC=180°，∠ABD+∠CBD+∠BCD+∠ACD+∠A=180°，∴2∠DBC+2∠BCD+∠A=180°，∴2（180°-∠BDC）+∠A=180°，∴∠BDC=90°+12∠A，∵∠A=70°，∴∠BDC=90°+12×70°=90°+35°=125°．②∠A=90°+12α．（2）∵BE、CE分别是△ABC两个外角∠MBC、∠NCB的平分线，∴∠EBC=12∠MBC，∠BCE=12∠BCM，∵∠CBM、∠BCN是△ABC的两个外角∴∠CBM+∠BCN=360°-（180°-∠A）=180°+∠A∴∠EBC+∠BCE=12（∠MBC+∠BCN）=12（180°+∠A）=90°+12∠A，在△DBC中，∵∠BEC=180°-（∠EBC+∠BCE）=180°-（90°+12∠A）=90°-12∠A，且∠A=α，∴∠BEC=90°-12α．7．已知：∠MON=40°，OE平分∠MON，点A、B、C分别是射线OM、OE、ON上的动点（A、B、C 不与点O重合），连接AC交射线OE于点D．设∠OAC=x°．（1）如图1，若AB∥ON，则①∠ABO的度数是_______②当∠BAD=∠ABD时，求∠OAC；③当∠BAD=∠BDA时，求∠OAC．（2）如图2，若AB⊥OM，且D在线段OB上，则是否存在这样的x的值，使得△ADB中有两个相等的角？若存在，求出x的值；若不存在，说明理由．【解答】【答案】（1）①20∘②120∘③60∘（2）存在，x=20∘,30∘,50∘,125∘二、全等三角形【知识探索】1．能够重合的两个图形叫做全等形．两个三角形是全等形，就说它们是全等三角形．两个全等三角形，经过运动后一定重合，相互重合的顶点叫做对应顶点；相互重合的边叫做对应边；相互重合的角叫做对应角．【错题精练】例1．两个三角形的两条边及其中一条边的对角对应相等，下面说法正确的有（）（1）这两个三角形一定全等；（2）这两个三角形不一定全等；（3）相等的角为锐角时，这两个三角形全等；（4）相等的角是钝角时，这两个三角形全等．A. 1种B. 2种C. 3种D. 4种【解答】解：两个三角形的两条边及其中一条边的对角对应相等，满足SSA，但是SSA不能判定三角形的全等．但当相等的角是钝角时，这两个三角形全等．则说法正确的只有（2）（4）．故选：B．【答案】B例2．已知：BE⊥CD，BE=DE，BC=DA，求证：①△BEC≌△DEA；②DF⊥BC．【答案】证明：（1）∵BE⊥CD，BE=DE，BC=DA，∴△BEC≌△DEA（HL）；（2）∵△BEC≌△DEA，∴∠B=∠D．∵∠D+∠DAE=90°，∠DAE=∠BAF，∴∠BAF+∠B=90°．即DF⊥BC．例3．【问题探究】（1）如图1，锐角△ABC中，分别以AB、AC为边向外作等腰△ABE和等腰△ACD，使AE=AB，AD=AC，∠BAE=∠CAD，连接BD，CE，试猜想BD与CE的大小关系，并说明理由．【深入探究】（2）如图2，四边形ABCD中，AB=5cm，BC=3cm，∠ABC=∠ACD=∠ADC=45°，求BD的长．（3）如图3，在（2）的条件下，当△ACD在线段AC的左侧时，求BD的长．例4．如图，点F、G分别是正五边形ABCDE边BC、CD上的点，且BF=CG，AF与BG交于点H．（1）求证：△ABF≌△BCG（2）求∠AHG的度数．【答案】（1）证明：∵正五边形ABCDE，∴AB=BC，∠ABF=∠C，∴在△ABF和△BCG中AB=CB∠ABF=∠C BF=CGAB=CB∠ABF=∠CBF=CG，∴△ABF≌△BCG（SAS）；（2）解：∵△ABF≌△BCG，∴∠BAF=∠CBG，∵∠BAF+∠ABH=∠AHG，∴∠CBH+∠ABH=∠AHG=∠ABC=(5-2)180°5=108°．∴∠AHG=108°．例5．如图，点A、B、C在⊙O上，AĈ=CB̂．（1）若D、E分别是半径OA、OB的中点，如图1，求证：CD=CE．（2）如图2，⊙O的半径为4，∠AOB=90°，点P是线段OA上的一个动点（与点A、O不重合），将射线CP绕点C逆时针旋转90°，与OB相交于点Q，连接PQ，求出PQ的最小值．【答案】解：（1）连接CO．∵AĈ═CB̂，∴∠AOC=∠BOC，∵D、E分别是半径OA、OB的中点，∴OD=12OA，OE=12OB，∴OD=OE，在△ODC和△OEC中，∵OD=OE，∠AOC=∠BOC，OC=OC，∴△ODC≌△OEC（SAS）∴CD=CE；（2）当CP⊥OA时，∵∠AOB=90°，∠PCQ=90°，∴∠CQO=90°，即CQ⊥OB．∵∠AOC=∠BOC，∴CP=CQ，当CP与OA不垂直时，如图，过点C作CM⊥OA，CN⊥OB，M、N为垂足．∵∠AOC=∠BOC，∴CM=CN，又∵∠AOB=90°，∴∠MCN=90°，∴四边形CMON是正方形，∵∠PCQ=90°，∴∠PCM=∠QCN，∴△PCM≌△QCN（AAS）∴CP=CQ，∴PQ=√2CP，∴当CP取得最小值即CM的长时，PQ有最小值，∴PQ=√2CP≥√2CM=CO=4，PQ的最小值为4．【举一反三】1．下列4个判断：①有两边及第三边上的高对应相等的两个三角形全等；②两个三角形的6个边．角元素中，有5个元素分别相等的两个三角形全等；③有两边及其中一边上的高对应相等的两个三角形全等；④有两边及第三边上的中线对应相等的两个三角形全等；其中正确判断的编号是______．【解答】解：①如图，△ABC与△ABC′中，AB=AB，AC=AC′，高AD相同，但是，△ABC与△ABC′不全等，，故选项错误；②设△ABC的三边长分别为AB=16AC=24，BC=36；△A′B′C′的三边长分别为A′B′=24A′C′=36，B′C′=54．由于△ABC与△A′B′C′的对应边成比例故△ABC∽△A′B′C′，从而它们有5个边角元素分别相等：∠A=∠A′，∠B=∠B′，∠C=∠C′，AC=A′B′，BC=A′C′，但它们不全等；故该选项错误；③有两边及其中一边上的高对应相等的两个三角形不一定全等，如图：△ABC和△ACD，的边AC=AC，BC=CD，高AE=AE，但△ABC和△ACD不全等，故选项错误；④可根据SSS证明△ABD≌△A′B′D′以及利用SAS证明△ABC≌△A′B′C′，故选项正确．故选④．【答案】④2．如图，△ABC的两条高AD、BE相交于H，且AD=BD，试说明下列结论成立的理由．（1）∠DBH=∠DAC；（2）BH=AC；（3）如果BC=14，AH=2，AC=10，求HE的长度．【答案】解：（1）∵AD，BE是△ABC的高∴∠ADC=∠BEC=90°，∴∠DBH+∠C=90°，∠DAC+∠C=90°∴∠DBH=∠DAC；（2）由（1）题已得∠DBH=∠DAC，∵在△BDH和△ADC中，∠BDH=∠A DC BD=AD∠DBH=∠DAC∠BDH=∠A DCBD=AD∠DBH=∠DAC，∴△BDH≌△ADC（ASA），∴BH=AC；（3）由（2）题已证△BDH≌△ADC，∴HD=DC（设长度为x）设AD=BD=y，∵BC=14，AH=2，AC=10∴x+y=14，y-x=2．解得x=6，y=8，∵12×AC×BE=12×BC×AD，∴10×BE=14×8，解得BE=11.2，∴HE=BE-BH=11.2-10=1.2．3．如图，已知∠1=∠2，P为BN上一点，且PD⊥BC于D，AB+BC=2BD，求证：∠BAP+∠BCP=180°．【答案】证明：如图，过点P作PE⊥AB于E，∵∠1=∠2，PD⊥BC，∴PD=PE，在Rt△BPE和Rt△BPD中，BP=BP PE=PDBP=BPPE=PD，∴Rt△BPE≌Rt△BPD（HL），∴BE=BD，∵AB+BC=2BD，∴BE-AE+BD+CD=2BD，∴AE=CD，在△APE和△CPD中，AE=CDPD=PE∠AEP=∠CDP=90°PD=PE∠AEP=∠CDP=90°AE=CD，∴△APE≌△CPD（SAS），∴∠BCP=∠PAE，∵∠BAP+∠PAE=180°，∴∠BAP+∠BCP=180°．4．已知，如图，AB=AC，BD=CD，DE⊥AB于点E，DF⊥AC于点F，（1）求证：DE=DF．（2）连接BC，求证：线段AD垂直平分线段BC．【答案】解：（1）如图，连接AD ．在△ACD 和△ABD 中，AC=AB CD=BD AD=ADAC=AB CD=BD AD=AD∴△ACD ≌△ABD （SSS ）． ∴∠FAD=∠EAD ，即AD 平分∠EAF ．又∵DE ⊥AE ，DF ⊥AF ， ∴DE=DF ．（2）∵△ACD ≌△ABD （已证）． ∴DC=DB ，∴点D 在线段BC 的垂直平分线上．又∵AB=AC∴点A 在线段BC 的垂直平分线上． ∵两点确定一条直线， ∴AD 垂直平分BC ．5．如图，AĈ是劣弧，M 是AC ̂的中点，B 为AM ̂上任意一点．自M 向BC 弦引垂线，垂足为D ，求证：AB+BD=DC ．【答案】证明：在CD 上取点N ，使CN=AB ，连接CM ，MN∵M 是AC ̂的中点， ∴AM̂=CM ̂， ∴AM=CM （等弧对等弦），又∵∠BAM=∠BCM ，在△ABM 和△CNM 中，{CN=AB∠BAM=∠BCMAM=CM，∴△ABM≌△CNM（SAS），∴BM=MN，∴△BMN为等腰三角形（BN为底），又∵MD⊥BN，∴D为BN中点（等腰三角形三线合一），∴BD=DN∴AB+BD=CD．三、等腰三角形【知识探索】1．有两边相等的三角形叫做等腰三角形2．三边都相等的三角形叫做等边三角形．【说明】等边三角形的三边都相等，它是特殊的等腰三角形．【错题精练】例1．如图，△ABC的面积为1cm2，BP平分∠ABC，AP⊥BP于P，则△PBC的面积为（）A. 0.4cm2B. 0.5cm2C. 0.6cm2D. 0.7cm2【解答】解：∵BP平分∠ABC，∴∠ABP=∠EBP，∵AP⊥BP，∴∠APB=∠EPB=90°，在△ABP和△EBP中，∠ABP=∠EB P BP=BP∠APB=∠EPB∠ABP=∠EB PBP=BP∠APB=∠EPB，∴△ABP≌△EBP（ASA），∴AP=PE，∴S△ABP=S△EBP，S△ACP=S△ECP，∴S△PBC=12S△ABC=12×1cm2=0.5cm2，故选：B．【答案】B例2．如图，在△ABC中，AB=AC，E在AC上，经过A，B，E三点的圆O交BC于点D，且D点是弧BE的中点，（1）求证AB是圆的直径；（2）若AB=8，∠C=60°，求阴影部分的面积；（3）当∠A为锐角时，试说明∠A与∠CBE的关系．例3．如图钢架中，∠A=n°，依次焊上等长的钢条P1P2，P2P3，…，来加固钢架，若P1A=P1P2，要使得这样的钢条只能焊上4根，则n的取值范围是______．【解答】解：∵AP1=P1P2，P1P2=P2P3，P3P4=P2P3，P3P4=P4P5，∴∠A=∠P1P2A，∠P2P1P3=∠P2P3P1，∠P3P2P4=∠P3P4P2，∠P4P3P5=∠P4P5P3，∴∠P3P5P4=4∠A，∵要使得这样的钢条只能焊上4根，∴∠P5P4C=5∠A，由题意4n＜905n≥904n＜905n≥90，∴18≤n＜22.5，故答案为：18≤n＜22.5．【答案】18≤n＜22.5例4．如图，∠AOB=45°，点M，N在边OA上，OM=3，ON=7，点P是直线OB 上的点，要使点P，M，N构成等腰三角形的点P有______个．【解答】解：过M作MM′⊥OB于M′，过N作NN′⊥OB于N′，∵OM=3，ON=7，∠AOB=45°，∴MN=4，MM′=OM×sin45°=32√2＜4，NN′=ON×sin45°=72√2＞4，MH=M′N′=4×sin45°=2√2＜4，所以只有一小两种情况：①以M为圆心，以4为半径画弧，交直线OB于P1、P2，此时△NP1M和△NMP2都是等腰三角形；②作线段MN的垂直平分线，交直线PB于P3，此时△MNP3是等腰三角形，即有3个点P符合，故答案为：3．【答案】3例5．如图，D和E分别是△ABC的边BC和AC上的点，若AB=AC，AD=AE，则下列说法正确的是（）A. 当∠1为定值时，∠CDE为定值B. 当∠2为定值时，∠CDE为定值C. 当∠3为定值时，∠CDE为定值D. 当∠B为定值时，∠CDE为定值【解答】解：A∵AB=AC，∴∠B=∠C，又∠ADC=∠1+∠B，∴∠ADE=∠ADC-∠CDE=∠1+∠B-∠CDE，∵AD=AE，∴∠ADE=∠3=∠CDE+∠C=∠CDE+∠B，∴∠1+∠B-∠CDE=∠CDE+∠B，∴∠1=2∠CDE，∴当∠1为定值时，∠CDE为定值，故选：A．【答案】A例6．等腰三角形一腰上的高等于腰长的一半，则顶角的度数是（）A. 30°B. 60°C. 30°或150°D. 不能确定【解答】解：本题分两种情况讨论：（1）当BD在三角形内部时，AB，∠ADB=90°，∵BD=12∴∠A=30°；（2）当BD在三角形外部时，AB，∠ADB=90°，∵BD=12∴∠DAB=30°，∠ABC=180°-∠DAB=30°=150°．故选：C．【答案】C例7．如图，已知直线PQ⊥MN于点O，点A，B分别在MN，PQ上，OA=1，OB=2，在直线MN或直线PQ上找一点C，使△ABC是等腰三角形，则这样的C点有______个．【解答】解：使△ABC是等腰三角形，当AB当底时，则作AB的垂直平分线，交PQ，MN的有两点，即有两个三角形．当让AB当腰时，则以点A为圆心，AB为半径画圆交PQ，MN有三点，所以有三个．当以点B为圆心，AB为半径画圆，交PQ，MN有三点，所以有三个．所以共8个，故答案为：8【答案】8例8．等腰三角形一腰上的中线把周长分为15和12两部分，求该三角形各边的长．【答案】解：在△ABC 中，AB=AC ，BD 是中线，设AB=x ，BC=y（1）当AB+AD=12时，则{x +12x =12y +12x =15，解得{x =8y =11．∴三角形三边的长为8、8、11；（2）当AB+AD=15时，则{x +12x =15y +12x =12，解得{x =10y =7．∴三角形三边的长为10、10、7经检验，两种情况均符合三角形三边关系定理因此这个三角形的三边长分别为8，8，11或10，10，7．例9．如图，在△ABC 中，AB=AC ，∠B=30°，点D 从点B 出发，沿B→C 方向运动到点C （D 不与B ，C 重合），连接AD ，作∠ADE=30°，DE 交线段AC 于点E ，设∠BAD=x°，∠AED=y°．（1）当BD=AD 时，求∠DAE 的度数；（2）求y 与x 的关系式；（3）当BD=CE 时，求x 的值．【答案】解：（1）当BD=AD 时，∠B=∠BAD=30°，∵△ABC 等腰三角形，∴∠BAC=120°，∴∠DAE=∠BAC-∠BAD=120°-30°=90° （2）由题可知，∠BAD+∠DAE=120°即x+∠DAE=120 ∠AED+∠DAE=180°-∠ADE=150°即y+∠DAE=150 两式相减得y-x=30即y=x+30（3）由题可知，∠B+∠BAD=∠ADE+∠EDC 且∠B=∠ADE=30° ∴∠BAD=∠EDC=x 又∵∠B=∠C 和BD=CE ∴△ABD ≌△DCE∴CD=AB=AC∴△ACD为等腰三角形且∠C=30°∴∠DAE=75°∴x=∠BAC-∠DAE=120°-75°=45即x=45【举一反三】1．如图，△ABC中，AB=AC，点D在AC边上，若AD=BD=BC，则∠A的度数为（）A. 70° B. 45° C. 36° D. 30°【解答】解：∵AB=AC，∴∠ABC=∠C，∵BD=BC=AD，∴∠A=∠ABD，∠C=∠BDC，，设∠A=∠ABD=x，则∠BDC=2x，∠C=180°−x2可得2x=180°−x，2解得：x=36°，则∠A=36°，故选：C．【答案】C2．如图，在△ABC中，AB=AC，∠BAC=108°，若AD、AE三等分∠BAC，则图中等腰三角形有（）A. 3个B. 4个C. 5个D. 6个【解答】解：∵AB=AC，∠BAC=108°，∴∠B=∠C=36°，△ABC是等腰三角形，∵∠BAC=108°，AD、AE三等分∠BAC，∴∠BAD=∠DAE=∠EAC=36°，∴∠DAC=∠BAE=72°，∴∠AEB=∠ADC=72°，∴BD=AD=AE=CE，AB=BE=AC=CD，∴△ABE、△ADC、△ABD、△ADE、△AEC是等腰三角形，∴一共有6个等腰三角形．故选：D．【答案】D3．如图，BD、CE分别是∠ABC和∠ACB的角平分线，已知AG⊥BD，AF⊥CE，若BF=2，ED=3，GC=4，则△ABC的周长为______．【解答】解：由AG⊥BD，BD是∠ABC的角平分线，则在△ABD和△GBD中，BD=BD∠ADB=GDB∠ABD=∠GBD∠ABD=∠GBDBD=BD∠ADB=GDB，∴△ABD≌△GBD，∴AB=BG．即△ABG是等腰三角形，同理：△ACF也是等腰三角形．∴AB=BG，AC=CF，又∵AG⊥BD，AF⊥CE，∴E、D分别是AF和AG 的中点，∴ED是△AFG的中位线，∴FG=2DE，则△ABC的周长为：AB+BC+AC=BG+CG+BC=BF+FG+BF+FG+CG+FG+CG，由BF=2，ED=3，GC=4，FG=2DE=6得△ABC的周长为30．故答案为：30．4．等腰三角形一腰上的高与另一腰所在直线的夹角为40°，该等腰三角形的顶角等于______．【解答】解：①如图，等腰三角形为锐角三角形，∵BD⊥AC，∠ABD=40°，∴∠A=50°，即顶角的度数为50°．②如图，等腰三角形为钝角三角形，∵BD⊥AC，∠DBA=40°，∴∠BAD=50°，∴∠BAC=130°．故答案为50°或130°．【答案】50°或130°5．等腰三角形一腰上的高与另一腰的夹角为30°，则底角为______．【解答】解：当等腰三角形为锐角三角形时，如图1，由已知可知，∠ABD=30°，又BD⊥AC，∴∠ADB=90°，∴∠A=60°，∴∠ABC=∠C=60°．当等腰三角形为钝角三角形时，如图2，由已知可知，∠ABD=30°，∴∠DAB=60°，∴∠C=∠ABC=30°．故答案为：60°或30°．【答案】60°或30°6．如图，已知在△ABC中，∠ACB=90°，在AB上截取AE=AC，BD=BC．求证：∠DCE=45°．【答案】证明：∵∠ACB=90°，∴∠A+∠B=90°，∵AC=AE，BD=BC，∴∠BCD=∠BDC=12（180°-∠B），∠ACE=∠AEC=12（180°-∠A），∴∠BCD+∠ACE=180°-12（∠A+∠B）=135°，∴∠DCE=∠BCD+∠ACE-∠ACB=135°-90°=45°．7．如图所示，△ABC中，AC=BC，以AC为直径的⊙O交AB于E，作△BCA的外角平分线CF交⊙O于F，连接EF，求证：EF=BC．【答案】证明：∵CA=CB，∴∠B=∠A，又∵∠DCA=2∠FCA，∠DCA=∠A+∠B=2∠A，∴∠FCA=∠A．∴CF∥AB．又∵∠FCA=∠FEA（同弧所对的圆周角相等），∴∠FEA=∠B．∴BC∥EF．∴四边形CFEB为平行四边形．∴EF=BC．8．如图，在△ABC中，AB=AC，⊙O是△ABC的外接圆，D为弧AC的中点，E是BA延长线上一点，∠DAE=105°．（1）求∠DAC的度数；（2）若⊙O的半径为3，求弧BC的长．【答案】解：（1）∵AB=AC，̂=AĈ，∴AB∴∠ABC=∠ACB，̂的中点，∵D为AĈ=CD̂，∴AD∴∠CAD=∠ACD，̂=2AD̂，∴AB∴∠ACB=2∠ACD，又∵∠DAE=105°，∴∠BCD=105°，×105°=35°，∴∠ACD=13∴∠CAD=35°；（2）∵∠DAE=105°，∠CAD=35°，∴∠BOC=80°，∴弧BC的长=80•π×32360=2π．1．等腰三角形一腰上的高线与底边的夹角等于（）A. 顶角B. 底角C. 顶角的一半D. 底角的一半【解答】解：如图，过点A作AE⊥BC，则AE平分∠BAC，∴∠2=12∠A，∵BD⊥AC，∴∠1+∠C=90°，又∠2+∠C=90°，∴∠1=∠2，∴∠1=12∠A，即等腰三角形一腰上的高与底边的夹角等于顶角的一半，故选：C．【答案】C2．如图，点D是△ABC的边BC上的一点，则在△ABC中∠C所对的边是______；在△ACD中∠C所对的边是______；在△ABD中边AD所对的角是______；在△ACD中边AD 所对的角是______．【解答】解：在△ABC中∠C所对的边是AB；在△ACD中边AD所对的角是∠C；故答案为：AB；AD；∠B；∠C．【答案】ABAD∠B∠C3．如图，△ABC中，∠A=96°，D是BC延长线上的一点，∠ABC与∠ACD（△ACB的外角）的平分线交于A1点，则∠A1=______度；如果∠A=α，按以上的方法依次作出∠BA2C，∠BA3C…∠BA n C（n为正整数），则∠A n=______度（用含α的代数式表示）．【解答】解：∵∠ABC与∠ACD（△ACB的外角）的平分线交于A1点，∴∠A1BC=12∠ABC，∠A1CA=∠A1CD=12∠ACD，∴∠A1=180°-（∠A1BC+∠A1CB）=180°-（12∠ABC+12∠ACD+∠ACB）=180°-[12∠ABC+12（∠ABC+∠A）+∠ACB]=180°-[∠ABC+∠ACB+12∠A]=180°-[180°-∠A+12∠A]=12∠A．∵∠A=96°，∴∠A1=48°．∵∠A=α，依此类推可知∠A n=12nα度．【答案】4812nα4．如图，将一张三角形纸片ABC的一角折叠，使点A落在△ABC外的A'处，折痕为DE．如果∠A=α，∠CEA′=β，∠BDA'=γ，则α，β，γ三者之间的等量关系是______．【解答】解：由折叠得：∠A=∠A'，∵∠BDA'=∠A+∠AFD，∠AFD=∠A'+∠CEA'，∵∠A=α，∠CEA′=β，∠BDA'=γ，∴∠BDA'=γ=α+α+β=2α+β，故答案为：γ=2α+β．【答案】γ=2α+β5．如图：将△ABC纸片沿DE折叠成图①，此时点A落在四边形BCDE内部，则∠A与∠1、∠2之间有一种数量关系保持不变，请找出这种数量关系并说明理由．（1）若折成图②或图③，即点A落在BE或CD上时，分别写出∠A与∠2；∠A与∠1之间的关系；（不必证明）（2）若折成图④，写出∠A与∠1、∠2之间的关系式；（不必证明）（3）若折成图⑤，写出∠A与∠1、∠2之间的关系式．（不必证明）【答案】解：延长BD、CE，交于点P；则△BCP即为折叠前的三角形，由折叠的性质知：∠DAE=∠DPE．图①中：连接AP；由三角形的外角性质知：∠1=∠DAP+∠DPA，∠2=∠EAP+∠EPA；则∠1+∠2=∠DAE+∠DPE=2∠DAE，即∠1+∠2=2∠A．图②中：由三角形的外角性质知：∠2=∠DPE+∠DAE=2∠DAE，即∠2=2∠A．图③中：∠1=2∠A，解法同图②．图④中：由三角形的外角性质，知：∠2=∠3+∠P，∠3=∠1+∠A，即∠2=∠P+∠1+∠A=2∠A+∠1，故∠2-∠1=2∠A．图⑤中：∠1-∠2=2∠A，解法同图④．故当点A落在四边形BCDE内部，∠1+∠2=2∠A．（1）图②中，∠2=2∠A；图③中，∠1=2∠A．（2）图④中，∠2-∠1=2∠A．（3）图⑤中，∠1-∠2=2∠A．6．如图，在△ABC中，AD是BC边上的中线．若△ABC的周长为35，BC=11，且△ABD与△ACD的周长差为3，求AB，AC的长．【答案】解：∵AD是BC边上的中线，△ABD与△ACD的周长差为3，∴AB-AC=3，∵△ABC的周长为35，BC=11，∴AB+AC=35-11=24，∴AC+3+AC=24，解得：AC=10.5，∴AB=13.5．7．已知△ABC．（1）如图1，若P点为∠ABC和∠ACB的角平分线的交点，试说明：∠P=90°+12∠A；（2）如图2，若P点为∠ABC和外角∠ACD的角平分线的交点，试说明：∠P=12∠A；（3）如图3，若P点为外角∠CBD和∠BCE的角平分线的交点，试说明：∠P=90°-12∠A．【答案】证明：（1）∠P=180°-12∠ABC-12∠ACB=180°-12（180°-∠A）=90+12∠A（2）∠P=∠PCD-∠PBD=12∠ACD-12∠ABC=12∠A（3）∠P=180°-12∠CBD-12∠BCE=180°-12（∠CBD+∠BCE）=180°-12（∠A+∠ACB+∠A+∠ABC）=180°-12（180°+∠A）=90°-12∠A．8．如图，在△ABC中，AD是∠BAC的外角平分线，P是AD上异于点A的任一点，试比较PB+PC与AB+AC的大小，并说明理由．【答案】解：PB+PC＞AB+AC．如图，在BA的延长线上取一点E，使AE=AC，连接EP，由AD是∠BAC的外角平分线，可知∠CAP=∠EAP，又AP是公共边，AE=AC，在△ACP与△AEP中，{AE=AC∠EAP=∠CAPAP=AP，∴△ACP≌△AEP（SAS），从而有PC=PE，在△BPE中，PB+PE＞BE，而BE=AB+AE=AB+AC，故PB+PE＞AB+AC，所以PB+PC＞AB+AC．9．已知AB是⊙O的直径，半径OC⊥AB，D为AĈ上任意一点，E为弦BD上一点，且BE=AD．（1）试判断△CDE的形状，并加以证明．（2）若∠ABD=15°，AO=4，求DE的长．证明如下：如图1，连接AC、BC，则∠DAC=∠DBC，∵AB为直径，CO⊥AB，∴△ABC为等腰直角三角形，∴AC=BC，在△ADC和△BEC中{AD=BE∠DAC=∠EBCAC=BC∴△ADC≌△BEC（SAS），∴CD=CE，∠DCA=∠BCE，∵∠ACB=90°，∴∠ACE+∠BCE=90°，∴∠DCA+∠ACE=90°，即∠DCE=90°，∴△CDE为等腰直角三角形；（2）如图2，连接OD，则∠AOD=2∠ABD=2×15°=30°，∵∠AOC=90°，∴∠DOC=60°，且OD=OC=OA=4，∴△OCD为等边三角形，∴CD=CE=OA=4，在Rt△CDE中，由勾股定理可得DE=√CD2+CE2=√42+42=4√2．10．如图，⊙O是△ABC的外接圆，AO⊥BC于F，D为AĈ的中点，E是BA延长线上一点，∠DAE=126°，则∠CAD等于（）A. 36°B. 42°C. 38°D. 27°【解答】解：∵AO⊥BC，且AO是⊙O的半径，∴AO垂直平分BC，∴AB=AC，即∠ABC=∠ACB，̂的中点，∵D是AC∴∠ABC=2∠DCA=2∠DAC，∴∠ACB=2∠DCA，∵四边形ABCD内接于⊙O，∴∠BCD=∠DAE=126°，∴∠ACB+∠DCA=126°，即3∠DCA=126°，∴∠DAC=∠DCA=42°．故选：B．【答案】B11．一个等腰三角形一个内角是另一个内角的2倍，则这个三角形底角为（）A. 72°或45°B. 45°或36°C. 36°或45°D. 72°或90°【解答】解：①设三角形底角为x，顶角为2x，则x+x+2x=180°，解得：x=45°，②设三角形底角为2x，顶角为x，则2x+2x+x=180°，解得：x=36°，∴2x=72°，综上所述，这个三角形底角为72°或45°，故选：A．【答案】A12．如图钢架中，焊上等长的钢条P1P2，P2P3，P3P4，P4P5…至多需要8根加固钢架，若P1A=P1P2，则∠A的取值范围为______．【解答】解：设∠A=x，∴∠P2P1P3=2x，∴∠P3P2P4=3x，…，∠P8P9P7=8x，∴8x≤90°且9x＞90°，则10°≤∠A＜11.25°．故答案为：10°≤∠A＜11.25°．【答案】10°≤∠A＜11.25°13．（1）如图1，在△ABC中，AB=AC，点D在AC上，且AD=BD=BC，求∠A的度数；（2）如图2，点B，D在射线AM上，点C，E在射线AN上，且AB=BC=CD=DE．①若∠EDM=84°，求∠A的度数：②若以E为圆心，ED为半径作弧，与射线DM上没有交点（除D点外），直接写出∠A的取值范围．【答案】解：（1）设∠A=x°，∵AD=BD，∴∠ABD=∠A=x°，∴∠BDC=∠A+∠ABD=2x°，∵BD=BC，∴∠C=∠BDC=2x°，∵AB=AC，∴∠ABC=∠C=2x°，在△ABC中，∠A+∠ABC+∠C=180°，∴x+2x+2x=180，解得：x=36，∴∠A=36°；（2）①∵AB=BC=CD=DE，∴∠A=∠BCA，∠CBD=∠BDC，∠ECD=∠CED，根据三角形的外角性质，∠A+∠BCA=∠CBD，∠A+∠CDB=∠ECD，∠A+∠CED=∠EDM，又∵∠EDM=84°，∴∠A+3∠A=84°，解得：∠A=21°；②∵以E为圆心，ED为半径作弧，与射线DM上没有交点（除D点外）∴E到射线AM的距离大于DE，∴90°≤∠EDM＜120°，14．在△ABC中，AB=AC．（1）如图1，如果∠BAD=30°，AD是BC上的高，AD=AE，则∠EDC=______（2）如图2，如果∠BAD=40°，AD是BC上的高，AD=AE，则∠EDC=______（3）思考：通过以上两题，你发现∠BAD与∠EDC之间有什么关系？请用式子表示：______（4）如图3，如果AD不是BC上的高，AD=AE，是否仍有上述关系？如有，请你写出来，并说明理由．【解答】解：（1）∵在△ABC中，AB=AC，AD是BC上的高，∴∠BAD=∠CAD，∵∠BAD=30°，∴∠BAD=∠CAD=30°，∵AD=AE，∴∠ADE=∠AED=75°，∴∠EDC=15°．（2）∵在△ABC中，AB=AC，AD是BC上的高，∴∠BAD=∠CAD，∵∠BAD=40°，∴∠BAD=∠CAD=40°，∵AD=AE，∴∠ADE=∠AED=70°，∴∠EDC=20°．∠BAD）（3）∠BAD=2∠EDC（或∠EDC=12（4）仍成立，理由如下∵AD=AE，∴∠ADE=∠AED，∴∠BAD+∠B=∠ADC=∠ADE+∠EDC=∠AED+∠EDC=（∠EDC+∠C）+∠EDC=2∠EDC+∠C又∵AB=AC，∴∠B=∠C∴∠BAD=2∠EDC．故分别填15°，20°，∠EDC=1∠BAD2【答案】15°20°∠BAD∠EDC=1215．已知：如图，BD、CE是△ABC的高，F是BC的中点，G是ED的中点，（1）求证：FG⊥DE；（2）若BC=16，ED=4，求FG的长．（结果保留根号）【答案】（1）证明：∵BD、CE是△ABC的高，F是BC的中点，BC，∴在Rt△CEB中，EF=12在Rt△BDC中，FD=1BC，2∴FE=FD，∵G是ED的中点，∴FG是等腰三角形EFD的中线，∴FG⊥DE；（2）解：由（1）得，EF=1BC=8，2∵FE=FD，G是ED的中点，∴EF=1ED=2，2在Rt△FGE中，FG=√EF2−EG2=4√15．。

人教版七年级下数学第七章_三角形_知识点+考点+典型例题(含答案)

第七章三角形【知识要点】一．认识三角形1．关于三角形的概念及其按角的分类定义：由不在同一直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

2．三角形的分类：①三角形按内角的大小分为三类：锐角三角形、直角三角形、钝角三角形。

②三角形按边分为两类：等腰三角形和不等边三角形。

2．关于三角形三条边的关系（判断三条线段能否构成三角形的方法、比较线段的长短）根据公理“两点之间，线段最短”可得：三角形任意两边之和大于第三边。

三角形任意两边之差小于第三边。

3．与三角形有关的线段．．：三角形的角平分线、中线和高三角形的角平分线：三角形的一个角的平分线与对边相交形成的线段；三角形的中线：连接三角形的一个顶点与对边中点的线段，三角形任意一条中线将三角形分成面积相等的两个部分；三角形的高：过三角形的一个顶点做对边的垂线，这条垂线段叫做三角形的高。

注意：①三角形的角平分线、中线和高都是线段，不是直线，也不是射线；②任意一个三角形都有三条角平分线，三条中线和三条高；③任意一个三角形的三条角平分线、三条中线都在三角形的内部。

但三角形的高却有不同的位置：锐角三角形的三条高都在三角形的内部；直角三角形有一条高在三角形的内部，另两条高恰好是它两条直角边；钝角三角形一条高在三角形的内部，另两条高在三角形的外部。

④一个三角形中，三条中线交于一点，三条角平分线交于一点，三条高所在的直线交于一点。

（三角形的三条高（或三条高所在的直线）交与一点，锐角三角形高的交点在三角形的内部，直角三角形高的交点是直角顶点，钝角三角形高（所在的直线）的交点在三角形的外部。

）4．三角形的内角与外角（1）三角形的内角和：180°引申：①直角三角形的两个锐角互余；②一个三角形中至多有一个直角或一个钝角；③一个三角中至少有两个内角是锐角。

（2）三角形的外角和：360°（3）三角形外角的性质：①三角形的一个外角等于与它不相邻的两个内角的和；——常用来求角度②三角形的一个外角大于任何一个与它不相邻的内角。

中考数学复习----《等边三角形》知识点总结与练习题(含答案解)

中考数学复习----《等边三角形》知识点总结与练习题（含答案解）知识点总结1. 等边三角形的概念：三条边都相等的三角形是等边三角形。

2. 等边三角形的性质：①等边三角形的三条边都相等，三个角也相等，且三个角都等于60°。

②等边三角形三条边都存在“三线合一”③等腰三角形是一个轴对称图形，有三条对称轴。

④等腰三角形的面积等于243a （a 为等腰三角形的边长）。

3. 等腰三角形的判定：①三条边都相等的三角形是等边三角形。

②三个角都相等（两个角是60°）的三角形是等腰三角形。

③底和腰相等的等腰三角形是等边三角形。

④有一个角是60°的等腰三角形是等边三角形。

练习题1、（2022•鞍山）如图，直线a ∥b ，等边三角形ABC 的顶点C 在直线b 上，∠2＝40°，则∠1的度数为（）A ．80°B ．70°C ．60°D ．50°【分析】先根据等边三角形的性质得到∠A ＝60°，再根据三角形内角和定理计算出∠3＝80°，然后根据平行线的性质得到∠1的度数．【解答】解：∵△ABC 为等边三角形，∴∠A ＝60°，∵∠A +∠3+∠2＝180°，∴∠3＝180°﹣40°﹣60°＝80°，∵a∥b，∴∠1＝∠3＝80°．故选：A．2、（2022•绵阳）下列关于等边三角形的描述不正确的是（）A．是轴对称图形B．对称轴的交点是其重心C．是中心对称图形D．绕重心顺时针旋转120°能与自身重合【分析】根据等边三角形的性质，轴对称图形的定义，中心对称图形的定义进行判断即可．【解答】解：等边三角形是轴对称图形，每条边的高线所在的直线是其对称轴，故A选项不符合题意；三条高线的交点为等边三角形的重心，∴对称轴的交点是其重心，故B选项不符合题意；等边三角形不是中心对称图形，故C选项符合题意；等边三角形绕重心顺时针旋转120°能与自身重合，故D选项不符合题意，故选：C．3、（2022•海南）如图，直线m∥n，△ABC是等边三角形，顶点B在直线n上，直线m交AB于点E，交AC于点F，若∠1＝140°，则∠2的度数是（）A．80°B．100°C．120°D．140°【分析】先根据等边三角形的性质可得∠A＝∠B＝∠C＝60°，由三角形外角的性质可得∠AEF的度数，由平行线的性质可得同旁内角互补，可得结论．【解答】解：∵△ABC是等边三角形，∴∠A＝60°．对于△AEF，∵∠1＝∠A+∠AEF＝140°，∴∠AEF＝140°﹣60°＝80°，∴∠DEB＝∠AEF＝80°，∵m∥n，∴∠2+∠DEB＝180°，∴∠2＝180°﹣80°＝100°，故选：B．4、（2022•张家界）如图，点O是等边三角形ABC内一点，OA＝2，OB＝1，OC＝3，则△AOB与△BOC的面积之和为（）A ．43B ．23C ．433D ．3【分析】将△AOB 绕点B 顺时针旋转60°得△CDB ，连接OD ，可得△BOD 是等边三角形，再利用勾股定理的逆定理可得∠COD ＝90°，从而解决问题．【解答】解：将△AOB 绕点B 顺时针旋转60°得△CDB ，连接OD ，∴OB ＝BD ，∠OBD ＝60°，CD ＝OA ＝2，∴△BOD 是等边三角形，∴OD ＝OB ＝1，∵OD 2+OC 2＝12+（）2＝4，CD 2＝22＝4，∴OD 2+OC 2＝CD 2，∴∠DOC ＝90°，∴△AOB 与△BOC 的面积之和为S △BOC +S △BCD ＝S △BOD +S △COD ＝×12+＝，故选：C ．。

八年级数学上册第十一章三角形知识点总结归纳完整版(带答案)

八年级数学上册第十一章三角形知识点总结归纳完整版单选题1、下列长度的三条线段与长度为5的线段能组成四边形的是（）A．1，1，1B．1，1，8C．1，2，2D．2，2，2答案：D分析：若四条线段能组成四边形，则三条较短边的和必大于最长边，由此即可完成．A、1+1+1<5，即这三条线段的和小于5，根据两点间距离最短即知，此选项错误；B、1+1+5<8，即这三条线段的和小于8，根据两点间距离最短即知，此选项错误；C、1+2+2=5，即这三条线段的和等于5，根据两点间距离最短即知，此选项错误；D、2+2+2>5，即这三条线段的和大于5，根据两点间距离最短即知，此选项正确；故选：D．小提示：本题考查了两点间线段最短，类比三条线段能组成三角形的条件，任两边的和大于第三边，因而较短的两边的和大于最长边即可，四条线段能组成四边形，作三条线段的和大于第四条边，因而较短的三条线段的和大于最长的线段即可．2、要得知作业纸上两相交直线AB，CD所夹锐角的大小，发现其交点不在作业纸内，无法直接测量．两同学提供了如下间接测量方案（如图1和图2）：对于方案Ⅰ、Ⅱ，说法正确的是（）A．Ⅰ可行、Ⅱ不可行B．Ⅰ不可行、Ⅱ可行C．Ⅰ、Ⅱ都可行D．Ⅰ、Ⅱ都不可行答案：C分析：用夹角可以划出来的两条线，证明方案Ⅰ和Ⅱ的结果是否等于夹角，即可判断正误方案Ⅰ：如下图，∠BPD即为所要测量的角∵∠HEN=∠CFG∴MN∥PD∴∠AEM=∠BPD故方案Ⅰ可行方案Ⅱ：如下图，∠BPD即为所要测量的角在△EPF中：∠BPD+∠PEF+∠PFE=180°则：∠BPD=180°−∠AEH−∠CFG故方案Ⅱ可行故选：C小提示：本题考查平行线的性质和判定，三角形的内角和；本题的突破点是用可画出夹角的情况进行证明3、刘零想做一个三角形的框架，她有两根长度分别为6cm和8cm的细木条，需要将其中一根木条分为两段，如果不考虑损耗和接头部分，那么可以分成两段的是（）A．6cm的木条B．8cm的木条C．两根都可以D．两根都不行答案：B分析：利用三角形的三边关系可得答案．解：利用三角形的三边关系可得应把8cm的木条截成两段，如将8cm的线段分成3cm和5cm或4cm和4cm，所截成的两段线段之和大于6，所以，可以，而6cm的线段无论如何分，分成的两段线段之和都小于8，所以，不可以．故选：B．小提示：此题主要考查了三角形的三边关系，关键是掌握三角形两边之和大于第三边．4、如图，若干个全等的正五边形排成圆环状，图中所示的是前3个正五边形，要完成这一圆环还需正五边形的个数为（）A．10B．9C．8D．7答案：D分析：先根据多边形的内角和公式（n−2)·180°求出正五边形的每一个内角的度数，再延长五边形的两边相交于一点，并根据四边形的内角和求出这个角的度数，然后根据周角等于360°求出完成这一圆环需要的正五边形的个数，然后减去3即可得解．解：∵五边形的内角和为(5−2)×180°=540°,∴正五边形的每一个内角为540°÷5=108°,∴正五边形的每一个外角为180°−108°=72°,如图，延长正五边形的两边相交于点O，则∠1=180°−2×72°=36°,360°÷36°=10,∵已经有3个五边形，∴10−3=7,即完成这一圆环还需7个五边形．故选：D．小提示：本题考查了多边形的内角和公式，延长正五边形的两边相交于一点，并求出这个角的度数是解题的关键，注意需要减去已有的3个正五边形．5、已知△ABC中，D、E分别是边AB、AC上的点，连接DE、BE、DC，下列各式中正确的是（）．A．S△ADES△ABC =ADABB．S△ADES△ABC=AEACC．S△ADCS△ABC =ADABD．S△ADES△EDC=AEAC答案：C分析：A选项，设点E、C到AB的距离分别为ℎ1，ℎ2，则ℎ1<ℎ2，根据三角形面积公式进行判断即可；B选项设点D、B到AC的距离分别为x，y，则x≠y，x<y，根据三角形面积公式进行判断即可；C选项，设点C到AB距离为h，△ADC=12AD⋅ℎ，S△ABC=12AB⋅ℎ，根据三角形面积公式进行判断即可；D选项，设点D到AC距离为ℎ3，则S△ADE=12AE⋅ℎ3，S△EDC=12CE⋅ℎ3，根据三角形面积公式进行判断即可A选项：设点E、C到AB的距离分别为ℎ1，ℎ2，则ℎ1<ℎ2，S△ADE=12AD⋅ℎ1，S△ABC=12AB⋅ℎ2，∴S△ADES△ABC =12AD⋅ℎ112AB⋅ℎ2=AD⋅ℎ1AB⋅ℎ2≠ADAB，故A错误；B选项：设点D、B到AC的距离分别为x，y，则x≠y，x<y，S△ADE=12AE⋅x，S△ABC=12AC⋅y，S△ADES△ABC=12AE⋅x12AC⋅y=AE⋅xAC⋅y≠AEAC，故B错误；C选项：设点C到AB距离为h，△ADC=12AD⋅ℎ，S△ABC=12AB⋅ℎ，∴S△ADCS△ABC =12AD⋅ℎ12AB⋅ℎ=ADAB，故C正确；D选项：设点D到AC距离为ℎ3，则S△ADE=12AE⋅ℎ3，S△EDC=12CE⋅ℎ3，∴S△ADES△EDC =12AE⋅ℎ312CE⋅ℎ3=AECE=AEAC−AE≠AEAC，故D错误.故选C．小提示：本题考查了与三角形的高有关的计算，掌握三角形的高的定义，根据三角形的面积计算是解题的关键．6、一个多边形截去一个角后，变成16边形，那么原来的多边形的边数为（）A．15或16或17B．15或17C．16或17D．16或17或18答案：A分析：分三种情况讨论，当截线不经过多边形的顶点时，当截线经过多边形的一个顶点时，当截线经过多边形的两个顶点时，再利用数形结合的方法可得答案.解：如图，当截线不经过多边形的顶点时，被截后的多边形比原多边形增加一条边，所以当被截后的多边形为16边形，则原多边形为15边形，如图，当截线经过多边形的一个顶点时，被截后的多边形与原多边形边数相同，所以当被截后的多边形为16边形，则原多边形为16边形，如图，当截线经过多边形的两个顶点时，被截后的多边形比原多边形少一条边，所以当被截后的多边形为16边形，则原多边形为17边形，故选：A.小提示：本题考查的是用直线截多边形的一个角后，被截后的多边形的边数与原多边形的边数之间的关系，解题的关键是清晰的分类讨论.7、当n边形边数增加2条时，其内角和增加（）A．180°B．360°C．540°D．720°答案：B分析：根据n边形的内角和定理即可求解．解：原来的多边形的边数是n，则新的多边形的边数是n＋2．（n＋2−2）•180−（n−2）•180＝360°．故选：B．小提示：本题主要考查了多边形的内角和定理，多边形的边数每增加一条，内角和就增加180度．8、在△ABC中，∠A=12∠B=13∠C，则△ABC为（）三角形．A．锐角B．直角C．钝角D．等腰答案：B分析：根据∠A=12∠B=13∠C分别设出三个角的度数，再根据三角形的内角和为180°列出一个方程，解此方程即可得出答案．∵∠A=12∠B=13∠C∴可设∠A=x，∠B=2x，∠C=3x根据三角形的内角和可得：x+2x+3x=180°解得：x=30°∴∠A=30°，∠B=60°，∠C=90°因此△ABC是直角三角形故答案选择B．小提示：本题主要考查的是三角形的基本概念．9、如图，CE是△ABC的外角∠ACD的平分线，若∠B=35°，∠ACE=60°，则∠A=( )A．35°B．95°C．85°D．75°答案：C分析：根据CE是△ABC的外角∠ACD的平分线，∠ACE=60°，得出∠ACD=120°；再根据三角形的外角等于与它不相邻的两个内角和即可求解.解：∵CE是△ABC的外角∠ACD的平分线，∠ACE=60°∴∠ACD=2∠ACE=120°∵∠ACD=∠B+∠A∴∠A=∠ACD-∠B=120°-35°=85°故选:C.小提示：本题考查了三角形外角性质，角平分线定义的应用，注意:三角形的一个外角等于和它不相邻的两个内角的和.10、能说明“锐角α，锐角β的和是锐角”是假命题的例证图是（）．A．B．C．D．答案：C分析：先将每个图形补充成三角形，再利用三角形的外角性质逐项判断即得答案．解：A、如图1，∠1是锐角，且∠1=α+β，所以此图说明“锐角α，锐角β的和是锐角”是真命题，故本选项不符合题意；B、如图2，∠2是锐角，且∠2=α+β，所以此图说明“锐角α，锐角β的和是锐角”是真命题，故本选项不符合题意；C、如图3，∠3是钝角，且∠3=α+β，所以此图说明“锐角α，锐角β的和是锐角”是假命题，故本选项符合题意；D、如图4，∠4是锐角，且∠4=α+β，所以此图说明“锐角α，锐角β的和是锐角”是真命题，故本选项不符合题意．故选：C．小提示：本题考查了真假命题、举反例说明一个命题是假命题以及三角形的外角性质等知识，属于基本题型，熟练掌握上述基本知识是解题的关键．填空题11、如图，∠A+∠B+∠C+∠D+∠E=______．答案：180度##180°分析：如图，连接BC,记CD,BE的交点为G,先证明∠D+∠E=∠GBC+∠GCB,再利用三角形的内角和定理可得答案.解：如图，连接BC,记CD,BE的交点为G,∵∠D+∠E=180°−∠DGE,∠GBC+∠GCB=180°−∠BGC,∠DGE=∠BGC,∴∠D+∠E=∠GBC+∠GCB,∴∠A+∠ABG+∠GBC+∠GCB+∠ACG=180°,∴∠A+∠ABG+∠ACG+∠D+∠E=180°,所以答案是：180°小提示：本题考查的是三角形的内角和定理，作出合适的辅助线构建三角形是解本题的关键.12、如图，点D在△ABC的边BA的延长线上，点E在BC边上，连接DE交AC于点F，若∠DFC=3∠B=117°，∠C=∠D，则∠BED=________．答案：102°分析：首先根据∠DFC＝3∠B＝117°，可以算出∠B＝39°，然后设∠C＝∠D＝x°，根据外角与内角的关系可得39＋x＋x＝117，再解方程即可得到x＝39，再根据三角形内角和定理求出∠BED的度数．解：∵∠DFC＝3∠B＝117°，∴∠B＝39°，设∠C＝∠D＝x°，39＋x＋x＝117，解得：x＝39，∴∠D＝39°，∴∠BED＝180°−39°−39°＝102°．所以答案是：102°．小提示：此题主要考查了三角形外角的性质，关键是掌握三角形的一个外角等于和它不相邻的两个内角的和．13、已知AD、AE分别是△ABC的高和中线，若BD=2，CD=1，则DE的长为______．答案：0.5或1.5分析：根据题意作出草图，分类讨论即可求解．解：AD、AE分别是△ABC的高和中线，BD=2，CD=1，如图，当△ABC是钝角三角形时，∴BC=BD−CD=1∴DE=BD−BE=BD−12BC=2−12=32当△ABC是锐角三角形时，∵BC=BD+DC=2+1=3∴BE=12BC=32∴DE=BD−BE=2−32=12当△ABC是直角三角形时，CD=0，不合题意，所以答案是：12或32 小提示：本题考查了三角形的高线，中线的定义，线段的和差关系，分类讨论是解题的关键．14、一个多边形外角和是内角和的29，则这个多边形的边数为________．答案：11分析：多边形的内角和定理为(n −2)×180°，多边形的外角和为360°，根据题意列出方程求出n 的值．解：根据题意可得：29×(n −2)×180°=360°，解得：n =11 ，所以答案是：11．小提示：本题主要考查的是多边形的内角和公式以及外角和定理，属于基础题型．记忆理解并应用这两个公式是解题的关键．15、如图，△ABC 中，∠A ＝60°，∠B ＝40°，DE ∥BC ，则∠AED 的度数是______．答案：80°分析：根据三角形内角和定理可得∠C =80°，根据平行线的性质即可得答案．∵∠A ＝60°，∠B ＝40°，∴∠C ＝180°﹣∠A ﹣∠B =80°，∵DE ∥BC ，∴∠AED ＝∠C ＝80°，所以答案是：80°小提示：本题考查三角形内角和定理及平行线的性质，任意三角形的内角和等于180°；两直线平行，同位角相等；熟练掌握相关性质及定理是解题关键．解答题16、如图，在△ABC中，AD是BC边上的中线，△ABD的周长比△ADC的周长多1，AB与AC的和为11(1)求AB、AC的长；(2)求BC边的取值范围．答案：(1)AB=6，AC=5(2)1＜BC＜11分析：（1）根据三角形中线的定义，BD=CD．所以△ABD和△ADC的周长之差也就是AB与AC的差，然后联立关于AB、AC的二元一次方程组，利用加减消元法求解即可．（2）根据三角形三边关系解答即可．（1）解：∵AD是BC边上的中线，∴BD=CD，∴△ABD的周长﹣△ADC的周长＝(AB+AD+BD)−(AC+AD+CD)=AB−AC=1，即AB−AC=1①，又AB+AC=11②，①+②得：2AB=12，解得AB=6，②−①得：2AC=10，解得AC=5，∴AB和AC的长分别为：AB=6，AC=5；（2）∵AB=6，AC=5；∴1＜BC＜11．小提示：本题考查了三角形的三边关系，三角形的中线定义，二元一次方程组的求解，利用加减消元法求解是解题的关键．17、如图，在△ABC中，CD平分∠BCA，E为CD延长线上一点，EF⊥AB于点F，已知∠ACB=70°，∠E= 30°．求∠A的度数．答案：25°分析：利用垂直的定义和三角形内角和定理求出∠EDF，利用对顶角的性质求出∠CDB，再利用角平分线的定义求出∠DCB，进而利用三角形内角和定理求出∠B，∠A．解：∵EF⊥AB，∴∠EFD=90°，又∵∠E=30°，∴∠EDF=180°−∠E−∠EFD=60°，∴∠CDB=∠EDF=60°．∵CD平分∠BCA，∠ACB=70°，∴∠DCB=12∠ACB=12×70°=35°．∴∠B=180°−∠CDB−∠DCB=180°−60°−35°=85°，∴∠A=180°−∠B−∠ACB=180°−85°−70°=25°，即∠A的度数为25°．小提示：本题考查角平分线、对顶角、三角形内角和定理的应用，解题的关键是熟练掌握对顶角的性质和三角形内角和定理．18、如图，在△ABC中，CD、CE分别是△ABC的高和角平分线，∠BAC=α,∠B=β(α>β)．(1)若α=70°,β=40°，求∠DCE的度数；(2)试用α、β的代数式表示∠DCE的度数_________．答案：(1)∠DCE=15°(2)α−β2分析：（1）根据三角形的内角和定理求出∠ACB的值，再由角平分线的性质以及直角三角形的性质求出∠DCE．（2）由（1）的解题思路即可得正确结果．（1）解：∵∠BAC=70°，∠B=40°∴∠ACB=180°−(∠BAC+∠B)=180°−(70°+40°)=70°，∵CE是∠ACB的平分线，∴∠ACE=12∠ACB=35°．∵CD是高线，∴∠ADC=90°，∴∠ACD=90°−∠BAC=20°，∴∠DCE=∠ACE−∠ACD=35°−20°=15°．（2）解：∵∠BAC=α，∠B=β∴∠ACB=180°−(∠BAC+∠B)=180°−(α+β)，∵CE是∠ACB的平分线，∴∠ACE=12∠ACB=12×[180°−(α+β)]=90°−α+β2．∵CD是高线，∴∠ADC=90°，∴∠ACD=90°−∠BAC=90°−α，∴∠DCE=∠ACE−∠ACD=90°−α+β2−90°+α=α−β2．小提示：本题主要考查角平分线，高线以及角的转换，掌握角平分线，高线的性质是解题的关键．。

初二三角形知识点总结和常考题

初二三角形知识点总结和常考题一、三角形的基本概念。

1. 定义。

- 由不在同一条直线上的三条线段首尾顺次相接所组成的图形叫做三角形。

2. 三角形的边、顶点、内角。

- 组成三角形的线段叫做三角形的边；相邻两边的公共端点叫做三角形的顶点；相邻两边所组成的角叫做三角形的内角，简称三角形的角。

3. 三角形的表示方法。

- 三角形用符号“△”表示，顶点是A、B、C的三角形记作“△ABC”，读作“三角形ABC”。

二、三角形的分类。

1. 按角分类。

- 锐角三角形：三个角都是锐角的三角形。

- 直角三角形：有一个角是直角的三角形。

直角三角形可以用符号“Rt△”表示，直角所对的边叫做斜边，另外两条边叫做直角边。

- 钝角三角形：有一个角是钝角的三角形。

2. 按边分类。

- 不等边三角形：三边都不相等的三角形。

- 等腰三角形：有两边相等的三角形。

相等的两边叫做腰，另外一边叫做底边；两腰所夹的角叫做顶角，底边与腰的夹角叫做底角。

等腰三角形中，三边都相等的三角形叫做等边三角形（也叫正三角形）。

三、三角形的三边关系。

1. 定理。

- 三角形两边的和大于第三边。

2. 推论。

- 三角形两边的差小于第三边。

四、三角形的高、中线与角平分线。

1. 高。

- 从三角形的一个顶点向它的对边所在直线作垂线，顶点和垂足之间的线段叫做三角形的高。

三角形的三条高所在直线相交于一点。

2. 中线。

- 在三角形中，连接一个顶点和它对边中点的线段叫做三角形的中线。

三角形的三条中线相交于一点，这点叫做三角形的重心。

3. 角平分线。

- 在三角形中，一个内角的平分线与它的对边相交，这个角的顶点与交点之间的线段叫做三角形的角平分线。

三角形的三条角平分线相交于一点。

五、三角形的内角和定理及推论。

1. 内角和定理。

- 三角形三个内角的和等于180°。

2. 推论。

- 直角三角形的两个锐角互余。

- 有两个角互余的三角形是直角三角形。

六、三角形的外角。

1. 定义。

- 三角形的一边与另一边的延长线组成的角，叫做三角形的外角。

解三角形(总结+题+解析)

解三角形一．正弦定理：A a sin =B b sin =C csin =2R ，其中R 是三角形外接圆半径.正弦定理的如下变形常在解题中用到1.(1) a=2RsinA(2) b=2RsinB(3) c=2RsinC2.(1) sinA=a/2R(2) sinB=b/2R(3) sinC=c/2R3.a ：b ：c=sinA ：sinB:sinC适用类型（1）AAS（2）SSA二．余弦定理：1. a^2 = b^2 + c^2 - 2·b ·c ·cosA2. b^2 = a^2 + c^2 - 2·a ·c ·cosB3. c^2 = a^2 + b^2 - 2·a ·b ·cosC余弦定理的如下变形常在解题中用到1. cosC = (a^2 + b^2 - c^2) / (2·a ·b)2. cosB = (a^2 + c^2 - b^2) / (2·a ·c)3. cosA = (c^2 + b^2 - a^2) / (2·b ·c ）适用类型1.SSA2.SAS3.SSS三．余弦定理和正弦定理的面积公式S △ABC =21absinC=21bcsinA=21acsinB（常用类型：已知三角形两边及其夹角）判断解的个数判断三角形的形状有两种途径：（1）将已知的条件统一化成边的关系，用代数求和法求解（2）将已知的条件统一化成角的关系，用三角函数法求解三．解三角形的实际应用测量中相关的名称术语仰角：视线在水平线以上时，在视线所在的垂直平面内，视线与水平线所成的角叫做仰角。

俯角：视线在水平线以下时，在视线所在的垂直平面内，视线与水平线所成的角叫俯角方向角：从指定方向线到目标方向的水平角测距离的应用测高的应用(一)已知两角及一边解三角形例1已知在△ABC中，c＝10，A＝45°，C＝30°，求a、b和B.∠B=180°-30°-45°=105°a=10sin45°/sin30°=10√2sin105°=sin(60+45)=√2/2(√3/2+1/2)=(√6+√2)/41/sin105=√6-√2b=10sin45°/sin105°=5√2(√6-√2)=10(√3-1)（二）已知两边和其中一边对角解三角形例2在△ABC中，已知角A，B，C所对的边分别为a，b，C，若a=2√3，b =√6，A=45°，求边长C由余弦定理，得b²+c²-2bccosA-a²=06+c²-2√3c-12=0c²-2√3c-6=0根据求根公式，得c=√3±3又c>0所以c=3+√3（三）已知两边及夹角，解三角形例3△ABC中，已知b＝3，c＝33，B＝30°，求角A，角C和边a.解：由余弦定理得∴a2-9a+18=0，得a=3或6当a=3时，A=30°，∴C=120°当a=6时，由正弦定理∴A=90°∴C=60°。

初中三角形有关知识点总结及习题大全

初中三角形有关知识点总结及习题大全一、三角形内角和定理一、选择题40°1.如图，在△ABC中，D是BC延长线上一点，∠B = 40°，∠ACD = 120°，则∠A等于（）A．60°B．70°C．80°D．90°????B°C2.将一副三角板按图中的方式叠放，则角?等于（）A．75 B．60 C．45D． ?∠1=55?，∠2=45?，3.如图，直线m∥n，则∠3的度数为（）A．80? B．90?C．100? D．110?【解析】选C. 如图，由三角形的外角性质得?4??1??2?550?450?1000，由m∥n，得?3??4?10005.（xx·中考）如图，将三角尺的直角顶点放在直尺的一边上，?1?30°，?2?50°，则?3的度数等于（） A．50°B．30°C．20°D．15°【解析】选C 在原图上标注角4，所以∠4=∠2，因为∠2=50°，所以∠4=50°，又因为∠1=30°，所以∠3=20°；6.（xx·朝阳中考）如图，已知AB∥CD,若∠A=20°，∠E=35°，则∠C等于（）. A.20°B. 35°C. 45°D.55°【解析】选D 因为∠A=20°，∠E=35°，所以∠EFB＝55o，又因为AB∥CD,所以∠C＝∠EFB＝55o；7.（xx·呼和浩特中考）已知△ABC的一个外角为50°，则△ABC一定是（） A．锐角三角形 B．钝角三角形C．直角三角形 D．钝角三角形或锐角三角形【解析】选B 因为△ABC的一个外角为50°，所以与△ABC的此外角相邻的内角等于130°，所以此三角形为钝角三角形. 8.（xx·聊城中考）如图，?1?100?，?2?145?，那么?3?（）6A．55°B．65°C．75°D．85°答案：选B 二、填空题9.（xx·常德中考）如图，已知AE//BD，∠1=130o，∠2=30o，则∠C=．【解析】由AE//BD得∠AEC=∠2=30o，∴∠C=180°-∠1-∠AEC=180°-130o-30o=20o 答案：20o10.（xx·邵阳中考）如图，AB//CD,直线EF与AB、CD分别相交于E、F两点，EP平分∠AEF,过点F作FP⊥EP,垂足为P，若∠PEF=30,则∠PFC=__________。

(完整版)八年级数学上知识点+习题+答案

（一）三角形部分一、知识点汇总1. 三角形的定义定义：不在同一条直线上的三条线段首尾顺次相接组成的图形叫做三角形。

组成三角形的线段叫做三角形的边，相邻两边所组成的角叫做三角形的内角，简称角，相邻两边的公共端点是三角形的顶点。

三角形ABC用符号表示为△ABC。

三角形ABC的顶点C所对的边AB可用c 表示，顶点B所对的边AC可用b 表示，顶点A所对的边BC可用a表示。

注意：（1）三条线段要不在同一直线上，且首尾顺次相接；(2）三角形是一个封闭的图形；（3）△ABC是三角形ABC的符号标记,单独的没有意义．2、(1）三角形按边分类：(2)三角形按角分类:3、三角形的三边关系三角形的任意两边之和大于第三边. 三角形的任意两边之差小于第三边.注意：(1）三边关系的依据是：两点之间线段最短；（2）围成三角形的条件是：任意两边之和大于第三边．4、和三角形有关的线段:（1）三角形的中线三角形中，连结一个顶点和它对边中点的线段表示法:1、AD是△ABC的BC上的中线. 2、BD=DC=0.5BC。

3、AD是ABC的中线；注意：①三角形的中线是线段；②三角形三条中线全在三角形的内部；③三角形三条中线交于三角形内部一点；④中线把三角形分成两个面积相等的三角形．（2）三角形的角平分线三角形一个内角的平分线与它的对边相交，这个角与交点之间的线段。

表示法：1、AD是△ABC的∠BAC的平分线.2、∠1=∠2=0。

5∠BAC。

3、AD平分BAC，交BC于D注意:①三角形的角平分线是线段；②三角形三条角平分线全在三角形的内部;③三角形三条角平分线交于三角形内部一点；（3）三角形的高三角形的高：从三角形的一顶点向它的对边作垂线，顶点和垂足之间的线段叫做三角形的高，表示法：1、AD是△ABC的BC上的高。

2、AD⊥BC于D。

3、∠ADB=∠ADC=90°.4、AD是△ABC的高.注意：①三角形的高是线段：高与垂线不同，高是线段，垂线是直线.②锐角三角形三条高全在三角形的内部，直角三角形有两条高是边，钝角三角形有两条高在三角形外；三角形三条高所在直线交于一点．（而锐三角形的三条高的交点在三角形的内部，直角三角形三条高的交战在角直角顶点,钝角三角形的三条高的交点在三角形的外部。

人教版初中八年级数学上册第十一章《三角形》知识点总结(含答案解析)(1)

一、选择题1．如图，在ABC中，AB边上的高为（）A．CG B．BF C．BE D．AD A解析：A【分析】在ABC中，过C点向AB所在的直线作垂线，顶点与垂足之间的线段是AB上的高，由此可得答案．【详解】CG解：ABC中，AB边上的高为：.故选：.A【点睛】本题考查的是三角形的高的含义，掌握钝角三角形的高是解题的关键．y 0，则以x、y的值为两边长的等腰三角形周长是2．已知实数x、y满足|x－8（）A．20或16 B．20 C．16 D．18B解析：B【分析】根据绝对值与二次根式的非负性即可求出x与y的值．由于没有说明x与y是腰长还是底边长，故需要分类讨论．【详解】由题意可知：x-4=0，y-8=0，∴x=4，y=8，当腰长为4，底边长为8时，∵4+4=8，∴不能围成三角形，当腰长为8，底边长为4时，∵4+8＞8，∴能围成三角形，∴周长为：8+8+4=20，故选：B ．【点睛】本题考查了算术平方根，以及三角形三边关系，解题的关键是正确理解非负性的意义，以及三角形三边关系，本题属于基础题型．3．下列四组线段中，不可以构成三角形的是（）A ．4，5，6B ．1.5，2，2.5C ．13，14，15D ．1，3D 解析：D【分析】计算较小两边的和，与最大的边比较，大于最大的边时三角形存在，依此判断即可.【详解】∵4+5＞6，∴能构成三角形；∵1.5+2＞2.5，∴能构成三角形； ∵14+15＞13， ∴能构成三角形；∵＜1+2=3，∴不能构成三角形；故选D.【点睛】本题考查了已知线段长判断三角形的存在，熟记三角形存在的条件是解题的关键. 4．已知两条线段15cm a =，8cm b =，下列线段能和a ，b 首尾相接组成三角形的是（）A ．20cmB ．7cmC ．5cmD ．2cm A解析：A【分析】根据三角形任意两边的和大于第三边，进行分析判断．【详解】A 、15+8=23>20，能组成三角形，符合题意；B 、7+8=15，不能组成三角形，不合题意；C 、5+8=13<15，不能组成三角形，不合题意；D 、2+8=10＜15，不能组成三角形，不合题意．故选：A ．【点睛】本题主要考查了三角形的三边关系，要注意三角形形成的条件：任意两边之和大于第三边，三角形的两边差小于第三边．但通常不需一一验证，其简便方法是将较短两边之和与较长边比较．5．如图，AD 是ABC 的外角CAE ∠的平分线，35B ∠=︒，60=︒∠DAC ，则ACD ∠的度数为（）A ．25︒B ．85︒C ．60︒D ．95︒D解析：D【分析】根据角平分线的定义可得∠DAC ＝∠DAE ，根据三角形的一个外角等于与它不相邻的两个内角的和可得∠D ，然后利用三角形的内角和定理列式计算即可得解．【详解】解：∵AD 是∠CAE 的平分线，60=︒∠DAC ，∴∠DAC ＝∠DAE ＝60°，又∵35B ∠=︒由三角形的外角性质得，∠D ＝∠DAE−∠B ＝60°−35°＝25°，∴在△ACD 中，∠ACD ＝180°−∠DAC －∠D ＝180°−60°−25°＝95°．故选：D ．【点睛】本题考查了三角形的一个外角等于与它不相邻的两个内角的和，三角形的内角和定理，熟记性质并准确识图理清图中各角度之间的关系是解题的关键．6．已知长度分别为3cm ，4cm ，xcm 的三根小棒可以摆成一个三角形，则x 的值不可能是（）A ．2.4B ．3C ．5D ．8.5D解析：D【分析】先根据三角形的三边之间的关系求解1＜x ＜7，从而可得答案．【详解】解：长度分别为3cm ，4cm ，xcm 的三根小棒可以摆成一个三角形， 43∴-＜x ＜43+，1∴＜x ＜7，x 的值不可能是8.5.故选：.D【点睛】本题考查的是三角形的三边之间的关系，掌握三角形的三边之间的关系是解题的关键． 7．以下列各组线段为边，能组成三角形的是( )A ．1，2，3B ．1，3，5C ．2，3，4D ．2，6，10C解析：C【分析】根据三角形三边关系逐一进行判断即可．【详解】A 、1+2=3，不能构成三角形，故不符合题意；B 、1+3=4＜5，不能构成三角形，故不符合题意；C 、2+3=5>4，可以构成三角形，故符合题意；D 、2+6=8＜10，不能构成三角形，故不符合题意，故选：C ．【点睛】本题主要考查三角形的三边关系，比较简单，熟记三边关系定理是解决本题的关键． 8．如图，在ABC ∆中，80,BAC ∠=︒点D 在BC 边上，将ABD △沿AD 折叠，点B 恰好落在AC 边上的点'B 处，若'20B DC ∠=．则C ∠的度数为（）A ．20B ．25C ．35D ．40D解析：D【分析】由折叠的性质可求得'B AB D ∠=∠，利用三角形内角和及外角的性质列方程求解．【详解】解：由题意可得'B AB D ∠=∠∵80,BAC ∠=︒∴∠B+∠C=100°又∵'='=20B AB D C B DC C ∠=∠+∠+∠∠，∴∠C+20°+∠C=100°解得：∠C=40°故选：D ．【点睛】本题考查三角形内角和及外角的性质，找准角之间的等量关系列出方程正确计算是解题关键．9．如图，盖房子时，在窗框没有安装之前，木工师傅常常先在窗框上斜钉一根木条，使其不变形，这种做法的根据是（）A ．两点之间线段最短B ．长方形的对称性C ．长方形四个角都是直角D ．三角形的稳定性D解析：D【分析】在窗框未安装之前，木工师傅常常先在窗框上斜钉一根木条，则分成了两个三角形，据此即可判断是利用了三角形的稳定性．【详解】在窗框未安装之前，木工师傅常常先在窗框上斜钉一根木条，则分成了两个三角形，利用了三角形的稳定性，D 正确．故答案选D ．【点睛】本题比较简单主要考查三角形稳定性的实际应用，通常要使一些图形具有稳定的结构，往往是将其转化为三角形而获得．10．下列说法正确的个数为（）①过两点有且只有一条直线；②两点之间，线段最短；③若ax ay =，则x y =；④若A 、B 、C 三点共线且AB BC =，则B 为AC 中点；⑤各边相等的多边形是正多边形． A ．①②④B ．①②③C ．①④⑤D ．②④⑤A解析：A【分析】根据直线的性质、两点间的距离、等式的性质、线段中点定义、多边形的定义依次判断．【详解】①过两点有且只有一条直线，故①正确；②两点之间，线段最短，故②正确；③若ax ay =，当0a =时，x 不一定等于y ，故③错误；④若A ，B ，C 三点共线且AB BC =，则B 为AC 中点，故④正确；⑤各角都相等且各边相等的多边形是正多边形，故⑤错误．∴正确的有①②④，故选：A ．【点睛】此题考查理解能力，正确掌握直线的性质、两点间的距离、等式的性质、线段中点定义、正多边形的定义是解题的关键．二、填空题11．从n 边形的一个顶点出发，连接其余各顶点，可以将这个n 边形分割成17个三角形，则n ＝______．19【分析】根据从n 边形的一个顶点出发连接这个点与其余各顶点可以把一个n边形分割成（n-2）个三角形的规律作答【详解】解：∵一个多边形从一个顶点出发连接其余各顶点可以把多边形分成(n-2)个三角形∴解析：19【分析】根据从n边形的一个顶点出发，连接这个点与其余各顶点，可以把一个n边形分割成（n-2）个三角形的规律作答．【详解】解：∵一个多边形从一个顶点出发，连接其余各顶点，可以把多边形分成(n-2)个三角形，∴n-2=17，n=．∴19故答案为：19．【点睛】本题主要考查多边形的性质，解题关键是熟记多边形顶点数与分割成的三角形个数的关系．12．如图，将一副直角三角尺按图③放置，使三角尺①的长直角边与三角尺②的某直角边在同一条直线上，则图③中的∠1=______°．105【分析】利用三角形外角性质求解【详解】如图∵∠2=∠3=∴∠4=∠2+∠3=∴∠1=故答案为：105【点睛】此题考查三角板的角度计算三角形外角的性质观察图形掌握各角度之间的位置关系是解题的关键解析：105【分析】利用三角形外角性质求解．【详解】如图，∵∠2=30，∠3=45︒，∴∠4=∠2+∠3=75︒，︒-∠=︒，∴∠1=1804105故答案为：105．．【点睛】此题考查三角板的角度计算，三角形外角的性质，观察图形掌握各角度之间的位置关系是解题的关键．13．设三角形三内角的度数分别为,,x y z ︒︒︒，如果其中一个角的度数是另一个角的度数的2倍、那我们称数对(,)()y z y z <是x 的和谐数对，当150x =时，对应的和谐数对有一个，它为(10,20)；当66x =时，对应的和谐数对有二个，它们是__________．当对应的和谐数对(,)y z 有三个时，请写出此时x 的范围_______．（3876）（3381）【分析】根据和谐数对的定义求出当x=66时的两组数对；再分当时当时当时三种情况讨论从而得出结论【详解】解：当时180-66=114则114÷3=3838×2=76此时和谐数对解析：（38，76），（33，81） 060x ︒<<︒【分析】根据“和谐数对”的定义求出当x=66时的两组数对；再分当060x ︒<<︒时，当60120x ︒<︒时，当120180x ︒<︒时，三种情况讨论，从而得出结论．【详解】解：当66x =时，180-66=114，则114÷3=38，38×2=76，此时和谐数对为（38，76），或66÷2=33，114-33=81，此时和谐数对为（33，81），若对应的和谐数对(,)y z 有三个，当060x ︒<<︒时，它的和谐数对有(1803,2)x x ︒-，3(,180)22x x ︒-，180(3x ︒-，2(180))3x ︒-；当60120x ︒<︒时，它的和谐数对有3(,180)22x x ︒-，180(3x ︒-，2(180))3x ︒-，当120180x ︒<︒时，它的和谐数对有180(3x ︒-，2(180))3x ︒-， ∴对应的和谐数对(,)y z 有三个时，此时x 的范围是060x ︒<<︒，故答案为：（38，76），（33，81）；060x ︒<<︒．【点睛】本题考查三角形内角和定理，解题的关键是明确题意，找出所求问题需要的条件，利用分类讨论的数学思想解答问题．14．七边形的外角和为________．360°【分析】根据多边形的外角和等于360°即可求解；【详解】∵多边形的外角和都是360°∴七边形的外角和为360°故答案为：360°【点睛】本题考查了多边形的外角的性质掌握多边形的外角和等于36 解析：360°【分析】根据多边形的外角和等于360°即可求解；【详解】∵ 多边形的外角和都是360°，∴七边形的外角和为360°，故答案为：360°．【点睛】本题考查了多边形的外角的性质，掌握多边形的外角和等于360°是解题的关键； 15．用边长相等的正三角形和正六边形铺满地面，一个结点周围有m 块正三角形，n 块正六边形，则m+n ＝______．4或5【分析】先求出正三角形和正六边形的内角大小然后列出关于mn 的二元一次方程然后确定mn 的值最后求m+n 即可【详解】解：∵正三边形和正六边形内角分别为60°120°∴60°m+120°n=360°解析：4或5【分析】先求出正三角形和正六边形的内角大小，然后列出关于m 、n 的二元一次方程，然后确定m 、n 的值，最后求m+n 即可．【详解】解：∵正三边形和正六边形内角分别为60°、120°∴60°m+120°n=360°，即m+2n=6∴当n=1时，m=4；当n=2时，m=2；∴m+n=5或m+n=4．故答案为：4或5．【点睛】本主要考查了正多边形的组合能否进行平面镶嵌，掌握位于同一顶点处的几个角之和能否为360°成为解答本题的关键．16．如图，将长方形纸片的一角折叠，使顶点A 落在F 处，折痕为BC ，FBD ∠的角平分线为BE ，将FBD ∠沿BF 折叠使BE ，BD 均落在FBC ∠的内部，且BE 交CF 于点M ，BD 交CF 于点N ，若BN 平分CBM ∠，则ABC ∠的度数为_________．5°【分析】根据角平分线的定义可得再根据折叠的性质可得再根据平分可得进而可得【详解】解：∵的角平分线为∴又∵与关于对称∴∵与关于对称∴又∵平分∴又∵为折痕∴∵∴又∵∴∴又∵∴故答案为：675°【点睛解析：5°．【分析】根据角平分线的定义可得1FBE ∠=∠，再根据折叠的性质可得1MBF FBE ∠=∠=∠，NBF FBD ∠=∠，CBA CBF ∠=∠，再根据BN 平分CBM ∠可得CBN NBM ∠=∠，进而可得318067.58ABC ∠=⨯=．【详解】解：∵FBD ∠的角平分线为BE ，∴1FBE ∠=∠，又∵BM 与BE 关于BF 对称，∴1MBF FBE ∠=∠=∠， ∵BN 与BD 关于BF 对称，∴NBF FBD ∠=∠FBE EBD =∠+∠11=∠+∠21=∠，又∵BN 平分CBM ∠，∴CBN NBM ∠=∠，又∵BC 为折痕，∴CBA CBF ∠=∠CBN NBF =∠+∠21NBM =∠+∠，∵NBM NBF MBF ∠=∠-∠211=∠=∠1=∠，∴31CBA ∠=∠，又∵180CBA CBF FBD ∠+∠+∠=，∴3112121180∠+∠+∠+∠=，∴81180∠=，又∵31ABC ∠=∠，∴318067.58ABC ∠=⨯=，故答案为：67.5°．【点睛】本题考查了折叠的性质，角平分线的定义，平角的定义，解题的关键是理解题意，找到31808ABC ∠=⨯． 17．如图，在ABC 中，已知66ABC ∠=︒，54ACB ∠=︒，BE 是AC 上的高，CF 是AB 上的高，H 是BE 和CF 的交点，EHF ∠的度数是________．120°【分析】先根据三角形内角和定理求出∠A 的度数再根据CF是AB 上的高得出∠ACF 的度数再由三角形外角的性质即可得出结论【详解】解：∵∠ABC=66°∠ACB=54°∴∠A=60°∵CF 是AB 上解析：120°【分析】先根据三角形内角和定理求出∠A 的度数，再根据CF 是AB 上的高得出∠ACF 的度数，再由三角形外角的性质即可得出结论．【详解】解：∵∠ABC=66°，∠ACB=54°，∴∠A=60°，∵CF 是AB 上的高，∴在△ACF 中，∠ACF=180°-∠AFC-∠A=30°，在△CEH 中，∠ACF=30°，∠CEH=90°，∴∠EHF=∠ACF+∠CEH=30°+90°=120°．故答案为120°．【点睛】本题考查的是三角形内角和定理及三角形外角的性质、三角形的高线等知识，解题的关键是熟练掌握基本知识，属于中考常考题型．18．如图，把ABC 折叠，点B 落在P 点位置，若12120∠+∠=︒，则B ∠=______．60°【分析】先根据折叠的性质得∠3＝∠4∠5＝∠6再利用平角的定义得∠3＋∠4＋∠1＝180°∠5＋∠6＋∠2＝180°根据等式的性质得到2∠4＋∠1＋2∠6＝360°把∠1＋∠2＝120°代入得解析：60°【分析】先根据折叠的性质得∠3＝∠4，∠5＝∠6，再利用平角的定义得∠3＋∠4＋∠1＝180°，∠5＋∠6＋∠2＝180°，根据等式的性质得到2∠4＋∠1＋2∠6＝360°，把∠1＋∠2＝120°代入得到∠4＋∠6＝120°，然后根据三角形内角和定理可计算出∠B的度数．【详解】∵把△ABC的∠B折叠，点B落在P的位置，∴∠3＝∠4，∠5＝∠6，∵∠3＋∠4＋∠1＝180°，∠5＋∠6＋∠2＝180°，∴2∠4＋∠1＋∠2＋2∠6＝360°，而∠1＋∠2＝120°，∴∠4＋∠6＝120°，∵∠4＋∠6＋∠B＝180°，∴∠B＝180°−120°＝60°．故答案为60°．【点睛】本题考查了三角形内角和定理，也考查了折叠的性质，“数形结合”是关键．19．如图，△ABC中，D为BC边上的一点，BD：DC=2：3，△ABC的面积为10，则△ABD 的面积是_________________4【分析】利用面积公式可得出△ABD与△ABC等高只需求出BD与BC的比值即可求出三角形ABD的面积【详解】解：∵BD：DC=2：3∴BD=BC△ABD的面积=BD•h＝× BC•h=△ABC的面积解析：4【分析】利用面积公式可得出△ABD与△ABC等高，只需求出BD与BC的比值即可求出三角形ABD 的面积．【详解】解：∵BD：DC=2：3，∴BD=25BC．△ABD的面积=12BD•h＝12×25BC•h=25△ABC的面积=25×10=4．故答案为：4．【点睛】本题考查了三角形面积公式以及根据公式计算三角形面积的能力．20．把一副直角三角板按如图所示的方式摆放在一起，其中90∠，90C=∠=，F∠+∠等于___________度．∠=，则12A∠=，4530D210【分析】由题意得：∠1=∠D+∠DGA∠2=∠F+∠FHB然后由对顶角相等的性质得∠1=∠D+CGH∠2=∠F+∠CHG最后由直角三角形两锐角互余的性质可以算出∠1+∠2的值【详解】解：如图给解析：210【分析】由题意得：∠1=∠D+∠DGA，∠2=∠F+∠FHB，然后由对顶角相等的性质得∠1=∠D+CGH，∠2=∠F+∠CHG，最后由直角三角形两锐角互余的性质可以算出∠1+∠2的值．【详解】解：如图，给两三角板的两个交点标上G、H符号，则∠1=∠D+∠DGA=∠D+CGH，∠2=∠F+∠FHB=∠F+∠CHG，∴∠1+∠2=∠D+CGH+∠F+∠CHG=∠D+∠F+（CGH+∠CHG）=30°+90°+90°=210°，故答案为210 ．【点睛】本题考查直角三角形的应用，灵活运用直角三角形两锐角互余、三角形的外角性质和对顶角相等的定理求解是解题关键．三、解答题⊥于E，已知21．如图，ABC中，AD平分BAC∠，P为AD延长线上一点，PE BC∠=︒，2480ACB∠的度数．B∠=︒，求P解析：28°【分析】在△ABC 中，利用三角形内角和定理可求出∠BAC 的度数，结合角平分线的定义可得出∠BAD 的度数，在△ABD 中，利用三角形外角性质可求出∠PDE 的度数，再在△PDE 中利用三角形内角和定理可求出∠P 的度数．【详解】解：在ABC 中，80ACB ∠=︒，24B ∠=︒，18076BAC ACB B ∴∠=︒-∠-∠=︒． AD 平分BAC ∠， 1382BAD BAC ∴∠=∠=︒． PDE ∠是ABD △的外角，243862PDE B BAD ∴∠=∠+∠=︒+︒=︒，PE BC ⊥于E ，90PED ∴∠=︒，906228P ∴∠=︒-︒=︒．【点睛】本题考查了三角形内角和定理、角平分线的定义以及对顶角，利用三角形内角和定理及角平分线的定义，求出∠ADC 的度数是解题的关键．22．如图，已知长方形ABCD 中，10cm AD =，6cm DC =，点F 是DC 的中点，点E 从A 点出发在AD 上以每秒1cm 的速度向D 点运动，运动时间设为t 秒．（假定0t 10<<）（1）当5t =秒时，求阴影部分（即三角形BEF ）的面积；（2）用含t 的式子表示阴影部分的面积；并求出当三角形EDF 的面积等于3时，阴影部分的面积是多少？（3）过点E 作//EG AB 交BF 于点G ，过点F 作//FH BC 交BE 于点H ，请直接写出在E 点运动过程中，EG 和FH 的数量关系．解析：（1）4522cm ；（2）23302t cm ⎛⎫- ⎪⎝⎭；218cm ；（3）53EG FH = 【分析】（1）由长方形的性质得出10cm BC AD ==，6cm AB DC ==，由5t =得AE=5，DE=10-5=5，根据ABCD BEF BE BCF DEF S S S S S =---△△A △△长方形即可求解；（2）由题意得AE=t ，DE=10-t ，根据ABCD BEF BE BCF DEF S S S S S =---△△A △△长方形表示出阴影部分的面积；由12EDF S DE DF =⋅△求出t 的值，代入计算即可；（3）由长方形ABCD 得AD CD ⊥，根据平行线的性质得EG HF ⊥，根据平行线间的距离相等可得DE ，AE ，DF ，CF 分别等于,,,EGF EGB EHF BHF △△△△的高，由BEF S的面积即可得出结论．【详解】解：（1）∵长方形ABCD 中，10cm AD =，6cm DC =，∴10cm BC AD ==，6cm AB DC ==，∵点F 是DC 的中点，∴3cm DF CF ==，当5t =秒时，AE=5cm ，DE=10-5=5 cm ，∵ABCD BEF BE BCF DEF S S S S S =---△△A △△长方形 =()()()1111066510353222⨯-⨯-⨯-⨯ =156015152--- =4522cm ；（2）由题意得AE=t ，DE=10-t ， ∵ABCD BEF BE BCF DEF S S S S S =---△△A △△长方形 =()()1111066103310222t t ⨯-⨯-⨯-⨯⨯- =360315152t t ---+=3302t -， ∴用含t 的式子表示阴影部分的面积为：23302t cm ⎛⎫-⎪⎝⎭；当三角形EDF 的面积等于3时，12EDF S DE DF =⋅△=()13102t ⨯⨯-=3，解得：8t =， 8t =时，38=30=182S ⨯-阴影2cm ；（3）∵长方形ABCD ∴AD CD ⊥，//,//AB CD AD BC ，∵//EG AB ，//FH BC ，∴EG HF ⊥，,AD EG CD HF ⊥⊥，∴DE ，AE 分别等于,EGF EGB △△的EG 边上的高，DF ，CF 分别等于,EHF BHF △△的FH 边上的高，∴11112222BEF S EG DE EG AE HF DF HF CF =⋅+⋅=⋅+⋅△， ∴()()1122EG DE AE HF DF CF +=+，即EG AD HF CD ⋅=⋅， ∵10cm AD =，6cm DC =，∴106EG HF =，即53EG FH =．【点睛】本题是一个动点问题，考查了平行线间的距离，三角形面积的计算，解题的关键是熟练掌握平行线的性质和三角形面积的计算方法．23．如图，AF ，AD 分别是ABC 的高和角平分线，且34B ∠=︒，76C ∠=︒，求DAF ∠的度数．解析：21︒【分析】运用三角形的内角和定理即可求出∠BAC 的度数；根据角平分线的定义、三角形的内角和定理的推论以及直角三角形的两个锐角互余即可求出∠FAC 的度数，再由DAF DAC FAC =-∠∠∠即可得出结论．【详解】解：∵AF 是ABC 的高，∴90AFC ∠=︒，∴90907614FAC C ∠=︒-∠=︒-︒=︒，∵180BAC B C ∠+∠+∠=︒，∴180180763470BAC B C ∠=︒-∠-∠=︒-︒-︒=︒，∵AD 是ABC 的角平分线， ∴11703522DAC BAC ==⨯︒=∠∠︒， ∴21DAF DAC FAC =-∠=∠∠︒．【点睛】本题考查的是三角形内角和定理，熟知三角形内角和是180°是解答此题的关键． 24．()1若n 边形的内角和等于它外角和的3倍，求边数n ．()2已知a ，b ，c 为三角形三边的长，化简：a b c b c a --+--．解析：()18；()22c ．【分析】（1）根据多边形的内角和与外角和公式列出方程即可求解；（2）根据三角形的三边关系可得a c b +>，b c a +>，再根据化简绝对值的方法即可求解．【详解】解：()1由题意得：()18023603n ︒-=︒⨯，解得：8n =．()2∵a ，b ，c 为三角形三边的长，∴a c b +>，b c a +>， ∴a b c b c a --+--()()2a b c b c a b c a a c b c =-++-+=+-++-=．【点睛】此题主要考查多边形的内角和与外角和、三角形的三边关系的应用，解题的关键是熟知多边形的性质及去绝对值的方法．25．如果一个n 边形的内角都相等，且它的每一个外角与内角的比为2：5，求这个多边形的边数n ．解析：7【分析】先根据外角与内角的比为2：5，求出每个外角度数，再依据外角和360°求边数n ．【详解】解：因为多边形的每一个外角与内角之和为180°，所以每个外角度数为180°27⨯=（3607）°．又n 边形每个内角度数相等，则每个外角度数也相等，根据多边形外角和360°，可得n ＝3603607÷=7．答：这个多边形的边数n是7．【点睛】本题主要考查多边形的内角和外角关系以及多边形外角和，运用外角计算边数是这一类题的通用方法．26．已知，a，b，c为ABC的三边，化简|a﹣b﹣c|﹣2|b﹣c﹣a|+|a+b﹣c|．解析：﹣2a+4b﹣2c【分析】根据三角形三边关系：两边之和大于第三边，两边之差小于第三边，来判定绝对值里的式子的正负值，然后去绝对值进行计算即可．【详解】解：∵a，b，c为ABC的三边，∴a+b＞c，b+c＞a，a+c＞b∴|a﹣b﹣c|﹣2|b﹣c﹣a|+|a+b﹣c|=|a-(b+c)|-2|b-(c+a)|+ |a+b﹣c|＝﹣[a﹣（b+c）]+2[b﹣（c+a）]+（a+b﹣c）=-a+(b+c)+2b-2(c+a)+a+b-c＝﹣a+b+c+2b﹣2c﹣2a+a+b﹣c＝﹣2a+4b﹣2c．【点睛】此题主要考查了三角形三边关系，以及绝对值的性质，关键是掌握三边关系定理．27．如图，A、O、B三点在同一直线上，OE，OF分别是∠BOC与∠AOC的平分线．求：（1）当∠BOC=30°时，∠EOF的度数；（2）当∠BOC=60°时，∠EOF等于多少度？（3）当∠BOC=n°时，∠EOF等于多少度？（4）观察图形特点，你能发现什么规律？解析：（1）∠EOF=90°；（2）∠EOF=90°；（3）∠EOF=90°；（4）∠EOF的度数与∠BOC 的大小无关，互为邻补角的两个角的角平分线所组成的角是一个直角．【分析】根据∠BOC求得∠AOC，再由∠BOC和∠AOC的角平分线，即可求得；【详解】解：（1）∵∠BOC=30°，∴∠AOC=180°－30°=150°，∵OE平分∠BOC，OF平分∠AOC，∴∠EOC=12∠BOC=15°，∠COF=12∠COA=75°，∴∠EOF=75°+15°=90°；（2）∵∠BOC=60°，∴∠AOC=180°－60°=120°，∵OE 平分∠BOC ，OF 平分∠AOC ，∴∠EOC=12∠BOC=30°，∠COF=12∠COA=60°， ∴∠EOF=60°+30°=90°；（3）∵∠BOC=n ，∴∠AOC=180°－n ，OE 平分∠BOC ，OF 平分∠AOC ，∴∠EOC=12∠BOC=90°－12n ，∠COF=12∠COA=12n ， ∴∠EOF=90°－12n+12n=90°；（4）∠EOF 的度数与∠BOC 的大小无关，互为邻补角的两个角的角平分线所组成的角是一个直角．【点睛】本题考查角平分线和规律的总结与归纳，掌握角平分线的性质是解题的关键．28．如图，是A 、B 、C 三个村庄的平面图，已知B 村在A 村的南偏西65°方向，C 村在A 村的南偏东15°方向，C 村在B 村的北偏东85°方向，求从C 村观测A 、B 两村的视角ACB ∠的度数．解析：80ACB ∠=︒【分析】根据平行线的性质以及三角形内角和定理即可得到结论.【详解】解：由已知，265∠=︒，315∠=︒，85DBC ∠=︒∵//BD AE∴1265∠=∠=︒∴41856520DBC ∠=∠-∠=︒-︒=︒在ABC 中18018065152080ACB ABC BAC ∠=︒-∠-∠=︒-︒-︒-︒=︒【点睛】本题考查的是方向角的概念，平行线的性质以及三角形内角和定理，熟练掌握三角形的内角和是解答此题的关键．。

人教版八年级数学-三角形-知识点+考点+典型例题(含答案)

人教版八年级数学-三角形-知识点+考点+典型例题(含答案)第七章三角形知识要点】一。

认识三角形1.三角形的定义和按角度分类三条不在同一直线上的线段首尾相接组成的图形称为三角形。

2.三角形的分类：按角度大小分为锐角三角形、直角三角形和钝角三角形。

按边长分为等腰三角形和不等边三角形。

3.三角形三边关系（判断构成三角形的方法、比较线段长度）根据公理“两点之间，线段最短”，可以得出：任意两边之和大于第三边。

任意两边之差小于第三边。

4.与三角形有关的线段：角平分线、中线和高三角形的角平分线：一个角的平分线与对边相交形成的线段。

三角形的中线：连接一个顶点与对边中点的线段，将三角形分成面积相等的两个部分。

三角形的高：过一个顶点做对边的垂线，这条垂线段称为三角形的高。

注意：三角形的角平分线、中线和高都是线段，不是直线或射线。

任意一个三角形都有三条角平分线、三条中线和三条高。

任意一个三角形的三条角平分线、三条中线都在三角形的内部。

但是三角形的高有不同的位置：锐角三角形的三条高都在三角形的内部；直角三角形有一条高在三角形的内部，另两条高恰好是它两条直角边；钝角三角形一条高在三角形的内部，另两条高在三角形的外部。

一个三角形中，三条中线交于一点，三条角平分线交于一点，三条高所在的直线交于一点。

锐角三角形高的交点在三角形的内部，直角三角形高的交点是直角顶点，钝角三角形高的交点在三角形的外部。

4.三角形的内角和外角1) 三角形的内角和为180°。

引申：直角三角形的两个锐角互余。

一个三角形中至多有一个直角或一个钝角。

一个三角形中至少有两个内角是锐角。

2) 三角形的外角和为360°。

3) 三角形外角的性质：一个外角等于与它不相邻的两个内角的和，常用来求角度。

一个外角大于任何一个与它不相邻的内角，常用来比较角的大小。

5.多边形的内角和外角多边形的内角和与外角和（识记）正n边形内角和外角和每一个内角3 180° 360° 60°4 360° 360° 90°5 540° 360° 108°6 720° 360° 120°8 1080° 360° 135°10 1440° 360°3.一个多边形的边数增加一倍，它的内角和增加了（A）。

《常考题》初中八年级数学上册第十一章《三角形》知识点总结(含答案解析)

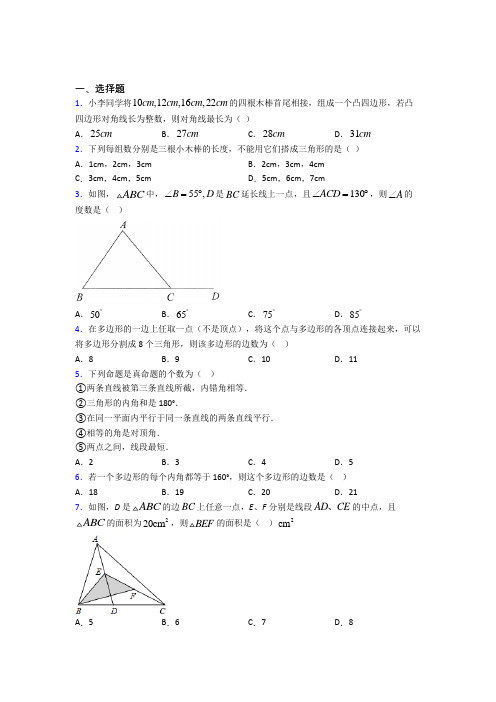
一、选择题1．小李同学将10,12,16,22cm cm cm cm 的四根木棒首尾相接，组成一个凸四边形，若凸四边形对角线长为整数，则对角线最长为（）A ．25cmB ．27cmC ．28cmD ．31cm 2．下列每组数分别是三根小木棒的长度，不能用它们搭成三角形的是（） A ．1cm ，2cm ，3cmB ．2cm ，3cm ，4cmC ．3cm ，4cm ，5cmD ．5cm ，6cm ，7cm 3．如图，ABC 中，55,B D ∠=︒是BC 延长线上一点，且130ACD ∠=︒，则A ∠的度数是（）A ．50︒B ．65︒C ．75︒D ．85︒4．在多边形的一边上任取一点（不是顶点），将这个点与多边形的各顶点连接起来，可以将多边形分割成8个三角形，则该多边形的边数为（）A ．8B ．9C ．10D ．115．下列命题是真命题的个数为（）①两条直线被第三条直线所截，内错角相等．②三角形的内角和是180°．③在同一平面内平行于同一条直线的两条直线平行．④相等的角是对顶角．⑤两点之间，线段最短．A ．2B ．3C ．4D ．5 6．若一个多边形的每个内角都等于160°，则这个多边形的边数是（）A ．18B ．19C ．20D ．21 7．如图，D 是ABC 的边BC 上任意一点，E 、F 分别是线段AD CE 、的中点，且ABC 的面积为220cm ，则BEF 的面积是（）2cmA ．5B ．6C ．7D ．88．下列长度的四根木棒，能与3cm ，7cm 长的两根木棒钉成一个三角形的是（） A ．3cm B ．10cm C ．4cm D ．6cm9．如图，已知,,90,//AD BC FG BC BAC DE AC ⊥⊥∠=︒．则结论①//FG AD ；②DE 平分ADB ；③B ADE ∠=∠；④CFG BDE ∠+∠90=︒．正确的是（）A ．①②③B ．①②④C ．①③④D ．②③④ 10．如图，小明从点A 出发沿直线前进9米到达点,B 向左转45后又沿直线前进9米到达点C ，再向左转45后沿直线前进9米到达点D ……照这样走下去，小明第一次回到出发点A 时所走的路程为（）A ．72米B ．80米C ．100米D ．64米 11．设四边形的内角和等于a ，五边形的外角和等于b ，则a 与b 的关系是（）． A ．a b = B ．180a b =+° C ．180b a =+︒ D ．360b a =+︒ 12．如图所示，ABC ∆的边AC 上的高是（）A ．线段AEB ．线段BAC ．线段BD D ．线段DA 13．某多边形的内角和是其外角和的3倍，则此多边形的边数是（）A ．5B ．6C ．7D ．8 14．如图，在ABC 中，48BAC ∠=︒，点 I 是ABC ∠、ACB ∠的平分线的交点．点D 是ABC ∠、 ACB ∠的两条外角平分线的交点，点E 是内角ABC ∠、外角ACG ∠的平分线的交点，则下列结论不正确．．．的是（）A ．180BDC BIC ∠+∠=︒B ．85ICE ∠=︒C ．24E ∠=︒D ．90DBE ∠=︒ 15．如图，王师傅用六根木条钉成一个六边形木框，要使它不变形，至少还要再钉上________根木条（）A ．2B ．3C ．4D ．5二、填空题16．如图，点D 在ABC 的边BA 的延长线上，点E 在BC 边上，连接DE 交AC 于点F ，若3117DFC B ∠∠==︒，C D ∠=∠，则BED ∠=________．17．2016年2月6日凌晨，宝岛高雄发生6.7级地震，得知消息后，中国派出武警部队探测队，探测队探测出某建筑物下面有生命迹象，他们在生命迹象上方建筑物的一侧地面上的,A B 两处，用仪器探测生命迹象C ，已知探测线与地面的夹角分别是30︒和60︒（如图)，则C ∠的度数是_________．18．如果三角形的三边长分别为5，8，a ，那么a 的取值范围为__．19．如果三角形两条边分别为3和5，则周长L 的取值范围是________20．如图，ACD ∠是ABC 的外角，ABC ∠的平分线与ACD ∠的平分线交于点1A ，1A BC ∠的平分线与1A CD ∠的平分线交于点2A ，…，1n A BC -∠的平分线与1n A CD -∠的平分线交于点n A ，设=A θ∠，则2=A ∠___________，=n A ∠___________．21．如图，若∠CGE=α，则∠A+∠B+∠C+∠D+∠E+∠F=____．22．如图所示，△ABC 中，∠BAC 、∠ABC 、∠ACB 的四等分线相交于D 、E 、F （其中∠CAD ＝3∠BAD ，∠ABE ＝3∠CBE ，∠BCF ＝3∠ACF ），且△DFE 的三个内角分别为∠DFE ＝60°、∠FDE ＝53°、∠FED ＝67°，则∠BAC 的度数为_________°．23．已知//AB CD ，点P 是平面内一点，若30,20BPD PBA ∠=︒∠=︒，则CDP ∠=___________度．24．如图所示，∠A+∠B+∠C+∠D+∠E+∠F=____．（填写度数）．25．如图，若//AB CD ，BF 平分ABE ∠，DF 平分CDE ∠，90BED ∠=，则BFD ∠=______．26．如图，ABC 的角平分线OB 、OC 相交于点O ，40A ∠︒＝，则BOC ∠＝______．三、解答题27．如图，∠CBF ，∠ACG 是△ABC 的外角，∠ACG 的平分线所在的直线分别与∠ABC ，∠CBF 的平分线BD ，BE 交于点D ，E ．（1）若∠A=70°，求∠D 的度数；（2）若∠A=a ，求∠E ；（3）连接AD ，若∠ACB=β，则∠ADB= ．28．（问题引入）（1）如图1，△ABC ，点O 是∠ABC 和∠ACB 相邻的外角平分线的交点，若∠A=40°，请求出∠BOC 的度数．（深入探究）（2）如图2，在四边形ABDC 中，点O 是∠BAC 和∠ACD 的角平分线的交点，若∠B+∠D=110°，请求出∠AOC 的度数．（类比猜想）（3）如图3，在△ABC 中，∠CBO=13∠DBC ，∠BCO= 13∠ECB ，∠A=α，则∠BOC=___（用α的代数式表示，直接写出结果，不需要写出解答过程）．（4）如果BO ，CO 分别是△ABC 的外角∠DBC ，∠ECB 的n 等分线，它们交于点O ，∠CBO=∠1n DBC ∠BCO=1n∠ECB ，则∠BOC=___（用n 、a 的代数式表示，直接写出结果，不需要写出解答过程）． 29．如图，在ABC 中，AD 是高，AE 、BF 是角平分线，它们相交于点O ，60BAC ∠=︒，70C ∠=︒．求EAD ∠和∠BOE 的度数．30．阅读材料在平面中，我们把大于180︒且小于360︒的角称为优角．如果两个角相加等于360︒，那么称这两个角互为组角，简称互组．（1）若1∠，2∠互为组角，且1135∠=︒，则2∠=______．习惯上，我们把有一个内角大于180︒的四边形俗称为镖形．（2）如图，在镖形ABCD 中，优角BCD ∠与钝角BCD ∠互为组角，试探索内角A ∠，B ，D ∠与钝角BCD ∠之间的数量关系，并至少用两种以上的方法说明理由．。

新人教版初中数学——三角形及其全等-知识点归纳及例题解析

新人教版初中数学——三角形及其全等知识点归纳及例题解析一、三角形的基础知识1．三角形的概念由三条线段首尾顺次相接组成的图形，叫做三角形．2．三角形的三边关系（1）三角形三边关系定理：三角形的两边之和大于第三边．推论：三角形的两边之差小于第三边．（2）三角形三边关系定理及推论的作用：①判断三条已知线段能否组成三角形；②当已知两边时，可确定第三边的范围；③证明线段不等关系．3．三角形的内角和定理及推论三角形的内角和定理：三角形三个内角和等于180°．推论：①直角三角形的两个锐角互余；②三角形的一个外角等于和它不相邻的两个内角的和；③三角形的一个外角大于任何一个和它不相邻的内角．4．三角形中的重要线段（1）三角形的一个角的平分线与这个角的对边相交，这个角的顶点和交点间的线段叫做三角形的角平分线．（2）在三角形中，连接一个顶点和它对边的中点的线段叫做三角形的中线．（3）从三角形一个顶点向它的对边做垂线，顶点和垂足之间的线段叫做三角形的高线（简称三角形的高）．（4）连接三角形两边中点的线段叫做三角形的中位线，三角形的中位线平行于第三边，且等于第三边的一半．二、全等三角形1．三角形全等的判定定理：（1）边角边定理：有两边和它们的夹角对应相等的两个三角形全等（可简写成“边角边”或“SAS”）；（2）角边角定理：有两角和它们的夹边对应相等的两个三角形全等（可简写成“角边角”或“ASA”）；（3）边边边定理：有三边对应相等的两个三角形全等（可简写成“边边边”或“SSS”）；（4）对于特殊的直角三角形，判定它们全等时，还有HL定理（斜边、直角边定理）：有斜边和一条直角边对应相等的两个直角三角形全等（可简写成“斜边、直角边”或“HL”）．2．全等三角形的性质：（1）全等三角形的对应边相等，对应角相等；（2）全等三角形的周长相等，面积相等；（3）全等三角形对应的中线、高线、角平分线、中位线都相等．考向一三角形的三边关系在判断三条线段能否组成一个三角形时，可以根据两条较短线段的长度之和是否大于第三条线段的长度来判断．典例1 小芳有两根长度为6 cm和9 cm的木条，她想钉一个三角形木框，桌上有下列长度的几根木条，她应该选择长度为__________的木条．A．2 cm B．3 cmC．12 cm D．15 cm【答案】C【解析】设木条的长度为x cm，则9–6<x<9+6，即3<x<15，故她应该选择长度为12 cm的木条．故选C．1．以下列各组线段为边，能组成三角形的是A．2 cm，5 cm，8 cm B．3 cm，3 cm，6 cmC．3 cm，4 cm，5 cm D．1 cm，2 cm，3 cm考向二三角形的内角和外角在同一个三角形中：等角对等边；等边对等角；大角对大边；大边对大角．典例2 小桐把一副直角三角尺按如图所示的方式摆放在一起，其中90E ∠=︒，90C ∠=︒，45°A ∠=，30D ∠=︒，则12∠+∠等于A ．150︒B ．180︒C ．210︒D ．270︒【答案】C【解析】如图，∵1D DOA ∠=∠+∠，2E EPB ∠=∠+∠， ∵DOA COP ∠=∠，EPB CPO ∠=∠， ∴12D E COP CPO ∠+∠=∠+∠+∠+∠ =180D E C ∠+∠︒+-∠ =309018090210︒︒︒︒++-=︒，故选C ．2．如图，CE 是△ABC 的外角ACD ∠的平分线，若3560，B ACE ∠=︒∠=︒，则A ∠=__________．3．如图，在△ABC 中，∠ACB =68°，若P 为△ABC 内一点，且∠1=∠2，则∠BPC =__________．考向三三角形中的重要线段三角形的高、中线、角平分线是三条线段，由三角形的高可得90°的角，由三角形的中线可得线段之间的关系，由三角形的角平分线可得角之间的关系．另外，要注意区分三角形的中线和中位线．中线：连接三角形一个顶点和它对边中点的线段；中位线：连接三角形两条边中点的线段.典例3 在△ABC中，AB=3，BC=4，AC=2，D，E，F分别为AB，BC，AC中点，连接DF，FE，则四边形DBEF的周长是A．5 B．7 C．9 D．11【答案】B【解析】∵D、E、F分别为AB、BC、AC中点，∴DF=12BC=2，DF∥BC，EF=12AB=32，EF∥AB，∴四边形DBEF为平行四边形，∴四边形DBEF的周长=2（DF+EF）=2×（2+32）=7，故选B．【名师点睛】三角形中位线定理：三角形的中位线平行于第三边，并且等于第三边的一半．典例4 在△ABC中，∠BAC=115°，DE、FG分别为AB、AC的垂直平分线，则∠EAG的度数为A．50°B．40°C．30°D．25°【答案】A【解析】∵∠BAC=115°，∴∠B+∠C=65°，∵DE、FG分别为AB、AC的垂直平分线，∴EA=EB，GA=GC，∴∠EAB=∠B，∠GAC=∠C，∴∠EAG=∠BAC–（∠EAB+∠GAC）=∠BAC–（∠B+∠C）=50°，故选A．4．如图，在Rt△ABC中，∠A=90°，BD平分∠ABC交AC于D点，AB=4，BD=5，点P是线段BC上的一动点，则PD 的最小值是__________．考向四全等三角形1．从判定两个三角形全等的方法可知，要判定两个三角形全等，需要知道这两个三角形分别有三个元素（其中至少有一个元素是边）对应相等，这样就可以利用题目中的已知边（角）准确地确定要补充的边（角），有目的地完善三角形全等的条件，从而得到判定两个三角形全等的思路：（1）已知两边SASHLSSS ⎧⎪⎨⎪⎩找夹角→找直角→找第三边→（2）已知一边、一角AASSASASAAAS⎧⎪⎧⎪⎨⎪⎨⎪⎪⎪⎩⎩一边为角的对边→找另一角→找夹角的另一边→一边为角的邻边找夹角的另一角→找边的对角→（3）已知两角ASAAAS ⎧⎨⎩找夹边→找其中一角的对边→2．若题中没有全等的三角形，则可根据题中条件合理地添加辅助线，如运用作高法、倍长中线法、截长补短法、分解图形法等来解决运动、拼接、旋转等探究性题目．典例5 如图，点B、F、C、E在同一条直线上，AB∥DE，∠A=∠D，BF=EC．（1）求证：△ABC≌△DEF；（2）若∠A=120°，∠B=20°，求∠DFC的度数．【解析】（1）∵AB∥DE，∴∠B=∠E，∵BF=EC∴BF+FC=EC+CF，即BC=EF，在△ABC和△DEF中，A DB E BC EF∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ABC≌△DEF．（2）∵∠A=120°，∠B=20°，∴∠ACB=40°，由（1）知△ABC≌△DEF，∴∠ACB=∠DFE，∴∠DFE=40°，∴∠DFC=40°．【名师点睛】本题考查了全等三角形的判定方法，①三边对应相等的两个三角形全等，简记为“SSS”；②两边及其夹角对应相等的两个三角形全等，简记为“SAS”；③两角及其夹边对应相等的两个三角形全等，简记为“ASA”；④两角及其中一角的对边对应相等的两个三角形全等，简记为“AAS”；⑤斜边及一直角边对应相等的两个三角形全等，根据这几种判定方法解答即可．5．如图，OA=OB，∠A=∠B，有下列3个结论：①△AOD≌△BOC，②△ACE≌△BDE，③点E在∠O的平分线上，其中正确的结论个数是A．0 B．1 C．2 D．36．如图，在△BCE中，AC⊥BE，AB=AC，点A、点F分别在BE、CE上，BF、AC相交于点D，BD=CE．求证：AD=AE．1．下列线段，能组成三角形的是A．2 cm，3 cm，5 cm B．5 cm，6 cm，10 cmC．1 cm，1 cm，3 cm D．3 cm，4 cm，8 cm2．下列图形不具有稳定性的是A．正方形B．等腰三角形C．直角三角形D．钝角三角形3．直角三角形中两锐角之差为20°，则较大锐角为A．45°B．55°C．65°D．50°4．如图，在△ABC中，∠C=90°，∠B=30°，AD是△ABC的角平分线，DE⊥AB，垂足为点E，DE=1，则BC=A3B．2 C．3 D3+25．如图所示，AB=DB，BC=BE，欲证△ABE≌△DBC，则需补充的条件是A．∠A=∠D B．∠E=∠CC．∠A=∠C D．∠1=∠26．如图，△ABC中，H是高AD、BE的交点，且BH=AC，则∠ABC=__________．7．如图，已知方格纸中是4个相同的正方形，则∠1＋∠2＋∠3=__________度．8．如图，已知AB∥CF，E为DF的中点，若AB=8，CF=5，则BD=__________．9．如图，在△ABC中，AB=AC，∠BAC=90°，BD是中线，AF⊥BD，F为垂足，过点C作AB的平行线交AF的延长线于点E．求证：（1）∠ABD=∠FAD；（2）AB=2CE．10．如图，在Rt△ABC中，∠ACB=90°，点D，F分别在AB，AC上，CF=C B．连接CD，将线段CD绕点C按顺时针方向旋转90°后得CE，连接EF．（1）求证：△BCD≌△FCE；（2）若EF∥C D．求∠BDC的度数．11．如图，操场上有两根旗杆CA与BD之间相距12 m，小强同学从B点沿BA走向A，一定时间后他到达M点，此时他测得CM和DM的夹角为90°，且CM=DM，已知旗杆AC的高为3 m，小强同学行走的速度为0.5 m/s，则：（1）请你求出另一旗杆BD的高度；（2）小强从M点到达A点还需要多长时间？1．下列长度的三条线段，能组成三角形的是 A ．2，2，4 B ．5，6，12 C ．5，7，2 D ．6，8，102．三角形的内角和等于 A ．90︒B ．180︒C ．270︒D ．360︒3．将一副直角三角板按如图所示的位置摆放，使得它们的直角边互相垂直，则1∠的度数是A ．95︒B ．100︒C ．105︒D ．110︒4．如图，在△ABC 中，BE 是∠ABC 的平分线，CE 是外角∠ACM 的平分线，BE 与CE 相交于点E ，若∠A =60°，则∠BEC 是A ．15°B ．30°C ．45°D ．60°5．如图，在ABC △中，ACB ∠为钝角．用直尺和圆规在边AB 上确定一点D ．使2ADC B ∠=∠，则符合要求的作图痕迹是A ．B ．C ．D ．6．如图，在ABC △中，90C ∠=︒，8AC =，13DC AD =，BD 平分ABC ∠，则点D 到AB 的距离等于A ．4B ．3C ．2D ．17．如图，DE 是ABC △的边AB 的垂直平分线，D 为垂足，DE 交AC 于点E ，且85AC BC ==，，则BEC △的周长是A ．12B ．13C ．14D ．158．如图，D 是AB 上一点，DF 交AC 于点E ，DE FE =，FC AB ∥，若4AB =，3CF =，则BD 的长是A ．0.5B ．1C ．1.5D ．29．如图，在四边形ABCD 中，AD ∥BC ，∠D =90°，AD =4，BC =3．分别以点A ，C 为圆心，大于12AC 长为半径作弧，两弧交于点E ，作射线BE 交AD 于点F ，交AC 于点O ．若点O 是AC 的中点，则CD 的长为A ．2B ．4C ．3D 1010．一副三角板如图摆放（直角顶点C 重合），边AB 与CE 交于点F ，DE BC ∥，则BFC ∠等于A ．105︒B ．100︒C ．75︒D ．60︒11．如图，BD 是△ABC 的角平分线，AE ⊥BD ，垂足为F ．若∠ABC =35°，∠C =50°，则∠CDE 的度数为A ．35°B ．40°C ．45°D ．50°12．如图，在OAB △和OCD △中，,,,40OA OB OC OD OA OC AOB COD ==>∠=∠=︒，连接,AC BD 交于点M ，连接OM ．下列结论：①AC BD =；②40AMB ∠=︒；③OM 平分BOC ∠；④MO 平分BMC ∠．其中正确的个数为A ．4B ．3C ．2D ．113．在△ABC 中，AB =AC ，∠A =40°，则∠B =__________．14．如图，要测量池塘两岸相对的A ，B 两点间的距离，可以在池塘外选一点C ，连接AC ，BC ，分别取AC ，BC 的中点D ，E ，测得DE =50 m ，则AB 的长是__________m ．15．如图，在△ABC 中，AB =AC ，点D ，E 都在边BC 上，∠BAD =∠CAE ，若BD =9，则CE 的长为__________．16．如图，△ABC 中，AB =BC ，∠ABC =90°，F 为AB 延长线上一点，点E 在BC 上，且AE =CF ，若∠BAE =25°，则∠ACF =__________度．17．如图，AB CD ∥，AD 和BC 相交于点O ，OA OD =．求证：OB OC =．18．如图，D 是AB 上一点，DF 交AC 于点E ，DE =FE ，FC ∥AB ，求证：ADE CFE △≌△．19．如图，在△ABC 中，AB =AC ，点D 、E 分别在AB 、AC 上，BD =CE ，BE 、CD 相交于点O ．△≌△；求证：（1）DBC ECB．（2）OB OC变式拓展1．【答案】C【解析】2cm+5cm<8cm，A不能组成三角形；3cm+3cm=6cm，B不能组成三角形；3cm+4cm＞5cm，C能组成三角形；1cm+2cm=3cm，D不能组成三角形；故选C．2．【答案】85°【解析】∵∠ACE=60°，CE是△ABC的外角∠ACD的平分线，∠ACD=2∠ACE=120°，∵∠ACD=∠A+∠B，∠B=35°，∴∠A=∠ACD-∠B=85°，故答案为：85°．3．【答案】112°【解析】∵∠1+∠PCB=∠ACB=68°，又∵∠1=∠2，∴∠2+∠PCB=68°，∵∠BPC+∠2+∠PCB=180°，∴∠BPC=180°-68°=112°，故答案为：112°．4．【答案】3【解析】由勾股定理知AD3=，BD平分∠ABC交AC于D点，所以PD=AD最小，PD=3，故答案为：3．5．【答案】D【解析】∵OA=OB，∠A=∠B，∠O=∠O，∴△AOD≌△BOC（ASA），故①正确；∴OD=CO，∴BD=AC，∴△ACE≌△BDE（AAS），故②正确；∴AE=BE，连接OE，∴△AOE≌△BOE（SSS），∴∠AOE=∠BOE，∴点E在∠O的平分线上，故③正确，故选D．6．【解析】∵AC⊥BE，∴∠BAD=∠CAE=90°，在Rt△ABD和Rt△ACE中，BD CE AB AC=⎧⎨=⎩，∴Rt△ABD≌Rt△ACE（HL），∴AD=AE．1．【答案】B【解析】A、3+2=5，故选项错误；B、5+6>10，故正确；C、1+1<3，故错误；D、4+3<8，故错误．故选B．2．【答案】A【解析】根据三角形具有稳定性可知，只有选项A不具有稳定性，故选A．3．【答案】B【解析】设两个锐角分别为x、y，由题意得，=90=20x yx y+︒-︒⎧⎨⎩，解得=55=35xy︒︒⎧⎨⎩，所以最大锐角为55°．故选B．4．【答案】C【解析】根据角平分线的性质可得CD=DE=1，根据Rt△ADE可得AD=2DE=2，根据题意可得△ADB为等腰三角形，则DE为AB的中垂线，则BD=AD=2，则BC=CD+BD=1+2=3．故选C．5．【答案】D【解析】根据全等“SAS”判定可知，要证△ABE≌△DBC还需补充条件AB，BE与BC，BD的夹角相等，即∠ABE=∠CBD或者∠1=∠2，故选D．6．【答案】45°【解析】∵AD⊥BC，BE⊥AC，∴∠ADB=∠ADC=∠BEC=90°，∴∠HBD+∠C=∠CAD+∠C=90°，∴∠HBD=∠CAD，∵在△HBD和△CAD中，HBD CADHDB CDA BH AC∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△HBD≌△CAD，∴AD=BD，∴∠DAB=∠DBA，∵∠ADB=90°，∴∠ABD=45°，即∠ABC=45°故答案为：45°．7．【答案】135【解析】如图所示：由题意可知△ABC≌△EDC，∴∠3=∠BAC，又∵∠1+∠BAC=90°，∴∠1+∠3=90°，∵DF=DC，∴∠2=45°，∴∠1+∠2+∠3=135度，故答案为：135．8．【答案】3【解析】∵AB∥CF，∴∠A=∠FCE，∠ADE=∠F，又∵DE=FE，∴△ADE≌△CFE，∴AD=CF=5，∵AB=8，∴BD=AB–AD=8–5=3，故答案为：3．9．【解析】(1)∵∠BAC=90°，∴∠FAD＋∠BAF=90°.∵AF⊥BD，∴在Rt△ABF中，∠ABD＋∠BAF=90°，∴∠ABD=∠FAD．(2)∵CE∥AB，∠BAC=90°，∴∠ACE=90°，在△BAD和△ACE中，∵∠ABD=∠CAE，AB=CA，∠BAC=∠ACE=90°，∴△BAD≌△ACE(ASA)，∴AD=CE.∵BD为△ABC中AC边上的中线．∴AC=2AD，∴AC=2CE.又∵AB=AC，∴AB=2CE.10．【解析】（1）∵将线段CD绕点C按顺时针方向旋转90°后得CE，∴CD=CE，∠DCE=90°，∵∠ACB=90°，∴∠BCD=90°–∠ACD=∠FCE，在△BCD和△FCE中，CB=CF，∵BCD=∠FCE，CD=CE，CB=CF，∠BCD=∠FCE，∴△BCD≌△FCE．（2）由（1）可知△BCD≌△FCE，∴∠BDC=∠E，∠BCD=∠FCE，∴∠DCE=∠DCA+∠FCE=∠DCA+∠BCD=∠ACB=90°，∵EF∥CD，∴∠E=180°–∠DCE=90°，∴∠BDC=90°．11．【解析】（1）如图，∵CM和DM的夹角为90°，∴∠1+∠2=90°，∵∠DBA=90°，∴∠2+∠D=90°，∴∠1=∠D，在△CAM 和△MBD 中，1A B D CM MD ∠=∠∠=∠=⎧⎪⎨⎪⎩，∴△CAM ≌△MBD （AAS ），∴AM =DB ，AC =MB ， ∵AC =3m ，∴MB =3m ，∵AB =12m ，∴AM =9m ，∴DB =9m ；（2）9÷0.5=18（s ）．答：小强从M 点到达A 点还需要18秒．1．【答案】D【解析】∵224+=，∴2，2，4不能组成三角形，故选项A 错误， ∵5612+<，∴5，6，12不能组成三角形，故选项B 错误， ∵527+=，∴5，7，2不能组成三角形，故选项C 错误， ∵6810+>，∴6，8，10能组成三角形，故选项D 正确，故选D ． 2．【答案】B【解析】因为三角形的内角和等于180度，故选B ． 3．【答案】C 【解析】如图，直通中考由题意得，2454903060∠=︒∠=︒︒=︒，-，∴3245∠=∠=︒，由三角形的外角性质可知，134105∠=∠+∠=︒，故选C ． 4．【答案】B【解析】∵BE 是∠ABC 的平分线，∴∠EBM =12∠ABC ， ∵CE 是外角∠ACM 的平分线，∴∠ECM =12∠ACM ，则∠BEC =∠ECM –∠EBM =12×（∠ACM –∠ABC ）=12∠A =30°，故选B ．5．【答案】B【解析】∵2ADC B ∠=∠且ADC B BCD ∠=∠+∠，∴B BCD ∠=∠，∴DB DC =， ∴点D 是线段BC 中垂线与AB 的交点，故选B ． 6．【答案】C【解析】如图，过点D 作DE AB ⊥于E ，∵8AC =，13DC AD =，∴18213CD =⨯=+， ∵90C ∠=︒，BD 平分ABC ∠，∴2DE CD ==，即点D 到AB 的距离为2，故选C ． 7．【答案】B【解析】∵DE 是ABC △的边AB 的垂直平分线，∴AE BE =，∵85AC BC ==，，∴BEC △的周长是：13BE EC BC AE EC BC AC BC ++=++=+=．故选B ． 8．【答案】B【解析】∵CF AB ∥，∴A FCE ∠=∠，ADE F ∠=∠，在ADE △和FCE △中，A FCEADE F DE FE ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴ADE CFE △≌△，∴3AD CF ==，∵4AB =，∴431DB AB AD =-=-=．故选B ． 9．【答案】A【解析】如图，连接FC ，则AF =FC ．∵AD ∥BC ，∴∠FAO =∠BCO ．在△FOA 与△BOC 中，FAO BCO OA OC AOF COB ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△FOA ≌△BOC （ASA ），∴AF =BC =3，∴FC =AF =3，FD =AD -AF =4-3=1．在△FDC 中，∵∠D =90°，∴CD 2+DF 2=FC 2，∴CD 2+12=32，∴CD 2A ． 10．【答案】A【解析】由题意知45E ∠=︒，30B ∠=︒，∵DE CB ∥，∴45BCF E ∠=∠=︒，在CFB △中，1801803045BFC B BCF ∠=︒-∠-∠=︒-︒-︒105=︒，故选A ． 11．【答案】C【解析】∵BD 是△ABC 的角平分线，AE ⊥BD ，∴∠ABD =∠EBD =12∠ABC =352︒，∠AFB =∠EFB =90°，∴∠BAF =∠BEF =90°-17.5°，∴AB =BE ，∴AF =EF ，∴AD =ED ，∴∠DAF =∠DEF ， ∵∠BAC =180°-∠ABC -∠C =95°，∴∠BED =∠BAD =95°，∴∠CDE =95°-50°=45°，故选C ． 12．【答案】B【解析】∵40AOB COD ∠=∠=︒，∴AOB AOD COD AOD ∠+∠=∠+∠，即AOC BOD ∠=∠，在AOC △和BOD △中，OA OBAOC BOD OC OD =⎧⎪∠=∠⎨⎪=⎩，∴AOC BOD △≌△，∴OCA ODB AC BD ∠=∠=，，①正确；∴OAC OBD ∠=∠，由三角形的外角性质得：AMB OAC AOB OBD ∠+∠=∠+∠， ∴40AMB AOB ∠=∠=°，②正确；作OG MC ⊥于G ，OH MB ⊥于H ，如图所示：则90OGC OHD ∠=∠=°，在OCG △和ODH △中，OCA ODB OGC OHD OC OD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴OCG ODH △≌△，∴OG OH =，∴MO 平分BMC ∠，④正确，正确的个数有3个，故选B ．13．【答案】70°【解析】∵AB =AC ，∴∠B =∠C ，∵∠A +∠B +∠C =180°，∴∠B =12（180°-40°）=70°．故答案为：70°． 14．【答案】100【解析】∵点D ，E 分别是AC ，BC 的中点，∴DE 是△ABC 的中位线，∴AB =2DE =2×50=100 m ．故答案为：100．15．【答案】9 【解析】∵AB =AC ，∴∠B =∠C ，在△BAD 和△CAE 中，BAD CAE AB AC B C ∠=∠⎧⎪=⎨⎪∠=∠⎩，∴△BAD ≌△CAE ，∴BD =CE =9，故答案为：9．16．【答案】70【解析】∵∠ABC =90°，AB =AC ，∴∠CBF =180°–∠ABC =90°，∠ACB =45°，在Rt △ABE 和Rt △CBF 中，AB CB AE CF=⎧⎨=⎩，∴Rt △ABE ≌Rt △CBF ， ∴∠BCF =∠BAE =25°，∴∠ACF =∠ACB +∠BCF =45°+25°=70°，故答案为：70．17．【解析】∵AB CD ∥，∴A D ∠=∠，B C ∠=∠，在AOB △和DOC △中，A D B C OA OD ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴AOB DOC △≌△，∴OB OC =．18．【解析】∵FC ∥AB ，∴∠A =∠FCE ，∠ADE =∠F ，所以在△ADE 与△CFE 中，A FCE ADE F DE EF ∠=∠⎧⎪∠=∠⎨⎪=⎩，∴△ADE ≌△CFE ．19．【解析】（1）∵AB =AC ，∴∠ECB =∠DBC ，在DBC △与ECB △中，BD CE DBC ECB BC CB =⎧⎪∠=∠⎨⎪=⎩，∴DBC △≌ECB △．（2）由（1）DBC △≌ECB △，∴∠DCB =∠EBC ，∴OB =OC ．。