比较线段的长短课件
合集下载
2024年秋季新冀教版7年级上册数学教学课件2.3 线段长短的比较

结 合
(2)如图所示,如果点B在线段CD上,就说线段AB小于CD,
记作AB<CD.
(3)如图所示,如果点B在线段CD外,就说线段AB大于CD, 记作AB>CD.
学生活动三【作一条线段等于已知线段】 我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
线段A'B'即为所求.
学生活动四【两点之间线段最短】
问 题 1 : 如图所示的是从北京到济南的铁路 线和公路线.请在图中画出这两个城市的线段. 在这三条线中,哪一条最短?请同学们用准备好 的细线比较一下。
问题2:一只小狗想吃到前方的一块骨头,有四条路 可选择,你说它会选择哪一条?为什么?
小狗
骨头
线段的基本事实:两点之间的所有连线中,线段最短. 容易地说:两点之间,线段最短.
如图所示,已知线段AB,CD,比较AB,CD的长短,有哪些方法? 先动手操作,再小组交流,探讨线段长短比较的方法。
A
B
C
D
A
B
归纳:观察法、度量法、叠合法
数
形
C
DLeabharlann 将两条线段的一个端点重合,另一个端点在这 个点的同一侧.
数 (1)如图所示,如果点B与点D重合,就说线段AB与CD相等, 形 记作AB=CD.
教学的艺术不在于传授本领,而在于 善于激励唤醒和鼓舞
第二章 几何图形的初步认识
2.3 线段长短的比较
1.了解比较线段的方法,注意图形与相应的符号表述. 2.掌握用直尺和圆规作一条线段等于已知线段的方法 3.理解和掌握“两点之间的所有连线中,线段最短”这 一线段的基本事实.
学习重点:比较线段的方法、线段的基本事实. 学习难点:叠合法比较两条线段大小.
北师大版七年级上册比较线段的长短(课件)

探索&交流
绿地里本没有路,走的人多了… …
根据生活经验,容易发现: 两点之间的所有连线中,线段最短.
探索&交流
这一事实可以简述为:两点之间线段最短. 我们把两点之间线段的长度,叫做这两点之间的距离.
探索&交流
将笔直的铁轨向两个方向无限延长形成了直线。直线没有端点。
例题欣赏 ☞
例题&解析
例1.如图,现实生活中有部分行人选择横穿马路而不走天桥
第四章 基本平面图形
2 比较线段的长短
北师大版七年级数学上册
学习&目标
1.借助具体情境,了解“两点之间的所有连线中,线段最短”的性质. 2.能借助直尺、圆规等工具比较两条线段的长短. 3.能用尺规作一条线段等于已知线段.
情境&导入
回顾:什么叫线段?射线和直线?它们之间的联系和区分是什么?
知识点一 线段的基本事实 为什么大家都喜欢走捷径呢?
AB A′ B′ C′
知识点四 线段的中点
探索&交流
若点M把线段AB分成相等的两条线段AM和BM, 则点M叫线段AB的
中点.
A
M
B
AM =
BM =
1 2
AB
探索&交流
2.对线段的中点的认识: (1)线段的中点是线段上的点,且把线段分成相等 的两条线段; (2)一条线段的中点有且只有一个; (3)如图,若M是AB的中点,则①AM=BM= AB; ②AB=2AM=2BM;③AM+BM=AB且AM=BM.反过来也成立.
哪支铅笔长?
探索&交流
窗框相邻的两条边哪条边长?
探索&交流
探索&交流
思考:请同学们思考并回答下面的问题:
《比较线段的长短》课件(共27张PPT)【推荐】

例3 比较图中各线段的长短.
例3 比较图中各线段的长短.
解析 线段AC<线段BC<线段AB 点拨 解答这类问题,可以利用叠合法,也可 以利用度量法.
知识点四 线段的和、差及尺规 作图
1.线段的和差:如图所示,点B在线段AC上,AB=a, BC=b,AC=c,则线段AC可表示为线段AB与BC的和, 即AC=AB+BC(或c=a+b);BC可表示为线段AC 与AB的差,即BC=AC-AB(或b=c-a);AB可表示为 线段AC与BC的差,即AB=AC-BC(或a=c-b).
提示: (1)连接两点的线有无数条,线段最短; (2)连线是指以两个点为端点的任意线,包括线 段、折线和曲线; (3)连接AB是指画线段AB.
例1 图中三条通往落马村的路线,哪条路线最短?请 在图中设计一条去落马村的最短的路线,并说明 理由.
解析:
①、②、③三条路线中,路线②最短如图,设计 的最短路线是路线④,理由是两点之间,线段最 短.
所以2x+3x+x=6,所以x=1.所以AC=1m,CD
=3m,BD=2m.
点拨
这种根据线段的比设出未知数,建立方程解决问 题的思想方法,数学中称为方程思想.
易错易混
易错点 忽视“直线”条件而导致漏解
例 已知点B在直线AC上,AB=6,AC=10,点P、Q分 别是AB、AC的中点,求PQ的长.
解析 有点B在线段AC上或在线段CA的延长线上两种可 能.由点P、Q分别为AB、AC的中点可知 AP= AB=3,AQ= AC=5. 如下图所示,当点B在线段AC上时,PQ=AQ-AP =2.
线段 的中 点
注意
内容
图例
把一条线段分 成两条相等线 段的点,叫做 点M是线段AB的中点,AM=BM 这条线段的中 = AB,即AB=2AM=2BM 点 (1)一条线段的中点一定在这条线段上; (2)一条线段只有一个中点.
比较线段的长短PPT教学课件
找到方法的朋友方可入内 你有办法吗?
房间1
小狗跑的远,
C
D
还是小猫跑的
A
B
远,你是怎么 比较的?
房间2
线段的大小比较
C
D
(1)度量法
A
B
(2)叠合法
房间2
AM BM 1 AB 2
A
MB
中点
点M把线段AB分成相 等的两条线段AM与
BM,点M叫做线段 AB的中点。
房1.间房A间、AB、、BC、在C同顺一次在同一条直线上, 条直A线B=上4、BC=3,则AC为多少? 2.房间A、B、C在同一条直线上,AB=4、
陶渊明的诗歌,以歌咏田园生活的居多,后世称他为田园诗人。陶渊明的 田园诗主要见于他的组诗《饮酒》、《归园田居》、《拟古》、《和郭主簿》。 他的五言诗成就最高,诗歌的意境下平和、静穆、深远,在中国诗歌史上有着 重要的地位。他那种淡泊明志的人生态度,对读书人的影响很深。
通过虚构(
)一
个和平、美好、没有剥…削、没有压迫、人
赞语说:黔娄的妻子曾经说过这样的话:“不为贫贱而忧虑, 不热衷于发财做官。”从这话来看,他应是五柳先生一类人吧 ? 一 边喝酒一边做诗,用这种方式使自己的心志得到快乐,他大概是无 怀氏的子民吧?或者是葛天氏的子民吧?
板书
归去来兮,田园将芜胡不归,自以心为形役,奚惆怅而独归,悟已往之不谏,知 来者可追。实迷途其未远,觉今是而昨非。
文章线索 抒情
自责自悔
自安自乐
乐天安命
叙事
辞官 归途 家中生活 纵情山水 抒发情怀
全文主旨
《归去来兮辞》 是陶渊明辞官归隐之际与上流社 会公开决裂的政治宣言。文章以 绝大篇幅写了他脱离官场的无限 喜悦,想家归隐田园的无限乐趣, 表现了作者对大自然和隐居生活
房间1
小狗跑的远,
C
D
还是小猫跑的
A
B
远,你是怎么 比较的?
房间2
线段的大小比较
C
D
(1)度量法
A
B
(2)叠合法
房间2
AM BM 1 AB 2
A
MB
中点
点M把线段AB分成相 等的两条线段AM与
BM,点M叫做线段 AB的中点。
房1.间房A间、AB、、BC、在C同顺一次在同一条直线上, 条直A线B=上4、BC=3,则AC为多少? 2.房间A、B、C在同一条直线上,AB=4、
陶渊明的诗歌,以歌咏田园生活的居多,后世称他为田园诗人。陶渊明的 田园诗主要见于他的组诗《饮酒》、《归园田居》、《拟古》、《和郭主簿》。 他的五言诗成就最高,诗歌的意境下平和、静穆、深远,在中国诗歌史上有着 重要的地位。他那种淡泊明志的人生态度,对读书人的影响很深。
通过虚构(
)一
个和平、美好、没有剥…削、没有压迫、人
赞语说:黔娄的妻子曾经说过这样的话:“不为贫贱而忧虑, 不热衷于发财做官。”从这话来看,他应是五柳先生一类人吧 ? 一 边喝酒一边做诗,用这种方式使自己的心志得到快乐,他大概是无 怀氏的子民吧?或者是葛天氏的子民吧?
板书
归去来兮,田园将芜胡不归,自以心为形役,奚惆怅而独归,悟已往之不谏,知 来者可追。实迷途其未远,觉今是而昨非。
文章线索 抒情
自责自悔
自安自乐
乐天安命
叙事
辞官 归途 家中生活 纵情山水 抒发情怀
全文主旨
《归去来兮辞》 是陶渊明辞官归隐之际与上流社 会公开决裂的政治宣言。文章以 绝大篇幅写了他脱离官场的无限 喜悦,想家归隐田园的无限乐趣, 表现了作者对大自然和隐居生活
【数学课件】比较线段的长短

最高级的技巧和艺术。——苏霍姆林斯基 5、没有时间教育儿子——就意味着没有时间做人。——(前苏联)苏霍姆林斯基 6、教育不是注满一桶水,而且点燃一把火。——叶芝 7、教育技巧的全部奥秘也就在于如何爱护儿童。——苏霍姆林斯基 8、教育的根是苦的,但其果实是甜的。——亚里士多德 9、教育的目的,是替年轻人的终生自修作准备。——R.M.H. 10、教育的目的在于能让青年人毕生进行自我教育。——哈钦斯 11、教育的实质正是在于克服自己身上的动物本能和发展人所特有的全部本性。——(前苏联)苏霍姆林斯基 12、教育的唯一工作与全部工作可以总结在这一概念之中——道德。——赫尔巴特 13、教育儿童通过周围世界的美,人的关系的美而看到的精神的高尚、善良和诚实,并在此基础上在自己身上确立美的品质。——苏霍姆林斯基 14、教育不在于使人知其所未知,而在于按其所未行而行。——园斯金 15、教育工作中的百分之一的废品,就会使国家遭受严重的损失。——马卡连柯 16、教育技巧的全部诀窍就在于抓住儿童的这种上进心,这种道德上的自勉。要是儿童自己不求上进,不知自勉,任何教育者就都不能在他的身
之间
思考题
如图是一个四边
形,现在取各边的中
点并连接成四边形, 想一想得到的四边形 与原四边形,哪一个 的周长大?如是在各
D H
A G
E
边任意取一点呢?
B
ቤተ መጻሕፍቲ ባይዱ
F
C
小结
1、线段的基本性质:两点之间线段最短。 两点之间的距离:两点之间线段的长度。
2、尺规作图:作一条线段等于已知线段。 3、线段的两种比较方法:叠合法和度量法。 4、线段的中点的概念及表示方法。
BN C
M
A
解:∵M为AC的中点,∴AC=2AM.
又∵AM=3cm,∴AC=2×3=6(cm) .
之间
思考题
如图是一个四边
形,现在取各边的中
点并连接成四边形, 想一想得到的四边形 与原四边形,哪一个 的周长大?如是在各
D H
A G
E
边任意取一点呢?
B
ቤተ መጻሕፍቲ ባይዱ
F
C
小结
1、线段的基本性质:两点之间线段最短。 两点之间的距离:两点之间线段的长度。
2、尺规作图:作一条线段等于已知线段。 3、线段的两种比较方法:叠合法和度量法。 4、线段的中点的概念及表示方法。
BN C
M
A
解:∵M为AC的中点,∴AC=2AM.
又∵AM=3cm,∴AC=2×3=6(cm) .
2024新人编版七年级数学上册《第六章6.2.2第1课时比较线段的长短》教学课件

探究新知
作一条线段等于已知线段.
已知:线段 a,作一条线段 AB,使 AB=a.
第一步:用直尺画射线 AF;
第二步:用圆规在射线 AF 上截取
AB = a.
Aa
所以 线段 AB 为所求.
a BF
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是
尺规作图.
探究新知
说一说
你们平时是如何比较两个同学的身高的?你能从比身 高的方法中得到启示来比较两条线段的长短吗?
义务教育(2024年)新人教版 七年级数学上册
第6章 几何图形初步 课件
第六章 几何图形初步
6.2.2 线段的比较与计算 第1课时 比较线段的长短
学习目标
1.用尺规画一条线段等于已知线段,会比较两条线段的长短. 2. 体会文字语言、符号语言和图形语言的相互转化;了解两 点间距离的意义,理解“两点之间,线段最短”的线段性 质,并学会运用.
两点的所有连线中,线段最短.
连接两点间的线段的长度,叫做 这两点的距离.
探究新知
1.如图,这是 A,B 两地之间的公路,在公路工程改造计 划时,为使 A,B 两地行程最短,应如何设计线路?请 在图中画出,并说明理由.
B. A.
两点之间线段最短.
探究新知
2.把原来弯曲的河道改直,A,B 两地间的河道长度 有什么变化?
两个端点的位置作比较.
C (A)
尺规作图
BD
探究新知
叠合法结论
A C (A)
A C(A) A (A)C
B
1. 若点 A 与点 C 重合,点 B 落
B D 在C,D之间,那么 AB <CD.
B (B) D
2. 若点 A 与点 C 重合,点 B 与 点 D 重合 ,那么 AB = CD.
比较线段的长短 ppt课件4
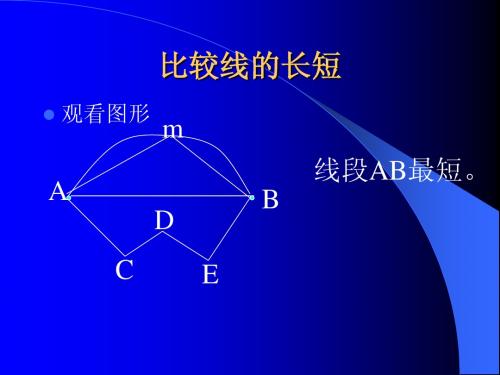
C B
2.如图,在正方体两个相距最远的 定点出逗留这一只苍蝇合一只蜘蛛。
(1)蜘蛛可以从哪条 最段的路径爬到苍蝇 处?说明你的理由?
(2)如果蜘蛛要沿着 棱爬到苍蝇处,最短的 路线有几条?
今天你学到了什么? 1.两点之间的所有连线中 线段最短Байду номын сангаас 或两点之间线段最短(线段公理) 2.两点之间线段的长度,叫做这两 点之间的距离。
比较线的长短
观看图形
m D B E 线段AB最短。
A C
比较线段的长短 1.两点之间的所有连线中 线段最短。 或两点之间线段最短(线段公理) 2.两点之间线段的长度,叫做这两 点之间的距离。
两条线段比较会有几种情况?
A
C A C
B
D D
(1).AB=CD
B
(2).AB>CD
A
C
B
D (3).AB<CD
3.比较线段的方法 (1)叠合法—从“形”的角度比较 (2)度量法—从“数值”的角度比 较
方法
(1)叠合法—从“形”的角度比较 (2)度量法—从“数值”的角度比 较
A
M
1
B
表示为:AB=BM-AB
2
或AB=2AM=2BM
线段的中点:把一条线段分成相等 的两段的点,叫做线段的中点。
能力挑战
1.已知线段AB=8cm,在直线AB上
画线段BC,使BC=3cm,求线段AC 的长度。 解: A AC=AB-BC =8-3 =5(cm).
2.如图,在正方体两个相距最远的 定点出逗留这一只苍蝇合一只蜘蛛。
(1)蜘蛛可以从哪条 最段的路径爬到苍蝇 处?说明你的理由?
(2)如果蜘蛛要沿着 棱爬到苍蝇处,最短的 路线有几条?
今天你学到了什么? 1.两点之间的所有连线中 线段最短Байду номын сангаас 或两点之间线段最短(线段公理) 2.两点之间线段的长度,叫做这两 点之间的距离。
比较线的长短
观看图形
m D B E 线段AB最短。
A C
比较线段的长短 1.两点之间的所有连线中 线段最短。 或两点之间线段最短(线段公理) 2.两点之间线段的长度,叫做这两 点之间的距离。
两条线段比较会有几种情况?
A
C A C
B
D D
(1).AB=CD
B
(2).AB>CD
A
C
B
D (3).AB<CD
3.比较线段的方法 (1)叠合法—从“形”的角度比较 (2)度量法—从“数值”的角度比 较
方法
(1)叠合法—从“形”的角度比较 (2)度量法—从“数值”的角度比 较
A
M
1
B
表示为:AB=BM-AB
2
或AB=2AM=2BM
线段的中点:把一条线段分成相等 的两段的点,叫做线段的中点。
能力挑战
1.已知线段AB=8cm,在直线AB上
画线段BC,使BC=3cm,求线段AC 的长度。 解: A AC=AB-BC =8-3 =5(cm).
6.3 线段的长短比较 教学课件 (共28张PPT)
讲授新课
作一条线段等于已知线段 已知:线段 a,作一条线段 AB,使 AB=a. 第一步:用直尺画射线 AF; 第二步:用圆规在射线 AF 上截取 AB = a. 所以线段 AB 为所求线段.
a Aa B F
在数学中,我们常限定用无刻度的直尺和圆规作图,这就是尺规作图.
讲授新课
尺规作图的要点: 1.直尺只能用来画线,不能量距; 2.尺规作图要求作出图形,说明结果,并保留作图痕迹.
生活中我们常常会比较两个物体的长短。如图两支铅笔 谁长?
我们可以把两支铅笔看成两条线段,这样我们就把实际 问题转化为了几何问题.
讲授新课
思考:怎样比较两条线段的长短??
Aa B
(1)度量法 用刻度尺量出它们的 长度,再进行比较.
Cb
D
(2) 叠合法 将其中一条线段“移动”, 使其一端点与另一线段的 一端点重合,两线段的另 一端点均在同一射线上.
(2)连接两点的线段叫两点间的距离;
(3)两点之间所有连线中,线段最短;
(4)射个
C.3个
D.4个
当堂检测
2.某同学用剪刀沿直线将一片平整的银杏叶减掉一部分(如图),发现剩下的银
杏叶的周长比原银杏叶的周长要小,能正确解释这一现象的数学知识是(
)
A.两点之间线段最短 C.垂线段最短
解:作图步骤如下:
aa b
(1)作射线 AM;
A B1 B2
BM
(2)在 AM 上顺次截取 AB1=a,B1B2=a,
B2B=b,则线段 AB=2a+b.
讲授新课 知识点三 有关线段的基本事实
探究
我要去书店 怎么走呀?
商场
礼堂
书店
讲授新课
根据生活经验,容易发现: 两点之间的所有连线中,线段最短
6.2.2线段的比较与运算 课件(共14张PPT)初中数学人教版(2024)七年级上册

(或AB=2AM=2MB)
反之也成立:因为AM=MB=
1 2
AB
(或AB=2AM=2MB)
所以M是线段AB的中点.
典例精讲
线段的运算
考点2-2
【例2】若AB=6cm,点C是线段AB的中点,点D是线段CB的中点,
求:线段AD的长是多少?
解:因为C是线段AB的中点.
A
所以AC=CB=
1 2
AB=
1 2
A.3 B.2 C.3或5 D.2或6
b
∴线段AB为所求.
A
B
CF
针对训练
线段的运算
考点3-1
1.如图1,点B,C在线段AD上则AB+BC=_A_C_,AD-CD=_A_C_,BC=_A_C_-_A_B_
=_B_D_-_C_D_. A
B
C
D
2.如图1,AB=CD,则图中另外两条相等的线段为_A_C_=_B_D__.
3.点A,B,C在同一条数轴上,其中点A,B表示的数分别是-3,1,若
方法总结:无图时求线段的长,应注意分类讨论,一般分以下 两种情况:点在某一线段上;点在该线段的延长线.
课堂小结
线段的比较与运算
中点
线段的和差
思想方法
方程思想 分类思想
知识梳理
针对训练
线段的比较与运算
查漏补缺
1.已知线段AB=6cm,延长AB到C,使BC=2AB,若D为AB的中点,则线段
DC的长为_1_5_c_m__.
BC=5,则AC=_1_1_或__1__.
目录
01
知识要点
02
线段的运算 线段的中点
精讲精练
新知探究
线段的运算---中点
《线段长短的比较》PPT教学课件

A.AB<CD
B.AB>CD
C.AB=CD
D.无法确定哪条长
2.如图,AB=CD,则AC与BD的大小关系是( C )
A.AC>BD B.AC<BD
C.AC=BD
D.无法确定
3.下列说法正确的是( C ) A.两点之间,直线最短 B.线段MN就是M,N两点间的距离 C.在连接两点的所有线中,最短的连线的长度就是这两点间的距离 D.从武汉到北京,火车行走的路程就是武汉到北京的距离
7.如图所示,在一条笔直公路a的两侧,分别有A,B两个村庄,现 要在公路a上建一个汽车站C,使汽车站到A,B两村的距离之和最小, 问汽车站C的位置应如何确定?
解:如答图,连接AB,交直线a于点C,这个点C的位置就是符合 条件的汽车站的位置.
判断平面上的点与线段的位置关系的方法: 若这个点到线段两端点的距离的和大于该线段的长,则点在线段外; 若这个点到线段两端点的距离的和等于该线段的长,则点在线段上.
线段A'B'即为所求.
步骤2 以点A'为圆心, AB为半径画弧, 交射线A'C于点B'.
1. 线段长短的比较方法: (1)估测法,在两条线段长短很明显的情况下使用; (2)度量法,用刻度尺分别量出两条线段的长度再比较; (3)叠合法,使两条线段的其中一个端点重合,另一个端点都位于重合
端点的同一侧,从而比较出两条线段的长短. 2. 线段的长短比较后,结果用“>”“<”或“=”表示.
(1)如右图,如果点B与点D重合,就说线段AB与CD相等, 记作AB=CD. (2)如右图,如果点B在线段CD上,就说线段AB小于CD, 记作AB<CD. (3)如右图,如果点B在线段CD外,就说线段大于CD,记 作 AB>CD.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两条线段的大小比较方法: 方法一: 测量法 (工具:刻度尺) 方法二: 叠合法 (工具:圆规) 说明:如果两条线段相差很大,直接观察就 可以进行比较
5. 请用两种方法比较下面AM 与 BM线段大小
结论:
AM=BM 线段的中点: 如果线段上的一个点把这条线段分成两 条相等的线段,那么这个点就叫做这条线 段的中点. 这时AM = BM =1/2AB (或AB=2AM=2BM).
8、,如图,△ABC中,你能说出线段AB+BC的长
与线段AC哪一条更长?你用什么方法比较?能
够不用工具比较吗?题
.如图是一个四边形,现在去各边的中点并 连接成四边形,想一想得到的四边形与原四边 形,哪一个的周长大?如是在各边任意取一点 呢? D
H A G E
B
C F
五.课堂小结10. 两点之间、 最短。 两点之间的距离是指 。 比较两天线段的大小的方法有 和 , 它们各自用的工具和具体做法是 。 用尺、规画一条线段等于已知线段的步骤是 。 六.11.作业 P113习题4.2第2和3题. 七.12.课外练习: (1)P113习题4.2全部做在练习本上。(课堂上已做的题和已布置的作业题除外). (2)预习下一节 八、教学反思
(学案,配课件)(P110-113)
学习目标:能了解“两点之间线段最短”的性质; 能借助于尺、规等工具比较两条线段的大小; 能用圆规作一条线段等于已知线段。
一.温故知新:
什么叫线段?射线和直线?它们之间的联系和
区别是什么?
二.学习新知:2.请猜测“从A到C的四条道路,哪条最短?” P110图4-6
6.例P111 (你能用圆规画出一条 线段等于已知线段吗?)
6.例P111
你能用圆规画出一条线段等于已知线段吗?
归纳出三步骤: 一、画出射线;二、度量已知线段; 三、移到射线上
7、已知线段a 、b如图,你能做出线段c,使c=a+b吗? P113第2题。
a
b
如果c=a-b呢?怎样画
归纳:作线段的和差实质就是先作一条线段, 然后再在线段的延长线上(或内部)作另外 的线段 即可。注意要保留 。
结论: 1.线段性质: 两点之间, 线 段
2.两点之间的距离: 两点之间 线段 的 的距离.
最短.
长度
叫两点之间
3. P110议一议:怎样比较两棵树的高矮? 怎样比较两根铅笔的长短? 怎样比较窗框相邻两边的长?P110图
实质上 就是怎样比较两条线段的长短?
4.画出两条线段,再比较它们长短。
讨论比较方法。
