C语言-用矩形法和梯形法求定积分
定积分的近似计算方法

定积分的近似计算方法定积分近似计算方法指的是利用数值计算方法来估算给定函数在一定区间上的积分值。
这些方法常常用于当函数在该区间内无法求得解析式时,或者解析式难以求得的情况下。
下面将介绍常用的数值积分近似计算方法。
一、矩形法矩形法即将积分区间等分为若干小区间,然后在每个小区间中选择一个代表点,将函数在该点的函数值作为近似积分的值。
具体可以分为左矩形法、右矩形法和中矩形法。
1.左矩形法左矩形法即取每个小区间的左端点作为代表点,近似积分的值为:∫[a, b]f(x)dx ≈ Δx * [f(a) +f(a+Δx) + … + f(a+(n-1)Δx)]其中,Δx=(b-a)/n,n为区间的等分数。
2.右矩形法右矩形法即取每个小区间的右端点作为代表点,近似积分的值为:∫[a, b]f(x)dx ≈ Δx * [f(a+Δx) + f(a+2Δx) + … +f(a+nΔx)]其中,Δx=(b-a)/n,n为区间的等分数。
3.中矩形法中矩形法即取每个小区间的中点作为代表点,近似积分的值为:∫[a, b]f(x)dx ≈ Δx * [f(a+Δx/2) + f(a+3Δx/2) + … +f(a+(2n-1)Δx/2)]其中,Δx=(b-a)/n,n为区间的等分数。
二、梯形法梯形法是通过将积分区间上的曲线拟合为多个梯形来近似计算定积分的方法。
将积分区间[a,b]等分为n个小区间,然后在每个小区间上用两个端点处的函数值拟合成一个梯形,然后将这些梯形的面积加起来即可得到近似的定积分的值。
具体计算公式为:∫[a, b]f(x)dx ≈ Δx/2 * [f(a) + 2f(a+Δx) + 2f(a+2Δx)+ … + 2f(a+(n-1)Δx) + f(b)]其中,Δx=(b-a)/n,n为区间的等分数。
三、辛普森法辛普森法是通过将积分区间上的曲线拟合为多个二次多项式的方法。
将积分区间[a,b]等分为n个小区间,每两个相邻区间拟合成一个二次多项式。
编程实现数值积分的几种--方法 c语言

编程实现数值积分的几种--方法c语言数值计算2010-11-05 09:52:43 阅读385 评论1 字号:大中小订阅复化梯形公式在区间不大时, 用梯形公式、辛卜生公式计算定积分是简单实用的, 但当区间较大时, 用梯形公式、辛卜生公式计算定积分达不到精确度要求 . 为了提高计算的精确度,我们将[a,b] 区间n等分,在每个小区间上应用梯形公式、辛卜生公式计算定积分,然后将其结果相加,这样就得到了复化梯形公式和复化辛卜生公式。
1. 复化梯形公式将积分区间等分, 设, 则节点为对每个小区间上应用梯形公式, 然后将其结果相加,则得(3.14)称(3.14) 式为复化梯形公式 .当在[a,b] 上有连续的二阶导数时,则复化梯形公式(3.14) 的余项推导如下:因为所以在区间[a,b] 上公式(3.14) 的误差为又因为在区间[a,b] 上连续,由连续函数的性质知,在区间[a,b] 上存在一点,于是( 3.15 )复化梯形公式,复化抛物线公式和Romberg求积法的算法程序:以下程序均定义误差限为1*10^-5;1)复化梯形公式:#include <stdio.h>#include <math.h>#define e 1e-5#define a 0 //积分下限a#define b 1 //积分上限b#define f(x) (4/(1+(x*x))) //被积函数f(x)int main(){int i,n;double h,t0,t,g;n=1; //赋初值h=(double)(b-a)/2;t=h*(f(a)+f(b));do{t0=t;g=0;for (i=1;i<=n;i++)g+=f((a+(2*i-1)*h));t=(t0/2)+(h*g); //复化梯形公式n*=2;h/=2;}while (fabs(t-t0)>e); //自定义误差限e printf("%.8lf",t); //输出积分的近似值return 0;}2)复化抛物线公式:#include <stdio.h>#include <math.h>#define e 1e-5#define a 0 //积分下限a#define b 1 //积分上限b#define f(x) (4/(1+(x*x))) //被积函数f(x)int main(){int i,n;double f1,f2,f3,h,s0,s;f1=f(a)+f(b); //赋初值f2=f(((double)(b+a)/2));f3=0;s=((double)(b-a)/6)*(f1+4*f2);n=2;h=(double)(b-a)/4;do //复化抛物线算法{f2+=f3;s0=s;f3=0;for (i=1;i<=n;i++)f3+=f((a+(2*i-1)*h));s=(h/3)*(f1+2*f2+4*f3);n*=2;h/=2;}while (fabs(s-s0)>e); //自定义误差限printf("%.8lf",s);return 0;}3)Romberg求积法:#include <stdio.h>#include <math.h>#define e 1e-5#define a 0 //积分下限a#define b 1 //积分上限b#define f(x) (4/(1+(x*x))) //被积函数f(x)double t[100][100];int main(){int n,k,i,m;double h,g,p;h=(double)(b-a)/2;t[0][0]=h*(f(a)+f(b));k=1;n=1;do //Romberg算法{g=0;for (i=1;i<=n;i++)g+=f((a+((2*i-1)*h)));t[k][0]=(t[k-1][0]/2)+(h*g);for (m=1;m<=k;m++){p=pow(4,(double)(m));t[k-m][m]=(p*t[k-m+1][m-1]-t[k-m][m-1])/(p-1);}m-=1;h/=2;n*=2;k+=1;}while (fabs(t[0][m]-t[0][m-1])>e); //自定义误差限eprintf("%.8lf",t[0][m]);return 0;}给定精度,定义误差限为1*10^-5,分别求出步长的先验估计值:用复化梯形公式计算,要求h<0. 007746。
c语言求解定积分(详细

淮北师范大学2010届学士学位论文C语言求解定积分系别、专业数学科学学院信息与计算科学研究方向计算机学生姓名谢贵龙学号06114303068指导教师姓名罗婷婷指导教师职称讲师2010年4月20日C语言求解定积分谢贵龙(淮北师范大学,数学科学学院,淮北,235000)摘要本文以连续函数在闭区间上的定积分为研究的出发点。
在简单介绍定积分、连续函数等相关定义后,论述了两种算法思想,并利用C语言编写相应的程序。
通过函数举例验证了算法的合理性和正确性,并讨论了这两种算法在适用范围及精确度上的略微差异。
最后通过本文的论述推广到其它求定积分的算法的实现。
关键词C语言,定积分,编程C Language to Solve Definite IntegralXie Guilong(School of Mathematical Science, Huaibei Normal University,huaibei,235000)AbstractIn this thesis, definite integral of a continuous function in the closed interval starting point for research.After a brief introduction of definite integral and continuous function definition,I discussed the ideas of two algorithms and used the corresponding program written in C.And then I verified through the example Function algorithm is correct and reasonable,discussed the scope of the two algorithms and the accuracy of the slight difference.Finally, the request will be extended to other points of the algorithm, through the discussion of this thesis.Keywords C Language, definite integral, programming目录引言 (1)一、C语言实现定积分计算的算法 (1)1.1定积分 (1)1.2C语言实现定积分计算的算法 (2)二、模块构成和各模块功能 (3)2.1关于算法一的模块构成和各模块功能 (3)2.2关于算法二的模块构成和各模块功能 (4)三、C语言求解定积分的具体程序 (4)3.1程序一(复合梯形公式求解定积分) (4)3.2程序二(辛甫生公式求解定积分) (5)四、程序编译运行及调试情况 (6)4.1程序一的编译运行及调试情况 (6)4.2程序二的编译运行及调试情况 (9)4.3程序简单分析 (11)参考文献 (12)致谢 (13)引言随着计算机的普及,计算机越来越多的运用于数学领域,但在早期,计算机实现的数学作用仅仅是四则运算、统计计算等简单的功能。
C语言常用算法

八、常用算法(一)考核知识要点1.交换、累加、累乘、求最大(小)值2.穷举3.排序(冒泡、插入、选择)4.查找(顺序、折半)5.级数计算(递推法)6.一元方程求解(牛顿迭代法、二分法)7.矩阵(转置)8.定积分计算(矩形法、梯形法)9.辗转相除法求最大公约数、判断素数10.数制转换(二)重点、难点精解教材中给出的算法就不再赘述了。
1.基本操作:交换、累加、累乘1)交换交换算法的要领是“借助第三者”(如同交换两个杯子里的饮料,必须借助第三个空杯子)。
例如,交换两个整型变量里的数值:int a=7,b=9,t;t=a; a=b; b=t;(不借助第三者,也能交换两个整型变量里的数值,但不通用,只是一个题目而已。
例如:int a=7,b=9; a=a+b; b=a-b; a=a-b;)2)累加累加算法的要领是形如“s=s+A”的累加式,此式必须出现在循环中才能被反复执行,从而实现累加功能。
“A”通常是有规律变化的表达式,s在进入循环前必须获得合适的初值,通常为0。
3)累乘累乘算法的要领是形如“s=s*A”的累乘式,此式必须出现在循环中才能被反复执行,从而实现累乘功能。
“A”通常是有规律变化的表达式,s在进入循环前必须获得合适的初值,通常为1。
2.非数值计算常用经典算法1)穷举法也称为“枚举法”,即将可能出现的各种情况一一测试,判断是否满足条件,一般采用循环来实现。
例如,用穷举法输出“将1元人民币兑换成1分、2分、5分硬币”的所有方法。
main(){int y,e,w;for(y=0;y<=100;y++)for(e=0;e<=50;e++)for(w=0;w<=20;w++)if(1*y+2*e+5*w==100)printf("%d,%d,%d\n",y,e,w);}2)有序序列的插入算法就是将某数据插入到一个有序序列后,该序列仍然有序。
以下给出用数组描述该算法的例子:将x插入一升序数列后,数列仍为升序排列。
C语言实现定积分求解方法

C语言实现定积分求解方法C语言可以通过数值积分的方法来实现定积分的求解,主要有矩形法、梯形法和辛普森法等几种常见的求解方法。
矩形法是最简单的一种数值积分方法,它将定积分区间等分成若干个小区间,然后在每个小区间上取一个点,将积分区间分成若干个小矩形,对每个小矩形的面积进行求和,即可得到近似的定积分值。
以下是使用矩形法实现定积分求解的C语言代码:```c#include<stdio.h>#include<math.h>double f(double x)//定义需要求解的函数return sqrt(1-x*x);double integrate(double a, double b, int n)//a:积分下限,b:积分上限,n:划分的矩形个数double dx = (b-a)/n; // 求解每个小矩形的宽度double sum = 0.0; // 求和变量int i;for(i=0; i<n; i++)double x = a + i*dx + dx/2; // 计算每个小矩形的横坐标中点sum += f(x)*dx; // 计算每个小矩形的面积并求和}return sum;int maindouble a = 0.0; // 积分下限double b = 1.0; // 积分上限int n = 1000; // 划分的矩形个数double result = integrate(a, b, n); // 求解定积分printf("The definite integral is: %.6f\n", result);return 0;```梯形法是一种比矩形法更精确的数值积分方法,它将积分区间等分成若干个小区间,然后将每个小区间上的函数图像近似为一个梯形,对每个梯形的面积进行求和,即可得到近似的定积分值。
以下是使用梯形法实现定积分求解的C语言代码:```c#include<stdio.h>#include<math.h>double f(double x)//定义需要求解的函数return sqrt(1-x*x);double integrate(double a, double b, int n)//a:积分下限,b:积分上限,n:划分的梯形个数double dx = (b-a)/n; // 求解每个小梯形的底边宽度double sum = 0.0; // 求和变量int i;for(i=0; i<n; i++)double x1 = a + i*dx; // 计算每个小梯形的左边横坐标double x2 = a + (i+1)*dx; // 计算每个小梯形的右边横坐标sum += (f(x1)+f(x2))*dx/2; // 计算每个小梯形的面积并求和}return sum;int maindouble a = 0.0; // 积分下限double b = 1.0; // 积分上限int n = 1000; // 划分的梯形个数double result = integrate(a, b, n); // 求解定积分printf("The definite integral is: %.6f\n", result);return 0;```辛普森法是一种更为精确的数值积分方法,它将积分区间等分成若干个小区间,然后在每个小区间上使用二次多项式来逼近积分函数的曲线,对每个小区间的积分值进行加权求和,即可得到近似的定积分值。
矩形法求函数的定积分

用矩形法求函数的定积分(C 语言实现)
在本程序中,先分别定义了 5 个 C 函数 f1、f2、f3、f4、f5,用来代表 5 个不同的函数。然后 定义了一个求定积分的函数 integral。现在介绍矩形法求函数定积分的数学思想。
设函数 在区间[a,b]上连续,在(a,b)上可导,将[a,b]之间的长度等分成 n 份(n 越大计算越精 确)。于是第 块小矩形的面积为 ,
printf("%lf\n",S[j]); } }
运行结果如图所示:
可以发现,计算值与理论值十分接近,当 N 取的足够大时,可以获得十分精确的值,但是运算 次数也会增加,本函数的时间复杂度为 O(n)。
从指针的用法上来讲,本程序使用了“指向函数的指针”。一个函数的函数名,代表了这个函 数的首地址,在主函数中,5 次调用 integral 函数,实现了对 5 个不同的函数求积分。integral 函 数包含了三个参数,前两个参数表示被积函数的上下限。
sum=sum+d*(*fun)(a+i*d);//定积分近似计算公式 }//fun 是指向函数的指针,该指针所指向的函数带有一个 double 型的形参, //同时,该函数的返回值类型为 double return sum; }
2
C 语言在计算中的应用
void main() {
double S[5]; int j; S[0]=integral(0,1,f1);//fun 指向 f1 S[1]=integral(0,1,f2);//fun 指向 f2 S[2]=integral(0,1,f3);//fun 指向 f3 S[3]=integral(0,1,f4);//fun 指向 f4 S[4]=integral(0,1,f5);//fun 指向 f5 printf("输出各个函数的积分值:\n"); for(j=0;j<5;j++) {
c++ 矩形法 梯形法 抛物线法求定积分

c++ 矩形法梯形法抛物线法求定积分矩形法、梯形法和抛物线法都是数值积分的常见方法,用于计算定积分的近似值。
矩形法(Rectangle Method)是最简单的数值积分方法之一。
它将积分区间等分为若干个小矩形,然后计算这些小矩形的面积之和作为整个区间上的定积分的近似值。
矩形法有两种常见的计算方式:左矩形法和右矩形法。
左矩形法(Left Rectangle Method)在每个子区间上选择区间左端点的函数值来计算小矩形的面积。
具体计算方法如下:```def left_rectangle(f, a, b, n):h = (b - a) / n # 子区间的宽度result = 0for i in range(n):x = a + i * h # 子区间的左端点result += f(x) * h # 计算小矩形的面积并累加return result```右矩形法(Right Rectangle Method)则选择区间右端点的函数值计算小矩形的面积:```def right_rectangle(f, a, b, n):h = (b - a) / n # 子区间的宽度result = 0for i in range(1, n + 1):x = a + i * h # 子区间的右端点result += f(x) * h # 计算小矩形的面积并累加return result```梯形法(Trapezoid Method)是一种稍微复杂一些的数值积分方法,它通过用梯形来逼近曲线下面积来计算定积分的近似值。
具体计算方法如下:```def trapezoid(f, a, b, n):h = (b - a) / n # 子区间的宽度result = (f(a) + f(b)) / 2 # 首先加上首尾两个端点的函数值for i in range(1, n):x = a + i * h # 子区间的点result += f(x) # 加上子区间内的函数值result *= h # 乘以子区间宽度return result```抛物线法(Parabolic Method)则采用二次插值的方式来逼近曲线下面积,计算定积分的近似值。
C语言实现定积分求解方法

C语⾔实现定积分求解⽅法求定积分的⽅法有很多种,下⾯是我总结的⼏种⽐较常⽤的⽅法。
#include <stdio.h>#include <stdlib.h>#include <math.h>#include <time.h>#define N 3double fun(double x){double y;y = sqrt(4-(x)*(x));//y = sin(x);return y;}/*随机点法求定积分*/double Darts(int n){double x, y;time_t t;int i = 0;int count = 0;srand((unsigned)time(&t));for (i=0; i<n; i++){x = rand()%100/100.0;y = rand()%100/100.0;if (y <= 1-pow(x,2)){count++;}}return (double)count/(double)n;}/*左矩形法求定积分*/double LeftRect(double down, double up, int n){double h, s;int i;/*计算步长*/h = (up-down)/n;s = fun(down)*h;for (i=1; i<n; i++){s = s + fun(down+i*h)*h;}return s;}/*梯形公式求定积分*/double Trape(double down, double up, int n){double h, s;int i = 0;/*计算步长*/h = (up-down)/n;s = 0.5*(fun(down)+fun(down+h))*h;for (i=1; i<n; i++){s = s + 0.5 * (fun(down+i*h) + fun(down+(i+1)*h))*h;}return s;}/*复合梯形公式*/double T(double x, double y, int z){double h, Tn;int i = 0;h = (y-x)/z;Tn = (fun(x)+fun(y))/2;for (i=0; i<z; i++){Tn = Tn+fun(x+i*h);}Tn = Tn*h;return Tn;}/*⾟普⽣公式求定积分,公式为:S[n]=(4*T[2*n]-T[n])/3,其中T[2n],T[n]为梯形公式计算结果*/ double Simposn(double down, double up, int n){double s;/*⾟普⽣公式*/s = (4*T(down, up, 2*n) - T(down, up, n))/3;return s;}/*⾼斯公式求定积分*/double Gass(double (*func)(double x), double a, double b, int n){int i = 0;//⾼斯点及其求积系数列表float x1[1]={0.0};float A1[1]={2};float x2[2]={-0.5573503,0.5573503};float A2[2]={1,1};float x3[3]={-0.7745967,0.0,0.7745967};float A3[3]={0.555556,0.888889,0.555556};float x4[4]={0.3399810,-0.3399810,0.8611363,-0.8611363};float A4[4]={0.6521452,0.6521452,0.3478548,0.3478548};float x5[5]={0.0,0.5384693,-0.5384693,0.9061799,-0.9061799};float A5[5]={0.5688889,0.4786287,0.4786287,0.2369269,0.2369269};float *p, *t;switch (n){case 1:p = x1;t = A1;break;case 2:p = x2;t = A2;break;case 3:p = x3;t = A3;break;case 4:p = x4;t = A4;break;case 5:p = x5;t = A5;break;default :printf("intput wrong!");}float g = 0;for (i=0; i<n; i++){g += (*func)((b-a)*p[i]/2+(a+b)/2)*t[i];}g *= (b-a)/2;return g;}int main(int argc, char *argv[]){printf("随机点法积分值%f\n", Darts(10000)); double down, up;int n;double sum = 0;printf("积分下限:\n");scanf("%lf", &down);printf("积分上限:\n");scanf("%lf", &up);printf("分隔数⽬:\n");scanf("%d", &n);sum = LeftRect(down, up, n);printf("左矩形法积分值为:%f\n", sum);sum = Trape(down, up, n);printf("梯形公式积分值为:%f\n", sum);sum = Simposn(down, up, n);printf("⾟普⽣公式积分值为:%f\n", sum);sum = Gass(fun, down, up, N);printf("⾼斯公式积分值为:%f\n", sum);return 0;}。
c语言表示积分

c语言表示积分积分是微积分的重要概念之一,用于求函数在某个区间上的总量或者累积变化量。
在C语言中,我们可以使用不同的方法来实现积分的计算。
一、定积分的计算方法定积分是指在某个区间上求函数与x轴之间的面积,可以用面积与区间长度的乘积来表示。
在C语言中,可以通过数值积分方法来近似计算定积分。
1.矩形法:矩形法是一种最简单的数值积分方法,它将区间划分为多个小矩形,然后用矩形面积的和来近似表示函数的总面积。
具体步骤如下:a.将区间[a, b]等分为n个小区间,每个小区间的宽度为h=(b-a)/n。
b.在每个小区间的右边选择一个点xi(i=0,1,2,...,n-1),计算出该点对应的函数值f(xi)。
c.将每个小矩形的面积f(xi)*h累加起来,得到总面积。
2.梯形法:梯形法是另一种常用的数值积分方法,它将区间划分为多个小梯形,然后用梯形面积的和来近似表示函数的总面积。
具体步骤如下:a.将区间[a, b]等分为n个小区间,每个小区间的宽度为h=(b-a)/n。
b.在每个小区间的两个端点上计算函数值,得到f(xi)和f(xi+1)。
c.将每个小梯形的面积[(f(xi)+f(xi+1))/2]*h累加起来,得到总面积。
二、代码示例下面是使用C语言实现上述两种数值积分方法的代码示例:1.矩形法代码示例:```c#include <stdio.h>double f(double x) {//定义被积函数return x*x;}double integral_rectangle(double a, double b, int n) { //计算矩形法近似积分double h = (b - a) / n;double sum = 0.0;for (int i = 0; i < n; i++) {double x = a + i * h;sum += f(x);}return sum * h;}int main() {double a = 0.0; //积分下限double b = 1.0; //积分上限int n = 100; //小区间个数double result = integral_rectangle(a, b, n); printf("矩形法求积分的结果为:%lf\n", result); return 0;}```2.梯形法代码示例:```c#include <stdio.h>double f(double x) {//定义被积函数return x*x;}double integral_trapezoid(double a, double b, int n) { //计算梯形法近似积分double h = (b - a) / n;double sum = 0.0;for (int i = 0; i < n; i++) {double x1 = a + i * h;double x2 = a + (i+1) * h;sum += (f(x1) + f(x2)) / 2;}return sum * h;}int main() {double a = 0.0; //积分下限double b = 1.0; //积分上限int n = 100; //小区间个数double result = integral_trapezoid(a, b, n);printf("梯形法求积分的结果为:%lf\n", result);return 0;}```三、总结以上是使用C语言实现数值积分的两种方法,定积分是微积分中的重要概念,可以通过数值积分方法来近似计算定积分的值。
C语言__用六种方法求定积分

C语言__用六种方法求定积分C语言是一种广泛应用于科学计算、算法设计和系统编程的程序设计语言。
虽然C语言本身并没有提供内置的定积分计算函数,但可以通过使用不同的方法来近似计算定积分。
以下将介绍六种常见的数值积分方法:矩形法、梯形法、辛普森法、龙贝格法、高斯-勒让德法和自适应辛普森法。
1. 矩形法(Reimann Sum):将积分区间等分成若干小区间,然后在每个小区间取一个函数值,最后将所有函数值相加,并乘以区间大小。
这相当于将每个小区间上的曲线近似为一个矩形。
2. 梯形法(Trapezoidal Rule):将积分区间分割成若干小区间,并在每个小区间使用梯形面积公式进行近似计算。
梯形的上底和下底分别为相邻两个小区间的函数值,高为小区间的宽度。
3. 辛普森法(Simpson's Rule):将积分区间分割成若干小区间,并在每个小区间使用三点拉格朗日插值多项式近似计算。
辛普森法使用二次多项式来逼近曲线,能够更好地近似曲线的曲率。
4. 龙贝格法(Romberg Method):龙贝格法是一种逐步逼近的方法,将积分区间多次分割,并使用多种精度的梯形法进行计算。
通过不断提高梯形法的精度,最终逼近定积分的值。
5. 高斯-勒让德法(Gauss-Legendre Method):高斯-勒让德法使用一组预先确定的节点和权重,将积分区间变换到[-1,1]上,然后使用插值多项式计算定积分的近似值。
该方法的优点是能够以很高的精度计算积分值。
6. 自适应辛普森法(Adaptive Simpson's Rule):自适应辛普森法根据曲线的变化程度自动调整子区间的大小。
在每个小区间上计算出辛普森值,并与高斯-勒让德法值进行比较,以决定是否需要进一步细分区间。
以上这些方法都可以使用C语言中的循环、条件语句和函数来实现。
具体实现的步骤包括:将积分区间分割成若干小区间,计算每个小区间上的函数值,然后将这些函数值进行加权求和,最后乘以相应的权重或宽度,得到定积分的近似值。
C语言—定积分

4.龙贝格求积公式,求解定积分C/C++ code#include<stdio.h>#include<math.h>#define f(x) (sin(x)/x)#define N 20#define MAX 20#define a 2#define b 4#define e 0.00001float LBG(float p,floatq,int n){ int i;float sum=0,h=(q-p)/n;for (i=1;i<n;i++)sum+=f(p+i*h);sum+=(f(p)+f(q))/2;return(h*sum);}void main(){ int i;int n=N,m=0;float T[MAX+1][2];T[0][1]=LBG(a,b,n);n*=2;for(m=1;m<Maxims++){ for(i=0;i<m;i++)T[i][0]=T[i][1];T[0][1]=LBG(a,b,n);n*=2;for(i=1;i<=m;i++)T[i][1]=T[i-1][1]+(T[i-1][1]-T[i-1][0])/(pow(2,2*m)-1); if((T[m-1][1]<T[m][1]+e)&&(T[m-1][1]>T[m][1]-e)) { prints("Answer=%f\n",T[m][1]); getch();return ;}}}6. 牛顿-科特斯求积公式,求定积分C/C++ code#include<stdio.h>#include<math.h>int NC(a,h,n,r,f)float (*a)[];float h;intn,f;float *r;{ intnn,i;float ds;if(n>1000||n<2){ if (f)printf("\n Faild! Check if 1<n<1000!\n",n);return(-1);}if(n==2){ *r=0.5*((*a)[0]+(*a)[1])*(h);return(0);}if (n-4==0){ *r=0;*r=*r+0.375*(h)*((*a)[n-4]+3*(*a)[n-3]+3*(*a)[n-2]+(*a)[n-1]); return(0);}if(n/2-(n-1)/2<=0)nn=n;elsenn=n-3;ds=(*a)[0]-(*a)[nn-1];for(i=2;i<=nn;i=i+2)ds=ds+4*(*a)[i-1]+2*(*a)[i];*r=ds*(h)/3;if(n>nn)*r=*r+0.375*(h)*((*a)[n-4]+3*(*a)[n-3]+3*(*a)[n-2]+(*a)[n-1]); return(0);}main(){floath,r;intn,ntf,f;int i;float a[16];printf("Input the x[i](16):\n");for(i=0;i<=15;i++)scanf("%d",&a[i]);h=0.2;f=0;ntf=NC(a,h,n,&r,f);if(ntf==0)printf("\nR=%f\n",r);elseprintf("\n Wrong!Return code=%d\n",ntf);getch();}C语言求函数定积分2011-8-14 09:38提问者:天空之柱|浏览次数:185次Auto.h中的内容:#include<stdio.h>#include<math.h>#include<string.h>#define g 9.81#define e 2.71828182845904523536028747135266249775724709369995 #define F float#define SC scanf#define SCS scanf_s#define PR printf#define D "%d\n"#define PF "%f\n"#define D2 D Dvoid swap( int * , int * );void swap(int *ph1,int *ph2){int temp;temp=*ph1;*ph1=*ph2;*ph2=temp;}___________________________分割线_____________________________ 定积分.c中的内容:#include"C:\Users\Administrator\Programs\Header\Auto.h"F f1( F );F f2( F );F f3( F );F f4( F );F f5( F );F integral( F , F , F(*pt)( F ) , F );void main(){int type;F u_limit,l_limit,precision=0.0000001,(*p_pt)(F);PR("请输入类型(1~5):\n");SCS("%d",&type);switch(type){case 1: p_pt=f1;break;case 2: p_pt=f2;break;case 3: p_pt=f3;break;case 4: p_pt=f4;break;case 5: p_pt=f5;break;default:PR("ERROR!");}PR("输入积分上限:\n");SCS("%f",&u_limit);PR("输入积分下限:\n");SCS("%f",&l_limit);PR("定积分值为:%f\n",integral(u_limit,l_limit,p_pt,precision)); }F f1(F x1){return(1+x1);}F f2(F x2){return(2*x2+3);}F f3(F x3){return(pow(e,x3)+1);}F f4(F x4){return(pow((1+x4),2));}F f5(F x5){return(pow(x5,3));}F integral(F ul,Fll,F (*pt)(F x),F pc){F sum=0;int counter;for(counter=0;counter*pc+ll<=ul;counter++){sum+=pc*(*pt)(ll+counter*pc);}return(sum);}_________________________运行报告____________________________ 1>------ 已启动生成: 项目: 定积分, 配置: Debug Win32 ------1>生成启动时间为2011/8/14 9:29:07。
C语言-用矩形法和梯形法求定积分

一.写一个用矩形法求定积分的函数,求sin(x)在(0,1)上的定积分。
#include <stdio.h>#include <math.h>float jifen(float a,float b){int i,l;float n=0.001,s=0; //n表示划分的单位宽度,n越小结果越精确,n是矩形的宽l=(b-a)/n; // l表示有多少个单位宽度for(i=0;i<l;i++)s=n*sin(a+n*i)+s; // sin(a+n*i)是矩形的长printf("用矩形法求得该函数在(%2.0f,%2.0f)上的积分为%f。
\n",a,b,s);}main(){jifen(0,1);}二.写一个用梯形法求定积分的函数,求sin(x)在(0,1)上的定积分。
#include <stdio.h>#include <math.h>float jifen(float a,float b){int i,l;float n=0.001,s=0;l=(b-a)/n;for(i=0;i<l;i++)s=(sin(a+n*i)+sin(a+n*(i+1)))*n/2+s; // (sin(a+n*i)是梯形的上底,sin(a+n*(i+1))是下底printf("用梯形法求得该函数在(%2.0f,%2.0f)上的积分为%f。
\n",a,b,s);}main(){jifen(0,1);}三.(综合)写一个用矩形法和梯形法求定积分的通用函数,分别求sin(x)在(0,1)上、cos(x)在(-1,1)上、exp在(0,2)上的定积分。
说明:jifen的函数定义中,double (*fun)(double)表示fun是指向函数的指针,被指的函数是一个实型函数,有一个实型形参,Fun是指向函数的指针变量。
用jifen(0,1,sin)语句调用jifen 函数时,给jifen函数传递了sin函数的入口地址,这时jifen函数中的fun函数就相当于是sin函数了,(*fun)(a+n*i)相当于sin(a+n*i)。
C语言__用六种方法求定积分

1. 描述问题利用①左矩形公式,②中矩形公式,③右矩形公式 ,④梯形公式,⑤simpson 公式,⑥Gauss 积分公式求解定积分。
2. 分析问题2.1定积分21.1定积分的定义定积分就是求函数()f x 在区间[],a b 中图线下包围的面积。
即()0,,,y x a x b y f x ====所包围的面积。
这个图形称为曲边梯形,特例是曲边梯形。
如下图:(图1)设一元函数()y f x =,在区间[],a b 内有定义。
将区间[],a b 分成n 个小区间[][][][]00112,,,,,......,i a x x x x x x b 。
设1i i i x x x -∆=-,取区间i x ∆中曲线上任意一点记做()i f ξ,作和式:()1lim n n i f i xi ξ→+∞=⎛⎫∆ ⎪⎝⎭∑ 若记λ为这些小区间中的最长者。
当0λ→时,若此和式的极限存在,则称这个和式是函数()f x 在区间[],a b 上的定积分。
记作:()ba f x dx ⎰其中称a 为积分下限,b 为积分上限,()f x 为被积函数,()f x dx 为被积式,∫ 为积分号。
之所以称其为定积分,是因为它积分后得出的值是确定的,是一个数,而不是一个函数。
21.2定积分的几何意义[1]它是介于x 轴、函数f(x)的图形及两条直线x=a ,x=b 之间的各个部分面积的代数和。
在x 轴上方的面积取正号;在x 轴下方的面积取负号。
如图2.2言实现定积分计算的算法22.1利用复合梯形公式实现定积分的计算假设被积函数为()f x ,积分区间为[],a b ,把区间[],a b 等分成n 个小区间,各个区间的长度为h ,即()/h b a n =-,称之为“步长”。
根据定积分的定义及几何意义,定积分就是求函数()f x 在区间[],a b 中图线下包围的面积。
将积分区间n 等分,各子区间的面积近似等于梯形的面积,面积的计算运用梯形公式求解,再累加各区间的面积,所得的和近似等于被积函数的积分值,n 越大,所得结果越精确。
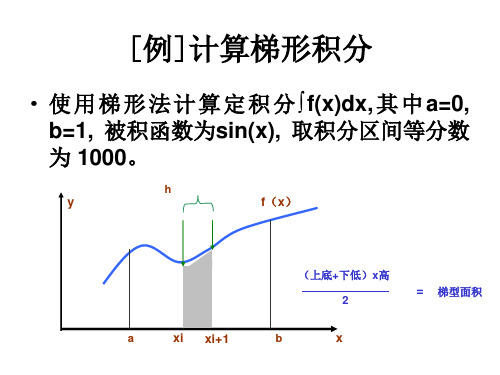
例---计算梯形积分
main() { double a,b,h,sum; /*积分的下限和上限、步长、 积分的下限和上限、 , , 积分的下限和上限 步长、 结果 */ int n,i; /* 积分区间等分数 ,i是循环变量 */ , 是循环变量 a = 0.0; b = 1.0; n = 1000; h = (b-a)/n; /* 计算小区间长度 */ /*---- 为工作变量赋初值 : 先计算不易循环运算的部分 ----*/ sum = (f(a)+f(b))/2; /*---- 循环计算公式中的Σ和式 -------------------------*/ 循环计算公式中的 和式 for(i=1;i<n;i=i+1) sum = sum+f(a+i*h); sum = sum*h; printf("The result is %f.\n",sum); }
h
y
f(x) ( )
下低) 高 (上底+下低)x高 上底 下低 2 a
=
梯型面积
xi
xi+1
b
x
计算原理和方法: 计算原理和方法 将积分区间等分为n份 其中第 其中第i个小区间上 将积分区间等分为 份,其中第 个小区间上 的定积分可以用如下梯形的面积来近似替 代: ∫f(x)dx≈(f(a+i*h)+f(a+(i+1)*h))*h/2 因此整个积分区间上的定积分可表示为 ∫f(x)dx≈Σ(f(a+i*h)+f(a+(i+1)*h))*h/2 = ((f(a)+f(b))/2+Σf(a+i*h))*h
/* 用梯形法计算定积分 */ #include <stdio.h> #include <math.h> /* 定义被积函数 */ double f(double x) { return sin(x); } /*注:sin(x)是C语言提供的标准库函数, 语言提供的标准库函数, 注 ( ) 语言提供的标准库函数 它的定义和说明在“ 它的定义和说明在“math.h”中。 */ 中
矩形法求定积分

矩形法求定积分矩形法是一种常用的数值积分方法,用于求解定积分。
它的原理是将被积函数的区间等分成若干个小矩形,再将这些小矩形的面积相加,从而得到定积分的近似值。
我们来看一个简单的例子,求解函数f(x)=x^2在区间[0,1]上的定积分。
假设我们将区间[0,1]等分成n个小区间,每个小区间的宽度为Δx=(b-a)/n=(1-0)/n=1/n。
那么,每个小矩形的宽度也为1/n。
接下来,我们需要确定每个小矩形的高度。
根据矩形法,我们可以使用被积函数在每个小区间的左端点、右端点或中点的函数值作为每个小矩形的高度。
在本例中,我们选择使用每个小区间的左端点作为每个小矩形的高度。
因此,第i个小矩形的高度为f(x_i),其中x_i为第i个小区间的左端点。
现在,我们可以计算每个小矩形的面积了。
每个小矩形的面积为宽度乘以高度,即Δx*f(x_i)。
我们将所有小矩形的面积相加,即可得到定积分的近似值。
在本例中,定积分的近似值为:∫[0,1]x^2dx ≈ Δx*f(x_1) + Δx*f(x_2) + ... + Δx*f(x_n) = Σ(Δx*f(x_i))当n趋近于无穷大时,这个近似值将趋近于定积分的精确值。
这是因为随着n的增大,每个小矩形的宽度将趋近于0,从而使近似值越来越接近于定积分的精确值。
矩形法的优点是简单易懂,计算量较小。
然而,它也有一些局限性。
首先,矩形法只是一种近似方法,得到的结果并不精确。
其次,矩形法对于某些函数可能会产生较大的误差。
例如,当被积函数在某些小区间内变化较大时,矩形法可能无法准确地估计定积分的值。
为了提高定积分的精确度,我们可以增加小区间的数量n。
当n足够大时,矩形法可以得到较为精确的结果。
此外,还可以使用其他更高级的数值积分方法,如梯形法则、辛普森法则等,来进一步提高精确度。
总结起来,矩形法是一种常用的数值积分方法,适用于求解定积分。
它的原理是将区间等分成若干个小矩形,通过计算这些小矩形的面积之和来近似定积分的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
for(i=0;i<l;i++)
s=n*sin(a+n*i)+s;// sin(a+n*i)是矩形的长
printf("用矩形法求得该函数在(%2.0f,%2.0f)上的积分为%f。\n",a,b,s);
}
main()
{
jifen(0,1);
}
二.写一个用梯形法求定积分的函数,求sin(x)在(0,1)上的定积分。
一.写一个用矩形法求定积分的函数,求sin(x)在(0,1)上的定积分。
#include <stdio.h>
#include <math.h>
floatjifen(float a,float b)
{int i,l;
float n=0.001,s=0;//n表示划分的单位宽度,n越小结果越精确,n是矩形的宽
#include <stdio.h>
#include <math.h>
floatjifen(float a,float b)
{int i,l;
float n=0.001,s=0;
l=(b-a)/n;
for(i=0;i<l;i++)
s=(sin(a+n*i)+sin(a+n*(i+1)))*n/2+s;// (sin(a+n*i)是梯形的上底,sin(a+n*(i+1))是下底
printf("用梯形法求得该函数在(%2.0f,%2.0f)上的积分为%f。\n",a,b,s);
}
main()
{
jifen(0,1);
}
三.(综合)写一个用矩形法和梯形法求定积分的通用函数,分别求sin(x)在(0,1)上、cos(x)在(-1,1)上、exp在(0,2)上的定积分。
说明:jifen的函数定义中,double (*fun)(double)表示fun是指向函数的指针,被指的函数是一个实型函数,有一个实型形参,Fun是指向函数的指针变量。用jifen(0,1,sin)语句调用jifen函数时,给jifen函数传递了sin函数的入口地址,这时jifen函数中的fun函数就相当于是sin函数了,(*fun)(a+n*i)相当于sin(a+n*i)。这样jifen函数就是一个通用求定积分的函数了。
{printf("1.sin函数:\n");
ji.cos函数:\n");
jifen(-1,1,cos);
printf("3.exp函数:\n");
jifen(0,2,exp);
}
s1=((*fun)(a+n*i)+(*fun)(a+n*(i+1)))*n/2+s1;
}
printf("用矩形法求得该函数在(%2.0f,%2.0f)上的积分为%f。\n",a,b,s);
printf("用梯形法求得该函数在(%2.0f,%2.0f)上的积分为%f。\n\n",a,b,s1);
}
main()
#include <stdio.h>
#include <math.h>
jifen(float a,float b,double (*fun)(double))
{int i,l;
float n=0.001,s=0,s1=0;
l=(b-a)/n;
for(i=0;i<l;i++)
{s=n*(*fun)(a+n*i)+s;
