2021年安徽中考数学总复习专题突破课件: 分类讨论思想
中考数学专题复习分类讨论课件(共23张PPT)

❖ 1. 一次函数y=kx+b的自变量的取值范围是
-3≤x≤ 6,,相应的函数值的取值范围是
-5≤y≤-2 ,则这个函数的解析式 。
-5=-3k+b
-5=6k+b
-2=6k+b
-2=-3k+b
解析式为 Y= 1 x-4, 或 y=- 1x-3 2. 函数y=ax2-ax+33x+1与x轴只有一3 个交点,求a的值与交
C
A
65° 65° 50°
BA C
110° 35°
35°
B
80°
20°
A
80°
BA
50°
50°
B
3. 如图,直线AB经过圆O的圆心,与圆O交于A、B两点,点C在O上, 且∠AOC=300,点P是直线AB上的一个动点(与点O不重合),直线PC 与圆O相交于点Q,问点P在直线AB的什么位置时,QP=QO?这样的点 P有几个?并相应地求出∠OCP的度数。
A
P
在矩形ABCD中:①当QAAB
= BACP
时,△QAP∽△ABC,则612 t
2t =6
,
解得t=
6 5
=1.2秒。所以当t=1.2秒时,△QAP∽△ABC。
②当
QA BC
=
AP AB
时,△PAQ∽△ABC,则
6
6
t
=
2 12
t
,
解得t=3(秒)。所以当t=3秒时,△PAQ∽△ABC。
角三角
C B
10。已知二次函数y=2x2-2的图像与x轴交于A、B两点(点 A在点B的左边),与y轴交于点C,直线x=m(m> 1)与x 轴交于点D。
中考数学专题《分类讨论思想在压轴题中的应用》原卷
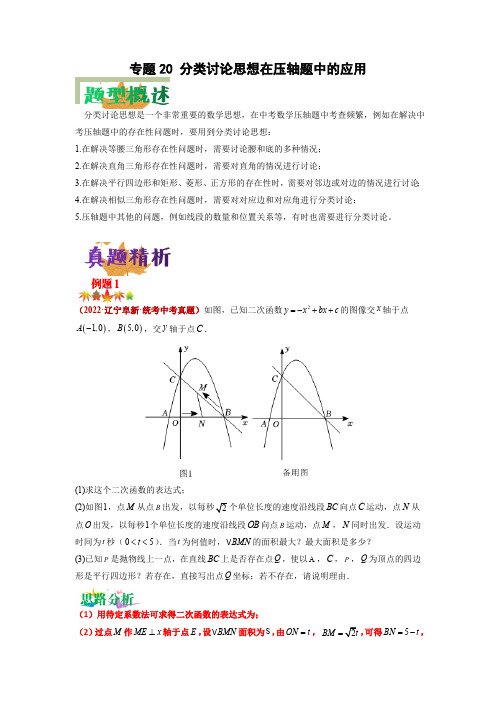
专题20 分类讨论思想在压轴题中的应用分类讨论思想是一个非常重要的数学思想,在中考数学压轴题中考查频繁,例如在解决中考压轴题中的存在性问题时,要用到分类讨论思想:1.在解决等腰三角形存在性问题时,需要讨论腰和底的多种情况;2.在解决直角三角形存在性问题时,需要对直角的情况进行讨论;3.在解决平行四边形和矩形、菱形、正方形的存在性时,需要对邻边或对边的情况进行讨论;4.在解决相似三角形存在性问题时,需要对对应边和对应角进行分类讨论;5.压轴题中其他的问题,例如线段的数量和位置关系等,有时也需要进行分类讨论。
(2022·辽宁阜新·统考中考真题)如图,已知二次函数2y x bx c =-++的图像交x 轴于点()1,0A -,()5,0B ,交y 轴于点C .(1)求这个二次函数的表达式;(2)如图1,点M 从点B BC 向点C 运动,点N 从点O 出发,以每秒1个单位长度的速度沿线段OB 向点B 运动,点M ,N 同时出发.设运动时间为t 秒(05t <<).当t 为何值时,BMN V 的面积最大?最大面积是多少?(3)已知P 是抛物线上一点,在直线BC 上是否存在点Q ,使以A ,C ,P ,Q 为顶点的四边形是平行四边形?若存在,直接写出点Q 坐标;若不存在,请说明理由.(1)用待定系数法可求得二次函数的表达式为;(2)过点M 作ME x ⊥轴于点E ,设BMN V 面积为S ,由ON t =,BM =,可得5BN t =-,45ME BMsin t =︒==,即得()21115255()22228S BN ME t t t =⋅=-⋅=--+,由二次函数性质可得当52t =秒时,BMN V 的面积最大,求得其最大面积;(3)由()5,0B ,()0,5C 得直线BC 解析式为5y x =-+,设(),5Q m m -+,()2,45P n n n -++,分三种情况进行讨论求解.【答案】(1)245y x x =-++(2)当52t =时,BMN V 的面积最大,最大面积是258(3)存在,Q 的坐标为()7,12-或()7,2-或()1,4或()2,3【详解】(1)将点()1,0A -,()5,0B 代入2y x bx c =-++中,得010255b c b c =--+⎧⎨=-++⎩,解这个方程组得45b c =⎧⎨=⎩,∴二次函数的表达式为245y x x =-++;(2)过点M 作ME x ⊥轴于点E ,如图:设BMN V 面积为S ,根据题意得:ON t =,BM =.()5,0B ,5BN t ∴=-,在245y x x =-++中,令0x =得5y =,()0,5C ∴,5OC OB ∴==,45OBC ∠∴=︒.45ME BMsin t ∴=︒==,()22111515255()2222228S BN ME t t t t t ∴=⋅=-⋅=-+=--+,05t << ,∴当52t =时,BMN V 的面积最大,最大面积是258;(3)存在点Q ,使以A ,C ,P ,Q 为顶点的四边形是平行四边形,理由如下:由()5,0B ,()0,5C 得直线BC 解析式为5y x =-+,设(),5Q m m -+,()2,45P n n n -++,又()1,0A -,()0,5C ,①当PQ ,AC 是对角线,则PQ ,AC 的中点重合,21054505m n m n n +=-+⎧∴⎨-+-++=+⎩,解得0(m =与C 重合,舍去)或7m =-,()7,12Q ∴-;②当QA ,PC 为对角线,则QA ,PC 的中点重合,21050455m n m n n -=+⎧∴⎨-++=-+++⎩,解得0(m =舍去)或7m =,()7,2Q ∴-;③当QC ,PA 为对角线,则QC ,PA 的中点重合,20155450m n m n n +=-⎧∴⎨-++=-+++⎩,解得1m =或2m =,()1,4Q ∴或()2,3,综上所述,Q 的坐标为()7,12-或()7,2-或()1,4或()2,3.本题考查二次函数的综合应用,涉及待定系数法,三角形面积,平行四边形的性质及应用,解题的关键是用含字母的式子表示相关点的坐标和相关线段的长度.(2022·湖南湘潭·统考中考真题)已知抛物线2y x bx c =++.(1)如图①,若抛物线图象与x 轴交于点()3,0A ,与y 轴交点()0,3B -.连接AB .①求该抛物线所表示的二次函数表达式;②若点P 是抛物线上一动点(与点A 不重合),过点P 作PH x ⊥轴于点H ,与线段AB 交于点M .是否存在点P 使得点M 是线段PH 的三等分点?若存在,请求出点P 的坐标;若不存在,请说明理由.(2)如图②,直线43y x n =+与y 轴交于点C ,同时与抛物线2y x bx c =++交于点()3,0D -,以线段CD 为边作菱形CDFE ,使点F 落在x 轴的正半轴上,若该抛物线与线段CE 没有交点,求b 的取值范围.(1)①直接用待定系数法求解;②先求出直线AB 的解析式,设点M (m ,m -3)点P (m ,m 2-2m -3)若点M 是线段PH 的三等分点,则13HM HP =或23HM HP =,代入求解即可;(2)先用待定系数法求出n 的值,再利用勾股定理求出CD 的长为5,因为四边形CDFE 是菱形,由此得出点E 的坐标.再根据该抛物线与线段CE 没有交点,分两种情况(CE 在抛物线内和CE 在抛物线右侧)进行讨论,求出b 的取值范围.【答案】(1)①2=23y x x --,②存在,点P 坐标为(2,-3)或(12,-154),理由见解析(2)b <32-或b >133【详解】(1)①解:把()3,0A ,()0,3B -代入2y x bx c =++,得20333b c c ⎧=++⎨-=⎩,解得:23b c =-⎧⎨=-⎩,∴2=23y x x --②解:存在,理由如下,设直线AB 的解析式为y =kx +b ,把()3,0A , ()0,3B -代入,得303k b b +=⎧⎨=-⎩,解得13k b =⎧⎨=-⎩,∴直线AB 的解析式为y =x -3,设点M (m ,m -3)、点P (m ,m 2-2m -3)若点M 是线段PH 的三等分点,则13HM HP =或23HM HP =,即232331m m m -=--或232332m m m -=--,解得:m =2或m =12或m =3,经检验,m =3是原方程的增根,故舍去,∴m =2或m =12∴点P 坐标为(2,-3)或(12,-154)(2)解:把点D (-3,0)代入直线43y x n =+,解得n =4,∴直线443y x =+,当x =0时,y =4,即点C (0,4)∴CD =5,∵四边形CDFE 是菱形,∴CE =EF =DF =CD =5,∴点E (5,4)∵点()3,0D -在抛物线2y x bx c =++上,∴(-3)2-3b +c =0,∴c =3b -9,∴239y b x bx =++-,∵该抛物线与线段CE 没有交点,分情况讨论当CE 在抛物线内时52+5b +3b -9<4解得:b <32-当CE 在抛物线右侧时,3b -9>4解得:b >133综上所述,b <32-或b >133此题考查了二次函数和一次函数以及图形的综合,解题的关键是数形结合和分情况讨论.1.(2023·安徽宿州·统考一模)如图,在平面直角坐标系中,矩形OABC 的顶点B 的坐标为()8,4,OA OC ,分别落在x 轴和y 轴上,将OAB V 绕点O 逆时针旋转,使点B 落在y 轴上,得到ODE V ,OD 与CB 相交于点F ,反比例函数()0k y x x=>的图象经过点F ,交AB 于点G .(1)求k 的值.(2)连接FG ,则图中是否存在与FBG △相似的三角形?若存在,请把它们一一找出来,并选其中一种进行证明;若不存在,请说明理由.(3)点M 在直线OD 上,N 是平面内一点,当四边形GFMN 是正方形时,请直接写出点N 的坐标.2.(2022·河南郑州·河南省实验中学校考模拟)在ABC V 中,AB AC =,E 为边AC 上一点,D 为直线BC 上一点,连AD 、BE ,交于点F .(1)如图1,若60BAC ∠=︒,D 点在线段BC 上,且AE CD =,过B 作BG AD ⊥,求证:12=FG BF ;(2)如图2,若BAC BFD ∠=∠,且3BF AF =,求BD BC 的值;(3)如图3,若60BAC ∠=︒.若3BD CD =,将线段AD 绕点A 逆时针旋转到AH ,并且使得HAC ADB ∠=∠,连接BH 交AC 于P ,直接写出AC PC= ______ .3.(2022·吉林长春·模拟)如图,在ABC V 中,5AB AC ==,6BC =.点P 从点B 出发,沿BC 以每秒2个单位长度的速度向终点C 运动,同时点Q 从点C 出发,沿折线CA AB -以每秒5个单位长度的速度运动,到达点A 时,点Q 停止1秒,然后继续运动.分别连接PQ 、BQ .设点P 的运动时间为t 秒.(1)求点A 与BC 之间的距离;(2)当3BP AQ =时,求t 的值;(3)当PQB V 为钝角三角形时,求t 的取值范围;(4)点P 关于直线AB 的对称点是点D ,连接DQ ,当线段DQ 与ABC V 的某条边平行时,直接写出t 的值.4.(2022·浙江金华·一模)如图,在平面直角坐标系xOy 中,菱形OABC 的顶点A 在x 轴的正半轴上,点C 的坐标为()3,4,点D 从原点O 出发沿O A B →→匀速运动,到达点B 时停止,点E 从点A 出发沿A B C →→随D 运动,且始终保持CDE COA ∠=∠.设运动时间为t .(1)当DE OB ∥时,求证:OCD BCE △≌△.(2)若点E 在BC 边上,当CDE △为等腰三角形时,求BE 的长.(3)若点D 的运动速度为每秒1个单位,是否存在这样的t ,使得以点C ,D ,E 为顶点的三角形与OCD V 相似?若存在,直接写出所有符合条件的t ;若不存在,请说明理由.5.(2022·重庆·模拟)如图,在平面直角坐标系中,抛物线2y x bx c ++=﹣交x 轴于点A 和C (1,0),交y 轴于点B (0,3),抛物线的对称轴交x 轴于点E ,交抛物线于点F .(1)求抛物线的解析式;(2)将线段OE 绕着点O 沿顺时针方向旋转得到线段OE ',旋转角为α(0°<α<90°),连接,AE BE '',求13BE AE '+'的最小值;(3)M 为平面直角坐标系中一点,在抛物线上是否存在一点N ,使得以A ,B ,M ,N 为顶点的四边形为矩形?若存在,请直接写出点N 的横坐标;若不存在,请说明理由.6.(2022·广东佛山·校考三模)已知抛物线223(0)y ax ax a a =--<交x 轴于点A ,(B A 在B 的左侧),交y 轴于点C .(1)求点A 的坐标;(2)若经过点A 的直线y kx k =+交抛物线于点D .①当0k >且1a =-时AD 交线段BC 于E ,交y 轴于点F ,求ΔΔEBD CEF S S -的最大值;②当0k <且k a =时,设P 为抛物线对称轴上一动点,点Q 是抛物线上的动点,那么以A ,D ,P ,Q 为顶点的四边形能否成为矩形?若能,求出点P 的坐标,若不能,请说明理由.7.(2022·广东江门·校考一模)如图,抛物线26y ax x =++的图象与直线y kx b =+有唯一交点()1,4A -.(1)求抛物线和直线的解析式;(2)若点拋物线与x 轴的交点分别为点M 、N ,抛物线的对称轴上是否存在一点P ,使PA PM +的值最小?如果有,请求出这个最小值,如果没有,请说明理由.(3)直线y kx b =+与x 轴交于点B ,点Q 是x 轴上一动点,请你写出使QAB V 是等腰三角形的所有点Q 的横坐标.8.(2022·广东佛山·校考三模)如图1,AD 、BD 分别是ABC ∆的内角BAC ∠、ABC ∠的平分线,过点A 作AE AD ⊥,交BD 的延长线于点E .(1)求证:12E C ∠=∠;(2)如图2,如果AE AB =,且:2:3BD DE =,求cos ABC ∠的值;(3)如果ABC ∠是锐角,且ABC ∆与ADE ∆相似,求ABC ∠的度数,并直接写出ADE ABC S S ∆∆的值.。
数学分类讨论思想课件

E
F a
2、在直角坐标系中,O为坐标原点, 已知 A(1,1),在x轴上确定点P, 使得△AOP为等腰三角形,则符合条 y 4 件的P点共有 个
1
P2(2 ,0)
A (1,1)
P1(2,0)
-1
o
-1
P4( 1, 0 )
1 P3(
2
,0) x
例7、在下图三角形的边上找出一点,使得 该点与三角形的两顶点构成等腰三角形!C
当AQ=AP时,△QAP为等腰直 角三角形, 即6-t=2t,解得t=2(秒) ∴当t=2秒时, △QAP为等腰直 角三角形。
16 17
(1)若顶角顶点与矩形顶点重合
A
F
D
16
E B
17
如图,当AE=AF=10时,S△AEF=
1 2 2×10×10=50(cm )
C
(2)若底角顶点与矩形顶点重合
A D E A D
E B F C B C
F
如图,当EA=EF=10时,BE=6, BF= 102 62 =8,
1 S△AEF= ×10×8=40(cm2) 2
例5
1、已知⊙O的半径为5cm,AB、CD是⊙O的弦, 且AB=6cm, CD=8cm,AB∥CD,则AB与CD之 间的距离为 7cm或1cm 。
A B C C A B D
O 2、在半径为1的圆O中,弦AB、AC的长分 别是 3、 2,则∠BAC的度数是 150或750 。
3、△ABC是半径为2cm的圆的内接三角形,若 0或1200 60 BC=2 cm,则∠ A的度数是 。
1)、对∠A进行讨论
110° 20° 50° B
3)、对∠C进行讨论
C
安徽中考数学第一轮复习策略课件(18张PPT)

2.对于公式、定理的证明或推导不可以口头描述证明, 实践发现,老师在课堂上省一个步骤,学生却给你省 了两个、甚至多个步骤,导致学生对公式、定理不知 道所有然。如,勾股定理的逆定理的运用学生大多数 会运用,但只有少数学生会证明这个定理,这就是我 当时是口头描述证明导致的后果。
A P 图3 B ∠CAB=∠DBA=∠CPD=ɑ.
内在联系:由 条件可知, ∠C+∠CPA=180°-α ,
∠DPB+∠CPA=180°-α , 所以,①∠C=∠DPB;②Δ CAPΔ PBD.
二、利用基本图形的特征,进行复杂图形分解
1.(中考题)如图点M在线段AB上,AE,BD交于C, AE,DM交于点F,ME,BD交于点G,∠DME=∠A=∠B=β . 试写出图中所有的相似三角形.
D
由基本图形1可得Δ CFDΔ DEA,所以, c CF=DE=3,在RtΔ CFD中可求CD= 10.
d
C
F
2.如图,四边形ABCD中,∠A=90°,∠B=120°,AD= 3, AB=6,AB∥DC,E在AB上,∠DEC=120°.求AE的长.
A
FE
B
D
C
G
1)作∠ADF=30°
2.作BG⊥DC于G.
3. 每个单元复习后都进行小测试,及时 批改与反馈,小结、分析学生学习的模 糊点、失分点。
4. 为夯实基础,快速完成基本题的答卷,布置 并跟踪与检查学生的配套作业,鼓励后进生反 复练习基本题。 5. 我校每月定期月考,及时开展组内分析、总结 不足,及时补缺补差。
6. 我校数学组信息共享、资源共享。
中考数学专题复习一分类讨论思想PPT课件

AC
∴AD=AC×sin 45°, 在Rt△ABD中,∠B=30°,
∴AB=2AD=2AC×sin 45°=750 2 m.
答案:750 2 m
【知识归纳】解直角三角形实际应用的两点技能 1.转化:利用直角三角形或构造直角三角形解决实际问题,一 般先把实际问题转化为数学问题,若题目中无直角三角形,需 要添加辅助线(如作三角形的高等)构造直角三角形,再利用解 直角三角形的知识求解. 2.前提:解直角三角形时结合图形分清图形中哪个三角形是直 角三角形,哪条边是角的对边、斜边、邻边,此外正确理解俯 角、仰角、坡度、坡角等名词术语是解答此类题目的前提条件.
5.一次函数:已知一次函数与坐标轴围成的三角形的面积,求k 的值,常分直线交于坐标轴正半轴和负半轴讨论;确定反比例函 数与一次函数交点个数,常分一、三象限或二、四象限两种情 况讨论. 6.圆:圆的一条弦(直径除外)对两条弧,常分优弧和劣弧两种情 况讨论;求圆中两条平行弦的距离,常分两弦在圆心的同旁和两 旁两种情况讨论;圆与圆的相切,此时要考虑分外切和内切两种 情况讨论.
4.在几何中的应用:对于几何问题,我们常通过图形,找出边、 角的数量关系,通过边、角的数量关系,得出图形的性质等.
【例2】(2013·兰州中考)已知反比例函数y1= k 的图象与
x
一次函数y2=ax+b的图象交于点A(1,4)和点B(m,-2). (1)求这两个函数的解析式. (2)视察图象,当x>0时,直接 写出y1>y2时自变量x的取值范围. (3)如果点C与点A关于x轴对称, 求△ABC的面积.
5.(2013·十堰中考)如图,在小山的东侧A点有一个热气球,由
2021中考安徽省专用数学重难点突破四 几何压轴题课件

(1)当 P 与 O 重合时(如图②所示),设点 C 是 AO 的中点,连接 BC. 求证:四边形 OCBM 是正方形;
AB OM (2)请利用如图①所示的情形,求证:PB=BM; (3)若 AO=2 6,且当 MO=2PO 时,请直接写出 AB 和 PB 的长.
【思路点拨】(1)先证明四边形 OCBM 是平行四边形,由于∠BMO= 90°,所以▱ OCBM 是矩形,最后根据直角三角形斜边上的中线的性质即 可证明四边形 OCBM 是正方形;(2)要证APBB=OBMM,只要由(1)的结论去推理 证明△ABC∽△PBM,即可得出结论;(3)由于点 P 的位置不确定,故需要 分情况进行讨论,共两种情况,第一种情况是点 P 在点 O 的左侧,第二 种情况是点 P 在点 O 的右侧,然后利用相似三角形的性质即可求出答案.
3
3
(1)解:如解图①,过 E 作 EH⊥AB 于 H,连接 CD,
设 EH=x,则 AE=2x,AH= 3x,
∵AE=EC,
∴AC=2AH=2 3x.
∵C 是 AB 的中点,
AD=BD,∴CD⊥AB,
∵∠ADB=120°,∴∠DAC=30°,
解图①
∴DC=2x,∴DC=CE=2x,
∵EH∥DC,∴∠HED=∠EDC=∠CED,
(3)解:如解图③,连接 DM,取 AC 的中点 N,连接 DN,
由(1)得 AE=EG,∴∠GAE=∠AGE,
在 Rt△ACD 中,N 为 AC 的中点,
∴DN=1AC=AN,∠DAN=∠ADN, 2
∴∠ADN=∠AGE,∴DN∥GF.
解图③
在 Rt△GDF 中,M 是 FG 的中点, ∴DM=12FG=GM,∠GDM=∠AGE, ∴∠GDM=∠DAN, ∴DM∥AE, ∴四边形 DMEN 是平行四边形, ∴EM=DN=12AC, ∵AC=AB=5,∴EM=52.
2021年中考数学复习之专题突破训练《专题五:二次函数》解析

2021年中考数学复习之专题突破训练《专题五:二次函数》参考答案与试题解析一、选择题1.已知原点是抛物线2(1)y m x =+的最高点,则m 的范围是( ) A .1m <-B .1m <C .1m >-D .2m >-【考点】3H :二次函数的性质【分析】由于原点是抛物线2(1)y m x =+的最高点,这要求抛物线必须开口向下,由此可以确定m 的范围.【解答】解:原点是抛物线2(1)y m x =+的最高点, 10m ∴+<,即1m <-. 故选:A .【点评】此题主要考查了二次函数的性质.2.将二次函数241y x x =--化为2()y x h k =-+的形式,结果为( ) A .2(2)5y x =++B .2(2)5y x =+-C .2(2)5y x =-+D .2(2)5y x =--【考点】9H :二次函数的三种形式 【专题】11:计算题【分析】把241y x x =--进行配方得到22445(2)y x x x =-+-=-,5-. 【解答】解:2241445y x x x x =--=-+-2(2)5x =--. 故选:D .【点评】本题考查了二次函数的三种形式:一般式2(y ax bx c a =++、b 、c 为常数,0)a ≠;顶点式2()y a x k h =-+,顶点坐标为(,)k h ;交点式12()()y x x x x =--,1x 、2x 为抛物线与x 轴交点的横坐标.3.将抛物线22y x =向左平移3个单位得到的抛物线的解析式是( )A .223y x =+B .223y x =-C .22(3)y x =+D .22(3)y x =-【考点】6H :二次函数图象与几何变换 【专题】1:常规题型【分析】根据“左加右减”的原则进行解答即可.【解答】解:将抛物线22y x =向左平移3个单位所得直线解析式为:22(3)y x =+; 故选:C .【点评】本题考查的是二次函数的图象与几何变换,熟知函数图象平移的法则是解答此题的关键.4.如图,以(1,4)-为顶点的二次函数2y ax bx c =++的图象与x 轴负半轴交于A 点,则一元二次方程20ax bx c ++=的正数解的范围是( )A .23x <<B .34x <<C .45x <<D .56x <<【考点】HB :图象法求一元二次方程的近似根【分析】先根据图象得出对称轴左侧图象与x 轴交点横坐标的取值范围,再利用对称轴1x =,可以算出右侧交点横坐标的取值范围.【解答】解:二次函数2y ax bx c =++的顶点为(1,4)-,∴对称轴为1x =,而对称轴左侧图象与x 轴交点横坐标的取值范围是32x -<<-,∴右侧交点横坐标的取值范围是45x <<.故选:C .【点评】此题主要考查了图象法求一元二次方程的近似根,解答本题首先需要观察得出对称轴左侧图象与x 轴交点横坐标的取值范围,再根据对称性算出右侧交点横坐标的取值范围.5.二次函数21y x =-+的图象与x 轴交于A 、B 两点,与y 轴交于点C ,下列说法错误的是( )A .点C 的坐标是(0,1)B .线段AB 的长为2C .ABC ∆是等腰直角三角形D .当0x >时,y 随x 增大而增大【考点】3H :二次函数的性质;HA :抛物线与x 轴的交点【分析】判断各选项,点C 的坐标可以令0x =,得到的y 值即为点C 的纵坐标;令0y =,得到的两个x 值即为与x 轴的交点坐标A 、B ;且AB 的长也有两点坐标求得,对函数的增减性可借助函数图象进行判断.【解答】解:A ,令0x =,1y =,则C 点的坐标为(0,1),正确;B ,令0y =,1x =±,则(1,0)A -,(1,0)B ,||2AB =,正确;C ,由A 、B 、C 三点坐标可以得出AC BC =,且222AC BC AB +=,则ABC ∆是等腰直角三角形,正确;D ,当0x >时,y 随x 增大而减小,错误.故选:D .【点评】本题考查了二次函数的性质,需学会判定函数的单调性及由坐标判定线段或点之间连线构成的图形的形状等问题.6.已知二次函数2(1)4y x =--,当0y <时,x 的取值范围是( ) A .31x -<<B .1x <-或3x >C .13x -<<D .3x <-或1x >【考点】3H :二次函数的性质;HA :抛物线与x 轴的交点 【专题】1 :常规题型【分析】先求出方程2(1)40x --=的解, 得出函数与x 轴的交点坐标, 根据函数的性质得出答案即可 .【解答】解:二次函数2(1)4y x =--,∴抛物线的开口向上, 当0y =时,20(1)4x =--,解得:3x =或1-,∴当0y <时,x 的取值范围是13x -<<,故选:C .【点评】本题考查了二次函数与x 轴的交点和二次函数的性质, 能熟记二次函数的性质的内容是解此题的关键 .7.已知1(1,)A y -,2(1,)B y ,3(2,)C y 三点在抛物线22y x x m =-+上,则1y 、2y 、3y 的大小关系为( ) A .123y y y <<B .321y y y <<C .213y y y <<D .231y y y <<【考点】5H :二次函数图象上点的坐标特征 【专题】11:计算题【分析】分别计算自变量为1-、1和2所对应的函数值,然后比较函数值的大小即可. 【解答】解:当1x =-时,212123y x x m m m =-+=++=+;当1x =时,222121y x x m m m =-+=-+=-+;当2x =时,23244y x x m m m =-+=-+=, 所以231y y y <<. 故选:D .【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式. 8.共享单车为市民出行带来了方便,某单车公司第一个月投放a 辆单车,计划第三个月投放单车y 辆,设该公司第二、三两个月投放单车数量的月平均增长率为x ,那么y 与x 的函数关系是( ) A .2(1)y a x =+B .2(1)y a x =-C .2(1)y x a =-+D .2y x a =+【考点】HD :根据实际问题列二次函数关系式 【专题】1:常规题型【分析】主要考查增长率问题,一般用增长后的量=增长前的量(1⨯+增长率),如果设该公司第二、三两个月投放单车数量的月平均增长率为x ,然后根据已知条件可得出方程. 【解答】解:设该公司第二、三两个月投放单车数量的月平均增长率为x , 依题意得第三个月第三个月投放单车2(1)a x +辆, 则2(1)y a x =+. 故选:A .【点评】此题主要考查了根据实际问题列二次函数关系式,求平均变化率的方法为:若设变化前的量为a ,变化后的量为b ,平均变化率为x ,则经过两次变化后的数量关系为2(1)a x b ±=.9.二次函数2y x mx =-+的图象如图,对称轴为直线2x =,若关于x 的一元二次方程20(x mx t t -+-=为实数)在15x <<的范围内有解,则t 的取值范围是( )A .5t >-B .53t -<<C .34t <D .54t -<【考点】HA :抛物线与x 轴的交点;HB :图象法求一元二次方程的近似根 【专题】68:模型思想【分析】如图,关于x 的一元二次方程20x mx t -+-=的解就是抛物线2y x mx =-+与直线y t =的交点的横坐标,利用图象法即可解决问题.【解答】解:如图,关于x 的一元二次方程20x mx t -+-=的解就是抛物线2y x mx =-+与直线y t =的交点的横坐标,由题意可知:4m =,当1x =时,3y =, 当5x =时,5y =-,由图象可知关于x 的一元二次方程20(x mx t t -+-=为实数)在15x <<的范围内有解, 直线y t =在直线5y =-和直线4y =之间包括直线4y =,54t ∴-<.故选:D .【点评】本题考查抛物线与x 轴的交点、一元二次方程等知识,解题的关键是学会利用图象法解决问题,画出图象是解决问题的关键,属于中考选择题中的压轴题. 10.二次函数23(2)5y x =--与y 轴交点坐标为( )A .(0,2)B .(0,5)-C .(0,7)D .(0,3)【考点】5H :二次函数图象上点的坐标特征 【专题】2B :探究型【分析】根据题目中的函数解析式,令0x =,求出相应的y 的值,即可解答本题. 【解答】解:23(2)5y x =--∴当0x =时,7y =,即二次函数23(2)5y x =--与y 轴交点坐标为(0,7), 故选:C .【点评】本题考查二次函数图象上点的坐标特征,解答本题的关键是明确二次函数与y 轴交点的横坐标等于0.11.对于函数25y x =,下列结论正确的是( ) A .y 随x 的增大而增大 B .图象开口向下 C .图象关于y 轴对称D .无论x 取何值,y 的值总是正的 【考点】3H :二次函数的性质 【专题】535:二次函数图象及其性质【分析】根据二次函数解析式结合二次函数的性质,即可得出结论. 【解答】解:二次函数解析式为25y x =,∴二次函数图象开口向上,当0x <时y 随x 增大而减小,当0x >时y 随x 增大而增大,对称轴为y 轴,无论x 取何值,y 的值总是非负. 故选:C .【点评】本题考查了二次函数的性质,根据二次函数的性质逐一对照四个选项即可得出结论. 12.某农产品市场经销一种销售成本为40元的水产品.据市场分析,若按每千克50元销售,一个月能售出500千克;销售单价每涨一元,月销售量就减少10千克.设销售单价为每千克x 元,月销售利润为y 元,则y 与x 的函数关系式为( ) A .(40)(50010)y x x =-- B .(40)(10500)y x x =--C .(40)[50010(50)]y x x =---D .(40)[50010(50)]y x x =---【考点】HD :根据实际问题列二次函数关系式 【专题】1:常规题型【分析】直接利用每千克利润⨯销量=总利润,进而得出关系式. 【解答】解:设销售单价为每千克x 元,月销售利润为y 元, 则y 与x 的函数关系式为:(40)[50010(50)]y x x =---. 故选:C .【点评】此题主要考查了根据实际问题抽象出二次函数关系式,正确表示出销量是解题关键. 13.如图,抛物线21y x =+与双曲线ky x=的交点A 的横坐标是1,则关于x 的不等式210kx x-->的解集是( )A .1x >B .1x <-C .01x <<D .10x -<<【考点】HC :二次函数与不等式若二次函数22(1)31y a x x a =-++-的图象经过原点,则a 的值必为( ) A .1或1-B .1C .1-D .0【考点】8H :待定系数法求二次函数解析式;1H :二次函数的定义【分析】先把原点坐标代入二次函数解析式得到a 的方程,解方程得到1a =或1a =-,根据二次函数的定义可判断1a =-.【解答】解:把(0,0)代入22(1)31y a x x a =-++-, 得210a -=,解得1a =或1a =-, 因为10a -≠, 所以1a ≠,即1a =-. 故选:C .【点评】本题考查了待定系数法求二次函数解析式,同时考查了二次函数的定义. 15.已知非负数a ,b ,c 满足2a b +=,34c a -=,设2S a b c =++的最大值为m ,最小值为n ,则m n -的值为( )A .9B .8C .1D .103【考点】7H :二次函数的最值【分析】用a 表示出b 、c 并求出a 的取值范围,再代入S 整理成关于a 的函数形式,然后根据二次函数的增减性求出m 、n 的值,再相减即可得解. 【解答】解:2a b +=,34c a -=, 2b a ∴=-,34c a =+, b ,c 都是非负数, ∴20340a a -⎧⎨+⎩①②,解不等式①得,2a , 解不等式②得,43a -, 423a ∴-, 又a 是非负数,02a ∴,22(2)34S a b c a a a =++=+-++, 226a a =++,∴对称轴为直线2121a =-=-⨯, 0a ∴=时,最小值6n =,2a =时,最大值2222614m =+⨯+=,1468m n ∴-=-=.故选:B .【点评】本题考查了二次函数的最值问题,用a 表示出b 、c 并求出a 的取值范围是解题的关键,难点在于整理出s 关于a 的函数关系式.16.如图,二次函数2(0)y ax bx c a =++≠的图象的顶点在第一象限,且过点(0,1)和(1,0)-,下列结论:①0ab <,②24b >,③02a b c <++<,④01b <<,⑤当1x >-时,0y >.其中正确结论的个数是( )A .2个B .3个C .4个D .5个【考点】4H :二次函数图象与系数的关系 【专题】31:数形结合【分析】利用抛物线开口方向得0a <,利用对称轴在y 轴的右侧得0b >,则可对①进行判断;根据二次函数图象上点的坐标特征得1c =,0a b c -+=,则1b a c a =+=+,所以01b <<,于是可对②④进行判断;由于1122a b c a a a ++=+++=+,利用0a <可得2a b c ++<,再根据抛物线的对称性得到抛物线与x 轴的另一个交点在(1,0)和(2,0)之间,则1x =时,函数值为正数,即0a b c ++>,由此可对③进行判断;观察函数图象得到1x >-时,抛物线有部分在x 轴上方,有部分在x 轴下方,则可对⑤进行判断.【解答】解:由抛物线开口向下, 0a ∴<,对称轴在y 轴的右侧, 0b ∴>,0ab ∴<,所以①正确;点(0,1)和(1,0)-都在抛物线2y ax bx c =++上, 1c ∴=,0a b c -+=,1b a c a ∴=+=+,而0a <,01b ∴<<,所以②错误,④正确; 1122a b c a a a ++=+++=+,而0a <,222a ∴+<,即2a b c ++<,抛物线与x 轴的一个交点坐标为(1,0)-,而抛物线的对称轴在y 轴右侧,在直线1x =的左侧,∴抛物线与x 轴的另一个交点在(1,0)和(2,0)之间,1x ∴=时,0y >,即0a b c ++>,02a b c ∴<++<,所以③正确;1x >-时,抛物线有部分在x 轴上方,有部分在x 轴下方,0y ∴>或0y =或0y <,所以⑤错误.故选:B .【点评】本题考查了二次函数图象与系数的关系:对于二次函数2(0)y ax bx c a =++≠,当0a >时,抛物线向上开口;当0a <时,抛物线向下开口;一次项系数b 和二次项系数a共同决定对称轴的位置:当a 与b 同号时当函数2(1)2y x =--的函数值y 随着x 的增大而减小时,x 的取值范围是( ) A .0x >B .1x <C .1x >D .x 为任意实数【考点】3H :二次函数的性质 【专题】31:数形结合【分析】利用二次函数的增减性求解即可,并画出了图形,可直接看出. 【解答】解:对称轴是:1x =,且开口向上,如图所示,∴当1x <时,函数值y 随着x 的增大而减小; 故选:B .【点评】本题主要考查了二次函数的性质,解题的关键是熟记二次函数的性质. 18.将抛物线2y x =平移得到抛物线2(3)y x =+,则这个平移过程正确的是( ) A .向左平移3个单位 B .向右平移3个单位C .向上平移3个单位D .向下平移3个单位【考点】6H :二次函数图象与几何变换 【专题】46:几何变换【分析】先利用顶点式得到两抛物线的顶点坐标,然后通过点的平移情况判断抛物线平移的情况.【解答】解:抛物线2y x =的顶点坐标为(0,0),抛物线2(3)y x =+的顶点坐标为(3,0)-, 点(0,0)向左平移3个单位可得到(3,0)-,∴将抛物线2y x =向左平移3个单位得到抛物线2(3)y x =+.故选:A .【点评】本题考查了二次函数图象与几何变换:由于抛物线平移后的形状不变,故a 不变,所以求平移后的抛物线解析式通常可利用两种方法:一是求出原抛物线上任意两点平移后的坐标,利用待定系数法求出解析式;二是只考虑平移后的顶点坐标,即可求出解析式. 19.把160元的电器连续两次降价后的价格为y 元,若平均每次降价的百分率是x ,则y 与x 的函数关系式为( )A .320(1)y x =-B .320(1)y x =-C .2160(1)y x =-D .2160(1)y x =-【答案】D【考点】根据实际问题列二次函数关系式【分析】由原价160元可以得到第一次降价后的价格是160(1)x -,第二次降价是在第一次降价后的价格的基础上降价的,为160(1)(1)x x --,由此即可得到函数关系式. 【解答】解:第一次降价后的价格是160(1)x -, 第二次降价为2160(1)(1)160(1)x x x -⨯-=- 则y 与x 的函数关系式为2160(1)y x =-. 故选:D .【点评】此题考查从实际问题中得出二次函数解析式,需注意第二次降价是在第一次降价后的价格的基础上降价的,所以会出现自变量的二次,即关于x 的二次函数. 20.下列函数中是二次函数的为( ) A .31y x =-B .231y x =-C .22(1)y x x =+-D .323y x x =+-【考点】1H :二次函数的定义【分析】根据二次函数的定义,可得答案.【解答】解:A 、31y x =-是一次函数,故A 错误;B 、231y x =-是二次函数,故B 正确;C 、22(1)y x x =+-不含二次项,故C 错误;D 、323y x x =+-是三次函数,故D 错误;故选:B .【点评】本题考查了二次函数的定义,形如2(0)y ax bx c a =++≠是二次函数,要先化简再判断.21.函数21y ax =+和(y ax a a =+为常数,且0)a ≠,在同一平面直角坐标系中的大致图象可能是( )A .B .C .D .【答案】D【考点】二次函数的图象;一次函数的图象【专题】推理能力;几何直观;一次函数及其应用;二次函数图象及其性质【分析】由二次函数21y ax =+的图象顶点(0,1)可排除A 、B 答案;由一次函数y ax a =+的图象过点(1,0)-可排除C 答案.此题得解. 【解答】解:21y ax =+,∴二次函数21y ax =+的图象的顶点为(0,1),故A 、B 不符合题意;当0y ax a =+=时,1x =-,∴一次函数y ax a =+的图象过点(1,0)-,故C 不符题意.故选:D .【点评】本题考查了一次函数的图象以及二次函数的图象,利用一次函数图象经过定点排除A 、B 、C 选项是解题的关键.22.点(,)P m n 在以y 轴为对称轴的二次函数24y x ax =++的图象上.则m n -的最大值等于( ) A .154B .4C .154-D .174-【答案】C【考点】二次函数图象上点的坐标特征;二次函数的性质 【专题】二次函数图象及其性质;应用意识【分析】根据题意,可以得到a 的值,m 和n 的关系,然后将m 、n 作差,利用二次函数的性质,即可得到m n -的最大值,本题得以解决.【解答】解:点(,)P m n 在以y 轴为对称轴的二次函数24y x ax =++的图象上, 0a ∴=,24n m ∴=+,222115(4)4()24m n m m m m m ∴-=-+=-+-=---,∴当12m =时,m n -取得最大值,此时154m n -=-, 故选:C .【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征,解答本题的关键是明确题意,利用二次函数的性质解答.23.已知抛物线22(26)3y x m x m =+-+-与y 轴交于点A ,与直线4x =交于点B ,当2x >时,y 值随x 值的增大而增大.记抛物线在线段AB 下方的部分为G ,M 为G 上任意一点,设M 的纵坐标为t ,若3t -,则m 的取值范围是( ) A .32mB .332m C .3m D .13m【答案】A【考点】二次函数图象与系数的关系;二次函数图象上点的坐标特征 【专题】二次函数图象及其性质;应用意识【分析】根据题意,22bx a=-,2434ac b a --【解答】解:当对称轴在y 轴的右侧时,2226026224(3)(26)34m m m m ⎧⎪-<⎪-⎪-⎨⎪⎪----⎪⎩, 解得332m <, 当对称轴是y 轴时,3m =,符合题意,当对称轴在y 轴的左侧时,260m ->,解得3m >, 综上所述,满足条件的m 的值为32m . 故选:A .【点评】本题考查二次函数图形与系数的关系,二次函数图象上的点的坐标特征,解题的关键是理解题意,学会用分类讨论的思想思考问题,属于中考选择题中的压轴题.24.若二次函数22y a x bx c =--的图象,过不同的六点(1,)A n -、(5,1)B n -、(6,1)C n +、D 1)y 、2(2,)E y 、3(4,)F y ,则1y 、2y 、3y 的大小关系是( )A .123y y y <<B .132y y y <<C .231y y y <<D .213y y y <<【答案】D【考点】二次函数图象上点的坐标特征;二次函数的图象 【专题】二次函数图象及其性质;推理能力【分析】由解析式可知抛物线开口向上,点(1,)A n -、(5,1)B n -、(6,1)C n +求得抛物线对称轴所处的范围,然后根据二次函数的性质判断可得.【解答】解:由题意22225513661a b c n a b c n a b c n ⎧+-=⎪--=-⎨⎪--=+⎩①②③②-①得,22461a b -=-④, ③-②得,2112a b -=⑤, ④6-⨯⑤得到,21342a =,可得5942b =, ∴抛物线的对称轴259226b x a -=-=, (2D ,1)y 、2(2,)E y 、3(4,)F y ,则213y y y <<, 故选:D .【点评】本题主要考查二次函数图象上点的坐标特征,根据题意得到抛物线的对称轴和开口方向是解题的关键.25.在同一平面直角坐标系中,若抛物线22y mx x n =+-与262y x x m n =--+-关于x 轴对称,则m ,n 的值为( )A .6m =-,3n =-B .6m =-,3n =C .6m =,3n =-D .6m =,3n =【答案】D【考点】6H :二次函数图象与几何变换;3H :二次函数的性质 【专题】535:二次函数图象及其性质;67:推理能力;69:应用意识 【分析】根据关于x 轴对称,函数y 是互为相反数即可求得.【解答】解:抛物线22y mx x n =+-与262y x x m n =--+-关于x 轴对称,22y mx x n ∴-=--+,22y mx x n ∴=--+与262y x x m n =--+-相同, 6m ∴-=-,n m n =-,解得6m =,3n =, 故选:D .【点评】本题考查了二次函数图象与几何变换,根据关于x 轴对称的坐标特征把抛物线22y mx x n =+-化成关于x 轴对称的抛物线的解析式是解题的关键.26.已知关于x 的二次函数24y x x m =-+在13x -的取值范围内最大值7,则该二次函数的最小值是( ) A .2- B .1-C .0D .1【答案】A【考点】二次函数的最值【专题】二次函数图象及其性质;运算能力【分析】先将二次函数写成顶点式,得出对称轴及开口方向,根据抛物线开口向上时离对称轴越远函数值越大,可知当1x =-时,7y =,从而可解得m 的值;再根据抛物线的顶点式可得其最小值. 【解答】解:24y x x m =-+2(2)4x m =-+-,∴对称轴为直线2x =,抛物线开口向上,二次函数在13x -的取值范围内最大值7, 当1x =-时,7y =,27(1)4(1)m ∴=--⨯-+, 解得:2m =,∴当2x =时,该二次函数有最小值,最小值为0242+-=-.故选:A .【点评】本题考查了二次函数的最值,熟练掌握二次函数的性质是解题的关键. 27.将二次函数2245y x x =-+的右边进行配方,正确的结果是( ) A .22(1)3y x =-- B .22(2)3y x =-- C .22(1)3y x =-+ D .22(2)3y x =-+【考点】9H :二次函数的三种形式【专题】66:运算能力;535:二次函数图象及其性质【分析】先提出二次项系数,再加上一次项系数一半的平方,即得出顶点式的形式. 【解答】解:提出二次项系数得,22(2)5y x x =-+, 配方得,22(21)52y x x =-++-, 即22(1)3y x =-+. 故选:C .【点评】本题考查了二次函数的三种形式,一般式:2y ax bx c =++,顶点式:2()y a x h k =-+;两根式:12()()y a x x x x =--.28.二次函数y =x 2﹣x +a ﹣4的图象与x 轴有两个公共点,a 取满足条件的最小整数,将图象在x 轴上方的部分沿x 轴翻折,其余部分保持不变,得到一个新图象,当直线y =kx ﹣2与新图象恰有三个公共点时,则k 的值不可能是 A .﹣1B .﹣2C .1D .2【考点】一次函数图象与系数的关系;一次函数图象上点的坐标特征;二次函数的性质;二次函数图象与几何变换;二次函数的最值;抛物线与x轴的交点.【专题】分类讨论;二次函数图象及其性质;数据分析观念.【答案】D【分析】由二次函数y=x2﹣x+a﹣4的图象与x轴有两个公共点,则△>0且a≠1,得到a=2.①当k>0时,直线y=kx﹣2与新图象恰有三个公共点时,此时直线过点B、C,故将点B的坐标代入y=kx﹣2,即可求解;②当k<0时,直线y=kx﹣2与新图象恰有三个公共点时,则此时直线过A、C点或直线与y=x2﹣x﹣2只有一个交点,进而求解.【解答】解:∵二次函数y=x2﹣x+a﹣4的图象与x轴有两个公共点,则△>0且a≠1,当△=2﹣4=8a﹣7>0时,解得a>,∵a取满足条件的最小整数,而a≠1,故a=2,当a=2时,y=x2﹣x+a﹣4=x2﹣x﹣2,设原抛物线交x轴于点A、B,交y轴于点C,将图象在x轴上方的部分沿x轴翻折,其余部分保持不变,得到一个新图象,如下图所示,对于y=x2﹣x﹣2,令y=0,则y=x2﹣x﹣2=0,解得x=﹣1或2,令x=0,则y=﹣2,故点A、B、C的坐标分别为、、,由直线y=kx﹣2知,该直线过点C,①当k>0时,∵直线y=kx﹣2与新图象恰有三个公共点时,则此时直线过点B、C,将点B的坐标代入y=kx﹣2得:0=2k﹣2,解得k=1;②当k<0时,∵直线y =kx ﹣2与新图象恰有三个公共点时,则此时直线过A 、C 点或直线与y =x 2﹣x ﹣2只有一个交点, 当直线过点A 、C 时,将点A 的坐标代入直线表达式得:0=﹣k ﹣2, 解得k =﹣2,当直线与y =x 2﹣x ﹣2只有一个交点时,联立直线和抛物线的表达式得:x 2﹣x ﹣2=kx ﹣2,即x 2﹣x =0, 则△=2﹣4×1×0=0, 解得k =﹣1,综上,k =1或﹣2或﹣1, 故选:D .【点评】本题考查的是抛物线与x 轴的交点,涉及到一次函数、根的判别式等知识点,分类求解是本题解题的关键.29.已知二次函数2y ax bx c =++与自变量x 的部分对应值如表,下列说法错误的是( )A .0a <B .方程22ax bx c ++=-的正根在4与5之间C .20a b +>D .若点1(5,)y 、3(2-,2)y 都在函数图象上,则12y y <【答案】B【考点】抛物线与x 轴的交点;图象法求一元二次方程的近似根;根的判别式;二次函数图象与系数的关系;根与系数的关系 【专题】推理能力;二次函数图象及其性质【分析】利用表中函数值的变换情况可判断抛物线的开口方向,则可对A 进行判断;利用抛物线的对称性可得1x =-和4x =的函数值相等,则可对B 进行判断;利用0x =和3x =时函数值相等可得到抛物线的对称轴方程,则可对C 进行判断;利用二次函数的性质则可对D 进行判断.【解答】解:二次函数值先由小变大,再由大变小,∴抛物线的开口向下,0a ∴<,故A 正确;1x =-时,3y =-,4x ∴=时,3y =-,∴二次函数2y ax bx c =++的函数值为2-时,10x -<<或34x <<,即方程22ax bx c ++=-的负根在1-与0之间,正根在3与4之间, 故B 错误;抛物线过点(0,1)和(3,1),∴抛物线的对称轴为直线32x =, 3122b a ∴-=>, 20a b ∴+>,故C 正确;3(2-,2)y 关于直线32x =的对称点为9(2,2)y ,952<, 12y y ∴<,故D 正确; 故选:B .【点评】本题考查了二次函数的图象与系数的关系,二次函数的性质.抛物线与x 轴的交点,熟练掌握二次函数的性质和抛物线的对称性是解决此题的关键. 30.在平面直角坐标系有一条抛物线241y x x =-+-,则在下列结论中: ①此抛物线的开口向下; ②此抛物线的对称轴是2x =; ③当12x x <时,则有12y y <;④当2x >时,若0m >,则有2()444x m x m -+++<; ⑤此抛物线中,当x 取任何实数时,y 值都不可能等于5; ⑥此抛物线与x 轴有两个交点.在下列给出的序号中,含有错误结论的是( ) A .①②③ B .①②④C .①②⑤D .①②⑥【答案】B【考点】抛物线与x 轴的交点;二次函数与不等式31.将函数224y x x =-+化为2()y a x h k =-+的形式为 2(1)3y x =-+ . 【考点】9H :二次函数的三种形式 【分析】利用配方法整理即可得解.【解答】解:2224(21)3y x x x x =-+=-++,2(1)3x =-+, 所以,2(1)3y x =-+. 故答案为:2(1)3y x =-+.【点评】本题考查了二次函数的三种形式,熟练掌握配方法是解题的关键.32.如果函数2(1)(y m x x m =-+是常数)是二次函数,那么m 的取值范围是 1m ≠ . 【考点】1H :二次函数的定义【专题】536:二次函数的应用;33:函数思想 【分析】依据二次函数的二次项系数不为零求解即可. 【解答】解:函数2(1)(y m x x m =-+为常数)是二次函数, 10m ∴-≠,解得:1m ≠,故答案为:1m ≠.【点评】本题主要考查的是二次函数的定义,掌握二次函数的特点是解题的关键. 33.如果函数232(3)1y x x -+=-++是二次函数,那么的值一定是 0 .【考点】二次函数的定义【分析】根据二次函数的定义,列出方程与不等式求解即可. 【解答】解:由题意得:2322-+=,解得0=或3=; 又30-≠,3∴≠.∴当0=时,这个函数是二次函数.故答案为:0.【点评】本题考查二次函数的定义,关键是掌握二次函数的定义:一般地,形如2(y ax bx c a =++、b 、c 是常数,0)a ≠的函数,叫做二次函数.34.设1(A x ,1)y 、2(B x ,2)y 是抛物线2242y x x =+-上的点,坐标系原点O 位于线段AB的中点处,则AB 的长为【考点】5H :二次函数图象上点的坐标特征【专题】11:计算题【分析】由于原点O 是线段AB 的中点得到A 点和B 点关于原点中心对称,则12x x =-,12y y =-,根据抛物线的位置可确定A 点和B 点在第一、三象限,设A 点在第一象限,再把点A 和B 点坐标代入解析式得到2111242y x x =+-,2111242y x x -=--,两式相加可得到11x =,则14y =,于是可确定A 点和B 点坐标,然后利用两点间的距离公式计算.【解答】解:原点是线段的中点,,与,关于原点中心对称,,,,抛物线的对称轴为直线,顶点坐标为,点和点在第一、三象限,设点在第一象限,点坐标为,,,,,,与,.O AB 1(A x ∴1)y 2(B x 2)y 12x x ∴=-12y y =-222422(1)4y x x x =+-=+-∴1x =-(1,4)--A ∴B A B ∴1(x -1)y -2111242y x x ∴=+-2111242y x x -=--11x ∴=14y ∴=(1,4)A ∴(1,4)B --AB ∴=故答案为.【点评】本题考查了二次函数图象上点的坐标特征:二次函数图象上点的坐标满足其解析式.也考查了两点间的距离公式.35.在一幢高的大楼上掉下一个苹果,苹果离地面的高度与时间大致有如下关系:. 5 秒钟后苹果落到地面.【考点】:二次函数的应用【分析】苹果落到地面,即的值为0,代入函数解析式求得的值即可解决问题.【解答】解:把代入函数解析式得,,解得,;答:5秒钟后苹果落到地面.故答案为:5.【点评】此题主要考查二次函数与一元二次方程的关系,解答时注意结合图象解答.36.如图,抛物线的对称轴为,点,点是抛物线与轴的两个交点,若点的坐标为,则点的坐标为 .【考点】二次函数的性质;抛物线与轴的交点【专题】二次函数图象及其性质【分析】根据抛物线的对称轴结合点的横坐标,即可求出点的横坐标,此题得解.【解答】解:抛物线的对称轴为直线,点的坐标为,点的横坐标为,点的坐标为.故答案为:.【点评】本题考查了抛物线与轴的交点以及二次函数的性质,牢记抛物线的对称性是解题125m ()h m ()t s 21255h t =-HE h t 0h =21255h t =-212550t -=15t =25t =-2y ax bx c =++1x =P Q x P (4,0)Q (2,0)-x P Q 1x =P (4,0)∴Q 1242⨯-=-∴Q (2,0)-(2,0)-x的关键.37.如图,在平面直角坐标系中,菱形的顶点在轴负半轴上,顶点在轴正半轴上.若抛物线经过点、,则点的坐标为 .【考点】菱形的性质;二次函数的性质;二次函数图象上点的坐标特征【专题】二次函数图象及其性质【分析】根据抛物线经过点、和二次函数图象具有对称性,可以求得该抛物线的对称轴和的长,然后根据菱形的性质和勾股定理可以求得的长,从而可以求得的长,进而写出点的坐标.【解答】解:抛物线,该抛物线的顶点的横坐标是,当时,,点的坐标为:,,抛物线经过点、,轴,,,,,,,,,点的坐标为,故答案为:【点评】本题考查二次函数的性质、二次函数图象上点的坐标特征、菱形的性质,解答本题的关键是明确题意,利用二次函数的性质和数形结合的思想解答.ABCD A x B x 2108(0)y ax ax a =-+>C D B(4,0)2108(0)y ax ax a =-+>C D CD AO OB B 22108(5)258y ax ax a x a =-+=--+∴5x =0x =8y =∴D (0,8)8OD ∴=2108(0)y ax ax a =-+>C D ////CD AB x 5210CD ∴=⨯=10AD ∴=90AOD ∠=︒8OD =10AD=6AO ∴====10AB =101064OB AO ∴=-=-=∴B (4,0)(4,0)。
2021年安徽省中考备考数学课件(共95张PPT)

一、总体思想
安徽省中考数学试卷一贯坚 持“考查基础,注重过程,渗透 思想,突出能力,强调应用,着 意创新”的指导思想,坚持 “稳中求变,变中求新”.
稳定第一,变化微小
多年来,安徽省数学中考试卷一直 保持全卷23题,其中选择题10题(1~ 10)、填空题4题(11~14)、解答题9 题(15~23),三种题型所占分数的百 分比平均为:27%,13%,60%. 全卷满 分150分,考试时间120分钟.
试题低、中、高三个档次
比基本保持为3:5:2,难度系 数能力保持在0.7左右;就数学
的代数、几何、概率统计三大板 块而言,代数占50%左右,几何 占38%左右,统计与概率12%左 右.
数学试卷的数学味越来越浓。 其实就是考虑数学的理性本质。
“数学课堂还是应该教数学”
顾泠沅教授,中国教育学会常务理事、学术 委员,全国数学教研会副理事长、学术委员会 主任。
⑴求AE和BD的长;
⑵若∠BAC=90°,△ABC的面积为S,求证: S=AE·BD
A
E
B
D
C
第20题图
模拟题及方法总结
第9题.如图,D、E分别是△ABC的边AB和AC上的点,设BC=a, AC=b,AB=c。
(1)当DE将△ABC分成周长相等的两部分, 且DE+BC=BD+CE,求DE的长; (2)当DE将△ABC分成周长相等的两部分, DE可否为AB的垂直平分线?请分析说明; (3)当DE将△ABC分成面积相等的两部 分,且a=5,b=12,c=13,求DE的最小值。
“兴趣产生动力,但不是所有的数学问题 对所有人都是有趣的”。
变化是对某一年来说的。对某一阶段来说 更大的特点是稳定,同时变化具有循环性。既 然稳定和循环,研究近期稳定循环的特点就显 得尤为重要。
安徽2021年中考专用数学课件 重难点突破三 多解题

22.(2019·六安霍邱县二模)如图,在矩形纸片 ABCD 中,AB=4,AD=8,现将纸片折叠,使点 B 与点 D 重合,再展开,折痕为线段 MN,点 P 在线段 MN 所在 直线上,若△PBD 的周长为 10+4 5,则 AP= _3__或___4_1_.
23.(2019·安庆一模)如图,△ABC 是一张等腰三角形纸 片,且 AB=AC=6,BC=4,将△ABC 沿着某条过一个顶点 的直线折叠,打开后再沿着所得到的折痕剪开,若剪开后 的两个三角形能够拼成一个与原△ABC 不全等的新三角形, 则折痕的长为___1_7_或__4___2__.
2.特殊图形的边不确定:①等腰三角形中的边分为底边和腰两种情 况;②直角三角形中的边分为直角边和斜边两种情况.
3.相似三角形中,未明确指明“一一对应”关系时,应考虑到所有 相似的情况.
4.图形的折叠、平移或旋转应充分考虑“方向性”,全面考虑是否 存在多解问题,防止漏解.
5.运用方程列等量关系时,若化简整理为一元二次方程,也会出现 多解情况.
2 (2)如图②所示,若 DA=DP,则 DP=8,在 Rt△BCD 中,BD= BC2+CD2 =10,∴BP=BD-DP=2.∵△PBE∽△DBC,∴PDEC=BBPD=15.∴PE=15CD=65. 综合以上两种情况从而得出结论.
【提分关键】几何图形中常见多解模型
1.特殊图形的角不确定:①等腰三角形中的角分为顶角和底角两种 情况;②直角三角形中的角分为直角和锐角两种情况;③平行四边形中 的角分为锐角和钝角两种情况.
7.如图所示,直线 y=x 与抛物线 y=x2-x-3 交于 A,B 两点,点 P 是抛物线上的一个动点,过点 P 作 PQ⊥x 轴交直线 y=x 于点 Q,设点 P 的横坐标为 m, 则线段 PQ 的长度随着 m 的增大而减小时 m 的取值范 围是____m_≤__-__1_或__1_≤__m_≤__3__.
中考数学《第36讲:分类讨论型问题》总复习讲解含真题分类汇编解析
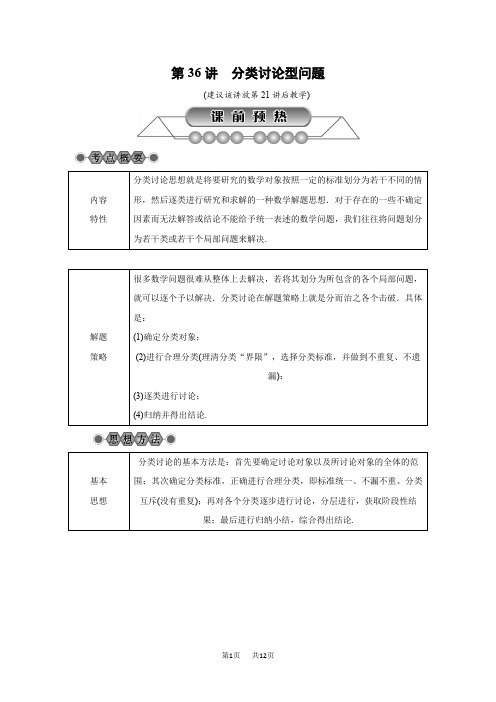
第36讲分类讨论型问题(建议该讲放第21讲后教学)内容特性分类讨论思想就是将要研究的数学对象按照一定的标准划分为若干不同的情形,然后逐类进行研究和求解的一种数学解题思想.对于存在的一些不确定因素而无法解答或结论不能给予统一表述的数学问题,我们往往将问题划分为若干类或若干个局部问题来解决.解题策略很多数学问题很难从整体上去解决,若将其划分为所包含的各个局部问题,就可以逐个予以解决.分类讨论在解题策略上就是分而治之各个击破.具体是:(1)确定分类对象;(2)进行合理分类(理清分类“界限”,选择分类标准,并做到不重复、不遗漏);(3)逐类进行讨论;(4)归纳并得出结论.基本思想分类讨论的基本方法是:首先要确定讨论对象以及所讨论对象的全体的范围;其次确定分类标准,正确进行合理分类,即标准统一、不漏不重、分类互斥(没有重复);再对各个分类逐步进行讨论,分层进行,获取阶段性结果;最后进行归纳小结,综合得出结论.类型一由计算化简时,运用法则、定理和原理的限制引起的讨论例1(·南通模拟)矩形一个角的平分线分矩形一边为1cm和3cm两部分,则这个矩形的面积为()A.3cm2B.4cm2C.12cm2D.4cm2或12cm2【解后感悟】解此题的关键是求出AB=AE,注意AE=1或3不确定,要进行分类讨论.1.(1)若关于x的函数y=kx2+2x-1与x轴仅有一个公共点,则实数k的值为____________________.(2)已知平面上有⊙O及一点P,点P到⊙O上一点的距离最长为6cm,最短为2cm,则⊙O的半径为cm.(3)若|a|=3,|b|=2,且a>b,则a+b=()A.5或-1 B.-5或1 C.5或1 D.-5或-1类型二在一个动态变化过程中,出现不同情况引起的讨论例2为了节约资源,科学指导居民改善居住条件,小王向房管部门提出了一个购买商品房的政策性方案.人均住房面积(平方米)单价(万元/平方米)不超过30(平方米)0.3超过30平方米不超过m平方米部分(45≤m≤60)0.5超过m平方米部分0.7根据这个购房方案:(1)若某三口之家欲购买120平方米的商品房,求其应缴纳的房款;(2)设该家庭购买商品房的人均面积为x平方米,缴纳房款y万元,请求出y关于x的函数关系式;(3)若该家庭购买商品房的人均面积为50平方米,缴纳房款为y万元,且57<y≤60时,求m的取值范围.【解后感悟】本题是房款=房屋单价×购房面积在实际生活中的运用,由于单价随人均面积而变化,所以用分段函数的解析式来描述.同时建立不等式组求解,解答本题时求出函数解析式是关键.2.(1)在平面直角坐标系中,直线y=-x+2与反比例函数y=1x的图象有唯一公共点,若直线y=-x+b与反比例函数y=1x的图象有2个公共点,则b的取值范围是()A.b>2 B.-2<b<2 C.b>2或b<-2 D.b<-2(2)如图,在平面直角坐标系中,四边形OBCD是边长为4的正方形,平行于对角线BD 的直线l从O出发,沿x轴正方向以每秒1个单位长度的速度运动,运动到直线l与正方形没有交点为止.设直线l扫过正方形OBCD的面积为S,直线l运动的时间为t(秒),下列能反映S与t之间函数关系的图象是()3.已知抛物线y1=ax2+bx+c(a≠0)与x轴相交于点A,B(点A,B在原点O两侧),与y轴相交于点C,且点A,C在一次函数y2=43x+n的图象上,线段AB长为16,线段OC长为8,当y1随着x的增大而减小时,求自变量x的取值范围.类型三由三角形的形状、关系不确定性引起的讨论例3(·湖州)如图,在平面直角坐标系xOy中,已知直线y=kx(k>0)分别交反比例函数y=1x和y=9x在第一象限的图象于点A,B,过点B作BD⊥x轴于点D,交y=1x的图象于点C,连结AC.若△ABC是等腰三角形,则k的值是________.【解后感悟】解题的关键是用k表示点A、B、C的坐标,再进行分类讨论.4.(1)在平面直角坐标系中,O为坐标原点,点A的坐标为(1,3),M为坐标轴上一点,且使得△MOA为等腰三角形,则满足条件的点M的个数为()A.4 B.5 C.6 D.8(2)(·北流模拟)如图,在Rt△ABC中,∠C=90°,AC=12,BC=6,一条线段PQ=AB,P、Q两点分别在AC和过点A且垂直于AC的射线AX上运动,要使△ABC和△QPA 全等,则AP=.(3)(·临淄模拟)如图,在正方形ABCD中,M是BC边上的动点,N在CD上,且CN=14CD ,若AB =1,设BM =x ,当x = 时,以A 、B 、M 为顶点的三角形和以N 、C 、M 为顶点的三角形相似.类型四 由特殊四边形的形状不确定性引起的讨论例4 (·鄂州模拟)如图1,在四边形ABCD 中,AD ∥BC ,AB =8cm ,AD =16cm ,BC =22cm ,∠ABC =90°,点P 从点A 出发,以1cm /s 的速度向点D 运动,点Q 从点C 同时出发,以3cm /s 的速度向点B 运动,其中一个动点到达端点时,另一个动点也随之停止运动,设运动时间为t 秒.(1)当t 为何值时,四边形ABQP 成为矩形?(2)当t 为何值时,以点P 、Q 与点A 、B 、C 、D 中的任意两个点为顶点的四边形为平行四边形?(3)四边形PBQD 是否能成为菱形?若能,求出t 的值;若不能,请说明理由,并探究如何改变Q 点的速度(匀速运动),使四边形PBQD 在某一时刻为菱形,求点Q 的速度.【解后感悟】解本题的关键是用方程(组)的思想解决问题,涉及四边形的知识,同时也是存在性问题,解答时要注意分类讨论及数形结合.5.(1)(·盐城模拟)在平面直角坐标系中有三点A(1,1),B(1,3),C(3,2),在直角坐标系中再找一个点D ,使这四个点构成平行四边形,则D 点坐标为 .(2)(·江阴模拟)如图,在等边三角形ABC 中,BC =6cm ,射线AG ∥BC ,点E 从点A 出发沿射线AG 以1cm /s 的速度运动,点F 从点B 出发沿射线BC 以2cm /s 的速度运动.如果点E 、F 同时出发,设运动时间为t(s ),当t = s 时,以A 、C 、E 、F 为顶点的四边形是平行四边形.(3) (·金华模拟)如图,B(6,4)在函数y =12x +1的图象上,A(5,2),点C 在x 轴上,点D 在函数y =12x +1上,以A 、B 、C 、D 四个点为顶点构成平行四边形,写出所有满足条件的D 点的坐标 .(4)(·萧山模拟)已知在平面直角坐标系中,点A 、B 、C 、D 的坐标依次为(-1,0),(m ,n),(-1,10),(-7,p),且p ≤n.若以A 、B 、C 、D 四个点为顶点的四边形是菱形,则n 的值是 .类型五 由直线与圆的位置关系不确定性引起的讨论例5 如图,已知⊙O 的半径为6cm ,射线PM 经过点O ,OP =10cm ,射线PN 与⊙O 相切于点Q.A 、B 两点同时从点P 出发,点A 以5cm /s 的速度沿射线PM 方向运动,点B 以4cm /s 的速度沿射线PN 方向运动.设运动时间为t(s ).(1)求PQ 的长;(2)当t 为何值时,直线AB 与⊙O 相切?【解后感悟】本题是直线与圆的位置关系应用,题目设置具有创新性.解决本题的关键是抓住直线与圆的两种情况位置关系,及其对应数量关系进行分析.6.(·泗洪模拟)如图,已知⊙P 的半径为2,圆心P 在抛物线y =12x 2-1上运动,当⊙P与x 轴相切时,圆心P 的坐标为 .【压轴把关题】如图,在平面直角坐标系中,点A ,B 的坐标分别是(-3,0),(0,6),动点P 从点O 出发,沿x 轴正方向以每秒1个单位的速度运动,同时动点C 从点B 出发,沿射线BO 方向以每秒2个单位的速度运动.以CP ,CO 为邻边构造▱PCOD ,在线段OP 延长线上取点E ,使PE =AO ,设点P 运动的时间为t 秒.(1)当点C 运动到线段OB 的中点时,求t 的值及点E 的坐标; (2)当点C 在线段OB 上时,求证:四边形ADEC 为平行四边形;(3)在线段PE 上取点F ,使PF =1,过点F 作MN ⊥PE ,截取FM =2,FN =1,且点M ,N 分别在第一、四象限,在运动过程中,设▱PCOD 的面积为S.①当点M ,N 中,有一点落在四边形ADEC 的边上时,求出所有满足条件的t 的值; ②若点M ,N 中恰好只有一个点落在四边形ADEC 内部(不包括边界)时,直接写出S 的取值范围.【方法与对策】本题是四边形的综合题,对于第(3)题解题的关键是正确分几种不同情况求解.①当点C在BO上时,第一种情况,当点M在CE边上时,由△EMF∽△ECO求解,第二种情况,当点N在DE边上时,由△EFN∽△EPD求解;【分类讨论应不重复、不遗漏】在△ABC中,P是AB上的动点(P异于A,B),过点P的一条直线截△ABC,使截得的三角形与△ABC相似,我们不妨称这种直线为过点P的△ABC的相似线.如图,∠A=36°,AB=AC,当点P在AC的垂直平分线上时,过点P的△ABC的相似线最多有________条.参考答案第36讲 分类讨论型问题【例题精析】例1 ∵四边形ABCD 是矩形,∴AB =CD ,AD =BC ,AD ∥BC ,∴∠AEB =∠CBE ,∵BE 平分∠ABC ,∴∠ABE =∠CBE ,∴∠AEB =∠ABE ,∴AB =AE ,①当AE =1cm 时,AB =1cm =CD ,AD =1cm +3cm =4cm =BC ,此时矩形的面积是1cm ×4cm =4cm 2;②当AE =3cm 时,AB =3cm =CD ,AD =4cm =BC ,此时矩形的面积是:3cm ×4cm =12cm 2;故选D .例2 (1)由题意,得三口之家应缴购房款为:0.3×90+0.5×30=42(万元); (2)由题意,得①当0≤x ≤30时,y =0.3×3x =0.9x ;②当30<x ≤m 时,y =0.9×30+0.5×3×(x -30)=1.5x -18;③当x >m 时,y =0.9×30+0.5×3(m -30)+0.7×3×(x -m)=2.1x -18-0.6m.∴y =⎩⎪⎨⎪⎧0.9x (0≤x ≤30)1.5x -18(30<x ≤m )2.1x -18-0.6m (x>m )(45≤m ≤60). (3)由题意,得①当50≤m ≤60时,y =1.5×50-18=57(舍).②当45≤m <50时,y =2.1×50-0.6m -18=87-0.6m.∵57<y ≤60,∴57<87-0.6m ≤60,∴45≤m <50.综合①②得45≤m <50.例3 ∵点B 是y =kx 和y =9x 的交点,y =kx =9x ,解得:x =3k ,y =3k ,∴点B 坐标为⎝⎛⎭⎫3k ,3k ,点A 是y =kx 和y =1x 的交点,y =kx =1x ,解得:x =1k ,y =k ,∴点A坐标为⎝⎛⎭⎫1k ,k ,∵BD ⊥x 轴,∴点C 横坐标为3k,纵坐标为13k=k3,∴点C 坐标为⎝ ⎛⎭⎪⎫3k ,k 3,∴BA ≠AC ,若△ABC 是等腰三角形,①AB =BC ,则⎝⎛⎭⎫3k -1k 2+(3k -k )2=3k -k 3,解得:k =377;②AC =BC ,则⎝⎛⎭⎫3k -1k 2+⎝⎛⎭⎫k 3-k 2=3k -k 3,解得:k =155;故答案为k =377或155.例4 (1)∵∠ABC =90°,AP ∥BQ ,∴当AP =BQ 时,四边形ABQP 成为矩形,由运动知,AP =t ,CQ =3t ,∴BQ =22-3t ,∴t =22-3t ,解得t =112.∴当t =112时,四边形ABQP成为矩形; (2)当P 、Q 两点与A 、B 两点构成的四边形是平行四边形时,就是(1)中的情形,此时t =112.当P 、Q 两点与C 、D 两点构成的四边形是平行四边形时,∵PD ∥QC ,∴当PD =QC 时,四边形PQCD 为平行四边形.此时,16-t =3t ,t =4;当P 、Q 两点与B 、D 两点构成的四边形是平行四边形时,同理,16-t =22-3t ,t =3;当P 、Q 两点与A 、C 两点构成的四边形是平行四边形时,同理,t =3t ,t =0,不符合题意;故当t =112或t =4或t =3时,以点P 、Q 与点A 、B 、C 、D 中的任意两个点为顶点的四边形为平行四边形. (3)四边形PBQD 不能成为菱形.理由如下:∵PD ∥BQ ,∴当PD =BQ =BP 时,四边形PBQD 能成为菱形.由PD =BQ ,得16-t =22-3t ,解得t =3,当t =3时,PD =BQ =13,AP =AD -PD =16-13=3.在Rt △ABP 中,AB =8,根据勾股定理得,BP =AB 2+AP 2=64+9=73≠13,∴四边形PBQD 不能成为菱形;如果Q 点的速度改变为v cm /s 时,能够使四边形PBQD 在时刻t s 为菱形,由题意得,⎩⎨⎧16-t =22-vt ,16-t =64+t 2,解得⎩⎪⎨⎪⎧t =6,v =2.故点Q 的速度为2cm /s 时,能够使四边形PBQD 在某一时刻为菱形.例5 (1)连结OQ ,∵PN 与⊙O 相切于点Q ,∴OQ ⊥PN ,即∠OQP =90°.∵OP =10,OQ =6,∴PQ =102-62=8(cm ). (2)过点O 作OC ⊥AB ,垂足为C.∵点A 的运动速度为5cm /s ,点B 的运动速度为4cm /s ,运动时间为t s ,∴PA =5t ,PB =4t.∵PO =10,PQ =8,∴PA PO =PB PQ =t2.∵∠P =∠P ,∴△PAB ∽△POQ ,∴∠PBA =∠PQO =90°.∵∠BQO =∠CBQ =∠OCB =90°,∴四边形OCBQ 为矩形,∴BQ =OC.∵⊙O 的半径为6,∴BQ =OC =6时,直线AB 与⊙O 相切.①当AB 运动到如图1所示的位置时,BQ =PQ -PB =8-4t ,由BQ =6,得8-4t =6,t =0.5.②当AB 运动到如图2所示的位置时,BQ =PB -PQ =4t -8,由BQ =6,得4t -8=6,t =3.5.综上,当t =0.5s 或3.5s 时,直线AB 与⊙O 相切.【变式拓展】1.(1)0或-1 (2)4或2 (3)C 2.(1)C (2)D3.根据OC 长为8可得一次函数中的n 的值为8或-8.分类讨论:①n =8时,易得A(-6,0),如图1,∵抛物线经过点A 、C ,且与x 轴交点A 、B 在原点的两侧,∴抛物线开口向下,则a <0,∵AB =16,且A(-6,0),∴B(10,0),而A 、B 关于对称轴对称,∴对称轴为直线x =-6+102=2,要使y 1随着x 的增大而减小,∵a <0,∴x ≥2;②n =-8时,易得A(6,0),如图2,∵抛物线过A 、C 两点,且与x 轴交点A ,B 在原点两侧,∴抛物线开口向上,则a >0,∵AB =16,且A(6,0),∴B(-10,0),而A 、B 关于对称轴对称,∴对称轴为直线x =6-102=-2,要使y 1随着x 的增大而减小,且a >0,∴x ≤-2.4.(1)C (2)6或12 (3)12或455.(1)(3,0)或(-1,2)或(3,4) (2)2或6 (3)(2,2)或(-6,-2)或(10,6) (4)2,5,186.(6,2)或(-6,2)【热点题型】【分析与解】(1)∵OB =6,C 是OB 的中点,∴BC =12OB =3.∴2t =3,即t =32s .∴OE =32+3=92,E(92,0). (2)如图1,连结CD 交OP 于点G ,在▱PCOD 中,CG =DG ,OG =PG ,∵AO =PE ,∴AG =EG .∴四边形ADEC 是平行四边形. (3)①(Ⅰ)当点C 在线段BO 上时,第一种情况:如图2,当点M 在CE 边上时,∵MF ∥OC ,∴△EMF ∽△ECO.∴MFCO=EF EO ,即26-2t =23+t,解得t =1.第二种情况:如图3,当点N 在DE 边时,∵NF ∥PD ,∴△EFN ∽△EPD.∴FN PD =EF EP 即16-2t =23,解得t =94.(Ⅱ)当点C 在BO 的延长线上时,第一种情况:如图4,当点M 在DE 边上时,∵MF ∥PD ,∴EMF ∽△EDP.∴MF DP =EF EP 即22t -6=23,解得t =92.第二种情况:如图5,当点N 在CE 边上时,∵NF ∥OC ,∴△EFN ∽△EOC.∴FN OC =EF EO 即12t -6=23+t ,解得t =5.综上所述,所有满足条件的t 的值为1,94,92,5.②278<S ≤92或272<S ≤20.【错误警示】当PD∥BC时,△APD∽△ABC,当PE∥AC时,△BPE∽△BAC,连结PC,∵∠A=36°,AB=AC,点P在AC的垂直平分线上,∴AP=PC,∠ABC=∠ACB =72°,∴∠ACP=∠PAC=36°,∴∠PCB=36°,∴∠B=∠B,∠PCB=∠A,∴△CPB ∽△ACB,故过点P的△ABC的相似线最多有3条.故答案为:3.。
中考数学复习解题方法突破+分类讨论课件

讲师:王保爱
2021年1Biblioteka 知识链接2021年
2
1. 涉及到分类定义概念和直接运用了分类研究的定理、性质、公式、法则的应用; 2. 含有的参变量的不同取值的分类应用; 3. 几何问题中几何图形的不确定的分类应用; 4. 由数学运算引起的分类应用.
2021年
3
直击中考
2021年
4
分情况讨论
2021年
12
例 4.(2013 年贵州黔西南 12 分)阅读材料: 小明在学习二次根式后,发现一些含根号的式子可以写成另一个
2021年
13
此课件下载后 可修改编辑
单击输入您的封面副标题
2021年
5
分情况讨论
2021年
6
分情况讨论
2021年
7
实战突破
2021年
8
【思想点拨】根据a的不同取值进行分类思考
2021年
9
【思想点拨】由等腰三角形中一条已知边对存在情况进行分类思考
2021年
10
【解析】 x2 (2k 1)x k 2 k 0
2021年
11
【思想点拨】分段函数的不同自变量取值进行分类思考
