广东省湛江市普通高中2017_2018学年高二数学下学期3月月考试题05
广东省湛江市普通高中2017-2018学年高二数学下学期3月月考试题01
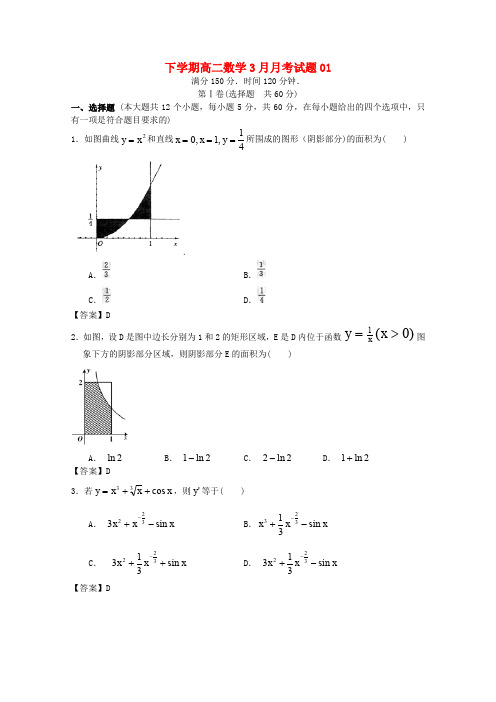
下学期高二数学3月月考试题01满分150分.时间120分钟. 第Ⅰ卷(选择题 共60分)一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.如图曲线2x y =和直线)的面积为( )A .B .C .D .【答案】D2.如图,设D 是图中边长分别为1和2的矩形区域,E 是D 象下方的阴影部分区域,则阴影部分E 的面积为( )A . 2lnB . 2ln 1-C . 2ln 2-D . 2ln 1+【答案】D3,则'y 等于( )A .BC .D .【答案】D4.一物体在力,2,4320,0)(⎩⎨⎧>+≤≤=x x x x F (单位:N)的作用下沿与力F 相同的方向,从x =0处运动到x =4(单位:m)处,则力F(x)作的功为( ) A .44 B .46 C .48 D .50【答案】B5.若0sin a xdx π=⎰,则二项式x 项的系数是( ) A .210 B .210-C .240D .240-【答案】C6( )A .223y e x e =-BC .2227y e x e =-D .222y e x e =- 【答案】B7.若函数()y f x =在区间(,)a b 内可导,且0(,)x a b ∈则的值为( ) A . '0()f xB . '02()f xC . '02()f x -D . 0【答案】B8.已知()ln f x x =,则()f e '的值为( )A .1B .-1C .eD 【答案】D9( )A . 1B . 2C .D . 3【答案】A10.某物体的运动方程为t t s +=23 ,那么,此物体在1=t 时的瞬时速度为( ) A . 4 ; B . 5 ;C . 6 ;D . 7【答案】D11图象上任意点处切线的斜率为k ,则k 的最小值是( )A . 1-B . 0C . 1D 【答案】A12( )A B C .0D 【答案】C第Ⅱ卷(非选择题 共90分)二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.定积分12n x e dx ⎰的值为 .【答案】114.已知函数()f x 在R 上满足22()(1)321f x f x x x +-=-+,则曲线()y f x =在点(1,(1))f 处的切线方程是 . 【答案】210x y --=15.一物体沿直线以()23(v t t t =-的单位:秒,v 的单位:米/秒)的速度做变速直线运动,则该物体从时刻t=0到5秒运动的路程s 为 米。
广东省湛江市普通高中2017_2018学年高二数学下学期3月月考试题03201804211179

下学期高二数学 3月月考试题 03满分 150分.时间 120分钟. 第Ⅰ卷(选择题 共 60分)一、选择题 (本大题共 12个小题,每小题 5分,共 60分,在每小题给出的四个选项中,只有 一项是符合题目要求的) 1.已知 f (x ) x 2 2xf ' (1) ,则 f ' (1) 等于()A . 0B .2 C .4 D . 2【答案】B 2.若函数 f (x )x 3 2x 2 1,则 f (1)( )A . 7B .1C .1D . 7【答案】C3.如下图,阴影部分的面积是()A . 2 3B . 2 3C . 32 3D .35 3【答案】C 4.若 f (x )xxln x ,则 f '(x )的解集为()A . (,)B . -(( ((+(C . (,)D . (- ,)【答案】C5.已知 f (x )=x 3 的切线的斜率等于 1,则其切线方程有( )A .1个B .2个C .多于两个D .不能确定【答案】B 6.过抛物线 y x 2 上的点 M(A .4B .31 1, )的切线的倾斜角为( )2 43 C .D .42【答案】C7.已知定义在 R 上的函数 f (x ) e x x 2 x sin x ,则曲线 yf (x ) 在点 (0, f (0)) 处的切线方程是( )A . yx 1 B . y 3x 2 C . y 2x 1 D . y2x 3- 1 -【答案】Ax 18.设曲线y在点(3,2)处的切线与直线 ax y 1 0垂直,则 a( )x 1A .2B .2C .1 D . 122【答案】B9.若曲线y与3在处的切线互相垂直,则x 0等于()x 21 y 1 x x x0等于( )A .3366 B .- 3366C .23 2 D . 或0 3【答案】A10.已知 a 0 函数 f (x )x 3 ax 在[1,)是单调增函数,则 a 的最大值是()A .0B .1C .2D .3【答案】D11.已知函数 f (x ) sin( x ) ,则要得到其导函数 y f '(x ) 的图象,只需将函数 y f (x )3的图象()22A .向左平移个单位B .向右平移个单位3 3C .向左平移 个单位D .向右平移 个单位22【答案】C12.如图所示,曲线 y x 2 和曲线 y x 围成一个叶形图(阴影部分),则该叶形图的面积是 ( )A .12B .14C .16D .13【答案】D第Ⅱ卷(非选择题 共 90分)二、填空题 (本大题共 4个小题,每小题 5分,共 20分,把正确答案填在题中横线上) 13.对于三次函数 f (x ) ax 3 bx 2 cx d ( a 0 ),定义:设 f (x )是函数 y =f(x)的导数 y = f(x ) 的导数,若方程 f (x )=0有实数解 x,则称点(x0,f(x0))为函数y=f(x)的“拐点”.有同学发现“任何一个三次函数都有‘拐点’;任何一个三次函数都有对称中心;且‘拐点’就是对称中心.”请你将这一发现为条件,函数()33231f x x x x,则它的对称中心为;24- 2 -1 2 3 2012 计算f () f ( ) f ( )f ( )=.2013 2013 2013 20131【答案】; 2012( ,1) 214.在曲线 y x 3 3x1的所有切线中,斜率最小的切线的方程为.【答案】y =3x +11 a15.对于函数 f (x ) | x 3| x 2(3 a ) | x | b ,若 f (x ) 有六个不同的单调区间,则 a3 2的取值范围为【答案】(0,3) 16.设函数 f (x )ax 3 bx 2 cx d 的图象在 x0处的切线方程 24x y 12 0 则c 2d【答案】0三、解答题 (本大题共 6个小题,共 70分,解答应写出文字说明,证明过程或演算步骤) 17.计算由曲线 y 2=2x,y=x-4所围成的图形的面积.【答案】首先根据曲线的方程画出图象(如图所示),确定出图形的范围,从而确定积分的上、下限,最后利用定积分求面积.为了确定图形的范围,先求出这两条曲线的交点坐标.x 2y2 ,解方程组得出交点坐标为(2,-2),(8,4). y x4.y 2y 2y3因此,所求图形的面积为 S=)4(y 4 )dx ( 4y 2 2 26a 318.已知函数 f (x ) 4ln x ax( a 0 )x(Ⅰ)讨论 f (x ) 的单调性;4=18.21(Ⅱ)当 a1时,设 g (x ) 2e x4x 2a ,若存在1g xx ,x[ ,2],使 f (x ) ( ) ,1 2 22求实数 a 的取值范围。
广东省湛江市普通高中2017-2018学年高二数学下学期3月月考试题09

下学期高二数学3月月考试题09一、选择题(本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、等差数列—3,1,5,…的第15项的值是( )A .40B .53C .63D .76 2、已知{a n }是等比数列,2512,4a a ==,则公比q=( )(A)21-(B)-2(C)2(D)21 3.在等差数列{}n a 中,3114a a +=,则此数列的前13项之和等于( )A .13B .26C .52D .1564.函数26x x y --=的定义域是( )(A))(2,3-(B) ),2[+∞(C) ]2,3[-(D)())(+∞⋃-∞-,23,5..若x ≠2或y ≠-1,M =x 2+y 2-4x +2y ,N =-5,则M 、N 的大小关系是( ) (A )M >N (B )M <N (C )M =N (D )不确定6.设等差数列{}n a 的前n 项和为n S ,若39S =,636S =,则789a a a ++=( )A .63B .45C .36D .27 7.已知)*n a n N =∈,则1210a a a +++L 的值为A 1B 1C 1D .28.{a n }为等差数列,若a 11a 10<-1,且它的前n 项和S n 有最小值,那么当S n 取得最小正值时,n=( )A .11B .17C .19D .20二、填空题(本大题共7小题,每小题5分,满分35分)9、已知f (x )=x 2—5x +6 则不等式f (x )>0的解集为10.、若数列{}n a 满足:111,2()n n a a a n N *+==∈,则5a = ;前8项的和8S = .(用数字作答)11、若数列{a n }的前n 项和S n =2n 2+n ,那么它的通项公式是12.己知不等式ax 2-5x+b>0的解集是{x|-3<x<-2},则不等式bx 2-5x+a<0的解集是_______.13、已知等差数列{}n a 的前n 项和为n S ,若1221S =,则25811a a a a +++= .14、设等差数列{}n a 的前n 项和为n S ,若535a a =则95S S = 15、定义:若数列{}n a 对任意的正整数n ,都有1||||n n a a d ++=(d 为常数),则称{}n a 为“绝对和数列”,d 叫做“绝对公和”,已知“绝对和数列”1{},2n a a =中,“绝对公和”2d =,则其前2010项和2010S 的最小值为三. 解答题(本大题共6小题,满分75分,解答题须写出文字说明,证明过程或演算步骤)16. (本小题满分12分) 等差数列{n a }的前n 项和记为S n .已知.50,302010==a a(Ⅰ)求通项n a ; (Ⅱ)求数列的前11项的和S 1117. (本小题满分12分)等比数列{n a }的前n 项和为n s ,已知1S ,3S ,2S 成等差数列 (1)求{n a }的公比q ; (2)求1a -3a =3,求n s18、(本小题满分12分)已知二次函数)(x f =c bx x ++2,且不等式0)(<x f 的解集为{}31<<x x 。
广东省湛江市普通高中2017_2018学年高二数学11月月考试题05

上学期高二数学11月月考试题05考试时间:120分钟总分:150分选择题:(本大题共10小题,每题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列给出的赋值语句中正确的是()A.3=A B. M= -M C. B=A=2 D. x+y=02.对于程序:试问,若输入m=-4,则输出的数为( )A.9 B.-7C.5或-7 D.53.图1中的程序框图的循环体执行的次数是()A. 49B.50 C.100 D.994、从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是( )(A) 至少1个白球,都是白球 (B) 至少1个白球,至少1个红球(C) 至少1个白球,都是红球 (D) 恰好1个白球,恰好2个白球5、用秦九韶算法求多项式654323567983512)(xxxxxxxf++++-+=的值,当4-=x图1时,4v 的值为( ) A .220 B .124 C .-845 D .-576、某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.每组命中个数的茎叶图如下.则下面结论中错误的一个是( ) A .甲的极差是29B .乙的众数是21 C .甲罚球命中率比乙高D .甲的中位数是247.是由一个圆、一个三角形和一个长方形构成的图形,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则相邻两个图形颜色不相同的概率为( ) A.34B.38C.14D.188.一个十字路口的交通信号灯,红灯、黄灯、绿灯亮的时间分别为30秒、5秒、60秒, 则某辆车到达路口,遇见绿灯的概率为( )A. 951B. 1912C. 1910D. 1919、下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是 A. 游戏1和游戏3 B.游戏1 C. 游戏2 D. 游戏310、甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a ,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中{},1,2,3,4,5,6a b∈,若1a b-≤,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( )A. 49 B.29 C.718D.19二.填空题:(每小题5分,共25分)11、已知程序如下,若 a = 35 ,则程序运行后结果是。
广东省湛江市普通高中2017-2018学年高二数学11月月考试题05

上学期高二数学11月月考试题05考试时间:120分钟总分:150分选择题:(本大题共10小题,每题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列给出的赋值语句中正确的是()A.3=A B. M= -M C. B=A=2 D. x+y=02.对于程序:试问,若输入m=-4,则输出的数为( )A.9 B.-7C.5或-7 D.53.图1中的程序框图的循环体执行的次数是()A. 49 B.50 C.100 D.994、从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是( )(A) 至少1个白球,都是白球 (B) 至少1个白球,至少1个红球(C) 至少1个白球,都是红球 (D) 恰好1个白球,恰好2个白球5、用秦九韶算法求多项式654323567983512)(xxxxxxxf++++-+=的值,当4-=x时,4v 的值为 ( ) A .220 B .124 C .-845D .-576、某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.每组命中个数的茎叶图如下.则下面结论中错误的一个是( ) A .甲的极差是29 B .乙的众数是21 C .甲罚球命中率比乙高 D .甲的中位数是247.是由一个圆、一个三角形和一个长方形构成的图形,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则相邻两个图形颜色不相同的概率为( ) A.34 B.38 C.14 D.188.一个十字路口的交通信号灯,红灯、黄灯、绿灯亮的时间分别为30秒、5秒、60秒, 则某辆车到达路口,遇见绿灯的概率为( )A. 951B. 1912C. 1910D. 1919、下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是 A. 游戏1和游戏3 B.游戏1 C. 游戏2 D. 游戏310、甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a ,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中{},1,2,3,4,5,6a b∈,若1a b-≤,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( )A. 49 B.29 C.718 D.19二.填空题:(每小题5分,共25分)11、已知程序如下,若 a = 35 ,则程序运行后结果是。
普通高中高二数学下学期3月月考试题09(2021学年)

广东省湛江市普通高中2017-2018学年高二数学下学期3月月考试题09 编辑整理:尊敬的读者朋友们:这里是精品文档编辑中心,本文档内容是由我和我的同事精心编辑整理后发布的,发布之前我们对文中内容进行仔细校对,但是难免会有疏漏的地方,但是任然希望(广东省湛江市普通高中2017-2018学年高二数学下学期3月月考试题09)的内容能够给您的工作和学习带来便利。
同时也真诚的希望收到您的建议和反馈,这将是我们进步的源泉,前进的动力。
本文可编辑可修改,如果觉得对您有帮助请收藏以便随时查阅,最后祝您生活愉快业绩进步,以下为广东省湛江市普通高中2017-2018学年高二数学下学期3月月考试题09的全部内容。
下学期高二数学3月月考试题09一、选择题(本大题共8小题,每小题5分,满分40分,在每小题给出的四个选项中,只有一项是符合题目要求的)1、等差数列-3,1,5,…的第15项的值是( )A.40B.53ﻩC.63D.762、已知{a n }是等比数列,2512,4a a ==,则公比q =( )ﻩ(A)21- (B)—2 ﻩﻩ(C)2 (D)213.在等差数列{}n a 中,3114a a +=,则此数列的前13项之和等于( )A.13 B .26ﻩ C.52ﻩD .1564.函数26x x y --=的定义域是( )(A))(2,3- (B) ),2[+∞ﻩ(C) ]2,3[- ﻩ(D)())(+∞⋃-∞-,23,5..若x≠2或y ≠-1,M =x 2+y2-4x+2y ,N =-5,则M、N的大小关系是( ) (A )M>N ﻩ(B )M <N ﻩ(C )M =N (D )不确定6.设等差数列{}n a 的前n 项和为n S ,若39S =,636S =,则789a a a ++=( )A .63 B.45 C.36 D.27 7.已知)*n a n N =∈,则1210a a a +++的值为1 B 1 ﻩC1 ﻩ D.28.{a n }为等差数列,若\f (a 11,a 10)<-1,且它的前n 项和S n有最小值,那么当S n 取得最小正值时,n =( )A.11B .17 C.19 D.20二、填空题(本大题共7小题,每小题5分,满分35分)9、已知f (x )=x 2—5x+6 则不等式f (x )〉0的解集为10.、若数列{}n a 满足:111,2()n n a a a n N *+==∈,则5a = ;前8项的和8S = 。
广东省湛江市普通高中2017_2018学年高二英语下学期3月月考试题05201804211190

下学期高二英语3月月考试题05第一部分:听力(共两节,满分20分)第一节(共5 小题;每小题1 分,满分5 分)听下面5段对话。
每段对话后有一个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有l0 秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
例:How much is the shirt?A.£19.15.B. £9.15.C.£9.18.答案是B。
1. What do we learn about the man?A. He slept well on the plane.B. He had a long trip.C. He had a meeting.2. Why will the woman stay home in the evening?A. To wait for a call.B. To watch a ball game on TV.C. To have dinner with afriend.3. What gift will the woman probably get for Mary?A. A school bag.B. A record.C. A theatre ticket.4. What does the man mainly do in his spare time?A. Learn a language.B. Do some sports.C. Play the piano.5. What did the woman like doing when she was young?A. Riding a bicycle with friends.B. Traveling the country.C. Reading alone.第二节(共15 小题;每小题 1 分,满分15 分)听下面5 段对话。
每段对话后有几个小题,从题中所给的A、B、C 三个选项中选出最佳选项,并标在试卷的相应位置。
广东省湛江市普通高中2017-2018学年高二数学11月月考试题03

上学期高二数学11月月考试题03一、选择题(本大题共10小题,每小题5分,共50分.在每小题给出的四个选项中,只有一项是符合题目要求的.)1. +10y -=的倾斜角是 ( )A .150º B.135º C.120º D.30º答案:C解析:直线斜率k =,则倾斜角为120º. 2. 下列说法中正确的有( )A .一组数据的平均数一定大于这组数据中的每个数据B .一组数据不可能有两个众数C .一组数据的中位数一定是这组数据中的某个数据D .一组数据的方差越大,说明这组数据的波动越大 答案:D解析:一组数据的平均数介于这组数据中的最大数据与最小数据之间,所以A 错;众数是一组数据中出现最多的数据,所以可以不止一个,B 错;若一组数据的个数有偶数个,则其中中位数是中间两个数的平均值,所以不一定是这组数据中的某个数据,C 错;一组数据的方差越大,说明这组数据的波动越大,D 对.3.抛掷一颗骰子,则事件“点数为奇数”与事件“点数大于5”是( )A .对立事件B .互斥事件但不是对立事件C .不是互斥事件D .以上答案都不对答案:B解析:事件“点数为奇数”即出现1点,3点,5点,事件“点数大于5”即出现6点,则两事件是互斥事件但不是对立事件. 4. 把(2)1010化为十进制数为( )A .20B .12C .10D .11答案:C3210(2)1010=12+02+12+02=10⨯⨯⨯⨯解析:5. 某程序框图如图1所示,现输入如下四个函数:则可以输出的函数是( ) A .2()f x x = B .()sin f x x =答案:B解析:有程序框图可知可以输出的函数既是奇函数,又要存在零点.满足条件的函数是B . 6. 设不等式组0202x y ≤≤⎧⎨≤≤⎩表示的平面区域为D ,在区域D 内随机取一个点,则此点到坐标原点的距离小于等于2的概率是( ) A .4π B .22π- C .6π D .44π- 答案:A解析:平面区域D 的面积为4,到坐标原点的距离小于等于2的点所到区域为π,有几何概型的概率公式可知区域D 内一个点到坐标原点的距离小于等于2的概率为4π. 7.采用系统抽样方法从960人中抽取32人做问卷调查,为此将他们随机编号为1,2,…,960,分组后在第一组采用简单随机抽样的方法抽到的号码为9.抽到的32人中,编号落入区间[]1,450的人做问卷A ,编号落入区间[]451,750的人做问卷B ,其余的人做问卷C .则抽到的人中,做问卷B 的人数为( ) A .7 B .9 C .10D .15 答案:C解析:方法一:从960中用系统抽样抽取32人,则每30人抽取一人,因为第一组号码为9,则第二组为39,公差为30.所以通项为2130)1(309-=-+=n n a n ,由7502130451≤-≤n ,即302125302215≤≤n ,所以25,17,16 =n ,共有1011625=+-人.方法二:总体中做问卷A 有450人,做问卷B 有300人,做问卷C 有210人,则其比例为15:10:7.抽到的32人中,做问卷B 有10321032=⨯人. 8.如图2等腰三角形和菱形,则该几何体体积为( )A . . C .4 D .2 答案:A解析:有三视图可知几何体是底面为菱形,对角线分别为2和图2面菱形对角线的交点,高为3,所以体积为11V=232⨯⨯⨯9.如图3是某算法的程序框图,则程序运行后输入的结果是( )A .1B .2C .3D .4 答案:C解析:当1,1,1;k a T === 当2,0,1;k a T ===当3,0,1;k a T ===当4,1,2;k a T ===当5,1,3k a T ===,则此时=16k k +=,所以输出T=3. 10.函数y =能成为该等比数列的公比的数是( ) A .34B C答案:D解析:函数等价为0,9)5(22≥=+-y y x ,表示为圆心在)0,5(半径为3的上半圆,圆上点到原点的最短距离为2,最大距离为8,若存在三点成等比数列,则最大的公比q 应有228q =,即2,42==q q ,最小的公比应满足282q =,所以21,412==q q ,所以公比的取值范围为221≤≤q 不可能成为该等比数列的公比. 二、填空题(本大题共5小题,每小题5分,共25分.把答案填在答题卡的相应位置上.)11.点B 是点A (1,2,3)在坐标面xOy 内的射影,其中O 为坐标原点,则OB 等于 ________.解析:点B 是点A (1,2,3)在坐标面xOy 内的射影,可知B (1,2,0),有空间两点的距离公式可知=5OB .12.从一堆苹果中任取10只,称得它们的质量如下(单位:克): 125 120 122 105 130114 116 95 120 134,则样本数据落在[)114124, 内的频率为________. 答案:0.7解析:样本数据落在[)114124, 内有7个,所以频率为0.7. 13.在平面直角坐标系中,设直线:0l kx y -+=与圆22:4C x y +=相交于A 、B 两点,M 为弦AB 的中点,且C 1M =,则实数k =________. 答案:1±解析:有圆的性质可知CM AB ⊥,又C 1M =,有点到直线距离公式可得1k =±. 14.某城市缺水问题比较突出,为了制定节水管理办法,对全市居民某年的月均用水量进行了抽样调查,其中4位居民的月均用水量 分别为1234,,,x x x x (单位:吨).根据如图4所示的程序框图, 若1234,,,x x x x 分别为1, 2,3, 4,则输出的结果S 为________. 答案:52解析:有算法的程序框图的流程图可知输出的结果S 为1234,,,x x x x 的平均值, 即为1+2+3+45=42. 15.设11(,)M x y ,22(,)N x y 为不同的两点,直线:0l ax by c ++=,1122ax by cax by cδ++=++,以下命题中正确的序号为 . ①不论δ为何值,点N 都不在直线l 上; ②若1δ=,则过M ,N 的直线与直线l 平行; ③若1δ=-,则直线l 经过MN 的中点;④若1δ>,则点M 、N 在直线l 的同侧且直线l 与线段MN 的延长线相交. 答案:①②③④解析:不论δ为何值,220ax by c ++≠,点N 都不在直线l 上,①对;若1δ=,则1212)()0a x x b y y -+-=(,即1212=MN l y y ak k x x b-==--,过M ,N 的直线与直线l 平行, ②对;若1δ=-则12121212+)(+)+)(+)+20+022x x y y a x x b y y c a b c +=⇒+=((,直线l 经过MN 的中点, ③对;点M 、N 到直线l的距离分别为12d d ==,若1δ>,则112212++ax by c ax by c d d +>+⇒>,且1122+(+ax by c ax by c ++())>0,即点M 、N 在直线l 的同侧且直线l 与线段MN 的延长.图4三、解答题(本大题共6小题,共75分.解答应写出文字说明,证明过程或演算步骤.) 16.(本题满分12分)某市对排污水进行综合治理,征收污水处理费,系统对各厂一个月内排出的污水量x 吨收取的污水处理费y 元,运行程序如图5所示: (Ⅰ)写出y 与x 的函数关系;(Ⅱ)求排放污水150吨的污水处理费用. 16解:(Ⅰ)y 与x 的函数关系为:…………8分(Ⅱ)因为150100,m =>所以15025(150100)1400y =+-=,故该厂应缴纳污水处理费1400元. …………12分17.(本题满分12分)已知向量(,1)a x =-,(3,)b y =,其中x 随机选自集合{1,1,3}-,y 随机选自集合{1,39},. (Ⅰ)求//a b 的概率; (Ⅱ)求a b ⊥的概率.17解析:则基本事件空间包含的基本事件有:(-1,1),(-1,3),(-1,9),(1,1),(1,3),(1,9),(3,1),(3,3),(3,9),共9种. …2分(Ⅰ)设“//a b ”事件为A ,则3xy =-. 事件A 包含的基本事件有(-1,3), 共1种. ∴//a b 的概率为()19P A =. …7分 (Ⅱ)设“a b ⊥” 事件为B ,则3y x =.事件A 包含的基本事件有(1,3), (3,9),共2种. ∴a b ⊥的概率为()29P B =. ………12分 18.(本题满分12分)如图6是歌手大奖赛中,七位评委给甲、乙两名选手打出的分数的茎叶图.(Ⅰ)现将甲、乙所得的一个最高分和一个最低分均去掉后,分别求甲、乙两名选手得分的众数,中位数,平均数;50131005015(50)15025(100)INPUT xIF x THEN y x ELSEIF x THEN y x ELSEy x END IF END IF END≤=≤=+-=+-图 566图613(50)5015(50)(50100)15025(100)(100)m m y m m m m ≤⎧⎪=+-<≤⎨⎪+->⎩(Ⅱ)在(Ⅰ)的条件下用方差说明甲、乙成绩的稳定性.(注:方差2222121[()()()]n s x x x x x x n=-+-+⋅⋅⋅+-,其中x ,为数据12,,,n x x x ⋅⋅⋅的平均数)18.解析:将甲、乙所得的一个最高分和一个最低分均去掉后,甲的分数为85,84,85,85,86;乙的分数为84,84,86,84,87. ……2分(Ⅰ)甲的众数,中位数,平均数分别为85,85,85;乙的众数,中位数,平均数分别为84,84,85. ………6分(Ⅱ)在(Ⅰ)的条件下,甲的方差为2222212[(8585)(8485)(8585)+(8585)+(8685)]=55-+-+---,乙的方差为2222218[(8485)(8485)(8685)+(8485)+(8785)]=55-+-+---.……10分甲的方差比乙的方差小,则甲的成绩稳定些. ………12分19.(本题满分12分)某校从高二年级学生中随机抽取60名学生,将其期中考试的政治成绩(均为整数)分成六段: [)40,50,[)50,60,…, []90,100后得到如下频率分布直方7. (Ⅰ)求分数在[)70,80内的频率;(Ⅱ)根据频率分布直方图,估计该校高二年级学生期中考试政治成绩的平均分;(Ⅲ)用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本,将该样 本看成一个总体,从中任意选取2人, 求其中恰有1人的分数不低于90分的概率. 19解析:(Ⅰ)分数在[)80,70内的频率为:1(0.0100.0150.0150.0250.005)1010.70.3-++++⨯=-= …3分(Ⅱ)平均分为:450.1550.15650.15750.3850.25950.0571x =⨯+⨯+⨯+⨯+⨯+⨯=……7分(Ⅲ)由题意,[)90,80分数段的人数为:0.256015⨯=人[]100,90分数段的人数为:0.05603⨯=人; ……9分∵用分层抽样的方法在80分以上(含80分)的学生中抽取一个容量为6的样本, ∴[)90,80分数段抽取5人,分别记为A ,B ,C ,D ,E ;[]100,90分数段抽取1人, 记为M. 因为从样本中任取2人,其中恰有1人的分数不低于90分,则另一人的图7分数一定是在[)90,80分数段,所以只需在分数段[)90,80抽取的5人中确定1人. 设“从样本中任取2人,其中恰有1人的分数不低于90分为”事件A , 则基本事件空间包含的基本事件有:(A ,B),(A ,C),(A ,D),(A ,E),(B ,C), (B ,D),(B ,E),(C ,D),(C ,E),(D ,E),(A ,M),(B ,M),(C ,M),(D ,M), (E ,M)共15种.事件A 包含的基本事件有(A ,M ),(B ,M ),(C ,M ),(D ,M ),(E ,M )5种. ∴恰有1人的分数不低于90分的 概率为()51.153P A ==. ……12分 20.(本题满分13分)如图8,圆柱1OO 内有一个三棱柱111ABC A B C -,三棱柱的底面为圆柱底面的内接三角形,且AB 是圆O 直径. (Ⅰ)证明:平面11A ACC ⊥平面11B BCC ;(Ⅱ)设12AB AA ==,在圆柱1OO 内随机选取一点,记该点取自于三棱柱111ABC A B C -内的概率为p . (i )当点C 在圆周上运动时,求p 的最大值;(ii )当p 取最大值时,求直线1CB 与平面11C COO 所成的角的正弦值. 20解析:(Ⅰ)因为1AA ⊥平面ABC ,BC ⊂平面ABC ,所以1AA ⊥BC ,因为AB 是圆O 直径,所以BC ⊥AC ,又AC ⋂1AA A =,所以BC ⊥平面11A ACC , 而11BC B BCC ⊂,所以平面11A ACC ⊥平面11B BCC . ……3分 (Ⅱ)(i )有AB=AA 1=2,知圆柱的半径=1r ,其体积2V=22r r ππ⋅=三棱柱111ABC-A B C 的体积为11V =BC AC 2BC AC 2r ⋅⋅=⋅,又因为222BC +AC =AB =4,所以22BC +AC BC AC =22⋅≤,当且仅当时等号成立,从而1V 2≤, 故11V p V π=≤当且仅当,即OC AB ⊥时等号成立, 所以p 的最大值是1π. ………8分(ii )由(i )可知,p 取最大值时,OC AB ⊥,即1111O C O B ⊥ , 111O O O B ⊥图8则11O B ⊥平面11C COO ,连1O C ,则11O CB ∠为直线1CB 与平面11C COO 所成的角,则11111sin O CB O B CB ∠=…………13分21.(本题满分14分)在平面直角坐标系xOy 中,已知圆221:(1)1C x y ++=,圆222:(3)(4)1C x y -+-=. (Ⅰ)若过点1(1,0)C -的直线l 被圆2C 截得的弦长为65, 求直线l 的方程;(Ⅱ)设动圆C 同时平分圆1C 的周长、圆2C 的周长,如图9(i )证明:动圆圆心C 在一条定直线上运动;(ii )动圆C 是否经过定点?若经过,求出定点的坐标;若不经过,请说明理由.21 解析:(Ⅰ)设直线l 的方程为(1)y k x =+,即0kx y k -+=.因为直线l 被圆2C 截得的弦长为65,而圆2C 的半径为1,所以圆心2(3 4)C ,到l :0kx y k -+=244451k k -=+.化简,得21225120k k -+=,解得43k =或34k =.所以直线l 的方程为4340x y -+=或3430x y -+=. ……4分(Ⅱ)(i )证明:设圆心( )C x y ,,由题意,得12CC CC =, .化简得30x y +-= 即动圆圆心C 在定直线30x y +-=上运动. …………8分(ii )圆C 过定点,设(3)C m m -,,则动圆C于是动圆C 的方程为222()(3)1(1)(3)x m y m m m -+-+=+++-整理,得22622(1)0x y y m x y +----+=.图9由2210 620x y x y y -+=⎧⎨+--=⎩,,得1 2x y ⎧=⎪⎨⎪=⎩或1 2x y ⎧=⎪⎨⎪=⎩所以定点的坐标为(1,(1++. ……14分。
【配套K12】广东省湛江市普通高中2017-2018学年高二数学下学期3月月考试题07

下学期高二数学3月月考试题07一.选择题:本大题共10小题,每小题3分,共30分,在每小题给出的四个选项中,只有一项是符合题目要求的.1.若a b >且c R ∈,则下列不等式中一定成立的是A .ac bc >B .22a b > C .a c b c +>+ D .22ac bc >2.设数列,,,,…,则是这个数列的A.第6项B.第7项C.第8项D.第9项 3.已知条件2:=x p ,条件0)3)(2(:=--x x q ,则p 是q 的 A.充分不必要条件 B .必要不充分条件 C .充要条件 D .既不充分也不必要条件 4.(理)在等差数列{a n }中,已知a 5=3,a 9=6,则a 13=A .9B .12C .15D .18 (文)1与5两数的等差中项是A .1B . 3C .2D .3±5.椭圆x 225 +y29 =1上一点P 到一个焦点的距离为5,则P 到另一个焦点的距离为A 、10B 、6C 、5D 、46.已知ABC ∆中,C B A 、、所对的边分别为c b a 、、,且ο60,3,2===B b a ,那么角A 等于A.ο30 B .ο45 C .ο135 D .οο45135或7.若实数x y ,满足1000x y x y x ⎧-+⎪+⎨⎪⎩,,,≥≥≤则2z x y =+的最小值是A . 0B .21 C .1 D . 28.抛物线 22y x -=的准线方程是A .21=y B .81=y C .41=x D .81=x9.(理)如图,在棱长为2的正方体ABCD —A 1B 1C 1D 1中,O 是底面ABCD 的中心,E 、F 分别是CC 1、AD 的中点.那么异面直线OE 和FD 1所成角的余弦值为 A.105B.155C.45D.23(文)曲线2+=x xy 在点)1,1(--处的切线方程是 A.12+=x y B.12-=x y C.32--=x y D.22--=x y10.已知直线l 过抛物线C 的焦点,且与C 的对称轴垂直,l 与C 交于A ,B 两点,||12AB =,P 为C 的准线上一点,则ABP ∆的面积为A.18B.24C. 36D. 48二、填空题:本大题共5小题,每小题4分,满分20分.11.命题2,240x R x x ∀∈-+≤的否定为12.已知双曲线的方程为2213y x -=,则它的离心率为______.13.函数322++-=x x y 的定义域是14.等比数列}{n a 中0>n a ,且243879236a a a a a a ++=,则38a a += .15.曲线C 是平面内与两个定点1(1,0)F -和2(1,0)F 的距离的积等于常数2(1)a a >的点的轨迹,给出下列三个结论: ①曲线C 过坐标原点;②曲线C 关于坐标原点对称;③若点P 在曲线C 上,则12F PF ∆的面积不大于212a . 其中,所有正确结论的序号是____ _____三、解答题:本大题共6小题,满分50分。
广东省湛江市普通高中2017-2018学年高二数学11月月考试题05

上学期高二数学11月月考试题05考试时间:120分钟总分:150分选择题:(本大题共10小题,每题5分,共50分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.下列给出的赋值语句中正确的是()A.3=A B. M= -M C. B=A=2 D. x+y=02.对于程序:试问,若输入m=-4,则输出的数为( )A.9 B.-7C.5或-7 D.53.图1中的程序框图的循环体执行的次数是()A. 49 B.50 C.100 D.994、从装有2个红球和2个白球的口袋里任取2个球,那么互斥而不对立的两个事件是( )(A) 至少1个白球,都是白球 (B) 至少1个白球,至少1个红球(C) 至少1个白球,都是红球 (D) 恰好1个白球,恰好2个白球5、用秦九韶算法求多项式654323567983512)(xxxxxxxf++++-+=的值,当4-=x图1时,4v 的值为 ( ) A .220 B .124 C .-845D .-576、某篮球队甲、乙两名运动员练习罚球,每人练习10组,每组罚球40个.每组命中个数的茎叶图如下.则下面结论中错误的一个是( ) A .甲的极差是29 B .乙的众数是21 C .甲罚球命中率比乙高 D .甲的中位数是247.是由一个圆、一个三角形和一个长方形构成的图形,现用红、蓝两种颜色为其涂色,每个图形只能涂一种颜色,则相邻两个图形颜色不相同的概率为( ) A.34 B.38 C.14 D.188.一个十字路口的交通信号灯,红灯、黄灯、绿灯亮的时间分别为30秒、5秒、60秒, 则某辆车到达路口,遇见绿灯的概率为( )A. 951B. 1912C. 1910D. 1919、下面有三个游戏规则,袋子中分别装有球,从袋中无放回地取球,问其中不公平的游戏是 A. 游戏1和游戏3 B.游戏1 C. 游戏2 D. 游戏310、甲、乙两人玩猜数字游戏,先由甲心中想一个数字,记为a ,再由乙猜甲刚才所想的数字,把乙猜的数字记为b,其中{},1,2,3,4,5,6a b∈,若1a b-≤,就称甲乙“心有灵犀”.现任意找两人玩这个游戏,则他们“心有灵犀”的概率为 ( )A. 49 B.29 C.718 D.19二.填空题:(每小题5分,共25分)11、已知程序如下,若 a = 35 ,则程序运行后结果是。
数学-广东省湛江市普通高中2017-2018学年下学期高二3月月考试题05

广东省湛江市普通高中2017-2018学年下学期高二3月月考试题05满分150分.时间120分钟.第Ⅰ卷(选择题共60分)一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数存在与直线平行的切线,则实数的取值范围是( ) A.B.C.D.2.下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是( ) A.B.C.D.3.若,则等于( )A.B.C.D.4.若函数,则( )A.B.1 C.D.5.若函数f(x)=x2+bx+c的图象的顶点在第四象限,则函数f /(x)的图象是( )6.对任意,函数不存在极值点的充要条件是( ) A.B.C.或D.或7.函数的导数为( )A.B.C.D.8.将和式的极限表示成定积分( ) A.B.C.D.9.已知二次函数的导数,且的值域为,则的最小值为( )A.3 B.C.2 D.10.变速运动的物体的速度为(其中为时间,单位:),则它在前内所走过的路程为( )A.B.C.D.11.下列求导运算正确的是( )A.B.C.D.12.用边长为6分米的正方形铁皮做一个无盖的水箱,先在四角分别截去一个小正方形,然后把四边翻转,再焊接而成(如图)。
设水箱底面边长为分米,则( )A.水箱容积最大为立方分米B.水箱容积最大为立方分米C.当在时,水箱容积随增大而增大D.当在时,水箱容积随增大而减小第Ⅱ卷(非选择题共90分)二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.一个物体的运动方程为其中的单位是米,的单位是秒,那么物体在秒末的瞬时速度是米/秒.14.若,则____________.15.曲线在点处的切线方程是,若+=0,则实数a=16.直线是曲线的一条切线,则实数b=____________。
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)17.2008年奥运会在中国召开,某商场预计2008 年从1月份起前.x.个月..,顾客对某种商品的需求总量....件与月份的近似关系是:该商品的进价元与月份的近似关系是:(1)写出今年第.x.个月..的需求量件与月份x的函数关系式;(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,则此商场今年销售该商品的月利润预计最大是多少元?18.已知函数在处取得极值为(1)求a、b的值;(2)若有极大值28,求在上的最大值.19.已知函数(),.(Ⅰ)当时,解关于的不等式:;(Ⅱ)若恒成立,求实数的取值范围;(Ⅲ)当时,记,过点是否存在函数图象的切线?若存在,有多少条?若不存在,说明理由;20.张林在李明的农场附近建了一个小型工厂,由于工厂生产须占用农场的部分资源,因此李明每年向张林索赔以弥补经济损失并获得一定净收入.工厂在不赔付农场的情况下,工厂的年利润(元)与年产量(吨)满足函数关系.若工厂每生产一吨产品必须赔付农场元(以下称为赔付价格).(1)将工厂的年利润(元)表示为年产量(吨)的函数,并求出工厂获得最大利润的年产量;(2)若农场每年受工厂生产影响的经济损失金额(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格是多少?21.用总长14.8m的钢条制作一个长方形容器的框架,如果容器底面的一边比另一边长0.5m,那么高为多少时这个容器的容积最大?并求出最大容积22.某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务部门上交元(为常数,2≤a≤5 )的税收。
广东省湛江市普通高中2017-2018学年高二第二学期3月月考英语试卷03

下学期高二英语3月月考试题03第Ⅰ卷(选择题满分70分)一、听力(共两节,满分17分)第一节(共5小题;每小题1分,满分5分)听下面5段对话,每段对话后有一个小题,从题中所给的A, B, C三个选项中选出最佳选项,并标在试卷的相应位置。
听完每段对话后,你都有10秒钟的时间来回答有关小题和阅读下一小题。
每段对话仅读一遍。
1.What was the weather like yesterday?A. Rainy.B. Sunny.C. Cloudy.2.When did the woman go to London?A. Last June.B. Last July.C. This July.3.What did the man think of the history lecture?A. It was great.B. It was boring.C. It was difficult to follow. 4.What do we know about the man?A. He is a fireman.B. His son wants to be a policeman.C. His son is having a birthday soon.5.Why did the woman fail the math exam?A. She didn’t study very hard.B. The exam was too difficult.C. She was sick that day.第二节:(共12小题;每小题1分, 满分12分)听下面四段对话或独白,每段对话或独白后有几个小题,从题中所给的A、B、C三个选项中选出最佳选项,并标在试卷的相应位置。
听每段对话或独白前,你都有时间阅读各个小题,每小题5秒钟;听完后,各小题将给出5秒钟的作答时间。
每段对话或独白读两遍。
听第6段材料,回答6、7题。
广东湛江市普通高中2016-2017学年下学期高二数学4月月

湛江市普通高中2016-2017学年下学期高二数学4月月考试题03(考试时间:120分钟 总分:150分)一、选择题(本题共12个小题,每小题5分,共60分。
在每小题给出的四个选项中,只有一项是符合题目要求的)1、在复平面内,点)1(2i ,所对应的复数是( ) A 、i +1 B 、i -1 C 、i +-1D 、i --12、在下列四组框图中,是工序流程图的是( )(1(3)(4)A 、(2)(4)B 、(1)(3)C 、(2)(3)D 、(1)(4)3、甲、乙两同学投篮进球的概率分别是43和54,现甲、乙各投篮一次,都不进球的概率是( ) A 、53B 、52 C 、203 D 、2014、已知幂函数αx x f =)(是增函数,而1-=x y 是幂函数,所以1-=x y 是增函数,上面推理错误是( )A 、大前提错误导致结论错B 、小前提错误导致结论错C 、推理的方式错误导致错D 、大前提与小前提都错误导致错5、在对某样本进行实验时,测得如下数据:则y 与x 之间的回归直线方程为( )A 、1ˆ+=x yB 、2ˆ+=x yC 、12ˆ+=x yD 、1ˆ-=x y6.在[]1,1-上任取两数x 和y 组成有序数对()y x ,,记事件A 为“122<+y x ”,则=)(A P ( )A 、4π B 、2πC 、πD 、π2 7、下列说法中正确的是( )A 、满足方程0)(='x f 的x 值为函数)(x f 的极值点B 、“0=m ”是“复数)()1()(2R m i m m m z ∈++-=为纯虚数”的充要条件C 、由“311321211,211211-=⨯+⨯-=⨯,……”,推出 “nn 11)1(1321211-=-+⋅⋅⋅+⨯+⨯”的过程是演绎推理 D 、“若c b a 、、成等差数列,则c a b +=2”类比上述结论:若c b a 、、成等比数列,则ac b =2.8、已知双曲线1222=-y ax 的一个焦点与抛物线x y 342=的焦点相同,则双曲线的渐近线方程是( )A 、x y 2±=B 、x y 2±=C 、x y 22±=D 、x y 21±= 9、已知函数3)(-=x xe x g 在点A 处的切线垂直于y 轴,则点A 的横坐标是( )A 、1B 、-1C 、e1D 、e10、设抛物线281x y =上一点P 到y 轴的距离为4,则点P 到该抛物线焦点的距离是( ) A 、4B 、6C 、8D 、1211、函数x a ax x x f 2233231)(+-=在)10(,内有极小值,则实数a 的取值范围是( ) A 、),0(+∞ B 、)3,(-∞ C 、(0 ,31) D 、)23,0(12、阅读如图所示程序框图,运行相应的程序(i 为虚数单位),则输出的S 的值为( )A 、-1B 、1C 、iD 、0二、填空题(每小题4分,共16分)13、已知复数z ,满足)3(43i iz z -=+,则=||z __________。
广东省湛江一中2017-2018学年高二下学期第一次月考数学试卷(文科) Word版含解析

2017-2018学年广东省湛江一中高二(下)第一次月考数学试卷(文科)一、选择题(本题共12小题,每小题5分,总分60分;每个小题仅有一个最恰当的选项)1.复数i(2﹣i)=()A.1+2i B.1﹣2i C.﹣1+2i D.﹣1﹣2i2.已知x>0,函数y=+x的最小值是()A.5 B.4 C.8 D.63.在△ABC中,sinA:sinB:sinC=3:2:4,则cosC的值为()A.B.C. D.4.已知数列{a n}满足a n+1=a n﹣1(n∈N+),且a2+a4+a6=18,则a5的值为()A.8 B.7 C.6 D.55.下列说法正确的是()A.“若x2=1,则x=1”的否为“若x2=1,则x≠1”B.“∀x≥0,x2+x﹣1<0”的否定是“∃x0<0,x02+x0﹣1≥0”C.“若x=y,则sin x=sin y”的逆否为假D.若“p∨q”为真,则p,q中至少有一个为真6.“|x﹣1|<2成立”是x(3﹣x)>0“成立”的()A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件7.等比数列{a n}的各项均为正数,且a5a6+a4a7=18,则log3a1+log3a2+…log3a10=()A.12 B.10 C.8 D.2+log358.下列各对曲线中,即有相同的离心率又有相同渐近线的是()A.=1和=1 B.=1和y2﹣=1C.y2﹣=1和x2﹣=1 D.=1和=19.设函数f (x)在定义域内可导,y=f (x)的图象如图所示,则导函数y=f′(x)的图象可能是()A. B.C.D.10.由不等式组确定的平面区域记为M,若直线3x﹣2y+a=0与M有公共点,则a的最大值为()A.﹣3 B.1 C.2 D.411.在平面上,若两个正三角形的边长之比1:2,则它们的面积之比为1:4,类似地,在空间中,若两个正四面体的棱长之比为1:2,则它的体积比为()A.1:4 B.1:6 C.1:8 D.1:912.函数f(x)=x+在(﹣∞,﹣1)上单调递增,则实数a的取值范围是()A.[1,+∞)B.(﹣∞,0)∪(0,1]C.(0,1]D.(﹣∞,0)∪[1,+∞)二、填空题(每空5分,共20分)之间的几组数据如表:则由表数据所得线性回归直线必过点..抛物线的焦点坐标是.15.将全体正整数排成一个三角形数阵;根据以上排列规律,数阵中第n(n≥3)行从左至右的第3个数是.16.如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为.三、解答题:解答应写出文字说明、证明过程或演算步骤17.在△ABC中,a,b,c分别是角A,B,C的对边,已知3(b2+c2)=3a2+2bc.(1)求sinA;(2)若a=,△ABC的面积S=,且b>c,求b,c.18.在数列{a n}中,a1=1,a n=a n+c(c为常数,n∈N*),且a1,a2,a5成公比不等于1的+1等比数列.(Ⅰ)求c的值;(Ⅱ)设b n=,求证:若数列{b n}的前n项和为S n,则≤S n<.19.某学校的课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩如下表所示:若单科成绩在85分以上(含85分),则该科成绩为优20.如图,椭圆C :+=1(a >b >0)经过点P (2,3),离心率e=,直线1的方程为y=4.(Ⅰ)求椭圆C 的方程;(Ⅱ)AB 是经过(0,3)的任一弦(不经过点P ),设直线AB 与直线l 相交于点M ,记PA ,PB ,PM 的斜率分别为k 1,k 2,k 3.问:是否存在常数λ,使得十=?若存在,求λ的值.21.已知函数f (x )=lnx ,g (x )=﹣bx ,设h (x )=f (x )﹣g (x ).(1)求函数F (x )=f (x )﹣x 的极值;(2)若g (2)=2,若a <0,讨论函数h (x )的单调性;(3)若函数g(x)是关于x的一次函数,且函数h(x)有两个不同的零点x1,x2,求b的取值范围.请在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-1:几何证明选讲](共1小题,满分10分)22.如图,C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB平分线DC交AE 于点F,交AB于D点.(Ⅰ)求∠ADF的度数;(Ⅱ)若AB=AC,求AC:BC.[选修4-4:坐标系与参数方程](共1小题,满分0分)23.在直角坐标系xOy中,过点P(1,﹣2)的直线l的倾斜角为45°.以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,直线l和曲线C 的交点为点A、B.(I)求直线l的参数方程;(Ⅱ)求|PA|•|PB|的值.[选修4-5:不等式选讲](共1小题,满分0分)24.已知函数f(x)=|2x+1︳+|2x﹣3︳(1)求不等式f(x)≤6 的解集;(2)若关于x的不等式|a﹣1︳<f(x)的解集为R,求实数a的取值范围.2015-2016学年广东省湛江一中高二(下)第一次月考数学试卷(文科)参考答案与试题解析一、选择题(本题共12小题,每小题5分,总分60分;每个小题仅有一个最恰当的选项)1.复数i(2﹣i)=()A.1+2i B.1﹣2i C.﹣1+2i D.﹣1﹣2i【考点】复数代数形式的乘除运算.【分析】利用复数的运算法则解答.【解答】解:原式=2i﹣i2=2i﹣(﹣1)=1+2i;故选:A.2.已知x>0,函数y=+x的最小值是()A.5 B.4 C.8 D.6【考点】基本不等式.【分析】由于x>0,利用基本不等式求得函数的最小值.【解答】解:∵x>0,函数≥2=4,当且仅当x=,x=2时,等号成立,故函数的最小值是4,故选:B.3.在△ABC中,sinA:sinB:sinC=3:2:4,则cosC的值为()A.B.C. D.【考点】余弦定理.【分析】根据正弦定理化简已知的比例式,得到a:b:c的比值,根据比例设出a,b及c,利用余弦定理表示出cosC,把表示出的a,b及c代入,化简即可求出值.【解答】解:由正弦定理==化简已知的比例式得:a:b:c=3:2:4,设a=3k,b=2k,c=4k,根据余弦定理得cosC===﹣.故选D4.已知数列{a n}满足a n+1=a n﹣1(n∈N+),且a2+a4+a6=18,则a5的值为()A.8 B.7 C.6 D.5 【考点】等差数列的通项公式.【分析】由已知可得数列{a n}是公差为﹣1的等差数列,再由a2+a4+a6=18结合等差数列的性质求得a4,则a5的值可求.=a n﹣1,得数列{a n}是公差为﹣1的等差数列,【解答】解:由a n+1又a2+a4+a6=18,得3a4=18,a4=6,∴a5=a4+d=6﹣1=5.故选:D.5.下列说法正确的是()A.“若x2=1,则x=1”的否为“若x2=1,则x≠1”B.“∀x≥0,x2+x﹣1<0”的否定是“∃x0<0,x02+x0﹣1≥0”C.“若x=y,则sin x=sin y”的逆否为假D.若“p∨q”为真,则p,q中至少有一个为真【考点】复合的真假;四种间的逆否关系;的否定.【分析】通过复合的定义,四种的关系,的否定,逐项进行判断.【解答】解:对于A:否为“若x2≠1,则x≠1”,故A错误;对于B:否定是“∃x0≥0,x02+x0﹣1≥0”,故B错误;对于C:逆否为:若“sin x≠sin y,则x≠y”,是真,故C错误;A,B,C,都错误,故D正确,故选:D.6.“|x﹣1|<2成立”是x(3﹣x)>0“成立”的()A.充分不必要条件B.必要不充分条件C.充分必要条件 D.既不充分也不必要条件【考点】必要条件、充分条件与充要条件的判断.【分析】解出对应的不等式,结合集合的包含关系求出答案即可.【解答】解:|x﹣1|<2⇔﹣1<x<3,由x(3﹣x)>0,解得:0<x<3,故“|x﹣1|<2成立”是x(3﹣x)>0“成立”的必要不充分条件,故选:B.7.等比数列{a n}的各项均为正数,且a5a6+a4a7=18,则log3a1+log3a2+…log3a10=()A.12 B.10 C.8 D.2+log35【考点】等比数列的性质;对数的运算性质.【分析】先根据等比中项的性质可知a5a6=a4a7,进而根据a5a6+a4a7=18,求得a5a6的值,最后根据等比数列的性质求得log3a1+log3a2+…log3a10=log3(a5a6)5答案可得.【解答】解:∵a5a6=a4a7,∴a5a6+a4a7=2a5a6=18∴a5a6=9∴log3a1+log3a2+…log3a10=log3(a5a6)5=5log39=10故选B8.下列各对曲线中,即有相同的离心率又有相同渐近线的是()A.=1和=1 B.=1和y2﹣=1C .y 2﹣=1和x 2﹣=1 D . =1和=1【考点】双曲线的应用;双曲线的简单性质.【分析】求解各个选项的离心率以及渐近线方程,排除不符号条件的选项,然后推出结果.【解答】解:对于A ,=1的离心率e=,渐近线方程为:y=;=1的离心率e=,渐近线方程为:y=;不满足题意,A 不正确.对于B , =1的离心率e=,渐近线方程为:y=;y 2﹣=1的离心率e=2,渐近线方程为:y=;不满足题意,B 不正确.对于C ,y 2﹣=1的离心率e=2,渐近线方程为:y=;x 2﹣=1的离心率e=2,渐近线方程为:y=;不满足题意,C 不正确.对于D , =1的离心率e=,渐近线方程为:y=;=1的离心率e=,渐近线方程为:y=;满足题意,D 正确.故选:D .9.设函数f (x )在定义域内可导,y=f (x )的图象如图所示,则导函数y=f ′(x )的图象可能是( )A .B .C .D .【考点】利用导数研究函数的单调性.【分析】先根据函数f (x )的图象判断单调性,从而得到导函数的正负情况,最后可得答案.【解答】解:原函数的单调性是:当x <0时,增;当x >0时,单调性变化依次为增、减、增故当x <0时,f ′(x )>0;当x >0时,f ′(x )的符号变化依次为+、﹣、+.故选:D.10.由不等式组确定的平面区域记为M,若直线3x﹣2y+a=0与M有公共点,则a的最大值为()A.﹣3 B.1 C.2 D.4【考点】简单线性规划.【分析】作出不等式对应的平面区域,利用线性规划的知识,通过平移即可求a的最大值.【解答】解:作出不等式组对应的平面区域如图:(阴影部分).由3x﹣2y+a=0得y=x+,平移直线y=x+,由图象可知当直线y=x+经过点A时,直线y=x+的截距最大,此时a最大.由得,即A(1,0),代入3x﹣2y+a=0得3+a=0.解得a=﹣3,即a的最大值为﹣3.故选:A11.在平面上,若两个正三角形的边长之比1:2,则它们的面积之比为1:4,类似地,在空间中,若两个正四面体的棱长之比为1:2,则它的体积比为()A.1:4 B.1:6 C.1:8 D.1:9【考点】类比推理.【分析】由平面图形面积类比立体图形的体积,结合三角形的面积比的方法类比求四面体的体积比即可.【解答】解:平面上,若两个正三角形的边长的比为1:2,则它们的面积比为1:4,类似地,由平面图形面积类比立体图形的体积,得出:在空间内,若两个正四面体的棱长的比为1:2,则它们的底面积之比为1:4,对应高之比为1:2,所以体积比为1:8故选C.12.函数f(x)=x+在(﹣∞,﹣1)上单调递增,则实数a的取值范围是()A.[1,+∞)B.(﹣∞,0)∪(0,1]C.(0,1]D.(﹣∞,0)∪[1,+∞)【考点】函数单调性的性质.【分析】求出函数的导数,由题意可得f′(x)≥0在(﹣∞,﹣1)上恒成立.运用参数分离可得≤x2在(﹣∞,﹣1)上恒成立.运用二次函数的最值,求出右边的范围即可得到.【解答】解:函数f(x)=x+的导数为f′(x)=1﹣,由于f(x)在(﹣∞,﹣1)上单调递增,则f′(x)≥0在(﹣∞,﹣1)上恒成立.即为≤x2在(﹣∞,﹣1)上恒成立.由于当x<﹣1时,x2>1,则有≤1,解得,a≥1或a<0.故选D.二、填空题(每空5分,共20分)则由表数据所得线性回归直线必过点(4.5,3.5).【考点】线性回归方程.【分析】根据线性回归方程必过样本中心点,即可得到结论.【解答】解:∵=4.5,=3.5,∴根据线性回归方程必过样本中心点,可得线性回归直线必过点(4.5,3.5),故答案为:(4.5,3.5).14.抛物线y=4x2的焦点坐标是.【考点】抛物线的简单性质.【分析】先化简为标准方程,进而可得到p的值,即可确定答案.【解答】解:由题意可知∴p=∴焦点坐标为故答案为15.将全体正整数排成一个三角形数阵;根据以上排列规律,数阵中第n(n≥3)行从左至右的第3个数是.【考点】归纳推理.【分析】先找到数的分布规律,求出第n行结束的时候一共出现的数的个数,再求第n+1行从左向右的第3个数即可.【解答】解:由排列的规律可得,第n﹣1行结束的时候排了1+2+3+…+(n﹣1)=个数.所以n行从左向右的第3个数+3=.故答案为.16.如图所示,已知抛物线y2=2px(p>0)的焦点恰好是椭圆的右焦点F,且两条曲线的交点连线也过焦点F,则该椭圆的离心率为﹣1.【考点】抛物线的简单性质;椭圆的简单性质.【分析】设椭圆的左焦点为F',抛物线与椭圆在第一象限的交点为A,连接AF',可得Rt△AFF'中,AF=FF'=p,从而AF'=p,再根据椭圆的定义,可得AF+AF'=2a=(1+)p,最后用椭圆的离心率的公式求出该椭圆的离心率.【解答】解:设椭圆的左焦点为F',抛物线与椭圆在第一象限的交点为A,连接AF',∴F(,0),F'(﹣,0),可得焦距FF'=p=2c,(c=为椭圆的半焦距)对抛物线方程y2=2px令x=,得y2=p2,所以AF=|y A|=p∴Rt△AFF'中,AF=FF'=p,可得AF'=p再根据椭圆的定义,可得AF+AF'=2a=(1+)p,∴该椭圆的离心率为e===﹣1故答案为:﹣1三、解答题:解答应写出文字说明、证明过程或演算步骤17.在△ABC中,a,b,c分别是角A,B,C的对边,已知3(b2+c2)=3a2+2bc.(1)求sinA;(2)若a=,△ABC的面积S=,且b>c,求b,c.【考点】余弦定理;正弦定理.【分析】(1)整理已知可得=,利用余弦定理可求cosA,结合A的范围,利用同角三角函数基本关系式可求sinA的值.(2)由已知利用三角形面积公式可求bc的值,由余弦定理可得:=b2+c2﹣1,结合b>c>0,联立即可解得b,c的值.【解答】(本题满分为12分)解:(1)∵3(b2+c2)=3a2+2bc,∴整理可得:=,∴cosA==,又∴A是三角形内角,A∈(0,π),∴sinA=.…(2)∵S==bcsinA=,∴bc=,①∵a=,cosA=,∴由余弦定理可得:=b2+c2﹣2×=b2+c2﹣1.②∵b>c>0,∴联立①②可得b=,c=1.…18.在数列{a n}中,a1=1,a n=a n+c(c为常数,n∈N*),且a1,a2,a5成公比不等于1的+1等比数列.(Ⅰ)求c的值;(Ⅱ)设b n=,求证:若数列{b n}的前n项和为S n,则≤S n<.【考点】数列的求和;等比数列的通项公式.【分析】(Ⅰ)由题意可知:a n=1+(n﹣1)c,求得a2=1+c,a5=1+4c.根据等比数列等比中项的性质,求得c=2;(Ⅱ)由(Ⅰ)可知,a n=2n﹣1,,根据“裂项法”即可求得数列{b n}的前n项和为S n,S n=(1﹣)=<,根据数列的单调性,可知当n=1时,S n有最小值,可证≤S n<.=a n+c,a=1,c为常数,【解答】解:(Ⅰ)∵a n+1∴a n=1+(n﹣1)c∴a2=1+c,a5=1+4c.又a1,a2,a5成等比数列,∴(1+c)2=1+4c,解得c=0或c=2,=a n不合题意,舍去.当c=0时,a n+1∴c=2 …(Ⅱ)证明:由(Ⅰ)知,a n=2n﹣1,∴,∴,=,∴>0,S n=(1﹣)=<,由单调性可知,当n=1时,S n有最小值,∴≤Sn<…19.某学校的课题组为了研究学生的数学成绩与物理成绩之间的关系,随机抽取高二年级20名学生某次考试成绩如下表所示:若单科成绩在85分以上(含85分),则该科成绩为优【分析】(1)根据科成绩在85分以上(含85分),则该科成绩为优秀,结合表格中的数据,即可得2×2列联表;(2)利用列联表中的数据,利用公式:,再与提供的临界值比较,即可得结论.1(2)根据列联表可以求得:,所以,我们有99%的把握认为:学生的数学成绩与物理成绩之间有关系20.如图,椭圆C :+=1(a >b >0)经过点P (2,3),离心率e=,直线1的方程为y=4.(Ⅰ)求椭圆C 的方程;(Ⅱ)AB 是经过(0,3)的任一弦(不经过点P ),设直线AB 与直线l 相交于点M ,记PA ,PB ,PM 的斜率分别为k 1,k 2,k 3.问:是否存在常数λ,使得十=?若存在,求λ的值.【考点】直线与圆锥曲线的综合问题;椭圆的简单性质.【分析】(Ⅰ)通过将点P(2,3)代入椭圆方程,结合离心率计算即得结论;(Ⅱ)分AB斜率存在、不存在两种情况讨论,结合韦达定理计算即得结论.【解答】解:(Ⅰ)∵椭圆C经过点P(2,3),∴+=1,又∵e==,a2=b2+c2,∴a2=16,b2=12,∴椭圆C的方程为:;(Ⅱ)结论:存在常数λ=2,使得十=.理由如下:①当AB斜率存在时,不妨设为y=kx+3,联立直线AB与椭圆方程,消去y整理得:(3+4k2)x2+24kx﹣12=0,设A(x1,y1),B(x2,y2),则x1+x2=﹣,x1x2=,∴十=+=+= [(1﹣)+(1﹣)]=(1﹣)=(1﹣)=﹣4,令y=4,则kx+3=4,从而M(,4),则=λ•=﹣2λ,∵十=,∴对比可知λ=2;②当AB斜率不存在时,不妨设A(0,2),B(0,﹣2),M(0,4),则十=+=﹣4,=﹣2,当λ=2时也成立;综上所述,存在常数λ=2,使得十=.21.已知函数f(x)=lnx,g(x)=﹣bx,设h(x)=f(x)﹣g(x).(1)求函数F(x)=f(x)﹣x的极值;(2)若g(2)=2,若a<0,讨论函数h(x)的单调性;(3)若函数g(x)是关于x的一次函数,且函数h(x)有两个不同的零点x1,x2,求b 的取值范围.【考点】利用导数研究函数的极值;利用导数研究函数的单调性.【分析】(1)求出F(x)的导数,解关于导函数的不等式,求出函数的单调区间,从而求出函数的极值即可;(2)求出h(x)的导数,通过讨论a的范围,解关于导函数的不等式,求出函数h(x)的单调区间即可;(3)求出h(x)的表达式,求出h(x)的导数,求出h(x)的单调性得到h(x)的最大值,从而求出b的范围即可.【解答】解:(1)∵F'(x)=﹣1,令F'(x)=0,即x=1,令F′(x)>0,解得:0<x<1,令F′(x)<0,解得:x>1,∴F(x)在(0,1)在(0,1)递增,在(1,+∞)递减,=F(1)=﹣1;∴F(x)极大值(2)h(x)=f(x)﹣g(x)=lnx﹣ax2+bx,其定义域为(0,+x).,又a<0,令h′(x)=0,得.1°..当a<﹣1时,则,所以函数h(x)在区间(0,)和(1,+∞)上单调递增;在区间(,1)上单调递减.2°.当a=﹣1时,h′(x)>0,数h(x)在区间(0,+∞)单调递增3°.当﹣1<a<0时,则,所以函数h(x)在区间(0,1)和(,+∞)上单调递增;在区间(1,)上单调递减.(3)∵函数g(x)是关于x的一次函数,故a=0,∴h(x)=lnx+bx,其定义域为(0,+∞),∵h(x)有两个不同的零点x1,x2,∴b<0,h′(x)=,令h′(x)>0,解得:0<x<﹣,令h′(x)<0,解得:x>﹣,∴h(x)在(0,﹣)递增,在(﹣,+∞)递减,∴x=﹣是极大值点,∴h(﹣)是最大值,∴h(﹣)>0,∴b的取值范围是(,0).请在第22、23、24题中任选一题作答,如果多做,则按所做的第一题记分.[选修4-1:几何证明选讲](共1小题,满分10分)22.如图,C点在圆O直径BE的延长线上,CA切圆O于A点,∠ACB平分线DC交AE 于点F,交AB于D点.(Ⅰ)求∠ADF的度数;(Ⅱ)若AB=AC,求AC:BC.【考点】相似三角形的判定;相似三角形的性质;圆的切线的性质定理的证明.【分析】(I)根据AC为圆O的切线,结合弦切角定理,我们易得∠B=∠EAC,结合DC是∠ACB的平分线,根据三角形外角等于不相邻两个内角的和,我们易得∠ADF=∠AFD,进而结合直径所对的圆周角为直角,求出∠ADF的度数;(II)若AB=AC,结合(1)的结论,我们易得∠ACB=30°,根据顶角为120°的等腰三角形三边之比为:1:1:,易得答案.【解答】解:(I)∵AC为圆O的切线,∴∠B=∠EAC又知DC是∠ACB的平分线,∴∠ACD=∠DCB∴∠B+∠DCB=∠EAC+∠ACD即∠ADF=∠AFD又因为BE为圆O的直径,∴∠DAE=90°∴(II)∵∠B=∠EAC,∠ACB=∠ACB,∴△ACE∽△ABC∴又∵AB=AC,∴∠B=∠ACB=30°,∴在RT△ABE中,[选修4-4:坐标系与参数方程](共1小题,满分0分)23.在直角坐标系xOy中,过点P(1,﹣2)的直线l的倾斜角为45°.以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,直线l和曲线C 的交点为点A、B.(I)求直线l的参数方程;(Ⅱ)求|PA|•|PB|的值.【考点】简单曲线的极坐标方程;参数方程化成普通方程.【分析】(1)求出直线的普通方程,令x=t,从而求出直线的参数方程;(2)求出曲线C的普通方程,联立方程组,求出A、B的坐标,根据两点间的距离公式求出|PA|•|PB|的值即可.【解答】解:(1)在直角坐标系xOy中,过点P(1,﹣2)的直线l的倾斜角为45°.∴k l=1,直线方程是:y+2=x﹣1,y=x﹣3,令x=t,则y=t﹣3,∴直线l的参数方程是;(2)以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为ρsin2θ=2cosθ,即为ρ2sin2θ=2ρcosθ,化为普通方程为:y2=2x,由,解得:或,∴|PA|•|PB|=•=4.[选修4-5:不等式选讲](共1小题,满分0分)24.已知函数f(x)=|2x+1︳+|2x﹣3︳(1)求不等式f(x)≤6 的解集;(2)若关于x的不等式|a﹣1︳<f(x)的解集为R,求实数a的取值范围.【考点】绝对值三角不等式;绝对值不等式的解法.【分析】(1)讨论2x﹣3和2x+1的正负化简绝对值代入到f(x)≤6中,求出并集即可;(2)|2x+1︳+|2x﹣3︳≥|2x+1﹣2x+3︳=4,关于x的不等式|a﹣1︳<f(x)的解集为R,所以|a﹣1︳<4,即可求出a的取值范围.【解答】解:(1)①当x≥时,解得x≤2,所以≤x≤2;②x≤﹣时,解得x≥﹣1,所以﹣1;③当﹣时,解得x∈R,所以﹣;综上:不等式的解集为x|﹣1≤x≤2};(2)因为|2x+1︳+|2x﹣3︳≥|2x+1﹣2x+3︳=4,关于x的不等式|a﹣1︳<f(x)的解集为R,所以,|a﹣1︳<4,解得﹣3<a<5 …2016年10月21日。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
下学期高二数学3月月考试题05
满分150分.时间120分钟. 第Ⅰ卷(选择题 共60分)
一、选择题 (本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.函数ax x x f +=ln )(存在与直线02=-y x 平行的切线,则实数a 的取值范围是( )
A .]2,(-∞
B . )2,(-∞
C . ),2(+∞
D . ),0(+∞ 【答案】B
2.下列曲线的所有切线构成的集合中,存在无数对互相垂直的切线的曲线是( )
A .x x f sin )(=
B .3)(x x f =
C .x e x f =)(
D .x x f ln )(=
【答案】A
3.若()sin cos f x x α=-,则'()f α等于( ) A .sin α B .cos α
C . sin cos αα+
D .2sin α
【答案】A
4.若函数32
()21f x x x =+-,则(1)f '-=( )
A .7-
B .1
C . 1-
D .7 【答案】C
5.若函数f(x)=x 2+bx+c 的图象的顶点在第四象限,则函数f /
(x)的图象是( )
【答案】A
6.对任意x R ∈,函数32()7f x ax ax x =++不存在极值点的充要条件是( ) A .021a ≤≤ B .021a <≤ C .0a <或21a > D .0a =或21a =
7
A B .
C .
D .
8( )
A B .
dx x
p
⎰1
C .
D 【答案】B
9.已知二次函数c bx ax x f ++=2)(的导数0)0('),('>f x f ,且)(x f 的值域为),0[+∞,则
( )
A .3
B
C .2
D 【答案】C
10.变速运动的物体的速度为2()1m/s v t t =-(其中t 为时间,单位:s ),则它在前2s 内所走过的路程为( )
A B C .2- D .2
【答案】D
11.下列求导运算正确的是( )
A . 12)2(-⋅='x x x
B . 11)(+-+--='x x e e
C .
D .【答案】B
12.用边长为6分米的正方形铁皮做一个无盖的水箱,先在四角分别截去一个小正方形,然后把四边翻转90︒,再焊接而成(如图)。
设水箱底面边长为
x 分米,则( )
A .水箱容积最大为8立方分米
B .水箱容积最大为64立方分米
C .当
x 在()0,3时,水箱容积()V x 随x 增大而增大
D .当x 在()0,3时,水箱容积()V x 随x 增大而减小
【答案】C
第Ⅱ卷(非选择题 共90分)
二、填空题 (本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上) 13.一个物体的运动方程为21t t s +-=其中s 的单位是米,t 的单位是秒,那么物体在3秒末的瞬时速度是 米/秒. 【答案】5
14
15.曲线()y f x =在点))3(,3(f P 处的切线方程是8y ax =+,若)3(f +)3('f =0,则实数a= 。
【答案】a=-2 16是曲线()ln 0y x x =>的一条切线,则实数b =____________。
【答案】ln2-1
三、解答题 (本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤) 17.2008年奥运会在中国召开,某商场预计2008 年从1月份起前.x .个月..,顾客对某种商品的需求总量....
件与月份的近似关系是:
该商品的进价元与月份的近似关系是:
(1)写出今年第.x .个月..
的需求量件与月份x 的函数关系式;
(2)该商品每件的售价为185元,若不计其他费用且每月都能满足市场需求,则此商场今年销售该商品的月利润预计最大是多少元? 【答案】(1)当时,
当
时,
验证符合
所以
(
,且
)
(2)该商场预计销售该商品的月利润为
(
,且
)
令
,解得(舍去)
当时,
,当
,
即函数
在[1,5)上单调递增,在(5,12]上单调递减,
所以当x=5时,
(元)
综上所述,5月份的月利润最大是3125元
18.已知函数3()f x ax bx c =++在2x =处取得极值为16c -
(1)求a 、b 的值;(2)若()f x 有极大值28,求()f x 在[3,3]-上的最大值.
【答案】(1)因3()f x ax bx c =++ 故2()3f x ax b '=+ 由于()f x 在点2x = 处取得极
值,故有(2)0(2)16f f c '=⎧⎨=-⎩即1208216a b a b c c +=⎧⎨++=-⎩ ,
化简得12048a b a b +=⎧⎨+=-⎩解得1
12a b =⎧⎨=-⎩
(2)由(Ⅰ)知 3()12f x x x c =-+,2()312f x x '=- 令()0f x '= ,得122,2x x =-=
当(,2)x ∈-∞-时,()0f x '>故()f x 在(,2)-∞-上为增函数; 当(2,2)x ∈- 时,()0f x '< 故()f x 在(2,2)- 上为减函数 当(2,)x ∈+∞ 时()0f x '> ,故()f x 在(2,)+∞ 上为增函数。
由此可知()f x 在12x =- 处取得极大值(2)16f c -=+,()f x 在22x = 处取得极小值
(2)16f c =- 由题设条件知1628c += 得12c =
此时(3)921,(3)93f c f c -=+==-+=,(2)164f c =-=- 因此()f x 上[3,3]-的最小值为(2)4f =-
19.已知函数()ln f x ax =(0,a a R ≠∈)(Ⅰ)当3a =时,解关于x 的不等式:()
()10f x e
g x ++>;
(Ⅱ)若()()()1f x g x x ≥≥恒成立,求实数a 的取值范围;
(Ⅲ)当1a =时,记()()()h x f x g x =-,过点()1,1-是否存在函数()y h x =图象的切线?若存在,有多少条?若不存在,说明理由;
【答案】(I)当3a =时,不等式等价于
(Ⅱ)
,将点T 坐标代入得:
①
0x >,
注意到()g x 在其定义域上的单调性知()0g x =
仅在
8分. 法2
(1)10ϕ=-<,而2()320e e e ϕ=-+>,故()t ϕ在(1,)e 上有唯一解.
. 法3:2
2
00000()ln 31K x x x x x =-+-,000000()2ln 3,()2ln 1K x x x x K x x '''=-+=+;
220000ln 310x x x x -+-=有必有一解,所以这样的切线存在,且只有一条。
()
ln x ax ≥
恒成立,所以ln ln a +
故()ln 10a h ≥=,min 1a =.
,()ln f x x =. ,即()1121k k λλλ
-+≤+, =()()112n f n λλ-⎡⎤+⎣⎦
. 20.张林在李明的农场附近建了一个小型工厂,由于工厂生产须占用农场的部分资源,因此
李明每年向张林索赔以弥补经济损失并获得一定净收入.工厂在不赔付农场的情况下,工厂的年利润x (元)与年产量t (吨)满足函数关系必须赔付农场s 元(以下称s 为赔付价格).
(1)将工厂的年利润w (元)表示为年产量t (吨)的函数,并求出工厂获得最大利润的年产量;
(2
)若农场每年受工厂生产影响的经济损失金额2002.0t y =(元),在工厂按照获得最大利润的产量进行生产的前提下,农场要在索赔中获得最大净收入,应向张林的工厂要求赔付价格s 是多少?
(0≥t ).
时,w 取得最大值. 吨).
(Ⅱ)设农场净收入为v 元,则2002.0t st v -=.
又
令0='v ,得20=s . 当20<s 时,0>'v ;当20>s 时,0<'v ,
所以20=s 时,v 取得最大值.
21.用总长14.8m 的钢条制作一个长方形容器的框架,如果容器底面的一边比另一边长0.5m ,那么高为多少时这个容器的容积最大?并求出最大容积。
,则
22.某商店经销一种奥运会纪念品,每件产品的成本为30元,并且每卖出一件产品需向税务
部门上交a 元(a 为常数,2≤a ≤5 )的税收。
设每件产品的售价为x 元(35≤x ≤41),根据市场调查,日销售量与x e (e 为自然对数的底数)成反比例。
已知每件产品的日售价为40元时,日销售量为10件。
(1)求该商店的日利润L (x )元与每件产品的日售价x 元的函数关系式;
)的最大值。
(2
∴当x=35时,L (x )取最大值为510(5)a e -
②当4<a ≤5时,35≤a+31≤36,'()0,31,L x x a ==+令得 易知当x=a+31时,L (x )取最大值为910a e - 综合上得5
max 910(5),(24)
()10,(45)
a
a e a L x e a -⎧-≤≤⎪=⎨<≤⎪⎩。
