点线面的投影规律总结
合集下载
简述直线上点的投影规律
简述直线上点的投影规律
直线上点的投影规律是指当一个点沿着一条直线移动时，它在垂直于该直线的平面上的投影的变化规律。
这里以一条水平直线作为例子进行说明。
1. 初始位置：当点位于直线上时，它的投影重合于直线上的相应位置。
2. 向上移动：当点沿直线向上移动时，其投影在直线上向上移动，但保持与初始位置的水平距离不变。
3. 向下移动：当点沿直线向下移动时，其投影在直线上向下移动，但同样保持与初始位置的水平距离不变。
4. 垂直投影：无论点在直线上的位置如何变化，其投影始终垂直于直线。
5. 投影长度变化：当点距离直线越远时，其投影在直线上的长度也相应增加。
通过以上规律，我们可以观察到点在直线上的投影变化是与该直线垂
直的平面上的投影。
这种规律在几何学、物理学等领域中都有广泛的应用，例如在光学中的成像原理、建筑设计中的阴影效果等。
直线上点的投影规律为我们理解和应用相关领域提供了基础。
点线面的投影工程图学
措施二 b" ab : cd不等于a'b': c'd‘
d b
举例： 试作一直线MN与AB、CD两直线相交 , 且平行 EF 能否作？有几条？
e ’
(m ’)
(a’) b’
d
’
分析
作图环节
X
f ’
c n’ ’
ac f
（1）过m’作直线 O m’n’平行e’f’
, 且与c’d’交于 (2) n’由n’求得n
复杂－－展为平面
1. 展开
V a
●
X
ax
a● H
Z
az
O
ay
Y
不动
W a
●
Y
ay
V a
●
X ax
向下翻
Z
向右翻
az
A
●
a● H
●a
O
W
ay
Y
2. 投影规律
Z
V
a
●
az
A
X ax
●
●a
W O
a●
ay
H Y
a ●
X ax
a●
Z az
a
●
O
Y
ay
ay
Y
从投影展开图能够看出: (1) aa⊥OX轴 aa⊥OZ轴
返回
§2.3 直线旳投影（续）
四、两直线旳相对位置
1. 两直线平行
b' d'
b
V
d
a
B
c
A
C
D
a' c'
a
c
c b
a
dH
d b
投影特征:
d b
举例： 试作一直线MN与AB、CD两直线相交 , 且平行 EF 能否作？有几条？
e ’
(m ’)
(a’) b’
d
’
分析
作图环节
X
f ’
c n’ ’
ac f
（1）过m’作直线 O m’n’平行e’f’
, 且与c’d’交于 (2) n’由n’求得n
复杂－－展为平面
1. 展开
V a
●
X
ax
a● H
Z
az
O
ay
Y
不动
W a
●
Y
ay
V a
●
X ax
向下翻
Z
向右翻
az
A
●
a● H
●a
O
W
ay
Y
2. 投影规律
Z
V
a
●
az
A
X ax
●
●a
W O
a●
ay
H Y
a ●
X ax
a●
Z az
a
●
O
Y
ay
ay
Y
从投影展开图能够看出: (1) aa⊥OX轴 aa⊥OZ轴
返回
§2.3 直线旳投影（续）
四、两直线旳相对位置
1. 两直线平行
b' d'
b
V
d
a
B
c
A
C
D
a' c'
a
c
c b
a
dH
d b
投影特征:
第3章 点线面的投影
b a a b a
b
投影特性：
三个投影都为类似 形。即: 都不反映空间 线段的实长及与三个投 影面夹角的实大，且与 三根投影轴都倾斜。
三、直线上点的投影
直线上的点具有两个特性：
1 从属性 若点在直线上，则点的各个投影必在直线 的各同面投影上。 利用这一特性可以在直线上找点，或 判断已知点是否在直线上。
两直线相交吗？ ★ 同名投影可能相交， 但 “交点”不符合空间 为什么？ 一个点的投影规律。 ★ “交点”是两直线上 的一 对重影点的投影， 用其可帮助判断两直线 的空间位置。
投影特性：
例：判断两直线的相对位置
c
1 a d d 1
相交吗？
b
X
a
c 1d
b
1c
判断两直线重影点的可见性
a k● b a
●
k
b
a k●
b
因k 不在a b 上， 故点K不在AB上。
另一判断法 如何判断 ? ?
应用定比定理
例3 ：已知点K在线段AB上，求点K正面投影。
解法一： （应用第三投影）
a k
b
●
解法二： （应用定比定理）
a
a k
● ●
●
k● b
怎么做?
b
b
k● a
求出侧面投影
⒉ 两直线相交
V a
A a c k b
注意：交点 为两直线共 有！
B c b k d
C
d K D d
k
a b
H
c
a c k
d
b
投影特性：
若空间两直线相交，则其同名投影必 相交，且交点的投影必符合空间一点的投 影规律。 (反之 用于判断） 。
04 点、线、面的投影
四、作图
1． 求直线的实长及对水平投影面的夹角角 2． 求直线的实长及对正面投影面的夹角角
3． 求直线的实长及对侧面投影面的夹角角
1． 求直线的实长及对水平投影面的夹角角
AB
|zA-zB|
|zA-zB|
ab
O
AB AB |zA-zB |
ab
|zA-zB|
2． 求直线的实长及对正面投影面的夹角 角
（解法1） （解法2） [例题7] 作正平线CD, 与直线AB相交于点D
[例题5] 已知线段AB的投影图，试将AB分成2﹕1两段， 求分点C的投影c、c' 。
c'
c
[例题6（解法1）] 已知点C在线段AB上，求点C 的正面投影。
bc
c' ca
[例题6（解法2）] 已知点C在线段AB上，求点C 的正面投影。
(a')b'
a"
b"
a'
b'
a"(b ")
a'
a b(a) b
a
b
（2）物体上垂直线的投影分析
§4.3 直线上的点
一、属于直线的点的投影 二、例题
一、属于直线的点的投影
e'
E
e'
e
e
二、例题
[例题5] 已知线段AB的投影图，试将AB分成2﹕1两段
[例题6] 已知点C在线段AB上，求点C 的正面投影
d'
d
三、两交叉直线
1. 交叉直线的投影
2. 交叉二直线重影点投影的可见性判断
3. 例题
1. 交叉二直线的投影
凡不满足平行和相交条件的直线为交叉二直线。
点线面的投影分析
一、点的投影分析
点的投影规律： (1)点的正面投影和水平投影的连线
垂直于OX 轴。即ss’⊥ OX
(2)点的正面投影和侧面投影的连线
垂直于OZ 轴。即s’s” ⊥ OZ (3)点的水平投影到OX轴的距离等于
侧面投影到OZ 的距离。
退出 节目录
§2－3 立体表面上点、线、面的投影分析
一、点的投影分析
影面。
退出 节目录
§2－3 立体表面上点、线、面的投影分析
三、平面的投影分析
1.一般位置平面 投影特性：
(1)三个投影都不 反映平面实形。 (2)三个投影均对 投影轴倾斜。
退出 节目录
§2－3 立体表面上点、线、面的投影分析 三、平面的投影分析
2.投影面平行面 投影特性：
（1）在所平行 的投影面上投 影反映实形。 （2）其他两个 投影面上的投 影积聚为直线， 且分别平行于 相应的投影轴。
2.投影面平行面 投影特性：
（1）在所平行 的投影面上投 影反映实形。 （2）其他两个 投影面上的投 影积聚为直线， 且分别平行于 相应的投影轴。
平行于侧面的平面称为侧平面
退出 节目录
§2－3 立体表面上点、线、面的投影分析 三、平面的投影分析
3.投影面垂直面 投影特性：
(1)在所垂直的投 影面内投影积聚 为一段斜线。 (2)其他两个投影 面上的投影均为 缩小的类似形。
平行于侧面的直线称为侧平线
退出 节目录
§2－3 立体表面上点、线、面的投影分析
二、直线的投影分析
3.投影面垂直线 投影特性：
（1）在所垂直的 投影面上投影积 聚为一点。
（2）其他两个投 影面上的投影反 映实长，且分别 垂直于相应的投 影轴。
垂直于水平面的直线称为铅垂线
点的投影规律： (1)点的正面投影和水平投影的连线
垂直于OX 轴。即ss’⊥ OX
(2)点的正面投影和侧面投影的连线
垂直于OZ 轴。即s’s” ⊥ OZ (3)点的水平投影到OX轴的距离等于
侧面投影到OZ 的距离。
退出 节目录
§2－3 立体表面上点、线、面的投影分析
一、点的投影分析
影面。
退出 节目录
§2－3 立体表面上点、线、面的投影分析
三、平面的投影分析
1.一般位置平面 投影特性：
(1)三个投影都不 反映平面实形。 (2)三个投影均对 投影轴倾斜。
退出 节目录
§2－3 立体表面上点、线、面的投影分析 三、平面的投影分析
2.投影面平行面 投影特性：
（1）在所平行 的投影面上投 影反映实形。 （2）其他两个 投影面上的投 影积聚为直线， 且分别平行于 相应的投影轴。
2.投影面平行面 投影特性：
（1）在所平行 的投影面上投 影反映实形。 （2）其他两个 投影面上的投 影积聚为直线， 且分别平行于 相应的投影轴。
平行于侧面的平面称为侧平面
退出 节目录
§2－3 立体表面上点、线、面的投影分析 三、平面的投影分析
3.投影面垂直面 投影特性：
(1)在所垂直的投 影面内投影积聚 为一段斜线。 (2)其他两个投影 面上的投影均为 缩小的类似形。
平行于侧面的直线称为侧平线
退出 节目录
§2－3 立体表面上点、线、面的投影分析
二、直线的投影分析
3.投影面垂直线 投影特性：
（1）在所垂直的 投影面上投影积 聚为一点。
（2）其他两个投 影面上的投影反 映实长，且分别 垂直于相应的投 影轴。
垂直于水平面的直线称为铅垂线
点线面正投影
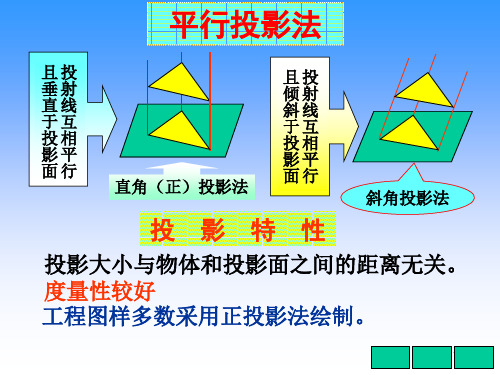
影上kn为可见。
还可通过重影点判别可见性。
47
⑵ 直线为特殊位置
m
空间及投影分析
b
直线MN为铅垂线，其
k●
水平投影积聚成一个点，
a
c ●1(2)
故交点K的水平投影也积聚
n
在该点上。
b
作图
a
mk(●●n2) ● 1
e f e(f) ●
b
b
d
●
a(b)
c
ef
投影特性:
① 在其垂直的投影面上，投影有积聚性。
② 另外两个投影，反映线段实长。且垂直 于相应的投影轴。
13
⑶ 一般位置直线
b
b
投影特性：
a
a
a b
三个投影都缩短。 即: 都不反映空间线段 的实长及与三个投影面 夹角的实大，且与三根 投影轴都倾斜。
14
二、直线与点的相对位置
是什么位置
的平面？ a
b
b
类似性
c c a
积聚性
βc
b
γ
a
投影特性：
铅垂面
在它垂直的投影面上的投影积聚成直
线。该直线与投影轴的夹角反映空间平面 与另外两投影面夹角的大小。
另外两个投影面上的投影有类似性。
34
⒉ 投影面平行面
积聚性
a b
积聚性
c a c b
a
实形性
c
水平面
b
投影特性：
在它所平行的投影面上的投影反映实形。
解法一:
a●
az ●a
通过作45°线 使aaz=aax
ax
a●
解法二:
用圆规直接量 取aaz=aax
点线面投影
两点中X值大的点 ——在左 两点中Y值大的点 ——在前 两点中Z值大的点 ——在上
1.3 重影点
a'
b'
被挡住的 投影加( )
(c')d' A B
被挡住的 投影加( )
C
D
A、B和C、D 分别为哪个投 影面的重影点 呢？
a(b)
c
d
1.3 重影点
被挡住的 投影加( )
b″
d″ c"
被挡住的 投影加( )
① 在与其垂直的投影面上，投影有积聚性。 ② 另外两个投影反映线段实长，且垂直于相应 的投影轴。
判断线的空间位置 特殊位置直线的投影特征
X
O
3、从属于投影面的直线
从属于投影面的直线
从属于投影面的铅垂线
从属于投影轴的直线
返回
从属于V面的直线
返回
从属于V投影面的铅垂线
返回
从属于OX轴的直线
返回
Y
3 、 a b 与OX、OZ 的夹角反映α、 角的真实大小
返回
3 、侧垂面 b’
z
c’
b’’
β c’’ α
x
a’ b
c
o
a’’ Y
a
投影特性：1、 a’’b’’c’’积聚为一条线 2 、 a’b’c’、 a’b’c’为 ABC的类似形
Y
3 、 a’’b’’c’’与OZ、 OY的夹角反映α、β角的真实大小 返回
例：已知点的两个投影，求第三投影。
解法一:
a● ax
az
●a
通过作45°线 使aaz=aax
a● 解法二: 用分规直接量 取aaz=aax
a●
ax az
点、线、面与体的投影
应用：在工程和设计中，投影是重要的几何概念，用于描述物体表面的形状和轮廓。
平面方程的一般形式：Ax + By + Cz + D = 0
平面方程的参数形式：通过点P(x0, y0, z0)且与向量v=(A, B, C)垂直的平面方程 为：A(x-x0) + B(y-y0) + C(z-z0) = 0
展览展示：利用投影技术，将展品或艺术品投影到屏幕上，让观众更全面地欣赏和了解
广告宣传：通过投影技术，将广告内容投影到建筑物、街道、车辆等物体上，吸引路人的注 意力
舞台演出：利用投影技术，将虚拟场景、人物、道具等投影到舞台上，增强演出的视觉效指点在垂直于平面的方向上向平面内投射形成的影子。
建筑图纸的规范与标准：介绍建筑图 纸的规范和标准，如制图比例、线型、 符号等，以及它们在实际应用中的作 用。
表达方式：点、线、 面与体的投影在工 程图样中的表示方 法
解读技巧：如何准 确理解工程图样的 投影关系和尺寸标 注
应用案例：介绍实际 工程中点、线、面与 体的投影在工程图样 中的应用实例
重要性：强调工程 图样的表达与解读 在工程建设中的重 要地位和作用
建筑图纸的绘制：点、线、面与体 的投影在实际建筑图纸中的应用， 如平面图、立面图和剖面图的绘制。
建筑图纸的投影原理：介绍投影的 基本原理，如正投影、斜投影等， 以及它们在建筑图纸中的应用。
添加标题
添加标题
添加标题
添加标题
建筑图纸的解读：如何通过点、线、 面与体的投影来理解建筑图纸，如从 平面图解读房间功能、从立面图了解 建筑外观等。
直线投影的应用：在工程设计中，常常需要利用直线的投影变换来绘制三维物体 的二维图形，或者根据二维图形想象出三维物体的形状。
平面方程的一般形式：Ax + By + Cz + D = 0
平面方程的参数形式：通过点P(x0, y0, z0)且与向量v=(A, B, C)垂直的平面方程 为：A(x-x0) + B(y-y0) + C(z-z0) = 0
展览展示：利用投影技术，将展品或艺术品投影到屏幕上，让观众更全面地欣赏和了解
广告宣传：通过投影技术，将广告内容投影到建筑物、街道、车辆等物体上，吸引路人的注 意力
舞台演出：利用投影技术，将虚拟场景、人物、道具等投影到舞台上，增强演出的视觉效指点在垂直于平面的方向上向平面内投射形成的影子。
建筑图纸的规范与标准：介绍建筑图 纸的规范和标准，如制图比例、线型、 符号等，以及它们在实际应用中的作 用。
表达方式：点、线、 面与体的投影在工 程图样中的表示方 法
解读技巧：如何准 确理解工程图样的 投影关系和尺寸标 注
应用案例：介绍实际 工程中点、线、面与 体的投影在工程图样 中的应用实例
重要性：强调工程 图样的表达与解读 在工程建设中的重 要地位和作用
建筑图纸的绘制：点、线、面与体 的投影在实际建筑图纸中的应用， 如平面图、立面图和剖面图的绘制。
建筑图纸的投影原理：介绍投影的 基本原理，如正投影、斜投影等， 以及它们在建筑图纸中的应用。
添加标题
添加标题
添加标题
添加标题
建筑图纸的解读：如何通过点、线、 面与体的投影来理解建筑图纸，如从 平面图解读房间功能、从立面图了解 建筑外观等。
直线投影的应用：在工程设计中，常常需要利用直线的投影变换来绘制三维物体 的二维图形，或者根据二维图形想象出三维物体的形状。
第三章点、直线及平面的投影详解
第三章 点、直线及平面投影
§3－1 点的投影 §3－2 直线的投影 §3－3 平面的投影
点线面的投影规律
通过上一节的学习及画图实践，可以体会到 画一个物体的三视图，实质上是画出组成物体的 各个面的投影，而各个面是由棱线围成的，各棱 线是由两个端点决定的。
因此，为了迅速而正确地画出物体的视图， 还需研究构成物体的基本几何元素点、线、面的 投影。
Y
H
向下翻
●a
O
W
ay
Y
a ●
X ax
a●
点的投影规律
Z az
a
●
Z
V a
●
az
O
Y
ay
A
X ax
●
●a
O
W
ay
Y
a●
ay
H
Y
① aa⊥OX轴
aa⊥OZ轴
连影垂轴
② aax= aaz= y = A 到 V 面的距离 aax= aay= z = A 到 H 面的距离 aay= aaz= x = A 到 W 面的距离
Z
X
V a′ A
a″ W
a b
a
Z a
b
O
YW
b′
B b″
b
判断方法：
YH
x
ab
H
Y
x 坐标大的在左 y 坐标大的在前
z 坐标大的在上
例2.已知B点在A下10，A后5，A左10 mm处，求B点的三投影。 作图步骤：（1）根据B的相对位置求 其V.H面的投影 b’,b;
（2）根据点的投影规律,求其第三投影 b”。
§3－1 点的投影
一、点在一个投影面上的投影
P
§3－1 点的投影 §3－2 直线的投影 §3－3 平面的投影
点线面的投影规律
通过上一节的学习及画图实践，可以体会到 画一个物体的三视图，实质上是画出组成物体的 各个面的投影，而各个面是由棱线围成的，各棱 线是由两个端点决定的。
因此，为了迅速而正确地画出物体的视图， 还需研究构成物体的基本几何元素点、线、面的 投影。
Y
H
向下翻
●a
O
W
ay
Y
a ●
X ax
a●
点的投影规律
Z az
a
●
Z
V a
●
az
O
Y
ay
A
X ax
●
●a
O
W
ay
Y
a●
ay
H
Y
① aa⊥OX轴
aa⊥OZ轴
连影垂轴
② aax= aaz= y = A 到 V 面的距离 aax= aay= z = A 到 H 面的距离 aay= aaz= x = A 到 W 面的距离
Z
X
V a′ A
a″ W
a b
a
Z a
b
O
YW
b′
B b″
b
判断方法：
YH
x
ab
H
Y
x 坐标大的在左 y 坐标大的在前
z 坐标大的在上
例2.已知B点在A下10，A后5，A左10 mm处，求B点的三投影。 作图步骤：（1）根据B的相对位置求 其V.H面的投影 b’,b;
（2）根据点的投影规律,求其第三投影 b”。
§3－1 点的投影
一、点在一个投影面上的投影
P
建筑识图的基本知识：点线面体的投影
V
Z
Z
a b
a
a
b
X
A
O
a
B
W
b
X
a
O
a
水平投影反H映实长及b 倾角，正Y面投影及侧b面投 YH 影垂直于OZ轴
b
YW
返回线目录 返回目录
V
a
X
正平线（平行V面，同时倾斜于H、W面的直线）
Z
b
Z
b
b
B
b
a
a
A
a W X
O
YW
O
a
b
a
b
正面投影反映H实长及倾角，水平投Y 影及侧
YH 返回线目录
面投影垂直于OY轴
图示特点：三斜
事实上，只要空间直线的任意两个投影都呈倾 斜状态，则该直线一定是一条一般位置直线。
返回线目录 返回目录
求一般位置线段的实长和倾角
一般线的直角三角形边角关系
以直线的某一投影为一直角边，直线的两个端点与这个投影 面的距离差（即坐标差）为另一直角边，所作出的直角三角形的 斜边，即为实长，斜边与直线投影的夹角，即为直线与这个投影 面的真实倾角。
V
下列五种方式可表达一平面：
（1）不在同一直线上的三
个点；
A
（2）一直线和直线外一点X；
（3）两相交直线；
（4）两平行直线；
（5）任意平面图形。
H
Z
B W
C Y
返回面目录 返回目录
相应地在投影图中，空间 平面可用下列五组几何元 素中的任意一组来表示。
（一）平面的表示方法
b
b
b
a c
a c
a c
a c
2家具制图(点线面投影)
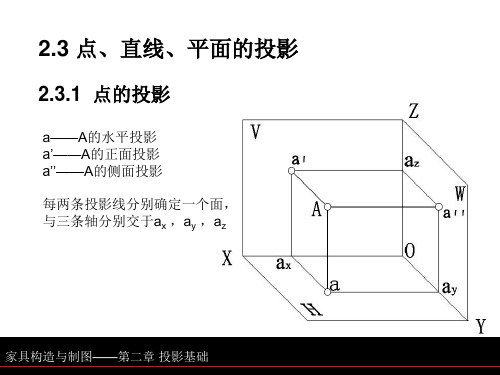
三、点与点的相对位置
指两点在空间的上下、左右、前后位置关系。 指两点在空间的上下、左右、前后位置关系。 例：给出三棱柱的投影图，及三棱柱上点A的V投影a’和点B的W 投影b’’，试分析A，B两点的相对位置。 a’’
a H投影反应左右、前后关系； V投影反应上下、左右关系； W投影反应上下、前后关系；
例：已知平行四边形ABCD的两边AB，CD的投影，试完成ABCD的投影。
家具构造与制图——第二章 投影基础
2、两直线相交 、
相交两直线的交点应符合点的投影规律。 如果某直线是投影面平行线，要通过第三个投影判断两直线是否相交。
家具构造与制图——第二章 投影基础
例：已知平行四边形ABCD的V投影a’b’c’d’，和两条边的H投影ab , bc，试 完成ABCD的H投影。
家具构造与制图——第二章 投影基础
ab //OX a’’b’’//OZ,长度变 短； a’b’反映实长； α、γ为实角, β=0
ab //OYH a’b’ //OZ,长度变 短； A’’b’’反映实长； α、β为实角, γ =0
家具构造与制图——第二章 投影基础
三、投影面垂直线
1、空间位置 投影面垂直线垂直于某一个投影面（因而平行于另外两个投影面） 与H面垂直——铅垂线（水平面垂直线） 与V面垂直——正垂线（正立面垂直线） 与W面垂直——侧垂线（侧立面垂直线） 二、投影特点 投影面垂直线在它所垂直的投影面上的投影积聚为一点。由于投影面垂直 线与其他两投影面平行，其上各点与相应的投影面等距，所以其他两个投 影平行于相应的投影轴，并反映该线段的实长。 ab //OYH a’’b’’//OYW 并 反应实长； a’b’积聚成一点；
二、投影面平行线
1、空间位置 投影面平行线平行于某一个投影面，但倾斜于其余两个投影面。 与H面平行——水平线 与V面平行——正平线 与W面平行——侧平线 二、投影特点 投影面平行线在它所平行的投影面上的投影是倾斜的，反映实长。此实形 投影与投影轴的夹角反映该投影面平行线对相应投影面的倾角的实形。 a’b’//OX a’’b’’//OYW ,长度变 短； ab 反映实长； β、γ为实角, α=0
汽车识图_投影_第三节_点、线、面的投影
第三节点、线、面的投影主要内容一、点的投影及标记二、点的三面投影规律三、特殊位置点的投影四、两点的相对位置五、直线的投影六、各种位置直线的投影特性七、直线上点的投影八、两点的相对位置九、各种位置平面的投影特性十、平面上的直线和点一、点的投影及标记XYZAaa 'a "1.点的投影及标记：将空间点A 分别向V 、H 、W 面投影，得正投影a ′,水平投影a ，侧投影a ″直观图a 'aa "点的三面投影图X AY A Z AX AZ AY A2.点的空间直角坐标Y HXY WZOO点是组成物体的最基本的几何元素，研究形体的投影问题应从点开始。
A 点坐标X A 、Y A 、Z A 分别为点到W 、V 、H 面的距离，已知空间点的位置，就可以画出点的投影。
二、点的三面投影规律XYZ Aaa 'a "直观图X AY A Z AOa 'aa "点的三面投影图Y HXY WZO1）a 'a ⊥OX 轴，a 'a "⊥OZ 轴2）点的水平投影到OX 轴的距离和点的侧面投影到OZ 轴的距离相等,都反映空间点的Y 坐标。
根据投影规律，若已知点的任何两个投影，就可求出它的第三个投影实例分析1.已知点A 到H 、V 、W 面的距离分别为20，10，25，求其三面投影。
a ＇a "20102510aY HY WOXZa z2.已知点A 的正面、侧面的投影，求其水平面投影。
a ＇a "aY HY WOXZ三、特殊位置的点空间点在投影面上或投影轴上，称为特殊位置的点。
XYZO a ＇a "aY HY WOXZBA aa ＇b ＇a "b "bb ＇b "b1.投影面上的点（点的一个坐标为零）：有两个投影在投影轴上，另一个投影和其空间点本身重合。
2.投影轴上的点（点的两个坐标为零）：有一个投影在原点上，另两个投影和其空间点本身重合。
点线面的投影
b
x
c
b
yW
a b
yH
Z
C c c
a A
a
O
b c
b
a
X
bB
A位于 空间
B位于 H面
C位于 V面
Y 11
第二节 直线的投影
直线的投影 直线上的点 各种位置直线的投影特性 线段的实长及倾角
一 直线的投影
直线的投影特性
1.直线平行于投影面，其投影反映实长。 2.直线垂直于投影面，其投影积聚成点。 3.直线倾斜于投影面，其投影长度缩短。
2、ab =AB 反映实长,倾斜于OZ轴，反映 、 角
投影面垂直线
垂直于一个投影面 平行于另外两个投影面。 垂直线分三种：
铅垂线⊥Ｈ面
正垂线⊥Ｖ面
侧垂线⊥Ｗ面
铅垂线（ Ｈ面、//Ｖ面、//Ｗ面）
Z a
Z
a
a
b X
A
O B a(b)
a
b
X
O
b
Y
a(b)
YH
b YW
投影特性：1、水平投影 a b 积聚 成一点 2、 a b // OZ ; a b // OZ； a bOX ; 3、 a b = a b = AB 反映实长
y 点B的Z坐标为0，故点B为H面上的
w 点。
b
yH
点C的x、y坐标为0，故点C为z轴 上的点。
例题7 已知点D 的三面投影，点C在点D的正前方15mm，
求作点C的三面投影，并判别其投影的可见性。
解： 由已知条件知：XC=XD
Z
ZC=ZD YC-YD=15mm
c' (d')
因为点C、D在V面上的投 影重影。
土木工程制图讲义点线面投影篇3
第二章
点、直线、面的投影 (3)
一、点的投影规律
Z
a ●
az
a
●
X ax a●
O
Y
ay
ay
Y
Z
V
a ●
az
X
yA A
ax
●
xA
O
a● zA
H
●a W ay
Y
① aa⊥OX轴 aa⊥OZ轴
② aax= aaz=A到V面的距离=yA
aax= aay=A到H面的距离=zA aay= aaz=A到W面的距离=xA
A a
线段实长。坐标差构 △YAB
成的直角边所对锐角
即为线段对该投影面
的倾角。
b'
△ZAB
B
.B
1
O
b
H
二、直角三角形法求实长和倾角
求AB的实长及对V面和H面的倾角。
b'
a0
b'
a' X
b 1O b
a' Xa1
a
b0 a
1. 直角三角形斜边长为实长。
O
b LAB
△YAB .
a’b'
2. 斜边与某个投影之间的夹角，即该直线与投影面的
二、两点的相对位置
Z
▲x 坐标大的在左 ▲y 坐标大的在前 ▲z 坐标大的在上
三、重影点
V
b' X bx
a'
az
A bz
a"
ax
O
W
B a
b H
ay b" by Y
重影点：是位于某一投影面的
V a●
同一条投射线上的空间两点。
点、直线、面的投影 (3)
一、点的投影规律
Z
a ●
az
a
●
X ax a●
O
Y
ay
ay
Y
Z
V
a ●
az
X
yA A
ax
●
xA
O
a● zA
H
●a W ay
Y
① aa⊥OX轴 aa⊥OZ轴
② aax= aaz=A到V面的距离=yA
aax= aay=A到H面的距离=zA aay= aaz=A到W面的距离=xA
A a
线段实长。坐标差构 △YAB
成的直角边所对锐角
即为线段对该投影面
的倾角。
b'
△ZAB
B
.B
1
O
b
H
二、直角三角形法求实长和倾角
求AB的实长及对V面和H面的倾角。
b'
a0
b'
a' X
b 1O b
a' Xa1
a
b0 a
1. 直角三角形斜边长为实长。
O
b LAB
△YAB .
a’b'
2. 斜边与某个投影之间的夹角，即该直线与投影面的
二、两点的相对位置
Z
▲x 坐标大的在左 ▲y 坐标大的在前 ▲z 坐标大的在上
三、重影点
V
b' X bx
a'
az
A bz
a"
ax
O
W
B a
b H
ay b" by Y
重影点：是位于某一投影面的
V a●
同一条投射线上的空间两点。
点线面的投影
例题5
已知点的坐标值为：A（20，10，15）和 B（0，15，20）求它们的三面投影图。
Z
b' 解：（1）量取坐标值； （2）作点的投影。
X O
b"
a'
a"
YW
a
b
YH
例题6
已知各点的两面投影，求作其第三投影，并判 断点对投影面的相对位置。
z
a' x
b'
c' c" o b" c
a
a"
点A的三个坐标值均不为0， A为一般位置。
b
A O B
X
b
b
b
a
Y
a
YH
两点中X 值大的点 ——在左 两点中Y 值大的点 ——在前 两点中Z 值大的点 ——在上
[二] 重影点的概念
H a b
A B X X O O
a b
由V投影 判断高低
a(b) 不可见投影点 的标记加括号
a(b) A与B 对H面重影
14
2、若两点的正面投影重合，可从 水平投影判别其可见性，y坐标值 大的点为可见（点C在前）。
O
YW
YH YH
规定：空间点A用大写字母表示，在H面的投影a，
在V面的投影用a'，在W面的投影用a"表示。
例题1
已知点A的正面与侧面投影，求点A的水平投影。 Z a a
X
O
YW
a YH
例题2 已知点 A的正面投影和侧面投影, 求其水平投影。
z a x a
O
y W
a
y H
注: 这是二求三问题的基础。
Z a Z a
工程制图 点、直线及平面的投影
工程制图
B b b
A a
a
a
b
Z
b
a
a
X a
b
O
YW
b
YH
27
工学院 机械系 张文斌
红河学院
从属于V 投影面的铅垂线
工程制图
Z
a
a
b
b
X
O
YW
a(b)
YH
28
工学院 机械系 张文斌
红河学院
从属于OX轴的直线
工程制图
Z
X a
b O
YW
(b)
a
b a(b)
YH
29
工学院 机械系 张文斌
红河学院
二、一般位置直线
(2) 正垂线
(3) 侧垂线
3.从属于投影面的直线
从属于投影面的直线
从属于投影面的铅垂线
从属于投影轴的直线 二、一般位置直线
20
工学院 机械系 张文斌
红河学院 (1) 水平线 — 只平行于水平投影面的直线 工程制图
z
a b
a
b
a
b
A
a
X
O
YW
B
b a
a
b
b YH
投影特性：1．ab OX ; ab OYW
O
YW
b
a(b)
YH
投影特性：1． a b 积聚 成一点
2． a bOX ; a b OYW 3． a b = a b = AB
24
工学院 机械系 张文斌
红河学院 （2）正垂线— 垂直于正面投影面的直线 工程制图
(a)b
(a)b
z a
b
A
2.2立体表面上的点、直线、平面的投影
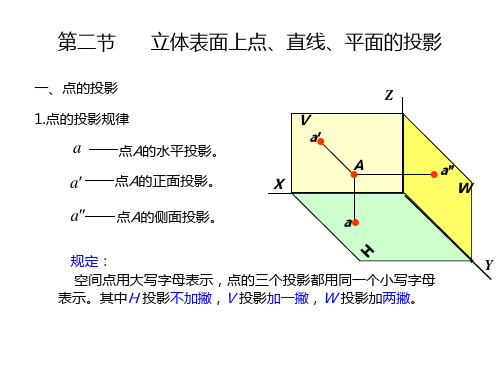
第二节
3.一般位置平面
立体表面上点、直线、平面的投影
对V，H，W面都倾斜， 不在同一直线上的三 点构成的平面。 投影特性 一般位置平 面的投影特 性：三面投 影仍为平面 图形，且面 积缩小。其 投影为和原 来形状类似 的图形。 （类似性）
a′ c′
b′ A
a″ B b b″ c″
C a c
第二节
Z
b●
bx X
12
bz
b
●
作图步骤： 1）在a′左方12 mm ， 上方8 mm 处确定b′；
a
8
az O
a
by YW ay
ax
a
2）作b′b⊥OX 轴，且在a 前 10 mm 处确定b ；
10
ay by
YH
b
●
3）按投影关系求得b″。
第二节
立体表面上点、直线、平面的投影
当空间两点位于对投影面的同一条投影线上时，这两点在该投影面上的 投影重合，称这两点为对该投影面的重影点。
W
V
●
a
●
az
O
W a
YW
X
ax
A
●
O
X
ax a
H
●
ay
a●
H
ay
Y
ay
YH
向下翻
第二节
立体表面上点、直线、平面的投影
1）、V、H两投影都反映横标，且投影连 线 垂直X轴；aa⊥OX轴。 2）、V、W两投影都反映高标，且投影 连线垂直Z轴；aa⊥OZ轴。 3）、H、W两投影都反映纵标，投影连 线是一条折线。
注意: 点的各个投影一定要写在它所属的投影面区域内。
第二节
点线面的投影规律总结
点线面的投影规律类型投影规律
点a'a⊥OX轴,a'a''⊥OZ轴,aa YH⊥Oa YH轴,a''a YW⊥Oa YW
轴,Oa YH=Oa YW
投影面
平行线
两投影线分别平行于不同轴，
根据实形斜线判断所平行的投影
面，
斜线反映与另外两投影面夹角
投影面
垂直线
两投影实长线平行于同一轴，
根据集聚点判断所垂直的投影
面，
一般位
置直线
三个投影都倾斜于投影轴，
均不反应夹角和实长
投影面
平行面
两面投影积聚成线，且平行于不
同轴，
根据实形面判定所平行的投影面
投影面
垂直面
两面投影相仿，
根据积聚斜线判定所垂直的投影
面，
斜线反映与另外两投影面夹角
一般位
置平面
三个投影都类似。
4第四章点线面投影
b′ a′ b″ b′ a″ a′ b Z B b″
β γ α A
b a
a″
X
a
Y
直线的投影特性：
一般来说，直线的投影 仍然为直线。当直线垂直 于投影面时，直线的投影 则积聚为一点。
A B b C D E F
a c
d
e(f)
H
直线对投影面的位置不同，直线可分为三类：
一般位置直线 —— 直线与三个投影面均倾斜。
b′
a′
△Z=15 △X=20 X=35
b″ a″
Z=10
b
a
Y=20 △Y=10
二、直线的投影(P51)
• 直线的投影
• 直线上的点
a′ V b′ β A b aH Y γ
Z B b″
W a″
• 两直线间的相对位置
X
α
1、直线的投影
直线的投影就是将直线上两端点投影求出，再将连接 同面投影即可得到。
1′ b′
k′
2′
c′
b 1 k 2
c
(三)平面上的点和直线
直线在平面上的几何条件： 若直线在平面上，则该直线 必通过平面上的两个已知点或通 过平面上的一个点且平行于平面 上某一直线。
V
b´
Z
B
b"
n´
点在平面上的几何条件： 若点在平面上，则该点必定位 于平面上的某一直线上。反之，若 一点位于平面上的某一直线上，则 该点必定位于平面上。 X
a ′ b ′ c ′z b ″a ″ c ″ a″ W c″
C
X
b
o
YW
x
a
H b
O
a
c
Y
c Y H
β γ α A
b a
a″
X
a
Y
直线的投影特性：
一般来说，直线的投影 仍然为直线。当直线垂直 于投影面时，直线的投影 则积聚为一点。
A B b C D E F
a c
d
e(f)
H
直线对投影面的位置不同，直线可分为三类：
一般位置直线 —— 直线与三个投影面均倾斜。
b′
a′
△Z=15 △X=20 X=35
b″ a″
Z=10
b
a
Y=20 △Y=10
二、直线的投影(P51)
• 直线的投影
• 直线上的点
a′ V b′ β A b aH Y γ
Z B b″
W a″
• 两直线间的相对位置
X
α
1、直线的投影
直线的投影就是将直线上两端点投影求出，再将连接 同面投影即可得到。
1′ b′
k′
2′
c′
b 1 k 2
c
(三)平面上的点和直线
直线在平面上的几何条件： 若直线在平面上，则该直线 必通过平面上的两个已知点或通 过平面上的一个点且平行于平面 上某一直线。
V
b´
Z
B
b"
n´
点在平面上的几何条件： 若点在平面上，则该点必定位 于平面上的某一直线上。反之，若 一点位于平面上的某一直线上，则 该点必定位于平面上。 X
a ′ b ′ c ′z b ″a ″ c ″ a″ W c″
C
X
b
o
YW
x
a
H b
O
a
c
Y
c Y H
点线面小结(工程制图基础)
A
E B
c
d
c b
直线和平面平行
• 几何条件
如果平面P 外的一条直线AB 与平面内的一条直线 平行,那么这条直线AB 和这个平面P 平行。 ∵ L∈P ；
L
A
L ∥AB ；
∴ AB ∥ P 。
B
反之，如果直线AB 与平面P 平行，那么在平面内 一定有一条直线与该直线AB 平行。
平面与平面平行
• 几何条件：
实长
α
α z 坐标差
水平投影
z 坐标差
实长
α
α
α
实长
z坐标差
实长
实长
水平投影 水平投影
z 坐标差 α
z 坐标差
两直线平行
两直线在空间平行则它们的各组同面投影必平行
即若AB∥CD B 则ab∥cd ； a’b’∥c’d’ 。
C A
D
c’ d’ X b’
a’
O d c
a d
b
c
b
a
两直线平行
① a a b c c b ② c d d c b a b
b m
c a n
b
m(n)
a
●
c
两平面相交
⑴ 两特殊位置平面 相交，根据交线的 投影特性分析交线 的空间位置，有时 可找出两平面的一 个共有点，画出交 线的投影。
a b e f
c
d a e c
d
b f
两平面相交
⑵ 一般位置平面与特殊 位置平面相交，可利 用特殊位置平面的积 聚性找出两平面的两 个共有点，求出交线。
平行于 面 （侧平线）
＝
反映 、实角
直线的位置
直 观 图
E B
c
d
c b
直线和平面平行
• 几何条件
如果平面P 外的一条直线AB 与平面内的一条直线 平行,那么这条直线AB 和这个平面P 平行。 ∵ L∈P ；
L
A
L ∥AB ；
∴ AB ∥ P 。
B
反之，如果直线AB 与平面P 平行，那么在平面内 一定有一条直线与该直线AB 平行。
平面与平面平行
• 几何条件：
实长
α
α z 坐标差
水平投影
z 坐标差
实长
α
α
α
实长
z坐标差
实长
实长
水平投影 水平投影
z 坐标差 α
z 坐标差
两直线平行
两直线在空间平行则它们的各组同面投影必平行
即若AB∥CD B 则ab∥cd ； a’b’∥c’d’ 。
C A
D
c’ d’ X b’
a’
O d c
a d
b
c
b
a
两直线平行
① a a b c c b ② c d d c b a b
b m
c a n
b
m(n)
a
●
c
两平面相交
⑴ 两特殊位置平面 相交，根据交线的 投影特性分析交线 的空间位置，有时 可找出两平面的一 个共有点，画出交 线的投影。
a b e f
c
d a e c
d
b f
两平面相交
⑵ 一般位置平面与特殊 位置平面相交，可利 用特殊位置平面的积 聚性找出两平面的两 个共有点，求出交线。
平行于 面 （侧平线）
＝
反映 、实角
直线的位置
直 观 图
相关主题
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
点线面的投影规律总结标准化文件发布号：（9312-EUATWW-MWUB-WUNN-INNUL-DDQTY-KII
点线面的投影规律 类型 投影规律 点 a'a ⊥OX 轴,a'a''⊥OZ 轴,aa YH
⊥Oa YH 轴,a''a YW ⊥Oa YW 轴,Oa YH =Oa YW
投影面
平行线 两投影线分别平行于不同
轴，
根据实形斜线判断所平行的投影面，
斜线反映与另外两投影面夹角
投影面
垂直线 两投影实长线平行于同一轴，
根据集聚点判断所垂直的投影面，
一般位置直线 三个投影都倾斜于投影轴， 均不反应夹角和实长
投影面
平行面 两面投影积聚成线，且平行于不同轴，
根据实形面判定所平行的投影面
投影面
垂直面 两面投影相仿，
根据积聚斜线判定所垂直的
投影面，
斜线反映与另外两投影面夹角
一般位置平面 三个投影都类似。