自动控制原理之第三章一时域性能指标时域分析5精品PPT课件
合集下载
自控原理课件第03-1,2章控制系统的时域分析

2020/4/6
8
典型响应:
C(s) G(s) R(s)
⒈ 单位脉冲函数响应:
C(s) G(s)1
⒉ 单位阶跃函数响应: ⒊ 单位斜坡函数响应: ⒋ 单位抛物线函数响应:
C(s) G(s) 1 s
C(s)
G(
s)
1 s2
C
(s)
G(s)
1 s3
[提示]:上述几种典型响应有如下关系:
积分
积分
单位脉冲
2020/4/6
14
❖第二节 一阶系统的时域分析
2020/4/6
15
用一阶微分方程描述的控制系统称为一阶系统。
R
其微分方程为
+
r(t)
i(t) C
+
c(t)
RC
duc dt
Uc
r(t)
•
T C(t) C(t) r(t)
(a) 电路图
其中C(t)为电路输出电压,r(t)为电 路输入电压,T=RC为时间常数。
c(t) t T (1 e T ) t T Te T
t
1t
e(t) r(t) c(t) T (1 e T )
所以一阶系统跟踪单位斜坡信号 的稳态误差为
ess
lim e(t)
t
T
2020/4/6
19
2 一阶系统的单位脉冲响应
当输入信号为理想单位脉冲函数时,R(s)=1,输出量的拉氏 变换与系统的传递函数相同,即
当初使条件为零时,其传递函数为 一阶系统的框图:
(s) C(s) 1
R(s) TS 1
a) 一阶系统框图 b) 等效框图
这种系统实际上是一个非周期性的惯性环节。
自动控制原理课件之第三章 (一) 时域性能指标,时域分析 (5)

故 20lg ( j) 3(dB)
b
系统带宽频率与带宽
一阶和二阶系统,带宽和系统参数具有解析关系。
自动控制原理教案
一阶系统的带宽: 一阶系统: 因为
1 (s) Ts 1
, 按带宽定义
1 1 T 2b
2
( j 0) 1
20lg ( jb ) 20lg
解 因为该系统为I型系统,单位速度输入下的稳态误差为 查表
1 K 9 K
60
0.62 % e
/ 1 2
7.5%
K 2 1 n , 2n n 2 K 11.6 T T 3.5 ts 0.506
n
自动控制原理教案
G ( j ) G ( j ) 1 G ( j ) A( )
1 2
[1 A2 ( ) 2 A( ) cos ( )] 1 1 [ cos ( )]2 sin 2 ( ) A( )
一般情况下,在M (ω)的极大值附近, γ(ω) 变化较小,且使M (ω)为极值的谐振频率ωr常位于ωc附近,即有
( j 0) 1 , 按带宽定义
b 2 2 b 2 (1 2 ) 4 2 2 2 n n
b n (1 2 2 ) (1 2 2 )2 1
1 2
二阶系统的带宽和自然频率成正比。与阻尼比成反比。
自动控制原理教案
带宽指标意义
根据一阶系统和二阶系统上升时间和过渡过程时间与参数的 关系,可以推论:系统的单位阶跃响应的速度和带宽成正比。 对于任意阶次的控制系统,这一关系仍然成立。 当系统的带宽扩大λ 倍,系统的响应速度则加快λ 倍。 对于输入端信号,带宽大,则跟踪控制信号的能力强;而在另一 方面, 抑制输入端高频干扰的能力则弱,因此系统带宽的选择在设计中应折 衷考虑,不能一味求大。
自动控制原理及应用课件(第三章)

即 s1,2=- n 临界阻尼情况的单位阶跃响应为
C(s) n2 1 (s n )2 s
设部分分式为
C(s) A1 A2 A3
s s n (s n )2
式中,待定系数分别为A1=1,A2=-1,A3=-n
于是有
C(s) 1 1 n s s n (s n )2
取C(s)的拉普拉斯逆变换,则有
R(s) A0 s2
3.抛物线信号 抛物线信号的数学表达式为
0
r(t)
1 2
A0t
2
(t 0) (t ≥ 0)
式中,A0为常数。
当A0=1时,称为单位抛物线信 号,也称为单位加速度信号。
抛物线信号如图所示,它表示
随时间以等加速度增长的信号。
图3-3 抛物线信号
抛物线信号在零初始条件下的拉普拉斯变换为
R(s) A0 s3
4.脉冲信号 脉冲信号是一个脉宽极短的信号,其数学表达式为
0 t < 0;t >
r
(t
)
A0
0<t <
脉冲信号如图3-4(a)所示,
当A0=1时,若令脉宽 →0,则
称为单位理想脉冲函数,记作
(t),单位脉冲函数如图3-4(
b)所示, (t)函数满足
(t)
0
(t 0) (t 0)
闭环传递函数为 系统特征根为
(s) n2 s2 n2
s1,2 jn
无阻尼情况的单位阶跃响应为
C(s) n2 1 1 s s2 n2 s s s2 n2
取C(s)的拉普拉斯逆变换,则有
c(t) 1 cosnt (t ≥ 0)
系统阶跃响应曲线为等幅振荡,超调量为100%,振荡频率为 自然振荡角频率 n 。由于曲线不收敛,系统处于临界稳定状 态。
自动控制原理的时域分析法ppt课件

精选课件PPT
13
系统的时域性能指标
• 稳定性 • 动态性能指标 • 稳态(静态)性能指标
精选课件PPT
14
单位阶跃响应性能指标:
H(t) 阶跃响应输出
1
0.9
误差带
0.5 Td
超调 稳态误差Ess
0.1 0
Tr Tp
Ts
上升时间
峰值时间 精选课调件PP整T 时间
t
15
1 延迟时间Td:指h(t)上升到稳态的50%所 需的时间。
稳定性是研究扰动去除后系统的运动情况,它与 系统的输入信号无关,因而可以用系统的脉冲响 应函数来描述,如果脉冲响应函数是收敛的,则 系统稳定。反之,系统不稳定。
精选课件PPT
22
设系统传递函数有 K 个实根 i(i 1K)
r 对共轭复根 (iji)(i1K)
则脉冲响应为:
K
r
y (t)C ie ite it(A ic o s it B isin it)
s 3 2 13 s 2 10 4
将s=z-1代入原方程得:
2 z 3 4 z 2 z 1 0
NEW ROUTH’S TABLE:
s3 2 1
s 1 12 . 2
s2 4 1
s0 4
s1 0 .5
故S右半平面无闭环
s0 1
极点。系统是稳定 的
精选课件PPT故有一个根在s=-1的右边33 。
精选课件PPT
27
劳斯判据
1、列出系统闭环特征方程:
F ( s ) a n s n a n 1 s n 1 a 1 s a 0 0 上式中所有系数均为实数,并设 an 0
2、按系统闭环特征方程列写劳斯行列表:
自动控制原理第三章

5
3-2 一阶系统的时域分析
用一阶微分方程描述的控制系统
3-2-1 一阶系统数学描述 RC电路 其微分方程为: 电路, 例如 RC电路,其微分方程为:
R + r(t) _ I
1 Cs
+ C c(t) _ C(s)
ɺ T c+c = r
其中:c(t) 为电路输出电压, 其中: 为电路输出电压, R(s) UR r(t) 为电路输入电压, 为电路输入电压, T=RC为时间常数 为时间常数 由原理图得系统结构图。 由原理图得系统结构图。 R(s) 当初始条件为零时,其传递函数为: 当初始条件为零时,其传递函数为 C ( s) 1 = Φ ( s) = 一阶惯性环节 R(s) Ts + 1
t − 1 2 c (t ) = t − Tt + T 2 1 − e T 2
误差: 误差:
(t ≥ 0)
t − e (t ) = r (t ) − c (t ) = Tt − T 1 − e T 2
(t ≥ 0)
跟踪误差随时间推移而增大,直至无限大。 跟踪误差随时间推移而增大,直至无限大。 因此,一阶系统不能跟踪加速度输入。 因此,一阶系统不能跟踪加速度输入。
1 R
-
1 Ts
C(s)
6
3-2-2 一阶系统单位阶跃响应 系统输入: 系统输入:R(s ) = 1 系统输出: 系统输出:C ( s ) = Φ ( s ) R( s ) = 1 ⋅ 1 Ts + 1 s 1 T = − s Ts + 1 变换, Λ−1变换,得:h( t ) = 1 − e ,t ≥ 0 阶跃响应的特点: 阶跃响应的特点: 1 1) 在 t=0 时的斜率最大,为: 时的斜率最大,
3-2 一阶系统的时域分析
用一阶微分方程描述的控制系统
3-2-1 一阶系统数学描述 RC电路 其微分方程为: 电路, 例如 RC电路,其微分方程为:
R + r(t) _ I
1 Cs
+ C c(t) _ C(s)
ɺ T c+c = r
其中:c(t) 为电路输出电压, 其中: 为电路输出电压, R(s) UR r(t) 为电路输入电压, 为电路输入电压, T=RC为时间常数 为时间常数 由原理图得系统结构图。 由原理图得系统结构图。 R(s) 当初始条件为零时,其传递函数为: 当初始条件为零时,其传递函数为 C ( s) 1 = Φ ( s) = 一阶惯性环节 R(s) Ts + 1
t − 1 2 c (t ) = t − Tt + T 2 1 − e T 2
误差: 误差:
(t ≥ 0)
t − e (t ) = r (t ) − c (t ) = Tt − T 1 − e T 2
(t ≥ 0)
跟踪误差随时间推移而增大,直至无限大。 跟踪误差随时间推移而增大,直至无限大。 因此,一阶系统不能跟踪加速度输入。 因此,一阶系统不能跟踪加速度输入。
1 R
-
1 Ts
C(s)
6
3-2-2 一阶系统单位阶跃响应 系统输入: 系统输入:R(s ) = 1 系统输出: 系统输出:C ( s ) = Φ ( s ) R( s ) = 1 ⋅ 1 Ts + 1 s 1 T = − s Ts + 1 变换, Λ−1变换,得:h( t ) = 1 − e ,t ≥ 0 阶跃响应的特点: 阶跃响应的特点: 1 1) 在 t=0 时的斜率最大,为: 时的斜率最大,
自动控制原理之 一 时域性能指标时域分析PPT课件

若要求ts=0.1s,求反馈系数Kh .
解题关键:化闭环传递函数为标准形式
第20页/共107页
3.3 二阶系统的时域分析
第21页/共107页
21
第22页/共107页
22
3.3.2 二阶系统的阶跃响应
闭环特征根决定了系统的响应形式。
第23页/共107页
23
第24页/共107页
24
欠阻尼二阶系统的单位阶响应由稳态和瞬态两部分
1
R( s ) 1 K1
Ts K1 1 T ' s 1
Ts 1
第12页/共107页
12
一阶系统的单位阶跃响应
1 1 1
1
C (s) G (s) R(s)
Ts 1 s s s 1
T
c(t ) 1 e t / T , t 0
方法:复数域求解,
组成
• 动态过程:在输入信号作用下系统输出量从初始状态到最终状态的响
应过程。
• 稳态过程:时间趋于无穷大时的响应
性能指标分为动态性能指标和稳态性能指标。
第2页/共107页
2
系统稳定性问题
稳定是控制系统运行的首要条件,只有动态
过程收敛研究系统性能才有意义。
任何系统在扰动作用下都会偏离原平衡状态,
产生初始偏差, 在扰动消失后,
求反变换
如图所示为典型一阶系统
的单位阶跃响应曲线。
第13页/共107页
13
一阶惯性环节的阶跃响应曲线
C(t)=1-e-t/T,t≥0
第14页/共107页
14
15
一阶系统的动态性能指标:
td=0.69T
解题关键:化闭环传递函数为标准形式
第20页/共107页
3.3 二阶系统的时域分析
第21页/共107页
21
第22页/共107页
22
3.3.2 二阶系统的阶跃响应
闭环特征根决定了系统的响应形式。
第23页/共107页
23
第24页/共107页
24
欠阻尼二阶系统的单位阶响应由稳态和瞬态两部分
1
R( s ) 1 K1
Ts K1 1 T ' s 1
Ts 1
第12页/共107页
12
一阶系统的单位阶跃响应
1 1 1
1
C (s) G (s) R(s)
Ts 1 s s s 1
T
c(t ) 1 e t / T , t 0
方法:复数域求解,
组成
• 动态过程:在输入信号作用下系统输出量从初始状态到最终状态的响
应过程。
• 稳态过程:时间趋于无穷大时的响应
性能指标分为动态性能指标和稳态性能指标。
第2页/共107页
2
系统稳定性问题
稳定是控制系统运行的首要条件,只有动态
过程收敛研究系统性能才有意义。
任何系统在扰动作用下都会偏离原平衡状态,
产生初始偏差, 在扰动消失后,
求反变换
如图所示为典型一阶系统
的单位阶跃响应曲线。
第13页/共107页
13
一阶惯性环节的阶跃响应曲线
C(t)=1-e-t/T,t≥0
第14页/共107页
14
15
一阶系统的动态性能指标:
td=0.69T
自动控制原理-第3章

响应曲线如图3-2所示。图中
为输出的稳态值。
第三章 线性系统的时域分析 法
图 3-2 动态性能指标
第三章 线性系统的时域分析 法
动态性能指标通常有以下几种:
延迟时间td: 指响应曲线第一次达到稳态值的一半所需的时间
上升时间tr: 若阶跃响应不超过稳态值, 上升时间指响应曲线从 稳态值的10%上升到90%所需的时间; 对于有振荡的系统, 上升时 间定义为响应从零第一次上升到稳态值所需的时间。上升时间越 短, 响应速度越快。
可由下式确定: (3.8)
振荡次数N: 在0≤t≤ts内, 阶跃响应曲线穿越稳态值c(∞)次 一半称为振荡次数。
上述动态性能指标中, 常用的指标有tr、ts和σp。上升时间tr 价系统的响应速度; σp评价系统的运行平稳性或阻尼程度; ts是同
时反映响应速度和阻尼程度的综合性指标。 应当指出, 除简单的一 、二阶系统外, 要精确给出这些指标的解析表达式是很困难的。
中可以看出, 随着阻尼比ζ的减小, 阶跃响应的振荡程度加剧。 ζ =0时是等幅振荡, ζ≥1时是无振荡的单调上升曲线, 其中临界阻尼 对应的过渡过程时间最短。 在欠阻尼的状态下, 当0.4<ζ<0.8时过
渡过程时间比临界阻尼时更短, 而且振荡也不严重。 因此在 控制工程中, 除了那些不允许产生超调和振荡的情况外, 通常都希
第三章 线性系统的时域分析法 4. 脉冲函数 脉冲函数(见图3-1(d))的时域表达式为
(3.4)
式中,h称为脉冲宽度, 脉冲的面积为1。若对脉冲的宽度取趋于 零的极限, 则有
(3.5) 及
(3.6)
称此函数为理想脉冲函数, 又称δ函数(见图3-1(e))。
第三章 线性系统的时域分析 法
自动控制原理课件之第三章 (一) 时域性能指标,时域分析 (1)
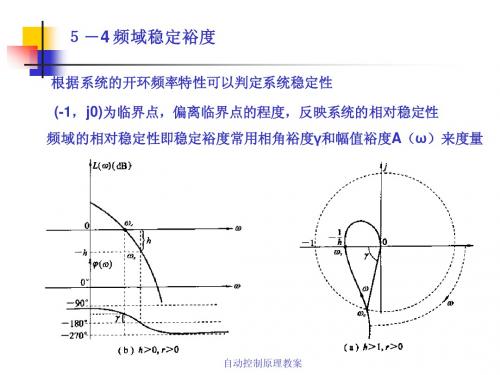
5-4 频域稳定裕度
根据系统的开环频率特性可以判定系统稳定性 (-1,j0)为临界点,偏离临界点的程度,反映系统的相对稳定性 频域的相对稳定性即稳定裕度常用相角裕度γ和幅值裕度A(ω)来度量
自动控制原理教案
相角裕度γ和幅值裕度A(ω)定义
相角裕度γ 设ωc为系统的截止频率
A ( c ) G ( j c ) H ( c ) 1
1 G ( j x ) H ( x )
对数坐标下 h 20 lg G ( j x ) H ( x )
幅值裕度h的含义是,对于闭环稳定系统,如果系统开环幅频特性再增大h倍, 则系统将处于临界稳定状态
自动控制原理教案
例5—12
已知单位反馈系统
G (s) K ( s 1)
3
设k分别为4和10时,试确定系统的稳定裕度。 解 系统开环频率特性
180 G ( j c ) H ( c )
相角裕度γ的含义是,对于闭环稳定系统,如果系统开环相频特性再 滞后γ度,则系统将处于临界稳定状态。 幅值裕度 设ωx为系统的穿越频率 定义幅值裕度为
h
( x ) G ( j x ) H ( x ) ( 2 k 1)
上例中减小开环增益可以增大系统的相角裕度,
但会增大系统的稳态误差,一般要求相角裕度达到 45º ~70º ,为满足这一要求在截止频率附近的斜率大 于-40dB/dec,且有一定的宽度. 若兼顾系统的稳态误差和过度过程的要求,有 必要应用校正方法
自动控制原理教案
自动控制原理教案
例5—13 典型二阶系统相角裕度γ
典型二阶系统如图所示,试确定系统的相角裕度γ。 解 典型二阶系统的开环频率特性为
G ( j )
根据系统的开环频率特性可以判定系统稳定性 (-1,j0)为临界点,偏离临界点的程度,反映系统的相对稳定性 频域的相对稳定性即稳定裕度常用相角裕度γ和幅值裕度A(ω)来度量
自动控制原理教案
相角裕度γ和幅值裕度A(ω)定义
相角裕度γ 设ωc为系统的截止频率
A ( c ) G ( j c ) H ( c ) 1
1 G ( j x ) H ( x )
对数坐标下 h 20 lg G ( j x ) H ( x )
幅值裕度h的含义是,对于闭环稳定系统,如果系统开环幅频特性再增大h倍, 则系统将处于临界稳定状态
自动控制原理教案
例5—12
已知单位反馈系统
G (s) K ( s 1)
3
设k分别为4和10时,试确定系统的稳定裕度。 解 系统开环频率特性
180 G ( j c ) H ( c )
相角裕度γ的含义是,对于闭环稳定系统,如果系统开环相频特性再 滞后γ度,则系统将处于临界稳定状态。 幅值裕度 设ωx为系统的穿越频率 定义幅值裕度为
h
( x ) G ( j x ) H ( x ) ( 2 k 1)
上例中减小开环增益可以增大系统的相角裕度,
但会增大系统的稳态误差,一般要求相角裕度达到 45º ~70º ,为满足这一要求在截止频率附近的斜率大 于-40dB/dec,且有一定的宽度. 若兼顾系统的稳态误差和过度过程的要求,有 必要应用校正方法
自动控制原理教案
自动控制原理教案
例5—13 典型二阶系统相角裕度γ
典型二阶系统如图所示,试确定系统的相角裕度γ。 解 典型二阶系统的开环频率特性为
G ( j )
自动控制原理第三章ppt课件

自动控制原理
.
1
第三章 线性系统的时域分析法
线性系统的时域分析法
引言 一阶系统时域分析 二阶系统时域分析 线性系统的稳定性分析 线性系统的稳态误差计算
.
3
自动控制系统好?差? 系统分析
典型的输入信号
时域分 析
复域分 单位析脉冲 频阶域跃分
斜析坡 正余弦
时域性能指标
稳态性能 指标
稳定性
动态性能 指标
2
0
1.8 0.4
0.1
1.6 0.5
0.2
1.4 0.6
0.3
1.2 0.7
1 0.8
0.8
0.6 0.4 0.2
0 0
0.9 1.0 1.5
246
阻尼比越小,超调量越大,上升时间越短。
2
nt
8 10 12
阻尼比取0.40.8时,超调 量适宜,调节
时间短
可以看出:随着 的增加,c(t)将从无衰减的周期运动变为有
能
指
标
稳态性能指标
1.动态性能指标
通常在阶跃函数作用下,测定或计算系统的动态性能。
一般认为,阶跃输入对系统来说是最严峻的工作状态。 如果系统在阶跃函数作用下的动态性能满足要求,那 么系统在其他形式的函数作用下,其动态性能也是令 人满意的。
描述稳定的系统在单位阶跃函数下,动态过程 随时间t的变化状况的指标,称为动态性能指标。
评价系统的阻尼程度。(稳)
稳定性能指标和抗干扰能力。越小, 系统精度越高。(准)
§3.3 典型一阶系统时域分析
一、典型一阶系统的数学模型 以一阶微分方程为运动方程的系 统 (s)C(s) 1 R(s) TS1
②
ui
.
1
第三章 线性系统的时域分析法
线性系统的时域分析法
引言 一阶系统时域分析 二阶系统时域分析 线性系统的稳定性分析 线性系统的稳态误差计算
.
3
自动控制系统好?差? 系统分析
典型的输入信号
时域分 析
复域分 单位析脉冲 频阶域跃分
斜析坡 正余弦
时域性能指标
稳态性能 指标
稳定性
动态性能 指标
2
0
1.8 0.4
0.1
1.6 0.5
0.2
1.4 0.6
0.3
1.2 0.7
1 0.8
0.8
0.6 0.4 0.2
0 0
0.9 1.0 1.5
246
阻尼比越小,超调量越大,上升时间越短。
2
nt
8 10 12
阻尼比取0.40.8时,超调 量适宜,调节
时间短
可以看出:随着 的增加,c(t)将从无衰减的周期运动变为有
能
指
标
稳态性能指标
1.动态性能指标
通常在阶跃函数作用下,测定或计算系统的动态性能。
一般认为,阶跃输入对系统来说是最严峻的工作状态。 如果系统在阶跃函数作用下的动态性能满足要求,那 么系统在其他形式的函数作用下,其动态性能也是令 人满意的。
描述稳定的系统在单位阶跃函数下,动态过程 随时间t的变化状况的指标,称为动态性能指标。
评价系统的阻尼程度。(稳)
稳定性能指标和抗干扰能力。越小, 系统精度越高。(准)
§3.3 典型一阶系统时域分析
一、典型一阶系统的数学模型 以一阶微分方程为运动方程的系 统 (s)C(s) 1 R(s) TS1
②
ui
自动控制原理 第三章 时域分析法ppt

离虚轴远的极点所决定的分量对响应产生的影响小, 有时甚至可以忽略不计。
过阻尼系统单位阶跃响应
与一阶系统阶跃响应的比较
二阶过阻尼系统阶跃响应指标分析 ( 1 ).稳 态 误 差 e s s l ti m [r (t) c (t)] 0
(2 ).响 应 没 有 振 荡 σ % = 0
2.欠阻尼 (0 1) 二阶系统的单位阶跃 响应
KKHH
一阶系统如图所示,试求:
1. 当KH=0.1时,求系统单位阶跃响应的调节时间ts,放大倍
数K,稳态误差ess。
2. 如果要求ts=0.1s,试问系统的反馈系数KH应调整为何值? 3. 讨论KH的大小对系统性能的影响及KH与ess的关系。
二、二阶系统的数学模型及单位阶跃响应
• 由二阶微分方程描述的系统称为二阶系统
第三章 时域分析法
主要内容
•3.1 •3.2 •3.3 •3.4 •3.5
时域分析基础 一、二阶系统分析与计算 高阶系统动态响应及简化分析 控制系统的稳定性分析及其代数判据 稳态误差分析计算
3.1 时域分析基础
1. 时域分析:根据系统微分方程,通过拉氏
变换,直接求出系统的时间响应。依据响应 的表达式及时间响应曲线来分析系统控制性 能,并找出系统结构、参数与这些性能之间 的关系。
3-2 一、二阶系统分析与计算
1.一阶系统的数学模型及单位阶跃响应
微分方程:
动态结构图:
传递函数:
一阶系统单位阶跃响应
输入: 输出:
初始斜率:
性能指标
1. 平稳性: 非周期、无振荡, =0
2. 快速性ts:
3. 准确性 ess:
例3-1
R(s) E(s) 110000 C(s)
过阻尼系统单位阶跃响应
与一阶系统阶跃响应的比较
二阶过阻尼系统阶跃响应指标分析 ( 1 ).稳 态 误 差 e s s l ti m [r (t) c (t)] 0
(2 ).响 应 没 有 振 荡 σ % = 0
2.欠阻尼 (0 1) 二阶系统的单位阶跃 响应
KKHH
一阶系统如图所示,试求:
1. 当KH=0.1时,求系统单位阶跃响应的调节时间ts,放大倍
数K,稳态误差ess。
2. 如果要求ts=0.1s,试问系统的反馈系数KH应调整为何值? 3. 讨论KH的大小对系统性能的影响及KH与ess的关系。
二、二阶系统的数学模型及单位阶跃响应
• 由二阶微分方程描述的系统称为二阶系统
第三章 时域分析法
主要内容
•3.1 •3.2 •3.3 •3.4 •3.5
时域分析基础 一、二阶系统分析与计算 高阶系统动态响应及简化分析 控制系统的稳定性分析及其代数判据 稳态误差分析计算
3.1 时域分析基础
1. 时域分析:根据系统微分方程,通过拉氏
变换,直接求出系统的时间响应。依据响应 的表达式及时间响应曲线来分析系统控制性 能,并找出系统结构、参数与这些性能之间 的关系。
3-2 一、二阶系统分析与计算
1.一阶系统的数学模型及单位阶跃响应
微分方程:
动态结构图:
传递函数:
一阶系统单位阶跃响应
输入: 输出:
初始斜率:
性能指标
1. 平稳性: 非周期、无振荡, =0
2. 快速性ts:
3. 准确性 ess:
例3-1
R(s) E(s) 110000 C(s)
自动控制原理-第3章 时域分析法82页PPT文档

因为劳思表第一列数符号变化2次,所以系统是不稳定的,有2个特征根在右 半S平面。
11
特殊情况(1):劳思表中某一行的第一列数为0,其余不为0。 解决办法:用一个很小的正数(也可以是负数) 然后继续列劳思表。
例3.4 已知系统的特征方程为 D (s)s43 s3s23 s 10
用劳思稳定判据判别系统稳定性。
b3an 1 1a a nn 1
an6an 1an6anan7
an7
an 1
直至其余 全为0。
c1b 11ab n1 1
an3b1an3b2an1
b2
b1
c2b 1 1ab n1 1
an5b1an5b3an1
b3
b1
c3b 1 1ab n1 1
an7b1an7b4an1
b4
b1
直至其余 c i 全为0。
系统的脉冲响应为
k
r
y(t) C ieit eit(A icods tiB isin dt)i
i 1
i 1
6
系统稳定的充分必要条件是稳定性分析的基础。 但直接检查全部特征根是否都具有负实部是困难的。 因此,后面将陆续介绍各种稳定性判据。如:
• 稳定性的代数稳定判据 • 李雅普诺夫稳定判据 • 奈奎斯特稳定判据
劳思表第一列数符号变化2次,所以系统是不稳定的,有2个特征根在右半S平面。
12
特殊情况(2):劳思表中某一行的数全为0
解决办法:用上一行的数构成辅助多项式,将辅助多项式对变量
得到一个新的多项式。然后用这个新多项式的系数代替全为0 一行的数,继续列劳斯表。
例3.5 已知系统的特征方程为
D (s ) s 6 s 5 2 s 4 3 s 3 7 s 2 4 s 4 0
11
特殊情况(1):劳思表中某一行的第一列数为0,其余不为0。 解决办法:用一个很小的正数(也可以是负数) 然后继续列劳思表。
例3.4 已知系统的特征方程为 D (s)s43 s3s23 s 10
用劳思稳定判据判别系统稳定性。
b3an 1 1a a nn 1
an6an 1an6anan7
an7
an 1
直至其余 全为0。
c1b 11ab n1 1
an3b1an3b2an1
b2
b1
c2b 1 1ab n1 1
an5b1an5b3an1
b3
b1
c3b 1 1ab n1 1
an7b1an7b4an1
b4
b1
直至其余 c i 全为0。
系统的脉冲响应为
k
r
y(t) C ieit eit(A icods tiB isin dt)i
i 1
i 1
6
系统稳定的充分必要条件是稳定性分析的基础。 但直接检查全部特征根是否都具有负实部是困难的。 因此,后面将陆续介绍各种稳定性判据。如:
• 稳定性的代数稳定判据 • 李雅普诺夫稳定判据 • 奈奎斯特稳定判据
劳思表第一列数符号变化2次,所以系统是不稳定的,有2个特征根在右半S平面。
12
特殊情况(2):劳思表中某一行的数全为0
解决办法:用上一行的数构成辅助多项式,将辅助多项式对变量
得到一个新的多项式。然后用这个新多项式的系数代替全为0 一行的数,继续列劳斯表。
例3.5 已知系统的特征方程为
D (s ) s 6 s 5 2 s 4 3 s 3 7 s 2 4 s 4 0
相关主题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
co ( s r)co ( s c)co 当s
A() 1 cos()
时有极值
Mr M(r)sin 1(r)s1in
电工学与电子技术
系统闭环和开环频域指标的关系
由于cos (ω) <l,故在闭环幅频特性的峰值处对应的 开环幅值A(ωr)>l,而A(ωc)=1,显然ωr≤ ωc 。
随着相角裕度γ的减小, ωc- ωr减小, γ =0时, ωr = ωc 。
一阶和二阶系统,带宽和系统参数具有解析关系。
电工学与电子技术
一阶系统的带宽:
一阶系统:
(s) 1
Ts 1
因为 (j0)1 , 按带宽定义
20 lg(jb)20 lg1T 12b2
20 lg1 2
b
1 T
一阶系统的带宽和时间常数成反比。
电工学与电子技术
二阶系统带宽:
对于二阶系统,闭环传递函数为
(s)
2 4n2
2n
根据定义 相角裕度γ
c (
1
44122)2
n
180G( jc)
18090arctgc arctg2n
2n
c
arctg[2( 44 12 2)12]
一般 30º≤γ≤70º
当选定γ后,可由γ-ξ曲线确定ξ,再由ξ确定б%,调节时间ts
电工学与电子技术
例5—14 设一单位反馈系统的开环传递函数
ωc 大的系统 ωb大
2. 闭环振荡性能指标谐振峰值Mr和开环指标相角裕度γ都能
表征系统的稳定程度.
Mr M(r)sin 1(r)s1in
证明
设系统开环相频特性可以表示为 () 18 0 ()
其中γ(ω)表示相角相对于-180º的相移。
开环频率特性可以表示为
G(j )A( )ej[180()] A() [cos()jsin()]
G(s) K
若已知单位速度信号输入下的稳态误差
s(Ts 1)
ess ( )
1 9
相角裕度 60
试确定系统时域指标 % , t s
解 因为该系统为I型系统,单位速度输入下的稳态误差为
1 K 9 K
查表 60 0.62 % e/ 1 27.5%
K T
n2,T1
2n
n
2K
11.6
ts
3.5
用于频域的分析和综合。
闭环系统频域指标:频带宽度 虽然能反映系统的跟踪速度和抗干扰能力,但需要通过闭环频率
特性(待定)加以确定.
工程上常用γ(相角裕度)和ωc (截止频率)(开环系统)来估算系统的 时域性能指标,可由开环特性确定。
电工学与电子技术
系统闭环和开环频域指标的关系
1.系统开环指标截止频率ωc与闭环指标带宽频率ωb有着密切的关系。
电工学与电子技术
系统闭环和开环频域指标的关系
闭环幅频特性
G ( j ) G ( j ) 1 G ( j )
A( )
1
[1 A 2 ( ) 2 A ( ) cos ( )] 2
1
[ 1 cos ( )] 2 sin 2 ( )
A( )
一般情况下,在M (ω)的极大值附近, γ(ω) 变化较小,且使M (ω)为极值的谐振频率ωr常位于ωc附近,即有
由此可知, γ较小时,近似程度较高。
控制系统的设计中,一般先根据控制要求提出闭 环频域指标ωb和Mr,再确定相角裕度γ和选择合适的 截止频率ωc ,然后根据γ和ωc选择校正网络的结构并 确定参数。
电工学与电子技术
开环频
j( j2n )
n2
90arctg
对于任意阶次的控制系统,这一关系仍然成立。 当系统的带宽扩大λ倍,系统的响应速度则加快λ 倍。
对于输入端信号,带宽大,则跟踪控制信号的能力强;而在另一 方面, 抑制输入端高频干扰的能力则弱,因此系统带宽的选择在设计中应折 衷考虑,不能一味求大。
电工学与电子技术
频域指标和时域指标关系
(闭环)系统时域指标: 超调量б%,调节时间ts 物理意义明确、直观,但仅运用于单位阶跃响应且不能直接应
s2
n2 2 nsn2
系统幅频特性
因为 (j0)1
(j)
1
(1n22)2
42
2 n2
, 按带宽定义
(1bn22)2
42
b2 n2
2
1 bn( 1 22 )( 1 22 )2 1 2
二阶系统的带宽和自然频率成正比。与阻尼比成反比。
电工学与电子技术
带宽指标意义
根据一阶系统和二阶系统上升时间和过渡过程时间与参数的 关系,可以推论:系统的单位阶跃响应的速度和带宽成正比。
n
0.506
电工学与电子技术
写在最后
成功的基础在于好的学习习惯
The foundation of success lies in good habits
11
谢谢聆听
·学习就是为了达到一定目的而努力去干, 是为一个目标去 战胜各种困难的过程,这个过程会充满压力、痛苦和挫折
Learning Is To Achieve A Certain Goal And Work Hard, Is A Process To Overcome Various Difficulties For A Goal
5-5闭环系统的频域性能指标
控制系统的频带宽度:
反馈控制系统的闭环传递函数为
(s) G(s)
1G(s)H(s)
当ω〉ωb时 2l0 g (j)2l0 g (j0)3
(0,ωb)为系统的频带宽度
对于I型和I型以上的开环系统,由于
20lg(j0) 0
故 20lg(j)3(dB )
b
系统带宽频率与带宽
