33二阶系统的时域分析PPT课件
合集下载
3.3 二阶系统的时域分析

ζ π π 1 2π 1 tp = = = Td = ωd 2 ωd 2 ωn 1 ζ 2
= tan( β + Kπ ) ω d t p + β = β + π
13
(3) 最大超调量σp%
ζ = 0 σ p % = 100 % ζ = 0.4 σ p % = 25.4%
最大超调量在峰值时间发生,故 ζ = 0 .8 σ p % = 1 . 5 % 1 ζω n t p h(t p ) = 1 e sin(ω d t p + β ) ζ =1 σ p% = 0 1ζ 2
18
�
1ζ 2
决定整个响应过程的衰减快慢. 无阻尼二阶系统: ζ =0 单位阶跃响应
h(t ) = 1 cos ω nt (t ≥ 0)
无阻尼二阶系统的单位阶跃响应围绕1的等幅振荡. 此时二阶系统不能完成控制任务.
7
三,临界阻尼二阶系统的单位阶跃响应
临界阻尼二阶系统有两个相等实根
s1, 2 = ζω n ± ω n ζ 2 1 = ω n
ωn2 ωn2 1 1 C ( s) = 2 = 2 s + 2ζω n s + ω n s ( s + 1 / T1 )( s + 1 / T2 ) s
e t / T1 e t / T2 + 过阻尼响应 h(t ) = 1 + T2 / T1 1 T1 / T2 1 (t ≥ 0 )
过阻尼二阶系统的单位阶跃响应是稳态值为1的无超 调单调上升过程.
R C R 实际阻尼系数 ζ= = = 2 L Rc 临界阻尼系数
2
故ζ 称为相对阻尼系数或阻尼比.
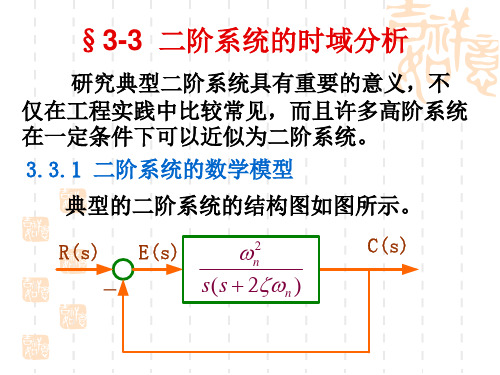
一,二阶系统的数学模型
R(s)
33二阶系统的时域分析PPT课件

求导可知,c(t)输出为一条单调上升的曲线。n 1,2,3时:
3 2 n 1
L[F(sa)]eatf(t)
一定时,随 n 的增大,系统的响应速度变快。
5) 1 (过阻尼)
c ( t ) 1 1
(s)1 G G (s()s)s22 n 2nsn 2
形式
结构图
G(s)
( s s
n2 2n)
R(s) -
2 n
C(s)
s(s 2 n )
:阻尼系数
n :自然频率(无阻尼振荡频率)
❖ 开环传函模拟电路
R1
R(s)
R1
比例 环节
R2
R3 + +
G(s) n2 s(s 2n)
积分 环节
惯性 环节
-1<ξ<0
振荡发散
❖
1时
(s)
s2
n2 2nsn2
,取 n
1
,阶跃响应为:
ξ = -1
c(t)输出为一单调发散形式的曲线。
❖ 1
C (s ) R (s ) (s ) 1 ss 2 2n 2 n sn 2 a s s b p 1 s c p 2
p 1 ( 2 1 )n p 2 ( 2 1 )n
由留数公式:
a[C(s)s]s01
C C(ss)1ss(ss2p12)n2(sn2nsp2) n2
1
b[C (s)(sp 1)]sp 1221(21)
c[C (s)(sp2)]sp222 1(1 2 1)
C(s)a b c s sp1 sp2
1
1
12
2 1(
21) 2
2 1(
2 1)
s s( 21)n s( 21)n
3 2 n 1
L[F(sa)]eatf(t)
一定时,随 n 的增大,系统的响应速度变快。
5) 1 (过阻尼)
c ( t ) 1 1
(s)1 G G (s()s)s22 n 2nsn 2
形式
结构图
G(s)
( s s
n2 2n)
R(s) -
2 n
C(s)
s(s 2 n )
:阻尼系数
n :自然频率(无阻尼振荡频率)
❖ 开环传函模拟电路
R1
R(s)
R1
比例 环节
R2
R3 + +
G(s) n2 s(s 2n)
积分 环节
惯性 环节
-1<ξ<0
振荡发散
❖
1时
(s)
s2
n2 2nsn2
,取 n
1
,阶跃响应为:
ξ = -1
c(t)输出为一单调发散形式的曲线。
❖ 1
C (s ) R (s ) (s ) 1 ss 2 2n 2 n sn 2 a s s b p 1 s c p 2
p 1 ( 2 1 )n p 2 ( 2 1 )n
由留数公式:
a[C(s)s]s01
C C(ss)1ss(ss2p12)n2(sn2nsp2) n2
1
b[C (s)(sp 1)]sp 1221(21)
c[C (s)(sp2)]sp222 1(1 2 1)
C(s)a b c s sp1 sp2
1
1
12
2 1(
21) 2
2 1(
2 1)
s s( 21)n s( 21)n
自动控制原理 3-3二阶系统的时域分析

(a)根分布
(b)单位阶跃响应
图3-12 临界阻尼情况(z =1)
3. >1,称为过阻尼情况 当阻尼比 >1时,系统有两个不相等的实数根:
s1,2 ( 2 1)n 对于单位阶跃输入,C(s)为
(3.27)
C(s) 1 [2 2 1(
2 1)]1 [2 2 1(
2 1)]1
% e 12 100%
e 或 %
tg
100%
取5%
ln
1 2
h(t) 由包络线求调节时间ts
取2%
ln 1 2
0.05 2.997
0.05 3.913
0.1 0.2 0.3
3.001 3.016 3.043
ts
31.5 n
,取5% e 1
n t
12
ts
4.5 n
,取2%
0.1 0.2 0.3
2%, 0.78; 5%, 0.7
当0< <0.9时,则
ts
3
n
3T
(按到达稳态值的95%~105%计)
或
ts
4
n
4T
(按到达稳态值的98%~102%计)
(3.40)
由此可见, n大,ts就小,当n一定,则ts与成反比,这与tp, tr与的关系正好相反。
根据以上分析,如何选取和n来满足系统设计要求,总结几点
令 dh(t) ab(c a) eat ab(a b) ebt 0
dt c(b a)
c(a b)
j
ca
分子正分母负,t<0,
ln 得:t c b
-c -b -a 0
零
无解!
ab
j
点
分子出错,无解! j
第三章2 线性系统的时域分析方法(33)PPT课件

0 虚轴上,瞬态响应变为等幅振荡,无阻尼
左 半 平 面 ξ>0
ξ= 0 jω
右 半 平 面 ξ<0
0< ξ< 1
jω n
ξ=1 两个相等根
ω d= ω n
单位阶跃 响应=0
ξ>1
jω n S1,2 nn 21
两个不等根
自动控制原理
图 3 - 9 二武汉阶 理系工统大学极自点动化分 学布院
n
d n 12
自动控制原理
武汉理工大学自动化学院
d n 12 称为阻尼自振频率
由极限求得 0 1 1 1 2 2n
将它们代入式(3-6)并将式中的第二项分成两项得
C (s) 1 s (s s n ) 2 n d 2 (s n ) n 2 d 2
因为
£ -1[(ssn )2 n d2]en tco ds t
3.3 二阶系统的时域分析
二阶系统:凡以二阶系统微分方程作为运动方程的 控制系统。
3.3.1 二阶系统的数学模型 随动系统A Servo System(位置控制系统)如图36所示。其任务是控制有黏性摩擦和转动惯量的负载, 使负载位置与输入手柄位置协调。
自动控制原理
武汉理工大学自动化学院
自动控制原理
自动控制原理
武汉理工大学自动化学院
1
1
e
2
n tsindt(
)
t0
1
自动控制原理
武汉理工大学自动化学院
(2)临界阻尼 ( 1 )的情况
当 时 ,1 系统具有两个相等的负实数极点,
,
如图S31-,211所示n。此时有
C(s)ss n 2n2 s0s 1n(s 2n)2 (3-7)
自动控制原理3.3~3.4 二阶系统时域分析

闭环特征方程: D( s ) s 2 2 s 2 0 n n 闭环特征根: s1, 2 n n
2
1
二、二阶系统单位阶跃响应
单位阶跃输入r(t)=1(t)时,其二阶系统的输出的拉氏变换为
2 2 n n 1 C ( s ) ( s ) R( s ) 2 2 s 2 n s n s s( s s1 )(s s2 )
e
(ζ ζ 2 1 ) n t
ζ 2 1 ) n t
c(t ) 1
1
2 ζ 2 1 (ζ ζ 2 1) 1 (ζ e 2 ζ 2 1 (ζ ζ 2 1)
e
(ζ ζ 2 1 ) n t
ζ 2 1 ) n t
c(t)
1
0 t
单调上升过程
2.0 1.8 1.6 1.4 1.2 c(t) 1.0 0.8 0.6 0.4 0.2 0
=0
0.4 0.5 0.6 0.7 0.8
0.1 0.2 0.3
1.0 2.0
1
2
3
4
5
• 在0<<1, 越小,超调量越大,平稳性越差,调节时间ts长; • =0.7,调节时间短,而超调量%<5%,平稳性也好,故称 ζ=0.7为最佳阻尼比。工程希望=0.4~0.8为宜; •在≥1 , 越大,系统响应速度慢,调节时间ts也长。
例题:设角度随动系统如图所示,T=0.1为伺服电机时间常数, 若要求系统的单位阶跃响应无超调,且调节时间ts≤1s,问K应 取多大?此时上升时间等于多少?
Θi(s)
_
K s(Ts 1)
Θo(s)
解:闭环传递函数为
K K K /T s (Ts 1) (s) 2 2 K Ts s K s s / T K / T 1 s (Ts 1)
3-3二阶系统的时域分析

输出为衰减振荡形 式(欠阻尼响应) ;
1:
s1, 2 n ;
c(t ) n te
2 t
C(t) t
;
输出为无振荡衰减形式(临界阻尼响应) ;
1 : T11 n n 2 1 s1 ,T21 n n 2 1 s2 ; n t / T t / T
2
s ( s 2 n )
; ( s)
a2 s a1s a2
2
;
典型二阶系统有两个参数。系统有两个极点:
1
极点在S平面上的位置不同(值,见图3-9) ,系统 的性质不同,对输入信号的响应过程不同。
0
0
0
s1, 2 jd
(a ) 1 0
s1, 2 n 1
2
s1, 2 jd
(c) 0 1
(b) 1
0
0
0
s1, 2 jn
(d ) 0
s1, 2 n
(e) 1
s1, 2 n 1
2
(f ) 1
n
衰减系数, d n
1
2
(阻尼)振荡频率
图3-9 二阶系统的闭环极点分布
☆二阶系统的单位脉冲响应:
0:
s1, 2 jn ;
c(t ) n sin( nt ) ;
输出为等幅振荡形式(无阻尼响应) ;
0 1 :s1, 2 jd ;c(t )
n
1
2
e
t
sin( d t ) ;
n
d
e
sin( d t 2 ) ;
3二阶系统的时域分析

式中: n 称为二阶系统的无阻尼振荡频率或自然振荡频率,单位是 rad/s,T 1 n称为二阶系统的时间常数, 称为阻尼比,一般无量纲。
U 0 ( s) 1 LC 1 其传递函数为 G(s) 2 2 U r (s) Lcs Rcs 1 s ( R C )s 1 LC
e nt 1 2
sin( d t )
由此可见误差的响应函数也是一个指数衰减的振荡响应形式。
(2)无阻尼( 0 )二阶系统单位阶跃响应
s 特征根: 1, 2 jn
c 单位阶跃响应: (t ) 1 cosn t (t 0)
分析结论:无阻尼二阶系统的单位阶跃响应曲线呈等幅振荡形式,其 振荡频率为 n ,幅值为1。 误差响应函数: e(t ) r (t ) c(t ) cosn t (t 0) 可见误差响应函数也是等幅振荡 形式,系统得不到稳态误差。
c (t )
1
0
t
四、欠阻尼二阶系统性能指标
c(t ) 1 ent 1 2 sin( 1 2 nt ) 式中, tg 1 1 2
(1)上升时间 t r :根据定义,当 t
t r 时,c(t)=1。
c(tr ) 1
entr 1 2
0
n e
整理得:
n t p 2
1
n
[sin( d t ) d cos( d t )] 0
1 2
[ sin(d t p ) 1 2 cos(d t p )] 0 [cos sin(d t p ) sin cos(d t p )] 0
100%
从上式可知超调量 M p % 仅与阻尼比 有关,而与自然振荡频率无关。 结论:阻尼比 越小,则超调量越大;阻尼比 越大,则超调量越小。
二阶系统的时域分析.ppt

d ds
[C
(s
)(
s
n
)
2
]s
n
1
2 [C(s) (s n )2 ]sn n
C(t) 1 ent ntent 1 ent (1 nt) (t 0)
j [s]
s1s2
n o
1
C(t) 1
1 是输出响应的单调和振荡过程的分界,通
常称为临界阻尼状态。
o
2020/3/29
3-3二阶系统的时域分析
况,故称为阻尼系数。
2020/3/29
3-3二阶系统的时域分析
10
3.二阶系统的性能指标(1)-上升时间
根据定义,当 t tr时,c(tr ) 1。 令 c(t) 1 et sin (dt+ ) =1
sin
c(t) 1 et sin (dt+ ) , t 0 sin
e t sin (d t+ ) 0 sin
T1 T2
n
T2
1
n
h(t)= 1 -(1临+ω界n阻t)尼0je-ωnt
0<0<ξ<ξ<1 1 S1,2= -ξ ωn ±jj ωn√1-ξξ2 =0
jj 0
0
0
e - h(t)=
ξ=1 0 1
2020/3/2√91-ξ2
-ξωSnt欠1s,2i阻n=(尼ω±d3t-j3+二ωβ阶n)系统的时域分析
为阻尼振荡圆频率。
2020/3/29
3-3二阶系统的时域分析
1 2 是振荡频率。称 d
5
2.二阶系统的单位阶跃响应(4)-过阻尼
极点:s1,2 n n 2 1
阶跃响应:c(t) 1
n
3-3 二阶系统的时域分析
1 C (s) = ⋅ ( s − s1 )( s − s2 ) s A3 A1 A2 = + + s s + ωn (ζ − ζ 2 − 1) s + ωn (ζ + ζ 2 − 1)
2 ωn
式中: 式中:A1 = 1,
A3 =
A2 =
−1
2 ζ − 1(ζ − ζ − 1)
2 2
,
1 2 ζ − 1(ζ + ζ − 1)
过阻尼二阶系统的单 位阶跃响应包含两个单调 衰减的指数项。 衰减的指数项。且响应为 非振荡的。 非振荡的。
(一对相等的负实根 一对相等的负实根) 一对相等的负实根 临界阻尼) 3. ζ = 1 时(临界阻尼) 2 s 闭环极点为: 闭环极点为:1,2 = −ζωn ± jωn 1 − ζ |ξ =1 = −ζωn 单位阶跃响应: 单位阶跃响应:
(Q e
− ζω n t r
≠ 0, 1 − ζ 2 ≠ 0 )
1− ζ 2
π −β ∴ tr = = ωd ωn 1 − ζ 2
π −β
( β = arctan(
t 成反比; 一定时, 越小, 成反比;当 ωn 一定时, 越小,r上升时间 ζ
也越小
β tr 一定时, 一定, 当 ζ 一定时, 一定,上升时间 ωn 与
ωn2 s ( s + 2ζωn )
系统的闭环传递函数为: 系统的闭环传递函数为: 2 ωn C ( s) Φ( s) = = 2 2 R( s ) s + 2ζωn s + ωn 系统阻尼比(阻尼系数) ζ —— 系统阻尼比(阻尼系数) ωn —— 无阻尼自然振荡角频率
2 闭环系统特征方程为:s 2 + 2ζωn s + ωn = 0 闭环系统特征方程为: 闭环系统特征根(闭环极点 闭环极点)为 闭环系统特征根 闭环极点 为:
2 ωn
式中: 式中:A1 = 1,
A3 =
A2 =
−1
2 ζ − 1(ζ − ζ − 1)
2 2
,
1 2 ζ − 1(ζ + ζ − 1)
过阻尼二阶系统的单 位阶跃响应包含两个单调 衰减的指数项。 衰减的指数项。且响应为 非振荡的。 非振荡的。
(一对相等的负实根 一对相等的负实根) 一对相等的负实根 临界阻尼) 3. ζ = 1 时(临界阻尼) 2 s 闭环极点为: 闭环极点为:1,2 = −ζωn ± jωn 1 − ζ |ξ =1 = −ζωn 单位阶跃响应: 单位阶跃响应:
(Q e
− ζω n t r
≠ 0, 1 − ζ 2 ≠ 0 )
1− ζ 2
π −β ∴ tr = = ωd ωn 1 − ζ 2
π −β
( β = arctan(
t 成反比; 一定时, 越小, 成反比;当 ωn 一定时, 越小,r上升时间 ζ
也越小
β tr 一定时, 一定, 当 ζ 一定时, 一定,上升时间 ωn 与
ωn2 s ( s + 2ζωn )
系统的闭环传递函数为: 系统的闭环传递函数为: 2 ωn C ( s) Φ( s) = = 2 2 R( s ) s + 2ζωn s + ωn 系统阻尼比(阻尼系数) ζ —— 系统阻尼比(阻尼系数) ωn —— 无阻尼自然振荡角频率
2 闭环系统特征方程为:s 2 + 2ζωn s + ωn = 0 闭环系统特征方程为: 闭环系统特征根(闭环极点 闭环极点)为 闭环系统特征根 闭环极点 为:
3.3.2 二阶系统的时域分析

2.动态性能指标
1.上升时间tr
当t t r时,y t r 1 y t r 1 即 e wntr 1 e wntr 1
2 2
e wntr 1
2
sin wn 1 2 t r 1
sin wn 1 2 t r 0 0 sin wn 1 2 t r 0 wn 1 2 t r k tr
t r为满足此式的最小正数
wn 1 2 t r
wn 1 2
wd
tr
wn 1 2
wd
上升时间和什么有关系?
增大自然频率 wn或减小阻尼比
均能减小tr,从而加快系统的初始 响应速度。
请大家回去思考一个问题 二阶系统初始斜率为多少?
2
闭环特征根
s1, 2 wn jwn 1 2
1 当输入信号为单位阶跃 函数时 Rs s 2 wn 1 Y s Rs GB s 2 2 s 2wn s wn s s wn 1 s s w 2 w 1 2 n n
三.欠阻尼二阶系统的动态性能指标 1.欠阻尼下根的分布
jwn
jwn 1 2
0
s w jw 1
1, 2 n n
2
s1
w jw
n
d
s2
wn
jwn 1 2
衰减系数 wn 是闭环极点到虚轴的距 离。 振荡频率wd wd wn 1 2 是闭环极点到实轴 的距离。无阻尼振荡频 率wn是闭环极点到原点 的距离。若直线 os1与负实轴的夹角为 ,则阻尼 比就等于的余弦,即 cos 。因此就是欠阻尼 二阶系统单位阶跃响应 的初相角。
33二阶系统的时域分析PPT课件

nt
8 10 12
可以看出:随着 的增加,c(t)将从无衰减的周期运动变为有
衰减的正弦运动,当 1 时c(t)呈现单调上升运动(无振荡)。
可见 反映实际系统的阻尼情况,故称为阻尼系数。
20.11.2020
10
三、典型二阶系统的动态过程分析
(一)衰减振荡瞬态过程 (01):欠阻尼
s1,2 njn 12
c (t) 1 e n t (cd o t s1 2sid n t), t 0
⒈ 上升时间 t r :根据定义,当 t tr时,c(tr)1。
c ( tr) 1 e n t r(cd o tr s1 2sid n tr) 1
cosdtr 1 2si ndtr0
tgdtr
1 2
20.11.2020
14
⒊ 最大超调量 % (书上用 %表示)
将峰值时间 tp
n
1 2
代入 c(t)得c(tp)cmax
c m a c (tx p ) 1 e n t p(cd o tp s1 2sin n tp )
1e 12(cos
sin)1e 12
12
% c(tp c )( c )( ) 1% 0 0 (c(tp) 1 ) 1% 00 c()1
1. [0,t1] 减小正向修正作用。附加与原误 e ( t ) t 1 t 2 t 3 t 4 差信号相反的信号。
调节时间主要由自然频 率决定。
20.11.2020
19
C(t)
1.4
1.2 1
0.8
0.6
0.4
0.2 0 0
2.86
4.38 5.2
2 4 6 3.38
4.75
7.04
自动控制原理第三章 二阶系统PPT

c(∞)
(4) 调节时间t s
0 tr tp
ts t
±(5上5)超%稳峰升系调(态值时统量或误时间输:±差间:出2输 离e%:输 升响s出量系s)一出 到应系 最响占统误次响 稳达统 终应稳输差到应 态到期 稳超态出范达从 值并望 态出值响围峰零所保值值稳的应内值开需持与之态百由,所始的在实间值分零所需第时稳际的的比开需时一间态输差最。始时间次。值出值大,间。上的的。偏第。
(±R5%(s))=
1 S
C(s)= tФs =(s4)•TS1
=
1 TS+1
•
1S(=±1S2%- S)+11/T
c(t)=1-e-t/T
第二节 一阶系统性能分析
一阶系统单位阶跃响应曲线
c(t)
0.98 1
0.95 0.86
0.632
0 T 2T3T4T
t
第二节 一阶系统性能分析
2.单位斜坡响应
c(t)
1 T
单位脉冲响应为:
0
c(t)=g(t)=
1 T
e-t/T
t
第二节 一阶系统性能分析
根据一阶系统三种响应的输入输出信号:
r(t)=δ(t)
r(t)=1(t)
c(t)=
1 T
e-t/T
c(t)=1-e-t/T
r(t)=t
c(t)=t-T+Te-t/T
可知: 系统输入信号导数的输出响应,等 于该输入信号输出响应的导数;根据一种 典型信号的响应,就可推知于其它。
得: ζωn= 0.5 ωd = 1.9
β=tg-1
1-ζ2 ζ
=75o
第三节 二阶系统性能分析
三、二阶系统的性能指标
33二阶系统解析

➢单位阶跃响应的变化率为:
dc(t) dt
n2tent
dc(t) 0 dt t0
dc(t) 0 dt t0
dc(t) 0 dt t
表明临界阻尼系统的阶跃响应是单调上升的。
➢ 单位阶跃响应变化率最大的时刻:
d 2h(t) dt 2
dh(t ) max
e2 nt n
(1
nt )
0
dt
解得 t 1/。n ➢ 整个暂态过程中,临界阻尼系统阶跃响应都是单调 增长的没有超调。如以达到稳态值的95%所经历的时 间做为调整时间,则
(1)平稳性
主要由最大超调量 % 和振荡次数 表征。 增大, %减 小,平稳性变好;若 不变,n 增大,d 增大, 增大,平
稳性变差。
(2)快速性
主大要,由则上tr升越时长间,t快r 速和性调越节差时;间当ts
表征。当 n 一定时,
越短,快速性越好。而对于ts ,则与 和n
一定时, 越
n 越大,则 tr
讨论: (1)欠阻尼情况下,二阶系统的单位阶跃响应是衰减的 正弦振荡曲线。衰减速度取决于特征根实部的绝对值
ζωn的大小,振荡角频率是特征根虚部的绝对值,即有 阻尼自振角频率ωd,
d n 1 2
(2)振荡周期为
Td
2 d
n
2 1 2
(3)ζ越大,振幅衰减越快,振荡周期越长(频率越低)。
(4)上升时间tr的计算:
dc(t)
( 2 1)n
e( 2 1)nt
dt 2 2 1( 2 1)
( 2 1)n
e( 2 1)nt
2 2 1( 2 1)
dc(t ) dt
0
0
t 0 t 0
《阶系统的时域分析》课件

04
阶系统的动态性能分析
阶系统的响应特性
阶系统的单位阶跃响应
描述了系统在单位阶跃函数输入下的输出特性,包括上升时间、峰值时间、调节时间和超调量等。
阶系统的单位速度响应
描述了系统在单位速度函数输入下的输出特性,主要用来分析系统的阻尼比和自然频率。
阶系统的频率响应
频率响应的定义
系统在正弦波输入下的稳态输出,表 示系统在不同频率下的增益和相位特 性。
03
通过状态空间描述可以方便地分析系统的动态特性和控制 系统的行为。
03
阶系统的稳定性分析
稳定性定义
平衡状态
系统在无外界干扰的情况下,能够保持静止或匀 速运动的状态。
稳定性
系统受到微小扰动后,能够恢复到平衡状态的性 能。
分类
根据系统对扰动的响应,可以分为线性稳定性和 非线性稳定性。
稳定性判据
劳斯-霍尔维茨判据
06
阶系统的仿真分析
仿真软件介绍
Simulink
MATLAB的一个组件,用于动态系统模拟和建 模。
Multisim
用于电路设计和仿真的软件。
LabVIEW
图形编程环境,适用于测试和测量应用。
阶系统的仿真模型建立
根据实际需求,设置模型 中的参数。
将数学方程转换为仿真软 件可识别的模型。
根据阶系统的特性,建立 相应的数学方程。
模型转换 建立数学模型
参数设置
仿真结果分析
时域波形
分析阶系统的时域响应,如超调和调节时间 等。
频域分析
通过频率响应分析,了解系统的稳定性。
误差分析
比较理论值与仿真结果的误差,评估模型的 准确性。
THANK YOU
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
开环传递函数为:
G(s)
s2
n2 2ns
闭环传递函数为: (s)1 G G (s()s)s22n 2 nsn 2
(s)称为典型二阶系统的传递函数,称为阻尼系数, n 称为无阻
尼振荡频率或自然频率。
20.11.2020
3
二、二阶系统的单位阶跃响应
特征方程为: s22 nsn 20
特征根为:s1,2nn 21,注意:当 不同时,特征根
o 1,欠阻尼 s1,2 njn 12
一对共轭复根(左 半平面)
衰减振荡
1,临界阻尼 s1,2 n(重根 ) 一对负实重根 单调上升
1,过阻尼 s1,2 nn 21 两个互异负实根 单调上升
20.11.2020
8
❖二阶系统在各种不同 情况下的闭环极点分布见P95 图3-9
Im [s]
s1
n 1 2
小写 ν ξ ο π ρ σ τ υ φ χ ψ ω
中文名 纽
克西 欧米克隆
派 柔 西格玛 陶 玉普西隆 弗爱 凯 普赛 奥米伽
20.11.2020
2
这是最常见的一种系统,很多高阶系统也可简化为二阶系统。
一、二阶系统的数学模型 下图所示为稳定的二阶系统的典型结构图。
R(s) -
2 n
C(s)
s(s 2 n )
nt
8 10 12
可以看出:随着 的增加,c(t)将从无衰减的周期运动变为有
衰减的正弦运动,当 1 时c(t)呈现单调上升运动(无振荡)。
可见 反映实际系统的阻尼情况,故称为阻尼系数。
20பைடு நூலகம்11.2020
10
三、典型二阶系统的动态过程分析
(一)衰减振荡瞬态过程 (01):欠阻尼
s1,2 njn 12
(闭环极点)有不同的形式,其阶跃响应的形式也不同,有振 荡和非振荡两大类情况。
⒈ 当时 0 ,特征方程有一对共轭的虚根,两极点位于S平
面的虚轴上,称为零(无)阻尼系统,系统的阶跃响应为持续的等 幅振荡。图3-9(d)
⒉ 当时 0 1,特征方程有一对实部为负的共轭复根,两
个极点位于S平面左半平面,称为欠阻尼系统,系统的阶跃响应为 衰减的振荡过程。图3-9(c)
解得:
tr
1
d
tg1(
12
)
20.11.2020
11
tr
1
d
tg1(
12
)
s1,2 njn 12
tg ()n1 n21 2
tg1( 12)
tr
d
jn
n
12 jd
n
n
jn 12
称为阻尼角,这是由于 cos 。
可见,当阻尼比一定时,系统的响应速度与自然频率成正 比;而当阻尼频率一定时,阻尼比越小,上升时间越短。
sin(
12
12nt)]
1
ent
12
sin(dt),
t0
d 称为阻尼振荡频率
20.11.2020
7
上述四种情况分别称为二阶无阻尼、欠阻尼、临界阻尼和 过阻尼系统。其阻尼系数、特征根、极点分布和单位阶跃响应 如下表所示:
阻尼系数
特征根
极点位置 单位阶跃响应
0,无阻尼 s1,2 jn 一对共轭虚根 等幅周期振荡
延迟时间见P97
20.11.2020
12
⒉ 峰值时间 t p :当t t p 时, c(tp) 0
e nt
c(t)1
s
12
i nd(t),
t0
其中
tg1 1 2
c (t) 1 n e 2 n tp sid n tp () e 1 n t2 p d co d tp s () 0
3-3 二阶系统的时域分析
20.11.2020
1
希腊字母中英对照一览表
大写 A B Γ Δ Ε Ζ Η Θ Ι Κ Λ Μ
小写 α β γ δ ε ζ η θ ι κ λ μ
中文名 阿尔法
贝塔 伽玛 德尔塔 伊普西隆 泽塔 伊塔 西塔 约塔 卡帕 兰姆达 米欧
大写 Ν Ξ Ο Π Ρ Σ Τ Υ Φ Χ Ψ Ω
6
闭环传递函数为: (s)1 G G (s()s)s22n 2 nsn 2
➢当 0 1的欠阻尼时, 极点为: s1,2 njn 12
阶跃响应为: C(s)1ss22n 2nsn2 1ss2s22nsnn2
根据表2-3
1ss2s2nsnn2
s22
n nsn2
c(t)1ent[cos(
12nt)
以上 01 属于振荡情况
20.11.2020
4
s1,2nn 21
⒊ 当 1 时,特征方程有一对相等的实根,两个极点位于S平
面负实轴上,系统时间响应无振荡,称为临界阻尼系统,系统的阶 跃响应为非振荡过程。图3-9(e)
⒋ 当 1时,特征方程有一对不等的实根,两个极点位于S平
面负实轴上,系统时间响应无振荡,称为过阻尼系统,系统的阶跃 响应为非振荡过程。图3-9(f)
c (t) 1 e n t (cd o t s1 2sid n t), t 0
⒈ 上升时间 t r :根据定义,当 t tr时,c(tr)1。
c ( tr) 1 e n t r(cd o tr s1 2sid n tr) 1
cosdtr 1 2si ndtr0
tgdtr
1 2
n 0 Re
Im [s]
s1 s2 0 Re
Im [s]
s2 s1 0 Re
(a) 0 1
(b) 1
(c) 1
Im [s]
s1
0 Re s2
(d) 0
20.11.2020
9
C (t)
2
1 .8
1 .6
1 .4
1 .2
1
0 .8
0 .6 0 .4 0 .2
0 0
246
以上 1 属于非振荡情况
20.11.2020
5
s1,2nn 21
当 0 ,二阶系统具有两个正实部的特征根,又分为两种情况:
5)如果特征根中有虚部,则输出是发散的振荡曲线,如图(a); 6)如果特征根中无虚部,则输出是发散的单调曲线,如图(b)
0 的情况一般不会出现,故这种情况不讨论。
20.11.2020
n s id tn p ( ) d c o d tp s ) (0
整理得:t
g (dtp)d n
12 t
g
dtpn,(n0,1 ,2,...)
20.11.2020
13
dtpn,(n0,1 ,2,...)
由于t
p
出现在第一次峰值时间,取n=1,有:tp
n
12 d
可见峰值时间与闭环极点的虚部数值成正比,阻尼比 一定时,闭环极点离负实轴距离越远,系统的峰值时间越 短。这也是因为当闭环极点离负实轴距离越远时,特征根S 中虚部的成分就越多,越容易产生振荡,响应上升越快, 系统的峰值时间越短。
