立体几何中的一个经典模型

合集下载

高中数学立体几何 2.(第二次修订版)八个有趣模型——搞定空间几何体的外接球与内切球(教师版)

八个有趣模型——搞定空间几何体的外接球与内切球当讲到付雨楼老师于2018年1月14日总第539期微文章，我如获至宝.为有了教学的实施，我以付老师的文章主基石、框架，增加了我个人的理解及例题，形成此文，仍用文原名，与各位同行分享.不当之处，敬请大家批评指正.一、有关定义1．球的定义：空间中到定点的距离等于定长的点的集合（轨迹）叫球面，简称球.2．外接球的定义：若一个多面体的各个顶点都在一个球的球面上，则称这个多面体是这个球的内接多面体，这个球是这个多面体的外接球.3．内切球的定义：若一个多面体的各面都与一个球的球面相切，则称这个多面体是这个球的外切多面体，这个球是这个多面体的内切球.二、外接球的有关知识与方法1．性质：性质1：过球心的平面截球面所得圆是大圆，大圆的半径与球的半径相等；性质2：经过小圆的直径与小圆面垂直的平面必过球心，该平面截球所得圆是大圆；性质3：过球心与小圆圆心的直线垂直于小圆所在的平面（类比：圆的垂径定理）；性质4：球心在大圆面和小圆面上的射影是相应圆的圆心；性质5：在同一球中，过两相交圆的圆心垂直于相应的圆面的直线相交，交点是球心（类比：在同圆中，两相交弦的中垂线交点是圆心）.初图1初图22．结论：结论1：长方体的外接球的球心在体对角线的交点处，即长方体的体对角线的中点是球心；结论2：若由长方体切得的多面体的所有顶点是原长方体的顶点，则所得多面体与原长方体的外接球相同；结论3：长方体的外接球直径就是面对角线及与此面垂直的棱构成的直角三角形的外接圆圆心，换言之，就是：底面的一条对角线与一条高（棱）构成的直角三角形的外接圆是大圆；结论4：圆柱体的外接球球心在上下两底面圆的圆心连一段中点处；结论5：圆柱体轴截面矩形的外接圆是大圆，该矩形的对角线（外接圆直径）是球的直径；结论6：直棱柱的外接球与该棱柱外接圆柱体有相同的外接球；结论7：圆锥体的外接球球心在圆锥的高所在的直线上；结论8：圆锥体轴截面等腰三角形的外接圆是大圆，该三角形的外接圆直径是球的直径；结论9：侧棱相等的棱锥的外接球与该棱锥外接圆锥有相同的外接球.3．终极利器：勾股定理、正定理及余弦定理（解三角形求线段长度）；三、内切球的有关知识与方法1．若球与平面相切，则切点与球心连线与切面垂直.（与直线切圆的结论有一致性）.2．内切球球心到多面体各面的距离均相等，外接球球心到多面体各顶点的距离均相等.（类比：与多边形的内切圆）.3．正多面体的内切球和外接球的球心重合.4．正棱锥的内切球和外接球球心都在高线上，但不一定重合.5．基本方法：（1）构造三角形利用相似比和勾股定理；（2）体积分割是求内切球半径的通用做法（等体积法）. 四、与台体相关的，此略. 五、八大模型第一讲柱体背景的模型类型一、墙角模型（三条棱两两垂直，不找球心的位置即可求出球半径）图1-1图1-2图1-3图1-4方法：找三条两两垂直的线段，直接用公式2222)2(c b a R ++=，即2222c b a R ++=，求出R 例1 （1）已知各顶点都在同一球面上的正四棱柱的高为4，体积为16，则这个球的表面积是（ C ） A ．π16 B ．π20 C ．π24 D ．π32 解： 162==h a V ，2=a ，24164442222=++=++=h a a R ，π24=S ，选C ；（2）若三棱锥的三个侧面两两垂直，且侧棱长均为3，则其外接球的表面积是 π9 解：933342=++=R ，ππ942==R S ；（3）在正三棱锥S ABC -中，M N 、分别是棱SC BC 、的中点，且MN AM ⊥,若侧棱SA =,则正三棱锥ABC S -外接球的表面积是 .π36 解：引理：正三棱锥的对棱互相垂直.证明如下：如图（3）-1，取BC AB ,的中点E D ,，连接CD AE ,，CD AE ,交于H ，连接SH ，则H 是底面正三角形ABC 的中心，∴⊥SH 平面ABC ，∴AB SH ⊥，ΘBC AC =，BD AD =，∴AB CD ⊥，∴⊥AB 平面SCD ， ∴SC AB ⊥，同理：SA BC ⊥，SB AC ⊥，即正三棱锥的对棱互垂直，本题图如图（3）-2， ΘMN AM ⊥，MN SB //，∴SB AM ⊥，ΘSB AC ⊥，∴⊥SB 平面SAC ， ∴SA SB ⊥，SC SB ⊥，ΘSA SB ⊥，SA BC ⊥， ∴⊥SA 平面SBC ，∴SC SA ⊥，故三棱锥ABC S -的三棱条侧棱两两互相垂直，(3)题-1(引理）AC(3)题-2（解答图）AC∴36)32()32()32()2(2222=++=R ，即3642=R ，∴正三棱锥ABC S -外接球的表面积是π36. （4）在四面体S ABC -中，ABC SA 平面⊥，,1,2,120====∠︒AB AC SA BAC 则该四面体的外接球的表面积为（ D ）π11.A π7.B π310.C π340.D 解：在ABC ∆中，7120cos 2222=⋅⋅-+=οBC AB AB AC BC ，7=BC ，ABC ∆的外接球直径为372237sin 2==∠=BAC BC r ，∴3404)372()2()2(2222=+=+=SA r R ，340π=S ，选D （5）如果三棱锥的三个侧面两两垂直，它们的面积分别为6、4、3，那么它的外接球的表面积是解：由已知得三条侧棱两两垂直，设三条侧棱长分别为c b a ,,（+∈R c b a ,,），则⎪⎩⎪⎨⎧===6812ac bc ab ，∴24=abc ，∴3=a ，4=b ，2=c ，29)2(2222=++=c b a R ，ππ2942==R S ，（6）已知某几何体的三视图如图所示，三视图是腰长为1的等腰直角三角形和边长为1的正方形，则该几何体外接球的体积为解：3)2(2222=++=c b a R ，432=R ，23=Rπππ2383334343=⋅==R V 球，类型二、对棱相等模型（补形为长方体）题设：三棱锥（即四面体）中，已知三组对棱分别相等，求外接球半径（CD AB =，BC AD =，BD AC =）第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为c b a ,,，x BC AD ==，y CD AB ==，z BD AC ==，列方程组，⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=， (6)题图（6）题直观图P图2-1补充：图2-1中，abc abc abc V BCD A 31461=⨯-=-. 第三步：根据墙角模型，22222222z y x c b a R ++=++=，82222z y x R ++=，8222z y x R ++=，求出R .思考：如何求棱长为a 的正四面体体积，如何求其外接球体积？例2（1）如下图所示三棱锥A BCD -，其中5,6,7,AB CD AC BD AD BC ======则该三棱锥外接球的表面积为 .解：对棱相等，补形为长方体，如图2-1，设长宽高分别为c b a ,,，110493625)(2222=++=++c b a ，55222=++c b a ，5542=R ，π55=S(1)题图B（2）在三棱锥BCD A -中，2==CD AB ，3==BC AD ，4==BD AC ，则三棱锥BCD A -外接球的表面积为 .π229 解：如图2-1，设补形为长方体，三个长度为三对面的对角线长，设长宽高分别为c b a ,,，则922=+b a ，422=+c b ，1622=+a c ∴291649)(2222=++=++c b a ，291649)(2222=++=++c b a ，229222=++c b a ，22942=R ，π229=S （3）正四面体的各条棱长都为2，则该正面体外接球的体积为（3）解答题解：正四面体对棱相等的模式，放入正方体中，32=R ，23=R ，ππ2383334=⋅=V （4）棱长为2的正四面体的四个顶点都在同一个球面上，若过该球球心的一个截面如下图，则图中三角形(正四面体的截面)的面积是 .(4)题解答图(4)题解：如解答图，将正四面体放入正方体中，截面为1PCO ∆，面积是2.类型三、汉堡模型（直棱柱的外接球、圆柱的外接球）图3-1图3-2 图3-3题设：如图3-1，图3-2，图3-3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）第一步：确定球心O 的位置，1O 是ABC ∆的外心，则⊥1OO 平面ABC ；第二步：算出小圆1O 的半径r AO =1，h AA OO 212111==（h AA =1也是圆柱的高）；第三步：勾股定理：21212O O A O OA +=⇒222)2(r hR +=⇒22)2(hr R +=，解出R例3（1）一个正六棱柱的底面上正六边形，其侧棱垂直于底面，已知该六棱柱的顶点都在同一个球面上，且该六棱柱的体积为89，底面周长为3，则这个球的体积为解：设正六边形边长为a ，正六棱柱的高为h ，底面外接圆的半径为r ，则21=a ，正六棱柱的底面积为833)21(4362=⋅⋅=S ，89833===h Sh V 柱，∴3=h ，4)3(14222=+=R 也可1)21()23(222=+=R ），1=R ，球的体积为34π=球V ；（2）直三棱柱111ABC A B C -的各顶点都在同一球面上，若12AB AC AA ===,120BAC ∠=︒，则此球的表面积等于 . 解：32=BC ，4120sin 322==οr ，2=r ，5=R ，π20=S ；（3）已知EAB ∆所在的平面与矩形ABCD 所在的平面互相垂直，︒=∠===60,2,3AEB AD EB EA ，则多面体ABCD E -的外接球的表面积为 .π16 解：折叠型，法一：EAB ∆的外接圆半径为31=r ，11=OO ，231=+=R ；法二：231=M O ，21322==D O r ，4413432=+=R ，2=R ，π16=表S ；法三：补形为直三棱柱，可改变直三棱柱的放置方式为立式，算法可同上，略.换一种方式，通过算圆柱的轴截面的对角线长来求球的直径：162)32()2(222=+=R ，π16=表S ；（4）在直三棱柱111C B A ABC -中，4,3,6,41====AA A AC AB π，则直三棱柱111C B A ABC -的外接球的表面积为 .π3160解：法一：282164236162=⋅⋅⋅-+=BC ，72=BC ，37423722==r ，372=r ， 3404328)2(2122=+=+=AA r R ，π3160=表S ；法二：求圆柱的轴截面的对角线长得球直径，此略.第二讲锥体背景的模型类型四、切瓜模型（两个大小圆面互相垂直且交于小圆直径——正弦定理求大圆直径是通法）图4-1图4-2图4-3图4-41．如图4-1，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点. 解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；（3）题第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R ；事实上，ACP ∆的外接圆就是大圆，直接用正弦定理也可求解出R .2．如图4-2，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且AC PA ⊥，则利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=3．如图4-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径） 21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=4．题设：如图4-4，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）第一步：易知球心O 必是PAC ∆的外心，即PAC ∆的外接圆是大圆，先求出小圆的直径r AC 2=；第二步：在PAC ∆中，可根据正弦定理R CcB b A a 2sin sin sin ===，求出R . 例4 （1）正四棱锥的顶点都在同一球面上，若该棱锥的高为1，底面边长为32，则该球的表面积为 . 解：法一：由正弦定理（用大圆求外接球直径）；法二：找球心联合勾股定理，72=R ，ππ4942==R S ；（2）正四棱锥ABCD S -的底面边长和各侧棱长都为2，各顶点都在同一球面上，则此球体积为解：方法一：找球心的位置，易知1=r ，1=h ，r h =，故球心在正方形的中心ABCD 处，1=R ，34π=V 方法二：大圆是轴截面所的外接圆，即大圆是SAC ∆的外接圆，此处特殊，SAC Rt ∆的斜边是球半径，22=R ，1=R ，34π=V . （3）一个正三棱锥的四个顶点都在半径为1的球面上，其中底面的三个顶点在该球的一个大圆上，则该正三棱锥的体积是（） A ．433 B ．33 C ．43 D ．123解：高1==R h ，底面外接圆的半径为1=R ，直径为22=R ，设底面边长为a ，则260sin 2==οaR ，3=a ，433432==a S ，三棱锥的体积为4331==Sh V ；（4）在三棱锥ABC P -中，3===PC PB PA ,侧棱PA 与底面ABC 所成的角为ο60，则该三棱锥外接球的体积为（） A ．π B.3π C. 4π D.43π 解：选D ，由线面角的知识，得ABC ∆的顶点C B A ,,在以23=r 为半径的圆上，在圆锥中求解，1=R ；（5）已知三棱锥S ABC -的所有顶点都在球O 的求面上,ABC ∆是边长为1的正三角形,SC 为球O 的直径,且2SC =，则此棱锥的体积为（）AA．6 BC．3 D．2解：36)33(12221=-=-=r R OO ，362=h ，62362433131=⋅⋅==Sh V 球类型五、垂面模型（一条直线垂直于一个平面）1．题设：如图5，⊥PA 平面ABC ，求外接球半径.解题步骤：第一步：将ABC ∆画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ；第二步：1O 为ABC ∆的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r C c B b A a 2sin sin sin ===），PA OO 211=；第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=.2．题设：如图5-1至5-8这七个图形，P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点.图5-1图5-2图5-3图5-4图5-6图5-7图5-8解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R 方法二：小圆直径参与构造大圆，用正弦定理求大圆直径得球的直径. 例5 一个几何体的三视图如图所示，则该几何体外接球的表面积为( )C A ．π3 B ．π2 C ．316πD ．以上都不对解：选C ，法一：（勾股定理）利用球心的位置求球半径，球心在圆锥的高线上，221)3(R R =+-,32=R ,ππ31642==R S ；法二：（大圆法求外接球直径）如图，球心在圆锥的高线上，故圆锥的轴截面三角形PMN 的外接圆是大圆，于是3460sin 22==οR ，下略；第三讲二面角背景的模型类型六、折叠模型题设：两个全等三角形或等腰三角形拼在一起，或菱形折叠(如图6)俯视图侧视图正视图解答图图6第一步：先画出如图6所示的图形，将BCD ∆画在小圆上，找出BCD ∆和BD A '∆的外心1H 和2H ；第二步：过1H 和2H 分别作平面BCD 和平面BD A '的垂线，两垂线的交点即为球心O ，连接OC OE ,；第三步：解1OEH ∆，算出1OH ，在1OCH Rt ∆中，勾股定理：22121OC CH OH =+ 注：易知21,,,H E H O 四点共面且四点共圆，证略.例6（1）三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 和△ABC 均为边长为2的正三角形，则三棱锥ABC P -外接球的半径为 . 解：如图，3460sin 22221===οr r ，3221==r r ，312=H O ， 35343121222=+=+=r H O R ，315=R ；法二：312=H O ，311=H O ，1=AH ， 352121222=++==O O H O AH AO R ，315=R ；（2）在直角梯形ABCD 中，CD AB //，ο90=∠A ，ο45=∠C ，1==AD AB ，沿对角线BD 折成四面体BCD A -'，使平面⊥'BD A 平面BCD ，若四面体BCD A -'的顶点在同一个球面上，则该项球的表面积为 π4(2)题-2(2)题-1→A(3)题解：如图，易知球心在BC 的中点处，π4=表S ；（1）题（3）在四面体ABC S -中，BC AB ⊥，2==BC AB ，二面角B AC S --的余弦值为33-，则四面体ABC S -的外接球表面积为 π6 解：如图，法一：33)2cos(cos 211-=+∠=∠πO OO B SO ， 33sin 21=∠O OO ，36cos 21=∠O OO ， 22cos 21211=∠=O OO O O OO ，232112=+=R ，ππ642==R S ；法二：延长1BO 到D 使111r BO DO ==，由余弦定理得6=SB ，2=SD ，大圆直径为62==SB R ；（4）在边长为32的菱形ABCD 中，ο60=∠BAD ，沿对角线BD 折成二面角C BD A --为ο120的四面体ABCD ，则此四面体的外接球表面积为 π28解：如图，取BD 的中点M ，ABD ∆和CBD ∆的外接圆半径为221==r r ，ABD ∆和CBD ∆的外心21,O O 到弦BD 的距离（弦心距）为121==d d ，法一：四边形21MO OO 的外接圆直径2=OM ，7=R ，π28=S ；法二：31=OO ，7=R ；法三：作出CBD ∆的外接圆直径CE ,则3==CM AM ， 4=CE ，1=ME ，7=AE ，33=AC ，72147227167cos -=⋅⋅-+=∠AEC ，7233sin =∠AEC ，72723333sin 2==∠=AEC AC R ，7=R ；(5)在四棱锥ABCD 中，ο120=∠BDA ，ο150=∠BDC ，2==BD AD ，3=CD ，二面角CBD A --(4)题图的平面角的大小为ο120，则此四面体的外接球的体积为解：如图，过两小圆圆心作相应小圆所在平面的垂线确定球心，→抽象化(5)题解答图-2(5)题解答图-11B32=AB ，22=r ，弦心距32=M O ，13=BC ，131=r ，弦心距321=M O ， ∴2121=O O ，72120sin 21==οO O OM ，法一：∴292222=+==OM MD OD R ，29=R ，∴329116π=球V ；法二：2522222=-=M O OM OO ，∴29222222=+==OO r OD R ，29=R ，∴329116π=球V . 类型七、两直角三角形拼接在一起(斜边相同,也可看作矩形沿对角线折起所得三棱锥)模型图7题设：如图7，ο90=∠=∠ACB APB ，求三棱锥ABC P -外接球半径（分析：取公共的斜边的中点O ，连接OC OP ,，则AB OP OC OB OA 21====，∴O 为三棱锥ABC P -外接球球心，然后在OCP 中求出半径），当看作矩形沿对角线折起所得三棱锥时与折起成的二面角大小无关，只要不是平角球半径都为定值.例7（1）在矩形ABCD 中，4=AB ，3=BC ，沿AC 将矩形ABCD 折成一个直二面角D AC B --，则四面体ABCD 的外接球的体积为（）A ．π12125 B ．π9125 C ．π6125 D ．π3125解：（1）52==AC R ，25=R ，6125812534343πππ=⋅==R V ，选C（2）在矩形ABCD 中，2=AB ，3=BC ，沿BD 将矩形ABCD 折叠，连接AC ，所得三棱锥BCDA -的外接球的表面积为．解：BD 的中点是球心O ，132==BD R ，ππ1342==R S .第四讲多面体的内切球问题模型类型八、锥体的内切球问题1．题设：如图8-1，三棱锥ABC P -上正三棱锥，求其内切球的半径. 第一步：先现出内切球的截面图，H E ,分别是两个三角形的外心；第二步：求BD DH 31=，r PH PO -=，PD 是侧面ABP ∆的高；第三步：由POE ∆相似于PDH ∆，建立等式：PDPODH OE =，解出r 2．题设：如图8-2，四棱锥ABC P -是正四棱锥，求其内切球的半径第一步：先现出内切球的截面图，H O P ,,三点共线；第二步：求BC FH 21=，r PH PO -=，PF 是侧面PCD ∆的高；第三步：由POG ∆相似于PFH ∆，建立等式：PFPOHF OG =，解出3．题设：三棱锥ABC P -是任意三棱锥，求其的内切球半径方法：等体积法，即内切球球心与四个面构成的四个三棱锥的体积之和相等第一步：先画出四个表面的面积和整个锥体体积；第二步：设内切球的半径为r ，建立等式：PBC O PAC O PAB O ABC O ABC P V V V V V -----+++=⇒r S S S S r S r S r S r S V PBC PAC PAB ABC PBC PAC PAB ABC ABC P ⋅+++=⋅+⋅+⋅+⋅=∆∆∆∆-)(3131313131第三步：解出PBCO PAC O PAB O ABC O ABCP S S S S V r -----+++=3例8 （1）棱长为a 的正四面体的内切球表面积是 62a π，解：设正四面体内切球的半径为r ，将正四面体放入棱长为2a的正方体中（即补形为正方体），如图，则 2622313133aa V V ABC P =⋅==-正方体，又Θr a r a Sr V ABC P 223343314314=⋅⋅⋅=⋅=-， ∴263332a r a =，62a r =，∴内切球的表面积为(1)题D图8-1A图8-26422a r S ππ==表（注：还有别的方法，此略）（2）正四棱锥ABCD S -的底面边长为2，侧棱长为37解：如图，正四棱锥ABCD S -的高7=h ，正四棱锥ABCD S -的体积为374=-ABCD S V 侧面斜高221=h ，正四棱锥ABCD S -的表面积为284+=表S ，正四棱锥ABCD S -的体积为r r S V ABCDS ⋅+==-328431表， ∴3743284=⋅+r ， 771427)122(7221728474-=-=+=+=r （3）三棱锥ABC P -中，底面ABC ∆是边长为2的正三角形，⊥PA 底面ABC ，2=PA ，则32解：如图，3=∆ABC S ，2==∆∆ACP ABP S S ，7=∆BCP S ，743++=表S ，三棱锥ABC P -的体积为332=-ABCP V ，另一表达体积的方式是r r S V ABC P ⋅++==-347331表， ∴3323473=⋅++r ，∴47332++=r习题： 1．若三棱锥ABC S -的三条侧棱两两垂直，且2=SA ，4==SC SB ，则该三棱锥的外接球半径为（） A.3 B.6 C.36 D.9 解：【A 】616164)2(2=++=R ，3=R【三棱锥有一侧棱垂直于底面，且底面是直角三角形】【共两种】2．三棱锥ABC S -中，侧棱⊥SA 平面ABC ，底面ABC 是边长为3的正三角形，32=SA，则该三(2)题(3)题B棱锥的外接球体积等于 . 332π解：260sin 32==οr ，16124)2(2=+=R ，42=R ，2=R ，外接球体积332834ππ=⋅ 【外心法（加中垂线）找球心；正弦定理求球小圆半径】3．正三棱锥ABC S -中，底面ABC 是边长为3的正三角形，侧棱长为2，则该三棱锥的外接球体积等于 .解：ABC ∆外接圆的半径为，三棱锥ABC S -的直径为3460sin 22==οR ，外接球半径32=R ，或1)3(22+-=R R ，32=R ，外接球体积2733233834343πππ=⋅==R V ， 4．三棱锥ABC P -中，平面⊥PAC 平面ABC ，△PAC 边长为2的正三角形，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：PAC ∆的外接圆是大圆，3460sin 22==οR ，32=R ， 5．三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，3==PC PA ，BC AB ⊥，则三棱锥ABC P -外接球的半径为 .解：973324992cos 222=⋅⋅-+=⋅-+=∠PC PA AC PC PA P ，81216)97(1sin 22⋅=-=∠P ，924sin =∠P ，42922992422===R ，829=R 6．三棱锥ABC P -中，平面⊥PAC 平面ABC ，2=AC ，PC PA ⊥，BC AB ⊥，则三棱锥ABCP -外接球的半径为 .解：AC 是公共的斜边，AC 的中点是球心O ，球半径为1=R。

▲立体几何中的外接球与内切球---模型知识点

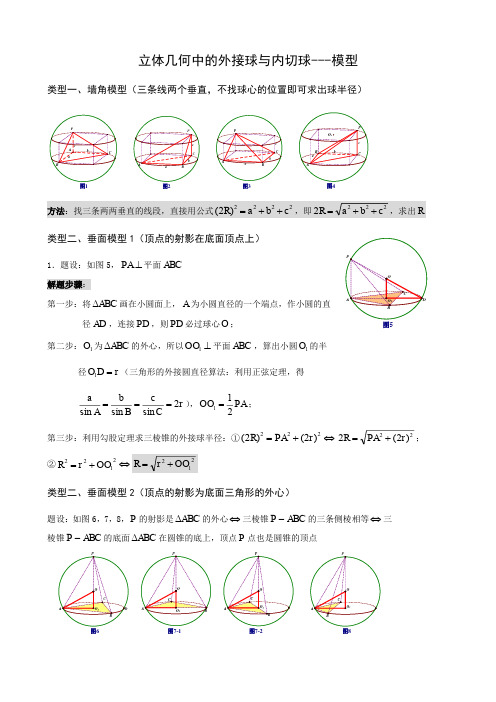
立体几何中的外接球与内切球---模型类型一、墙角模型（三条线两个垂直，不找球心的位置即可求出球半径）类型二、垂面模型1（顶点的射影在底面顶点上）1．题设：如图5，⊥PA 平面ABC 解题步骤：第一步：将ABC ∆画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ，连接PD ，则PD 必过球心O ；第二步：1O 为ABC ∆的外心，所以⊥1OO 平面ABC ，算出小圆1O 的半径r D O =1（三角形的外接圆直径算法：利用正弦定理，得r C cB b A a 2sin sin sin ===），PA OO 211=；第三步：利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=类型二、垂面模型2（顶点的射影为底面三角形的外心）题设：如图6，7，8，P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱锥ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点图2图3图7-1图7-2图5解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R 方法二：小圆直径参与构造大圆。

类型三、切瓜模型（两个平面互相垂直，一个面为直角三角形）1．题设：如图9-1，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径）解题步骤：第1步：易知球心O 必是PAC ∆的外心，即PAC ∆的外接圆是大圆，先求出小圆的直径r AC 2=；第2步：在PAC ∆中，可根据正弦定理R CcB b A a 2sin sin sin ===，求出R 2．如图9-2，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径） 21212O O C O OC +=⇔2122O O r R +=⇔2122O O R AC -=3．如图9-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且P 的射影是ABC ∆的外心⇔三棱锥ABC P -的三条侧棱相等⇔三棱ABC P -的底面ABC ∆在圆锥的底上，顶点P 点也是圆锥的顶点解题步骤：第一步：确定球心O 的位置，取ABC ∆的外心1O ，则1,,O O P 三点共线；第二步：先算出小圆1O 的半径r AO =1，再算出棱锥的高h PO =1（也是圆锥的高）；第三步：勾股定理：21212O O A O OA +=⇒222)(r R h R +-=，解出R图8-1图8-2图8-3图9-1图9-2图9-3图9-44．如图9-3，平面⊥PAC 平面ABC ，且BC AB ⊥（即AC 为小圆的直径），且AC PA ⊥，则利用勾股定理求三棱锥的外接球半径：①222)2()2(r PA R +=⇔22)2(2r PA R +=；②2122OO r R +=⇔212OO r R +=类型四、汉堡模型（直棱柱的外接球、圆柱的外接球）题设：如图10-1，图10-2，图10-3,直三棱柱内接于球（同时直棱柱也内接于圆柱，棱柱的上下底面可以是任意三角形）解题步骤：第一步：确定球心O 的位置，1O 是ABC ∆的外心，则⊥1OO 平面ABC ；第二步：算出小圆1O 的半径r AO =1，h AA OO 212111==（h AA=1也是圆柱的高）；第三步：勾股定理：21212O O A O OA +=⇒222)2(r hR +=⇒R =题设：两个全等三角形或等腰三角形拼在一起，或菱形折叠(如图解题步骤：第一步：先画出如图所示的图形，将BCD ∆画在小圆上，找出BCD ∆和BD A '∆的外心1H 和2H ；第二步：过1H 和2H 分别作平面BCD 和平面BD A '的垂线，两垂线的交点即为球心O ，连接OC OE ,；第三步：解1OEH ∆，算出1OH ，在1OCH Rt ∆中，勾股定理：22121OC CH OH =+类型六、对棱相等模型（补形为长方体）题设：三棱锥（即四面体）中，已知三组对棱分别相等，求外接球半径（CD AB =，BC AD =，BD AC =）第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为c b a ,,，x BC AD ==，y CD AB ==，z BD AC ==，列方程组，图11⎪⎩⎪⎨⎧=+=+=+222222222z a c y c b x b a ⇒2)2(2222222z y x c b a R ++=++=，补充：abc abc abc V BCD A 31461=⨯-=- 第三步：根据墙角模型，22222222z y x c b a R ++=++=，82222z y x R ++=，8222z y x R ++=，求出R ，例如，正四面体的外接球半径可用此法。

立体几何专题：外接球问题中常见的8种模型(学生版)

立体几何专题：外接球问题中常见的8种模型1.知识梳理一、墙角模型适用范围：3组或3条棱两两垂直；可在长方体中画出该图且各顶点与长方体的顶点重合直接用公式(2R )2=a 2+b 2+c 2，即2R =a 2+b 2+c 2，求出R【补充】图1为阳马，图2和图4为鳖臑二、麻花模型适用范围：对棱相等相等的三棱锥对棱相等指四面体的三组对棱分别对应相等，且这三组对棱构成长方体的三组对面的对角线。

推导过程：三棱锥(即四面体)中，已知三组对棱分别相等，(AB =CD ，AD =BC ，AC =BD )第一步：画出一个长方体，标出三组互为异面直线的对棱；第二步：设出长方体的长宽高分别为a ,b ,c ，AD =BC =x ，AB =CD =y ，AC =BD =z ，列方程组，a 2+b 2=x 2b 2+c 2=y 2c 2+a 2=z 2⇒(2R )2=a 2+b 2+c 2=x 2+y 2+z 22，补充：V A −BCD =abc −16abc ×4=13abc 第三步：根据墙角模型，2R =a 2+b 2+c 2=x 2+y 2+z 22，R 2=x 2+y 2+z 28，R =x 2+y 2+z 28，求出R .三、垂面模型适用范围：有一条棱垂直于底面的棱锥。

推导过程：第一步：将ABC 画在小圆面上，A 为小圆直径的一个端点，作小圆的直径AD ,连接PD ,则PD 必过球心O .第二步：O 1为ABC 的外心，所以OO 1⊥平面ABC ，算出小圆O 1的半径O 1D =r(三角形的外接圆直径算法:利用正弦定理a sin A =b sin B=csin C =2r ,OO 1=12PA .第三步：利用勾股定理求三棱锥的外接球半径：(1)(2R )2=PA 2+(2r )2⇔2R =PA 2+(2r )2；(2)R 2=r 2+OO 21⇔R =r 2+OO 21.公式：R 2=r 2+h 24四、切瓜模型适用范围：有两个平面互相垂直的棱锥推导过程：分别在两个互相垂直的平面上取外心O 1、O 2过两个外心做两个垂面的垂线，两条垂线的交点即为球心0，取B C 的中点为E ，连接OO 1、OO 2、O 2E 、O 1E 为矩形由勾股可得|OC |2=|O 2C |2+|OO 2|2=|O 2C |2+|O 1C |2-|CE |2∴R 2=r 21+r 22-l 24公式：R 2=r 21+r 22-l 24五、斗笠模型适用于：顶点的投影在底面的外心上的棱锥推导过程：取底面的外心01，连接顶点与外心，该线为空间几何体的高h ，在h 上取一点作为球心0，根据勾股定理R 2=(h -R )2+r 2⇔R =r 2+h 22h公式：R =r 2+h 22h六、矩形模型适用范围：两个直角三角形的斜边为同一边，则该边为球的直径推导过程：图中两个直角三角形ΔPAB 和ΔQAB ，其中∠APB =∠AQB =90°，求外接圆半径取斜边AB 的中点O ，连接OP ,OQ ，则OP =12AB =OA =OB =OQ 所以O 点即为球心，然后在ΔPOQ 中解出半径R 公式：R 2=l22(l 为斜边长度)七、折叠模型适用范围：两个全等三角形或等腰三角形拼在一起，或菱形折叠.推导过程：两个全等的三角形或者等腰拼在一起，或者菱形折叠，设折叠的二面角∠A EC =α,CE =A E =h .如图，作左图的二面角剖面图如右图：H 1和H 2分别为△BCD ,△A BD 外心，分别过这两个外心做这两个平面的垂线且垂线相交于球心O CH 1=r =BD 2sin ∠BCD,EH 1=h -r ,OH 1=(h -r )tanα2由勾股定理可得：R 2=OC 2=OH 21+CH 21=r 2+(h -r )2tan 2α2.公式：R 2=r 2+(h -r )2tan 2α2八、鳄鱼模型适用范围：所有二面角构成的棱锥，普通三棱锥方法：找两面外接圆圆心到交线的距离m ,n ，找二面角α，找面面交线长度l 推导过程：取二面角两平面的外心分别为O 1,O 2并过两外心作这两个面的垂线，两垂线相交于球心O ，取二面角两平面的交线中点为E ，则O ,O 1,E ,O 2四点共圆，由正弦定理得：OE =2r =O 1O 2sin α①在ΔO 1O 2E 中，由余弦定理得：O 1O 2 2=O 1E 2+O 2E 2-2O 1E O 2E cos α②由勾股定理得：OD 2=O 1O 2+O 1D 2③由①②③整理得：OD2=O 1O 2+O 1D 2=OE 2-O 1E 2+O 1D 2=O 1O 2sin α2-O 1E 2+O 1D 2=O 1E2+O 2E 2-2O 1E O 2E cos αsin 2α-O 1E 2+O 1D 2=O1E2+O2E2-2O1EO2Ecosαsin2α-O1E2+O1B2记O1E=m,O2E=n,AB=l,则R2=m2+n2-2mn cosαsin2α+l22公式：R2=m2+n2-2mn cosαsin2α+l222.常考题型3.题型精析题型一:墙角模型1(2023·高一单元测试)三棱锥A-BCD中，AD⊥平面BCD，DC⊥BD，2AD=BD=DC=2，则该三棱锥的外接球表面积为()A.3π2B.9π2C.9πD.36π1.(2022秋·陕西西安·高一统考期末)在《九章算术》中，将四个面都为直角三角形的三棱锥称之为鳖臑．已知在鳖臑A-BCD中，满足AB⊥平面BCD，且AB=BD=5，BC=3，CD=4，则此鳖臑外接球的表面积为()A.25πB.50πC.100πD.200π2.(2023·高一课时练习)《九章算术》是我国古代数学名著，它在几何学中的研究比西方早1000多年．在《九章算术》中，将底面为矩形且一侧棱垂直于底面的四棱锥称为阳马．如图P-ABCD是阳马，PA⊥平面ABCD，PA=5，AB=3，BC=4．则该阳马的外接球的表面积为()A.1252π3B.50πC.100πD.500π33.(2023·广西南宁·统考二模)在《九章算术》中，将四个面都是直角三角形的四面体称为鳖臑，在鳖臑A -BCD 中，AB ⊥平面BCD ，CD ⊥AD ，AB =BD =2，已知动点E 从C 点出发，沿外表面经过棱AD 上一点到点B 的最短距离为10，则该棱锥的外接球的体积为.4.(2023春·辽宁朝阳·高二北票市高级中学校考阶段练习)已知四棱锥P -ABCD 的外接球O 的表面积为64π，PA ⊥平面ABCD ，且底面ABCD 为矩形，PA =4，设点M 在球O 的表面上运动，则四棱锥M -ABCD 体积的最大值为.题型二:麻花模型1(2023春·广东梅州·高二统考期中)已知三棱锥S -ABC 的四个顶点都在球O 的球面上，且SA =BC =2，SB =AC =7，SC =AB =5，则球O 的体积是()A.83π B.3223π C.423π D.823π1.(2022春·江西景德镇·高一景德镇一中校考期中)在△ABC 中，AB =AC =2，cos A =34，将△ABC 绕BC 旋转至△BCD 的位置，使得AD =2，如图所示，则三棱锥D -ABC 外接球的体积为．2.(2023秋·吉林·高一吉林一中校考阶段练习)如图，在△ABC 中，AB =25,BC =210,AC =213，D ，E ，F 分别为三边中点，将△BDE ,△ADF ,△CEF 分别沿DE ,EF ,DF 向上折起，使A ，B ，C 重合为点P ，则三棱锥P -DEF 的外接球表面积为()A.72π B.7143π C.14π D.56π3.(2023·江西·统考模拟预测)在三棱锥P -ABC 中，已知PA =BC =213,AC =BP =41,CP =AB =61，则三棱锥P -ABC 外接球的表面积为()A.77πB.64πC.108πD.72π4.(2022·全国·高三专题练习)已知四面体ABCD 的棱长满足AB =AC =BD =CD =2，BC =AD =1，现将四面体ABCD 放入一个轴截面为等边三角形的圆锥中，使得四面体ABCD 可以在圆锥中任意转动，则圆锥侧面积的最小值为．题型三:垂面模型1(2023·高一单元测试)在三棱锥P -ABC 中，PA ⊥平面ABC ，PA =6，BC =3，∠CAB =π6，则三棱锥P -ABC 的外接球半径为()A.3B.23C.32D.61.(2023·全国·高一专题练习)已知A ，B ，C ，D 在球O 的表面上，△ABC 为等边三角形且边长为3，AD ⊥平面ABC ，AD =2，则球O 的表面积为()A.4πB.8πC.16πD.32π2.(2020春·天津宁河·高一校考期末)在三棱锥P -ABC 中，AP =2,AB =3,PA ⊥面ABC ，且在△ABC 中，C =60°，则该三棱锥外接球的表面积为()A.20π3B.8πC.10πD.12π3.(2023·全国·高一专题练习)已知A ，B ，C ，D 在球O 的表面上，△ABC 为等边三角形且其面积为334，AD ⊥平面ABC ，AD =2，则球O 的表面积为()A.πB.2πC.4πD.8π4.(2022春·山东聊城·高一山东聊城一中校考阶段练习)在四棱锥P -ABCD 中，PA ⊥平面ABCD ，四边形ABCD 为矩形，BC =2，PC 与平面PAB 所成的角为30o ，则该四棱锥外接球的体积为()A.433π B.43πC.823πD.833π题型四:切瓜模型1(2023·贵州贵阳·校联考模拟预测)在三棱锥A -BCD 中，已知AC ⊥BC ,AC =BC =2,AD =BD =6，且平面ABD ⊥平面ABC ，则三棱锥A -BCD 的外接球表面积为()A.8πB.9πC.10πD.12π1.(2023·四川达州·统考二模)三棱锥A -BCD 的所有顶点都在球O 的表面上，平面ABD ⊥平面BCD ，AB =AD =6，AB ⊥AD ，∠BDC =2∠DBC =60°，则球O 的体积为()A.43πB.32π3C.49π3D.323π2.(2023春·陕西西安·高一长安一中校考期中)在直三棱柱ABC -A 1B 1C 1中，AB ⊥BC ，AB =BC =AA 1=4，点P 为B 1C 1的中点，则四面体PABC 的外接球的体积为()A..41416π B.41413π C.41412π D.4141π3.(2022·高一单元测试)四棱锥P -ABCD 的顶点都在球O 的表面上，△PAD 是等边三角形，底面ABCD 是矩形，平面PAD ⊥平面ABCD ，若AB =2，BC =3，则球O 的表面积为()A.12πB.16πC.20πD.32π4.(2021·高一课时练习)在四棱锥P -ABCD 中，平面PAD ⊥平面ABCD ，且ABCD 为矩形，∠DPA =π2，AD =23，AB =2，PA =PD ，则四棱锥P -ABCD 的外接球的体积为()A.163π B.323π C.643π D.16π5.(2023春·全国·高一专题练习)在四棱锥P-ABCD中，ABCD是边长为2的正方形，AP=PD=10，平面PAD⊥平面ABCD，则四棱锥P-ABCD外接球的表面积为()A.4πB.8πC.136π9D.68π3题型五:斗笠模型1(2023·全国·高一专题练习)正四面体S-ABC内接于一个半径为R的球，则该正四面体的棱长与这个球的半径的比值为()A.64B.33C.263D.31.(2022·高一专题练习)已知正四棱锥P-ABCD(底面四边形ABCD是正方形，顶点P在底面的射影是底面的中心)的各顶点都在同一球面上，底面正方形的边长为10，若该正四棱锥的体积为50 3，则此球的体积为()A.18πB.86πC.36πD.323π2.(2022·全国·高一专题练习)某四棱锥的底面为正方形，顶点在底面的射影为正方形中心，该四棱锥内有一个半径为1的球，则该四棱锥的表面积最小值是()A.16B.8C.32D.243.(2022春·安徽·高三校联考阶段练习)在三棱锥P-ABC中，侧棱PA=PB=PC=10，∠BAC=π4，BC=22，则此三棱锥外接球的表面积为．题型六:矩形模型1(2022春·全国·高一期末)已知三棱锥A-BCD中，CD=22，BC=AC=BD=AD=2，则此几何体外接球的表面积为()A.2π3B.2π C.82π3D.8π1.(2022春·广东惠州·高一校考期中)在矩形ABCD中，AB=6,BC=8，现将△ABC沿对角线AC翻折，得到四面体DABC，则该四面体外接球的体积为()A.1963π B.10003π C.4003π D.5003π2.(2022春·河北沧州·高一校考阶段练习)矩形ABCD中，AB=4,BC=3，沿AC将三角形ABC折起，得到的四面体A-BCD的体积的最大时，则此四面体外接球的表面积值为()A.25πB.30πC.36πD.100π3.(2022春·四川成都·高一统考期末)在矩形ABCD 中，AB =6，AD =8，将△ABC 沿对角线AC 折起，则三棱锥B -ACD 的外接球的表面积为()A.36πB.64πC.100πD.与二面角B -AC -D 的大小有关题型七:折叠模型1(2022春·陕西西安·高一长安一中校考期末)已知菱形ABCD 的边长为3，∠ABC =60°，沿对角线AC 折成一个四面体，使平面ACD 垂直平面ABC ，则经过这个四面体所有顶点的球的体积为()．A.5152π B.6πC.515πD.12π1.已知等边△ABC 的边长为2，将其沿边AB 旋转到如图所示的位置，且二面角C -AB -C 为60°，则三棱锥C -ABC 外接球的半径为2.(2023·广西南宁·统考二模)蹴鞠，又名“蹴球”“蹴圈”等，“蹴”有用脚蹴、踢的含义，鞠最早系外包皮革、内饰米糠的球，因而“蹴鞠”就是指古人以脚蹴、踢皮球的活动，类似今日的足球，现已知某“鞠”的表面上有四个点A ,B ,C ,D 满足AB =BC =CD =DA =DB =433cm ，AC =23cm ，则该“鞠”的表面积为cm 2.3.(2022秋·福建泉州·高三校考开学考试)在三棱锥S -ABC 中，SA =SB =AC =BC =2,SC =1，二面角S -AB -C 的大小为60°，则三棱锥S -ABC 的外接球的表面积为.4.(2022秋·山东德州·高二统考期中)已知在三棱锥中，S -ABC 中，BA ⊥BC ，BA =BC =2，SA =SC =22，二面角B -AC -S 的大小为5π6，则三棱锥S -ABC 的外接球的表面积为()A.56π3B.58π3C.105π4D.124π9题型八:鳄鱼模型1(2022春·四川成都·高一树德中学校考期末)已知在三棱锥S-ABC中，AB⊥BC，AB=BC=2，SA =SC=22，二面角B-AC-S的大小为2π3，则三棱锥S-ABC的外接球的表面积为()A.124π9B.105π4C.105π9D.104π91.(2023春·全国·高一专题练习)如图，在三棱锥P-ABC，△PAC是以AC为斜边的等腰直角三角形，且CB=22，AB=AC=6，二面角P-AC-B的大小为120°，则三棱锥P-ABC的外接球表面积为()A.5103π B.10π C.9π D.4+23π2.(2023·陕西榆林·统考三模)在三棱锥A-BCD中，AB⊥BC,BC⊥CD,CD=2AB=2BC= 4，二面角A-BC-D为60°，则三棱锥A-BCD外接球的表面积为()A.16πB.24πC.18πD.20π3.(2023春·安徽阜阳·高三阜阳市第二中学校考阶段练习)如图1，四边形ABCD中，AB=AD =2，CB=CD=2，AB⊥AD，将△ABD沿BD翻折至△PBD，使二面角P-BD-C的正切值等于2，如图2，四面体PBCD的四个顶点都在同一个球面上，则该球的表面积为()A.4πB.6πC.8πD.9π4.(2023·江西南昌·校联考模拟预测)在平面四边形ABCD中，AD=CD=3，∠ADC=∠ACB =90°，∠ABC=60°，现将△ADC沿着AC折起，得到三棱锥D-ABC，若二面角D-AC-B的平面角为135°，则三棱锥D-ABC的外接球表面积为.5.(2023春·广东广州·高三统考阶段练习)在三棱锥P-ABC中，△ABC为等腰直角三角形，AB=AC=2，△PAC为正三角形，且二面角P-AC-B的平面角为π6，则三棱锥P-ABC的外接球表面积为．。

立体几何四个重要模型

立体几何四个重要模型广州市第六十五中学朱星如模型1：在棱长为a 的正面体ABCD 中：1.求证它是一个正三棱锥。

证明：即证顶点A 在底面BCD 的中心H 的连线与底面垂直。

取BC 的中点E，BD 的中点F，连CF，DE 相交于点H，则H 是三角形BCD 的中心，且H 是CF，DE 的一个三等分点，连AH，由BC ⊥DE，BC ⊥AE，AE 交DE=E,AE,DE 的平面AED 内，得BC ⊥平面AED，由此得BC ⊥AH，即AH ⊥BC。

（1）同理：AH ⊥BD。

（2）由BC 交BD=B，BC，BD 在平面BCD 内及（1）（2）得：AH ⊥平面BCD。

所以四面体ABCD 是正三棱锥。

2.设E、F、S、T 分别是BC、BD、AD、AC 的中点，求证：四边形EFST 是正方形。

证明：由于E、F、S、T 分别是BC、BD、AD、AC 的中点，故有ST 12DC EF，ST EF，所四边形EFST 是平行四边形。

同理：SF 12AB TE ，DC=AB ，所以四边形EFST 是菱形。

仿题1可证DC ⊥平面ABH，故DC ⊥AB,故有四边形EFST 是正方形。

注;由此可得到相对的两棱所成角为90o 。

3.设E、S 分别是BC、AD 的中点，求证：ES ⊥BC，ES ⊥AD，并求ES 的长。

证明：可证BC ⊥平面AED，从而BC ⊥ES；可得AD ⊥平面BCS，从而AD ⊥ES。

在直角三角形SBE 中，SB=32a,BE=12a,从而，2222ES SB BE =-=4.求任何一条棱与它相交的面所成角的正弦值。

解：只要求AB 与平面BCD 所成的角。

AH ⊥平面BCD，∴AB 与平面BCD 所成的角是ABH ∠。

22333323BH DE ==⨯=，在直角三角形ABH 中，2263AH AB BH =-=，故6sin 3AH ABH AB ∠==。

5.求相邻两个面的夹角的余弦值。

解：只要求二面角A-BD-C 的平面的余弦值。

立体几何中外接球与内切球模型归纳

立体几何中外接球与内切球模型归纳
在立体几何中，外接球和内切球是两个重要的概念。

外接球和内切球分别指在几何体上找到的可以用一个球切割出来的最大和最小的球形结构。

在实际应用中，外接球和内切球可以应用到各种领域，例如机械制造、建筑设计等。

一、外接球
外接球是指能够切割几何体上所有顶点的球，也就是说，外接球的球心在几何体的所以顶点上。

常见的外接球有以下几种类型：
1. 立方体的外接球
立方体的外接球是一个边长等于立方体对角线长度的球。

由于立方体的对角线长度是边长的$\sqrt{3}$倍，因此，立方体的外接球半径为边长的$\frac{\sqrt{3}}{2}$倍。

圆锥的外接球是一个球心位于圆锥顶点上，且半径等于圆锥母线长度的一半的球。

圆锥的外接球直径等于底面圆的直径加上圆锥高的二倍，即外接球直径等于
$\sqrt{d^2+4h^2}$。

二、内切球
立方体的内切球是一个正八面体，正八面体的体心即为立方体重心。

2. 正四面体的内切球
正四面体的内切球是一个球心位于四面体重心处，且半径等于四面体高的
$\frac{1}{3}$倍的球。

4. 圆锥的内切球
圆锥的内切球是一个球心位于圆锥顶点上，且半径等于圆锥母线长度与底面半径之差的一半的球。

初中数学九大几何模型

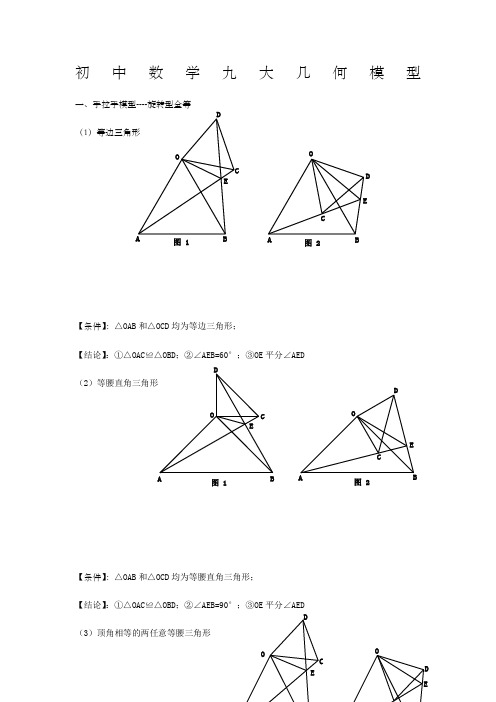
初中数学九大几何模型一、手拉手模型----旋转型全等（1）等边三角形【条件】：△OAB 和△OCD 均为等边三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=60°；③OE 平分∠AED（2）等腰直角三角形【条件】：△OAB 和△OCD 均为等腰直角三角形；【结论】：①△OAC ≌△OBD ；②∠AEB=90°；③OE 平分∠AED（3）顶角相等的两任意等腰三角形OB C DE图 1OABCD E图 2OABCDE图 1OACDE图 2OCDEOD E【条件】：△OAB 和△OCD 均为等腰三角形；且∠COD=∠AOB【结论】：①△OAC ≌△OBD ； ②∠AEB=∠AOB ； ③OE 平分∠AED二、模型二：手拉手模型----旋转型相似（1）一般情况【条件】：CD ∥AB ，将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA （2）特殊情况【条件】：CD ∥AB ，∠AOB=90° 将△OCD 旋转至右图的位置【结论】：①右图中△OCD ∽△OAB →→→△OAC ∽△OBD ； ②延长AC 交BD 于点E ，必有∠BEC=∠BOA ；OAB COBCDEOB CDEOA CD③===OAOBOC OD AC BD tan ∠OCD ；④BD ⊥AC ； ⑤连接AD 、BC ，必有2222CD AB B C AD +=+；⑥BD AC 21S △BCD ⨯=三、模型三、对角互补模型（1）全等型-90°【条件】：①∠AOB=∠DCE=90°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=2OC ；③2△OCE △OCD △DCE OC 21S S S =+= 证明提示：①作垂直，如图2，证明△CDM ≌△CEN②过点C 作CF ⊥OC ，如图3，证明△ODC ≌△FEC ※当∠DCE 的一边交AO 的延长线于D 时（如图4）：以上三个结论：①CD=CE ；②OE-OD=2OC ；③2△OCD △OCE OC 21S S =-（2）全等型-120°【条件】：①∠AOB=2∠DCE=120°；②OC 平分∠AOB【结论】：①CD=CE ；②OD+OE=OC ；③2△OCE △OCD △DCE OC 43S S S =+=AOBCDE 图 1A OBCDEM N图 2A OBCDEF图 3A O BCDEMN 图 4证明提示：①可参考“全等型-90°”证法一；②如右下图：在OB 上取一点F ，使OF=OC ，证明△OCF 为等边三角形。

立体几何经典模型——直观感受作图篇

立体几何经典模型——直观感受作图篇
通过下列文字描述（有的并不严谨，自己感受一下），作出所描述几何体的直观图和三视图，并自选棱长，标出三视图所有平面图形的边长
1.底面水平，有一个面正朝你的正方体
2.底面水平，有一条侧棱竖直正朝你的正方体
3.底面水平，有一条棱正朝你的正四面体
4.底面水平，有一条底边所在直线指向你的正四面体
5.从1中挖出来的“墙角”
6.“墙角”是正棱锥，让它底面水平，有一条棱正朝你放置
7.从1中挖出的正四面体
8.从1中挖出的鳖臑（四个面都是直角三角形的三棱锥）
9.从1中挖出的阳马（底面是矩形，一条侧棱垂直于底面的四棱锥）
10.1和它的内切球
11.1和它的棱切球
12.1和它的外接球
13.一枚（视作正方体）旋转的足够快的时候，你看到的几何体
14.正八面体：两个侧棱长等于底边长的正四棱锥底面重合组成；四棱锥底面水平放置，有一条底边正对着你
15.将正方体的一条体对角线竖直放置，一条侧棱正朝你放置（这道题做出来有奖励）。

八个超强模型——彻底解决立体几何的外接球和内切球问题

八个超强模型——彻底解决立体几何的外接球和内切球问题摘要本文介绍了八个超强模型，这些模型可以用来彻底解决立体几何中的外接球和内切球问题。

每个模型都具有独特的特点和优势，能够有效地求解球的外接和内切问题，为立体几何的研究提供了有力的工具和方法。

引言在立体几何中，外接球和内切球问题是非常常见的问题。

求解这些问题通常需要借助一些数学模型和方法。

本文介绍了八个超强模型，这些模型在解决外接球和内切球问题方面表现出色。

模型一：球心法线模型该模型基于球的法线方程，通过求解法线方程的交点来得到球心坐标。

利用该模型可以快速准确地求解外接球和内切球的球心坐标。

模型二：点坐标向量模型该模型利用点的坐标向量来表示球心坐标，通过计算坐标向量的运算得到球心坐标。

该模型适用于各种类型的球体，求解效果良好。

模型三：坐标平移模型该模型基于坐标平移的概念，通过平移球心坐标来求解外接球和内切球的球心坐标。

该模型简单易懂，适用于多种立体几何结构。

模型四：线段接触模型该模型利用线段的接触点来求解外接球和内切球的球心坐标。

通过求解线段接触点的几何关系，可以得到球心坐标。

该模型适用于特定的立体几何结构。

模型五：平面交线模型该模型基于平面交线的概念，通过求解平面交线的方程来得到球心坐标。

该模型对于立体几何结构较复杂的情况下求解效果较好。

模型六：圆心半径模型该模型通过求解球的圆心和半径来得到球心坐标。

该模型适用于已知球的圆心和半径的情况下求解。

模型七：曲线拟合模型该模型通过对曲线进行拟合来得到球心坐标。

该模型适用于曲线较为复杂的情况下求解。

模型八：图像处理模型该模型利用图像处理的方法来得到球心坐标。

通过处理球体的图像，可以得到球心坐标。

该模型适用于图像处理技术较为成熟的情况下求解。

结论本文介绍了八个超强模型，这些模型可以用来彻底解决立体几何中的外接球和内切球问题。

每个模型都有其独特的特点和优势，能够有效地求解球的外接和内切问题。

这些模型为立体几何的研究提供了有力的工具和方法，有助于推动该领域的发展。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

立体几何中的一个经典几何模型
由四个直角三角形围成的四面体是一个经典的几何模型i ，俗称“三节棍”模型，如图1四面体A BCD -中，,,ABC ABD ∠∠
,BDC ADC ∠∠均为直角.我们研究它的产生背
景、各面所成的角及其棱所在直线与相关面所成的角的性质，为此，定义BDC ⌝为底面，ADC ⌝为斜面，ABC ⌝为主垂面，ABD ⌝为副垂面.(主副垂面之分在于BC BD >)AC 为
BDC ⌝
的主斜线，AD 为BDC ⌝副斜线，它们在
底面内的摄影BC BD 和也分别称作主射影和副射影.设,ACB α∠=,BCD β∠=.ACD γ∠=
这个模型的几何结构特点决定，在其
中，空间直角坐标系的建立以及相关向量的计算不易直接实现，因此我们有必要探讨在这种模型中如何避开利用空间向量的解析法而用纯几何的手段解决有关角的问题.
1. “三节棍”模型的背景：
①线面角背景：如图1，AB 是平面BCD 的垂线，B 为垂足，AC 是平面BCD 的斜线，C 是斜足，CD 是平面BCD 内另一异于BC 的直线，过B 作BD CD ⊥，垂足为D ，ABC ∠就是斜线AC 与底面BCD 所成的角，四面体A BCD - 即为“三节棍”模型
②长方体切割背景：如图2，在长方体 ABCD A B C D ''''-中两个平面A AC '和A BC '切割所得四面体A ABC '-即为“三节棍”模型.
③球体切割背景：如图3，球O 的直径为AB ，过AB 作球的两个不同截面,ABD ABC ，再分别过AD
和BC 分别作共弦CD 的截面ACD 和BCD ，四面体A BCD -即为“三节棍”模型.
2. “三节棍”模型的性质：
在图1的“三节棍”模型中，我们可以得出下面的性质， ①最小角定理：
斜线AC 与BDC ⌝所成的角，是斜线AC 与BDC ⌝内过斜足的所有直线所成角中最小的角.
②三面角公式：cos cos cos γαβ=⋅———公式1
在图1中，,,αβγ满足cos cos cos γαβ=⋅.不仅如此，“三节棍”模型中各顶点的三个角中，对应斜面上的角的余弦等于其它两个互相垂直的面中对应角余弦之积.
如cos cos ADC BDC ∠=∠⋅cos ADB ∠.
由各面直角三角形锐角的互余关系，公式1还可化为：
sin sin sin CAD CAB CBD ∠=∠⋅∠———公式1'
③二面角公式：
1) 主、副垂面所成的二面角C AB D --，它的平面角CBD ∠等于2
πβ-
2) 主垂面与底面所成的角A BC D --为直二面角. 3) 副垂面与底面所成的二面角A BD C --为直二面角
B
A
C
D
图1
4)副垂面与斜面所成的二面角B AD C
--为直二面角
5)斜面与底面所成的二面角A CD B
--的平面角为ADB
∠，
ADB
∠满足：cos ADB
∠= tan
tan
β
γ
————公式2
证明：设1
CD=，则tan,
BDβ
=tan
ADγ
=，
所以cos ADB
∠= tan tan
β
γ
6)主垂面与斜面所成的二面角B AC D
--，设其平面角为,θ
cosθ= tan
tan α
γ
————公式3
证明：如图4，作,
DO BC
⊥垂足为O，连接AO.
设=1
CD，则cos
OCβ
=，
1
cos
AC
γ
=，
tan,
ADγ
=
④线面角
1).副斜线与主垂面所成的角为ϕ，ϕ满
足sin
sin
tan β
ϕ
γ
=.——公式4
证明：如图4，按照6)的作图，OAD
∠即为副斜线AD与主截面ABC所成的角，即OADϕ
∠=，同样设CD=1
则sin,
ODβ
=tan
ADγ
=，
sin sin
tan
OD
AD
β
ϕ
γ∴==
2).主射影与斜面所成的角为ψ
则ψ满足sin sin tan tan
sin
sin tan
αβαβ
ψ
γγ
==————公式5
证明：如图5，过B作BE AD
⊥，连接CE，
则BCE
∠即为主射影BC
与斜面ACD所成的角，
设1
BC=，则sin
BDβ
=
在ABD
∆中利用等面积关系得：
tan sin
cos tan
AB BD
BE
AD
αβ
βγ
⋅
==，
3.“三节棍”模型的应用举例
为说明“三节棍”模型及其相关规律在解题中的作用，我们试举下面例题
例1.
如图，在三棱柱
111
ABC A B C
-中，11
AAC C是边长为4的正方形平面ABC⊥平面
11
AAC C，3, 5.
AB BC
==
(I)求证：
1
AA⊥平面ABC；
(II)求二面角
111
A BC B
--的余弦值；
(III)证明：在线段
1
BC存在点D，使得
1
AD A B
⊥，并求
1
BD
BC
的值.
分析：该题中的几何关系尽管适合建立空
间直角坐标系，但我们直接用公式3更快
捷的解决问题.
解：(I)略
(II)由(I)知
1
BB⊥平面111
A B C，11
A C⊥
11
BB A，1A B=5
B
A
C
D
O
图4
图5
C
D
E
B
A
C
B
C1
B1
设二面角111A BC B --为η，则
11114
tan 16
5cos 5tan 25
4
BC B BC A η∠===
∠ (III)证明(略)
例2.如图，AB 是圆O 的直径，点C 是圆
是圆O 上异于上异于,A B 的点，直线平面直线PC ⊥,ABC ,E F 分别是
,PA PC 的中点
(I)记平面BEF 与ABC 的交线为l ，判断直线l 与平面PAC 的位置关系，并加以证明；
(II)设(I)中的直线l 与圆O 的另一个交点为D ，且
点Q DQ 12
CP =.记直线PQ 与平面ABC 所成的角为θ，异面直线PQ 与EF 所成的角为α，二面角E l C --的大小为β，求证：sin sin sin θαβ=
解析：本题直接用到了“三节棍”模型，除了建系用解析法外，我们用公式1可以更迅捷的解决问题. 解(I)（略）
(II)证明：由(I)知DB ⊥平面BCF ，连接DF ，DF 平行于PQ ，则
,,FDC FDB FBC θαβ∠=∠=∠=.在四面体F CBD -中，
即)cos()cos()2
2
2
πππ
θαβ-=--cos(
所以sin sin sin θαβ=. 证毕.
例2图。