中数学中考中的开放题、探索题

合集下载

初中数学开放型试题含答案-

开放型试题开放型试题重在开发思维，促进创新，提高数学素养，所以是近几年中考试题的热点考题。

观察、实验、猜想、论证是科学思维方法，是新课标思维能力新添的内容，学习中应重视并应用。

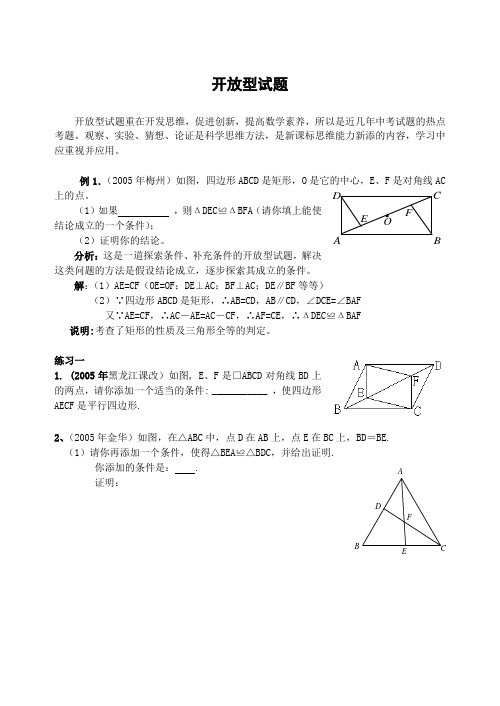
例1．（2005年梅州）如图，四边形ABCD 是矩形，O 是它的中心，E 、F 是对角线AC上的点。

（1）如果，则ΔDEC ≌ΔBFA （请你填上能使结论成立的一个条件）；（2）证明你的结论。

分析：这是一道探索条件、补充条件的开放型试题，解决这类问题的方法是假设结论成立，逐步探索其成立的条件。

解：（1）AE=CF （OE=OF ；DE ⊥AC ；BF ⊥AC ；DE ∥BF 等等）（2）∵四边形ABCD 是矩形，∴AB=CD ，AB ∥CD ，∠DCE=∠BAF 又∵AE=CF ，∴AC －AE=AC －CF ，∴AF=CE ，∴ΔDEC ≌ΔBAF 说明:考查了矩形的性质及三角形全等的判定。

练习一1. (2005年黑龙江课改）如图, E 、F 是□ABCD 对角线BD 上的两点，请你添加一个适当的条件: ___________ ，使四边形AECF 是平行四边形.2、（2005年金华）如图，在△ABC 中，点D 在AB 上，点E 在BC 上，BD ＝BE. （1）请你再添加一个条件，使得△BEA ≌△BDC ，并给出证明.你添加的条件是： . 证明：A D E FO F EDCBA（2）根据你添加的条件，再写出图中的一对全等三角形： . （只要求写出一对全等三角形，不再添加其他线段，不再标注或使用其他字母，不必写出证明过程） 3、（2005年玉溪）如图，在梯形ABCD 中，AD ∥BC ，BD ＝CD ，AB ＜CD 且∠ABC 为锐角，若AD ＝4，BC ＝12，E 为BC 上一点。

问：当CE 分别为何值时，四边形ABED 是等腰梯形？直角梯形？请分别说明理由。

例2、（2005年长沙）己知点E 、F 在ABC ∆的边 AB 所在的直线上，且AE BF =，FH EG AC ，FH 、EG 分别交边BC 所在的直线于点H 、G ．⑴如图l ，如果点E 、F 在边AB 上，那么EG FH AC +=；⑵如图2，如果点E 在边AB 上，点F 在AB 的延长线上，那么线段EG 、FH 、AC 的长度关系是_______________ ；⑶如图3，如果点E 在AB 的反向延长线上，点F 在AB 的延长线上，那么线段EG 、FH 、AC 的长度关系是_________ ；对⑴⑵⑶三种情况的结论，请任选一个给予证明．分析：这是一道探索、确定结论的开放型试题，解决这类问题的方法是根据条件，结合已学的知识、数学思想方法，通过分析、归纳逐步得出结论，或通过观察、实验、猜想、论证的方法求解。

中考数学重难点突破专题一：规律探索型问题试题(含答案)

精品基础教育教学资料，仅供参考，需要可下载使用！专题一规律探索问题类型1 数字规律1．甲、乙、丙三位同学进行报数游戏，游戏规则为：甲报1，乙报2，丙报3，再甲报4，乙报5，丙报6，…依次循环反复下去，当报出的数为2020时游戏结束，若报出的数是偶数，则该同学得1分．当报数结束时甲同学的得分是__337__分．解析：甲报的数中第一个数为1，第2个数为1＋3＝4，第3个数为1＋3×2＝7，第4个数为1＋3×3＝10，…，第n 个数为1＋3(n －1)＝3n －2，3n －2＝2020，则n ＝674，甲报出了674个数，一奇一偶，所以偶数有674÷2＝337个，得337分．2．如图，给正五边形的顶点依次编号为1，2，3，4，5，若从某一顶点开始，沿五边形的边顺时针行走，顶点编号是几，就走几个边长，则称这种走法为一次“移位”．如：小宇在编号为3的顶点上时，那么他应走3个边长，即从3→4→5→1为第一次“移位”，这时他到达编号为1的顶点；然后从1→2为第二次“移位”．若小宇从编号为2的顶点开始，第10次“移位”，则他所处顶点的编号为__3__．3．(2017·六盘水)计算1＋4＋9＋16＋25＋…的前29项的和是__8555__．解析：12＋22＋32＋42＋52＋…＋292＋…＋n 2＝0×1＋1＋1×2＋2＋2×3＋3＋3×4＋4＋4×5＋5＋…(n －1)n ＋n＝(1＋2＋3＋4＋5＋…＋n)＋[0×1＋1×2＋2×3＋3×4＋…＋(n －1)n]＝n （n ＋1）2＋{13(1×2×3－0×1×2)＋13(2×3×4－1×2×3)＋13(3×4×5－2×3×4)＋…＋13[(n －1)·n·(n ＋1)－(n －2)·(n －1)·n]}＝n （n ＋1）2＋13[(n －1)·n·(n ＋1)]＝n （n ＋1）（2n ＋1）6， ∴当n ＝29时，原式＝29×（29＋1）×（2×29＋1）6＝8555. 类型2 图形规律4．(2017·天水)观察下列的“蜂窝图”则第n 个图案中的“”的个数是__3n ＋1__．(用含有n 的代数式表示)5．(2017·临沂)将一些相同的“○“按如图所示摆放，观察每个图形中的“○“的个数，若第n 个图形中“○“的个数是78，则n 的值是( B )A ．11B ．12C ．13D ．14解：第1个图形有1个小圆；第2个图形有1＋2＝3个小圆；第3个图形有1＋2＋3＝6个小圆；第4个图形有1＋2＋3＋4＝10个小圆；第n 个图形有1＋2＋3＋…＋n ＝n （n ＋1）2个小圆；∵第n 个图形中“○“的个数是78，∴78＝n （n ＋1）2，解得：n 1＝12，n 2＝－13(不合题意舍去)．6．(2017·德州)观察下列图形，它是把一个三角形分别连接这个三角形三边的中点，构成4个小三角形，挖去中间的一个小三角形(如图1)；对剩下的三个小三角形再分别重复以上做法，…将这种做法继续下去(如图2，图3…)，则图6中挖去三角形的个数为( C )A ．121B ．362C ．364D ．729解：图1挖去中间的1个小三角形，图2挖去中间的(1＋3)个小三角形，图3挖去中间的(1＋3＋32)个小三角形，…则图6挖去中间的(1＋3＋32＋33＋34＋35)个小三角形，即图6挖去中间的364个小三角形，类型3 坐标变化规律7．在平面直角坐标系中，对于平面内任一点(a ，b)，若规定以下三种变换：①△(a ，b)＝(－a ，b)；②○(a ，b)＝(－a ，－b)；③Ω(a ，b)＝(a ，－b)，按照以上变换例如：△(○(1，2))＝(1，－2)，则○(Ω(3，4))等于__(－3，4)__．8．(2017·衢州)如图，正△ABO 的边长为2，O 为坐标原点，A 在x 轴上，B 在第二象限，△ABO 沿x 轴正方向作无滑动的翻滚，经一次翻滚后得到△A 1B 1O ，则翻滚3次后点B的对应点的坐标是__(5，3)__，翻滚2017次后AB 中点M 经过的路径长为 (134633＋896)π ．解析：如图作B 3E ⊥x 轴于E ，易知OE ＝5，B 3E ＝3，∴B 3(5，3)，观察图象可知三次一个循环，一个循环点M 的运动路径为120·π·3180＋120π·1180＋120π·1180＝(23＋43)π，∵2017÷3＝672…1，∴翻滚2017次后AB 中点M 经过的路径长为672·(23＋43)π＋233π＝(134633＋896)π.9．(2017·菏泽)如图，AB ⊥y 轴，垂足为B ，将△ABO 绕点A 逆时针旋转到△AB 1O 1的位置，使点B 的对应点B 1落在直线y ＝－33x 上，再将△AB 1O 1绕点B 1逆时针旋转到△A 1B 1O 2的位置，使点O 1的对应点O 2落在直线y ＝－33x 上，依次进行下去…若点B 的坐标是(0，1)，则点O 12的纵坐标为__(－9－93，9＋33)__．解：观察图象可知，O 12在直线y ＝－33x 时，OO 12＝6·OO 2＝6(1＋3＋2)＝18＋63， ∴O 12的横坐标＝－(18＋63)·cos30°＝－9－93，O 12的纵坐标＝12OO 12＝9＋33，∴O 12(－9－93，9＋33)． 10．定义：直线l 1与l 2相交于点O ，对于平面内任意一点M ，点M 到直线l 1、l 2的距离分别为p 、q ，则称有序实数对(p ，q)是点M 的“距离坐标”，根据上述定义，“距离坐标”是(1，2)的点的个数是( C )A ．2B ．3C ．4D ．5解析：如图，∵到直线l 1的距离是l 的点在与直线l 1平行且与l 1的距离是1的两条平行线a 1、a 2上，到直线l 2的距离为2的点在与直线l 2平行且与l 2的距离是2的两条平行线b 1、b 2上，∴“距离坐标”是(1，2)的点是M 1，M 2，M 3，M 4，一共4个．11．(2017·绍兴模拟)在平面直角坐标系中，对图形F 给出如下定义：如图形F 上的所有点都在以原点为顶点的角的内部或边界上，在所有满足条件的角中，其度数的最小值称为图形的坐标角度．例如，图中的矩形ABCD 的坐标角度是90°.现将二次函数y ＝ax 2(1≤a ≤3)的图象在直线y ＝1下方的部分沿直线y ＝1向上翻折，则所得图形的坐标角度α的取值范围是( B )A ．30°≤α≤60°B ．60°≤α≤90°C ．90°≤α≤120°D ．120°≤α≤150°12．(2017·昆山二模)赵爽弦图是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形，如图所示，若这四个全等直角三角形的两条直角边分别平行于x 轴和y 轴，大正方形的顶点B 1，C 1，C 2，C 3，…，C n 在直线y ＝－12x ＋72上，顶点D 1，D 2，D 3，…，D n 在x 轴上，则第n 个阴影小正方形的面积为__(23)2n －2__．解：设第n 个大正方形的边长为a n ，则第n 个阴影小正方形的边长为55a n，当x ＝0时，y ＝－12x ＋72＝72，∴72＝55a 1＋52a 1，∴a 1＝ 5.∵a 1＝a 2＋12a 2，∴a 2＝235，同理可得：a 3＝23a 2，a 4＝23a 3，a 5＝23a 4，…，∴a n ＝(23)n －1a 1＝5(23)n －1，∴第n 个阴影小正方形的面积为(55a n )2＝[(23)n －1]2＝(23)2n －2.。

含答案中考数学复习专题六规律探索题

专题六规律探索题类型一数式规律1. 设a n 为正整数n 4的末位数，如a 1＝1，a 2＝6，a 3＝1，a 4＝6，…，则a 1＋a 2＋a 3＋…＋a 2019＋a 2020＋a 2021＝________．2. 如图，阶梯图的每个台阶上都标着一个数，从下到上的第1个至第4个台阶上依次标着－5，－2，1，9，且任意相邻四个台阶上数的和都相等．则第5个台阶上的数x ＝________，从下到上前35个台阶上数的和＝________．第2题图3. 将从1开始的连续奇数按如图所示的规律排列，例如：位于第4行第3列的数为27，则位于第32行第13列的数是________．第3题图4. 如图，下列各正方形中的四个数具有相同的规律，根据规律，x 的值为________．第4题图5. 已知a ＞0，S 1＝1a ，S 2＝－S 1－1，S 3＝1S 2，S 4＝－S 3－1，S 5＝1S 4，…(即当n 为大于1的奇数时，S n ＝1S n －1；当n 为大于1的偶数时，S n ＝－S n －1－1)，按此规律，S 2018＝________(用含a 的代数式表示)．6. 观察下列等式：(x －1)(x ＋1)＝x 2－1；(x －1)(x 2＋x ＋1)＝x 3－1；(x －1)(x 3＋x 2＋x ＋1)＝x 4－1；(x －1)(x 4＋x 3＋x 2＋x ＋1)＝x 5－1；…根据以上规律，计算22020＋22019＋22018＋…＋23＋22＋2＋1的结果是________，个位数字是________．7. 人们把5－12这个数叫做黄金分割数，著名数学家华罗庚优选法中的0.618法就应用了黄金分割数．设a ＝5－12，b ＝5＋12，得ab ＝1，记S 1＝11＋a ＋11＋b ，S 2＝11＋a 2＋11＋b 2，…，S 10＝11＋a 10＋11＋b 10.则S 1＋S 2＋…＋S 10＝________． 8.如图，某校礼堂的座位分为四个区域，前区一共有8排，其中第1排共有20个座位(含左、右区域)，往后每排增加两个座位，前区最后一排与后区各排的座位数相同，后区一共有10排，则该礼堂的座位总数是________．第8题图9.观察下列等式：x 1＝1＋112＋122＝32＝1＋11×2； x 2＝1＋122＋132＝76＝1＋12×3； x 3＝1＋132＋142＝1312＝1＋13×4； …根据以上规律，计算x 1＋x 2＋x 3＋…＋x 2020－2021＝________.10.“干支纪年法”是我国历法的一种传统纪年法，甲、乙、丙、丁、戊、己、庚、辛、壬、癸被称为“十天干”；子、丑、寅、卯、辰、巳、午、未、申、酉、戌、亥叫做“十二地支”；“天干”以“甲”字开始，“地支”以“子”字开始，两者按干支顺序相配，组成了干支纪年法，其相配顺序为甲子、乙丑、丙寅…癸酉；甲戌、乙亥、丙子…癸未；甲申、乙酉、丙戌…癸巳；…共得到60个组合，称六十甲子，周而复始，无穷无尽.2021年是“干支纪年法”中的辛丑年，那么2050年是“干支纪年法”中的________．类型二图形变化规律1. 如图，在平面直角坐标系中，函数y ＝3x 和y ＝－x 的图象分别为直线l 1，l 2，过点(1，0)作x 轴的垂线交l 1于点A 1，过点A 1作y 轴的垂线交l 2于点A 2，过点A 2作x 轴的垂线交l 1于点A 3，过点A 3作y 轴的垂线交l 2于点A 4，…，依次进行下去，则点A 6的坐标为________，点A2022的坐标为________．第1题图2. 如图，菱形ABCD中，∠ABC＝120°，AB＝1，延长CD至A1，使DA1＝CD，以A1C为一边，在BC的延长线上作菱形A1CC1D1，连接AA1，得到△ADA1；再延长C1D1至A2，使D1A2＝C1D1，以A2C1为一边，在CC1的延长线上作菱形A2C1C2D2，连接A1A2，得到△A1D1A2，…，按此规律，得到△A2020D2020A2021，记△ADA1的面积为S1，△A1D1A2的面积为S2，…，△A2020D2020A2021的面积为S2021，则S2021＝________．第2题图3. 如图，在Rt△ABC中，∠ACB＝90°，∠B＝30°，AC＝1，且AC在直线l上，将△ABC 绕点A顺时针旋转到①，可得到点P1，此时AP1＝2；将位置①的三角形绕点P1顺时针旋转到位置②，可得到点P2，此时AP2＝2＋3；将位置②的三角形绕点P2顺时针旋转到位置③，可得到点P3，此时AP3＝3＋3，…，按此规律继续旋转，直到点P2020为止，则AP2020等于________．第3题图4. 已知菱形A1B1C1D1的边长为2，∠A1B1C1＝60°，对角线A1C1，B1D1相交于点O.以点O 为坐标原点，分别以OA1，OB1所在直线为x轴、y轴，建立如图所示的平面直角坐标系．以B1D1为对角线作菱形B1C2D1A2∽菱形A1B1C1D1，再以A2C2为对角线作菱形A2B2C2D2∽菱形B1C2D1A2，再以B2D2为对角线作菱形B2C3D2A3∽菱形A2B2C2D2，…，按此规律继续作下去，在x轴的正半轴上得到点A1，A2，A3，…，A n，则点A n的坐标为________．第4题图5. 如图，在矩形ABCD 中，AB ＝1，BC ＝2，连接AC ，过点D 作DC 1⊥AC 于C 1；以C 1A 、C 1D 为邻边作矩形AA 1DC 1，连接A 1C 1，交AD 于O 1，过点D 作DC 2⊥A 1C 1于C 2，交AC 于M 1，以C 2A 1，C 2D 为邻边作矩形A 1A 2DC 2，连接A 2C 2，交A 1D 于O 2，过点D 作DC 3⊥A 2C 2于C 3，交A 1C 1于M 2；以C 3A 2，C 3D 为邻边作矩形A 2A 3DC 3，连接A 3C 3，交A 2D 于O 3，过点D 作DC 4⊥A 3C 3于C 4，交A 2C 2于M 3；…若四边形AO 1C 2M 1的面积为S 1，四边形A 1O 2C 3M 2的面积为S 2，四边形A 2O 3C 4M 3的面积为S 3，…，四边形A n －1O n C n ＋1M n 的面积为S n ，则S n ＝________．(结果用含正整数n 的式子表示)第5题图6. 如图，在平面直角坐标系中，菱形OABC 的边OC 在x 轴的正半轴上，且点C 的坐标为(2，0)，∠OCB ＝45°，将菱形OABC 绕点O 顺时针旋转45°后得到菱形OA 1B 1C 1，…，依此方式，绕点O 连续旋转2021次后得到菱形OA 2021B 2021C 2021，则点A 2021的坐标为________．第6题图7. 如图，在平面直角坐标系中，AB ⊥y 轴，垂足为B ，将△ABO 绕点A 逆时针旋转到△AB 1O 1的位置，使点B 的对应点B 1落在直线y ＝－34x 上，再将△AB 1O 1绕点B 1逆时针旋转到△A 1B 1O 2的位置，使点O 1的对应点O 2也落在直线y ＝－34x 上，以此进行下去…，若点B 的坐标为(0，3)，则点B 21的纵坐标．．．为________．第7题图专题六规律探索题类型一数式规律1. 6667 【解析】∵a 1＝1，a 2＝6，a 3＝1，a 4＝6，a 5＝5，a 6＝6，a 7＝1，a 8＝6，a 9＝1，a 10＝0，…，即每10个数一循环，∴a 1＋a 2＋a 3＋…＋a 10＝1＋6＋1＋6＋5＋6＋1＋6＋1＋0＝33，2021÷10＝202……1，∴33×202＋1＝6667.2. －5；18 【解析】第1个至第4个台阶上数的和为－5＋(－2)＋1＋9＝3，∵任意相邻四个台阶上数的和都相等，∴－2＋1＋9＋x ＝3，解得x ＝－5，则第5个台阶上的数x 是－5.由题意知，台阶上的数字每4个一循环，∵35÷4＝8……3，∴从下到上前35个台阶上数的和为8×3－5－2＋1＝18.3. 2023 【解析】观察数字的变化，发现规律：第n 行，第n 列的数为2n (n －1)＋1，∴第32行，第32列的数为2×32×(32－1)＋1＝1985，根据排列规律，偶数行的数从右往左依次增加2，∴第32行，第13列的数为1985＋2×(32－13)＝2023.4. 170 【解析】分析题目可得4＝2×2，6＝3×2，8＝4×2；2＝1＋1，3＝2＋1，4＝3＋1；∴18＝2b ，b ＝a ＋1.∴a ＝8，b ＝9.∵9＝2×4＋1，20＝3×6＋2，35＝4×8＋3，∴x ＝18b ＋a ＝18×9＋8＝170.5. －a ＋1a 【解析】S 1＝1a ，S 2＝－1a －1＝－a ＋1a ，S 3＝－a a ＋1，S 4＝－1a ＋1，S 5＝－(a ＋1)，S 6＝a ，S 7＝1a ，…，∴每6个数是一个循环，∵2018÷6＝336……2，∴S 2018＝S 2＝－a ＋1a .6. 22021－1 ；1 【解析】根据题意得：(x －1)(x n ＋x n －1＋…＋x ＋1)＝x n ＋1－1，∵(2－1)×(22020＋22019＋…＋2＋1)＝22020＋1－1，∴22020＋22019＋…＋2＋1＝22021－1，∵21＝2，个位数字是2，22＝4，个位数字是4，23＝8，个位数字是8，24＝16，个位数字是6，25＝32，个位数字是2，…，∵2021÷4＝505……1，∴22021的个位数字是2，∴22021－1的个位数字是1. 7. 10 【解析】∵a ＝5－12，b ＝5＋12，∴ab ＝5－12×5＋12＝1，∵S n ＝11＋a n ＋11＋b n ＝2＋a n ＋b n （1＋a n ）（1＋b n ）＝2＋a n ＋b n 1＋（ab ）n ＋a n ＋b n ＝2＋a n ＋b n2＋a n ＋b n ＝1，∴S 1＝S 2＝S 3＝…＝S n ＝1，∴S 1＋S 2＋S 3＋…＋S 10＝10.8. 556个【解析】∵前区一共有8排，其中第1排共有20个座位(含左、右区域)，往后每排增加两个座位，∴前区最后一排座位数为20＋2×(8－1)＝34，∴前区座位数为(20＋34)×8÷2＝216，∵前区最后一排与后区各排的座位数相同，后区一共有10排，∴后区的座位数为10×34＝340，∴该礼堂的座位总数是216＋340＝556个．9. －12021 【解析】x 1＝1＋11×2＝1＋1－12，x 2＝1＋12×3＝1＋12－13，x 3＝1＋13×4＝1＋13－14，…，x n ＝1＋1n （n ＋1）＝1＋1n －1n ＋1，∴x 1＋x 2＋x 3＋…＋x n ＝1＋1－12＋1＋12－13＋1＋13－14＋…＋1＋1n －1n ＋1＝n ＋1－1n ＋1，∴x 1＋x 2＋x 3＋…＋x 2020－2021＝2020＋1－12021－2021＝－12021.10. 庚午年【解析】公元纪年换算成干支纪年方法如下：天干算法：用公元纪年数减3，除以10(不管商数)所得余数，就是天干所对应的位数，地支算法：用公元纪年数减3，除以12(不管商数)所得余数，就是地支所对应的位数，2050－3＝2047，2047÷10余数为7，∴天干为“庚”，2047÷12余数为7，∴地支为“午”，∴2050年为“庚午”年．类型二图形变化规律1. (－27，27)，(－31011，31011) 【解析】当x ＝1时，y ＝3x ＝3，∴点A 1的坐标为(1，3)；当y ＝－x ＝3时，x ＝－3，∴点A 2的坐标为(－3，3)；同理可得A 3(－3，－9)，A 4(9，－9)，A 5(9，27)，A 6(－27，27)，A 7(－27，－81)，…，∴A 4n ＋1(32n ，32n ＋1)，A 4n ＋2(－32n ＋1，32n ＋1)，A 4n ＋3(－32n ＋1，－32n ＋2)，A 4n ＋4(32n ＋2，－32n ＋2)(n 为自然数)．∵2022＝505×4＋2，∴点A 2022的坐标为(－31011，31011)．2. 24038· 3 【解析】∵四边形ABCD 是菱形，∴AB ＝AD ＝BC ＝CD ＝1，AD ∥BC ，AB ∥CD ，∵∠ABC ＝120°，∴∠BCD ＝60°，∴∠ADA 1＝∠BCD ＝60°，∵DA 1＝CD ，∴DA 1＝AD ，∴△ADA 1为等边三角形，同理可得△A 1D 1A 2，…，△A 2020D 2020A 2021都为等边三角形，如解图，过点B 作BE ⊥CD 于点E ，∴BE ＝BC ·sin ∠BCD ＝32＝A 1D ，∴S 1＝12A 1D ·BE ＝34A 1D 2＝34，同理可得，S 2＝34A 2D 12＝34×22＝3，S 3＝34A 3D 22＝34×42＝43，…，∴由此规律可得，S n ＝3·22n －4，∴S 2021＝3×22×2021－4＝24038· 3.第2题解图3. 2021＋673 3 【解析】∵∠ACB ＝90°，∠B ＝30°，AC ＝1，∴AB ＝2，BC ＝3，∴将△ABC 绕点A 顺时针旋转到①，可得到点P 1，此时AP 1＝2；将位置①的三角形绕点P 1顺时针旋转到位置②，可得到点P 2，此时AP 2＝2＋3；将位置②的三角形绕点P 2顺时针旋转到位置③，可得到点P 3，此时AP 3＝3＋3，…，∵2020÷3＝673……1，∴AP 2020＝673×(3＋3)＋2＝2021＋673 3.4. (3n －1，0) 【解析】根据题意得△A 1B 1C 1是等边三角形，∴A 1C 1＝2，则点A 1的坐标是(1，0)，B 1O ＝3，在Rt △A 2OB 1中，tan30°＝B 1O A 2O ，得A 2O ＝3，则点A 2的坐标为(3，0)，同理求出点A 3的坐标是(9，0)，A 4的坐标是(27，0)，…，即点A 3(32，0)，A 4(33，0)，…，∴点A n 的坐标为(3n －1，0)5. 9×4n －15n ＋1 【解析】∵在矩形ABCD 中，AB ＝1，BC ＝2，∴AC ＝5，∵DC 1⊥AC ，∴DC 1＝AD ·CD AC ＝255，∴CC 1＝CD 2－DC 21＝12－（255）2＝55，∴AC 1＝455，∵四边形AA 1DC 1是矩形，∴AA 1＝DC 1＝255，∵DC 2⊥A 1C 1，∴∠AC 1A 1＝∠C 1DM 1，∴tan ∠AC 1A 1＝tan ∠C 1DM 1＝AA 1AC 1＝C 1C 2DC 2＝12，∴由勾股定理可得C 1C 2＝25，∴M 1C 2＝15，∵点O 1是矩形AA 1DC 1对角线的交点，∴点O 1到AC 1的距离＝12DC 1＝55，∴S 1＝S △AO 1C 1－S △C 1C 2M 1＝12×455×55－12×15×25＝925＝9×152；同理可得A 1C 2＝85，DC 2＝45，C 2C 3＝4525，M 2C 3＝2525，点O 2到A 1C 1的距离＝12DC 2＝25，∴S 2＝S △A 1O 2C 2－S △C 2C 3M 3＝12×85×25－12×4525×2525＝36125＝9×453；同理可得S 3＝9×4254，S 4＝9×4355，…，以此类推可得S n ＝9×4n －15n ＋1.6. (0，－2) 【解析】如解图，∵四边形OABC 是菱形，且OC ＝2，∴OA ＝2，又∵∠OCB ＝45°，∴∠OAB ＝45°，∴A (－1，1)，由旋转的性质得OA ＝OA 1＝OA 2＝…＝OA 7＝ 2.∵菱形OABC 绕点O 顺时针旋转45°后得到菱形OA 1B 1C 1，相当于将线段OA 绕点O 顺时针旋转45°得到线段OA 1，易知点A 与A 2关于y 轴对称，点A 2与A 4关于x 轴对称，点A 与点A 6关于x 轴对称，其余点均在x 轴、y 轴上，∴A (－1，1)，A 1(0，2)，A 2(1，1)，A 3(2，0)，A 4(1，－1)，A 5(0，－2)，A 6(－1，－1)，A 7(－2，0)，….∵360°÷45°＝8，∴图形在旋转过程中每8次为一个循环，∵2021÷8＝252……5，∴点A 2021的坐标与点A 5的坐标相同，∴点A 2021的坐标为(0，－2)．第6题解图7. 3875 【解析】∵AB ⊥y 轴，点B (0，3)，∴OB ＝3，则点A 的纵坐标为3，将y ＝3代入y ＝－34x ，解得x ＝－4，即A (－4，3)，∴OB ＝3，AB ＝4，OA ＝32＋42＝5，由旋转可知：OB ＝O 1B 1＝O 2B 1＝O 2B 2＝...＝3，OA ＝O 1A ＝O 2A 1＝...＝5，AB ＝AB 1＝A 1B 1＝A 2B 2＝ (4)∴OB 1＝OA ＋AB 1＝5＋4＝9，B 1B 3＝3＋4＋5＝12，∴OB 21＝OB 1＋B 1B 21＝9＋(21－1)÷2×12＝129，设B 21(a ，－34a )，则OB 21＝a 2＋（－34a ）2＝129, 解得a ＝－5165或5165(舍)，则－34a ＝－34×(－5165)＝3875，即点B 21的纵坐标为3875.。

开放探究题-中考数学

开放探究题-中考数学开放探索性试题在中考中越来越受到重视，由于条件与结论的不确定性，使得解题的方法与答案呈多样性，学生犹如八仙过海，各显神通。

探索性问题的特点是：问题一般没有明确的结论，没有固定的形式和方法，需要自己通过观察、分析、比较、概括、推理、判断等探索活动来确定所需求的结论或条件或方法，这类题主要考查学生分析问题和解决问题的能力和创新意识。

这类题对同学们的综合素质要求比较高，这类题往往作为中考试卷中的压轴题出现，在中考中所占比例在9％左右。

1．条件开放与探索给出问题的结论，让解题者分析探索使结论成立应具备的条件，而满足结论的条件往往不惟一，这样的问题是条件开放性问题。

它要求解题者善于从问题的结论出发，逆向追索，多途寻因。

[例1] 已知△ABC 内接于⊙O ，⑴当点O 与AB 有怎样的位置关系时，∠ACB 是直角？⑵在满足⑴的条件下，过点C 作直线交AB 于D ，当CD 与AB 有什么样的关系时，△ABC ∽△CBD ∽△ACD ？ ⑶画出符合⑴、⑵题意的两种图形，使图形的CD ＝2cm 。

[解析]：⑴要使∠ACB ＝90°，弦AB 必须是直径，即O 应是AB 的中点；⑵当CD ⊥AB 时，结论成立；⑶由⑵知DB AD CD ⋅=2，即422==⋅DB AD ，可作直径AB 为5的⊙O ，在AB 上取一点D ，使AD ＝1，BD ＝4，过D 作CD⊥AB 交⊙O 于C 点，连结AC 、BC ，即得所求。

⑴当点O 在AB 上（即O 为AB 的中点）时，∠ACB 是直角； ⑵∵∠ACB 是直角，∴当CD ⊥AB 时，△ABC ∽△CBD ∽△ACD ；⑶作直径AB 为5的⊙O ，在AB 上取一点D ，使AD ＝1，BD =4，过D 点作CD ⊥AB 交⊙O 于C 点，连结AC 、BC ，即为所求（如下图所示）。

[评注]：本题是一个简单的几何条件探索题，它突破了过去“假设——求证”的封闭式论证，而是给出问题的结论，逆求结论成立的条件，强化了对学生通过观察、分析、猜想、推理、判断等探索活动的要求。

中考数学第二轮复习：开放探索问题

及语言表达能力．
16
答案所设计图形如下所示(答案不唯一，可供参考)：
17
【例题6】 (2012· 广东佛山)(1)任选以下三个条件中的一个，求二次函数y＝ax2＋bx＋c的解析式；①y随x变化的部分数值规律如下表：
x
－1
0
1
2
3
y
0
3
4
3
0
18
②有序数对(－1，0)、(1，4)、(3，0)满足y＝ax2＋bx ＋c；
专题五开放探索问题
1
专题解读
2
考情透析
所谓开放探索问题是指已知条件、解题依据、解题方法、问题结论这四项要素中，缺少解题要素两个或两个以上，或者条件、结论有待探求、补充等.
3
思路分析
在解决开放探索问题的时候，需解题者经过探索确定结论或补全条件，将开放性问题转化为封闭性问题，然后选择合适的解题途径完成最后的解答.
2 3 (2)∠E＝30°，CD＝，求⊙O 的半径 r. 3
9
分析此题结论开放，可从不同角度去考虑，例如圆中同弧所对的圆周角，也可以考虑直线之间的位置关系，或从三角形全等与相似方面考虑．
解 (1)由切线的性质及垂径定理，结合题意，我们不
难得出如下结论： BC⊥AB，AD⊥BD，DF＝FE，BD＝BE，
7
分析由已知BD＝CD，又∠EDC＝∠FDB，因为三角形全等条件中必须是SSS，SAS，ASA或 AAS，故添加的条件是：DE＝DF(或CE∥BF或 ∠ECD＝∠FBD或∠DEC＝∠DFB等)．
证明在△BDF和△CDE中，
∵BD＝CD(已知)， ∠EDC＝∠FDB(对顶角相等)，
DE＝DF(添加)，

中考数学探索题---新题型训练(含答案)-

中考数学探索题新题型训练1、我们平常用的数是十进制数，如2639=2×103+6×102+3×101+9×100，表示十进制的数要用10个数码（又叫数字）：0，1，2，3，4，5，6，7，8，9。

在电子数字计算机中用的是二进制，只要两个数码：0和1。

如二进制中101=1×22+0×21+1×20等于十进制的数5，10111=1×24+0×23＋1×22＋1×21＋1×20等于十进制中的数23，那么二进制中的1101等于十进制的数。

2、从1开始，将连续的奇数相加，和的情况有如下规律：1=1=12；1+3=4=22；1+3+5=9=32；1+3+5+7=16=42；1+3+5+7+9=25=52；…按此规律请你猜想从1开始，将前10个奇数（即当最后一个奇数是19时），它们的和是。

3、小王利用计算机设计了一个计算程序，输入和输出的数据如下表：A 、618 B 、638 C 、658 D 、6784、如下左图所示，摆第一个“小屋子”要5枚棋子，摆第二个要11枚棋子，摆第三个要17枚棋子，则摆第30个“小屋子”要枚棋子.5、如下右图是某同学在沙滩上用石子摆成的小房子，观察图形的变化规律，写出第n 个小房子用了块石子。

6、如下图是用棋子摆成的“上”字：(1)(2)(3)第4题第一个“上”字第二个“上”字第三个“上”字如果按照以上规律继续摆下去，那么通过观察，可以发现：（1）第四、第五个“上”字分别需用和枚棋子；（2）第n个“上”字需用枚棋子。

7、如图一串有黑有白，其排列有一定规律的珠子，被盒子遮住一部分，则这串珠子被盒子遮住的部分有_______颗.8、根据下列5个图形及相应点的个数的变化规律：猜想第6个图形有个点，第n个图形中有个点。

9、下面是按照一定规律画出的一列“树型”图：经观察可以发现：图（2）比图（1）多出2个“树枝”，图（3）比图（2）多出5个“树枝”，图（4）比图（3）多出10个“树枝”，照此规律，图（7）比图（6）多出个“树枝”。

中考数学复习第二讲《开放探究型问题》经典题型含答案

中考数学复习专题第二讲开放探究型问题【要点梳理】开放探究型问题的内涵：所谓开放探究型问题是指已知条件、解题依据、解题方法、问题结论这四项要素中，缺少解题要素两个或两个以上，需要通过观察、分析、比较、概括、推理、判断等探索活动来确定所需求的条件或结论或方法．(1)常规题的结论往往是唯一确定的，而多数开放探究题的结论是不确定或不是唯一的，它是给学生有自由思考的余地和充分展示思想的广阔空间；(2)解决此类问题的方法，可以不拘形式，有时需要发现问题的结论，有时需要尽可能多地找出解决问题的方法，有时则需要指出解题的思路等．对于开放探究型问题，需要通过观察、比较、分析、综合及猜想，展开发散性思维，充分运用已学过的数学知识和数学方法，经过归纳、类比、联想等推理的手段，得出正确的结论．在解开放探究题时，常通过确定结论或补全条件，将开放性问题转化为封闭性问题．【学法指导】三个解题方法(1)条件开放型问题：由已知的结论反思题目应具备怎样的条件，即从题目的结论出发，结合图形挖掘条件，逆向追索，逐步探寻，是一种分析型思维方式．它要求解题者善于从问题的结论出发，逆向追索，多途寻因；(2)结论开放型问题：从剖析题意入手，充分捕捉题设信息，通过由因导果，顺向推理或联想、类比、猜测等，从而获得所求的结论；(3)条件和结论都开放型：此类问题没有明确的条件和结论，并且符合条件的结论具有多样性，需将已知的信息集中进行分析，探索问题成立所必须具备的条件或特定的条件应该有什么结论，通过这一思维活动得出事物内在联系，从而把握事物的整体性和一般性．【考点解析】条件开放型问题（2017贵州安顺）如图，DB∥AC，且DB=AC，E是AC的中点，（1）求证：BC=DE；（2）连接AD、BE，若要使四边形DBEA是矩形，则给△ABC添加什么条件，为什么？【考点】LC：矩形的判定；L7：平行四边形的判定与性质．【分析】（1）要证明BC=DE，只要证四边形BCED是平行四边形．通过给出的已知条件便可．（2）矩形的判定方法有多种，可选择利用“对角线相等的平行四边形为矩形”来解决．【解答】（1）证明：∵E是AC中点，∴EC=AC．∵DB=AC，∴DB∥EC．又∵DB∥EC，∴四边形DBCE是平行四边形．∴BC=DE．（2）添加AB=BC．（ 5分）理由：∵DB AE，∴四边形DBEA是平行四边形．∵BC=DE，AB=BC，∴AB=DE．∴▭ADBE是矩形．结论开放型问题（2017广西河池）（1）如图1，在正方形ABCD中，点E，F分别在BC，CD 上，AE⊥BF于点M，求证：AE=BF；（2）如图2，将（1）中的正方形ABCD改为矩形ABCD，AB=2，BC=3，AE ⊥BF于点M，探究AE与BF的数量关系，并证明你的结论．【考点】S9：相似三角形的判定与性质；KD：全等三角形的判定与性质；LE：正方形的性质．【分析】（1）根据正方形的性质，可得∠ABC与∠C的关系，AB与BC的关系，根据两直线垂直，可得∠AMB的度数，根据直角三角形锐角的关系，可得∠ABM与∠BAM的关系，根据同角的余角相等，可得∠BAM与∠CBF的关系，根据ASA，可得△ABE≌△BCF，根据全等三角形的性质，可得答案；（2）根据矩形的性质得到∠ABC=∠C，由余角的性质得到∠BAM=∠CBF，根据相似三角形的性质即可得到结论．【解答】（1）证明：∵四边形ABCD是正方形，∴∠ABC=∠C，AB=BC．∵AE⊥BF，∴∠AMB=∠BAM+∠ABM=90°，∵∠ABM+∠CBF=90°，∴∠BAM=∠CBF．在△ABE和△BCF中，，∴△ABE≌△BCF（ASA），∴AE=BF；（2）解：AB=BC，理由：∵四边形ABCD是矩形，∴∠ABC=∠C，∵AE⊥BF，∴∠AMB=∠BAM+∠ABM=90°，∵∠ABM+∠CBF=90°，∴∠BAM=∠CBF，∴△ABE∽△BCF，∴=，∴AB=BC．存在开放型问题（2017广东）如图，在平面直角坐标系中，O为原点，四边形ABCO是矩形，点A，C的坐标分别是A（0，2）和C（2，0），点D是对角线AC上一动点（不与A，C重合），连结BD，作DE⊥DB，交x轴于点E，以线段DE，DB为邻边作矩形BDEF．（1）填空：点B的坐标为（2，2）；（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD 的长度；若不存在，请说明理由；（3）①求证： =；②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值．【考点】SO：相似形综合题．【分析】（1）求出AB、BC的长即可解决问题；（2）存在．连接BE，取BE的中点K，连接DK、KC．首先证明B、D、E、C 四点共圆，可得∠DBC=∠DCE，∠EDC=∠EBC，由tan∠ACO==，推出∠ACO=30°，∠ACD=60°由△DEC是等腰三角形，观察图象可知，只有ED=EC，推出∠DBC=∠DCE=∠EDC=∠EBC=30°，推出∠DBC=∠BCD=60°，可得△DBC是等边三角形，推出DC=BC=2，由此即可解决问题；（3）①由（2）可知，B、D、E、C四点共圆，推出∠DBC=∠DCE=30°，由此即可解决问题；②作DH⊥AB于H．想办法用x表示BD、DE的长，构建二次函数即可解决问题；【解答】解：（1）∵四边形AOCB是矩形，∴BC=OA=2，OC=AB=2，∠BCO=∠BAO=90°，∴B（2，2）．故答案为（2，2）．（2）存在．理由如下：连接BE，取BE的中点K，连接DK、KC．∵∠BDE=∠BCE=90°，∴KD=KB=KE=KC，∴B、D、E、C四点共圆，∴∠DBC=∠DCE，∠EDC=∠EBC，∵tan∠ACO==，∴∠ACO=30°，∠ACB=60°①如图1中，△DEC是等腰三角形，观察图象可知，只有ED=EC，∴∠DBC=∠DCE=∠EDC=∠EBC=30°，∴∠DBC=∠BCD=60°，∴△DBC是等边三角形，∴DC=BC=2，在Rt△AOC中，∵∠ACO=30°，OA=2，∴AC=2AO=4，∴AD=AC﹣CD=4﹣2=2．∴当AD=2时，△DEC是等腰三角形．②如图2中，∵△DCE是等腰三角形，易知CD=CE，∠DBC=∠DEC=∠CDE=15°，∴∠ABD=∠ADB=75°，∴AB=AD=2，综上所述，满足条件的AD的值为2或2．（3）①由（2）可知，B、D、E、C四点共圆，∴∠DBC=∠DCE=30°，∴tan∠DBE=，∴=．②如图2中，作DH⊥AB于H．在Rt△ADH中，∵AD=x，∠DAH=∠ACO=30°，∴DH=AD=x，AH==x，∴BH=2﹣x，在Rt△BDH中，BD==，∴DE=BD=•，∴矩形BDEF的面积为y= []2=（x2﹣6x+12），即y=x2﹣2x+4，∴y=（x﹣3）2+，∵＞0，∴x=3时，y有最小值．综合开放型问题（2017山东泰安）如图，四边形ABCD是平行四边形，AD=AC，AD⊥AC，E 是AB的中点，F是AC延长线上一点．（1）若ED⊥EF，求证：ED=EF；（2）在（1）的条件下，若DC的延长线与FB交于点P，试判定四边形ACPE 是否为平行四边形？并证明你的结论（请先补全图形，再解答）；（3）若ED=EF，ED与EF垂直吗？若垂直给出证明．【考点】LO：四边形综合题．【分析】（1）根据平行四边形的想知道的AD=AC，AD⊥AC，连接CE，根据全等三角形的判定和性质即可得到结论；（2）根据全等三角形的性质得到CF=AD，等量代换得到AC=CF，于是得到CP=AB=AE，根据平行四边形的判定定理即可得到四边形ACPE为平行四边形；（3）过E作EM⊥DA交DA的延长线于M，过E作EN⊥FC交FC的延长线于N，证得△AME≌△CNE，△ADE≌△CFE，根据全等三角形的性质即可得到结论．【解答】（1）证明：在▱ABCD中，∵AD=AC，AD⊥AC，∴AC=BC，AC⊥BC，连接CE，∵E是AB的中点，∴AE=EC，CE⊥AB，∴∠ACE=∠BCE=45°，∴∠ECF=∠EAD=135°，∵ED⊥EF，∴∠CEF=∠AED=90°﹣∠CED，在△CEF和△AED中，，∴△CEF≌△AED，∴ED=EF；（2）解：由（1）知△CEF≌△AED，CF=AD，∵AD=AC，∴AC=CF，∵DP∥AB，∴FP=PB，∴CP=AB=AE，∴四边形ACPE为平行四边形；（3）解：垂直，理由：过E作EM⊥DA交DA的延长线于M，过E作EN⊥FC交FC的延长线于N，在△AME与△CNE中，，∴△AME≌△CNE，∴∠ADE=∠CFE，在△ADE与△CFE中，，∴△ADE≌△CFE，∴∠DEA=∠FEC，∵∠DEA+∠DEC=90°，∴∠CEF+∠DEC=90°，∴∠DEF=90°，∴ED⊥EF．【真题训练】训练一：（2017日照）如图，已知BA=AE=DC，AD=EC，CE⊥AE，垂足为E．（1）求证：△DCA≌△EAC；（2）只需添加一个条件，即AD=BC（答案不唯一），可使四边形ABCD 为矩形．请加以证明．训练二：（2017湖北荆州）如图，在矩形ABCD中，连接对角线AC、BD，将△ABC沿BC方向平移，使点B移到点C，得到△DCE．（1）求证：△ACD≌△EDC；（2）请探究△BDE的形状，并说明理由．训练三：如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．（1）证明：AF=CE；（2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．训练四：（2017广东）如图，在平面直角坐标系中，O为原点，四边形ABCO 是矩形，点A，C的坐标分别是A（0，2）和C（2，0），点D是对角线AC上一动点（不与A，C重合），连结BD，作DE⊥DB，交x轴于点E，以线段DE，DB 为邻边作矩形BDEF．（1）填空：点B的坐标为（2，2）；（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD 的长度；若不存在，请说明理由；（3）①求证： =；②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值．训练五：（2017•黑龙江）在四边形ABCD中，对角线AC、BD交于点O．若四边形ABCD是正方形如图1：则有AC=BD，AC⊥BD．旋转图1中的Rt△COD到图2所示的位置，AC′与BD′有什么关系？（直接写出）若四边形ABCD是菱形，∠ABC=60°，旋转Rt△COD至图3所示的位置，AC′与BD′又有什么关系？写出结论并证明．参考答案：训练一：（2017日照）如图，已知BA=AE=DC，AD=EC，CE⊥AE，垂足为E．（1）求证：△DCA≌△EAC；（2）只需添加一个条件，即AD=BC（答案不唯一），可使四边形ABCD 为矩形．请加以证明．【考点】LC：矩形的判定；KD：全等三角形的判定与性质．【分析】（1）由SSS证明△DCA≌△EAC即可；（2）先证明四边形ABCD是平行四边形，再由全等三角形的性质得出∠D=90°，即可得出结论．【解答】（1）证明：在△DCA和△EAC中，，∴△DCA≌△EAC（SSS）；（2）解：添加AD=BC，可使四边形ABCD为矩形；理由如下：∵AB=DC，AD=BC，∴四边形ABCD是平行四边形，∵CE⊥AE，∴∠E=90°，由（1）得：△DCA≌△EAC，∴∠D=∠E=90°，∴四边形ABCD为矩形；故答案为：AD=BC（答案不唯一）．训练二：（2017湖北荆州）如图，在矩形ABCD中，连接对角线AC、BD，将△ABC沿BC方向平移，使点B移到点C，得到△DCE．（1）求证：△ACD≌△EDC；（2）请探究△BDE的形状，并说明理由．【考点】LB：矩形的性质；KD：全等三角形的判定与性质；Q2：平移的性质．【分析】（1）由矩形的性质得出AB=DC，AC=BD，AD=BC，∠ADC=∠ABC=90°，由平移的性质得：DE=AC，CE=BC，∠DCE=∠ABC=90°，DC=AB，得出AD=EC，由SAS即可得出结论；（2）由AC=BD，DE=AC，得出BD=DE即可．【解答】（1）证明：∵四边形ABCD是矩形，∴AB=DC，AC=BD，AD=BC，∠ADC=∠ABC=90°，由平移的性质得：DE=AC，CE=BC，∠DCE=∠ABC=90°，DC=AB，∴AD=EC，在△ACD和△EDC中，，∴△ACD≌△EDC（SAS）；（2）解：△BDE是等腰三角形；理由如下：∵AC=BD，DE=AC，∴BD=DE，∴△BDE是等腰三角形．训练三：如图，在△ABC中，∠ACB=90°，点D，E分别是边BC，AB上的中点，连接DE并延长至点F，使EF=2DF，连接CE、AF．（1）证明：AF=CE；（2）当∠B=30°时，试判断四边形ACEF的形状并说明理由．【考点】L9：菱形的判定；KX：三角形中位线定理；L7：平行四边形的判定与性质．【分析】（1）由三角形中位线定理得出DE∥AC，AC=2DE，求出EF∥AC，EF=AC，得出四边形ACEF是平行四边形，即可得出AF=CE；（2）由直角三角形的性质得出∠BAC=60°，AC=AB=AE，证出△AEC是等边三角形，得出AC=CE，即可得出结论．【解答】（1）证明：∵点D，E分别是边BC，AB上的中点，∴DE∥AC，AC=2DE，∵EF=2DE，∴EF∥AC，EF=AC，∴四边形ACEF是平行四边形，∴AF=CE；（2）解：当∠B=30°时，四边形ACEF是菱形；理由如下：∵∠ACB=90°，∠B=30°，∴∠BAC=60°，AC=AB=AE，∴△AEC是等边三角形，∴AC=CE，又∵四边形ACEF是平行四边形，∴四边形ACEF是菱形．训练四：（2017广东）如图，在平面直角坐标系中，O为原点，四边形ABCO 是矩形，点A，C的坐标分别是A（0，2）和C（2，0），点D是对角线AC上一动点（不与A，C重合），连结BD，作DE⊥DB，交x轴于点E，以线段DE，DB 为邻边作矩形BDEF．（1）填空：点B的坐标为（2，2）；（2）是否存在这样的点D，使得△DEC是等腰三角形？若存在，请求出AD 的长度；若不存在，请说明理由；（3）①求证： =；②设AD=x，矩形BDEF的面积为y，求y关于x的函数关系式（可利用①的结论），并求出y的最小值．【考点】SO：相似形综合题．【分析】（1）求出AB、BC的长即可解决问题；（2）存在．连接BE，取BE的中点K，连接DK、KC．首先证明B、D、E、C 四点共圆，可得∠DBC=∠DCE，∠EDC=∠EBC，由tan∠ACO==，推出∠ACO=30°，∠ACD=60°由△DEC是等腰三角形，观察图象可知，只有ED=EC，推出∠DBC=∠DCE=∠EDC=∠EBC=30°，推出∠DBC=∠BCD=60°，可得△DBC是等边三角形，推出DC=BC=2，由此即可解决问题；（3）①由（2）可知，B、D、E、C四点共圆，推出∠DBC=∠DCE=30°，由此即可解决问题；②作DH⊥AB于H．想办法用x表示BD、DE的长，构建二次函数即可解决问题；【解答】解：（1）∵四边形AOCB是矩形，∴BC=OA=2，OC=AB=2，∠BCO=∠BAO=90°，∴B（2，2）．故答案为（2，2）．（2）存在．理由如下：连接BE，取BE的中点K，连接DK、KC．∵∠BDE=∠BCE=90°，∴KD=KB=KE=KC，∴B、D、E、C四点共圆，∴∠DBC=∠DCE，∠EDC=∠EBC，∵tan∠ACO==，∴∠ACO=30°，∠ACB=60°①如图1中，△DEC是等腰三角形，观察图象可知，只有ED=EC，∴∠DBC=∠DCE=∠EDC=∠EBC=30°，∴∠DBC=∠BCD=60°，∴△DBC是等边三角形，∴DC=BC=2，在Rt△AOC中，∵∠ACO=30°，OA=2，∴AC=2AO=4，∴AD=AC﹣CD=4﹣2=2．∴当AD=2时，△DEC是等腰三角形．②如图2中，∵△DCE是等腰三角形，易知CD=CE，∠DBC=∠DEC=∠CDE=15°，∴∠ABD=∠ADB=75°，∴AB=AD=2，综上所述，满足条件的AD的值为2或2．（3）①由（2）可知，B、D、E、C四点共圆，∴∠DBC=∠DCE=30°，∴tan∠DBE=，∴=．②如图2中，作DH⊥AB于H．在Rt△ADH中，∵AD=x，∠DAH=∠ACO=30°，∴DH=AD=x，AH==x，∴BH=2﹣x，在Rt△BDH中，BD==，∴DE=BD=•，∴矩形BDEF的面积为y= []2=（x2﹣6x+12），即y=x2﹣2x+4，∴y=（x﹣3）2+，∵＞0，∴x=3时，y有最小值．训练五：（2017•黑龙江）在四边形ABCD中，对角线AC、BD交于点O．若四边形ABCD是正方形如图1：则有AC=BD，AC⊥BD．旋转图1中的Rt△COD到图2所示的位置，AC′与BD′有什么关系？（直接写出）若四边形ABCD是菱形，∠ABC=60°，旋转Rt△COD至图3所示的位置，AC′与BD′又有什么关系？写出结论并证明．【考点】LE：正方形的性质；KD：全等三角形的判定与性质；L8：菱形的性质；R2：旋转的性质．【分析】图2：根据四边形ABCD是正方形，得到AO=OC，BO=OD，AC⊥BD，根据旋转的性质得到OD′=OD，OC′=OC，∠D′OD=∠C′OC，等量代换得到AO=BO，OC′=OD′，∠AOC′=∠BOD′，根据全等三角形的性质得到AC′=BD′，∠OAC′=∠OBD′，于是得到结论；图3：根据四边形ABCD是菱形，得到AC⊥BD，AO=CO，BO=DO，求得OB=√3OA，OD=√3OC，根据旋转的性质得到OD′=OD，OC′=OC，∠D′OD=∠C′OC，求得OD′=√3OC′，∠AOC′=∠BOD′，根据相似三角形的性质得到BD′=√3AC′，于是得到结论．【解答】解：图2结论：AC′=BD′，AC′⊥BD′，理由：∵四边形ABCD是正方形，∴AO=OC，BO=OD，AC⊥BD，∵将Rt△COD旋转得到Rt△C′OD′，∴OD′=OD，OC′=OC，∠D′OD=∠C′OC，∴AO=BO，OC′=OD′，∠AOC′=∠BOD′，在△AOC′与△BOD′中，{AO=BO∠AOC′=∠BOD′OC′=OD′，∴△AOC′≌△BOD′，∴AC′=BD′，∠OAC′=∠OBD′，∵∠AO′D′=∠BO′O，∠O′BO+∠BO′O=90°，∴∠O′AC′+∠AO′D′=90°，∴AC′⊥BD′；图3结论：BD′=√3AC′，AC′⊥BD’理由：∵四边形ABCD是菱形，∴AC⊥BD，AO=CO，BO=DO，∵∠ABC=60°，∴∠ABO=30°，∴OB=√3OA，OD=√3OC，∵将Rt△COD旋转得到Rt△C′OD′，∴OD′=OD，OC′=OC，∠D′OD=∠C′OC，∴OD′=√3OC′，∠AOC′=∠BOD′，∴OBOA =OD′OC′=√3，∴△AOC′∽△BOD′，∴BD′AC′=OBOA=√3，∠OAC′=∠OBD′，∴BD′=√3AC′，∵∠AO′D′=∠BO′O，∠O′BO+∠BO′O=90°，∴∠O′AC′+∠AO′D′=90°，∴AC′⊥BD′．【点评】本题考查了正方形的性质，菱形的性质，全等三角形的判定和性质，相似三角形的判定和性质，旋转的性质，正确的识别图形是解题的关键．。

初中数学中考总复习冲刺：创新、开放与探究型问题--巩固练习题及答案(提高)

中考冲刺：创新、开放与探究型问题—巩固练习（提高）【巩固练习】一、选择题1. 下列图形都是由同样大小的平行四边形按一定的规律组成，其中，第①个图形中一共有1个平行四边形，第②个图形中一共有5个平行四边形，第③个图形中一共有11个平行四边形，…则第⑥个图形中平行四边形的个数为（）A、55B、42C、41D、292．如图，直角三角形纸片ABC中，AB=3，AC=4，D为斜边BC中点，第1次将纸片折叠，使点A与点D 重合，折痕与AD交与点P1；设P1D的中点为D1，第2次将纸片折叠，使点A与点D1重合，折痕与AD交于点P2；设P2D1的中点为D2，第3次将纸片折叠，使点A与点D2重合，折痕与AD交于点P3；…；设P n﹣1D n﹣2的中点为D n﹣1，第n次将纸片折叠，使点A与点D n﹣1重合，折痕与AD交于点P n（n＞2），则AP6的长为（）A．512532⨯B．69352⨯C．614532⨯D．711352⨯3．下面两个多位数1248624…、6248624…，都是按照如下方法得到的：将第一位数字乘以2，若积为一位数，将其写在第2位上，若积为两位数，则将其个位数字写在第2位．对第2位数字再进行如上操作得到第3位数字……，后面的每一位数字都是由前一位数字进行如上操作得到的．当第1位数字是3时，仍按如上操作得到一个多位数，则这个多位数前100位的所有数字之和是( ) A．495 B．497 C．501 D．503二、填空题4. 如图所示，一个4×2的矩形可以用3种不同的方式分割成2或5或8个小正方形，那么一个5×3的矩形用不同的方式分割后，小正方形的个数可以是____ ____．5. 一园林设计师要使用长度为4L 的材料建造如图1所示的花圃，该花圃是由四个形状、大小完全一样的扇环面组成，每个扇环面如图2所示，它是以点O 为圆心的两个同心圆弧和延长后通过O 点的两条直线段围成，为使得绿化效果最佳，还须使得扇环面积最大．(1)使图①花圃面积为最大时R －r 的值为，以及此时花圃面积为，其中R 、r 分别为大圆和小圆的半径；(2)若L ＝160 m ，r ＝10 m ，使图面积为最大时的θ值为．6．如图所示，已知△ABC 的面积1ABC S =△，在图(a)中，若11112AA BB CC AB BC CA ===，则11114A B C S =△；在图(b)中，若22213AA BB CC AB BC CA ===，则222A B C 13S =△；在图(c)，若33314AA BB CC AB BC CA ===，则333716A B C S =△．…按此规律，若88819AA BB CC AB BC CA ===，则888A B C S =△________．三、解答题7．如图所示，∠ABM 为直角，C 为线段BA 的中点，D 是射线BM 上的一个动点(不与点B 重合)，连接AD ，作BE ⊥AD ，垂足为E ，连接CE ，过点E 作EF ⊥CE ，交BD 于F ．(1)求证：BF ＝FD ；(2)∠A 在什么范围内变化时，四边形ACFE 是梯形?并说明理由；(3)∠A在什么范围内变化时，线段DE上存在点G，满足条件14DG DA？并说明理由．8.如图(a)、(b)、(c)，在△ABC中，分别以AB，AC为边，向△ABC外作正三角形、正四边形、正五边形，BE，CD相交于点O．(1)①如图(a)，求证：△ADC≌△ABE；②探究：图(a)中，∠BOC＝________；图(b)中，∠BOC＝________；图(c)中，∠BOC＝________；(2)如图(d)，已知：AB，AD是以AB为边向△ABC外所作正n边形的一组邻边；AC，AE是以AC为边向△ABC外所作正n边形的一组邻边．BE，CD的延长相交于点O．①猜想：图(d)中，∠BOC＝________________；(用含n的式子表示)②根据图(d)证明你的猜想．9. 如图(a)，梯形ABCD中，AD∥BC，∠ABC＝90°， AD＝9，BC＝12，AB＝a，在线段BC上任取一点P(P 不与B，C重合)，连接DP，作射线．PE⊥DP，PE与直线AB交于点E．(1)试确定CP＝3时，点E的位置；(2)若设CP＝x(x＞0)，BE＝y(y＞0)，试写出y关于自变量x的函数关系式；(3)若在线段BC上能找到不同的两点P1，P2，使按上述作法得到的点E都与点A重合，试求出此时a的取值范围．10. 点A，B分别是两条平行线m，n上任意两点，在直线n上找一点C，使BC＝k·AB．连接AC，在直线AC上任取一点E，作∠BEF＝∠ABC，EF交直线m于点F．(1)如图(a)，当k＝1时，探究线段EF与EB的关系，并加以说明；说明：①如果你经过反复探索没有解决问题，请写出探索过程(要求至少写三步)；②在完成①之后，可以自己添加条件(添加的条件限定为∠ABC为特殊角)，在图(b)中补全图形，完成证明．(2)如图(c)，若∠ABC＝90°，k≠l，探究线段EF与EB的关系，并说明理由．【答案与解析】一、选择题1.【答案】C；【解析】找出规律：∵图②平行四边形有5个=1+2+2，图③平行四边形有11个=1+2+3+2+3，图④平行四边形有19=1+2+3+4+2+3+4，∴图⑥的平行四边形的个数为1+2+3+4+5+6+2+3+4+5+6=41.故选C.2.【答案】A；【解析】由题意得，AD=12BC=52，AD1=AD﹣DD1=158，AD2=25532⨯，AD3=37532⨯，AD n=21532nn+⨯，故AP1=54，AP2=1516，AP3=26532⨯…APn=12532nn-⨯，故可得AP6=512532⨯.故选A.3.【答案】A ；【解析】根据题意，当第1位数字是3时，按操作要求得到的数字是3624862486248…，从第2位数字起每隔四位数重复一次6248，因为(100-1)被4整除得24余3，所以这个多位数前100位的所有数字之间和是3+(6+2+4)+(6+2+4+8)×24＝495，答案选A ．二、填空题4.【答案】4或7或9或12或15；【解析】一个5×3的矩形可以有下面几种分割方式，如图所示．5.【答案】（1）R －r 的值为4L ，以及此时花圃面积为24L ；（2）θ值为240π．【解析】要使花圃面积最大，则必定要求扇环面积最大．设扇环的圆心角为θ，面积为S ，根据题意得：2()180180R rL R r θπθπ=++- ()2()180R r R r πθ+=+-g ，∴180[2()]()L R r R r θπ--=+∴2222()360360360R r S R r θπθππθ=-=-22180[2()]()360()L R r R r R r ππ--=-+gg1[2()]()2L R r R r =---g 21()()2R r L R r =--+-22()416L L R r ⎡⎤=---+⎢⎥⎣⎦．∵02L R r <-<， ∴S 在4LR r -=时取最大值为216L ．∴花圃面积最大时R －r 的值为4L，最大面积为224164L L ⨯=．(2)∵当4LR r -=时，S 取大值， ∴1604044L R r -===(m)，40401050R r =+=+=(m)，∴180[2()]180(160240)240()60L R r R r θπππ---⨯===+．6.【答案】1927．【解析】1111111-3=224A B C S =⨯⨯△222A B C 2111-3=333S =⨯⨯△3331-3=4416A B C S =⨯⨯△…8888157191-3==998127A B C S =⨯⨯△2131-3=111(1)AnBnCn n nS n n n =⨯⨯-+++△三、解答题 7．【答案与解析】解：(1)Rt △AEB 中，∵AC ＝BC ，∴CE ＝12AB ． ∴CB ＝CE ．∴∠CEB ＝∠CBE ．∵∠CEF ＝∠CBF ＝90°，∴∠BEF＝∠EBF．∴EF＝BF．∵∠BEF+∠FED＝90°，∠EBD+∠EDB＝90°．∴∠FED＝∠EDF．∴EF＝FD．∴BF＝FD．(2)由(1)得BF＝FD，而BC＝CA，∴CF∥AD，即AE∥CF．若AC∥EF，则AC＝EF，∴BC＝BF．∴BA＝BD，∠A＝45°．∴当0°＜∠A＜45°或45°＜∠A＜90°时，四边形ACFE为梯形．(3)作GH⊥BD，垂足为H，则GH∥AB．∵DG＝14DA，∴DH＝14DB．又F为BD的中点，∴H为DF的中点．∴GH为DF的中垂线．∴∠GDF＝∠GFD．∵点G在ED上，∴∠EFD≥∠GFD．∵∠EFD+∠FDE+∠DEF＝180°，∴∠GFD+∠FDE+∠DEF≤180°．∴3∠EDF≤180°．∴∠EDF≤60°．又∠A+∠EDF＝90°，∴30°≤∠A＜90°．∴30°≤∠A＜90°时，DE上存在点G，满足条件DG＝14 DA，8．【答案与解析】(1)证法一：∵△ABD与△ACE均为等边三角形，∴AD＝AB，AC＝AE，且∠BAD＝∠CAE＝60°．∴∠BAD+∠BAC＝∠CAE+∠BAC，即∠DAC＝∠BAE．∴△ADC≌△ABE．证法二：∵△ABD与△ACE均为等边三角形，∴AD＝AB，AC＝AE，且∠BAD＝∠CAE＝60°．∴△ADC可由△ABE绕着点A按顺时针方向旋转60°得到．∴△ABE ≌△ADC ．②120°，90°，72°． (2)①360n°． ②证法一：依题意，知∠BAD 和∠CAE 都是正n 边形的内角，AB ＝AD ，AE ＝AC ， ∴∠BAD ＝∠CAE ＝(2)180n n-°．∴∠BAD －∠DAE ＝∠CAE －∠DAE ，即∠BAE ＝∠DAC ． ∴△ABE ≌△ADC ． ∴∠ABE ＝∠ADC ．∵∠ADC+∠ODA ＝180°， ∴∠ABO+∠ODA ＝180°．∴∠ABO+∠ODA+∠DAB+∠BOC ＝360°． ∴∠BOC+∠DAB ＝180°． ∴∠BOC ＝180°－∠DAB ＝(2)180360180n n n--=°°°．证法二：延长BA 交CO 于F ，证∠BOC ＝∠DAF ＝180°-∠BAD ．证法三：连接CE ．证∠BOC ＝180°－∠CAE ．9．【答案与解析】解：(1)作DF ⊥BC ，F 为垂足．当CP ＝3时，四边形ADFB 是矩形，则CF ＝3． ∴点P 与点F 重合．又∵BF ⊥FD ，∴此时点E 与点B 重合．(2)(i)当点P 在BF 上(不与B ，F 重合)时，(见图(a))∵∠EPB+∠DPF ＝90°，∠EPB+∠PEB ＝90°， ∴∠DPF ＝∠PEB ．∴Rt △PEB ∽△ARt △DPF ．∴BE FPBP FD=． ① 又∵ BE ＝y ，BP ＝12-x ，FP ＝x-3，FD ＝a ，代入①式，得312y x x a-=- ∴1(12)(3)y x x a =--，整理，得21(1536)(312)y x x x a=-+<< ②(ii)当点P 在CF 上（不与C ，F 重合）时，（见上图(b))同理可求得BE FPBP FD=．由FP ＝3-x 得21(1536)(03)y x x x a=-+<<．∴ 221(1536)(03)1(1536)(312).x x x ay x x a⎧--+<<⎪⎪=⎨⎪--+<<⎪⎩(3)解法一：当点E 与A 重合时，y ＝EB ＝a ，此时点P 在线段BF 上．由②式得21(1536)a x x a=--+．整理得2215360x x a -++=． ③∵在线段BC 上能找到两个不同的点P 1与P 2满足条件， ∴方程③有两个不相等的正实根．∴△＝(-15)2－4×(36+a 2)＞0．解得2814a <．又∵a ＞0， ∴902a <<．解法二：当点E 与A 重合时，∵∠APD ＝90°，∴点P 在以AD 为直径的圆上．设圆心为M ，则M 为AD 的中点． ∵在线段BC 上能找到两个不同的点P 1与P 2满足条件， ∴线段BC 与⊙M 相交．即圆心M 到BC 的距离d 满足02ADd <<． ④ 又∵AD ∥BC ， ∴d ＝a ． ∴由④式得902a <<． 10．【答案与解析】解：(1)EF ＝EB ．证明：如图(d)，以E 为圆心，EA 为半径画弧交直线m 于点M ，连接EM ．∴EM ＝EA ，∴∠EMA ＝∠EAM ． ∵BC ＝k ·AB ，k ＝1， ∴BC ＝AB ．∴∠CAB ＝∠ACB ．∵m ∥n ，∴∠MAC ＝∠ACB ，∠FAB ＝∠ABC ．∴∠MAC＝∠CAB．∴∠CAB＝∠EMA．∵∠BEF＝∠ABC，∴∠BEF＝∠FAB．∵∠AHF＝∠EHB，∴∠AFE＝∠ABE．∴△AEB≌△MEF．∴EF＝EB．探索思路：如上图(a)，∵BC＝k·AB，k＝1，∴BC＝AB．∴∠CAB＝∠ACB．∵m∥n，∴∠MAC＝∠ACB．添加条件：∠ABC＝90°．证明：如图(e)，在直线m上截取AM＝AB，连接ME．∵ BC＝k·AB，k＝1，∴ BC＝AB．∵∠ABC＝90°，∴∠CAB＝∠ACB＝45°．∵ m∥n，∴∠MAE＝∠ACB＝∠CAB＝45°，∠FAB＝90°．∵ AE＝AE，∴△MAE∽△BAE．∴ EM＝EB，∠AME＝∠ABE．∵∠BEF＝∠ABC＝90°，∴∠FAB+∠BEF＝180°．又∵∠ABE+∠EFA＝180°，∴∠EMF＝∠EFA．∴ EM＝EF．∴ EF＝EB．(2)EF＝1k EB．说明：如图(f)，过点E作EM⊥m，EN⊥AB，垂足为M，N．∴∠EMF＝∠ENA＝∠ENB＝90°．∵ m∥n，∠ABC＝90°，∴∠MAB＝90°．∴四边形MENA为矩形．∴ ME＝NA，∠MEN＝90°．∵∠BEF＝∠ABC＝90°．∴∠MEF＝∠NEB．∴△MEF∽△NEB．∴ME EF EN EB=，∴AN EF EN EB=在Rt△ANE和Rt△ABC中，tanEN BCBAC kAN AB∠===，∴1EF EBk=．。

中考数学专题训练第3课时开放探究题(含答案)

中考数学专题训练第3课时开放探究题(含答案)第3课时开放探究题开放探究题是一种新的题型,关于开放题的概念，主要有下列几种描述：（1）答案不固定或者条件不完备的习题成为开放题；（2）具有多种不同的解法或有多种可能的解答的问题称为开放题.开放探究题的特点是：（1）条件多余需选择,条件不足需补充；（2）答案不固定；（3）问题一般没有明确的结论，没有固定的形式和方法，需要自己通过观察、分析、比较、概括、推理、判断等探索活动来确定所需求的结论或条件或方法.开放探究题常见的类型有：（1）条件开放型：即问题的条件不完备或满足结论的条件不唯一；（2）结论开放型：即在给定的条件下，结论不唯一；（3）策略开放型：即思维策略与解题方法不唯一；（4）综合型：即条件、结论、策略中至少有两项均是开放的.在解决开放探究题的时候，需解题者经过探索确定结论或补全条件，将开放性问题转化为封闭性问题，然后选择合适的解题途径完成最后的解答.这类题主要考查我们分析问题和解决问题的能力和创新意识.类型之一条件开放型问题解这种类型的开放性问题的一般思路是：由已知的结论反思题目应具备怎样的条件，即从题目的结论出发，结合图形挖掘条件，逆向追索，逐步探寻，是一种分析型思维方式.它要求解题者善于从问题的结论出发，逆向追索，多途寻因。

1.（郴州市）已知四边形ABCD中，∠A=∠B=∠C=90°，若添加一个条件即可判定该四边形是正方形，那么这个条件可以是_________．2.（庆阳市）如下左图，D、E分别是△ABC的边AB、AC上的点，则使△AED∽△ABC的条件是类型之二结论开放型问题解决这种类型的问题的时候要充分利用已知条件或图形特征，进行猜想、归纳、类比，透彻分析出给定条件下可能存在的结论现象，然后经过论证作出取舍，这是一种归纳类比型思维.它要求解题者充分利用条件进行大胆而合理的猜想，发现规律，得出结论，这类题主要考查解题者的发散性思维和所学基本知识的应用能力。

2024年中考数学复习重难点题型训练—规律探索题(含答案解析)

2024年中考数学复习重难点题型训练—规律探索题（含答案解析）类型一数式规律1．（2023·云南·统考中考真题）按一定规律排列的单项式：2345,a ，第n 个单项式是（）AB1n -CnD1n -【答案】Ca ，指数为1开始的自然数，据此即可求解．【详解】解：按一定规律排列的单项式：2345,a ，第nn ，故选：C ．【点睛】本题考查了单项式规律题，找到单项式的变化规律是解题的关键．2．（2023·山东·统考中考真题）已知一列均不为1的数123n a a a a ，，，，满足如下关系：1223121111a a a a a a ++==--，34131111n n na a a a a a +++==-- ，，，若12a =，则2023a 的值是（）A ．12-B ．13C ．3-D ．2【答案】A【分析】根据题意可把12a =代入求解23a =-，则可得312a =-，413a =，52a =……；由此可得规律求解．【详解】解：∵12a =，∴212312a +==--，3131132a -==-+，411121312a -==+，51132113a +==-，…….；由此可得规律为按2、3-、12-、13四个数字一循环，∵20234505.....3÷=，∴2023312a a ==-；故选A ．【点睛】本题主要考查数字规律，解题的关键是得到数字的一般规律．3．（2023·湖南常德·统考中考真题）观察下边的数表（横排为行，竖排为列），按数表中的规律，分数202023若排在第a 行b 列，则a b -的值为()11122113223114233241……A ．2003B ．2004C ．2022D ．2023【答案】C【分析】观察表中的规律发现，分数的分子是几，则必在第几列；只有第一列的分数，分母与其所在行数一致．【详解】观察表中的规律发现，分数的分子是几，则必在第几列；只有第一列的分数，分母与其所在行数一致，故202023在第20列，即20b =；向前递推到第1列时，分数为201912023192042-=+，故分数202023与分数12042在同一行．即在第2042行，则2042a =．∴2042202022.a b -=-=故选：C ．【点睛】本题考查了数字类规律探索的知识点，解题的关键善于发现数字递变的周期性和趋向性．4．（2023·四川内江·统考中考真题）对于正数x ，规定2()1xf x x =+，例如：224(2)213f ⨯==+，1212212312f ⨯⎛⎫== ⎪⎝⎭+，233(3)312f ⨯==+，1211313213f ⨯⎛⎫== ⎪⎝⎭+，计算：11111(1)1011009932f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫+++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭(2)(3)(99)(100)(101)f f f f f +++++= （）A ．199B ．200C ．201D ．202【答案】C【分析】通过计算11(1)1,(2)2,(3)223f f f f f ⎛⎫⎛⎫=+=+= ⎪ ⎪⎝⎭⎝⎭，⋯可以推出11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭结果．【详解】解：2(1)1,11f ==+ 12441212(2),,(2)2,112323212f f f f ⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+122331113(3),,(3)2,113232313f f f f ⨯⨯⎛⎫⎛⎫====+= ⎪ ⎪+⎝⎭⎝⎭+…2100200(100)1100101f ⨯==+，1212100()11001011100f ⨯==+，1(100)(2100f f +=，11111(1)(2)(3)(99)(100)(101)1011009932f f f f f f f f f f f ⎛⎫⎛⎫⎛⎫⎛⎫⎛⎫++++++++++++ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭⎝⎭21001=⨯+201=故选：C ．【点睛】此题考查了有理数的混合运算，熟练掌握运算法则，找到数字变化规律是解本题的关键．5.（2021·湖北鄂州市·中考真题）已知1a 为实数﹐规定运算：2111a a =-，3211a a =-，4311a a =-，5411a a =-，……，111n n a a -=-．按上述方法计算：当13a =时，2021a 的值等于（）A．23-B．13C．12-D．23【答案】D 【分析】当13a =时，计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅，会发现呈周期性出现，即可得到2021a 的值．【详解】解：当13a =时，计算出23421,,3,32a a a ==-=⋅⋅⋅⋅⋅⋅，会发现是以：213,,32-，循环出现的规律，202136732=⨯+ ，2021223a a ∴==，故选：D ．【点睛】本题考查了实数运算规律的问题，解题的关键是：通过条件，先计算出部分数的值，从中找到相应的规律，利用其规律来解答．6.（2021·湖北随州市·中考真题）根据图中数字的规律，若第n 个图中的143q =，则p的值为（）A．100B．121C．144D．169【答案】B 【分析】分别分析n 的规律、p 的规律、q 的规律，再找n 、p 、q 之间的联系即可．【详解】解：根据图中数据可知：1,2,3,4n =，……22221,2,3,4,p =……222221,31,41,51,q =----……则2p n =，2(1)1q n =+-，∵第n 个图中的143q =，∴2(1)1=143q n =+-，解得：11n =或13n =-(不符合题意，舍去)∴2=121p n =，故选：B ．【点睛】本题主要考查数字之间规律问题，将题中数据分组讨论是解决本题的关键．7.（2021·山东济宁市·中考真题）按规律排列的一组数据：12，35，□，717，926，1137，…，其中□内应填的数是（）A．23B．511C．59D．12【答案】D 【分析】分子为连续奇数，分母为序号的平方1+，根据规律即可得到答案．【详解】观察这排数据发现，分子为连续奇数，分母为序号的平方1+，∴第n 个数据为：2211n n -+当3n =时W 的分子为5，分母为23110+=∴这个数为51102=故选：D ．【点睛】本题考查了数字的探索规律，分子和分母分别寻找规律是解题关键．8.（2021·湖北十堰市·）将从1开始的连续奇数按如图所示的规律排列，例如，位于第4行第3列的数为27，则位于第32行第13列的数是（）A．2025B．2023C．2021D．2019【答案】B 【分析】根据数字的变化关系发现规律第n 行，第n 列的数据为：2n(n-1)+1，即可得第32行，第32列的数据为：2×32×(32-1)+1=1985，再依次加2，到第32行，第13列的数据，即可．解：观察数字的变化，发现规律：第n行，第n列的数据为：2n(n-1)+1，∴第32行，第32列的数据为：2×32×(32-1)+1=1985，根据数据的排列规律，第偶数行从右往左的数据一次增加2，∴第32行，第13列的数据为：1985+2×(32-13)=2023，故选：B．【点睛】本题考查了数字的变化类，解决本题的关键是观察数字的变化寻找探究规律，利用规律解决问题．9.（2020•天水）观察等式：2+22＝23﹣2；2+22+23＝24﹣2；2+22+23+24＝25﹣2；…已知按一定规律排列的一组数：2100，2101，2102，…，2199，2200，若2100＝S，用含S的式子表示这组数据的和是（）A．2S2﹣S B．2S2+S C．2S2﹣2S D．2S2﹣2S﹣2【分析】根据已知条件和2100＝S，将按一定规律排列的一组数：2100，2101，2102，…，2199，2200，求和，即可用含S的式子表示这组数据的和．【解析】∵2100＝S，∴2100+2101+2102+…+2199+2200＝S+2S+22S+…+299S+2100S＝S（1+2+22+…+299+2100）＝S（1+2100﹣2+2100）＝S（2S﹣1）＝2S2﹣S．10．（2023·湖南岳阳·统考中考真题）观察下列式子：21110-=⨯；22221-=⨯；23332-=⨯；24443-=⨯；25554-=⨯；…依此规律，则第n （n 为正整数）个等式是．【答案】()21n n n n -=-【分析】根据等式的左边为正整数的平方减去这个数，等式的右边为这个数乘以这个数减1，即可求解．【详解】解：∵21110-=⨯；22221-=⨯；23332-=⨯；24443-=⨯；25554-=⨯；…∴第n （n 为正整数）个等式是()21n n n n -=-，故答案为：()21n n n n -=-．【点睛】本题考查了数字类规律，找到规律是解题的关键．11．（2023·山东临沂·统考中考真题）观察下列式子21312⨯+=；22413⨯+=；23514⨯+=；……按照上述规律，2n =．【答案】()()111n n -++【分析】根据已有的式子，抽象出相应的数字规律，进行作答即可．【详解】解：∵21312⨯+=；22413⨯+=；23514⨯+=；……∴()()2211n n n ++=+，∴()()2111n n n -++=．故答案为：()()111n n -++【点睛】本题考查数字类规律探究．解题的关键是从已有的式子中抽象出相应的数字规律．12．（2023·四川成都·统考中考真题）定义：如果一个正整数能表示为两个正整数m ，n 的平方差，且1m n ->，则称这个正整数为“智慧优数”．例如，221653=-，16就是一个智慧优数，可以利用22()()m n m n m n -=+-进行研究．若将智慧优数从小到大排列，则第3个智慧优数是；第23个智慧优数是．【答案】1545【分析】根据新定义，列举出前几个智慧优数，找到规律，进而即可求解．【详解】解：依题意，当3m =，1n =，则第1个一个智慧优数为22318-=当4m =，2n =，则第2个智慧优数为224214-=当4m =，1n =，则第3个智慧优数为224115-=，当5m =，3n =，则第5个智慧优数为225316-=当5m =，2n =，则第6个智慧优数为225221-=当5m =，1n =，则第7个智慧优数为225324-=……6m =时有4个智慧优数，同理7m =时有5个，8m =时有6个，12345621+++++=第22个智慧优数，当9m =时，7n =，第22个智慧优数为2297814932-=-=，第23个智慧优数为9,6m n ==时，2296813645-=-=，故答案为：15，45．【点睛】本题考查了新定义，平方差公式的应用，找到规律是解题的关键．13．（2023·山东聊城·统考中考真题）如图，图中数字是从1开始按箭头方向排列的有序数阵．从3开始，把位于同一列且在拐角处的两个数字提取出来组成有序数对：()3,5；()7,10；()13,17；()21,26；()31,37…如果单把每个数对中的第一个或第二个数字按顺序排列起来研究，就会发现其中的规律．请写出第n 个数对：．【答案】()221,22n n n n ++++【分析】根据题意单另把每个数对中的第一个或第二个数字按顺序排列起来研究，可发现第n 个数对的第一个数为：()11n n ++，第n 个数对的第二个位：()211n ++，即可求解．【详解】解：每个数对的第一个数分别为3，7，13，21，31，…即：121⨯+，231⨯+，341⨯+，451⨯+，561⨯+，…则第n 个数对的第一个数为：()2111n n n n ++=++，每个数对的第二个数分别为5，10，17，26，37，…即：221+；231+；241+；251+；261+…，则第n 个数对的第二个位：()221122n n n ++=++，∴第n 个数对为：()221,22n n n n ++++，故答案为：()221,22n n n n ++++．【点睛】此题考查数字的变化规律，找出数字之间的排列规律，利用拐弯出数字的差的规律解决问题．14．（2023·内蒙古通辽·统考中考真题）点Q 的横坐标为一元一次方程37322x x +=-的解，纵坐标为a b +的值，其中a ，b 满足二元一次方程组2428a b a b -=⎧⎨-+=-⎩，则点Q 关于y 轴对称点Q '的坐标为___________．【答案】()5,4--【分析】先分别解一元一次方程37322x x +=-和二元一次方程组2428a b a b -=⎧⎨-+=-⎩，求得点Q的坐标，再根据直角坐标系中点的坐标的规律即可求解．【详解】解：37322x x +=-，移项合并同类项得，525x =，系数化为1得，5x =，∴点Q 的横坐标为5，∵2428a b a b -=⎧⎨-+=-⎩①②，由2+⨯①②得，3=12b -，解得：4b =-，把4b =-代入①得，24=4a +，解得：0a =，∴=04=4a b +--，∴点Q 的纵坐标为4-，∴点Q 的坐标为()5,4-，又∴点Q 关于y 轴对称点Q '的坐标为()5,4--，故答案为：()5,4--．【点睛】本题考查解一元一次方程和解二元一次方程组、代数值求值、直角坐标系中点的坐标的规律，熟练掌握解一元一次方程和解二元一次方程组的方法求得点Q 的坐标是解题的关键．15．（2023·湖北恩施·统考中考真题）观察下列两行数，探究第②行数与第①行数的关系：2-，4，8-，16，32-，64，……①0，7，4-，21，26-，71，……②根据你的发现，完成填空：第①行数的第10个数为；取每行数的第2023个数，则这两个数的和为．【答案】1024202422024-+【分析】通过观察第一行数的规律为(2)n -，第二行数的规律为(2)1n n -++，代入数据即可.【详解】第一行数的规律为(2)n -，∴第①行数的第10个数为10(2)1024-=；第二行数的规律为(2)1n n -++，∴第①行数的第2023个数为2023(2)-，第②行数的第2023个数为2023(2)2024-+，∴202422024-+，故答案为：1024；202422024-+．【点睛】本题主要考查数字的变化，找其中的规律，是今年考试中常见的题型.16.（2021·湖南怀化市·中考真题）观察等式：232222+=-，23422222++=-，2345222222+++=-，……，已知按一定规律排列的一组数：1002，1012，1022，……，1992，若1002=m ，用含m 的代数式表示这组数的和是___________．【答案】100(21)m -【分析】根据规律将1002，1012，1022，……，1992用含m 的代数式表示，再计算0199222+++ 的和，即可计算1001011011992222++++ 的和．【详解】由题意规律可得：2399100222222++++=- ．∵1002=m∴23991000222222=2m m +++++== ，∵22991001012222222+++++=- ，∴10123991002222222=++++++ 12=2m m m m =+=．102239910010122222222+=++++++ 224=2m m m m m =++=．1032399100101102222222222=++++++++ 3248=2m m m m m m =+++=．……∴1999922m =．故10010110110199992222222m m m ++++=+++ ．令012992222S ++++= ①12310022222S ++++= ②②-①，得10021S-=∴10010110110199992222222m m m ++++=+++ =100(21)m -故答案为：100(21)m -．【点睛】本题考查规律问题，用含有字母的式子表示数、灵活计算数列的和是解题的关键．17.（2022·湖南怀化）正偶数2，4，6，8，10，……，按如下规律排列，2468101214161820……则第27行的第21个数是______．【答案】744【分析】由图可以看出，每行数字的个数与行数是一致的，即第一行有1个数，第二行有2个数，第三行有3个数••••••••第n行有n个数，则前n行共有(1)2n n+个数，再根据偶数的特征确定第几行第几个数是几．【详解】解：由图可知，第一行有1个数，第二行有2个数，第三行有3个数，•••••••第n行有n个数．∴前n行共有1+2+3+⋯+n=(1)2n n+个数．∴前26行共有351个数，∴第27行第21个数是所有数中的第372个数．∵这些数都是正偶数，∴第372个数为372×2=744．故答案为：744．【点睛】本题考查了数字类的规律问题，解决这类问题的关键是先根据题目的已知条件找出其中的规律，再结合其他已知条件求解．18.（2021·四川眉山市·中考真题）观察下列等式：1311 212x===+⨯；2711623x ===+⨯；313111234x ===+⨯；……根据以上规律，计算12320202021x x x x ++++-= ______．【答案】12016-【分析】根据题意，找到第n 个等式的左边为1与1n(n 1)+的和；利用这个结论得到原式＝112+116+1112+…+1120202021⨯﹣2021，然后把12化为1﹣12，16化为12﹣13，120152016⨯化为12015﹣12016，再进行分数的加减运算即可．【详解】11(1)n n =++，20201120202021x =+⨯12320202021x x x x ++++- ＝112+116+1112+…+1120202021⨯﹣2021＝2020+1﹣12+12﹣13+…+12015﹣12016﹣2021＝2020+1﹣12016﹣2021＝12016-．故答案为：12016-．【点睛】本题考查了二次根式的化简和找规律，解题关键是根据算式找的规律，根据数字的特征进行简便运算．19.（2022·安徽）观察以下等式：第1个等式：()()()22221122122⨯+=⨯+-⨯，第2个等式：()()()22222134134⨯+=⨯+-⨯，第3个等式：()()()22223146146⨯+=⨯+-⨯，第4个等式：()()()22224158158⨯+=⨯+-⨯，……按照以上规律．解决下列问题：(1)写出第5个等式：________；(2)写出你猜想的第n 个等式（用含n 的式子表示），并证明．【答案】(1)()()()2222516101610⨯+=⨯+-⨯(2)()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅，证明见解析【分析】（1）观察第1至第4个等式中相同位置的数的变化规律即可解答；（2）观察相同位置的数变化规律可以得出第n 个等式为()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅，利用完全平方公式和平方差公式对等式左右两边变形即可证明．(1)解：观察第1至第4个等式中相同位置数的变化规律，可知第5个等式为：()()()2222516101610⨯+=⨯+-⨯，故答案为：()()()2222516101610⨯+=⨯+-⨯；(2)解：第n 个等式为()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅，证明如下：等式左边：()2221441n n n +=++，等式右边：[][]22(1)21(1)2n n n n +⋅+-+⋅[][](1)21(1)2(1)21(1)2n n n n n n n n =+⋅+++⋅⋅+⋅+-+⋅[](1)411n n =+⋅+⨯2441n n =++，故等式()[][]22221(1)21(1)2n n n n n +=+⋅+-+⋅成立．【点睛】本题考查整式规律探索，发现所给数据的规律并熟练运用完全平方公式和平方差公式是解题的关键．20.（2021·贵州铜仁市·中考真题）观察下列各项：112，124，138，1416，…，则第n 项是______________．【答案】12nn +【分析】根据已知可得出规律：第一项：1111122=+，第二项：2112242=+，第三项：3113382=+…即可得出结果．【详解】解：根据题意可知：第一项：1111122=+，第二项：2112242=+，第三项：3113382=+，第四项：41144162=+，…则第n 项是12n n +；故答案为：12nn +．【点睛】此题属于数字类规律问题，根据已知各项的规律得出结论是解决此类题目的关键．0.618≈这个数叫做黄金比，著名数学家华罗庚优选法中的“0.618法”就应用了黄金比．设12a =，b =11111S a b =+++，2222211S a b =+++，…，10010010010010011S a b=+++，则12100S S S +++= _______．【答案】5050【分析】利用分式的加减法则分别可求S 1=1，S 2=2，S 100=100，•••，利用规律求解即可．【详解】解： 12a =，b =11122ab =⨯=∴，1112211112a ba ba b b ba bS a a ++++=+==+++++++ ，222222222222222222221112a b a b S a b a b a b a b ++++=+=⨯=⨯=+++++++，…，10101001001001010101010010011100100111a b S a b a b a b +++=+=⨯=+++++∴12100S S S +++= 121005050++⋯⋯+=故答案为：5050【点睛】本题考查了分式的加减法，二次根式的混合运算，求得1ab =，找出的规律是本题的关键．22.（2021·江西中考真题）下表在我国宋朝数学家杨辉1261年的著作《详解九章算法》中提到过，因而人们把这个表叫做杨辉三角，请你根据杨辉三角的规律补全下表第四行空缺的数字是______．【答案】3【分析】通过观察每一个数字等于它上方相邻两数之和．【详解】解：通过观察杨辉三角发现每一个数字等于它上方相邻两数之和的规律，例如：第3行中的2，等于它上方两个相邻的数1，1相加，即：211=+；第4行中的3，等于它上方两个相邻的数2，1相加，即：321=+；⋅⋅⋅⋅⋅⋅由此规律：故空缺数等于它上方两个相邻的数1，2相加，即空缺数为：3，故答案是：3．【点睛】本题考查了杨辉三角数的规律，解题的关键是：通过观察找到数与数之间的关系，从来解决问题．23.（2022·山东泰安）将从1开始的连续自然数按以下规律排列：若有序数对(),n m 表示第n 行，从左到右第m 个数，如()3,2表示6，则表示99的有序数对是_______．【答案】()10,18【分析】分析每一行的第一个数字的规律，得出第n 行的第一个数字为211n +-（），从而求得最终的答案．【详解】第1行的第一个数字：()2111=+-1第2行的第一个数字：()22121=+-第3行的第一个数字：()25131=+-第4行的第一个数字：()210141=+-第5行的第一个数字：()217151=+-…..，设第n 行的第一个数字为x ，得()211x n =+-设第1n +行的第一个数字为z ，得21z n =+设第n 行，从左到右第m 个数为y 当99y =时221(1)991n n +-≤<+∴22(1)98n n -≤<∵n 为整数∴10n =∴21182x n =+-=（）∴9982118m =-+=故答案为：()10,18．【点睛】本题考查数字规律的性质，解题的关键是熟练掌握数字规律的相关性质．24.（2022·浙江舟山）观察下面的等式：111236=+，1113412=+，1114520=+，……(1)按上面的规律归纳出一个一般的结论（用含n 的等式表示，n 为正整数）(2)请运用分式的有关知识，推理说明这个结论是正确的．【答案】(1)1111(1)n n n n =+++(2)见解析【分析】（1）根据所给式子发现规律，第一个式子的左边分母为2，第二个式子的左边分母为3，第三个式子的左边分母为4，…；右边第一个分数的分母为3，4，5，…，另一个分数的分母为前面两个分母的乘积；所有的分子均为1；所以第（n+1）个式子为1111(1)n n n n =+++．（2）由（1）的规律发现第（n+1）个式子为1111(1)n n n n =+++，用分式的加法计算式子右边即可证明．(1)解：∵第一个式子()1111123621221=+=+++，第二个式子()11111341231331=+=+++，第三个式子()11111452041441=+=+++，……∴第（n+1）个式子1111(1)n n n n =+++；(2)解：∵右边=111111(1)(1)(1)(1)n n n n n n n n n n n n ++=+==+++++=左边，∴1111(1)n n n n =+++．【点睛】此题考查数字的变化规律，分式加法运算，解题关键是通过观察，分析、归纳发现其中各分母的变化规律．类型二图形规律25．（2023·重庆·统考中考真题）用长度相同的木棍按如图所示的规律拼图案，其中第①个图案用了9根木棍，第②个图案用了14根木棍，第③个图案用了19根木棍，第④个图案用了24根木棍，……，按此规律排列下去，则第⑧个图案用的木棍根数是（）A ．39B ．44C ．49D ．54【答案】B 【分析】根据各图形中木棍的根数发现计算的规律，由此即可得到答案．【详解】解：第①个图案用了459+=根木棍，第②个图案用了45214+⨯=根木棍，第③个图案用了45319+⨯=根木棍，第④个图案用了45424+⨯=根木棍，……，+⨯=根，第⑧个图案用的木棍根数是45844故选：B．【点睛】此题考查了图形类规律的探究，正确理解图形中木棍根数的变化规律由此得到计算的规律是解题的关键．25．（2023·重庆·统考中考真题）用圆圈按如图所示的规律拼图案，其中第①个图案中有2个圆圈，第②个图案中有5个圆圈，第③个图案中有8个圆圈，第④个图案中有11个圆圈，…，按此规律排列下去，则第⑦个图案中圆圈的个数为（）A．14B．20C．23D．26【答案】B【分析】根据前四个图案圆圈的个数找到规律，即可求解.=⨯-；【详解】解：因为第①个图案中有2个圆圈，2311=⨯-；第②个图案中有5个圆圈，5321=⨯-；第③个图案中有8个圆圈，8331=⨯-；第④个图案中有11个圆圈，11341…，⨯-=；所以第⑦个图案中圆圈的个数为37120故选：B.【点睛】本题考查了图形类规律探究，根据前四个图案圆圈的个数找到第n个图案的规律为31n -是解题的关键.27．（2023·山东日照·统考中考真题）数学家高斯推动了数学科学的发展，被数学界誉为“数学王子”，据传，他在计算1234100+++++ 时，用到了一种方法，将首尾两个数相加，进而得到100(1100)12341002⨯++++++= ．人们借助于这样的方法，得到(1)12342n n n ++++++= （n 是正整数）．有下列问题，如图，在平面直角坐标系中的一系列格点(),i i i A x y ，其中1,2,3,,,i n = ，且,i i x y 是整数．记n n n a x y =+，如1(0,0)A ，即120,(1,0)a A =，即231,(1,1)a A =-，即30,a = ，以此类推．则下列结论正确的是（）A ．202340a =B ．202443a =C ．2(21)26n a n -=-D ．2(21)24n a n -=-【答案】B 【分析】利用图形寻找规律()211,1n A n n ---，再利用规律解题即可．【详解】解：第1圈有1个点，即1(0,0)A ，这时10a =；第2圈有8个点，即2A 到()91,1A ；第3圈有16个点，即10A 到()252,2A ，；依次类推，第n 圈，()211,1n A n n ---；由规律可知：2023A 是在第23圈上，且()202522,22A ，则()202320,22A 即2023202242a =+=，故A 选项不正确；2024A 是在第23圈上，且()202421,22A ，即2024212243a =+=，故B 选项正确；第n 圈，()211,1n A n n ---，所以2122n a n -=-，故C 、D 选项不正确；故选B ．【点睛】本题考查图形与规律，利用所给的图形找到规律是解题的关键．28.（2022·江西）将字母“C”，“H”按照如图所示的规律摆放，依次下去，则第4个图形中字母“H”的个数是（）A．9B．10C．11D．12【答案】B 【分析】列举每个图形中H 的个数，找到规律即可得出答案．【详解】解：第1个图中H 的个数为4，第2个图中H 的个数为4+2，第3个图中H 的个数为4+2×2，第4个图中H 的个数为4+2×3=10，故选：B．【点睛】本题考查了规律型：图形的变化类，通过列举每个图形中H 的个数，找到规律：每个图形比上一个图形多2个H 是解题的关键．29.（2022·重庆）用正方形按如图所示的规律拼图案，其中第①个图案中有5个正方形，第②个图案中有9个正方形，第③个图案中有13个正方形，第④个图案中有17个正方形，此规律排列下去，则第⑨个图案中正方形的个数为（）A．32B．34C．37D．41【答案】C 【分析】第1个图中有5个正方形，第2个图中有9个正方形，第3个图中有13个正方形，……，由此可得：每增加1个图形，就会增加4个正方形，由此找到规律，列出第n 个图形的算式，然后再解答即可．【详解】解：第1个图中有5个正方形；第2个图中有9个正方形，可以写成：5+4=5+4×1；第3个图中有13个正方形，可以写成：5+4+4=5+4×2；第4个图中有17个正方形，可以写成：5+4+4+4=5+4×3；．．．第n 个图中有正方形，可以写成：5+4（n-1）=4n+1；当n=9时，代入4n+1得：4×9+1=37．故选：C．【点睛】本题主要考查了图形的变化规律以及数字规律，通过归纳与总结结合图形得出数字之间的规律是解决问题的关键．30.（2021·广西玉林市·中考真题）观察下列树枝分杈的规律图，若第n 个图树枝数用n Y 表示，则94Y Y -=（）A．4152⨯B．4312⨯C．4332⨯D．4632⨯【答案】B【分析】根据题目中的图形，可以写出前几幅图中树枝分杈的数量，从而可以发现树枝分杈的变化规律，进而得到规律21nn Y =-，代入规律求解即可．【详解】解：由图可得到：11223344211213217211521n n Y Y Y Y Y =-==-==-==-==-则：9921Y =-，∴944942121312Y Y -=--+=⨯，故答案选：B．【点睛】本题考查图形规律，解答本题的关键是明确题意，利用数形结合的思想解答31.（2021·黑龙江大庆市·中考真题）如图，3条直线两两相交最多有3个交点，4条直线两两相交最多有6个交点，按照这样的规律，则20条直线两两相交最多有______个交点【答案】190【分析】根据题目中的交点个数，找出n 条直线相交最多有的交点个数公式：1(1)2n n -．【详解】解：2条直线相交有1个交点；3条直线相交最多有1123322+==⨯⨯个交点；4条直线相交最多有11236432++==⨯⨯个交点；5条直线相交最多有1123410542+++==⨯⨯个交点；⋯20条直线相交最多有120191902⨯⨯=．故答案为：190．【点睛】本题考查的是多条直线相交的交点问题，解答此题的关键是找出规律，即n 条直线相交最多有1(1)2n n -．32．（2023·四川遂宁·统考中考真题）烷烃是一类由碳、氢元素组成的有机化合物，在生产生活中可作为燃料、润滑剂等原料，也可用于动、植物的养护．通常用碳原子的个数命名为甲烷、乙烷、丙烷、……、癸烷（当碳原子数目超过10个时即用汉文数字表示，如十一烷、十二烷……）等，甲烷的化学式为4CH ，乙烷的化学式为26C H ，丙烷的化学式为38C H ……，其分子结构模型如图所示，按照此规律，十二烷的化学式为．【答案】1226C H 【分析】根据碳原子的个数，氢原子的个数，找到规律，即可求解．【详解】解：甲烷的化学式为4CH ，乙烷的化学式为26C H ，丙烷的化学式为38C H ……，碳原子的个数为序数，氢原子的个数为碳原子个数的2倍多2个，十二烷的化学式为1226C H ，故答案为：1226C H ．【点睛】本题考查了规律题，找到规律是解题的关键．33．（2023·山西·统考中考真题）如图是一组有规律的图案，它由若干个大小相同的圆片组成．第1个图案中有4个白色圆片，第2个图案中有6个白色圆片，第3个图案中有8个白色圆片，第4个图案中有10个白色圆片，…依此规律，第n 个图案中有个白色圆片（用含n 的代数式表示）【答案】()22n +【分析】由于第1个图案中有4个白色圆片4221=+⨯，第2个图案中有6个白色圆片6222=+⨯，第3个图案中有8个白色圆片8223=+⨯，第4个图案中有10个白色圆片10224=+⨯，⋯，可得第(1)n n >个图案中有白色圆片的总数为22n +．【详解】解：第1个图案中有4个白色圆片4221=+⨯，第2个图案中有6个白色圆片6222=+⨯，第3个图案中有8个白色圆片8223=+⨯，第4个图案中有10个白色圆片10224=+⨯，⋯，∴第(1)n n >个图案中有()22n +个白色圆片．故答案为：()22n +．【点睛】此题考查图形的变化规律，通过从一些特殊的数字变化中发现不变的因素或按规律变化的因素，然后推广到一般情况．解题关键是总结归纳出图形的变化规律．34．（2023·黑龙江绥化·统考中考真题）在求123100++++ 的值时，发现：1100101+=，299101+= ，从而得到123100++++= 101505050⨯=．按此方法可解决下面问题．图（1）有1个三角形，记作11a =；分别连接这个三角形三边中点得到图（2），有5个三角形，记作25a =；再分别连接图（2）中间的小三角形三边中点得到图（3），有9个三角形，记作39a =；按此方法继续下去，则123n a a a a ++++= ．（结果用含n 的代数式表示）【答案】22n n -/22n n -+【分析】根据题意得出()14143n a n n =+-=-，进而即可求解．【详解】解：依题意，()1231,5,9,14143n a a a a n n ===⋅⋅⋅=+-=-，，∴123n a a a a ++++= ()21432122n n n n n n +-==-=-，故答案为：22n n -．【点睛】本题考查了图形类规律，找到规律是解题的关键．35.（2022·山东泰安）观察下列图形规律，当图形中的“○”的个数和“．”个数差为2022时，n 的值为____________．【答案】不存在【分析】首先根据n=1、2、3、4时，“•”的个数分别是3、6、9、12，判断出第n 个图形中“•”的个数是3n；然后根据n=1、2、3、4，“○”的个数分别是1、3、6、10，判断出第n 个“○”的个数是()12n n +；最后根据图形中的“○”的个数和“．”个数差为2022，列出方程，解方程即可求出n 的值是多少即可．【详解】解：∵n=1时，“•”的个数是3=3×1；n=2时，“•”的个数是6=3×2；n=3时，“•”的个数是9=3×3；n=4时，“•”的个数是12=3×4；……∴第n 个图形中“•”的个数是3n；又∵n=1时，“○”的个数是1=1(11)2⨯+；n=2时，“○”的个数是2(21)32⨯+=，n=3时，“○”的个数是3(31)62⨯+=，n=4时，“○”的个数是4(41)102⨯+=，……∴第n 个“○”的个数是()12n n +，由图形中的“○”的个数和“．”个数差为2022()1320222n n n +∴-=①，()1320222n n n +-=②解①得：无解解②得：12n n ==故答案为：不存在【点睛】本题考查了图形类规律，解一元二次方程，找到规律是解题的关键．36.（2022·四川遂宁）“勾股树”是以正方形一边为斜边向外作直角三角形，再以该直角三角形的两直角边分别向外作正方形，重复这一过程所画出来的图形，因为重复数次后的形状好似一棵树而得名．假设如图分别是第一代勾股树、第二代勾股树、第三代勾股树，按照勾股树的作图原理作图，则第六代勾股树中正方形的个数为______．【答案】127【分析】由已知图形观察规律，即可得到第六代勾股树中正方形的个数．【详解】解：∵第一代勾股树中正方形有1+2=3（个），第二代勾股树中正方形有1+2+22=7（个），第三代勾股树中正方形有1+2+22+23=15（个），.....．∴第六代勾股树中正方形有1+2+22+23+24+25+26=127（个），故答案为：127．【点睛】本题考查图形中的规律问题，解题的关键是仔细观察图形，得到图形变化的规律．37.（2021·湖南常德市·中考真题）如图中的三个图形都是边长为1的小正方形组成的网格，其中第一个图形有11⨯个正方形，所有线段的和为4，第二个图形有22⨯个小正方形，所有线段的和为12，第三个图形有33⨯个小正方形，所有线段的和为24，按此规律，则第n 个网格所有线段的和为____________．(用含n 的代数式表示)【答案】2n 2+2n【分析】本题要通过第1、2、3和4个图案找出普遍规律，进而得出第n 个图案的规律为S n =4n+2n ×(n-1)，得出结论即可．【详解】解：观察图形可知：第1个图案由1个小正方形组成，共用的木条根数141221,S =⨯=⨯⨯第2个图案由4个小正方形组成，共用的木条根数262232,S =⨯=⨯⨯第3个图案由9个小正方形组成，共用的木条根数383243,S =⨯=⨯⨯第4个图案由16个小正方形组成，共用的木条根数4104254,S =⨯=⨯⨯…由此发现规律是：第n 个图案由n 2个小正方形组成，共用的木条根数()22122,n S n n n n =+=+ 故答案为：2n 2+2n．【点睛】本题考查了规律型-图形的变化类，熟练找出前四个图形的规律是解题的关键．38.（2021·黑龙江绥化市·中考真题）下面各图形是由大小相同的三角形摆放而成的，图①中有1个三角形，图②中有5个三角形，图③中有11个三角形，图④中有19个三角形…，依此规律，则第n 个图形中三角形个数是_______．【答案】21n n +-【分析】此题只需分成上下两部分即可找到其中规律，上方的规律为(n-1)，下方规律为n 2，结合两部分即可得出答案．【详解】解：将题意中图形分为上下两部分，则上半部规律为：0、1、2、3、4……n-1，下半部规律为：12、22、32、42……n 2，∴上下两部分统一规律为：21n n +-．故答案为：21n n +-．【点睛】本题主要考查的图形的变化规律，解题的关键是将图形分为上下两部分分别研究．类型三与函数有关规律39．（2023·山东烟台·统考中考真题）如图，在直角坐标系中，每个网格小正方形的边长均为1个单位长度，以点P 为位似中心作正方形123PA A A ，正方形456,PA A A ⋯，按此规律作下去，所作正方形的顶点均在格点上，其中正方形123PA A A 的顶点坐标分别为()()()123,0,2,1,1,0P A A ---，()32,1A --，则顶点100A 的坐标为（）。

中考数学专题12探索性问题(第03期)-2017年中考数学试题分项版解析汇编(原卷版)

一、选择题目1．（2017四川省绵阳市）如图所示，将形状、大小完全相同的“●”和线段按照一定规律摆成下列图形，第1幅图形中“●”的个数为a1，第2幅图形中“●”的个数为a2，第3幅图形中“●”的个数为a3，…，以此类推，则1a1+1a2+1a3+⋯+1a19的值为（）A．2021B．6184C．589840D．4217602．（2017四川省达州市）如图，将矩形ABCD绕其右下角的顶点按顺时针方向旋转90°至图①位置，继续绕右下角的顶点按顺时针方向旋转90°至图②位置，以此类推，这样连续旋转2017次．若AB=4，AD=3，则顶点A在整个旋转过程中所经过的路径总长为（）A．2017πB．2034πC．3024πD．3026π3．（2017江苏省连云港市）如图所示，一动点从半径为2的⊙O上的A0点出发，沿着射线A0O方向运动到⊙O上的点A1处，再向左沿着与射线A1O夹角为60°的方向运动到⊙O上的点A2处；接着又从A2点出发，沿着射线A2O方向运动到⊙O上的点A3处，再向左沿着与射线A3O夹角为60°的方向运动到⊙O上的点A4处；…按此规律运动到点A2017处，则点A2017与点A0间的距离是（）A．4B．C．2D．04．（2017重庆市B 卷）下列图象都是由相同大小的按一定规律组成的，其中第①个图形中一共有4颗，第②个图形中一共有11颗，第③个图形中一共有21颗，…，按此规律排列下去，第⑨个图形中的颗数为（）A ．116B ．144C ．145D ．150 二、填空题目 5．（2017山东省济宁市）请写出一个过点（1，1），且与x 轴无交点的函数解析式：．6．（2017山东省济宁市）如图，正六边形A 1B 1C 1D 1E 1F 1的边长为1，它的六条对角线又围成一个正六边形A 2B 2C 2D 2E 2F 2，如此继续下去，则正六边形A 4B 4C 4D 4E 4F 4的面积是．三、解答题7．（2017四川省南充市）如图，在正方形ABCD 中，点E 、G 分别是边AD 、BC 的中点，AF =14AB ．（1）求证：EF ⊥AG ；（2）若点F 、G 分别在射线AB 、BC 上同时向右、向上运动，点G 运动速度是点F 运动速度的2倍，EF ⊥AG 是否成立（只写结果，不需说明理由）？（3）正方形ABCD 的边长为4，P 是正方形ABCD 内一点，当PAB OABS S ∆∆=，求△P AB 周长的最小值．8．（2017四川省达州市）如图，在△ABC中，点O是边AC上一个动点，过点O作直线EF∥BC分别交∠ACB、外角∠ACD的平分线于点E、F．（1）若CE=8，CF=6，求OC的长；（2）连接AE、AF．问：当点O在边AC上运动到什么位置时，四边形AECF是矩形？并说明理由．9．（2017四川省达州市）探究：小明在求同一坐标轴上两点间的距离时发现，对于平面直角坐标系内任意两点P1（x1，y1），P2（x2，y2），可通过构造直角三角形利用图1得到结论：()()22 122121 PP x x y y =-+-他还利用图2证明了线段P1P2的中点P（x，y）P的坐标公式：122x xx+=，122y yy+=．（1）请你帮小明写出中点坐标公式的证明过程；运用：（2）①已知点M（2，﹣1），N（﹣3，5），则线段MN长度为；②直接写出以点A（2，2），B（﹣2，0），C（3，﹣1），D为顶点的平行四边形顶点D的坐标：；拓展：（3）如图3，点P（2，n）在函数43y x=（x≥0）的图象OL与x轴正半轴夹角的平分线上，请在OL、x轴上分别找出点E、F，使△PEF的周长最小，简要叙述作图方法，并求出周长的最小值．10．（2017山东省枣庄市）如图，在△ABC中，∠C=90°，∠BAC的平分线交BC于点D，点O在AB上，以点O为圆心，OA为半径的圆恰好经过点D，分别交AC，AB于点E，F．（1）试判断直线BC与⊙O的位置关系，并说明理由；（2）若BD=BF=2，求阴影部分的面积（结果保留π）．11．（2017山东省枣庄市）已知正方形ABCD，P为射线AB上的一点，以BP为边作正方形BPEF，使点F 在线段CB的延长线上，连接EA，EC．（1）如图1，若点P在线段AB的延长线上，求证：EA=EC；（2）如图2，若点P在线段AB的中点，连接AC，判断△ACE的形状，并说明理由；（3）如图3，若点P在线段AB上，连接AC，当EP平分∠AEC时，设AB=a，BP=b，求a：b及∠AEC 的度数．12．（2017山西省）如图，△ABC内接于⊙O，且AB为⊙O的直径，OD⊥AB，与AC交于点E，与过点C 的⊙O的切线交于点D．（1）若AC=4，BC=2，求OE的长．（2）试判断∠A与∠CDE的数量关系，并说明理由．13．（2017江苏省盐城市）如图，矩形ABCD中，∠ABD、∠CDB的平分线BE、DF分别交边AD、BC于点E、F．（1）求证：四边形BEDF是平行四边形；（2）当∠ABE为多少度时，四边形BEDF是菱形？请说明理由．14．（2017江苏省盐城市）如图，在平面直角坐标系中，Rt△ABC的斜边AB在y轴上，边AC与x轴交于点D，AE平分∠BAC交边BC于点E，经过点A、D、E的圆的圆心F恰好在y轴上，⊙F与y轴相交于另一点G．（1）求证：BC是⊙F的切线；（2）若点A、D的坐标分别为A（0，﹣1），D（2，0），求⊙F的半径；（3）试探究线段AG、AD、CD三者之间满足的等量关系，并证明你的结论．15．（2017江苏省盐城市）（探索发现】如图①，是一张直角三角形纸片，∠B=60°，小明想从中剪出一个以∠B为内角且面积最大的矩形，经过多次操作发现，当沿着中位线DE、EF剪下时，所得的矩形的面积最大，随后，他通过证明验证了其正确性，并得出：矩形的最大面积与原三角形面积的比值为．【拓展应用】如图②，在△ABC中，BC=a，BC边上的高AD=h，矩形PQMN的顶点P、N分别在边AB、AC上，顶点Q、M在边BC上，则矩形PQMN面积的最大值为．（用含a，h的代数式表示）【灵活应用】如图③，有一块“缺角矩形”ABCDE ，AB =32，BC =40，AE =20，CD =16，小明从中剪出了一个面积最大的矩形（∠B 为所剪出矩形的内角），求该矩形的面积．【实际应用】如图④，现有一块四边形的木板余料ABCD ，经测量AB =50cm ，BC =108cm ，CD =60cm ，且tan B =tan C =43，木匠徐师傅从这块余料中裁出了顶点M 、N 在边BC 上且面积最大的矩形PQMN ，求该矩形的面积．16．（2017江苏省连云港市）如图，已知等腰三角形ABC 中，AB =AC ，点D 、E 分别在边AB ．AC 上，且AD =AE ，连接BE 、CD ，交于点F ．（1）判断∠ABE 与∠ACD 的数量关系，并说明理由；（2）求证：过点A 、F 的直线垂直平分线段BC ．17．（2017江苏省连云港市）问题呈现：如图1，点E 、F 、G 、H 分别在矩形ABCD 的边AB 、BC 、CD 、DA 上，AE =DG ，求证：2ABCDEFGHS S 矩形四边形．（S 表示面积）实验探究：某数学实验小组发现：若图1中AH ≠BF ，点G 在CD 上移动时，上述结论会发生变化，分别过点E 、G 作BC 边的平行线，再分别过点F 、H 作AB 边的平行线，四条平行线分别相交于点A 1、B 1、C 1、D 1，得到矩形A 1B 1C 1D 1．如图2，当AH ＞BF 时，若将点G 向点C 靠近（DG ＞AE ），经过探索，发现：2S四边形EFGH =S矩形ABCD +S．如图3，当AH ＞BF 时，若将点G 向点D 靠近（DG ＜AE ），请探索S四边形EFGH 、S矩形ABCD与S之间的数量关系，并说明理由．迁移应用：请直接应用“实验探究”中发现的结论解答下列问题：（1）如图4，点E 、F 、G 、H 分别是面积为25的正方形ABCD 各边上的点，已知AH ＞BF ，AE ＞DG ，S四边形EFGH=11，HF，求EG 的长．（2）如图5，在矩形ABCD中，AB=3，AD=5，点E、H分别在边AB、AD上，BE=1，DH=2，点F、G分别是边BC、CD上的动点，且FG=10，连接EF、HG，请直接写出四边形EFGH面积的最大值．18．（2017湖北省襄阳市）如图，在△ABC中，∠ACB=90°，CD是中线，AC=BC，一个以点D为顶点的45°角绕点D旋转，使角的两边分别与AC、BC的延长线相交，交点分别为点E，F，DF与AC交于点M，DE与BC交于点N．（1）如图1，若CE=CF，求证：DE=DF；（2）如图2，在∠EDF绕点D旋转的过程中：①探究三条线段AB，CE，CF之间的数量关系，并说明理由；②若CE=4，CF=2，求DN的长．祝你考试成功!祝你考试成功!。

中考数学专题复习开放性问题-人教版初中九年级全册数学试题

开放性问题【专题点拨】开放探索问题是指已知条件、解题依据、解题方法、问题结论这四项要素中，缺少解题要素两个或两个以上，或者条件、结论有待探求、补充等.【解题策略】在解决开放探索问题的时候，需解题者经过探索确定结论或补全条件，将开放性问题转化为封闭性问题，然后选择合适的解题途径完成最后的解答.【典例解析】类型一：条件开放型问题例题1：（2016·某某省滨州市·14分）如图，已知抛物线y=﹣x2﹣x+2与x轴交于A、B两点，与y轴交于点C（1）求点A，B，C的坐标；（2）点E是此抛物线上的点，点F是其对称轴上的点，求以A，B，E，F为顶点的平行四边形的面积；（3）此抛物线的对称轴上是否存在点M，使得△ACM是等腰三角形？若存在，请求出点M的坐标；若不存在，请说明理由．【考点】二次函数综合题．【专题】压轴题；函数及其图象．【分析】（1）分别令y=0，x=0，即可解决问题．（2）由图象可知AB只能为平行四边形的边，易知点E坐标（﹣7，﹣）或（5，﹣），由此不难解决问题．（3）分A、C、M为顶点三种情形讨论，分别求解即可解决问题．【解答】解：（1）令y=0得﹣x2﹣x+2=0，∴x2+2x﹣8=0，x=﹣4或2，∴点A坐标（2，0），点B坐标（﹣4，0），令x=0，得y=2，∴点C坐标（0，2）．（2）由图象可知AB只能为平行四边形的边，∵AB=EF=6，对称轴x=﹣1，∴点E的横坐标为﹣7或5，∴点E坐标（﹣7，﹣）或（5，﹣），此时点F（﹣1，﹣），∴以A，B，E，F为顶点的平行四边形的面积=6×=．（3）如图所示，①当C为顶点时，CM1=CA，CM2=CA，作M1N⊥OC于N，在RT△CM1N中，==，∴点M1坐标（﹣1，2+），点M2坐标（﹣1，2﹣）．②当M3为顶点时，∵直线AC解析式为y=﹣x+1，线段AC的垂直平分线为y=x，∴点M3坐标为（﹣1，﹣1）．③当点A为顶点的等腰三角形不存在．综上所述点M坐标为（﹣1，﹣1）或（﹣1，2+）或（﹣1.2﹣）．【点评】本题考查二次函数综合题、平行四边形的判定和性质、勾股定理等知识，解题的关键是熟练掌握抛物线与坐标轴交点的求法，学会分类讨论的思想，属于中考压轴题．变式训练1：（2016·某某某某）如图，抛物线y=x2+bx+c与x轴交于A、B两点，B点坐标为（3，0），与y轴交于点C（0，﹣3）（1）求抛物线的解析式；（2）点P在抛物线位于第四象限的部分上运动，当四边形ABPC的面积最大时，求点P 的坐标和四边形ABPC的最大面积．（3）直线l经过A、C两点，点Q在抛物线位于y轴左侧的部分上运动，直线m经过点B和点Q，是否存在直线m，使得直线l、m与x轴围成的三角形和直线l、m与y轴围成的三角形相似？若存在，求出直线m的解析式，若不存在，请说明理由．类型二：结论开放型问题例题2：（2016·某某随州·3分）二次函数y=ax2+bx+c（a≠0）的部分图象如图所示，图象过点（﹣1，0），对称轴为直线x=2，下列结论：（1）4a+b=0；（2）9a+c＞3b；（3）8a+7b+2c ＞0；（4）若点A（﹣3，y1）、点B（﹣，y2）、点C（，y3）在该函数图象上，则y1＜y3＜y2；（5）若方程a（x+1）（x﹣5）=﹣3的两根为x1和x2，且x1＜x2，则x1＜﹣1＜5＜x2．其中正确的结论有（）A．2个 B．3个 C．4个 D．5个【解析】二次函数图象与系数的关系．（1）正确．根据对称轴公式计算即可．（2）错误，利用x=﹣3时，y＜0，即可判断．（3）正确．由图象可知抛物线经过（﹣1，0）和（5，0），列出方程组求出a、b即可判断．（4）错误．利用函数图象即可判断．（5）正确．利用二次函数与二次不等式关系即可解决问题．【解答】解：（1）正确．∵﹣ =2，∴4a+b=0．故正确．（2）错误．∵x=﹣3时，y＜0，∴9a﹣3b+c＜0，∴9a+c＜3b，故（2）错误．（3）正确．由图象可知抛物线经过（﹣1，0）和（5，0），∴解得，∴8a+7b+2c=8a﹣28a﹣10a=﹣30a，∵a＜0，∴8a+7b=2c＞0，故（3）正确．（4）错误，∵点A（﹣3，y1）、点B（﹣，y2）、点C（，y3），∵﹣2=，2﹣（﹣）=，∴＜∴点C离对称轴的距离近，∴y3＞y2，∵a＜0，﹣3＜﹣＜2，∴y1＜y2∴y1＜y2＜y3，故（4）错误．（5）正确．∵a＜0，∴（x+1）（x﹣5）=﹣3/a＞0，即（x+1）（x﹣5）＞0，故x＜﹣1或x＞5，故（5）正确．∴正确的有三个，故选B．变式训练2：（2016·某某某某·3分）如图，抛物线y=ax2+bx+c（a≠0）的对称轴为直线x=1，与x 轴的一个交点坐标为（﹣1，0），其部分图象如图所示，下列结论：①4ac＜b2；②方程ax2+bx+c=0的两个根是x1=﹣1，x2=3；③3a+c＞0④当y＞0时，x的取值X围是﹣1≤x＜3⑤当x＜0时，y随x增大而增大其中结论正确的个数是（）A．4个B．3个C．2个D．1个类型三：解题策略开放型例题3：(2014 年某某襄阳)如图 Z3-1，在△ABC 中，点D，E 分别在边 AC，AB 上，BD 与 CE 交于点 O，给出下列三个条件：①∠EBO＝∠DCO；②BE＝CD；③OB＝OC.(1)上述三个条件中，由哪两个条件可以判定△ABC 是等腰三角形？(用序号写出所有成立的情形)（2）选择其中的成立条件进行证明。

中考数学总复习第三编综合专题闯关篇专题1规律探索猜想类试题(2021-2022学年)

专题一规律探索猜想类规律探索与猜想是中考中常见题型之一,它主要用于考查学生观察、分析、归纳、猜想等方面的能力,既可以命基础题，也可命中高档题，题型不限,方法灵活,主要有数式规律、图形规律、坐标规律等,解这类问题要善于发现其过程中的特点，抓住其周期是解决此类问题的关键.纵观遵义近五年中考,每年都会涉及一道规律探索问题，一般难度不大，预计20１８年遵义中考也有可能命一道中基础（选择或填空)规律探索题．,中考重难点突破）数字规律【例1】（临夏中考)古希腊数学家把数1，3，6,１0,15,２1,…叫做三角形数,它有一定的规律性，若把第一个三角形数记为x1，第二个三角形数记为ｘ2,…第n个三角形数记为x n，则x n＋x n+1＝____＿_＿_．【解析】根据三角形数得到ｘ1＝1，x2＝3=1+2，x3＝6=１＋２＋３,x4=10＝1＋２＋３＋4,ｘ5＝１5=1+2＋3+4+5，即三角形数为从1到它的顺号数之间所有整数的和,即ｘｎ＝１＋2+3+…+n=错误!未定义书签。

，xｎ＋1=错误!,然后计算ｘn＋ｘｎ＋1可得.【答案】(n＋1)2◆模拟题区1．（２017遵义二中二模)计算下列各式的值:92+１9;错误!;错误!；错误!.观察所得结果，总结存在的规律，应用得到的规律可得错误!未定义书签。

+１99…9,２０15个9））＝_＿102__0１5＿_.2．（2017遵义六中三模)将自然数按以下规律排列：第一列第二列第三列第一行１４ 5…第二行 2 3 ６…第三行98７………表中数2在第二行第一列，与有序数对（2，1)对应;数5与(１,3)对应；数１4与（3,4)对应；根据这一规律,数2 014对应的有序数对为＿_(４５，１2)_＿.3．（2０17遵义十一中三模)已知：错误!未定义书签。

＝＼ｆ（1，3)；错误!=错误!;计算:错误!未定义书签。

=__错误!__；猜想：错误!未定义书签。

＝__错误!未定义书签。

_＿.4．（天水中考)观察下列运算过程:S=1＋3＋32＋33+…＋3２ 012+32 01３①，①×3得3S=3+32＋33+…+32 ０１3+32 014 ②,②－①得2S＝32014－1,S＝错误!未定义书签。

中考数学复习专题3：开放性问题(含详细参考答案)

中考数学复习专题三：开放性问题一、中考专题诠释开放型问题是相对于有明确条件和明确结论的封闭型问题而言的，它是条件或结论给定不完全、答案不唯一的一类问题．这类试题已成为近年中考的热点，重在考查同学们分析、探索能力以及思维的发散性，但难度适中．根据其特征大致可分为：条件开放型、结论开放型、方法开放型和编制开放型等四类．二、解题策略与解法精讲解开放性的题目时，要先进行观察、试验、类比、归纳、猜测出结论或条件，然后严格证明；同时，通常要结合以下数学思想方法：分类讨论，数形结合，分析综合，归纳猜想，构建数学模型等。

三、中考考点精讲考点一：条件开放型条件开放题是指结论给定，条件未知或不全，需探求与结论相对应的条件．解这种开放问题的一般思路是：由已知的结论反思题目应具备怎样的条件，即从题目的结论出发，逆向追索，逐步探求．例1 （•义乌市）如图，在△ABC中，点D是BC的中点，作射线AD，在线段AD及其延长线上分别取点E、F，连接CE、BF．添加一个条件，使得△BDF≌△CDE，并加以证明．你添加的条件是．（不添加辅助线）．考点：全等三角形的判定。

专题：开放型。

分析：由已知可证∠ECD﹦∠FBD，又∠EDC﹦∠FDB，因为三角形全等条件中必须是三个元素，并且一定有一组对应边相等．故添加的条件是：DE=DF（或CE∥BF或∠ECD=∠DBF 或∠DEC=∠DFB等）；解答：解：（1）添加的条件是：DE=DF（或CE∥BF或∠ECD=∠DBF或∠DEC=∠DFB等）．（2）证明：在△BDF和△CDE中∵∴△BDF≌△CDE．点评：三角形全等的判定是中考的热点，一般以考查三角形全等的方法为主，判定两个三角形全等，先根据已知条件或求证的结论确定三角形，然后再根据三角形全等的判定方法，看缺什么条件，再去证什么条件．考点二：结论开放型：给出问题的条件，让解题者根据条件探索相应的结论并且符合条件的结论往往呈现多样性，这些问题都是结论开放问题．这类问题的解题思路是：充分利用已知条件或图形特征，进行猜想、类比、联想、归纳，透彻分析出给定条件下可能存在的结论，然后经过论证作出取舍．例2 （•宁德）如图，点E、F分别是AD上的两点，AB∥CD，AB=CD，AF=DE．问：线段CE、BF有什么数量关系和位置关系？并加以证明．考点：全等三角形的判定与性质；平行线的性质；平行线的判定与性质。

2023中考数学开放探究型压轴大题(最新模拟50道)学生版

2023中考数学开放探究型压轴大题一、解答题1.(2023春·陕西延安·九年级专题练习)如图1，在Rt △ABC 中，∠B =90°，AB =4，BC =2，点D 、E 分别是边BC 、AC 的中点，连接DE ．将△CDE 绕点C 逆时针方向旋转，记旋转角为α．(1)问题发现①当α=0°时，AE BD =______；②当α=180°时，AE BD=______．(2)拓展探究试判断：当0°≤α<360°时，AE BD的大小有无变化？请仅就图2的情形给出证明．(3)问题解决△CDE 绕点C 逆时针旋转至A 、B 、E 三点在同一条直线上时，请直接写出线段BD 的长______．2.(2023春·河南驻马店·九年级驻马店市第二初级中学校考开学考试)点E是矩形ABCD边AB延长线上一动点(不与点B重合)，在矩形ABCD外作Rt△ECF其中∠ECF=90°，过点F作FG⊥BC 交BC的延长线于点G，连接DF交CG于点H．(1)发现如图1，若AB=AD，CE=CF，猜想线段DH与HF的数量关系是(2)探究如图2，若AB=nAD，CF=nCE，(1)中的猜想是否仍然成立？若成立，请给予证明；若不成立，请说明理由．(3)拓展在(2)的基础上，若FC的延长线经过AD的三等分点，且AD=3，AB=4，请直接写出线段EF的值3.(2023·河北·模拟预测)在平面直角坐标系xOy中，⊙O的半径是10，A，B为⊙O外两点，AB= 22．给出如下定义：平移线段AB，使平移后的线段A′B′成为⊙O的弦(点A′，B′分别为点A，B 的对应点)，线段AA′长度的最小值成为线段AB到⊙O的“优距离”．(1)如图1，⊙O中的弦P1P2、P3P4是由线段AB平移而得，这两条弦的位置关系是；在点P1，P2，P3，P4中，连接点A与点的线段长度等于线段AB到⊙O的“优距离”；(2)若点A(0，7)，B(2，5)，线段AA′的长度是线段AB到⊙O的“优距离”，则点A′的坐标为；(3)如图2，若A，B是直线y=-x+6上两个动点，记线段AB到⊙O的“优距离”为d，则d的最小值是；请你在图2中画出d取得最小值时的示意图，并标记相应的字母．4.(2023春·全国·八年级期中)如图1，在矩形ABCD中，AB=a，BC=6，动点P从B出发沿射线BC方向移动，作△PAB关于直线PA的对称△PAB′．(1)如图2，当点P在线段BC上运动时，直线PB′与CD相交于点M，连接AM，若∠PAM=45°，请直接写出∠B′AM和∠DAM的数量关系；(2)在(1)的条件下，请求出此时a的值：(3)当a=8时，①如图3，当点B′落在AC上时，请求出此时PB的长；②当点P在BC的延长线上时，请直接写出△PCB′是直角三角形时PB的长度．5.(2023春·广东深圳·八年级统考阶段练习)已知△ABC是边长为4的等边三角形，点D是射线BC上的动点，将AD绕点A逆时针方向旋转60°得到AE，连接DE．(1)如图1，猜想△ADE是什么三角形？；(直接写出结果)(2)如图2，点D在射线CB上(点C的右边)移动时，证明∠BCE+∠BAC=180°．(3)点D在运动过程中，△DEC的周长是否存在最小值？若存在．请求出△DEC周长的最小值；若不存在，请说明理由．6.(2023·山东济南·统考一模)如图1，已知正方形AFEG与正方形ABCD有公共顶点A，点E在正方形ABCD的对角线AC上(AG<AD).(1)如图2，正方形AFEG绕A点顺时针方向旋转α(0°<α<90°)，DG和BF的数量关系是，位置关系是；(2)如图3，正方形AFEG绕A点逆时针方向旋转α(0°<α<90°)，求CEDG的值以及直线CE和直线DG所夹锐角的度数；(3)如图4，AB=8，点N在对角线AC上，CN=22，将正方形AFEG绕A顺时针方向旋转α(0°<α<360°)，点M是边CD的中点，过点M作MH∥DG交EC于点H；在旋转过程中，线段NH的长度是否变化？如果不变，请直接写出NH的长度；如果改变，请说明理由.7.(2023春·全国·八年级期中)如图1，D、E、F是等边三角形ABC中不共线三点，连接AD、BE、CF，三条线段两两分别相交于D、E、F．已知AF=BD，∠EDF=60°．(1)证明：EF=DF；(2)如图2，点M是ED上一点，连接CM，以CM为边向右作△CMG，连接EG．若EG=EC+ EM，CM=GM，∠GMC=∠GEC，证明：CG=CM．(3)如图3，在(2)的条件下，当点M与点D重合时，若CD⊥AD，GD=4，请问在△ACD内部是否存在点P使得P到△ACD三个顶点距离之和最小，若存在请直接写出距离之和的最小值；若不存在，试说明理由．8.(2023春·重庆南岸·九年级重庆市珊瑚初级中学校校联考阶段练习)已知△ABC为等边三角形，D是边AB上一点，连接CD，点E为CD上一点，连接BE．(1)如图1，延长BE交AC于点F，若∠ABF=15°，BF=6，求AF的长；(2)如图2，将△BEC绕点C顺时针旋转60°到△AGC，延长BC至点H，使得CH=BD，连接AH交CG于点N，猜想线段CE，GN，DE之间存在的数量关系，并证明你的猜想；(3)如图3，AB=8，点H是BC上一点，且BD=2CH，连接DH，点K是AC上一点，CK=AD，连接DK，BK，将△BKD沿BK翻折到△BKQ，连接CQ，当△ADK的周长最小时，直接写出△CKQ 的面积．9.(2023·福建三明·校考一模)在矩形ABCD中，连接AC，线段AE是线段AC绕点A逆时针旋转90°得到，平移线段AE得到线段DF(点A与点D对应，点E与点F对应)，连接BF，分别交AC，CE于点M，N，连接EF．(1)求证：BN=FN；(2)求∠ABF的大小；(3)若BM=x，FN=y，求矩形ABCD的面积(用含有x，y的式子表示)．10.(2023·湖北省直辖县级单位·校联考一模)如图，正方形ABCD的对角线AC，BD相交于点O.将∠AOB绕点O沿逆时针方向旋转α0°≤α<90°得到∠EOF，OE，OF分别交AB，BC于点E，F，连接EF交OB于点G．(1)求证：①△OEF是等腰直角三角形；②△COF∽△BFG；(2)在旋转过程中，探究线段AC，EF，OG的数量关系，并说明理由；(3)若AB=3BE，OE=5，求线段OG，BF的长度．11.(2023·江苏盐城·统考一模)【问题思考】如图1，点E是正方形ABCD内的一点，过点E的直线AQ，以DE为边向右侧作正方形DEFG，连接GC，直线GC与直线AQ交于点P，则线段AE与GC之间的关系为．【问题类比】如图2，当点E是正方形ABCD外的一点时，【问题思考】中的结论还成立吗？若成立，请证明你的结论；若不成立，请说明理由；【拓展延伸】如图3，点E是边长为6的正方形ABCD所在平面内一动点，【问题思考】中其他条件不变，则动点P 到边AD的最大距离为(直接写出结果)．12.(2023春·安徽合肥·八年级合肥市五十中学西校校考期中)(1)如图1，在边长为1个单位长度的小正方形组成的网格中，△ABC的三个顶点均在格点上，现将△ABC绕点A按顺时针方向旋转90°，点B 的对应点为B ，点C的对应点为C ，连接BB ，如图所示则∠AB B=．(2)如图2，在等边△ABC内有一点P，且PA=2，PB=3，PC=1，如果将△BPC绕点B逆时针旋转60°得出△BP A，求∠BPC的度数和PP 的长；(3)如图3，将(2)题中“在等边△ABC内有一点P”改为“在等腰直角三角形ABC内有一点P”，且BA=BC，PA=6，BP=4，PC=2，求∠BPC的度数．13.(2023春·重庆合川·九年级重庆市合川中学校考阶段练习)如图1，△ABC与△EDC为等腰直角三角形，AC=BC=6，DE=DC=2，∠ACB=∠CDE=90°，将△EDC绕着点C旋转．(1)如图2，在旋转过程中，当A、C、E三点共线(E在AC延长线上)时，连接BE，过D点作AE的垂线交AE于点G，交BE于点F，求BF的长；(2)如图3，在旋转过程中，连接AE、BE，过点D作DF⊥AE于点G，交BE于点F，请写出EF与BF的数量关系并证明．(3)如图4，在(2)的条件下，连接CF、AF，当AF最小时，请直接写出△ACF的面积．14.(2023春·湖北十堰·九年级统考阶段练习)如图1，在△ABC中，∠BAC=90°，AB=AC，过点A作AD⊥BC于点D，点M为线段AD上一点(不与A，D重合)，在线段BD上取点N，使DM=DN，连接AN，CM．(1)观察猜想：线段AN与CM的数量关系是，AN与CM的位置关系是；(2)类比探究：将△DMN绕点D旋转到如图2所示的位置，请写出AN与CM的数量关系及位置关系，并就图2的情形说明理由；(3)问题解决：已知AD=32，DM=3，将△DMN绕点D旋转，当以A、D、M、N四点为顶点的四边形为平行四边形时，直接写出BN的长．15.(2023·河南商丘·校考一模)综合与实践二轮复习中，刘老师以“最值问题”为专题引导同学们进行复习探究．问题模型：等腰三角形ABC，∠BAC=120°，AB=AC=2，(1)探究1：如图1，点D为等腰三角形ABC底边BC上一个动点，连接AD，则AD的最小值为，判断依据为；(2)探究2：在探究1的结论下，继续探究，作∠BAD的平分线AE交BC于点E，点F，G分别为AE，AD上一个动点，求DF+FG的最小值；(3)探究3：在探究1的结论下，继续探究，点M为线段CD上一个动点，连接AM，将AM顺时针旋转60°，得到线段AN，连接ND，求线段DN的最小值．16.(2023·广东东莞·东莞市厚街海月学校校考模拟预测)如图(1)，在Rt△ABC中，∠ACB=90°，tan∠BAC=3．点D是BC边上任意一点(不与B，C重合)，连接AD，过点D作DE⊥AB于点E，连接CE，点F为AD中点，连接CF，EF．(1)当BD=2CD时，判断四边形CDEF的形状，并证明．(2)点D在线段BC上的什么位置时，△DEF的面积最大？请说明理由．(3)如图(1)中的△BDE绕点B旋转到如图(2)所示位置，得到△BD E ，使得点A在直线D E 上，连接CE ，点F 为AD 中点，AD 与BC交于点G，其他条件不变．求证：AE -D E =2CF ．17.(2023·福建厦门·福建省厦门第六中学校考一模)如图，在正方形ABCD中，点E在边AD上，点A关于直线BE的对称点为点F，连接AF，CF．设∠ABE=α，(1)试用含α的代数式表示∠DCF；(2)作CG⊥AF，垂足为G，点G在AF的延长线上，连接DG，试判断DG与CF的位置关系，并加以证明；(3)把△ABE绕点B顺时针旋转90°得到△CBH，点E的对应点为点H，连接BF，HF，若△HBF是等腰三角形，求sinα的值．18.(2023·北京海淀·清华附中校考模拟预测)在平面直角坐标系xOy中，对于线段AB，点P和图形G定义如下：线段AB绕点P逆时针旋转90°得到线段A B (A 和B 分别是A和B的对应点)，若线段AB 和A B 均在图形G的内部(包括边界)，则称图形G为线段AB关于点P的旋垂闭图．(1)如图，点C1,0．，D3,0①已知图形G1：半径为3的⊙O；G2：以O为中心且边长为6的正方形；G3：以线段OD为边的等边三角形．在G1，G2，G3中，线段CD关于点O的旋垂闭图是．②若半径为5的⊙O是线段CD关于点T t,0的旋垂闭图，求t的取值范围；(2)已知长度为4的线段AB在x轴负半轴和原点组成的射线上，若存在点Q2+a,2-a，使得对半径为2的⊙Q上任意一点P，都有线段AB满足半径为r的⊙O是该线段关于点P的旋垂闭图，直接写出r的取值范围．19.(2023春·四川成都·九年级四川省成都市第七中学初中学校校考阶段练习)如图，抛物线y=ax2+2ax+c经过B1，0两点，与x轴交于另一点A，点D是抛物线的顶点．，C0，3(1)求抛物线的解析式及点D的坐标；(2)如图1，连接AC，点E在直线AC上方的抛物线上，连接EA，EC，当△EAC面积最大时，求点E坐标；(3)如图2，连接AC、BC，在抛物线上是否存在点M，使∠ACM=∠BCO，若存在，求出M点的坐标；若不存在，请说明理由．20.(2023春·浙江宁波·九年级浙江省余姚市实验学校校考阶段练习)如图，直线y=-2x+10与x轴交于点A，与y轴交于点B，以OB为直径的⊙M交AB于另一点C，点D在⊙M上．分别过点O，B 作直线CD的垂线段，垂足为E，F，连接OC．(1)求点A，B，C的坐标．(2)当点D在直线BC右侧时，①求证：EC⋅CF=OE⋅BF；②求证：EC=DF．(3)CD与EF的距离和是否为定值？若是，请直接写出定值；若不是，请直接写出取到最小值时直线CD的解析式．21.(2023春·江苏无锡·九年级校考阶段练习)如图，平面直角坐标系中，已知A(-2，0)，B(4，0)，点C是在y轴的负半轴上，且△ABC的面积为9．(1)点C的坐标为；(2)P是第四象限内一点且横坐标为m，tan∠PBA=32．①连接AP，交线段BC于点D．根据题意画出示意图并求PDDA的值(用含m的代数式表示)；②连接CP，是否存在点P，使得∠BCO+2∠PCB=90°，若存在，求m的值；若不存在，请说明理由．22.(2023·北京海淀·中关村中学校考模拟预测)如图，矩形AOBC的顶点B，A分别在x轴，y轴上，点C坐标是5，4，D为BC边上一点，将矩形沿AD折叠，点C落在x轴上的点E处，AD的延长线与x 轴相交于点F(1)如图1，求点D的坐标；(2)如图2，若P是AF上一动点，PM⊥AC交AC于M，PN⊥CF交CF于N，设AP=t，FN=s，求s与t之间的函数关系式；(3)在(2)的条件下，是否存在点P，使△PMN为等腰三角形？若存在，请直接写出点P的坐标；若不存在，请说明理由23.(2023春·重庆沙坪坝·九年级重庆八中校考阶段练习)如图，在平面直角坐标系中，抛物线y=-x2+bx+c经过A0,1．直线AB交x轴于点C，P是直线AB上方且在对称轴右侧的一个，B4,-1动点，过P作PD⊥AB，垂足为D，E为点P关于抛物线的对称轴的对应点．(1)求抛物线的函数表达式；(2)当5PD+PE的最大值时，求此时点P的坐标和5PD+PE的最大值；(3)将抛物线y关于直线x=3作对称后得新抛物线y ，新抛物线与原抛物线相交于点F，M是新抛物线对称轴上一点，N是平面中任意一点，是否存在点N，使得以C，F，M，N为顶点的四边形是菱形，写出所有符合条件的点N的坐标，并写出求解点N的坐标的其中一种情况的过程．24.(2023·吉林长春·统考一模)如图，在△ABC中，∠C=90°，AC=10，BC=20，点D从点A出发，以每秒5个单位长度的速度沿AB方向运动，到点B停止．当点D与A、B两点不重合时，作DP⊥AC交AC于点P，作DQ⊥BC交BC于点Q．E为射线CA上一点，且∠CQE=∠BAC．设点D 的运动时间为t(秒)．(1)AB的长为．(2)求CQ的长．(用含有t的代数式表示)(3)线段QE将矩形PDQC分成两部分图形的面积比为1:3时，求t的值．(4)当t为某个值时，沿PD将以D、E、Q、A为顶点的四边形剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形．请直接写出所有符合上述条件的t值．25.(2023·广东云浮·校考一模)如图，在平面直角坐标系中，矩形AOBC的其中两边分别在坐标轴上，它的两条对角线交于点E，其中OA=6cm，OB=8cm，动点M从点C出发，以1cm/s的速度在CB上向点B运动，动点N同时从点B出发，以2cm/s的速度在BO上向点O运动．当其中一个动点到达终点时，它们同时停止运动．设它们运动时间是ts．(1)请直接写出BM，BN的长度；(2)当t为何值时，△MNB与△OBC相似；(3)记△MNE的面积为S，求出S与t的函数表达式，并求出S的最小值及此时t的值．26.(2023春·福建厦门·九年级厦门市松柏中学校考阶段练习)如图，以AB为直径的⊙O与AH相切于点A，点C在AB左侧圆弧上，弦CD⊥AB交⊙O于点D，连接AC，AD，点A关于CD的对称点为E，直线CE交⊙O于点F，交AH于点G．(1)求证：∠CAG=∠AGC；(2)当点E在AB上，连接AF交CD于点P，若EFCE =25，求DPCP的值；(3)当点E在射线AB上，AB=2，四边形ACOF中有一组对边平行时，求AE的长．27.(2023春·吉林长春·九年级校考阶段练习)在△ABC中，AB=AC=10，△ABC的面积为30，点D为AC的中点，动点P由点A以每秒5个单位的速度向点B运动，连接PD，以PD、DC为邻边作▱PDCQ，设▱PDCQ与△ABC的重叠部分面积为S，设点P的运动时间为t t>0．(1)tan A=(2)求点Q落在BC上时t的值．(3)在点P运动的过程中，求S与t之间的函数关系式．(4)若点A关于PD所在直线的对称点为A ，当点A 落在△ABC一边上的高上时，直接写出t的值．28.(2023·山西晋中·统考一模)问题情境：在综合实践课上，同学们以“正方形的旋转”为主题开展活动．如图①，四边形ABCD和四边形EFGH都是正方形，边长分别是12和13，将顶点A与顶点E重合，正方形EFGH绕点A逆时针方向旋转，连接BF，DH．初步探究：(1)试猜想线段BF与DH的关系，并加以证明；(2)如图②，在正方形EFGH的旋转过程中，当点F恰好落在BC边上时，连接CG，求线段CG的长；(3)在图②中，若FG与DC交于点M，请直接写出线段MG的长．29.(2023·江苏无锡·校联考一模)抛物线y=ax2+bx+3过点A-1，0，顶点为C．，点B3，0(1)直接写出抛物线的表达式及点C的坐标；(2)如图1，点P在抛物线上，连接CP并延长交x轴于点D，连接AC，若△DAC是以AC为底的等腰三角形，求点P的坐标；(3)如图2，在(2)的条件下，点E是线段AC上(与点A，C不重合)的动点，连接PE，作∠PEF=∠CAB，边EF交x轴于点F，设点F的横坐标为m，求m的最大值．30.(2022春·上海徐汇·九年级统考期中)已知⊙O的直径AB=4，点P为弧AB上一点，连接PA、PO，点C为劣弧AP上一点(点C不与点A、P重合)，连接BC交PA、PO于点D、E．(1)如图，当AD=DP时，求DEEB；(2)当点C为劣弧AP的中点，且△EDP与△AOP相似时，求∠ABC的度数；(3)当AD=2DP，且△BEO为直角三角形时，求BC的长．31.(2022·广东东莞·一模)如图，△ADE 由ΔABC 绕点A 按逆时针方向旋转90°得到，且点B 的对应点D 恰好落在BC 的延长线上，AD ，EC 相交于点P ．(1)求∠BDE 的度数；(2)F 是EC 延长线上的点，且∠CDF =∠DAC ．①判断DF 和PF 的数量关系，并证明；②求证：EP PF =PC CF．32.(2023春·山东东营·九年级东营市胜利第一初级中学校考阶段练习)(1)问题发现：如图①，△ABC和△ADE均为等边三角形，点A,D,E在同一直线上，连接BD,CE．①线段BD,CE之间的数量关系为；②∠BEC的度数为．(2)拓展探究：如图②，△ABC和△ADE均为等腰直角三角形，∠ACB=∠AED=90°，点B,D,E在同一直线上，连接BD,CE，求BDCE的值及∠BEC的度数．(3)解决问题：如图③，在△ABC和△ADE中，∠BAC=∠DAE=90°，∠B=∠ADE=30°，AC与DE相交于点F，点D在BC上，AD=3BD，求DFCF的值．33.(2023春·辽宁本溪·九年级统考阶段练习)如图(1)，在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=AC，EC=DC，点E在△ABC内部，直线AD与BE相交于点F．小明和小军想要探究线段AF，BF，CF之间存在怎样的数量关系．(1)问题探究：他们先将问题特殊化如图(2)，当点D，F重合时，直接写出一个等式，表示AF，BF，CF之间的数量关系；(2)再探究一般情形如图(1)，当点D，F不重合时，(1)中的结论是否成立．若成立请证明，若不成立请写出正确结论并说明理由．(3)问题拓展：如图(3)，在△ABC和△DEC中，∠ACB=∠DCE=90°，BC=kAC，EC=kDC(k是常数)，点E在△ABC内部，直线AD与BE交于点F．直接写出一个等式，表示线段AF，BF，CF 之间的数量关系．34.(2023·河南洛阳·统考一模)综合与实践综合与实践课上，老师让同学们以“正方形的折叠”为主题开展数学活动．(1)操作判断操作一：折叠正方形纸片ABCD，使顶点A落在边DC上点P处，得到折痕EF，把纸片展平；(如图1)操作二：折叠正方形纸片ABCD，使顶点B也落在边DC上点P处，得到折痕GH，GH与EF交于点O．连接OA，OB，OP．根据以上操作，直接写出图2中与OP相等的两条线段和．(2)探究发现把图2中的纸片展平，得到图3，小亮通过观察发现无论点P在线段DC上任何位置，线段OE和线段OF始终相等，请你直接用第一问发现的结论帮小亮写出完整的证明过程．(3)拓展应用已知正方形纸片ABCD的边长为6cm，在以上的探究过程中，当点O到AB距离是73cm时，请直接写出PC的长．35.(2023春·江苏南京·八年级校考期中)如图，将△ABC纸片沿中位线EH折叠，使点A的对称点D落在BC边上，再将纸片分别沿等腰△BED和等腰△DHC的底边上的高线EF，GH折叠，折叠后的三个三角形拼合形成一个矩形．类似地，对多边形进行折叠，若翻折后的图形恰能拼成一个无缝隙、无重叠的矩形，这样的矩形称为叠合矩形．(1)将▱ABCD纸片按图①的方式折叠成一个叠合矩形AEFG，则操作形成的折痕分别是线段∶S▱ABCD=．，；S矩形AEFG(2)▱ABCD纸片还可以按图②的方式折叠成一个叠合矩形EFGH，若EF=5，EH=12，求AD的长．(3)如图③，四边形ABCD纸片满足AD∥BC，AD<BC，AB⊥BC，AB=8，CD=10.小明把该纸片折叠，得到叠合正方形．请你帮助画出叠合正方形的示意图，并求出AD，BC的长．36.(2023·吉林长春·校联考一模)如图，BD是▱ABCD的对角线，AB⊥BD，BD=8cm，AD=10cm．动点P从点D出发，以5cm/s的速度沿DA运动到终点A，同时动点Q从点B出发，沿折线BD-DC运动到终点C，在BD、DC上分别以8cm/s、6cm/s的速度运动，过点Q作QM⊥AB，交射线AB于点M，连结PQ；以PQ与QM为边作▱PQMN，设点P的运动时间为t s t>0，▱PQMN 与▱ABCD重叠部分图形的面积为S cm2．(1)AP=cm(用含t的代数式表示)．(2)当点N落在边AB上时，求t的值．(3)当点Q在线段DC上运动时，t为何值时，S有最大值？最大值是多少？(4)连结NQ，当NQ与△ABD的一边平行时，直接写出t的值．37.(2023·江苏淮安·统考一模)【基础模型】：如图1，在△ABC中，D为AB上一点，∠ACD=∠B，求证：AC2=AD⋅AB．【尝试应用】：如图2，在平行四边形ABCD中，E为BC上一点，F为CD延长线上一点，∠BFE=∠A，若BF=6，BE=4，求AD的长．【更上层楼】：如图，在菱形ABCD中，E是直线AB上一点，F是菱形ABCD内一点，EF⎳AC，AC=2EF，∠BAD，AE=2，DF=5，请直接写出菱形ABCD的边长．∠EDF=1238.(2023·广东深圳·统考一模)将正方形ABCD的边AB绕点A逆时针旋转至AE，记旋转角为α，连接BE，过点B作BF⊥直线DE，垂足为点F，连接CF．(1)如图1，当α=30°时，△BEF的形状为，DECF的值为；(2)当90°<α<180°时，①(1)中的两个结论是否仍然成立？如果成立，请根据图2的情形进行证明；如果不成立，请说明理由；②如图3，正方形ABCD边长为4，DN⊥BE，CM⊥BE，在AE旋转的过程中，是否存在△AMN与△BEF相似？若存在，则CF的值为，若不存在，请说明理由．39.(2023年浙江省宁波市初中学业水平考试数学模拟试卷(探花卷))(1)【问题初探】如图1，E是正方形ABCD的边BC上一点，延长BA至点F，使AF=CE，连接DE，DF．求证：△DCE≌△DAF．(2)【问题再探】如图2，E，M分别是正方形ABCD的边BC，AB上一点，分别过点M，E作MP⊥CD于点P，EQ⊥AD于点Q，线段QE，MP相交于点N．连接DM，DE，ME，PQ，若∠MDE= 45o．①求证：AM+CE=ME．②探究△NME和△NPQ的面积关系，并说明理由．(3)【问题延伸】如图3，在正方形ABCD中，E，M分别是射线CB，BA上一点，【问题再探】中的其余条件不变，请直接判断△NME和△NPQ的面积关系是否仍成立．40.(2023·湖南·校联考一模)定义：有一组邻边相等且对角互补的四边形称为“等补四边形”．(1)下列选项中一定是“等补四边形”的是；A.平行四边形；B.矩形；C.正方形；D.菱形(2)如图1，在边长为a的正方形ABCD中，E为CD边上一动点(E不与C、D重合)，AE交BD于点F，过F作FH⊥AE交BC于点H．①试判断四边形AFHB是否为“等补四边形”并说明理由；②如图2，连接EH，求△CEH的周长；③若四边形ECHF是“等补四边形”，求CE的长．41.(2023春·吉林长春·九年级校考阶段练习)如图，在△ABC中，∠ACB=90°，AC=6，BC=8，D为边AB的中点．动点P从点B出发以每秒1个单位的速度沿BA运动到终点A．连结CP，作点D关于CP的对称点D ，连结PD ，设点P的运动时间为t秒．(1)点C、D之间的距离为．(2)用含t的代数式表示PD 的长．(3)当PD ⊥AB时，求△BCP的面积．(4)当点D 在△ABC内部时，直接写出t的取值范围．42.(2023春·四川成都·九年级四川省成都市第七中学初中学校校考阶段练习)模型建立：(1)如图1，在△ABC中，D是AB上一点，∠ACD=∠B，求证：AC2=AD⋅AB；∠BAD，射(2)类比探究：如图2，在菱形ABCD中，E、F分别为边BC、DC上的点，且∠EAF=12线AE交DC的延长线于点M，射线AF交BC的延长线于点N．①求证：FA2=FC⋅FM；②若AF=4，CF=2，AM=10，求FN的长．43.(2023春·河南商丘·九年级校考阶段练习)如图，AB是半圆O的直径，点C是半圆上一点(不与点A，B重合)，连接AC，BC．(1)请在图1中用无刻度的直尺和圆规作出∠ABC的平分线，交半圆O于点D．(保留作图痕迹，不写做法)(2)如图2，在(1)的条件下，过点D作半圆的切线，交BC的延长线于点F，作DE⊥AB于点E，连接BD．①求证：△BED≌△BFD．②若AB=8，BC=2CF，请直接写出DE的长．44.(2023春·广东广州·九年级华南师大附中校考阶段练习)四边形ABCD是正方形，E是直线BC上一点，连接AE，在AE右侧，过点E作射线EP⊥AE，F为EP上一点．(1)如图1，若点E是BC边的中点，且EF=AE，连接CF，则∠DCF=°；(2)如图2，若点E是BC边上一点(不与B，C重合)，∠DCF=45°，判断线段EF与AE的数量关系，并说明理由；(3)若正方形边长为1，且EF=AE，当AF+BF取最小值时，求△BCF的面积．45.(2023·湖北武汉·校联考一模)问题提出：如图(1)，在△ABC中，∠BAC=90°，∠ABC=30°，D是△ABC内一点，AD⊥CD，∠ACD=30°，若AD=1，连接BD，求BD的长．(1)问题探究：请你在图(1)中，用尺规作图，在AB左侧作△ABE，使△ABE∽△ACD．(用直尺、圆规作图，保留作图痕迹，不写作法，不说明理由)(2)根据(1)中作图，你可以得到CD与BE的位置关系是；你求得BD的长为；(3)问题拓展：如图(2)，在△ABC中，∠BAC=90°，∠ABC=30°，D是△ABC内一点，若AD=7，BD=27，CD=4，求BC的长．46.(2023春·河北保定·九年级统考阶段练习)如图1，已知直线l 1：y =x +3，点B 0,b 在直线l 1上．y =mx +n 是过定点P 1,0 的一簇直线．嘉淇用绘图软件观察m 与n 的关系．记y =mx +n 过点B 时的直线为l 2．(1)求b 的值及l 2的解析式；(2)探究m 与n 的数量关系；当y =mx +n 与y 轴的交点为0,1 时，记此时的直线为l 3，l 3与l 1的交点记为A ，求AB 的长；(3)当y =mx +n 与直线l 1的交点为整点(横、纵坐标均为整数)，且m 的值也为整数时，称y =mx +n 为“美好直线”．①在如图2所示的视窗下(-2.5≤x ≤2.5，-2.5≤y ≤2.5)，求y =mx +n 为“美好直线”时m 的值；②视窗的大小不变，改变其可视范围，且变化前后原点O 始终在视窗中心．现将图2中坐标系的单位长度变为原来的1k，使得在视窗内能看到所有“美好直线”与直线y =x +3的交点，求k 的最小整数值．47.(2023·山东济南·统考一模)(1)①如图1，等腰△ABC(BC为底)与等腰△ADE(DE为底)，∠BAC=∠DAE，则BD与CE的数量关系为；②如图2，矩形ABCD中，AB=3，AD=4，则sin∠DAC=；(2)如图3，在(1)②的条件下，点E在线段CD上运动，将AE绕点A顺时针旋转得到AF，使∠EAF=∠DAC，连接CF．当AE=32时，求CF的长度；(3)如图4，矩形ABCD中，若AB=23，AD=6，点E在线段CD上运动，将AE绕点A顺时针旋转得到AF，旋转角等于∠BAC，连结CF，AE中点为G，CF中点为H，若GH=13，直接写出DE的长．48.(2023·浙江温州·统考一模)如图，点E，F分别为矩形ABCD边AD，CD上的点，以BE为直径作⊙O交BF于点G，且EF与⊙O相切，连结EG．(1)若AE=EG，求证：△ABE≌△GBE．(2)若AB=2，tan∠EBF=12．①求DE的长．②连结AG，若△ABG是以AG为腰的等腰三角形，求所有满足条件的BC的长．(3)连结CG，若CG的延长线经过点A，且ED=EG，求CGEF的值．49.(2023春·山东济南·九年级校考阶段练习)小明同学和小红同学分别拿着一大一小两个等腰直角三角板，可分别记作△ABC和△ADE，其中∠BAC=∠DAE=90°．问题的产生：两位同学先按照图1摆放，点D，E在AB、AC上，发现BD和CE在数量和位置关系分别满足BD= CE，BD⊥CE．问题的探究：(1)将△ADE绕点A逆时针旋转一定角度，如图2，点D在△ABC内部，点E在△ABC外部，连接BD，CE，上述结论依然成立吗？如果成立，请证明，如果不成立，并说明理由．问题的延伸：继续将△ADE绕点A逆时针旋转，如图3，点D、E都在△ABC的外部，连接BD，CE，CD，EB，BD和CE相交于点H．(2)若BD=19，求四边形BCDE的面积．(3)若AB=3，AD=2，设CD2=x，EB2=y，直接写出y和x的函数关系式．50.(2023·湖南长沙·校联考模拟预测)对于平面直角坐标系xOy中的图形W1和图形W2，给出如下定义：在图形W1上存在两点A，B(点A，B可以重合)，在图形W2上存在两点M，N(点M，N可以重合)使得AM=2BN，则称图形W1和图形W2满足限距关系．(1)如图1，点C(3,0),D(0,-1),E(0,1)，点P在线段CE上运动(点P可以与点C，E重合)，连接OP,DP．①线段DP的最小值为，最大值为；线段OP的取值范围是；②点O与线段DE(填“是”或“否”)满足限距关系；(2)在(1)的条件下，如图2，⊙O的半径为1，线段FG与x轴、y轴正半轴分别交于点F，G，且FG∥EC，若线段FG与⊙O满足限距关系，求点G纵坐标的取值范围；(3)⊙O的半径为r(r>0)，点H，K是⊙O上的两个点，分别以H，K为圆心，3为半径作圆得到⊙H和⊙K，若对于任意点H，K，⊙H和⊙K都满足限距关系，直接写出r的取值范围；。

2022年中考数学专题复习：开放探究题

2022年中考数学专题复习：开放探究题1．点E 是矩形ABCD 边AB 延长线上一动点（不与点B 重合），在矩形ABCD 外作Rt△ECF 其中△ECF ＝90°，过点F 作FG △BC 交BC 的延长线于点G ，连接 DF 交CG 于点H ．(1)发现如图1，若AB ＝AD ，CE ＝CF ，猜想线段DH 与HF 的数量关系是______ (2)探究如图2，若AB ＝nAD ，CF ＝nCE ，（1）中的猜想是否仍然成立？若成立，请给予证明；若不成立，请说明理由． (3)拓展在（2）的基础上，若FC 的延长线经过AD 的三等分点，且AD ＝3，AB ＝4，请直接写出线段EF 的值2．如图1，在Rt ABC 中，90B ∠=︒，4AB =，2BC =，点D 、E 分别是边BC 、AC 的中点，连接DE ．将CDE △绕点C 逆时针方向旋转，记旋转角为α．(1)问题发现△当0α=︒时，AE BD =________；△当180α=︒时，AEBD=______． (2)拓展探究试判断：当0360α︒≤<︒时，AEBD的大小有无变化？请仅就图2的情形给出证明． (3)问题解决CDE △绕点C 逆时针旋转至A 、B 、E 三点在同一条直线上时，请直接写出线段BD 的长________．3．如图1，在Rt△ABC 中，△ACB ＝90°，CA ＝CB ，点D 为AB 边上一动点，连接CD ，并将CD 绕点C 逆时针旋转90°得到CE ，连接BE 、DE ，点F 为DE 中点，连接BF ．（1）求证：△ACD ≅△BCE ；（2）如图2所示，在点D 的运动过程中，当ADn BD=时（n ＞1），分别延长AC 、BF 相交于G ：△当32n =时，求CG 与AB 的数量关系； △当AD BD ＝n 时（n ＞1），ABCG＝．（3）当点D 运动时，在线段CD 上存在一点M ，使得AM +BM +CM 的值最小，若CM ＝2，则BE ＝．4．如图，在Rt △ABC 中，△ACB ＝90°，AC ＝6，△ABC ＝30°，点D ，E 分别在边AB ，AC 上，在线段ED 左侧构造Rt △DEF ，使△DEF △△BCA ．（1）如图1，若AD ＝BD ，点E 与点C 重合，DF 与BC 相交于点H ．求证：2CH ＝BH ．（2）当AE ＝2时，连接BF ，取BF 的中点G ，连接DG ． △如图2，若点F 落在AC 边上，求DG 的长．△是否存在点D ，使得△DFG 是直角三角形？若存在，求AD 的长；若不存在，试说明理由．5．【教材呈现】（1）如图1，在同一平面内，将两个全等的等腰直角三角形ABC 和AFG 摆放在一起，A 为公共顶点，△BAC ＝△G ＝90°，BC ＝6，若△ABC 固定不动，将△AFG 绕点A 旋转，边AF 、AG 与边BC 分别交于点D ，E （点D 不与点B 重合，点E 不与点C 重合）△求证：AE 2＝DE •BE ； △求BE •CD 的值；【拓展探究】（2）如图2，在△ABC 中，△C ＝90°，点D ，E 在边BC 上，△B ＝△DAE ＝30°，且34AD AE，请直接写出DE BC的值．6．（1）[问题发现]如图1，在Rt△ABC中，AB＝AC＝4，△BAC＝90°，点D为BC的中点，以CD为一条边作正方形CDEP，点E恰好与点A重合．则线段BE与AF的数量关系为；（2）[拓展研究]在（1）的条件下，如果正方形CDEF绕点C旋转，连接BE，CE，AF，线段BE与AF的数量关系有无变化？请就图2的情形给出证明；（3）[问题发现]当正方形CDEF旋转到B，E，F三点共线时候，直接写出线段AF的长．7．综合与实践在△ABC中，BD△AC于点D，点P为射线BD上任一点（点B除外），连接AP，将线段P A绕点P顺时针方向旋转α，α=△ABC，得到PE，连接CE．（1）如图1，当BA=BC，且△ABC=60°时，BP与CE的数量关系是，BC与CE的位置关系是（2）如图2，当BA=BC，且△ABC=90°时，（1）中的结论是否成立？若成立，请予以证明；若不成立，请说明理由．（请选择图2，图3中的一种情况予以证明或说理）（3）在（2）的条件下，若AB=8，AP=CE的长．8．【问题情境】如图1，四边形ABCD是正方形，M是BC边上的一点，E是CD边的中点，AE平分△DAM．【探究展示】（1）请你判断AM，AD，MC三条线段的数量关系，并说明理由；（2）AM = DE + BM是否成立？若成立，请给出证明；若不成立，请说明理由．【拓展延伸】（3）若四边形ABCD是长与宽不相等的矩形，其他条件不变，如图2，探究展示（1）、（2）中的结论是否仍然成立？请分别作出判断，不需要证明．9．【背景】如图1，在△ABC中，AB＝AC，过点A的直线MN△BC，点D是直线MN 上的一动点，将射线DB绕着点D逆时针旋转，交线段AC于点P，使△BDP＝△BAC，试说明：DB＝DP．小丽提出了自己的想法：如图2在线段AB上取一点F，使DA＝DF，通过证明△BDF△△PDA可以解决问题．【尝试】△请你帮助小丽完成说理过程．△若AC＝6，BC＝4，AD＝3，求AP的长．【拓展】如图3，过点A的直线MN△BC，AB＝3 cm，AC＝4cm，点D是直线MN上一点，点P是线段AC上的一点，连接DP，使得△BDP＝△BAC，求DBDP的值．10．如图1，E是直线AB，CD内部一点，AB△CD，连接EA，ED．（1）探究猜想：△若∠A=30°，∠D=40°，则∠AED等于_______度；△若∠A=20°，∠D=60°，则∠AED等于_______度；△猜想图1中∠AED，∠EAB，∠EDC的关系并证明你的结论．（2）拓展应用：如图2，射线FE与矩形ABCD的边AB交于点E，与边CD交于点F，△△△△分别是被射线FE隔开的4个区域（不含边界，其中区域△、△位于直线AB上方，P是位于以上四个区域上的点，猜想：∠PEB，∠PFC，∠EPF的关系并选择其中一个证明．11．在△ABC中，AC＝BC，△ACB＝90°，点P为△ABC外一点，点P与点C位于直线AB异侧，连接AP，△APB＝45°，过点C作CD△P A，垂足为D．（1）当△ABP＝90°时，直接写出线段AP与CD的数量关系为AP＝_____________；（2）如图，当△ABP＞90°时．△试探究（1）中的结论是否成立；△在线段AP上取一点K，使得△ABK＝△ACD，画出图形并直接写出KPBP的值．12．如图1，已知两条直线AB，CD被直线EF所截，分别交于点E，点F，EM平分△AEF 交CD 于点M ，且△FEM =△FME ．（1）若2△AEF = △MFE ，求△AEF 的度数．（2）如图2，点G 是射线 MD 上一动点（不与点M ，F 重合），EH 平分△FEG 交CD 于点H ，过点H 作HN △EM 于点N ，设△EHN =α，△EGF = β． △当点G 在点F 的右侧时，若β= 50°，求α的度数；△当点G 在运动过程中，α 和β之间有怎样的数量关系？请写出你的猜想，并加以证明．13．已知：点E 是矩形ABCD 边AB 延长线上的一动点，在矩形ABCD 外作RtECF △，90ECF ∠=︒．FG BC ⊥交BC 的延长线于点G ，连接DF ，交CG 于点H ．（1）初步发现：如图1，若AB AD =，CE CF =．求证：DH HF =．（2）深入探究：如图2，若AB nAD =，CF nCE =．DH 与HF 是否仍然相等？若相等，进行证明；若不相等，写出新的数量关系并证明；（3）拓广延伸：在（2）的条件上，3AD =，4AB =，且射线FC 过边AD 的三等分点，直接写出线段EF 的长．14．【感知】如图△，在四边形AEFC 中，EB 、FD 分别是边AE 、CF 的延长线，我们把△BEF 、△DFE 称为四边形AEFC 的外角，若△A ＋△C ＝260°，则△BEF ＋△DFE ＝度．【探究】如图△，在四边形AECF 中，EB 、FD 分别是边AE 、AF 的延长线，我们把△BEC 、△DFC 称为四边形AECF 的外角，试探究△A 、△C 与△BEC 、△DFC 之间的数量关系．【结论】综合以上，请你用文字描述上述关系：．【应用】如图△，FM 、EM 分别是四边形AEFC 的外角△DFE 、△BEF 的平分线，若△A ＋△C ＝210°，求△M 的度数．15．ABC 中，AB AC =，ABC α∠=，过点A 作直线MN ，使//BC MN ，点D 在直线MN 上（不与点A 重合），作射线BD ，将射线BD 绕点B 顺时针旋转α后交直线AC 于点E ．（1）如图1，点D 在射线AN 上，60α=︒，求证：AB AD AE +=；（2）如图2，点D 在射线AN 上，45α=︒，线段AB ，AD ，AE 之间又有何数量关系？写出你的结论，并证明；（3）若30α=︒，15ABE ∠=︒，BC =AD 的长．16．综合与探究：如图△，在△ABC 中，△C ＞△B ，AD 是△BAC 角平分线．（1）探究与发现：如图△，AE △BC 于点E ，△若△B =20º， △C =70º，则△CAD =_______º， △DAE =_____º； △若△B =40º，△C =80ºº，则△DAE =_____º；△试探究△DAE 与△B 、△C 的数量关系，并说明理由．（2）判断与思考：如图△，F 是AD 上一点，FE △BC 于点E ，这时△DFE 与△B 、△C 又有怎样的数量关系？17．在ABC 中，AB AC =．（1）如图1、求证：B C ∠=∠：（2）如图2，D 为AB 上一点，连接CD ，E 为CD 中点，过点E 作EF CD ⊥于点E ，连接,FC FD ，求证：FC FD =；（3）如图3，在（2）的条件下，过点F 作FH AC ⊥于点H ，连接AF ，若AF△BC ，FH=4，CH=20，BD=10，求ADF 的面积18．如图1，四边形ABCD 为正方形，△AEF 为等腰直角三角形，△EAF ＝90°，连接BE、DF．（1）求证：△ABE△△ADF；（2）如图2，延长DF交AB于点G，交BE于点H，连结AH．△求△EHA的度数；△过点D作DM△HA交HA的延长线于点M，请你写出线段AM与BH之间的数量关系，并证明你的结论．19．在ABC中，AB＝AC，△BAC＝90°，点D在射线BC上（与B、C两点不重合），以AD为边作正方形ADEF，使点E与点B在直线AD的异侧，射线BA与直线CF相交于点G．（1）若点D在线段BC上，如图1，判断：线段BC与线段CG的数量关系，位置关系；（2）如图2，△若点D在线段BC的延长线上，（1）中判断线段BC与线段CG的数量关系与位置关系是否仍然成立，并说明理由；△当G为CF中点，BC＝2时，求正方形ADEF的面积（直接写出结果）.20．如图1，在正方形ABCD和正方形BEFG中，点A、B、E在同一直线上，连接DF，且点M是DF的中点，连接MC、MG．（1）在图1中，MC与MG的位置关系是，数量关系是；（2）如图2，将条件“正方形ABCD和正方形BEFG”改为“矩形ABCD和矩形BEFG”，其他条件不变，求证：MC＝MG；（3）如图3，若将条件“正方形ABCD和正方形BEFG”改为“菱形ABCD和菱形BEFG”，点A、B、E在同一直线上，连接DF，且点M是DF的中点，连接MC、MG，且△ABC＝△BEF＝60°求MCMG的值．。