弹性力学-极坐标求解.共80页
合集下载
弹性力学第七章平面问题的极坐标解
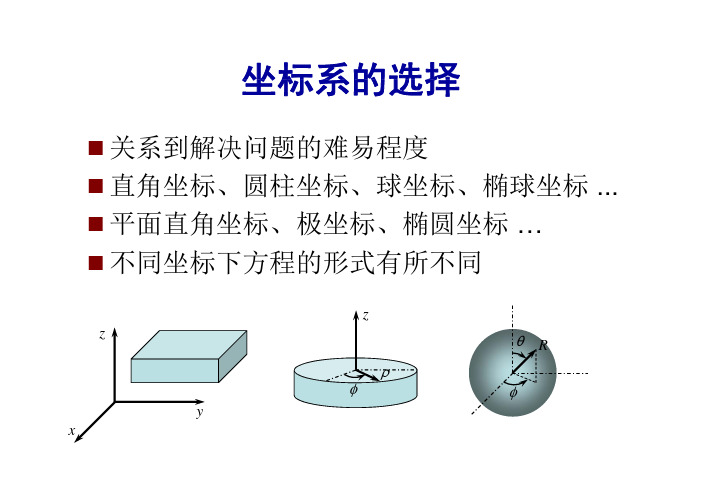
第七章 平面问题的极坐标解知识点极坐标下的应力分量 极坐标下的应变分量 极坐标系的 Laplace 算符 轴对称应力分量 轴对称位移和应力表达式 曲梁纯弯曲 纯弯曲位移与平面假设 带圆孔平板拉伸问题 楔形体问题的应力函数 楔形体应力 楔形体受集中力偶作用、内容介绍在弹性力学问题的处理时，坐标系的选择从本质上讲并不影响问题的求解， 但是坐标的选取直接影响边界条件的描述形式，从而关系到问题求解的难易程 度。
对于圆形，楔形，扇形等工程构件，采用极坐标系统求解将比直角坐标系统 要方便的多。
本章的任务就是推导极坐标表示的弹性力学平面问题基本方程， 且求解一些典型问题。
极坐标平衡微分方程 几何方程的极坐标表达 应力函数 轴对称位移 厚壁圆筒作用均匀压力 曲梁弯曲应力 曲梁作用径向集中力 孔口应力 楔形体边界条件 半无限平面作用集中力二、重点1、基本未知量和基本方程的极坐标形式；2、双调和方程的极坐标形式；3、轴对称应力与厚壁圆筒应力；4、曲梁纯弯曲、楔形体和圆孔等典型问题§7.1平面问题极坐标解的基本方程学习思路：选取极坐标系处理弹性力学平面问题，首先必须将弹性力学的基本方程以及边界条件通过极坐标形式描述和表达。
本节的主要工作是介绍基本物理量，包括位移、应力和应变的极坐标形式；并且将基本方程，包括平衡微分方程、几何方程和本构关系转化为极坐标形式。
由于仍然采用应力解法，因此应力函数的极坐标表达是必要的。
应该注意的是坐标系的选取与问题求解性质无关，因此弹性力学直角坐标解的基本概念仍然适用于极坐标。
学习要点:1、极坐标下的应力分量；2、极坐标平衡微分方程；3、极坐标下的应变分量；4、几何方程的极坐标表达；5、本构方程的极坐标表达；6极坐标系的LaPIaCe算符；7、应力函数。
1、极坐标下的应力分量为了表明极坐标系统中的应力分量，从考察的平面物体中分割出微分单元体ABCD ,其由两个相距茁的圆柱面和互成d「的两个径向面构成，如图所示在极坐标系中，用二表示径向正应力，用二表示环向正应力，「,和•二:分别表示圆柱面和径向面的切应力，根据切应力互等定理，.J=.二:。
弹性力学第三章极坐标
2
1
0
的系数均应等于0。由此得三个常微分方程,
第三章 平面问题的直角坐标解答
半逆解法
从而解出: f Ay 3 By 2 cy D,
3 2 f1 Ey Fy Gy, A y 5 B y 4 Hy 3 Ky 2 . f 2 10 6 式(b)中已略去 Φ 的一次式。
(b)
将式(b)代入式(a)，即得Φ 。
第三章 平面问题的直角坐标解答
半逆解法
⑷ 由 Φ 求应力。
在无体力下，应力公式如书中式( f ),
(g),(h)所示。 对称性条件─由于结构和荷载对称于
y轴，∴ Φ, σ x , σ y 应为 x 的偶函数， xy 为 x的奇函数，故 E F G 0 。
(e)
第三章 平面问题的直角坐标解答
逆解法
从而得出，在面力(e)作用下的解
答，就是上述 Φ 和应力。
逆解法没有针对性，但可以积累基
本解答。
第三章 平面问题的直角坐标解答
逆解法
例1 一次式 Φ =ax+by+c,对应于无体力， 无面力，无应力状态。 故应力函数中加减一次式，不影响应力。 2 例2 二次式 Φ ax2 bxy cy，分别表示常量 的应力和边界面力。如图示。
2a b b
o
2a
x
b
o
y b
x
2c
o
y
2c
x
y
第三章 平面问题的直角坐标解答
逆解法
例3 设图中所示的矩形长梁，l >>h，试考
F 察应力函数 Φ 3 xy (3h 2 4 y 2 )能解决什么 2h
样的受力问题？ o
《弹塑性力学》第七章 弹性力学平面问题的极坐标系解答.ppt
x
应力：r, ,r= r 应变：r, ,r= r
P
y
位移：u r , u
2020/10/9
3
§7-1平面极坐标下的基本公式
直角坐标与极坐标之间关系:
x=rcos, y=rsin
r cos sin
x r x x
r r
r sin cos
y r y y
r
r
2 r
r )( f r
r
f 1
r
fr 0 0 f
fr ) r
2＝ 2 1 1 2
r 2 r r r 2 2
力的边界条件如前所列。
2020/10/9
14
§7-1平面极坐标下的基本公式
1.8 应力函数解法
当体力为零 fr=f=0时, 应力法基本方程中的应
力分量可以转为一个待求的未知函数 ( r, ) 表示,而应力函数 ( r, ) 所满足方程为
16
§7-2 轴对称问题
2.1 轴对称问题的特点
1.截面的几何形状为圆环、圆盘。
2.受力和约束对称于中心轴,因此，可知体 积力分量 f=0 ； 在边界上 r=r0 ：F 0， u （0 沿环向的受力和约束为零） 。
3.导致物体应力、应变和位移分布也是轴 对称的：
2020/10/9
17
§7-2 轴对称问题
上式代入平衡微分方程可得到用位移表 示的平衡微分方程,即位移法的基本方程。
r
r
1 r r
( r
r
)
Kr
0
r
r
1 r
2 r
r
K
0
力的边界条件也同样可以用位移表示。
2020/10/9
弹性力学 第四章 平面问题的极坐标解答
s = sσ
(3) 多连体中的位移单值条件
§ 4-4 应力分量的坐标变换式
·问题的提出
工程中有些问题, 用极坐标计算方便, 但应力分量用直角坐 标表述更直观. 反之也存在.
由此需要对应力分量进行坐标变换.
§ 4-4 应力分量的坐标变换式
·坐标变换
已知 σx、σy、τxy , 求 σρ、συ、τρυ？
y
fρ τ + ∂τρυdρ ρυ ∂ρ ∂συ dυ συ+ ∂σρ ∂υ σρ+ dρ ∂τυρ C ∂ρ dυ τυρ+ ∂υ
B
fυ
§ 4-1 极坐标中的平衡微分方程
·平衡微分方程
x
υ dυ ρ
Σ Fρ = 0 :
συ
A
σρ τρυ P τυρ
∂σρ σρ+ dρ (ρ+dρ)dυ - σρ ρdυ ∂ρ ∂συ dυ - συ+ dυ dρ sin ∂υ 2 + τυρ+ - συ dρ sin
Σ Fυ = 0 :
συ = ?
§ 4-4 应力分量的坐标变换式
·坐标变换
συ = ?
将两坐标系下微元体组合
τyx σy σx συ
τυρ τxy
§ 4-4 应力分量的坐标变换式
·坐标变换
已知 σx、σy、τxy , 求 σρ、συ、τρυ？
O x
υ
τyx
σy σx
συ y
τυρ τxy
Σ Fυ = 0 :
O h/2 h/2 lqx源自(v)x=0, l = 0
应力边界条件： ( σy ) y=-h/2 = - q (τyx ) y=-h/2 = 0 ( σy ) y= h/2 = 0 (τyx ) y= h/2 = 0
弹性力学第七章平面问题的极坐标解
第七章 平面问题的极坐标解知识点极坐标下的应力分量 极坐标下的应变分量 极坐标系的 Laplace 算符 轴对称应力分量 轴对称位移和应力表达式 曲梁纯弯曲 纯弯曲位移与平面假设 带圆孔平板拉伸问题 楔形体问题的应力函数 楔形体应力 楔形体受集中力偶作用、内容介绍在弹性力学问题的处理时，坐标系的选择从本质上讲并不影响问题的求解， 但是坐标的选取直接影响边界条件的描述形式，从而关系到问题求解的难易程 度。
对于圆形，楔形，扇形等工程构件，采用极坐标系统求解将比直角坐标系统 要方便的多。
本章的任务就是推导极坐标表示的弹性力学平面问题基本方程， 且求解一些典型问题。
极坐标平衡微分方程 几何方程的极坐标表达 应力函数 轴对称位移 厚壁圆筒作用均匀压力 曲梁弯曲应力 曲梁作用径向集中力 孔口应力 楔形体边界条件 半无限平面作用集中力二、重点1、基本未知量和基本方程的极坐标形式；2、双调和方程的极坐标形式；3、轴对称应力与厚壁圆筒应力；4、曲梁纯弯曲、楔形体和圆孔等典型问题§7.1平面问题极坐标解的基本方程学习思路：选取极坐标系处理弹性力学平面问题，首先必须将弹性力学的基本方程以及边界条件通过极坐标形式描述和表达。
本节的主要工作是介绍基本物理量，包括位移、应力和应变的极坐标形式；并且将基本方程，包括平衡微分方程、几何方程和本构关系转化为极坐标形式。
由于仍然采用应力解法，因此应力函数的极坐标表达是必要的。
应该注意的是坐标系的选取与问题求解性质无关，因此弹性力学直角坐标解的基本概念仍然适用于极坐标。
学习要点:1、极坐标下的应力分量；2、极坐标平衡微分方程；3、极坐标下的应变分量；4、几何方程的极坐标表达；5、本构方程的极坐标表达；6极坐标系的LaPIaCe算符；7、应力函数。
1、极坐标下的应力分量为了表明极坐标系统中的应力分量，从考察的平面物体中分割出微分单元体ABCD ,其由两个相距茁的圆柱面和互成d「的两个径向面构成，如图所示在极坐标系中，用二表示径向正应力，用二表示环向正应力，「,和•二:分别表示圆柱面和径向面的切应力，根据切应力互等定理，.J=.二:。
弹性力学第4章-平面问题的极坐标解答
两面不平行, d 夹角为 φ; 两
ρ 面面积不等,分别为 ρdφ, ( ρ + d ρ) dφ. ρ从原点出发为正, 从 x 轴向 y 轴方向转动为正.
微分体上的作用力有: 微分体上的作用力有
体力-- f ρ , f φ , 以坐标正向为正. -应力---
作用力
±ρ
面, φ 面分别表示应力及其增量. ±
第一节 第二节 第三节 第四节 第五节
极坐标中的平衡微分方程 极坐标中的几何方程及物理方程 极坐标中的应力函数与相容方程 应力分量的坐标变换式 轴对称应力和相应的位移
第六节 第七节 第八节 第九节 第十节 例题
圆环或圆筒受均布压力 压力隧洞 圆孔的孔口应力集中 半平面体在边界上受集中力 半平面体在边界上受分布力
基本方程的区别. 对于圆形,弧形,扇形及由径向线和环向围成的物 体,宜用极坐标求解.用极坐标表示边界简单,使边界条 件简化.
在A内任一点(ρ, )取出一个微分体,考虑其平 衡条件. 微分体:由夹 角为d φ的两 径向线和距离 为d ρ的两环 向线围成.
§4-1 极坐标中的平衡微分方程
注意: 注意:
即 Φ是通过中间变量 ρ,φ ,为 x, y 的复合函数. 有: Φ = Φ ρ + Φ φ, Φ=Φρ +Φφ. 而
ρ x φ x y ρ y φ y sin cos ρ ρ = , = sin; = cos, . = ρ x y ρ y x x
代入,即得一阶导数的变换公式,
Φ sin Φ sinφ Φ=cosφ =(cosφ )Φ x ρ ρ φ ρ ρ φ
u = uρ cos u sin, v = uρ sin + u cos.
(c) (d)
弹性力学平面问题的极坐标解答课件
b
a
2
ln
a
b2
a
2
0
位移的确定
H, I, K待定
u
1 E
(1 )
A
(1 3 )B
2(1 )B(ln
1)
2(1
)C
I
sin
K
cos
u
4B
E
H
I
cos
K
sin
左端固定：(u )0 0
0,
(u ) 0 0
0,
u
0
0
0
常数的确定：
H
I
0,
K
1 E
极坐标下的双调和方程
代入协调方程，得到应力函数U需满足
的双调和方程
2
2
1
1
2
2
2
2U
2
1
U
1
2
2U
2
0
§7-2 轴对称应力及其位移
应力函数与无关，双调和方程为
d2
d 2
1
d
d
d2 U
d 2
1
dU
d
0
4
d4 U
d 4
23
d3 U
d 3
2
d2 U
d 2
dU
问题描述 任一截面上的弯矩：
M () F cos R tan F R sin
应力函数：
U f () sin
O
m
ba
F
x
n
y
f()的求解及应力表达式
微分方程及其通解
d2
d 2
1
d
d
1
2
d2 f
弹性力学-第八章 平面问题的极坐标解答
(2) 只有环向变形，无径向变形。 O
径向线段PA的相对伸长：
r2
PA PA PA
dr dr 0 dr （f）
径向线段PA的转角：
2
u
u dr r
dr
u
y
u r
d
B
B
rP
2
P
dr
u
2 A
x
A
u
（g） u
u
d
u r
dr
环向线段PB的相对伸长：
2
PB PB PB
BB PP PB
u
u d rd
xy
sin
2
x
y
2
x
y
2
cos 2
xy
sin
2
r
x
y
2
sin
2
xy
cos 2
第八章 平面问题的极坐标解答 §8.2 平面轴对称应力问题
§8.2 平面轴对称应力问题
A. 轴对称问题应力分量与协调方程
无体积力,且与θ无关.求解方法：
（1）应力分量
r
1 r
d
dr
d 2
dr 2
r 0
主 要内容
§8-1 §8-2 §8-3 §8-4 §8-5 §8-6 §8-7 §8-8 §8-9
基本方程 平面轴对称应力问题 内外壁受均布压力作用的圆筒或圆环板 匀速转动的圆盘 曲梁的纯弯曲 曲梁一端受径向集中力作用 圆孔对应力分布的影响 集中力作用于全平面 在顶端受集中力或集中力偶作用的楔形体
第八章 平面问题的极坐标解答 §8-1 基本方程
1 r
)
e2 (sin
r
cos
弹性力学1
2 Fy 0, 0 [(σ ρ )ρρ sin φρ d φ (τ ρφ)ρρ cos φρ d φ] 0,
Mo 0,
2 0
(
τ
ρ
)
ρ
ρ
ρ
2
d
φ
0。
将应力代入上式，其中第二、三式自然满足， 而第一式得出
B F 2 。
(a)
第四章 平面问题的极坐标解答
由几何方程第二式，
uρ ρ
1 ρ
uφ φ
2F
πE
sinρφ,
得
uφ φ
2 μF πE
sin
φ
2F πE
sin
φln
ρ
f1
(φ)。
第四章 平面问题的极坐标解答
第四章例题
两边对 φ积分，得
uφ
2μF πE
cosφ
2F πE
cosφln
ρ
f1(φ)dφ f2()。
(b)
第四章例题
在半平面体的左半表面，铅直沉陷是
η
(uφ
)
φπ
2
F
(1 2E
μ)
Hρ;
水平位移是
(uρ
)φπ
2
2F
E
ln
ρ
K。
取B点 (ρ s) 为参考点，则M点 ( ρ ρ)的相
对水平位移 是
M
B
2F πE
ln
s。 ρ
第四章 平面问题的极坐标解答
2B],
εφ
1 E
弹性力学平面问题极坐标解法
2
sin θ cosθ ∂ 2 − r2 ∂θ 2
极坐标下的应力函数和相容方程（ 极坐标下的应力函数和相容方程（3）
∂2 ∂2 ∂2 1 ∂ 1 ∂2 + 2 = 2 + + 2 2 r ∂r r ∂θ 2 ∂x ∂y ∂r
应力函数的相容方程
∂2 ∂2 2 ∂2 1 ∂ 1 ∂2 2 ∇ 2ϕ = ( 2 + 2 ) ϕ = ( 2 + + 2 ) ϕ =0 2 ∂x ∂y ∂r r ∂r r ∂θ
极坐标系是正交曲线坐标系 极坐标系是正交曲线坐标系 正交
r坐标曲线：坐标θ为常数的曲线（过原点和空间点的直线） 坐标曲线：坐标 为常数的曲线 过原点和空间点的直线） 为常数的曲线（ 坐标曲线 θ坐标曲线：坐标 为常数的曲线（过空间点的圆弧） 坐标曲线： 为常数的曲线（ 坐标曲线 坐标r为常数的曲线 过空间点的圆弧） 由坐标确定的空间点， 由坐标确定的空间点，既是两条坐标曲线的交点 过一个空间点的两条坐标曲线都是唯一的，且相互正交。 过一个空间点的两条坐标曲线都是唯一的，且相互正交。其 切线构成局部正交坐标标架
极坐标和直角坐标的坐标变换
∂r 2 x = = cos θ ∂x 2r ∂r 2 y = = sin θ ∂y 2r ∂θ 1 −y y sin θ = ⋅ 2 =− 2 =− 2 y x ∂x r r 1+ 2 x 1 1 x cos θ ∂θ = ⋅ 2 = 2 = 2 y x ∂y r r 1+ 2 x
ε
(1) r
P′A′ − PA AA′ − PP′ = = PA PA ∂u (u r + r d r ) − u r ∂ur ∂r = = dr dr ∂r
ε θ(1) =
sin θ cosθ ∂ 2 − r2 ∂θ 2
极坐标下的应力函数和相容方程（ 极坐标下的应力函数和相容方程（3）
∂2 ∂2 ∂2 1 ∂ 1 ∂2 + 2 = 2 + + 2 2 r ∂r r ∂θ 2 ∂x ∂y ∂r
应力函数的相容方程
∂2 ∂2 2 ∂2 1 ∂ 1 ∂2 2 ∇ 2ϕ = ( 2 + 2 ) ϕ = ( 2 + + 2 ) ϕ =0 2 ∂x ∂y ∂r r ∂r r ∂θ
极坐标系是正交曲线坐标系 极坐标系是正交曲线坐标系 正交
r坐标曲线：坐标θ为常数的曲线（过原点和空间点的直线） 坐标曲线：坐标 为常数的曲线 过原点和空间点的直线） 为常数的曲线（ 坐标曲线 θ坐标曲线：坐标 为常数的曲线（过空间点的圆弧） 坐标曲线： 为常数的曲线（ 坐标曲线 坐标r为常数的曲线 过空间点的圆弧） 由坐标确定的空间点， 由坐标确定的空间点，既是两条坐标曲线的交点 过一个空间点的两条坐标曲线都是唯一的，且相互正交。 过一个空间点的两条坐标曲线都是唯一的，且相互正交。其 切线构成局部正交坐标标架
极坐标和直角坐标的坐标变换
∂r 2 x = = cos θ ∂x 2r ∂r 2 y = = sin θ ∂y 2r ∂θ 1 −y y sin θ = ⋅ 2 =− 2 =− 2 y x ∂x r r 1+ 2 x 1 1 x cos θ ∂θ = ⋅ 2 = 2 = 2 y x ∂y r r 1+ 2 x
ε
(1) r
P′A′ − PA AA′ − PP′ = = PA PA ∂u (u r + r d r ) − u r ∂ur ∂r = = dr dr ∂r
ε θ(1) =
弹性力学-04平面问题的极坐标解答 (2)PPT
ur , u 为边界上已知的位移分量。
应力边界条件：
lrsm rsfr m slrsf
f r , f 为边界上已知的面力分量。lcos(N,r) mcos(N,)
特别地，对r =常数的边界，应力边界条件简化为：
r r常数＝pn
r r常数＝pt
对 =常数的边界，应力边界条件简化为：
常数＝pn
y
x r2
cos
r
x y
x r xr xcos r sinr cosrsinr
y r yr ysin r cors sinrcors
2 x 2 c o s r sin r c o s r sin r
x x
cos2 2 r 2 sin21 r rr12 2 2
r 常数＝pt
0
r l
q0
r 0 0
0 r 0
r ra 0 r ra 0
r rb 0 r rb 0
b
a 0 dr0
b
a r 0 dr 0
b
a
0
rd
rM
ur /2 0 u /2 0
lr
r
r
0 0 r0
0 180 r0
r 0 0 r0
r 180 0 r0
r r
1 r r
r
r
fr
0
y
F 0,
d r
r
P r
x
(rdr)d
r
rd B
dr
fr
f
A
r
r
r
d
C
r
r
r
d
r
r
dr dr
dd
r
dr
弹性力学 平面问题的极坐标解答2
r 0
由此可见，应变分量也只是r的 函数，与无关，即应变绕z轴对 称
2、位移分量
u r 1 A r [(1 ) 2 (1 3 ) B r E r 2(1 ) B ln r 2(1 )C ]
积分得：
1 A ur [(1 ) (1 3 ) Br E r 2(1 ) Br (ln r 1) 2(1 )Cr ] 平衡微分方程 4—2 极坐标中的几何方程和物理方程 4—3 极坐标中的应力函数与相容方程 4—4 应力分量的坐标变换式 4—5 轴对称应力和相应的位移
4—6 圆环或圆筒受均布压力 4—8 圆孔的孔边、应力集中
4—9 半平面体在边界上受集中力
4—10 半平面体在边界上受分布力
A r 2 B(1 2 ln r ) 2C r A 2 B(3 2 ln r ) 2C r
r r
由此可以看出，应力分量只是r得函数，不 随而变化，且只有正应力，无剪应力
一、轴对称问题的应变和位移
1、应变分量
1 A r [(1 ) 2 (1 3 ) B E r 2(1 ) B ln r 2(1 )C ] 1 A [(1 ) 2 (3 ) B E r 2(1 ) B ln r 2(1 )C ]
1 sin yx ds sin 1 cos 0
r x cos y sin 2 xy sin cos
2 2
同理，由平衡方程：
F 0
2 2
r ( y x ) sin cos xy (cos sin )
o
x
y yx
弹性力学-04极坐标求解-贾
第四章
平面问题的极坐标解答
要点： （1）极坐标中平面问题的基本方程： —— 平衡方程、几何方程、物理方程、
相容方程、边界条件。
（2）极坐标中平面问题的求解方法 及应用 应用： 圆盘、圆环、厚壁圆筒、楔形体、 半无限平面体等的应力与变形分析。
对于圆形、楔形、扇形等，边界条件用直角坐 标可能十分复杂，而用极坐标却十分简单。
为边界上已知的面力分量。 （位移单值条件）
ur , u 为边界上已知位移， k r , k
r r
r
0 r q0
r 0 0
l
lr
0
r 0
r r a 0 r r a 0 r r b 0 r r b 0
径向线段PA的转角： 线段PB的相对伸长： 环向线段PB的转角：
ur
ur ur dr r A A
x
1
1 0
PB PB (r ur )d rd u r （c） PB rd r
（b）
tan 1 1
ur (ur d ) ur BB PP 1 u r PB r rd
r C 1 r 2 r r dr k 0 y r r r r r d d r （4－1）
方程（4－1）中包含三个未知量，而只有二个方程，是一次超静 定问题，需考虑变形协调条件才能求解。
B
y
u u dr）
P
u
2
A
u u d
u A u r dr
环向线段PB的相对伸长：
2
u PB PB BB PP u d u 1 u PB PB r rd
平面问题的极坐标解答
要点： （1）极坐标中平面问题的基本方程： —— 平衡方程、几何方程、物理方程、
相容方程、边界条件。
（2）极坐标中平面问题的求解方法 及应用 应用： 圆盘、圆环、厚壁圆筒、楔形体、 半无限平面体等的应力与变形分析。
对于圆形、楔形、扇形等，边界条件用直角坐 标可能十分复杂，而用极坐标却十分简单。
为边界上已知的面力分量。 （位移单值条件）
ur , u 为边界上已知位移， k r , k
r r
r
0 r q0
r 0 0
l
lr
0
r 0
r r a 0 r r a 0 r r b 0 r r b 0
径向线段PA的转角： 线段PB的相对伸长： 环向线段PB的转角：
ur
ur ur dr r A A
x
1
1 0
PB PB (r ur )d rd u r （c） PB rd r
（b）
tan 1 1
ur (ur d ) ur BB PP 1 u r PB r rd
r C 1 r 2 r r dr k 0 y r r r r r d d r （4－1）
方程（4－1）中包含三个未知量，而只有二个方程，是一次超静 定问题，需考虑变形协调条件才能求解。
B
y
u u dr）
P
u
2
A
u u d
u A u r dr
环向线段PB的相对伸长：
2
u PB PB BB PP u d u 1 u PB PB r rd
第七章_弹性力学平面问题的极坐标系解答
1 ∂u r ∂uθ uθ + − ∂r r ∂θ r
1.3 变形协调方程
1 ∂ 2ε r 1 ∂ 2 1 ∂2 1 ∂ε r + (rε θ ) − 2 (rγ rθ ) − =0 r ∂r r 2 ∂θ 2 r ∂r 2 r ∂r∂θ
1.4 物理方程 平面应力问题：
εr =
1 1 2(1 + ν ) (σ r − νσ θ ) ， ε θ = (σ θ − νσ r ) ， γ rθ = τ rθ E E E E ν E→ 平面应变问题将上式中 ，ν → 即得。 1 −ν 1 −ν 2
θ
r P y
x
σ σθ ,τrθ=τθ r 应变：εr, εθ ,γrθ=γθ r
应力： r, 位移：u r
, uθ
直角坐标与极坐标之间关系:
y=rsinθ ∂ ∂ ∂r ∂ ∂θ ∂ sin θ ∂ = + = cos − ∂x ∂r ∂x ∂θ ∂x ∂r r ∂θ
x=rcosθ,
∂ ∂ ∂r ∂ ∂θ ∂ cosθ ∂ = + = sin θ − r ∂θ ∂y ∂r ∂y ∂θ ∂y ∂r
2
则
d 2 1 d 1 d dφ 1 d d 1 d dφ ∇ φ =( 2 + ) (r ) = (r ) = 0 r r dr r dr dr r dr dr r dr dr dr
4
逐次积分（四次）可将轴对称问题的φ
(r)基本形式得到：
1 d2 1 dε r ⇒ (rε θ ) − =0 2 r dr r dr
⇒
d (rε θ ) = ε r ——变形协调方程 dr
由几何方程： rε θ
弹性力学： 极坐标解答
由于极坐标和直角坐标都是正交坐标系，因此，极坐标和 直角坐标的物理方程应该有相同的形式。 极坐标下的物理方程：
1 ( ) E （4－3） 1 ( ) E 1 2(1 ) G E
平面坐标下的物理方程：
1 x y E 1 y y x E 2 1 xy xy E
由径向应变引起的： 径向线应变： 1 环向线应变： 1 切应变：
P ' B ' PB P 'C PB 1 PB PB u d d u d
1
Northeastern university
§4－2 极坐标中的几何方程及物理方程
2 f 0
1
C
考虑 d 、 d 增量引起应力 的增量
M 0
注意：PA面与BC面不平行， PB面与AC面面积不同。
Northeastern university
§4－1 极坐标中的平衡微分方程
Northeastern university
§4－3 极坐标中的应力函数与相容方程
二阶导数：
2 2 2sin cos 2 2 cos 2 2 x
sin
2
2sin cos
sin
2 2
由环向位移引起的径向线段PBiblioteka 的线应变 径向线应变：2 0
2
Northeastern university
§4－2 极坐标中的几何方程及物理方程
2、只有环向位移
1 ( ) E （4－3） 1 ( ) E 1 2(1 ) G E
平面坐标下的物理方程：
1 x y E 1 y y x E 2 1 xy xy E
由径向应变引起的： 径向线应变： 1 环向线应变： 1 切应变：
P ' B ' PB P 'C PB 1 PB PB u d d u d
1
Northeastern university
§4－2 极坐标中的几何方程及物理方程
2 f 0
1
C
考虑 d 、 d 增量引起应力 的增量
M 0
注意：PA面与BC面不平行， PB面与AC面面积不同。
Northeastern university
§4－1 极坐标中的平衡微分方程
Northeastern university
§4－3 极坐标中的应力函数与相容方程
二阶导数：
2 2 2sin cos 2 2 cos 2 2 x
sin
2
2sin cos
sin
2 2
由环向位移引起的径向线段PBiblioteka 的线应变 径向线应变：2 0
2
Northeastern university
§4－2 极坐标中的几何方程及物理方程
2、只有环向位移
弹性力学：第四章 平面问题的极坐标解答 (3)
属于轴 对称应 力问 题，可 以引用 轴对称 应力问 题的通 解。
σρ
A ρ2
B(1 2 ln
ρ) 2C,
σφ
1 ρ2
B(3
2 ln
ρ)
2C,
(a)
τ ρφ 0.
边界条件是
(σ ρ ) ρr q1, (τ ρφ ) ρr 0, (σ ρ )ρR q2 , (τ ρφ )ρR 0.
轴对称应力问题
§4－5 轴对称应力和相应的位移
轴对称，即绕轴对称，凡通过此轴的任何面均为对称面。
轴对称应力问题：
应力数值轴对称 -- 仅为 r 的函数，
应力方向轴对称 -- τ ρφ τφρ 0.
相应的应力函数 Φ Φ，ρ所以应力公式为：
σ
ρ
1 ρ
dΦ dρ
,
σ
φ
d2Φ d ρ2
,
r 0.
(a)
边界条件
边界条件--应用极坐标时，弹性体的 边界面通常均为坐标面，即：
r 常数，或 常数,
故边界条件形式简单。
导数的变换：
ቤተ መጻሕፍቲ ባይዱ
将对 x, y 的导数，变换为对 r, 的导数：
F (x, y) 可看成是 F (r, )，而 r, 又是 x, y
的函数，即 F 是通过中间变量 r, 为 x, y
ur
1 [(1 ) A 2(1 )Br(ln r 1)
E
r
2(1 )Cr I cos K sin，
(1
3)
Br
(e)
u
4B E
r
H
r
I
sin
K
cos。
其中 I，K — 为 x、y 向的刚体平移，
弹性力学双语课件第四章平面问题极坐标解答
徐汉忠第一版2000/7
弹性力学 第四章
7
Only the radial displacement takes place只有径向位移
• PP=ur AA=ur+ur/ rdr BB= ur+ur/ d
• r=(PA -PA)/PA=(AA-PP)/PA=[(ur+ur/rdr)ur]/dr=ur/r
徐汉忠第一版2000/7
弹性力学 第四章
13
rxy=u/y+v/x中的一般规律
• 由rxy=u/y+v/x，总结出一般规律，即设有 两个正交坐标方向，一个坐标方向的位移（如 u）对另一个坐标方向（y）求导为该坐标方向 （y）线段的转角。
1. u/y--x方向的位移 u 对y坐标求导为y方向线 段的转角。
Equations yields the axisymmetrical strain
components.
徐汉忠第一版2000/7
弹性力学 第四章
23
[/(rr)+2/r2 ]2 =0
• [/(rr)+2/r2 ] [ /(rr)+2 /r2 ] =0 • /(rr) /(rr)=r-2 ’’-r-3 ’ /(rr) [2 /r2 ]=r-1’’’
r4’’’’+2r3 ’’’ -r2 ’’ +r’=0
• Assume r=et
• =Alnr+Br2lnr+Cr2+D
(4.5.2)
徐汉忠第一版2000/7
弹性力学 第四章
25
the corresponding strains and displacements 相应的应变及位移
• Substitution of Eqs. (4.5.3)-(4.5.5) into physical Equations yields the axisymmetrical strain components. 将式 (4.5.3)-(4.5.5) 的应力代入物 理方程得应变分量，为轴对称。