平行四边形对角线最小值二例
第5讲四边形最值问题-尖子班

【例1】(1)如图所示,正方形ABCD 的面积为12,△ABE 是等边三角形,点E 在正方形ABCD 内,在对角线AC 上有一点P ,使PD +PE 的和最小,则这个最小值为()A .6B .32C .3D .62(2)如图所示,在Rt △ABC 中,已知∠B=90°,AB=6,BC=8,D ,E ,F 分别是三边AB ,BC ,CA 上的点,则DE+EF+FD 的最小值为.(3)如图,在五边形ABCDE 中,∠BAE =120°,∠B =∠E =90°,AB =BC ,AE =DE ,在直线BC ,DE 上分别找一点M ,N ,使得△AMN 的周长最小时,则∠AMN +∠ANM 的度数为.四边形最值问题模块一两点之间,线段最短【例1】(1)如图,菱形ABCD 中,AB =4,∠A =120°,点M 、N 、P 分别为线段AB 、AD 、BD 上的任意一点,则PM +PN 的最小值为________.(2)以边长为2的正方形的中心O 为端点,引用两条垂直的射线,分别与正方形的边交于A ,B 两点,则线段AB 的最小值为.(3)如图,在Rt △ABC 中,∠B=90°,AB=3,BC=4,点D 在BC 上,以AC 为对角线的所有平行四边形ADCE 中,DE 最小的值是().A.2B.3C.4D.5(4)如图在∆ABC 中,AB=3,AC=4,BC=5,P 是BC 边上的一动点,PE 垂直于AB 于E 点,PF 垂直于AC 于点F,M 是EF 的中点,则AM 的最小值为.模块二点到直线的距离,垂线段最短【例1】(1)如图,正方形ABCD 中,AB=8,O 为AB 的中点,P 为正方形ABCD 外一点,且AP ⊥CP,则线段的OP 最大值为.(2)如图,已知菱形ABCD 中,BC=10,∠BCD=60°两顶点B 、D 分别在平面直角坐标系的y 轴、x 轴的正半轴上滑动,连接OA ,则OA 的长的最小值是.【巩固】如图,正方形ABCD 中,E 、F 是AD 上两个动点,且AE DF ,连接CF 交BD 于点G ,连接BE 交AG 于点H ,若正方形的边长为2,求DH的最小值.模块三三角形三边关系,两边之和>第三边>两边之差最值问题:OA 与OB 共用顶点O ,固定OA 将OB 绕点O 旋转过程中的,会出现AB 的最大值与最小值,如图.【例1】(1)如图所示,ABD ∆是等边三角形,在ABC ∆中,BC a =,CA b =,问:当ACB∠为何值时,C 、D 两点的距离最大?最大值是多少?DCBA (2)已知:2PA =,4PB =,以AB 为一边作正方形ABCD ,使P 、D 两点落在直线AB的两侧.①如图,当45APB ∠=︒时,求AB 及PD 的长;②当APB ∠变化,且其它条件不变时,求PD 的最大值及相应APB ∠的大小.【例2】如图1,已知ABC ∆是等腰直角三角形,︒=∠90BAC ,点D 是BC 的中点.作正方形DEFG ,使点A 、C 分别在DG 和DE 上,连接AE ,BG .(1)试猜想线段BG 和AE 的数量关系是________________;(2)将正方形DEFG 绕点D 逆时针方向旋转)3600(︒≤<︒αα,①判断(1)中的结论是否仍然成立?请利用图2证明你的结论;②若4==DE BC ,当AE 取最大值时,求AF 的值.费马点与旋转☞考点说明:到三个定点的三条线段之和最小,夹角都为120°.旋转与最短路程问题主要是利用旋转的性质转化为两点之间线段最短的问题,同时与旋转有关路程最短的问题,比较重要的就是费马点问题结论:(1)平面内一点P 到△ABC 三顶点的之和为PA PB PC ++,当点P 为费马点时,距离之和最小.特殊三角形中:(2).三内角皆小于120°的三角形,分别以AB ,BC ,CA 为边,向三角形外侧做正三角形1ABC 1ACB ,1BCA ,然后连接1AA ,1BB ,1CC ,则三线交于一点P ,则点P 就是所求的费马点.(3).若三角形有一内角大于或等于120度,则此钝角的顶点就是所求的费马点.(4)当ABC ∆为等边三角形时,此时内心与费马点重合下面简单说明如何找点P 使它到ABC ∆三个顶点的距离之和PA PB PC ++最小?这就是所谓的费尔马问题.解析:如图1,把APC ∆绕A 点逆时针旋转60°得到△AP ′C ′,连接PP ′.则△APP ′为等边三角形,AP =PP ′,P ′C ′=PC ,所以PA PB PC ++=PP ′+PB +P ′C ′.点C ′可看成是线段AC 绕A 点逆时针旋转60°而得的定点,BC ′为定长,所以当B 、P 、P ′、C ′四点在同一直线上时,PA PB PC ++最小.这时∠BPA =180°-∠APP ′=180°-60°=120°,∠APC =∠A P ′C ′=180°-∠AP ′P =180°-60°=120°,∠BPC =360°-∠BPA -∠APC =360°-120°-120°=120°因此,当ABC ∆的每一个内角都小于120°时,所求的点P 对三角形每边的张角都是120°,可在AB 、BC 边上分别作120°的弓形弧,两弧在三角形内的交点就是P 点;当有一内角大于或等于120°时,所求的P 点就是钝角的顶点.费尔马问题告诉我们,存在这么一个点到三个定点的距离的和最小,解决问题的方法是运用旋转变换.【例1】阅读下列材料对于任意的ABC ∆,若三角形内或三角形上有一点P ,若PA PB PC ++有最小值,则取到最小值时,点P 为该三角形的费马点.①若三角形内有一个内角大于或等于120︒,这个内角的顶点就是费马点②若三角形内角均小于120︒,则满足条件120APB BPC APC ∠=∠=∠=︒时,点P 既为费马点.解决问题:(1)如图,ABC∆、ACE∆,∆中,三个内角均小于120︒,分别以AB、AC为边向外作等边ABD连接CD、BE交于点P,证明:点P为ABC++=∠=∠=∠=︒)且PA PB PC CD ∆的费马点.(即证明120APB BPC APC++>++(2)如图,点Q为三角形内部异于点P的一点,证明:QA QC QB PA PB PC(3)若30BC=,直接写出PA PB PC++的最小值AB=,4ABC∠=︒,3【例2】小华遇到这样一个问题,如图1,△ABC中,∠ACB=30º,BC=6,AC=5,在△ABC 内部有一点P,连接PA、PB、PC,求PA+PB+PC的最小值.他先后尝试了翻折、旋转、平移的方法,发现通过旋转可以解决这个问题.他的做法是,如图2,将△APC绕点C顺时针旋转60º,得到△EDC,连接PD、BE,则BE的长即为所求.(1)请你写出图2中,PA+PB+PC的最小值为________;(2)参考小华的思考问题的方法,解决下列问题:①如图3,菱形ABCD中,∠ABC=60º,在菱形ABCD内部有一点P,请在图3中画出并指明长度等于PA+PB+PC最小值的线段(保留画图痕迹,画出一条即可);②若①中菱形ABCD 的边长为4,请直接写出当PA+PB+PC值最小时PB的长.图1图2图3【例3】如图,四边形ABCD 是正方形,ABE ∆是等边三角形,M 为对角线BD 上任意一点,将BM 绕点B 逆时针旋转60︒得到BN ,连接AM 、CM 、EN .⑴求证:AMB ENB∆∆≌⑵①当M 点在何处时,AM CM +的值最小;②当M 点在何处时,AM BM CM ++的值最小,并说明理由;⑶当AM BM CM ++的最小值为31+时,求正方形的边长.【巩固】A 、B 、C 、D 四个城市恰好为一个正方形的四个顶点,现在要设立P 、Q 两个交通枢纽,并建设公路连接AP 、BP 、PQ 、QC 、QD ,使个城市之间都有公路相通,并使整个公路系统的总长为最小,则这个公路系统应当如何修建?【例4】(1)已知:ABC ∆中,120A ∠︒≥,P 是不与A 重合的定点,求证PA PB PC AB AC ++>+.P CBA(2)如图所示,在四边形ABCD中,AB BC∠=︒,P为四边形ABCD内部一点,ABC=,60++≥.∠=︒,证明:PA PD PC BD120APDAP DBC【题1】如图,∠MON=90°,正方形ABCD的顶点A、B分别在OM、ON上运动,当正方.形的边长为2时,OD的最大值为CE=,点M、N在对角线AC 上运动,且2周长的最小值.MN=,连接BM、EN.求四边形BMNE【题4】如图,已知菱形ABCD的边长为2,∠DAB=60︒,E、F分别是AD、CD上的两个动点,且满足AE+CF=2,连接BD,当∆BEF的面积取得最小值时,试判断此时EF与BD的位置关系。
二次函数平行四边形对角线公式

二次函数平行四边形对角线公式平行四边形是一个具有两对平行边的四边形,它具有一些特殊的性质。
其中之一是对角线的长度以及它们之间的关系可以使用二次函数的公式来计算。
在本文中,我们将探讨平行四边形对角线的公式,推导该公式,并给出一个详细的解释。
首先,我们定义一个平行四边形,并将其四个角分别标记为A、B、C和D。
设对角线AC和BD相交于点O。
我们用d1表示对角线AC的长度,用d2表示对角线BD的长度。
现在,我们的目标是找到d1和d2之间的关系。
我们可以从两个三角形ABC和CDA入手来推导此公式。
首先,我们观察到这两个三角形是相似的,因为它们有一组相等的角(∠A和∠C)。
由此,我们可以写出一个比例关系:d1/d2=BC/AD(1)接下来,我们关注三角形ABC和三角形ODB。
这两个三角形也是相似的,因为它们具有一组相等的角(∠ABC和∠ODB)。
同样,我们可以写出以下比例关系:BC/OD=AB/OD+AC(2)然而,我们的目标是找到d1和d2之间的关系,而不是BC和OD之间的关系。
为了解决这个问题,我们需要找到一个化简公式来消除BC和OD。
我们注意到,三角形ODB的两个边长为OD和OB。
这两个边长构成了平行四边形的两条边。
因此,我们可以将它们表示为两条边的长度之和:OD=d1+d2OB=d2将这两个长度代入到比例关系(2)中,我们可以得到新的比例关系:BC/d2=AB/(d1+d2+AC)(3)现在,我们需要解决一个问题,即:如何获取AB和AC的表达式,以便将其代入比例关系中。
我们继续研究平行四边形,并注意到四个角A、B、C和D是共享的。
因此,对角线AC和BD是对角线AD和BC的平分线。
我们可以利用这些信息来找到AB和AC的表达式。
让我们先来看对角线AD。
根据平分线定理,我们可以得到以下关系:AB/BD=AC/CD(4)同样,我们注意到对角线BD是对角线AC和BD的平分线,因此:AB/AC=BD/CD(5)观察比例关系(4)和(5),我们可以看到CD是一个共同的值。
5.1.2 平行四边形的对角线性质 课件(共33张PPT) 鲁教版数学八年级上册

如图,过点A作AE⊥BC于E,
∵在直角三角形ABE中,∠B=30°,
∴AE=
1 2
×AB=
1 2
×4=2.
∴平行四边形ABCD的面积=BC·AE=6×2=12.
感悟新知
归纳
求平行四边形的面积时,根据平行四 边形的面积公式,要知道平行四边形的一 边长及这边上的高.
平行四边形的高不一定是过顶点的垂 线段,因为平行线间的距离处处相等.
结构导图
课堂小结
错解:∵四边形ABCD为平行四边形, ∴OA=OC,∵OE⊥AD于点E,OF⊥BC于点F, ∴∠AEO=∠CFO=90°,又∠AOE=∠COF, ∴△AOE≌△COF,∴OE=OF.
结构导图
课堂小结
诊断:错解误认为已知E,O,F三点共线,从而得到 ∠AOE=∠COF,而已知条件中并没有这个. E,O,F三点共线需要在解题过程中加以推理, 否则就犯了逻辑错误.
结构导图
课堂小结
正解:∵四边形ABCD为平行四边形, ∴AD∥BC,OA=OC, ∴∠EAO=∠FCO, ∵OE⊥AD,OF⊥BC, ∴∠AEO=∠CFO=90°, ∴△AOE≌△COF, ∴OE=OF.
作业1 必做: 请完成教材课后练习 作业2 补充: 请完成本课时习题
课后作业
感悟新知
4. 如图,▱ABCD的对角线AC与BD相交于点O,AE⊥BC,
垂足为E,AB=3,AC=2,BD=4,则AE的长为( D )
A. 3 2
B. 3 2
21
2 21
C. 7 D. 7
感悟新知 5. 如图,EF过▱ABCD对角线的交点O,交AD于E,
交BC于F,若▱ABCD的周长为18,OE=1.5,则 四边形EFCD的周长为( C ) A.14 B.13 C.12 D.10
平行四边形的对角线平行性质

平行四边形的对角线平行性质平行四边形是几何学中的重要概念,它具有许多有趣的性质和特点。
其中之一就是对角线的平行性质。
本文将探讨平行四边形对角线的平行性质,并介绍一些相关的定理和证明。
一、对角线的定义和性质在开始讨论平行四边形的对角线平行性质之前,我们先来回顾一下对角线的定义和性质。
对角线是连接一个多边形的两个非相邻顶点的线段。
对于平行四边形来说,它有两条对角线,分别连接了相对的顶点。
对角线的性质有以下几点:1. 两条对角线相等:对于平行四边形ABCD来说,对角线AC和BD的长度相等,即AC=BD。
2. 对角线互相平分:对于平行四边形ABCD来说,对角线AC和BD互相平分,即它们的中点重合。
3. 对角线交于一点:对于平行四边形ABCD来说,对角线AC和BD交于一点O,即它们的交点唯一。
二、对角线平行的性质和定理接下来,我们重点讨论平行四边形对角线的平行性质。
定理1:平行四边形的对角线互相平行。
证明:设平行四边形ABCD的对角线AC和BD相交于点O,我们需要证明AC∥BD。
首先,根据平行四边形的定义,我们知道AB∥CD和AD∥BC。
因为AB∥CD,所以∠BAC=∠CDA。
同理,因为AD∥BC,所以∠ADB=∠CDB。
又因为∠BAC+∠ADB=180°(补角定理),所以∠CDA+∠CDB=180°。
根据平行线性质,当两条平行线被一条横截线截断时,同旁内角相等,即∠CDA=∠CDB。
综上所述,我们可以得出∠CDA=∠CDB,即AC∥BD。
根据定理1,我们可以得出平行四边形的对角线互相平行的结论。
三、例题应用为了更好地理解和应用平行四边形对角线的平行性质,这里我们通过一个例题来说明。
例题:在平行四边形ABCD中,AC=10cm,BD=8cm,求AC与BD的夹角。
解:首先,根据定理1,我们知道AC∥BD。
由于平行四边形的对角线互相平分,所以AC和BD的中点重合于点O。
根据对角线平分性质,我们可以推知AO=OC,BO=OD。
平行四边形解题方法与技巧

◆解读平行四边形1.正确理解平行四边形的概念有两组对边分别平行的四边形叫做平行四边形.用数学语言表示为:在四边形ABCD中,若AB∥DC,AD∥BC,则四边形ABCD是平行四边形.记作□ ABCED.平行四边形的定义也是判定一个四边形是不是平行四边形的一种方法.2.掌握平行四边形的性质平行四边形的性质可以从以下三个方面去理解:(1)从边着眼:平行四边形的两组对边分别平行且相等;(2)从角着眼:平行四边形的两组对角分别相等,邻角互补;(3)从对角线着眼:平行四边形的对角线互相平分.事实上,平行四边形的对角线除了互相平分外,它还是将四边形转化为三角形的”桥梁”,在处理许多与平行四边形有关的问题时,常用”对角线”互相平分这一性质解决.如:□ABCD的周长为26,对角线AC 和BD相交于点O,若△AOB的周长比△AOD的周长多1,这样我们就可以利用平行四边形的对边相等和对角线互相平分得到AB+AD=13,,AB-AD=1,从而求得AB=7,AD=6.3.掌握平行四边形的判定方法判定一个四边形是平行四边形的方法主要有:(1)两组对边分别平行;(2)两组对边分别相等;(3)一组对边平行且相等;(4)两组对角分别相等;(5)两条对角线互相平分.◆平行四边形性质的活用平行四边形除了具有一般四边形的性质外,还具有以下特性:(1)对边平行且相等;(2)对角相等,邻角互补;(3)对角线互相平分;(4)是中心对称图形,对角线的交点是它的对称中心;(5)平行四边形被对角线分成的4个三角形的面积相等.例1: 已知:如图,在□ABCD中,E、F分别是AB、CD的中点.求证:(1)△AFD≌△CEB;(2)四边形AECF是平行四边形.例2: 如图,在平行四边形ABCD中,E、F分别是AB、CD上的点,且∠DAF=∠BCE.(1)求证:△DAF≌△BCE;(2)若∠ABC=60°,∠ECB=20°,∠ABC的平分线BN交AF与M,交AD于N,求∠AMN的度数.◆判定平行四边形的五种基本方法判定平行四边形的五种方法1.两组对边分别平行例: 如图1,已知△ABC是等边三角形,D、E分别在边BC、AC上,且CD=CE,连结DE并延长至点F,使EF=AE,连结AF、BE和CF(1)请在图中找出一对全等三角形,并加以证明;(2)判断四边形ABDF是怎样的四边形,并说明理由。
由对角线的关系判定平行四边形

知2-讲
导引:两条线段的数量关系有相等或倍分,位置关系 有平行或相交,而相交的特殊情况有垂直、互 相平分,如图,连接AF,CE,分析本题可证 四边形AECF是平行四边形,则AC与EF互相 平分.
解:AC与EF互相平分.
知2-讲
方法一:连接AF,CE,如图.
∵四边形ABCD是平行四边形,
∴DC=AB,CF∥AE,
知1-讲
证明: 连接BD,交AC于点O. ∵四边形ABCD是平行四边形, ∴OB=OD,OA=OC (平行 四边形的对角线互相平分). 又∵AE=CF, ∴OA-AE=OC-CF,即OE=OF. ∴四边形BFDE是平行四边形(对角线互相平分
的 四边形是平行四边形).
知1-练
1 如图,延长△ABC的中线AD至点E,使DE=AD, 那么四边形ABEC是平行四边形吗?为什么?
知1-练
2 如图,在 ABCD中,两条对角线AC和BD相 交于点O, E、F、G、H分别是AO、BO、CO、 DO的中点,以图中标明字母的点为顶点,尽可 能多地画出平行四边形.
知1-练
3 如图,在四边形ABCD中,对角线AC,BD相交于点 O,下列条件不能判定四边形ABCD为平行四边形的 是( ) A.AB∥CD,AD∥BC B.OA=OC,OB=OD C.AD=BC,AB∥CD D.AB=CD,AD=BC
要点精析:
知2-讲
(1)判定平行四边形的五种方法各有妙用,应仔细观
察题图所给Байду номын сангаас件,看它与哪种方法接近,灵活选
择适合题目的判定方法;
(2)这五种方法与平行四边形的性质相呼应,每一种
方法都对应着一条性质,要注意它们的区别与联
系.
①由平行四边形这一条件得到边、角、对角线关
专题02 特殊平行四边形中的四种最值问题(解析版)-2024年常考压轴题攻略(9年级上册人教版)
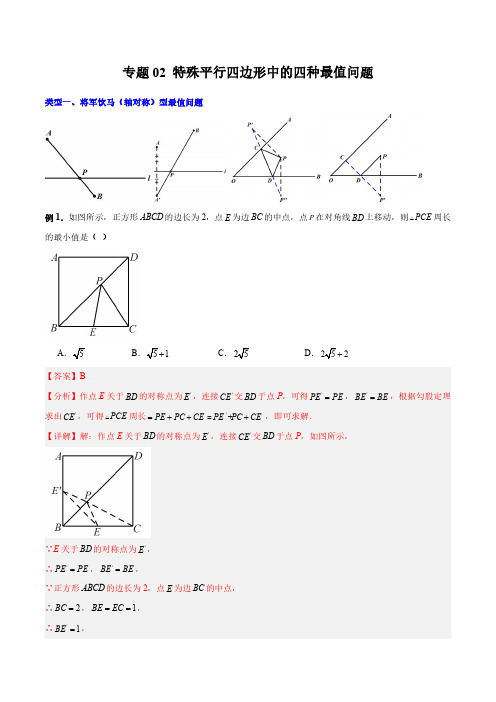
专题02特殊平行四边形中的四种最值问题类型一、将军饮马(轴对称)型最值问题A .5B .【答案】B 【分析】作点E 关于BD 的对称点为∵E 关于BD 的对称点为'E ,∴'PE PE =,'BE BE =,∵正方形ABCD 的边长为2,点A.0B.3【答案】C【分析】要使四边形APQE的周长最小,由于在BC边上确定点P、Q的位置,可在与BC交于一点即为Q点,过A点作后过G点作BC的平行线交DC的延长线于长度.∵四边形ABCD 是矩形,∴8BC AD ==,90D Ð=°,∠QCE =90°,∵2PQ =,∴6DF AD AF =-=,∵点F 点关于BC 的对称点G ,∴FG AD⊥∴90DFG ∠=︒∴四边形FGHD 是矩形,∴GH =DF =6,∠H =90°,∵点E 是CD 中点,∴CE =2,∴EH =2+4=6,∴∠GEH =45°,∴∠CEQ =45°,设BP =x ,则CQ =BC ﹣BP ﹣PQ =8﹣x ﹣2=6﹣x ,在△CQE 中,∵∠QCE =90°,∠CEQ =45°,∴CQ =EC ,∴6﹣x =2,解得x =4.故选:C .【点睛】本题考查了矩形的性质,轴对称﹣最短路线问题的应用,题目具有一定的代表性,是一道难度较大的题目,对学生提出了较高的要求.例3.如图,在矩形ABCD 中,26AB AD ==,,O 为对角线AC 的中点,点P 在AD 边上,且2AP =,点Q【答案】210【分析】①连接PO并延长交BC 明四边形APHB是矩形可得AB②过点O作关于BC的对称点PQ OQ+的最小值为PO'的长度,延长∵GO AD'⊥,点O是AC的中点,∴132AG AD==,【点睛】本题考查矩形的性质、全等三角形的判定与性质、勾股定理及轴对称识是解题的关键.【变式训练1】如图,正方形ABCD的周长为24,P为对角线AC上的一个动点,E是CD的中点,则PE PD+的最小值为()A .35B .32C .6D .5【答案】A 【详解】解:如图,连接BE ,设BE 与AC 交于点P',∵四边形ABCD 是正方形,∴点B 与D 关于AC 对称,∴P'D =P'B ,∴P'D +P'E =P'B +P'E =BE 最小.即P 在AC 与BE 的交点上时,PD +PE 最小,即为BE 的长度.∵正方形ABCD 的周长为24,∴直角△CBE 中,∠BCE =90°,BC =6,CE =12CD =3,∴226335BE =+=故选A.【变式训练2】如图,在矩形ABCD 中,AB =2,AD =3,动点P 满足S △PBC =14S 矩形ABCD ,则点P 到B ,C 两点距离之和PB +PC 的最小值为()A 10B 13C 15D .3【答案】B 【详解】解:设△PBC 中BC 边上的高是h .∵S △PBC =14S 矩形ABCD .∴12BC •h =14AB •AD ,∴h =12AB =1,∴动点P 在与BC 平行且与BC 的距离是1的直线l 上,如图,作B 关于直线l 的对称点E ,连接CE ,则CE 的长就是所求的最短距离.在Rt △BCE 中,∵BC =3,BE =BA =2,∴CE 2213+AB BC 即PB +PC 13故选:B .【变式训练3】如图,在正方形ABCD 中,4AB =,AC 与BD 交于点O ,N 是AO 的中点,点M 在BC 边上,且3BM =,P 为对角线BD 上一点,则PM PN -的最大值为_____________.【答案】1【分析】作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,可判定当点P ,E ,M 三点共线时,PM -PE 的值最大,为ME 的长,求出CE ,CQ ,得到EQ ,利用垂直平分线的性质得到EM =CM =1即可.【详解】解:如图:作N 关于BD 的对称点E ,连接PE ,ME ,过点M 作MQ ⊥AC ,垂足为Q ,∴PN =PE ,则PM -PN =PM -PE ,【答案】13【分析】连接CF、AF+=+,故当EF MN EF AF类型二、翻折型最值问题例1.如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上的一动点,将△AMN 沿MN所在直线翻折得到△A'MN,连接A'C,则A'C长度的最小值是()【变式训练1】如图,在矩形ABCD 中,3AB =,4=AD ,E 在AB 上,1BE =,F 是线段BC 上的动点,将EBF △沿EF 所在的直线折叠得到'EB F △,连接'B D ,则'B D 的最小值是()A .6B .4C .2D .1-【答案】D 【详解】解:如图,'B 的运动轨迹是以E 为圆心,以BE 的长为半径的圆.所以,当'B 点落在DE 上时,'B D 取得最小值.根据折叠的性质,△EBF ≌△EB’F ,∴E 'B ⊥'B F ,∴E 'B =EB ,∵1BE =∴E 'B =1,∵3AB =,4=AD ,∴AE =3-1=2,∴DE =D 'B =.故选:D .【变式训练2】如图,在正方形ABCD 中,AB =6,E 是CD 边上的中点,F 是线段BC 上的动点,将△ECF 沿EF 所在的直线折叠得到EC F '△,连接AC ',则的最小值是AC '_______.【答案】3【详解】解:∵四边形ABCD 是正方形,∴6CD AB AD ===,∵E 是CD 边上的中点,∴132EC CD ==∵△ECF 沿EF 所在的直线折叠得到EC F '△,∴3EC EC '==,∴当点A ,C ',E 三点共线时,AC '最小,如图,在Rt ADE △中,由勾股定理得:AE ==3AE EC '-=-,∴AC '的最小值为3.类型三、旋转型最值问题【答案】353-【分析】过点M 作MP CD ⊥,垂足为P ,连接CM ,根据正方形的性质求出CE ,证明EDC DMP △≌△股定理求出CM ,根据CN MN CM +≥即可求出CN 【详解】解:过点M 作MP CD ⊥,垂足为P ,连接由旋转可得:DE DM =,3EF MN ==,90EDM ∠=例2.如图,长方形ABCD 中,6AB =,8BC =,E 为BC 上一点,且2BE =,F 为AB 边上的一个动点,连接EF ,将EF 绕着点E 顺时针旋转30°到EG 的位置,连接FG 和CG ,则CG 的最小值为______.【答案】2+【详解】解:如图,将线段BE 绕点E 顺时针旋转30°得到线段ET ,连接GT ,过E 作EJ CG ⊥,垂足为J ,∵四边形ABCD 是矩形,∴AB =CD =6,∠B =∠BCD =90°,∵∠BET =∠FEG =30°,∴∠BEF =∠TEG ,在△EBF 和△TEG 中,EB ET BEF TEG EF EG =⎧⎪∠=∠⎨⎪=⎩,∴△EBF ≌△ETG (SAS ),∴∠B =∠ETG =90°,∴点G 的在射线TG 上运动,∴当CG ⊥TG 时,CG 的值最小,∵∠EJG =∠ETG =∠JGT =90°,∴四边形ETGJ 是矩形,∴∠JET =90°,GJ =TE =BE =2,∵∠BET =30°,∴∠JEC =180°-∠JET -∠BET =60°,∵8BC =,∴226,3,3EC BC BE EJ CJ EC EJ =-===-=,∴CG =CJ +GJ =332+.∴CG 的最小值为332+.故答案为:332.【变式训练1】如图,已知正方形ABCD 的边长为a ,点E 是AB 边上一动点,连接ED ,将ED 绕点E 顺时针旋转90︒到EF ,连接DF ,CF ,则当DF CF +之和取最小值时,DCF 的周长为______.(用含a 的代数式表示)【答案】()51a +【分析】连接BF ,过点F 作FG AB ⊥交AB 延长线于点G ,先证明AED GFE △≌△,即可得到点F 在CBG ∠的角平分线上运动,作点C 关于BF 的对称点C ',当点D ,F ,C 三点共线时,DF CF DC +='最小,根据勾股定理求出DC DF CF '=+的最小值为35,即可求出此时DCF 的周长为353+.将ED绕点E顺时针旋转90︒到EF,=,∴⊥,EF DEEF DEDEA FEG DEA ADE∴∠+∠=∠+∠=︒,90∴∠=∠,ADE FEG又90,∠=∠=︒DAE FGE(1)试猜想线段BG 和AE 的数量关系,并证明你得到的结论;(2)将正方形DEFG 绕点D 逆时针方向旋转一定角度后(旋转角度大于过观察或测量等方法判断(1)中的结论是否仍然成立?如果成立,请予以证明;如果不成立,请说明理由;(3)若2BC DE ==,在(2)的旋转过程中,①当AE 为最大值时,则AF =___________.ABC 是等腰直角三角形,AD BC ∴⊥,BD CD =,90ADB ADC ∴∠=∠=︒.四边形DEFG 是正方形,DE DG ∴=.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)ADE BDG ∴△≌△,BG AE ∴=;(2)(1)中的结论仍然成立,BG AE =,BG AE ⊥.理由如下:如图②,连接AD ,延长EA 交BG 于K ,交DG 于O .在Rt BAC 中,D 为斜边BC 中点,AD BD ∴=,AD BC ⊥,90ADG GDB ∴∠+∠=︒.四边形EFGD 为正方形,DE DG ∴=,且90GDE ∠=︒,90ADG ADE ∴∠+∠=︒,BDG ADE ∴∠=∠.在BDG 和ADE V 中,BD AD BDG ADE GD ED =⎧⎪∠=∠⎨⎪=⎩,(SAS)BDG ADE ∴△≌△,BG AE ∴=,BGD AED ∠=∠,2,==BC DEBG∴=+=.213AE∴=.3在Rt AEF中,由勾股定理,得222=+=+3AF AE EF中,如图②中,在BDGBG∴-≤≤+,2112∴的最小值为1,此时如图④中,AE在Rt AEF中,2=AF EF【点睛】本题属于四边形综合题,考查了旋转的性质的运用,等腰直角三角形的性质的运用,勾股定理的运用,全等三角形的判定及性质的运用,正方形的性质的运用,解答时证明三角形全等是关键.类型四、PA+KPB型最值问题3A.27B.23【答案】C【分析】连接AC与EF相交于∵四边形ABCD是菱形,∠=∠,∴OAE OCFA.3B.22【答案】D【分析】连接AF,利用三角形中位线定理,可知四边形ABCD是菱形,∴==,AB BC23,H分别为AE,EF的中点,GGH∴是AEF△的中位线,【答案】51-【分析】连接BD交EF的中点,求出OB的长,得到AH AM MH>=-–51直线l平分正方形∴O是BD的中点,四边形ABCD是正方形,∴==,BD AB24【答案】26【分析】利用轴对称的性质作出如图的辅助线,在【详解】解:延长DC '''∴E F G H E '''、、、、在同一直线上时,四边形EFCH 作E K AB '⊥交AB 延长于点K ,则23EK BE CD A E AB CD '''=++=+=,E K BC '=+在△ABH中,∠AHB=90°,∠ABH过点D作DE∥AC交BC延长线于点E,作点C【点睛】本题考查了对称的性质,勾股定理,等边三角形的判定和性质,最值问题,直角三角形的性质,多边形的面积,知识点较多,难度较大,解题的关键是作出辅助线,得出当且仅当B,D,F三点共线时,BD+CD取得最小值.。
平行四边形几何辅助线专题详解
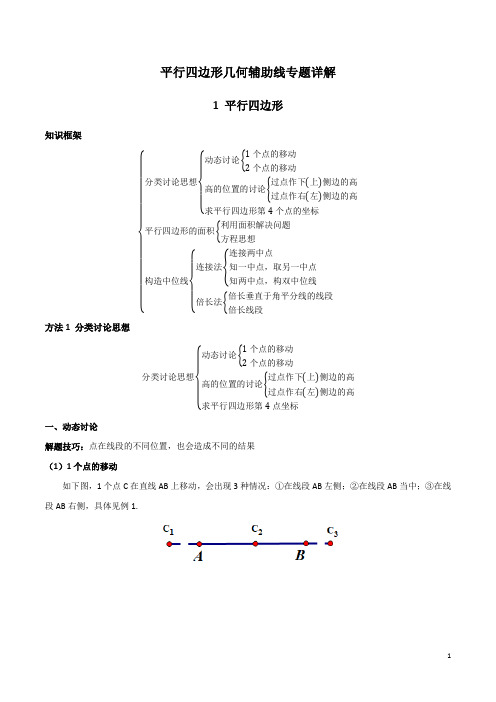
平行四边形几何辅助线专题详解1 平行四边形知识框架{分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4个点的坐标平行四边形的面积{利用面积解决问题方程思想构造中位线{连接法{连接两中点知一中点,取另一中点知两中点,构双中位线倍长法{倍长垂直于角平分线的线段倍长线段 方法1 分类讨论思想分类讨论思想{动态讨论{1个点的移动2个点的移动高的位置的讨论{过点作下(上)侧边的高过点作右(左)侧边的高求平行四边形第4点坐标一、动态讨论解题技巧:点在线段的不同位置,也会造成不同的结果 (1)1个点的移动如下图,1个点C 在直线AB 上移动,会出现3种情况:①在线段AB 左侧;②在线段AB 当中;③在线段AB 右侧,具体见例1.(2)2个点的移动如下图,2个点C、D在线段AB上移动(C、D两点在AB中),会出现2种情况:①点C在点D的左侧;②点C在点D的右侧,具体见例2.例1.▱ABCD的内角∠BCD的平分线CE交射线DA于点E,若AE=3,DE=4,求▱ABCD的周长。
例2.在▱ABCD中,AD=8,AE平分∠BAD交BC于点E,DF平分∠ADC交BC于点F,且EF=2,求AB的长。
二、高的位置的讨论解题技巧:在平行四边形中作高,会出现2种情况:①在图形内;②在图形外。
(1)过点作下(上)侧边的高如下图,过点A作▱ABCD下侧的边CD上的高AE。
因▱ABCD倾斜方向的变化,高会存在两种情况,具体见例1(2)过点右(左)侧边的高如下图,过点B作▱ABCD的右侧边AD上的高AE。
因▱ABCD倾斜大小的变化,高会存在两种情况,具体见例2上述两种情况实质是同一种情况经过翻折后得到的,为同一种情况。
例1.在面积为15的平行四边形ABCD中,过点A作AE垂直于直线BC于点E,若AB=5,BC=6,求CE的值。
例2.在▱ABCD中,AD=BD=4,BE是AD边上的高,∠EBD=30°,求△ABD的面积。
直角坐标系中平行四边形对角线法则

直角坐标系中平行四边形对角线法则
【原创版】
目录
1.平行四边形对角线法则的定义
2.平行四边形对角线法则的性质
3.平行四边形对角线法则的应用
4.总结
正文
一、平行四边形对角线法则的定义
在直角坐标系中,一个平行四边形的对角线是指连接不相邻顶点的线段。
平行四边形对角线法则指的是,对于一个平行四边形,其对角线互相平分,且对角线的中点连线互相垂直。
二、平行四边形对角线法则的性质
1.平行四边形的对角线互相平分:平行四边形的两条对角线,分别连接不相邻的顶点,它们互相平分,即对角线的中点重合。
2.对角线的中点连线互相垂直:平行四边形对角线的中点连线,互相垂直,且长度相等。
三、平行四边形对角线法则的应用
平行四边形对角线法则在几何学中有广泛的应用,特别是在解决一些与平行四边形相关的几何问题时,使用对角线法则可以简化问题,提高解题效率。
例如,在计算平行四边形的面积时,可以利用对角线法则求出对角线的长度,然后应用面积公式求解。
四、总结
在直角坐标系中,平行四边形对角线法则是一个基本的几何性质,掌
握这一性质,对于解决一些复杂的几何问题有很大的帮助。
八年级数学下册平行四边形的判定练习题

BDCAO图1FEDCBA图2F E D CBA HG FEOAB C DOM ABCD图1FE DCB A4321图3F ED CBA H G 图2F E DCB A八年级数学下册平行四边形的判定练习题识记知识1)定义:两组对边分别平行的四边形是平行四边形.∵ , ∴四边形ABCD 是平行四边形.2)定理:两组对边分别相等的四边形是平行四边形.∵∴四边形ABCD 是平行四边形.3)定理:一组对边平行且相等的四边形是平行四边形.∵∴四边形ABCD 是平行四边形.4)定理:对角线互相平分的四边形是平行四边形.∵∴四边形ABCD 是平行四边形.5)定理:两组对角分别相等的四边形是平行四边形∵∴四边形ABCD 是平行四边形. 二、平行四边形性质与判定的综合应用例1: 如图, 已知:E 、F 是平行四边形ABCD 对角线AC 上的两点,并且AE=CF 。
求证:四边形BFDE 是平行四边形变式一:在□ABCD 中,E ,F 为AC 上两点,BE//DF .求证:四边形BEDF 为平行四边形.变式二:在□ABCD 中,E,F 分别是AC 上两点,BE ⊥AC 于E ,DF ⊥AC 于F.求证:四边形BEDF 为平行四边形想一想:在□ABCD 中, E ,F 为AC 上两点, BE =DF .那么可以证明四边形 BEDF 是平行四边形吗?例2:如图,平行四边形ABCD 中,AF =CH ,DE =BG 。
求证:EG 和HF 互相平分。
练习1、如图所示,在四边形ABCD 中,M 是BC 中点,AM 、BD 互相平分于点O ,那么请说明AM=DC 且AM ∥DC:1、以不在同一直线上的三点为顶点作平行四边形,最多能作( )A 、4个B 、3个C 、2个D 、1个 2、如图,在□ABCD 中,已知两条对角线相交于点O ,E 、F 、G 、H 分别是AO 、BO 、CO 、DO 的中点,以图中的点为顶点,尽可能多地画出平行四边形在四边形ABCD 中,AD ∥BC ,且AD >BC ,BC = 6cm ,P ,Q 分别从A ,C 同时出发,P 以1厘米/秒的速度由A 向D 运动,Q 以2厘米/秒的速度由C 向B 运动,几秒后四边形ABQP 成为平行四边形?1、下列条件中,能判定四边形是平行四边形的是( )A 、一组对边相等,另一组对边平行;C 、一组对角相等,一组邻角互补;B 、一组对边平行,一组对角互补;D 、一组对角互补,另一组对角相等。
平行四边形的对角线关系

平行四边形的对角线关系平行四边形是一种特殊的四边形,具有一些独特的性质和特点。
其中,对角线关系是平行四边形的一个重要性质之一。
本文将探讨平行四边形对角线的关系,并分析其性质和应用。
一、对角线的定义和性质平行四边形是指四边形的对边两两平行。
根据平行四边形的定义,我们可以得出平行四边形的对角线有以下性质:1. 对角线互相平分:平行四边形的两条对角线互相平分。
也就是说,平行四边形的任意一条对角线将另一条对角线平分为两个相等的线段。
2. 对角线相交于一点:平行四边形的两条对角线相交于一点,称为对角线的交点或对角点。
这个交点将对角线分成两段,分别连接了四边形的两个非相邻顶点。
二、对角线的长度关系对于平行四边形的对角线,我们可以得出它们的长度关系:1. 对角线相等:平行四边形的两条对角线相等。
这是平行四边形特有的性质,可以通过几何证明来得到。
2. 对角线比例关系:平行四边形的对角线分割四边形成比例。
具体说来,如果一条对角线把平行四边形分成两个三角形,那么这两个三角形的底边与对角线之比相等,即:AB/AD = BC/CD。
三、对角线的应用平行四边形的对角线关系具有一定的应用价值。
以下是几个常见的应用:1. 确定平行四边形:通过测量四边形的对角线长度,我们可以判断一个四边形是否为平行四边形。
如果对角线相等,则可以确定该四边形是平行四边形。
2. 确定四边形的性质:由于平行四边形对角线的长度关系,我们可以通过对角线的测量结果来判断四边形的性质。
例如,如果四边形的对角线相等,则可以推断出这是一个矩形或菱形。
3. 解决几何问题:在几何问题中,我们经常需要利用平行四边形的性质来解决一些复杂的计算或证明。
对角线关系是解决这类问题的重要工具之一。
四、总结平行四边形的对角线关系是平行四边形的一个重要性质,它们对平行四边形的形状和性质有着重要的影响。
对角线的长度关系和应用使我们能够通过对角线的测量结果来确定四边形的性质,并应用于解决各种几何问题。
平行四边形的定律

平行四边形的定律平行四边形是一种具有特殊性质的四边形。
在平行四边形中,有一些重要的定律可以帮助我们解决与其相关的几何问题。
本文将介绍平行四边形的定律以及它们的应用。
一、平行四边形的定义平行四边形是指具有两组对边分别平行的四边形。
根据平行四边形的定义,我们可以得出以下定律。
二、平行四边形的性质1. 相对边相等定律:在平行四边形中,对边是平行的,因此相对边相等。
2. 对角线互相平分定律:平行四边形的对角线互相平分。
也就是说,平行四边形的对角线相交于一点,并且将对角线分成两段相等的线段。
3. 相邻角互补定律:在平行四边形中,相邻角互补,即相邻的两个内角的和等于180度。
4. 同位角相等定律:平行四边形中,同位角相等。
同位角是指两组平行线中位于同一边的对应角。
5. 余角相等定律:平行四边形中,余角相等。
余角是指两组平行线中位于同一边的非对应角。
三、平行四边形的应用平行四边形的定律在解决几何问题时有着广泛的应用。
下面我们将通过一些具体例子来说明它们的应用。
例1:已知平行四边形ABCD中,AB=6cm,BC=8cm,求对角线AC的长度。
解:根据平行四边形的对角线互相平分定律,我们知道AC将对角线BD平分。
因此,AC的长度等于BD的长度。
根据相对边相等定律,我们知道AB=CD,BC=AD,所以BD=AB+BC=6+8=14cm。
因此,AC的长度也为14cm。
例2:已知平行四边形ABCD中,AB=6cm,AD=10cm,角BAD=60度,求平行四边形的面积。
解:我们可以通过计算平行四边形的高和底边的乘积来求解面积。
在平行四边形ABCD中,我们可以通过绘制高BE,使其与AD垂直相交。
由于角BAD=60度,所以角BAE也为60度。
根据三角形的性质,我们可以得知三角形BAE是一个等边三角形,即BE=AE=6cm。
因此,平行四边形的高为6cm。
底边的长度为AD=10cm。
所以,平行四边形的面积为6cm×10cm=60cm²。
北师大版数学八年级下册期末复习(六) 平行四边形

期末复习(六) 平行四边形01 各个击破)命题点1 平行四边形的性质与判定【例1】 (桂林中考)如图,在▱ABCD 中,E ,F 分别是AB ,CD 的中点. (1)求证:四边形EBFD 为平行四边形;(2)对角线AC 分别与DE ,BF 交于点M ,N ,求证:△ABN≌△CDM.【思路点拨】 (1)先根据平行四边形的性质得AB∥CD,AB =CD ,再根据一组对边平行且相等的四边形是平行四边形即可得证;(2)因为AB =CD ,∠CAB =∠ACD 已知,则只需要再证明一组对应角相等即可. 【解答】 证明:(1)∵四边形ABCD 是平行四边形, ∴ABCD.∵E ,F 分别是AB ,CD 的中点, ∴BE =12AB ,DF =12DC. ∴BEDF.∴四边形EBFD 为平行四边形. (2)∵四边形ABCD 是平行四边形, ∴ABCD.∴∠CAB =∠ACD.∵四边形EBFD 为平行四边形, ∴∠ABN =∠CDM. 又∵AB=CD ,∴△ABN ≌△CDM(ASA).【方法归纳】 1.判定平行四边形的基本思路:(1)若已知一组对边平行,可以证这一组对边相等或另一组对边平行;(2)若已知一组对边相等,可以证这一组对边平行或另一组对边相等;(3)若已知一组对角相等,可以证另一组对角相等;(4)若已知条件与对角线有关,可以证明对角线互相平分. 2.利用平行四边形的性质进行计算的方法:(1)利用平行四边形的性质,通过角度或线段之间的等量转化进行相应的计算;(2)找出所求线段或角所在的三角形,若三角形为直角三角形,通过直角三角形的性质或勾股定理求解;若三角形为任意三角形,可通过三角形全等的性质进行求解.1.如图,在四边形ABCD 中,已知AB =CD ,AD =BC ,AC ,BD 相交于点O ,若AC =6,则AO 的长度等于3.2.如图,已知D 是△ABC 的边AB 上一点,CE ∥AB ,DE 交AC 于点O ,且OA =OC ,猜想线段CD 与线段AE 的大小关系和位置关系,并说明理由.解:线段CD 与线段AE 的大小关系和位置关系是相等且平行. 理由:∵CE∥AB, ∴∠DAO =∠ECO.∵OA =OC ,∠AOD =∠COE, ∴△ADO ≌△CEO.∴AD =CE. 又∵AD∥CE,∴四边形ADCE 是平行四边形. ∴CD ∥AE ,CD =AE.3.如图,E 是▱ABCD 的边CD 的中点,延长AE 交BC 的延长线于点F. (1)求证:△ADE≌△FCE;(2)若∠BAF=90°,BC =5,EF =3,求CD 的长.解:(1)证明:∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AB ∥CD.∴∠DAE =∠F,∠D =∠ECF. ∵E 是▱ABCD 的边CD 的中点, ∴DE =CE.在△ADE 和△FCE 中,⎩⎨⎧∠DAF=∠F,∠D =∠ECF,DE =CE ,∴△ADE ≌△FCE(AAS). (2)∵△ADE≌△FCE, ∴AE =EF =3. ∵AB ∥CD ,∴∠AED =∠BAF=90°. 在▱ABCD 中,AD =BC =5, ∴DE =AD 2-AE 2=52-32=4. ∴CD =2DE =8.命题点2 三角形的中位线【例2】 (邵阳中考)如图,等边三角形ABC 的边长是2,D ,E 分别为AB ,AC 的中点,延长BC 至点F ,使CF =12BC ,连接CD 和EF. (1)求证:DE =CF ; (2)求EF 的长.【思路点拨】 (1)欲证DE =CF ,由三角形中位线定理可知DE =12BC ,而条件中有CF =12BC 故易证得;(2)欲求EF 的长,可证四边形DEFC 是平行四边形,因此只需求出CD 的长.在等边三角形ABC 中,点D 是AB 的中点,因此运用勾股定理可求出,问题获解.【解答】 (1)证明:∵D,E 分别为AB ,AC 的中点,∴DE =12BC ,且DE∥BC. ∵点F 在BC 的延长线上,且CF =12BC ,∴DE ∥CF ,且DE =CF.(2)由(1)知DE∥CF,且DE =CF , ∴四边形DEFC 为平行四边形.∵△ABC 是等边三角形,边长是2,点D 是AB 的中点,AB =BC =2, ∴CD ⊥AB ,∠BDC =90°,BD =12AB =1. ∴CD =BC 2-BD 2=22-12= 3. ∵四边形DEFC 为平行四边形, ∴EF =CD = 3.【方法归纳】 若题中有中点通常考虑到三角形的中线和中位线,而在等边三角形(等腰三角形)中,中线同时也是高和角平分线.4.如图,CD 是△ABC 的中线,点E ,F 分别是AC ,DC 的中点,EF =2,则BD =4.5.如图所示,在四边形ABCD 中,AB =CD ,M ,N ,P 分别是AD ,BC ,BD 的中点,∠ABD =20°,∠BDC =70°,求∠PMN 的度数.解:∵M,N ,P 分别是AD ,BC ,BD 的中点,∴MP ,PN 分别是△ABD,△BCD 的中位线, ∴MP12AB, PN12CD.∴∠MPD =∠ABD=20°,∠BPN =∠BDC=70°. ∴∠DPN =110°.∴∠MPN =∠MPD+∠DPN=20°+110°=130°. 又∵AB=CD ,∴MP =PN. ∴∠PMN =∠PNM. ∴∠PMN =25°.命题点3 多边形的内角和与外角和【例3】(泰安中考)如图,五边形ABCDE中,AB∥CD,∠1,∠2,∠3分别是∠BAE,∠AED,∠EDC的外角,则∠1+∠2+∠3等于(B)A.90°B.180°C.210°D.270°【思路点拨】由AB∥CD,推导∠B+∠C=180°,故∠B,∠C两角的外角和是180°,根据多边形外角和等于360°可计算∠1+∠2+∠3度数.【方法归纳】对于求多边形的外角和或部分外角的和的问题,都要根据任意多边形的外角和是360°以及邻角和其补角的互补关系这两个知识点,来解决问题.6.正多边形的一个内角的度数恰好等于它的外角的度数的3倍,则这个多边形的边数为8.7.如图,在六边形ABCDEF中,AB⊥AF,BC⊥DC,∠E+∠F=260°,求两外角和α+β的度数.解:∵AB⊥AF,BC⊥DC,∴∠A=∠C=90°.又∵∠E+∠F=260°,∴∠EDC+∠ABC=(6-2)×180°-90°×2-260°=280°.∴β+α=(180°-∠EDC)+(180°-∠ABC)=360°-(∠EDC+∠ABC)=80°.故两外角和α+β的度数为80°.02整合集训一、选择题(每小题3分,共24分)1.已知平行四边形ABCD的周长为32 cm,AB=4 cm,则BC的长为(B)A.4 cm B.12 cmD.16 cm D.24 cm2.(西宁中考)如果等边三角形的边长为4,那么等边三角形的中位线长为(A)A.2 B.4 C.6 D.83.(临沂中考)将一个n边形变成n+1边形,内角和将(C)A.减少180°B.增加90°C.增加180°D.增加360°4.(乐山中考)如图,点E是▱ABCD的边CD的中点,AD,BE的延长线相交于点F,DF=3,DE=2,则▱ABCD 的周长为(D)A.5B.7C.10D.145.某平行四边形的对角线长为x,y,一边长为6,则x与y的值可能是(C)A.4和7 B.5和7C.5和8 D.4和176.(葫芦岛中考)如图,在五边形ABCDE中,∠A+∠B+∠E=300°,DP,CP分别平分∠EDC,∠BCD,则∠P 的度数是(A)A.60°B.65°C.55°D.50°7.如图,在▱ABCD中,AB=4,∠BAD的平分线与BC的延长线交于点E,与DC交于点F,且点F为边DC的中点,DG⊥AE,垂足为G,若DG=1,则AE的长为(B)A.2 3 B.43C.4 D.88.已知在正方形的网格中,每个小方格的边长都相等,A,B两点在小方格的顶点上,位置如图所示,则以A,B 为顶点的网格平行四边形的个数为(D)A.6个B.8个C.10个D.12个二、填空题(每小题4分,共24分)9.(陕西中考)一个正多边形的外角为45°,则这个正多边形的边数是8.10.如图所示,在▱ABCD中,E,F分别为AD,BC边上的一点,若添加一个条件AE=FC或∠ABE=∠CDF,则四边形EBFD为平行四边形.11.(娄底中考)如图,▱ABCD的对角线AC,BD交于点O,点E是AD的中点,△BCD的周长为18,则△DEO 的周长是9.12.(泉州中考)如图,顺次连接四边形ABCD四边的中点E,F,G,H,则四边形EFGH的形状一定是平行四边形.13.如图,在▱ABCD中,∠ABC=60°,E,F分别在CD,BC的延长线上,AE∥BD,EF⊥BC,CF=3,则AB 的长为3.14.在某张三角形纸片上,取其一边的中点,沿着过这点的两条中位线分别剪去两个三角形,剩下的部分就是如图所示的四边形;经测量这个四边形的相邻两边长为10 cm ,6 cm ,一条对角线的长为8 cm ;则原三角形纸片的周长是48_cm 或(32+813)cm .三、解答题(共52分)15.(6分)一个多边形的内角和与外角和的差为1 260度,求它的边数. 解:设多边形的边数是n ,则(n -2)·180-360=1 260.解得n =11. 答:它的边数为11.16.(8分)(陕西中考)如图,在▱ABCD 中,连接BD ,在BD 的延长线上取一点E ,在DB 的延长线上取一点F ,使BF =DE ,连接AF ,CE ,求证:AF∥CE.证明:∵四边形ABCD 是平行四边形, ∴AD ∥BC ,AD =BC. ∴∠ADB =∠CBD. ∵BF =DE ,∴BF +BD =DE +BD , 即DF =BE.在△ADF 和△CBE 中,⎩⎨⎧AD =CB ,∠ADF =∠CBE,DF =BE ,∴△ADF ≌△CBE(SAS). ∴∠AFD =∠CEB. ∴AF ∥CE.17.(8分)(永州中考)如图,M 是△ABC 的边BC 的中点,AN 平分∠BAC,BN ⊥AN 于点N ,延长BN 交AC 于点D ,已知AB =10,BC =15,MN =3. (1)求证:BN =DN ; (2)求△ABC 的周长.解:(1)证明:∵AN 平分∠BAC, ∴∠BAN =∠DAN. ∵BN ⊥AN ,∴∠ANB =∠AND=90°. 又∵AN=AN ,∴△ABN ≌△ADN(ASA).∴BN=DN. (2)∵△ABN≌△ADN, ∴AD =AB =10,DN =NB. 又∵点M 是BC 中点,∴MN 是△BDC 的中位线. ∴CD =2MN =6.∴△ABC 的周长为AB +AC +BC =AB +AD +CD +BC =10+10+6+15=41.18.(10分)如图,在△ABC 中,点D ,E 分别是AB ,AC 的中点,连接DE 并延长到点F ,使EF =ED ,连接CF.(1)四边形DBCF 是平行四边形吗?说明理由;(2)DE 与BC 有什么样的位置关系和数量关系?说明理由. 解:(1)四边形DBCF 是平行四边形. 理由:∵E 是AC 的中点, ∴AE =CE.又∵EF=ED ,∠CEF =∠AED, ∴△AED ≌△CEF(SAS). ∴AD =CF ,∠A =∠ECF. ∴AD ∥CF ,即CF∥BD.又∵D 为AB 的中点,∴BD =AD.∴BD=CF. ∴四边形DBCF 是平行四边形. (2)DE∥BC,DE =12BC. 理由:∵EF=ED ,∴DE =12DF. 又∵四边形DBCF 是平行四边形, ∴DF =BC ,DF ∥BC. ∴DE ∥BC ,DE =12BC.19.(10分)(怀化中考)已知:如图,在△ABC 中,DE ,DF 是△ABC 的中位线,连接EF ,AD ,其交点为点O.求证: (1)△CDE≌△DBF; (2)OA =OD.证明:(1)∵DE,DF 是△ABC 的中位线, ∴DF =CE ,DF ∥CE ,DB =DC. ∵DF ∥CE , ∴∠C =∠BDF.在△CDE 和△DBF 中,⎩⎨⎧DC =BD ,∠C =∠BDF,CE =DF ,∴△CDE ≌△DBF(SAS).(2)∵DE,DF 是△ABC 的中位线, ∴DF =AE ,DF ∥AE.∴四边形DEAF 是平行四边形. ∵EF 与AD 交于点O , ∴OA =OD.20.(10分)(扬州中考改编)如图,AC 为长方形ABCD 的对角线,将边AB 沿AE 折叠,使点B 落在AC 上的点M 处,将边CD 沿CF 折叠,使点D 落在AC 上的点N 处. (1)求证:四边形AECF 是平行四边形;(2)若AB =6,AC =10,求四边形AECF 的面积.解:(1)证明:由折叠的性质可知:AM =AB ,CN =CD ,∠FNC =∠D=90°,∠AME =∠B=90°, ∴∠ANF =90°,∠CME =90°. ∵四边形ABCD 为长方形, ∴AB =CD ,AD ∥BC.∴AM =CN ,∠FAN =∠ECM. ∴AM -MN =CN -MN , 即AN =CM.在△ANF 和△CME 中,∠FAN =∠ECM,AN =CM ,∠ANF =∠CME, ∴△ANF ≌△CME(ASA). ∴AF =CE. 又∵AF∥CE,∴四边形AECF 是平行四边形. (2)∵AB=6,AC =10,∴BC =8.设CE =x ,则EM =8-x ,CM =10-6=4. 在Rt △CEM 中,(8-x)2+42=x 2, 解得x =5.∴S 四边形AECF =EC·AB=5×6=30.。
2022-2023学年初二数学第二学期培优专题06 平行四边形中的最值问题

2022-2023学年初二数学第二学期培优专题06 平行四边形中的最值问题【例题讲解】如图,在平行四边形ABCD 中,30BCD ∠=︒,6BC =,33CD =,(1)平行四边形ABCD 的面积为________.(2)若M 是AD 边的中点,N 是AB 边上的一个动点,将AMN 沿MN 所在直线翻折得到A MN '△,连接A C ',则A C '长度的最小值是________.解:(1)过点C 作CF ⊥AB ,交AB 延长线于F ,∵四边形ABCD 是平行四边形,∴AB ∥CD ,BC =6,AB =CD =33,∵∠BCD =30°=∠CBF ,∴CF =12BC =3, ∴四边形ABCD 的面积=AB CF ⨯=333⨯=93;(2)连接MC ,过点M 作ME ⊥CD 于E ,交CD 的延长线于点E ;∵四边形ABCD 为平行四边形,∴AD ∥BC ,AD =BC =6,∵点M 为AD 的中点,∠BCD =30°,∴DM =MA =3,∠MDE =∠BCD =30°,∴ME =12DM =32,DE =332,∴CE =CD +DE =33332+=932,由勾股定理得:CM 2=ME 2+CE 2, ∴CM=2239322⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭=37,由翻折变换的性质得:MA ′=MA =3,∵MA ′+A ′C ≥MC , ∴A ′C ≥MC- MA ′= MC -3,显然,当折线MA ′C 与线段MC 重合时,线段A ′C 的长度最短,此时A ′C =373-,故答案为:(1)93;(2)373-.【综合演练】1.如图 ,在平行四边形ABCD 中 ,120C ∠=︒ ,AB =4 ,AD =8 , 点H 、G 分别是边CD 、BC 上的动点.连接AH 、HG ,点E 为AH 的中点 ,点F 为GH 的中点 ,连接EF .则EF 的最大值与最小值的差为( )A .2B .232-C .3D .43-2.如图,在△ABC 中,∠ACB =60°,∠CAB =45°,BC =4,点D 为AB 边上一个动点,连接CD ,以DA 、DC 为一组邻边作平行四边形ADCE ,则对角线DE 的最小值是( )A .2+6B .1+3C .4D .2+23第II 卷(非选择题)二、填空题(共0分)3.如图,在Rt ABC 中,90,3,4B AB BC ∠=︒==,点D 为BC 上一动点(不与点C 重合),以AD ,CD 为一组邻边作平行四边形ADCE ,当DE 的值最小时,平行四边形ADCE 的周长..为_____. 4.如图,在ABCD 中,=60B ∠︒,10AB =,8BC =,点E 为边AB 上的一个动点,连接ED ,EC , 以ED 、CE 为邻边构造EDGC ,连接EG ,则EG 的最小值为__________.5.如图,平行四边形ABCD 中,AB =2,AD =1,∠ADC =60°,将平行四边形ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点D 处,折痕交CD 边于点E .若点P 是直线l 上的一个动点,则PD '+PB 的最小值_______.6.如图,平行四边形ABCD中,8∠=︒,E是边AD上且2AAB=,6AD=,60=,F是边AB上AE DE+的最小值__________.的一个动点,将线段EF绕点E逆时针旋转60︒,得到EG,连接BG、CG,则BG CG7.如图,CD是直线x=1上长度固定为1的一条动线段.已知A(﹣1,0),B(0,4),则四边形ABCD 周长的最小值为_________________.8.如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC 为边作平行四边形PCQD,则对角线PQ的长的最小值是_____.9.如图,四边形ABCD中,∠B=∠D=90°,∠C=50°,在BC、CD边上分别找到点M、N,当△AMN 周长最小时,∠AMN+∠ANM的度数为______.10.如图,在ABCD 中,对角线AC 、BD 相交于点O ,点E 、F 分别是边AD 、AB 上的点,连结OE 、OF 、EF .若7AB =,52BC =,45DAB ∠=︒,则OEF 周长的最小值是_______.11.如图,点(1,3),(6,1),(,0),(2,0)A B P a N a --+为四边形的四个顶点,当四边形PABN 的周长最小时,=a ________.12.如图,在四边形ABCD 中,90,5,4,A D AB AD ∠=∠=︒==3,CD =点P 是边AD 上的动点,则PBC 周长的最小值为( )A .8B .45C .12D .65三、解答题(共0分)13.如图,四边形ABCD 为平行四边形,延长AD 到点E ,使DE AD =,且BE DC ⊥.(1)求证:四边形DBCE 为菱形;(2)若DBC △是边长为2的等边三角形,点P 、M 、N 分别在线段BE 、BC 、CE 上运动,求PM PN +的最小值.14.如图,在平行四边形ABCD 中,2,1,60AB AD B ==∠=︒,将平行四边形ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点'D 处,折痕交CD 边于点E .(1)求证:四边形'BCED 是菱形;(2)若点P 是直线l 上的一个动点,请作出使'PD PB +为最小值的点P ,并计算'PD PB +.15.如图,在平行四边形ABCD 中,30BCD ∠=︒,6BC =,33CD =,(1)平行四边形ABCD 的面积为________.(2)若M 是AD 边的中点,N 是AB 边上的一个动点,将AMN 沿MN 所在直线翻折得到A MN '△,连接A C ',则A C '长度的最小值是________.答案与解析【例题讲解】如图,在平行四边形ABCD 中,30BCD ∠=︒,6BC =,33CD =,(1)平行四边形ABCD 的面积为________.(2)若M 是AD 边的中点,N 是AB 边上的一个动点,将AMN 沿MN 所在直线翻折得到A MN '△,连接A C ',则A C '长度的最小值是________.解:(1)过点C 作CF ⊥AB ,交AB 延长线于F ,∵四边形ABCD 是平行四边形,∴AB ∥CD ,BC =6,AB =CD =33,∵∠BCD =30°=∠CBF ,∴CF =12BC =3, ∴四边形ABCD 的面积=AB CF ⨯=333⨯=93;(2)连接MC ,过点M 作ME ⊥CD 于E ,交CD 的延长线于点E ;∵四边形ABCD 为平行四边形,∴AD ∥BC ,AD =BC =6,∵点M 为AD 的中点,∠BCD =30°,∴DM =MA =3,∠MDE =∠BCD =30°,∴ME =12DM =32,DE =332,∴CE =CD +DE =33332+=932,由勾股定理得:CM 2=ME 2+CE 2, ∴CM=2239322⎛⎫⎛⎫+ ⎪ ⎪ ⎪⎝⎭⎝⎭=37,由翻折变换的性质得:MA ′=MA =3,∵MA ′+A ′C ≥MC , ∴A ′C ≥MC- MA ′= MC -3,显然,当折线MA ′C 与线段MC 重合时,线段A ′C 的长度最短,此时A ′C =373-,故答案为:(1)93;(2)373-.【综合演练】1.如图 ,在平行四边形ABCD 中 ,120C ∠=︒ ,AB =4 ,AD =8 , 点H 、G 分别是边CD 、BC 上的动点.连接AH 、HG ,点E 为AH 的中点 ,点F 为GH 的中点 ,连接EF .则EF 的最大值与最小值的差为( ) A .2 B .232- C .3 D .43- 【答案】C【分析】如图,取AD 的中点M ,连接CM 、AG 、AC ,作AN ⊥BC 于N .首先证明∠ACD =90°,求出AC ,AN ,利用三角形中位线定理,可知EF =12AG ,求出AG 的最大值以及最小值即可解决问题. 【解答】解:如图,取AD 的中点M ,连接CM 、AG 、AC ,作AN ⊥BC 于N .∵四边形ABCD 是平行四边形,∠BCD =120°,28AD AB ==∴∠D =180°−∠BCD =60°,AB =CD =4,∵AM =DM =DC =4,∴△CDM 是等边三角形,∴∠DMC =∠MCD =60°,AM =MC ,∴∠MAC =∠MCA =30°,∴∠ACD =90°,∴AC =43在Rt △ACN 中,∵AC =43,∠ACN =∠DAC =30°,∴AN =12AC =23∵AE =EH ,GF =FH ,∴EF =12AG ,∵点G 在BC 上,∴AG 的最大值为AC 的长,最小值为AN 的长,∴AG 的最大值为43,最小值为23,∴EF 的最大值为23,最小值为3,∴EF的最大值与最小值的差为:3故选C.【点评】本题考查平行四边形的性质、三角形的中位线定理、等边三角形的判定和性质、直角三角形30度角性质、垂线段最短等知识,解题的关键是学会添加常用辅助线,本题的突破点是证明∠ACD=90°,属于中考选择题中的压轴题.2.如图,在△ABC中,∠ACB=60°,∠CAB=45°,BC=4,点D为AB边上一个动点,连接CD,以DA、DC为一组邻边作平行四边形ADCE,则对角线DE的最小值是()A.2+6B.1+3C.4 D.2+23【答案】ABC=2,AF=BF=3CF 【分析】设DE交AC于O,作BF⊥AC于F,由直角三角形的性质得出CF=12AC=1+3,DO=EO,当OD⊥AB =23,求出AC=CF+AF=2+23,由平行四边形性质得出AO=CO=12时,DO的值最小,即DE的值最小,则△AOD是等腰直角三角形,即可得出结果.【解答】解:设DE交AC于O,作BF⊥AC于F,如图所示:则∠BFC=∠BF A=90°,∵∠ACB=60°,∠CAB=45°,∴∠CBF=30°,∠ABF=45°=∠CAB,BC=2,AF=BF=3CF=23,∴CF=12∴AC=CF+AF=2+23,∵四边形ADCE是平行四边形,AC=1+3,DO=EO,∴AO=CO=12∴当OD ⊥AB 时,DO 的值最小,即DE 的值最小,则△AOD 是等腰直角三角形,∴OD =22AO =622+, ∴DE =2OD =26+.故选:A .【点评】本题主要考查解直角三角形,平行四边形的性质,掌握平行四边形的性质和特殊角的三角函数值是解题的关键.3.如图,在Rt ABC 中,90,3,4B AB BC ∠=︒==,点D 为BC 上一动点(不与点C 重合),以AD ,CD 为一组邻边作平行四边形ADCE ,当DE 的值最小时,平行四边形ADCE 的周长..为_____. 【答案】4+213【分析】根据题意,可知当DE ⊥AE 时,DE 取得最小值,然后根据题目中的数据,即可得到A D 、CD 的长,从而可以得到当DE 的值最小时,平行四边形ADCE 周长.【解答】解:当DE ⊥AE 时,DE 取得最小值,设此时CD =x ,∵四边形ADCE 是平行四边形,∴CD =AE ,AD =CE ,BC ∥AE ,∵∠B =90°,DE ⊥AE ,∴四边形BAED 是矩形,∴BD =AE ,∴BD =CD =x ,∵BC =BD +CD ,BC =4,∴BD =CD =2,∵AB =3,∠B =90°,∴AD =22222313BD AB +=+=,∴当DE 的值最小时,平行四边形ADCE 周长为:2+13+2+13=4+213,故答案为:4+213.【点评】本题考查平行四边形的性质、矩形的判定与性质、垂线段最短,解答本题的关键是明确题意,利用数形结合的思想解答. 4.如图,在ABCD 中,=60B ∠︒,10AB =,8BC =,点E 为边AB 上的一个动点,连接ED ,EC , 以ED 、CE 为邻边构造EDGC ,连接EG ,则EG 的最小值为__________.【答案】83【分析】根据平行四边形的性质得到EG ,FG ,根据垂线段最短得到EG ⊥CD 时取最小值,过点C 作CH ⊥AB 于点H ,求出CH 的长度,从而得到结果.【解答】解:∵四边形EDGC 是平行四边形,∴EF =FG ,∴当EF ⊥CD 时,EF 最小,此时EG 最小,过点C 作CH ⊥AB 于点H ,则CH =EF ,∵∠B =60°,∴∠BCH =30°,∵BC =8,∴BH =4,∴CH =2284-=43,∴EF 的最小值为43,∴EG 的最小值为83,故答案为:83.【点评】本题考查了平行四边形的性质,垂线段最短,直角三角形的性质,勾股定理,解题的关键是理解题意,找到EG最短时满足的条件.5.如图,平行四边形ABCD中,AB=2,AD=1,∠ADC=60°,将平行四边形ABCD沿过点A的直线l 折叠,使点D落到AB边上的点D处,折痕交CD边于点E.若点P是直线l上的一个动点,则PD +PB 的最小值_______.【答案】7【分析】不管P点在l上哪个位置,PD始终等于PD',故求PD'+PB可以转化成求PD+PB,显然当D、P、D'共线时PD+ PB最短.【解答】过点D作DM⊥AB交BA的延长线于点M,∵四边形ABCD是平行四边形,AD=1,AB=2,∠ADC=60°,∴∠DAM=60°,由翻折变换可得,AD=AD′=1,DE=D′E,∠ADC=∠AD′E=60°,∴∠DAM=∠AD′E=60°,∴AD∥D′E,又∵DE∥AB,∴四边形ADED′是菱形,∴点D与点D′关于直线l对称,连接BD交直线l于点P,此时PD′+PB最小,PD′+PB=BD,在Rt△DAM中,AD=1,∠DAM=60°,∴AM=12AD=12,DM=32AD=32,在Rt△DBM中,DM=32,MB=AB+AM=52,∴BD=DM2+MB2=322+522=7,即PD′+PB最小值为7,故答案为:7.【点评】本题考查平行四边形性质和菱形性质,掌握这些是本题解题关键.6.如图,平行四边形ABCD中,8∠=︒,E是边AD上且2AAD=,60AB=,6=,F是边AB上AE DE+的最小值__________.的一个动点,将线段EF绕点E逆时针旋转60︒,得到EG,连接BG、CG,则BG CG【答案】221【分析】如图,取AB的中点N.连接EN,EC,GN,作EH⊥CD交CD的延长线于H.利用全等三角形的性质证明∠GNB=60°,点G的运动轨迹是射线NG,由“SAS”可证△EGN≌△BGN,可得GB=GE,推出GB+GC=GE+GC≥EC,求出EC即可解决问题.【解答】解:如图,取AB的中点N.连接EN,EC,GN,作EH⊥CD交CD的延长线于H,∵AE=2DE,∴AE=4,DE=2,∵点N是AB的中点,∴AN=NB=4,∴AE=AN,∵∠A=60°,∴△AEN是等边三角形,∴∠AEN=∠FEG=60°,∴∠AEF=∠NEG,∵EA=EN,EF=EG,∴△AEF≌△NEG(SAS),∴∠ENG=∠A=60°,∵∠ANE=60°,∴∠GNB=180°-60°-60°=60°,∴点G的运动轨迹是射线NG,∵BN=EN,∠BNG=∠ENG=60°,NG=NG∴△EGN≌△BGN(SAS),∴GB=GE,∴GB+GC=GE+GC≥EC,在Rt△DEH中,∵∠H=90°,DE=2,∠EDH=60°,DE=1,EH=3,∴DH=12在Rt△ECH中,EC=22221+=,EH CH∴GB+GC≥221,∴GB+GC的最小值为221,故答案为:221.【点评】本题考查旋转变换,轨迹,平行四边形的性质,全等三角形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造全等三角形解决问题,学会用转化的思想思考问题,属于中考常考题型.7.如图,CD是直线x=1上长度固定为1的一条动线段.已知A(﹣1,0),B(0,4),则四边形ABCD 周长的最小值为_________________.【答案】17132++【分析】在y轴上取点E,使BE=CD=1,则四边形BCDE为平行四边形,根据勾股定理得到AB,作点A关于直线x=1的对称点A',得到A'、E、D三点共线时,AD+DE最小值为A'E的长,根据勾股定理求出A'E,即可得解;【解答】解:如图,在y轴上取点E,使BE=CD=1,则四边形BCDE为平行四边形,∵B(0,4),A(﹣1,0),∴OB=4,OA=1,∴OE=3,AB=22+=,1417作点A关于直线x=1的对称点A',∴A'(3,0),AD=A'D,∴AD+DE=A'D+DE,即A'、E、D三点共线时,AD+DE最小值为A'E的长,在Rt△A'OE中,由勾股定理得A'E=22+=,3332∴C四边形ABCD最小值=AB+CD+BC+AD=AB+CD+A'E=17+1+32.故答案为:17132++.【点评】本题主要考查了轴对称最短路线问题、勾股定理、位置与坐标,准确分析作图计算是解题的关键.8.如图四边形ABCD,AD∥BC,AB⊥BC,AD=1,AB=2,BC=3,P为AB边上的一动点,以PD,PC 为边作平行四边形PCQD,则对角线PQ的长的最小值是_____.【答案】4【分析】根据题意在平行四边形PCQD中,设对角线PQ与DC相交于点O,可得O是DC的中点,过点Q作QH⊥BC,交BC的延长线于H,易证得Rt△ADP≌Rt△HCQ,即可求得BH=4,则可得当PQ⊥AB 时,PQ的长最小,即为4.【解答】解:在平行四边形PCQD中,设对角线PQ与DC相交于点O,则O是DC的中点,过点Q作QH⊥BC,交BC的延长线于H,∵AD ∥BC ,∴∠ADC=∠DCH ,即∠ADP+∠PDC=∠DCQ+∠QCH ,∵PD ∥CQ ,∴∠PDC=∠DCQ ,∴∠ADP=∠QCH ,又∵PD=CQ ,在Rt △ADP 与Rt △HCQ 中,ADP QCH A QHCPD CQ ⎧⎪⎨⎪∠∠⎩∠∠=== ∴Rt △ADP ≌Rt △HCQ (AAS ),∴AD=HC ,∵AD=1,BC=3,∴BH=4,∴当PQ ⊥AB 时,PQ 的长最小,即为4.故答案为:4.【点评】本题考查梯形的中位线的性质,注意掌握梯形的中位线等于两底和的一半且平行于两底.9.如图,四边形ABCD 中,∠B =∠D =90°,∠C =50°,在BC 、CD 边上分别找到点M 、N ,当△AMN 周长最小时,∠AMN +∠ANM 的度数为______.【答案】100°【分析】根据要使△AMN 的周长最小,即利用点的对称,让三角形的三边在同一直线上,作出A 关于BC和CD 的对称点A′,A″,即可得出∠AA′M+∠A″=180°-∠DAB =∠C=50°,进而得出∠AMN+∠ANM=2(∠AA′M+∠A″)即可得出答案.【解答】解:作A 关于BC 和CD 的对称点A′,A″,连接A′A″,交BC 于M ,交CD 于N ,则A′A″即为△AMN 的周长最小值.∵∠B =∠D =90°,∠C =50°,∵∠DAB=130°,∴∠AA′M+∠A″=180°-130°=50°,由对称性可知:∠MA′A=∠MAA′,∠NAD=∠A″,且∠MA′A+∠MAA′=∠AMN ,∠NAD+∠A″=∠ANM ,∴∠AMN+∠ANM=∠MA′A+∠MAA′+∠NAD+∠A″=2(∠AA′M+∠A″)=2×50°=100°,故答案为:100°.【点评】此题主要考查了平面内最短路线问题求法以及三角形的内角和定理及外角的性质和轴对称的性质等知识,根据已知得出M ,N 的位置是解题关键.10.如图,在ABCD 中,对角线AC 、BD 相交于点O ,点E 、F 分别是边AD 、AB 上的点,连结OE 、OF 、EF .若7AB =,52BC =,45DAB ∠=︒,则OEF 周长的最小值是_______.【答案】1322【分析】作点O 关于AB 的对称点M ,点O 关于AD 的对称点N ,连接MN 交AB 于F ,交AD 于E ,此时△OEF 的周长最小,周长的最小值=MN ,由作图得AN =AO =AM ,∠NAD =∠DAO ,∠MAB =∠BAO ,于是得到∠MAN =90°,过D 作DP ⊥AB 于P ,则△ADP 是等腰直角三角形,根据等腰直角三角形的性质得到AP =DP =22AD ,求得AP =DP =5,根据三角形的中位线的性质得到OQ =12DP =52,BQ =12BP=12(AB−AP )=1,根据勾股定理求出AO =132,然后根据等腰直角三角形的性质即可得到结论. 【解答】解:作点O 关于AB 的对称点M ,点O 关于AD 的对称点N ,连接MN 交AB 于F ,交AD 于E ,此时△OEF 的周长最小,周长的最小值=MN ,∴AN =AO =AM ,∠NAD =∠DAO ,∠MAB =∠BAO ,∵∠DAB =45°,∴∠MAN =90°,过D 作DP ⊥AB 于P ,则△ADP 是等腰直角三角形,∴AP =DP =22AD , ∵AD =BC =52,∴AP =DP =5,设OM ⊥AB 于Q ,则OQ ∥DP ,∵OD =OB ,∴OQ =12DP =52,BQ =12BP =12(AB−AP )=1, ∴AQ =6,∴AO =2222513622AQ OQ , ∴AM =AN =AO =132, ∴MN =2AM =1322, ∴△OEF 周长的最小值是1322. 故答案为:1322. 【点评】此题主要考查轴对称−−最短路线问题,平行四边形的性质,等腰直角三角形的性质,勾股定理以及三角形中位线定理等,正确的作出辅助线是解题的关键.11.如图,点(1,3),(6,1),(,0),(2,0)A B P a N a --+为四边形的四个顶点,当四边形PABN 的周长最小时,=a ________.【答案】13 4【分析】作点A关于x轴的对称点A′,则A′(1,3),将A′向右平移2个单位,即A″(3,3),连接A″B,与x轴交于点N,可判断出AP+BN=A″N+BN≥A″B,即此时四边形ABNP的周长最小,求出A″B的表达式,得到与x轴的交点,即为点N,从而可得a值.【解答】解:如图,作点A关于x轴的对称点A′,则A′(1,3),将A′向右平移2个单位,即A″(3,3),连接A″B,与x轴交于点N,则此时AP=A′P=A″N,则AP+BN=A″N+BN≥A″B,在四边形ABNP中,PN和AB均为定值,∴此时四边形ABNP的周长最小,设A″B的表达式为y=kx+b,则3361k bk b+=⎧⎨+=-⎩,解得:437kb⎧=-⎪⎨⎪=⎩,∴直线A″B的表达式为473y x=-+,令y=0,则214x=,即此时N(214,0),2124a+=,解得:a=134,故答案为:134. 【点评】本题考查了轴对称-最短路线问题:通过对称,把两条线段的和转化为一条线段,利用两点之间线段最短解决问题.12.如图,在四边形ABCD 中,90,5,4,A D AB AD ∠=∠=︒==3,CD =点P 是边AD 上的动点,则PBC 周长的最小值为( )A .8B .45C .12D .65【答案】D【分析】根据勾股定理可求BC 的长,所以要使△PBC 的周长最小,即BP+PC 最短,利用对称性,作点C 关于AD 的对称点E ,即可得出最短路线,从而求解可.【解答】解:过点C 作CG ⊥AB ,由题意可知四边形DAGC 是矩形∴CG=AD=4,BG=AB-AG=AB-CD=2∴在Rt △BCG 中,222425BC =+=作点C 关于AD 的对称点E ,连接BE ,交AD 于点P',连接'CP此时'P BC 的周长为最小值,即''''BP CP BC BP EP BC BE BC ++=++=+过点E 作EF ⊥BA ,交BA 的延长线于点F由题意可知四边形EFAD 为矩形∴EF=AD=4,DE=CD=AF=3∴在Rt △EBF 中,224(35)45BE =++=∴此时'P BC 的周长为:65BE BC +=故选:D .【点评】本题考查勾股定理解直角三角形及应用对称的性质求最短路线,掌握相关性质定理正确添加辅助线进行推理计算是解题关键.13.如图,四边形ABCD 为平行四边形,延长AD 到点E ,使DE AD =,且BE DC ⊥.(1)求证:四边形DBCE 为菱形;(2)若DBC △是边长为2的等边三角形,点P 、M 、N 分别在线段BE 、BC 、CE 上运动,求PM PN +的最小值. 【答案】(1)证明见解析(2)3【分析】(1)先根据四边形ABCD 为平行四边形的性质和DE AD =证明四边形DBCE 为平行四边形,再根据BE DC ⊥,即可得证;(2)先根据菱形对称性得,得到'PM PN PM PN +=+,进一步说明PM PN +的最小值即为菱形的高,再利用三角函数即可求解.(1)证明:∵四边形ABCD 是平行四边形,∴AD BC ∥,AD BC =,∵DE AD =,∴DE BC =,又∵点E 在AD 的延长线上,∴DE BC ∥,∴四边形DBCE 为平行四边形,又∵BE DC ⊥,∴四边形DBCE 为菱形.(2)解:如图,由菱形对称性得,点N 关于BE 的对称点'N 在DE 上,∴'PM PN PM PN +=+,当P 、M 、'N 共线时,''PM PN PM PN MN +=+=,过点D 作DH BC ⊥,垂足为H ,∵DE BC ∥,∴'MN 的最小值即为平行线间的距离DH 的长,∵DBC △是边长为2的等边三角形,∴在Rt DBH 中,60DBC ∠=︒,2DB =,sin DH DBC DB ∠=, ∴3sin 232DH DB DBC =∠=⨯=, ∴PM PN +的最小值为3.【点评】本题考查了最值问题,考查了菱形的判定和性质,平行四边形的判定和性质,三角函数等知识,运用了转化的思想方法.将最值问题转化为求菱形的高是解答本题的关键.14.如图,在平行四边形ABCD 中,2,1,60AB AD B ==∠=︒,将平行四边形ABCD 沿过点A 的直线l 折叠,使点D 落到AB 边上的点'D 处,折痕交CD 边于点E .(1)求证:四边形'BCED 是菱形;(2)若点P 是直线l 上的一个动点,请作出使'PD PB +为最小值的点P ,并计算'PD PB +.【答案】(1)见解析;(2)作图见解析,7得到DAD E'是菱形,作DG BA⊥)将ABCD沿过点A的直线∠=EA,D//DE AD∴∠=DEA∴∠=,DAE EA∴∠'DAD∴四边形=AD ADAB=,2∴=AD AD∴'是菱形;BCED(2)四边形∴与D'D连接BD交CD AB//∴∠=DAGAD=,112AG ∴=,32DG =, 52BG ∴=, 227BD DG BG ∴=+=,PD PB ∴'+的最小值为7.【点评】本题考查了平行四边形的性质,最短距离问题,勾股定理,菱形的判定和性质,正确的作出辅助线是解题的关键.。
平行四边形的对角线关系与推论

平行四边形的对角线关系与推论平行四边形是四边形中最简单也是最基础的一种类型。
它具有两对平行边,并且对边长度相等。
当我们考虑平行四边形的对角线时,我们会发现它们之间存在着一些有趣的关系与推论。
本文将探讨平行四边形的对角线关系,并推导出一些相关的结论。
一、平行四边形的对角线一个平行四边形由两条互相平行的边和与它们相交的两条对边组成。
对角线是连接平行四边形两个非相邻顶点的线段。
如图所示,ABCD是一个平行四边形,AC和BD是它的对角线。
[插入一张平行四边形的示意图]二、平行四边形的对角线交点当我们观察平行四边形的对角线时,会发现它们有一个有趣的性质:对角线相交于同一点。
也就是说,对角线AC和BD相交于点O。
[插入一张平行四边形对角线交点的示意图]这个性质可以通过数学证明得到。
不过在此处,我们将直接接受这一事实,并继续探究基于这个性质的推论。
三、平行四边形对角线的长度关系在平行四边形ABCD中,我们可以观察到一些有关对角线的长度关系。
首先,我们注意到对角线AC和BD长相等。
这是因为平行四边形的定义要求对边长度相等。
其次,我们可以观察到对角线AC和BD的中点之间构成了一条线段,假设为M。
很明显,M是AC和BD的中点,即M是线段AC和BD的交点。
由于AC和BD是平行的,所以点M也同时是直线AC和BD的中点。
基于这个观察,我们可以得出一个重要的推论:平行四边形的对角线中点相连的线段长度等于对边的长度。
即\[AM = BM = CM = DM =\frac{1}{2}(AB + CD)\]。
[插入一张平行四边形对角线的长度关系示意图]四、平行四边形内部角的关系平行四边形ABCD的内部角度也存在一些有意思的关系。
以点O为圆心,以OC为半径,我们可以画出一个圆。
这个圆将平行四边形的两组对角线分成了两个相等的扇形。
[插入一张平行四边形内部角关系的示意图]根据圆的性质,我们知道扇形的圆心角等于扇形所对的圆弧。
因此,平行四边形ABCD的两个内部角∠ADC和∠ABC等于半圆的角度。
判定平行四边形的五种方法

判别平行四边形的基本方法如何判别一个四边形是平行四边形呢?下面举例予以说明.一、运用“两条对角线互相平分的四边形是平行四边形”判别例1 如图1,在平行四边形ABCD中,E、F 在对角线AC上,且AE=CF,试说明四边形DEBF 是平行四边形.分析:由于已知条件与对角线有关,故考虑运用“两条对角线互相平分的四边形是平行四边形”进行判别.为此,需连接BD.解:连接BD交AC于点O.因为四边形ABCD是平行四边形,所以AO=CO,BO=DO. 又AE=CF,所以AO-AE=CO-CF,即EO=FO.所以四边形DEBF是平行四边形.二、运用“两组对边分别相等的四边形是平行四边形”判别例2 如图2,是由九根完全一样的小木棒搭成的图形,请你指出图中所有的平行四边形,图1AB C DEF并说明理由.分析:设每根木棒的长为1个单位长度,则图中各四边形的边长便可求得,故应考虑运用“两组对边分别相等的四边形是平行四边形”进行判别.解:设每根木棒的长为1个单位长度,则AF=BC=1,AB=FC=1,所以四边形ABCF是平行四边形.同样可知四边形FCDE、四边形ACDF都是平行四四边形.因为AE=DB=2,AB=DE=1,所以四边形ABDE也是平行四边形.三、运用“一组对边平行且相等的四边形是平行四边形”判别例3 如图3,E、F是四边形ABCD的对角线AC上的两点,AE=CF,DF=BE,DF∥BE,试说明四边形ABCD是平行四边形.分析: 题目给出的条件都不能直接判别四边形ABCD是平行四边形,但仔细观察可知,由已知条件可得△ADF≌△CBE,由此就可得到判图3别平行四边形所需的“一组对边平行且相等”的条件.解:因为DF∥BE,所以∠AFD=∠CEB.因为AE=CF,所以AE+EF=CF+EF,即AF=CE.又DF=BE,所以△ADF≌△CBE,所以AD=BC,∠DAF=∠BCE,所以AD∥BC.所以四边形ABCD是平行四边形.四、运用“两组对边分别平行的四边形是平行四边形”判别例 4 如图4,在平行四边形ABCD中,∠DAB、∠BCD的平分线分别交BC、AD边于点E、F,则四边形AECF是平行四边形吗?为什么?分析:由平行四边形的性质易得AF∥EC,又题目中给出的是有关角的条件,借助角的条件可得到平行线,故本题应考虑运用“两组对边分别平行的四边形是平行四边形”进行判别.解:四边形AECF是平行四边形.AB CDEF图41 32理由:因为四边形ABCD 是平行四边形,所以AD ∥BC ,∠DAB=∠BCD ,所以AF ∥EC.又因为∠1=21∠DAB ,∠2=21∠BCD ,所以∠1=∠2.因为AD ∥BC ,所以∠2=∠3, 所以∠1=∠3,所以AE ∥CF.所以四边形AECF 是平行四边形.判定平行四边形的五种方法平行四边形的判定方法有:(1)证两组对边分别平行;(2)证两组对边分别相等;(3)证一组对边平行且相等;(4)证对角线互相平分;(5)证两组对角分别相等。
平行边形的对角线比例与关系研究

平行边形的对角线比例与关系研究对角线是平行边形中一个重要的性质,它们的比例和关系对于数学研究和实际问题都有重要的意义。
本文将对平行边形的对角线比例与关系进行研究和探讨。
一、对角线比例的基本性质1. 平行四边形的对角线比例首先,我们来研究平行四边形的对角线比例。
设平行四边形ABCD 的对角线AC和BD交于点O,连接AO和OC,BO和OD。
根据相似三角形的性质,可以得到以下结论:① ∆AOB ∽ ∆COD (相似三角形的对应角相等)② ∆BOC ∽ ∆DOA (相似三角形的对应角相等)由此可知,对角线AC和BD所分割的平行四边形ABCD可以分成四个全等的三角形,即∆AOB ≌ ∆COD 且∆BOC ≌ ∆DOA。
由全等三角形的性质可知,对应边的比例相等,因此我们可以得出结论:AC/BD = AO/OD = BO/OC这就是平行四边形的对角线比例的基本性质。
2. 非平行四边形的对角线比例对于非平行四边形,同样可以通过相似三角形的性质得到对角线比例。
设非平行四边形ABCD的对角线AC和BD交于点O,连接AO和OC,BO和OD。
由于非平行四边形的对角线不一定平分彼此,所以无法像平行四边形那样得到对应边全等,但是,我们可以通过相似三角形的性质得到以下结论:① ∆AOB ∽ ∆COD (相似三角形的对应角相等)② ∆BOC ∽ ∆DOA (相似三角形的对应角相等)同样可以得出结论:AC/BD = AO/OD ≠ BO/OC这个结论告诉我们,在非平行四边形中,对角线的比例通常是不相等的,因此要根据具体问题来进行具体分析和计算。
二、对角线比例的应用平行边形的对角线比例和关系在几何学和实际应用中有多种应用。
1. 确定平行四边形的性质通过对角线比例,我们可以确定一个平行四边形的性质。
当对角线的比例为1时,说明该平行四边形是一个矩形;当对角线的比例为2时,说明该平行四边形是一个菱形。
2. 计算平行四边形的面积通过对角线比例,我们可以计算平行四边形的面积。
平行边形的多边形对角线比例关系

平行边形的多边形对角线比例关系平行边形是指具有两组平行边的多边形,它们之间存在一种特殊的对角线比例关系。
本文将探讨平行边形内部各个对角线的比例关系。
1. 平行四边形的对角线比例关系平行四边形是一种特殊的平行边形,它的两组对边恒定平行。
设平行四边形的对角线交点为O,则连接O与相邻的顶点A、B、C、D得到四条对角线。
在平行四边形ABCD中,连接对角线AC和对角线BD,我们可以观察到以下比例关系:AD:BC = AO:CO = BO:DO = AB:CD这个比例关系可以通过平行四边形的性质进行证明。
由于ABCD是平行四边形,所以AB ∥ CD,AC ∥ BD。
根据平行线的性质,我们可以得知三角形AOD与三角形BOC相似。
因此,我们推导出AO:BO = DO:CO。
同理,根据三角形AOC与三角形BOD的相似性,我们得到AO:CO = BO:DO。
综上所述,我们得到了平行四边形的对角线比例关系。
2. 平行六边形的对角线比例关系平行六边形是一种具有六条平行边的多边形。
设平行六边形的对角线交点为O,则连接O与相邻的顶点A、B、C、D、E、F得到六条对角线。
在平行六边形ABCDEF中,连接对角线AD、BE和CF,我们可以观察到以下比例关系:AD:BE:CF = AO:BO:CO = DO:EO:FO = AB:CD:FE这个比例关系可以通过平行六边形的性质进行证明。
由于ABCDEF 是平行六边形,所以AD ∥ BE ∥ CF。
根据平行线的性质,我们可以得知三角形ADO与三角形BEO、三角形CEF的相似关系,因此AO:BO = DO:EO = CO:FO。
同理,我们可以得到三角形ABO与三角形CDO、三角形BED与三角形EFC的相似关系。
综上所述,我们得到了平行六边形的对角线比例关系。
3. 平行多边形的对角线比例关系类似于平行四边形和平行六边形,平行多边形的对角线也具有一定的比例关系。
无论是平行四边形还是平行六边形,我们都可以推广到具有更多边的平行多边形,其对角线比例关系仍然成立。
解平行四边形的对角线与边长问题

解平行四边形的对角线与边长问题在平面几何中,平行四边形是指具有两组对边分别平行,两组对边长度相等的四边形。
解决平行四边形的对角线与边长问题,是通过已知条件推导出未知条件的过程。
本文将从不同角度探讨该问题,并提供相关的解决方法。
一、平行四边形的基本性质平行四边形的一些基本性质可以帮助我们解决对角线与边长之间的关系问题。
这些性质如下:1. 平行四边形的对边是平行的;2. 平行四边形的对边长度相等;3. 平行四边形的对角线互相平分;4. 平行四边形的对角线长度相等。
根据这些性质,我们可以通过已知的边长或对角线长度,推导出其他未知的边长或对角线长度。
二、已知边长求对角线长度如果我们已知平行四边形的边长,想要求出对角线长度,可以采用以下方法之一:1. 利用勾股定理。
设平行四边形的边长分别为a和b,对角线的长度为d1和d2。
根据勾股定理,可得d1^2 = a^2 + b^2,d2^2 = a^2 +b^2。
因此,通过计算边长的平方和再开平方根,即可求出对角线的长度。
2. 利用对角线平分性质。
设平行四边形的边长分别为a和b,对角线的长度分别为d1和d2。
由于对角线互相平分,所以d1 = d2。
因此,可以通过已知的边长求出对角线的长度。
三、已知对角线长度求边长如果我们已知平行四边形的对角线长度,想要求出边长,可以采用以下方法之一:1. 利用勾股定理。
设平行四边形的对角线长度为d1和d2,边长为a和b。
根据勾股定理,可得a^2 + b^2 = d1^2,a^2 + b^2 = d2^2。
因此,通过计算对角线长度的平方和再开平方根,即可求出边长。
2. 利用对角线平分性质。
设平行四边形的对角线长度为d1和d2,边长为a和b。
由于对角线互相平分,所以d1 = d2。
因此,可以通过已知的对角线长度求出边长。
四、实际问题应用平行四边形的对角线与边长问题在实际问题中有广泛的应用。
以下是几个典型的例子:1. 电子屏幕尺寸确定。
