【精品奥数】五年级下册数学奥数讲义-第一讲 共边模型 通用版(含答案)
小学五年级下册奥数题型分类讲义(附答案)

小学五年级下册奥数题型分类讲义(附答案)图形问题专题1长方形、正方形的周长一、专题解析同学们都知道,长方形的周长=(长+宽)×2,正方形的周长=边长×4.长方形、正方形的周长公式只能用来计算标准的长方形和正方形的周长。
那么如何应用所学知识巧求表面上看起来不是长方形或正方形的图形的周长呢?还需同学们灵活应用已学知识,掌握转化的思考方法,把复杂的图形转化为标准的图形,以便计算它们的周长。
二、精讲精练例题1】有5张同样大小的纸如下图(a)重叠着,每张纸都是边长6厘米的正方形,重叠的部分为边长的一半,求重叠后图形的周长。
思路导航】根据题意,我们可以把每个正方形的边长的一半同时向左、右、上、下平移(如图b),转化成一个大正方形,这个大正方形的周长和原来5个小正方形重叠后的图形的周长相等。
因此,所求周长是18×4=72厘米。
操演11、右图由8个边长都是2厘米的正方形组成,求这个图形的周长。
2、右图由1个正方形和2个长方形组成,下方长方形长为50cm,求这个图形的周长。
3、有6块边长是1厘米的正方形,如例题中所说的这样重叠着,求重叠后图形的周长。
1例题2】一块长方形木板,沿着它的长度不同的两条边各截去4厘米,截掉的面积为192平方厘米。
现在这块木板的周长是多少厘米?思路导航】把截掉的192平方厘米分红A、B、C三块(如图),个中AB的面积是192-4×4=176(平方厘米)。
把A和B移到一同拼成一个宽4厘米的长方形,而此长方形的长就是这块木板剩下部分的周长的一半。
176÷4=44(厘米),现在这块木板的周长是44×2=88(厘米)。
练21、有一个长方形,如果长减少4米,宽减少2米,面积就比原来减少44平方米,且剩下部分恰好是一个正方形。
求这个正方形的周长。
2、有两个相同的长方形,长是8厘米,宽是3厘米,如果按下图叠放在一起,这个图形的周长是几何?3、有一块长方形广场,沿着它不同的两条边各划出2米做绿化带,剩下的部分仍是长方形。
五年级下册数学竞赛试题-14讲图形-五大模型全国通用(含答案)
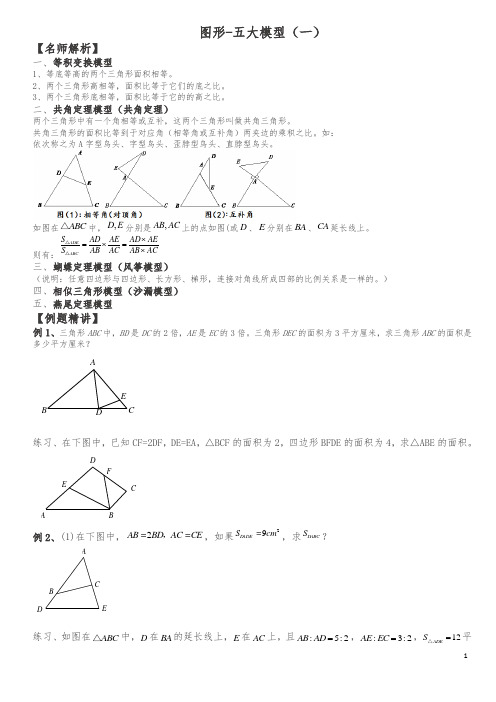
图形-五大模型(一)【名师解析】一、等积变换模型1、等底等高的两个三角形面积相等。
2、两个三角形高相等,面积比等于它们的底之比。
3、两个三角形底相等,面积比等于它的的高之比。
二、共角定理模型(共角定理)两个三角形中有一个角相等或互补,这两个三角形叫做共角三角形。
共角三角形的面积比等到于对应角(相等角或互补角)两夹边的乘积之比。
如: 依次称之为A 字型鸟头、字型鸟头、歪脖型鸟头、直脖型鸟头。
如图在ABC △中,,D E 分别是,AB AC 上的点如图(或D 、E 分别在BA 、CA 延长线上。
则有:ADE ABC S AD AE AD AES AB AC AB AC⨯=⨯=⨯△△三、蝴蝶定理模型(风筝模型)(说明:任意四边形与四边形、长方形、梯形,连接对角线所成四部的比例关系是一样的。
)四、相似三角形模型(沙漏模型) 五、燕尾定理模型【例题精讲】例1、三角形ABC 中,BD 是DC 的2倍,AE 是EC 的3倍。
三角形DEC 的面积为3平方厘米,求三角形ABC 的面积是多少平方厘米?EADCB练习、在下图中,已知CF=2DF ,DE=EA ,△BCF 的面积为2,四边形BFDE 的面积为4,求△ABE 的面积。
FEDC BA例2、(1)在下图中,2AB BD AC CE ==,,如果29ADE S cm D =,求ABC S D ?EDC B A练习、如图在ABC △中,D 在BA 的延长线上,E 在AC 上,且:5:2AB AD =,:3:2AE EC =,12ADE S =△平方厘米,求ABC △的面积.D EABC例3、正方形ABCD 边长为6 厘米,BC CF AC AE 3131==,.三角形DEF 的面积为多少平方厘米?A B CDE练习、如图,1ABC S =△,5BC BD =,4AC EC =,DG GS SE ==,AF FG =.求FGS S V .SGF E DCBA例4、一个长方形,被两条直线分成四个长方形,其中三个的面积是20亩、25亩和30亩.问另一个长方形的面积是多少亩?练习、下图中,长方形被两条直线分成四个小长方形,其中三个的面积分别是12平方米、8平方米、20平方米,求另一个(图中阴影都分)长方形的面积。
五年级数学奥数精品讲义1-34讲

五年级数学奥数精品讲义1-34讲(总87页)-CAL-FENGHAI.-(YICAI)-Company One1-CAL-本页仅作为文档封面,使用请直接删除目录第一讲消去问题(一)第二讲消去问题(二)第三讲一般应用题第四讲盈亏问题(一)第五讲盈亏问题(二)第六讲流水问题第七讲等差数列第八讲找规律能力测试(一)第九讲加法原理第十讲乘法法原理第十一讲周期问题(一)第十二讲周期问题(二)第十三讲巧算(一)第十四讲巧算(二)第十五讲数阵问题(一)第十六讲数阵问题(二)能力测试(二)第十七讲平面图形的计算(一)第十八讲平面图形的计算(二)第十九讲列方程解应用题(一)第二十讲列方程解应用题(二)第二十一讲行程问题(一)第二十二讲行程问题(二)第二十三讲行程问题(三)第二十四讲行程问题(四)能力测试(三)第二十五讲平均数问题(一)第二十六讲平均数问题(二)第二十七讲长方体和正方体(一)第二十八讲长方体和正方体(二)第二十九讲数的整除特征第三十讲奇偶性问题第三十一讲最大公约数和最小公倍数第三十二讲分解质因数(一)第三十三讲分解质因数(二)第三十四讲牛顿问题能力测试(四)2第一讲消去问题(一)在有些应用题里,给出了两个或者两个以上的未知数量间的关系,要求出这些未知数的数量。
我们在解题时,可以通过比较条件,分析对应的未知数量变化的情况,想办法消去其中的一个未知量,从而把一道数量关系较复杂的题目变成比较简单的题目解答出来。
这样的解题方法,我们通常把它叫做“消去法”。
例题与方法在学习例题前,我们先进行一些基本数量关系的练习,为用消去法解题作好准备。
(1)买1个皮球和1个足球共用去40元,买同样的5个皮球和5个足球一共用去多少元?(2)3袋子、大米和3袋面粉共重225、千克,1袋大米和1袋面粉共重多少千克?(3)6行桃树和6行梨树一共120棵,照这样子计算8行桃树和8行梨树一共有多少棵?(4)学校买了4个水瓶和25个茶杯,一共用去172元,每个水瓶18元,每个茶杯多少元?例1学校第一次买了3个水瓶和20个茶杯,共用去134元;第二次又买了同样的3个水瓶和16个差杯,共用去118元。
【精品奥数】五年级下册数学奥数讲义-第一讲 共边模型 通用版(含答案)

共边模型
一、等积模型
由三角形面积公式可以得到,若两个三角形底相等,高也相等,那么它们的面积必然也是相等的。
如图所示:
b
a
由图示可直接得到
,
结论1:两个三角形,底相等,高相等,面积相等;
结论1:夹在一组平行线之间的同底(等底)三角形面积相等;
结论2:夹在一组平行线之间的两个同底三角形,会有三对三角形面积相等.
补充:
1.
两个三角形,若底相等,一个高是另外一个高的几倍,那么它的面积也是另一个的几倍.如图所示:
2.两个三角形,若底相等,一个高是另外一个高的几倍,那么它的面积也是另一个的几倍.
如图所示:
b
a
练习题
1.如图所示,四边形ABCD是边长为18的正方形,E、F、G分别是AB、BC、CD的三等分
点,H是AD上任意一点,求图中的阴影部分面积.
H
2. 如图所示,四边形ABCD 是边长为8的正方形,四边形GIHJ 的面积为5,求图中阴影部分
的面积.
3.
如图所示,已知,求图中阴影部分面积.
B C
参考答案
1. 【解答】108
【解析】连接HC、HB,如图所示:
H
2. 【解答】22
【解析】
3. 【解答】12.5
【解析】连接CF,如图所示:
B
C。
五年级同步奥数讲义(全册)

第一讲最不利原则例1.盒子里有5支红笔,3支蓝笔,10支黑笔。
现在随意抓一把笔要确保其中至少有1支红笔,则一把必须不少于几支?分析:抓得巧,只要抓1支即可。
然而并不能保证实现这种情况。
最不利的情况是抓了13支,都是不想要的黑笔与蓝笔。
不过,只要再多抓1支就必定包含红的了。
解:10+3+1=14(支)例2.一列2个小方格,每个方格中随意涂红黑两种颜色中的一种,当涂毕第几列时,至少有2列是相同的?(有一列与另一列重复)。
分析:不妨这样想:要实现两列所用颜色一样,涂的顺序也相同。
然而,由于是任意选的,据最不利原则总是先考虑已涂各列没有重复的。
如:红红黑黑……红黑黑红……实际上各不相同的列数总共只有4列。
到第5列就必定重复前面涂过的4种中的某一种。
如果并非遇到最不利情况,那么在前5列中重复的列数就不止2列。
这与“至少2列”并不矛盾。
解:4+1=5(列)练习一1.盒子里有3支红笔,6支蓝笔,10支黑笔。
现在随意抓一把笔要确保其中至少有1支红笔,则一把必须不少于几支?2.鱼池中有30条白鳞鱼,50条黑鳞鱼,50条金鳞鱼。
至少在多少名钓鱼者中才可保证他们一次钓出的鱼中,必有金鳞鱼?3.在一个口袋中有10个黑球、 6个白球、 4个红球。
问:至少从中取出多少个球,才能保证其中有白球?4.口袋中有三种颜色的筷子各10根,问:至少取多少根才能保证三种颜色都取到?5.在三个口袋中各有10个黑球、10个白球、10个红球。
问:至少从中取出多少个球,才能保证其中有白球?第二讲抽屉原理专题简析:如果给你5盒饼干,让你把它们放到4个抽屉里,那么可以肯定有一个抽屉里至少有2盒饼干。
如果把4封信投到3个邮箱中,那么可以肯定有一个邮箱中至少有2封信。
如果把3本联练习册分给两位同学,那么可以肯定其中有一位同学至少分到2本练习册。
这些简单内的例子就是数学中的“抽屉原理”。
基本的抽屉原理有两条:(1)如果把x+k(k≥1)个元素放到x 个抽屉里,那么至少有一个抽屉里含有2个或2个以上的元素。
小学五年级下册基础奥数教程含答案(精品)

10.一只猴子每天都要吃桃子,如果它每天吃桃子的数量 Math-y
互不 2
IMO
相同,那么 100 个桃子最多够这只猴子吃多少天? 11.某同学把他最喜爱的书顺序编号为 1, 2,3,…,所有编号之和是 100 的倍数且小
于 1000,则他编号的最大数是多少?(2002 年小学数学奥林匹克预赛题) 12. 有若干人的年龄的和是 4476 岁, 其中年龄最大的不超过 79 岁, 最小的不低于
解法一:用大长方形的面积,减去阴影周围空白部分的面积。长方形的面积是 6×5= 30,左上角三角形的面积是 2×2÷2=2,左下角三角形的面积是 3×1÷2=1.5,右下角左 边三角形的面积是 2×1÷2=1,右边梯形的面积是(1+4)×3÷2=7.5,右上角左边三角形
Math-y
3
IMO
的面积是 2×1÷2=1,右边梯形的面积是(1+2)×3÷2=4.5,所以阴影部分的面积是 30-(2
1.计算:23.91+37.78+51.65+65.52+79.39+93.26+107.13=? 2.计算 1+2+3+2+4+6+3+6+9+…+100+200+300。 3.计算:1+3+4+6+7+9+10+12+13+…+66+67+69+70。 4.计算 100×95-95×90+90×85-85×80+80×75-75×70+…+20×15-15×10 +10×5。(吉林省第九届小学数学邀请赛试题) 5.计算(1994+1992+1990+…+4+2)-(1+3+5+…+1991+1993)。 6.计算 (2004-1)+(2003-2)+(2002-3)+…+(1003-1002)。(吉林省第 九届小学数学邀请赛试题) 7.如图,照这样摆下去,若摆到 80 层,一共需要□多少个?■多少个?
数学共边模型课件(五年级)奥数

点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
您的内容打在这里,或者通过复制的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。
01 点击此处添加标题 02 点击此处添加标题 03 点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
S2+S4=O+☆+△+? 相等
知识链接
面积等分三角形 三角形平分底边,那么,将会平分 三角形的面积
例题四(★ ★ ★ )
如图所示,长方形ABCD内的阴影部分的面积之和为70,AB
=8,AD=15,四边形EFGO的面积为
。
长方形面积:15×8=120 △AFC和△DFB的面积之和为 120÷2=60而空白部分的面积: 120-70=50所以四边形EFGO的面 积是60-50=10
阴=4.5(cm2 )
△AED=4.5
知识链接
3、三角形等分面积;得分底边,即可等分面积
例题【三】(★ ★ ★ )
如图,E、F、G、H分别是四边形ABCD各边四边形ABC各边的中点 ,S1、S2、S3及S4分别表示四个小四边形的面积. 试比较S1+S3与S2+S4的大小。
最新小学五年级奥数全册讲义(1-30讲)(含详解)【值得拥有】

小学五年级奥数全册讲义第1讲数字迷(一)第2讲数字谜(二)第3讲定义新运算(一)第4讲定义新运算(二)第5讲数的整除性(一)第6讲数的整除性(二)第7讲奇偶性(一)第8讲奇偶性(二)第9讲奇偶性(三)第10讲质数与合数第11讲分解质因数第12讲最大公约数与最小公倍数(一)第13讲最大公约数与最小公倍数(二)第14讲余数问题第15讲孙子问题与逐步约束法第16讲巧算24第17讲位置原则第18讲最大最小第19讲图形的分割与拼接第20讲多边形的面积第21讲用等量代换求面积第22 用割补法求面积第23讲列方程解应用题第24讲行程问题(一)第25讲行程问题(二)第26讲行程问题(三)第27讲逻辑问题(一)第28讲逻辑问题(二)第29讲抽屉原理(一)第30讲抽屉原理(二)第1讲数字谜(一)数字谜的内容在三年级和四年级都讲过,同学们已经掌握了不少方法。
例如用猜想、拼凑、排除、枚举等方法解题。
数字谜涉及的知识多,思考性强,所以很能锻炼我们的思维。
这两讲除了复习巩固学过的知识外,还要讲述数字谜的代数解法及小数的除法竖式问题。
例1 把+,-,×,÷四个运算符号,分别填入下面等式的○内,使等式成立(每个运算符号只准使用一次):(5○13○7)○(17○9)=12。
分析与解:因为运算结果是整数,在四则运算中只有除法运算可能出现分数,所以应首先确定“÷”的位置。
当“÷”在第一个○内时,因为除数是13,要想得到整数,只有第二个括号内是13的倍数,此时只有下面一种填法,不合题意。
(5÷13-7)×(17+9)。
当“÷”在第二或第四个○内时,运算结果不可能是整数。
当“÷”在第三个○内时,可得下面的填法:(5+13×7)÷(17-9)=12。
例2 将1~9这九个数字分别填入下式中的□中,使等式成立:□□□×□□=□□×□□=5568。
小学奥数五年级测试及答案(共边模型、共角模型)

一、共边模型
如果你的文档出现显示不全的问题,请调整页边距,或将图片缩小查看。
第1题
第2题
第3题
第4题
第5题
第6题
试题答案第1题:
答案解析
第2题:正确答案:D 答案解析
第3题:正确答案:D 答案解析
第4题:正确答案:C 答案解析
正确答案:C
答案解析
第6题:
正确答案:D
答案解析
二、共角模型第1题
第2题
第3题
第4题
第5题
第6题
试题答案
第1题:
正确答案:C 答案解析
第2题:
正确答案:C 答案解析
第3题:
正确答案:B 答案解析
第4题:
正确答案:D 答案解析
第5题:正确答案:D 答案解析
第6题:正确答案:C 答案解析。
【教材同步】春季学期五年级奥数教程下册【讲义】

春季学期北师大版数学五年级奥数讲义2020年3月制目录第一讲多边形的面积1.1面积计算1.2等积变形1.3列方程求面积第二讲二元一次方程组第三讲牛吃草问题第四讲分数的简算(加减法)第五讲分数的简算(乘法)第六讲分数除法应用题第七讲较复杂分数应用题第八讲浓度问题(百分数)第九讲长方体和正方体的表面积第十讲长方体和正方体的体积第十一讲应用题综合练习(一)第十二讲应用题综合练习(二)第一讲多边形的面积面积的计算[同步巩固演练]1、求下图中每个小图形的阴影部分的面积(单位:厘米)[能力拓展平台]1、已知三角形ABC的周长是20厘米,三角形内一点到三角形三条边的距离都是3厘米,求三角形的面积。
第1题2、如图,ABCG是4×7的长方形,DEFG是2×10的长方形,那么三角形BCM的面积与三角形DEM的面积之差是多少?(单位:厘米)第2题3、求阴影部分的面积(单位:厘米)4、长方形ABCD 的边上有二点E 、F 、AF 、BE 、BE 把长方形分成若干块,其中三个小块的面积标注在图上,求阴影部分面积。
第4题5、(第五届华杯赛试题)涂阴影部分的小正六角星形面积是16平方厘米,问大正六角星的面积是多少平方厘米第5题等积变形[同步巩固演练]1、如图所示,已知矩形ABCD 中,BE=21EC ,则△ABE 和△ABC 的面积之比是多少?第1题2、如图所示,梯形ABCD 中共有8个三角形,其中,面积相等的三角形有多少对?第2题3、如图,三角形ABC 的面积是18平方厘米,BD=2DC ,AE=EC ,则三角形BDE 的面积是多少平方厘米?第3题4、如图已知BC=6BD ,AB=5BE ,三角形BDE 的面积是1,则三角形ABC 的面积是多少?第4题5、如图ABCD 是平行四边形,AE=32AB ,则梯形EBCD 的面积是三角形AED 的面积是多少倍?6、如图所示,三角形ABC 中,BD=DC ,ED=2AE ,BF=FD ,三角形ABC 的面积是1,三角形DFE 的面积是多少?第6题[能力拓展平台]1、如图E 、F 分别为平行四边形ABCD 两条邻边的中点,若平行四边行的面积是1,则图中面积为41的三角形有多少个。
五年级奥数之共边模型
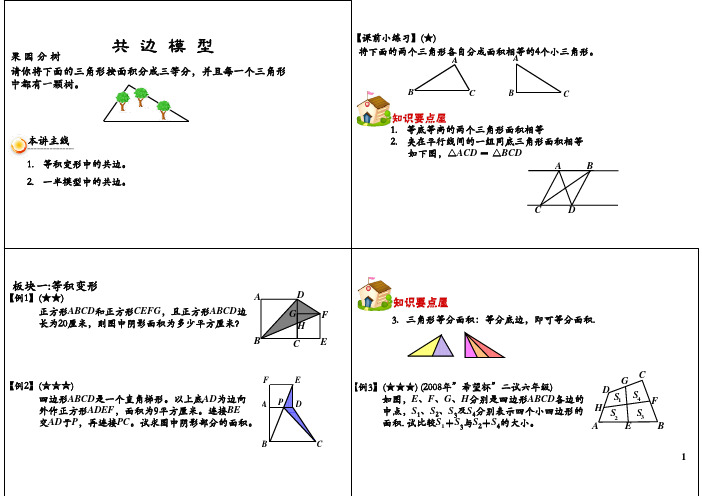
1等积变形中的共边
本讲主线
1.等积变形中的共边。
2.一半模型中的共边。
1.等底等高的两个三角形面积相等
夹在行线间的2.夹在平行线间的一组同底三角形面积相等如下图,△E P
D
C
3. 三角形等分面积:等分底边,即可等分面积.
【例3】(★★★)(2008年”希望杯”二试六年级)(2008年希望杯二试六年级)如图,E 、F 、G 、H 分别是四边形中点S 1、S 2、S 及S 4分别表示四个小四边形的中点,面积. 试比较S 1+与S 2+S 4的大小。
板块二:一半模型
4. 一半模型
长方形中,
平行四边形中,
【例5】(★★)
如下图长方形
如下图,长方形AFEB和长方形FDCE拼成了长
方形ABCD,长方形ABCD的长是20,宽是12,
则它内部阴影部分的面积是
则它内部阴影部分的面积是______。
知识大总结
1三角形面积底×高÷2A
1.三角形面积=底×高÷2
平行线性质:夹在平行线间的一
组同底三角形面积相等
组同底三角形面积相等.
面积等分三角形:
C
4.一半模型:
例1,例4,超常大挑战
______________________________________________。
_______________________________________________。
高斯小学奥数五年级下册含答案第01讲_圆与扇形初步

第一讲圆与扇形初步- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -圆是宇宙中最简单的图形:天上的太阳、月亮、行星和恒星,它们在太空中呈现圆和球形;地上的滚滚车轮,家里的盘子、碗、钟表也都是圆的.在自然界中,没有像圆那样美的图形了.圆匀称、饱满、光滑、对称,常用来象征吉祥如意,表达人们的良好愿望:圆满、圆梦、团圆……古希腊毕达哥拉斯学派认为:“一切立体图形中最美的是球体,一切平面图形中最美的是圆形”.他们认为,圆是神创造出来的最完美的东西.在纸上画一点O ,并在纸上找到所有与O 距离为1的点,如A 、B 、C 、D 、E 、F 、G ……等.这些点合到一起,就构成一个圆..点O 就称为该圆的圆心..;圆心与圆周上任意一点的连线(例如线段OA 、OB 、OC 、OD 等)叫半径..;通过圆心,并且两端都在圆上的线段叫直.径..直径长恰好是半径长的两倍.圆心确定了圆所在的位置,半径长度确定了圆的大小.一个圆只要确定了“圆心”和“半径”,就能完全确定下来.圆周长与直径的比值是一个固定不变的数,我们称之为圆周率...,用希腊字母π表示.很早的时候,人们就利用滚圆法知道了π大约是3.随着科学的进步,现在我们已经知道圆周率是一个无限不循环小数,无法写成分数的形式.在实际问题的计算中,常常取近似值3.14.直径长度通常用字母d 来表示,半径长度通常用r 来表示,圆周长通常用C 来表示.于是有圆周长公式:习惯上,圆面积用字母S 来表示.它的计算公式为:这一计算公式可以通过圆的周长公式推导出来.大家仔细观察下图,想想看应该如何推导?练一练下面的题目中,π都取为3.14.1.已知一个圆的半径为3厘米,那么这个圆的周长为_______厘米;2.已知一个圆的周长为50.24厘米,那么这个圆的直径为_______厘米;3.已知一个圆的半径为3厘米,那么这个圆的面积为_______平方厘米;4.已知一个圆的面积为78.5平方厘米,那么这个圆的半径为_______厘米.扇形是指圆上被两条半径和半径之间的弧所包围的部分.其中,圆的半径也称为扇形的半径,而两条半径所成的夹角称为扇形的圆心角.扇形是圆的一部分.要想知道扇形的弧长与面积,只要知道它是所在圆的几分之几就可以.它是圆的几分之几,它的弧长就是圆周长的几分之几,它的面积也同样就是圆面积的几分之几.需要注意的是,扇形的弧长不是它的周长...........,扇形的周长还必须加上两条半径!练一练5. 已知一个扇形的半径是2厘米,圆心角是45°,那么这个扇形所在圆的面积是_______平方厘米;扇形的圆心角占圆周角的____分之____,它的面积占圆面积的____分之____,这个扇形的面积是______.6. 已知一个扇形的半径为6厘米,圆心角为120°,那么这个扇形的弧长为________厘米,周长是_______厘米;面积为_______平方厘米.7. 已知一个扇形的半径为4厘米,面积为12.56平方厘米,它的弧长等于_______厘米,周长等于______厘米.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - 例题1.有一个圆形花坛,直径为20米,一只小蜜蜂沿着花坛外周飞了一圈,请问它飞了多少米?如果小蜜蜂沿着图中的虚线,飞一个“8”字,路线构成过花坛圆心的两个小圆,那么这次它飞了多少米?(π取3.14) 分析:小圆的直径是多少?练习1.半径分别为1、2、3、4厘米的四个圆的周长之和是多少厘米?(π取3.14)例题2.如图,在一块面积为28.26平方厘米的圆形铝板中,裁出了7个同样大小的圆铝板.问:余下的边角料的总面积是多少平方厘米?(π取3.14) 分析:大圆的半径是多少?小圆的半径又是多少?练习2.如图,在一块面积为12.56平方厘米的纸板中,裁出了2个同样大小的圆纸板.问:余下的纸板的总面积是多少平方厘米?(π取3.14)- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -一个规则的圆或扇形直接利用公式就可以求解,但一个不规则图形就没那么容易.在求解之前,先得当一回“裁缝”,将图形拆分、重组,然后再利用规则图形的相加或相减来进行求解.- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例题3.如图,图中的三角形都是等腰直角三角形,求各图中阴影部分的面积.(π取3.14)分析:经过适当的分割和移动,图中不规则的阴影部分可以拼成规则的几何图形.练习3.图中的4个圆的圆心恰好是正方形的4个顶点,如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?(π取3.14)444例题4.如图是一个直径是3厘米的半圆,AB 是直径.如图所示,让A 点不动,把整个半圆逆时针转60°,此时B 点移动到C 点.请问:图中阴影部分的面积是多少平方厘米?(π取3.14)分析:图(2)中整个图形的面积是多少,空白部分的面积又是多少?先列出算式,看看有没有可以抵消的部分.练习4.下图(1)是一个半径为3厘米的半圆,AB 是直径.如图(2)所示,让A 点不动,把整个半圆顺时针转30°,此时B 点移动到C 点.请问:图中阴影部分的面积是多少平方厘米?小知识圆有很多有意思的性质:➢ 圆心到圆上的每个点的距离都相等,这是圆的定义.➢ 每条经过圆心的直线都把圆平分为两半,都是圆的对称轴,因而圆有无数条对称轴. ➢ 圆绕着圆心任意旋转,所得的图形与原来的圆重合.➢ 所有的圆之间都可以通过缩放相互转换,因而圆只有唯一一种形状,任意两个圆都是相似的.➢ 所有平面图形在周长相同的情况下,圆的面积是最大的.因而圆也被称为平面上最完美的图形.A BB (1)(1) A A B B (2)例题5.图中的4个圆的圆心是正方形的4个顶点,它们的公共点是该正方形的中心.如果每个圆的半径都是1厘米,那么阴影部分的总面积是多少平方厘米?分析:图中的阴影部分虽然很对称,但并不规则,无法用公式直接计算.那能不能通过恰当的割补将其变为一个规则图形进行求解呢?同学们不妨动手试一试.- - - - - - - - - - - - - - - - - - - - - -- - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - - -例6. 右图是由一个圆与一个直角扇形重叠组成的,其中圆的直径与扇形的半径都是4.图中阴影部分的面积是多少?(π取3.14)分析:阴影部分的两个小弓形可以拼到哪里?圆的历史圆形,是一个看来简单,实际上十分奇妙的图形.古代人最早是从太阳、阴历十五的月亮得到圆的概念的.在一万八千年前的山顶洞人曾经在兽牙、砾石和石珠上钻孔,那些孔有的就很圆.到了陶器时代,许多陶器都是圆的.圆的陶器是将泥土放在一个转盘上制成的.当人们开始纺线,又制出了圆形的石纺锤或陶纺锤.古代人还发现搬运圆的木头时滚着走比较省劲.后来他们在搬运重物的时候,就把几段圆木垫在大树、大石头下面滚着走,这样当然比扛着走省劲得多.约在6000年前,美索不达米亚人,做出了世界上第一个轮子——圆形的木盘.大约在4000多年前,人们将圆的木盘固定在木架下,这就成了最初的车子.会作圆,但不一定就懂得圆的性质.古代埃及人就认为:圆,是神赐给人的神圣图形.一直到两千多年前我国的墨子(约公元前468~前376年)才给圆下了一个定义:圆,一中同长也.意思是说:圆有一个圆心,圆心到圆周的长都相等.这个定义比希腊数学家欧几里得(约公元前330~前275年)给圆下定义要早100年.任意一个圆的周长与它直径的比值是一个固定的数,我们把它叫做圆周率,用字母π表示.它是一个无限不循环小数,π=3.1415926535…但在实际运用中一般只取它的近似值,即π≈3.14.如果用C表示圆的周长:C=πd或C=2πr.《周髀算经》上说“周三径一”,把圆周率看成3,但是这只是一个近似值.美索不达米亚人在作第一个轮子的时候,也只知道圆周率是3.魏晋时期的刘徽于公元263年给《九章算术》作注时,发现“周三径一”只是圆内接正六边形周长和直径的比值.他创立了割圆术,认为圆内接正多边形边数无限增加时,周长就越逼近圆周长.他算到圆内接正3072边形的圆周率,π=3927/1250.刘徽把极限的概念运用于解决实际的数学问题之中,这在世界数学史上也是一项重大的成就.祖冲之(公元429~500年)在前人的计算基础上继续推算,求出圆周率在3.1415926与3.1415927之间,是世界上最早的七位小数精确值,他还用两个分数值来表示圆周率:22/7称为约率,355/113称为密率.在欧洲,直到1000年后的十六世纪,德国人鄂图(公元1573年)和安托尼兹才得到这个数值.现在有了电子计算机,圆周率已经算到了小数点后12400亿位了.作业1. 面积为78.5平方厘米的圆,周长是多少厘米?(π取3.14)作业2. 一个半径为3分米的扇形,面积为6.28平方分米,那么它的圆心角是多少度?(π取3.14) 作业3. 如图,三角形ABC 为等边三角形,边长为2,D 为BC 边中点.分别以B 、C 为圆心、1为半径作两个扇形(即图中阴影部分).那么阴影部分的面积是多少?(π取近似值3.14,结果保留2位小数) 作业4. 如图,ABCD 是正方形,且F A =AD =DE =1,阴影部分的面积是多少?(π取3.14)作业5. 图中阴影部分的面积是多少平方厘米?(图中长度单位为厘米,π取3.14)第4题图第3题图第一讲 圆与扇形初步例题1.答案:62.8米详解:小圆半径是5米,飞行路线为两个小圆周长,所以是2π5262.8⨯⨯=米.无论小圆有多少个,大小是否相等,只要所有小圆的直径之和等于大圆,那么它们的周长之和也等于大圆. 例题2.答案:6.28平方厘米详解:228.26 3.143÷=,大圆半径是3厘米.小圆半径是1厘米,所以边角料面积为228.2671 3.14 6.28-⨯⨯=平方厘米.例题3.答案:4;4.56;8详解:(1)割补法,将右边的弓形补到左边,两块阴影面积之和恰好为等腰直角三角形面积的一半.即44224⨯÷÷=.(2)割补法,如图,将图中的叶子形从中间分成面积相等的两个小弓形,阴影部分可拼成一个完整弓形,面积为1144 3.1444 4.5642⨯⨯⨯-⨯⨯=. (3)割补法.正好是把第二问的过程反过来,把两个小弓形补到空白部分,阴影部分面积之和正好是等腰直角三角形的面积,即4428⨯÷=.例题4.答案:4.71详解:图中阴影部分面积为整个图形面积减去半圆的面积,而整个图形面积为一个半圆面积与一个圆心角为60°的扇形面积之和.因此阴影面积等于圆心角为60°的扇形面积,即21π3 4.716⨯⨯=.例题5.答案:8平方厘米详解:如图,阴影部分总面积等于虚边正方形面积,该正方形的对角线长为圆直径的两倍,等于4厘米,所以面积为平方厘米.例题6.答案:4.56详解:如图,把两个阴影部分的小弓形补到空白部分之后,可以看出阴影部分的面积之和等于大扇形的面积减去圆中正方形的面积.21π4442 4.564⨯⨯-⨯÷=.4428⨯÷= 444练习1. 答案:62.8简答:()1234 3.14262.8+++⨯⨯=.练习2. 答案:6.28简答:大圆的面积是12.56,可求出大圆的半径是2,那么小圆的半径是1,面积是3.14.阴影部分的面积是12.56 3.14 3.14 6.28--=.练习3. 答案:10.28简答:图中的阴影部分恰好可以拼成一个边长为2的正方形和两个半径为1的圆,22 3.1411210.28⨯+⨯⨯⨯=.练习4. 答案:9.42简答:类似例题4的分析,可知阴影部分的面积与30°的扇形面积是相同的,都是21π69.4212⨯⨯=.作业1.答案:31.4 简答:278.5 3.1425r =÷=,5r =.2 3.14531.4C =⨯⨯=厘米. 作业2. 答案:80简答:扇形所在大圆的面积是23.14328.26⨯=,圆心角是6.283608028.26⨯=度. 作业3. 答案:1.05简答:阴影部分是两个60°的扇形,面积是213.1412 1.056⨯⨯⨯≈. 作业4. 答案:0.6075简答:连接BD ,将最左边的弓形补过来.阴影部分的面积就是平行四边形BDEC 的面积减去扇形的面积.24511 3.141=0.6075360S =⨯-⨯⨯n 影. 作业5. 答案:12平方厘米 简答:阴影部分可以合成三个斜边是4的等腰直角三角形,面积是344412⨯⨯÷=平方厘米;。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
共边模型
一、等积模型
由三角形面积公式可以得到,若两个三角形底相等,高也相等,那么它们的面积必然也是相等的。
如图所示:
b
a
由图示可直接得到
,
结论1:两个三角形,底相等,高相等,面积相等;
结论1:夹在一组平行线之间的同底(等底)三角形面积相等;
结论2:夹在一组平行线之间的两个同底三角形,会有三对三角形面积相等.
补充:
1.
两个三角形,若底相等,一个高是另外一个高的几倍,那么它的面积也是另一个的几倍.如图所示:
2.两个三角形,若底相等,一个高是另外一个高的几倍,那么它的面积也是另一个的几倍.
如图所示:
b
a
练习题
1.如图所示,四边形ABCD是边长为18的正方形,E、F、G分别是AB、BC、CD的三等分
点,H是AD上任意一点,求图中的阴影部分面积.
H
2. 如图所示,四边形ABCD 是边长为8的正方形,四边形GIHJ 的面积为5,求图中阴影部分
的面积.
3.
如图所示,已知,求图中阴影部分面积.
B C
参考答案
1. 【解答】108
【解析】连接HC、HB,如图所示:
H
2. 【解答】22
【解析】
3. 【解答】12.5
【解析】连接CF,如图所示:
B
C。
