张量与连续介质力学基本公式总结
第四章 连续介质力学的基本定律

br 0 b 0
bz 0
在球面坐标系中,平衡方程可化为:
T rr r
1 T r r
1 T r
1
T r
r sin
1 r
2 T
1
rr
cot T r T T b r 0
f fb fc
其中
fb
V
bdV
tdS
fc
S
物体的动量为:
m
V
vdV
Dx Dt dV
V
V
adV
S
tdS
V
bdV
可将上式改写为:
S
n TdS
V
bdV
V
adV
利用高斯公式,得到:
即:
V
T dV
左边两项分别 表示连续介质 的动能和内能 的时间变化率
右边分别表示 接触力和体力 所做的功率
DK Dt
V
D : T dV
S
t v dS
V
b v dV
若令U表示内能,则能量方程也可简洁地写成:
DK Dt DU Dt DW Dt
即:
动能变化率+内能变化率=外力作用功率 表示接触力和 体力的功率
v y y
v z z
0
在柱面坐标系中,连续性方程为:
t
1 rv r r
连续介质力学柯西公式

连续介质力学柯西公式
连续介质力学中的柯西公式是描述物质的运动和变形的基本方程之一。
它由法国数学家奥古斯丁·路易·柯西(Augustin-Louis Cauchy)在19世纪初提出。
柯西公式以张量形式表示,描述了在连续介质中任意一点的应力与该点的速度梯度之间的关系。
下面是柯西公式的一般形式:σ = C : ε
在这个公式中,σ代表应力张量,ε代表速度梯度张量,C 代表弹性常数张量,":"表示张量的内积运算。
具体来说,应力张量σ描述了物质内部的力的分布情况,速度梯度张量ε描述了物质的形变情况,而弹性常数张量C则是物质的弹性性质的度量。
柯西公式是连续介质力学的重要方程之一,它揭示了物质在受力作用下的行为规律,为研究固体力学、流体力学和弹性力学等领域提供了基础。
张量力学与连续介质力学

张量力学与连续介质力学张量力学与连续介质力学的联系与应用引言:张量力学和连续介质力学是力学领域中的两个重要分支,它们在物理现象的研究和工程设计中都扮演着重要的角色。
本文将探讨张量力学和连续介质力学的联系以及它们在现实生活中的应用。
一、张量力学的特点与基本概念1. 张量的定义与表示张量是一个多维数组,可以用来表示物体的性质或物理量。
它具有方向和大小,并且根据其阶数可分为零阶张量(标量)、一阶张量(向量)和二阶张量等。
2. 张量的运算张量的运算包括加法、减法、乘法和除法等。
其中,张量的乘法是通过将对应分量进行相乘,并按规定的法则求和得到新的张量。
3. 张量的对称性张量的对称性是指在某些条件下具有某种对称特性。
对称性可以帮助我们简化张量方程的求解,并从中得到更多有用的信息。
二、连续介质力学的基本原理1. 连续介质假设连续介质力学将物体看作连续分布的物质,忽略了其中的微观离散性,从而使问题的求解更加简化。
2. 连续介质的宏观特性连续介质力学研究了物质的宏观性质,如质量、能量和动量等。
通过运用质量守恒、动量守恒和能量守恒等基本原理,可以推导出连续介质的运动方程和守恒方程等。
3. 弹性力学与流体力学弹性力学和流体力学是连续介质力学的两个重要分支。
弹性力学研究物体在外力作用下的弹性变形,而流体力学则研究了物体内部的流动和扩散等现象。
三、张量力学在连续介质力学中的应用1. 应力张量与应变张量张量力学提供了一种描述物体内部变形性质的方法,通过引入应力张量和应变张量的概念,可以定量地描述物体在外力作用下的变形状态。
2. 连续介质的弹性性质利用张量力学的理论,可以推导连续介质的弹性模量、刚度系数和泊松比等弹性性质,从而帮助工程师设计耐用的结构。
3. 流体的运动与扩散流体力学的研究中,通过张量力学的方法可以得到流体的速度场与压力场的解析解。
这对于气象学、水动力学以及工程设计等领域都具有重要的意义。
4. 数值模拟与计算流体力学在现代科学中,数值模拟和计算流体力学成为了研究连续介质力学的重要工具。
从张量的角度推导流体力学三大基本方程

从张量的角度推导流体力学三大基本方程首先要讲一点,从张量的角度来看,流体力学的三大基本方程就是物理学家们在最初探讨介质流动的基本思路,也就是物理四大基本方程组的应用。
因此,我们可以借助张量的思维,来解释它们之间的联系和关系。
物理学家莱布尼茨首次提出物理的四大基本方程,有基于的物质的物理过程,包括动能守恒定律、牛顿第二定律、热力学定理和电磁学方程,这四个定理被称为"物理四大基本方程"。
运用张量计算,物理四大基本方程组可以表示为扩散方程(物体总动能守恒)、质量守恒方程(物体质量守恒)、动量守恒方程(物体总动量守恒)和能量守恒方程(物体总能量守恒)。
因此,从张量的角度来看,流体力学的三大基本方程就可以被推导出来了,它们分别是物质及能量流量守恒方程(散度定律)、恒定流体能量方程(动量守恒方程)和变量流体压力方程(勒莱塔方程)。
物质及能量流量守恒方程,就是基于张量计算的变量物质流动的物理过程,它表示物体总本量的流动的等离子体及其能量的守恒,其正视图扩散方程可以表示为:∇•∇*T=0,T表示物质总本量的流动及其能量;恒定流体能量方程,主要对物体动量而言,基于张量表示,比如动量方程:。
∇•(Y×Y )=0, Y表示动量;最后是变量流体压力方程,这是在勒莱塔方程的基础上的进一步发展,它结合了物质及能量流浪的特性,表示为:Φ=Φ(F/L-q*h),其中F表示动量、L表示动量流浪速度、q表示物质流浪的密度以及h表示压力的空间变化。
总之,流体力学三大基本方程实质上都是应用物理四大基本方程和张量思维,在有限时间和空间范围内对物体总本量和其能量变化和动力学过程进行守恒性分析的方法。
鉴于其复杂性,可以用来研究复杂物理过程,比如流体动力学。
连续介质力学第二章.

即得( i ),将( i )作相应的指标替换, 展开化简,将得其余三式。
二维置换符号 e (, 1, 2)
从三维退化得到
e ei j3 e 3
其中
e11 e22 0, e12 e21 1
有下列恒等式
e e
又如,方程
12
2 2
32
111
2 22
333
用指标法表示,可写成
i i i ii i ii i ii
i 不参与求和,只在数值上等于 i
1.2 Kronecker 符号
在卡氏直角坐标系下,Kronecker 符号定义为:
ij
表示
e1 A11e1 A12e2 A13e3 e2 A21e1 A22e2 A23e3 e3 A31e1 A32e2 A33e3
ei Aije j i 为自由指标,j 为哑标
表示
e1 A11e1 A12e2 A13e3 e2 A21e1 A22e2 A23e3 e3 A31e1 A32e2 A33e3
新旧基矢量夹角的方向余弦:
ei e j | ei || e j | cos(ei , e j ) cos(ei , e j ) ij
1.5.1 坐标系的变换关系
ij cos(ei , e j ) ei e j
旧 新
e1
e 2 e 3
e1
11 21 31
ai xi a1x1 a2 x2 a3x3 bjj b11 b22 b33
cmem c1e1 c2e2 c3e3
双重求和
33
S
第二连续介质力学之张量分析

, n 0
n l n 0 m
l m l m 0 m l l 0 m m x l 0 yx 0 l x m yx
2 2
n n
x
2
y
x
2
y
cos 2 xy sin 2
x
2
(2-4)
y
sin 2 xy cos 2
三.最大应力
n l n m 1.最大正应力
n
m x l yx
xy l y m
x l m y m x l y
y
y
P ( x , y ), ( x , y )
c
x x x c o s y sin
A B
o
D
x
y x sin y c o s
应力变换
n l n m
z yz xz 0
2 12 ) (
由(2~12)式可求解出
x , y , xy
x E y
1 求
1
1
1
x 1 y
x m 2 yxxy l 2 y m 2
l1
o l2 l1 2 m 2
x m1 yx
xy l 2 y m 2
2 ( l1 l 2 m 1 m 2 ) l1
第二章 连续介质力学之张量分析

f ,
y
g
。假设上端的约束
y
y
反力为均布力,那么y=L处的边界条件为
( xy ) y L f x 0 ( y ) y L f y gL
按照材料力学的计算结果, L y处的应力为
x 0,
y
L
gy , xy 0
(1)
O
y x O x
1.考察应力分量(1)式能否满足平衡微分方程
x xy 0 x y xy y g 0 x y (2)
(1)式代入能够满足平衡方程。 2.考察应力分量(1)式能否满足应力相容方程(2.22)
(
2 2
y
(9)
对上式中的前两式积分得到
gyx f1 ( y ) u E 2 gy v f2 ( y) 2E
(10 )
式中 f ( y )与 f ( x ) 都是待定函数。把(10)式代入 (9)式中的第三式,得
1 2
df 2 ( x ) dx
gx
(b )
根据复合函数微分理论,上式为
d ds ( y ) s f x d ( ) f y ds x s ( 2 . 34 )
在A,B区间,对上面两式积分得到:
( y ) B ( ) x B
(
d ds dx x ds dy y ds (d )
在A,B区间内,对(d)积分得:
d 采用分部积分
A B B A
x
B
dx
B A
y
dy
连续介质力学2-2

[
λ2
ˆ λ3 • P
]
1 ˆ = P • diag λ1
T
1
λ2
1 ˆ •P λ3
ˆ ˆ ˆ R = F • U −1
例1. 图示二维线元变形 v v v v ˆ ˆ • dX + F • dX ˆ dx = F • dX = F I II dx1 = F1I dX I + F1II dX II = x1,I dX I + x1,II dX II x2 v dx 2 e 2 dx 2 = F2 I dX I + F2 II dX II = x 2,I dX I + x 2,II dX II
L形式 形式: 形式
B XⅢ
v ∂r v v dr = dX K R ∂X K O v ∂ ( xi ei ) XⅠ dX K = ∂X K v v v ∂ xi ei E K = • d X M EM ∂X K
v dR P
XⅡ
v dr
p
v r
b(t)
(
) (
)
∂x i FiK = ∂X K
v v v v dr = ( x∇ X ) • dR
同理: 同理
2 E IJ = U I , J + U J , I + U M , I U M , J 2e ij = ui , j + u j ,i − um ,i um , j
v v 是同一个矢量。 注:U与u是同一个矢量。
讨论: 讨论:
v v (dr )2 = dr • dr = δ ij dxi dx j
1ˆ ˆ ˆ e= I − F −1 2
( )
T
ˆ • F −1
张量与连续介质力学基本公式总结

第一章:矢量和张量重要矢量等式:()()()⨯⨯=⋅-⋅c a b b c a a c b 指标记法:哑指标求和约定 自由指标规则 协变基底和逆变基底:张量概念i i'i'i β=g g i'i'i i β=g gi'i'i i v v β= i i 'i 'iv v β= i'j'i'j'k l ij..k'l'i j k'l'..kl T T ββββ= i i i i v v ==v g g ..kl i j ij k l T =⊗⊗⊗T g g g g度量张量ij i i i j i i g =⊗=⊗=⊗G g g g g g g⋅=⋅=⋅=⋅=v G G v vT G G T T.j kj i ik T T g =张量的商法则lm ijk T(i,j,k,l,m )S U = ijk...lm T(i,j,k ,l,m )T =置换符号i i ir s t j j j ijk ijk ijkr s t rst rst rstk k kr s t e e δδδδδδεεδδδδ=== ijk j k j k jk ist s t t s st δδδδδδ=-2ijk k ijt t δδ= 6ijk ijk δ=置换张量i j k ijk ijk i j k εε=⊗⊗=⊗⊗εg g g g g gijk i j k ijk ()e ε=⋅⨯=g g gijkijki j k ()ε=⋅⨯=g g g ()::()i j k ijk ijk i j k a b a b εε⨯===⊗=⊗a b g g a b εεa b第二章: 二阶张量重要性质:T =T.u u.T 主不变量1.()i i Tr T ζ==T 212i j l ml m .i .j T T ζδ= 3()det ζ=T1()()(())(())()ζ⋅⋅⨯⋅⋅⨯⋅⨯⋅=⋅⨯T u v w +u T v w +u v T w u v w2)[)][()(]()[()]()ξ⋅⋅⋅⨯⋅⋅⨯⋅⋅⋅⨯⋅=⋅⨯T u (T v w +u T v T w)+T u (v T w u v w (()[()()]det()()⋅⋅⋅⨯⋅=⋅⨯T u T v T w T u v w标准形1. 特征值、特征向量λ⋅=T v v ()λ-⋅=T G v 0 321230λζλζλζ-+-= 2. 实对称二阶张量标准形123112233i iλλλ=⋅⊗=⊗+⊗+⊗N N g g g g g g g g 3. 正交张量(了解方法)12112233(cos()sin())(sin()cos())ϕϕϕϕ=+⊗+-+⊗+⊗R e e e e e e e e4. 反对称二阶张量的标准形21123μμμ=⊗-⊗=⨯Ωe e e e e G⋅=⨯Ωu ωu31:2μ=-=⨯ωεΩe u=-⋅Ωεω 5. 正则张量极分解 =⋅=⋅T R U V R第三章 张量函数概念:各项同性张量函数、解析函数 计算 e T sin()T 重要定理:1. Hamilton-Cayley 定理:32321231230λςλςλςςςς-+-=⇒-+-=T T T G 0 2.对称各向同性张量函数表示定理:2012()f k k k ==++H N G N N ;其中T T ;==H H N N ;而系数i k 是N 的主不变量的函数。
连续介质力学1-3

3. 对称张量与反对称张量 命题一、对称性与反对称性与坐标系无关。 命题一、对称性与反对称性与坐标系无关。 证明: 证明:
Ti′j′ = β i′m β j′nTmn T j′i′ = β j′m β i′nTmn
命题二、 命题二、任意二阶张量可以唯一分解成一个对称 张量与一个反对称张量之和。 张量与一个反对称张量之和。 证明: 证明: 存在性 唯一性
证明: 证明:I 12 = (λ1 + λ2 + λ3 )
2
2 = λ1 + λ2 + λ2 + 2 λ1 λ 2 + λ 2 λ 3 + λ 3 λ1 2 3
(
) (
)
ˆ = T2
( )
kk
+ 2I2
§3-3 二阶实对称张量 ˆ的三个主值都是实数。 1. T的三个主值都是实数。 v v v 证明: 为主值, 是主方向, ˆ 证明:λ为主值,x是主方向,即T • x = λx v v ˆ • x # = λ# x # 则T v ˆ v# v 或x • T • x ˆ对称, ˆ v ˆ Q T对称,故T • x # = x # • T v# ˆ v = x •T • x v# ˆ # v# ∴ x •T = λ x v v v ˆ v x # • T • x = λ# x # • x
Tij a j = β ii ′ β jj′Ti ′j′ β jk ′ ak ′ = β ii ′δ k ′j′Ti ′j′ a k ′ = β ii ′Ti ′k ′ ak ′
λa i = λβ ik ′ a k ′ β ii ′Ti ′k ′ a k ′ = λβ ik ′ ak ′ β im′ β ii ′Ti ′k ′ ak ′ = λβ im′ β ik ′ ak ′
连续介质力学第二章
其中: T ip ekjp jTik
小 结:
哈密顿算子
梯度
i ei gradf f eii f
散度
diva a iai
旋度
curla a
2.2 Laplace算子
公式:
2 f f
展开后有:
原式 (i ei ) ( j f ej ) (i j f )ij
第二章 张量分析
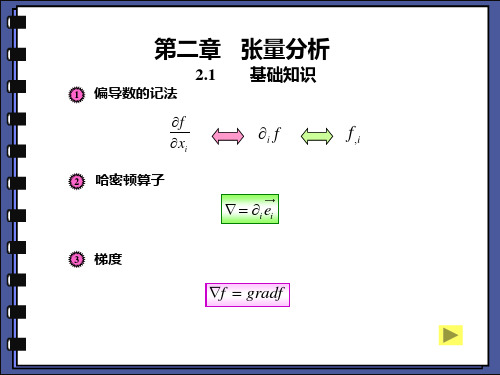
2.1 基础知识
1 偏导数的记法
f
xi
i f
f,i
2 哈密顿算子
i ei
3 梯度
f gradf
标量的梯度:
标量函数:
f f (r)
则梯度为:
f gradf eii f 展开后有: 原式 1 f e1 2 f e2 3 f e3
f i f j f k x y z
a (P、Q、R)
根据Gauss定理有:
左边 (a1n1 a2n2 a3n3)dS S ainidS S
a ndS a d S
S
S
右边 (1a1 2a2 3a3)dV V
iaidV adV
V
V
a d S adV
S
V
2 Stokes定理
Pdx Qdy Rdz
ii f 11 f 22 f 33 f
2 f 2 f 2 f
x2 y2 z2
2.3 物质导数
若 f f (t, r(t))
则:Df f f r f f x f y f z
Dt t r t t x t y t z t
f
x
y
z
t (1 f ) t (2 f ) t (3 f ) t
S
(1a2 2a1)dl1dl2 ]
第三连续介质力学之张量分析
(3)考察边界条件:无体力、无面力,
(4)结论:线性函数对应于无荷载的情况,应力函数 Ф 的线性项不影响应力分布,研究问题时可舍去。
2. 二次函数
考察其能解决的问题。 (1)检查Φ 是否满足 4 0
4
1) ax
2
4
x
2
4 2
2
x y
4
4
y
0
能被满足
(2)根据(2—23)求出应力分量{;
2 fxx 0 x 2 y 2 f y y 2a y 2 x 2 0 xy xy
x
4
2
4
x y
v y
u y
xy
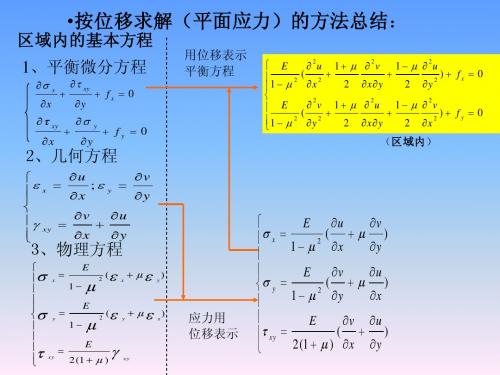
3、物理方程
x
E
2
(
x
y
)
y
1
E
2
(
y
x
)
应力用 位移表示
xy
2 (1 )
E u ( x 2 1 x E v ( y 2 1 y E v xy ( 2(1 ) x
u y u y
)] s f x )] s f y
(
( S S )
us u ( S S u ) vs v
未知函数—应力、 应变、位移
位移分量
u,v
连续介质力学2-2
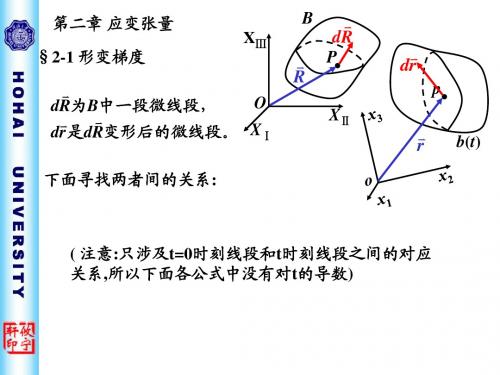
记E IJ
1 x i x j ij IJ 2 X I X J
E IJ
1 x i x j ij IJ 2 X I X J
ˆ 1 x i x j E E E ij IJ I J 2 X I X J
N K N L KL 1
取泛函 N K N K N L E KL 1 KL N K N L
其中Ψ为Lagrange乘子
泛函 N K N K N L E KL 1 KL N K N L
由d dN K d 0 N K
ˆ ˆ U P T diag 1
ˆ 2 3 P
2
ˆ 3 P
ˆ U
1
1 ˆ P diag 1
T
1
2
1 ˆ P 3
ˆ ˆ ˆ R F U 1
例1. 图示二维线元变形 ˆ dx F dX FiK ei E K dX L E L FiK dX K ei
同理:
2 E IJ U I , J U J , I U M , I U M , J 2e ij ui , j u j ,i um ,i um , j
注:U与u是同一个矢量。
讨论:
dr2 dr dr ij dxi dx j
x i x i dX I dX J X I X J
ˆ dr F dR
( 2) dR (1) dR
dr ( 2 )
(1) dr
ˆ 1 FT F I ˆ ˆ ˆ E 2 ˆ T U I ˆ F X
连续介质力学1-5
不为零 的只有
i = j = k = l; i = k ≠ j = l;
i= j≠k=l i=l≠ j=k
(2)绕x3旋转 0 绕 旋转90
0 1 0 {β i′j } = − 1 0 0 0 0 1
x1′ = x 2 , x 2′ = − x1 , x 3′ = x 3
推论:在任意置换下,张量的每一分量被换成另一分量, 推论 在任意置换下,张量的每一分量被换成另一分量, 在任意置换下 如该张量为各向同性张量,则这两个分量相等。 如该张量为各向同性张量,则这两个分量相等。 (1)先说明置换是旋转变换的特例 先说明置换是旋转变换的特例
T11 T12 T13 T21 T22 T23 T T32 T33 31
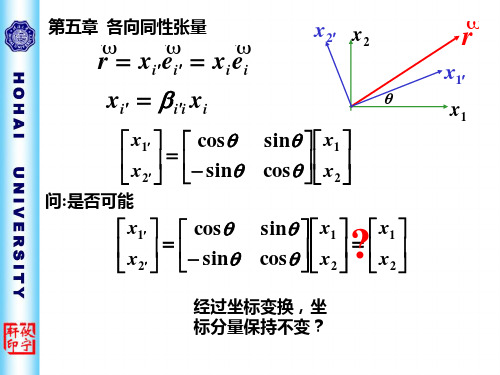
第五章 各向同性张量
r = xi ′ ei ′ = xi ei xi ′ = β i ′i xi
x1′ cos θ = x 2′ − sin θ
问:是否可能 是否可能
x2′ x 2
θ
r
x1′
x1
sin θ x1 x cos θ 2 sin θ x1 x1 x = x cos θ 2 2
− 1 0 0 {β i′j } = 0 − 1 0 0 0 1
Aijkl = Ai′j′k′l ′ = β i′i β j′j β k′k β l ′l Aijkl
i ′、j ′、k ′、l ′中有单数个 3时, Ai ′j′k ′l ′ = 0
再由置换知, 2 3 1 再由置换知,、、任意一个数值 如在下标中只出现单数 次,则该项 Aijkl = 0。
A11 A21 A 31
连续介质力学第二章new

T T
3、散度
矢量场的散度,为标量 矢量场的左散度定义为:
r r diva a
u r ur 原式 ( i ei )( a j e j )
i a jij i ai
1a1 2 a2 3a3
ax ay az x y z
ekjp j Tik
一 般
T T
小
结: 哈密顿算子
u r i ei
梯
度
u r gradf f ei i f
散
度
r r diva a i ai
curla a
旋
度
2.2
定义:
克里斯托弗尔符号
在基矢量组 g 1,g 2 ,g 3中把 i g j 按下式分解
r ir g
r ir
i g
g
i log g
k k 由于 l g j g ,故有
i g j g k i g j g k i g k g j 0
于是
i g k g j ijk
i g j ipj g p
T pk e p e k
其中:
T pk
e jip j Tik
右旋度定义为:
c url T T
Tik e i e k e j
e kjp j Tik e i e k
T ip e i e p
其中:
j
T ip
i g j ijp g p
ig j pij g p
这里分解系数 ijp和 ij分别称为第一类和第二类克 里斯托弗尔(Christoffel ijk关于指标i和j对称。
连续介质力学1d

G gi
G g
j
G ...g
k
G g
l
=
T ...kl ij...
G g
i
G g
j
G ...gk
G gl
论
张 量 复 习
散 度 旋
右左散 散度 度张量∇TG的⋅⋅T∇G散==度gG∂∂s:xT⋅Gs∂∂x⋅TGgsG
= T s
... ks
ij... ;s
=
∇
sT
sj... ...kl
G g G g
i j
左、右梯度均为n+1阶张量,一般是两个不同的张量
张 量 复
仅对标量场有ϕ∇ = ∇ϕ
G
G
对矢量场有 F∇ = (∇F )T
习
•张量场的微分:
GG GG G
梯
dT = (T∇) ⋅ dx = dx ⋅ (∇T ) (1.102)
度 以上运算均涉及张量场对坐标的偏导数—协变导数
8
—
3)协变导数的G 定义
Γ ij ,l
= Γijk gkl
=
∂g j ∂xi
⋅
G g
k
g
kl
=
∂g j ∂xi
G ⋅ gl
=
∂
2
G x
∂xi∂x j
G ⋅ gl
(1.92)
复 习
∴ Γij,l = Γ ji,l
(1.93)
—
张 量 的
Γ ij ,l
=
1 2
(
∂g ∂x
il j
+
∂g jl ∂xi
−
∂g ij ∂xl
)
(1.94)
第 一 章
连续介质力学第二章

V
r u r r ∫∫ a ⋅ d S = ∫∫∫ ∇ ⋅ adV
S V
2
Stokes定理 Stokes定理
∫ Pdx + Qdy + Rdz
C
= ∫∫ [(
S
∂R ∂Q ∂P ∂R ∂Q ∂P − )dydz + ( − )dzdx + ( − )dxdy ] ∂y ∂z ∂z ∂x ∂x ∂y r a = ( P、Q、R ) r dl = (dx、dy、dz )
dS1
u r r1
dS3
uu r ur u r d S1 = d r2 × d r3 uu r u r u r d S 2 = d r3 × d r1 uu r u r ur d S3 = d r1 × d r2
r a = ( P、Q、R )
根据Gauss定理有: 根据Gauss定理有: Gauss定理有 左边
ur + (e123∂1a2 + e213∂ 2 a1 )e3 ur uu r ur = (∂ 2 a3 − ∂ 3 a2 )e1 + (∂ 3 a1 − ∂1a3 )e2 + (∂1a2 − ∂ 2 a1 )e3
∂az ∂a y r ∂ax ∂az r ∂a y ∂ax r = ( )+ i( )+ j( ) k ∂y ∂z ∂z ∂x ∂x ∂y
ur D ∂ () = () + V ⋅ ∇ () D t ∂t
2.4
1
积分定理
Gauss定理
∂P ∂Q ∂R ∫∫ ( P cos α + Q cos β + R cos r )ds = ∫∫∫ ( ∂x + ∂y + ∂z )dxdydz S V
黄生洪张量分析和连续介质力学概论

vx vy vz
wx u x wy u y wz u z uu uw
vx vy vz v u vv
wx wz
ux wx
uy vy wy
uz ux vz u y wz u z
vx vy vz
wx wy wz
wy v x
w u wv
wi vi u v
vw ww
(e1 )
t
(e3 )
31e1 32e2 33e3 t
(ei )
ije j
(ei )
t
(ei )
ije j
ij t
' ' ' '
e j
' ' ' ' ' ' ' '
ij ik ek jl el ik jl ijek el k l ek el
“,” 表示求导 j: 哑标 i: 自由标
ij , j f i 0
(i, j 1,2,3)
表达式简洁;如 r p x ,
i i
(i 1,2,3)
ik ,k f i 0
(i, k 1,2,3)
用张量写出的方程(张量方程),与参考系无关,
亦即在所有参考系中都成立。
主讲:黄生洪
中国科学技术大学近代力学系
0 绪论
0.1 张量概念的引入
标量
温度 密度 高度
t
矢量 物理世界 e3
位移 速度 作用力
e1
e2
值+方向
S1, S2,S3
标示客观物理量 共性: 具有坐标不变性 满足客观的数学运算规则
连续介质力学之张量分析

应变分量(工程应变)不是张量,不服从张量坐标变换式, 将 xy
yz
zx 等乘上1/2以后才形成一个张量
张量形式为
1 ui u j ij x x 2 j i
yz
2
zx
2
2
xy
xx ij yx zx
方程用矩阵表示:
1 1
D
1 0 0 0 1 2 2(1 ) 0 0 0 0 0 0 1 2 2(1 ) 0 0 0 0 0 1 2 2(1 ) 0
式中[D]为弹性矩阵表示为:
由 Fy 0和 Fz 0 可得类似表达式,整理并两边除以 :
dxdydz
x
,注意到剪应力互等关系,得:
x
zx f x 0 y z
yx
x
xy
y
y
z
zy
fy 0
(8-1)
xz
x
z f z 0 y z
x
yz zx xy
2(1 ) yz E 2(1 ) zx E 2(1 ) xy E
ij ij uk,k G u j,i ui,j) (
四、体积应变:
各向同性材料的体积应变 构件每单位体积的体积变化, 称为体积应变用θ表示. 各向同性材料在三向应力状态下的体应变 如图所示的单元体,三个边长为 a1 , a2 , a3 2 变形后的边长分别为 a1(1+,a2(1+2 ,a3(1+3 变形后单元体的体积为 V1=a1(1+· 2(1+2 · 3(1+3 a a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
张量与连续介质力学基本公式总结
在连续介质力学中,有一些基本的公式被广泛应用于系统建模和问题
求解。
这些公式包括牛顿第二定律、应力应变关系、连续性方程和能量守
恒等。
1.牛顿第二定律
连续介质力学的基础是牛顿第二定律,它描述了质点的运动情况。
对
于一个连续介质,牛顿第二定律可以推广为控制体中动量的变化率等于力
的和,即
∂(ρv)/∂t=∇•σ+ρg
其中,ρ是介质的密度,v是介质的速度矢量,t是时间,σ是应力
张量,g是重力矢量。
这个方程可以用来描述介质的运动。
2.应力应变关系
应力应变关系描述了介质中力与变形之间的关系。
在连续介质力学中,通常假设介质是线性弹性的,即应力张量与应变张量之间存在线性关系。
在各向同性的介质中,应力张量与应变张量之间的关系可以用胡克定律表示,即
σ=λ(∇•v)I+2μE
其中,λ和μ是介质的弹性常数,I是单位张量,E是应变张量。
这个方程可以用来计算各向同性介质中的应力分布。
3.连续性方程
连续性方程描述了质点数密度的守恒。
在连续介质力学中,这个方程被推广为质量守恒方程,即
∂ρ/∂t+∇•(ρv)=0
这个方程说明了质点的数密度随时间和空间的变化率。
它告诉我们质点不会凭空消失或产生,而是通过流体的运动来重新分布。
4.能量守恒
能量守恒方程描述了介质中能量的转化和分布。
在连续介质力学中,可将能量守恒方程表示为
∂(ρe)/∂t + ∇•(ρve + q) = ρg•v + ∇•σ•v
其中,e是单位质量的内能,v是速度矢量,q是热通量矢量。
这个方程考虑了能量的传输、转化和产生与消耗。
它可以用来分析介质中的热传导、热膨胀和内部能量变化等现象。
这些公式构成了连续介质力学的基本框架,可以用来描述各种各样的物理现象,如流体力学、固体力学、热力学等。
通过结合实际问题和适当的边界条件,这些公式可以用于求解各种与连续介质力学相关的工程和科学问题。
总之,张量与连续介质力学基本公式是研究介质在连续性假设下力学行为的关键工具。
它们提供了描述质点运动、力与变形关系、质量守恒和能量守恒等方面的基本框架和理论基础。
在实际应用中,我们可以利用这些公式解决各种与连续介质力学有关的工程和科学问题。
