光学_郭永康_5.光在各向同性介质界面的反射和折射
物理光学与应用光学(第二版)第一章

n=
c
υ
= µ rε r
(1.1-15)
除铁磁性介质外,大多数介质的磁性都很弱,可以认为µr≈1。 因此, 折射率可表示为
n = εr
(1.1-16)
此式称为麦克斯韦关系。对于一般介质,εr或n都是频率的函数, 具体的函数关系取决于介质的结构。
第 1 章 光在各向同性介质中的传播特性 5. 光电磁场的能流密度 光电磁场的能流密度 电磁理论指出,电磁场是一种特殊形式的物质,既然是物 质,就必然有能量。而光电磁场是一种电磁波,它所具有的能 量将以速度v向外传播。为了描述电磁能量的传播,引入能流 密度——玻印亭(Poynting)矢量S,它定义为 S=E×H (1.1-17)
式中,ε=ε0εr ,为介电常数,描述介质的电学性质,ε0 是真空中 介电常数,εr是相对介电常数;µ=µ0µr,为介质磁导率,描述介 质的磁学性质,µ0是真空中磁导率,µr是相对磁导率;σ为电导率, 描述介质的导电特性。
第 1 章 光在各向同性介质中的传播特性 应当指出的是,在一般情况下,介质的光学特性具有不均 匀性,ε、µ和σ应是空间位置的坐标函数,即应当表示成ε(x, y, z)、µ(x, y, z)和σ(x, y, z); 若介质的光学特性是各向异性的,则ε、 µ和σ应当是张量,因而物质方程应为如下形式:
(1.1-8) (1.1-9) (1.1-10) (1.1-11)
第 1 章 光在各向同性介质中的传播特性 对(1.1-10)式两边取旋度, 并将(1.1-11)式代入, 可得
∂2 E ∇ × (∇ × E ) = − µε 2 ∂t
利用矢量微分恒等式
∇ × (∇ × A) = ∇ × (∇ ⋅ A) = −∇ A
第 1 章 光在各向同性介质中的传播特性 下面,我们从麦克斯韦方程组出发,推导出电磁波动方程, 并且限定所讨论的区域远离辐射源,不存在自由电荷和传导 电流,介质为各向同性的均匀介质。此时,麦克斯韦方程组 可简化为
光波在各向同性介质界面反射和折射

在θ1>450时,随θ1的增大,Rn较快地变大;
(ii)光密到光疏。在入射角大于临界角范围 内,将发生全反射;
(iiPi)r特=1殊,情故况,,反当射θ光1=为θB完时全,偏由振于光R。p=0,
举例
5/20/2021
第1章 光的特性
光由空气以布儒斯特角射向玻璃
由布反儒射斯率特公角式为及折射定B律可a得rcRts=ann112n5%5,6因4此0',反射光强
对于θ1非零、小角度入射时,都 将近似产生π相位突变,或半波 损失。
② n1>n2,光密到光疏。
5/20/2021
第1章 光的特性
② n1>n2,光密到光疏
先考察θ1=00的正入射情况。
由图1-24(b),有
rs 0,rp 0
考虑P30 T1-23,有关光场振动正方向的规定,则
有
可见:在入射点处,合成的 反射光矢量Er相对入射光场Ei 同向,相位相同,反射光没 有半波损失。
薄膜两侧介质相同时,上下表面的反射光场除了有光程差的贡献外, 还有的附加相位差,或称有的额外光程差/2。
产生额外光程差/2的条件是: 上下表面的光学性质不同。
结论
5/20/2021
返回
第1章 光的特性
1.2.5 反射和折射的偏振特性
偏振度 反射和折射的偏振特性
自然光的反射、折射特性 线偏振光的反射的振动面旋转
Rs rs2 ssiinn22((1122))
Rp
rp2
ta ta
n2(12) n2(12)
入射光中s分量和p分量的透射率(不相同)为
Tsn n2 1c co o1 2ssts2ssii2 2n (n11 si2n 2 )2
光学_郭永康_解答

光学_郭永康_解答摘要:本文将解答关于光学的一些常见问题,包括光的特性、光的传播、光的折射等内容。
通过对这些问题的解答,将帮助读者更好地理解光学领域的知识。
1. 光的特性光是一种电磁波,具有波动性和粒子性。
其波动性表现在光可以产生干涉、衍射等现象,而其粒子性表现在光具有能量和动量。
光的波长决定了其颜色,不同波长的光被人眼感知为不同的颜色,我们将其称为光谱。
光谱包括可见光谱、紫外线、红外线等等。
2. 光的传播光的传播遵循直线传播原理,也就是说光在真空中直线传播,但在其他介质中会发生折射。
光线从一种介质进入另一种介质时会发生折射现象,其折射角和入射角之间遵循折射定律。
折射现象是为什么水中的物体看起来“折断”了的原因。
除了折射,光还可以发生反射。
反射分为漫反射和镜面反射,漫反射是指光在粗糙表面上发生的反射,而镜面反射则是光在光滑表面上发生的反射。
3. 光的折射光的折射现象是由光从一种介质进入另一种介质时发生的。
当光从光疏介质进入光密介质时,折射角大于入射角;当光从光密介质进入光疏介质时,折射角小于入射角。
这是因为光在不同介质中传播速度不同,根据斯涅尔定律我们可以通过折射角和入射角的正弦比来计算出两种介质的折射率之比。
4. 光的干涉光的干涉是光的波动性在特定条件下的表现。
干涉分为相长干涉和相消干涉两种情况。
相长干涉指的是两束相干光叠加时,光强增强的现象;相消干涉则是两束相干光叠加时,光强减弱或完全消失的现象。
干涉现象在我们的日常生活中有很多应用,比如光的薄膜干涉可以用于制作反光镜、彩色滤光片等光学元件。
5. 光的衍射光的衍射是光通过一个物体或者一个缝隙时发生的现象。
衍射是由于光波传播过程中被物体或缝隙遮挡而发生的波前的弯曲或扩散现象。
比如光通过一个狭缝时会发生单缝衍射,这种现象也是夫琅禾费衍射的基础。
光的衍射也是我们在实验室和工程中经常遇到的现象,比如在天文学中,利用衍射现象可以观测到遥远的星系和行星。
光学 第三章

S
0
iC 90 0
s 2arctan n2
(n2 / n1)2 sin2 i11 n1 cosi1
p 2arctan n1
(n2 / n1)2 sin2 i11 n2 cosi1
1.0
•折射时相位跃迁:t p , tS 0
折射光r与s 入射光同相位
0 rp
-0.50 图3.i1B-33振0i1i幅c/(反o)射6率0 曲线
0 .5
2. 反射、折射时的相位跃迁(相移) 0
-0 .5
外反射:光从光疏介质进入光密介质
-1 .0
内反射:光从光密介质进入光疏介质 0
t
p
r
t
s
p
r
s
30
60
i1/(o)
1 .0
0 .5
0 90 0
|t |
p
|t |
s
|r |
s
|r |
p
30
60
90
i1/(o)
① 外反射时相位跃迁(n1<n2)
图3.1-2 振幅反射率与振幅透射率曲线(n1=1,n2=1.5)
90
(n1=1.5,n2=1)
z
P2
k2
n2
i2
S2
O
x n1
k1 i1 i1' P1
P'1
S1
S'1 k'1
§1 光在各向同性介质界面上的反射和折射
3.光在反射和折射时振动分量改变的真实情况
p
S
0
i1 iB
90 0 0
n1 n2
i1
90 0
物理光学与应用光学第二版课件及课后习题答案

由式(1-12)
2 所以有: ( E ) ) E
由式(1-16)得:
2
即 E 0
E 2 E 2 t
(1-17)
同理对式(1-15)两边 取旋度,得
2 2 D B E H ( D) 2 2 t t t t
即:
E E 2 t
2
(1-16)
利用矢量微分恒等式
2 ( A) ( A) A
有:
2 ( E ) ( E ) E
D 0
可知 E 0
同理,利用矢量微分恒等式,可得:
2 有以上两式得: H H 2 t
2
2 ( H ) H
(1-18)
v 令
1
可将式(1-17)式(1-18)变为:
2 1 2E 2 E 2 2 0 (1-19) 2 H 1 H 0 v t v 2 t 2
4.波动方程
麦克斯韦方程组描述了电磁现象的变化规律, 指出随时间变化的电场将在周围空间产生变化的磁 场,随时间变化的磁场将在周围空间产生变化的电 场,变化的电场和磁场之间相互联系,相互激发, 并且以一定速度向周围空间传播。因此,时变电磁 场就是在空间以一定速度由近及远传播的电磁波。
一、 电磁场波动方程:
D H j t
符号的意义:
哈密顿算符:
i j k x y z
具有矢量和求导的双重功能 Dx Dy Dz 散度: D D
x y z
(完整版)物理光学-第一章习题与答案

物理光学习题 第一章 波动光学通论一、填空题(每空2分)1、.一光波在介电常数为ε,磁导率为μ的介质中传播,则光波的速度v= 。
【εμ1=v 】2、一束自然光以 入射到介质的分界面上,反射光只有S 波方向有振动。
【布儒斯特角】3、一个平面电磁波波振动表示为 E x =E z =0, E y =cos[⎪⎭⎫⎝⎛-⨯t c x 13102π], 则电磁波的传播方向 。
电矢量的振动方向 【x 轴方向 y 轴方向】4、在光的电磁理论中,S 波和P 波的偏振态为 ,S 波的振动方向为 , 【线偏振光波 S 波的振动方向垂直于入射面】5、一束光强为I 0的自然光垂直穿过两个偏振片,两个偏振片的透振方向夹角为45°,则通过两偏振片后的光强为 。
【I 0/4】6、真空中波长为λ0、光速为c 的光波,进入折射率为n 的介质时,光波的时间频率和波长分别为 和 。
【c/λ0 λ0 /n 】7、证明光驻波的存在的维纳实验同时还证明了在感光作用中起主要作用是 。
【电场E 】8、频率相同,振动方向互相垂直两列光波叠加,相位差满足 条件时,合成波为线偏振光波。
【0 或Π】9、会聚球面波的函数表达式 。
【ikre rA r E -)(=】 10、一束光波正入射到折射率为1.5的玻璃的表面,则S 波的反射系数为 ,P 波透射系数: 。
【-0.2 0.2 】11、一束自然光垂直入射到两透光轴夹角为θ的偏振片P 1和P 2上,P 1在前,P 2在后,旋转P 2一周,出现 次消光,且消光位置的θ为 。
【2 Π/2】12、当光波从光疏介质入射到光密介质时,正入射的反射光波 半波损失。
(填有或者无) 【有】13、对于部分偏振光分析时,偏振度计算公式为 。
(利用正交模型表示) 【xy x y I I I I P +-=】二、选择题(每题2分)1.当光波从光密介质入射到光疏介质时,入射角为θ1,布儒斯特角为θB ,临界角为θC ,下列正确的是 ( )A .0<θ1<θB , S 分量的反射系数r S 有π位相突变 B .0<θ1<θB , P 分量的反射系数r P 有π位相突变C .θB <θ1<θC , S 分量的反射系数r S 有π位相突变D .θB <θ1<θC , P 分量的反射系数r P 有π位相突变 【B 】2.下面哪种情况产生驻波 ( ) A .两个频率相同,振动方向相同,传播方向相同的单色光波叠加 B .两个频率相同,振动方向互相垂直,传播方向相反的单色光波叠加 C .两个频率相同,振动方向相同,传播方向相反的单色光波叠加 D .两个频率相同,振动方向互相垂直,传播方向相同的单色光波叠加 【C 】3.平面电磁波的传播方向为k ,电矢量为E ,磁矢量为B, 三者之间的关系下列描述正确的是 ( ) A .k 垂直于E , k 平行于B B .E 垂直于B , E 平行于k C .k 垂直于E , B 垂直于k D .以上描述都不对 【C 】4、由两个正交分量]cos[0wt kz A x E x -= 和]87cos[0π+-=wt kz A y E y表示的光波,其偏振态是( )A 线偏振光B 右旋圆偏振光C 左旋圆偏振光D 右旋椭圆偏振光 【D 】5、一列光波的复振幅表示为ikre rA r E =)(形式,这是一列( )波 A 发散球面波 B 会聚球面波 C 平面波 D 柱面波 【A 】6、两列频率相同、振动方向相同、传播方向相同的光波叠加会出现现象( ) A 驻波现象 B 光学拍现象 C 干涉现象 D 偏振现象 【C 】7、光波的能流密度S 正比于( )A E 或HB E 2或H 2C E 2,和H 无关D H 2,和E 无关 【B 】8、频率相同,振动方向互相垂直两列光波叠加,相位差满足( )条件时,合成波为二、四象限线偏振光波。
第五章光在各向同性介质界面上的反射和折射 光学课件

r
1.0
内反射垂直入射时无相位变化
i1 00
反射光与入 射光同相位
0.2 0.2
1.0
rs
rp iB i c
公式
90 0 i1
E s1
E P1 E 1 E s1
E P 1 E 1
p
s
0
iB i c 90 0
i1
光在各向同性的介质界面反射时, 一般会引起偏振态的变化:
若知入射光的偏振态和入射角, 可以由其反射特征辨别 反射光的偏振态, 方法可以分为两步:
得 p 分量 振幅反射比:
rp
Ep1 Ep1
tg(i1i2), tg(i1i2)
振幅透射比:
tp
Ep2 Ep1
2sini2cois1. sini1(i2)
返回
(b) 讨论S分量
对于 s 分量, 同理有
H pc 1 io 1 H sp c 1 io 1 H spc 2 io 2 , s
Es1Es1Es2 .
若圆偏振光的光矢量随时间变化是右旋的,
则这种圆偏振光叫做右旋圆偏振光,反之,叫做
左旋圆偏振光. 若光矢量在时间上是右旋的,
则在空间上一定是左旋, 即“空左时右”.
y
y
x
z
0
x
ห้องสมุดไป่ตู้
在垂直于光传播方向的平面 内,右旋圆偏振光的电矢量
随时间变化顺时针旋转
右旋圆偏振光在 三维空间中电矢量左旋
(3) 椭圆偏振光
在垂直于光传播方向的固定平面内, 光矢量的 方向和大小都在随时间改变, 光矢量的端点描出一 个椭圆, 这样的 偏振光 叫做椭圆偏振光.
y
以上三种偏振光称为完 全偏振光, 可以由两个互相 垂直的,有相位关系的, 同 频率的线偏振光合成. 反之, 一完全偏振光也可以分解为 两个任意方向, 相互垂直, 有相位关系的同频率的线偏 振光.
光在各向同性介质界面的反射和折射-四川大学

δs π
π/2 i1
o
iB iC
π/2 i1 o
iC
π/2 i1
图 3.5-5 相移变化曲线
2. 相位突变 (1) 近于正入射的外反射
已知n1< n2,i1 ≈ 0
rp
=
rs
= n2 − n1 n2 + n1
rp>0,rs<0
·
·
·
n1 n2 图 3.5-6 正入射的相位突变(外反射)
n1 n2
图 3.5-7 正入射无相位突变(内反射)
− n1 + n1
tp
= ts
=
2n1 n2 + n1
思考:怎样理解式中的 “-”与设定的s、p比较。
注意: tp , ts 大于1是可能的。
3.5.2 能流反射率和透射率
四川大学精品课程《光学》
反射光、折射光和入射光间的光强关系
w1
=
I 1σ
cos i1
=
n1 2
ε0 μ0
E12σ
cos
i1
w
' 1
i2 ta
rra
tt'a i1
M O
R ra
①N ②
ta i2 tr'a tra
T
(a)
T
(b)
图 3.5-4 斯托克斯关于反射的处理方法
r 2a + t'ta = a , rta + r'ta = 0
斯托克斯公式
r2 (i1) + t'(i2 )t(i1) = 1 r(i1) = −r'(i2)
四.反射光的相位变化 菲涅耳公式中负号的理解:入射点处E'1和E1间的相位差或称反射光的附加相移
光学课件:第三章各向同性介质及其界面

§1 光在各向同性介质界面上的反射和折射
各向同性介质: 折射率或波速沿各个方向相同。
1.1 菲涅耳反射折射公式
问题 光通过各向同性介质时会发生反射、 折射等各种物理现象。反射、折射定律 只解决了入射、反射、折射光传播方向 间的关系,未涉及到三者间的振幅、位 相、偏振态间的关系。 菲涅耳公式可以解决上述问题。
rs< 0 有的位相跃变 rp > 0 没有的位相跃变 对观察者来说
p
k
k
反射光P、S分量都与入射光P、S分量方向相反 ※ 反射光在界面处发生了的位相跃变
光波正入射
i1=0, i2=0 ( i1 0, i2 0 )
rp= - rs=n2-n1 / n2+n1
若 n1 >n2
rs> 0 没有的位相跃变 rp< 0 有的位相跃变
(3)位相跃变(相移)
为什么图中r 的值 会有正、有负?负值 表示什么?
1)r, t 为正值表示 其分量方向与约定 的正方向相同。若 为负值,则分量方 向与约定方向相反
2)r,t 是瞬时值比,也可看作是复振幅比。 对复振幅比,比值中即包含振幅比的大 小,也包含相位的变化。
rs E1S / E1S E1S eit / E1S eit E1S / E1S
2
iB
)
n2 n1
tgiB
n2 n1
有
iB
tg 1(
n2 n1
上) 式称为布儒斯特定律
例. 当自然光以起偏角入射到折射率为 1.5的玻璃上时,求折射光的偏振度
解:已知 n1=1.0, n2=1.5, 自然光的 E1s=E1p , iB+i2=π /2
光波在各向同性介质界面的反射和折射34页PPT

42、只有在人群中间,才能认识自 己。——德国
43、重复别人所说的话,只需要教育; 而要挑战别人所说的话,则需要头脑。—— 玛丽·佩蒂博恩·普尔
44、卓越的人一大优点是:在不利与艰 难的遭遇里百折不饶。——贝多芬
45、自己的饭量自己知道。——苏联
光波在各向同性介质界面的反射和折 射
16、自己选择的路、跪着也要把它走 完。 17、一般情况下)不想三年以后的事, 只想现 在的事 。现在 有成就 ,以后 才能更 辉煌。
18、敢于向黑暗宣战的人,心里必须 充满光 明。 19、学习的关键--重复。
20、懦弱的人只会裹足不前,莽撞的 人只能 引为烧 身,只 有真正 勇敢的 人才能 所向披 靡。
大物二NO.4答案

《大学物理AII 》作业 No.4 光的偏振班级 ________ 学号 ________ 姓名 _________ 成绩 _______一、判断题:(用“T ”和“F ”表示)[ F ] 1.横波具有偏振性,纵波不具有偏振性。
解:由横波、纵波、偏振定义P91可得。
[ T ] 2.偏振片让平行于偏振化方向的电场分量通过,吸收垂直于这个方向的电场分量。
解:由偏振片性质P94知。
[ F ] 3.自然光入射到介质分界面时,如果入射角大于它的布儒斯特角,则反射光为线偏振光。
解:由光入射到介质分界面时形成反射、折射的起偏规律P95知。
[ T ] 4.双折射晶体中,光沿光轴方向传播,不发生双折射现象。
解:由双折射晶体中光轴定义P96知。
[ T ] 5.光是一种电磁波,我们把电场强度矢量称为光矢量。
解:由P90只有电场强度矢量引起视觉和感光作用知。
二、选择题:1.如图所示的偏振片可以得到偏振化方向平行于y 轴的偏振光。
当自然光入射时,将偏振片绕如图所示的光传播的方向顺时针转动︒40,通过偏振片的光强是: [ ] (A) 增大 (B) 减小(C) 不变 (D) 不能确定解:因自然光是非偏振光,故将偏振片绕如图所示的光传播的方向顺时针转动︒40,并没改变自然光振动方向与偏振片偏振化方向关系,故光强不变。
故选C2.当第三块偏振片以45º插入两块偏振方向正交的偏振片时,会有部分的光出射。
如果不是用单一的一块45º偏振片插入,而是中间插入N 块偏振片组,每片的偏振化方向平均转过90º/(N+1)。
[ ] (A) 没有光出射 (B) 出射的光更少(C) 出射的光一样多 (D) 出射的光更多解:设两块偏振方向正交的偏振片放置在 x 方向y ,自然光入射,则当第三块偏振片以45º插入时由偏振片起偏规律和右偏振化方向关系有 自然光通过偏振片1后光强为:21I I =强度为1I 线偏振光通过偏振片2后光强为:(马吕期定律))45(cos 2)45(cos 20212︒=︒=I I I 强度为2I 线偏振光通过偏振片3后光强为:)45(cos )45(cos 2)45(cos 220223︒︒=︒=I I I 80I =若中间插入N 块偏振片组,每片的偏振化方向平均转过90º/(N+1),由偏振片起偏规律和y x︒45右偏振化方向关系有出射光光强为)190(cos 2)190(cos )190(cos )190(cos 2)1(202220+︒=+︒+︒+︒=+N I N N N I I N(其中:共有N +1项)190(cos 2+︒N 连乘) 例:若N=1,则有0)11(20125.0)1190(cos 2I I I =+︒=+若N=2,则有0)12(20211.0)1290(cos 2I I I =+︒=+若N=3,则有0)13(20265.0)1390(cos 2I I I =+︒=+上述例子表明N 越大,透射光强越多。
光波及其在各向同性介质界面的反射和折射

2020年2月8日
7
光学教程专题 光波及其在各向同性介质界面的反射和折射
菲涅耳公式: 反射比与透射比关系:
rp t p 1; rs ts 1
正入射时:
rp
rs
n2 n2
n1 n1
tp
ts
2n1 n2 n1
2020年2月8日
8
光学教程专题 光波及其在各向同性介质界面的反射和折射
沿z轴方向传播的一维平面简谐波的波函数:
E(
p, t )
A c os [ (t
z) v
0
]
E hv,T 2 , h / 2 , P h /
k 2 , v
E(
p, t )
A exp
i [Et
P
r0 ]
2020年2月8日
2
E
2020年2月8日
A
exp
i[
(t
z v
)
0
E* Aexp{i[(t
] z
v
)
0
]}
4
光学教程专题 光波及其在各向同性介质界面的反射和折射
波函数的复数表达 复振幅:
当略去含有时间的指数因子时:
E~
Aexpi[k
r 0
]
称为复振幅。而根据复函数的运算法则:
相位突变 对入射波和反射波而言,则因:
rp
E1p ' E1 p
n2 n2
cosi1 cosi1
n1 cosi2 n1 cosi2
rs
第3章光通过各向同性介质及其界面所发生的现象

P58:例3.3 一束右旋圆偏振光正入射至一玻璃表面, 试确定反射光的偏振态。 解: 将右旋圆偏振光的振动分解为x方向的P分量和y 方向的S分量。
Ex Ap cos t , E y As cos(t
Ap As , i1 i2 0, rp n2 n1 rs n2 n1 Ap As
§1 光在各向同性介质界面上的反射和折射
1.1
1.2 1.3 1.4 1.5
菲涅耳反射折射公式
振幅反射(透射)比 布儒斯特定律 反射光与折射光的偏振态 相位跃变(相移) (能流)反射率和透射率
1.6 全反射与隐失波(近场光学) 1.7 受抑全反射(光子隧道效应)
复习 第一章 几何光学
折射定律:
n1 sin i1 n2 sin i2
一般取 E1s , E1 p 为正,所以反射波和折射波的 两个分量的正负号与入射角和两介质的折射率有关。
1.2
振幅反射(透射)比
相位跃变(相移)
1. 外反射(n1 < n2) (取n1 =1.0, n2 =1.5 )
+
iB
-
P51 从图中 可以看出: ① tp>0,ts>0 ② rs<0 ③ iB i1+i2=90° iB
n2 W2 I 2 cos i2 2
0 2 A2 cos i2 0
W1s A1s 2 2 能流反射率:Rs R r 2 rs , p p 2 W1 p A1 p W1s A1s W2 s n2 cos i2 A2 s 2 n2 cos i2 2 能流透射率: Ts ts 2 W1s n1 cos i1 A1s n1 cos i1
n2 n1 rp rs n2 n1 2n1 t p ts n2 n1
物理光学-在各向同性介质界面上反、折射(1.2.1-2)
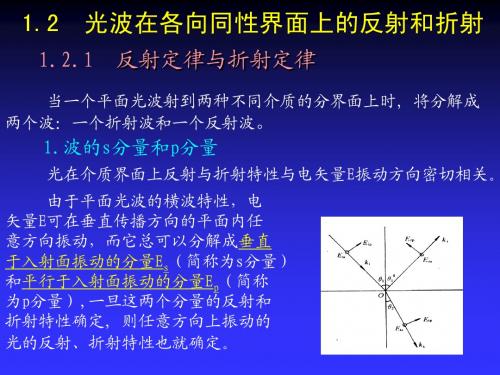
2.菲涅耳公式
消去Ers分量
⇒ ts =
[Eis − ( Ets − Eis )]n1 cosθ1 = Ets n2 cosθ 2
Ets 2 n1 cos θ1 2 n1 cos θ1 = = Eis n1 cos θ1 + n2 cos θ 2 n1 cos θ1 + ( n1 sin θ1 sin θ 2 ) cos θ 2 2 sin θ 2 cos θ 1 sin( θ 1 + θ 2 )
消去Etp分量
2E ip n1 cosθ1 = E tp (n 2 cosθ1 + n1 cosθ 2 )
⇒ tp = E
tp
E ip
=
2 n 1 cos θ 1 n 2 cos θ 1 + n 1 cos θ 2
=
2 cosθ1 sinθ 2 sin(θ1 + θ 2 ) cos(θ1 − θ 2 )
H is + H rs = H ts
n1 ( E ip + E rp ) = E tp n2
1 1 E ip + E µ 1V1 µ 1V1
rp
=
1 E µ 1V 2
tp
n1 (Eip + Erp ) cosθ2 n2
Erp (n 2 cosθ1 + n1 cosθ2 ) = Eip (n 2 cosθ1 − n1 cosθ2 )
光学 郭永康 高等教育出版社 期末考试试卷A 四川大学本科生专用

第 4 页 教务处编号
一.1.D 2.A 3.B 4.D 二. 1. 2π (n −1) e / λ 4 103 2. 3. 4. 5. 2d / λ
5.D,
6.B,
7.D,
8.D,
9.C
2分 2分 3 分
225 3 分
2 .
用波长为λ的单色光垂直照射如图所示的牛顿环装置,观察从 空气膜上下表面反射的光形成的牛顿环.若使平凸透镜慢慢地垂直 向上移动,从透镜顶点与平面玻璃接触到两者距离为 d 的移动过程 中,移过视场中某固定观察点的条纹数 目等于_______________. (3 分) 3.
λ
一平凸透镜,凸面朝下放在一平玻璃板上.透镜刚好与玻璃板接触.波长分别为
四 川 大 学 期 末 考 试 试 题
(2004-2005 学年第一学期(秋季) )
课程号: 课序号: 课程名称:光学 任课教师:王磊 成绩: 适用专业年级:2003 级物理类 学生人数:78 印题份数:85 学号: 姓名: 一.填空题(27 分)。 1. 用白光光源进行双缝实验,若用一个纯红色的滤光片遮盖一条缝,用一个纯蓝 色的滤光片遮盖另一条缝,则 (A) 干涉条纹的宽度将发生改变. (B) 产生红光和蓝光的两套彩色干涉条纹. (C) 干涉条纹的亮度将发生改变. (D) 不产生干涉条纹. [ ] 这条光路的光程改变了 (A) 2 ( n- 1 ) d. (B) 2nd. (C) 2 ( n- 1 ) d+λ / 2. (D) nd. (E) ( n- 1 ) d. [ ] 3.在夫琅禾费单缝衍射实验中,对于给定的入射单色光,当缝宽度变小时,除中央亮 纹的中心位置不变外,各级衍射条纹 (A) 对应的衍射角变小. (B) 对应的衍射角变大. (C) 对应的衍射角也不变. (D) 光强也不变. [ ] 4 . 在如图所示的单缝的夫琅禾费衍射实验中,将 x 单缝K沿垂直于光的入射方向(沿图中的 x 方向)稍微平移, 则 S (A) 衍射条纹移动,条纹宽度不变. L1 (B) 衍射条纹移动,条纹宽度变动. (C) 衍射条纹中心不动,条纹变宽. K L2 E (D) 衍射条纹不动,条纹宽度不变. (E) 衍射条纹中心不动,条纹变窄. [ ]
光学教程-答案-郭永康

1.4 在充满水的容器底部放一平面反射镜,人在水面上正视镜子看自己的像。
若眼睛高出水面h 1=5.00cm ,水深h 2=8.00cm ,求眼睛的像和眼睛相距多远?像的大小如何?设水的折射率n =1.33。
解:如图,人见水中镜离自己的距离为nh h h h 2121'+=+ 所以眼睛的像和眼睛的距离为)(03.22)33.100.800.5(2)(221cm n h h =+=+1.8 一个顶角为60º之冕玻璃棱镜,对钠黄光的折射率为1.62。
已知光线在棱镜第一面上的入射角i 1=70º,求:(1)在第一面上的偏向角;(2)在第二面上的偏向角;(3)总的偏向角。
解:由图可知'2835)70sin 62.11(sin )sin 1(sin 001112===--i n i00012'603528'2432'i i α=-=-=110021'sin (sin ')sin (1.62sin 2432')4227'i n i --===A习题图1.8习题图1.4因此,在第一、第二面上的偏向角分别为011202213432'''1755'i i i i δδ=-==-=总偏向角为0125217'δδδ=+=1.11 一根长玻璃棒的折射率为 1.6350,将它的左端研磨并抛光成半径为2.50cm 的凸球面。
在空气中有一小物体位于光轴上距球面顶点9.0cm 处。
求: (1)球面的物方焦距和像方焦距;(2)光焦度;(3)像距;(4)横向放大率;(5)用作图法求像。
解:已知1,' 1.6350, 2.50,9.0n n r cm s cm ====- (1) 2.50 3.94' 1.63501n f r n n =-=-=---(㎝) ' 1.6350 2.50' 6.44' 1.63501n f r n n ⨯===--(㎝)(2)2' 1.635025.4(D)' 6.4410n f -Φ===⨯ (3)由'''n n n n s s r --=得 ' 1.653011''/() 1.6530/()11.402.509.0n n n s n r s --=+=+=-(㎝)(4)由'11.400.777' 1.6350(9.0)ns n s β===-⨯-,是一倒立的缩小的实像。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
耳 公 式
ts
2 c o s i1 s in i2 s in ( i1 i2 ) c o s ( i1
i2 )
说明 1. Es 和 Ep 是同一矢量 E 的 s 分量和 p 分量。频率 相同。可以表瞬时量,也可表复振幅;
2. 正负随规定不同而不同,物理实质不变;
3. S 分量与 p 分量相互独立。
可得s光
振幅反射率
振幅透射率
rs
E1s E1s
n1coi1sn2coi2s n1coi1sn2coi2s
s光
ts
E2s E1s
2n1coi1s n1coi1sn2coi2s
同样分析TM光,可得p光
振幅反射率
rp
E1p E1p
n2coi1sn1coi2s n2coi1sn1coi2s
p光
振幅透射率
W1
A1
W 1
A1
n 1 i1 i1 A
光通量
W1 I1A1 I1Acosi1 W1 I1A1 I1Acosi1 W2 I2 A2 I2 Acosi2
能流反射率
n2
i2
A2
W2
Ts
W2s W1s
I2s cosi2 I1s cosi1
cosi2 cosi1
Ts
Tp
W2p W1p
I2p cosi2 I1p cosi1
2 2
rs 2
Rp
I 1p I1 p
n1 E 1p n1 E1 p
2 2
rp
2
光强透射率
Ts
I2s I1s
n2 E2s 2 n1 E1s 2
n2 n1
ts
2
2
Tp
I2p I1 p
n2• 能流反射率 能流折射率
能流比: 通过界面上某一面积的入射光、反射光 和折射光通量之比
cosi2 cosi1
Tp
R
s
W1s W1s
I 1s I1s
Rs
R
p
W1p W1 p
I 1 p I1 p
Rp
能流透射率
能量守恒
R s Ts 1 R p Tp 1
自然光入射 总能流反射率 R总 总入 反射 射 W W 1 1 能 能 W W 1 1ss流 流 W W 1 1p p
自然光二正交线偏振分量强度相等 W1s W1p 12W1
n1 n1
n2 n2
rp
rs
n 21 n 21
1 1
n2 n2
n1 n1
ts
tp
2 n 21 1
2 n1 n1 n2
(2) 无论外反射和内反射都有一特殊角度
ib
tan1
n2 1
tan1
n2 n1
i1 ib rp 0.
ib ib
n1
n2
ib 称为布儒斯特(D.Brewster)角
i2
(3) 对内反射(光密到光疏),存在一角度
ic
sin1 n21
sin1
n2 n1
i1 ic rs rp 1
ic 称为全反射临界角
二. 反射、折射能流比与光强比 • 光强反射率 光强折射率 光强正比于光振动振幅平方
注意:一般折射反射问题中,考虑不同折射率的影响
12 , InE 02
光强反射率
Rs
I 1s I1s
n1 E 1s n1 E1s
CH 3-5
光在各向同性介质界面的反射折射
reflection and diffraction at the interface of isotropic dielectrics of light wave
3.5 光在各向同性介质界面的反射折射
电磁理论
反射定律、折射定律
边界条件
菲涅耳公式
菲涅耳公式反射、折射---振幅、强度、能流
注意:正入射时,无论外反射内反射
Rs
Rp
R(n211)2 n211
(n1 n2)2 n2 n1
Ts
Tp
T
4n21 (n211)2
4n1n2 (n1 n2)2
对空气-玻璃界面,R = 0.04,T = 0.96。外反射时,R
一般随入射角 i1 的增加而增大,当 i1 即90掠 入射 Rs
和 RP 均趋近于1。
E 1s
E1s
n1
H 1P
k 1 k 1
i1 i1
H 1 p
p态—振动矢量在入射面内 s态—振动矢量垂直于入射面
n2
i2 k 2E 2s
H 2p
TE波界面折射、反射
TE波—E为s态, H为p态 TM波—E为p态H为s态
任一偏振态的入射光均可依据正交 分解看作TE和TM两种线偏振叠加
一. 反射、折射的振幅比 菲涅耳公式
菲涅耳公式以 i1 表示
r s cos i1 cos i1
n 21 2 sin 2 i1 n 21 2 sin 2 i1
ts cos
2 cos i1 i1 n 21 2 sin
2 i1
rp
n 21 2 cos n 21 2 cos
i1 i1
n 21 2 sin 2 i1 n 21 2 sin 2 i1
TE波
E 1s
E1s
n1 H 1P
k 1 k 1
i1 i1
H 1 p
E、H矢量在界面处切向连续
反射和折射不改变E、H的振 动态
n2
i2 k 2E 2s
H 2p
光学介质-非磁介质
E1sE1sE2s H1pcoi1 sH1pcoi1 sH2pcoi2s
120Hn0cE n 1 (E 1 s E 1 s)cio 1 n s2 E 2 scio 2
tp
n 21 2 cos
2 n 21 cos i1 i1 n 21 2 sin
2 i1
n21n2/n1
内反射— n2n1,n211从光疏介质射向光密介质
外反射— n2n1,n211从光密介质射向光疏介质
◆ 三个特殊角度
(1) 正入射 i1 = 0,不论内反射还是外反射
rs
n 21 n 21
1 1
例如:在湖岸边观察水下物体时,近物要比远物更加 清楚,相反,远处物体在湖面的倒影则比近物更加清 晰。
RW 1 sW 1 W 1 p2 W W 1 1 ss2 W W 1 1 p p1 2(RsRp)
类似可得总光强反射率:
R 总 总入 反 I I1 1 射 射 I I1 1 s s I I1 1 光 光 p p1 2(R 强 强 sR p) R 由能量守恒 RT 1
总能流透射率 T1-R1R
总光强透射率 T总 总透 入II1 2射 射 II2 1s s 光 光 II1 2p p1 2 强 强 (T sT p)
tp
E2p E1p
2n1coi1s n2coi1sn2coi2s
利用关系 n1siin 1n2siin 2
rs
s in ( i1 s in ( i1
i2 ) i2 )
ts
2 c o s i1 s in i2 s in ( i1 i2 )
菲 涅
rp
ta n ( i1 i2 ) ta n ( i1 i2 )
