201单自由度体系运动方程(力学)

合集下载

结构力学专题七(单自由度体系的动力计算)

设： 2
k11 m
1
m11
运动方程： y(t) 2 y(t) 0
1、运动方程的解
y(t) c1sin t c2 cos t
(a)
或 y(t) csin( t )(ຫໍສະໝຸດ )当 y0、y0 为已知时
y(t)
y 0
sin
t
y
0
cos
t
(c)
方程（a）、（b）、（c）称为位移方程。
2、位移方程的几何意义
A1 5cm2
W 0.1kN
3m
（1）求竖向振动时的频率和周期，
(2)设： y0 10cm(向下），y0 0;
求： t
4
90
时质体的绝对位移。
A2 10cm2
4m
补2（选作）：求图示体系的自振频率：
m
EI
m
k
l
l
l EI
FP (t)
EI
l/2 l/2
三、举例与讨论
例1：建立图示体系运动微分方程 FP (t)
m EI
l/2 l/2
方程：
L3 48EI
(my(t)
cy(t))
y(t)
L3 48EI
FP (t)
my(t) cy(t)
48EI L3
y(t)
FP (t)
例2：建立图示体系运动微分方程
FP (t)
EI0
m
h EI
EI
方程：
my(t) cy(t)
m
EI FP (t)
l/2 l/2
例3：求图示体系的自振频率。
FP (t)
EI0
m
h EI
EI

第3章单自由度体系1(时域)

第三章单自由度体系自由振动和强迫振动时域分析3.1力学模型•单自由度体系：SDOF（Single－Degree－of－Freedom ）System•结构的运动状态仅需要一个几何参数即可以确定•分析单自由度体系的意义：1、单自由度系统包括了结构动力分析中涉及的所有物理量及基本概念。

2、很多实际的动力问题可以直接按单自由度体系进行分析计算。

3、多自由度系统在很多情况下可以转变为单自由度系统进行分析重力的影响1、考虑重力影响时，结构体系的运动方程与无重力影响时的运动方程完全一样，此时u是由动荷载引起的动力反应。

在研究结构的动力反应时，可以完全不考虑重力的影响，建立体系的运动方程，直接求解动力荷载作用下的运动方程，即得到结构体系的动力解。

2、当需要考虑重力影响时，结构的总位移为总位移=静力解+动力解应用叠加原理将结构的动力反应和静力反应相加即得到结构的总体反应。

在结构反应问题中，应用叠加原理可将静力问题（一般是重力问题）和动力问题分开计算。

重力的影响3、注意1：由于应用了叠加原理，上述结论是用于线弹性体系。

4、注意2，在以上推导过程中，假设悬挂的弹簧―质点体系只发生竖向振动，在动荷载作用之前，重力被弹簧的弹性变形所平衡，而施加荷载后，重力始终被弹性变形所平衡。

如果重力的影响没有预先被平衡，则在施加动力荷载产生进一步变形后，可以产生二阶影响问题，例如P―Δ效应。

1.1无阻尼自由振动运动方程的通解为：121212()n n i ti ts ts tu t c e c ec ec eωω−=+=+指数函数与三角函数的关系：cos sin cos sin ixixe x i x ex i x−=+=−运动方程的解：()cos sin n n u t A t B tωω=+A ，B —待定常数，由初始条件确定。

一些重要性质：（1）自振周期只与结构的质量和结构的刚度有关，与外界的干扰因素无关。

（2）自振周期与质量的平方根成正比，质量越大，周期越大（频率越小）；自振周期与刚度的平方根成反比，刚度越大，周期越小（频率越大）；要改变结构的自振周期，只有从改变结构的质量或刚度着手。

动力学(第1章)

f
(t)
=
2P0
ωt π
∫ ∫ bi
=
2 T
T 0
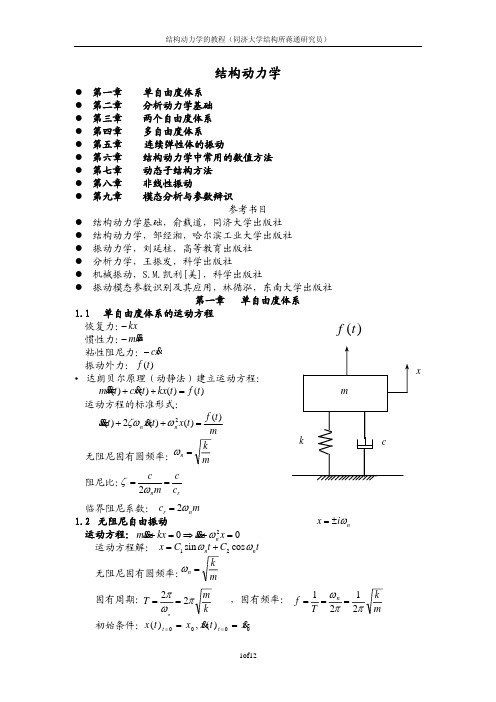
f (t) sin(iωt)dt = 4ω π
π 2ω 0
f
(t) sin(iωt)dt
=
8P0 i2π 2
i −1
(−1) 2 (i
= 1,3,5,⋅⋅⋅)
6of12
结构动力学的教程（同济大学结构所蒋通研究员）
∑ 取
i=1~3
β1 算得：
=
1
−
1 ω2
= 1−ω
2ζω 3 2 + (2ζω )2
1+ 4ζ 2ω 2 (1− ω 2 )2 + (2ζω )2
5of12
结构动力学的教程（同济大学结构所蒋通研究员）
隔振要求：频率比： ω
=
ω
>
2⇒
ωn
阻尼比小：ζ ↓⇒ A ↓
B
A <1 B
但过小通过共振区不利
主动隔振：将振源隔开，使振动传播不出去（隔振器）
+ϕ)
振幅与相位角： A=
x02
+
⎜⎜⎝⎛
x&0 ωn
⎟⎟⎠⎞2
,ϕ
=
arctg
ωn x0 x&0
x
A
x&0
x0
t ϕ /ωn
t t +T
例题 1-1 求图示体系的固有频率
悬臂梁刚度：k1
=
3EI l3
与 K2 并联后等效刚度：k = k1 + k2 固有频率:ωn = k / m （串联弹簧）
l m
• •
能量守衡：We +Wd + Wf = 0 → ω = ωn →

结构力学-单自由度体系的自由振动

mh3 T 2 24 EI
Vibration Characteristic
y(t ) Asin( t )
Acceleration： Inertia Force：
(t ) A 2 sin(t ) y (t ) mA 2 sin(t ) I (t ) m y
这是一个齐次方程，其通解为
y(t ) C1 cost C2 sin t
C1 和 C2 可由初始条件确定，设初始位移和初始速度分别为
y(0) y0 C1 y0
(0) v0 y
C2
v0
v0

,
y (t ) y0 cos t

sin t
y (t ) y0 cos t
在无阻尼自由振动中，位移、加速度和惯性力都按正弦规律
变化，且作相位相同的同步运动，即它们在同一时刻均达极值，
而且惯性力的方向与位移的方向一致。
幅值产生于
sin(t ) 1 时，其值分别为：
y A
A 2 y
I mA

2
由于在运动的任一瞬时质体都处于平衡状态，在幅值出现时
l

1 m
EA ml
st Wl T 2 2 g EAg
例: 求图示结构自振频率。（EI 为常数，杆件自身质量不计） [分析] 图乘法求位移
A m C l h
1 1 2 2 1 2 h2 B ( h h hl h) (h l ) EI 2 3 2 3 3EI
y y

v0

sin t
T
0
t
y cos t
-y
y

单自由度系统(自由振动)

第二章单自由度系统的自由振动本章以阻尼弹簧质量系统为模型,讨论单自由度系统的自由振动。

§2-1 无阻尼系统的自由振动无阻尼单自由度系统的动力学模型如图1.1所示。

设质量为m ，单位是kg 。

弹簧刚度为K ，单位是N ／m ，即弹簧单位变形所需的外力。

弹簧在自由状态位置如图中虚线所示。

当联接质量块后，弹簧受重力W=mg 作用而产生拉伸变形∆：，同时也产生弹簧恢复力K ∆，当其等于重力W 时，则处于静平衡位置，即 W=K ⋅∆若系统受到外界某种初始干扰，使系统静平衡状态遭到破坏．则弹簧力不等于重力，这种不平衡的弹性恢复力，便使系统产生自由振动。

首先建立座标，为简便起见，可选静平衡位置为座标原点，建立铅垂方向的座标x ，从原点算起，向下为正，向上为负，表示振动过程中质量块的位置。

现设质量m 向下运动到x ，此时弹簧恢复力为K(∆+x)，显然大于重力W ，由于力不平衡，质量块在合力作用下，将产生加速度运动，故可按牛顿运动定律(作用于一个质点上所有力的合力，等于该质点的质量和沿合力方向的加速度的乘积)，建立运动方程，取与x 正方向一致的力、加速度、速度为正，可列如下方程改写为 0=+kx xm (1-1-1 令mkp =2(1-1-2)单自由度无阻尼系统自由振动运动方程为02=+x p x(1-1-3)设方程的特解为 ste x =将上式代入(1-1-3)处特征方程及特征根为ips p s ±==+2,1220则(1-1-3)的通解为ptD pt C e C e C x ipt ipt sin cos 11+=+=- (1-1-4)C 、D 为任意积分常数，由运动的初始条件确定，设t=0时00,x xx x == （1-1-5）()x m x k W F=+∆-=∑量位静平衡位置一自由度弹簧—质量系统 ∆==k mgW xx)则pt pxpt x x sin cos 00 += （1-1-6）经三角变换，又可表示为)sin(α+=pt A x（1-1-7）其中 001220,x px tg p x x A -=⎪⎪⎭⎫ ⎝⎛+=α （1-1-8）自由振动的振幅A 和初相位角α与系统的参数和初始条件有关。

电大土木工程力学-选择判断

电大土木工程力学-选择判断1.对图示平面体系进行几何组成分析，以下体系是（无多余约束的几何不变体系）。

2.对图示平面体系进行几何组成分析，该体系是（瞬变体系）。

3.对图示平面体系进行几何组成分析，该体系是（有两个多余约束的几何不变体系）。

4.对图示平面体系进行几何组成分析，该体系是（可变体系）。

5.对图示平面体系进行几何组成分析，该体系是（有一个多余约束的几何不变体系）。

6.对图示平面体系进行几何组成分析，该体系是（几何可变体系）。

7.三刚片组成几何不变体系的规则是（三铰两两相联，三铰不在一直线上）。

8.刚结点在结构发生变形时的特征是（结点处各杆端之间的夹角保持不变）。

9.一个平面体系的计算自由度W>0，则该体系是（可变体系）。

10.在无多余约束的几何不变体系上增加或去掉一个二元体后构成（无多余约束的几何不变体系）。

11.图乘法的假设为（Mp及M图中至少有一图是由直段组成、杆件EI为常数、杆件为直杆）。

12.图示结构AB杆件A截面的剪力等于（Fp）。

13.瞬变体系在很小的荷载作用下会产生很大的内力。

14.如果在一个体系中增加一个约束，而体系的自由度并不因此减少，则称此约束为多余约束。

15.体系的实际自由度绝对不小于其计算自由度。

16.如果体系的计算自由度等于其实际自由度，那么体系中没有多余约束。

17.如果体系的计算自由度大于零，那么体系一定时几何可变体系。

18.仅利用静力平衡条件即可确定结构全部反力和内力，且解答唯一，这样的结构称为静定结构。

19.两个刚片用不全平行也不全交于一点的三根链杆相联，组成的体系是无多余约束的几何不变体系。

20.两刚片用三个链杆相联，且三链杆平行不等长，则构成瞬变体系。

21.当结构中某个杆件的EI为无穷大时，其含义是这个杆件无弯曲变形（无轴向变形）。

1.对图a所示结构，按虚拟力状态b将求出（A、D连线的转动）。

2.图示虚拟状态是为了求（A截面转角）。

3.图示为刚架的虚设力状态，按此力状态及位移计算公式可求出（）。

结构力学单自由度体系强迫振动

l3 4 EI
A16 FPl3 7 4EI.
3
FFPPssiinnω3 4t t
l
3mm 2
l 2
l
求质点处的最大动位移及最大动弯矩图,EI=常数
l3 4 EI
A1619FPl3 7 48EI .
FI 1298FPsint
FPsint
m
l/ 2
l/ 2
4 EI
3ml 3
求质点m处的最大动位移及最大动弯矩图,EI=常数
0
t<0
FP0
t
FP(t)= FP0 0<t<u
u
0 t> u
.
阶段Ⅰ：（ 0≤t ≤ u ） y(t) = yst (1- cosωt)
FP(t)
yt2yst
sint
2
2
FP0
u
.
阶段Ⅰ：（ 0≤t ≤ u ）
yt2yst
sint
2
2
ytmax
2yst
2yst
sinu
2
2
.
U≥T/2 U≤T/2
FP(t)
• m ÿ+ k y = F P(t)
•y•(t)2yFPt
m
.
二、动荷载作用在结构的任意位置
FP(t)
••
m y
m
y
.
• 动位移方程：y(t)(m•y•)11FPt1P
若令等效荷载 FP'tFPt111P 只对质点位移等效
•y•(t)2yFP't 运动微分方程的标准
m 表达式（强迫振动）
2
3
A
l/2
l/2
2l3 3 EI

结构动力学-第三章单自由度体系 (Part 1)

结构动力学Dynamics of Structures 第三章单自由度体系Chapter 3 Single-Degree-of-Freedom SystemsPart 1华南理工大学土木工程系马海涛/陈太聪本章主要目的及内容目的:z 通过单自由度体系介绍动力学的基本概念z 若干实际问题的解内容:(1)无阻尼自由振动(2)有阻尼自由振动(3)对简谐荷载的反应(4)对周期荷载的反应(5)对任意荷载的反应(6)体系的阻尼和振动过程中的能量(7)隔振(震)原理(8)结构地震反应分析的反应谱法自由振动free vibration强迫振动forced vibration第三章单自由度体系SDOF Systems自由振动：结构受到扰动离开平衡位置以后，不再受任何外力影响的振动过程。

0mucu ku ++= 无阻尼自由振动单自由度系统的运动方程()mucu ku P t ++=00c muku =⇒+= 自由振动运动方程单自由度系统无阻尼自由振动的运动方程0muku += 初始扰动：00(0)(0)t t u u uu ==== 初始位移初始速度二阶齐次常微分方程Homogeneous second orderordinary differential equation无阻尼自由振动的数学模型000;(0),(0)t t muku u u uu ==+=== 初始条件Initial conditions2()0stC ms k e +=设解有以下形式()stu t Ce=代入方程得 C 和s 为待定常数。

因此，方程通解为：121212()n n i ti ts t s tu t C e C eC eC eωω−=+=+或模型求解0muku += 2ms k ⇒+=1,2n ks i mω⇒=±=±()cos sin n n u t A t B tωω=+三角函数形式通解()sin cos n n n n ut A t B t ωωωω=−+00(0)(0)t n t u A u uB u ω====== (0)()(0)cos sin n n nuu t u t tωωω=+(0)(0),nuA uB ω⇒==利用初始条件，我们有单自由度系统无阻尼自由振动问题的解其中n kmω=无阻尼自由振动为简谐运动Simple harmonic motion ωn 称为圆频率或角速度Angular frequency / velocity ()cos sin n n u t A t B tωω=+三角函数形式通解()sin cos n n n n ut A t B t ωωωω=−+振幅无阻尼自由振动问题解的图示（1）振幅–Amplitude of motion[]220(0)(0)n u u u ω⎡⎤=+⎢⎥⎣⎦基本参数（2）固有周期–Natural period of vibration2n nT πω=（3）固有频率–Natural frequency of vibration1n nf T =Hz (赫兹)固有频率s (秒)固有周期rad/s (弧度/秒)固有圆频率单位定义物理量名称2n nT πω=1n nf T =n k m ω=单自由度系统无阻尼自由振动系统参数§3.2 有阻尼自由振动0c uk u m u ++= 运动方程2()0stC ms cs k e ++=设解有以下形式()stu t Ce =代入方程得解为：221,222nc c s m m ω⎛⎞=−±−⎜⎟⎝⎠粘性阻尼模型2ms cs k ++=2c k s s m m++=22n c s s mω++=阻尼系数影响此项的取值进一步决定解的特征Critical damping and damping ration临界阻尼22022n cr n c c m m k c m ωω⎛⎞−=⇒⎜⎟⎝⎠===此时运动方程的解为12ns s ω==−()()n tu t A Bt e ω−=+0mucu ku ++= 验证—分别将两个解代入方程()n tu t Aeω−=()n tu t Bteω−=()22220n t nnnAem m m ωωωω−=−+=()2n t nnAem c k ωωω−−+左端=()()221n t nnnBem t c t kt ωωωω−⎡⎤−++−+⎣⎦左端=()2220n tnnnBec m t m k ωωωω−⎡⎤=−+−+=⎣⎦Critical damping and damping ration运动方程的解为()()n tu t A Bt e ω−=+()()(0)(1)(0)n tn u t u t ut e ωω−=++ (0)(0)n u AuA B ω==−+ 因此，解为根据初始条件，有()()n tn u t A Bt B eωω−=−++⎡⎤⎣⎦ 对应的速度表达式为(0)(0)(0)n A u B u uω==+ 或者(0)()(0)1(0)n t n uu t u t e u ωω−⎡⎤⎛⎞=++⎢⎥⎜⎟⎝⎠⎣⎦(0)()(0)1(0)n t n uu t u t e u ωω−⎡⎤⎛⎞=++⎢⎥⎜⎟⎝⎠⎣⎦ 解的特征由此项控制当阻尼大于临界阻尼时，0mucu ku ++= 220n n uu u ζωω++= 2n crc cm c ζω==其中，阻尼比1221120()s ts ts s u t C e C e<<=+临界阻尼可定义为：体系自由振动反应中不出现往复振动所需的最小阻尼值。

2-1结构动力学(单自由度)

c 2 m
O
t
这条曲线仍具有衰减性，但不具有波动性。
1, cr 2m
c 2m
c cr
阻尼比
（2）ξ> 1（强阻尼）情况
1,2 2 1 0
y t C1e1t C2e2t
t

y( t )
O
y (t ) e t C1 sinh 2 1 t C 2 cosh 2 1 t
g y st
y st m T 2 2 k g
频率只取决于体系的质量和刚度，而与外界因素无关，是体系本身固有的属性，所以又称为固有频率
（natural frequency）。
（3）简谐自由振动的特性
y(t ) Asin( t )
(t ) A 2 sin(t ) y 加速度为：惯性力为： FI (t ) m (t ) mA 2 sin(t ) y
特征根一般解
2 2 2 0
1, 2 2 1

y(t ) C1e
1t
C2 e
2t
（1）ξ= 1（临界阻尼）情况
1,2
y C1 C2 t e t
y( t )
tan v

t
y y0 (1 t ) v0t e
d
阻尼对自振频率、周期的影响
,
d
Td T
在工程结构问题中，若0.01<ξ<0.1，可近似取:
d , Td T
y(t ) e t Asin ( d t )
阻尼对振幅的影响
yk Aetk Td e y k 1 Ae (tk Td )

结构力学课件单自由度体系复习版

W
FP(t)
由作用力和反作用力的关系 FS(t ) FS (t )
FI (t) FD(t) FP (t) W
y FS(t )
FI (t) FD (t) FP (t) W
yd (myd cyd FP (t))
单自由度体系动力平衡方程
myd cyd kyd FP (t)
非质量处的位移动力系数
单自由度体系受迫振动当动荷载不作用在质点上时，质点的位移动力系数仍与原动荷载作用于质点上相同，但体系其它部位的位移和内力的动力系数通常不再相同，即体系没有统一的动力系数。
第十章结构动力计算
10.2 单自由度体系运动方程的建立
General Equation of Motion
1. 建立体系运动方程方法
反映体系各自由度方向上位移随时间变化的规律的函数表达式称为体系的运动方程.
建立运动方程的途径： 1. 利用达朗伯原理 —— 动静法； 2. 利用哈密顿原理 —— 变分法。
稳态受迫振动分析
稳态受迫振动
yt
m(
F 2
2
)
sin
t
F
m 2
1
1
2 2
s in
t
yst sin
t
yst
F
m 2
F11
荷载幅值作为静荷载所引起的静位移
1 2
1
2
A yst
质量的位移动力系数稳态振幅
质量位移动力系数的讨论
1
1
2 2
1. 当θ/ω→0时, →1，荷载变化得
很慢，可当作静荷载处理。
当荷载未作用在质量上
注意：此时内力动力系数和位移动力系数并不相同，而各截面对应的动弯矩和静弯矩的比值也不同。各区段没有一个统一的放大系数。

《结构力学》结构动力学(2)

为最大的动力位移与静力位移之比，称为位移动力系数。
简谐荷载作用下，与之间关系曲线分析。
1、无阻尼条件
（1） 0 时， 5.0
1, ymax ( t ) yst。
4.0
（2）0 1 0 时，
随着增加增大，
3.0
0
FP ( t ) FP sint。 y( t ) yst sint。
（3）当ξ=1时的阻尼称为临界阻尼；相应的值称为
临界阻尼系数，用cr 表示，则
cr 2mk 2m ，
k 2mk 2m cr
阻尼比即为阻尼系数与临界阻尼系数 cr 之比。
§14-4 单自由度结构在简谐荷载作用下的强迫振动
当干扰力 F(t) 直接作用在质点上，质点的受力将如图14-10所示，
且 y( t )与FP ( t ) 同步。
2.0
（3） 1 时， 1.0
, ymax ( t ) , 共振。
（4）1 时，
1.0 2 2.0
3.0
随着增加减小，且 y( t )与 FP ( t ) 反向。
（5）时， 0, 在静平衡位置附近作微小
振动。
y0
cos 't
y0
ky0
'
sin
't
y bekt sin( 't ')
其中
b
y02
(ห้องสมุดไป่ตู้
y0
ky0
'
)2
tan ' ' y0
/ 为有阻尼自振频率。
y0 ky0
令 k ，称为阻尼比。
' 2 k2 1 ( k )2 1 2
通常当ξ<0.1时，则 ' 和的差别很小。

电大开放教育土木工程力学选择判断复习提纲

土木工程力学选择判断题复习提纲（本提纲按每道题的第一个字的首字母排序。

●代表单选题，◆代表判断）B 部●不考虑杆件的轴向变形，下图所示体系的振动自由度为(A1)C 部◆超静定结构的内力状态与刚度有关。

(√)◆超静定结构的内力与材料的性质元关。

(╳)◆超静定结构的力法基本结构不是唯一的。

(√)◆超静定结构的力法基本结构是唯一的。

(╳)●超静定结构的超静定次数等于结构中(B 多余约束的数目) ●超静定结构产生内力的原因(D.以上原因都可以)。

◆超静定结构由于支座位移可以产生内力。

(√)●超静定结构在荷载作用下产生的内力与刚度(B 相对值有关) ◆超静定次数一般不等于多余约束的个数。

（×）D 部◆当AB 杆件刚度系数SAB=3i 时，杆件的B 端为定向支座。

(╳)◆当结构中某个杆件的EA 为无穷大时，其含义是这个杆件元轴向变形。

(√)◆当结构中某个杆件的EI 为无穷大时，其含义是这个杆件无弯曲变形。

(√) ◆当结构中某杆件的刚度增加时，结构的自振频率不一定增大。

(√) ◆对称结构在反对称荷载作用下，对称轴穿过的截面只有反对称的内力。

(√) ◆对称刚架在反对称荷载作用下的内力图都是反对称图形。

（×）●对称结构作用正对称荷载时，对称轴穿过的截面(D. 既有轴力，又有弯矩)。

◆对于超静定梁，塑性铰的数目不一定等于结构的超静定次数。

(√) ●单自由度体系运动方程为y+2wy+w 2y=P(t)/m ，其中未考虑质体重力，这是因为(C.以重力作用时的静平衡位置为y 坐标零点)F 部◆反映结构动力特性的参数是振动质点的数目。

(╳)◆反映结构动力特性的参数是振动质点的振幅。

(╳)●反映结构动力特性的重要物理参数是(C.自振频率)。

G 部◆干扰力只影响振动质点振幅，不影响结构的自振频率。

(√)●根据影响线的定义，图示悬臂梁A 截面的弯矩(下侧受拉为正)影响线在B 点的纵坐标为(B. -4m)。

单自由度体系自由振动

单自由度体系自由振动一、无阻尼振动单自由度体系自由振动可分为有阻尼和无阻尼振动两种。

在模型建立过程当中，可以直接进行建立。

在运行时，只需将c=0即可。

ω增加，单位时间内振动次数增加。

无阻尼振动是简谐振动，振幅和初相位仅取决于初位移和速度。

初始干扰反映了外部初始赋予体系能量的大小。

由于不考虑振动过程中体系能量的耗散，因而体系的总能量保持不变，这就表现为振幅Ａ保持不变，永不衰减。

于是振动一旦发生便永不停息，但这仅是一种理想状态。

二、对阻尼自由振动的讨论当阻尼系数ｃ不为０时，体系做阻尼运动。

由于有能量的耗散，体系的运动幅度会逐渐减小，最终停止振动。

有阻尼单自由度体系，自由振动的运动方程为ωξωm c m k t ky t y c t y m 2,0)()()(2===++∙∙∙，则原式可变为022=++∙∙∙ωξωy y 。

解微分方程有如下结果：2.1 当1<ξ时，即小阻尼运动，方程的解为：)sin(A )sin cos ()(000ϕωωωξωωξωξω+=++=--t e t y v t y e t y d t d d d t 其中2200201)(ξωωωξω-=++=d d y v y A可画出小阻尼体系自由振动时的ｙ－ｔ曲线如图所示：是一条逐渐衰减的波动曲线2.2 当1>ξ时，即大阻尼的情况，方程的解为：⎥⎥⎦⎤⎢⎢⎣⎡-+--+=-t ch y t sh v y e t y o t ωξωξξξωωξ11)1()(20220 上式不含有简谐振动的因子，是因为体系受干扰后偏离平衡位置所积蓄起来的初始能量在恢复平衡位置的过程中全部消耗克服阻尼，由于阻尼很大，不足以引起振动。

当初始速度，初始位移都大于０时，可画出大阻尼体系自由振动时的ｙ－ｔ曲线如图所示：2.3 当1=ξ时，即临界阻尼的情况，方程的解为：[]t v t y e t y t 00)1)(++=-ωω（当初始速度，初始位移都大于０时，可画出临界阻尼体系自由振动时的ｙ－ｔ曲线如下图所示；当体系在临界阻尼时，其运动衰减的最快，即他能在最短时间内无振动的回到平衡位置。

第三章结构动力学单自由度体系

DTD 2
ui 1 TD eTD ui 1 e
相邻振动峰值比仅与阻尼比有关而与i的取值无关
小阻尼比时
ui 2 ln ui 1 1 2
D 2m
1 0.11 ln 2 2J 50% J 50%
2
3.自由振动试验
自振周期：Natural Period (of vibration) ——结构的重要动力特性
3.1.1 无阻尼自由振动结构自振频率和自振周期及其关系
k 自振圆频率： n (单位：弧度/秒, rad/s) m
自振周期：
Tn
2
n
(单位：秒, sec)
自振频率：
n fn (单位：周/秒, 赫兹, Hz) 2
TD 2
ωD—阻尼体系的自振频率
Tn 1
2
n 1
2

TD—阻尼体系的自振周期
ωn和Tn分别为无阻尼体系的自振频率和自振周期
(1) 阻尼的存在使体系自由振动的自振频率变小 (2) 阻尼的存在使体系的自振周期变长，当ζ＝1时，自振周期TD=∞
3.1.2 有阻尼自由振动
3.低阻尼体系
现场实测：ωD 和 TD 理论计算：ωn 和 Tn 工程中结构的阻尼比ζ 在1—5%之间，一般不超过20%，因此可以用无阻尼体系的结果代替有阻尼结果。
D n 1
2
TD
Tn 1 2
TD Tn
D n
图3.6 阻尼对自振频率和自振周期的影响
3.1.2 有阻尼自由振动
ku 0 mu
初始条件：
t 0 u (0) u t 0 u(0), u
3.1.1 无阻尼自由振动

自由度体系的运动方程

边界条件的处理
边界条件是运动方程中需要考虑的重要因素，它决定了系统的行为和响应。
处理边界条件的方法包括直接约束法、引入虚拟约束法、罚函数法等。根据具体问题选择适当的处理方法，以保证求解的准确性和有效性。
04 自由度体系的稳定性分析
线性稳定性分析
线性化方程
将非线性自由度体系线性化，得到线性微分方程。
通过建立自由度体系的运动方程，可以分析飞行器的气动性能、稳定性、控制性能等，为航空航天器设计提供重要的技术支持。
THANKS FOR WATCHING
感谢您的观看

解析法求解需要对方程进行数学变换，如分离变量法、傅里叶变换等，以简化方程并找到解。
数值法求解
数值法求解运动方程是通过对方程进行离散化，用一系列离散点上的数值近似代替连续的解。这种方法适用于复杂的问题，如多自由度振动或非线性动力学问题。
数值法求解需要选择适当的离散化方法和迭代算法，如有限差分法、有限元法、龙格-库塔法等，以获得满足精度要求的解。
确定需要优化的参数，并给出其取值范围和约束条件。
建立约束条件
根据设计要求和实际情况，建立各种约束条件，如几何约束、性能约束等。
优化算法的选择与实现
优化算法分类
根据设计问题的特点和要求，选择合适的优化算法，如梯度下降法、遗传算法、模拟退火算法等。
算法实现
根据选定的优化算法，编写相应的计算程序，实现优化设计的过程。
航天器姿态控制
航天器的姿态调整是通过控制其自由度实现的，如俯仰、偏航和滚动三个方向的转动。
车辆动力学
车辆的运动状态可以通过控制其轮毂电机的自由度进行调节，实现车辆的稳定性和操控性。
02 运动方程的建立

第五章单自由度体系运动方程数值方法

p i1
pi1
1 [
t 2
ui
1
t
ui
(
1
2
1)ui ]m
[ t
ui
(
1)ui
t 2
(
2)ui ]c
5.4 Newmark —β法与其它积分方法的关系
通过对Newmark —β法中控制参数β取不同的值也可以得到其它时域逐步积分方法。下表给出了β取不同值时 Newmark —β法所对应的逐步积分法。
结构动力学
（2003秋）
结构动力学
第五章
单自由度体系运动方程数值解法
5.1 数值求解的数学基础
• 单自由度体系运动微分方程（时间连续）
利用微分与差分的关系转化为代数方程（时间离散）
u&i (ui 1 ui ) / (ti 1 ti ) (ui 1 ui ) / t
u&&i (u&i 1 u&i ) / (ti 1 ti ) (ui 2 2u i 1ui ) 方程2：加速度、速度和位移的积分关系
ui1－ui
ti1 u&( )d
ti
ti1 ti
ti1 u&&( )d
ti
u&it
方程3：补充方程：
假定&u&（）在ti和ti＋1时间段的变化规律
5.3 逐步积分法介绍：常加速度法
5.3 逐步积分法介绍：常加速度法
评价的标准：求解无阻尼单自由度振子：
u&& 02u 0
初值：u(0)=1和u&(0)=0
5.5 逐步积分法的评价
数值计算的稳定性：无条件稳定：时
间步距无关，计算结果总是稳定的

第三章_单自由度机械系统动力学

2. 等效构件的角加速度
d d d d dt d dt d
二、等效转动惯量是常数，等效力矩是速度的函数时
以电动机驱动的鼓风机、搅拌机、离心泵以及车床等之类机械属于这种情况。这些机器的驱动力是速度的函数，而生产阻力是常数或者是速度的函数，机器的速比是常数。因此，其等效力矩仅仅是速度的函数，而等效转动惯量是常数，此时，用力矩形式的运动方程式求解比较方便。
广义坐标为一个角位移时，广义力F为一等效力矩Me，它可按下式计算：
m j Fk vk cos k F Me ( ) ( M j ) q q k 1 j 1 m
、vk / q 是由机构的尺度和位置决定的， Me表示式中的广义传动比 j / q 的变化无关。 Me仅仅是机构广义坐标q的函数，与广义速度 q
单自由度机械系统的动力学方程2 q
三、等效力学模型
机械系统是复杂多样的，在进行动力学研究时，通常要将复杂的机械系统，按一定的原则简化为一个便于研究的等效动力学模型。为了研究单自由度机械系统的真实运动，可将机械系统等效转化为只有一个独立运动的等效构件，等效构件的运动与机构中相应构件的运动一致。
§3.1 概述
机械的真实运动规律是由作用于机械上的外力、各构件的质量、尺寸及转动惯量等因素决定的，而研究机械在外力作用下的真实运动则是机械动力学的基本问题（机械动力学的正问题）。本章主要研究两个问题: 第一，研究单自由度机械系统在外力作用下的真实运动规律，即机械系统的运动随时间的变化规律。掌握通过建立动力学模型建立力与运动参数之间的运动微分方程来研究真实运动规律的方法。
例题P72
§3.4 动力学方程式的求解
注意：关键是确定等效转动惯量和等效力矩的关系式（解析式、图表形式等）

单自由度机械系统的动力学分析

§3 单自由度机械系统的动力学分析1e 21111111d d 21F qq J q J =+ 一、基于拉格朗日方程的动力学方程☐若 q 1 为位移，则 J 11 称为等效质量 ( m e )，F e1称为等效力 ( F e ) ；☐若 q 1 为角位移，则 J 11 称为等效转动惯量 ( J e )，F e1称为等效力矩 ( M e ) 。

∑∑==⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫⎝⎛+⎪⎪⎭⎫⎝⎛=⎪⎭⎪⎬⎫⎪⎩⎪⎨⎧⎪⎪⎭⎫⎝⎛+⎥⎥⎦⎤⎢⎢⎣⎡⎪⎪⎭⎫ ⎝⎛+⎪⎪⎭⎫⎝⎛=n j j S S j n j jS S S jq J q v m q J q y q x m J j j j j j 12121121212111d d d d d d ωϕ∑∑∑∑====±+=±+⎪⎪⎭⎫ ⎝⎛+=l j m k k kj j j lj m k kk j jy j jx q M q v F q M q y F q x F F 1111111111e cos ωθω单自由度机械系统的动力学分析“±” 取决于 M k 与的方向是否相同，相同为“＋”，相反则为“－” 。

k ω1. 等效动力学模型二、基于等效动力学模型的动力学方程单自由度机械系统的动力学分析☐单自由度机械系统仅有一个广义坐标，无论其组成如何复杂，均可将其简化为一个等效构件。

等效构件的角位移(位移)即为系统的广义坐标。

☐等效构件的等效质量(等效转动惯量)所具有的动能，应等于机械系统的总动能；等效构件上的等效力(等效力矩)所产生的功率，应等于机械系统的所有外力与外力矩所产生的总功率。

单自由度机械系统的动力学分析定轴转动构件直线移动构件求出位移 S 或角位移的变化规律，即可获得系统中各构件的真实运动。

等效转动惯量等效质量等效力等效力矩☐等效量不仅与各运动构件的质量、转动惯量及作用于系统的外力、外力矩有关，而且与各运动构件与等效构件的速比有关，但与机械系统的真实运动无关；☐等效力（等效力矩）只是一个假想的力（力矩），并非作用于系统的所有外力的合力（外力矩的合力矩）；等效质量（等效转动惯量）也只是一个假想的质量（或转动惯量），它并不是系统中各构件的质量（或转动惯量）的总和。

第四节单自由度体系在简谐荷载作用下的强迫振动

稳态强迫振动
下面分别就考虑和不考虑阻尼两种情况来讨论。下面分别就考虑和不考虑阻尼两种情况来讨论。二．不考虑阻尼的纯强迫振动 1.运动方程及方程的解运动方程
令ξ = 0 ，质点m的运动方程为质点的运动方程为
&&(t ) + ω 2 y = y
P sin θt m
由式(11-28)的第三项可知纯强迫振动质点的位移为的第三项可知纯强迫振动质点的位移为由式
[
]
取第三项，取第三项，并令
(ω 2 − θ 2 ) P = A cos ϕ 2 2 2 2 2 2 m[(ω − θ ) + 4ξ ω θ ] 2ξωθP − = − A sin ϕ 2 2 2 2 2 2 m[(ω − θ ) + 4ξ ω θ ]
则有
y(t) = Asin(θt − ϕ)
3.讨论 β 与 ω 的变化曲线讨论 (1) θ < < ω 时, β → 1.
当
1 θ = ω时 5
θ
,β=
1 1 1− 25
= 1 .041
, 这表明当简谐荷载
的周期T= 为结构自振周期的五倍以上时，的周期 2π / θ 为结构自振周期的五倍以上时，可将其视为静力荷载。可将其视为静力荷载。 (2)0＜ ω ＜1时，β 值随 ω 的增大而增大，动＜的增大而增大，时力系数 β ＞1。。
β= A = y st 1 θ2 1− 2 ω
y (t ) =
y(t ) = −
P P sin θt = sin(θt − π) 2 2 2 2 m(θ − ω ) m(θ − ω )
P sin θt 2 2 m (ω − θ )