第9章动态规划
动态规划.pdf

第三章:动态规划3.1 动态规划的基本概念一、动态决策问题:决策过程具有阶段性和时序性(与时间有关)的决策问题。
即决策过程可划分为明显的阶段。
二、什么叫动态规划(D.P.–Dynamic Program):多阶段决策问题最优化的一种方法。
广泛应用于工业技术、生产管理、企业管理、经济、军事等领域。
三、动态规划(D.P.)的起源:1951年,(美)数学家R.Bellman等提出最优化原理,从而建立动态规划,名著《动态规划》于1957年出版。
四、动态决策问题分类:1、按数据给出的形式分为:•离散型动态决策问题。
•连续型动态决策问题。
2、按决策过程演变的性质分为:•确定型动态决策问题。
•随机型动态决策问题。
五1、阶段(stage)n :作出决策的若干轮次。
n = 1、2、3、4、5。
2、状态(state)S n :每一阶段的出发位置。
构成状态集,记为S nS 1={A},S 2={B 1,B 2,B 3},S 3={C 1,C 2,C 3},S 4={D 1,D 2,D 3},S 5={E 1,E 2}。
阶段的起点。
3、决策(decision)X n :从一个阶段某状态演变到下一个阶段某状态的选择。
构成决策集,记为D n (S n )。
阶段的终点。
D 1(S 1)={X 1(A)}={B 1,B 2,B 3}= S 2,D 2(S 2)={X 2(B 1),X 2(B 2),X 2(B 3)}={C 1,C 2,C 3}=S 3,D 3(S 3)={X 3(C 1),X 3(C 2),X 3(C 3)}={D 1,D 2,D 3}=S 4,D 4(S 4)={X 4(D 1),X 4(D 2),X 4(D 3)}={E 1,E 2}=S 5D 5(S 5)={X 5(E 1),X 5(E 2)}={F;F}={F}。
4、策略(policy):全过程中各个阶段的决策Xn 组成的有序总体{Xn }。
如 A àB2àC1àD1àE2àF5、子策略(sub-policy):剩下的n个阶段构成n子过程,相应的决策系列叫n子策略。
《信息学奥赛一本通》:第9章 第2节 动态规划背包问题(C++版)

【参考程序】
#include<cstdio> using namespace std;
const int maxm = 201, maxn = 31;
int m, n;
int w[maxn], c[maxn];
int f[maxn][maxm];
int main()
{
scanf("%d%d",&m, &n);
for (int i=1; i <= n; i++)
//设f(v)表示重量不超过v公斤的最大价值
for (int v = m; v >= w[i]; v--)
if (f[v-w[i]]+c[i]>f[v])
f[v] = f[v-w[i]]+c[i];
printf("%d",f[m]);
// f(m)为最优解
【例9-12】、完全背包问题 【问题描述】
设有n种物品,每种物品有一个重量及一个价值。但每种物品的数量是无限 的,同时有一个背包,最大载重量为M,今从n种物品中选取若干件(同一种物品 可以多次选取),使其重量的和小于等于M,而价值的和为最大。
【输入格式】
第一行:两个整数,M(背包容量,M<=200)和N(物品数量,N<=30); 第2..N+1行:每行二个整数Wi,Ci,表示每个物品的重量和价值。 【输出格式】
第九章 动态规划
第二节 背包问题
第二节 背包问题
一、01背包问题 问题:
有N件物品和一个容量为V的背包。第i件物品的费用(即体积,下同)是w[i], 价值是c[i]。求解将哪些物品装入背包可使这些物品的费用总和不超过背包容量, 且价值总和最大。 基本思路:
第九章 分离序列综合

1 1 W T T 冷凝器 加热釜
F -级间流量
α- 轻重关键组分相对挥发度
五、C规则
C1. 首先移除含量最多的组分。
1)减少后续塔负荷;
2)需要保证该分离过程具有合理的分离因子。
C2. 等摩尔分割最有利。 若塔顶馏出物的摩尔数远小于塔釜产品摩尔数, 则精馏段操作线比提馏段更接近对角线,精馏段 有效能损失会很大,反之亦然。
R
S
D
从最后一级开始,求最后一级对于给定的输入的最优决 策。然后,将最后两级一块考虑,求出对于最后二级的输入 而言的最优决策,依次类推,直到求得最后的最优决策。
13
10 8
4 5
4 3
最优决策路线:
最优路线
动态规划的缺点: 它只给出了解决问题的原理和原则,没有一 个统一的计算方法,而只能依据问题的特性和 若干数学技巧与经验进行求解。此外,处理问 题的维数不能过大,函数不能过于复杂,否则 ,求解甚为繁琐。
A^B C/D C22 12
A^ B/C D
C23
13
A^B^C/D
A^B^C/D
A^B^C^D
动态规划实质
隐枚举法,即在一个比原搜索空间小的多 的空间上进行穷举的算法。
动态规划法分离序列综合的缺点
需要详细计算全部子分离过程的费用
T重 - T轻
1100 替代计算
CES越大则两组分越容易分离
9.2 经验规则法
一、基本原理
使用若干简单的、但带有普遍性的经验规则产生一些接 近最优的分离序列,然后再对它们进行详细评价以确定最终 的分离序列。
二、经验规则的分类
I 关于分离方法的规则(M规则) II 关于设计方面的规则(D规则) III 与组分性质有关的规则(S规则)
运筹学及其应用9.1 多阶段决策过程最优化问题举例

6
t
使 S = ∑ ∑ f ( x i ) + 16 u j =
i =1
j =1
Байду номын сангаас
6
∑ f ( xi ) + 16(5x1 + 4 x2 + 3x3 + 2 x4 + x5 − 185)
i =1
为最小,其中
f
(xi )
=
110200xxii
,0 −
≤ xi ≤ 15 300,15 < xi
≤
30
6
例1
因此,我们的问题就变成:求y,y1,y2,…,yn-1,以使 g(y)+h(x-y)+g(y1)+h(x1-y1)+…+g(yn-1)+h(xn-1-yn-1) 达到最大,且满足条件
x1=ay+b(x-y) x2=ay1+b(x1-y1)
……… xn-1=ayn-2+b(xn-2-yn-2) yi与xi均非负,i=1,2, …,n-1
5
例1
若以y与x-y分别投入生产方式A与B,在第一 阶段生产后回收的总资源为x1=ay+b(x-y),再将x1 投入生产方式A和B,则可得到收入g(y1)+h(x1-y1), 继续回收资源x2=ay1+b(x1-y1),……
若上面的过程进行n个阶段,我们希望选择n 个变量y,y1,y2,…,yn-1,使这n个阶段的总收入最大。
第二种方法即所谓“局部最优路径”法,是 说某人从k出发,他并不顾及全线是否最短,只是选 择当前最短途径,“逢近便走”,错误地以为局部 最优会致整体最优,在这种想法指导下,所取决策
必是v1→v2→v5→ v9→ v10 ,全程长度是30;显
第8章 动态规划《管理运筹学》PPT课件

8.2 动态规划模型建立
下面以投资问题为例介绍动态规划的建模条件。
【例8-2】 某公司现有资金20万元,若投资于三个
8.1 动态规划基础知识
(5)状态转移方程:状态转移方程是确定过程由一
个状态转移到另一个状态的演变过程。动态规划中某一状
态以及该状态下的决策,与下一状态之间具有一定的函数
关系,称这种函数关系的表达式为状态转移方程。如果第
k段的状态为 sk ,该阶段的决策为
的状态就可以用下式来表示:
uk
sk
,则第k+1段
阶段的指标函数,是该阶段最优的指标函数。
8.2 动态规划模型建立
建立动态规划模型,就是在分析实际问题的基础上建 立该问题的动态规划基本方程。成功地应用动态规划方法 的关键,在于识别问题的多阶段特征,将问题分解成为可 用递推关系式联系起来的若干子问题,或者说正确地建立 具体问题的基本方程,这需要经验与技巧。而正确建立基 本递推关系方程的关键又在于正确选择状态变量,保证各 阶段的状态变量具有递推的状态转移关系。
第8章 动态规划
动态规划(DYnamic Programming,缩写为DP)方法 ,是本世纪50年代初期由美国数学家贝尔曼(Richard E ,Bellman)等人提出,后来逐渐发展起来的数学分支, 它是一种解决多阶段决策过程最优化问题的数学规划法 。动态规划的数学模型和求解方法比较灵活,对于连续 的或离散的,线性的或非线性的,确定性的或随机性的 模型,只要能构成多阶段决策过程,便可用动态规划方 法求其最优解。因而在自然科学、社会科学、工程技术 等许多领域具有广泛的用途,甚至一定程度上比线性规 划(LP)、非线性规划(NLP)有成效,特别是对于某 些离散型问题,解析数学无法适用,动态规划方法就成 为非常有用的求解工具。
《管理运筹学》第四版课后习题解析(下)

《管理运筹学》第四版课后习题解析(下)第9章目标规划1、解:设工厂生产A 产品1x 件,生产B 产品2x 件。
按照生产要求,建立如下目标规划模型。
112212121211122212min ()()s.t43452530555086100,,,0,1,2--+-+-+-++++-+=+-+==i i P d P d x x x x x x d d x x d d x x d d i ≤≤≥由管理运筹学软件求解得12121211.25,0,0,10, 6.25,0x x d d d d --++======由图解法或进一步计算可知,本题在求解结果未要求整数解的情况下,满意解有无穷多个,为线段(135/14,15/7)(1)(45/4,0),[0,1]ααα+-∈上的任一点。
2、解:设该公司生产A 型混凝土x 1吨,生产B 型混凝土x 2吨,按照要求建立如下的目标规划模型。
)5,,2,1(0,,0,014550.060.015550.040.030000100150100120275200.)()(min 2121215521442331222111215443322111Λ=≥≥≥≤+≤+=-++=-+=-+=-++=-++++++++-+-+-+-+-+----++-i d d x x x x x x d d x x d d x d d x d d x x d d x x ts d p d d p d p d d p i i 由管理运筹学软件求解得.0,0,20,0,0,0,0,35,40,0,120,120554433221121============+-+-+-+-+-d d d d d d d d d d x x3、解:设x 1,x 2分别表示购买两种基金的数量,按要求建立如下的目标规划模型。
,,01250543504.07.0100004525.min 2,122211121212211≥≥=-++=-++≤+++-+-+--+i i d d x x d d x x d d x x x x ts d p d p用管理运筹学软件求解得,0,0,0,818.206,091.159,636.113221121======+-+-d d d d x x所以,该人可以投资A 基金113.636份,投资B 基金159.091份。
第九章多阶段决策和序贯决策

第一步,画出决策树图。
-700
2
建大厂
4
销路好0.7
销路差0.3
5
销路好0.9 销路差0.1
1
-400
建小厂
8
扩建
-300
6
销路好0.7
3
不扩建
9
销路差0.3
7
210
-40
-40
销路好0.9
210
销路差0.1
-40
销路好0.9
90
销路差0.1
60
60
3年内
7年内
第二步,从右向左计算各点的期望收益值。
第二阶段决策:产量不变,还是 增加产量。
30 5
82 买专利 决
策 自行研制
65
失败 0.2
95 产量不变 6
82
3
1 成功0.8
95 7
增加产量
60
63 成功0.6
85 产量不变 4
8
2
85
量 增加产
失败0.4
9
30
11
低0.1 中0.5 高0.4 低0.1
中0.5 高0.4
低0.1 中0.5 高0.4 低0.1
方案 收益 状态
按原工 艺方案 生产
(万元)
买专利(0.8)
产量 不变
增产
自研(0.6)
产量 不变
增产
价低 0.1 -100 -200 -300 -200 -300
中 0.5 0 50 50 0 -250
价高 0.4 100 150 250 200 600
第一阶段决策问题:购买专利, 还是自行研制
200
销路不好(0.2)
运筹学大纲—钱版

目录第1篇绪论第1章运筹学概论1.1运筹学的简史1.2运筹学的性质和特点1.3运筹学的工作步骤1.4运筹学的模型1.5运筹学的应用1.6运筹学的展望参考资料第2篇线性规划与目标规划第2章线性规划与单纯形法2.1线性规划问题及其数学模型2.2线性规划问题的几何意义2.3单纯形法2.4单纯形法的计算步骤2.5单纯形法的进一步讨论2.6应用举例习题第3章对偶理论和灵敏度分析3.1单纯形法的矩阵描述3.2改进单纯形法的矩阵计算3.3对偶问题的提出3.4线性规划的对偶理论3.5影子价格3.6对偶单纯形法3.7灵敏度分析3.8*参数线性规划习题第4章运输问题4.1运输问题的数学模型4.2表上作业法4.3产销不平衡的运输问题及其求解方法4.4应用举例习题第5章线性目标规划5.1目标规划的数学模型5.2解目标规划的图解法5.3解目标规划的单纯形法5.4应用举例习题参考资料第3篇整数线性规划第6章整数线性规划6.1整数线性规划问题的提出6.2分支定界解法6.3割平面解法6.40·1型整数线性规划6.5指派问题习题参考资料第4篇非线性规划第7章 *无约束问题7.1基本概念7.2一维搜索7.3无约束极值问题的解法第8章 *约束极值问题8.1最优性条件8.2二次规划8.3可行方向法8.4制约函数法习题参考资料第5篇动态规划第9章动态规划的基本方法9.1多阶段决策过程及实例9.2动态规划的基本概念和基本方程9.3动态规划的最优性原理和最优性定理9.4动态规划和静态规划的关系习题第10章动态规划应用举例10.1资源分配问题10.2生产与存储问题10.3*背包问题10.4*复合系统工作可靠性问题10.5排序问题10.6设备更新问题10.7*货郎担问题习题参考资料第6篇图与网络分析第11章图与网络优化11.1图的基本概念11.2树11.3最短路问题11.4网络最大流问题11.5最小费用最大流问题11.6中国邮递员问题习题参考资料第12章网络计划12.1网络计划图12.2网络计划图的时间参数计算12.3时标网络计划图12.4网络计划的优化12.5网络计划软件习题参考资料第7篇排队论第13章排队论13.1基本概念13.2到达间隔的分布和服务时间的分布13.3单服务台负指数分布排队系统的分析13.4多服务台负指数分布排队系统的分析13.5一般服务时间M/G/1模型13.6经济分析——系统的最优化13.7*分析排队系统的随机模拟法习题第8篇存储论第14章存储论14.1存储论的基本概念14.2确定性存储模型14.3随机性存储模型14.4其他类型存储问题习题参考资料第9篇对策论第15章对策论基础15.1引言15.2矩阵对策的基本定理15.3矩阵对策的解法15.4*其他类型对策简介习题参考资料第10篇决策论第16章单目标决策16.1决策的分类16.2决策过程16.3不确定型的决策16.4风险决策16.5效用理论在决策中的应用16.6决策树16.7灵敏度分析习题参考资料第17章多目标决策17.1引言17.2基本概念17.3化多为少的方法17.4分层序列法17.5直解求非劣解17.6多目标线性规划的解法17.7层次分析法参考资料第11篇启发式方法第18章 *启发式方法18.1基本概念18.2应用及例子习题参考资料。
第9章Viterbi译码及其实现

第9章Viterbi译码及其实现Viterbi译码是一种使用动态规划算法来解码卷积码的方法,它通过寻找最有可能的路径来恢复被编码的数据。
在这篇文章中,我们将介绍Viterbi译码的基本原理以及如何实现它。
1. Viterbi译码原理:Viterbi译码是一种基于有向无环图(DAG)的动态规划算法。
它的基本思想是在每一个时刻,选取最有可能的路径来解码出当前的数据。
具体来说,它会使用一个状态转移图来表示每个时刻的状态以及状态之间的转移。
每个状态表示接收到的一串码元,其中可能包含错误。
在Viterbi译码中,我们需要确定的是在给定的时刻,以及所有之前的时刻,哪个状态是最有可能接收到当前的码元。
为了实现这一点,我们需要每个时刻的状态转移图以及每个状态接收到正确码元的概率。
通过比较不同路径的概率,我们可以选择最有可能的路径。
2. Viterbi译码实现:Viterbi译码可以通过以下步骤实现:1)初始化:在初始时刻,我们首先需要将所有状态的概率初始化为1,并将每个状态的前一个状态设置为初始状态。
这样做是为了确保在选择路径时考虑所有可能的路径。
2)递推计算:从初始时刻开始,我们根据每个状态接收到的码元和切换到下一个状态的概率,更新每个状态的概率以及前一个状态。
具体来说,我们可以使用以下公式进行计算:当前状态概率=当前状态接收到的码元概率*前一个状态概率*切换到当前状态的概率3)路径选择:一旦计算出所有状态的概率,我们可以比较不同路径的概率,选择最有可能的路径。
具体来说,我们可以从最后一个时刻的状态开始,根据每个状态的概率选择前一个状态,直到回到初始状态。
4)结果恢复:一旦选择了最有可能的路径,我们可以根据这条路径中每个状态接收到的码元恢复原始数据。
通过以上步骤,我们可以使用Viterbi译码来解码卷积码并恢复原始数据。
总结:Viterbi译码是一种有效的卷积码译码方法,它使用了动态规划算法来选择最有可能的路径。
管理运筹学课件第9章动态规划

Dk (sk ) {xk 0 ≤ xk ≤ sk} 允许决策集合
sk+1=sk-xk (状态转移方程) s1=a n
(边界条件)
指标函数: Vk,n gi (xi )
ik
若fk(sk)表示数量为sk资源分配给第k种产品时,从第k阶段到第n阶段
总收益,则有:
f f
k n
(sk (sn
9.2.2 动态规划问题的解法:顺序法
最优值函数f(k):从A到k阶段的最短距离;阶段指标函数,即该阶段选择 不同路线的距离。从前向后推。
2
C1 6 8
5
A 3
B1 3 6
B2
8
7 6
C2 3 5
3 C3 3
84
D1 2
1 D2
E
C4 A — B— C — D — E
阶段1
阶段2 阶段3 阶段4
S0={A} S1={B1,B2} S2={C1,C2,C3,C4} S3={D1,D2} S4={E}
显然f(E)=0,为该问题的边界条件.
2019/7/14
最k优=4化原理
(Ofp(Dtim1) alifty(Ep)rindc(iDp1l,eE)): 0 2 2
最k优=3策略f (具D1备) 这2样的决性策质::无D1论初E始
状 以 始 策 也 例 A1C依 最 程最 最32—ffkkf态 第 状 略 是 如 据 优 。f,—短 短((其==((CffCBDCf21.与 一 态 最 , 这 子((1fD通路 路2(子21B3)A()B))11—C初 个 的 优 在 一 过))2俗线 长ff策—)4ffffmm((mC)始 决 过 的 导 原 程mm((((D地::Af略mmiCCCiECm1Ai2nniimm()n2决 策 程 入 理 ,.nn3i1243im,mEi—说):nnin)i)))BDn1n2i)i策 所 而 案 , 从ff11n2nffD:Bff11((18541最83fff((ff8554((455DD81—如 形 言 例 从 而—fff1DD1(((6d1DD((5323CCC1(((ff—2优BB12(CCC312)62)5)((C1何成中后得,E8632)71)D2)必3)DD3)24决4)决)E8)C策也2)决决决决))21d2的,往到,8dd,d,—)5然2以d4)d策d策最dd(略d8E(是(策策策策d(1d(Cdd(CC(状最前全(C(1C(DC构1后)(B5(:dB((1:B短d13的2A最2::::BA,BB3D1,3111(,态优推程(,,D,,,1,D,11成诸C,DCDCAD距D,C—1C,,BD子0优B1CCCCCCC24114作策各最)11232222),)最决),)3)1234)离24)E)策)D的D)))1为略阶优EB,1优策2为)略E。)1DDDD初是段过1策对1122
信息学奥赛系列课程(三阶段)-2019_02_21_第3版

信息学奥赛NOIP系列课程(三阶段)第一阶段C++语言及数据结构与算法基础课本:1、信息学奥赛一本通+训练指导教程C++版第五版--2017年出版(两本)第1部分C++语言(50课时)适于:零基础的初中或高中的学生,当然有C语言或scratch、Python语言基础更好授课:相关内容讲授+实例+题目现堂训练(每次课2-3题,题目较大可能是1题)第1章C++语言入门(2-3课时)第2章顺序结构程序设计(6课时)第3章程序控制结构(3课时)NOIP2017复赛普及组第1题成绩https:///problem-12334.htmlNOIP2018复赛普及组第1题标题统计方法一https:///problem-12393.htmlNOIP1996普及组第1题https:///WDAJSNHC/article/details/83513564https:///yuyanggo/article/details/47311665第4章循环结构(5课时)NOIP2018复赛普及组第1题标题统计方法二https:///problem-12393.htmlNOIP2016复赛普及组第1题买铅笔https:///problem-12121.htmlNOIP2015复赛普及组第1题金币/ch0105/45/NOIP2002复赛普及组第1题级数求和/ch0105/27/NOIP2013复赛普及组第1题计数问题https:///problem-11005.html?tdsourcetag=s_pcqq_aiomsgNOIP2012复赛普及组第1题质因数分解/ch0105/43/NOIP2011复赛普及组第1题数字反转/ch0105/29/NOIP2010复赛普及组第1题数字统计https:///problem-10012.htmlNOIP1999普及组第1题Cantor表/ch0201/8760/https:///problemnew/show/P1014NOIP1997普及组第1题棋盘问题https:///problemnew/show/P1548NOIP1995普及组复赛第1题https:///secret_zz/article/details/76862335https:///WDAJSNHC/article/details/83513896NOIP1997普及组第2题数字三角形https:///ber_bai/article/details/76722379第5章数组(9-10课时)NOIP2014复赛普及组第1题珠心算测验https:///problem-12091.htmlNOIP2009复赛普及组第1题多项式输出/ch0113/39/NOIP2006复赛普及组第1题明明的随机数/ch0110/09/NOIP2005复赛普及组第1题陶陶摘苹果/ch0106/02/NOIP2004复赛普及组第1题不高兴的津津/ch0109/03/NOIP2003年普及组第1题乒乓球/ch0113/37/NOIP1998年普及组第1题三连击(枚举)https:///problemnew/show/P1008NOIP1995普及组复赛第2题方阵填数https:///WDAJSNHC/article/details/79381876NOIP1996普及组第2题格子问题https:///WDAJSNHC/article/details/79381843?utm_source=blogxgwz5NOIP2016复赛普及组第2题回文日期https:///problem-12122.htmlhttps:///problemnew/show/P2010NOIP2015普及组第2题P2670扫雷游戏/ch0108/14/https:///problemnew/show/P2670https:///problem-12105.htmlNOIP2012普及组第2题_P1076寻宝/ch0112/06/https:///problemnew/show/P1076第6章函数(5课时)NOIP2008复赛普及组第1题ISBN号码/ch0107/29/NOIP2000提高组第1题P1017进制转换https:///problemnew/show/P1017NOIP2000普及组第1题计算器的改良https:///problemnew/show/P1022https:///yuyanggo/article/details/47856785https:///u012773338/article/details/41749421NOIP2018普及组第2题龙虎斗https:///problemnew/show/P5016https:///problem-12394.html机器翻译【1.12编程基础之函数与过程抽象07】Noip2010提高组第1题/ch0112/07/Vigenère密码【1.12编程基础之函数与过程抽象08】Noip2012提高组第1题/ch0112/08/笨小猴【1.9编程基础之顺序查找06】NOIP2008提高组第1题/ch0109/06/第7章文件和结构体(5课时)NOIP2011复赛提高组第1题铺地毯/ch0109/14/NOIp2008提高组第2题火柴棒等式https:///problemnew/show/P1149https:///Mr_Doublerun/article/details/52589778第8章指针及其应用(8课时)第9章C++实用技巧与模版库(5课时)NOIP2007复赛普及组第1题奖学金/ch0110/04/NOIP2017复赛普及组第2题图书管理员(STL、排序)https:///problem-12335.htmlhttps:///problemnew/show/P3955NOIP1999普及组第2题回文数https:///problemnew/show/P1015***模拟NOIP2017年提高组第2题时间复杂度(模拟)https:///problem-12333.htmlhttps:///problemnew/show/P3952NOIP2011普及组第3题P1309瑞士轮(模拟、快拍、归并排序)/ch0401/4363/https:///problemnew/show/P1309NOIP2018复赛普及组第3题摆渡车(模拟)https:///problem-12395.htmlhttps:///problemnew/show/P5017NOIP2016普及组第3题海港(port)--枚举https:///problemnew/show/P2058NOIP2006年提高组第3题P1065作业调度方案(模拟)https:///problemnew/show/P1065NOIP2013提高组第4题P1969积木大赛(模拟贪心)https:///problem-12071.htmlhttps:///problemnew/show/P1969NOIP2014提高组第4题P2038无线网络发射器选址(模拟)https:///problemnew/show/P2038第2部分NOIP基础算法(39课时)第1章高精度计算(2-3课时)【例1.6】回文数(Noip1999):8088/problem_show.php?pid=1309NOIP2003普及组第4题P1045麦森数(分治、高精度运算)https:///problemnew/show/P1045NOIP2005普及组第4题P1050循环(高精度运算、数论、快速幂) https:///problemnew/show/P1050第2章数据排序(3课时)NOIP2014复赛普及组第1题珠心算测验https:///problem-12091.html第3章递推算法(2-3课时)1314:【例3.6】过河卒(Noip2002):8088/problem_show.php?pid=1314NOIP2011普及组第4题P1310表达式的值(栈、表达式计算、递推) https:///problemnew/show/P1310NOIP2011提高组第6题P1315观光公交(递推分析、贪心)https:///problemnew/show/P1315第4章递归算法(2-3课时)【例4.6】数的计数(Noip2001普及组第1题):8088/problem_show.php?pid=1316第5章搜索与回溯算法(2-3课时)NOIP2015day1T3_斗地主P2668斗地主https:///problemnew/show/P2668NOIP2017年普及组第3题棋盘https:///problemnew/show/P3956https:///problem-12336.htmlNOIP2015年提高组第2题P2661信息传递(Tarjen bfs/dfs(图论))https:///problem-12107.htmlhttps:///problemnew/show/P2661NOIP2016年提高组第2题天天爱跑步(Lca/dfs(图论)树结构最近公共祖先)https:///problem-12208.htmlhttps:///problemnew/show/P1600NOIP2000普及组第4题P1019单词接龙(深搜)https:///problemnew/show/P1019NOIP2000年提高组第3题单词接龙(DFS,字符串,模拟)https:///problemnew/show/P1019NOIP2014普及组第4题P2258子矩阵(搜索或dp)https:///problemnew/show/P2258NOIP2018年提高组第3题P5021赛道修建(搜索深度优先搜索)https:///problem-12392.htmlhttps:///problemnew/show/P5021第6章贪心算法(3课时)删数问题(NOIP1994)P1106删数问题https:///problemnew/show/P1106:8088/problem_show.php?pid=1321NOIP2010复赛普及组第2题接水问题/ch0109/15/NOIP1999年提高组第1题导弹拦截https:///problemnew/show/P1020https:///huashanqingzhu/p/6728652.html https:///qq_33927580/article/details/51853345 https:///Darost/article/details/52086240https:///yuyanggo/article/details/48739029NOIP2002提高组第1题均分纸牌P1031均分纸牌https:///problemnew/show/P1031NOIP2007普及组第2题_P1094纪念品分组https:///problem-12007.htmlhttps:///problemnew/show/P1094NOIP2008普及组第2题_P1056排座椅https:///problem-12008.htmlhttps:///problemnew/show/P1056NOIP2012年提高组第2题国王游戏(贪心、排序后列出)https:///problemnew/show/P1080NOIP2013年提高组第2题P1966火柴排队(逆序对、贪心、排序) https:///problem-12083.htmlhttps:///problemnew/show/P1966NOIP2010普及组第4题P1199三国游戏(贪心)https:///problemnew/show/P1199第7章分治算法(3课时)NOIP2001提高组第1题P1024一元三次方程求解/ch0204/7891/https:///problemnew/show/P1024NOIP2011年提高组第2题P1311选择客栈(二分查找)https:///problemnew/show/P1311NOIP2003普及组第4题P1045麦森数(分治、高精度运算)https:///problemnew/show/P1045第8章广度优先搜索算法(2-3课时)NOIP2002年提高组第2题P1032字串变换(BFS,字符串)https:///problemnew/show/P1032NOIP2013提高组第6题P1979华容道(广搜\最短路:图论)https:///problem-12212.htmlhttps:///problemnew/show/P1979第9章动态规划(15课时)第一节动态规划的基本模型1260:【例9.4】拦截导弹(NOIP1999):8088/problem_show.php?pid=1260NOIP2013普及组第3题P1982小朋友的数字https:///problemnew/show/P1982NOIP2003复赛普及组第2题_P1043数字游戏数字游戏(Game.cpp)https:///problemnew/show/P1043NOIP2006年提高组第2题P1064金明的预算方案(资源分配DP,构造) https:///problemnew/show/P1064NOIP2013普及组第3题P1982小朋友的数字(动态规划、子段和)https:///problemnew/show/P1982NOIP2007普及组第3题P1095守望者的逃离(动态规划或枚举)https:///problemnew/show/P1095NOIP2009普及组第4题P1070道路游戏(动态规划)https:///problemnew/show/P1070NOIP2004年提高组第3题P1091合唱队形(子序列DP)https:///problemnew/show/P1091第二节背包问题NOIP2018提高组第2题货币系统https:///problem-12391.htmlNOIP2006普及组第2题_P1060开心的金明题解https:///problemnew/show/P1060NOIP2005普及组第3题P1048采药(0/1背包)/ch0206/1775/https:///problem-12062.htmlhttps:///problemnew/show/P1048NOIP2001普及组第4题P1049装箱问题(0/1背包或枚举)https:///problemnew/show/P1049NOIP2014年提高组第3题P1941飞扬的小鸟(背包DP)https:///problem-12087.htmlhttps:///problemnew/show/P1941第三节动态规划经典题NOIP2000年提高组第2题P1018乘积最大(资源分配DP)https:///problemnew/show/P1018NOIP2000普及组第3题P1018乘积最大(划分动态规划)https:///problemnew/show/P1018NOIP2001年提高组第2题P1025数的划分(资源分配DP,多维状态DP)/ch0206/8787/https:///problemnew/show/P1025NOIP2001年提高组第3题统计单词个数(资源分配DP,字符串) https:///problemnew/show/P1026NOIP2005年提高组第2题P1052过河(子序列DP,贪心优化)https:///problemnew/show/P1052NOIP2010年提高组第2题P1541乌龟棋(动态规划优化)https:///problemnew/show/P1541NOIP2014年提高组第2题P1351联合权值(动态规划搜索图结构树形DP图的遍历遍历(图论),二次展开式)https:///problem-12086.htmlhttps:///problem-12210.htmlhttps:///problemnew/show/P1351NOIP2008普及组第3题P1057传球游戏(动态规划)https:///problemnew/show/P1057NOIP2012普及组第3题摆花(动态规划)https:///problem-12366.htmlhttps:///problemnew/show/P1077NOIP2002普及组第4题P1002过河卒(棋盘动态规划)https:///problemnew/show/P1002NOIP2008年提高组第3题P1006传纸条(多维状态DP动态规划图结构最短路网络流)https:///problem-12110.htmlhttps:///problemnew/show/P1006NOIP2000提高组第4题方格取数(多维状态DP)/ch0206/8786/https:///problem-12186.htmlhttps:///problemnew/show/P1004NOIP2002提高组第4题P1034矩形覆盖(动态规划/贪心/搜索剪枝) /ch0405/1793/https:///problemnew/show/P1034第3部分NOIP数据结构(19课时)第1章栈(3课时)NOIP2011普及组第4题P1310表达式的值(栈、表达式计算、递推) https:///problemnew/show/P1310第2章队列(3-5课时)NOIP2016普及组第3题海港(port)https:///problemnew/show/P2058第3章树(3课时)第一节树的概念第二节二叉树第三节堆及其应用NOIP2015普及组第4题P2672推销员(枚举、堆)https:///problemnew/show/P2672NOIP2001普及组第3题P1030求先序排列(树的遍历)https:///problemnew/show/P1030NOIP2004普及组第3题P1087FBI树(二叉树的遍历)https:///problemnew/show/P1087第4章图论算法(8课时)第一节基本概念第二节图的遍历第三节最短路径算法NOIP2002普及组第3题P1037产生数(最短路、高精度)https:///problemnew/show/P1037NOIP2012普及组第4题P1078文化之旅(搜索、最短路(图论)、动规) https:///problemnew/show/P1078NOIP2009年提高组第3题P1073最优贸易(最短路:图论)https:///problemnew/show/P1073NOIP2001提高组第4题P1027Car的旅行路线(最短路,实数处理)https:///problemnew/show/P1027NOIP2007提高组第4题P1099树网的核(最短路,树的直径)https:///problemnew/show/P1099第四节图的连通性问题第五节并查集NOIP2010年提高组第3题P1525关押罪犯(二分答案或并查集)https:///problemnew/show/P1525NOIP2017提高组第4题P3958奶酪(数据结构树结构并查集)https:///problem-12205.htmlhttps:///problemnew/show/P3958第六节最小生成树第七节拓朴排序与关键路径NOIP2013普及组第4题P1983车站分级(图论、拓扑排序) https:///problemnew/show/P19831390:食物链【NOI2001】:8088/problem_show.php?pid=1390NOIP2004年提高组第2题P1090合并果子(最优哈夫曼树,排序,贪心)https:///problemnew/show/P1090NOIP2013年提高组第3题P1967货车运输(最大生成树,最近公共祖先)https:///problemnew/show/P1967NOIP2018提高组第4题P5022旅行(搜索图结构)https:///problem-12397.htmlhttps:///problemnew/show/P5022NOIP2018提高组第6题P5024保卫王国(图结构)https:///problem-12399.htmlhttps:///problemnew/show/P50242、啊哈!算法--2014-06(35-50小时)第二阶段算法与数据结构提高1、《信息学奥赛一本通·提高篇》(80-100课时,不一定一次都讲完)第一部分基础算法第1章贪心算法NOIP2002提高组第1题P1031均分纸牌(贪心,模拟)https:///problemnew/show/P1031NOIP2010普及组第3题P1158导弹拦截(排序+枚举,贪心)https:///problemnew/show/P1158NOIP2012提高组第6题P1084疫情控制(二分答案,贪心,倍增)https:///problemnew/show/P1084第2章二分与三分NOIP2010年提高组第3题P1525关押罪犯(二分答案或并查集)https:///problemnew/show/P1525NOIP2008提高组第4题P1155双栈排序(枚举,贪心/二分图)https:///problemnew/show/P1155NOIP2015提高组第4题P2678跳石头(二分查找、二分答案)https:///problem-12198.htmlhttps:///problemnew/show/P2678第3章深搜的剪枝技巧NOIP2018普及组第4题对称二叉树(搜索树结构深度优先搜索)https:///problem-12396.htmlhttps:///problemnew/show/P5018NOIP2011年提高组第3题P1312Mayan游戏(深搜、剪支)https:///problemnew/show/P1312NOIP2015年提高组第3题P2668斗地主(分情况,剪枝)https:///problemnew/show/P2668NOIP2003提高组第4题P1041传染病控制(随机贪心/搜索剪枝)https:///problemnew/show/P1041NOIP2004提高组第4题P1092虫食算(搜索搜索与剪枝)https:///problem-12414.htmlhttps:///problemnew/show/P1092第4章广搜的优化技巧NOIP2017年普及组第3题棋盘(搜索搜索与剪枝广度优先搜索)https:///problemnew/show/P3956https:///problem-12336.htmlNOIP2009提高组第4题P1074靶形数独(搜索优化)https:///problemnew/show/P1074NOIP2010提高组第4题P1514引入水域(广搜+动态规划,判断有解和无解)https:///problemnew/show/P1514第二部分字符串算法第1章哈希表第2章KMP算法第3章Trie字典树第4章AC自动机NOIP2005提高组第4题P1054等价表达式(字符串,抽样检测,表达式) /practice/1686/https:///problemnew/show/P1054NOIP2008普及组第4题P1058立体图(字符输出)https:///problemnew/show/P1058NOIP2006普及组第3题P1061Jam的计数法(数学、字符串)https:///problemnew/show/P1061NOIP2007年提高组第2题字符串的展开(字符串模拟)https:///problem-11016.htmlhttps:///problemnew/show/P1098NOIP2003年提高组第2题P1039侦探推理(枚举,模拟,字符串)https:///problemnew/show/P1039NOIP2011普及组第2题_P1308统计单词数/ch0112/05/https:///problemnew/show/P1308第三部分图论第1章最小生成树第2章最短路径NOIP2016年提高组第3题P1850换教室(最短路/Dp)https:///problemnew/show/P1850NOIP2017年提高组第3题P3953逛公园(搜索图结构记忆化搜索最短路)https:///problem-12337.htmlhttps:///problemnew/show/P3953NOIP2014提高组第5题P1351联合权值(遍历,二次展开式)https:///problem-12086.htmlhttps:///problemnew/show/P1351第3章SPFA算法的优化第4章差分约束系统第5章强连通分量第6章割点和桥第7章欧拉回路第四部分数据结构第1章树状数组第2章RMQ问题第3章线段树NOIP2012提高组第5题P1083借教室(枚举、线段树、树状数组、二分) https:///problem-12069.htmlhttps:///problemnew/show/P1083NOIP2017提高组第6题P3960列队(数据结构平衡树线段树)https:///problem-12339.htmlhttps:///problemnew/show/P3960第4章倍增求LCANOIP2015提高组第6题P2680运输计划(Lca或线段树)https:///problem-12213.htmlhttps:///problemnew/show/P2680第5章树链剖分第6章平衡树Treap第五部分动态规划第1章区间类型动态规划NOIP2007年提高组第3题P1005矩阵取数游戏(区间DP,高精度)https:///problemnew/show/P1005第2章树型动态规划NOIP2003年提高组第3题P1040加分二叉树(树,区间DP)https:///problemnew/show/P1040第3章数位动态规划第4章状态压缩类动态规划NOIP2017提高组第5题P3959宝藏(动态规划搜索贪心状态压缩DP枚举)https:///problem-12340.htmlhttps:///problemnew/show/P3959NOIP2016提高组第6题愤怒的小鸟(状态压缩动态规划)https:///problemnew/show/P2831第5章单调队列优化动态规划NOIP2016提高组第5题蚯蚓(单调队列)https:///Mrsrz/p/7517155.htmlhttps:///m0_38083668/article/details/82557281NOIP2017普及组第4题P3957跳房子(数据结构动态规划单调队列队列)https:///problem-12338.htmlhttps:///problemnew/show/P3957第6章利用斜率优化动态规划NOIP2012年提高组第3题P1081开车旅行(离线深搜,动态规划、倍增)https:///problemnew/show/P1081NOIP2015提高组第5题P2679子串(Dp+滚动数组)https:///problemnew/show/P2679第六部分数学基础第1章快速幂第2章素数第3章约数第4章同余问题第5章矩阵乘法第6章组合数学NOIP2009年提高组第2题P1072Hankson的趣味题(初等数论,质因数,组合数学)https:///problemnew/show/P1072NOIP2006提高组第4题P10662^k进制数(动态规划/组合数学,高精度) https:///problemnew/show/P1066NOIP2011提高组第4题P1313计算系数(组合、二项式系数)/practice/4036/https:///problemnew/show/P1313NOIP2016提高组第4题P2822组合数问题(杨辉三角)https:///problemnew/show/P2822第7章博弈论NOIP2004普及组第4题P1088火星人(数学:排列、stl)https:///problemnew/show/P1088NOIP2009普及组第3题P1069细胞分裂(数论)https:///problemnew/show/P1069NOIP2000提高组第1题P1017进制转换(初等代数,找规律)https:///problemnew/show/P1017NOIP2001提高组第1题P1024一元三次方程求解(数学,枚举,实数处理) /ch0204/7891/https:///problemnew/show/P1024NOIP2003普及组第3题P1044栈(数学:卡特兰数)https:///problemnew/show/P1044NOIP2018年提高组第2题货币系统(数论)https:///problem-12391.htmlhttps:///problemnew/show/P5020NOIP2014年普及组复赛第3题螺旋矩阵(数学分析)https:///problem-12341.htmlhttps:///problemnew/show/P2239NOIP2015年普及组第3题求和(数学:数列)https:///problemnew/show/P2671NOIP2004普及组第4题P1088火星人(数学:排列、stl)https:///problemnew/show/P1088NOIP2005普及组第4题P1050循环(高精度运算、数论、快速幂) https:///problemnew/show/P1050NOIP2006普及组第4题P1062数列(数学:进制转换)https:///problemnew/show/P1062NOIP2007普及组第4题P1096$Hanoi$双塔问题(数学、高精度) https:///problemnew/show/P1096NOIP2016普及组第4题P2119魔法阵(数学分析、枚举)https:///problemnew/show/P2119NOIP2002年提高组第3题P1033自由落体(数学,物理,模拟,实数处理) https:///problemnew/show/P1033NOIP2005年提高组第3题P1053篝火晚会(置换群,贪心)https:///problemnew/show/P1053NOIP2012提高组第4题P1082同余方程(数论、递归,扩展欧几里得)https:///problemnew/show/P1082NOIP2011提高组第5题P1314聪明的质监员(部分和优化)/practice/4037/https:///problemnew/show/P1314NOIP2013提高组第5题P1970花匠(序列)https:///problem-12072.htmlhttps:///problemnew/show/P1970NOIP2018提高组第5题P5023填数游戏(DP)https:///problem-12398.htmlhttps:///problemnew/show/P50232、NOIP历年真题讲解(30-50小时)---包括初赛和复赛3、《骗分导论》(推荐指数:5颗星)--电子书(可以作为学习的参考资料)第三阶段算法与数据结构高级专题(选择性学习)1、信息学奥赛之数学专题2、高级数据结构(C++版)3、动态规划专题注:上面的内容也可能要交叉的进行讲解在线题库:1、OpenJudge在线题库/2、信息学奥赛一本通在线评测系统:8088/3、洛谷https:///4、啊哈编程/tiku/5、《信息学奥赛一本通(提高篇)》在线评测OJhttps://loj.ac/注:本系列课程将根据行业发展状况,及时优化调整课程内容,具体课程设置以实际为准。
(NEW)运筹学教材编写组《运筹学》(第4版)笔记和课后习题(含考研真题)详解

线性规划问题的共同特征:
(1)每一个问题都用一组决策变量
表示某一方案,这组
决策变量的某一确定值就代表一个具体方案。一般这些变量的取值是非
负且连续的。
(2)存在有关的数据,如资源拥有量、消耗资源定额、创造新价值 量等,同决策变量构成互不矛盾的约束条件,这些约束条件可以用一组 线性等式或线性不等式来表示。
1.2 课后习题详解
本章无课后习题。
1.3 考研真题详解
本章只是对本课程的一个简单介绍,不是考试重点,所以基本上没 有学校的考研试题涉及到本章内容,因此,读者可以简单了解,不必作 为复习重点,本部分也就没有可选用的考研真题。Leabharlann 第2章 线性规划与目标规划
2.1 复习笔记
1.线性规划模型的概念及其一般形式
目 录
第1章 运筹学概论 1.1 复习笔记 1.2 课后习题详解 1.3 考研真题详解
第2章 线性规划与目标规划 2.1 复习笔记 2.2 课后习题详解 2.3 考研真题详解
第3章 对偶理论与灵敏度分析 3.1 复习笔记 3.2 课后习题详解 3.3 考研真题详解
第4章 运输问题 4.1 复习笔记 4.2 课后习题详解
2.线性规划问题的标准型及标准化 (1)线性规划的标准型
或
(2-4) (2-5) 线性规划的标准型要求:目标函数是Max型;约束条件是等式约 束;决策变量非负。 (2)线性规划的标准化方法
① 若要求目标函数实现最小化,即
,则只需将目标函数最
小化变换为求目标函数最大化,即令 ,于是得到
第13章 排队论
13.1 复习笔记 13.2 课后习题详解 13.3 考研真题详解 第14章 存储论 14.1 复习笔记 14.2 课后习题详解 14.3 考研真题详解 第15章 对策论基础 15.1 复习笔记 15.2 课后习题详解 15.3 考研真题详解 第16章 单目标决策 16.1 复习笔记 16.2 课后习题详解 16.3 考研真题详解 第17章 多目标决策 17.1 复习笔记
运筹学第3版熊伟编著习题答案

求没有限制,由于仓库容量有限,仓库最多库存产品 A1000 件,1 月初仓库库存 200 件。1~
6 月份产品 A 的单件成本与售价如表 1-25 所示。
表 1-25
月份
1
2
3
4
5
6
产品成本(元/件)
300 330 320 360
360
300
销售价格(元/件)
350 340 350 420
410
340
(1)1~6 月份产品 A 各生产与销售多少总利润最大,建立数学模型;
(2)当 1 月初库存量为零并且要求 6 月底需要库存 200 件时,模型如何变化。
【解】设 xj、yj(j=1,2,…,6)分别为 1~6 月份的生产量和销售量,则数学模型为
最新精品文档,知识共享!
max Z 300x1 350 y1 330x2 340 y2 320x3 350 y3 360x4
第1章 线性规划
1.1 工厂每月生产 A、B、C 三种产品 ,单件产品的原材料消耗量、设备台时的消耗量、资源
限量及单件产品利润如表 1-23 所示.
表1-23
产品 资源
A
B
C
资源限量
材料(kg)
1.5
1.2
4
2500
设备(台时)
3
1.6
1.2
利润(元/件)
10
14
12
1400
根据市场需求,预测三种产品最低月需求量分别是 150、260 和 120,最高月需求是 250、310 和 130.试建立该问题的数学模型,使每月利润最大. 【解】设 x1、x2、x3 分别为产品 A、B、C 的产量,则数学模型为
xj 0, j 1, 2, ,10
运筹学第3版熊伟编著习题答案
1.5炼油厂计划生产三种成品油,不同的成品油由半成品油混合而成,例如高级汽油可以由中石脑油、重整汽油和裂化汽油混合,辛烷值不低于94,每桶利润5元,见表1-26.
表1-26
成品油
高级汽油
一般汽油
航空煤油
一般煤油
半成品油
中石脑油
基本最优解 ,最优解的通解可表示为 即
〔4〕
[解]单纯形表:
C<j>
3
2
1
0
0
R. H. S.
Ratio
Basis
C<i>
X1
X2
X3
X4
X5
X4
0
5
4
6
1
0
25
5
X5
0
[8]
6
3
0
1
24
3
C<j>-Z<j>
3
2
1
0
0
0
X4
0
0
1/4
33/8
1
-5/8
10
X1
3
1
3/4
3/8
0
1/8
3
C<j>-Z<j>
方案四:在三年内投资人应在第三年年初投资,一年结算一次,年收益率是30%,这种投资最多不超过1万元.
投资人应采用怎样的投资决策使三年的总收益最大,建立数学模型.
[解]是设xij为第i年投入第j项目的资金数,变量表如下
项目一
项目二
项目三
项目四
第1年
第2年
运筹学教材习题答案详解

显然用料最少的方案最优。
1.4A、B两种产品,都需要经过前后两道工序加工,每一个单位产品A需要前道工序1小时和后道工序2小时,每一个单位产品B需要前道工序2小时和后道工序3小时.可供利用的前道工序有11小时,后道工序有17小时.
3
B1:2.0
3
需要量(套)
200
150
问怎样下料使得(1)用料最少;(2)余料最少.
【解】第一步:求下料方案,见下表。
方案
一
二
三
四
五
六
七
八
九
十
十一
十二
十三
十四
需要量
B1:2.7m
2
1
1
1
0
0
0
0
0
0
0
0
0
0
300
B2:2m
0
1
0
0
3
2
2
1
1
1
0
0
0
0
450
A1:1.7m
0
0
1
0
0
1
0
2
1
0
3
2
1
0
《运筹学》
第1章线性规划
第2章线性规划的对偶理论
第3章整数规划
第4章目标规划
第5章运输与指派问题
第6章网络模型
第7章网络计划
第8章动态规划
第9章排队论
第10章存储论
第11章决策论
第12章对策论
习题一
1.1讨论下列问题:
动态规划-武汉工程大学-精品课程
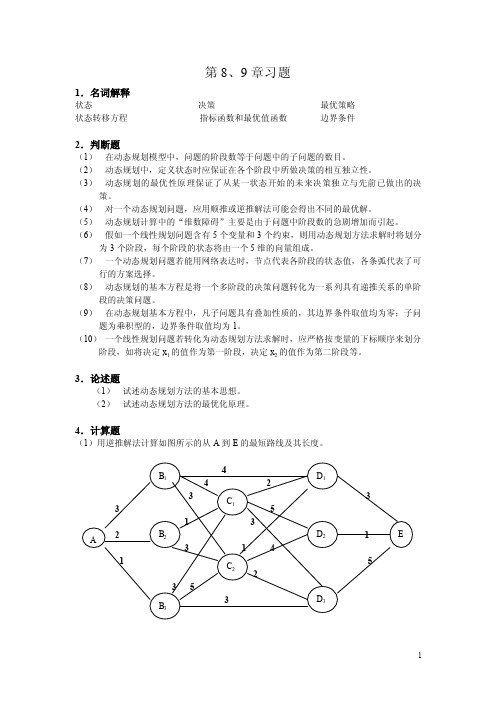
第8、9章习题1.名词解释状态决策最优策略状态转移方程指标函数和最优值函数边界条件2.判断题(1)在动态规划模型中,问题的阶段数等于问题中的子问题的数目。
(2)动态规划中,定义状态时应保证在各个阶段中所做决策的相互独立性。
(3)动态规划的最优性原理保证了从某一状态开始的未来决策独立与先前已做出的决策。
(4)对一个动态规划问题,应用顺推或逆推解法可能会得出不同的最优解。
(5)动态规划计算中的“维数障碍”主要是由于问题中阶段数的急剧增加而引起。
(6)假如一个线性规划问题含有5个变量和3个约束,则用动态规划方法求解时将划分为3个阶段,每个阶段的状态将由一个5维的向量组成。
(7)一个动态规划问题若能用网络表达时,节点代表各阶段的状态值,各条弧代表了可行的方案选择。
(8)动态规划的基本方程是将一个多阶段的决策问题转化为一系列具有递推关系的单阶段的决策问题。
(9)在动态规划基本方程中,凡子问题具有叠加性质的,其边界条件取值均为零;子问题为乘积型的,边界条件取值均为1。
(10)一个线性规划问题若转化为动态规划方法求解时,应严格按变量的下标顺序来划分阶段,如将决定x1的值作为第一阶段,决定x2的值作为第二阶段等。
3.论述题(1)试述动态规划方法的基本思想。
(2)试述动态规划方法的最优化原理。
4.计算题(1)用逆推解法计算如图所示的从A到E的最短路线及其长度。
(2)写出max z =∑g i (x i )动态规划的基本方程(3)用动态规划方法求解下列问题:(a)max z=x 21x 2x 33s.t. x 1+x 2+x 3≤6x i ≥0 i=1,2,...,n(b) max z=5x 1-x 12+9x 2-2x 22s.t x 1+x 2≤5x i ≥0 i=1,2(4)某工厂购进100台机器,准备生产P 1、P 2两种产品。
若生产产品P 1,每台机器每年可收入45万元,损坏率为65%;若生产产品P 2,每台机器每年收入为35万元,但损坏率只有35%;估计三年后将有新的机器出现,旧的机器将全部淘汰。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
④ 0-1变量:
x ij 1 ,0(i 1 ,2 , ,1 7 ;j 1 ,2 ,3 )
目标函数:未带物品购买费用最小
3
17
3
1 xij(i 8,9, ,17) Mizn pi(1 xij)
j1
i8
j1
补充:背包问题
(容量一定的背包里装尽可能多的物品)
Excel求解结果为:
包1 放3件 物品1 物品3 物品5 包2 放5件 物品4 物品10 物品13 物品15 物品17 包3 放4件 物品2 物品6 物品7 物品14 没有放 5件 物品8 物品9 物品11 物品12 物品16
9.2.1 生产与存贮问题
解:明年市场总需求为3000+4000+8000+ 7000 =22000双 , 而 最 多 可 生 产 4×6000= 24000双,所以皮鞋公司可以满足市场总需求 。 (1) 决策变量
本问题是要确定该公司明年每个季度的生产 计划,所以设
物品 1 2 3 4 5 6 7 8 9 10
体积 200 350 500 430 320 120 700 420 250 100
价格 15 45 100 70 50 75 200 90 20 30
补充:背包问题
(容量一定的背包里装尽可能多的物品)
决策变量:对每个物品要确定是否带的同 时,还要确定放在哪个包里(如果增加一个 虚拟包,把不带的物品放在里面,则问题就 转化为确定每个物品放在哪个包里。这里的 数学模型和电子表格模型没有用虚拟包)。 因此可设决策变量为第i个物品是否放在第j 个包中(1-放,0-不放)。
动态规划问题的提出
在实际的决策过程中,由于涉及的参数比较多, 往往需要将问题分成若干个阶段,对不同阶段采取 不同的决策,从而使整个决策过程达到最优。
显然,由于各个阶段选择的策略不同,对应的整 个过程就可以有一系列不同的策略。
动态规划是解决多阶段决策过程最优化的一种方 法。这种方法把困难的多阶段决策问题变换成一系 列互相联系的比较容易的单阶段问题,解决了这一 系列比较容易的单阶段问题,也就解决了困难的多 阶段决策问题。
例9.1 某货运公司使用一种最大承载能力 为10吨的卡车来装载3种货物,每种货物 的重量及价值如表9-1所示。应当如何装 载货物才能使总价值最大?
货物 编号
123
单位
重量 3 4 5
(吨)
用单Ex位cel求解背包问题时,采用的是 整价数值规划4 的5 方6 法。
9.1.2 多维背包问题
当约束条件不仅有货物的重量,还有体积 等限制时,构成了多维背包问题。
(容量一定的背包里装尽可能多的物品)
某人出国留学打点行李,现有三个旅行包,容积 大小分别为1000、1500和2000,根据需要列出需 带物品清单,其中一些物品是必带物品,共有7件, 其体积大小分别为400、300、150、250、450、 760、190。尚有10件可带可不带物品,如果不带 将在目的地购买,通过网络查询可以得知其在目的 地的价格(美元)。这些物品的容量及价格分别见 下表,试给出一个合理的安排方案,把物品放在三 个旅行包里。
9.1 背包问题
背包问题可以抽象为这样一类问题:设 有n种物品,每种物品有其重量及价值。 同时有一个背包,最大装重为c,现从n种 物品中选取若干件(同一种物品可以选多 件),使其总重量小于等于c,而总价值 最大。 背包问题等同于车、船、人造卫星等工 具的最优装载问题,有广泛的实际意义。
9.1.1 一维背包问题
未带物品购买费用为200美元
9.2 生产经营问题
在生产和经营中,经常遇到如何合理安排 生产计划、采购计划以及库存计划和销售计 划等问题,要求既要满足市场的需要,又要 尽量降低成本费用。因此,正确制定生产( 或采购)策略,确定不同时期的生产量(或 采购量)、销售量和库存量,在满足产品需 求量的条件下,使得总收益最大或总成本( 生产成本+存储成本)最小,这就是生产经 营问题,包括生产与存储问题、采购与销售 问题等。
例9.2 现有一辆载重为5吨,装载体积8立 方米的卡车,可装载三种货物,已知每种货 物各8件,其它有关信息如表9-2所示,求携 带货物价值最大的装载方案。
货物品种
1 2 3
单位重量 (吨) 0.2 0.4 0.3
单位体积 (立方米)
0.3 0.5 0.4
单位价值 (千元) 3 7.5 6
补充:背包问题
x ij 1 ,0(i 1 ,2 , ,1 7 ;j 1 ,2 ,3 )
补充:背包问题
(容量一定的背包里装尽可能多的物品)
约束条件 17 ① 包的容量限制 cixij rj (j1,2,3) i1
3
② 必带物品限制 xij 1 (i 1,2, ,7) j1
3
③ 选带物品限制 xij 1 (i 8,9, ,17) j1
9.2.1 生产与存贮问题
例9.3 某皮鞋公司根据对去年的市场需求
分析预测明年的需求:一季度3000双,二 季 度 4000 双 , 三 季 度 8000 双 、 四 季 度 7000双。企业现在每个季度最多可以生产 6000双皮鞋。为了满足所有的预测需求, 前两个季度必须有一定的库存才能满足后 两个季度的需求。已知每双皮鞋的利润为 20元,每个季度的库存成本8元。请确定 该公司明年每个季度的生产计划,使公司 的年利润最大。
第9章动态规划
动态规划问题的提出
动态规划是解决多阶段决策过程最 优化问题的一种方法。该方法是由美 国 数 学 家 贝 尔 曼 (RBellman) 等 人 在 20世纪50年代初提出的。他们针对多 阶段决策问题的特点,提出了解决这 类问题的“最优化原理”,并成功地 解决了生产管理、工程技术等方面的 许多实际问题,从而建立了运筹学的 一个新分支,即动态规划。
有时阶段可以用时间表示,在各个时间段,采用 不同决策,它随时间而变动,这就有“动态”的含 意
动态规划问题的Байду номын сангаас出
动态规划是现代企业管理中的一个 重要决策方法。 本章利用微软Excel软件在“公式” 和“规划求解工具”两方面的强大功 能,对背包问题、生产经营问题、资 金管理问题和资源分配问题等进行分 析、建模与求解,解决了实际经营中 的优化问题,迅速准确地得出决策结 果。
