高一数学人教A版必修3课件:程序框图
合集下载
人教a版必修3数学教学课件第1章算法初步第1节算法与程序框图

HISHISHULI
HONGNANJUJIAO
D典例透析
2.算法的特征
特征
有限性
确定性
可行性
有序性
说明
一个算法运行完有限个步骤后必须结束,而不能无限
地运行
算法的每一步计算,都必须有确定的结果,不能模棱
两可,即算法的每一步只有唯一的执行路径,对于相
同的输入只能得到相同的输出结果
算法中的每一步必须能用实现算法的工具精确表达,
并能在有限步内完成
算法从初始步骤开始,分为若干明确的步骤,每一个
步骤只能有一个确定的后续步骤,只有执行完前一步
才能执行后一步
IANLITOUXI
目标导航
特征
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
说明
算法一般要适用于不同形式的输入值,而不是局限于
目标导航
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
1.算法的概念
12 世纪的算法 用阿拉伯数字进行算术运算的过程
按照一定规则解决某一类问题的明确和有限的步
数学中的算法
骤
通常可以编成计算机程序,让计算机执行并解决
现代算法
问题
名师点拨1.算法没有一个精确化的定义,可以理解为由基本运算
题型四
设计含有重复步骤的算法
【例4】 写出求1×2×3×4×5×6的算法.
分析:思路一:采取逐个相乘的方法;思路二:由于重复作乘法,故可
以设计作重复乘法运算的步骤.
解:算法1:第一步,计算1×2得到2.
HONGNANJUJIAO
D典例透析
2.算法的特征
特征
有限性
确定性
可行性
有序性
说明
一个算法运行完有限个步骤后必须结束,而不能无限
地运行
算法的每一步计算,都必须有确定的结果,不能模棱
两可,即算法的每一步只有唯一的执行路径,对于相
同的输入只能得到相同的输出结果
算法中的每一步必须能用实现算法的工具精确表达,
并能在有限步内完成
算法从初始步骤开始,分为若干明确的步骤,每一个
步骤只能有一个确定的后续步骤,只有执行完前一步
才能执行后一步
IANLITOUXI
目标导航
特征
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
说明
算法一般要适用于不同形式的输入值,而不是局限于
目标导航
Z 知识梳理 Z重难聚焦
HISHISHULI
HONGNANJUJIAO
D典例透析
IANLITOUXI
1.算法的概念
12 世纪的算法 用阿拉伯数字进行算术运算的过程
按照一定规则解决某一类问题的明确和有限的步
数学中的算法
骤
通常可以编成计算机程序,让计算机执行并解决
现代算法
问题
名师点拨1.算法没有一个精确化的定义,可以理解为由基本运算
题型四
设计含有重复步骤的算法
【例4】 写出求1×2×3×4×5×6的算法.
分析:思路一:采取逐个相乘的方法;思路二:由于重复作乘法,故可
以设计作重复乘法运算的步骤.
解:算法1:第一步,计算1×2得到2.
高中数学新人教A版必修三课件程序框图

讲授新课
1.程序框图的概念 程序框图简称框图,是一种用规定的图形、指
向线及文字说明来准确、直观地表示算法的图形.
第六页,编辑于星期一:点 八分。
例如:
开始
输入a11,a12,a21,a22,b1,b2
D=a11a22-a12a21
D=0
否
x1
(b1a22
-b a ) 2 12
D
x2
(b2a11
-b a 1
输出y
结束
第十七页,编辑于星期一:点 八分。
反馈练习
《名师》 精题大淘金
1,2,3,12,13
第十八页,编辑于星期一:点 八分。
作业:
第9页A组2,B组1
作业: 设计房租收费的算法,其要求是:住房面积 80平方米以内,每平方米收费3元,住房面积超过80 平方米时,超过部分,每平方米收费5元.输入住房面 积数,输出应付的房租.
第二步, 用3除7,得到余数1.因为余数不为0,
所以3不能整除7.
第三步, 用4除7,得到余数3.因为余数不为0, 所以4不能整除7.
第四步, 用5除7,得到余数2.因为余数不为0, 所以5不能整除7.
第五步, 用6除7,得到余数1.因为余数不为0, 所以6不能整除7.因此,7是质数.
第五页,编辑于星期一:点 八分。
第三页,编辑于星期一:点 八分。
算法的表示
⑴用日常语言和数学语言 ⑵程序框图(简称框图)。 ⑶形式语言(算法程序语言)。
算法的要求
(1)可行性
(2)确定性 (3)有限性
(4)有输出
(5)通用性 (6)不唯一性
第四页,编辑于星期一:点 八分。
设计一个算法判断7是否为质数.
高中数学人教A版必修3课件1121程序框图顺序结构

3.如图所示程序框图中,其中不含有的程序框是 ( )
A.终端框
B.输入、输出框
C.判断框
D.处理框
【解析】选C.含有终端框,输入、输出框和处理框,不
含有判断框.
4.如图所示的程序框图,输入a1=3,a2=4,则输出的结果
是
.
【解析】输入a1=3,a2=4,b=a1a2=3×4=12.则输出b=12. 答案:12
类型三 利用顺序结构表示算法 【典例】已知直线l:Ax+By+C=0(A2+B2≠0),点P(x0,y0), 设计一个算法计算点P到直线l的距离,并画出程序框图.
【审题路线图】直线l的方程和点P的坐标⇒利用点到
直线的距离公式d=Ax0 By0,给 C公式中的字母赋值,
A2 B2
再代入计算.
【解析】用自然语言描述算法如下:
【典例】阅读程序框图,若输入的a=1,
b=2,输出的结果是 ( D )
A.0,2
B.2,0
C.1,3
D.3,1
【失误案例】由题意,输入a=1,b=2,执行程序 a=b=2,b=a=1,进而b=2-1=1,a=2+1=3.
【错解分析】分析解题过程,请找出错误之处. 提示:错误的根本原因是忽视了程序执行过程中变量数 值的变化,实际上执行完a=b,b=a后,a和b的值都是b 的初始值2.执行完b=a-b后,计算a=a+b时b的值为0.
第一步,输入点P的横、纵坐标x0,y0, 输入直线方程的系数,即常数A,B,C.
第二步,计算z1=Ax0+By0+C. 第三步,计算z2=A2+B2. 第四步,计算d= z1 .
z2
第五步,输出d.
人教A版高中数学必修三课件程序框图、顺序结构

变式训练2把【例3】中的直线l改为圆C:(x-a)2+(y-b)2=r2,写出求
点P0(x0,y0)到圆上的点的距离最大值的算法,并画出程序框图. 解:算法如下:第一步,输入点P0的横、纵坐标x0,y0,输入圆心C的横、
纵坐标a,b,圆的半径r.
第二步,计算 z= (������0-������)2 + (������0-������)2.
提示第一步,输入球的半径R.
第二步,计算S=4πR2.
第三步,计算V=
4 3
πR3.
第四步,输出S,V.
2.上述算法有何特点?
提示按照顺序从上到下依次执行.
3.你能画出该算法的程序框图吗? 提示
课前篇自主预习
4.如何定义顺序结构? 提示顺序结构是由若干个依次执行的步骤组成的.这是任何一个 算法都离不开的基本结构.
课前篇自主预习
5.顺序结构可以用怎样的程序框图来表示? 提示顺序结构可以用程序框图表示为:
6.做一做3:判断题 (1)顺序结构中一定含有判断框. ( ) (2)处理框既可以用来对变量赋值,也可以用来计算. ( )
答案:(1)× (2)√
课前篇自主预习
7.做一做4:已知如图所示的程序框图,若输入x=32,则输出y的值
课堂篇探究学习
探究一
探究二
探究三
当堂检测
互动探究(1)在【例2】中,若已知梯形上、下底边长和面积,求该 梯形的高.
(2)在【例2】中,若已知梯形上底边长、高和面积,求该梯形的下 底长.
分析(1)首先根据梯形面积公式列出方程,表示出梯形的高,然后 根据高的表达式设计相应的算法,最后用框图语言表示相应的算法 步骤.
行的顺序,用来连接程序框,是带箭头的直线或折线,应用时必须带 箭头;连接点是连接同一个程序框图的不同部分的.
高一数学人教A版必修3课件:1.1.2 程序框图6.2

1.1.2 程序框图
第一页,编辑于星期日:二十二点 四分。
图形符号
名称
起止框
含义
表示一个算法的 起始与结束
输入,输出框 表示一个算法输
入输出信息
处理框(执行框) 赋值、计算
判断框
流程线
判断某一条件是否成立, 成立时在出口处标明“是” 或“Y”;不成立时标明 “否”或“N”
算法中从上一步骤指向
下一步骤(连接程序框)
左图是包含直到型循 环结构的程序框图,你 能画出当型循环结构框 图吗?
开始
n=2005 a=200
t=0.05a
a=a+t
n=n+1
a>300? 是
输出n 结束
否
第十一页,编辑于星期日:二十二点 四分。
程序框图:
开始
n=2005 a=200
a≤300?
否 输出n
结束
n=n+1 a=a+t
t=0.05a
输出S
第三次循环s= 3+3=6
S=1+2+3
结束
……S=1+2+3+…100
第七页,编辑于星期日:二十二点 四分。
思考?
如何用自然语言表述右图中 的算法?
1. S=0; 2. i=1; 3. S=S+i; 4. i=i+1;
5. 如果i大于100,结束算法,得到S值,否 则返回重新执行第3步,第4步,第5步.
常见的条件结构可以用程序框图表示为下面两种形式
满足条件?
是
步骤 A
否
B
满足条件?
否
是
步骤A
第五页,编辑于星期日:二十二点 四分。
第一页,编辑于星期日:二十二点 四分。
图形符号
名称
起止框
含义
表示一个算法的 起始与结束
输入,输出框 表示一个算法输
入输出信息
处理框(执行框) 赋值、计算
判断框
流程线
判断某一条件是否成立, 成立时在出口处标明“是” 或“Y”;不成立时标明 “否”或“N”
算法中从上一步骤指向
下一步骤(连接程序框)
左图是包含直到型循 环结构的程序框图,你 能画出当型循环结构框 图吗?
开始
n=2005 a=200
t=0.05a
a=a+t
n=n+1
a>300? 是
输出n 结束
否
第十一页,编辑于星期日:二十二点 四分。
程序框图:
开始
n=2005 a=200
a≤300?
否 输出n
结束
n=n+1 a=a+t
t=0.05a
输出S
第三次循环s= 3+3=6
S=1+2+3
结束
……S=1+2+3+…100
第七页,编辑于星期日:二十二点 四分。
思考?
如何用自然语言表述右图中 的算法?
1. S=0; 2. i=1; 3. S=S+i; 4. i=i+1;
5. 如果i大于100,结束算法,得到S值,否 则返回重新执行第3步,第4步,第5步.
常见的条件结构可以用程序框图表示为下面两种形式
满足条件?
是
步骤 A
否
B
满足条件?
否
是
步骤A
第五页,编辑于星期日:二十二点 四分。
人教版高中数学必修3课件程序框图

结束
否 否
d=d+1
否 n不是质数
程序框图:又称流程图,是一种用规定的图形、指向线及文字说明来准确、
直观的表示算法的图形.
名称
作用 终端框或起止框
表示算法的 起始和结束
名称
输入、输出框 作用 表示算法的输入 和输出的信息
名称
作用
处理框或执行框
赋值、计算
名称 判断框 作用
判断某一条件是否成立, 成立在出口处标明“是”或“Y” 不成立标明“否”或“N”
5;
结束
指向②处时,输出 sum 15 .
5.下图为求1~1000的所有的偶数的和而设计的一个程 序框图,将空白处补上,并指明它是循环结构中的哪一 种类型,并画出它的另一种循环结构框图.
开始
i=2
sum=0 i<=1000
i=i+2 sum=sum+i
输出sum 结束
课堂小结:
1.要掌握程序框的作用; 2.掌握三种逻辑结构,并能正确使用这三种结构画流程图; 3.在循环结构中,一定有条件结构,通常都有一个起到循环计数作用的变量; 4.确实明确当型和直到型的区别和联系,不要混用。
输出S 结束
输出S 结束
练习:
1.就(1)、(2)两种逻辑结构,说出各自的算法功能 ຫໍສະໝຸດ 1)开始(2) 开始
输入a,b
输入a,b
2.已知梯形上底为2,下底为4, 高为5,求其面积,设计出该 问题的流程图.
开始
d a2 b2
sum=a+b
a 2,b 4, h 5
c d
输出c
结束
输出sum 结束
S 1 (a b)h 2
高中数学人教A版必修3ppt课件-.2程序框图优质课件

开始
输入A,B,C Y A>B? N
A>C? N N
Y 输出A
输出C
B>C? Y
输出输B出B
结束
五、课时小结
1、程序框图的概念: 程序框图又称流程图,是一种用程序框、流程线
及文字说明来准确、直观的表示算法的图形。
2、基本的程序框图(课本P6,表1-2)
3、能理解两种结构(顺序结构和条件结构)的特 点和区别,能运用两种结构解决简单的算法问题。
作业
习题1.1 A组 第3题 预习程序框图P12-19
第一步,输入3个系数a,b,c。 时在出口处标明“是”或“Y”; 算法的流程根据条件是否成立有不同的流向.
随练、设计一个算法,判断一元二次方程ax2 +bx + c=0是否有实数根,并画出程序框图表示。
算法分析:
第一步,输入3个系数a,b,c。 第二步,计算△=b2-4ac。 第三步,判断△≥0是否成立。若是, 则输出“方程有实数根”;若否,则 输出“方程无实数根”。结束算法。
a+b>c, a+c>b,
则存在这样的三角形;若否,
ቤተ መጻሕፍቲ ባይዱ
b+c>a是否同时
则不存在这样的三角形。
是
成立?
否
存在这样的 三角形
不存在这样 的三角形
结束
三、例题分析
例2、任意给定3个正实数,设计一个算法,判断分别 以这3个数为三边边长的三角形是否存在,并画出程序 框图。
判断某一条件是否成立,成立
随练、设计一个算法,判断一元二次方程ax +bx + a+b>c, a+c>b,
一、知识回顾 程序框、流程线及其功能
输入A,B,C Y A>B? N
A>C? N N
Y 输出A
输出C
B>C? Y
输出输B出B
结束
五、课时小结
1、程序框图的概念: 程序框图又称流程图,是一种用程序框、流程线
及文字说明来准确、直观的表示算法的图形。
2、基本的程序框图(课本P6,表1-2)
3、能理解两种结构(顺序结构和条件结构)的特 点和区别,能运用两种结构解决简单的算法问题。
作业
习题1.1 A组 第3题 预习程序框图P12-19
第一步,输入3个系数a,b,c。 时在出口处标明“是”或“Y”; 算法的流程根据条件是否成立有不同的流向.
随练、设计一个算法,判断一元二次方程ax2 +bx + c=0是否有实数根,并画出程序框图表示。
算法分析:
第一步,输入3个系数a,b,c。 第二步,计算△=b2-4ac。 第三步,判断△≥0是否成立。若是, 则输出“方程有实数根”;若否,则 输出“方程无实数根”。结束算法。
a+b>c, a+c>b,
则存在这样的三角形;若否,
ቤተ መጻሕፍቲ ባይዱ
b+c>a是否同时
则不存在这样的三角形。
是
成立?
否
存在这样的 三角形
不存在这样 的三角形
结束
三、例题分析
例2、任意给定3个正实数,设计一个算法,判断分别 以这3个数为三边边长的三角形是否存在,并画出程序 框图。
判断某一条件是否成立,成立
随练、设计一个算法,判断一元二次方程ax +bx + a+b>c, a+c>b,
一、知识回顾 程序框、流程线及其功能
人教A版高中数学必修3第一章.2算法与程序框图课件

❖输入 a,b,c
❖a+ b>c, a+ c>b,
❖否
❖
b+ c>a是否同时
❖成立?
❖是
❖存在这样的三角形
❖不存在这样的三角形
❖结束
三、循环结构
1.含义:循环结构是指在算法中从某处开 始,按照一定的条件反复执行某些步骤的算 法结构.反复执行的步骤称为循环体。
在科学计算中,有许多有规律的重复计算,如 累加求和、累乘求积等问题要用到循环结构.
步骤B
❖ 如果学生的成绩大于或等于60分,则输出 “及格”,否则输出“不及格”.
❖用程序框图表示这一算法过程❖开. 始
❖程序框图:
❖输入 A
算法步骤:
第一步: 输入一个学生 成绩; 第二步:判断这个学生 的成绩是否小于60; 第三步: 若是则成绩不
及格,若不是则成绩 及格.
❖否
❖A<60?
❖是
❖输出“不及格”
算法分析:
Sum=0
第一步:从1开始将自然 数1,2,3,…,100逐个相加;
第二步:输出累加结果.
Sum=Sum + 1 Sum=Sum + 2 Sum=Sum + 3 … Sum=Sum + 100
思பைடு நூலகம்:
Sum=Sum + i
1.上边的式子有怎样的规律呢?
2.怎么用程序框图表示呢?
在一些算法中,经常会出现从某处开始,反 复执行某一处理步骤,这就是循环结构.
顺序结构
条件结构
循环结构
尽管不同的算法千差万别,但它们都是由三 种基本的逻辑结构构成的。
算法三种基本逻辑结构(顺序结构、条件结构、循环结构) 流程图表示,实例,程序演示:
❖a+ b>c, a+ c>b,
❖否
❖
b+ c>a是否同时
❖成立?
❖是
❖存在这样的三角形
❖不存在这样的三角形
❖结束
三、循环结构
1.含义:循环结构是指在算法中从某处开 始,按照一定的条件反复执行某些步骤的算 法结构.反复执行的步骤称为循环体。
在科学计算中,有许多有规律的重复计算,如 累加求和、累乘求积等问题要用到循环结构.
步骤B
❖ 如果学生的成绩大于或等于60分,则输出 “及格”,否则输出“不及格”.
❖用程序框图表示这一算法过程❖开. 始
❖程序框图:
❖输入 A
算法步骤:
第一步: 输入一个学生 成绩; 第二步:判断这个学生 的成绩是否小于60; 第三步: 若是则成绩不
及格,若不是则成绩 及格.
❖否
❖A<60?
❖是
❖输出“不及格”
算法分析:
Sum=0
第一步:从1开始将自然 数1,2,3,…,100逐个相加;
第二步:输出累加结果.
Sum=Sum + 1 Sum=Sum + 2 Sum=Sum + 3 … Sum=Sum + 100
思பைடு நூலகம்:
Sum=Sum + i
1.上边的式子有怎样的规律呢?
2.怎么用程序框图表示呢?
在一些算法中,经常会出现从某处开始,反 复执行某一处理步骤,这就是循环结构.
顺序结构
条件结构
循环结构
尽管不同的算法千差万别,但它们都是由三 种基本的逻辑结构构成的。
算法三种基本逻辑结构(顺序结构、条件结构、循环结构) 流程图表示,实例,程序演示:
人教A版高中数学必修三课件程序框图

出它的面积,画出
步骤n+1 它的程序框图.
开始
算法分析:
先算出的值,再将它代入公式, 最后输出结果.因此只用顺序结构就能 表达出来.
输入a,b,c
输出s 结束
烧水泡茶问题:
烧水泡茶可分下面四步开完始成: 第一步:洗好开水壶;洗水壶 第二步:灌好凉水,放烧在水火上,等待水开; 第三步:洗好茶杯,茶杯里放好茶叶; 第四步:水开后再洗冲茶水杯泡,茶放。茶叶
流程线 连接点
赋值、计算 判断某一条件是否成立,成立时在 出口处标明“是”或“Y”;不成立时 标明“否”或“N”.
表示流程的路径和方向
连接程序框图的两部分
“判断整数n(n>2)是否为质数”的算法用程序框图的表示:
开始 输入n
i=2 求n除以i的余数r
i的值增加1, 仍用i表示
i>n-1或r=0
是
r=0?
是
输出“n不是质数”
结束
顺序结构
循环结构
否
条件结构
否
输出“n是质数”
算法的基本逻辑结构:
①顺序结构 ②条件结构(选择结构 ③循环结构
步骤n
)
While(当型)循环 Until(直到型)循环
成立
不成立
P
A
A
步骤n+1
A
B
P 成立
不成立
P 不成立
成立
①顺序结构 由若干个依次执行的处理步骤组成的。
步骤n 例1 已知一个三角形的三边边长分别为a、b、c,利用
输入a、b、c
a+b>c,a+c>b,
否
b+c>a是否同时成立
是 存在这样的三角形 不存在这样的三角形
步骤n+1 它的程序框图.
开始
算法分析:
先算出的值,再将它代入公式, 最后输出结果.因此只用顺序结构就能 表达出来.
输入a,b,c
输出s 结束
烧水泡茶问题:
烧水泡茶可分下面四步开完始成: 第一步:洗好开水壶;洗水壶 第二步:灌好凉水,放烧在水火上,等待水开; 第三步:洗好茶杯,茶杯里放好茶叶; 第四步:水开后再洗冲茶水杯泡,茶放。茶叶
流程线 连接点
赋值、计算 判断某一条件是否成立,成立时在 出口处标明“是”或“Y”;不成立时 标明“否”或“N”.
表示流程的路径和方向
连接程序框图的两部分
“判断整数n(n>2)是否为质数”的算法用程序框图的表示:
开始 输入n
i=2 求n除以i的余数r
i的值增加1, 仍用i表示
i>n-1或r=0
是
r=0?
是
输出“n不是质数”
结束
顺序结构
循环结构
否
条件结构
否
输出“n是质数”
算法的基本逻辑结构:
①顺序结构 ②条件结构(选择结构 ③循环结构
步骤n
)
While(当型)循环 Until(直到型)循环
成立
不成立
P
A
A
步骤n+1
A
B
P 成立
不成立
P 不成立
成立
①顺序结构 由若干个依次执行的处理步骤组成的。
步骤n 例1 已知一个三角形的三边边长分别为a、b、c,利用
输入a、b、c
a+b>c,a+c>b,
否
b+c>a是否同时成立
是 存在这样的三角形 不存在这样的三角形
高一数学人教A版必修3第一章1.1.2算法与程序框图课件(19张PPT)

高一数学人教A版必修3第一章1.1.2算 法与程 序框图 课件( 19张PP T)
第一步,给定实数 x .
第二步,判断 x 0
是否成立.若成立,
则 y x;若不成立, 则 y x .
开始
输入 x
x 0? 否
是
y x y x
高一数学人教A版必修3第一章1.1.2算 法与程 序框图 课件( 19张PP T)
开始 输入
条件结构
a,b, c
ab c bc a
否
c a b是否同时成立?
是
存在这样的 三角形
不存在这样的 三角形
高一数学人教A版必修3第一章1.1.2算 法与程 序框图 课件( 19张PP T)
结束
高一数学人教A版必修3第一章1.1.2算 法与程 序框图 课件( 19张PP T) 高一数学人教A版必修3第一章1.1.2算 法与程 序框图 课件( 19张PP T)
高一数学人教A版必修3第一章1.1.2算 法与程 序框图 课件( 19张PP T)
课后作业:
必做:
课本第20页 习题1.1A组1题.2题
选做:
1. 任意给定一个大于1的整数n,设计一
个算法求出n的所有因数,并画出程 序框图表示.
2. 请用所学知识推导例1中的三角形面积
高一数学人教A版必修3第一章1.1.2算 法与程 序框图 课件( 19张PP T)
输出 x
x2
b 2a
输出 x1, x2 输出:“方程没有实数根”
结束
高一数学人教A版必修3第一章1.1.2算 法与程 序框图 课件( 19张PP T)
回顾反思:
1.本节课大家学到了哪些知识? 2.如何得到程序框图?
高一数学人教A版必修3第一章1.1.2算 法与程 序框图 课件( 19张PP T)
人教A版 高中数学 必修3 第一章 1.1.2 循环结构的程序框图课件(共16张PPT)
巩固提高
1、设计一算法,求 积:1×2×3×…×100, 画出流程图
思考:该流程图与前面 的例1中求和的流程图有 何不同?
开始 i=0,S=1
i=i+1 S=S*i 否 i>=100?
是 输出S 结束
巩固提高
2、设计一算法输出1~1000以内能被3整除的整数
开始
算法:
i=0
S1:确定i的初始值为0;
开始 i=0,S=0
否 i<100? 是 i=i+1 S=S+ i
输出S 结束
思考:将步骤A和步骤B交换位 置,结果会怎样?能达到预期结果 吗?为什么?要达到预期结果,还 需要做怎样的修改?
步骤A
步骤B 答:达不到预期结果;
当i = 100时,退出循环,i 的值未能加入到S中;修 改的方法是将判断条件改 为i<101
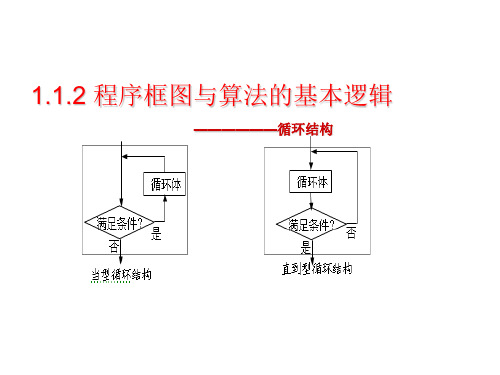
1.1.2 程序框图与算法的基本逻辑
——————循环结构
复习回顾
1、程序框图(流程图)的概念: 2、算法的三种逻辑结构: 3、顺序结构的概念及其程序框图: 4、条件结构的概念及其程序框图:
复习回顾
i) 顺序结构
ii) 条件结构
Yp N A
A
B
B
循环结构
循环结构:在一些算法中,也经常会出现从某处开始,
小结:
4.画循环结构流程图前: ①确定循环变量和初始条件; ②确定算法中反复执行的部分,即循环体; ③确定循环的转向位置; ④确定循环的终止条件.
循环结构的三要素:
循环变量,循环体、循环的终止条件。
其中顺序结构是最简单的结构,也是最基 本的结构,循环结构必然包含条件结构,所以 这三种基本逻辑结构是相互支撑的,无论怎样 复杂的逻辑结构,都可以通过这三种结构来表 达。
人教A版高中数学必修3第一章.2算法与程序框图优秀课件

流程线 连接 程序框
连接点 连接程序框图的两部分
新课 1、程序框图基本概念: (1)程序框图的概念:
程序框图又称流程图,是一种用规定 的图形、指向线及文字说明来准确、 直观地表示算法的图形。 (2)程序框图的组成: 一个程序框图包括以下几部分: 表示相应操作的程序框; 带箭头的流程线; 程序框内必要文字说明。
(3)基本程序框的符号及其功能
程序框
名称
功能
终端框(起止 表示一个算法的起始和结束 框)
输入、输出框 表示算法的输入和输出的信 息
处理框(执行 框) 判断框
流程线
赋值、计算
判断一个条件是否成立,用 “是”、“否”或“Y”、 “N”标明 表示从某一框到另一框的流
一、对程序框图的认识和理解 例 2. (1)下列关于程序框图的说法正确的是( ) A.程序框图是描述算法的语言 B.程序框图中可以没有输出框,但必须要有输入框给 变量赋值 C.在程序框图中,一个判断框可能同时产生两种结果 D.程序框图与流程图不是同一个概念 【解】由于算法设计时要求返回执行的结果,故必须要有输 出框,对于变量的赋值可通过处理框完成,故算法设计时不 一定要有输入框,因此 B 错;一个判断框产生的结果是唯一 的,故 C 错;程序框图就是流程图,所以 D 错.故选 A. 【答案】 A
1.1.2算法的基本结构和 程序框图(1)
复习回顾
1.算法的概念:算法实际上是解决问题的一种程序
性方法,它通常解决某一个或一类问题,在用算法解决
问题时,显然体现了特殊与一般的数学思想. 2.算法的性质有:①有限性,②确定性,③有序性,
④不唯一性,⑤可行性.解答有关算法的概念判断题应
根据算法的这五大特点.
2、简单程序框图的画法:
高中数学 程序框图课件 新人教A版必修3

i=1
sum=0 i=i+1 sum=sum+1 i≤100? 否 输出sum 输出 结束
是
练习2 练习 城区一中学生数学模块学分 认定由模块成绩决定, 认定由模块成绩决定,模块 成绩由模块考试成绩和平时 成绩构成,各占50%,若模 成绩构成,各占 , 块成绩大于或等于60分 块成绩大于或等于 分,获 学分, 得2学分,否则不能获得学分 学分 设计一算法, (为0分),设计一算法,通 分),设计一算法 过考试成绩和平时成绩计算 学分, 学分,并画出程序框图 开始 输入a,b 输入 S=(a+b)*0.5 否 S>=60? 是 credit=2 输出credit 输出 结束 credit=0
课堂作业P11
练习1
开始
输入a
N
a ≥0
Y
输出 |a|=a
输出 |a|=-a
结束
开始 X1=1
练习2
X2=2
m=(x1+x2)/2 N m*m -3<>0 y (x1*x1 -3)*(m*m -3) >0
x1=m N |x1 -x2|<0.005 y m=(x1+x2)/2
x2=m
输出所求的近似值m
条件结构: 条件结构:
满足条件? 满足条件? 是 步骤A 步骤
否
满足条件? 满足条件? 是
否
步骤B 步骤
步骤A 步骤
例3:设计求︱x︱的算法,并画出程序框图表示。 :设计求︱ ︱的算法,并画出程序框图表示。 算法分析: 算法分析: 第一步: 第一步:输入 x 第二步: 第二步:若x≥0,则 , ︱x︱= x ︱ 第三步: < , 第三步:若x<0,则 ︱x︱=-x ︱ 第四步:输出︱ ︱ 第四步:输出︱x︱的值
高中数学人教A版必修三《程序框图、顺序结构》课件

连接点
连接程序框图的两部分
高中数学人教A版必修三1.1.2《程序 框图、 顺序结 构》课 件(共26 张PPT)
高中数学人教A版必修三1.1.2《程序 框图、 顺序结 构》课 件(共26 张PPT)
思考2:在逻辑结构上,“判断整数n(n>2)是否为质数”的程序框图
由几种组成?
开始
输入n
顺序结构
i=2
算法的顺序结构 任何一个算法各步骤之间都有明确的顺序性,在算法
的程序框图中,由若干个依次执行的步骤组成的逻辑结构, 称为顺序结构.顺序结构是任何一个算法都离不开的基本 结构,用程序框图可以表示为:
步骤n
步骤n+1
高中数学人教A版必修三1.1.2《程序 框图、 顺序结 构》课 件(共26 张PPT)
高中数学人教A版必修三1.1.2《程序 框图、 顺序结 构》课 件(共26 张PPT)
判断框
开始
输入n
i=2
求n除以i的余数r
i的值增加1,仍用i表示
i>n-1或r=0?
否
是
否
r=0?
判断某一条件是否 成立,成立时在出 口处标明“是”或 “Y”;不成立时 标明“否”或 “N”.
输出“n是质数”
结束
高中数学人教A版必修三1.1.2《程序 框图、 顺序结 构》课 件(共26 张PPT)
高中数学人教A版必修三1.1.2《程序 框图、 顺序结 构》课 件(共26 张PPT)
思考1:在上述程序框图中,有4种程序框,2种流程线,它们分别有
何特定的名称和功能?
开始
输入n
i=2 求n除以i的余数r
i的值增加1,仍用i表示
i>n-1或r=0?
高一数学人教A版必修3课件:1.1.2-1程序框图与顺序结构(共16张PPT)

二、算法的三种基本逻辑结构
输入n i=2
用n除以i,得余数r
顺序结构
i=i+1
循环结构
否 i>n-1或r=0?
是 r=0是?
否
条件
输出“n不是质数” 输出“n是质数” 结构
1.顺序结构 是最简单的算法结构,它是由若干个依
次执行的步骤组成的,语句与语句之间,框 与框之间是按从上到下的顺序进行的,这是 任何一个算法都离不开的基本结构.用程序框 图可以表示为: 左图中,语句A和语
1.1.2 程序框图与算法 的基本逻辑结构
第一课时
1.1.2-1 程序框图与顺序结构
一、程序框图 1. 概念 教材第6页 思考:用程序框图表示算法,相对于 自然语言描述的算法有什么优点? 程序框图相对于自然语言表述算法,看 起来更清晰,更明确,也更接近于计算机 的程序设计.
2.常见的程序框图
图形符号 名 称
3.画流程图的规则 (1)使用标准的框图符号; (2)框图一般按从上到下,从左到右的方向画
(3)一个完整的程序框图必须有起止框,用于 表示一个算法的开始和结束.
(3)除判断框外,大多数程序框图符号只有 一个进入点和一个退出点,判断框是唯一具 有超过一个退出点的框图符号.
(4)一类判断框是“是”与“否”两分支的 判断,而且有且仅有两个结果;另一类是多分 支判断,有几种不同的结果. (5)在图形符号内描述的语言要非常简练清楚
第五步:判断“i>(n-1)”或“r=0”是否成 立.若是,再判断“r=0”是否成立,否则, 返回第三步;
若“r=0”成立,则n不是质数,否则,n是 质数.
开始
输入n
i=2 用n除以i,得余数r
i=i+1
人教A版高中数学必修3课件:1.1.2程序框图与算法的基本逻辑结构

0(x 0)
设计一个算法计算分段函数 y 1(0 x 1)
画出程序框图。
x(x 1)
, 的函数值,并
第一步、输入x
第二步、判断“x<0”是否成立, 若
是,则输出y=0,否则执行第三步;
第三步、判断“x<1”是否成立, 若
是,则输出y=1,否则输出y=x。
1、设计一个算法判断任意给定一个整数N是 奇数还是偶数,并画出程序框图;
第三步:将所有步骤的程序框图用流程线连接起来,并加上 终端框,得到表示整个算法的程序框图.
2、算法的逻辑结构
(1)顺序结构
由若干个依次执行的处理步骤组成的结构.它是任 何一个算法都离不开的结构.
画顺序结构程序框图时注意事项
步骤n 步骤n+1
(1)在程序框图中,开始框 和结束框不可少; (2)在算法过程中,第一步 输入语句是必不可少的; (3)顺序结构在程序框图中 的体现就是用流程线将程 序框自上而下地连接起来, 按顺序执行算法步骤.
循环结构的三要素 循环变量,循环体、循环的终止条件.
循环结构的设计步骤 (1)确定循环结构的循环变量和初始条件; (2)确定算法中需要反复执行的部分,即循环体; (3)确定循环的终止条件.
循环结构一定包含条件结构,用以控制循环过程,避免出现 “死循环”.判断框内写上条件,两个出口分别对应终止条件成 立与否,其中一个指向循环体,经过循环体回到判断框的入口处.
0 有两个不相等的实数根
b b2 4ac
b
0 有两个相等的实数根 x 0 没有实数根
2a
2a 2a
算法
第一步:输入三个系数 a, b, c
第二步:计算 b2 4ac
第三步:判断 0 是否成立.若是,计算
人教A版高中数学必修3第一章.2算法与程序框图课件_3

人教A版高中数学必修3第一章.2算法 与程序 框图课 件_3
2.循环结构的框图表示
直
到
型
循环体
循
环 结
满足 否
条件?
是
构
直到型循环执行了一次循环体之后,对控 制循环条件进行判断,当条件不满足时执行循 环体,直到满足则终止循环.
人教A版高中数学必修3第一章.2算法 与程序 框图课 件_3
2.循环结构的框图表示
1.1.2程序框图与算法的基本逻辑结构
循环结构
温故知新
算法的基本逻辑结构
①顺序结构
是由若干个 依次执行的处理 步骤组成的. 这是任何一个算法都离不
开的基本结构.
示意图
步骤 n
步骤n+1
温故知新
②条件结构
条件结构就是算法中, 根据条件是否成立有不同的 流向的结构.
名称
形式一
形式二
结构形 式
特征
两个步骤A,B根据条 件,选择 一个 执 行
课堂实例例1 设计一算法,求和:1+2+3+…+100
第1步,0+1=1. 第2步,1+2=3. 第3步,3+3=6. 第4步,6+4=10.
…… 第100步,4950+100=5050.
我们发现这个算法中存在一些反复执行的步骤,于 是我们尝试用循环结构表示。如何用循环结构表示 出来呢?
人教A版高中数学必修3第一章.2算法 与程序 框图课 件_3
否 输出S
人教A版高中数学必修3第一章.2算法 与程序 框图课 件_3
结束
i=i+1
S=S+i 是
当型循环 结构
人教A版高中数学必修3第一章.2算法 与程序 框图课 件_3
2.循环结构的框图表示
直
到
型
循环体
循
环 结
满足 否
条件?
是
构
直到型循环执行了一次循环体之后,对控 制循环条件进行判断,当条件不满足时执行循 环体,直到满足则终止循环.
人教A版高中数学必修3第一章.2算法 与程序 框图课 件_3
2.循环结构的框图表示
1.1.2程序框图与算法的基本逻辑结构
循环结构
温故知新
算法的基本逻辑结构
①顺序结构
是由若干个 依次执行的处理 步骤组成的. 这是任何一个算法都离不
开的基本结构.
示意图
步骤 n
步骤n+1
温故知新
②条件结构
条件结构就是算法中, 根据条件是否成立有不同的 流向的结构.
名称
形式一
形式二
结构形 式
特征
两个步骤A,B根据条 件,选择 一个 执 行
课堂实例例1 设计一算法,求和:1+2+3+…+100
第1步,0+1=1. 第2步,1+2=3. 第3步,3+3=6. 第4步,6+4=10.
…… 第100步,4950+100=5050.
我们发现这个算法中存在一些反复执行的步骤,于 是我们尝试用循环结构表示。如何用循环结构表示 出来呢?
人教A版高中数学必修3第一章.2算法 与程序 框图课 件_3
否 输出S
人教A版高中数学必修3第一章.2算法 与程序 框图课 件_3
结束
i=i+1
S=S+i 是
当型循环 结构
人教A版高中数学必修3第一章.2算法 与程序 框图课 件_3
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数据的输入 或结果的输出
赋值、执行计算语句、 结果的传送
判断框 根据给定条件判断
图形符号
名称
流程线 连结点 注释框
功能
连接循环框 连接循环框图的两部分 帮助理解框图
3.说明事项
(1)起止框:起止框是必不可少的;
(2)输入、输出框:可用在算法中任意需要输入输 出的位置,框内填写输入、输出的字母、符号等;
第三步:输出应交纳的 水费y.
是 y=1.2x
y=1.9x-4.9
输出y 结束
反馈练习
《名师》 精题大淘金 1,2,3,12,13
作业:
第9页A组2,B组1
作业: 设计房租收费的算法,其要求是:住房 面积80平方米以内,每平方米收费3元,住房面 积超过80平方米时,超过部分,每平方米收费5 元.输入住房面积数,输出应付的房租.
第三步, 用4除7,得到余数3.因为余数不为0, 所以4不能整除7.
第四步, 用5除7,得到余数2.因为余数不为0, 所以5不能整除7.
第五步, 用6除7,得到余数1.因为余数不为0, 所以6不能整除7.因此,7是质数.
讲授新课
1.程序框图的概念
程序框图简称框图,是一种用规定的 图形、指向线及文字说明来准确、直观地表示 算法的图形.
解:y与x之间的函数关系为:
1.2x, (当0≤x≤7时) y 1.9x 4.9(当x>7时)
解:y与x之间的函数关系为: 程序框图
y
1.2 x, 1.9x
4.9
(当0≤x≤7时) (当x>7时)
开始 输入x>0
算法分析:
否
0<x≤7?
第一步:输入每月用水 量x;
第二步:判断x是否不超 过7.若是,则y=1.2x;若 否,则y=1.9x-4.9.
§1.1.2 程序框图
【教学目标】 ➢掌握程序框图的概念;会用通用的图形符号 表示算法
➢掌握画程序框图的基本规则,能正确画出 程序框图. 【教学重点】 ➢框图的概念及画框图的规则
【教学难点】
➢框图符号的意义 .
一、算法的概念 复习
算法可以理解为由基本运算及规定的运算顺序所构 成的完整的解题步骤,或者看成按照要求设计好的有限 的确切的计算序列,并且这样的步骤或序列能解决一类 问题。
x.
结束
例4 为了加强居民的节水意识,某市制订了 以下生活用水收费标准:每户每月用水未超过 7m3时,每立方米收费1.0元,并加收0.2元的城 市污水处理费;超过7m3的部分,每立方米收费 1.5元,并加收0.4元的城市污水处理费,请你 写出某户居民每月应交纳的水费y(元)与用水 量x(m3)之间的函数关系,然后设计一个求该 函数值的算法,并画出程序框图.
x2 b 2a
输出x1,x2
否
输出“方程没
有实数根”
结束
例3 设计一个求任意数的绝对值的算法,并画出
பைடு நூலகம்
程序框图.
程序框图:
x(当x 0时) | x | x(当x<0时)
算法分析:
开始 输入x
第一步:输入数x;
x≥0? 否
第二步:判断x≥0是 否成立?若是,则
是 输出x
输出-x
|x|=x;若否,则|x|=-
(3)处理框(执行框):算法中需要的算式、 公式、 对变量进行赋值等要用处理框表示.
(4)判断框:当算法要求在不同的情况下执行不同 的运算时,需要判断框.框内填写判断条件.
(5)连接点:如果一个框图需要分开来画,要 在断开处画上连接点,并标出连接的号码。
4.画流程图的规则
为了使大家彼此之间能够读懂各自画出的框图,必须遵
守一些共同的规则,下面对一些常用的规则作一简单的介绍.
(1)使用标准的框图符号. (2)框图一般按从上到下、从左到右的方向画. (3)除判断框外,大多数程序框图符号只有一个进入 点和一个退出点,判断框是具有超过一个退出点的唯 一符号,但任何时候只有一条流出线起作用. (4)一类判断框是“是”与“否”两分支的判断,而且 有且仅有两个结果;另一类是多分支判断,有几种不同 的结果. (5)在图形符号内描述的语言要非常简练清楚.
算法的表示
⑴用日常语言和数学语言 ⑵程序框图(简称框图)。 ⑶形式语言(算法程序语言)。
算法的要求
(1)可行性 (2)确定性 (3)有限性 (4)有输出 (5)通用性 (6)不唯一性
设计一个算法判断7是否为质数.
第一步, 第二步,
用2除7,得到余数1.因为余数不为0, 所以2不能整除7.
用3除7,得到余数1.因为余数不为0, 所以3不能整除7.
例如:
开始
输入a11,a12,a21,a22,b1,b2
D=a11a22-a12a21
D=0
否
x1
(
b
1
a
2
2
-
b
2
a
1
)
2
D
x2
(
b
2
a
1
1
-
b
1
a
2
)
1
D
输出x1,x2
是
输出无法求 解信息
结束
2. 程序框图中常用的图形符号和连接线
图形符号
名称 起、止
框
输入、 输出框
处理框
功能
框图的开始或结 束
开始
例1 :(1) 输入a,b,c
下列程序框图 表示的算法是?
是
否
c>a,c>b
是
b>a
否
输出c
输出b
输出a
结束
开始
(2)
输入a
若输入-4,则输出 的结果是?
是
a0
否
输出 a
输出“ 是负数”
结束
例2 : 写出求一元 二次方程
ax2+bx+c=0
的根的程序框图
开始
输入a,b,c
b24ac
0
是
x1 b 2a
赋值、执行计算语句、 结果的传送
判断框 根据给定条件判断
图形符号
名称
流程线 连结点 注释框
功能
连接循环框 连接循环框图的两部分 帮助理解框图
3.说明事项
(1)起止框:起止框是必不可少的;
(2)输入、输出框:可用在算法中任意需要输入输 出的位置,框内填写输入、输出的字母、符号等;
第三步:输出应交纳的 水费y.
是 y=1.2x
y=1.9x-4.9
输出y 结束
反馈练习
《名师》 精题大淘金 1,2,3,12,13
作业:
第9页A组2,B组1
作业: 设计房租收费的算法,其要求是:住房 面积80平方米以内,每平方米收费3元,住房面 积超过80平方米时,超过部分,每平方米收费5 元.输入住房面积数,输出应付的房租.
第三步, 用4除7,得到余数3.因为余数不为0, 所以4不能整除7.
第四步, 用5除7,得到余数2.因为余数不为0, 所以5不能整除7.
第五步, 用6除7,得到余数1.因为余数不为0, 所以6不能整除7.因此,7是质数.
讲授新课
1.程序框图的概念
程序框图简称框图,是一种用规定的 图形、指向线及文字说明来准确、直观地表示 算法的图形.
解:y与x之间的函数关系为:
1.2x, (当0≤x≤7时) y 1.9x 4.9(当x>7时)
解:y与x之间的函数关系为: 程序框图
y
1.2 x, 1.9x
4.9
(当0≤x≤7时) (当x>7时)
开始 输入x>0
算法分析:
否
0<x≤7?
第一步:输入每月用水 量x;
第二步:判断x是否不超 过7.若是,则y=1.2x;若 否,则y=1.9x-4.9.
§1.1.2 程序框图
【教学目标】 ➢掌握程序框图的概念;会用通用的图形符号 表示算法
➢掌握画程序框图的基本规则,能正确画出 程序框图. 【教学重点】 ➢框图的概念及画框图的规则
【教学难点】
➢框图符号的意义 .
一、算法的概念 复习
算法可以理解为由基本运算及规定的运算顺序所构 成的完整的解题步骤,或者看成按照要求设计好的有限 的确切的计算序列,并且这样的步骤或序列能解决一类 问题。
x.
结束
例4 为了加强居民的节水意识,某市制订了 以下生活用水收费标准:每户每月用水未超过 7m3时,每立方米收费1.0元,并加收0.2元的城 市污水处理费;超过7m3的部分,每立方米收费 1.5元,并加收0.4元的城市污水处理费,请你 写出某户居民每月应交纳的水费y(元)与用水 量x(m3)之间的函数关系,然后设计一个求该 函数值的算法,并画出程序框图.
x2 b 2a
输出x1,x2
否
输出“方程没
有实数根”
结束
例3 设计一个求任意数的绝对值的算法,并画出
பைடு நூலகம்
程序框图.
程序框图:
x(当x 0时) | x | x(当x<0时)
算法分析:
开始 输入x
第一步:输入数x;
x≥0? 否
第二步:判断x≥0是 否成立?若是,则
是 输出x
输出-x
|x|=x;若否,则|x|=-
(3)处理框(执行框):算法中需要的算式、 公式、 对变量进行赋值等要用处理框表示.
(4)判断框:当算法要求在不同的情况下执行不同 的运算时,需要判断框.框内填写判断条件.
(5)连接点:如果一个框图需要分开来画,要 在断开处画上连接点,并标出连接的号码。
4.画流程图的规则
为了使大家彼此之间能够读懂各自画出的框图,必须遵
守一些共同的规则,下面对一些常用的规则作一简单的介绍.
(1)使用标准的框图符号. (2)框图一般按从上到下、从左到右的方向画. (3)除判断框外,大多数程序框图符号只有一个进入 点和一个退出点,判断框是具有超过一个退出点的唯 一符号,但任何时候只有一条流出线起作用. (4)一类判断框是“是”与“否”两分支的判断,而且 有且仅有两个结果;另一类是多分支判断,有几种不同 的结果. (5)在图形符号内描述的语言要非常简练清楚.
算法的表示
⑴用日常语言和数学语言 ⑵程序框图(简称框图)。 ⑶形式语言(算法程序语言)。
算法的要求
(1)可行性 (2)确定性 (3)有限性 (4)有输出 (5)通用性 (6)不唯一性
设计一个算法判断7是否为质数.
第一步, 第二步,
用2除7,得到余数1.因为余数不为0, 所以2不能整除7.
用3除7,得到余数1.因为余数不为0, 所以3不能整除7.
例如:
开始
输入a11,a12,a21,a22,b1,b2
D=a11a22-a12a21
D=0
否
x1
(
b
1
a
2
2
-
b
2
a
1
)
2
D
x2
(
b
2
a
1
1
-
b
1
a
2
)
1
D
输出x1,x2
是
输出无法求 解信息
结束
2. 程序框图中常用的图形符号和连接线
图形符号
名称 起、止
框
输入、 输出框
处理框
功能
框图的开始或结 束
开始
例1 :(1) 输入a,b,c
下列程序框图 表示的算法是?
是
否
c>a,c>b
是
b>a
否
输出c
输出b
输出a
结束
开始
(2)
输入a
若输入-4,则输出 的结果是?
是
a0
否
输出 a
输出“ 是负数”
结束
例2 : 写出求一元 二次方程
ax2+bx+c=0
的根的程序框图
开始
输入a,b,c
b24ac
0
是
x1 b 2a
