人教版数学五年级下册体积和表面积

人教版数学五年级下册典型题讲解

总和：24+30+32+30=116（cm） 116cm=1.16m
答：彩带长1.16m。
10.用一根2米的铁丝焊接好一个长方体框架，长22cm、宽16cm，高是多少？
方法一： 2m=200cm 200÷4=50（cm）
高：50-22-16=12（cm）
方法二：200-22×4-16×4 =112-64 =48（cm） 48÷4=12（cm）答：高是12cm。
=20×15×0.8 =240（dm³）
v水=abh水 =20×15×0.5 =150（dm³）
v石=v总-v水
=240-150 =90（dm³）答：石块的体积是90立方分米。
方法二： v石=abh下降
=20×15×（0.8-0.5） =90（dm³）答：石块的体积是90立方分米。
放入石块 8cm
方法一： a=6×3=18（cm） s表=（ab+ah+bh）×2
=（18×6+18×6+6×6）×2 =（108+108+36）×2 =504（cm²）
504cm²=5.04dm² 答：它的表面积是5.04平方分米。
方法二： s表=s正×数量
=6×6×14 =504（cm²） 504cm²=5.04dm² 答：它的表面积是5.04平方分米。
答：正方体木料体积27立方分米，切去部分木料体积18立方分米。
20dm
15dm
下降的高度 5cm
取出石块 20dm
15dm
在一个棱长6cm的正方体上放一个棱长2cm的小正方体，此时表面积是多少平方分米？
方法1、读题看单位，看问题是否需要换算单位。方法二
2cm
2、s大=6a大²

人教版小学五年级数学下册长方体和正方体表面积和体积解决问题专项训练试题(含答案)

人教版五年级数学下册长方体和正方体表面积和体积解决问题专项训练（50道含答案）1.学校活动室长15米，宽8米，高5米，门窗面积共24平方米。

要把活动室的天花板和四周的墙刷上涂料，一共要刷多少平方米?2.一种无盖的长方体水箱,长2.5dm,宽2.5dm,高3.5dm,制作一个这样的水箱,至少需要白铁皮多少平方分米?3.如图，这是一个铝合金框组成的鱼缸，侧面的每个面都是正方形，且边长为25厘米。

这个鱼缸的侧面准备全用玻璃，那么玻璃的总面积和铝合金框的总长度各是多少?4.如图，求这个正方体的表面积.5.爸爸买了一个长为30cm、宽为20cm、高为15cm的长方体礼盒,里面装有妈妈爱吃的长方体形状的花生酥,每块花生酥长5cm,宽3cm,高2cm。

（1）礼盒用彩纸包装,需要多少彩纸?(重叠部分不计算)（2）这个礼盒最多能装多少块花生酥?6.纸盒厂生产一种正方体纸板箱,棱长为40cm,做一个纸盒要多少平方厘米的纸板?它占空间多少立方厘米?合多少立方分米?7.有一个长8厘米，宽6厘米，高5厘米的长方体零件，在每个面的正中间挖去一个棱长为2厘米的小正方体，这个零件的体积与表面积各是多少?8.一个长方体形状的游泳池,长50m,宽30m,深2m。

要给游泳池的底面和四壁抹一层水泥,如果每平方米用水泥12千克,22吨水泥够不够用?9.有一个正方体木块,把它分成两个长方体木块后,表面积增加了24cm2,这个正方体木块原来的表面积是多少平方厘米?10.用纸皮做一个长1.2米、宽20分米、高60厘米无盖的长方体箱子用来堆放同学们收聚的矿泉水空瓶，至少要用多少平方分米的纸皮?11.一个集装箱长9米，宽3.2米，高2.5 米。

（1）制作这样一个集装箱至少需要多少平方米的钢板？（2）这个集装箱的容积大约是多少立方米？(箱壁厚度忽略不计)12.用240厘米唱的铁丝做一个最大的正方体框架，然后用纸板将6个面包起来做一个正方体纸盒，至少需要多少平方厘米纸板？这个纸盒的体积是多少立方厘米？13.求下面组合图形的面积．(单位：厘米)14.一个正方体的棱长之和是48厘米，那么它的表面积是多少平方厘米？15.一个正方体的表面积是48平方米，它的一个面的面积是多少平方米？16.做一个棱长为4分米的正方体无盖纸盒，至少需要用硬纸多少平方分米？17.小亚的房间长4.2米，宽3.5米，高3米，除去门窗的面积4.5平方米，房间的墙壁和天花板都贴上墙纸，这个房间至少需要多少平方米墙纸？18.一个长方体的食品盒长10厘米，宽6厘米，高13厘米．如果围着它贴一圈商标纸(上下面不贴)，这张商标纸的面积至少要多少平方厘米？19.五年级一班的教室长9米、宽7.2米，学校计划暑假把四面墙粉刷绿色的墙围，要求从地面起1.1米高，计算一下这间教室粉刷墙围的面积是多少平方米.如果每平方米的粉刷费是5元，则粉刷这间教室需要多少钱？20.把一根144厘米的铁丝焊接成一个正方体框架，再在外面糊一层纸，糊纸的面积是多少平方米？21.如图，求这个长方体的表面积.22.做一个长5厘米、宽4厘米、高3厘米的长方体纸盒，至少要用多少平方厘米的硬纸板？23.一块正方体魔方的棱长是8厘米，它的表面积是多少？24.做一个没有盖的长方体玻璃缸，长60厘米，宽60厘米，高40厘米，共需要玻璃多少平方厘米？合多少平方米？25.一间教室长10米、宽6米、高4米，门窗面积为19.6平方米，要粉刷教室的四壁和顶棚，如果每平方米用涂料0.25千克，则共需要涂料多少千克？26.有一个棱长10厘米的正方体包装盒，在它的四壁贴上商标纸，这张商标纸的面积是多少？27.一个长方体玻璃钟罩，长15厘米，宽10厘米，高16厘米，它的表面积是多少平方厘米？28.一间教室长9 米，宽7 米，高3 米。

人教版小学数学五年级下册长方体和正方体的体积

（
）
3.棱长总和相等的长方体，体积一定相等。
（
）
4.长宽高相等的长方体，体积一定相等。
（
）
5.体积相等的长方体，它们的长宽高一定相等。
（
）
6.长宽高相等的长方体，它们的体积相等，它们的
（
）
表面积也相等。
练一练
判断：
1.体积相等的长方体，形状也一定相同。
4
厘
米
3厘米
2厘米
（
2
厘
米
6厘米
3 × 2 × 4 = 24
米。
10厘
米
5厘米
知识应用
6. 有两个大小相等的正方体，将它们拼成下图的形状。表面
积比原来减少了32平方厘米。这个长方体的体积是多少？
正方体的一个面：32 ÷ 2 = 16（cm²）
减少32cm²
知识应用
6. 有两个大小相等的正方体，将它们拼成下图的形状。表面
积比原来减少了32平方厘米。这个长方体的体积是多少？
体积又可以样求呢？
底
面
长方体的体积 = 长 × 宽 × 高
底面积
底
面
正方体的体积 = 棱长 × 棱长 × 棱长
探索发现
长方体和正方体的
体积又可以样求呢？
底
面
底
面
长方体的体积 = 长 × 宽 × 高正方体的体积 = 棱长 × 棱长 × 棱长
底面积
底面积
探索发现
长方体（或正方体）的体积 = 底面积 × 高
关注单位名称的不同。
知识应用
4. 一段方钢长2米，横截面是边长10厘米的正方形。现把它
锻造成横截面为25平方厘米的长方体钢材，长是多少厘米？

人教版小学数学五年级下册第三单元《长方体和正方体》教材分析

人教版小学数学五年级下册第三单元《长方体和正方体》教材分析1.通过观察、操作，学生能够认识长方体和正方体的特征以及它们的展开图。

2.学生能够理解体积（包括容积）的含义，并能够使用常用的度量单位（立方米、立方分米、立方厘米、升、毫升）建立1立方米、1立方分米、1立方厘米以及1升、1毫升的表象，并能够进行简单的换算。

3.学生能够掌握长方体、正方体的体积和表面积的计算方法，并能够解决一些简单的实际问题。

4.学生能够探索某些实物体积的测量方法。

长方体和正方体的认识本小节介绍了长方体和正方体的特征和形状，学生需要理解长方体各部分的名称，面、棱、顶点，并能够形成长方体和正方体的概念。

长方体一般是由6个长方形（特殊情况有两个相对的面是正方形）围成的立体图形，而正方体是由6个完全相同的正方形围成的立体图形，所有的棱长度相等。

长方体和正方体的体积和表面积计算本小节介绍了长方体和正方体的体积和表面积的计算方法，学生需要掌握体积计算公式的推导和体积单位间的进率及名数的换算。

同时，学生需要理解表面积的含义，并能够计算出长方体和正方体的表面积。

容积和容积单位本小节介绍了容积和容积单位的概念，学生需要理解容积的含义，并能够使用常用的容积单位（升、毫升）进行换算。

不规则物体的体积本小节介绍了如何测量不规则物体的体积，学生需要探索并掌握测量不规则物体体积的方法。

总体来说，本单元的教学目标是让学生通过观察、操作，认识长方体和正方体的特征以及它们的展开图，理解体积（包括容积）的含义，掌握长方体、正方体的体积和表面积的计算方法，并能够解决一些简单的实际问题。

同时，学生需要探索某些实物体积的测量方法。

同。

第二个价值是通过操作让学生深入理解长、宽、高的概念。

建议在活动中引导学生思考：为什么要把12条棱分成三组？为什么这三组棱分别叫长、宽、高？通过思考和操作，学生会逐渐理解长、宽、高的概念和它们之间的关系。

练五是应用题，要求学生根据长方体的特征计算面积、体积等。

五年级数学下册各单元知识点归纳(附常见题型

第二单元因数和倍数1、因数、倍数：①一个数的因数的个数是有限的，最小的因数是1，最大的因数是它本身。

一个数的因数的求法：成对地按顺序找。

②一个数的倍数的个数是无限的，最小的倍数是它本身。

一个数的倍数的求法：依次乘以自然数。

③一个数的最大因数和最小倍数都是它本身。

如15的最大因数和最小倍数都是15。

2例题：1、从0、4、5、8、9中取出三个数字组成三位数，①在能被2整除的数中，最大的是（），最小的是（）②在能被3整除的数中，最大的是（），最小的是（）③在能被5整除的数中，最大的是（），最小的是（）2、在四位数21□0的方框中填入一个数，使它能同时被2、3、5整除，最多能（）种填法。

分别是。

3、质数和合数（1）质数和合数的意义：一个数，如果只有1和它本身两个因数，这样的数叫做质数；一个数，如果除了1和它本身还有别的因数，这样的数叫做合数。

判断题：①所有的奇数都是质数。

（）如②所有的偶数都是合数（）如③在1，2，3……自然数中，除了质数以外都是合数。

（）如④两个质数的和是偶数。

（）如（2）质数×质数=合数每个合数都可以由几个质数相乘得到，质数相乘一定得合数。

（3）20以内的质数：有8个（2、3、5、7、11、13、17、19）100以内的质数有25个：2、3、5、7、11、13、17、19、23、29、31、37、41、43、47、53、59、61、67、71、73、79、83、89、97100以内找质数、合数的技巧：看是否是2、3、5、7、11、13…的倍数，是就是合数，不是的就是质数。

4、最大、最小A的最小因数是：1；A的最大因数是：A；A的最小倍数是：A；最小的奇数是：1；最小的偶数是：0；最小的质数是：2；最小的合数是：4最小的自然数是：0；连续的两个质数是2、3。

例题：猜电话号码0592－A B C D E F G提示：A——5的最小倍数 B——最小的自然数 C——5的最大因数 D——它既是4的倍数，又是4的因数 E ——它的所有因数是1，2，3，6 F——它的所有因数是1， 3 G——它只有一个因数，这个号码就是附：判断（1）因为7×8＝56，所以56是倍数，7和8是因数（）因为（2）1是1，2，3，4，5…的因数（）（3）14比12大，所以14的因数比12的因数多（）（4）因为1.2÷0.6=2，所以1.2是0.6的倍数。

五年级下册数学课堂课件--长方体与正方体表面积人教版(38张)

宽、高
已知，利用长方体的表面积公式即可求解
【解答】解：5×5×2+5×20×4 =50+400 =450（平方厘米）答：做一只这样的纸盒至少需要硬纸450平方厘米．
17
走进生活，解决问题
一个长方体的长是宽的3倍，高是宽的2倍．已知这个长方体的长是 12厘米，求长方体的表面积．
18
走进生活，解决问题
（2）要使割后的表面积之和最小，沿平行6×8面切割，这样表面积就会增加两个原来长方体的最小的面，由此把原来长方体的表面积加上增加的面积就是切割后的长方体表面积之 25
切把一拼个问长16题厘米，宽6厘米，高8厘米的大长方体切成两个小长方
体，这两个小长方体的表面积的和最大是多少平方厘米，最小是多少？
22
走进生活，解决问题
有个长方体铁盒，它的高与宽相等．如果长缩短15厘米，就成为表面积是54平方厘米的正方体，这个长方体盒的宽是长的几分之几？
【解答】解：54÷6=9（平方厘米），
因为3×3=9平方厘米，
所以正方体的棱长为3厘米，
则长方体的长为3+15=18厘米，宽为3厘米，
3÷18=16．
答：这个长方体盒的宽是长的1．
走进生活，解决问题
纸盒厂加工一批装工具的纸盒，盒长20厘米，宽和高都是5厘米，做一只这样的纸盒至少需要硬纸多少平方厘米？
16
走进生活，解决问题
纸盒厂加工一批装工具的纸盒，盒长20厘米，宽和高都是5厘米，做一只这样的纸盒至少需要硬纸多少平方厘米？
【分析】求制作这样一个纸盒积，实际上是求纸盒的表面积，长方体的长、
2.一个正方体的木料，它的底面积是10cm ，把它横截成4段，表面积增加（）。

新人教版小学数学五年级下册《长方体和正方体的表面积》精品教案

板书：长方体表面积的计算方法=（长×宽）×2 +（长×高）×2 +（宽×高）×2
出示例1、学生读题，独立完成，小组交流。
教师巡视指导
集体订正
师：我们学会了如何求长方体的表面积，你能想象一下正方体展开后会发现什么呢？
学生：（答略）
师：演示正方体展开图。
师：我们怎样求出正方体的表面积呢？
师：如果知道正方体的数据，你能求出它的表面积吗?
（2）粉刷教室的内壁和天花板。
（3）要给长方体的游泳池里面贴瓷砖。
（4）两盒磁带，有下面三种包装方式，请同学们交流讨论一下，哪种包装方式省包装纸？说明理由。
（5）一个长方形木块，被切成两块后，它的表面积增加了多少？
【设计意图：数学学习，从理解知识到具体应用，解决实际问题，这是一次飞跃。本节课所设计的练习题都是学生熟悉的生活中的求六个、五个、四个面的面积，并结合教材题目进行,灵活应用长方体和正方体表面积的意义和计算方法解题，让学生运用所学知识解决实际问题，逐渐学会用数学的眼光去看待周围世界，去认识身边熟悉的事物，体会到生活中处处有数学，还数学本来面目。】
4、一个游泳池，长50米，宽40米，平均深1.5米.在池底和四壁抹上一层水泥, 抹水泥的面积至少是多少平方米?如果每平方米用水泥4.5千克,共需要水泥多少千克?(先求五个面的面积和,再求水泥的重量。)
学生独立完成，小组内相互修改，小组长记录下问题，集体交流，解决全班存在的问题。
【设计意图:本环节给学生设计了部分自主检测题，学生通过自主检测发现自己在做题中存在的问题和不足，同时也能尝到成功的快乐，给自己这一部分的学习有一个正确的评价。】
二．分层练习，强化提高
1.出示练习六第一题
学生先独立完成，然后小组内交流。

人教版五年级数学下册长方体和正方体表面积和体积解决问题专项训练2(50道含答案)

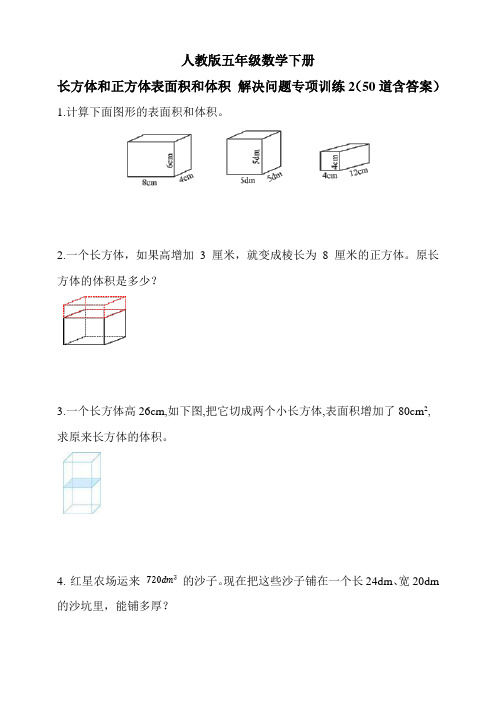
人教版五年级数学下册长方体和正方体表面积和体积解决问题专项训练2（50道含答案）1.计算下面图形的表面积和体积。

2.一个长方体，如果高增加3 厘米，就变成棱长为8 厘米的正方体。

原长方体的体积是多少？3.一个长方体高26cm,如下图,把它切成两个小长方体,表面积增加了80cm2,求原来长方体的体积。

4.红星农场运来的沙子。

现在把这些沙子铺在一个长24dm、宽20dm 的沙坑里，能铺多厚？5.在一个长为120cm、宽为60cm的长方体水箱里,浸没一块长方体的铁块后,水面就比原来上升2cm。

求铁块的体积。

6.一个游泳池长50米，宽25米，内蓄满水2500立方米。

（1）这个游泳池的高是多少米？（2）如果要把游泳池内贴上瓷砖，需下面规格的瓷砖多少块？边长是：5分米×5分米的正方形方砖（3）如果每块方砖1.4元，你会到哪个商店去购买更合算？7.有一个长方体的木料，截面是一个正方形，正方形的边长是2dm，这块木料的体积是．这块木料的长是多少分米？8.如图是一个长方体的空心管，掏空部分的长方体的长为10厘米，宽为7厘米。

求这根空心管的体积是多少？如果每立分米重7.8千克，这根管子重多少千克?（单位：厘米）9.有甲、乙两个水箱，从里面测量，甲水箱长12dm、宽8dm、高5dm，乙水箱长8dm、宽8dm、高6dm.甲水箱装满水，乙水箱空着.现将甲水箱里的一部分水抽到乙水箱中，使两箱水面高度一样.现在两个水箱的水面高多少分米？10.把下图所示的长方体木料切割成最大的正方体，正方体的体积是多少立方分米？最多能切成几个这样的正方体？11.有一个长方体的铁块，底面积是，高是4cm．把它锻造成一个截体的长是多少厘米．12.用右面的两块铁皮做一个无盖的长方体水箱。

（1）做好后里外都刷上防锈漆，刷漆的面积是多少？（2）这个水箱的容积是多少升？(忽略铁皮厚度和接头)13.一块正方体铁锭，棱长5分米．每立方分米的铁重7.8千克，这块铁锭重多少千克？14.一个长方体油箱的容积是30升．已知这个油箱底面长3分米，宽2.5分米，油箱的深是多少分米？(用方程解)15.有一个长方体，高2米，底面的周长是14米，宽3米．这个长方体的体积是多少？16.有一个正方体，底面周长是32分米，这个正方体的体积是多少？17.一个长方形水箱，长5分米，宽4分米，高3分米．装满水后倒入一个棱长是5分米的水箱内，水深多少分米？18.如图所示，在一个大长方体中挖去一个小长方体，求这个物体的表面积和体积．(单位：厘米)(按表面积、体积的顺序填写)19.一辆运土机运了36立方米的沙子，准备铺在一个长45米，宽20米的长方体沙坑里，所铺沙子的厚度是多少厘米?20.一个从里面量长和宽都是10厘米，高14厘米的长方体容器，装有8厘米深的水，现将一个铁球浸没在水中，这时量得水深是12厘米，铁球的体积是多少立方厘米?21.一个正方体容器,从里面量棱长是10厘米。

五年级数学下册长方体和正方体的表面积练习题(人教版)

五年级数学下册长方体和正方体的表面积练习题(人教版)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（五年级数学下册长方体和正方体的表面积练习题(人教版)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为五年级数学下册长方体和正方体的表面积练习题(人教版)的全部内容。

长方体和正方体表面积练习题一、填空。

1、一根长96厘米的铁丝围成一个正方体,这个正方体的棱长是（）厘米。

2、一个长方体的棱长总和是80厘米，长10厘米，宽是7厘米。

高是（）厘米。

3、至少需要（）厘米长的铁丝,才能做一个底面周长是18厘米，高3厘米的长方体框架。

4、一个长方体的长、宽、高都扩大2倍，它的表面积就( ）.二、应用题。

1、一个面的面积是36平方米的正方体，它所有的棱长的和是多少厘米？2、用一根铁丝刚好焊成一个棱长8厘米的正方体框架，如果用这根铁丝焊成一个长10厘米、宽7厘米的长方体框架，它的高应该是多少厘米？3、天天游泳池，长25米，宽10米，深1.6米，在游泳池的四周和池底砌瓷砖，如果瓷砖的边长是1分米的正方形，那么至少需要这种瓷砖多少块4、把棱长12厘米的正方体切割成棱长是3厘米的小正方体，可以切割成多少块？5、一种长方体硬纸盒，长10厘米,宽6厘米，高5厘米，有2平方米的硬纸板210张,可以做这样的硬纸盒多少个?(不计接口）6、一个长方体的棱长和是72厘米，它的长是9厘米，宽6厘米，它的表面积是多少平方厘米？长方体和正方体表面积练习题1、填空。

(3）一个长方体的长是6分米，宽1。

5分米,高3分米，它的表面积是( )平方分米.（4)一个正方体的棱长是0.5分米，它的表面积是（）平方分米。

2021最新人教版数学五年级下册长方体和正方体的体积《整理与复习》优质课件

人教版数学五年级下册
3 长方体和正方体
3 长方体和正方体的体积
整理和复习
人教版数学五年级下册
1
体积的意义和体积单位：
物体所占空间的大小叫做物体的体积。计量体积要用体积单位，常用的体积单位有立方厘米、立方分米和立方米，可以分别写成 cm ³、 dm ³和 m ³。
2
长方体和正方体体积计算公式:
9
7. 算一算。
4³= 64 4×3 = 12 4+4+4 = 12
8²= 64 8×2 = 16 8+8 = 16
10
8. 建筑工地要挖一个长 50m、宽 30m、深 50cm的长方体土坑，一共要挖出多少方的土？ 50cm = 0.5m 50×30×0.5 = 1500×0.5 = 750（m³）= 750方答：一共要挖出 750方的土。
50800cm³ 6.039m² 1500dm
5080dm³ 603900cm² 15m
5080000cm³ 60.39m² 150dm
27
7. 一个长方体的无盖水族箱，长是 6 m，宽是 60 cm，
高是 1.5 m。这个水族箱占地面积有多大？需要用多
少平方米的玻璃？它的体积是多少？ 60 cm = 0.6 m 6×0.6 = 3.6（m²）
答：这面墙一共用了 36000 块积木。
25
5. 学校运来 7.6m³，铺在一个长 5 m、宽 38dm的沙坑里，可以铺多厚？
38dm = 3.8m 7.6÷(5×3.8)
= 7.6÷19
= 0.4（m）答：可以铺 0.4m厚。
26
6. 请你圈出每组数据中与其他数据不相等的那个数。
（1）5.08m³ （2）6039dm² （3）1500cm

人教版五年级数学下册第三单元《长方体和正方体的体积》PPT课件

36立方厘米
24立方厘米
27立方厘米
要知道一个物体的体积，就要看这个物体含有多少个体积单位
物体含有多少个体积单位，体积就是多少。
二新课探究
?
长方体所占空间的大小叫做长方体的体积。长方体的体积可以怎样算呢？数体积单位个数的方法求长方体的体积。
下面的长方体都是用棱长1cm的小正方体摆成的，你知道这个长方体的体积吗？
答：这个铁球的体积是70立方分米。
用12个棱长为1厘米的小正方体摆出不同的长方体
长(厘米) 宽(厘米) 高(厘米) 正方体的个数体积(厘米3)
第一个长方体
第二个长方体
第三个长方体
第四个长方体
长 12 cm
高 1 cm
宽 1 cm
高 1 cm 长 6 cm
宽 2 cm
高 1 cm 长 4 cm
?
正方体的体积怎么样计算呢？正方体的是特殊的长方体是长宽高都相等的长方体。
棱长
棱长
棱长
正长方体的体积＝棱长长 × 棱宽长 ×棱高长
棱长a a棱长
棱a长
正方体的体积V ＝= 棱a长长a×a棱宽长 ×棱高长 V = a3
V = a3 3a
a×a×a
{
a+a+ 3 ×a
a
比较a×3和a3 a×3表示3和a相乘 a3表示3个a相乘
一个长方体,长7cm,宽4cm,高3cm,它的体积是多少?
V=abh
=7×4×3 =84(cm3)
计算下面长方体的体积
3 分米
0.8 分米 2 分米
6米 2. 2 米 0. 4 米
V = abh = 2×0.8×3 = 4.8（立方分米）

人教版小学五年级数学下册长方体和正方体表面积和体积解决问题专项训练试题(含答案)

人教版五年级数学下册长方体和正方体表面积和体积解决问题专项训练（50道含答案）1.学校活动室长15米，宽8米，高5米，门窗面积共24平方米。

要把活动室的天花板和四周的墙刷上涂料，一共要刷多少平方米?2.一种无盖的长方体水箱,长2.5dm,宽2.5dm,高3.5dm,制作一个这样的水箱,至少需要白铁皮多少平方分米?3.如图，这是一个铝合金框组成的鱼缸，侧面的每个面都是正方形，且边长为25厘米。

这个鱼缸的侧面准备全用玻璃，那么玻璃的总面积和铝合金框的总长度各是多少?4.如图，求这个正方体的表面积.5.爸爸买了一个长为30cm、宽为20cm、高为15cm的长方体礼盒,里面装有妈妈爱吃的长方体形状的花生酥,每块花生酥长5cm,宽3cm,高2cm。

（1）礼盒用彩纸包装,需要多少彩纸?(重叠部分不计算)（2）这个礼盒最多能装多少块花生酥?6.纸盒厂生产一种正方体纸板箱,棱长为40cm,做一个纸盒要多少平方厘米的纸板?它占空间多少立方厘米?合多少立方分米?7.有一个长8厘米，宽6厘米，高5厘米的长方体零件，在每个面的正中间挖去一个棱长为2厘米的小正方体，这个零件的体积与表面积各是多少?8.一个长方体形状的游泳池,长50m,宽30m,深2m。

要给游泳池的底面和四壁抹一层水泥,如果每平方米用水泥12千克,22吨水泥够不够用?9.有一个正方体木块,把它分成两个长方体木块后,表面积增加了24cm2,这个正方体木块原来的表面积是多少平方厘米?10.用纸皮做一个长1.2米、宽20分米、高60厘米无盖的长方体箱子用来堆放同学们收聚的矿泉水空瓶，至少要用多少平方分米的纸皮?11.一个集装箱长9米，宽3.2米，高2.5 米。

（1）制作这样一个集装箱至少需要多少平方米的钢板？（2）这个集装箱的容积大约是多少立方米？(箱壁厚度忽略不计)12.用240厘米唱的铁丝做一个最大的正方体框架，然后用纸板将6个面包起来做一个正方体纸盒，至少需要多少平方厘米纸板？这个纸盒的体积是多少立方厘米？13.求下面组合图形的面积．(单位：厘米)14.一个正方体的棱长之和是48厘米，那么它的表面积是多少平方厘米？15.一个正方体的表面积是48平方米，它的一个面的面积是多少平方米？16.做一个棱长为4分米的正方体无盖纸盒，至少需要用硬纸多少平方分米？17.小亚的房间长4.2米，宽3.5米，高3米，除去门窗的面积4.5平方米，房间的墙壁和天花板都贴上墙纸，这个房间至少需要多少平方米墙纸？18.一个长方体的食品盒长10厘米，宽6厘米，高13厘米．如果围着它贴一圈商标纸(上下面不贴)，这张商标纸的面积至少要多少平方厘米？19.五年级一班的教室长9米、宽7.2米，学校计划暑假把四面墙粉刷绿色的墙围，要求从地面起1.1米高，计算一下这间教室粉刷墙围的面积是多少平方米.如果每平方米的粉刷费是5元，则粉刷这间教室需要多少钱？20.把一根144厘米的铁丝焊接成一个正方体框架，再在外面糊一层纸，糊纸的面积是多少平方米？21.如图，求这个长方体的表面积.22.做一个长5厘米、宽4厘米、高3厘米的长方体纸盒，至少要用多少平方厘米的硬纸板？23.一块正方体魔方的棱长是8厘米，它的表面积是多少？24.做一个没有盖的长方体玻璃缸，长60厘米，宽60厘米，高40厘米，共需要玻璃多少平方厘米？合多少平方米？25.一间教室长10米、宽6米、高4米，门窗面积为19.6平方米，要粉刷教室的四壁和顶棚，如果每平方米用涂料0.25千克，则共需要涂料多少千克？26.有一个棱长10厘米的正方体包装盒，在它的四壁贴上商标纸，这张商标纸的面积是多少？27.一个长方体玻璃钟罩，长15厘米，宽10厘米，高16厘米，它的表面积是多少平方厘米？28.一间教室长9 米，宽7 米，高3 米。

人教版五年级数学下册第三单元长方体和正方体的体积——体积单位间的进率(l两课时)

21>18，可以装下。
2.一个长方体包装盒，从里面量长 28 厘米，宽 20
厘米，体积 8.96 立方分米。用它包装一个长 25 厘
米，宽 15 厘米、高 18 厘米的玻璃器皿，是否可以
装得下？
方法一
8.96 dm³= 8960 cm³ 25×15×18 ＝ 6750（cm³） 6750 cm3＜8960 cm3 所以装得下。
42×5×0.1 = 21（dm3） 21dm3 = 0.021 m3
体积单位间的进率（2）
状元成才路
R·五年级下册
一基础复习回顾
3m3=_3_0_0_0__dm3 4.5dm3=_4_5_0_0__cm3 700dm3=__0_.7__m3 95cm3=_0_._0_9_5_dm3 2300cm3=__2_.3__dm3 3.5dm3=_3_5_0_0__cm3 3020立方厘米=__3_.0_2__立方分米 2.05立方米=__2_0_5_0_0_0_0_立方厘米
1 m3 = 1000 dm3
下面是我们学过的计量单位，请把下表补充完整。
单位名称
相邻两个单位间的进率
长度米、分米、厘米
面积
平方米、平方分米、平方厘米
体积
立方米、立方分米、立方厘米
10 100 1000
三理解应用，巩固提高
（1）3.8 m3 是多少立方分米？想：1 m3＝1000 dm3 3.8 m3＝__3_8_0_0_dm3
2.在 6085 dm2，6.085 m2，608500 cm2，60.85 m2
这四个数据中，相等的数据有（ C
D.4
【选自教材P37 练习八第10题】
30×30×30÷（20×20×10）＝6.75（盒）最多 6 盒，竖着放 4 盒，横着放 2 盒。

(完整版)新人教版五年级数学下册各单元知识点总结

(完整版)新人教版五年级数学下册各单元知识点总结(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（(完整版)新人教版五年级数学下册各单元知识点总结(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为(完整版)新人教版五年级数学下册各单元知识点总结(word版可编辑修改)的全部内容。

人教版五年级数学下册知识点班级: 姓名：第一单元观察物体1、由几个大小相同的小正方体摆成的立体图形,从同一个方向观察，看到的图形可能是相同的,也可能是不同的。

根据一个方向看到的图形摆立体图形，有多种摆法。

2、从同一个方向观察物体最多只能看到三个面。

几何视图一般是根据三个方向观察到的形状进行绘制。

3、根据两个方向观察到的形状能确定所用小正方体的个数。

根据三个方向观察到的形状摆小正方体结果只有一种。

第二单元因数和倍数1、在整数除法中，如果商是整数而没有余数，我们就说被除数是除数的倍数,除数是被除数的因数。

因数和倍数是相互依存的，不能单独存在。

）2、注意：为了方便，在研究因数和倍数时候，我们所说的数指的是自然数(一般不包括0）3、找因数的方法：①乘法②除法; 找倍数的方法：逐次乘自然数。

4、①一个数的最小因数是1，最大因数是它本身.一个数的最小倍数是它本身，没有最大的倍数。

②一个数的因数的个数是有限的,一个数的倍数的个数是无限的。

一个数的最大因数和最小倍数是相等的都是它本身.③1是所有非0自然数的因数。

也是任一自然数（0除外）的最小因数。

④一个数的因数至少有1个,这个数是1。

⑤一个数的因数都小于等于他本身，一个数的倍数都大于等于他本身。

五年级下册数学_2长方体与正方体的表面积与体积人教版(39张)精品课件

（2）30×20×3÷6=1800÷6=300（分钟）答：200分钟后水深能到达2m，300分钟后能将池塘注满水．解：（1）30×20×2÷6=1200÷6=200（分钟）
（2）30×20×3÷6=1800÷6=300（分钟）答：200分钟后水深能到达2m，300分钟后能将池塘注满水．这个游泳池可装多少立方米的水？ 5平方分米= （）平方厘米先求出假山和水一共的体积：46×25×28=32200（立方厘米）拼成的这个长方体的表面积比原来16个小正方体的表面积之和少了多少平方分米？
（2）同理，用池塘的容积，除以每分钟注水量6立方米，即可求出注水的时间．
29
真题训练营
2.小明家门前有一个长30m，宽20m，深3m的池塘，现在要养鱼，需要往池塘注水，如果每分钟能注水6m3，那么多少分钟后水深能到达 2m，多少分钟后能将池塘注满水？解：（1）30×20×2÷6=1200÷6=200（分钟）
没第？三关---实物5实0验×班25×2=2500（立方米）
6
旧识回顾
在一个长60cm,宽30cm的水箱中放入两个大小一样的西瓜（西瓜完全浸没），水面上升了8cm,平均每个西瓜的体积是多少？
7
旧识回顾
在一个长60cm,宽30cm的水箱中放入两个大小一样的西瓜（西瓜完全浸没），水面上升了8cm,平均每个西瓜的体积是多少？解：根据长方体体积公式：长×宽×高
14
3.长方体与正方体的体积之会旧友
什么是体积：物体所占空间的大小叫做物体的体积计量体积要用体积单位：常用的体积单位有立方厘米(cm^3)、立方分米(dm^3)、立方米(m^3)
15
3.制胜宝典
长方体体积=长×宽×高 (V=abh)或底面积×高(V=sh) 正方体体积=棱长×棱长×棱长(V=a*a*a) • 长方体或正方体底面的面积叫做底面积

(人教版)五年级数学下册长方体和正方体的表面积和体积

（人教版）五年级数学下册长方体和正方体的表面积和体积（人教版）五年级数学下册长方体和正方体的表面积和体积班级姓名分数一、填空题。

1.一个长方体框架长8厘米，宽6厘米，高4厘米，做这个框架共要（）厘米铁丝，是求长方体（），在表面贴上塑料板，是求长方体（），在里面能盛（）升水是求（），这个盒子有（）立方米是求（）。

长方体的短就是6厘米，阔就是4厘米，低就是4厘米，它的棱长总和就是（）厘米，六个面中最小的面积就是（）平方厘米，表面积就是（）平方厘米，体积就是（）立方厘米，（）条棱成正比。

2.一瓶可乐的容积大约是230（）；一个雪糕的体积是20（）；一台冰箱的容积大约是180（）；一瓶眼药水约有12（）。

3.1立方分米的1个正方体可以分为（）个1立方厘米的小正方体，如果把这些大正方体排在一排，一共短（）分后米。

4.用长2厘米、宽1厘米、高1厘米的长方体木块拼成一个正方体，至少用（）个这样的长方体。

拼成的正方体的表面积是（）平方厘米。

5.搞一个长6分米，阔4分米，低1.5分米的抽屉，至少须要木板（）。

6．一根铁丝长36厘米，如果搞一个正方体框架，棱长就是（）厘米；如果搞一个低和阔都就是2厘米的长方体框架，短就是（）厘米。

7．一个长方体水池占地6平方米，他深1.5米，池内最多能容水（）升。

8．把一个棱长2分米的正方体，切成两个相等的长方体，表面积增加了（）。

9．至少（）个棱长2厘米的小正方体可以拼成一个大正方体。

10．一个长方体的长、阔、低各不断扩大了3倍，它的体积不断扩大了（）倍。

11．把5个棱长1厘米的小正方体拆成长方体，这个长方体的表面积就是（）。

12．一个长方体的玻璃缸，长4分米、宽3分米、高5分米，倒入水后量得水深3.5分米，倒入的水有（）升。

13.用两个长6厘米，阔3厘米，低1厘米的长方体拆成一个表面积尽可能大的正方体，这个拆成的长方体的表面积就是（）平方厘米。

14.一个长方体的体积是30立方厘米，长是5厘米，高是3厘米，宽是（）。

五年级数学下册长方体的表面积人教版ppt课件

为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
左左。
上
上
后前
下下
右右
前
为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
1.6
2、这题求长方体几个面的面积。
5个面的面积
自己独立解答：
0.75 0.5
方法一：
（0.75×0.5＋0.75×1.6＋0.5×1.6）×2－0.75×0.5
方法二： 0.75×1.6×2＋0.5×1.6×2＋0.75×0.5
为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
课前准备： 1. 任意一个长方体纸盒。 2. 一把剪刀。 3. 一支水彩笔。 4. 笔和练习本。
为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
左
上
后后
右
下
前、后每个面长＝长方体的长宽＝长方体的高
前
为深入学习习近平新时代中国特色社会主义思想和党的十九大精神,贯彻全国教育大会精神,充分发挥中小学图书室育人功能
左
上
后后
右
下
左、右每个面长＝长方体的宽宽＝长方体的高

人教版数学五年级下册体积和表面积

人教版数学五年级下册典型题讲解

人教版小学五年级数学下册长方体和正方体表面积和体积 解决问题专项训练试题(含答案)

人教版小学数学五年级下册 长方体和正方体的体积

人教版小学数学五年级下册第三单元《长方体和正方体》教材分析

五年级数学下册各单元知识点归纳(附常见题型

五年级下册数学课堂课件--长方体与正方体表面积人教版(38张)

新人教版小学数学五年级下册《长方体和正方体的表面积》精品教案

人教版五年级数学下册长方体和正方体表面积和体积 解决问题专项训练2(50道含答案)

五年级数学下册长方体和正方体的表面积练习题(人教版)

2021最新人教版数学五年级下册长方体和正方体的体积《整理与复习》优质课件

人教版五年级数学下册第三单元《长方体和正方体的体积》PPT课件

人教版小学五年级数学下册长方体和正方体表面积和体积 解决问题专项训练试题(含答案)

人教版五年级数学下册第三单元长方体和正方体的体积——体积单位间的进率(l两课时)

(完整版)新人教版五年级数学下册各单元知识点总结

五年级下册数学_2长方体与正方体的表面积与体积人教版(39张)精品课件

(人教版)五年级数学下册 长方体和正方体的表面积和体积

五年级数学下册长方体的表面积人教版ppt课件

人教版小学五年级数学下册长方体和正方体表面积和体积解决问题专项训练试题(含答案)

人教版小学数学五年级下册长方体和正方体的体积

人教版五年级数学下册长方体和正方体表面积和体积解决问题专项训练2(50道含答案)

人教版小学五年级数学下册长方体和正方体表面积和体积解决问题专项训练试题(含答案)

(人教版)五年级数学下册长方体和正方体的表面积和体积