高中数学知识清单手绘大招之第二部分

高中数学知识点完整结构图

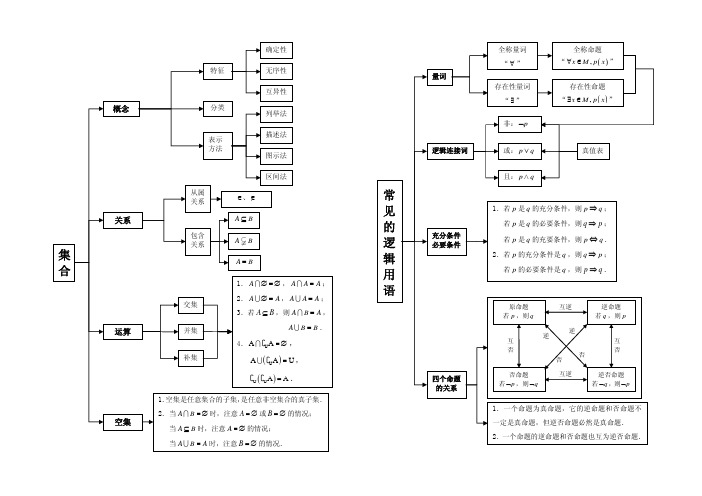
高中数学知识点1集合123412n x A x B A B A B A n A ∈∉⎧⎪⎪⎨⎪⎪⎩∈⇒∈⊆（）元素与集合的关系：属于（）和不属于（）（）集合中元素的特性：确定性、互异性、无序性集合与元素（）集合的分类：按集合中元素的个数多少分为：有限集、无限集、空集（）集合的表示方法：列举法、描述法（自然语言描述、特征性质描述）、图示法、区间法子集：若，则，即是的子集。

、若集合中有个元素，则集合的子集有个，注关系集合集合与集合{}00(2-1)23,,,,.4/n A A A B C A B B C A C A B A B x B x A A B A B A B A B A B x x A x B A A A A A B B A A B ⎧⎪⎧⎪⎪⎪⊆⎪⎪⎨⎪⊆⊆⊆⎨⎪⎪⎪⎩⎪⎪⊆≠∈∉⎪⊆⊇⇔=⎪⎩⋂=∈∈⋂=⋂∅=∅⋂=⋂⋂⊆真子集有个。

、任何一个集合是它本身的子集，即、对于集合如果，且那么、空集是任何集合的（真）子集。

真子集：若且（即至少存在但），则是的真子集。

集合相等：且定义：且交集性质：，，，运算{}{},/()()()-()/()()()()()()U U U U U U U U A A B B A B A B A A B x x A x B A A A A A A B B A A B A A B B A B A B B Card A B Card A Card B Card A B C A x x U x A A C A A C A A U C C A A C A B C A C B ⎧⎪⎨⋂⊆⊆⇔⋂=⎪⎩⎧⋃=∈∈⎪⎨⋃=⋃∅=⋃=⋃⋃⊇⋃⊇⊆⇔⋃=⎪⎩⋃=+⋂=∈∉=⋂=∅⋃==⋂=⋃，定义：或并集性质：，，，，，定义：且补集性质：，，，， ()()()U U U C A B C A C B ⎧⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⋃=⋂⎪⎪⎩⎩⎩⎩函数,,,A B A x B y f B A B x y x f y y x y →映射定义：设，是两个非空的集合，如果按某一个确定的对应关系，使对于集合中的任意一个元素，在集合中都有唯一确定的元素与之对应，那么就称对应：为从集合到集合的一个映射传统定义：如果在某变化中有两个变量并且对于在某个范围内的每一个确定的值，定义按照某个对应关系都有唯一确定的值和它对应。

高中数学_必修2知识点第一章到第二章 2

高中数学必修2知识点第一章空间几何体1.1柱、锥、台、球的结构特征1.2空间几何体的三视图和直观图1 三视图：正视图：从前往后侧视图：从左往右俯视图：从上往下2 画三视图的原则：长对齐、高对齐、宽相等3直观图：斜二测画法4斜二测画法的步骤：（1）.平行于坐标轴的线依然平行于坐标轴；（2）.平行于y 轴的线长度变半，平行于x ，z 轴的线长度不变；（3）.画法要写好。

5 用斜二测画法画出长方体的步骤：（1）画轴（2）画底面（3）画侧棱（4）成图1.3 空间几何体的表面积与体积（一）空间几何体的表面积1棱柱、棱锥的表面积：各个面面积之和2 圆柱的表面积3 圆锥的表面积2r rl S ππ+=4 圆台的表面积22R Rl r rl S ππππ+++=5 球的表面积24R S π=（二）空间几何体的体积1柱体的体积 h S V ⨯=底 2锥体的体积h S V ⨯=底31 3台体的体积 h S S S S V ⨯++=)31下下上上（ 4球体的体积 334R V π= 第二章直线与平面的位置关系2.1空间点、直线、平面之间的位置关系 2.1.1 1 平面含义：平面是无限延展的 2 平面的画法及表示（1）平面的画法：水平放置的平面通常画成一个平行四边形，锐角画成450，且横边画成邻边的2倍长（如图）（2）平面通常用希腊字母α、β、γ等表示，如平面α、平面β等，也可以用表示平面的平行四边形的四个顶点或者相对的两个顶点的大写字母来表示，如平面AC 、平面ABCD 等。

3 三个公理：（1）公理1：如果一条直线上的两点在一个平面内，那么这条直线在此平面内符号表示为 222r rl S ππ+= DC BA αA ∈LB ∈L => L α A ∈αB ∈α 公理1作用：判断直线是否在平面内（2）公理2：过不在一条直线上的三点，有且只有一个平面。

符号表示为：A 、B 、C 三点不共线 => 有且只有一个平面α，使A ∈α、B ∈α、C ∈α。

高中数学知识结构图全部

,
+∞
⎞ ⎠⎟
为减函数．
① 图像是双曲线；
当 k < 0 时，
② 定义域为{x x ∈ R, x ≠ 0} ，
值域为{y y ∈ R, y ≠ 0} ；
③ 奇函数． ④ 没有零点；
在 (−∞,0) 和 (0, +∞) 为增函数
①
值域为
⎡ ⎢ ⎣
4ac − 4a
b2
,
+∞
⎞ ⎟ ⎠
②
在
⎛ ⎜⎝
−∞,
−
顶点坐标是
⎛ ⎜ ⎝
−
b 2a
,
4ac − 4a
b2
⎞ ⎟ ⎠
④ 当 b = 0 时是偶函数；
⑤ 当 Δ > 0 ，有两个零点；当 Δ = 0 ，
有一个零点；当 Δ < 0 ，没有零点．
①
值域为
⎛ ⎜ ⎝
−∞,
4ac − 4a
b2
⎤ ⎥ ⎦
②
在
⎛ ⎜⎝
−∞,
−
b 2a
⎞ ⎟⎠
为增函数，
在
⎛ ⎜⎝
−
b 2a
辑
2．若 p 的充分条件是 q ，则 q ⇒ p ；
用
若 p 的必要条件是 q ，则 p ⇒ q ．
语
原命题若 p ，则 q
互否
互逆
逆
逆
否否
逆命题若 q ，则 p
互否
四个命题的关系
否命题若 ¬p ，则 ¬q
互逆
逆否命题若 ¬q ，则 ¬p
1．一个命题为真命题，它的逆命题和否命题不一定是真命题，但逆否命题必然是真命题． 2．一个命题的逆命题和否命题也互为逆否命题．

高中数学知识点思维导图--21张图梳理高中数学知识结构

高中数学知识点思维导图
----21张图理清高中数学知识结构
目录
一、集合与简易逻辑 (1)
二、函数与基本初等函数 (2)
三、导数及其应用 (3)
四、三角函数 (4)
五、解三角形与平面向量 (5)
六、数列 (6)
七、不等式 (7)
八、三视图与空间位置关系 (8)
九、立体几何 (9)
十、空间向量与立体几何 (10)
十一、直线的方程 (11)
十二、圆的方程 (12)
十三、直线系、圆系、直线与圆锥曲线关系 (13)
十四、圆锥曲线 (14)
十五、椭圆的定义与几何性质 (15)
十六、双曲线的定义与几何性质 (16)
十七、抛物线的定义与几何性质 (17)
十八、计数原理、二项式定理、推理与证明 (18)
十九、概率与统计 (20)
二十、复数 (21)
二十一、算法 (22)
一、集合与简易逻辑
二、函数与基本初等函数
三、导数及其应用
四、三角函数
五、解三角形与平面向量
六、数列
七、不等式
八、三视图与空间位置关系
九、立体几何
十、空间向量与立体几何
十一、直线的方程
十二、圆的方程
十三、直线系、圆系、直线与圆锥曲线关系
十四、圆锥曲线
十五、椭圆的定义与几何性质
十八、计数原理、二项式定理、推理与证明
十九、概率与统计
二十、复数
二十一、算法。

高中数学知识点完整结构图

高中数学知识点1集合123412n x A x B A B A B A n A ∈∉⎧⎪⎪⎨⎪⎪⎩∈⇒∈⊆（）元素与集合的关系：属于（）和不属于（）（）集合中元素的特性：确定性、互异性、无序性集合与元素（）集合的分类：按集合中元素的个数多少分为：有限集、无限集、空集（）集合的表示方法：列举法、描述法（自然语言描述、特征性质描述）、图示法、区间法子集：若，则，即是的子集。

、若集合中有个元素，则集合的子集有个，注关系集合集合与集合{}00(2-1)23,,,,.4/n A A A B C A B B C A C A B A B x B x A A B A B A B A B A B x x A x B A A A A A B B A A B ⎧⎪⎧⎪⎪⎪⊆⎪⎪⎨⎪⊆⊆⊆⎨⎪⎪⎪⎩⎪⎪⊆≠∈∉⎪⊆⊇⇔=⎪⎩⋂=∈∈⋂=⋂∅=∅⋂=⋂⋂⊆真子集有个。

、任何一个集合是它本身的子集，即、对于集合如果，且那么、空集是任何集合的（真）子集。

真子集：若且（即至少存在但），则是的真子集。

集合相等：且定义：且交集性质：，，，运算{}{},/()()()-()/()()()()()()U U U U U U U U A A B B A B A B A A B x x A x B A A A A A A B B A A B A A B B A B A B B Card A B Card A Card B Card A B C A x x U x A A C A A C A A U C C A A C A B C A C B ⎧⎪⎨⋂⊆⊆⇔⋂=⎪⎩⎧⋃=∈∈⎪⎨⋃=⋃∅=⋃=⋃⋃⊇⋃⊇⊆⇔⋃=⎪⎩⋃=+⋂=∈∉=⋂=∅⋃==⋂=⋃，定义：或并集性质：，，，，，定义：且补集性质：，，，， ()()()U U U C A B C A C B ⎧⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎧⎪⎨⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⎪⎪⎧⎪⎪⎪⎪⎪⎪⎪⎨⎪⎪⎪⎪⎪⋃=⋂⎪⎪⎩⎩⎩⎩函数,,,A B A x B y f B A B x y x f y y x y →映射定义：设，是两个非空的集合，如果按某一个确定的对应关系，使对于集合中的任意一个元素，在集合中都有唯一确定的元素与之对应，那么就称对应：为从集合到集合的一个映射传统定义：如果在某变化中有两个变量并且对于在某个范围内的每一个确定的值，定义按照某个对应关系都有唯一确定的值和它对应。

高一数学第二张知识点框架图

高一数学第二张知识点框架图高一数学第二章知识点框架图高一数学的第二章主要涉及到函数的基本概念、性质与图像以及反函数的相关内容。

下面将以框架图的形式进行论述。

一、函数的基本概念1. 函数的定义函数是一种特殊的关系，每个自变量x都对应唯一的因变量y。

2. 函数的表示方法（1）显式表示法：y = f(x)，其中f(x)表示函数关系。

（2）隐式表示法：F(x, y) = 0，其中F(x, y)表示函数关系。

二、函数的性质与图像1. 定义域和值域（1）定义域：自变量x的取值范围。

（2）值域：因变量y的取值范围。

2. 奇偶性与周期性（1）奇函数：f(-x) = -f(x)，图像关于原点对称或关于原点旋转180°对称。

（2）偶函数：f(-x) = f(x)，图像关于y轴对称或关于原点旋转360°对称。

（3）周期函数：f(x + T) = f(x)，其中T为正常数，图像在区间[a, a + T]内完全相同。

3. 单调性与极值（1）单调增函数：f(x1) < f(x2)（x1 < x2），图像从左向右递增。

（2）单调减函数：f(x1) > f(x2)（x1 < x2），图像从左向右递减。

（3）极大值：f(x)在某段区间上的值大于或等于该区间内任意其他点的函数值。

（4）极小值：f(x)在某段区间上的值小于或等于该区间内任意其他点的函数值。

三、反函数1. 反函数的定义若函数f的值域为Y，对于Y中的任一元素y，若存在唯一的x使得f(x) = y，则称x是函数f的反函数g的值，记作g(y) = x。

2. 图像与性质（1）函数与反函数的图像关于直线y = x对称。

（2）若函数f在[a, b]上单调递增（或递减），则其反函数在[f(a), f(b)]上单调递增（或递减）。

总结：高一数学的第二章主要介绍了函数的基本概念、性质与图像以及反函数的相关内容。

在函数的基本概念部分，我们了解到函数是一种特殊的关系，每个自变量对应唯一的因变量；函数可以用显式表示法或隐式表示法来表示。

高中数学知识梳理----13张图理清高中数学知识结构

高中数学知识梳理
----十三张图理清高中数学知识结构
目录
一、集合与简易逻辑 (1)
二、函数与基本初等函数 (2)
三、导数及其应用 (3)
四、三角函数 (4)
五、平面向量 (5)
六、数列 (6)
七、三视图与立体几何 (7)
八、立体几何 (8)
九、空间向量与立体几何 (9)
十、直线的方程 (10)
十一、圆的方程 (11)
十二、直线系、圆系、直线与圆锥曲线关系 (12)
十三、圆锥曲线 (13)
一、集合与简易逻辑
二、函数与基本初等函数
三、导数及其应用
四、三角函数
五、平面向量
六、数列
七、三视图与立体几何
八、立体几何
九、空间向量与立体几何
十二、直线系、圆系、直线与圆锥曲线关系
十三、圆锥曲线。

高中数学知识点总结图框架图

高中数学知识点总结图框架图一、代数1. 集合与函数概念- 集合的表示与运算- 函数的定义与性质- 常见函数（线性函数、二次函数、幂函数、指数函数、对数函数、三角函数）2. 代数式的运算- 整式的加减乘除- 因式分解- 分式的运算- 二次根式的运算3. 方程与不等式- 一元一次方程与不等式- 二元一次方程组- 一元二次方程- 不等式及其解集- 绝对值不等式4. 函数的应用- 函数的图像与性质- 函数的最值问题- 函数的单调性与周期性- 反函数与复合函数二、几何1. 平面几何- 点、线、面的基本性质- 三角形的性质与分类- 四边形的性质与计算- 圆的性质与方程- 相似与全等的判定与应用2. 空间几何- 空间图形的基本性质- 空间直线与平面的位置关系- 空间角的计算- 立体图形的表面积与体积3. 解析几何- 坐标系的建立与应用- 直线与圆的方程- 圆锥曲线（椭圆、双曲线、抛物线）的方程与性质三、概率与统计1. 概率论基础- 随机事件与概率的定义- 概率的计算与加法定理- 条件概率与乘法定理- 事件的独立性与贝叶斯定理2. 统计初步- 数据的收集与整理- 描述性统计（平均数、中位数、众数、方差、标准差） - 概率分布与正态分布- 抽样与估计四、数学思维与方法1. 逻辑推理- 演绎推理与归纳推理- 数学归纳法2. 数学证明- 直接证明与间接证明- 反证法3. 问题解决策略- 分类讨论- 转化与化归- 函数与方程思想以上框架图总结了高中数学的主要知识点，涵盖了代数、几何、概率与统计以及数学思维与方法四个方面。

每个部分都细分为若干小节，详细列出了各知识点及其内在联系。

通过这样的框架图，学生可以系统地复习和掌握高中数学的核心内容，为进一步的数学学习打下坚实的基础。

【高考数学】全部知识点结构图汇总

高中数学全部知识点结构图汇总1、集合、映射、函数、导数及微积分2、三角函数与平面向量3、数列与不等式4、解析几何5、立体几何6、统计与概率7、其他部分内容菊怒放秋菊傲骨秋色迷人秋色宜人金桂飘香秋天的景色果实,累累北雁南飞, 满山红叶五谷丰登芦花飘扬冬天天寒地冻北风呼啸滴水成冰寒冬腊月瑞雪纷飞冰天雪地冬天的景色冰封雪盖漫天飞雪白雪皑皑冰封大地冰天雪地早晨东方欲晓旭日东升万物初醒空气清醒雄鸡报晓晨雾弥漫晨光绚丽中,午烈日当头丽日临空艳阳高照万里无云碧空如洗傍晚日落西山夕阳西斜残阳如血炊烟四起百鸟归林华灯初上夜幕低垂日薄西山夜晚夜深人静月明星稀夜色柔美夜色迷人深更半夜漫漫长夜城镇风光秀丽人山人海车水马龙宁静和谐村庄草木苍翠竹篱瓦舍山幽路辟小桥流,水大楼、饭店直指青云古色古香青砖素瓦耸入碧云工厂, 机器轰鸣铁流直泻热气腾腾钢花飞溅商店粉饰一新门可罗雀冷冷清清错,落有致馆场富丽堂皇设施齐全气势雄伟金碧辉煌学校风景如画闻名遐迩桃李满天下车站、码头井然有序杂乱无章布局巧妙错落有致街道宽阔平坦崎岖不平拥挤不堪畅通无,阻花花红柳绿,花色,迷人花香醉人花,枝招展百花齐放百花盛开百花争艳, 绚丽多彩五彩缤纷草绿草如, 标准答案一、填空题。

（每空1分, , , , 共,22分）1、4120500000 41.205 2092 2、3、12 4、14 32 7:7、1080cm2 8、, 6 9、2a2 10、3 11、3:2 12、558 810 13、20 14、18 ,二、判断题。

（对的打“√”, 错的打“×”）, （共5分）15、×, 16、√17、√18、×19、√, 三、选择（将正确答案的字母填入括号里）。

（5份）20、A 21、B 22、B 23、C 24、B 四、计算。

（30分,）28、3、3 62 6、6 第(1)题画图正确计2分, 数对表示正确计2分29、表面积：8×8×＋4×4×4＋2×2×4体积：8×8×8＋4×4×4＋×2×2 30、d=16.56÷（1 3.14)＝4dm r=2dm 容积:3.14×22×4= 六、解决问题。

【高中】数学超全知识点结构图汇总,扫清三年知识点,建议收藏!

高中各科学习具有知识量大、理论性强、系统性强、综合性强以及能力要求高五个方面的特点。

然而，知识点是零乱的，不利于记忆和掌握。

只有把它们串起来，形成一个体系，才有助于快速高效掌握知识。

我们需要做的，就是找到并运用一定的方法（尤其是思维方法）用“红线”把知识“串”起来。

今天，老师为大家汇集整理了高中数学知识框架图，方便同学们整体把握知识之间的联系。

如果都掌握了，你的学习成绩一定会更上一层楼！！
集合、映射、函数、导数及微积分
三角函数与平面向量
数列与不等式
解析几何
立体几何
统计与概率
其他部分内容
延伸阅读
新高考的人才选拔机制
痛彻心扉：教师的十大痛苦，个个戳中老师们的“痛点”！
【小学】人教版PEP三至六年级英语电子课本
【初中】中考学霸：现代文阅读拿满分，靠的就是这18个套路
【高中】数学21种解题方法与技巧全汇总，太实用！
长按识别二维码关注考辅网
为您助力考试，助您金榜题名
(二维码自动识别)。

高中数学知识点脉络图

1.导数是平均变化率的极限，导数的几何意义；
理
解
2.极大值、极小值、最大值、最小值的概念；
3.函数在一点处的导数的定义和导数的几何意义；
1.多项式函数的单调区间、极大值、极小值及闭区间上的最大值和最小值；
掌
2.函数的导数公式，多项式函数的导数；
握
3.两个函数和、差、积、商的求导法则。
十三复数、推理与证明
1.两个（不扩展到三个）正数的算术平均数不小于它们的几何平均数的定理；
掌握
2.分析法、综合法、比较法证明简单的不等式；
3.二次不等式，简单的绝对值不等式和简单的分式不等式的解法。
六数列
•
•
1.数列通项公式的意义；
了
解
2.递推公式是给出数列的一种方法，并能根据递推公式写出数列的前几项；
1.数列的概念；
1. 双曲线的定义、标准方程、渐近线，几何性质；
解 2.圆锥曲线的第二定义；
1.数形结合的思想；
理解
2.抛物线的定义、标准方程和抛物线的简单几何性质；
掌
1.椭圆的定义、标准方程和椭圆的简单几何性质；
握
2.直线与椭圆的应用。
九直线、平面、简单几何体
1.棱柱、棱锥、棱台、球的概念，棱柱的性质，会画直棱柱的直观图；
高中数学知识点脉络图
高中数学
必修
代数集合函数Fra bibliotek不等式
三角函数
平面向量
数列
几何
直线. 平面. 简单几何体
直线与圆
圆锥曲线概率 .排列组合与二项式定理
选修导数与极限
统计复数. 推理与证明 .算法
一．集合、简易逻辑

高中数学知识点完整结构图

高中数学知识点完整结构图Revised at 2 pm on December 25, 2020.高中数学知识点1集合函数附：一、函数的定义域的常用求法：1、分式的分母不等于零；2、偶次方根的被开方数大于等于零；3、对数的真数大于零；4、指数函数和对数函数的底数大于零且不等于1；5、三角函数正切函数tan y x =中()2x k k Z ππ≠+∈；余切函数cot y x =中；6、如果函数是由实际意义确定的解析式，应依据自变量的实际意义确定其取值范围。

二、函数的解析式的常用求法：1、定义法；2、换元法；3、待定系数法；4、函数方程法；5、参数法；6、配方法三、函数的值域的常用求法：1、换元法；2、配方法；3、判别式法；4、几何法；5、不等式法；6、单调性法；7、直接法四、函数的最值的常用求法：1、配方法；2、换元法；3、不等式法；4、几何法；5、单调性法五、函数单调性的常用结论：1、若(),()f x g x 均为某区间上的增（减）函数，则()()f x g x +在这个区间上也为增（减）函数2、若()f x 为增（减）函数，则()f x -为减（增）函数3、若()f x 与()g x 的单调性相同，则[()]y f g x =是增函数；若()f x 与()g x 的单调性不同，则[()]y f g x =是减函数。

4、奇函数在对称区间上的单调性相同，偶函数在对称区间上的单调性相反。

5、常用函数的单调性解答：比较大小、求值域、求最值、解不等式、证不等式、作函数图象。

六、函数奇偶性的常用结论：1、如果一个奇函数在0x =处有定义，则(0)0f =，如果一个函数()y f x =既是奇函数又是偶函数，则()0f x =（反之不成立）2、两个奇（偶）函数之和（差）为奇（偶）函数；之积（商）为偶函数。

3、一个奇函数与一个偶函数的积（商）为奇函数。

4、两个函数()y f u =和()u g x =复合而成的函数，只要其中有一个是偶函数，那么该复合函数就是偶函数；当两个函数都是奇函数时，该复合函数是奇函数。

高中数学知识点完整结构图

高中数学知识点1集合函数附：一、函数的定义域的常用求法：1、分式的分母不等于零；2、偶次方根的被开方数大于等于零；3、对数的真数大于零；4、指数函数和对数函数的底数大于零且不等于1；5、三角函数正切函数tan y x =中()2x k k Z ππ≠+∈；余切函数cot y x =中；6、如果函数是由实际意义确定的解析式，应依据自变量的实际意义确定其取值范围。

二、函数的解析式的常用求法：1、定义法；2、换元法；3、待定系数法；4、函数方程法；5、参数法；6、配方法三、函数的值域的常用求法：1、换元法；2、配方法；3、判别式法；4、几何法；5、不等式法；6、单调性法；7、直接法四、函数的最值的常用求法：1、配方法；2、换元法；3、不等式法；4、几何法；5、单调性法五、函数单调性的常用结论：1、若(),()f x g x 均为某区间上的增（减）函数，则()()f x g x +在这个区间上也为增（减）函数2、若()f x 为增（减）函数，则()f x -为减（增）函数3、若()f x 与()g x 的单调性相同，则[()]y f g x =是增函数；若()f x 与()g x 的单调性不同，则[()]y f g x =是减函数。

4、奇函数在对称区间上的单调性相同，偶函数在对称区间上的单调性相反。

5、常用函数的单调性解答：比较大小、求值域、求最值、解不等式、证不等式、作函数图象。

六、函数奇偶性的常用结论：1、如果一个奇函数在0x =处有定义，则(0)0f =，如果一个函数()y f x =既是奇函数又是偶函数，则()0f x =（反之不成立）2、两个奇（偶）函数之和（差）为奇（偶）函数；之积（商）为偶函数。

3、一个奇函数与一个偶函数的积（商）为奇函数。

4、两个函数()y f u =和()u g x =复合而成的函数，只要其中有一个是偶函数，那么该复合函数就是偶函数；当两个函数都是奇函数时，该复合函数是奇函数。

高中数学知识清单手绘大招之第二部分

高中数学知识点完整结构图

高中数学_必修2知识点第一章到第二章 2

高中数学知识结构图 全部

高中数学知识点思维导图--21张图梳理高中数学知识结构

高中数学知识点完整结构图

高一数学第二张知识点框架图

高中数学知识梳理----13张图理清高中数学知识结构

高中数学知识点总结图框架图

【高考数学】全部知识点结构图汇总

【高中】数学超全知识点结构图汇总,扫清三年知识点,建议收藏!

高中数学知识点脉络图

高中数学知识点完整结构图

高中数学知识点完整结构图

高中数学知识结构图全部