上海海洋大学高数下册测试题
上海市2020〖人教版〗高一数学下册期末复习试卷6

上海市2020年〖人教版〗高一数学下册期末复习试卷创作人:百里安娜 创作日期:202X.04.01 审核人: 北堂王会创作单位: 明德智语学校一. 选择题(每小题5分,共60分)1.点sin 2015,cos 25()01A ︒︒位于( ) A .第一象限 B .第二象限 C .第三象限D .第四象限2.一个容量为N 的总体抽取容量为n 的样本,当选取简单随机抽样、系统抽样和分层抽样三种不同方法抽取样本时,总体中每个个体被抽中的概率分别为1p 、2p 、3p ,则( )A.123p p p =<B.123p p p >=C.132p p p =<D.132p p p ==3.已知非零向量a 、b ,满足a b ⊥,则函数()()f x ax b =+·(2)(R)ax b x -∈( ) A.是偶函数 B. 是奇函数 C. 有最大值 D.是增函数4.已知角βα,均为锐角,且,31)tan(,53cos -=-=βαα=βtan 则( )A .3B .31C .139 D .9135.实数m 是[]0,6上的随机数,则关于x 的方程240x mx -+=有实根的概率为( )A. 14B.13C.12D.236.已知tan 2α=,则22sin 3cos αα+=( )A. 51B.511 C. 521 D. 531 7.已知(cos 70,sin 70),(cos10,sin10),a b ==则a b -=( )A.0B.1C.2D.3 8.从某高中随机选取5名高三男生,其身高和体重的数据如下表所示:身高x (cm) 160 165 170 175 180 体重y (kg)6366707274根据上表可得回归直线方程ˆˆ0.56yx a =+,据此模型预报身高为172cm 的高三男生的体重为 ( )A .70.09kgB .70.12kgC .70.55kgD .71.05kg9.某从某次考试成绩中抽取若干名学生的分数,并绘制成如图1所示的频率分布直方图,样本数据分组为[)50,60、[)60,70、[)70,80、[)80,90、[]90,100.若用分层抽样的方法从样本中抽取分数在[]80,100范围内的数据16个,则其中分数在[]90,100范围内的样本数据有( )A.5个B.6个C.8个D.10个10.如图是某算法的程序框图,若任意输入[1,19]中的实数x ,则输出的x 大于49的概率为( )A .38B .23C .58D .71211.将函数()cos 2f x x =的图象向右平移4π个单位后得到函数()g x ,则()g x 具有性质( )A .最大值为1,图象关于直线2x π=对称 B .在(0,)4π上单调递增,为奇函数C .在3(,)88ππ-上单调递增,为偶函数 D .周期为π,图象关于点3(,0)8π对称 12.已知函数)3cos()(x a x f π=,a 为抛掷一颗骰子所得的点数,则函数)(x f 在]4,0[上零点的个数小于5或大于6的概率为( )A.32 B. 65 C. 52 D. 31 二、填空题(每小题5分,共20分) 13.若tan θ+1tan θ=4,则sin2θ=_________.14.若等腰梯形ABCD 中,//AB CD ,3AB =,2BC =,45ABC ∠=,则AC BD ⋅的值为____.15.执行如图所示的程序框图,则输出S 的值为.16.在直角ABC ∆中,2,23AB AC ==,斜边BC 上有异于端点两点B C 、的两点E F 、,且=1EF ,则AE AF ⋅的取值范围是.三、解答题(本大题共6小题,共70分.解答时应写出必要的文字说明、证明过程或演算步骤)17.(10分)某学校有男老师45名,女老师15名,按照分层抽样的方法组建了一个4人的学科攻关小组。
知到网课答案高等数学下经管类上海海洋大学版课后作业答案.docx

知到网课答案高等数学下经管类上海海洋大学版课后作业答案问:燃料棒在组件内排列规律答:对问:肖斯塔科维奇的《第七交响曲》时间最长的是哪一乐章:()答:一问:丁香结能在登山者在速降过程中来达到固定的效果。
()答:正确问:尽管在苹果馅饼中存在苹果籽,但它不会导致出现食品安全问题。
答:对问:人体肌肉之间的固定是依靠骨骼固定来完成的。
()答:错误问:案例:患者男性,38岁,发热5天,尿量减少3天,于2006年1月入院,查体:体温39OC,球结合膜充血,水肿,腋窝处皮肤可见条索状出血点,右臀部皮肤可见5cm×8cm瘀斑,浅表淋巴结未见肿大。
实验室检查:血小板21×109/L,BU34.5mmol/L。
下列哪项处理是不恰当的答:肥皂水灌肠问:案例“西游记团队的几点管理启示”告诉我们,作为一名优秀的管理者或领导者,要做到()?答:准确把握团队的前进目标和方向在完成目标的过程中坚定不移高超的用人艺术和技巧合理分工,用人所长问:案例表明,心脏病发作病例中,大部分的患者表现为猝死,之前没有心脏病的症状而突然发病。
()答:错问:案例的分析需要()的指导。
答:理论问:案例分析:一个处男,以前谈过女朋友,但没有破处。
新女友不是处女,和前三任都发生过性关系,而且诚实坦白,刚在一起时没有处女情节,但时间久了,处女情结越来越严重困扰他,每天都睡不着觉。
针对此案例中这个男生痛苦的原因,下列说法正确的是答:因为他的女友违背了宜慢不宜快原则男性心底里想要的是纯洁的女性刚开始不爱她,但是因为越来越爱,所以越来越在乎中国传统文化对女性贞洁态度影响较深问:下列哪些是按钮元件的正确状态和拥有的功能?答:一共四帧状态可做多个图层拥有点击热区拥有滤镜问:下列哪些是表示层的例子?()答:MPEGJPEGASCII问:下列哪些是病毒性肝炎的易感人群?答:婴幼儿问:下列哪些是产品部件之间的划分原则()?答:功能能生部件装配之后,还要能满足拆卸符合流水线生产要求问:下列哪些是澄江动物群发现的重要意义答:展现了动物多样性起源的突发性揭示了现代动物各大分支系统诞生的秘密潘多拉魔盒中的第一颗明珠问:中国菜的真谛,就是()俱全答:色香味型问:中国菜分为汉族菜、苗族菜、傣族菜等,划分的依据是()答:民族风格问:中国菜命名中的“荷叶鸡”的命名方式为()答:以料命名问:中国参加了第一届世博会。
高数C下整理

上海海洋大学试卷标准答案姓名:学号:专业班名:一、[/30103=⨯'] 选择:将您认为正确的答案代号填入下列表格内。
1、设5)2(,3)2(,1)0(/===f f f ,则dx x xf ⎰2//)(的值为( )A )12B )8C )7D )6 2、设定积分⎰=exdx I 11ln ,⎰=exdx I122ln ,则()A )12I I <B )122I I <C )122I I >D )12I I > 3、定积分dx e x ⎰1的值为( )A )eB )21C )21e D )24、由1,,===-x e y e y xx 所围成的平面图形的面积是( ) A )ee 1+B )e e 1-C )21-+e eD )21+-e e5、曲边梯形b y a y f x ≤≤≤≤≤0),(0绕y 轴旋转所形成的旋转体的体积为( ) A )dy y fba⎰)(2π B )dy y f b a⎰)(π C )dy y yf b a⎰)(π D )dy y yf ba⎰)(2π6、函数)1ln(y x z --=的定义域为() A ){}1,1),(<<y x y x ; B ){}1),(≤+y x y x ;C ){}1),(<+y x y x ; D )在xOy 平面上处处无定义。
7、二元函数 ),(y x f z = 在点),(00y x 处可导与可微的关系为( )A )可导必可微;B )可导一定不可微;C )可微必可导;D )可微不一定可导 8、⎰⎰=Ddxdy ( ) 其中 222:a y x D ≤+ A )2a B )π C )2 a π D )不能求9、级数∑∞=--11)1(n pn n 当( ) A )1>p 时条件收敛 B )10≤<p 时绝对收敛 C )10≤<p 时条件收敛 D )10≤<p 时发散10、求方程0)(2//=-y yy 的通解时,可令()A )p y =/,则///p y =B )p y =/,则dydppy =//C )p y =/,则dx dp py=//D )p y =/,则dydp p y ///= 二、[8163'=⨯'] 填空: 1、函数22),(yx xy y x f +=,则=),1(y x f 22xy x y +; 2、=++→→221)ln(limyx e x y y x ln 2;3、设)23ln(z y x u +-=,则=du 3232dx dy dzx y z-+-+;4、交换积分秩序:dy y x f dx xe),(ln 01⎰⎰=1(,)y eedy f x y dx ⎰⎰;5、若级数∑∞=1n nu收敛,则)(1n n nu u+∑∞=绝对收敛(填绝对收敛、条件收敛或发散)6、02///=+-y y y 的通解为xe x C C y )(+=;三、[//4058=⨯]计算:1、设v u z ln 2=,而y x v y x u 23,-==,求yz x z ∂∂∂∂,; 解:22221232ln 3ln(32)(32)z z u z v u x x u v x y x u x v x y v y y x y ∂∂∂∂∂=+=+⨯=-+∂∂∂∂∂-(4分) 222232222ln ()(2)ln(32)(32)z z u z v x u x x u v x y y u y v y y v y y x y ∂∂∂∂∂=+=-+⨯-=---∂∂∂∂∂-(8分) 2、),(22xye y xf z -=,其中f 具有连续二阶偏导数,求 22xz ∂∂;解:设22u x y =-,xyv e =,(,)z f u v =122xy z z u z v xf ye f x u x v x∂∂∂∂∂''=+=+∂∂∂∂∂(3分) 因此2122()(2)xy z z xf ye f x x x x∂∂∂∂''==+∂∂∂∂ 2121222xy xy f f f xy e f ye x x''∂∂''=+++∂∂(4分) 而11111122xy f f f u vxf ye f x u x v x'''∂∂∂∂∂''''=+=+∂∂∂∂∂ 22221222xy f f f u vxf ye f x u x v x'''∂∂∂∂∂''''=+=+∂∂∂∂∂(7分) 所以221212222xy xy f f z f x y e f ye x x x''∂∂∂''==+++∂∂∂2111122212222(2)(2)xy xy xy xy f x xf ye f y e f ye xf ye f ''''''''''=+++++ 222211112222244xy xy xy f x f xye f y e f y e f ''''''''=++++(8分) 3、⎰⎰+dxdy y x )(,D 是由2y x =,2-=x y 所围成的闭区域;解:2222221121()()2y y Dy x y dxdy dy x y dx x xy dy y +--+⎡⎤+=+=+⎢⎥⎣⎦⎰⎰⎰⎰⎰(5分) 2243131(42)22y y y y dy -=++--⎰ 9.45=(8分)4、⎰⎰+Ddxdy y x 222)(,D 是由x y 33=,x y =,122=+y x 及422=+y x (0,0≥≥y x )所围成的闭区域;解:令θθsin ,cos r y r x ==,则积分区域D 可表示为⎪⎩⎪⎨⎧<<<<2146r πθπ(2分)所以,22224416()Dx y dxdy d r rdr ππθ+=⎰⎰⎰⎰(6分) 621()1466r ππ⎡⎤=-⨯⎢⎥⎣⎦ 637728ππ==(8分) 5、求微分方程y y x '''=+的通解; 解:令,/p y =则,///p y = 原方程化为:x p p +=/(2分)因为)(111⎰+⎰⎰=---C dx xe e p dxdx)(1⎰+=-C dx xe e x xx e C x 11+--=(6分)从而2121)1(C e C x x dx e C x y x x++--=+--=⎰,即为所求通解。
上海海洋大学15-16高数C期末A卷

上海海洋大学试卷(本试卷不准使用计算器)诚信考试承诺书本人郑重承诺:我已阅读且透彻理解了“上海海洋大学学生考场规则”和“上海海洋大学学生违反校纪校规处理规定”,承诺在考试中自觉遵守,如有违反,按有关条款接受处理。
承诺人签名: 日 期:考生姓名: 学号: 专业班名:一、选择题 (每题3分,共21分) 1. 21lim 2n n →+∞⎛⎫++=+ ( ) (A)21; (B) 32; (C) 1; (D) 不存在. 2.设2)(0='x f ,则000(2)()limx f x x f x x∆→-∆-=∆ ( )(A) -2; (B) -4; (C) 1; (D) 不存在.3.若()y f x = 在(,)a b 内满足'''()0,()0,f x f x <> 则曲线()y f x = 在(,)a b 内是 ( )(A) 单调上升且是凹的; (B) 单调下降且是凹的;(C) 单调上升且是凸的; (D) 单调下降且是凸的.4.ln 2xdx =⎰( )(A) ln 22x x x C -+; (B) ln 42xx x C -+;(C) ln 2x x x C -+; (D) ln 2xx x C ++.5.下列等式正确的是( )(A) ()()d f x dx f x =⎰; (B) '()()f x dx f x C =+⎰; (C) ()()df x f x dx =⎰; (D) ()()df x dx f x C dx =+⎰. 6. 曲线24(1)2x y x +=-总共有几条渐近线 ( )(A) 1条; (B) 2条; (C) 3条; (D) 4条.7.设函数111()1xx e f x e -=+,则0x =是 )(x f 的 ( )(A) 可去间断点; (B) 跳跃间断点;(C) 第二类间断点; (D) 连续点.二、计算下列极限 (每题6分,共24分). 1.03sin 3lim (1cos )ln(12)x x x x x →--+ 2. 23(1)lim xt x e dt x -→-⎰3.)lim x xx →+∞4. 3lim 1x x x x +→∞⎛⎫⎪+⎝⎭三、计算下列导数 (共14分).1.(7分) 求曲线221169x y +=在处的切线方程.2.(7分) 设函数)(x f y =由参数方程221t x y t⎧=⎪⎨⎪=-⎩确定,求dx dy ,22dx y d .四、计算下列定积分 (20分).1.(6分)⎰exdx x 1ln 2.(6分)40⎰3.(8分)计算抛物线2y x = 与2y x = 所围成的图形的面积.五、(7分) 设函数()⎩⎨⎧>+≤=1,1,2x b ax x x x f ,为了使函数()x f 在1=x 处连续且可导,b a ,应取什么值?六、某商品的需求量Q 为价格P 的函数22150P Q -=。
上海海洋大学高数下册测试题

题目部分,(卷面共有100题,分,各大题标有题量和总分) 一、选择 (16小题,共分) (2分)[1] (3分)[2]二重积分Dxydxdy ⎰⎰(其中D :0≤y ≤x 2,0≤x ≤1)的值为 (A )16 (B )112 (C )12 (D )14答 ( ) (3分)[3]若区域D 为0≤y ≤x 2,|x |≤2,则2Dxy dxdy =⎰⎰=(A )0; (B )323 (C )643(D )256 答 ( )(3分)[4]设D 1是由ox 轴,oy 轴及直线x +y =1所圈成的有界闭域,f 是区域D :|x |+|y |≤1上的连续函数,则二重积分22(,)Df x y dxdy =⎰⎰__________122(,)D f x ydxdy ⎰⎰(A )2 (B )4 (C )8 (D )12答 ( ) (3分)[5]设f (x ,y )是连续函数,则二次积分011(,)x dx f x y dy -+⎰=(A)112111(,)(,)y dy f x y dx dy f x y dx ---+⎰⎰⎰(B)111(,)y dy f x y dx --⎰⎰(C)11111(,)(,)y dy f x y dx f x y dx ---+⎰⎰⎰(D)21(,)dy f x y dx -⎰⎰答 ( ) (3分)[6] 设函数f (x ,y )在区域D :y 2≤-x ,y ≥x 2上连续,则二重积分(,)Df x y dxdy⎰⎰可化累次积分为(A)201(,)x dx f x y dy -⎰(B)21(,)x dx f x y dy -⎰⎰(C)21(,)y dy f x y dx -⎰⎰(D)21(,)y dy f x y dx ⎰答 ( ) (3分)[7]设f (x ,y )为连续函数,则二次积分21102(,)y dy f x y dx ⎰⎰可交换积分次序为(A)1010(,)(,)dx f x y dy f x y dy +⎰(B)112102(,)(,)(,)dx f x y dy f x y dy f x y dy ++⎰⎰⎰(C)1(,)dx f x y dy ⎰(D)222cos 0sin (cos ,sin )d f r r rdr πθθθθθ⎰⎰答 ( ) (3分)[8]设f (x ,y )为连续函数,则积分212201(,)(,)x xdx f x y dy dx f x y dy -+⎰⎰⎰⎰可交换积分次序为 (A)12201(,)(,)y ydy f x y dx dy f x y dx -+⎰⎰⎰⎰(B)212201(,)(,)x xdy f x y dx dy f x y dx -+⎰⎰⎰⎰(C)120(,)y dy f x y dx -⎰(D)2120(,)xxdy f x y dx -⎰⎰答 ( ) (4分)[9]若区域D 为(x -1)2+y 2≤1,则二重积分(,)Df x y dxdy ⎰⎰化成累次积分为(A)2cos 0(,)d F r dr πθθθ⎰⎰(B)2cos 0(,)d F r dr πθπθθ-⎰⎰(C)2cos 202(,)d F r dr πθπθθ-⎰⎰(D)2cos 202(,)d F r dr πθθθ⎰⎰其中F (r ,θ)=f (r cos θ,r sin θ)r .答 ( )(3分)[10]若区域D 为x 2+y 2≤2x ,则二重积分22()Dx y x y dxdy ++⎰⎰化成累次积分为(A)2cos 202(cos sin )2cos d r rdr πθπθθθθ-+⎰⎰(B)2cos 30(cos sin )d r dr πθθθθ+⎰⎰(C)2cos 3202(cos sin )d r dr πθθθθ+⎰⎰(D)2cos 3222(cos sin )d r dr πθπθθθ-+⎰⎰答 ( ) (4分)[11]设777123[ln()],(),sin ()DDDI x y dxdy I x y dxdy I x y dxdy =+=+=+⎰⎰⎰⎰⎰⎰其中D 是由x =0,y =0,12x y +=,x +y =1所围成的区域,则I 1,I 2,I 3的大小顺序是 (A)I 1<I 2<I 3; (B)I 3<I 2<I 1; (C)I 1<I 3<I 2; (D)I 3<I 1<I 2.答 ( ) (5分)[12]设2211cos sin x y dxdyI x y +≤=++⎰⎰,则I 满足 (A)223I ≤≤ (B)23I ≤≤ (C)12D I ≤≤ (D)10I -≤≤答 ( ) (4分)[13]设12x y +=其中D 是由直线x =0,y =0,及x +y =1所围成的区域,则I 1,I 2,I 3的大小顺序为(A)I 3<I 2<I 1; (B)I 1<I 2<I 3; (C)I 1<I 3<I 2; (D)I 3<I 1<I 2.答 ( ) (3分)[14]设有界闭域D 1与D 2关于oy 轴对称,且D 1∩D 2=,f (x ,y )是定义在D 1∪D 2上的连续函数,则二重积分2(,)Df x y dxdy =⎰⎰(A)122(,)D f x y dxdy ⎰⎰ (B)224(,)D f x y dxdy ⎰⎰(C)124(,)D f x y dxdy ⎰⎰(D)221(,)2D f x y dxdy ⎰⎰ 答 ( )(3分)[15]若区域D 为|x |≤1,|y |≤1,则cos()sin()xy Dxe xy dxdy =⎰⎰ (A) e; (B) e -1; (C) 0; (D)π.答 ( ) (4分)[16]设D :x 2+y 2≤a 2(a >0),当a =___________时,.Dπ=答 ( ) 二、填空 (6小题,共分)(4分)[1]设函数f (x ,y )在有界闭区域D 上有界,把D 任意分成n 个小区域Δσi (i =1,2,…,n ),在每一个小区域Δσi 任意选取一点(ξi ,ηi ),如果极限 01lim(,)niiii f λξησ→=∆∑(其中入是Δσi (i =1,2,…,n )的最大直径)存在,则称此极限值为______________的二重积分。
上海海洋大学16-17高数C期末A卷(答案)
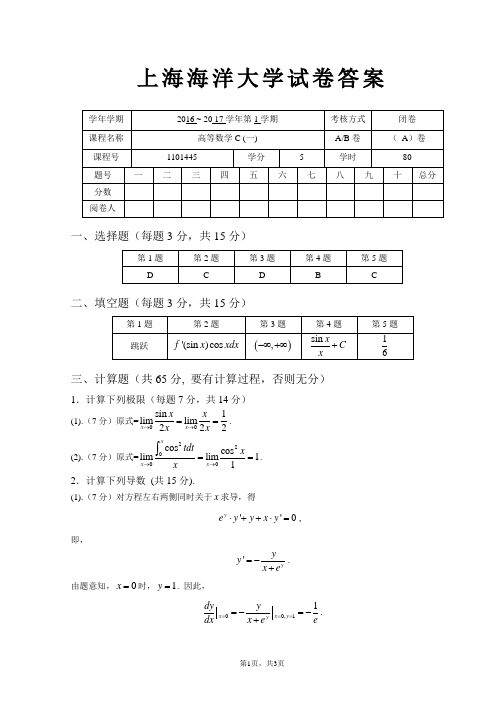
上海海洋大学试卷答案一、选择题(每题3分,共15分)二、填空题(每题3分,共15分)三、计算题(共65分, 要有计算过程,否则无分)1.计算下列极限(每题7分,共14分)(1).(7分)原式=00sin 1limlim 222x x x x x x →→==. (2).(7分)原式=2200cos cos limlim 11xx x tdt xx→→==⎰. 2.计算下列导数 (共15分).(1).(7分)对方程左右两侧同时关于x 求导,得''0y e y y x y ⋅++⋅=,即,'yyy x e=-+. 由题意知,0x =时,1y =. 因此,0,11x x y y dy y dxx e e====-=-+.(2).(8分)2//(1)1t tt dy dy dt e e dx dx dt t e t-===--; 222323/(32)/(1)32/(1)(1)t tt dy d dt d y t e t t dx e dx dx dt t e t -⎛⎫ ⎪---⎝⎭===--. 3. 计算下列定积分 (18分).(1).(6分)43322200cos 1sin cos cos cos |44d d πππϕϕϕϕϕϕ=-=-=⎰⎰;(2).(6分)111222112111|xxx e dx e d e e x x=-=-=-⎰⎰ (3).(6t =,则21x t =-,故8333223222(1)|42t t te dt t e e e ==-=-⎰⎰.4. (8分)设2,[0,1)(),[1,2].x x f x x x ⎧∈=⎨∈⎩求0()()x x f t dt ϕ=⎰在[0,2]上的表达式,并讨论()x ϕ在(0,2)内的连续性..解:由题意得32012201,01,013()31,12,126xxx x t dt x x x t dt tdt x x ϕ⎧⎧≤<≤<⎪⎪⎪==⎨⎨-⎪⎪+≤≤≤≤⎩⎪⎩⎰⎰⎰, 显然,()x ϕ在(0,1)和(1,2)内连续,又由于1(10)(10)(1)3ϕϕϕ-=+==,故()x ϕ在(0,2)内连续. 5. (10分) 某产品的总成本(万元)的变化率为()1C q '=(万元/百台),总收入(万元)的变化率为产量q (百台)的函数()5R q q '=-(万元/百台). (1) 求产量q 为多少时,利润最大?(2) 在上述产量(使利润最大)的基础上再生产100台,利润将减少多少?解: (1)利润函数为2001()()()('()'())(4)42q q L q R q C q R q C q dq q dq q q =-=-=-=-⎰⎰(万元),因此,4q =(百台)时利润最大。
上海市2020〖人教版〗高一数学下册期末复习试卷3

上海市2020年〖人教版〗高一数学下册期末复习试卷创作人:百里安娜 创作日期:202X.04.01 审核人: 北堂王会创作单位: 明德智语学校一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)1.函数y =sin 2x +cos 2x 是( )A .周期为π的偶函数B .周期为π的奇函数C .周期为2π的增函数D .周期为2π的减函数2.已知向量a =(1,3),b =(3,x ),若a ⊥b ,则实数x 的值为( )A .9 B. -9 C .1 D .-1zxxk3.已知{a n }是等差数列,前n 项和为S n ,a 1=120,公差d =-4,若S n ≤a n (n ≥2),则n 的最小值为( )zxxkA .60B .62C .70D .724.设|a |=5,|b |=4,a ·b =-10,则a 与b 的夹角为( )A .30°B .60°C .120°D .150° 5.若实数x ,y 满足⎩⎪⎨⎪⎧x -y +1≤0,x>0,则yx的取值范围是( )A .(0,1)B .(0,1]C .(1,+∞)D .[1,+∞)6.已知角θ的终边与单位圆交于点P 错误!-错误!,错误!错误!,则cos(π-θ)的值为( )A .-255B .-55C.55D.2557.已知数列{a n }是等比数列,且a n >0,公比q ≠1,则a 1+a 8与a 4+a 5的大小关系是( )A .a 1+a 8>a 4+a 5B .a 1+a 8≥a 4+a 5C .a 1+a 8<a 4+a 5D .a 1+a 8≤a 4+a 58.定义在R 上的函数f (x )既是偶函数又是周期函数,若f (x )的最小正周期为π,且当x ∈[0,π2]时,f (x )=sin x ,则f 错误!5π3错误!的值为( )A .-12B. -32C.32 D.129.若α,β均为锐角,sin α=255,sin(α+β)=35,则cos β等于( )A.255 B.2525C.255或2525D .-252510.下列结论中正确的是( )A .若ac >bc ,则a >bB .若a 8>b 8,则a >b C .若a >b ,c <0,则ac <bc D .若a <b ,则a >b二、填空题(本大题共5小题,每小题4分,满分20分)11.已知α∈错误!错误!,π错误!,且sin α=错误!,则tanα的值为____________.12.若三点A (2,2),B (a,0),C (0,4)共线,则a 的值等于_________.13.不等式(x +1)2(x -1)<0的解集为__________.14.在△ABC 中,角A ,B ,C 所对的边分别为a ,b ,c ,若c =2,b =6,B =120°,则a =________.15.设x ,y 满足约束条件⎩⎪⎨⎪⎧3x -y -6≤0x -y +2≥0x≥0,y≥0,若目标函数z =ax+by (a >0,b >0)的最大值为12,则2a+3b的最小值为________.三、解答题:本大题共6小题,满分80分.解答须写出文字说明、证明过程和演算步骤.16.(本题满分12分)已知函数f(x)=A sin(ωx+φ)错误!A>0,ω>0,0<φ<错误!错误!的周期为π,其图象上一个最高点为M错误!错误!,2错误!.(1)求f(x)的解析式;(2)当x∈[0,π4]时,求f(x)的最值及相应x的值.17.(本题满分14分)集合D={平面向量},定义在D上的映射f,满足对任意x∈D,均有f(x)=λx(λ∈R且λ≠0).(1)若|a|=|b|,且a与b不共线,试证明:[f(a)-f(b)]⊥(a+b);(2)若A(1,2),B(3,6),C(4,8),且f错误!错误!错误!=错误!,求f(AC→)·AB→.18.(本题满分14分)已知向量a=错误!-错误!,错误!错误!,错误!=a-b,错误!=a+b,△AOB是以O为直角顶点的等腰直角三角形.(1)求向量b;(2)求△AOB的面积.19.(本题满分14分)某工厂用两种不同的原料均可生产同一产品,若釆用甲种原料,每吨成本1 000元,运费500元,可生产产品90千克;若釆用乙种原料,每吨成本 1 500元,运费400元,可生产100千克.若每日预算总成本不得超过 6 000元,运费不得超过 2 000元,问此工厂每日最多可生产多少千克产品?20.(本题满分14分)已知数列{a n}的前n项和为S n,设a n是S n与2的等差中项,数列{b n}中,b1=1,b n+1=b n+2.(1)求a n,b n;(2)若数列{b n}的前n项和为B n,比较1B1+1B2+…+1Bn与2的大小;(3)令T n =b1a1+b2a2+…+bnan,是否存在正整数M ,使得T n <M 对一切正整数n 都成立?若存在,求出M 的最小值;若不存在,请说明理由.参考答案一、选择题(本大题共10小题,每小题5分,满分50分.在每小题给出的四个选项中,只有一项是符合题目要求的)19.(本题满分14分)设工厂每日需用甲原料x 吨,乙原料y 吨,可生产产品z 千克.则⎩⎪⎨⎪⎧1 000x +1 500y≤6 000,500x +400y≤2 000,x≥0,y≥0,即⎩⎪⎨⎪⎧2x +3y≤12,5x +4y≤20,x≥0,y≥0,画出可行域,如图所示.过直y 100+x 90=z .当直线)克千(y 100+x 90=z 目标函数,取得最大值z 时,⎝ ⎛⎭⎪⎫127,207A 交点02=y 4+x 5和21=y 3+x 2线千044产.工厂每日最多生)克千(440=207100·+12790·=max z 即克产品.创作人:百里安娜创作日期:202X.04.01 审核人: 北堂王会创作单位: 明德智语学校。
级(下)期中考试试卷(11学分)解答

第 1 页/共 6 页华东理工大学2023年年–2023年年学年第二学期 《高等数学(下)11学分》课程期中考试试卷 2023年年.4 开课学院:理学院, 专业:大面积, 考试形式:闭卷,所需时光 120 分钟考生姓名: 学号: 年级 任课教师一.填空题(本大题共11小题,每小题4分,共44分): 1、微分方程222'y x e yx y -=的通解为 。
答:C e xe e xx y +-=22412122、微分方程0''9)4(=+y y 的通解为 。
答:x C x C x C C y 3sin 3cos 4321+++=3、函数 z x yu )(= 对变量x 的偏导数 =x u 。
答:12)(--=z x x yx yz u4、设 ))arctan(,,(xyz e y xze f u z y +=,其中f 关于所有变量有一阶延续偏导数, 则=∂∂yu。
答:3222211f zy x xz f f xze y u y +++=∂∂ 5、设函数z z x y =(,)由方程 ),(yzxz f z = 所决定,其中f 关于所有变量有一阶延续偏导数,则∂∂zy= 。
答:21222yf f xy y zf ---6、设1)(-=⋅⨯c b a,则=+⨯+⋅)]()[(c b b a b 。
答: 17、函数)ln(22z y x u ++=在点)1,0,1(处最大的方向导数等于 。
答:228、微分方程 0'2''=+y xy 的通解=y 。
答: 21C xC y +-= 9、设平面π过直线⎩⎨⎧=+-=++04,05:z x z y x L 则原点到平面π距离d 的范围是 。
答: ]22,0[10、设),(y x z z =由方程2xyz e z =所决定,则=dz 。
答: dy xyze xz dx xyz e yz dz z z 2222-+-=11、求一个最低阶的常系数线性齐次微分方程,使得x 和x x cos sin +都是它的特解,则该常系数线性齐次微分方程为 。
09~10高数下试题

第 1 页 共 6 页上 海 海 事 大 学 试 卷2009 — 2010 学年第二学期期末考试《 高等数学A (二)》(A 卷) (本次考试不能使用计算器)班级 学号 姓名 总分(本大题分5小题, 每小题4分, 共20分)1、设f x y x y xy x y (,)=+-+-32231,则f y '(,)32=( ) (A) 41 (B) 40(C) 42 (D) 392、设圆域D :x 2+y 2≤1,f 是域D 上的连续函数,则答 ( )3、如果81lim1=+∞→nn n a a ,则幂级数∑∞=03n n n x a (A)当2<x 时,收敛; (B) 当8<x 时,收敛;(C) 当81>x 时,发散; (D) 当21>x 时,发散;答( )--------------------------------------------------------------------------------------装订线------------------------------------------------------------------------------------第 2 页 共 6 页4、设Ω为球体x 2+y 2+z 2≤1,f (x ,y ,z )在Ω上连续,I =x 2yzf (x ,y 2,z 3),则I =(A) 4x 2yzf (x ,y 2z 3)d v (B) 4x 2yzf (x ,y 2,z 3)d v(C) 2x 2yzf (x ,y 2,z 3)d v (D) 0 答 ( )5、设L 是圆周 x 2+y 2=a 2 (a >0)负向一周,则曲线积分( )二、填空题(将正确答案填在横线上) (本大题分5小题, 每小题4分, 共20分)1、设)ln(),,(222z y x z y x f ++=,则=-)2,1,1(f d gra2、=-=+++dz z y x xyz 处全微分在)1,0,1(,22223、设L 为圆周122=+y x ,则⎰=Lds x 24、如果幂级数n n x a ∑在x = -2处条件收敛,则收敛半径为R=5、曲面32=+-xy e z z 在(1,2,0)处切平面方程为三 计算题(必须有解题过程) (本大题分7小题,共 60分) 1、(本小题8分)已知22)1()1(ln -+-=y x u ,试求:2222yux u ∂∂∂∂+第 3 页 共 6 页2、(本小题8分)求函数223333y x y x z --+=的极值。
上海海洋大学概率论(共32页)

上海海洋大学试卷(shìjuàn)学年学期20 11 ~ 20 12 学年第 1 学期考核方式闭卷课程名称概率论与数理统计B A/B卷( A )卷课程号1106403学分 3 学时48题号一二三四五六七八九十总分分数阅卷人姓名(xìngmíng):学号:专业班名:一、填空题(本大题共7小题,每小题3分,总计(zǒngjì)21分)1. 已知P(A)=0.6, P(B|A)=0.3, 则P(A B)= __________2.一个(yīɡè)袋内有5个红球,3个白球,2个黑球,任取3个球恰为一红一白一黑的概率为_____3. 三个人独立地向一架飞机射击,每个人击中飞机的概率都是0.4,则飞机被击中的概率为__________4.已知连续型随机变量的概率密度为则P{X 1.5}=_______5.设随机变量X服从参数为的泊松分布,且,则______6. 设随机变量X服从二项分布B(5, 0.5),则E(2X+1)=______________7.已知X~N(0,1), , 且X与Y独立, 则服从________分布 (正态,,).二、选择题(在各小题四个备选答案中选出一个正确答案,填在题末的括号中,本大题共7个小题,每小题3分,总计21分)1. 某人射击(shèjī)三次,以A i表示(biǎoshì)事件“第i次击中目标”(i=1,2,3),则A1∪A2∪A3表示(biǎoshì)()A.“恰好(qiàhǎo)击中目标一次”B.“至少击中目标一次”C.“至多击中目标一次”D.“三次都击中目标”2. 设A、B相互独立,且P(A)>0,P(B)>0,则下列等式成立的是( )A.P(AB)=0B.P(A-B)=P(A)P()C.P(A)+P(B)=1D.P(A | B)=03. 设F(x)和f(x)分别为某随机变量的分布函数和概率密度,则必有( )A. f(x)单调不减B.C.D.4. 以下数列中,可以成为某一离散型随机变量的分布律的是()A.,k=1,2,…B.,k=0,1,2,…C.,k=0,1,2,…D.…5.设随机变量X~N(1,4),已知,则P{1≤X≤2}=( )A. 0.6915B. 0.1915C. 0.5915D. 0.39156. 设随机变量X的数学期望存在,则()A. 0B.C.D.7.样本X1,X2,X3取自总体X,E(X)=μ, D(X)=σ2, 则下列估计量中方差最小的是( )A. B.C. D.三、计算题(本大题共5小题,共计58分)1.(10分)设某地区男性居民中肥胖者占25%,中等者占60%,瘦者占15%,又知肥胖者患高血压病的概率为20%,中等者患高血压病的概率为8%,瘦者患高血压病的概率为2%,试求:(1)该地区成年男性居民患高血压病的概率;(5分)(2)若某成年男性居民患高血压病,则他属于肥胖者的概率有多大?(5分)2.(10分)已知随机变量(suí jī biàn liànɡ)X服从(fúcóng)区间(qū jiān)(0,1)上的均匀分布,Y=2X +1,求Y的概率密度函数。
知到答案大全高等数学下经管类上海海洋大学版满分考试答案.docx

知到答案大全高等数学下经管类上海海洋大学版满分考试答案问:企业的使命描述的是企业关注的市场。
()答:错误问:企业的所有权原则是企业运行无可争辩的基础前提。
答:正确问:企业的特征有()答:组织性商品性经济性独立性问:企业的投资人既可以是国家,也可以是法人,自然人。
()答:对问:企业的投资者也可以以固定资产进行投资,企业收到投资者投入的固定资产,在办理了固定资产移交手续之后,应按投资合同或协议约定的价值加上应支付的税费作为固定资产的入账价值,但合同或协议约定价值不公允的除外。
()答:对问:企业的外包决策首先考虑的问题有()。
答:资金需要量资本成本企业的风险态度问:企业的外源融资包括:()。
答:IPO银行借贷配股增发融资租赁问:企业的下列项目中可以在计算应纳税所得额时享受加计扣除优惠政策的是()。
答:开发新技术、新产品、新工艺发生的研究开发费用安置残疾人员及国家鼓励安置的其他就业人员所支付的工资问:企业的显著标志在于:它是价格机制的替代物,是一种替代市场进行资源配置的组织。
答:正确问:企业的现金流量包括经营活动产生的现金流量、投资活动产生的现金流量和筹资活动产生的现金流量。
答:正确问:企业的现金流越大越好答:错误问:企业的销售业务,只有在收取货款后,才能确认为销售收入实现。
答:×问:企业的性质不同对应聘者的哪一方面要求也不同:()答:政治面貌问:企业的性质分为股份有限公司和有限责任公司两种。
()答:对问:企业的性质分为有限责任公司和股份有限公司两种。
()答:√问:企业的隐含成本一般难以体现在会计的账目上。
答:正确问:企业的盈余公积可用于(?0?2?0?2?0?2)。
?0?2答:分派现金股利?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0? 2?0?2?0?2?0?2?0?2?0?2?0?2转增资本?0?2弥补亏损?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0? 2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2?0?2问:企业的营销活动不可能脱离周围环境而孤立地进行,企业营销活动要主动地去()。
高等数学A(二)B期末考卷及解答海大

高等数学A(二)B期末考卷及解答海大一、选择题(每题1分,共5分)1. 设函数f(x)在x=0处可导,且f'(0)=2,则下列选项中正确的是()A. lim(x→0) [f(x)f(0)]/x = 0B. lim(x→0) [f(x)f(0)]/x = 2C. lim(x→0) [f(x)f(0)]/x = 1D. lim(x→0) [f(x)f(0)]/x = 22. 设函数f(x)在区间[0,1]上连续,且满足0≤f(x)≤1,则下列选项中正确的是()A. ∫(0,1) f(x) dx = 0B. ∫(0,1) f(x) dx = 1C. ∫(0,1) f(x) dx = 0.5D. 无法确定3. 设矩阵A为3阶方阵,且|A|=3,则下列选项中正确的是()A. A可逆B. A不可逆C. A的行列式为0D. A的行列式为34. 设函数y=f(x)在点(x0,y0)处的切线方程为yy0=2(xx0),则下列选项中正确的是()A. f'(x0)=0B. f'(x0)=1C. f'(x0)=2D. f'(x0)不存在5. 设函数f(x)在区间[a,b]上可导,且f'(x)>0,则下列选项中正确的是()A. f(x)在[a,b]上单调递增B. f(x)在[a,b]上单调递减C. f(x)在[a,b]上取得最大值D. f(x)在[a,b]上取得最小值二、判断题(每题1分,共5分)1. 函数f(x)在x=0处可导,则f(x)在x=0处连续。
()2. 若函数f(x)在区间[a,b]上可导,则f(x)在[a,b]上一定连续。
()3. 矩阵A的行列式为0,则A不可逆。
()4. 二重积分的值与积分次序无关。
()5. 若函数f(x)在区间[a,b]上单调递增,则f'(x)>0。
()三、填空题(每题1分,共5分)1. 设函数f(x)=x^33x,则f'(x)=______。
上海海洋大学高数C期末A卷

上海海洋大学试卷(本试卷不准使用计算器)诚信考试承诺书本人郑重承诺:我已阅读且透彻理解了“上海海洋大学学生考场规则”和“上海海洋大学学生违反校纪校规处理规定”,承诺在考试中自觉遵守,如有违反,按有关条款接受处理。
承诺人签名:日期:考生姓名:学号:专业班名:一、选择题(每题3分,共15分)1.设A 为常数,0lim (),x x f x A →=则()f x 在0x 处()()A 一定有定义()B 一定无定义()C 有定义且0()f x A =()D 可以有定义也可以无定义2.若0lim2,(3)x x f x →=则0(2)lim x f x x→=()3.函数sin y x =在0x =处是()()A 连续又可导()B 不连续也不可导()C 不连续但可导()D 连续但不可导4.设()f x 的一个原函数是2,x e -则()f x =() 5.121(sin )x dx -=⎰()()A π()B 2π()C 23()D 0二、填空题(每题3分,共15分).1.已知函数11,1x x y e-=-则1x =是它的间断点;2.设(sin ),y f x =其中f 可导,则dy =;3.曲线26x y e x x =-+在区间是凹的;4.sin x dx x '⎛⎫= ⎪⎝⎭⎰;5.曲线y =y x =所围成图形的面积是_____________. 三、计算题(共65分,要有计算过程,否则无分) 1.计算下列极限(每题7分,共14分)(1).0ln(1sin )lim tan 2x x x→+;(2).200cos lim .tan xx tdt x →⎰ 2.计算下列导数(共15分).(1).(7分)设函数()y y x =由方程y e xy e +=所确定,求x dydx=;(2).(8分)设,,t tx te y e -⎧=⎨=⎩求dy dx ,22d ydx . 3.计算下列定积分(18分).(1).(6分)320sin cos d πϕϕϕ⎰;(2).(6分)1221xedx x⎰; (3).(6分)83⎰.4.(8分)设2,[0,1)(),[1,2].x x f x x x ⎧∈=⎨∈⎩求0()()x x f t dt ϕ=⎰在[0,2]上的表达式,并讨论()x ϕ在(0,2)内的连续性..5.(10分)某产品的总成本(万元)的变化率为()1C q '=(万元/百台),总收入(万元)的变化率为产量q (百台)的函数()5R q q '=-(万元/百台). (1)求产量q 为多少时,利润最大?(2)在上述产量(使利润最大)的基础上再生产100台,利润将减少多少? 四、证明题(共5分)利用罗尔定理证明拉格朗日中值定理:若函数()f x 在[,]a b 上连续,在(,)a b 内可导,则存在点(,),a b ξ∈使得()()()().f b f a f b a ξ'-=-。
上海海洋大学2017-2018学年第2学期线性代数试卷

上海海洋大学试卷姓名: 学号: 专业班名:一、填空题(每小题4分,共24分)1、四阶行列式中含有因子1334a a 且带正号的项是 ;2、设A 为n 级方阵,3||2A =,则1*|(2)|A A --= ; 3、设矩阵123045002A ⎛⎫ ⎪= ⎪ ⎪⎝⎭,100510231B ⎛⎫ ⎪=- ⎪ ⎪⎝⎭,则行列式=AB _______ .;4、设n 元齐次线性方程组0Ax =的系数矩阵的秩()r A r n =<,则该方程组的基础解系所含的向量个数为5、设矩阵3121A ⎛⎫=⎪--⎝⎭,则=-1A ;6、设12312323k A k k -⎛⎫ ⎪=-- ⎪ ⎪-⎝⎭,若()2r A =,则k =二、选择题(每小题3分,共12分)1、设A 、 B 是n 阶方阵,下列等式正确的是 。
A. 111()AB A B ---= B. ()T T T A B A B +=+C. ()T TTAB A B = D. ))((22B A B A B A -+=-2、下列矩阵中不是初等矩阵的是 。
A . 1010,100001P ⎛⎫ ⎪= ⎪ ⎪⎝⎭ B. 2100010101P ⎛⎫ ⎪= ⎪⎪⎝⎭C. 1101,010101P ⎛⎫ ⎪= ⎪ ⎪⎝⎭ D. 2102010001P -⎛⎫⎪= ⎪ ⎪⎝⎭3、设向量组123411110221,,,0032a b c d αααα-⎛⎫⎛⎫⎛⎫⎛⎫⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪==== ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭⎝⎭,其中,,,a b c d 是任意常数,则A. 123,,ααα总线性相关B. 1234,,,αααα总线性相关C. 123,,ααα总线性无关D. 1234,,,αααα总线性无关4、设矩阵n m A ⨯的秩n m A r <=)(,下述结论中正确的是 。
A .A 的任意m 个列向量必线性无关;B. A 的任意一个m 阶子式不等于零; C. 齐次方程组0=Ax 只有零解; D. 非齐次方程组b Ax =必有无穷多解.三、计算行列式(每小题9分,共18分)1、11111234149161827642、na b a aaa ab aa a a a ba a a aa b----四、设101301110110012014X ⎛⎫⎛⎫ ⎪ ⎪-= ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭,求X (10分)五、(共10分)方阵A 满足223A A E O --=,(1)证明:2A E +可逆,并求其逆;(8分) (2)A E +是否可逆?试说明理由。
上海海洋大学15-16高数C期末A卷

上海海洋大学试卷(本试卷不准使用计算器)诚信考试承诺书本人郑重承诺:我已阅读且透彻理解了“上海海洋大学学生考场规则”和“上海海洋大学学生违反校纪校规处理规定”,承诺在考试中自觉遵守,如有违反,按有关条款接受处理。
承诺人签名: 日 期:考生姓名: 学号: 专业班名:一、选择题 (每题3分,共21分) 1. 1lim 2n →+∞⎛⎫+=L ( ) (A)21; (B) 32; (C) 1; (D) 不存在. 2.设2)(0='x f ,则000(2)()limx f x x f x x∆→-∆-=∆ ( )(A) -2; (B) -4; (C) 1; (D) 不存在.3.若()y f x = 在(,)a b 内满足'''()0,()0,f x f x <> 则曲线()y f x = 在(,)a b 内是( )(A) 单调上升且是凹的; (B) 单调下降且是凹的; (C) 单调上升且是凸的; (D) 单调下降且是凸的.4.ln 2xdx =⎰ ( )(A) ln 22x x x C -+; (B) ln 42xx x C -+;(C) ln 2x x x C -+; (D) ln 2xx x C ++.5. 下列等式正确的是 ( ) (A) ()()d f x dx f x =⎰; (B) '()()f x dx f x C =+⎰;(C) ()()df x f x dx =⎰; (D) ()()df x dx f x C dx =+⎰. 6. 曲线24(1)2x y x+=-总共有几条渐近线 ( ) (A) 1条; (B) 2条; (C) 3条; (D) 4条.7.设函数111()1xxe f x e -=+,则0x =是 )(x f 的 ( )(A) 可去间断点; (B) 跳跃间断点; (C) 第二类间断点; (D) 连续点.二、计算下列极限 (每题6分,共24分). 1.03sin 3lim (1cos )ln(12)x x x x x →--+ 2. 23(1)lim xt x e dt x-→-⎰3.)lim x xx →+∞4. 3lim 1x x x x +→∞⎛⎫⎪+⎝⎭三、计算下列导数 (共14分).1.(7分) 求曲线221169x y +=在处的切线方程.2.(7分) 设函数)(x f y =由参数方程221t x y t⎧=⎪⎨⎪=-⎩确定,求dx dy ,22dx y d .四、计算下列定积分 (20分).1.(6分)⎰exdx x 1ln 2.(6分)4⎰3.(8分)计算抛物线2y x = 与2y x = 所围成的图形的面积.五、(7分) 设函数()⎩⎨⎧>+≤=1,1,2x b ax x x x f ,为了使函数()x f 在1=x 处连续且可导,b a ,应取什么值?六、某商品的需求量Q 为价格P 的函数22150P Q -=。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
题目部分,(卷面共有100题,分,各大题标有题量和总分) 一、选择 (16小题,共分) (2分)[1] (3分)[2]二重积分Dxydxdy ⎰⎰(其中D :0≤y ≤x 2,0≤x ≤1)的值为 (A )16 (B )112 (C )12 (D )14答 ( ) (3分)[3]若区域D 为0≤y ≤x 2,|x |≤2,则2Dxy dxdy =⎰⎰=(A )0; (B )323 (C )643(D )256 答 ( )(3分)[4]设D 1是由ox 轴,oy 轴及直线x +y =1所圈成的有界闭域,f 是区域D :|x |+|y |≤1上的连续函数,则二重积分22(,)Df x y dxdy =⎰⎰__________122(,)D f x ydxdy ⎰⎰(A )2 (B )4 (C )8 (D )12答 ( ) (3分)[5]设f (x ,y )是连续函数,则二次积分011(,)x dx f x y dy -+⎰=(A)112111(,)(,)y dy f x y dx dy f x y dx ---+⎰⎰⎰(B)111(,)y dy f x y dx --⎰⎰(C)11111(,)(,)y dy f x y dx f x y dx ---+⎰⎰⎰(D)21(,)dy f x y dx -⎰⎰答 ( ) (3分)[6] 设函数f (x ,y )在区域D :y 2≤-x ,y ≥x 2上连续,则二重积分(,)Df x y dxdy⎰⎰可化累次积分为(A)201(,)x dx f x y dy -⎰(B)21(,)x dx f x y dy -⎰⎰(C)21(,)y dy f x y dx -⎰⎰(D)21(,)y dy f x y dx ⎰答 ( ) (3分)[7]设f (x ,y )为连续函数,则二次积分21102(,)y dy f x y dx ⎰⎰可交换积分次序为(A)1010(,)(,)dx f x y dy f x y dy +⎰(B)112102(,)(,)(,)dx f x y dy f x y dy f x y dy ++⎰⎰⎰(C)1(,)dx f x y dy ⎰(D)222cos 0sin (cos ,sin )d f r r rdr πθθθθθ⎰⎰答 ( ) (3分)[8]设f (x ,y )为连续函数,则积分212201(,)(,)x xdx f x y dy dx f x y dy -+⎰⎰⎰⎰可交换积分次序为 (A)12201(,)(,)y ydy f x y dx dy f x y dx -+⎰⎰⎰⎰(B)212201(,)(,)x xdy f x y dx dy f x y dx -+⎰⎰⎰⎰(C)120(,)y dy f x y dx -⎰(D)2120(,)xxdy f x y dx -⎰⎰答 ( ) (4分)[9]若区域D 为(x -1)2+y 2≤1,则二重积分(,)Df x y dxdy ⎰⎰化成累次积分为(A)2cos 0(,)d F r dr πθθθ⎰⎰(B)2cos 0(,)d F r dr πθπθθ-⎰⎰(C)2cos 202(,)d F r dr πθπθθ-⎰⎰(D)2cos 202(,)d F r dr πθθθ⎰⎰其中F (r ,θ)=f (r cos θ,r sin θ)r .答 ( )(3分)[10]若区域D 为x 2+y 2≤2x ,则二重积分22()Dx y x y dxdy ++⎰⎰化成累次积分为(A)2cos 202(cos sin )2cos d r rdr πθπθθθθ-+⎰⎰(B)2cos 30(cos sin )d r dr πθθθθ+⎰⎰(C)2cos 3202(cos sin )d r dr πθθθθ+⎰⎰(D)2cos 3222(cos sin )d r dr πθπθθθ-+⎰⎰答 ( ) (4分)[11]设777123[ln()],(),sin ()DDDI x y dxdy I x y dxdy I x y dxdy =+=+=+⎰⎰⎰⎰⎰⎰其中D 是由x =0,y =0,12x y +=,x +y =1所围成的区域,则I 1,I 2,I 3的大小顺序是 (A)I 1<I 2<I 3; (B)I 3<I 2<I 1; (C)I 1<I 3<I 2; (D)I 3<I 1<I 2.答 ( ) (5分)[12]设2211cos sin x y dxdyI x y +≤=++⎰⎰,则I 满足 (A)223I ≤≤ (B)23I ≤≤ (C)12D I ≤≤ (D)10I -≤≤答 ( ) (4分)[13]设12x y +=其中D 是由直线x =0,y =0,及x +y =1所围成的区域,则I 1,I 2,I 3的大小顺序为(A)I 3<I 2<I 1; (B)I 1<I 2<I 3; (C)I 1<I 3<I 2; (D)I 3<I 1<I 2.答 ( ) (3分)[14]设有界闭域D 1与D 2关于oy 轴对称,且D 1∩D 2=,f (x ,y )是定义在D 1∪D 2上的连续函数,则二重积分2(,)Df x y dxdy =⎰⎰(A)122(,)D f x y dxdy ⎰⎰ (B)224(,)D f x y dxdy ⎰⎰(C)124(,)D f x y dxdy ⎰⎰(D)221(,)2D f x y dxdy ⎰⎰ 答 ( )(3分)[15]若区域D 为|x |≤1,|y |≤1,则cos()sin()xy Dxe xy dxdy =⎰⎰ (A) e; (B) e -1; (C) 0; (D)π.答 ( ) (4分)[16]设D :x 2+y 2≤a 2(a >0),当a =___________时,.Dπ=答 ( ) 二、填空 (6小题,共分)(4分)[1]设函数f (x ,y )在有界闭区域D 上有界,把D 任意分成n 个小区域Δσi (i =1,2,…,n ),在每一个小区域Δσi 任意选取一点(ξi ,ηi ),如果极限 01lim(,)niiii f λξησ→=∆∑(其中入是Δσi (i =1,2,…,n )的最大直径)存在,则称此极限值为______________的二重积分。
(4分)[2]若D 是以(0,0),(1,0)及(0,1)为顶点的三角形区域,由二重积分的几何意义知(1)Dx y --⎰⎰=___________.(3分)[3]设:00D y x ≤≤≤,由二重积分的几何意义知D=___________.(3分)[4]设D :x 2+y 2≤4,y ≥0,则二重积分32sin()Dx y d σ=⎰⎰__________。
(4分)[5]设区域D 是x 2+y 2≤1与x 2+y 2≤2x 的公共部分,试写出(,)Df x y dxdy ⎰⎰在极坐标系下先对r 积分的累次积分_________________.(3分)[6]设D :0≤x ≤1,0≤y ≤2(1-x ),由二重积分的几何意义知12D y x dxdy ⎛⎫-- ⎪⎝⎭⎰⎰=_______________. 三、计算 (78小题,共分)(3分)[1]设f (x ,y )为连续函数,交换二次积分2102(,)yydy f x y dx ⎰⎰的积分次序。
(3分)[2]设f (x ,y )为连续函数,交换二次积分220(,)xxdx f x y dy ⎰⎰的积分次序。
(3分)[3]设f (x ,y )为连续函数,交换二次积分10021(,)(,)dy f x y dx dy f x y dx ---+⎰⎰⎰⎰的积分次序。
(3分)[4]设f (x ,y )为连续函数,交换二次积分211111ln (,)(,)e x xdx f x y dx dx f x y dy -+⎰⎰⎰⎰的积分次序。
(4分)[5]计算二重积分2()Dx ydxdy -⎰⎰其中D :0≤y ≤sin x ,0≤x ≤π. (3分)[6]计算二重积分Dxydxdy ⎰⎰其中D 是由曲线y =x 2,直线y =0,x =2所围成区域。
(3分)[7]计算二重积分Dx ydxdy ⎰⎰其中D 为由y =x ,y =2x ,x =4所围成的区域。
(3分)[8]计算二重积分Dxydxdy ⎰⎰其中D :x ≤y ≤x ,1≤x ≤2.(3分)[9]计算二重积分cos()Dx y dxdy +⎰⎰其中D 是由直线x =0,y =π和y =x 围成的区域。
(4分)[10]计算二重积分22()Dx y y dxdy +-⎰⎰ 其中D 是由直线y =x ,y =x +1,y =1及y =3所围成的区域。
(3分)[11]计算二重积分cos(2)Dx xy dxdy ⎰⎰其中D:0,114x y π≤≤-≤≤(3分)[12]计算二重积分()Dx y dxdy +⎰⎰其中D 为由y =x ,x =0,y =1所围成的区域。
(3分)[13]计算二重积分(6)Dx y dxdy +⎰⎰其中D 是由直线y =x ,y =5x 及x =1所围成的区域。
(3分)[14]计算二重积分Dxydxdy ⎰⎰其中D 是由双曲线1y x=,直线y =x 及x =2所围成的区域。
(3分)[15]计算二重积分Dydxdy x⎰⎰其中D 是由直线y =2x ,y =x ,x =2及x =4所围成的区域。
(3分)[16]计算二重积分Dy dxdy ⎰⎰其中D :|x |+|y |≤1. (3分)[17]计算二重积分Dxy d σ⎰⎰其中D :|x |+|y |≤1. (4分)[18]计算二重积分2xy dxdy ⎰⎰其中1D:,12xy x x ≤≤≤≤ (4分)[19]计算二重积分22()Dx y dxdy +⎰⎰ 其中D 是由直线y =x ,y =x +a ,y =a 及y =3a (a >0)所围成的区域。
(4分)[20]计算二次积分330(2)xdx x y dy -+⎰⎰(4分)[21]计算二重积分Dxydxdy ⎰⎰其中D 是由y =x ,xy =1,x =3所围成的区域。
(4分)[22]计算二重积分22()Dx y x dxdy +-⎰⎰ 其中D 是由y =2,y =x ,y =2x 所围成的区域。
(4分)[23]计算二重积分(1)Dx ydxdy -⎰⎰其中D 是由曲线1x y =+,y =1-x 及y =1所围成的区域。
(4分)[24]计算二重积分411Ddxdy x +⎰⎰ 其中D 是由y =x ,y =0,x =1所围成的区域。
(4分)[25]计算二重积分2Dxy dxdy ⎰⎰ 其中D 为与x =0所围成的区域。
