混沌系统的电路实现与仿真分析

合集下载

混沌电路实验报告

混沌电路实验报告混沌电路实验报告引言：混沌理论是一门非常有趣和重要的领域，它研究的是一种看似无序但实际上具有内在规律的系统行为。

混沌电路是应用混沌理论的一种实验装置，通过构建电路来模拟混沌现象的发生和演化。

本次实验旨在通过搭建混沌电路，观察和分析混沌现象，并探讨其在实际应用中的潜力。

实验步骤：1. 准备工作在开始实验之前，我们需要准备一些基本的器件和元件，包括电阻、电容、运算放大器等。

同时，还需要一块实验板和一台示波器，用于观测电路的输出信号。

2. 搭建电路根据实验指导书上的电路图，我们开始搭建混沌电路。

首先，将电阻和电容按照一定的连接方式连接起来，然后将运算放大器与电路连接。

在搭建过程中，我们需要仔细检查每个连接点，确保电路的正常工作。

3. 调试电路完成电路的搭建后，我们开始调试电路，使其能够产生混沌现象。

通过调整电阻和电容的数值，我们可以改变电路的参数，从而改变电路的行为。

在调试过程中，我们需要观察示波器上的波形，判断电路是否进入了混沌状态。

4. 观察混沌现象一旦电路进入混沌状态，我们可以开始观察混沌现象的特征。

混沌现象通常表现为信号的不规则变化，具有高度的复杂性和敏感性。

我们可以通过示波器上的波形来观察混沌现象的变化，并用数学工具对其进行分析和描述。

实验结果：经过一系列的实验和观察，我们成功地搭建了混沌电路，并观察到了混沌现象的发生和演化。

通过调整电路的参数，我们发现电路的行为可以从有序到混沌再到周期性，呈现出多样的动态行为。

讨论与分析：混沌电路的研究不仅仅是为了满足科学的好奇心，更是为了实际应用中的需要。

混沌现象具有高度的复杂性和随机性，可以用于密码学、通信和图像处理等领域。

例如，在密码学中，混沌现象可以用来生成随机数序列，增加密码系统的安全性。

在通信中，混沌现象可以用来抵御干扰和窃听，提高通信系统的稳定性和可靠性。

然而，混沌电路也存在一些挑战和问题。

首先，混沌现象的产生和演化非常复杂，需要精确调整电路的参数才能实现。

基于DSP Builder的四维时滞混沌系统数字电路设计与仿真

合理，计算机仿真结果表明在ＤＰＢｉｅ下与ＭａａＳｕｄｒｌｔｂ下结果一致．而使得基于ＦＧＬ从ＰＡ混沌系统的开发变得快速、捷．有实际应用价值便具关键词：时滞混沌系统；计算机仿真；ＰＢｉｅ：ＰＡＤＳｕｌｒＦＧｄ
号【ＦＧＡ指现场可编程门阵列（ｉｌｒｇａｌＰｌ。ＦｅｄＰｏｒｍｍｅｄ
为对自身参数扰动非常敏感．系统配置不灵活、备运设
行与维护都比较麻烦．从而限制了模拟电路混沌系统
的实际应用现在多数算法都能在数字系统（如例
基于ＤＰＢｉｅ的四维时滞混沌系统Ｓｕｌｒｄ数字电路设计与仿真
张之光一，杨杰。。李明
（．１中国人民解放军６７９部队，原０２０；．西理工大学信息＿学院，州３１０；１６太３１０２江Ｔ程赣４００３中国人民解放军６９２部队，ＩＩ．１０￣Ｊ宜宾６４０；．州广播电视大学，州３１０）ｔＩ４００４赣赣４００
设计混沌系统的固有缺陷．混沌系统进行离散化处理．出基于ＤＳｕｌｅ软件设计时将提ＰＢｉｒｄ滞混沌吸引子的方法。通过数字电路的优化设计．数的合理配置．系统的信号幅度控制参该

新的三维自治混沌系统及其电路仿真

收稿日期：０９Ｏ — ４２０一９１稿件编号：０９９４２０００６
作者简介：阿娟（９８）女，西阎良人。研究方向：赵１８一，陕混沌电路的构造与分析。
－
１４－
赵阿娟。等
新的三维自治混沌系统及其电路仿真
轨迹逐渐运动到一个吸引子上，过分析和数值仿真可知路仿真实现
对该系统设计仿真电路，图７示。其电路方程为：如所
￣
图３时域图
＝３丽Ｒ
１— ５
动力学系统随时间变化的动态特性．有１Ｌａｕｏ数若个ｙｐｎｖ指
大于０则系统处于混沌状态。Ｌａｕｏ，ｙｐｎｖ指数图如图６所示。
由计算机得出该系统的非周期性时域波形图和频谱图，
如图３和图４所示。
Ｄ＋＿Ａ＋＝篇＝１１ｕ２２ ¨ ＝毫２＋雪．亡２ ∞
（４）
由式（）知，系统是一个耗散系统。实际中，统的４可该系
（西北农林科技大学水利与建筑工程学院，陕西杨凌７２０）１１０
摘要：了丰富非线性电路领域的研究内容，出一个新的三维自治混沌系统，造其数学模型。运用ＭＡＬ为提构ＴＡＢ对它

一个新五阶超混沌系统分析与电路仿真 (1)

一个新五阶超混沌系统分析与电路仿真-机电论文一个新五阶超混沌系统分析与电路仿真周小勇韩晓新（江苏理工学院电气信息工程学院，江苏常州213001）摘要：提出了一个新的五阶自治超混沌系统，通过系统的理论分析、数值仿真、Lyapunov指数和维数证明该超混沌系统的存在性，还利用Lyapunov指数谱和分岔图说明随着系统参数的改变，系统呈现复杂周期、混沌和超混沌状态，具有丰富的动力学特性。

最后，运用Multisim软件设计了系统的电路并进行了仿真实验，数值仿真和电路仿真证实了该超混沌系统与以往发现的混沌系统并不拓扑等价，是一个新的超混沌系统。

关键词：超混沌系统；Lyapunov指数谱；分岔图；超混沌电路项目名称：江苏省产学研前瞻性联合研究项目，项目编号：BY201302503 0引言现今，在混沌加密的保密通信研究中发现，低维混沌系统用作密钥时容易被破译，而高维的超混沌系统却难以破译［12］。

主要原因是低维系统产生的混沌信号频带较窄，容易被数字滤波器分离，失去加密保护作用，但对于高维混沌系统或超混沌系统来说，其混沌动力学特性较为复杂，产生的混沌序列信号具有比较宽的频率范围，难以被滤波器滤除［35］，这对于信息加密具有非常重要的应用价值，因此，围绕超混沌系统产生与应用的研究成为混沌理论的研究热点之一。

本文在一个三维混沌系统的基础上通过变量拓展与状态反馈构造了一个五阶自治超混沌系统。

通过理论推导、数值仿真、Lyapunov指数与维数、Lyapunov指数谱和分岔图等研究了该超混沌系统的动力学特性，验证了系统的超混沌特性。

最后，采用模块化电路设计方法，根据系统数学模型设计了系统的硬件电路原理图，并进行了电路的EWB 仿真实验，验证了系统的物理可实现性。

1新五阶超混沌系统的基本分析1.1新五阶超混沌系统模型本文提出的新五阶自治超混沌系统是在文献［6］的三维混沌系统的基础上，通过拓展系统变量并实施反馈控制来实现的，其数学模型描述为：式中的a、b、c、d是实常数，当a=25、b=35、c=30、d=35时，系统存在一个典型的混沌吸引子如图1所示，由图可见，吸引子的轨线在其吸引域中具有遍历性。

Lorenz混沌系统的电路仿真

毕业论文（设计）题目：Lorenz混沌系统的电路仿真指导教师：学生姓名：学生学号：信息工程系-电气自动化专业-08自动化2班2011年 04月 15日摘要混沌学研究从早期探索到重大突破,经以至到本世纪70年代以后形成世界性研究热潮，其涉及的领域包括数学、物理学、生物学、气象学、工程学和经济学等众多学科，其研究的成果，不只是增添了一个新的现代科学学科分支，而且几乎渗透和影响着现代科学的整个学科体系。

混沌学的研究是现代科学发展的新篇章.许多学者把混沌理论称为继量子力学和相对论以后二十世纪最有影响的科学理论之一,人们对混沌信号的产生和混沌振荡器等内容的研究非常感兴趣.本文将论述混沌的概念、混沌同步和混沌控制的一些方法,并针对Lorenz 系统提出了以一定的祸合比例系数，实现主动系统和被动系统的同步控制以及计算机仿真.计算机仿真结果表明：在控制的过程中，控制周期随着松弛系数值的增大而减小,较大的松弛系数导致较快的控制。

这个控制法则来源于李雅普诺夫稳定性原理，可以用来控制非同步系统达到同步,最终实现所要求的P同步，即通过加入微小的控制可以在短时间内按任意比例系数实现对主动系统的响应的放大或缩小。

电路实现证实了所提新方法的有效性，并且可以按照实际需要的祸合比例实现同步控制。

关键词：混沌同步；控制;祸合比例系数;电路实现ABSTRACTChaos studies from early exploration to significant breakthrough in the 1970s by up to this century after the hot forming worldwide, the field that involves including mathematics, physics, biology, meteorology, engineering and economics，and so many subject，the research achievement，not just added a new modern scientific disciplines branch，and almost permeates and affects the whole subject system of modern science. Chaos study of the development of modern science is a new chapter。

Multisim仿真—混沌电路

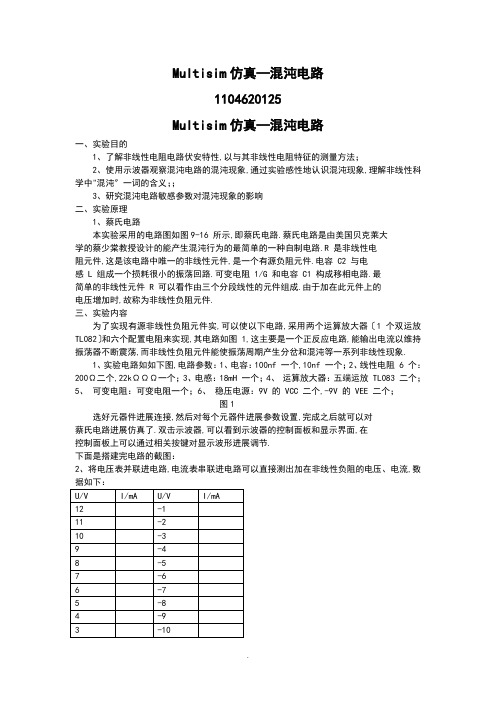
Multisim仿真—混沌电路1104620125Multisim仿真—混沌电路一、实验目的1、了解非线性电阻电路伏安特性,以与其非线性电阻特征的测量方法；2、使用示波器观察混沌电路的混沌现象,通过实验感性地认识混沌现象,理解非线性科学中"混沌〞一词的含义；；3、研究混沌电路敏感参数对混沌现象的影响二、实验原理1、蔡氏电路本实验采用的电路图如图9-16 所示,即蔡氏电路.蔡氏电路是由美国贝克莱大学的蔡少棠教授设计的能产生混沌行为的最简单的一种自制电路.R 是非线性电阻元件,这是该电路中唯一的非线性元件,是一个有源负阻元件.电容 C2 与电感 L 组成一个损耗很小的振荡回路.可变电阻 1/G 和电容 C1 构成移相电路.最简单的非线性元件 R 可以看作由三个分段线性的元件组成.由于加在此元件上的电压增加时,故称为非线性负阻元件.三、实验内容为了实现有源非线性负阻元件实,可以使以下电路,采用两个运算放大器〔1 个双运放TL082〕和六个配置电阻来实现,其电路如图 1,这主要是一个正反应电路,能输出电流以维持振荡器不断震荡,而非线性负阻元件能使振荡周期产生分岔和混沌等一系列非线性现象.1、实验电路如如下图,电路参数：1、电容：100nf 一个,10nf 一个；2、线性电阻 6 个：200Ω二个,22kΩΩΩ一个；3、电感：18mH 一个；4、运算放大器：五端运放 TL083 二个；5、可变电阻：可变电阻一个；6、稳压电源：9V 的 VCC 二个,-9V 的 VEE 二个；图1选好元器件进展连接,然后对每个元器件进展参数设置,完成之后就可以对蔡氏电路进展仿真了.双击示波器,可以看到示波器的控制面板和显示界面,在控制面板上可以通过相关按键对显示波形进展调节.下面是搭建完电路的截图：2、将电压表并联进电路,电流表串联进电路可以直接测出加在非线性负阻的电压、电流,数据如下：经过线性拟合得到如下伏安特性曲线：3、使用示波器成像法例如图中,RN 就是我们所需要进展研究的有源非线性负阻.元件的详细参数如原理图所示,运放的工作电源取 9V.信号源为三角波,输出波幅从-3.75V 至 3.75V.为测量电流 i,在电路中串联了一个 10Ω的取样电阻 R,其电压与电流成正比.示波器记录的结果也如如下图所示.我们可以观察到,仿真得到的伏安特性曲线与通过实验数据绘制得出的伏安特性曲线一致,根本相符.实验曲线中有如下几个特殊点：电压为0V时,电流符合理论值0A；电压分别在-10V和10V 左右时,电流的数值大小出现最大值,该两点为曲线的转折点；电压分别在-2V和2V左右时曲线斜率发生改变,故该两点也可算为曲线的转折点.ΩΩ这一X围的状态.kΩ,电路状态变化中k1与k2相图为稳定焦点,呈蝌蚪型,为衰减振荡,这就是不动点.R=1.93 kΩ时R=2.0 kΩ时Ω,此时等幅振荡：Ω,增幅振荡开始,一倍周期：ΩΩ时,2 倍周期：当R = 1 819kΩ~1 818kΩ时：当R = 1 787kΩ时：Ω时：ΩΩ两个图像的比照,可以发现：当电路处于单涡旋混沌状态时,改变电路的初始状态,可以观察到向左和向右两种单涡旋混沌吸引子相图.Ω时为单吸引子图形,这是电路第一次进入单吸引子混沌.当 R 继续减小,当R = 1. 7165kΩ时,出现双吸引子混沌图形：Ω时：Ω时,呈单叶周期：混沌图像分析：通过以上数据和图案发现,改变初始电路参数时,在混沌现象中电路是非周期性的,时而稳定,时而混乱,虽然出现平衡点,但并不稳定.在理想实验条件下观察到了不同参数条件下出现的极限环、单吸引子、双吸引子、奇异吸引子等一系列不同的混沌现象.随着混沌电路电感R 值的逐渐减小,混沌现象提前,边界化也越来越明显.四、实验结论1、该实验是根据图书馆资料和网上介绍的根底上做的,实验中所需要的非线性负电阻电路并不唯一,而我所选用的以两个运算放大器和六个配置电阻的形式来实现是其中最简单的电路之一,通过使用Multisim11.0仿真软件得到了如上的波形,所得实验结果与要求根本符合.混沌现象表现了非周期有序性,看起来似乎是无序状态,但呈现一定的统计规律：〔1．频谱分析：R很大时,系统只有一个稳定的状态〔对应一个解〕,随R的变化系统由一个稳定状态变成在两个稳定状态之间跳跃〔两个解〕,即由一周期变为二周期,进而两个稳定状态分裂为四个稳定状态〔四周期,四个解〕,八个稳定状态〔八周期,八个解〕………直至分裂进入无穷周期,即为连续频谱,接着进入混沌,系统的状态无法确定；〔2．无穷周期后,由于产生轨道排斥,系统出现局部不稳定.〔3．奇异吸引子存在．奇异吸引子有一个复杂但明确的边界,这个边界保证了在整体上的稳定,在边界内部具有无穷嵌套的自相似结构,运动是混合和随机的,它对初始条件十分敏感.2、面前在中国,对混沌理论研究有突破的人士较少,然而,混沌与人类生存环境间有十分密切的关联,混沌学的进步不仅将进一步解释那些尚未为人所知的东西,而且还孕育着一场深刻的科技革命,涉与各种学科包括电子、激光、化学、生物、医学、机械等.预期的混沌应用X围涉与疾病的混沌诊断与混沌医疗、混沌控制与混沌制导、混沌通信、混沌振荡以与混沌在农业生产中的应用.。

一个新的三维混沌系统分析及电路实现

１混沌模型及特性分析
１１混沌模型．本文在文献［０中研究的基础上，出了一个新的三１］提
系统之间都是拓扑不等价的，但都是一个简单的三阶二次
自治微分方程．此后国内外的许多文献中又报道了若干新的混沌系统．本文在文献［０］１中研究的基础上，出提了一个新的三维混沌系统，该系统含有３个参数，２个方第程和第３个方程各含有一个非线性乘积项．中第２个方其程中的非线性项为交叉乘积，３个方程中的非线性项第
统．０２年Ｃｅ２０ｈｎ和Ｌ又进一步提出在Ｌｒｚ系统与ｎｏｎｅＣｅ统之间起关键桥梁的混沌系统，ｈｎ系即系统．３个这
算机数值模拟，用模块化方法设计了一个模拟电路，并并进行了电路实验，从理论分析、算机模拟和电路实验３个计方面证实了该系统的混沌特性．
沌吸引子，图１示．如所
图ｌ系统（）２混沌吸引子在相平面上的投影
需要强调的是，（）表示的三维混沌系统与文献式１所１２系统的基本特性分析．
１２１对称性和不变性．．
［０中的三维混沌系统相比，主要的差别是方程中的第１］最
｛收稿日期：０９— ２—２Ｉ｝２０１０基金项目：山东省科技发展计划项目（０９Ｇ００００；２０Ｇ１０１３）滨州学院科研基金项目（ＺＹ００）ＢＸＧ９２作者简介：连新（９２）男，孙１８一，主要从事计算机应用技术研究．

一个混沌系统仿真研究及其电路分析

，
ｃａｔｓｍ，ｈｓｙｔｈｓｔｅｐｒｔｒｄｕｔｎｏｙｎｅｔｅｓｍｐｅｎｈｉｈｅｉｂｌｔｎｄｇｈｏｉｓｔｃｙｅｔｉｓｓｍａｈａｍｅｊｓｅａｅａｍｅｔｓｃｎｅｉ，ａｔｉｌｉｎｙｏｍｅｔｇｒｌａｉｉｙａｏ０ｄ
，
ｒａ－ｔｍｅａＯｏｅｌｉｎｄＳｎ．Ｋｃｗｏｒ：ｃｏｉｙｓｅｓｙｄｓｈａｔｃｓｔｍ；Ｍｕｌｉｉ１１ｕｔｎｏｍｏｕｈａｉｖｓｅｔＳｍ０；ａｏｓｃｏｔｃｓｔｍ
．
★基金项目：聊城大学东昌学院青年教师基金项目（９ｇ０）ｘ１３资助。ＯＯ
关键词：混沌系统；ｌＳｍ１．自治混沌系统Ｍｕｔｉ０１ｉ；
中图分类号：Ｐ３．Ｔ３２２文献标识码：Ａ
Ｓｍｕａｉｉｌｔｏｎｈａｉｙｓｅｎｄｉｃｔａｌｉｏｆａｃｏｔｃｓｔｍａｃｒｕｉｎａｙｓｓ
，
ａｔｉｄ・ＮｕｍｅｉａｎｌｓｓｓｔｍａｈｏｔｃＥｘｒｍｅｓａｅｇｖｅｕｌｉｍ０１ｏｆｗａｅｓｓｅｏｐｏｇｎｄｕｄｅｒｃｌａａｙｉｙｓｅｃｎｂｅｃａｉｐｅｉｎｔｒｉｎＭｔＳｉ１ｓｔｒｙｔｍｔｏｌｙ
统类似但不拓扑等价的Ｃｅｈｎ混沌系统口；０２１年０
和２００２年，吕金虎等人相继发现了Ｌｔｉ混沌系统
ＷｕＧｕｅｇ．ｏｚｎ

混沌电路系统的模型仿真与电路实现_林若波

2009 年 6月 JOURNAL OF CIRCUITS AND SYSTEMS June ， 2009 文章编号：1007-0249 (2009) 03-0121-05混沌电路系统的模型仿真与电路实现*林若波1,2（1. 揭阳职业技术学院，广东揭阳 522051；2. 湖南大学电气信息工程学院，湖南长沙 410082）摘要：通过对混沌电路系统的分析方法的介绍，指出模型仿真和电路实现的重要性；以二个典型混沌系统为例，阐述了基于Matlab/Simulink 环境下的仿真方法，同时介绍基于Multisim 8平台的电路仿真和实现过程；最后指出混沌电路的发展前景和研究方向。

关键词：混沌；仿真；Lorenz；Simulink；Multisim 8中图分类号：N945.1 文献标识码：A1 引言非线性科学是一门研究非线性现象共性的基础科学，而混沌理论是非线性科学最重要的成就之一。

“混沌”的发现冲破了传统的决定性观念，著名物理学家福特（J. Ford ）认为混沌的发现是继相对论、量子力学之后，20世纪物理学的第三次革命。

目前混沌系统理论有三个主要的发展方向：应用、综合、和引入比较复杂的数学工具，以求机理研究、分类与构造理论等的进一步发展；寻求数学与物理模型的新范例，研究混沌的应用及其工程系统实现。

2 混沌电路系统的分析方法[1]混沌系统模型的研究一般包括以下几个基本步骤：问题描述、模型建立、仿真实验、结果分析、电路实现，其流程如图1所示。

（1）建立数学模型数学模型是指描述系统的输入、输出变量以及各变量之间关系的数学表达式。

混沌系统中最常用、最基本的数学模型是微分方程与差分方程。

（2）建立仿真模型仿真模型是借助计算机对数学模型进行数值分析计算的模型。

仿真模型的建立是最重要的，它是混沌系统分析的关键点。

有些混沌模型不能直接用于数值计算的，如微分方程，必须进行相应的转换。

（3）仿真与实验变量之间的联系必须通过编制程序来实现，常用的数值仿真编程语言有MATLAB 、C 、FORTRAN 等。

Lorenz混沌系统的分析与电路实现

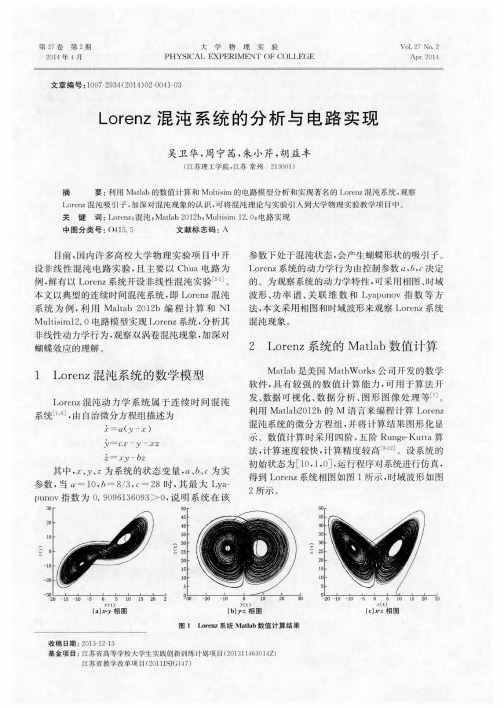
图５Ｌｏｒｅｎｚ系统电路模型实现的时域波形
图５为Ｌｏｒｅｎｚ系统电路模型实现的三个状
态变量，，的时域波形，可以实时动态观察其
波形的变化。
图３Ｌｏｒｅｎｚ系统的电路模型
Ｌｏｒｅｎｚ混沌系统的分析与电路实现
图１为Ｌｏｒｅｎｚ系统通过Ｍａｔｌａｂ编程实现的
—
在电路模型中设置元件的电阻值和电容值，启动仿真按钮，同时在示波器属性框设置合适的参数，如纵横轴的标度、起始值等，通过示波器模块可以观察到Ｌｏｒｅｎｚ系统相图如图４所示，时域
图４中为Ｌｏｒｅｎｚ系统电路模型实现的相，
运算放大器，型号采用ＬＦ３５３Ｄ，Ａ１和Ａ２为模拟乘法器，采用集成芯片ＡＤ６３３，ＶＣＣ和ＶＤＤ分
别为＋１２Ｖ和一１２Ｖ。
从电路仿真结果同样可以动态地观察到Ｌｏｒｅｎｚ系统的蝴蝶状混沌吸引子，双涡卷现象。仿真实验表明该电路设计是可行的。
电路与系统学报，２００９，１４（３）：１２１ — １２５．
［１Ｏ］张建忠．用Ｍａｔｌａｂ数值模拟非线性电路混沌实验［Ｊ］．实验技术与管理，２００７，２４（ｉ１）：８６ — ９１．［１１］姚齐国．Ｌｏｒｅｎｚ系统动力学行为的ＭＡＴＬＡＢ仿真与分析［Ｊ］．水电能源科学，２００７，２５（５）：１２１１２３．［１２］杨纪华．基于Ｍａｔｌａｂ混沌系统的数值仿真［Ｊ］．绵阳

蔡氏混沌电路的分析与仿真

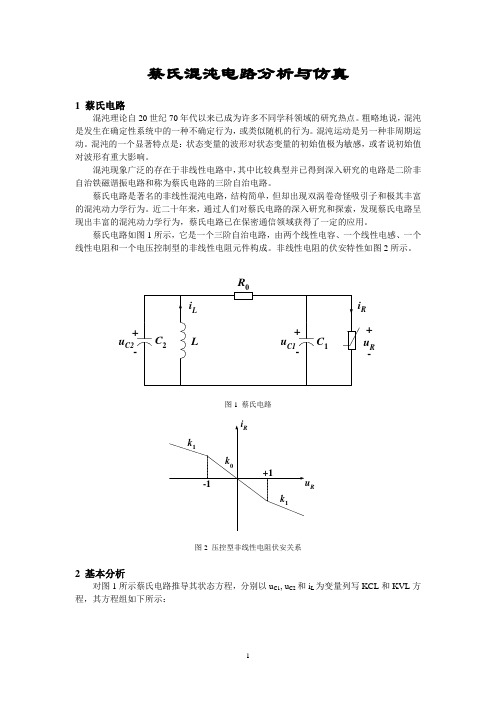
蔡氏混沌电路分析与仿真1 蔡氏电路混沌理论自20世纪70年代以来已成为许多不同学科领域的研究热点。

粗略地说，混沌是发生在确定性系统中的一种不确定行为，或类似随机的行为。

混沌运动是另一种非周期运动。

混沌的一个显著特点是：状态变量的波形对状态变量的初始值极为敏感，或者说初始值对波形有重大影响。

混沌现象广泛的存在于非线性电路中，其中比较典型并已得到深入研究的电路是二阶非自治铁磁谐振电路和称为蔡氏电路的三阶自治电路。

蔡氏电路是著名的非线性混沌电路，结构简单，但却出现双涡卷奇怪吸引子和极其丰富的混沌动力学行为。

近二十年来，通过人们对蔡氏电路的深入研究和探索，发现蔡氏电路呈现出丰富的混沌动力学行为，蔡氏电路已在保密通信领域获得了一定的应用。

蔡氏电路如图1所示，它是一个三阶自治电路，由两个线性电容、一个线性电感、一个线性电阻和一个电压控制型的非线性电阻元件构成。

非线性电阻的伏安特性如图2所示。

u C2RR+-uR 图1 蔡氏电路R图2 压控型非线性电阻伏安关系2 基本分析对图1所示蔡氏电路推导其状态方程，分别以u C1, u C2和i L为变量列写KCL和KVL方程，其方程组如下所示：2212112210C C C L C C C R L C du u u C i dt R u u du C i R dt di u L dt -⎧+=⎪⎪⎪-⎪=+⎨⎪⎪=-⎪⎪⎩式中，i R = g(u R )。

整理上述各式，且令u C1=x, u C2=y, i L =z ，取电路中各参数的值为L=7/100 H, C 1=1/9 F, C 2=1 F, R 0=1 Ω, k 0= -8/7, k 1= -5/7。

方程可变换为标准的蔡氏方程，即为：[()]dxa y f x dt dyx y z dt dzby dt ⎧=-⎪⎪⎪=-+⎨⎪⎪=-⎪⎩其中，1010101()...........(1)()............................(1)() (1)m x m m x f x m x x m x m m x +-≥⎧⎪=≤⎨⎪--≤-⎩式中，a=9, b=100/7, m 0= -1/7, m 1=2/7。

混沌电路实验报告

一、实验目的1. 理解混沌现象的产生原理及其在电路中的应用。

2. 掌握混沌电路的基本搭建方法。

3. 通过实验观察混沌现象，并分析其特性。

4. 研究混沌电路在通信、加密等领域的应用潜力。

二、实验原理混沌现象是指在确定性系统中，由于初始条件的微小差异，导致系统行为表现出高度复杂、不可预测的特性。

混沌电路是一种模拟混沌现象的电路系统，通过非线性元件和反馈环路实现。

本实验采用蔡氏电路（Chua’s circuit）作为研究对象。

蔡氏电路是一种三阶互易非线性自治电路，由电阻、电容和电感元件组成，其中包含一个有源非线性元件。

通过改变电路参数，可以观察到混沌现象的产生。

三、实验仪器与设备1. 蔡氏电路实验板2. 双踪示波器3. 数字万用表4. 信号发生器5. 计算机及数据采集软件四、实验步骤1. 搭建蔡氏电路，确保电路连接正确。

2. 使用示波器观察电路的输出波形，记录初始状态下的波形特征。

3. 改变电路参数，如电阻、电容或电感，观察波形变化。

4. 逐步调整参数，观察混沌现象的产生、发展及消失过程。

5. 使用数字万用表测量电路关键参数，如电压、电流等。

6. 使用信号发生器输入不同频率的信号，观察电路对不同信号的响应。

五、实验结果与分析1. 混沌现象的产生：当电路参数调整至一定范围时，输出波形呈现出复杂、无规律的特性，即混沌现象。

2. 混沌现象的特性：敏感依赖初始条件：混沌现象对初始条件非常敏感，微小差异会导致截然不同的结果。

长期行为的不可预测性：混沌现象的长期行为具有不可预测性，即使初始条件相同，系统的状态也会随时间演化而发生变化。

分岔现象：混沌现象的产生与分岔现象密切相关。

当电路参数发生变化时，系统状态会出现分岔，从而产生混沌现象。

3. 混沌电路的应用：通信：混沌通信利用混沌信号的自相似性和非线性特性，实现信号的加密和解密。

加密：混沌密码学利用混沌现象的复杂性和不可预测性，设计出具有较高安全性的加密算法。

控制：混沌控制利用混沌现象的特性，实现对系统的精确控制。

蔡氏混沌电路的混沌现象及其simulink仿真PPT

从上图中可以看出，当电阻的值为 2.1K时，蔡氏电路的运行状态有一个渐进稳定点，并且在稳定点附近运动。
2、蔡氏电路simulink数值仿真分析
• 2.1.2、R 1.91 K • 当 R 1.91 K 时，b=21.2098,simulink仿真结果如下：
• 当电阻的值减小到 R 1.91K 时，蔡氏电路的运动状态出现单漩涡混沌振荡。从以上相轨图中可以观察到明显的倍周期现象。
2、蔡氏电路simulink数值仿真分析
• 2.2、调节电容 • 给定初始值：u1 0.1V , u 2 0.1V , iL 0.001 A ，固定电路参数 ,C2=100nF 、 L2=17.2mH、,此时b的值是14.51395保持不变，与以上内容不同，下面的内容保持b的值不变，改变a的值。电容c1的值可变，simulink数值仿真可得到在不同C1值时蔡氏电路的运行状态。
0、混沌现象及混沌电路介绍
• 0.4、混沌吸引子 • 混沌吸引子也称奇异吸引子，是反映混沌系统运动特征的产物，也是一种混沌系统中无序稳态的运动形态，它具有复杂的拉伸、扭曲的结构。奇异吸引子是系统总体稳定性和局部不稳定性共同作用的产物，具有自相似性，具有分形结构。从整体上讲，系统是稳定的，即吸引之外的一切运动最终都要收敛到吸引子上。但就局部来说，吸引子内的运动又是不稳定的，即相邻运动轨道要相互排斥而按指数型分离。
2、蔡氏电路simulink数值仿真分析
• 2.2.1、令C1=20nF，则a=5,simulink仿真结果为：
• 有以上图可以得出，改变电容的值改变a系数同样可以得到蔡氏电路的稳定状态，此时的运动轨迹基本上在一点处，是稳定状态。
2、蔡氏电路simulink数值仿真分析

洛伦兹混沌系统的电路仿真与设计

洛伦兹混沌系统的电路仿真与设计【摘要】本文基于Lorenz混沌系统的动力学方程，利用Matlab软件中的simulink模块搭建方程进行仿真，并将Lorenz方程进行标度变换为一个新的标准方程，使用Mutisim软件进行电路设计与模拟，得到了理想的结果。

【关键词】Lorenz混沌系统；Matlab仿真；模拟电路设计0 引言混沌系统对初始值非常敏感，并且具有类随机性，可控及同步性。

近年来，混沌保密通讯、混沌电路及加密发展成为一个前沿领域。

混沌加密等应用问题首先要解决的问题即混沌电路的设计。

本文基于Lorenz混沌系统，分析其基本特性，并进行了电路仿真及模拟电路的设计。

1963年著名的气象学家E.N.Lorenz研究大气热对流运动时发现了一种特殊的混沌现象，即蝴蝶效应。

Lorzen吸引子是目前文献记载最早的奇怪吸引子，因此Lorenz也被成为“混沌之父”。

至今，Lorzen系统族的发展虽然有很长的历史，但是Lorzen系统族丰富的动力学行为依然值得更加深入的研究，并进行更多的应用发展。

lorenz系统的动力学方程为：■=-σx+σy■=-y+rx-xz■=-bz+xy （1）式中，x，y和z表示对流强弱，水平温差和与温差有关的变量；σ、γ和b 则分别为Rayleigh数、Rayleigh数和容器大小有关的参数。

当σ =10，b=8/3，γ=28时，lorenz系统出现混沌现象。

1999年，我国学者陈关荣等人提出了一个新的混沌吸引子，即Chen吸引子，它的动力学方程为：■=a（y-x）■=（c-a）x-xz+cy■=-bz+xy （2）当a=35，b=3，c=28时，Chen系统产生混沌现象。

2002年，吕金虎提出了LU系统，它的动力学方程为：■=a（y-x）■=-xz+cy■=xy-bz （3）当a=36，b=3，c=20时，LU系统出现混沌现象。

这三个系统具有类似却不相同的动力学行为，被称为Lorzen系统族[1]，它对于混沌系统的理论研究以及控制、同步、加密应用等都具有重要的意义。

一个新四维混沌系统的电路设计与仿真

ｃｌａａｙｉ．ａｎｌｓｓＫｅｒｓ：ａｔｉｃｉ，，ａｔｃｓｓｅｙｗｏｄＣｈｏｉｃｒｕｔ４ＤＣｈｏｉｙｔｍｃ
Ｏ前言
在混沌理论的研究中，重要的一研究方向很是对现有的混沌系统进行重新构造，出一些具得
第２９卷
第６期
江
西
科
学
Ｖｏ．９Ｎｏ．Ｉ２６
Ｄｅ．Ｏｌｃ２ｌ
２１年ｌ０１２月
ｌＡＮＧＸＩＳＥＮＣＥＪＩＣＩ
文章编号：０１— ６９２１）６— ６１０１０３７（０１００９ — ４
一
个新四维混：系统的电路设计与仿真沌
ｂｅｅｉｎｄａｄｓｍｕａｅａｅｎｔｅＭｕｉｉＴｅｓｍｕａｉｎｒｓｌｃｏｄｗｔｈｈｏｅｉｅｎｄｓｅｎｉｌｔｄｂｓｄｏｈｈｓｇｍ．ｈｉｌｔｅｕｔａｃｒｉｔｅｔｅｒｔｏｓｈＬ
Ａｂｓｒｃ：ｎｗｔａｔＡｅ４Ｄｕｏｏｕｈｏｉｙｔｍｓｒｓｎｅｎｔｉａｅ，ｈｈｏｉｉｃｔｈａａｔｎｍｏｓｃａｔｃｓｓｅｉｐｅｅｔｄｉｈｓｐｐｒｔｅｃａｔｃｒｕｉｃｓ
其，积电模的分子控混中索是分路块积因，制沌电频。７南，４通的线电路率令．则个道非性路
方程组为
ｄｚ一＋９＋．，

混沌系统的电路实现与仿真分析

混沌系统的电路实现与仿真分析1. 设计思路混沌系统模块化设计方法的主要思路是，根据系统的无量纲状态方程，用模块化设计理念设计相应的混沌电路，其中主要的模块包括：反相器模块、积分器模块、反相加法比例运算模块和非线性函数产生模块。

2. 设计过程第一步，对混沌系统采用Matlab 进行数值分析，观察状态变量的时序图、相图，观察系统状态变量的动态范围；第二步，对变量进行比例压缩变换。

我们通常取电源电压为±15V ，集成运放的动态范围为±13.5V ，如果系统状态变量的动态范围超过±13.5，则状态变量的动态范围超过了集成运放的线性范围，需要进行比例压缩变换，如没有超出，则不需要进行变换。

举例：变换的基本方法⎪⎪⎩⎪⎪⎨⎧===w k z v k y uk x 321 代入原状态方程，然后重新定义u →x ，v →y ，w →z 得到的状态方程即为变量压缩后的状态方程。

第三步，作时间尺度变换。

将状态方程中的t 变换为τ0t ，其中τ0为时间尺度变换因子，设τ0=1/R 0C 0，从而将时间变换因子与积分电路的积分时间常数联系起来。

第四步，作微分-积分变换。

第五步，考虑到模块电路中采用的是反相加法器，将积分方程作标准化处理。

第六步，根据标准积分方程，可得到相应的实现电路。

第七步，采用Pspice 仿真软件或Multisim 仿真软件对电路进行仿真分析。

3. 设计举例：Lorenz 系统的电路设计与仿真Lorenz 系统的无量纲归一化状态方程为bz xy zy xz cx yay ax x--=--=+-= （1）其中当a=10，b=8/3，c=28时，该系统可以展现出丰富的混沌行为。

MATLAB 仿真程序如下：function dx=lorenz(t,x) %¶¨Òåº¯Êý a=10; b=8/3;c=28; %¶¨ÒåÏµÍ³²ÎÊý %***************************************** dx=zeros(3,1); dx(1)=a*(x(2)-x(1));dx(2)=c*x(1)-x(1).*x(3)-x(2); dx(3)=x(1).*x(2)-b*x(3);%*********************************¶¨Òå×´Ì¬·½³Ì clear;options=odeset('RelTol',1e-6,'AbsTol',[1e-6,1e-6,1e-6]); t0=[0 500]; x0=[1,0,0];[t,x]=ode45('Lorenz',t0,x0,options); n=length(t);n1=round(n/2);figure(1);plot(t(n1:n),x(n1:n,1)); %×´Ì¬xµÄÊ±ÐòÍ¼xlabel('t','fontsize',20,'fontname','times new roman','FontAngle','normal'); ylabel('x1','fontsize',20,'fontname','times new roman','FontAngle','normal');figure(2);plot(x(n1:n,1),x(n1:n,3)); %x-zÏàÍ¼xlabel('x','fontsize',20,'fontname','times new roman','FontAngle','italic'); ylabel('Z','fontsize',20,'fontname','times new roman','FontAngle','italic');figure(3);plot3(x(n1:n,1),x(n1:n,2),x(n1:n,3)); %x-y-zÏàÍ¼xlabel('x','fontsize',20,'fontname','times new roman','FontAngle','italic'); ylabel('y','fontsize',20,'fontname','times new roman','FontAngle','italic');zlabel('z','fontsize',20,'fontname','times new roman','FontAngle','italic')；t x 1xzxyz图1 lorenz 系统的时序图和相图由于状态变量的范围超过了±13.5，所以先必须进行变量压缩，按均匀压缩10倍进行处理后得到的状态方程为z xy z y xz x yy x x)3/8(1010281010-=--=+-= （2）作时间尺度变换，令τ=τ0t ，τ0=100，得zy x z y xz x y y x x )3/800()(10001001000)(2800)(10001000---=----=---= （3）图2 lorenz 系统的电路实现根据图2可以得到电路的状态方程为zC R y x C R zy C R xz C R x C R y y C R x C R x 3931025262814111)(1011101)(1)(11---=----=---= （4）设电路中的电容C1=C2=C3=10nF ，比较(3)式、(4)式可得K R C R K R C R KR R C R C R K R C R K C R R C R C R 37513800100011001010110110007.351280010010001111000939525106310268281411411=→==→===→===→====→== Time0s200ms 400ms 500msV(x)V(y)V(z)-5.0V0V5.0VFrequency0Hz0.5KHz 1.0KHz 1.5KHz 2.0KHzV(x)0V250mV500mVV(x)-2.0V0V 2.0VV(z)0V 2.5V5.0VV(x)-2.0V0V 2.0VV(y)-2.0V0V2.0V图3 Pspice 仿真得到的时序图、频谱图和相图设计课题及要求共提供了10个典型的混沌系统，每个混沌系统的设计项目限选4人。

一类特殊受控混沌系统的电路仿真实验

一类特殊受控混沌系统的电路仿真实验混沌电路仿真与实现是非线性混沌研究中的一项重要内容。

基于具有一对位置对称、稳定性态相反平衡点的混沌系统，文章通过混合控制得到一个新的混沌系统。

运用混沌电路理论，设计出实现新混沌吸引子的电路信号源，并通过Multisim软件进行实验仿真。

实验结果和分析结果一致。

标签：混沌系统；Multisim；电路实验；数值仿真Abstract：The simulation and realization of chaotic circuits is an important part of nonlinear chaos research. In this paper，a new chaotic system is obtained by hybrid control. Using the chaotic circuit theory，the circuit signal source to realize the new chaotic attractor is designed，and the experimental simulation is carried out by Multisim software. The experimental results are consistent with the analysis results.Keywords：chaotic system；Multisim；circuit experiment；numerical simulation1 概述混沌及其相关研究是当今非线性科学研究的热点问题，自上世纪Lorenz混沌吸引子发现以来[1]，对混沌系统研究得到了学者们的极度关注[2，3]。

实践表明，混沌系统在各个领域有普遍的应用价值。

在混沌理论及应用研究中，混沌电路是一项非常重要的内容，混沌电路实验是这项内容的基础部分。

电路中混沌现象的研究始于1927年，荷兰物理学家Van der Pol在氖气灯物理电路实验中发现了“不规则噪声”，即我们后面所说的混沌现象。

Liu混沌系统的LabVIEW仿真研究及其电路设计

信息安全刘兴云:Liu混沌系统的LabV IEW 仿真研究及其电路设计Liu 混沌系统的LabVIEW 仿真研究及其电路设计刘兴云1 ,2(1. 湖北师范学院湖北黄石435002 ;2. 湖北大学材料科学与技术学院湖北武汉430062)摘要:分析了Liu 混沌系统动力学特性,设计了基于虚拟仪器Liu 混沌系统的软件系统,给出了基于虚拟仪器技术实验系统的拓扑结构,并进行了硬件电路的设计以及相关的电路实验研究。

虚拟仪器技术为研究非线性系统提供了可行的方案,此实验系统具有良好的实验效果,与传统的自治混沌系统相比,此系统具有参数调节方便、易实现、可靠性高,实时性好等优点。

关键词:Liu 混沌系统;虚拟仪器;LabV IEW ;自治混沌系统中图分类号:O415. 5 ; TM132 文献标识码:B 文章编号:10042373 X(2008) 092098202LabVIEW Simulation Research and Circuit Design of Liu Chaotic SystemL IU Xingyun1 ,2(1. Hubei Normal University , Huangshi ,435002 ,China ;2. Faculty of Material Science and Engineering , Hubei University ,Wuhan ,430062 ,China)Abstract : The chaotic dynamic characteristic of Liu ch aotic sy stem is f urth er investigated. The software system of Liu cha2 otic sy stem based on virtual in str um ent is designed. Topology constr uction of experimental sy stem based on virt ual in str um ent technique is given. The hardware circuit design is designed an d the interrelated circuit implementation is realized. A feasible program is provided fo r the research of nonlinear system. As the approach has been used ,the result of experimental system is satisfactory. To compare the t raditional autonomo us chaotic sy stem ,it has many advantages , such as a convenient parameter changin g ,easy gainin g ,high accuracy ,goo d real2time capability and so on.Keywords :Liu chaotic sy stem ;virtual in str ument ;LabVI EW ;autonomous chaotic system1 引言自从1963 年,Lorenz 在三维自治系统中发现了第一个混沌吸引子以来[ 1 ] ,其混沌理论研究和实际应用得到了极大的关注,但供研究的混沌系统并不多。