第7章-惯性矩与惯性积
07第七章 截面的几何性质

y b
y1
C(zc, yc)
dA
面积A
z1
a z
o
已知: 已知: I y
, Izc , I yczc c
计算: 计算:
y = y1 +a
I y , Iz , I yz
z = z1 +b
z1 —y1为形心坐标系
Iz = ∫ y dA
2
= ∫( y1 +a )2dA = ∫ y dA+2a∫ y1dA+a ∫dA
y1 H B y A C D G
ycosθ = y1 +GF
2、再减去GF 得y1
y1 = ycosθ −GF = ycosθ − z sinθ
θ
z1
θ
O F
E
z
《z 变 z1 的操作》 的操作》
OF) 1、z(OF)向z1 轴投影得 z1 - GD z cosθ = z1 −GD 2、再加上GD 得z1
实质 —— 1、数学,不是力学 、数学,
目的 —— 1、翦除弯曲前面的拦路虎之一(惯性矩 、翦除弯曲前面的拦路虎之一(惯性矩) 2、从更高的观点,统一截面几何性质 、从更高的观点, 3、便于学习(弊病:只有大厦,无脚手架) 、便于学习(弊病:只有大厦, 脚手架) 大厦
5.1 静矩(Statical moment)、 形 心(Centroid) 静矩( 、 零次矩: 零次矩: A = ∫ dA y 一次矩(静矩): 一次矩(静矩): C(zc, yc) dA 面积A 面积
已知: 已知:截面对 y、z 轴的惯性矩、惯性积 、 轴的惯性矩、 求解:截面对 轴的惯性矩、 求解:截面对y1、z1轴的惯性矩、惯性积
2 Iz1 = ∫ y1 dA= ∫(ycosθ − zsinθ)2 dA
惯性矩和惯性积的平行移轴公式
20 140
zc
20
1
yc
2
y
100
A1 20140 A2 100 20
Z1 80 Z2 0
所以截面的形心坐标为
ZC
A1 Z1 A1
A2 Z2 A2
46.7mm
20 140zc20源自1ycxc
ob
x
二、组合截面的惯性矩 惯性积
Ixi , Iyi , Ixyi —— 第 i个简单截面对 x ,y 轴的惯性矩、
惯性积。
组合截面的惯性矩,惯性积
n
I x I xi i1
n
I y I yi i1
n
I xy I xyi i 1
例 3 -1 求梯形截面对其形心轴 yc 的惯性矩。
解:将截面分成两个矩形截面。
xc
b
x
Ix , Iy , Ixy _____ 截面对 x , y 轴的惯性矩和惯性积。
Ixc ,Iyc , Ixc yc —— 截面对形心轴 xc , yc 的惯性矩和惯性积。
则平行移轴公式为
y
yc
I x I xc a2 A
Iy Iyc b2 A
I xy I xcyc abA
a
C(a,b)
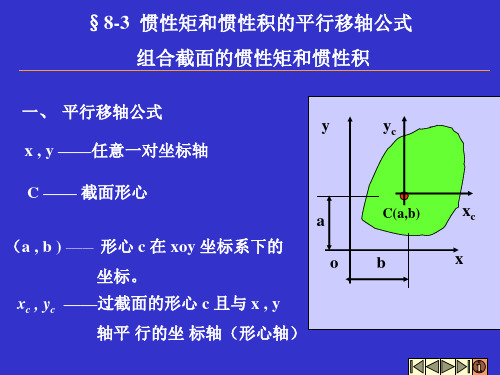
§8-3 惯性矩和惯性积的平行移轴公式 组合截面的惯性矩和惯性积
一、 平行移轴公式
y x , y ——任意一对坐标轴
C —— 截面形心
a
(a , b ) _____ 形心 c 在 xoy 坐标系下的
坐标。
o
xc , yc ——过截面的形心 c 且与 x , y 轴平 行的坐 标轴(形心轴)
第7章 截面几何性质答案

第七章 截面几何性质基本要求与重点1.形心与重心(1)理解重心与形心,熟知常见规则图形形心的位置。
(2)记住以下常见规则几何图形的形心位置:圆及圆环、矩形、三角形。
(3)能熟练计算,由规则图形构成的组合图形的形心位置。
2.面积静矩(又称静矩或面矩)(1)了解面积静矩的积分定义,掌握其有限式定义。
(2)能熟练计算组合图形的静矩。
(3)熟知面积静矩的重要性质。
3.惯性矩与极惯性矩。
(1)理解惯性矩与极惯性矩(2)了解惯性矩与极惯性矩的定义(3)掌握惯性矩与极惯性矩之间的关系(4)掌握平行轴定理及组合图形惯性矩的计算方法。
(5)记住圆及圆环对圆心的极惯性矩(6)记住矩形截面对其对称轴的惯性矩。
4.了解惯性积、形心主轴的概念主要内容1.形心与重心(1)概念与性质重心是物体的重力中心,形心是几何体的形状中心。
对均质物体,重心与形心位置重合。
若存在几何对称同,则形心必在对称轴上。
(2)计算形心位置的计算公式分积分式与代数式两种。
其中,常用的是代数形式的计算公式:11n n ic i ic ii i c c x A y A x y A A==⋅∆⋅∆==∑∑, 2.面积静矩(又称静矩或面矩)(1)定义:分为代数式和积分式两种形式有限式:几何图形的面积乘以形心到某轴的距离的坐标值,称为该图形对该轴的静矩。
积分式:几何图形的元面积乘以点到某轴的距离的坐标值,称为该元面积对该轴的静矩;所有点的元面积静矩之和,为几何图形的对该轴的静矩。
(2)面积静矩的重要性质:若图形对某轴的面积静矩为零,则该轴过这一图形的形心;反之亦然。
也就是说,静矩为零与轴过形心互为充要条件。
(3)计算根据实际情况可选用代数式或积分式进行计算,工程中主要是利用代数式进行计算。
11S S n nx ix i i c i i y A y A ====⋅∆=⋅∑∑11S S n ny iy i i c i i x A x A ====⋅∆=⋅∑∑3.惯性矩与极惯性矩。
建筑力学第七章 截面的几何性质

第七章平面图形的几何性质研究截面几何性质的意义从上章介绍的应力和变形的计算公式中可以看出,应力和变形不仅与杆的内力有关,而且与杆件截面的横截面面积A、极惯性矩I P、抗扭截面系数W P等一些几何量密切相关。
因此要研究构件的的承载能力或应力,就必须掌握截面几何性质的计算方法。
另一方面,掌握截面的几何性质的变化规律,就能灵活机动地为各种构件选取合理的截面形状和尺寸,使构件各部分的材料能够比较充分地发挥作用,尽可能地做到“物尽其用”,合理地解决好构件的安全与经济这一对矛盾。
第一节 静矩一、静距的概念Ay S z d d =Az S y d d =⎰⎰⎰⎰====AAy y AAz z Az S S A y S S d d d d zy d A yz静距是面积与它到轴的距离之积。
平面图形的静矩是对一定的坐标而言的,同一平面图形对不同的坐标轴,其静矩显然不同。
静矩的数值可能为正,可能为负,也可能等于零。
它常用单位是m 3或mm 3。
形心d A zyy zCx Cy ⎪⎪⎭⎪⎪⎬⎫⋅∆∑=⋅∆∑=A y A y Az A z C C ⎪⎪⎭⎪⎪⎬⎫==⎰⎰A ydA y A zdA z AC A C ⎪⎪⎭⎪⎪⎬⎫==A S y A S z z C y C ⎭⎬⎫⋅=⋅=C y C z z A S y A S 平面图形对z 轴(或y 轴)的静矩,等于该图形面积A 与其形心坐标y C (或z C )的乘积。
当坐标轴通过平面图形的形心时,其静矩为零;反之,若平面图形对某轴的静矩为零,则该轴必通过平面图形的形心。
如果平面图形具有对称轴,对称轴必然是平面图形的形心轴,故平面图形对其对称轴的静矩必等于零。
⎭⎬⎫⋅=⋅=C y C z z A S y A S二、组合图形的静矩根据平面图形静矩的定义,组合图形对z 轴(或y 轴)的静矩等于各简单图形对同一轴静矩的代数和,即⎪⎪⎭⎪⎪⎬⎫=+++==+++=∑∑==ni Ci i Cn n C C y ni Ci i Cn n C C z z A z A z A z A S y A y A y A y A S 1221112211 式中 y Ci 、z Ci 及A i 分别为各简单图形的形心坐标和面积;n 为组成组合图形的简单图形的个数。
第七章 静矩及其性质

Iy Iy i i 1 n I z I z i i 1 n I yz I yz i i 1
n
I z i 、 I y i、 I yz i 分别为第个i简单图形对y轴和z轴的惯 式中, 性矩和惯性积。
22
§7-3
17
例2
求图示矩形的 I z , I y , I yz ,i y ,iz z
dz z
h
c
y
b
1 3 b 3 bh I y z dA z A 12 3 h 2 1 3 2 I z y dA hb A 12 Iy 3 iy h A 6
2
h 2
Iz 3 iz b A 6 I yz yzdA 0
z
60 96 65 (77 ) 39.7(mm ) 96 77 13
§7-2
惯性矩和惯性积
y
z y dA z
一、简单图形的惯性矩 1、定义: dA对z轴的惯性距: dA对y轴的惯性距: 图形对z轴的惯性矩:
2
dIz y dA 2 dIy z dA o
I z y 2 dA,
求圆环圆形的 I z , I y z D d y
I P I P大 I P小
1 1 D 4 d 4 32 32 1 D 4 ( 1 4 ) 32
d D
I y I z I z大 I z小
1 D 4 (1 4 ) 64
21
三、组合图形的惯性矩及惯性积 根据定义可知,组合图形对某坐标轴的惯性矩 等于各个简单图形对同一轴的惯性矩之和;组合图 形对于某一对正交坐标轴的惯性积等于各个简单图 形对同一对轴的惯性积之和。用公式可表示为
第七章 截面几何性质 平行移轴公式

课时授课计划
第七章截面的几何性质
通过例子引入(让学生知道截面的重要性)
截面尺寸和形状完全相同的杆件,因为放置的方式不同,
其承载能力是大不相同的。
思考:抗弯能力与截面形状有何关系?
一、静矩与形心
平面图形对某轴的静矩等于其面积与形心
坐标(形心到该轴的距离)的乘积。
特性:
当坐标轴通过该平面图形的形心(简称形心轴)时,静矩等于零;反之,若平面图形对某轴的静矩等于零,则该轴必通过形心。
二、惯性矩
简单图形对其形心轴的的惯性矩
(见课本111页表7-1)
三、惯性矩的平行移轴公式
已知
对z 轴的惯性矩:
平行移轴定理,或称为平行移轴公式:截面对任意轴的惯性矩,等于截面对与该轴平行的形心轴的惯性矩加上截面面积与两轴间距离平方的乘积。
四、例题分析
1、T 字形截面尺寸及形心位置如下图所示,求该截面对其形心轴的惯性矩。
2、讲解:例8-7
五、讨论
形心的计算。
⎩⎨⎧+=+=b z z a y y C
C
⎰=A c z dA y I C
2
⎰=A z dA
y I 2⎰⎰++=+=A
C C A C z dA a a y y dA a y I )2()(2
2
2。
惯性矩抵抗矩面积矩

例6-4-1 在矩形内挖去一与上边 解 : 、建立坐标系如图。
内切的圆,求图形的形心主轴。
(b=1.5dy)
yc
x
xi A
、求形心位置。
Ai 0 0 A
O
x1
x
xc
y
yi Ai A
d d 2
2 3d 2
4
d 2
0.177d
4
、建立形心坐标系;求:Iyc , Ixc ,Ixcyc
1、主惯性轴和主惯性矩:坐标旋转到= 0 时;恰好有
Ix 0y 0 (Ix 2Iysi2n 0 Ixc y o 20s ) 0
与 0 对应的旋转轴x 0 y 0 称为主惯性轴;平面图形对主轴 之惯性矩主惯性矩。
tg20
2Ixcyc Ixc Iyc
主惯 I Ix y性 0 0Ix 2 矩 Iy: (Ix 2Iy)2Ix 2y
I I abA
点
xy xcyc
必
I I (a b)2A P Pc
须 为
形
心
y
例6-3-1 求图示圆对其切线AB的惯性矩.
解 :求解此题有两种方法:一是安
定义直接积分;二是用平行移轴
d
x
定理等知识求。
O
建立形心坐标如图,求图形对形心轴
的惯性矩。
B
I
d
4
I
I
圆 2 I
P 32
三、惯性积:面积与其到两轴距离之积。
A
I xy xydA
A
!如果 x 或 y 是对称轴,则,Ix y =0
第7章-截面图形的几何性质(PDF)

第7章 截面图形的几何性质教学提示:在对构件进行应力和强度等计算时,需要用到构件截面图形的几何性质,即与构件截面几何形状和尺寸有关的一些量,例如形心、静矩、惯性矩、惯性半径、极惯性矩、惯性积等。
本章的主要内容就是讨论这些几何性质的定义和计算。
教学要求:通过本章学习,要求理解形心、静矩、惯性矩、极惯性矩、惯性积和主惯性矩的概念,会用平行移轴公式计算组合截面对形心轴的惯性矩、主惯性矩等。
受力构件的承载能力,不仅与材料性能和加载方式有关,而且与构件截面的几何形状和尺寸有关。
当研究构件的强度、刚度和稳定性问题时,都要涉及到一些与截面形状和尺寸有关的几何量。
这些几何量包括:形心、静矩、惯性矩、惯性半径、极惯性矩、惯性积、主惯性矩等,统称为“截面图形的几何性质”。
研究这些几何性质时,完全不需考虑研究对象的物理和力学因素,只作为纯几何问题处理。
7.1 静矩与形心考察如图7.1所示任意截面几何图形。
在其上取面积微元d A ,设该微元在Oyz 坐标系中的坐标为(y 、z )。
定义下列积分d y AS z A =∫, d z AS y A =∫(7.1)图7.1分别为截面图形对y 轴和z 轴的静矩(或称为面积矩)。
其量纲为长度的三次方。
常用单位是3m 或3mm 。
由于均质等厚薄板的重心与薄板截面图形的形心有相同的坐标(C y 、C z ),而薄板的重心坐标由式(2.24)给出,即d d AAzCy V y A S y V AA ===∫∫d d y AAC z Vz A S z VAA===∫∫第7章 截面图形的几何性质·91··91·所以,形心坐标为d Az Cy A Sy AA==∫, d y ACz A S z AA==∫ (7.2a)或y C S A z =⋅,z C S A y =⋅(7.2b)由式(7.2)可知,若某坐标轴通过形心轴,则图形对该轴的静矩等于零,即若0C y =,则0z S =,或若0C z =,则0y S =;反之,若图形对某一坐标轴的静矩等于零,则该坐标轴必然通过图形的形心。
第7章-惯性矩与惯性积方案

10
y
I yc1
b1h13 12
a12h1
I yc1
10 125 3 12源自62.5 41.92
10 125
2.16 106 mm 4
矩形②对yc轴的惯性矩为:
I yc2
b2h23 12
a22h2
I yc2
70 103 12
5 41.92 70 10
截面对水平形心轴yc和垂直形心轴zc的惯性积
应等于矩形①对水平形心轴yc和垂直形心轴zc
yc
的惯性积加上矩形②对水平形心轴yc和垂直 形心轴zc的惯性积。即:
I I I yczc
yc zc 1
yczc 2
10
矩形①对yc和zc轴的惯性积为:
y
Iyczc 1 I yc1zc1 a1b1A1
A
惯性半径(工程中表示惯性矩的方法):
ix
Ix A
iy
Iy A
5
建筑力学
组合截面的惯性矩和惯性积 当截面由n个简单图形组合而成时,截面对于某根轴的惯
性矩等于这些简单图形对于该轴的惯性矩之和。即:
n
I y I y1 I y2 I y3 I yn I yi i 1 n
4
建筑力学
7.2 惯性矩和惯性积
惯性矩:面积对某轴的二次矩。
Ix
y 2 dA
A
I y
x2dA
A
极惯性矩:平面内任意面积dA与其到坐标原点距离平方的乘积。
IP
2dA
A
Ip Ix Iy
惯性积:面积与其到x轴、y轴距离的乘积称为该面积对坐
建筑力学 第7章 平面图形的

A2=200×40=8000,yc2=40/2=20 截面对Z轴的静矩为:
Sz1 Ai yci A1 yc1 A2 yc2 8000140 8000 20 1.28106
图7-7
7.2 惯性矩和惯性积
【例7-1】试求如图7-4所示工字形截面的 形心坐标。
解:将平面图形分割为三个矩形,每个图 形的面积和形心坐标分别为:
A1=80×40=3200,z1=0, y1=40+120+40/2=180
A2=120×40=4800, z2=0, y2=40+120/2=100
A3=40×120=4800, z3=0, y3=40/2=20
图7-6
2.组合平面图形的静矩 在工程实际中,经常会遇到由简单几何图形组合而
成的横截面构件,根据平面图形静矩的定义,组合图形对 z轴(或y轴)的静矩等于各简单图形对同一轴静矩的代数 和,即
S z
A1 yC1 A2 yC2 An yCn
n
Ai yCi
S y
我们把这些只与平面图形几何形状和尺
寸有关的几何量称之为平面图形的几何性质, 它是纯粹的几何问题,与研究对象的力学性 质无关,但它是影响构件承载力的重要因素。 例如,在前两章介绍的应力和变形的计算公 式中可以看出,应力和变形不仅与杆的内力 有关,还与杆件截面的横截面积A、极惯性 矩IP、抗扭截面系数WP等一些几何量密切 相关,以后在弯曲等问题中我们还会遇到平 面图形其它的一些几何性质。
2 19953750
Iy
I1y
I2y
640
惯性矩总结(含常用惯性矩公式)

惯性矩是一个物理量,通常被用作描述一个物体抵抗扭动,扭转的能力。
惯性矩的国际单位为(m^4)。
工程构件典型截面几何性质的计算2.1面积矩1.面积矩的定义图2-2.1任意截面的几何图形如图2-31所示为一任意截面的几何图形(以下简称图形)。
定义:积分和分别定义为该图形对z轴和y轴的面积矩或静矩,用符号S z和S y,来表示,如式(2—2.1)(2—2.1)面积矩的数值可正、可负,也可为零。
面积矩的量纲是长度的三次方,其常用单位为m3或mm3。
2.面积矩与形心平面图形的形心坐标公式如式(2—2.2)(2—2.2)或改写成,如式(2—2.3)(2—2.3)面积矩的几何意义:图形的形心相对于指定的坐标轴之间距离的远近程度。
图形形心相对于某一坐标距离愈远,对该轴的面积矩绝对值愈大。
图形对通过其形心的轴的面积矩等于零;反之,图形对某一轴的面积矩等于零,该轴一定通过图形形心。
3.组合截面面积矩和形心的计算组合截面对某一轴的面积矩等于其各简单图形对该轴面积矩的代数和。
如式(2—2.4)(2—2.4)式中,A和y i、z i分别代表各简单图形的面积和形心坐标。
组合平面图形的形心位置由式(2—2.5)确定。
(2—2.5)2.2极惯性矩、惯性矩和惯性积1.极惯性矩任意平面图形如图2-31所示,其面积为A。
定义:积分称为图形对O点的极惯性矩,用符号I P,表示,如式(2—2.6)(2—2.6)极惯性矩是相对于指定的点而言的,即同一图形对不同的点的极惯性矩一般是不同的。
极惯性矩恒为正,其量纲是长度的4次方,常用单位为m4或mm4。
(1)圆截面对其圆心的极惯性矩,如式(2—7)(2—2.7)(2)对于外径为D、内径为d的空心圆截面对圆心的极惯性矩,如式(2—2.8)(2—2.8)式中,d/D为空心圆截面内、外径的比值。
2.惯性矩在如图6-1所示中,定义积分,如式(2—2.9)(2—2.9)称为图形对z轴和y轴的惯性矩。
惯性矩是对一定的轴而言的,同一图形对不同的轴的惯性矩一般不同。
1、静矩与形心2、惯性矩、极惯性矩和惯性积3、平行移轴公

1. 转轴公式
y
y
A dA
C E
D
O
x
B
新坐标系ox1y1 旧坐标系o x y
x1 x cos y sin y1 y cos x sin
将上述关系代入平 面图形对x1轴的惯性矩:
x
I x1 A y12 d A
Ix1
cos2
y2 d A sin2
(4)由转轴公式得
80 aⅡ 20 10
40 C
bⅠ Ⅰ
aⅠ
xC
tan 20
2I xc yc I xc I yc
1.093
=113°.8
yc0
bⅡ
20 227 .6 0 113 .8
10 Ⅱ
I xc0
Imax
I xc
I yc 2
1 2
I xc
目录
§ I-2 极惯性矩 ·惯性矩 ·惯性积
1.极惯性矩(或截面二次极矩)
y
I p
2d A
A
2.惯性矩(或截面二次轴矩)
y
I y
x2 d A
A
I x
y2d A
A
O
由于 2 y2 x2
dA
x
x
所以
Ip
2 d A
A
(y2
A
x2)
dA IxIy
(B) Ixy<0 (D) Ix=Iy
(思考题I—2)A
y
bO
(思考题I—3)
x
a
y a
x
Ba
D
思考题I—3:等腰直角三角形如图所示,x、y轴是过斜边中点的
惯性矩的计算方法及常用截面惯性矩计算公式讲解

惯性矩的计算方法及常用截面惯性矩计算公式截面图形的几何性质一.重点及难点:(一).截面静矩和形心1.静矩的定义式如图1所示任意有限平面图形,取其单元如面积dA ,定义它对任意轴的一次矩为它对该轴的静矩,即ydAdSx xdAdS y == 整个图形对y 、z 轴的静矩分别为⎰⎰==AAy ydASx xdAS (I-1) 2.形心与静矩关系 图I-1设平面图形形心C 的坐标为C C z y , 则 0A S y x=, AS x y = (I-2) 推论1 如果y 轴通过形心(即0=x ),则静矩0=y S ;同理,如果x 轴通过形心(即0=y ),则静矩0=Sx ;反之也成立。
推论2 如果x 、y 轴均为图形的对称轴,则其交点即为图形形心;如果y 轴为图形对称轴,则图形形心必在此轴上。
3.组合图形的静矩和形心设截面图形由几个面积分别为n A A A A ⋯⋯321,,的简单图形组成,且一直各族图形的形心坐标分别为⋯⋯332211,,,y x y x y x ;;,则图形对y 轴和x 轴的静矩分别为∑∑∑∑========ni ni ii xi x ni ii n i yi y y A S S x A S 1111S (I-3)截面图形的形心坐标为∑∑===ni ini ii AxA x 11 , ∑∑===ni ini ii AyA y 11 (I-4)4.静矩的特征(1) 界面图形的静矩是对某一坐标轴所定义的,故静矩与坐标轴有关。
(2) 静矩有的单位为3m 。
(3) 静矩的数值可正可负,也可为零。
图形对任意形心轴的静矩必定为零,反之,若图形对某一轴的静矩为零,则该轴必通过图形的形心。
(4) 若已知图形的形心坐标。
则可由式(I-1)求图形对坐标轴的静矩。
若已知图形对坐标轴的静矩,则可由式(I-2)求图形的形心坐标。
组合图形的形心位置,通常是先由式(I-3)求出图形对某一坐标系的静矩,然后由式(I-4)求出其形心坐标。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
上式为计算惯性矩及惯性积的转轴公式。 若Iy1z1=0,则坐标轴y1和z1轴称为截面的主惯性轴;Iy1与Iz1 称为主惯性矩。当主惯性轴y1和z1通过形心时,则为形心主轴, 截面对形心主轴的惯性矩称为形心主矩。
11
建筑力学
主惯性矩Iyp与Izp的计算公式为:
I yp I zp Iy Iz 2 Iy Iz 2 1 2 1 2
i 1
n
I yz I yz1 I yz 2 I yz3 I yzn I yzi
i 1
6
n
建筑力学
[例] 求图示截面对x轴的惯性矩。
200mm
200mm
R80mm
x
解:图示截面看成是矩形截面在左右各方, 挖去两个半圆构成,因此,图示截面对x轴 的惯性矩等于矩形对x轴的惯性矩减去两个 半圆的惯性矩,即:
I yc zc I yc zc 1 I yc zc 2
C2
②
80
10
矩形①对yc和zc轴的惯性积为:
y
I yc zc 1 I yc1zc1 a1b1 A1
I yc zc 1 0 5 19.36 62.5 41.910125 3.7 105 mm4
I
2 I 4 I y z yz 2 2 I 4 I y z yz 2
tg 2 p
2 I yz Iy Iz
I
形心主惯性轴和形心主惯性矩的计算步骤:
(1) 确定组合截面形心的位置;
(2) 计算通过截面形心的一对坐标轴yc与zc的惯性矩Iyc 、 Izc 和惯性积Iyczc ; (3) 通过转轴公式确定形心主惯性轴的方位角α,并计算
10
建筑力学
7.4 主惯性轴和主惯性矩
z y z
dA
I y1 I z1
Iy Iz 2 Iy Iz 2 Iy Iz 2
I y Iz 2 Iy Iz 2
cos 2 I yz sin 2 cos 2 I yz sin 2
o
y
I y1z1
sin 2 I yz cos 2
建筑力学
7.1 静矩和形心
质心:物体总质量集中于一点。 重心:物体的重力的合力作用点 。
形心:截面图形的几何中心。质心是针对实物体而言的,而 形心是针对抽象几何体而言的,对于密度均匀的实物 体,质心和形心重合。
xC xdA
A
A
yC
A
ydA A
(10-1)
静矩:面积对某轴的一次矩。一般用S来表示。
z
10
单位:mm
解:将该截面看成由矩形①和矩形②组成,每个矩形 的面积和形心坐标分别为:
①
125 C1
矩形①:A1=1250 mm2,y1=5mm, z1=62.5mm
矩形②:A2=700 mm2,y2=45mm,
z2=5mm
C2
②
80
10
y
y1 A1 y2 A2 19.36mm A1 A2 z1 A1 z2 A2 zc 41.9mm A1 A2 yc
ix Ix A
iy
Iy A
5
建筑力学
组合截面的惯性矩和惯性积
当截面由n个简单图形组合而成时,截面对于某根轴的惯 性矩等于这些简单图形对于该轴的惯性矩之和。即:
I y I y1 I y 2 I y 3 I yn I yi
i 1
n
I z I z1 I z 2 I z 3 I zn I zi
A
惯性矩:面积对某轴的二次矩。
I y x 2 dA
A
极惯性矩:平面内任意面积dA与其到坐标原点距离平方的乘积。 I P 2 dA I p Ix I y A 惯性积:面积与其到x轴、y轴距离的乘积称为该面积对坐 标轴的惯性积。
I xy xydA
A
惯性半径(工程中表示惯性矩的方法):
3
I yc 2
所以可得:
I yc I yc1 I yc 2 3.119106 mm4
9
[例] 试计算截面对水平形心轴yc和垂直形心轴zc的惯性积。
z
10
zc
单位:mm
①
125 C1
C
yc
解:已算出该截面形心C的坐标为: yc=19.36mm,zc=41.9mm 截面对水平形心轴yc和垂直形心轴zc的惯性积 应等于矩形①对水平形心轴yc和垂直形心轴zc 的惯性积加上矩形②对水平形心轴yc和垂直 形心轴zc的惯性积。即:
解:已算出该截面形心C的坐标为: yc=19.36mm,zc=41.9mm 截面对轴yc的惯性矩应等于矩形①对轴yc的惯 性矩加上矩形②对yc轴的惯性矩。即:
C
yc
I yc I yc1 I yc 2
矩形①对yc轴的惯性矩为: 3 b1h1 2 I yc1 a1 h1 12
C2
②
80
10
C2
②
80
10
y
I yc zc 103 .2 104 mm4
0.981
可得:
tg 2α p
2 I yc zc I yc I z c
α p 22.30
I yp Izp
1 2 2 6 4 I yc I z c 4 I y 3 . 54 10 m m c zc 2 2 I yc I z c 1 2 2 5 4 I yc I z c 4 I y 6 . 0 10 m m c zc 2 2
I x I x矩形 I x圆形
bh3 d 4 200 2003 1604 Ix 1.01108 m m4 12 64 12 64
7
建筑力学
7.3 平移轴公式
I x I xc a 2 A I y I yc b2 A I xy I xc y c abA
形心主惯性矩Iyp和Izp 。
12
[例] 试确定截面形心主轴的位置以及计算截面的形心主矩。
z
10
单位:mm ①
125 C1
解:已算出该截面形心C的坐标为: yc=19.36mm,zc=41.9mm 并且已算出截面对于水平形心轴yc和铅直形 心轴zc的惯性矩和惯性积:
C
yc
I yc 311 .9 104 mm4 I zc 101 .4 104 mm4
矩形②对yc和zc轴的惯性积为: I yc zc 2 I yc 2 zc 2 a2b2 A2
I yc zc 2 0 45 19.36 5 41.9 7010 6.62105 mm4
所以可得:
I yc zc I yc zc 1 I yc zc 2 1.032106 mm4
S x ydA
A
S y xdA
A
(10-2)
1
建筑力学
S x yC A
S y xC A
从上式可以看出来,(1) 静矩为代数值,静矩的单位是m3、 mm3。(2) 平面图形的面积A与其形心到某一坐标轴的距离的 乘积称为平面图形对该轴的静矩。(3)不同截面对同一坐标轴 的静矩不同;同一截面对不同坐标轴的静矩也不同。(4)若图 形对某一轴的静距等于零,则该轴必然通过图形的形心;若 某一轴通过图形的形心,则图形对该轴的静距必然等于零。
截面对y轴的静矩 为:
S z A1z1 A2 z2 1250 62.5 700 5mm3 8.16104 mm3
Sz AzC A1 A2 zC 1250 700mm2 41.9mm
或
4
建筑力学
7.2 惯性矩和惯性积
I x y 2 dA
y
I yc 1
101253 2 62.5 41.9 10125 2.16106 m m4 12 70103 2 5 41.9 7010 9.59105 m m4 12
矩形②对yc轴的惯性矩为:
I yc 2
bh 2 2 2 a2 h2 12
y dA
C
y yC
O
xC x
x
2
建筑力学
组合图形的静矩和形心 截面对某一轴的静距等于其组成部分对同一轴的静距之和。 设截面图形由几个面积分别为A1、A2、A3…An,的简单图形 组成,且各图形的形心坐标分别为(x1,y1)、(x2,y2)、(x3, y3)…(xn,yn),则图形对x轴和y轴的静矩为:
I yc I z c
13
S x S xi Ai yi
i 1 i 1 n n
S y S yi Ai xi
i 1 i 1
n
n
截面图形的形心坐标为:
xC
Ax
i 1 n
n
i i
A
i 1
yC
Ay
i 1 n i
n
i
i
A
i 1
i
3
[例] 截面图形如图所示,试计算该截面图形形心位置和对y轴的静矩。
上式说明,截面图形对任一轴的惯性矩,等于图形对其平行 的形心轴的惯性矩加上两轴间距离的平方与图形面积之积;而 截面图形对于任意一对互相垂直轴的惯性积,等于图形对于与 其平行的一对形心轴的惯性积加上图形形心坐标与其面积之积。
8
[例] 试计算截面对水平形心轴yc的惯性矩。
z
10
单位:mm ①
125 C1
