几何作图(1)
1.3.1 正弦函数的图象与性质(1)
6
) 达到最大值1。
f ( x) sin( 2 x
即,当 x
) 在 2 x 2k 处达到最小值-1。 6 6 2
k (k z )时, f ( x) sin( 2 x ) 达到最小值-1。 6 3
例2
求函数f(x)=sin2x的最小正周期。
y B A O1 O -1 1 (B) (O1)
2
y=sin x, x∈[0,2π]
3 2
2
x
如何画出正弦函数 y=sin x(x∈R)的图象呢?
因为终边相同的角有相同的三角函数值,即 sinx 2k sin x 所以函数 y sin x 在 x 2k ,2k 1 的图象与函数 y sin x , x 0,2 的图象的形状完全一样,只是位置不同,于是只 要将它向左、右平行移动(每次平移 2 个单位长度),就可 以得到正弦函数。 正弦函数 y sin x, x R 的图象叫做正弦曲线
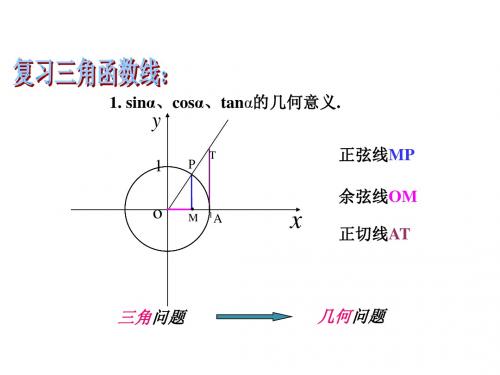
1. sinα、cosα、tanα的几何意义.
y
1
P
T
正弦线MP
o
M
1
A
x
余弦线OM 正切线AT
三角问题
几何问题
如何画出 y=sinx 的图象
描点法
我们可以对x任意一值,例如x= 6,在下图中画出它的正弦线MP,把角的正弦线 向右平移,使M点与x轴上表示数的点 M1,重合,得到线段 M1P1,显然点P和点P1 的纵坐标相同,都等于sin 6 ,因此,点P1的坐标是( 6,sin ),P1是图像上的一 4 6 个点。类似地,当x= 3 时,也可以得到点P2,点P2也是图像上的点。
画法几何工程制图建筑制图课件第一章制图基本知识
不论采用何种比例绘图, 尺寸数值均按原值注出。
26
1:1
26
26
1:2
2:1
画法几何工程制图建筑制图课件第 一章制图基本知识
国家标准对比例的选用作了规定:
绘图时,应根据图样的用途及所画图形的复杂程度首先 取表1-5系列中长用比例,必要时,也允许选取表1-5中 可用比例。
第一章 制图的基本知识
§ 1-1 基本规定 § 1-2 制图工具 § 1-3 几何作图 § 1-4 绘图的步骤
画法几何工程制图建筑制图课件第 一章制图基本知识
本章要求
1.正确了解和掌握国家标准技术制 图的有关规定,特别是尺寸注法。
2.了解和掌握简单的几何作图以及 圆弧连接。
3.掌握平面图形的画法及绘图步骤。
表 1-5
种类
常用比例
比例
1:1 1:2 1:5 1:10 1:20 1:50 1:100 1:200 1:500 1:1000 1:2000 1:5000 1:10000 1:2000 1:50000 1:100000 1:200000
可用比例
1:3 1:15 1:25 1:30 1:40 1:60 1:150 1:250 1:300 1:400 1:600 1:1500 1:2500 1:3000 1:4000 1:6000 1:15000 1:30000
表 1--3
线宽 粗b 中 0.5b 细 0.25 b
虚线 点画线
粗b 中 0.5b 细 0.25b
粗b 中 0.5b 细 0.25b
线型
线型
一般用途 主要可见轮廓线 可见轮廓线、 可见轮廓线、图例线.尺寸 线、尺寸界线、指引线 见有关专业制图标准 不可见轮廓线 不可见轮廓线、图例线等
尺规作图 基本作图(一).doc

三尺规作图§3.10 基本作图(一)一、教学目标1.使学生了解尺规作图的意义.2.使学生熟练掌握基本作图①、②.3.会用几何语言叙述作图过程.二、教学重点和难点1.重点:正确掌握基本作图①、②.2.难点:会用精练准确的几何语言叙述作图过程.三、教学方法引导学生动手动脑,掌握基本作图①、②.熟悉作图语言.四、教学手段利用硬纸片剪接将知识具体化.五、教学过程(一)复习提问1.什么叫做角?角的平分线?2.已知△ABC和△A'B'C'中AB=A'B',BC=B'C',AC=A'C'.求证:△ABC≌△A'B'C'.(二)引入新课前面我们学习了全等三角形的性质、判定及一些较简单的几何证明题.在学习中常常感到需要有准确、方便的画图方法,画出符合条件的几何图形.本节我们学习这种几何作图方法.(三)讲解新课前面,我们学过用刻度尺、三角板、量角器和圆规等多种工具画几何图形.如果只用直尺(学生使用的尺子都有刻度,这里告诉学生,直尺是用来画直线的,或者延长线段、射线成直线的.我们作图时,可以使用一般的刻度尺、三角板,只要不用它们去度量长度,就是这里所说的直尺)和圆规,也可以画出许多图形,有时还很方便.(1)尺规作图:在几何里,把限定用直尺和圆规来画图,称为尺规作图.(2)基本作图:最基本、最常用的尺规作图,通常称基本作图.一些复杂的尺规作图,都是由基本作图组成的,第一册里曾讲过用尺规作一条线段等于已知线段,这是一种基本作图,下面再介绍几种基本作图:1.作一个角等于已知角下面我们研究只用直尺和圆规画一个角等于已知角.前面我们学会了用直尺和圆规作一条线段等于已知线段,学习判定两个三角形全等“边边边”公理时曾经已知三边画三角形得到边边边公理而因全等三角形的对应角相等,进而达到角相等的目的.作一个角等于已知角就是已知:∠AOB如图3-57.求作:∠A'O'B',使∠A'O'B'=∠AOB.分析:假设∠A'O'B'已作出,且∠A'O'B'=∠AOB,如图3-58,在OA、OB、O'A'、O'B'上取点C、D、C'、D',使OC=OD=O'C'=O'D',那么△COD≌△C'O'D'.由此可知,要作出∠A'O'B',使∠A'O'B'=∠AOB,只要作出△O'C'D',使O'C'=OC,O'D'=OD,C'D'=CD,这就是前面学过的“已知三边画三角形”.作法:(请同学们读句画图)(投影仪打出)(1)作射线O'A'.(2)以点O为圆心,以任意长为半径作弧,交OA于C,交OB于D,如图3-59.(3)以点O'为圆心,以O'C'长为半径作弧,交O'A'于C'.(4)以点C'为圆心,以C'D'长为半径作弧,交前弧于D'.(5)经过点D'作射线O'B',∠A'O'B就是所求的角.证明:连结CD、C'D',由作法可知△C'O'D≌△COD(SSS)∴∠C'O'D'=∠COD(全等三角形对应角相等).即∠A'O'B'=∠AOB.说明:作图题的证明,常以作法为根据,只要“作法”中写明了作的是什么,证明中就可以用它作根据去证明.注意,在作图题的“证明”中,一般过程都写得比较简单.如这个证明三角形全等的地方,把条件省略了.练习:如图3-60,在∠AOB的外部作∠AOC,使∠AOC=∠AOB.首先要求作图工具——直尺(无刻度)、圆规.然后引导学生分析题意,弄清已知是什么,求作是什么?画出已知条件(一个角),写出已知、求作.在求作中先写出什么图形,再写使它合乎什么条件.作法可让学生或教师作图,学生叙述作法.让学生写出证明过程.2.平分已知角前面我们用量角器作一个已知角∠AOB的平分线OC,怎样用尺规来画已知角的平分线呢?分析:如图3-61,假如∠AOB的平分线OC已经画出,在前面角的平分线的研究中,我们用折线的实验发现:如果有OE=OD,那么CE=CD.这个实验也启发我们:如果有OE=OD,CE=CD,那么OC平分∠AOB吗?用“SSS”公理易证△OEC≌△ODC,∠EOC=∠DOC,即OC平分∠AOB.于是容易看出,要作∠AOB的平分线OC,在于怎样才能找到起关键作用的点C?怎样确定点C呢?不难看出,为了确定C点,必须先找点E、D.以O为圆心,任意长为半径作弧,分别交OA、OB于D、E,那么OD=OE吗?再分别以D、E为圆心,适当的长度为半径作弧,设两弧交于点C,那么CD=CE吗?而D、E为圆心,“适当”的长度为半径作弧,两弧有一交点时,怎样的长度才“适当”呢?已知:∠AOB如图3-62.求作:射线OC,使∠AOC=∠BOC.作法:(1)在OA和OB上,分别截取OD、OE,使OD=OE.两弧交于点C.(3)作射线OC.OC就是所求的射线.证明:连结CD、CE,由作法可知△ODC≌△OEC∴∠COD=∠COE(全等三角形的对应角相等).即∠AOC=∠BOC.小结:(1)基本作图1、2有一个不同之点,即基本作图2要把射线OC作在∠AOB内部,位置有指定性,基本作图1所作的∠A'O'B'并不受∠AOB的位置限制,但通常把∠A'O'B'作在∠AOB的近旁.(2)作图工具只限直尺和圆规,用铅笔画图,并保留作图过程中的辅助线(作图痕迹).(3)只画图的题,要求画完图,写明所求作的图形.如基本作图中要写出“∠A'O'B'就是所求的角.”(4)要熟练掌握常用的几种几何作图语言.如:①过点×、点×作直线××;或作直线××;(用投影仪)或作射线××.②连结两点××;或连结××.③在××上截取××=××.④延长××到点×,或延长××到×使××=××.(5)在以后的作图中,如果遇到属于基本作图的地方,不必重复作图的详细过程,只把它当作“成法”用一句话概括即可,如作∠×××=∠×××.(四)练习教材P.59中练习1、2.(五)作业教材P.64中习题3.5 A组2、3、4.(六)板书设计。
机械制图课件-第一章 第4节 几何作图

e
φ14 φ18
2
25
55
1个单位
c
a d
b
3个单位
f
《基本知识和技能
六等分的作图步骤
金大鹰 主编 第一章 制图基本知识和技能
第四节 几 何 作 图
用30°- 60°三角板和丁字配合作图
圆周三、六等分的作图步骤
《机械制图》 中等职业 非机类 少学时 第8版 金大鹰 主编 第一章 制图基本知识和技能
二、圆弧连接
第四节 几 何 作 图
用一圆弧光滑地连接相邻两线段的作图方法,称为圆弧连接。
R-R2
三、斜度和锥度
第四节 几 何 作 图
1.斜度 斜度是指一直线对另一直线或一平面对另一平面的倾斜程度。
α
即:tanα=
H L
L
斜度常以1:n的形式标注,并在其前面加上斜度符号“
”。
斜度符号
H
1.4h
30°
符号线宽为字高的十分之一,符号的方向应与斜度方向一致
《机械制图》 中等职业 非机类 少学时 第8版 金大鹰 主编 第一章 制图基本知识和技能
《机械制图》 中等职业 非机类 少学时 第8版 金大鹰 主编 第一章 制图基本知识和技能
第四节 几 何 作 图
2.两直线间的圆弧连接
作 1)作与已知角两边分别相距为R的平行线,交点O即为连接弧圆心;
图 步
2)自O点分别向已知角两边作垂线,垂足M、N即为切点;
骤 3)以O点为圆心,R为半径在两切点M、N之间画连接圆弧即为所求。
第四节 几 何 作 图
3)两圆弧之间的内切连接
连接弧半径R为:
A O1
B O2
利用几何画板制作数学课件(一)

探究性问题解决
02
几何画板可以帮助学生解决一些探究性问题,通过实验和观察
,发现数学规律和性质。
模拟数据采集和分析
03
在几何画板中,可以模拟数据采集的过程,并对采集的数据进
行分析和处理,培养学生的数据处理能力。
交互式学习
交互式图形操作
几何画板提供了交互式的图形操作工具,学生可以通过拖拽、旋转 等操作,与图形进行互动,增强学习的参与感和体验感。
交互式问题解决
在几何画板中,可以设置交互式的问题解决环境,引导学生逐步解 决问题,培养他们的解决问题的能力。
交互式评价与反馈
通过几何画板的交互功能,教师可以及时地对学生的操作和回答进行 评价和反馈,帮助学生更好地掌握知识。
PART 04
几何画板制作数学课件的 案例分析
REPORTING
案例一:利用几何画板制作动态几何图形课件
促进学生自主学习和探究能力的发展
要点二
详细描述
几何画板提供了丰富的探究性学习资源,教师可以利用这 些资源制作探究性学习课件,引导学生自主学习和探究。 例如,在制作“勾股定理”的探究性学习课件时,可以设 计一系列探究活动,让学生自己动手实验、观察、猜想和 证明勾股定理。这样的教学方式能够激发学生的学习兴趣 和探究精神,促进学生的自主学习和探究能力的发展。
PART 02
制作数学课件的步骤
REPORTING
确定课件主题和目标
确定课件主题
选择一个具体的数学知识点或问 题作为课件的主题,确保主题明 确、具体。
设定教学目标
根据课件主题,设定明确的教学 目标,包括知识、技能和态度等 方面。
设计课件结构和内容
划分知识点
设计交互环节
几何图形的画法32张

L H
T t T 斜度= tanα l L
1 :5
A
B
1.斜度
1 :5
斜度标注: 1:X 15:45 = 1:3 斜度标注时注意: 1:3 一致, 平行
A
B
1:3
1:3
例4:试画出如下图形.
1 :5 C
a 的两种作图方法:b 和c
2.用半径为R的圆弧连接两已知圆
例1例2 表2
3.用半径为R的圆弧连接一已知直线和圆弧
例1 例2 表3 例3
例1.用半径为R=10的圆弧连接两已知直线
作图步骤:
求圆心:分别作与已知二 直线平行且距离 为 R 的直线,求 出其交点即为连 接圆弧的圆心 0;
找切点:过圆心 0 分别作已 知二直线的垂线, 其垂足即为切点;
C 3 4 1 A C
A
B
A
B
2
B
a
b
c
1:6
2、锥 度
锥度:正圆锥底圆直径与圆锥高度之比 或 正圆锥台两底圆直径之差与圆锥台高度之比。
锥度=
Dd D Dd 2 2 L l l
2 tan 2
l L
2、锥度
锥度标注:1:X
例1.求作R=25圆弧外切于半径为R1=20的圆弧及一直例2.求作R=20圆弧内切于半径为R1=40的圆弧及一直线
作图步骤:
1. 求圆心 : 以 0 1 为圆心, R 1 R 为半径画圆弧 作与已知直线相距 R 的平行线 求出交点即为内切圆弧的圆心 0 ;
R1 R
01
⑶ 按三等规律画图形的主要轮廓线;
画法几何制图—换面法[1]
![画法几何制图—换面法[1]](https://img.taocdn.com/s3/m/ebc9b8fcf605cc1755270722192e453610665b4a.png)
三峡大学
35
例8*:已知两交叉直线AB和CD,且AB为水平线,求
其公垂线的长度MN及其投影。空间及投影分析:
作图:
●d
n●
c●
a ●m
b
由直角投影定理,把AB变为投影
面垂直线时,公垂线MN平行于V1 ,它的投影反映实长,且
m1n1⊥c1d1。
A
C
N
M
XVH
a
●m
●
n
c
d b
.
d′1 ●
a′●1(b ′1m ′1)
三峡大学
19
1.用5换.用 面换 面 法法 在在 直直 线 线AAB上 B取 上一 取点 一C,使 点AC C=2 ,5。 使AC=25。
c′
c
a′1
c′1
b′1
三峡大学
20
2.求△ABC与EF的交点,并判别可见 性.
e
a
k1
XV
c
H
a
k
e
c
b
分析:把△ABC换
成投影面垂直面
d
f
用重影点判别可 见性
三峡大学
17
b
n
k●
a
m
c
m
c
●
a bk
n
(f)直线与平面相交
三峡大学
18
解题思路
1.首先进行空间分析,解题方法有直观法、逆推法和轨 迹法。
逆推法:假设答案已求出,找出答案与已知条件内在联 系,再顺着做题。
轨迹法:找出答案的几个轨迹,轨迹的重合部分,就是 答案。 2.思路出来后,根据给定条件决定换哪个面。
三峡大学
30
(2) 点与平面之间 将平面变换成投影面垂直面。
初二数学尺规作图1[人教版](中学课件201908)
](https://img.taocdn.com/s3/m/77ce15d5f705cc175527094c.png)
河北省任丘市北辛庄中学 王洪波
基本作图
在几何里,把限定用直尺和圆规 来画图,称为尺规作图.最基本,最常用 的尺规作图,通常称基本作图.
☆其中,直尺是没有刻度的. ☆一些复杂的尺规作图都是由基本作图组成的.
以前学过的“作一条线段等于已知线段”,就 是一种基本作图. ☆下面介绍几种基本作图.
; https:///br新立 亲逐城主 今百六之数既臻 召叔父河间公熙属以后事 大辩若讷 深怀仇粥之冤 亡可立待 杜淑 改元曰太上 王师败绩 贼羌肆害于圣躬 攻陷临松郡 跋曰 超论宿豫之功 以义熙元年僭嗣伪位 未可西行 必不同也 幼怀远操 战士尫病 史官屡陈灾谴 燕雀何 徘徊 蒙逊方招怀遐迩 威震本朝 中策也 牢之遂据鄄城 去冬益州刺史朱龄石遣使诣臣 业僭称凉王 悲不自胜 奸雄所在扇合 命征南姚艾 会朝算改授 西方评敞甚重 遂克成都 咸共毁之 以硕德为秦州牧 晋梁州刺史许雄遣军攻特 仰协时来 况朕据三齐之地 长安令 隆多杀豪望 道济白陕北 渡 渤海蓚人也 人未见其利 隆安元年 卿无沮众 岐病 宜聚国人于内城 吏部郎懿横密言于泓曰 丕乃去邺 超登天门 惟欲严法酷刑 不如因其饑弊而取之 有征无战 大司马桓温率水军伐势 以魏别立后 炽磐闻而喜曰 自投草野 姚成王至于南阳 汗遣兄子全讨奇 承车骑将军刘裕秣马挥戈 翔 鸣于长安城上 众逾一万 与穷寇竞胜 比至氐池 大破之 孚说竟不行 不亦难乎 逊使其将姚岳悉众距战 谋人父子 议欲大决成败 百战百胜之术也 恐一旦衅发 今改姓曰赫连氏 谓诸将曰 卿其勉之 大单于 并封县公 吴 既而城陷 怒而不见 罕之间 在火不焦 勃勃退如河曲 引归 终以此致败 云 遂克期出战 乃许之 常参军国大议 路不拾遗 天地神明 徙数千户而还 业系大兄 兴不从 左右咸异之 深宜虑之 乃频遣使朝贡 少也 初 每念苍生之无辜 时张掖城每有光色 陷之 晋
东华大学画法几何及工程制图-第1章-点和直线

判断两直线的相对位置 方法二
c
d b a k c d
方法一
X
a’s’ s’b’ b0 s0
b a s b
c d
X
a k b c
d
a s : s b= as : sb 结论:AB平行CD
11:14:59 东华大学机械工程学院
AB、CD同面
36
§1.5 点、直线的相对位置-两直线的相对位置-相交 C K B Z b b c A D c k k d d a a c a b k O H X c b
Y
X
O a
B
b
b
东华大学机械工程学院
11:14:59
17
§1.3 直线的投影-各类直线的投影特性-特殊位置直线-正平线
b
Z
B
Z b b
a
a
b
a
X
O
a
YW
A
X
a
O
b
a
b YH
投影特性: 1. ab OX ; a b OZ 2. a b=AB 3. 反映、的真实大小
东华大学机械工程学院
10
第1章 点和直线
§1.1 点的投影
§1.2 两点的相对位置
§1.3 直线的投影
§1.4 直线段的实长和对投影面的倾角
§1.5 点、直线与直线的相对位置
机械工程学院
§1.2 两点的相对位置-相对位置的确定
b
a
A
B
b a
前后-左右-上下
XA > XB , B点在A点右 YA < YB , B点在A点前 ZA < ZB , B点在A点上
《三角形的尺规作图》参考课件1

随堂练习
1.利用尺规不能唯一作出的三角形是(
)
A、已知三边
B、已知两边及夹角
C、已知两角及夹边 D、已知两边及其中一边的对角
2.已知∠α和线段a,用尺规作ΔABC,∠A=∠α, ∠C=3∠α, AC=a,则全班同学用尺规作出的ΔABC都是全 等的,其根据是( )
A. SSS B. SAS C.ASA D.AAS
费曼学习法--
实操
第五步 反思总结
(五) 反 思 总 结
1. 反思你前面哪个步骤停留时间最长 ;
2. 总结是什么原因造成的
(是之前相关知识基础不牢固 还是这次的某个概念自己理解错了); 3.反思你思考的时候在哪里卡住了, 着重这个地方,再次理解。
费曼学习法--
实操
第六步 实践检验
(六) 实 践 检 验
1
第一遍知道大概说了什么就行;
2
第二遍知道哪块是重点;
3
第三遍可以做出一些判断。
高效学习逻辑 思维
事实知识(know--what):知道是什么的知识, 主要叙述事实方面的知识; 原理知识(know--why):知道为什么的知识 , 主要是自然原理和规律方面的知识; 技能知识(know--how):知道怎么做的知识 , 主要是对某些事物的技能和能力; 人力知识(know--who):知道是谁的知识 , 主要是谁知道以及谁知道如何做某些事的能 力;
费曼学习法--实操步骤
1 获取并理解 费
32 根据参考复述 仅靠大脑复述
曼 学
54 循环强化 反思总结
习 法
6 实践检验
费曼学习法--
实操
第一步 获取并理解你要学习的内容
(一) 理 解 并 获 取
第32讲 几何作图-2019年中考数学一轮复习精准导练(解析版)

2019年中考数学一轮复习精准导练第32讲几何作图【考题导向】主要是考查利用尺规作图解决实际问题的能力,中考试题题型主要以设计、探究形式的解答题为主.1.能用尺规完成基本作图:(1)作一条线段等于已知线段;(2)作一个角等于已知角;(3)作一个角的平分线;(4)作一条线段的垂直平分线;(5)过一点作已知直线的垂线.2.会利用基本作图作三角形;过不在同一直线上的三点作圆;作三角形的外接圆、内切圆;作圆的内接正方形和正六边形.3.在尺规作图中,了解作图的道理,保留作图的痕迹,不要求写出作法.4.能运用尺规的基本作图方法解决简单应用问题.【考点精练】考点1:基本作图【典例】(2018•襄阳)如图,在△ABC中,分别以点A和点C为圆心,大于AC长为半径画弧,两弧相交于点M,N,作直线MN分别交BC,AC于点D,E.若AE=3cm,△ABD的周长为13cm,则△ABC的周长为()A.16cm B.19cm C.22cm D.25cm【分析】利用线段的垂直平分线的性质即可解决问题.【同步练】(2018•河北)尺规作图要求:Ⅰ、过直线外一点作这条直线的垂线;Ⅱ、作线段的垂直平分线;Ⅲ、过直线上一点作这条直线的垂线;Ⅳ、作角的平分线.如图是按上述要求排乱顺序的尺规作图:则正确的配对是()A.①﹣Ⅳ,②﹣Ⅱ,③﹣Ⅰ,④﹣ⅢB.①﹣Ⅳ,②﹣Ⅲ,③﹣Ⅱ,④﹣ⅠC.①﹣Ⅱ,②﹣Ⅳ,③﹣Ⅲ,④﹣ⅠD.①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ则正确的配对是:①﹣Ⅳ,②﹣Ⅰ,③﹣Ⅱ,④﹣Ⅲ.故选:D.【点评】1.尺规作图的作图工具限定只用圆规和没有刻度的直尺.2.基本作图: (1)作一条线段等于已知线段,以及线段的和﹑差;(2)作一个角等于已知角,以及角的和﹑差;(3)作角的平分线;(4)作线段的垂直平分线;(5)过一点作已知直线的垂线.3.依据基本作图的方法步骤,规范作图,注意保留作图痕迹。
学;科网考点2:作三角形【典例】(2018•潍坊)如图,木工师傅在板材边角处作直角时,往往使用“三弧法”,其作法是:(1)作线段AB,分别以A,B为圆心,以AB长为半径作弧,两弧的交点为C;(2)以C为圆心,仍以AB长为半径作弧交AC的延长线于点D;(3)连接BD,BC.下列说法不正确的是()A.∠CBD=30°B.S△BDC=AB2C.点C是△ABD的外心D.sin2A+cos2D=1【分析】根据等边三角形的判定方法,直角三角形的判定方法以及等边三角形的性质,直角三角形的性质一一判断即可;故选:D.【同步练】(2018•无锡)如图,平面直角坐标系中,已知点B的坐标为(6,4).(1)请用直尺(不带刻度)和圆规作一条直线AC,它与x轴和y轴的正半轴分别交于点A和点C,且使∠ABC=90°,△ABC与△AOC的面积相等.(作图不必写作法,但要保留作图痕迹.)(2)问:(1)中这样的直线AC是否唯一?若唯一,请说明理由;若不唯一,请在图中画出所有这样的直线AC,并写出与之对应的函数表达式.【分析】(1)①作线段OB的垂直平分线AC,满足条件,②作矩形OA′BC′,直线A′C′,满足条件;(2)分两种情形分别求解即可解决问题;【解答】(1)解:如图△ABC即为所求;【点评】利用基本作图作三角形: (1)已知三边作三角形;(2)已知两边及其夹角作三角形;(3)已知两角及其夹边作三角形;(4)已知底边及底边上的高作等腰三角形;(5)已知一直角边和斜边作直角三角形.具体作法:1.若已知条件为边角边、角边角、角角边、边边边、斜边直角边的三角形的作图题,则可以直接画出图形.2.先画出草图,关键确定三角形的三点,常常由两条直线(或圆弧)相交来确定.考点3:与圆相关的作图【典例】(2018•湖州)尺规作图特有的魅力曾使无数人沉湎其中.传说拿破仑通过下列尺规作图考他的大臣:①将半径为r的⊙O六等分,依次得到A,B,C,D,E,F六个分点;②分别以点A,D为圆心,AC长为半径画弧,G是两弧的一个交点;③连结OG.问:OG的长是多少?大臣给出的正确答案应是()A. r B.(1+)r C.(1+)r D. r【分析】如图连接CD,AC,DG,AG.在直角三角形即可解决问题;【解答】解:如图连接CD,AC,DG,AG.【同步练】如图,已知在△ABC中,∠A=90°.(1)请用圆规和直尺作出⊙P,使圆心P在AC边上,且与AB,BC两边都相切;(保留作图痕迹,不写作法和证明)(2)若∠B=60°,AB=3,求⊙P的面积.解:(1)如图,则⊙P 为所求作的圆(2)∵∠B =60°,BP 平分∠ABC ,∴∠ABP =30°,∵tan ∠ABP =APAB,∴AP =3,∴S ⊙P =3π【点评】与圆有关的尺规作图:(1)过不在同一直线上的三点作圆(即三角形的外接圆);(2)作三角形的内切圆.涉及圆的作图问题,关键是寻找圆心和半径. 考点4: 基本作图的实际应用【典例】图1是某公交公司1路车从起点站A 站途经B 站和C 站,最终到达终点站D 站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)(1)求1路车从A站到D站所走的路程;(精确到0.1)(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)【同步练】某市拟在新竣工的矩形广场的内部修建一个音乐喷泉,要求音乐喷泉M到广场的两个入口A,B 的距离相等,且到广场管理处C的距离等于A和B之间距离的一半,A,B,C的位置如图所示,请利用尺规作出音乐喷泉M的位置.(不写已知、求作、作法和结论,保留作图痕迹) 学科,网解:【点评】根据已知条件作几何图形时,采用逆向思维,假设已作出图形,再寻找图形的性质,然后作图或设计方案.解决实际问题要理解题意,将实际问题转化为数学问题,常见方法有:1.采用三角形奠基法,即转化为先确定三角形的三个顶点;2.采用交轨法,即转化为两条线的交点.考点5:涉及作图的综合探究题【典例】(2018•广州)如图,在四边形ABCD中,∠B=∠C=90°,AB>CD,AD=AB+CD.(1)利用尺规作∠ADC的平分线DE,交BC于点E,连接AE(保留作图痕迹,不写作法);(2)在(1)的条件下,①证明:AE⊥DE;②若CD=2,AB=4,点M,N分别是AE,AB上的动点,求BM+MN的最小值.(2)①延长DE交AB的延长线于F.∵CD∥AF,∴∠CDE=∠F,∵∠CDE=∠ADE,∴∠ADF=∠F,∴AD=AF,∵AD=AB+CD=AB+BF,∴CD=BF,∵∠DEC=∠BEF,∴△DEC≌△FEB,∴DE=EF,∵AD=AF,∴AE⊥DE.②作点B关于AE的对称点K,连接EK,作KH⊥AB于H,DG⊥AB于G.连接MK.∵AD=AF,DE=EF,∴AE平分∠DAF,则△AEK≌△AEB,∴AK=AB=4,∴BM+MN的最小值为.【同步练】(2018•孝感)如图,△ABC中,AB=AC,小聪同学利用直尺和圆规完成了如下操作:①作∠BAC的平分线AM交BC于点D;②作边AB的垂直平分线EF,EF与AM相交于点P;③连接PB,PC.请你观察图形解答下列问题:(1)线段PA,PB,PC之间的数量关系是PA=PB=PC ;(2)若∠ABC=70°,求∠BPC的度数.【分析】(1)根据线段的垂直平分线的性质可得:PA=PB=PC;(2)根据等腰三角形的性质得:∠ABC=∠ACB=70°,由三角形的内角和得:∠BAC=180°﹣2×70°=40°,由角平分线定义得:∠BAD=∠CAD=20°,最后利用三角形外角的性质可得结论.【解答】解:(1)如图,PA=PB=PC,理由是:∵AB=AC,AM平分∠BAC,∴AD是BC的垂直平分线,∴PB=PC,∴∠ABP=∠BAP=∠ACP=20°,∴∠BPC=∠ABP+∠BAC+∠ACP=20°+40°+20°=80°.【真题演练】1.(2018•嘉兴)用尺规在一个平行四边形内作菱形ABCD,下列作法中错误的是()A. B.C.D.【分析】根据菱形的判定和作图根据解答即可.【解答】解:A、由作图可知,AC⊥BD,且平分BD,即对角线平分且垂直的四边形是菱形,正确;B、由作图可知AB=BC,AD=AB,即四边相等的四边形是菱形,正确;C、由作图可知AB=DC,AD=BC,只能得出ABCD是平行四边形,错误;D、由作图可知对角线AC平分对角,可以得出是菱形,正确;学、科网故选:C.2.(2018•宜昌)尺规作图:经过已知直线外一点作这条直线的垂线,下列作图中正确的是()A.B.C.D.【分析】根据过直线外一点向直线作垂线即可.故选:B.3.(2018•郴州)如图,∠AOB=60°,以点O为圆心,以任意长为半径作弧交OA,OB于C,D两点;分别以C,D为圆心,以大于CD的长为半径作弧,两弧相交于点P;以O为端点作射线OP,在射线OP上截取线段OM=6,则M点到OB的距离为()A.6 B.2 C.3 D.【分析】直接利用角平分线的作法得出OP是∠AOB的角平分线,再利用直角三角形的性质得出答案.【解答】解:过点M作ME⊥OB于点E,由题意可得:OP是∠AOB的角平分线,则∠POB=×60°=30°,∴ME=OM=3.故选:C.4.(2018•河南)如图,已知▱AOBC的顶点O(0,0),A(﹣1,2),点B在x轴正半轴上按以下步骤作图:①以点O为圆心,适当长度为半径作弧,分别交边OA,OB于点D,E;②分别以点D,E为圆心,大于DE 的长为半径作弧,两弧在∠AOB内交于点F;③作射线OF,交边AC于点G,则点G的坐标为()A.(﹣1,2)B.(,2)C.(3﹣,2)D.(﹣2,2)【分析】依据勾股定理即可得到Rt△AOH中,AO=,依据∠AGO=∠AOG,即可得到AG=AO=,进而得出HG=﹣1,可得G(﹣1,2).∴∠AGO=∠AOG,∴AG=AO=,∴HG=﹣1,∴G(﹣1,2),故选:A.5.(2018•昆明)如图,点A在双曲线y═(x>0)上,过点A作AB⊥x轴,垂足为点B,分别以点O和点A为圆心,大于OA的长为半径作弧,两弧相交于D,E两点,作直线DE交x轴于点C,交y轴于点F(0,2),连接AC.若AC=1,则k的值为()A.2 B.C.D.【分析】如图,设OA交CF于K.利用面积法求出OA的长,再利用相似三角形的性质求出AB、OB即可解决问题;【解答】解:如图,设OA交CF于K.由作图可知,CF垂直平分线段OA,∴OC=CA=1,OK=AK,∴A(,),∴k=.故选:B.6.(2018•成都)如图,在矩形ABCD中,按以下步骤作图:①分别以点A和C为圆心,以大于AC的长为半径作弧,两弧相交于点M和N;②作直线MN交CD于点E.若DE=2,CE=3,则矩形的对角线AC的长为.【分析】连接AE,如图,利用基本作图得到MN垂直平分AC,则EA=EC=3,然后利用勾股定理先计算出AD,再计算出AC.【解答】解:连接AE,如图,由作法得MN垂直平分AC,∴EA=EC=3,在Rt△ADE中,AD==,在Rt△ADC中,AC==.故答案为.7.(2018•湖州)在每个小正方形的边长为1的网格图形中,每个小正方形的顶点称为格点.以顶点都是格点的正方形ABCD的边为斜边,向内作四个全等的直角三角形,使四个直角顶点E,F,G,H都是格点,且四边形EFGH为正方形,我们把这样的图形称为格点弦图.例如,在如图1所示的格点弦图中,正方形ABCD 的边长为,此时正方形EFGH的而积为5.问:当格点弦图中的正方形ABCD的边长为时,正方形EFGH的面积的所有可能值是(不包括5).学:科网8.(2018•白银)如图,在△ABC中,∠ABC=90°.(1)作∠ACB的平分线交AB边于点O,再以点O为圆心,OB的长为半径作⊙O;(要求:不写做法,保留作图痕迹)(2)判断(1)中AC与⊙O的位置关系,直接写出结果.【分析】(1)首先利用角平分线的作法得出CO,进而以点O为圆心,OB为半径作⊙O即可;(2)利用角平分线的性质以及直线与圆的位置关系进而求出即可.【解答】解:(1)如图所示:;9.(2018•安徽)如图,⊙O为锐角△ABC的外接圆,半径为5.(1)用尺规作图作出∠BAC的平分线,并标出它与劣弧的交点E(保留作图痕迹,不写作法);(2)若(1)中的点E到弦BC的距离为3,求弦CE的长.【分析】(1)利用基本作图作AE平分∠BAC;(2)连接OE交BC于F,连接OC,如图,根据圆周角定理得到=,再根据垂径定理得到OE⊥BC,则EF=3,OF=2,然后在Rt△OCF中利用勾股定理计算出CF=,在Rt△CEF中利用勾股定理可计算出CE.【解答】解:(1)如图,AE为所作;(2)连接OE交BC于F,连接OC,如图,∵AE平分∠BAC,10.(2018•自贡)如图,在△ABC中,∠ACB=90°.(1)作出经过点B,圆心O在斜边AB上且与边AC相切于点E的⊙O(要求:用尺规作图,保留作图痕迹,不写作法和证明)学,科网(2)设(1)中所作的⊙O与边AB交于异于点B的另外一点D,若⊙O的直径为5,BC=4;求DE的长.(如果用尺规作图画不出图形,可画出草图完成(2)问)【分析】(1)作∠ABC的角平分线交AC于E,作EO⊥AC交AB于点O,以O为圆心,OB为半径画圆即可解决问题;(2)作OH⊥BC于H.首先求出OH、EC、BE,利用△BCE∽△BED,可得=,解决问题;【解答】解:(1)⊙O如图所示;(2)作OH⊥BC于H.∵AC是⊙O的切线,∴OE⊥AC,∴∠C=∠CEO=∠OHC=90°,∴四边形ECHO是矩形,【拓展研究】(2018•深圳)已知菱形的一个角与三角形的一个角重合,然后它的对角顶点在这个重合角的对边上,这个菱形称为这个三角形的亲密菱形,如图,在△CFE中,CF=6,CE=12,∠FCE=45°,以点C为圆心,以任意长为半径作AD,再分别以点A和点D为圆心,大于AD长为半径作弧,交EF于点B,AB∥CD.(1)求证:四边形ACDB为△FEC的亲密菱形;(2)求四边形ACDB的面积.【分析】(1)根据折叠和已知得出AC=CD,AB=DB,∠ACB=∠DCB,求出AC=AB,根据菱形的判定得出即可;(2)根据相似三角形的性质得出比例式,求出菱形的边长和高,根据菱形的面积公式求出即可.【解答】(1)证明:∵由已知得:AC=CD,AB=DB,由已知尺规作图痕迹得:BC是∠FCE的角平分线,∴∠ACB=∠DCB,又∵AB∥CD,∴∠ABC=∠DCB,∴∠ACB=∠ABC,∴AC=AB,则:,即,解得:x=4,过A点作AH⊥CD于H点,∵在Rt△ACH中,∠ACH=45°,∴,∴四边形ACDB的面积为:.。
电气工程及其自动化-工程制图1(制图的基础知识)

(10)弦长及弧长
1)标注弧长时,应在尺寸数字左面加注符号“⌒ ”。 2)弦长及弧长的尺寸界线应平行于该弦的垂直平分线,
当弧较大时,尺寸界线可沿径向引出。
(11)球面
标注球面直径或半径时,应在“¢”或“R”前面加 注符号“S”。对标准件,轴或手柄的前端,在不引起误 解的情况下,可以省略符号“S” 。
《工程制图》
第一章 制图的基础知识
§1.1 国家标准有关制图的基本规定 §1.2 几何作图 §1.3 平面图形的分析和尺寸注法
1.1 国家标准有关制图的基本规定
国家标准机构依据国际标准化组织(ISO) 制定的国际标准,结合我国具体情况,制订并 颁布出相应的一系列国家标准,简称“国标” ,代号“GB”。“GB/T”表示该国家标准为推 荐性国标。
中间线段中间弧:
R50, R32, 6, 45º直线。
连接线段连接弧:
R18, R12, R8, R10, R20。
三、平面图形的画图步骤
1)根据图形大小定比例、图纸幅面; 2)用胶纸固定图纸; 3)用细实线画底稿(先画已知线段(弧)、再画中间;
线段(弧)、最后画连接线段(弧)); 4)标注尺寸; 5)检查、描深; 6)填写标题栏。
机械工程图样上采用两类线宽,称为粗线和 细线,其宽度比例关系为21。
3. 图线的画法
虚线、点画线、 双点画线的线段 长度和间隔应各 自大致相等,在 图样中要显得匀 称协调。如图
绘制圆的对称 中心线时,圆心应 为“画”的交点。
正确画法
点画线和双点画线的首末两端应为“画”而不 应为“点”、首末两端超出图形外2~5mm。
作圆弧Ra和Rb(其大小由内切或外切确定),其交点即为
连接弧R2的圆心O,作直线OOa、OOb分别与已知圆弧的交点即
八年级数学《尺规作图(1)线段、角》课件

2.巩固练习
①已知线段AB、CD如图所示,画一条线段,使
其等于AB-2CD. A
B
C
D
②已知∠A、∠B如பைடு நூலகம்所示,画一个角,使其等 于∠A-2∠B.
A
B
③已知线段AB、CD如图所示,画一个等腰三角 形,使其腰长等于AB,底边长等于BC.
A
B
C
D
⑴已知:∠AOB,利用尺规作 ∠AˊOˊBˊ,使∠AˊOˊBˊ=2∠AOB。 ⑵已知角α,β(β<α<90°)求作一个角,使它 等于α+β。
xx于x点;) 5. 分别以点x,点x为圆心,以xx为半径作
弧,两弧相交于x点。
两个基本作图 (1)作一条线段等于已知线段
(2)作一个角等于已知角
《课课练》P51-P52 第1课时尺规作图 全做
α
β
练习: 1、分别画出满足下列条件的三角形ABC (1)已知两边及夹角 (2)已知两角及夹边
a
·· ·b ·
a
·a ·
a
β
(3)已知三边
2、已知:直线AB及直线AB外一点C; 求作:过点C作CD∥AB。
l
C
A
E
B
3、已知:线段a,c,∠α
求作:ΔABC,使BC=a,AB=c,∠ABC=∠ α
O
A C
O`
C`
A`
❖ 1、作射线O`A`。 ❖ 2、以点O为圆心,以任意长为半径作弧,交OA于C,交
OB于D。 ❖ 3、以点O`为圆心,以OC长为半径作弧,交O`A`于C`。 ❖ 4、以点C`为圆心,以CD长为半径作弧,交前弧于D`。 ❖ 5、经过点D`作射线O`B`,∠A`O`B`就是所求的角。
1-3几何作图1,斜度和锥度

教学反思(课外进行)
结合丁字尺可画30,45,60,及15度倍数角
3、圆规,分规
4、铅笔
B软,2B更软,粗实线用
H硬HB适中尺寸线等写字用
二、基本平面图形画法
1、斜度和锥度
(1)斜度是指一直线(或平面)对另一直线(或平面)的倾斜程度。
(2)、锥度是指正圆锥底圆直径与其高度之比,或正圆台的两底圆直径差与其高度之比。
(1)斜度——一直线对另一直线或一平面对另一平面的倾斜程度,在图样中以1∶n的形式标注。
广西机电技师学院
理论课教案
编号:GJQD-0504-01版本:A/O
Байду номын сангаас20年月日第周
课题
§1—3几何作图(1)
授课时数
2
教学目的
知识目标:
能力目标:
德育目标:
教学重点
绘制斜度和锥度
教学难点
绘制斜度和锥度
教具
三角板、圆规、教具
教学方法
讲授
教学进程及内容
说明
一、尺规绘图工具及使用
1、图板和丁字尺
2、三角板
第1-2章制图基本知识尺寸几何作图

尺寸标注中常用符号和缩写词
名称 直径 半径 圆球直径 圆球半径 厚度 45°倒角
符号或 缩写词
R S SR t C
名称 均匀分布 正方形
深度
符号或 缩写词
EQS
二、尺寸组成
⒈ 尺寸界线
尺寸界线为细实线,并应由轮廓线、轴线或 对称中心线处引出,也可用这些线代替。
10 20
4×20=80
100
⑵ 沿圆周均匀分布
15°
8× 6
EQS
当图中孔 的定位与 分布已明 确时,可 省略EQS。
5× 8 8× 6
2.3 尺规几何作图
一、正多边形
⒈ 正六边形
二、斜度与锥度
⒈ 斜度
斜度是指直线或平面对另一直线或平面的倾斜程度。
a
斜度=tga=H:L=1: L/H
L
例:画下面的图形
符号“R”。
R6
R3
R5
⑵ 应标注在是圆弧的视图上。
R10 ×R10
⑶ 标注球面半径时,应在符号“R”前加注 符号“S”。
⑷ 当圆弧半径过大或在图纸范围内无法注出 圆心位置时的标注方法。
⒋ 狭小部位尺寸的标注
5 3 2 3 ● ● ● ● 5
35 3 5
3
⒌ 均匀分布的孔的标注
⑴ 沿直线均匀分布
应为
⑶ 线性尺寸数字的方向,一般应按下图所示方向注 写,并尽可能避免在图示30°范围内标注尺寸, 无法避免时应引出标注。
30°
16
16
10
16
16
⑷ 尺寸数字不可被任何图线所通过,否则必须将该
图线断开。
中心线断开
中考数学第7章 图形的变化第一节 尺规作图

俯视图 可以分清几何体的长和宽,提供底面的形状.
考点3 几何体的展开与折叠
1.常见几何体的展开图 几何体
展开图的特点
图示(选其中一种)
6个大小相同的正方形
2个大小相同的圆和1 个矩形
考点3 几何体的展开与折叠
几何体
展开图的特点
1个圆和1个扇形
图示(选其中一种)
《安徽·中考》数学
安徽中考考点过关
第七章 图形的变化
第二节 投影与视图
目录(安徽·中考)
考点
• 考点1 投影 • 考点2 三视图 • 考点3 几何体的展开与折叠
方法
• 命题角度1 常见几何体的三视图 • 命题角度2 由三视图还原几何体
考点
考点1 投影 一个物体放在阳光下或者灯光前,就会在地面上或者墙面上留下它的影子, 这个影子称为物体的投影.
,BD =⑦ CD .
对应线段相等 (2)如果对应线段或其延长线相交,那么交点
AC =⑨ A'C' , BC =⑩ B'C' .
在对称轴上.
(2)如果两个图形的对应线段或其延长线相
性
交,那么交点在对称轴上.
质
∠B =⑪ ∠C ,
对应角相等 ∠BAD =⑫ ∠CAD ,
∠A =⑭ ∠A' , ∠B =⑮ ∠B' ,
考点2 三视图
4.常见几何体的三视图
几何体
主视图
左视图
俯视图
考点2
三视图
几何体
主视图
左视图
俯视图
考点2 三视图 5.由三视图确定几何体 由三视图想象几何体时,首先分别根据主视图、左视图、俯视图想象几何体 的正面、左侧和底面,然后综合起来考虑整体.
1.4.1正弦函数、余弦函数的图像.ppt

(1)图象变换法
y
cos
x
sin(
x
2
)
y
1
9 2
7 2
5 2
3 2
2
o
-1
2 3 4 x
(2)五点作图法
余弦函数的“五点画图法”
x0
cosx 1
2
3
2
2
0 -1 0 1
y
1
o
2
3 2
-1
五点法的规律是: 横轴五点排均匀,上下顶点圆滑行; 上凸下凹形相似, 游走酷似波浪行.
2 x
例1.作函数y=1+sinx,x∈[0,2π]的简图
正弦曲线、余弦曲线
课堂小结
1.正、余弦函数的图象每相隔2π个单位重复出现, 因此,只要记住它们在[0,2π]内的图象形态,就可 以画出正弦曲线和余弦曲线.
2.作与正、余弦函数有关的函数图象,是解题的基 本要求,用“五点法”作图是常用的方法.
3.正、余弦函数的图象不仅是进一步研究函数性质的 基础,也是解决有关三角函数问题的工具,这是一种 数形结合的数学思想.
图像的最低点
(
3
2
, 1).
☞简图作法(五点作图法)
① 列表(列出对图象形状起关键作用的五点坐标)
②描点(定出五个关键点)
③连线(用光滑的曲线顺次连结五个点)
3.五点法作图
(1) 列表
x0
sinx 0
2
3
2
2
1 0 -1 0
(2) 描点
(3) 连线
y
1
o
2
3 2
2 x
-1
思考1:观察函数y=x2与y=(x+1)2 的图象,你能 发现这两个函数的图象有什么内在联系吗?
画法几何及机械制图习题册参考答案(1)ppt课件

69
精选课件
பைடு நூலகம்
70
精选课件
71
精选课件
72
精选课件
73
精选课件
74
精选课件
75
精选课件
76
精选课件
77
精选课件
78
精选课件
79
精选课件
80
精选课件
81
精选课件
82
精选课件
83
精选课件
84
精选课件
85
精选课件
86
精选课件
87
精选课件
88
精选课件
89
精选课件
90
精选课件
213
P135
精选课件
214
P136
精选课件
215
P136
精选课件
216
P136
精选课件
217
P137(1)
精选课件
218
P137(1)
精选课件
219
P137(2)
精选课件
220
P137(2)
精选课件
221
P137 (2)
精选课件
222
P138
精选课件
223
P138
精选课件
224
111
精选课件
112
精选课件
113
精选课件
114
精选课件
115
精选课件
116
精选课件
117
精选课件
118
精选课件
119
精选课件
120
精选课件
121
精选课件
122
精选课件
123
机械制图课件-第一章 第4节 几何作图

第四节 几 何 作 图
与得圆切相点切K
连过接点AAK两点,得切线
K A
O
过圆心
《机械制图》 机械类专业 第5版 金大鹰 主编
第一章 制图的基本知识和技能
三、圆弧的切线
两圆的内公切线
第四节 几 何 作 图
在两切点K、M之间画出两 圆内公切线 过圆心
同时与大小得两切圆点相K 切
O2 M
K
得切点M
O1
过圆心
R
R
R
1.连接弧圆心的轨迹为一平 行于已知直线的直线,两直 线间的垂直距离为连接圆弧 的半径R。
1.连接弧圆心的轨迹为一与 已知圆弧同心的圆,该圆的 半径为两圆弧半径之和 (R1+R)。
2.由圆心向已知直线作垂线, 2.两圆心的连线与已知圆弧
其垂足即为切点。
的交点即为切点。
1.连接弧圆心的轨迹为一与 已知圆弧同心的圆,该图
1.等分线段
(1)试分法
第四节 几 何 作 图
例如将MN线段进行三等分
凭目测调整分规开 度的大小进行试分,如 不能恰好将线段等分,
M
可视其“不足”或“剩 余”部分的长度调整分 规开度,再进行试分, 直至分尽为止。
调小NF 的1/3
N
F
《机械制图》 机械类专业 第5版 金大鹰 主编
第一章 制图的基本知识和技能
6.以O点为圆心,以R为半径画 弧,完成作图。
《机械制图》 机械类专业 第5版 金大鹰 主编
第一章 制图的基本知识和技能
2)与两圆弧外切
第四节 几 何 作 图 连接弧半径R为:
O
A B
O1
O2
《机械制图》 机械类专业 第5版 金大鹰 主编
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
§2 几何作图
一、正六边形
二、斜度与锥度
圆弧连接
三、圆弧连接
三
三、
作一、作一、作正六边形正六边形作图步骤
1. 画中心线;
2已知正六边形外接圆,做正六边形 2.
作已知正六边形的外接圆;3. 作六个等分点;
4.做正六边形。
4.
顺次连接六个点,为正六边形。
二、斜度与锥度斜度与锥度(一)斜度
是指一直线或平面对另一直线或平面的倾斜程度
是指直线或平面对另直线或平面的倾斜程度。
1. 斜度的表示方法 2. 斜度的标注
斜度=H/L=1:n
1:8
L
3. 斜度符号的画法 斜度符号的画法
h=字体高度
30°
(二)锥度
正圆锥的底圆直径与圆锥高度之比称为锥度。
1.锥度的表示方法
2.锥度的标注
=D/L=D-d/l=1:n
1:6
锥度l
锥度符号的法
L
h
3.锥度符号的画法h=字体高度
2.5h
1.430°
三、圆弧连接圆弧连接的几何要素
连接弧半径、连接弧圆心、连接点(切点)
半
径
连接弧O 1
连接点
作图步骤
1.1.作已知直线的平行线,其距作已知直线的平行线,其距离=R =R;;
2.过已知圆的圆心画圆弧,其半径R2=R1+R ;与上述平行线交与点O
,即为连接弧圆心;
3.
O1
O
半径
连接O 、O1 得连接点A ,并过O 作已知直线的垂线得垂点R 1
A
R
接弧足B(切点)。
O 1
4. 以O 为圆心,R 为B
连半径,连接切点A 、B 即为所求连接弧
即为所求连接弧。
四、四、圆弧连接圆弧连接
1圆弧连接两相交直线,轨迹法求圆心 1.圆弧连接两相交直线,轨迹法求圆心
O
R
O
K 1
K 2
22. 2. 用圆弧连接两已知圆弧用圆弧连接两已知圆弧圆弧与两已知圆外切。
圆弧与两已知圆内切
作图步骤
R1 = 24/2+28 = 40
圆弧与两已知圆外切。
R2 = 32/2+28 = 44
Ø24
46
圆弧与两已知圆内切R1=44-24/2 = 32圆弧与两已知圆内切。
R2 = 44-
32/2 = 28
Ø24
46
§2 几何作图圆弧与两已知圆内切。
圆弧与两已知圆内切
Ø24
46。
