一次函数特殊平行四边形存在性.doc
八年级(下)数学 同步讲义 四边形的存在性

四边形的存在性内容分析本节包含两部分,平行四边形的存在性及梯形的存在性,常见题型是存在菱形和正方形,根据题目中的条件及特殊的平行四边形的性质构造等量关系,求出相应的点的坐标;常见的梯形的问题中,经常需要添加辅助线,考察学生的分类讨论思想及逻辑思维能力.知识结构模块一平行四边形的存在性知识精讲平行四边形的问题是近几年来考试的热点,考察学生的分类讨论的思想.常见的题型是在平面直角坐标系中已知三点和第四点构成平行四边形,求第四点;或者已知两点,另外两点在某函数图像上,四点构成平行四边形;利用两点间的距离公式和平移的思想,结合题目中的条件构造等量关系进行求解即可.在几何中,平行四边形的判定方法有如下几条:①两组对边互相平行;②两组对边分别相等;③一组对边平行且相等;④对角线互相平分;⑤两组对角相等。
在压轴题中,往往与函数(坐标轴)结合在一起,运用到④⑤的情况较少,更多的是从边的平行、相等角度来得到平行四边形.- 2 -ABCM 1M 2M 31、 知识内容:已知三点后,其实已经固定了一个三角形(平行四边形的一半),如图ABC .第四个点M 则有3种取法,过3个顶点作对边的平行线且取相等长度即可(如图中3个M 点).2、 解题思路:(1) 根据题目条件,求出已知3个点的坐标; (2) 用一点及其对边两点的关系,求出一个可能点; (3) 更换顶点,求出所有可能的点;(4) 根据题目实际情况,验证所有可能点是否满足要求并作答.【例1】 如图所示,在梯形ABCD 中,AD ∥BC ,∠B =90°,AD =24 cm ,BC =26 cm ,动点P 从点A 出发沿AD 方向向点D 以1cm /s 的速度运动,动点Q 从点C 开始沿着CB 方向向点B 以3cm /s 的速度运动.点P 、Q 分别从点A 和点C 同时出发,当其中一点到达端点时,另一点随之停止运动.(1)经过多长时间,四边形PQCD 是平行四边形; (2)经过多长时间,四边形PQBA 是矩形.例题解析思路剖析【例2】 如图,在平面直角坐标系中,点A 的坐标为A (3, 0),点B 的坐标为B (0, 4).(1)求直线AB 的解析式;(2)点C 是线段AB 上一点,点O 为坐标原点,点D 在第二象限,且四边形BCOD 为菱形,求点D 坐标;(3)在(2)的条件下,点E 在x 轴上,点P 在直线AB 上,且以B 、D 、E 、P 为顶点 的四边形是平行四边形,请写出所有满足条件的点P 的坐标.【例3】 如图,在平面直角坐标系中,过点(2,3)的直线y =kx +2与x 轴交于点A ,与y 轴交于点B ,将此直线向下平移3个单位,所得到的直线l 与x 轴交于点C . (1)求直线l 的表达式;(2)点D 为该平面直角坐标系内的点,如果以点A 、B 、C 、D 为顶点的四边形是平行 四边形,求点D 的坐标.ABOxyAB Oxy【例4】如图,已知直线l1经过点A(-5,-6)且与直线l2:362y x=-+平行,直线l 2与x轴、y轴分别交于点B、C.(1)求直线l1的表达式及其与x轴的交点D的坐标;(2)判断四边形ABCD是什么四边形.并证明你的结论;(3)若点E是直线AB上一点,平面内存在一点F,使得四边形CBEF是正方形,求点E的坐标,请直接写出答案.【例5】直线364y x=-+与坐标轴分别交与点A、B两点,点P、Q同时从O点出发,同时到达A点,运动停止.点Q沿线段OA运动,速度为每秒1个单位长度,点P沿O B A→→运动.(1)直接写出A、B两点的坐标;(2)设点Q的运动时间为t秒,△OPQ的面积为S,求出S与t之间的函数关系式.(3)当485S=时,求出点P的坐标,并直接写出以点O、P、Q为顶点的平行四边形的第四个顶点M的坐标.xOy- 4 -【例6】 已知:如图,四边形ABCD 是菱形,∠B 是锐角,AF ⊥BC 于点F , CH ⊥AD 于点H , 在AB 边上取点E ,使得AE =AH ,在CD 边上取点G ,使得CG =CF .联结EF 、FG 、GH 、HE .(1)求证:四边形EFGH 是矩形;(2)当∠B 为多少度时,四边形EFGH 是正方形.并证明.【例7】 如图所示,平面直角坐标系中,O 是坐标原点,正比例函数y =kx (x 为自变量)的图像与双曲线2y x=-交于点A ,且点A 的横坐标为2-.(1)求k 的值;(2)将直线y =kx (x 为自变量)向上平移4个单位得到直线BC ,直线BC 分别交x 轴、y 轴于B 、C ,如点D 在直线BC 上,在平面直角坐标系中求一点,使以O 、B 、D 、P 为顶点的四边形是菱形.ABC OxyABCDEFGH- 6 -【例8】 在直角△ABC 中,∠C =90°,∠A =30°,AB =4,将一个30°角的顶点P 放在AB边上滑动,保持30°角的一边平行于BC ,且交边AC 于点E ,30°的另一边交射线BC 于点D ,连ED .(1)如图,当四边形PBDE 为等腰梯形时,求AP 长;(2)四边形PBDE 有可能为平行四边形吗.若可能,求出PBDE 为平行四边形时,AP 的长,若不可能,说明理由;(3)若点D 在BC 边上(不与B 、C 重合),试写出线段AP 的取值范围.ABCDE P梯形的分类讨论题多见于各类压轴题中,由于这类题目都与图形的运动有关,需要学生有一定的想象力、分析力和运算力.梯形的主要特征是两底平行,特殊梯形又可分为等腰梯形和直角梯形两大类.常见题型为在直角坐标平面内已知三点求第四点,抓住梯形两底平行的特征,对应的一次函数的解析式的k 相等而b 不相等.若是等腰梯形,常需添设辅助线,过上底的两个顶点作下底的垂线,构造两个全等的直角三角形.若是直角梯形,则需连接对角线或过上底的一顶点作下底的高构造直角三角形.【例9】 在梯形ABCD 中,AD ∥BC ,AD =12cm ,DC =8cm ,且∠C =60°,动点P 以1cm/s的速度从点A 出发,沿AD 方向向点D 移动,同时,动点Q 以2cm /s 的速度从点C 出发,沿C 出发,沿CB 方向向点B 移动,连接PQ ,(1)得四边形ABQP 和四边形PQCD .若设移动的时间为t 秒(0<t <7),四边形PQCD 的面积为ycm ²,求y 与t 的函数关系式;(2)当t 为何值时,四边形QPCD 是等腰梯形.说明理由; (3)当t 为何值时,四边形PQCD 是直角梯形.模块二 梯形的存在性知识精讲例题解析QPBCDA- 8 -【例10】 如图,一次函数33y x b =+的图像与x 轴相交于点A (53,0)、与y 轴相交于点B . (1)求点B 的坐标及∠ABO 的度数;(2)如果点C 的坐标为(0,3),四边形ABCD 是直角梯形,求点D 的坐标【例11】 如图,在平行四边形ABCD 中,O 为对角线的交点,点G 为BC 的中点,点E 为线段BC 延长线上的一点,且CE =12BC ,过点E 作EF //CA ,交CD 于点F ,联结OF .(1)求证:OF //BC ;(2)如果四边形OBEF 是等腰梯形,判断四边形ABCD 的形状,并给出证明.【例12】 如图,在平面直角坐标系中,直线l 1经过O 、A (1,2)两点,将直线l 1向下平移6AB C OxyABCDEFGO个单位得到直线l 2,交x 轴于点C ,B 是直线l 2上一点,且四边形ABCO 是平行四边形.(1)求直线l 2的表达式及点B 的坐标;(2)若D 是平面直角坐标系内的一点,且以O 、A 、C 、D 四个点为顶点的四边形是等腰梯形,求点D 的坐标.【例13】 已知一次函数142y x =-+的图像与x 轴、y 轴分别相交于点A 、B ,梯形AOBC 的边AC =5.(1) 求点C 的坐标;(2) 如果点A 、C 在一次函数y =kx +b (k 、b 为常数,且k <0)的图像上,求这个一次 函数的解析式【例14】 如图1,在平面直角坐标系中,已知点A (0,2),点P 是x 轴上一动点,以线段APAOC xy为一边,在其一侧作等边三角形APQ.当点P运动到原点O处时,记Q的位置为B.(1)求点B的坐标;(2)当点P在x轴上运动(P不与O重合)时,求证:∠ABQ=90°;(3)是否存在点P,使得以A、O、Q、B为顶点的四边形是梯形.若存在,请求出点P 的坐标;若不存在,请说明理由.ABOPQ xyABO xy图1备用图- 10 -【例15】 在直角平面内,O 为原点,点A 的坐标为(1,0),点C 的坐标为(0,4),直线CM ∥x 轴(如图所示).点B 与点A 关于原点对称,直线y =x +b (b 为常数)经过点B ,且与直线CM 相交于点D ,连接OD . (1)求b 的值和点D 的坐标;(2)设点P 在x 轴的正半轴上,若△POD 是等腰三角形,求点P 的坐标;(3)若动点P 在x 轴的正半轴上,以每秒2个单位长的速度向右运动;动点Q 在射线CM 上,且以每秒1个单位长的速度向右运动,若P 、Q 分别由O 点、C 点同时出发,问几秒后,以P 、Q 、O 、D 为顶点的四边形可以成为平行四边形;以P 、Q 、O 、D 为顶点的四边形是否可以成为等腰梯形.写出理由.1AO4CxMy- 12 -【习题1】 如图,在平面直角坐标系中,函数y =2x +12的图像分别交x 轴、y 轴于A 、B两点.过点A 的直线交y 轴正半轴于点C ,且点C 为线段OB 的中点. (1)求直线AC 的表达式;(2)如果四边形ACPB 是平行四边形,求点P 的坐标.【拓展】如果以A 、C 、P 、B 为顶点的四边形是平行四边形,求点P 的坐标.【习题2】 如图,在平面直角坐标系中,直线162y x =-+与y 轴交于点A ,与直线12y x =相交于点B ,点C 是线段OB 上的点,且△AOC 的面积为12. (1)求直线AC 的表达式;(2)设点P 为直线AC 上的一点,在平面内是否存在点Q ,使四边形OAPQ 为菱形, 若存在,求点Q 的坐标,若不存在,请说明理由.随堂检测ABCOxy ABO xy【习题3】 如图,已知在梯形ABCD 中,AD//BC ,∠B =90°,AD =24cm ,AB =8cm ,BC =26cm ,动点P 从A 点开始沿AD 边以1cm /s 的速度向D 运动,动点Q 从C 点开始沿CB 边以3 cm /s 的速度向B 运动,P 、Q 分别从A 、C 同时出发,当其中一点到端点时,另一点也随之停止运动.设运动时间为t 秒,当t 为何值时,线段PQ =CD .【作业1】 如图,在平面直角坐标系中,一次函数的图像与反比例函数的图像相交于A 、B两点,点A 的坐标为(2,3),点B 的横坐标为6. (1)求反比例函数与一次函数的解析式;(2)如果点C 、D 分别在x 轴、y 轴上,四边形ABCD 是平行四边形,求直线CD 的表达式.课后作业ABCDQPAB CDABOxy【作业2】已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.(1)求点A的坐标;(2)若k<0,在直角坐标平面内有一点D,使四边形ABOD是一个梯形,且AD∥BO,其面积又等于20,试求点D的坐标.【作业3】定义[p,q]为一次函数y=px+q的特征数.(1)若特征数为[3,k-1]的一次函数为正比例函数,求k的值;(2)一次函数y=kx+b的图像与x轴交于点A(3-,0),与y轴交于点B,且与正比例函数43y x=的图像的交点为C (m,4).求过A、B两点的一次函数的特征数;(3)在(2)的条件下,若点D与A、O、C构成的四边形为平行四边形,直接..写出所有符合条件的点D的坐标.A BCO x y- 14 -【作业4】 如图所示,直线y =-2x +12,分别与x 轴、y 轴交于点A 、B ,点C 是线段AB 的中点,点D 在线段OC 上,点D 的纵坐标是4. (1) 求点C 的坐标和直线AD 的解析式;(2) P 是直线AD 上的点,请你找出一点Q ,使得以O 、A 、P 、Q 这四个点为顶点的 四边形是菱形,写出所有满足条件的Q 的坐标.BA Cyx。
一次函数之平行四边形存在性问题

一次函数与平行四边形1.线段中点公式平面直角坐标系中,点A 坐标为(x 1,y 1),点B 坐标为(x 2,y 2),则线段AB 的中点P 的坐标为 (2,22121y y x x ++) 例:如图,已知点A (-2,1),B (4,3),则线段AB 的中点P 的坐标是________.2.线段的平移平面内,线段AB 平移得到线段A'B' ,则①AB ∥A'B' ,AB =A'B' ;②AA'∥BB',AA'= BB'. 如图,线段AB 平移得到线段A'B' ,已知点A (-2,2),B (-3,-1), B' (3,1),则点A'的坐标是________.%例:如图,在平面直角坐标系中,□ABCD 的顶点坐标分别为A (x 1,y 1)、B (x 2,y 2)、C (x 3,y 3)、D (x 4,y 4),已知其中3个顶点的坐标,如何确定第4个顶点的坐标"例:如图,已知□ABCD 中A (-2,2),B (-3,-1), C (3,1),则点D 的坐标是________. 方法一:利用线段平移总结:x 1-x 2= x 4-x 3,y 1-y 2= y 4-y 3 或者 x 4-x 1= x 3-x 2,y 4-y 1= y 3-y 2 等方法二:利用中点公式总结:x 1+x 3= x 2+x 4,y 1+y 3= y 2+y 4类型一:三定一动例1 、如图,平面直角坐标中,已知中A(-1,0),B(1,-2),C (3,1),点D是平面内一动点,若以点A、B、C、D为顶点的四边形是平行四边形,则点D的坐标是_________________________________.*总结:三定一动问题,可以通过构造中点三角形得以解决.说明:若题中四边形ABCD是平行四边形,则点D的坐标只有一个结果________【例1】.一次函数y =x +3与y =﹣x +q 的图象都过点A (m ,0),且与y 轴分别交于点B 、C .(1)试求△ABC 的面积;(2)点D 是平面直角坐标系内的一点,且以点A 、C 、B 、D 为顶点的四边形是平行四边形,请直接写出点D 的坐标;(3)过△ABC 的顶点能否画一条直线,使它能平分△ABC 的面积若能,求出直线的函数关系式,若不能,说明理由.【解答】解:(1)将点A (m ,0)代入y =x +3中,得$m +3=0,解得m =﹣3,即点A (﹣3,0),将点A (﹣3,0)代入y =﹣x +q 中,得q =﹣3,∴点B (0,3)、C (0,﹣3),故S =12×BC ×AO =9;(2)满足条件的D 点坐标为D (﹣3,6)、D (﹣3,﹣6)、D (3,0);(3)若过点A ,则得直线l :y =0;若过点C ,则得直线l :y =﹣3x ﹣3;@若过点B ,则得直线l :y =3x +3.例2.如图,在平面直角坐标系xOy 中,已知直线PA 是一次函数y =x +m (m >0)的图象,直线PB 是一次函数y =﹣3x +n (n >m )的图象,点P 是两直线的交点,点A 、B 、C 、Q 分别是两条直线与坐标轴的交点.(1)用m 、n 分别表示点A 、B 、P 的坐标及∠PAB 的度数;(2)若四边形PQOB 的面积是112,且CQ :AO =1:2,试求点P 的坐标,并求出直线PA 与PB的函数表达式;(3)在(2)的条件下,是否存在一点D ,使以A 、B 、P 、D 为顶点的四边形是平行四边形若存在,求出点D 的坐标;若不存在,请说明理由.【解答】解:(1)在直线y =x +m 中,令y =0,得x =﹣m .∴点A (﹣m ,0).…在直线y =﹣3x +n 中,令y =0,得x =x 3. ∴点B (x 3,0). 由{x =x +x x =−3x +x ,得{x =x −x 4x =x +3x 4,∴点P (x −x 4,x +3x 4). 在直线y =x +m 中,令x =0,得y =m ,∴|﹣m |=|m |,即有AO =QO .又∵∠AOQ =90°,∴△AOQ 是等腰直角三角形,∴∠PAB =45°.(2)∵CQ :AO =1:2,,∴(n ﹣m ):m =1:2,整理得3m =2n ,∴n =32m , ∴x +3x 4=32x +3x 4=98m , 而S 四边形PQOB =S △PAB ﹣S △AOQ =12(x 3+m )×(98m )−12×m ×m =1132m 2=112, 解得m =±4,∵m >0,∴m =4,∴n =32m =6,∴P (12,92). !∴PA 的函数表达式为y =x +4,PB 的函数表达式为y =﹣3x +6.(3)存在.过点P 作直线PM 平行于x 轴,过点B 作AP 的平行线交PM 于点D 1,过点A 作BP 的平行线交PM 于点D 2,过点A 、B 分别作BP 、AP 的平行线交于点D 3.①∵PD 1∥AB 且BD 1∥AP ,∴PABD 1是平行四边形.此时PD 1=AB ,易得x 1(132,92); ②∵PD 2∥AB 且AD 2∥BP ,∴PBAD 2是平行四边形.此时PD 2=AB ,易得x 2(−112,92);③∵BD 3∥AP 且AD 3∥BP ,此时BPAD 3是平行四边形.】∵BD 3∥AP 且B (2,0),∴y BD 3=x ﹣2.同理可得y AD 3=﹣3x ﹣12{x =x −2x =−3x −12, 得{x =−52x =−92,∴x 3(−52,−92).3.如图,在等边△ABC 中,BC =8cm ,射线AG ∥BC ,点E 从点A 出发沿射线AG 以1cm /s 的速度运动,同时点F 从点B 出发沿射线BC 以2cm /s 的速度运动,设运动时间为t (s ).(1)连接EF ,当EF 经过AC 边的中点D 时,求证:△ADE ≌△CDF ;(2)填空:#①当t 为 s 时,以A 、F 、C 、E 为顶点的四边形是平行四边形;②当t 为 s 时,四边形ACFE 是菱形.【解答】(1)证明:∵AG ∥BC ,∴∠EAD =∠DCF ,∠AED =∠DFC ,∵D 为AC 的中点,∴AD =CD ,∵在△ADE 和△CDF 中,{∠xxx =∠xxx∠xxx =∠xxx xx =xx,∴△ADE ≌△CDF (AAS );(2)解:①当点F 在C 的左侧时,根据题意得:AE =tcm ,BF =2tcm ,·则CF =BC ﹣BF =6﹣2t (cm ),∵AG ∥BC ,∴当AE =CF 时,四边形AECF 是平行四边形,即t =8﹣2t ,解得:t =83; 当点F 在C 的右侧时,根据题意得:AE =tcm ,BF =2tcm ,则CF =BF ﹣BC =2t ﹣8(cm ),∵AG ∥BC ,∴当AE =CF 时,四边形AEFC 是平行四边形,即t =2t ﹣8,]解得:t =8;综上可得:当t =83或8s 时,以A 、C 、E 、F 为顶点四边形是平行四边形.②若四边形ACFE 是菱形,则有CF =AC =AE =8,则此时的时间t =8÷1=8(s );故答案是:83或8;8.|4.已知,Rt △OAB 的两直角边OA 、OB 分别在x 轴和y 轴上,如图1,A ,B 坐标分别为(﹣2,0),(0,4),将△OAB 绕O 点顺时针旋转90°得△OCD ,连接AC 、BD 交于点E .(1)求证:△ABE ≌△DCE .(2)M 为直线BD 上动点,N 为x 轴上的点,若以A ,C ,M ,N 四点为顶点的四边形是平行四边形,求出所有符合条件的M 点的坐标.(3)如图2,过E 点作y 轴的平行线交x 轴于点F ,在直线EF 上找一点P ,使△PAC 的周长最小,求P 点坐标和周长的最小值.【分析】(1)由A 、B 的坐标可求得AO 和OB 的长,由旋转的性质可求得OC 、OD 的长,从而可求得∠AEB =90°,再由勾股定理可求得CD 和AB 的长,可求得AB =CD ,可证得△ABE ≌△DCE ;(2)由B 、D 坐标可求得直线BD 解析式,当M 点在x 轴上方时,则有CM ∥AN ,则可求得M 点纵坐标,代入直线BD 解析式可求得M 点坐标,当M 点在x 轴下方时,同理可求得M 点纵坐标,则可求得M 点坐标;)(3)由AE =DE 可知A 、D 关于EF 对称,连接CD 交EF 于点P ,则P 点即为满足条件的点,由C 、D 坐标可求得直线CD 的解析式,则可求得P 点坐标,利用勾股定理可分别求得AC 和CD 的长,则可求得此时△PAC 的周长.【解答】解:(1)∵A (﹣2,0),B (0,4),∴OA =2,OB =4,∵将△OAB 绕O 点顺时针旋转90°得△OCD ,∴OC =OA =2,OD =OB =4,AB =CD ,∴∠ACO =∠ECB =∠CBE =45°,∴∠CEB =90°,∴∠AEB =∠CED ,且CE =BE ,在Rt △ABE 和Rt △DCE 中:{xx =xx xx =xx∴Rt △ABE ≌Rt △DCE (HL );(2)由(1)可知D (4,0),且B (0,4),∴直线BD 解析式为y =﹣x +4,当M 点在x 轴上方时,则有CM ∥AN ,即CM ∥x 轴,∴M 点到x 轴的距离等于C 点到x 轴的距离,∴M 点的纵坐标为2,在y =﹣x +4中,令y =2可得x =2,∴M (2,2);当M 点在x 轴下方时,同理可得M 点的纵坐标为﹣2,(在y =﹣x +4中,令y =﹣2可求得x =6,∴M 点的坐标为(6,﹣2);综上可知M 点的坐标为(2,2)或(6,﹣2);(3)由(1)可知AE =DE ,∴A 、D 关于直线EF 对称,连接CD 交EF 于点P ,则PA =PD , ∴PA +PC =PD +PC =CD ,∴满足△PAC 的周长最小,∵C (0,2),D (4,0),∴可设直线CD 解析式为y =kx +2,∴4k +2=0,解得k =−12, ∴直线CD 解析式为y =−12x +2,∵A (﹣2,0),D (4,0),∴F (1,0),即直线EF 解析式为x =1,在y =−12x +2中,令x =1可得y =32, ∴P (1,32), 在Rt △AOC 中,由勾股定理可求得AC =2√2, 在Rt △COD 中,由勾股定理可求得CD =√22+42=2√5, ∴PA +PC +AC =CD +AC =2√5+2√2, 即△PAC 的周长最小值为2√5+2√2.。
一次函数的性质

一次函数的性质一次函数y=kx+b (k≠0) k>0,b>0,则图象过1,2,3象限k>0,b<0,则图象过1,3,4象限k<0,b>0,则图象过1,2,4象限k<0,b<0,则图象过2,3,4象限当k>0时,y随x的增大而增大;图像经过一、三象限当k<0时,y随x的增大而减小;图像经过二、四象限二次函数y=ax^2+bx+ca>0开口向上a<0开口向下a,b同号,对称轴在y轴左侧,反之,再y轴右侧|x1-x2|=根号下b^2-4ac除以|a|与y轴交点为(0,c)b^2-4ac>0,ax^2+bx+c=0有两个不相等的实根b^2-4ac<0,ax^2+bx+c=0无实根b^2-4ac=0,ax^2+bx+c=0有两个相等的实根对称轴x=-b/2a顶点(-b/2a,(4ac-b^2)/4a)顶点式y=a(x+b/2a)^2+(4ac-b^2)/4a函数向左移动d(d>0)个单位,解析式为y=a(x+b/2a+d)^2+(4ac-b^2)/4a,向右就是减函数向上移动d(d>0)个单位,解析式为y=a(x+b/2a)^2+(4ac-b^2)/4a+d,向下就是减正比例函数与反比例函数形如y=kx(k为常数,且k不等于0),y就叫做x的正比例函数.图象做法:1.带定系数2.描点3.连线图象是一条直线,一定经过坐标轴的原点性质:当k>0时,图象经过一,三象限,y随x的增大而增大当k<0时,图象经过二,四象限,y随x的增大而减小形如y=k/x(k为常数且k≠0) 的函数,叫做反比例函数。
自变量x的取值范围是不等于0的一切实数。
反比例函数的图像为双曲线。
它可以无限地接近坐标轴,但永不相交.性质:当k>0时,图象在一,三象限,在每个象限内,y随x的增大而减小,当k<0时,图象在二,四象限,在每个象限内,y随x的增大而增大.一次函数是有规律的:一、定义:如果y=kx+b(k、b是常数且k不等于0),那么y叫做x 的一次函数。
专题训练4 平行四边形的存在性问题

专题训练4 平行四边形的存在性问题针对训练1、 如图已知抛物线y=-x 2-2x+3与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C 顶点为P.若以A 、C 、P 、M 为顶点的四边形是平行四边形,求点M 的坐标2、 如图,在平面直角坐标系xOy 中,已知抛物线y=-x 2+2x+3与x 轴交于A 、B 两点,点M 在这条抛物线上,点P 在y 轴上,如果以点P 、M 、A 、B 为顶点的四边形是平行四边形,求点M 的坐标3、 将抛物线c1:y=23x 3-+沿x 轴翻折,得到抛物线c2如图所示现将抛物线c1向左平移m 个单位长度,平移后得到新抛物线的顶点为M ,与x 轴的交点从左到右依次为A 、B :将抛物线c2向右也平移m 个单位长度,平移后得到新抛物线的顶点为N ,与x 轴的交点从左到右依次为D E 在平移过程中,是否存在以点A 、N 、F,M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理曰如图,4、 抛物线y=25x bx c 4-++与y 轴交于点A (0,1),过点A 的直线与抛物线交于为一点B (3.2),过点B 作BC ⊥x 轴,垂足为C(1)求抛物线的表达式;(2)点P 是x 轴正半轴上的一动点,过点P 作PN ⊥x 轴交直线AB 于点M ,交抛物线于点N 设OP 的长度为m ,连结CM 、BN ,当m 为何值时,四边形BCMN 为平行四边形?5、如图,在Rt△ABC中,∠C=90°,AC=6,BC=8,动点P从点A开始沿边AC向点C秒1个单位长度的速度运动,动点Q从点C开始沿边CB向点B以每秒2个单位长度的速度过点P作PD∥BC,交AB于点D,连结PQ点P、Q分别从点A、C同时出发,当其中一点到达终点时,另一点也随之停止运动,设运动的时间为t秒(t≥0)(1)直接用含t的代数式分别表示:QB=,PD=(2)是否存在t的值,使四边形PDBQ为菱形?若存在,求出t的值;若不存在,说明理由,并探究如何改变点Q的速度(匀速运动),使四边形PDBQ在某一时刻为菱形,求点Q的速度6、如图,在平面直角坐标系中,直线AB与x轴、y轴分别交于点A(4,0)、B(0,3),点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴正半轴上的一动点,且满足O=2x,连结DE,以DE、DA 为边作平行匹边形DEFA(1)如果平行四边形DEFA为矩形,求m的值(2)如果平行四边形DEFA为菱形,请直接写出m的值真题演练7、(18衢州24)如图,Rt△OAB的直角边OA在x轴上,顶点B的坐标为(6,8),直线CD交AB于点D(6,3),交x轴于点C(12,0)(1)求直线CD的函数表达式;(2)动点P在x轴上从点(-10,0)出发,以每秒1个单位的速度向x轴正方向运动,过点P作直线l垂直于x轴,设运动时间为t①点P在运动过程中,是否存在某个位置,使得∠PDA=∠B?若存在,请求出点P的坐标;若不存在,请说明理由②请探索当t为何值时,在直线l上存在点M,在直线CD上存在点Q,使得以OB为一边,O、B、M、Q为顶点的四边形是菱形?并求出此时t的值8、(19连云港26)如图,在平面直角坐标系xOy 中,抛物线L1:y=x 2+bx+c 过点C (0,-3),与抛物线L2:y=213222x x --+的一个交点为A ,且点A 的横坐标为2,点P 、Q 分别是抛物线L1,L2上的动点(1)求抛物线L1的函数表达式(2)若以A 、C 、P 、Q 为顶点的四边形恰为平行四边形,求点P 的坐标;(3)设点R 为抛物线L1上另一个动点,且CA 平分∠PCR 若OQ ∥PR ,求点Q 的坐标9、(19南充25)抛物线y=ax 2+bx+c 与x 轴交于点A (-1,0)、点B (-3,0)与y 轴交于点C ,且OB=OC (如图所示) (1)求抛物线的解析式;(2)若点P 在抛物线上,且∠POB=∠ACB ,求点P 的坐标;(3)抛物线上有两点M 、N ,点M 的横坐标为m ,点N 的横坐标为m+4.点D 是抛物线上M 、N 之间的动点,过点D 作y 轴的平行线交MN 于点①求DE 的最大值 ②点D 关于点E 的对称点为F ,当m 为何值时,四边形MDNF 为矩形?10(17泰安28)如图是将抛物线y=-x 2平移后得到的抛物线,其中对称轴为x=1,与x 轴的一个交点为A (-1,0),另一个交点为B ,与y 轴的交点为C.(1)求抛物线的函数表达式;(2)若点N 为抛物线上一点,且BC ⊥NC ,求点N 的坐标;(3)点P 是抛物线上一点,点Q 是一次函数y=2x+2的图象上一点,若四边形OAPQ 为平行四边形,这样的点P 、Q 是否存在?若存在,分别求出点P 、Q 的坐标;若不存在,请说明理由模拟训练11、(2018年长沙市中考模拟(三)第26题)如图,已知抛物线y=x2-2x+a(a<0)与y轴相交于点A,顶点为M直线y=2x-a分别与x轴、y轴相交于B、C两点,并且与直线M相交于点N.(1)试用含a的代数式分别表示点M与N的坐标;(2)如图,将△NAC沿y轴翻折,若点N的对应点N恰好落在抛物线上,AN与x轴交于点D,连结CD,求a的值和四边形ADCN的面积;(3)在抛物线y=x2-2x+a上是否存在一点P,使得以P、A、 C、N为顶点的四边形是平行四边形?若存在,求出点P的坐标;若不存在,试说明理由12、(2019年内蒙古准格尔旗中考模拟第24题)如图所示,已知抛物线y=-x2+bx+c与一直线相交于A (-1,0)、C(2,3)两点,其顶点为D(1)求抛物线及直线AC的函数关系式(2)若抛物线的对称轴与直线AC相交于点B,E为直线AC上的任意一点,过点E作EF∥BD交抛物线于点F,以B、D、E、F为顶4O点的四边形能否为平行四边形?若能,求点E的坐标;若不能,请说明理由(3)若P是抛物线上位于直线AC上方的一个动点,直接写出△APC的面积的最大值及此时点P的坐标专题预测13、如图,在平面直角坐标系中,矩形1BC的顶点A、C分别在x轴和y轴上,点B的坐标为(3.33)。
一次函数与四边形

一次函数与四边形教学目标:知识与技能:1.利用一次函数比例系数k 值特征证明直线位置关系与四边形的形状;2.利用平行四边形的性质,求一次函数解析式.过程与方法:通过一次函数与四边形的想和转换,感受数形结合的思想方法. 情感态度与价值观:通过思考,让学生体会学习数学方法对于学习数学的重要性.教学重难点:教学重点:一次函数比例系数k 值与平行四边形的性质与判定的相互转换. 教学难点:利用数形结合思想解决函数与几何问题.教学过程:课前一练:1.若一次函数的图像经过点),(01A 和点),(22-B ,则这个一次函数的解析式为 .2.已知直线b kx y l +=11:与直线x y l 2:22=相互平行,且经过点)(1,2,则直线1l 的函数解析式为 .知识回顾:问题1:平面直角坐标系中求一次函数解析式的方法? 问题2:待定系数法求一次函数解析式的两种常见类型?一、利用一次函数证明四边形的形状例1:如图,直线b kx y +=经过),(3203-A 、),(45-B 两点,过点A 作x AD ⊥轴点D ,过点B 作y BC ⊥轴于点C ,AB 与x 轴相交于点E .(1)求点E 坐标;(2)证明:AB CD ∥;(3)判断四边形BCDE 的形状.二、利用特殊四边形的性质求一次函数解析式例2:如图,一次函数4y的图象与x、y轴=x2+分别相交于点A、B,以AB为边在直线AB右侧作正方形四边形ABCD.(1)求点A、B、D的坐标;(2)求直线BD的函数解析式;(3)求直线AC的函数解析式.例3:如图所示,矩形ABCD中,5AD,==AB,3点A的坐标为)=:.l+(1,2,作直线bykx(1)当3k时,若直线l与矩形ABCD相交,求-=b的取值范围;(2)在(1)的条件下,若直线l平分矩形ABCD 面积,求直线l的解析式;(3)当2b时,若直线l平分矩形ABCD面积,=-求直线l的解析式;(4)在(3)的条件下,若直线l与矩形ABCD相交,求k的取值范围.。
八年级数学培优第十三讲平行四边形与一次函数

八年级数学培优第十三讲平行四边形与一次函数第十二讲平行四边形与一次函数考点•方法•破译⒈理解并掌握平行四边形的定义、性质、和判定方法,并运用它们进行计算与证明.⒉理解三角形中位线定理并会应用.⒊了解平行四边形是中心对称图形.经典•考题•赏析【例3】(南昌)如图:在平面直角坐标系中,有A(0,1),B(-1,0),C(1,0)三点.⑴若点D与A、B、C三点构成平行四边形,请写出所有符合条件的点D 的坐标;⑵选择⑴中符合条件的一点D,求直线BD的解析式.【解法指导】已知固定的三个点,作平行四边形应有三种可能性,如图所示,因而本题D点坐标应有三种可能性.【解】⑴D1(2,1)D2(-22,1)D3(0,-1)⑵若选择D3(0,-1),可求得解析式:y =-x-1【变式题组】已知固定的三个点,作平行四边形时应有三种可能性,如图所示,因而本题D点坐标应有三种可能性.【解】⑴D1(2,1)D2(-2,1)D3(0,-1)⑵若选择D3(0,-1),可求得解析式:y =-x-1【变式题组】3+3与y01.如图,直线l1:y =-x2轴交于点A,与直线l2交于x轴上同一点B,直线l2交y轴于点3C,且点C与点A关于x轴对称.⑴求直线l2的解析式;⑵设D(0,-1),平行于y轴的直线x=t分别交直线l1和l2于点E、F.是否存在t的值,使得以A、D、E、F为顶点的四边形是平行四边形,若存在,求出t的值;若不存在,请说明理由.02.如图,在直角坐标系中,A(1,0),B(3,1x上是否0),P是y轴上一动点,在直线y=2存在点Q,使A、B、P、Q为顶点的四边形为平行四边形?若存在,求出对应的Q点的坐标;若不存在,请说明理由.4503.(四川资阳)若一次函数y =2x -1和反比例函数y =x k 2的图象都经过点(1,1).⑴求反比例函数的解析式;⑵已知点A 在第三象限,且同时在两个函数的图象上,求点A 的坐标;⑶利用⑵的结果,若点B 的坐标为(2,0),且以点A 、O 、B 、P 为顶点的四边形是平行四边形,请你直接写出点P 的坐标.【例4】(齐齐哈尔)如图1.在四边形ABCD 中,AB=CD,E、F分别是BC、AD的中点,连接EF并延长,分别与BA、CD的延长线交于点M、N,则∠BME=∠CNE(不需证明)(温馨提示:在图1中,连接BD,取BD的中点H,连接HE、HF,根据三角形中位线定理,证明HE=HF,从而∠1=∠2,再利用平行线性质,可证得∠BME=∠CNE.)问题一:如图2,在四边形ADBC中,AB 与CD相交于点O,AB=CD,E、F分别是BC、AD的中点,连接EF,分别交DC、AB于M、N,判断∆OMN的形状,请直接写出结论.67问题二:如图3,在∆ABC 中,AC >AB ,D 点在AC 上,AB =CD ,E 、F 分别是BC 、AD 的中点,连接EF 并延长,与BA 的延长线交于点G ,若∠EFC =60°,连接GD ,判断∆AGD 的形状并证明.【解法指导】出现中点,联想到三角形中位线是常规思路,因为三角形中位线不仅能进行线段的替换,也可通过平行进行角的转移.【解】⑴△OMN 为等腰三角形.⑵△AGD 为含有30°的直角三角形.证明:连接BD ,取BD 的中点M ,连接FM 、EM .∵AF =FD ,BM =MD ∴MF //21AB 同理ME //21CD .∵AB =CD ∴MF =ME ,RP D CB A EF又∵∠2=∠1=60°,∴△MEF为等边三角形,∴∠4=∠3=60°,∠5=60°∴△AGF为等边三角形∴FG=FD∴∠ADG=30°∴△AGD为含有30°的直角三角形.【变式题组】01.(扬州)如图,已知四边形ABCD中,R、P分别是BC、CD上的点,E、F分别是AP、RP的中点,当点P在CD上从C向D移动而点R不动时,那么下列结论成立的是()A、线段EF的长逐渐增大B、线段EF的长逐渐减小C、线段EF的长不变D、线段EF的长与点P的位置有关02.如图,在△ABC中,M是BC的中点,AD是∠A的平89分线, BD ⊥AD 于D ,AB =12,AC =22,则MD 的长为( ).A .3B .4C .5D .6【例5】(浙江竞赛)如图1,在△ABC 中,∠C =90°,点M 在BC 上,且BM =AC ,点N 在AC 上,且AN =MC ,AM 与BN 相交于点P ,求证:∠BPM =45°.【解法指导】题中相等线段关联性不强,能否把相等的线段(或角)通过改变位置,将分散的条件集中,从而构造全等三角形解决问题.【解】方法一、如图2,过M 作 ME AN ,连接BE ,EN ,则得 AMEN , ∴ME ⊥BC ,AM =EN在△AMC 和△BEM 中 ,AC =BN ,∠BNE=∠C=90°, ME=MC∴△AMC≌△BEM∴BE=AM=EN,∠3=∠4 ∵∠1=∠2,∠1+∠4=90°∴∠2+∠3=90°, ∴△BEN为等腰直角三角形,∠BNE=45°,∴∠BPM=45°方法2:如图3,过B作BF AN,连接AF,FM也可证得.【变式题组】01.如图,在等腰△ABC中,AB=AC,延长边AB到点D,延长CA到点E,连接DE,若AD=BC=CE=DE,求∠BAC的度数.10演练巩固反馈提高05.(浙江金华)某广场有一个形状是平行四边形的花坛(如图)分别种有红黄蓝绿橙紫6得颜色的花,如果有AB∥EF∥DC,BC∥GH ∥AD,那么下列说法错误的是A.红花,绿花种植面积一定相等B.紫花,橙花种植面积一定相等C.红花,蓝花种植面积一定相等D.蓝花,黄花种植面积一定相等06.(陕西)如图,l1∥l2BE∥CF, BA⊥l1DC⊥l2,下面四个结论中①AB=DC;②BE=CF③S△ADE=S△DCF④S□ABCD =S□BCFE,其中正确的有()A.4个B .3个C.2个D .1个07.(成都)已知四边形ABCD,有以下四个条件:①AB∥CD②AB=CD③BC∥AD④BC=AD从这四个条件中任选两个,能使四边形ABCD为平行四边形的选法种数有()A.6种B.5种C.4种D.3种08.(厦门)如图,在四边形ABCD中,P是对角线BD的中点,E,F分别是AB,CD的中点,AD=BC,∠PEF=180,则∠PFE的度数为________09..如图,平行四边形ABCD中,点E在边AD中,以BE为折痕,将△ABE向上翻折,点A恰好落在CD上的F点,若△FDE的周长为8,△FCB的周长为22,则FC的长为_________10.如图,在Rt△ABC中,∠BAC=90°,AB=3,AC=4,将△ABC沿直线BC向右平移2.5个单位得到△DEF,AC与DE相交于点G,连接AD,AE,则下列结论中成立的是____①四边形ABED是平行四边;②△AGD≌△CGE③△ADE为等腰三角形④AC平分∠EAD11.(长春)如图□ABCD中,E是BC边上一点,且AB=AE.求证:△ABC≌△EAD若AE平分∠DAB,∠EAC=25°,求∠AED的度数.12.(荆州)如图,□ABCD内一点E满足ED⊥AD于D,且∠EBC=∠EDC,∠ECB=45°,找出图中一条与EB相等的线段,并加以证明.13.已知,如图,△ABC是等边三角形,D是AB边上的点,将线段DB绕点D顺时针旋转60°得到线段DE,延长ED交AC于点F,连接DC,AE.⑴求证:△ADE≌△DFC⑵过点E作EH∥DC交DB于点G ,交BC于点H,连接AH,求∠AHE的度数.。
特殊四边形存在性问题-二次函数特殊四边形存在性问题

特殊四边形存在性问题平行四边形:如果已知三个定点,则形成三条定线段,把每条定线段看成对角线,利用对角形互相平分解决。
如果已知两个定点,一般是把确定的一条线段按照边或对角线分为两种情况.菱形:通常转化为等腰三角形存在问题。
矩形:通常转化为直角三角形存在问题。
正方形:通常转化为等腰直角三角形存在问题。
针对训练1.如图,已知抛物线y =-x 2-2x +3与x 轴交于A 、B 两点(点A 在点B 的左侧),与y 轴交于点C ,顶点为P .若以A 、C 、P 、M 为顶点的四边形是平行四边形,求点M 的坐标.2.如图,在平面直角坐标系xOy 中,已知抛物线y =-x 2+2x +3与x 轴交于A 、B 两点,点M 在这条抛物线上,点P 在y 轴上,如果以点P 、M 、A 、B 为顶点的四边形是平行四边形,求点M 的坐标.3.如图(1),抛物线与x 轴交于A 、B 两点,与y 轴交于点C ,其中点A 的坐标为(﹣2,0).(1)求此抛物线的解析式;(2)①若点D 是第一象限内抛物线上的一个动点,过点D 作DE ⊥x 轴于E ,连接CD ,以OE 为直径作⊙M ,如图(2),试求当CD 与⊙M 相切时D 点的坐标;②点F 是x 轴上的动点,在抛物线上是否存在一点G ,使A 、C 、G 、F 四点为顶点的四边形是平行四边形?若存在,求出点G 的坐标;若不存在,请说明理由.21y x x c 4=-++4.如图1,在平面直角坐标系中,抛物线y =ax 2+bx -3a 经过A (-1,0)、B (0,3)两点,与x 轴交于另一点C ,顶点为D .(1)求该抛物线的解析式及点C 、D 的坐标;(2)经过点B 、D 两点的直线与x 轴交于点E ,若点F 是抛物线上一点,以A 、B 、E 、F 为顶点的四边形是平行四边形,求点F 的坐标;(3)如图2,P (2,3)是抛物线上的点,Q 是直线AP 上方的抛物线上一动点,求△APQ 的最大面积和此时Q 点的坐标.5.如图,在平面直角坐标系中,直线AB 与x 轴、y 轴分别交于点A ,B ,直线CD 与x 轴、y 轴分别交于点C ,D ,AB 与CD 相交于点E ,线段OA ,OC 的长是一元二次方程x 2﹣18x+72=0的两根(OA >OC ),BE=5,tan ∠ABO=.(1)求点A ,C 的坐标;(2)若反比例函数y=的图象经过点E ,求k 的值; (3)若点P 在坐标轴上,在平面内是否存在一点Q ,使以点C ,E ,P ,Q 为顶点的四边形是矩形?若存在,请写出满足条件的点Q 的个数,并直接写出位于x 轴下方的点Q 的坐标;若不存在,请说明理由.43kx6.将抛物线c 1:2y =x 轴翻折,得到抛物线c 2,如图所示.现将抛物线c 1向左平移m 个单位长度,平移后得到新抛物线的顶点为M ,与x 轴的交点从左到右依次为A 、B ;将抛物线c 2向右也平移m 个单位长度,平移后得到新抛物线的顶点为N ,与x 轴的交点从左到右依次为D 、E .在平移过程中,是否存在以点A 、N 、E 、M 为顶点的四边形是矩形的情形?若存在,请求出此时m 的值;若不存在,请说明理由.7.已知平面直角坐标系xOy (如图),一次函数334y x =+的图像与y 轴交于点A ,点M 在正比例函数32y x =的图像上,且MO =MA .二次函数y =x 2+bx +c 的图像经过点A 、M .(1)求线段AM 的长; (2)求这个二次函数的解析式;(3)如果点B 在y 轴上,且位于点A 下方,点C 在上述二次函数的图像上,点D 在一次函数334y x =+的图像上,且四边形ABCD 是菱形,求点C 的坐标.8.如图,直线y=x ﹣4与x 轴、y 轴分别交于A 、B 两点,抛物线经过A 、B 两点,与x 轴的另一个交点为C ,连接BC .(1)求抛物线的解析式及点C 的坐标; (2)点M 在抛物线上,连接MB ,当∠MBA+∠CBO=45°时,求点M 的坐标;(3)点P 从点C 出发,沿线段CA 由C 向A 运动,同时点Q 从点B 出发,沿线段BC 由B 向C 运动,P 、Q 的运动速度都是每秒1个单位长度,当Q 点到达C 点时,P 、Q 同时停止运动,试问在坐标平面内是否存在点D ,使P 、Q 运动过程中的某一时刻,以C 、D 、P 、Q 为顶点的四边形为菱形?若存在,直接写出点D 的坐标;若不存在,说明理由.9.已知抛物线2(2)y a x b =-+ (0)ab <的顶点为A ,与x 轴的交点为B ,C (点B 在点C 的左侧).(1)直接写出抛物线对称轴方程;(2)若抛物线经过原点,且△ABC 为直角三角形,求a ,b 的值;(3)若D 为抛物线对称轴上一点,则以A 、B 、C 、D 为顶点的四边形能否为正方形?若能,请求出a ,b 满足的关系式;若不能,说明理由.21y x bx c 3=++10.如图,已知双曲线6yx与直线AB交于A、B两点,与直线CD交于C、D两点.(1)求证四边形ACBD是平行四边形;(2)四边形ACBD可能是矩形吗?可能是正方形吗?(3)如果点A的横坐标为3,点C的横坐标为m(m>0),四边形ACBD的面积为S,求S与m的之间的关系式.。
“一般”与“特殊”

“一般”与“特殊”我们常把要研究的对象分为“一般对象”或“特殊对象”,例如,当我们把平行四边形看作一般对象时,矩形、菱形和正方形就是其中的几种特殊对象,即几种特殊的平行四边形.又如,当我们把一次函数y=kx+b(k≠0)看作一般对象时,正比例函数y=kx(k≠0)就是一种特殊对象,即一种特殊的一次函数.一般对象与特殊对象的关系是:一般对象中包含了特殊对象.一般对象的性质,指的是其中各个特殊对象都具有的共性.例如,任一平行四边形都有“对边相等”“对角相等”“对角线互相平分”等性质.特殊对象存在于一般对象之中,特殊对象不仅具有一般对象都具有的共性,而且还有自己的特性.例如,矩形不仅具有平行四边形的所有性质,而且还有“四个角都是直角”“两条对角线相等”等特性,这些特性并非任一平行四边形都会具有.我们研究对象时,有两种不同的途径.一种是从研究一般对象发展到研究特殊对象,另一种是从研究特殊对象发展到研究一般对象,我们需要根据研究对象的特点,选择适当的研究途径,一、“从一般到特殊”的研究途径举例回顾人教版初中数学教科书的第十八章《平行四边形》,大家会发现教科书展现的是“从一般到特殊”的研究途径.这章的第一节,从认识平行四边形的定义出发,以平行四边形的基本特征(两组对边分别平行)为基础,推导出平行四边形的性质,并由性质的逆命题推导出判定一个四边形是平行四边形的条件(“两组对边分别相等”“两组对角分别相等”“对角线互相平分”“一组对边平行且相等”等).这章的第二节,依次认识矩形、菱形和正方形.矩形是有一个角是直角的平行四边形.相对于一般平行四边形,矩形特殊在“有一个角是直角”.根据这一特征,再加上一般平行四边形的共性,就能推导出矩形的特性以及判定方法.菱形是有一组邻边相等的平行四边形.相对于一般平行四边形,菱形特殊在“有一组邻边相等”,根据这一特征,再加上一般平行四边形的共性,就能推导出菱形的特性(“四条边都相等”“对角线互相垂直,并且每一条对角线平分一组对角”等)以及判定方法.正方形是四条边都相等并且四个角都相等的四边形,它既是特殊的矩形,又是特殊的菱形,所以它不仅具有一般平行四边形的共性,而且具有矩形和菱形的特性,在认识了平行四边形、矩形和菱形之后,对正方形这种特殊性更强的平行四边形的认识就水到渠成了.平行四边形、矩形、菱形和正方形的包含关系,可以用图1来表示.图1直观地显示出一般对象(平行四边形)包含了特殊对象(矩形和菱形),特殊对象又包含了更特殊的对象(正方形).由图l可以看出,特殊对象处于一般对象范围之内的特定区域,这表示它除具有一般对象的属性之外,还具有特定的性质,一般地说,如果对象4包含对象B,那么A的外延(即范围)大,B的外延小;A的内涵(即属性)少,B的内涵多.纵观这章的体系结构,“先研究一般平行四边形,再研究特殊平行四边形”这一“从一般到特殊”的发展脉络十分清晰,三、“从特殊到一般”的研究途径举例回顾人教版初中数学教科书第十九章《一次函数》第二节“一次函数”,大家会发现教科书展现的是“从特殊到一般”的研究途径.这节的第一小节,从认识正比例函数的定义出发,以正比例函数的基本对应关系y=kx(k≠0)为基础,由描点法得出正比例函数的图象是通过原点的一条直线.而由“k>0时,图象经过第一、三象限,从左到右上升;k0时,随着x的增大y也增大;k<0时,随着x的增大y反而减小).至此,完成了用“定义一图象一性质”这一模式研究正比例函数的过程.这节的第二小节,在正比例函数关系y=kx(k≠0)的基础上,添加常数6,使函数关系发展成为y=kx+b(k≠0),引出了一般的一次函数的定义.按一次函数的定义可知,正比例函数是一种特殊的一次函数,其特殊性在于常数b=0.在研究一次函数的图象时,教科书没有重复描点法这一“原始的”方法,而是引导我们发现y=kx与y=kx+b(k≠0)的联系,借助正比例函数的图象得出一般的一次函数的图象.具体的认识过程是,先提出问题:画函数y=-6x和y=-6x+5的图象,由于y=-6x是正比例函数,其图象是第一小节已经研究过的问题,我们很容易得出它是过原点和点(1,-6)的一条直线.对比两个函数的解析式,可以联想到一次函数y=-6x+5的图象是平行于直线y=-6x并且比它高5个单位的一条直线(图2).进一步,容易得出一般的一次函数y=kx+b(k≠0)的图象为过点(0,b)和点(1,k+b)的一条直线,掌握了一次函数的图象后,联系正比例函数的增减性,借助图象的直观描述,容易得出一次函数的增减性(k>0时,随着x的增大y也增大;k<0时,随着x的增大y反而减小).至此,完成了用“定义一图象一性质”这一模式研究一次函数的过程.纵观这节的体系结构,“先研究正比例函数这种特殊的一次函数,再研究一般的一次函数”这一“从特殊到一般”的发展脉络十分清晰,三“由浅入深,由简至繁,由易到难”进行研究“从一般到特殊”和“从特殊到一般”是两种过程相反的研究途径,但它们并非是“一对一错”的对立关系,它们各自都有用武之地,关键在于要用得恰到好处,要适合研究的对象,“由浅入深,由简至繁,由易到难”是一般研究过程的规律,不论是“从一般到特殊”,还是“从特殊到一般”,都应遵循这样的规律.例如,矩形、菱形和正方形是特殊的平行四边形,它们的内涵比一般平行四边形更多,性质更复杂,判定条件更严苛,而且对它们的研究不能脱离对一般平行四边形的认识,因此“从一般到特殊”地研究平行四边形是符合认识规律的,又如,正比例函数y=kx(k≠0)是特殊的一次函数,与一般的一次函数y=kx+b(k≠0)相比,正比例函数所具有的b=0的特征使其在形式上更简单,由此其图象的位置也更容易确定(必定过原点).正是由于这些特性,使正比例函数成为一次函数中最简单的特殊对象,而且在认识它的基础上很容易扩展到一般的一次函数,因此“从特殊到一般”地研究一次函数是符合认识规律的,俗话说“到什么山唱什么歌”“看菜吃饭,量体裁衣”,研究不同的对象,有可能采取不同的研究途径,要具体问题具体分析,没有一成不变的方法.同学们,回顾并总结研究问题的方法,对于提高研究问题的能力非常有益.认识一般对象与特殊对象的辩证关系,对于更全面地认识事物十分重要.。
特殊平行四边形-中考数学第一轮总复习课件(全国通用)

中考数学第一轮总复习典例精讲考点聚集查漏补缺拓展提升第五单元 四边形专题5.2 特殊平行四边形知识点矩 形01菱 形02正 方 形03中点四边形04拓展训练05【例1-1】如图,在□ABCD中,E为BC的中点,连接AE并延长交DC的延长线于点F,连接BF,AC,若AD=AF.求证:四边形ABFC是矩形.A EFD CB利用对角线相等的平行四边形是矩形证明方法一:利用△ABE≌△FCE证平行四边形;证法二:利用△ABE∽△FCE证平行四边形考点聚焦一个角为直角对角线相等平行四边形平行四边形直角证明四边形ABCD 是矩形的方法(三种)①先证明四边形ABCD为___________,再证明□ABCD的任意_____________;②先证明四边形ABCD为___________,再证明□ABCD的____________;【例1-2】如图,在矩形ABCD中,AB=3,BC=6,若点E,F分别在AB,CD上,且BE=2AE,DF=2FC,G,H分别是AC的三等分点,则四边形EHFG的面积为( ) A.1 B.1.5 C.2 D.4AHGECBD F C 考点聚焦对边平行且相等四角都是直角对角线互相平分且相等矩形的性质(1)边:________________;(2)角:________________;(3)对角线:______________________.1.已知□ABCD,下列条件中,不能判定这个平行四边形为矩形的是( ) A.∠A=∠B B.∠A=∠C C.AC=BD D.AB⊥BC2.如图,矩形ABCD的对角线AC=10,P,Q分别为AO,AD的中点,则PQ=_____.3.如图,矩形ABCD中,AB=3,BC=4,则图中四个小矩形的周长之和为____.4.如图,矩形OCDE,矩形OFGH,矩形OMNP各有一边在半⊙O的直径AB上,D,G,N都在半⊙O上,比较EC,HF,MP的大小_________.B 2.514EC=HF=EP5.如图,在矩形ABCD中,AB=8,AD=4,E为CD边上一点,CE=5,点P从B点出发,以每秒1个单位的速度沿着BA边向终点A运动,设点P运动的时间为t秒,则当t=_______时,△PAE是以PE为腰的等腰三角形.6.如图,将矩形ABCD绕点B顺时针旋转,得到矩形EBFG,且点E落在CD上,过点C作FG的垂线,垂足为H,若FH=HG,则BC:AB的值为_______.7.如图,在Rt△ABC中,∠BAC=90º,BA=3,AC=4,点D是斜边BC上的一个动点,过点D分别作DM⊥AB于点M,DN⊥AC于点N,连接MN,则线段MN的最小最为_____.M2.4知识点矩 形01菱 形02正 方 形03中点四边形04拓展训练05【例2-1】如图,在等腰△ABC中,AD平分顶角∠BAC,交底边BC于点H,点E在AD上,BE=BD,求证:四边形BDCE是菱形.考点聚焦证明四边形ABCD 是菱形的方法(三种)①先证明四边形ABCD为___________,再证明□ABCD的任意_____________;②先证明四边形ABCD为___________,再证明□ABCD的________________平行四边形一组邻边相等平行四边形对角线互相垂直四边相等AH E DCB利用“三线合一”得出AD 垂直平分BC,从而得出四边相等。
专题05 二次函数中特殊平行四边形存在性问题(原卷版)--2023 年中考数学压轴真题汇编

挑战2023年中考数学解答题压轴真题汇编专题05二次函数中特殊平行四边形存在性问题一.平行四边形的存在性1.(2022•重庆)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c与x轴交于点A(4,0),与y轴交于点B(0,3).(1)求抛物线的函数表达式;(2)点P为直线AB上方抛物线上一动点,过点P作PQ⊥x轴于点Q,交AB于点M,求PM+AM的最大值及此时点P的坐标;(3)在(2)的条件下,点P′与点P关于抛物线y=﹣x2+bx+c的对称轴对称.将抛物线y=﹣x2+bx+c向右平移,使新抛物线的对称轴l经过点A.点C在新抛物线上,点D在l上,直接写出所有使得以点A、P′、C、D为顶点的四边形是平行四边形的点D的坐标,并把求其中一个点D的坐标的过程写出来.2.(2022•郴州)已知抛物线y=x2+bx+c与x轴相交于点A(﹣1,0),B(3,0),与y轴相交于点C.(1)求抛物线的表达式;(2)如图1,将直线BC向上平移,得到过原点O的直线MN.点D是直线MN上任意一点.①当点D在抛物线的对称轴l上时,连接CD,与x轴相交于点E,求线段OE的长;②如图2,在抛物线的对称轴l上是否存在点F,使得以B,C,D,F为顶点的四边形是平行四边形?若存在,求出点F与点D的坐标;若不存在,请说明理由.3.(2022•攀枝花)如图,二次函数y=ax2+bx+c的图象与x轴交于O(O为坐标原点),A两点,且二次函数的最小值为﹣1,点M(1,m)是其对称轴上一点,y轴上一点B(0,1).(1)求二次函数的表达式;(2)二次函数在第四象限的图象上有一点P,连结PA,PB,设点P的横坐标为t,△PAB的面积为S,求S与t的函数关系式;(3)在二次函数图象上是否存在点N,使得以A、B、M、N为顶点的四边形是平行四边形?若存在,直接写出所有符合条件的点N的坐标,若不存在,请说明理由.4.(2022•内蒙古)如图,抛物线y=ax2+x+c经过B(3,0),D(﹣2,﹣)两点,与x轴的另一个交点为A,与y轴相交于点C.(1)求抛物线的解析式和点C的坐标;(2)若点M在直线BC上方的抛物线上运动(与点B,C不重合),求使△MBC面积最大时M点的坐标,并求最大面积;(请在图1中探索)(3)设点Q在y轴上,点P在抛物线上,要使以点A,B,P,Q为顶点的四边形是平行四边形,求所有满足条件的点P的坐标.(请在图2中探索)5.(2022•资阳)已知二次函数图象的顶点坐标为A(1,4),且与x轴交于点B (﹣1,0).(1)求二次函数的表达式;(2)如图,将二次函数图象绕x轴的正半轴上一点P(m,0)旋转180°,此时点A、B的对应点分别为点C、D.①连结AB、BC、CD、DA,当四边形ABCD为矩形时,求m的值;②在①的条件下,若点M是直线x=m上一点,原二次函数图象上是否存在一点Q,使得以点B、C、M、Q为顶点的四边形为平行四边形,若存在,求出点Q的坐标;若不存在,请说明理由.二.矩形的存在性6.(2022•泸州)如图,在平面直角坐标系xOy中,已知抛物线y=ax2+x+c经过A(﹣2,0),B(0,4)两点,直线x=3与x轴交于点C.(1)求a,c的值;(2)经过点O的直线分别与线段AB,直线x=3交于点D,E,且△BDO与△OCE的面积相等,求直线DE的解析式;(3)P是抛物线上位于第一象限的一个动点,在线段OC和直线x=3上是否分别存在点F,G,使B,F,G,P为顶点的四边形是以BF为一边的矩形?若存在,求出点F的坐标;若不存在,请说明理由.8.(2021•齐齐哈尔)综合与探究如图,在平面直角坐标系中,抛物线y=ax2+2x+c(a≠0)与x轴交于点A、B,与y轴交于点C,连接BC,OA=1,对称轴为直线x=2,点D为此抛物线的顶点.(1)求抛物线的解析式;(2)抛物线上C、D两点之间的距离是2;(3)点E是第一象限内抛物线上的动点,连接BE和CE,求△BCE面积的最大值;(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.9.(2022•随州)如图1,平面直角坐标系xOy中,抛物线y=ax2+bx+c(a<0)与x轴分别交于点A和点B(1,0),与y轴交于点C,对称轴为直线x=﹣1,且OA=OC,P为抛物线上一动点.(1)直接写出抛物线的解析式;(2)如图2,连接AC,当点P在直线AC上方时,求四边形P ABC面积的最大值,并求出此时P点的坐标;(3)设M为抛物线对称轴上一动点,当P,M运动时,在坐标轴上是否存在点N,使四边形PMCN为矩形?若存在,直接写出点P及其对应点N的坐标;若不存在,请说明理由.10.(2023•秦都区校级二模)如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0)、B两点(点B在点A的右侧),与y轴交于点C,且OC=3OA,点D为抛物线的对称轴与x轴的交点,连接CD.(1)求抛物线的函数表达式;(2)点F为坐标平面内一点,在第一象限的抛物线上是否存在点E,使得以点C、D、E、F为顶点的四边形是以CD为边的矩形?若存在,请求出符合条件的点E的横坐标;若不存在,请说明理由.7.(2022•元宝区校级二模)如图,在平面直角坐标系中,抛物线y=ax2+bx+3(a≠0)与x轴交于点A、B,与y轴交于点C,连接BC,OA=1,对称轴为直线x=2,点D为此抛物线的顶点.(1)求抛物线的解析式;(2)抛物线上C、D两点之间的距离是11;(3)点E是第一象限内抛物线上的动点,连接BE和CE,求△BCE面积的最大值;(4)点P在抛物线对称轴上,平面内存在点Q,使以点B、C、P、Q为顶点的四边形为矩形,请直接写出点Q的坐标.8.(2022•鱼峰区模拟)如图,在平面直角坐标系中,抛物线y=x2+bx+c与坐标轴交于A(0,﹣2),B(4,0)两点,直线BC:y=﹣2x+8交y轴于点C.(1)求该抛物线的解析式;(2)在第二象限内是否存在一点M,使得四边形ABCM为矩形?如果存在,求出点M的坐标;如果不存在,请说明理由.三.菱形的存在性9.(2022•朝阳)如图,在平面直角坐标系中,抛物线y=ax2+2x+c与x轴分别交于点A(1,0)和点B,与y轴交于点C(0,﹣3),连接BC.(1)求抛物线的解析式及点B的坐标.(2)如图,点P为线段BC上的一个动点(点P不与点B,C重合),过点P 作y轴的平行线交抛物线于点Q,求线段PQ长度的最大值.(3)动点P以每秒个单位长度的速度在线段BC上由点C向点B运动,同时动点M以每秒1个单位长度的速度在线段BO上由点B向点O运动,在平面内是否存在点N,使得以点P,M,B,N为顶点的四边形是菱形?若存在,请直接写出符合条件的点N的坐标;若不存在,请说明理由.10.(2021•湘潭)如图,一次函数y=x﹣图象与坐标轴交于点A、B,二次函数y=x2+bx+c图象过A、B两点.(1)求二次函数解析式;(2)点B关于抛物线对称轴的对称点为点C,点P是对称轴上一动点,在抛物线上是否存在点Q,使得以B、C、P、Q为顶点的四边形是菱形?若存在,求出Q点坐标;若不存在,请说明理由.11.(2021•鄂尔多斯)如图,抛物线y=x2+2x﹣8与x轴交于A,B两点(点A 在点B左侧),与y轴交于点C.(1)求A,B,C三点的坐标;(2)连接AC,直线x=m(﹣4<m<0)与该抛物线交于点E,与AC交于点D,连接OD.当OD⊥AC时,求线段DE的长;(3)点M在y轴上,点N在直线AC上,点P为抛物线对称轴上一点,是否存在点M,使得以C、M、N、P为顶点的四边形是菱形?若存在,请直接写出点M的坐标;若不存在,请说明理由.12.(2021•通辽)如图,抛物线y=ax2+bx+3交x轴于A(3,0),B(﹣1,0)两点,交y轴于点C,动点P在抛物线的对称轴上.(1)求抛物线的解析式;(2)当以P,B,C为顶点的三角形周长最小时,求点P的坐标及△PBC的周长;(3)若点Q是平面直角坐标系内的任意一点,是否存在点Q,使得以A,C,P,Q为顶点的四边形是菱形?若存在,请直接写出所有符合条件的点Q的坐标;若不存在,请说明理由.13.(2021•娄底)如图,在直角坐标系中,二次函数y=x2+bx+c的图象与x轴相交于点A(﹣1,0)和点B(3,0),与y轴交于点C.(1)求b、c的值;(2)点P(m,n)为抛物线上的动点,过P作x轴的垂线交直线l:y=x于点Q.①当0<m<3时,求当P点到直线l:y=x的距离最大时m的值;②是否存在m,使得以点O、C、P、Q为顶点的四边形是菱形,若不存在,请说明理由;若存在,请求出m的值.14.(2021•山西)综合与探究如图,抛物线y=x2+2x﹣6与x轴交于A,B两点(点A在点B的左侧),与y轴交于点C,连接AC,BC.(1)求A、B,C三点的坐标并直接写出直线AC,BC的函数表达式.(2)点P是直线AC下方抛物线上的一个动点,过点P作BC的平行线l,交线段AC于点D.①试探究:在直线l上是否存在点E,使得以点D,C,B,E为顶点的四边形为菱形,若存在,求出点E的坐标,若不存在,请说明理由;②设抛物线的对称轴与直线l交于点M,与直线AC交于点N.当S△DMN=S△AOC时,请直接写出DM的长.15.(2020•阜新)如图,二次函数y=x2+bx+c的图象交x轴于点A(﹣3,0),B(1,0),交y轴于点C.点P(m,0)是x轴上的一动点,PM⊥x轴,交直线AC于点M,交抛物线于点N.(1)求这个二次函数的表达式;(2)①若点P仅在线段AO上运动,如图,求线段MN的最大值;②若点P在x轴上运动,则在y轴上是否存在点Q,使以M,N,C,Q为顶点的四边形为菱形.若存在,请直接写出所有满足条件的点Q的坐标;若不存在,请说明理由.。
09 专题九:一次函数与平行四边形存在性问题(方法专题)

1、如图,在平面直角坐标系xOy中,已知A(2,-2),B(4,0),若C是坐标平面内一点,且以A,B,C,O为顶点的平行四边形是_______________________。
【答案】(-2,-2),(6,-2)或(2,2)。
2、已知M(1,1)是AB的中点,若点A的坐标为(3,2)则点B的坐标为_________。
【答案】(-1,0)。
1.线段中点坐标公式平面直角坐标系中,点A坐标为(x1,y1),点B坐标为(x2,y2),则线段AB的中点坐标为1212,22x x y y++⎛⎫⎪⎝⎭。
2.平行四边形顶点坐标公式ABCD的顶点坐标分别为A(x A,y A)、B(x B,y B)、C(x C,y C)、D(x D,y D),则:x A+x C=x B+x D;y A+y C=y B+y D。
即平行四边形对角线两端点的横坐标、纵坐标之和分别相等。
解法点睛专题导入一次函数与平行四边形存在性问题3.一个基本事实,确定动点位置如图,已知不在同一直线上的三点A 、B 、C ,在平面内另找一个点D ,使以A 、B 、C 、D 为顶点的四边形是平行四边形.答案有三种:以AB 为对角线的ACBD 1,以AC 为对角线的ABCD 2,以BC 为对角线的ABD 3C 。
例1、已知:在平面直角坐标系中,点(1,0)A ,点(4,0)B ,点C 在y 轴正半轴上,且2OB OC =.(1)试确定直线BC 的解析式;(2)在平面内确定点M ,使得以点M 、A 、B 、C 为顶点的四边形是平行四边形,请直接写出点M 的坐标. 【答案】解:(1)(4,0)B ,4OB ∴=,又2OB OC =,C 在y 轴正半轴上,(0,2)C ∴.设直线BC 的解析式为(0)y kx b k =+≠.过点(4,0)B ,(0,2)C ,∴402k b b +=⎧⎨=⎩, 解得122k b ⎧=-⎪⎨⎪=⎩,∴直线BC 的解析式为122y x =-+. 专题精析(2)如图,①当BC 为对角线时,易求1(3,2)M ;②当AC 为对角线时,//CM AB ,且CM AB =.所以2(3,2)M -;③当AB 为对角线时,//AC BM ,且AC BM =.则||2y M OC ==,||5x M OB OA =+=,所以3(5,2)M -. 综上所述,符合条件的点M 的坐标是1(3,2)M ,2(3,2)M -,3(5,2)M -.【举一反三】如图,在平面直角坐标系中,直线4y x =-+与x 轴、y 轴分别交于A ,B 两点,直线3y kx =-经过点A ,且与y 轴交于点C ,若点M 在直线AB 上运动,点N 在直线AC 上运动,且以O ,B ,M ,N 为顶点的四边形是平行四边形,则点M 的坐标 ______ .【答案】解:把0x =代入4y x =-+得:4y =,即点B 的坐标为:(0,4),线段OB 的长度为:4,把0y =代入4y x =-+得:40x -+=,解得:4x =,即点A 的坐标为:(4,0),把点(4,0)A 代入直线3y kx =-的:430k -=,解得:34k =,即直线AC 的解析式为:334y x =-,设点M 的横坐标为m ,则M 的坐标为:(,4)m m -+,根据题意得:点N 的坐标为:3(,3)4m m -当04m <<时,3(4)(3)44m m -+--=, 解得:127m =, 即点M 的坐标为:12(7,16)7, 当4m >时, 3(3)(4)44m m ---+=, 解得:447m =, 即点M 的坐标为:44(7,16)7-, 综上,点M 的坐标为:12(7,16)7或44(7,16)7-,如下图所示: 故答案为:12(7,16)7或44(7,16)7-.2.如图在平面直角坐标系中,点A 在x 轴的正半轴上,点B 在y 轴的正半轴上,且OA、OB 的长满足|2|0OA -.(1)求AB 的长;(2)若直线y kx b =+与线段AB 交于点E ,与坐标轴分别交于C 、D 两点,且点3(0,)2D ,(1,2)E ,求点C 的坐标;(3)在(2)的条件下,在坐标平面内是否存点P ,使以A 、B 、C 、P 为顶点的四边形是平行四边形?若存在,请直接写出点P 的坐标;若不存在,请说明理由.【答案】解:|2|0OA -,2OA ∴=,4OB =,在RtAOB ∆中,根据勾股定理得,AB(2)将点3(0,)2D ,(1,2)E 代入直线y kx b =+中得,232k b b +=⎧⎪⎨=⎪⎩, ∴1232k b ⎧=⎪⎪⎨⎪=⎪⎩, ∴直线CD 是解析式为1322y x =+, 令0y =,则13022x +=,3x ∴=-, ∴点C 的坐标(3,0)-;(3)如图,连接BC ,由(1)知,2OA =,4OB =,点A 在x轴的正半轴上,点B 在y 轴的正半轴上,(2,0)A∴,(0,4)B,由(2)知,(3,0)C-,5AC∴=,以A、B、C、P为顶点的四边形是平行四边形,①当AC为边时,//BP AC,5BP AC==,(5,4)P∴-或(5,4);②当AC为对角线时,点B向下平移4个单位,再向右平移2个单位,∴点C向下平移4个单位,再向右平移2个单位得到点P的坐标(32,04)-+-,(1,4)P∴--,即:点P的坐标为(5,4)-或(5,4)或(1,4)--.例2、如图,在已建立直角坐标系的44⨯正方形方格纸中,若每个小正方形的边长为1,将ABC∆绕点B顺时针旋转90︒到DBE∆(1)求线段BC扫过的面积;(2)平移线段DE后的像为GF,在正方形格点上是否存在点F,G,使得以D,E,F,G为顶点的四边形是菱形,求线段FG所在的直线解析式.【答案】解:(1)2902360Sππ==;(2)当(2,2)F ,(0,3)G 时,D ,E ,F ,G 为顶点的四边形是菱形,设直线FG 的解析式为y kx b =+,223k b b +=⎧⎨=⎩, 解得123k b ⎧=-⎪⎨⎪=⎩,132FG y x =-+; 当(4,2)F ,(2,3)G 时,D ,E ,F ,G 为顶点的四边形是菱形,设直线FG 的解析式为y mx n =+,4223m n m n +=⎧⎨+=⎩, 解得124m n ⎧=-⎪⎨⎪=⎩,142FG y x =-+.【举一反三】如图,在平面直角坐标系xOy 中,直线21y x =-+与坐标轴分别交于A ,B 两点,与直线y x a =+交于点D ,点B 绕点A 顺时针旋转90︒的对应点C 恰好落在直线y x a =+上.(1)求直线CD 的表达式;(2)若点E 在y 轴上,且CDE ∆的周长最小,求点E 的坐标;(3)点F 是直线21y x =-+上的动点,G 为平面内的点,若以点C ,D ,F,G 为顶点的四边形是菱形,请直接写出点G 的坐标.【答案】解:(1)如图1中,连接AC ,作CE x ⊥轴于E .90BAC ∠=︒,90ABO BAO ∴∠+∠=︒,90BAO CAE ∠+∠=︒,ABO CAE ∴∠=∠,AB OC =,90AOB CEA ∠=∠=︒,ABO CAE ∴∆≅∆,12CE OA ∴==,1AE OB ==, 3(2C ∴,1)2, 把3(2C ,1)2代入y x a =+,得到1322a =+, 1a ∴=-,∴直线CD 的解析式为1y x =-.(2)如图2中,作D 关于y 轴的对称点D ',连接CD '交y 轴于E ,此时CDE ∆的周长最小.由121y x y x =-⎧⎨=-+⎩解得2313x y ⎧=⎪⎪⎨⎪=-⎪⎩, 2(3D ∴,1)3-,2(3D '-,1)3-, ∴直线CD '的解析式为511313y x =-,1(0,)13E ∴-.(3)如图3中,①如图3中,当DF 为菱形对角线时,四边形DCFG 是菱形,C ∴、G 关于AB 对称,易求直线CG 的解析式为1124y x =-, 由112421y x y x ⎧=-⎪⎨⎪=-+⎩,解得120x y ⎧=⎪⎨⎪=⎩,G ∴与C 关于1(2,0)对称,可得1(2G -,1)2-.②如图4中,当AC 为菱形的对角线时,F 、G 关于CD 对称,求出线段CD 的垂直平分线,同法可得7(3G ,7)6-. ③如图5中,当CF为菱形的对角线时,可得3(2G,12或32+,12.综上所述,满足条件的点G 坐标为1(2-,1)2-或7(3,7)6-或3(2,12+或32+,12.1.如图,直角坐标系中的网格由单位正方形构成,在格点ABC ∆中,点A 的坐标为(2,3)(1)若以A 、B 、C 及点D 为顶点的四边形是矩形,直接写出点D 的坐标: (0,4) ;(2)若以A 、B 、C 及点E 为顶点的四边形是平行四边形,请画出所有点E 的位置.【答案】解:(1)如图1所示:四边形ADBC是矩形,5CD AB ∴=,1OD =,4OD ∴=,(0,4)D ∴,故答案为:(0,4);专题过关(2)如图2所示:2.如图,直线2y =+与坐标轴分别交于A ,B 两点,点C 在y 轴上,且12OA AC =,直线CD AB ⊥于点P ,交x 轴于点D (1)求点P 的坐标(2)坐标系内是否存在点M ,使以点B ,P ,D ,M 为顶点的四边形为平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由.【答案】解:(1)对于直线2y +,令0x =得到2y =,令0y =得到-(0,2)A ∴,(B -0),2AC AO =,4AC ∴=,(0,6)C ∴,CD AB ⊥,∴直线CD 的解析式为6y =+,由26y x y ⎧+⎪⎨⎪=+⎩,解得3x y ⎧=⎪⎨=⎪⎩P ∴,3).(2)存在,P 点坐标3),(23D,0),(B -0), BD ∴=,当1PM BD是平形四边形, 则1BD PM ==1(M ∴-3),当2PBDM 是平形四边形,则2BD PM ==2M ∴,3),P 到x 轴距离等于3M 到x 轴距离,故3M 的纵坐标为3-,BE DF BD DE ==-=FO ∴3M ∴的横坐标为 3M ∴的坐标为(3)-;综上所述M 点的坐标为:1(M -3),2M3),3(M ,3)-.3.如图, 在平面直角坐标系xOy ,直线1y x =+与24y x =-+交于点A ,两直线与x 轴分别交于点B 和点C ,D 是直线AC 上的一个动点, 直线AB 上是否存在点E ,使得以E ,D ,O ,A 为顶点的四边形是平行四边形?若存在, 求出点E 的坐标;若不存在, 请说明理由 .【答案】解:①如下图: 当//OE AD 时,//OE AC ,所以直线OE 的解析式为2y x =-, 联立OE 、AB ,得12y x y x =+⎧⎨=-⎩①②,解得1323x y ⎧=-⎪⎪⎨⎪=⎪⎩,即11(3E -,2)3;②如下图: 当//DE OA 时,//OD AB 时,//OD AB ,∴直线OD 的解析式为y x =,联立OD 、AC ,得24y xy x =⎧⎨=-+⎩,解得4343x y ⎧=⎪⎪⎨⎪=⎪⎩,4(3D ,4)3. 联立AB 、AC 得241y x y x =-+⎧⎨=+⎩,解得12x y =⎧⎨=⎩,(1,2)A .OA 的解析式为2y x =, //DE OA ,∴设直线DE 的解析式为2y x b =+,将点D 的坐标代入直线的解析式得:42y x =-联立DE 、AB 得4231y x y x ⎧=-⎪⎨⎪=+⎩,解得73103x y ⎧=⎪⎪⎨⎪=⎪⎩,27(3E ,10)3. ③当OA 为对角线时,(1,2)A ,OA ∴的中点坐标为1(2,1),点D 在直线24y x =-+上,∴设(,24)D m m -+,点E 在直线1y x =+上,∴设(,1)E n n +,DE ∴的中点坐标为(2m n +,241)2m n -+++, ∴122m n +=,24112m n -+++=, 43m ∴=,13n =-,1(3E ∴-,2)3综上所述:11(3E -,2)3,27(3E ,10)3.4.如图,四边形OABC 为矩形,A 点在x 轴上,C 点在y 轴上,矩形一角经过翻折后,顶点B 落在OA边的点G 处,折痕为EF ,F 点的坐标是(4,1),30FGA ∠=︒. (1)求B 点坐标. (2)求直线EF 解析式.(3)若点M 在y 轴上,直线EF 上是否存在点N ,使以M 、N 、F 、G 为顶点的四边形是平行四边形?若存在,求N 点的坐标;若不存在,请说明理由.【答案】解:(1)F点的坐标是(4,1),1FA∴=,4OA=,30 FGA∠=︒,GA∴=,2FG=,由折叠的性质知2BF FG==,3AB∴=,四边形OABC为矩形,4CB OA∴==,B∴点坐标为(4,3);(2)903060AFG∠=︒-︒=︒,由折叠的性质知1(18060)602EFB EFG∠=∠=︒-︒=︒,BE∴=4CE∴=-(4E∴-3),设直线EF的解析式是y kx b=+,∴41(44k bk b+=⎧⎪⎨-+=⎪⎩,解得1kb⎧=⎪⎪⎨⎪=+⎪⎩,∴直线EF的解析式是1y=++(3)①如图1中,当四边形MNGF是平行四边形时,易知点N的横坐标为点N在直线EF上,(N ∴2.②如图2中,当四边形MNFG 是平行四边形时,易知点N 点N 在直线EF 上,N ∴.③如图3中,当四边形MFNG 是平行四边形时,易知点N 的横坐标为8(8N ∴2).5.平面直角坐标系中,直线132y x =-+与x 轴交于点A ,与y 轴交于点B ,与直线(0)y kx k =≠交于点(2,)C m .(1)求k 的值;(2)求OBC ∆的面积;(3)点M 为直线132y x =-+上一动点,过M 作/MN x 轴交直线y kx =于点N ,作MP x ⊥轴于点P ,过N作NQ x ⊥轴于点Q ,当以M ,N ,Q ,P 为顶点的四边形是正方形时,直接写出点M 的坐标.【答案】解:(1)(2,)C m 在直线132y x =-+上2m ∴=(2,2)C ∴将(2,2)C 代入(0)y kx k =≠中得:1k =(2)直线132y x =-+与x 轴交于点A ,与y 轴交于点B ,(6,0)A ∴,(0,3)B (2,2)COBC ∴∆的面积为:13232⨯⨯= (3)MP x ⊥轴,NQ x ⊥轴//MP NQ ∴,90MPQ ∠=︒/MN x 轴,即/MN PQ∴以M ,N ,Q ,P 为顶点的四边形是矩形当以M ,N ,Q ,P 为顶点的四边形是正方形时,即四边形MNQP 为正方形∴当满足MN NQ =时,必有以M ,N ,Q ,P 为顶点的四边形是正方形设(,)N a a ,则(62,)M a a -|63|MN a ∴=-,||NQ a =|63|||a a ∴-=3a ∴=或32(0,3)M ∴或3(3,)26.已知,如图,在平面直角坐标系xoy 中,直线1:3l y x =+分别交x 轴、y 轴于点A 、B 两点,直线2:3l y x =-过原点且与直线1l 相交于C ,点P 为y 轴上一动点. (1)求点C 的坐标;(2)在平面坐标系中是否存在点M ,使以A 、O 、C 、M 为顶点的四边形为平行四边形.若存在,求出点M 的坐标;若不存在,请说明理由;(3)当PA PC +的值最小时,求此时点P 的坐标,并求PA PC +的最小值.【答案】解:(1)直线1:3l y x =+①与直线2:3l y x =-②相交于C , 联立①②解得,34x =-,94y =,3(4C ∴-,9)4;(2)直线3y x =+交x 轴于点A ,(3,0)A ∴-,由(1)知,3(4C -,9)4,以A 、O 、C 、M 为顶点的四边形为平行四边形, 设(,)M m n 如图1,∴①当AC 是对角线时,131(3)242m --=,191(0)242n +=,154m ∴=-,94n =, 15(4M ∴-,9)4, ②当OC 是对角线时,131(0)(3)242m -=-+,191(0)(0)242n +=+,94m ∴=,94n =,19(4M ,9)4, ③当OA 为对角线时,113(03)()224m -=-,119(00)()224m +=+,94m ∴=-,94n =-.29(4M -,9)4,(3)如图2,作点(3,0)A -关于y 轴的对称点(3,0)A ',连接CA '交y 轴于点P ,此时,PC PA +最小,最小值为CA '= 由(1)知,3(4C -,9)4,(3,0)A ',∴直线A C '的解析式为3955y x =-+, 9(0,)5P ∴.。
一次函数与平行四边形存在性问题

一次函数与平行四边形存在性问题1.坐标系中的平行四边形:(1)对边平行且相等2. 线段中点坐标公式平面直角坐标系中,点A坐标为(x1,y1),点B坐标为(x2,y2),则线段AB的中点坐标为(221xx+,221yy+).2.1平行四边形顶点坐标公式□ABCD的顶点坐标分别为A(x A,y A)、B(x B,y B)、C(x C,y C)、D(x D,y D),则:x A+x C=x B+x D;y A+y C=y B+y D.证明:如图2,连接AC、BD,相交于点E.∵点E为AC的中点,∴E点坐标为(2CA xx+,2CA yy+).又∵点E为BD的中点,∴E点坐标为(2DB xx+,2DB yy+).∴x A+x C=x B+x D;y A+y C=y B+y D.即平行四边形对角线两端点的横坐标、纵坐标之和分别相等.以上两条可统一为:总结:平面直角坐标系中,平行四边形两组相对顶点的横坐标之和相等,纵坐标之和相等方法归纳:1、列出四个点坐标2、分三组对角线讨论列方程组,解方程组3、验证点是否符合题意如图,已知一次函数y=kx+b的图象经过A(﹣2,﹣1),B(1,3)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的表达式;(2)求△AOB的面积;(3)平面内是否存在一点M,使以点M、C、O、B为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标,若不存在,请说明理由.如图,在平面直角坐标系中,矩形OABC的顶点A在y轴的正半轴上,点C在x轴的正半轴上,线段OA,OC的长分别是m,n且满足(m﹣6)2+=0,点D是线段OC上一点,将△AOD沿直线AD翻折,点O落在矩形对角线AC上的点E处(1)求线段OD的长;(2)求点E的坐标;(3)DE所在直线与AB相交于点M,点N在x轴的正半轴上,以M、A、N、C为顶点的四边形是平行四边形时,求N点坐标.如图,在平面直角坐标系中,已知矩形OABC的两个顶点A、B 的坐标分别A(32-,0)、B(32-,2),∠CAO=30°.(1)求对角线AC所在的直线的函数表达式;(2)把矩形OABC以AC所在的直线为对称轴翻折,点O落在平面上的点D处,求点D的坐标;(3)在平面内是否存在点P,使得以A、O、D、P为顶点的四边形为平行四边形?若存在,求出点P的坐标;若不存在,请说明理由.如图1,在平面直角坐标系中,直线l1:y=x+1与y轴交于点A,过B(6,1)的直线l2与直线l1交于点C(m,﹣5).(1)求直线l2的解析式;(2)若点D是第一象限位于直线l2上的一动点,过点D作DH∥y轴交l1于点H.当DH=8时,试在x轴上找一点E,在直线l1上找一点F,使得△DEF的周长最小,求出周长的最小值;(3)如图2,将直线l2绕点A逆时针旋转90°得到直线l3,点P是直线l3上一点,到y轴的距离为2且位于第一象限.直线l2与x轴交于点M,与y轴交于点N,将△OMN沿射线NM方向平移2个单位,平移后的△OMN记为△O'M'N'.在平面内是否存在一点Q,使得以点M′,C,P,Q顶点的四边形是平行四边形,若存在,请直接写出点Q的坐标;若不存在,请说明理由.如图1,在平面直角坐标系xOy中,直线l2:y=﹣x+与x轴交于点B,与直线l1:y=x+b交于点C,C 点到x轴的距离CD为2,直线l1交x轴于点A.(1)求直线l1的函数表达式;(2)如图2,y轴上的两个动点E、F(E点在F点上方)满足线段EF的长为,连接CE、AF,当线段CE+EF+AF 有最小值时,求出此时点F的坐标以及CE+EF+AF的最小值;(3)如图3,将△ACB绕点B逆时针方向旋转60°,得到△BGH,使点A与点H对应,点C与点G对应,将△BGH沿着直线BC平移,平移后的三角形为△B′G′H′,点M为直线AC上的动点,是否存在分别以C、O、M、G′为顶点的平行四边形,若存在,请求出M的坐标;若不存在,说明理.。
压轴题06二次函数与特殊四边形存在性问题(四大类型)-2023年中考数学压轴题专项训练(全
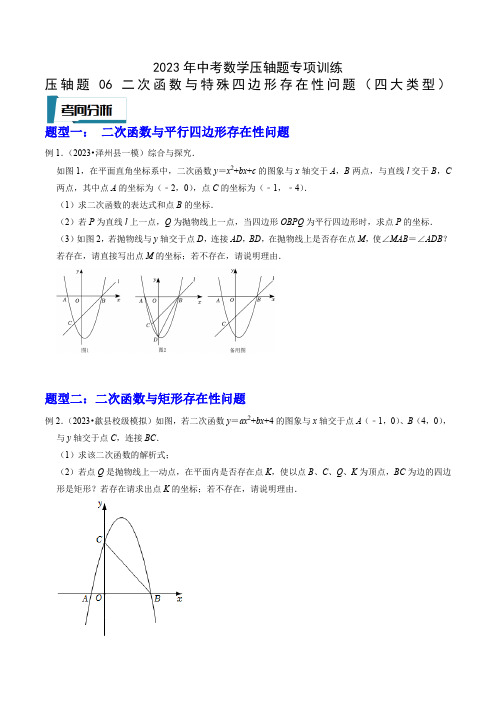
2023年中考数学压轴题专项训练压轴题06二次函数与特殊四边形存在性问题(四大类型)题型一:二次函数与平行四边形存在性问题例1.(2023•泽州县一模)综合与探究.如图1,在平面直角坐标系中,二次函数y=x2+bx+c的图象与x轴交于A,B两点,与直线l交于B,C 两点,其中点A的坐标为(﹣2,0),点C的坐标为(﹣1,﹣4).(1)求二次函数的表达式和点B的坐标.(2)若P为直线l上一点,Q为抛物线上一点,当四边形OBPQ为平行四边形时,求点P的坐标.(3)如图2,若抛物线与y轴交于点D,连接AD,BD,在抛物线上是否存在点M,使∠MAB=∠ADB?若存在,请直接写出点M的坐标;若不存在,请说明理由.题型二:二次函数与矩形存在性问题例2.(2023•歙县校级模拟)如图,若二次函数y=ax2+bx+4的图象与x轴交于点A(﹣1,0)、B(4,0),与y轴交于点C,连接BC.(1)求该二次函数的解析式;(2)若点Q是抛物线上一动点,在平面内是否存在点K,使以点B、C、Q、K为顶点,BC为边的四边形是矩形?若存在请求出点K的坐标;若不存在,请说明理由.题型三: 二次函数与菱形存在性问题例3.(2023春•沙坪坝区校级月考)如图,在平面直角坐标系中,抛物线y=﹣x2+bx+c经过A(0,1),B (4,﹣1).直线AB交x轴于点C,P是直线AB上方且在对称轴右侧的一个动点,过P作PD⊥AB,垂足为D,E为点P关于抛物线的对称轴的对应点.(1)求抛物线的函数表达式;(2)当√5PD+PE的最大值时,求此时点P的坐标和√5PD+PE的最大值;(3)将抛物线y关于直线x=3作对称后得新抛物线y',新抛物线与原抛物线相交于点F,M是新抛物线对称轴上一点,N是平面中任意一点,是否存在点N,使得以C,F,M,N为顶点的四边形是菱形,写出所有符合条件的点N的坐标,并写出求解点N的坐标的其中一种情况的过程.题型四: 二次函数与正方形存在性问题例4.(2023•前郭县一模)如图,在平面直角坐标系中,抛物线y=x2﹣4x+c与y轴相交于点A(0,2).(1)求c的值;(2)点B为y轴上一点,其纵坐标为m(m≠2),连接AB,以AB为边向右作正方形ABCD.①设抛物线的顶点为P,当点P在BC上时,求m的值;②当点C在抛物线上时,求m的值;③当抛物线与正方形ABCD有两个交点时,直接写出m的取值范围.一.解答题(共20小题)1.(2023春•兴化市月考)已知:二次函数y=ax2+2ax﹣8a(a为常数,且a>0)的图象与x轴交于点A、B(点A在点B的左侧),与y轴交于点C,顶点为点D.(1)分别求点A、B的坐标;(2)若△ABC是直角三角形,求该二次函数相应的表达式;(3)当a=12时,一次函数y=12x+b的图象过B点,与二次函数的对称轴交于Q点,N为一次函数图象上一点,过N点作y的平行线交二次函数图象于M点,当D、M、N、Q四点组成的四边形是平行四边形时,求N点的坐标.2.(2023春•沙坪坝区校级月考)如图1,在平面直角坐标系中,抛物线y=ax2+bx+8(a≠0)与x轴交于点B(﹣4,0),点C(8,0),与y轴交于点A.点D的坐标为(0,4).(1)求二次函数的解析式及点C的坐标.(2)如图1,点F为该抛物线在第一象限内的一动点,过E作FE∥CD,交CD于点F,求EF+√55DF的最大值及此时点E的坐标.(3)如图2,在(2)的情况下,将原抛物线绕点D旋转180°得到新抛物线y',点N是新抛物线y'上一点,在新抛物线上的对称轴上是否存在一点M,使得点D,E,M,N为顶点的四边形为平行四边形,若存在,请直接写出点M的坐标,并写出其中一个点M的求解过程.3.(2023•武清区校级模拟)在平面直角坐标系中,二次函数y=ax2+bx+3的图象与x轴交于A(﹣4,0),B(2,0)两点,与y轴交于点C.(1)求这个二次函数的解析式;(2)抛物线上是否存在点Q,且满足AB平分∠CAQ,若存在,求出Q点坐标;若不存在,说明理由;(3)点N为x轴上一动点,在抛物线上是否存在点M,使以B,C,M,N为顶点的四边形是平行四边形?若存在,直接写出点M的坐标;若不存在,说明理由.4.(2023春•承德县月考)已知二次函数y=14x2−32x−4与x数轴交于点A、B(A在B的左侧),与y轴交于点C,连接BC.发现:点A的坐标为,求出直线BC的解析式;拓展:如图1,点P是直线BC下方抛物线上一点,连接PB、PC,当△PBC面积最大时,求出P点的坐标;探究:如图2,抛物线顶点为D,抛物线对称轴交BC于点E,M是线段BC上一动点(M不与B、C两点重合),连接PM,设M点的横坐标为m(0<m<8),当m为何值时,四边形PMED为平行四边形?5.(2023春•梅江区校级月考)如图,在平面直角坐标系中,△AOC绕原点O逆时针旋转90°得到△DOB,其中OA=1,OC=3.(1)若二次函数经过A、B、C三点,求该二次函数的解析式;(2)在(1)条件下,在二次函数的对称轴l上是否存在一点P,使得P A+PC最小?若P点存在,求出P点坐标;若P点不存在,请说明理由.(3)在(1)条件下,若E为x轴上一个动点,F为抛物线上的一个动点,使得B、C、E、F构成平行四边形时,求E点坐标.6.(2022秋•云州区期末)综合与探究如图,二次函数y=ax2+bx+4的图象经过x轴上的点A(6,0)和y轴上的点B,且对称轴为直线x=7 2.(1)求二次函数的解析式.(2)点E位于抛物线第四象限内的图象上,以OE,AE为边作平行四边形OEAF,当平行四边形OEAF 为菱形时,求点F的坐标与菱形OEAF的面积.(3)连接AB,在直线AB上是否存在一点P,使得△AOP与△AOB相似,若存在,请直接写出点P坐标,若不存在,请说明理由.7.(2023春•开福区校级月考)【定义】对于函数图象上的任意一点P(x,y),我们把x+y称为该点的“雅和”,把函数图象上所有点的“雅和”的最小值称为该函数的“礼值”.根据定义回答问题:(1)①点P(9,10)的“雅和”为;(直接写出答案)②一次函数y=3x+2(﹣1≤x≤3)的“礼值”为;(直接写出答案)(2)二次函数y=x2﹣bx+c(bc≠0)(3≤x≤5)交x轴于点A,交y轴于点B,点A与点B的“雅和”相等,若此二次函数的“礼值”为1﹣b,求b,c的值;(3)如图所示,二次函数y=x2﹣px+q的图象顶点在“雅和”为0的一次函数的图象上,四边形OABC 是矩形,点B的坐标为(5,﹣3),点O为坐标原点,点C在x轴上,当二次函数y=x2﹣px+q的图象与矩形的边有四个交点时,求p的取值范围.8.(2023春•无锡月考)在平面直角坐标系中,O为坐标原点,二次函数y=ax2﹣2ax﹣3a(a>0)的图象分别与x轴交于A、B两点(点A在点B左侧),与y轴交于点C,过点B作BC的垂线交对称轴于点M,以BM、BC为邻边作矩形BMNC.(1)求A、B的坐标;(2)当点N恰好落在函数图象上时,求二次函数的表达式;(3)作点N关于MC的对称点N',则点N'能否落在函数图象的对称轴上,若能,请求出二次函数的表达式;若不能,请说明理由.9.(2022秋•开福区校级期末)若凸四边形的两条对角线所夹锐角为60°,我们称这样的凸四边形为“美丽四边形”.(1)①在“平行四边形、矩形、菱形、正方形”中,一定不是“美丽四边形”的有;②若矩形ABCD是“美丽四边形”,且AB=1,则BC=;(2)如图1,“美丽四边形”ABCD内接于⊙O,AC与BD相交于点P,且对角线AC,为直径,AP=2,PC=8,求另一条对角线BD的长;(3)如图2,平面直角坐标系中,已知“美丽四边形”ABCD的四个顶点A(﹣2,0),C(1,0),B在第三象限,D在第一象限,AC与BD交于点O,且四边形ABCD的面积为6√3,若二次函数y=ax2+bx+c (a、b、c为常数,且a≠0)的图象同时经过这四个顶点,求a的值.10.(2022秋•南关区校级期末)在平面直角坐标系中,二次函数y=x2﹣2x+n(x>0)的图象记为G1,将G1绕坐标原点旋转180°得到图象G2,图象G1和G2合起来记为图象G.(1)若点P(﹣2,3)在图象G上,求n的值.(2)当n=﹣1时.①若O(t,1)在图象G上,求t的值.②当k≤x≤3(k<3)时,图象G对应函数的最大值为2,最小值为﹣2,直接写出k的取值范围.(3)当以A(﹣2,2),B(﹣2,﹣1),C(1,﹣1),D(1,2)为顶点的矩形ABCD的边与图象G有且只有3个公共点时,直接写出n的取值范围.11.(2022•株洲)已知二次函数y=ax2+bx+c(a>0).(1)若a=1,b=3,且该二次函数的图象过点(1,1),求c的值;(2)如图所示,在平面直角坐标系xOy中,该二次函数的图象与x轴相交于不同的两点A(x1,0)、B (x2,0),其中x1<0<x2、|x1|>|x2|,且该二次函数的图象的顶点在矩形ABFE的边EF上,其对称轴与x轴、BE分别交于点M、N,BE与y轴相交于点P,且满足tan∠ABE=3 4.①求关于x的一元二次方程ax2+bx+c=0的根的判别式的值;②若NP=2BP,令T=1a2+165c,求T的最小值.阅读材料:十六世纪的法国数学家弗朗索瓦•韦达发现了一元二次方程的根与系数之间的关系,可表述为“当判别式Δ≥0时,关于x的一元二次方程ax2+bx+c=0(a≠0)的两个根x1、x2有如下关系:x1+x2=−b a,x1x2=ca”.此关系通常被称为“韦达定理”.12.(2023春•南关区月考)已知抛物线y=−12x2+bx+c(b、c是常数)的顶点B坐标为(﹣1,2),抛物线的对称轴为直线l,点A为抛物线与x轴的右交点,作直线AB.点P是抛物线上的任意一点,其横坐标为m,过点P作x轴的垂线交直线AB于点Q,过点P作PN⊥l于点N,以PQ、PN为边作矩形PQMN.(1)b=,c=.(2)当点Q在线段AB上(点Q不与A、B重合)时,求PQ的长度d与m的函数关系式,并直接写出d的最大值.(3)当抛物线被矩形PQMN截得的部分图象的最高点纵坐标与最低点纵坐标的距离为2时,求点P的坐标.13.(2023春•南关区校级月考)在平面直角坐标系中,抛物线y =﹣x 2+bx +c (b 、c 是常数)经过点A (﹣1,0)和点B (3,0).点P 在抛物线上,且点P 的横坐标为m . (1)求b 、c 的值;(2)当△P AB 的面积为8时,求m 的值;(3)当点P 在点A 的右侧时,抛物线在点P 与点A 之间的部分(包含端点)记为图象G ,设G 的最高点与最低点的纵坐标之差为h ,求h 与m 之间的函数关系式;(4)点Q 的横坐标为1﹣3m ,纵坐标为m +1,以PQ 为对角线构造矩形,且矩形的边与坐标轴平行.当抛物线在矩形内部的点的纵坐标y 随x 的增大而增大或y 随x 的增大而减小时,直接写出m 的取值范围.14.(2023•九台区校级一模)在平面直角坐标系中,已知抛物线y =x 2﹣2ax ﹣a (a 为常数). (1)若点(2,﹣1)在抛物线上. ①求抛物线的表达式;②当x 为何值时y 随x 的增大而减小?(2)若x ≤2a ,当抛物线的最低点到x 轴的距离恰好是1时,求a 的值;(3)已知A (﹣1,1)、B(−1,2a −12),连结AB .当抛物线与线段AB 有交点时,该交点为P (点P 不与A 、B 重合),将线段PB 绕点P 顺时针旋转90°得到线段PM ,以PM 、P A 为邻边构造矩形PMQA .当抛物线在矩形PMQA 内部(包含边界)图象所对应的函数的最大值与最小值的差为32时,直接写出a 的值.15.(2023•靖江市校级模拟)如图,在平面直角坐标系中,抛物线y=−12x2+bx+32与x轴正半轴交于点A,且点A的坐标为(3,0),过点A作垂直于x轴的直线l.P是该抛物线上的任意一点,其横坐标为m,过点P作PQ⊥l于点Q,M是直线l上的一点,其纵坐标为﹣m+32,以PQ、QM为边作矩形PQMN.(1)求b的值.(2)当点Q与点M重合时,求m的值.(3)当矩形PQMN是正方形,且抛物线的顶点在该正方形内部时,求m的值.(4)当抛物线在矩形PQMN内的部分所对应的函数值y随x的增大而减小时.直接写出m的取值范围.16.(2022秋•临朐县期末)如图,在平面直角坐标系中,O是坐标原点,菱形OABC的顶点A(3,4),C 在x轴的负半轴,抛物线y=ax2+bx+c的对称轴x=2,且过点O,A.(1)求抛物线y=ax2+bx+c的解析式;(2)若在线段OA上方的抛物线上有一点P,求△P AO面积的最大值,并求出此时P点的坐标;(3)若把抛物线y=ax2+bx+c沿x轴向左平移m个单位长度,使得平移后的抛物线经过菱形OABC的顶点B.直接写出平移后的抛物线解析式.17.(2023•道外区一模)如图,在平面直角坐标系中,点O为坐标原点,抛物线y=ax2﹣2ax+c经过点A (﹣4,0),点C(0,6),与x轴交于另一点B.(1)求抛物线的解析式;(2)点D为第一象限抛物线上一点,连接AD,BD,设点D的横坐标为t,△ABD的面积为S,求S关于t的函数解析式(不要求写出自变量t的取值范围);(3)在(2)的条件下,点P为第四象限抛物线上一点,连接P A交y轴于点E,点F在线段BC上,点G在直线AD上,若tan∠BAD=12,四边形BEFG为菱形,求点P的坐标.18.(2023春•九龙坡区校级月考)如图,在平面直角坐标系中,抛物线y=12x2+bx+c与x轴交于A(﹣1,0),B(4,0),与y轴于点C,连接BC,D为抛物线的顶点.(1)求该抛物线的解析式;(2)点P为直线BC下方抛物线上的一动点,过P作PE⊥BC于点E,过P作PF⊥x轴于点F,交直线BC于点G,求PE+PG的最大值,以及此时点P的坐标;(3)将抛物线y=12x2+bx+c沿射线CB方向平移,平移后的图象经过点H(2,﹣1),点M为D的对应点,平移后的抛物线与y轴交于点N,点Q为平移后的抛物线对称轴上的一点,且点Q在第一象限.在平面直角坐标系中确定点R,使得以点M,N,Q,R为顶点的四边形为菱形,请写出所有符合条件的点R的坐标,并写出求解点R的坐标的其中一种情况的过程.19.(2023•安徽一模)如图,在平面直角坐标系中,抛物线C 1:y =−14x 2+bx +c 的图象与坐标轴交于A 、B 、C 三点,其中点A 的坐标为(0,8),点B 的坐标为(﹣4,0),点D 的坐标为(0,4).(1)求该二次函数的表达式及点C 的坐标;(2)若点F 为该抛物线在第一象限内的一动点,求△FCD 面积的最大值;(3)如图2,将抛物线C 1向右平移2个单位,向下平移5个单位得到抛物线C 2,M 为抛物线C 2上一动点,N 为平面内一动点,问是否存在这样的点M 、N ,使得四边形DMCN 为菱形,若存在,请直接写出点N 的坐标;若不存在,请说明理由.20.(2023•九台区一模)在平面直角坐标系中,抛物线y =x 2+bx +c (b 、c 是常数)经过点(﹣2,﹣1),点(1,2).点A 在抛物线上,且点A 的横坐标为m (m ≠0).以点A 为中心,构造正方形POMN ,PQ =2|m |,且PQ ⊥x 轴.(1)求该抛物线对应的函数表达式;(2)若点B 是抛物线上一点,且在抛物线对称轴右侧.过点B 作x 轴的平行线交抛物线于另一点C ,连接BC .当BC =6时,求点B 的坐标;(3)若m <0,当抛物线在正方形内部的点的纵坐标y 随x 的增大而增大或y 随x 的增大而减小时,求m 的取值范围;(4)当抛物线与正方形PQMN 的边只有2个交点,且交点的纵坐标之差为34时,直接写出m 的值.。
平行四边形存在性问题(三定一动)

平行四边形存在性问题
平行四边形存在性问题 第一篇
主讲人: 日 期:2022-11-15
2
平行四边形存在性问题
平行四边形存在性问题分类
类型一、三定点一动点
此种情况是三个点固定,另外一个动点可能在正比例函数、一次函数、反比例 函数、二次函数上,也可能在x轴、y轴或者坐标平面上。
问题是先找动点位置,再求出动点坐标可以使这四个点构成平行四边形;
B、P两点为对点,则B、P中点坐标 5 x0 , 2 y0
2
2
4 2 5 x0
2
2
2
2
2
5
平行四边形存在性问题
例题解析:如图,抛物线y= - x2 + x +2 与x轴的交点为A、B,与y轴的交点为C
,点P是平面内一点,判断有几个点P能使以点A、B、C、P为顶点的四边形是平
C
则P1、P2、P3就是所求的动点的具体位置,可以使四 边形ABCP为平行四边形。
4
1 平行四边形存在性问题
问题二:如图,在平面直角坐标系中,已知□ABCD的顶点坐标分别是A(-4,2), B(-5,-2),C(2,1),如何确定点P(x0,y0)?
y
A(-4,2)
7
O
7
B(-5,-2)
P(x0,y0)
顶点的四边形是平行四边形,求出P点坐标。
y
第一步:先求出A(1,0),B (0,1),C(-1,-1),
连接A、B、C组成三角形
P1
第二步:过A点做BC平行线,
(0,1)B
P3
O
C
(-1,-1)
A(1,0)
过B点做AC平行线,
过C点做BC平行线, 则三条平行线的三个交点即为P1、P2、 x 第P三3 步:利用点的平移法或者对点法进行点P坐标求解 ∴ P1(2,2),P2(-2,0),P3(0,-2)
一次函数平行四边形存在性

1平行四边形存在性Ø知识点睛1.存在性问题处理框架:①研究背景图形.②根据不变特征,确定分类标准.③分析特殊状态的形成因素,画出符合题意的图形并求解.④结果验证.2.平行四边形存在性问题特征举例:①三定一动,连接定点出现三条定线段.定线段分别作为平行四边形的________,利用________确定点的坐标.②两定两动,连接定点出现一条定线段.若定线段作为平行四边形的________,则通过________确定点的坐标;若定线段作为平行四边形的________,则定线段绕________旋转,利用________________确定点的坐标.Ø精讲精练1.如图,在平面直角坐标系中,点A 的坐标为(1,0),点B 的坐标为(4,0),点C 在y 轴正半轴上,且OB =2OC .若M 是坐标平面内一点,且以点M ,A ,B ,C 为顶点的四边形是平行四边形,则点M 的坐标为_____________________.2.如图,在平面直角坐标系中,已知A (3,0),B (0,1),C (2,2),若D 是坐标平面内一点,且以点A ,B ,C ,D 为顶点的四边形是平行四边形,则点D 的坐标为______________.CB A yOxxC BAy O3. 如图,在平面直角坐标系中,直线323y x =+与坐标轴分别交于点A ,B ,点C 在y 轴正半轴上,且12OA AC =,直线CD ⊥AB 于点P ,交x 轴于点D .在坐标平面内是否存在点M ,使得以点B ,P ,D ,M 为顶点的四边形是平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由.的坐标;若不存在,请说明理由.xy ABCD OPxy ABCD OP4. 如图,在平面直角坐标系中,直线334y x =-+与x 轴、y 轴分别交于点A ,B ,点C 的坐标为(0,2-).若点D 在直线AB 上运动,点E 在直线AC 上运动,当以点O ,A ,D ,E 为顶点的四边形是平行四边形时,求点D 的坐标.的坐标.y xCB AO5. 如图,在平面直角坐标系中,四边形OABC 是直角梯形,是直角梯形,BC ∥OA ,∠OCB =90°,AB =5,BC =1,直线112y x =-+经过点A ,且与y轴交于点D .若M 是直线AD 上的一个动点,则在x 轴上是否存在点N ,使得以点O ,B ,M ,N 为顶点的四边形是平行四边形?若存在,求出点N 的坐标;若不存在,请说明理由.标;若不存在,请说明理由.y xCB AO y x DC BA O y xD C BAO6. 如图,在平面直角坐标系中,在平面直角坐标系中,四边形四边形OABC 是矩形,顶点A ,C 分别在x 轴、y 轴上,顶点B 的坐标为(3,4),点E 在OC 边上,点F 的坐标为(2,4).将矩形OABC 沿直线EF 折叠,点C 落在AB 边上的点G 处,若点N 在x 轴上,则直线EF 上是否存在点M ,使得以点F ,G ,M ,N 为顶点的四边形是平行四边形?若存在,求出点M 的坐标;若不存在,请说明理由.的坐标;若不存在,请说明理由.GF OAB C E xy GFOAB CE xy【参考答案】Ø 知识点睛 1. ①对角线①对角线 平移②边②边 平移平移 对角线对角线 其中点其中点 中点坐标公式 Ø 精讲精练1. (3,2),(-3,2),(5,-2) 2. (5,1),(-1,3),(1,-1) 3. 存在存在 (53,3),(33-,3),(3-,-3) 4. (125,65),(285,-65) 5. 存在存在 (-3,0),(7,0),(3,0) 6. 存在存在 (4333-,3),(4313-,3-),(4313+,83-) 。
二次函数与特殊四边形存在问题(学生版)

二次函数与几何综合专题---- 平行四边形存在性问题【模型解读】考虑到求证平行四边形存在,必先了解平行四边形性质: (1)对应边平行且相等; (2)对角线互相平分.这是图形的性质,我们现在需要的是将其性质运用在在坐标系中: (1)对边平行且相等可转化为:A B D CAB DC x x x x y y y y -=-⎧⎨-=-⎩,可以理解为点B 移动到点A ,点C 移动到点D ,移动路径完全相同.(2)对角线互相平分转化为:2222A CB DAC BD x x x x y y y y ++⎧=⎪⎪⎨++⎪=⎪⎩,可以理解为AC 的中点也是BD 的中点.【小结】虽然由两个性质推得的式子并不一样,但其实可以化为统一:A B D C A C D BA B D C AC D B x x x x x x x x y y y y y y y y -=-+=+⎧⎧→⎨⎨-=-+=+⎩⎩, 2222A CB DAC BD x x x x y y y y ++⎧=⎪⎪⎨++⎪=⎪⎩→A C B D A C B D x x x x y y y y +=+⎧⎨+=+⎩. 当AC 和BD 为对角线时,结果可简记为:A C B D +=+(各个点对应的横纵坐标相加)y D -y Cx D -x Cy A -y Bx A -x BABC DDCBA引例:已知A (1,1)、B (3,2),点C 在x 轴上,点D 在y 轴上,且以A 、B 、C 、D 为顶点的四边形是平行四边形,求C 、D 坐标.【分析】设C 点坐标为(m ,0),D 点坐标为(0,n ),又A (1,1)、B (3,2). (1)当AB 为对角线时,130120m n +=+⎧⎨+=+⎩,解得43m n =⎧⎨=⎩,故C (4,0)、D (0,3);(2)当AC 为对角线时,130102m n +=+⎧⎨+=+⎩,解得21m n =⎧⎨=-⎩,故C (2,0)、D (0,-1);(3)当AD 为对角线时,103120m n +=+⎧⎨+=+⎩,解得21m n =-⎧⎨=⎩,故C (-2,0)、D (0,1).【动点综述】“三定一动”的动点和“两定两动”的动点性质并不完全一样,“三定一动”中动点是在平面中,横纵坐标都不确定,需要用两个字母表示,这样的我们姑且称为“全动点”,而有一些动点在坐标轴或者直线或者抛物线上,用一个字母即可表示点坐标,称为“半动点”.从上面例子可以看出,虽然动点数量不同,但本质都是在用两个字母表示出4个点坐标.若把一个字母称为一个“未知量”也可理解为:全动点未知量=半动点未知量×2.找不同图形的存在性最多可以有几个未知量,都是根据图形决定的,像平行四边形,只能有2个未知量.究其原因,在于平行四边形两大性质: (1)对边平行且相等; (2)对角线互相平分.但此两个性质统一成一个等式: A C B DAC BD x x x x y y y y +=+⎧⎨+=+⎩,两个等式,只能允许最多存在两个未知数,即我们刚刚所讲的平行四边形存在性问题最多只能存在2个未知量.【模型实例】1.如图,已知抛物线y=ax2+bx+4经过A(﹣1,0),B(4,0)两点,交y轴于点C.(1)求抛物线的解析式;(2)连接BC,求直线BC的解析式;(3)请在抛物线的对称轴上找一点P,使AP+PC的值最小,求点P的坐标,并求出此时AP+PC的最小值;(4)点M为x轴上一动点,在抛物线上是否存在一点N,使得以A、C、M、N四点为顶点的四边形是平行四边形?若存在,求出点N的坐标;若不存在,请说明理由.2.将抛物线y=ax2(a≠0)向左平移1个单位,再向上平移4个单位后,得到抛物线H:y=a(x﹣h)2+k.抛物线H与x轴交于点A,B,与y轴交于点C.已知A(﹣3,0),点P是抛物线H上的一个动点.(1)求抛物线H的表达式;(2)如图1,点P在线段AC上方的抛物线H上运动(不与A,C重合),过点P作PD⊥AB,垂足为D,PD 交AC于点E.作PF⊥AC,垂足为F,求△PEF的面积的最大值;(3)如图2,点Q是抛物线H的对称轴l上的一个动点,在抛物线H上,是否存在点P,使得以点A,P,C,Q为顶点的四边形是平行四边形?若存在,求出所有符合条件的点P的坐标;若不存在,说明理由.3.如图,抛物线y=ax2+bx﹣3的图象与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C,直线l与抛物线交于点B,交y轴于点D(0,3).(1)求该抛物线的函数表达式;(2)点P(m,0)为线段OB上一动点,过点P作x轴的垂线EF,分别交抛物线与直线l于点E,F,连接CE,CF,BE,求四边形CEBF面积的最大值及此时m的值;(3)点M为y轴右侧抛物线上一动点,过点M作直线MN∥AC交直线l于点N,是否存在点M,使以A,C,M,N四点为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标;若不存在,请说明理由.【课后练习】1.如图,已知二次函数y=−38x2+bx+c的图象与x轴交于点A、C,与y轴交于点B,直线y=34x+3经过A、B两点.(1)求b、c的值.(2)若点P是直线AB上方抛物线上的一动点,过点P作PF⊥x轴于点F,交直线AB于点D,求线段PD 的最大值.(3)在(2)的结论下,连接CD,点Q是抛物线对称轴上的一动点,在抛物线上是否存在点G,使得以C、D、G、Q为顶点的四边形是平行四边形,若存在,请直接写出点G的坐标;若不存在,请说明理由.2.已知,抛物线y=x2+bx+c与x轴交点为A(﹣1,0)和点B,与y轴交点为C(0,﹣3),直线L:y=kx﹣1与抛物线的交点为点A和点D.(1)求抛物线和直线L的解析式;(2)如图,点M为抛物线上一动点(不与A、D重合),当点M在直线L下方时,过点M作MN∥x轴交L 于点N,求MN的最大值;(3)点M为抛物线上一动点(不与A、D重合),M'为直线AD上一动点,是否存在点M,使得以C、D、M、M′为顶点的四边形是平行四边形?如果存在,请直接写出点M的坐标,如果不存在,请说明理由.二次函数与几何综合专题---- 菱形存在性问题【模型解读】作为一种特殊的平行四边形,我们已经知道可以从以下几种方式得到菱形: (1)有一组邻边相等的平行四边形菱形; (2)对角线互相垂直的平行四边形是菱形; (3)四边都相等的四边形是菱形.坐标系中的菱形存在性问题也是依据以上去得到方法.和平行四边形相比,菱形多一个“对角线互相垂直”或“邻边相等”,故若四边形ABCD 是菱形,则其4个点坐标需满足:A CB D AC BD x x x x y y y y ⎧+=+⎪⎪+=+⎨=即根据菱形的图形性质,我们可以列出关于点坐标的3个等式, 故菱形存在性问题点坐标最多可以有3个未知量.因此就常规题型而言,菱形存在性至少有2个动点,多则有3个动点,可细分如下两大类题型: (1)2个定点+1个半动点+1个全动点 (2)1个定点+3个半动点引例:如图,在坐标系中,A 点坐标(1,1),B 点坐标为(5,4),点C 在x 轴上,点D 在平面中,求D 点坐标,使得以A 、B 、C 、D 为顶点的四边形是菱形.【分析】设C 点坐标为(m ,0),D 点坐标为(p ,q ). (1)当AB 为对角线时,由题意得:(AB 和CD 互相平分及AC =BC ) ()()()()2222151********m p q m m ⎧+=+⎪⎪+=+⎨⎪-+-=-+-⎪⎩,解得:398985m p q ⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩(2)当AC 为对角线时,由题意得:(AC 和BD 互相平分及BA =BC )()()()()2222151041514504m p qm ⎧+=+⎪⎪+=+⎨⎪-+-=-+-⎪⎩,解得:223m p q =⎧⎪=-⎨⎪=-⎩或843m p q =⎧⎪=⎨⎪=-⎩ (3)当AD 为对角线时,由题意得:()()()()2222151401514110p mq m ⎧+=+⎪⎪+=+⎨⎪-+-=-+-⎪⎩,解得:153m p q ⎧=+⎪⎪=+⎨⎪=⎪⎩153m p q ⎧=-⎪⎪=-⎨⎪=⎪⎩【模型实例】1.如图,已知直线与x 轴、y 轴分别交于B 、C 两点,抛物线y =ax 2+3x +c 经过B 、C 两点,与x 轴的另一个交点为A ,点E 的坐标为.(1)求抛物线的函数表达式;(2)点E ,F 关于抛物线的对称轴直线l 对称,Q 点是对称轴上一动点,在抛物线上是否存在点P ,使得以E 、F 、P 、Q 为顶点的四边形是菱形?若存在,求出点P 的坐标;若不存在,请说明理由.2.如图,在平面直角坐标系中,抛物线y=﹣x2﹣x+2交x轴于点A、B,交y轴于点C.(1)求△ABC的面积;(2)如图,过点C作射线CM,交x轴的负半轴于点M,且∠OCM=∠OAC,点P为线段AC上方抛物线上的一点,过点P作AC的垂线交CM于点G,求线段PG的最大值及点P的坐标;(3)将该抛物线沿射线AC方向平移个单位后得到的新抛物线为y′=ax2+bx+c(a≠0),新抛物线y′与原抛物线的交点为E,点F为新抛物线y′对称轴上的一点,在平面直角坐标系中是否存在点Q,使以点A、E、F、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.3.如图,抛物线y=ax2+bx+c与x轴交于A,B(﹣1,0)两点,与y轴交于点C,直线AC的解析式为y=x﹣2.(1)求抛物线的解析式;(2)已知k为正数,当0<x≤1+k时,y的最大值和最小值分别为m,n,且m+n=,求k的值;(3)点P是平面内任意一点,在抛物线对称轴上是否存在点Q,使得以点A,C,P,Q为顶点的四边形是菱形?若存在,求出点Q的坐标;若不存在,请说明理由.【课后练习】1.如图1,抛物线y=ax2+bx+c与x轴相交于点B、C(点B在点C左侧),与y轴相交于点A.已知点B坐标为B(1,0),BC=3,△ABC面积为6.(1)求抛物线的解析式;(2)如图1,点P为直线AC下方抛物线上一动点,过点P作PD∥AB,交线段AC于点D.求PD长度的最大值及此时P点的坐标;(3)如图2,将抛物线向左平移个单位长度得到新的抛物线,M为新抛物线对称轴l上一点,N为平面内一点,使得以点A、B、M、N为顶点的四边形为菱形,请直接写出点N的坐标,并写出求解其中一个N点坐标的过程.2.如图,抛物线y=ax2+bx+3交x轴于点A(﹣1,0)和点B(3,0),与y轴交于点C,连接BC,交对称轴于点D.(1)求抛物线的解析式;(2)点P是直线BC上方的抛物线上一点,连接PC,PD.求△PCD的面积的最大值以及此时点P的坐标;(3)将抛物线y=ax2+bx+3向右平移1个单位得到新抛物线,新抛物线与原抛物线交于点E,点F是新抛物线的对称轴上的一点,点G是坐标平面内一点.当以D、E、F、G四点为顶点的四边形是菱形时,直接写出点F的坐标,并写出求解其中一个点F的坐标的过程.二次函数与几何综合专题---- 矩形存在性问题【模型解读】矩形的判定:(1)有一个角是直角的平行四边形;(2)对角线相等的平行四边形; (3)有三个角为直角的四边形.【题型分析】矩形除了具有平行四边形的性质之外,还有“对角线相等”或“内角为直角”,因此相比起平行四边形,坐标系中的矩形满足以下3个等式:A CB D AC BD x x x x y y y y ⎧+=+⎪⎪+=+⎨=(AC 为对角线时)因此在矩形存在性问题最多可以有3个未知量,代入可以得到三元一次方程组,可解. 确定了有3个未知量,则可判断常见矩形存在性问题至少有2个动点,多则可以有3个. 题型如下:(1)2个定点+1个半动点+1个全动点; (2)1个定点+3个半动点.引例:已知A (1,1)、B (4,2),点C 在x 轴上,点D 在坐标系中,且以A 、B 、C 、D 为顶点的四边形是矩形,求D 点坐标.【分析】设C 点坐标为(a ,0),D 点坐标为(b ,c ),又A (1,1)、B (4,2). 先考虑平行四边形存在性:(1)AB 为对角线时,14120a b c +=+⎧⎨+=+⎩,满足此条件的C 、D 使得以A 、B 、C 、D 为顶点的四边形是平行四边形,另外AB =CD=综合以上可解:323a b c =⎧⎪=⎨⎪=⎩或233a b c =⎧⎪=⎨⎪=⎩.故C (3,0)、D (2,3)或C (2,0)、D (3,3).(2)AC为对角线时,14102a bc+=+⎧⎨+=+⎩,另外AC=BD得:143531abc⎧=⎪⎪⎪=⎨⎪⎪=-⎪⎩.故C14,03⎛⎫⎪⎝⎭、D5,13⎛⎫-⎪⎝⎭.(3)AD为对角线时,14120b ac+=+⎧⎨+=+⎩,另外AD=BC综合以上可解得:431331abc⎧=⎪⎪⎪=⎨⎪⎪=⎪⎩.故C14,03⎛⎫⎪⎝⎭、D13,13⎛⎫⎪⎝⎭.【小结】这个方法是在平行四边形基础上多加一个等式而已,剩下的都是计算.【模型实例】1.如图,在平面直角坐标系xOy中,已知抛物线y=ax2+x+c经过A(﹣2,0),B(0,4)两点,直线x=3与x轴交于点C.(1)求a,c的值;(2)经过点O的直线分别与线段AB,直线x=3交于点D,E,且△BDO与△OCE的面积相等,求直线DE 的解析式;(3)P是抛物线上位于第一象限的一个动点,在线段OC和直线x=3上是否分别存在点F,G,使B,F,G,P为顶点的四边形是以BF为一边的矩形?若存在,求出点F的坐标;若不存在,请说明理由.2.如图,抛物线y=ax2+2x+c的对称轴是直线x=1,与x轴交于点A,B(3,0),与y轴交于点C,连接AC.(1)求此抛物线的解析式;(2)已知点D是第一象限内抛物线上的一个动点,过点D作DM⊥x轴,垂足为点M,DM交直线BC于点N,是否存在这样的点N,使得以A,C,N为顶点的三角形是等腰三角形.若存在,请求出点N的坐标,若不存在,请说明理由;(3)已知点E是抛物线对称轴上的点,在坐标平面内是否存在点F,使以点B、C、E、F为顶点的四边形为矩形,若存在,请直接写出点F的坐标;若不存在,请说明理由.3.如图,在平面直角坐标系中,抛物线y=ax2+bx﹣3交x轴于A、B两点(点A在点B的左侧),交y轴于点E,一次函数y=x+1与抛物线交于A、D两点,交y轴于点C,且D(4,5).(1)求抛物线的解析式;(2)若点P是第四象限内抛物线上的一点,过点作PQ⊥AD交AD于点Q,求PQ的最大值以及相应的P点坐标;(3)将抛物线向右平移1个单位长度,再向上平移1个单位长度得到新抛物线,新抛物线与原抛物线交于点R,M点在原抛物线的对称轴上,在平面内是否存在点N,使得以点A、R、M、N为顶点的四边形是矩形?若存在,请直接写出N点的坐标;若不存在,请说明理由.【课后练习】1.如图,在平面直角坐标系中,抛物线y=ax2+bx+c(a<0)与x轴交于A(﹣2,0)、B(4,0)两点,与y轴交于点C,且OC=2OA.(1)试求抛物线的解析式;(2)直线y=kx+1(k>0)与y轴交于点D,与抛物线交于点P,与直线BC交于点M,记m=,试求m 的最大值及此时点P的坐标;(3)在(2)的条件下,m取最大值时,点Q是x轴上的一个动点,点N是坐标平面内的一点,是否存在这样的点Q、N,使得以P、D、Q、N四点组成的四边形是矩形?如果存在,请求出点N的坐标;如果不存在,请说明理由.2.如图,抛物线y=ax2+bx+c与x轴交于A(﹣1,0),B(3,0)两点,与y轴交于点C.点D(2,3)在该抛物线上,直线AD与y轴相交于点E,点F是直线AD上方的抛物线上的动点.(1)求该抛物线对应的二次函数的关系式;(2)当点F到直线AD距离最大时,求点F的坐标;(3)如图,点M是抛物线的顶点,点P的坐标为(0,n),点Q是坐标平面内一点,以A,M,P,Q为顶点的四边形是AM为边的矩形.①求n的值;②若点T和点Q关于AM所在直线对称,求点T的坐标.二次函数与几何综合专题----正方形存在性问题【模型解读】作为特殊四边形中最特殊的一位,正方形拥有更多的性质,因此坐标系中的正方形存在性问题变化更加多样,从判定的角度来说,可以有如下:(1)有一个角为直角的菱形;(2)有一组邻边相等的矩形;(3)对角线互相垂直平分且相等的四边形.依据题目给定的已知条件选择恰当的判定方法,即可确定所求的点坐标.从未知量的角度来说,正方形可以有4个“未知量”,因其点坐标满足4个等量关系,考虑对角线性质,互相平分(2个)垂直(1个)且相等(1个).从动点角度来说,关于正方形存在性问题可分为:(1)2个定点+2个全动点;(2)1个定点+2个半动点+1个全动点;甚至可以有:(3)4个半动点.不管是哪一种类型,要明确的是一点,我们肯定不会列一个四元一次方程组求点坐标!常用处理方法:思路1:从判定出发若已知菱形,则加有一个角为直角或对角线相等;若已知矩形,则加有一组邻边相等或对角线互相垂直;若已知对角线互相垂直或平分或相等,则加上其他条件.思路2:构造三垂直全等若条件并未给关于四边形及对角线的特殊性,则考虑在构成正方形的4个顶点中任取3个,必是等腰直角三角形,若已知两定点,则可通过构造三垂直全等来求得第3个点,再求第4个点.引例:在平面直角坐标系中,A(1,1),B(4,3),在平面中求C、D使得以A、B、C、D为顶点的四边形是正方形.如图,一共6个这样的点C 使得以A 、B 、C 为顶点的三角形是等腰直角三角形.至于具体求点坐标,以1C 为例,构造△AMB ≌△1C NA ,即可求得1C 坐标.至于像5C 、6C 这两个点的坐标,不难发现,5C 是3AC 或1BC 的中点,6C 是2BC 或4AC 的中点.题无定法,具体问题还需具体分析,如上仅仅是大致思路.【模型实例】1.如图,某一次函数与二次函数y =x 2+mx +n 的图象交点为A (﹣1,0),B (4,5).(1)求抛物线的解析式;(2)点C 为抛物线对称轴上一动点,当AC 与BC 的和最小时,点C 的坐标为 (1,2) ;(3)点D 为抛物线位于线段AB 下方图象上一动点,过点D 作DE ⊥x 轴,交线段AB 于点E ,求线段DE 长度的最大值;(4)在(2)条件下,点M 为y 轴上一点,点F 为直线AB 上一点,点N 为平面直角坐标系内一点,若以点C ,M ,F ,N 为顶点的四边形是正方形,请直接写出点N 的坐标.2.如图,抛物线y=x2+bx+c经过A(﹣3,0),B(1,0)两点,与y轴交于点C,P为y轴上的动点,连接AP,以AP为对角线作正方形AMPN.(1)求抛物线的解析式;(2)当正方形AMPN与△AOP面积之比为5:2时,求点P的坐标;(3)当正方形AMPN有两个顶点在抛物线上时,直接写出点P的坐标.3.如图,抛物线y=x2+2x的顶点为A,与x轴交于B、C两点(点B在点C的左侧).(1)请求出A、B、C三点的坐标;(2)平移抛物线,记平移后的抛物线的顶点为D,与y轴交于点E,F为平面内一点,若以A、D、E、F为顶点的四边形是正方形,且平移后的抛物线的对称轴在y轴右侧,请求出满足条件的平移后抛物线的表达式.【课后练习】1.已知抛物线L:y=﹣ax2+2ax+c与x轴交于A、B两点(点A在点B的左侧),且AB=4.(1)求A、B两点的坐标;(2)将抛物线L沿x轴翻折后得到的新抛物线记为L',且记L和L'的顶点分别记为M、M',要使点A、B、M、M'为顶点的四边形是正方形,请求抛物线L的解析式.。
专题55 一次函数背景下的图形存在性问题(解析版)

例题精讲考点一:一次函数中等腰三角形存在性问题【例1】.如果一次函数y=﹣x+6的图象与x轴、y轴分别交于A、B两点,M点在x轴上,并且使得以点A、B、M为定点的三角形是等腰三角形,则M点的坐标为(﹣8,0)或(﹣2,0)或(18,0)或(﹣,0).解:一次函数y=﹣x+6中令x=0,解得y=6;令y=0,解得x=8,∴A(8,0),B(0,6),即OA=8,OB=6,在直角三角形AOB中,根据勾股定理得:AB=10,分四种情况考虑,当BM=BA时,由BO⊥AM,根据三线合一得到O为MA的中点,此时M1(﹣8,0);当AB=AM时,由AB=10,得到OM=﹣2或18,此时M2(﹣2,0),M3(18,0);当MA=MB时,∵A(8,0),B(0,6),∴AB的中点的坐标为(4,3),设直线AB的垂直平分线的解析式为y=x+b,代入(4,3)得3=+b,解得b=﹣,∴直线AB的垂直平分线的解析式为y=x﹣,令y=0,解得x=,此时M4(,0).综上,这样的M点有4个,分别为(﹣8,0)或(﹣2,0)或(18,0)或(,0).故答案为(﹣8,0)或(﹣2,0)或(18,0)或(,0).变式训练【变1-1】.如图,在平面直角坐标系中,直线MN的函数解析式为y=﹣x+3,点A在线段MN上且满足AN=2AM,B点是x轴上一点,当△AOB是以OA为腰的等腰三角形时,则B点的坐标为(2,0)或(,0)或(,0).解:∵在y=﹣x+3中,令x=0,则y=3;令y=0,则﹣x+3=0,解得x=3,∴N(3,0),M(0,3),∴OM=ON=3,∵AN=2AM,∴A(1,2),∴OA==,当AO=OB时,则OB=,∴点B的坐标为(﹣,0)或(,0);②当AO=AB时,设点B的坐标为(m,0),则=,整理得,(1﹣m)2=1,解得m=2或m=0(舍去),∴点B的坐标为(2,0).综上所述:点B的坐标为(2,0)或(,0)或(,0).【变1-2】.如图,在平面直角坐标系中,直线y=﹣2x+12与x轴交于点A,与y轴交于点B,与直线y=x交于点C.(1)求点C的坐标.(2)若P是x轴上的一个动点,直接写出当△OPC是等腰三角形时P的坐标.解:(1)联立两直线解析式成方程组,得,解得:,∴点C的坐标为(4,4);(2)设点P(m,0),而点C(4,4),点O(0,0);PC2=(m﹣4)2+16,PO2=m2,OC2=42+42=32;当PC=PO时,(m﹣4)2+16=m2,解得:m=4;当PC=OC时,同理可得:m=0(舍去)或8;当PO=OC时,同理可得:m=±4;故点P的坐标为(4,0)或(8,0)或(4,0)或(﹣4,0).考点二:一次函数中直角三角形存在性问题【例2】.已知点A、B的坐标分别为(2,2)、(5,1),试在x轴上找一点C,使△ABC为直角三角形.解:当△ABC为直角三角形时,设点C坐标为(x,0),分三种情况:①如果A为直角顶点,则AB2+AC2=BC2,即(2﹣5)2+(2﹣1)2+(2﹣x)2+22=(5﹣x)2+1,解得:x=,②如果B为直角顶点,那么AB2BC2=AC2,即(2﹣5)2+(2﹣1)2+(5﹣x)2+1=(2﹣x)2+22,解得x=,③如果C为直角顶点,那么AB2=AC2+BC2,即(2﹣5)2+(2﹣1)2=(2﹣x)2+22+(5﹣x)2+1,解得x=3或4,综上可知,使△PAB为直角三角形的点C坐标为(,0)或(,0)或(3,0)或(4,0).变式训练【变2-1】.如图,一次函数y=kx+1的图象过点A(1,2),且与x轴相交于点B.若点P 是x轴上的一点,且满足△ABP是直角三角形,则点P的坐标是(1,0)或(3,0).解:∵一次函数y=kx+1的图象过点A(1,2),∴2=k+1,解得k=1,∴一次函数的解析式为y=x+1.∴当∠APB=90°时,P1(1,0);当∠BAP=90°时,∵一次函数的解析式为y=x+1,∴设直线AP的解析式为y=﹣x+b,∵A(1,2),∴2=﹣1+b,解得b=3,∴直线AP的解析式为y=﹣x+3,∴当y=0时,x=3,∴P2(3,0).综上所述,点P的坐标是(1,0)或(3,0).【变2-2】.如图,已知一次函数y=x﹣2的图象与y轴交于点A,一次函数y=4x+b的图象与y轴交于点B,且与x轴以及一次函数y=x﹣2的图象分别交于点C、D,点D的坐标为(﹣2,﹣4).(1)关于x、y的方程组的解为.(2)求△ABD的面积;(3)在x轴上是否存在点E,使得以点C,D,E为顶点的三角形是直角三角形?若存在,求出点E的坐标;若不存在,请说明理由.解:(1)∵一次函数y=x﹣2的图象与一次函数y=4x+b的图象交于点D,且点D的坐标为(﹣2,﹣4),∴关于x、y的方程组的解是,∴关于x、y的方程组的解是,故答案为:;(2)把点D的坐标代入一次函数y=4x+b中得:﹣8+b=﹣4,解得:b=4,∴B(0,4),∵A(0,﹣2),∴AB=4﹣(﹣2)=6,==6;∴S△ABD(3)存在,如图1,当点E为直角顶点时,过点D作DE⊥x轴于E,∵D(﹣2,﹣4),∴E(﹣2,0);当点C为直角顶点时,x轴上不存在点E;当点D为直角顶点时,过点D作DE⊥CD交x轴于点E,作DF⊥x轴于F,设E(t,0),当y=0时,4x+4=0,∴x=﹣1,∴C(﹣1,0),∵F(﹣2,0),∴CE=﹣1﹣t,EF=﹣2﹣t,∵D(﹣2,﹣4),∴DF=4,CF=﹣1﹣(﹣2)=1,在Rt△DEF中,DE2=EF2+DF2=42+(﹣2﹣t)2=t2+4t+20,在Rt△CDF中,CD2=12+42=17,在Rt△CDE中,CE2=DE2+CD2,∴(﹣1﹣t)2=t2+4t+20+17,解得t=﹣18,∴E(﹣18,0),综上,点E的坐标为:(﹣2,0)或(﹣18,0).考点三:一次函数中平行四边形存在性问题【例3】.如图,已知一次函数y=kx+b的图象经过A(1,3),B(﹣2,﹣1)两点,并且交x轴于点C,交y轴于点D.(1)求该一次函数的表达式;(2)求△AOB的面积;(3)平面内是否存在一点M,使以点M、C、O、B为顶点的四边形是平行四边形,若存在,请直接写出点M的坐标,若不存在,请说明理由.解:(1)将A(1,3)、B(﹣2,﹣1),代入y=kx+b得:,解得,∴一次函数的表达式为y=x+;(2)在y=x+中,令x=0得y=,∴OD=,=OD•|x A|=××1=,∴S△AODS△BOD=OD•|x B|=××2=,=S△BOD+S△AOD=;∴△AOB的面积S△AOB(3)存在,理由如下:在y=x+中,令y=0得y=﹣,∴C(﹣,0),设M(m,n),而B(﹣2,﹣1),O(0,0),①以OB、CM为对角线,则OB的中点即是CM的中点,如图:∴,解得,∴M(﹣,﹣1);②以BC、OM为对角线,则BC的中点即是OM的中点,如图:∴,解得,∴M(﹣,﹣1);③以BM、CO为对角线,则BM的中点即是CO的中点,如图:∴,解得,∴M(,1);综上所述,M的坐标为:(﹣,﹣1)或(﹣,﹣1);或(,1).变式训练【变3-1】.如图1,在平面直角坐标系中,直线y=﹣x+3与x轴、y轴相交于A、B两点,点C在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当B'C'经过点D时,求△BCD平移的距离及点D的坐标;(3)若点P在y轴上,点Q在直线AB上,是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的P点的坐标;若不存在,请说明理由.(1)证明:∵∠BOC=∠BCD=∠CED=90°,∴∠OCB+∠OBC=90°,∠OCB+∠ECD=90°,∴∠OBC=∠ECD.∵将线段CB绕着点C顺时针旋转90°得到CD,∴BC=CD.在△BOC和△CED中,,∴△BOC≌△CED(AAS).(2)解:∵直线y=﹣x+3与x轴、y轴相交于A、B两点,∴点B的坐标为(0,3),点A的坐标为(6,0).设OC=m,∵△BOC≌△CED,∴OC=ED=m,BO=CE=3,∴点D的坐标为(m+3,m).∵点D在直线y=﹣x+3上,∴m=﹣(m+3)+3,解得:m=1,∴点D的坐标为(4,1),点C的坐标为(1,0).∵点B的坐标为(0,3),点C的坐标为(1,0),∴直线BC的解析式为y=﹣3x+3.设直线B′C′的解析式为y=﹣3x+b,将D(4,1)代入y=﹣3x+b,得:1=﹣3×4+b,解得:b=13,∴直线B′C′的解析式为y=﹣3x+13,∴点C′的坐标为(,0),∴CC′=﹣1=,∴△BCD平移的距离为.(3)解:设点P的坐标为(0,m),点Q的坐标为(n,﹣n+3).分两种情况考虑,如图3所示:①若CD为边,当四边形CDQP为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P1的坐标为(0,);当四边形CDPQ为平行四边形时,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P2的坐标为(0,);②若CD为对角线,∵C(1,0),D(4,1),P(0,m),Q(n,﹣n+3),∴,解得:,∴点P的坐标为(0,).综上所述:存在,点P的坐标为(0,)或(0,).考点四:一次函数中矩形存在性问题【例4】.Rt△AOB的两直角边OA、OB分别在x轴的负半轴和y轴的正半轴上,且OA、OB的长满足|OA﹣8|+(OB﹣6)2=0,∠ABO的平分线交x轴于点C过点C作AB的垂线,垂足为点D,交y轴于点E.(1)求线段AB的长;(2)求直线CE的解析式;(3)若M是射线BC上的一个动点,在坐标平面内是否存在点P,使以A、B、M、P为顶点的四边形是矩形?若存在,请直接写出点P的坐标;若不存在,请说明理由.解:(1)∵|OA﹣8|+(OB﹣6)2=0,∴OA=8,OB=6,在直角△AOB中,AB===10;(2)∵BC平分∠ABO,CD⊥AB,AO⊥BO,∴OC=CD,设OC=x,则AC=8﹣x,CD=x.∵△ACD和△ABO中,∠CAD=∠BAO,∠ADC=∠AOB=90°,∴△ACD相似于△ABO,∴,即,解得:x=3.即OC=3,则C的坐标是(﹣3,0).设AB的解析式是y=kx+b,根据题意得解得:则直线AB的解析式是y=x+6,设CD的解析式是y=﹣x+m,则4+m=0,则m=﹣4.则直线CE的解析式是y=﹣x﹣4;(3)①当AB为矩形的边时,如图所示矩形AM1P1B,易知BC的直线方程为y=2x+6,设M1(m,2m+6),P1(x,y),因为A(﹣8,0),B(0,6),则AM12=(m+8)2+(2m+6)2,=5m2+40m+100,BM12=m2+(2m+6﹣6)2=5m2,AB=10,根据AB2+AM12=BM12得100+5m2+40m+100=5m2,m=﹣5,∴M1(﹣5,﹣4),根据平移规律可以解得P1(3,2)②当AB为矩形的对角线时,此时有AB2=AM22+BM22,即100=5m2+40m+100+5m2,m =﹣4或m=0(舍去),∴M2(﹣4,﹣2),根据平移规律可以解得P2(﹣4,8)综上可得,满足条件的P点的坐标为P1(3,2)或P2(﹣4,8).变式训练【变4-1】.如图,四边形OABC是矩形,点A、C在坐标轴上,△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H,线段BC、OC的长是方程x2﹣4x+3=0的两个根,且OC>BC.(1)求直线BD的解析式;(2)求点H到x轴的距离;(3)点M在坐标轴上,平面内是否存在点N,使以点D、F、M、N为顶点的四边形是矩形?若存在,请直接写出点N的坐标;若不存在,请说明理由.解:(1)x2﹣4x+3=0,解得:x=3或1,故BC=1,OC=3,即点C(0,3)、点A(﹣1,0),则点B(﹣1,3),点D(3,0),点E(3,1),将B、D点的坐标代入一次函数表达式:y=kx+b得:,解得:,故直线BD的表达式为:y=﹣x+…①;(2)同理可得:直线OE的表达式为:y=x…②,联立①②并解得:y=,即点H到x轴的距离为:;(3)直线BD的表达式为:y=﹣x+,则点F(0,),①当FD是矩形的一条边时,当点M在x轴上时,∵MF⊥BD,则直线MF的表达式为:y=x+,当y=0,x=﹣,即点M(﹣,0),点F向右平移3个单位向下平移单位得到D,则点M向右平移3个单位向下平移单位得到N,则点N(,﹣);当点M在y轴上时,同理可得:点N(﹣3,﹣);②当FD是矩形的对角线时,此时点M在原点O,则点N(3,);综上,点N的坐标为:(,﹣)或(﹣3,﹣)或(3,).考点五:一次函数中菱形存在性问题【例5】.如图1,直线y=x+6与x,y轴分别交于A,B两点,∠ABO的角平分线与x轴相交于点C.(1)求点C的坐标;(2)在直线BC上有两点M,N,△AMN是等腰直角三角形,∠MAN=90°,求点M 的坐标;(3)点P在y轴上,在平面上是否存在点Q,使以点A、B、P、Q为顶点的四边形为菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)对于直线y=x+6,令x=0,得到y=6,∴B(0,6),令y=0,得到x=﹣8,∴A(﹣8,0).∵A(﹣8,0),B(0,6),∴OA=8,OB=6,∵∠AOB=90°,∴AB==10,过点C作CH⊥AB于H,设OC=t,∵BC平分∠ABO,∠AOB=90°,∴CH=OC=t,=S△ABC+S△BCO,∵S△ABO∴OA•OB=AB•CH+OC•OB,∴6×8=10t+6t,∴t=3,∴OC=3,∴C(﹣3,0);(2)设线BC的表达式为:y=kx+b,∵B(0,6),C(﹣3,0),∴直线BC的表达式为:y=2x+6,设点M(m,2m+6)、N(n,2n+6),过点M作MF⊥x轴于点F,过点N作NE⊥x轴于点E,∵△AMN为等腰直角三角形,故AM=AN,∵∠NAE+∠MAF=90°,∠MAF+∠AMF=90°,∴∠NAE=∠AMF,∵∠AFM=∠NEA=90°,AM=AN,∴△FMA≌△EAN(AAS),∴EN=AF,MF=AE,即﹣2n﹣6=m+8,2m+6=8+n,解得:m=﹣2,n=﹣6,故点M的坐标为(﹣2,2)、点N(﹣6,﹣6);由于M,N的位置可能互换,故点N的坐标为(﹣2,2)、点M(﹣6,﹣6);综上所述,点M的坐标为(﹣2,2)或(﹣6,﹣6);(3)设点P(0,p),∴BP2=(p﹣6)2,AP2=82+p2,①当AB是边时,如图,∵点A、B、P、Q为顶点的四边形为菱形,∴BP=AB=10,BP′=AB=10,OB=OP″,∵B(0,6),∴P(0,16),P′(0,﹣4),P″(0,﹣6),∵A(﹣8,0),∴Q(﹣8,10),Q′(﹣8,﹣10),Q″(8,0);②当AB是对角线时,如图,∵点A、B、P、Q为顶点的四边形为菱形,∴AP=BP,∴BP2=AP2,∴(p﹣6)2=82+p2,解得p=﹣,∴P(0,﹣),∵A(﹣8,0),B(0,6),∴Q(﹣8,);综上所述,点Q的坐标为(﹣8,10)或(﹣8,﹣10)或(8,0)或(﹣8,).变式训练【变5-1】.如图,在平面直角坐标系中,直线y=x+4与x轴、y轴分别交于点D、C,直线AB与y轴交于点B(0,﹣2),与直线CD交于点A(m,2).(1)求直线AB的解析式;(2)点E是射线CD上一动点,过点E作EF∥y轴,交直线AB于点F,若以O、C、E、F为顶点的四边形是平行四边形,请求出点E的坐标;(3)设P是射线CD上一点,在平面内是否存在点Q,使以B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)∵点A(m,2)在直线y=x+4上∴m+4=2解得m=﹣2∴点A的坐标为(﹣2,2)设直线AB的解析式为y=kx+b∴解得∴直线AB的解析式为y=﹣2x﹣2;(2)如图1,由题意设点E的坐标为(a,a+4),则∵EF∥y轴,点F在直线y=﹣2x﹣2上∴点F的坐标为(a,﹣2a﹣2)∴EF=|a+4﹣(﹣2a﹣2)|=|3a+6|,∵以点O、C、E、F为顶点的四边形是平行四边形,且EF∥OC∴EF=OC∵直线y=x+4与y轴交于点C∴点C的坐标为(0,4)∴OC=4,即|3a+6|=4解得:a=﹣或a=﹣∴点E的坐标为(﹣,)或(﹣,);(3)如图2,当BC为对角线时,点P,Q都是BC的垂直平分线,且点P和点Q关于BC对称,∵B(0,﹣2),C(0,4),∴点P的纵坐标为1,将y=1代入y=x+4中,得x+4=1,∴x=﹣3,∴P''(﹣3,1),∴Q''(3,1)当CP是对角线时,CP是BQ的垂直平分线,设Q(m,n),∴BQ的中点坐标为(,),代入直线y=x+4中,得+4=①,∵CQ=CB,∴m2+(n﹣4)2=36②,联立①②得,(舍)或,∴Q'(﹣6,4),当PB是对角线时,PC=BC=6,设P(c,c+4),∴c2+(c+4﹣4)2=36,∴c=3(舍)或c=﹣3,∴P(﹣3,﹣3+4),设Q(d,e)∴(﹣3+0)=(0+d),(﹣3+4﹣2)=(e+4),∴d=﹣3,e=﹣3﹣2,∴Q(﹣3,﹣3﹣2),即:点Q的坐标为(3,1),(﹣6,4)或(﹣3,﹣3﹣2).1.一次函数y=x+4分别交x轴、y轴于A、B两点,在x轴上取一点C,使△ABC为等腰三角形,则这样的点C的坐标为(﹣8,0)(3,0)(2,0)(,0).解:当x=0时,y=4,当y=0时,x=﹣3,即A(﹣3,0),B(0,4),OA=3,OB=4,由勾股定理得:AB=5,有三种情况:①以A为圆心,以AB为半径交x轴于两点,此时AC=AB=5,C的坐标是(2,0)和(﹣8,0);②以B为圆心,以AB为半径交x轴于一点(A除外),此时AB=BC,OA=OC=3,C的坐标是(3,0);③作AB的垂直平分线交x轴于C,设C的坐标是(a,0),A(﹣3,0),B(0,4),∵AC=BC,由勾股定理得:(a+3)2=a2+42,解得:a=,∴C的坐标是(,0),故答案为:(﹣8,0)(3,0)(2,0)(,0).2.如图,在平面直角坐标系中,点A坐标为(2,1),连接OA,点P是x轴上的一动点,如果△OAP是等腰三角形,请你写出符合条件的点P坐标P1(4,0),P2(,0),P3(﹣,0),P4(,0).解:设P(x,0),当OA=AP时,∵A(2,1),∴P1(4,0);当OA=OP时,∵A(2,1),∴OA==,∴P2(,0),P3(﹣,0);当AP=OP时,∵P(x,0),(2,1),∴(2﹣x)2+12=x2,解得x=,∴P4(,0).综上所述,P点坐标为:P1(4,0),P2(,0),P3(﹣,0),P4(,0).故答案为:P1(4,0),P2(,0),P3(﹣,0),P4(,0).3.如图,在平面直角坐标系中,点A的坐标为(1,0),点B的坐标为(4,0),点C在y 的正半轴上,且OB=2OC,在直角坐标平面内确定点D,使得以点D、A、B、C为顶点的四边形是平行四边形,请写出点D的坐标为(3,2)(﹣3,2)(5,﹣2).解:如图,①当BC为对角线时,易求M1(3,2);②当AC为对角线时,CM∥AB,且CM=AB.所以M2(﹣3,2);③当AB为对角线时,AC∥BM,且AC=BM.则|M y|=OC=2,|M x|=OB+OA=5,所以M3(5,﹣2).综上所述,符合条件的点D的坐标是M1(3,2),M2(﹣3,2),M3(5,﹣2).故答案为:(3,2)(﹣3,2)(5,﹣2).4.如图,一次函数y=k2x+b的图象与y轴交于点B,与正比例函数y=k1x的图象相交于点A(3,4),且OA=OB.(1)分别求出这两个函数的解析式;(2)求△AOB的面积;(3)点P在x轴上,且△POA是等腰三角形,请直接写出点P的坐标.解:(1)∵正比例函数y=k1x的图象经过点A(3,4),∴3k1=4,∴k1=,∴正比例函数解析式为y=x.如图1中,过A作AC⊥x轴于C,在Rt△AOC中,OC=3,AC=4,∴AO==5,∴OB=OA=5,∴B(0,﹣5),∴,解得,∴一次函数的解析式为y=3x﹣5.(2)如图1中,过A作AD⊥y轴于D,∵A(3,4),∴AD=3,=;∴S△AOB(3)当OP=OA时,P1(﹣5,0),P2(5,0),当AO=AP时,P3(6,0),当PA=PO时,线段OA的垂直平分线为y=﹣,∴,满足条件的点P的坐标(﹣5,0)或(5,0)或(6,0)或.5.直线l1交x轴于点A(6,),交y轴于B(0,6).(1)如图,折叠△AOB,使BA落在y轴上,折痕所在直线为l2,直线l2与x轴交于C 点,求C点坐标及l2的解析式;(2)在直线l1上找点M,使得以M、A、C为顶点的三角形是等腰三角形,求出所有满足条件的M点的坐标.解:∵点A(6,0),交y轴于B(0,6).∴OA=6,OB=6,∴tan∠OAB==,∴∠OAB=30°,∴∠OBA=60°,∵折叠△AOB,∴∠OBC=∠ABC=30°,∴BC=2OC,BO=OC=6,∴OC=2,∴点C(2,0),设直线BC解析式为:y=kx+b,解得:∴直线BC解析式为:y=﹣x+6;(2)当点M与点B重合时,由(1)可知:∠AMC=∠MAC=30°,∴CM=AC,∴△ACM是等腰三角形,∴当M为(0,6)时,△ACM是等腰三角形,∵OC=2,OA=6,∴AC=4,若AM=AC=4,如图1:过点M作MH⊥AC,∵∠MAH=30°,∴MH=AM=2,AH=2MH=6,∴OH=6﹣6或6+6,∴点M(6﹣6,2)或(6+6,﹣2)若AM=MC,如图2,过点M作MH⊥AC,∵AM=MC,MH⊥AC,∴AH=CH=2,∴OC=4,∵∠MAH=30°,∴AH=MH,∴MH=2,∴点M(4,2),综上所述:点M(6﹣6,2)或(6+6,﹣2)或(4,2)或(0,6).6.在平面直角坐标系中,直线y=kx+8k(k是常数,k≠0)与坐标轴分别交于点A,点B,且点B的坐标为(0,6).(1)求点A的坐标;(2)如图1,将直线AB绕点B逆时针旋转45°交x轴于点C,求直线BC的解析式;(3)在(2)的条件下,直线BC上有一点M,坐标平面内有一点P,若以A、B、M、P 为顶点的四边形是菱形,请直接写出点P的坐标.解:(1)令y=kx+8k=0,解得x=﹣8,故点A的坐标为(﹣8,0);(2)过点A作AD⊥AB交BC于点D,过点A作y轴的平行线交过点B与x轴的平行线于点M,交过点D与x轴的平行线于点N,∵∠ABC=45°,故△ABD为等腰直角三角形,则AD=AB,∵∠BAM+∠DAN=90°,∠DAN+∠ADN=90°,∴∠BAM=∠ADN,∵∠BMA=∠AND=90°,∴△BMA≌△AND(AAS),∴AN=BM=8,ND=AM=6,故点D的坐标为(﹣2,﹣8),设直线BC的表达式为y=kx+b,则,解得,故直线BC的表达式为y=7x+6;(3)设点M的坐标为(m,7m+6),点P(s,t),而点A、B的坐标分别为(﹣8,0)、(0,6),①当AB是边时,点A向右8个单位向上6个单位得到点B,同样,点M(P)向右8个单位向上6个单位得到点P(M),且AB=BP(AB=BM),则或,解得或或(不合题意的值已舍去);故点P的坐标为(﹣8,7)或(﹣﹣8,﹣7)或(6,﹣2);②当AB是对角线时,由中点坐标公式和AM=BM得:,解得,故点P的坐标为(﹣7,7);综上,点P的坐标为(﹣8,7)或(﹣﹣8,﹣7)或(6,﹣2)或(﹣7,7).7.如图,在平面直角坐标系中,一次函数的图象与x轴交于点A(﹣4,0),与y轴交于点B,且与正比例函数y=x的图象交于点C(m,6).(1)求一次函数的解析式;(2)求△BOC的面积;(3)在x轴上是否存在一点P,使得△ABP是等腰三角形?若存在,请直接写出符合条件的所有点P的坐标;若不存在,请说明理由.解:(1)∵将点C(m,6)代入y=x,∴6=m,∴m=4,∴C(4,6),设一次函数的解析式为y=kx+b,∴,∴,∴y=x+3;(2)在y=x+3中,令x=0得y=3,∴B(0,3),=OB•|x C|=×3×4=6;∴S△BOC(3)在x轴上存在一点P,使得△ABP是等腰三角形,理由如下:∵A(﹣4,0),B(0,3),∴AB=5,OA=4,当B为等腰三角形顶角顶点时,P点与A点关于y轴对称,∴P(4,0);当A为等腰三角形顶角顶点时,AP=AB=5,∴P(﹣9,0)或P(1,0);当P为等腰三角形顶角顶点时,设P(t,0),∵PA=PB,∴(t+4)2=t2+9,解得t=﹣,∴P(﹣,0),综上所述:P点坐标为(﹣9,0)或(1,0)或(4,0)或(﹣,0).8.如图,已知一次函数y=x+m的图象与x轴交于点A(﹣6,0),交y轴于点B.(1)求m的值与点B的坐标(2)问在x轴上是否存在点C,使得△ABC的面积为16?若存在,求出点C的坐标;若不存在,说明理由.(3)问在x轴是否存在点P,使得△ABP为等腰三角形,求出点P坐标.(4)一条经过点D(0,2)和直线AB上的一点的直线将△AOB分成面积相等的两部分,请求出这条直线的函数表达式.解:(1)把点A(﹣6,0)代入y=x+m,得m=8,∴点B坐标为(0,8).(2)存在,设点C坐标为(a,0),由题意•|a+6|•8=16,解得a=﹣2或﹣10,∴点C坐标(﹣2,0)或(﹣10,0).(3)如图1中,①当AB=AP时,AP=AB==10,可得P1(﹣16,0),P2(4,0).②当BA=BP时,OA=OP,可得P3(6,0).③当PA=PB时,∵线段AB的垂直平分线为y=﹣x+,可得P4(,0),综上所述,满足条件的点P坐标为(﹣16,0)或(4,0)或(6,0)或(,0).(4)如图2中,设过点D的直线交AB于E,设E(b,),由题意BD•(﹣b)=××6×8,∴b=﹣4,∴点E坐标(﹣4,),设直线DE的解析式为y=kx+b则有,解得,∴这条直线的函数表达式y=﹣x+2.9.在平面直角坐标系中,一次函数y=﹣x+2的图象交x轴、y轴分别于A、B两点,交直线y=kx于P(2,a).(1)求点A、B的坐标;(2)若Q为x轴上一动点,△APQ为等腰三角形,直接写出Q点坐标;(3)点C在直线AB上,过C作CE⊥x轴于E,交直线OP于D,我们规定若C,D,E 中恰好有一点是其他两点所连线段的中点,则称C,D,E三点为“和谐点”,求出C,D,E三点为“和谐点”时C点的坐标.解:(1)当x=0时,y=﹣x+2=2,∴点B的坐标为(0,2);当y=0时,有﹣x+2=0,解得:x=4,∴点A的坐标为(4,0);(2)∵一次函数y=﹣x+2的图象交直线y=kx于P(2,a).∴a=﹣×2+2=1,∴点P的坐标为(2,1),设点Q(m,0),而点A、P的坐标分别为:(4,0)、(2,1),则AP==,AQ=|4﹣m|,PQ=,当AP=AQ时,则=|4﹣m|,解得m=4±,∴点Q(4±,0);当AP=PQ时,=,解得m=0或4(舍去),∴点Q(0,0);当PQ=AQ时,即=|4﹣m|,解得:m=,∴点Q(,0);综上,点Q的坐标为(4±,0)或(0,0)或(,0);(3)∵y=kx过P(2,1).∴2k=1,解得k=,∴y=x,设点C的坐标为(n,﹣n+2),则点D的坐标为(n,n),点E的坐标为(n,0),∴CD=|﹣n+2﹣n|=|2﹣n|,DE=|n|,CE=|﹣n+2|=|n﹣2|,当D为CE的中点时,CD=DE,∴|2﹣n|=|n|,解得n=或4(舍去),∴点C的坐标为(,);当C为DE的中点时,CD=CE,∴|2﹣n|=|n﹣2|,解得n=或0(舍去),∴点C的坐标为(,);当E为CD的中点时,DE=CE,∴|n|=|n﹣2|,无解;综上,C,D,E三点为“和谐点”时C点的坐标为(,)或(,).10.如图所示,直线l:y=﹣x+2与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4).(1)求△AOB的面积;(2)动点M从A点以每秒1个单位的速度沿x轴向左移动,求△COM的面积S与M的移动时间t之间的函数关系式;(3)当动点M在x轴上移动的过程中,在平面直角坐标系中是否存在点N,使以点A,C,N,M为顶点的四边形为菱形,若存在,请直接写出点N的坐标;若不存在,请说明理由.解:(1)令y=0,,解得x=.令x=0,y=.∴A(,0),B(0,).=.∴△AOB的面积为12.(2)∵动点M从A点以每秒1个单位的速度沿x轴向左移动,∴AM=t.当0≤t≤时,OM=,OC=.∴==.当t>时,OM=t﹣.∴==.综上,△COM的面积S与M的移动时间t之间的函数关系式:S=.(3)在平面直角坐标系中存在点N,使以点A,C,N,M为顶点的四边形为菱形.①当AC,AM为菱形的边时,情况一:如图1,当点M在点A的左侧时,Rt△AOC中,=,∴NC=AC=.∵NC∥AM,∴点N(,).情况二,如图1′,当点M在点A的右侧时,由情况一同理可得点N的坐标为.②当AC为菱形的对角线时,如图2,此时M,O重合,四边形OANC为正方形,则点N(,).③如图3,当AC为菱形的边,AM为菱形的对角线时,此时点C,N关于x轴对称,∴点N(0,﹣).综上,在平面直角坐标系中存在点N,使以点A,C,N,M为顶点的四边形为菱形,此时点N的坐标为:(,),,(,),(0,﹣).11.如图,直线y=﹣x+4与x轴、y轴分别交于A、B两点,直线BC与x轴、y轴分别交于C、B两点,连接BC,且OC=OB.(1)求点A的坐标及直线BC的函数关系式;(2)点M在x轴上,连接MB,当∠MBA+∠CBO=45°时,求点M的坐标;(3)若点P在x轴上,平面内是否存在点Q,使点B、C、P、Q为顶点的四边形是菱形?若存在,请直接写出点Q的坐标;若不存在,请说明理由.解:(1)对于直线y=﹣x+4,令x=0的y=4,令y=0得x=4,∴A(4,0),B(0,4),∴OB=OA=4,∵OC=OB,∴OC=3,∴C(﹣3,0),设直线BC的解析式为y=kx+b,则有,解得,∴直线BC的解析式为y=x+4.(2)如图1中,当点M在点A的左边时,∵OB=OA=4,∠AOB=90°,∴∠ABO=45°,∴∠CBO+∠MBA=∠MBA+∠MBO=45°,∴∠CBO=∠OBM,∵∠CBO+∠BCO=90°,∠BMO+∠OBM=90°,∴∠BCO=∠BMO,∴BC=BM,OC=OM=3,∴M(3,0),作点M关于直线AB的对称点N,作直线BN交x轴于M1,则∠M1BA=∠MBA,点M1满足条件.∵N(4,1),B(0,4),∴直线BN的解析式为y=﹣x+4,令y=0,得x=,∴M1(,0),综上所述,满足条件的点M的坐标为(3,0)或(,0).(3)如图2中,∵BC==5,当BC为菱形的边时,四边形CP1Q1B,四边形CP3Q3B,四边形BCQ2P2是菱形,此时Q1(﹣5,4),Q3(5,4),Q2(0,4),当BC是菱形的对角线时,四边形CP4BQ4是菱形,可得Q4(﹣,4).综上所述,满足条件的点Q的坐标为(﹣5,4)或(5,4)或(0,﹣4)或.12.已知,一次函数y=的图象与x轴、y轴分别交于点A、点B,与直线y=相交于点C.过点B作x轴的平行线l.点P是直线l上的一个动点.(1)求点A,点B的坐标.(2)求点C到直线l的距离.=S△BCP,求点P的坐标.(3)若S△AOC(4)若点E是直线y=上的一个动点,当△APE是以AP为直角边的等腰直角三角形时,请直接写出点E的坐标.解:(1)∵一次函数y=的图象与x轴、y轴分别交于点A、点B,∴令y=0,则=0,∴x=8,令x=0,则y=6,∴点A、B的坐标分别为:(8,0)、(0,6);(2)解:得,,∴点C(3,),则C到直线l的距离为6﹣=;=×8×=15=S△BCP=×BP×(y P﹣y C)=BP×,(3)∵S△AOC解得:BP=,故点P(,6)或(﹣,6);(4)设点E(m,m)、点P(n,6);①当∠EPA=90°时,当点P在y轴右侧时,当点P在点E的左侧时,如图1,∵∠MEP+∠MPE=90°,∠MPE+∠NPA=90°,∴∠MEP=∠NPA,AP=PE,∵△EMP≌△PNA(AAS),则ME=PN=6,MP=AN,即m﹣n=6,m﹣6=8﹣n,解得:m=,当点P在点E的右侧时,如图,同理可得m=16,当∠EAP=90°时,当点P在y轴左侧时,如图2,同理可得:m﹣8=6,m=8﹣n,解得:m=14,故点E(14,);故点E(,)或(14,)或(16,20);如图3,同理可得:△AMP≌△ANE(AAS),故MP=EN,AM=AN=6,即m=n﹣8,|8﹣m|=6,解得:m=2或14(不合题意舍去),故点E(2,);综上,E(,)或(16,20)或(2,)或(14,).13.如图,在平面直角坐标系xOy中,直线y=﹣x+与y=x相交于点A,与x轴交于点B.(1)求点A,B的坐标;(2)在平面直角坐标系xOy中,是否存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形?如果存在,试求出所有符合条件的点C的坐标;如果不存在,请说明理由;(3)在直线OA上,是否存在一点D,使得△DOB是等腰三角形?如果存在,试求出所有符合条件的点D的坐标,如果不存在,请说明理由.解:(1)∵直线y=﹣x+与y=x相交于点A,∴联立得,解得,∴点A(1,1),∵直线y=﹣x+与x轴交于点B,∴令y=0,得﹣x+=0,解得x=3,∴B(3,0),(2)存在一点C,使得以O,A,B,C为顶点的四边形是平行四边形.①如图1,过点A作平行于x轴的直线,过点O作平行于AB的直线,两直线交于点C,∵AC∥x轴,OC∥AB,∴四边形CABO是平行四边形,∵A(1,1),B(3,0),∴AC=OB=3,∴C(﹣2,1),②如图2,过点A作平行于x轴的直线,过点B作平行于AO的直线,两直线交于点C,∵AC∥x轴,BC∥AO,∴四边形CAOB是平行四边形,∵A(1,1),B(3,0),∴AC=OB=3,∴C(4,1),③如图3,过点O作平行于AB轴的直线,过点B作平行于AO的直线,两直线交于点C,∵OC∥AB,BC∥AO,∴四边形CBAO是平行四边形,∵A(1,1),B(3,0),∴AO=BC,OC=AB,作AE⊥OB,CF⊥OB,易得OE=EF=FB=1,∴C(2,﹣1),(3)在直线OA上,存在一点D,使得△DOB是等腰三角形,①如图4,当OB=OD时,作DE⊥x轴,交x轴于点E∵OB=3,点D在OA上,∠DOE=45°∴DE=OE=,∴D(﹣,﹣),②如图5,当OD=OB时,作DE⊥x轴,交x轴于点E∵OB=3,点D在OA上,∠DOE=45°∴DE=OE=,∴D(,),③如图6,当OB=DB时,∵∠AOB=∠ODB=45°,∴DB⊥OB,∵OB=3,∴D(3,3),④如图7,当DO=DB时,作DE⊥x轴,交x轴于点E∵∠AOB=∠OBD=45°,∴OD⊥DB,∵OB=3,∴OE=,AE=,∴D(,).综上所述,在直线OA上,存在点D(﹣,﹣),D(,),D(3,3)或D(,),使得△DOB是等腰三角形,14.如图,经过点B(0,2)的直线y=kx+b与x轴交于点C,与正比例函数y=ax的图象交于点A(﹣1,3)(1)求直线AB的函数的表达式;(2)直接写出不等式(kx+b)﹣ax<0的解集;(3)求△AOC的面积;(4)点P是直线AB上的一点,且知△OCP是等腰三角形,写出所有符合条件的点P的坐标.解:(1)依题意得:,解得,∴所求的一次函数的解析式是y=﹣x+2.(2)观察图形可知:不等式(kx+b)﹣ax<0的解集;x<﹣1.(3)对于y=﹣x+2,令y=0,得x=2∴C(1,0),∴OC=2.=×2×3=3.∴S△AOC(4)①当点P与B重合时,OP1=OC,此时P1(0,2);②当PO=PC时,此时P2在线段OC的垂直平分线上,P2(1,1);③当PC=OC=2时,设P(m.﹣m+2),∴(m﹣2)2+(﹣m+2)2=4,∴m=2±,可得P3(2﹣,),P4(2+,﹣),综上所述,满足条件的点P坐标为:(1,1)或(0,2)或P(2+,﹣)或(2﹣,).15.如图1,已知直线l1:y=kx+4交x轴于A(4,0),交y轴于B.(1)直接写出k的值为﹣1;(2)如图2,C为x轴负半轴上一点,过C点的直线l2:经过AB的中点P,点Q(t,0)为x轴上一动点,过Q作QM⊥x轴分别交直线l1、l2于M、N,且MN=2MQ,求t的值;(3)如图3,已知点M(﹣1,0),点N(5m,3m+2)为直线AB右侧一点,且满足∠OBM=∠ABN,求点N坐标.解:(1)把A(4,0)代入y=kx+4,得0=4k+4.解得k=﹣1.故答案是:﹣1;(2)∵在直线y=﹣x+4中,令x=0,得y=4,∴B(0,4),∵A(4,0),∴线段AB的中点P的坐标为(2,2),代入,得n=1,∴直线l2为,∵QM⊥x轴分别交直线l1、l2于M、N,Q(t,0),∴M(t,﹣t+4),,∴,MQ=|﹣t+4|=|t﹣4|,∵MN=2MQ,∴,分情况讨论:①当t≥4时,,解得:t=10.②当2≤t<4时,,解得:.③当t<2时,,解得:t=10>2,舍去.综上所述:或t=10.(3)在x轴上取一点P(1,0),连接BP,作PQ⊥PB交直线BN于Q,作QR⊥x轴于R,∴∠BOP=∠BPQ=∠PRQ=90°,∴∠BPO=∠PQR,∵OA=OB=4,∴∠OBA=∠OAB=45°,∵M(﹣1,0),∴OP=OM=1,∴BP=BM,∴∠OBP=∠OBM=∠ABN,∴∠PBQ=∠OBA=45°,∴PB=PQ,∴△OBP≌△RPQ(AAS),∴RQ=OP=1,PR=OB=4,∴OR=5,∴Q(5,1),∴直线BN的解析式为,将N(5m,3m+2)代入,得3m+2=﹣×5m+4解得,∴.16.如图,平面直角坐标系中,直线l分别交x轴、y轴于A、B两点(OA<OB)且OA、OB的长分别是一元二次方程x2﹣(+1)x+=0的两个根,点C在x轴负半轴上,且AB:AC=1:2(1)求A、C两点的坐标;(2)若点M从C点出发,以每秒1个单位的速度沿射线CB运动,连接AM,设△ABM 的面积为S,点M的运动时间为t,写出S关于t的函数关系式,并写出自变量的取值范围;(3)点P是y轴上的点,在坐标平面内是否存在点Q,使以A、B、P、Q为顶点的四边形是菱形?若存在,请直接写出Q点的坐标;若不存在,请说明理由.解:(1)x2﹣(+1)x+=0,(x﹣)(x﹣1)=0,解得x1=,x2=1,∵OA<OB,∴OA=1,OB=,∴A(1,0),B(0,),∴AB=2,又∵AB:AC=1:2,∴AC=4,∴C(﹣3,0);(2)∵AB=2,AC=4,BC=2,∴AB2+BC2=AC2,即∠ABC=90°,由题意得:CM=t,CB=2.①当点M在CB边上时,S=2﹣t(0≤t);②当点M在CB边的延长线上时,S=t﹣2(t>2);(3)存在.①当AB是菱形的边时,如图所示,在菱形AP1Q1B中,Q1O=AO=1,所以Q1点的坐标为(﹣1,0),在菱形ABP2Q2中,AQ2=AB=2,所以Q2点的坐标为(1,2),在菱形ABP3Q3中,AQ3=AB=2,所以Q3点的坐标为(1,﹣2),②当AB为菱形的对角线时,如图所示的菱形AP4BQ4,设菱形的边长为x,则在Rt△AP4O中,AP42=AO2+P4O2,即x2=12+(﹣x)2,解得x=,所以Q4(1,).综上可得,平面内满足条件的Q点的坐标为:Q1(﹣1,0),Q2(1,2),Q3(1,﹣2),Q4(1,).17.如图1,在平面直角坐标系中.直线与x轴、y轴相交于A、B两点,动点C 在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上时,过点D作DE⊥x轴于点E.(1)求证:△BOC≌△CED;(2)如图2,将△BCD沿x轴正方向平移得△B'C'D',当直线B′C′经过点D时,求点D的坐标;(3)若点P在y轴上,点Q在直线AB上.是否存在以C、D、P、Q为顶点的四边形是平行四边形?若存在,直接写出所有满足条件的Q点坐标;若不存在,请说明理由.(1)证明:∵∠BOC=∠BCD=∠CED=90°,∴∠OCB+∠DCE=90°,∠DCE+∠CDE=90°,∴∠BCO=∠CDE,在△BOC和△CED中,。
一次函数与平行四边形存在性问题

一次函数与平行四边形存在性问题问题描述在平面几何中,我们知道一次函数可以用来表示一条直线的方程,而平行四边形则是具有平行边的四边形。
我们现在想研究以下问题:一次函数是否存在与平行四边形的边平行的斜率?解决方案我们将通过讨论一次函数的斜率和平行四边形的边进行分析。
一次函数的斜率一次函数可以用如下的一般方程表示:y = mx + c其中,`m` 表示斜率,`c` 表示截距。
斜率 `m` 是函数直线斜率的关键参数,它决定了直线的倾斜程度。
我们知道,当两条直线的斜率相等时,它们是平行的。
平行四边形的边平行四边形是一种特殊的四边形,它的对边是平行的。
我们可以定义平行四边形的边为 `AB` 和 `CD`,并假设它们是平行的。
讨论现在,我们来探讨一次函数是否可能存在与平行四边形的边平行的斜率 `m`。
假设 `AB` 和 `CD` 是平行四边形的边,我们可以通过求解两个点的斜率来判断函数的斜率是否与平行四边形的边平行。
假设点 `A` 的坐标为 `(x1, y1)`,点 `B` 的坐标为 `(x2, y2)`,我们可以计算出两点的斜率 `m_AB`:m_AB = (y2 - y1) / (x2 - x1)同理,如果点 `C` 的坐标为 `(x3, y3)`,点 `D` 的坐标为 `(x4, y4)`,我们可以计算出另一条边的斜率 `m_CD`:m_CD = (y4 - y3) / (x4 - x3)如果 `m_AB` 等于 `m_CD`,那么一次函数存在与平行四边形的边平行的斜率。
总结通过对一次函数的斜率和平行四边形的边进行分析,我们得出结论:一次函数存在与平行四边形的边平行的斜率。
请注意,此结论仅在满足题设条件的情况下成立,具体问题具体分析。
此解决方案仅提供了一种可能的方法,具体问题的解决需要进一步讨论和推导。
参考资料:。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
特殊平行四边形存在性
课前预习
1.一般情况下我们如何处理存在性问题
(1)研究背景图形
坐标系背景下研究 ____________ 、 ____________ ;几何图形研究____________、 ____________、____________.
(2)根据不变特征,确定分类标准
研究定点,动点,定线段,确定分类标准
不变特征举例:
① 等腰三角形(两定一动)
以定线段作为 _________或者 ___________来分类,利用
_______________确定点的位置.
② 等腰直角三角形(两定一动)
以________________来分类,然后借助 _________或者
___________确定点的位置.
(3)分析特殊状态的形成因素,画出符合题意的图形并求解
(4)结果验证
2.用铅笔做讲义第1,2 题,并将计算、演草保留在讲义上,先看知识点睛,再
做题,思路受阻时(某个点做了 2~3 分钟)重复上述动作,若仍无法解决,课堂重点听.
知识点睛
1.存在性问题处理框架:①研究背景图形.②根据不变特征,
确定分类标准.③分析特殊状态的形成因素,画出符合题意
的图形并求解.④结果验证.
2.特殊平行四边形存在性问题不变特征举例:
①菱形存在性问题(两定两动)
转化为等腰三角形存在性问题;
以定线段作为底边或者腰确定分类标准,利用两圆一线确定一动点的位置,
然后通过平移确定另一动点坐标.
②正方形存在性问题(两定两动)
转化为等腰直角三角形存在性问题;
根据直角顶点确定分类标准,利用两腰相等或者45°角确定一动点的位置,
然后通过平移确定另一动点坐标.
精讲精练
1. 如图,在平面直角坐标系xOy 中,直线 l :y2x 4 与x轴交于点A,与y
轴交于点 B.
( 1)求点 A,B 的坐标.
( 2)若 P 是直线 x2上的一动点,则在坐标平面内是否存在点Q,使得以 A,
B,P,Q为顶点的四边形是菱形若存在,求出点Q的坐标;若不存在,请说
明理由.
y
O A x
y
B
O A x
B
2.如图,在平面直角坐标系 xOy 中,直角梯形 OABC的顶点 A 在 y 轴正半轴上,
顶点C的坐标为(18,0 ), A B∥O C,∠OCB=45°,且 BC=12 2 .
(1)求点 B 的坐标.
(2)直线 BE与线段 OA交于点 E,且 OE=6.若 P 是直线 BE上的一动点,则在坐标平面内是否存在点 Q,使得以 O, E,P,Q为顶点的四边形是菱形若存在,求出点 Q的坐标;若不存在,请说
明理由.
y
B A
E
C O x
y
B A
E
C O x
3.如图,在平面直角坐标系 xOy 中,□ABCD的顶点 A,B 的坐标分别为 A(0 ,
3) ,B( 3 ,0),顶点C在x轴正半轴上,顶点D在第一象限,且AD= 2 3 .若
M 为坐标平面内一点,则在第一象限内是否存在点F,使得以A, C, F, M 为顶点的四边形是正方形若存在,求出点F的坐标;若不存在,请说明理由.
y
A D
B O
C x
y
A D
B O
C x
4.如图,在平面直角坐标系中,已知点 A,B,C的坐标分别为 A( 9 ,0) ,B(16 ,
0) ,C(0 ,12) , D是线段 BC上的一动点(不与点 B, C重合),过点 D作直
线
DE⊥OB,垂足为点 E.若 M为坐标平面内一点,则在直线DE上是否存在点 N,使得以 C,B,M,N 为顶点的四边形是正方形若存在,求出点N 的坐标;若不存在,请说明理由.
y
C
D
A O E
B x
y
C
A O
B x
y
C
A O
B x
【参考答案】
课前预习
1.(1)坐标、表达式;边、角、形
(2)①腰底两圆一线
②直角顶点两腰相等45 °角
精讲精练
A ,
0) ,B ,
-4)
1.(1) (2 (0
(2)存在,点 Q的坐标为 (0 ,4) ,(-4 ,-2) , (-4 , -6) 或(4 ,7 )
2 2.(1)B(-6 ,12)
(2)存在,点 Q 的坐标为 (6 , 6) ,( 3 2 , 3 2 ) ,( 3 2 , 3 2 ) 或( 3 , 3)
.存在,点 F 的坐标为 (3 , 3 3 ) , 3 3 , 3
)
3 (
或 (
3
3 , 3 3 )
2
2
.存在,点 N 的坐标为 (12 , 28) , (4 , 16) , (14 , 14) 或 (2 , 2) 4。
