平行线的判定和性质经典题
平行线的判定与性质的综合应用 专题练习

平行线的判定与性质的综合应用专题练习平行线的判定与性质的综合运用专题一、推理填空题1.已知:如图,DE∥BC,∠ADE=∠XXX,将说明∠1=∠2成立的理由填写完整。
解:因为DE∥BC,所以∠ADE=∠XXX。
又因为DE∥BC,所以DB∥EF。
由平行线性质可知,∠1=∠ADE=∠XXX∠2.2.已知:如图所示,∠1=∠2,∠A=∠3.求证:XXX。
证明:因为∠1=∠2,所以XXX。
又因为∠A=∠3,所以AC∥BD。
由平行线性质可知,AC∥DE。
3.已知:如图,∠XXX∠ADC,BF、DE分别平分∠ABC 与∠ADC,且∠1=∠3.求证:AB∥DC。
证明:因为∠XXX∠ADC,所以∠XXX∠ADC。
又因为BF、DE分别平分∠ABC与∠ADC,所以∠1=∠ABC,∠3=∠ADC。
由∠1=∠3可得,∠2=∠ADC。
由平行线性质可知,AB∥DC。
二、证明题4.如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37º,求∠D的度数。
证明:因为AB∥CD,所以∠A+∠D=180º。
又因为DE⊥AE,所以∠ADE=90º。
由∠A=37º可得,∠ADE=53º。
由三角形内角和定理可得,∠D=80º。
5.如图,已知AB∥CD,∠1=100°,∠2=120°,求∠α的度数。
证明:因为AB∥CD,所以∠1+∠α+∠2=180º。
由∠1=100º,∠2=120º可得,∠α= -40º。
由于∠α是角度,所以∠α=320º。
6.如图,XXX,AE平分∠BAD,求证:XXX与AE相交于F,∠XXX∠EAF。
证明:因为XXX,所以∠BAD=∠ACD。
又因为AE平分∠BAD,所以∠XXX∠DAF。
由相邻角的性质可得,∠EAF+∠DAF=∠BAD=∠ACD。
又因为CD与AE相交于F,所以∠CFE+∠EAF+∠ACD=180º。
初二平行线的判定经典练习题

初二平行线的判定经典练习题平行线是初中数学中的重要概念之一,它在几何学中有着广泛的应用。
平行线的判定方法有很多种,下面将介绍一些经典的练习题,帮助大家掌握平行线的判定方法。
1. 判断下列直线是否平行:(1)直线l1:y = 2x + 1,直线l2:3x - 4y = 7(2)直线l1:2x - y + 3 = 0,直线l2:4x - 2y + 6 = 0(3)直线l1:x - 2y - 3 = 0,直线l2:2x - 4y - 6 = 0解答:(1)两直线斜率相等,l1的斜率为2,l2的斜率为3/4,不相等,因此两直线不平行。
(2)两直线斜率相等,l1的斜率为2/1,l2的斜率为4/2,相等,因此两直线平行。
(3)两直线斜率相等,l1的斜率为1/2,l2的斜率为2/4,相等,因此两直线平行。
2. 已知线段AB且CD平行于AB,点E是线段CD上的点,若DE = 2cm,DC = 5cm,BC = 10cm,求AE的长度。
解答:由线段比例定理可知:AE/EC = AB/BC代入已知条件,得到:AE/5 = 10/10解方程得到:AE = 5cm3. 如图,AB // DE,CB是三角形ACD的角平分线,若∠ACD = 60°,求∠CAB和∠ECB。
解答:由平行线性质可知,∠CAB = ∠ACD = 60°由角平分线性质可知,∠ECB = 1/2 * ∠ACD = 1/2 * 60° = 30°4. 在平面直角坐标系中,有四点A(1, 2),B(3, -1),C(4, 5),D(6, 2),判断线段AB和线段CD是否平行。
解答:利用斜率公式计算:线段AB的斜率为:(2 - (-1))/(1 - 3) = 3/(-2) = -3/2线段CD的斜率为:(2 - 5)/(6 - 4) = -3/2两斜率相等,因此线段AB与线段CD平行。
5. 如图,已知AB // EF,且∠BCD = 90°,AC = 6cm,BC = 8cm,DE = 4cm,求EF的长度。
平行线的判定及性质

平行线的判定、性质专练
姓名:
例1:如图所示:AD∥BC,∠A=∠C,试说明AB∥DC.
变式:如图所示:AB∥DC,∠A=∠C,试说明AD∥BC.
变式2:如图,点E为DF上的点,点B为AC上的点,∠1= ∠2,∠C= ∠D,求证:DF ∥AC
变式3:如图,点B、E分别在AC、DF上,BD、CE均与AF相交,∠1=∠2,∠C=∠D,试问:∠A与∠F相等吗?请说出你的理由。
变式4:如图,已知∠A=∠F,∠C=∠D,求证:BD//CE.
例2:已知AB ∥CD,GP,HQ 分别平分∠EGB, ∠EHD,判断GP 与HQ 是否平行?
变式1:如图11,直线AB 、CD 被EF 所截,∠1 =∠2,∠CNF =∠BME。
求证:AB∥CD,MP∥NQ.
F 2
A B C D Q E 1 P M N 图11
变式2:已知AB∥CD,GP,HQ分别平分∠AGF, ∠EHD,判断GP与HQ是否平行?
例3:如图,已知AB∥CD,∠1=∠2,求证∠E=∠F.
变式1:如图,已知∠E=∠F,∠1=∠2,:求证AB∥CD .
变式2:如图,已知AB∥CD,∠E=∠F,:求证∠1=∠2.
变式3:如图,已知AB∥CD, AF∥DE, :求证∠1=∠2.
变式4:如图,已知∠1=∠2, AF∥DE, :求证AB∥CD.。
平行线典型例题

一.解答题(共21小题)
1.如图,AD⊥BC于D,EG⊥BC于G,∠E=∠1,可得AD平分∠BAC.
理由如下:∵AD⊥BC于D,EG⊥BC于G,(已知)
∴∠ADC=∠EGC=90°,(垂直的定义),
∴AD∥EG,(同位角相等,两直线平行)
∴∠1=∠2,(两直线平行,内错角相等)
∠E=∠3,(两直线平行,同位角相等)
解答:
解:AD与BC平行;理由如下:
∵BE∥DF,
∴∠B+∠BCD=180°(两直线平行,同旁内角互补)
∵∠B=∠D,
∴∠D+∠BCD=180°,
点评:
本题考查了平行线的性质及判定,熟记定理是正确解题的关键.
4.如图,已知BE∥DF,∠B=∠D,则AD与BC平行吗?试说明理由.
考点:
平行线的判定与性质.
专题:
探究型.
分析:
利用两直线平行,同旁内角互补可得∠B+∠C=180°,即∠C+∠D=180°;根据同旁内角互补,两直线平行可证得AD∥BC.
这是一道结论开放的探究性问题,由于E点位置的不确定性,可引起对E点不同位置的分类讨论。本题可分为AB,CD之间或之外。
结论:①∠AEC=∠A+∠C②∠AEC+∠A+∠C=360°③∠AEC=∠C-∠A④∠AEC=∠A-∠C⑤∠AEC=∠A-∠C⑥∠AEC=∠C-∠A.
例、如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )
(3)如图3,点 、 是直线CM、DN内部的一个点,连结 、 、 .
试求 的度数;
(4)若按以上规律,猜想并直接写出 … 的度数(不必写出过程).
例、如图,已知直线l1∥l2,且l3和l1、l2分别交于A、B两点,点P在AB上.
平行线的判定及性质 例题及练习

平行线的判定及性质一、【基础知识精讲】1、平行线的判定(1)平行公理:经过直线外一点,有且只有一条直线与已知直线平行. (2)平行公理的推论:平行于同一条直线的两条直线. (3)在同一平面内,垂直于同一条直线的两条直线. (4)同位角相等,两直线平行. (5)内错角相等,两直线平行.(6)同旁内角互补,两直线平行.3、平行线的性质(1)两直线平行,同位角相等. (2)两直线平行,内错角相等.(3)两直线平行,同旁内角互补.二、【例题精讲】专题一:余角、补角、对顶角与三线八角例题1:∠A的余角与∠A的补角互为补角,那么2∠A是()A.直角 B.锐角 C.钝角 D.以上三种都有可能【活学活用1】如图2-79中,下列判断正确的是()A.4对同位角,2对内错角,4对同旁内角B.4对同位角,2对内错角,2对同旁内角C.6对同位角,4对内错角,4对同旁内角D.6对同位角,4对内错角,2对同旁内角【活学活用2】如图2-82,下列说法中错误的是( )A.∠3和∠5是同位角B.∠4和∠5是同旁内角C.∠2和∠4是对顶角D.∠1和∠2是同位角【活学活用3】如图,直线AB与CD交于点O,OE⊥AB于O,图中∠1与∠2的关系是()A.对顶角B.互余C.互补D相等例题2:如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角分别是_______.【活学活用4】如图,∠AOC +∠DOE +∠BOF = .专题二:平行线的判定例题3:如图,已知∠EFB+∠ADC=180°,且∠1=∠2,试说明DG ∥AB.1 2A BCDF E G【活学活用】1、长方体的每一对棱相互平行,那么这样的平行棱共有 ( )A .9对B .16对 C.18对 D .以上答案都不对2、已知:如图2-96,DE ⊥AO 于E,BO ⊥AO,FC ⊥AB 于C ,∠1=∠2,求证:DO ⊥AB.3、如图2-97,已知:∠1=∠2=,∠3=∠4,∠5=∠6.求证:AD ∥BC.4、如图2—101,若要能使AB ∥ED ,∠B 、∠C 、∠D 应满足什么条件?ABCDOE F5、同一平面内有四条直线a 、b 、c 、d ,若a ∥b ,a ⊥c ,b ⊥d ,则c 、d 的位置关系为( ) A.互相垂直 B .互相平行 C.相交 D .没有确定关系专题三:平行线的性质1、如图,110,ABC ACB BO ∠+∠=、CO 分别平分ABC ∠和,ACB EF ∠过点O 与BC 平行,则BOC ∠= . 2、如图,AB //CD ,BC //DE ,则∠B+∠D = .3、如图,直线AB 与CD 相交于点O ,OB 平分∠DOE .若60DOE ∠=,则∠AOC 的度数是 .4、 如图,175,2120,375∠=∠=∠=,则4∠= .13 425、如图,//AB CD ,直线EF 分别交AB 、CD 于E 、F ,ED 平分BEF ∠,若172∠=,则2∠= .【例题讲解】例1:如图,已知:AD ∥BC, ∠AEF=∠B,求证:AD ∥EF 。
平行线判定大题30道

平行线判定大题30道摘要:一、引言1.问题背景及重要性2.文章目的与结构二、平行线判定方法1.同位角相等2.内错角相等3.同侧角相等4.两直线平行,同位角相等5.两直线平行,内错角相等6.两直线平行,同侧角相等三、平行线判定大题解析1.例题1:同位角相等判定2.例题2:内错角相等判定3.例题3:同侧角相等判定4.例题4:两直线平行,同位角相等判定5.例题5:两直线平行,内错角相等判定6.例题6:两直线平行,同侧角相等判定四、平行线判定大题练习1.练习1:同位角相等判定2.练习2:内错角相等判定3.练习3:同侧角相等判定4.练习4:两直线平行,同位角相等判定5.练习5:两直线平行,内错角相等判定6.练习6:两直线平行,同侧角相等判定五、总结与展望1.平行线判定方法总结2.平行线判定大题技巧概述3.后续学习建议正文:一、引言1.问题背景及重要性在初中数学几何部分,平行线的判定与性质是重点内容。
掌握平行线的判定方法,对于解决各类几何问题具有重要意义。
本文将为大家详细解析平行线判定大题30道,帮助大家更好地理解和应用平行线判定方法。
2.文章目的与结构本文旨在通过解析平行线判定大题,使大家对平行线的判定方法有更深刻的理解。
文章共分为五个部分,分别为:引言、平行线判定方法、平行线判定大题解析、平行线判定大题练习和总结与展望。
二、平行线判定方法1.同位角相等若两条直线被第三条直线所截,且有同位角相等,则这两条直线平行。
2.内错角相等若两条直线被第三条直线所截,且有内错角相等,则这两条直线平行。
3.同侧角相等若两条直线被第三条直线所截,且有同侧角相等,则这两条直线平行。
4.两直线平行,同位角相等若两条直线平行,则它们被第三条直线所截时的同位角相等。
5.两直线平行,内错角相等若两条直线平行,则它们被第三条直线所截时的内错角相等。
6.两直线平行,同侧角相等若两条直线平行,则它们被第三条直线所截时的同侧角相等。
三、平行线判定大题解析1.例题1:同位角相等判定已知直线AB与CD被直线EF所截,若∠AEF = ∠CED,证明AB平行于CD。
初三平行线知识点以及经典例题

初三平行线知识点以及经典例题平行线是初中数学中的重要概念之一。
本文将介绍初三学生需要掌握的平行线的知识点,并提供几个经典例题供大家练。
知识点1. 平行线定义:如果两条直线在同一个平面内,且没有交点,那么它们被称为平行线。
平行线可以用符号"// "表示。
平行线定义:如果两条直线在同一个平面内,且没有交点,那么它们被称为平行线。
平行线可以用符号"// "表示。
2. 平行线的判定方法:以下是几种判定平行线的方法:平行线的判定方法:以下是几种判定平行线的方法:- (a) 两条直线的斜率相等,且不重合。
- (b) 两条直线之间的对应角相等。
- (c) 一条直线与另一平行线的任意直线交角为180°。
3. 平行线的性质:平行线具有以下性质:平行线的性质:平行线具有以下性质:- (a) 平行线之间的距离在每个交点处相等。
- (b) 平行线之间的夹角为0°,即平行线之间没有夹角。
- (c) 平行线与同一直线相交的角被称为"同位角",同位角的对应角相等。
经典例题例题1已知AB//CD,AB=6cm,BC=4cm,EF=5cm,求EF的长度。
例题2已知直线l与平行线m及n相交,交角1为120°,求交角2的度数。
例题3已知直线k与平行线p及q相交,交角a为40°,求交角b的度数。
例题4已知平行四边形ABCD中,AB=10cm,BC=6cm,求AD的长度。
以上是初三平行线知识点以及经典例题的介绍。
希望能对初三学生理解和掌握平行线有所帮助。
平行线的判定与性质练习题

平行线的判定与性质练习题平行线的判定与性质练习题平行线是几何学中的基本概念之一,它在我们的日常生活中无处不在。
从道路上的交叉口到建筑物的设计,平行线都扮演着重要的角色。
在几何学中,我们需要学会判定平行线,并掌握它们的性质。
下面,我将给大家提供一些平行线的判定与性质练习题,希望能帮助大家更好地理解和应用平行线的知识。
练习题一:判定平行线1. 在下图中,判断线段AB和线段CD是否平行。
A-----B| |C-----D2. 在下图中,判断线段AB和线段EF是否平行。
A-----B| || |E-----F3. 在下图中,判断线段AB和线段CD是否平行。
A-----B\ /\ /C-----D练习题二:平行线的性质1. 若两条平行线被一条横线所截,那么对应的内角互补。
2. 若两条平行线被一条横线所截,那么对应的外角相等。
3. 若两条直线分别与一条平行线相交,那么对应的内角相等。
4. 若两条直线分别与一条平行线相交,那么同旁内角互补。
练习题三:平行线的应用1. 若两条平行线被一条横线所截,且已知其中一个内角的度数为60°,求对应的内角和外角的度数。
2. 若两条平行线被一条横线所截,且已知其中一个外角的度数为120°,求对应的内角和另一个外角的度数。
3. 若两条直线分别与一条平行线相交,且已知其中一个内角的度数为70°,求对应的内角和同旁内角的度数。
4. 若两条直线分别与一条平行线相交,且已知其中一个同旁内角的度数为45°,求对应的内角和另一个同旁内角的度数。
通过以上练习题,我们可以加深对平行线的判定与性质的理解。
判定平行线需要观察线段的走向,若两条线段的走向相同,即不相交且不重合,则可以判定它们为平行线。
而平行线的性质则是通过观察线段之间的关系得出的。
掌握这些性质可以帮助我们解决更复杂的几何问题。
在应用平行线的过程中,我们可以根据已知条件利用平行线的性质进行推导。
(完整)七年级上册平行线经典题型及答案解析(经典)

1、如图,∠1=∠2,∠3=110°,求∠4.2、如图,AB ∥CD ,AE 交CD 于点C ,DE ⊥AE ,垂足为E ,∠A=37°,求∠D 的度数.3、如图,AB ,CD 是两根钉在木板上的平行木条,将一根橡皮筋固定在A ,C 两点,点E 是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,请你探索∠A ,∠AEC ,∠C 之间具有怎样的关系并说明理由。
(提示:先画出示意图,再说明理由)提示:这是一道结论开放的探究性问题,由于E 点位置的不确定性,可引起对E 点不同位置的分类讨论。
本题可分为AB ,CD 之间或之外。
结论:①∠AEC =∠A +∠C ②∠AEC +∠A +∠C =360°③∠AEC =∠C -∠A④∠AEC =∠A -∠C ⑤∠AEC =∠A -∠C ⑥∠AEC =∠C -∠A .4、如图,将三角板的直角顶点放在直角尺的一边上,∠1=30°,∠2=50°,则∠3的度数为( )A 、80B 、50C 、30D 、205、将一个直角三角板和一把直尺如图放置,如果∠α=43°,则∠β的度数是( )A 、43°B 、47°C 、30°D 、60°6、如图,点A 、B 分别在直线CM 、DN 上,CM ∥DN .(1)如图1,连结AB ,则∠CAB +∠ABD = ;(2)如图2,点错误!未找到引用源。
是直线CM 、DN 内部的一个点,连结错误!未找到引用源。
、错误!未找到引用源。
.求证:错误!未找到引用源。
=360°;(3)如图3,点错误!未找到引用源。
、错误!未找到引用源。
是直线CM 、DN 内部的一个点,连结错误!未找到引用源。
、错误!未找到引用源。
、错误!未找到引用源。
.试求错误!未找到引用源。
的度数;(4)若按以上规律,猜想并直接写出错误!未找到引用源。
…错误!未找到引用源。
七年级上册平行线经典题型及答案解析(经典)

七年级上册平行线经典题型及答案解析(经典)1、已知∠1=∠2,∠3=110°,求∠4的度数。
2、已知AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,且∠A=37°,求∠D的度数。
3、在图中,AB,CD是两根钉在木板上的平行木条,将一根橡皮筋固定在A,C两点,点E是橡皮筋上的一点,拽动E点将橡皮筋拉紧后,探索∠A,∠AEC,∠C之间具有的关系并说明理由。
根据提示,可分类讨论E点在AB,CD之间或之外。
结论:①∠AEC=∠A+∠C②∠AEC+∠A+∠C=360°③∠AEC=∠C-∠A④∠AEC=∠A-∠C⑤∠AEC=∠A-∠C⑥∠AEC=∠C-∠A.4、在图中,将三角板的直角顶点放在直角尺的一边上,已知∠1=30°,∠2=50°,求∠3的度数。
5、在图中,将一个直角三角板和一把直尺放置,已知∠α=43°,求∠β的度数。
6、在图中,点A、B分别在直线CM、DN上,且CM∥DN。
1)连接AB,则∠CAB+∠ABD=180°;2)连接AC、BD,则∠CAD=∠BDA,即∠CAB+∠CAD+∠ABD+∠BDA=360°;3)连接AC、BD、AD,则∠CAB+∠CAD+∠ABD+∠BDA+∠CDA=540°,又∠CDA=180°,故∠CAB+∠CAD+∠ABD+∠BDA=360°;4)根据(2)和(3)的结果,猜想∠CAB+∠CAD+∠ABD+∠BDA+∠EDA=720°。
2、当点P在A、B两点之间运动时,∠1、∠2、∠3之间的关系不发生变化。
3、当点P在A、B两点外侧运动时,∠1、∠2、∠3之间的关系取决于点P的具体位置。
如果P在AB的延长线上,则∠1、∠2、∠3之和为180度;如果P在AC和BD的交点之外,则∠1=∠PAC,∠2=∠APB,∠3=∠PBD,且∠1+∠2+∠3=180度。
平行线的判定与性质(重点题专项讲练)(人教版)(解析版)
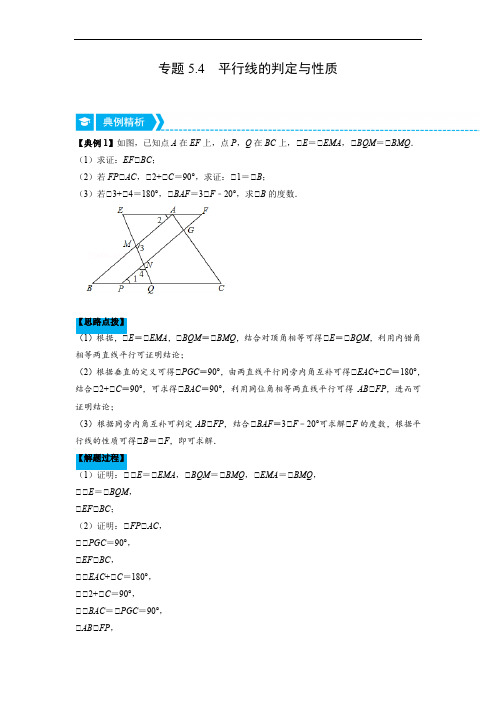
专题5.4 平行线的判定与性质【典例1】如图,已知点A在EF上,点P,Q在BC上,∠E=∠EMA,∠BQM=∠BMQ.(1)求证:EF∠BC;(2)若FP∠AC,∠2+∠C=90°,求证:∠1=∠B;(3)若∠3+∠4=180°,∠BAF=3∠F﹣20°,求∠B的度数.【思路点拨】E=∠EMA,∠BQM=∠BMQ,结合对顶角相等可得∠E=∠BQM,利用内错角相等两直线平行可证明结论;(2)根据垂直的定义可得∠PGC=90°,由两直线平行同旁内角互补可得∠EAC+∠C=180°,结合∠2+∠C=90°,可求得∠BAC=90°,利用同位角相等两直线平行可得AB∠FP,进而可证明结论;(3)根据同旁内角互补可判定AB∠FP,结合∠BAF=3∠F﹣20°可求解∠F的度数,根据平行线的性质可得∠B=∠F,即可求解.【解题过程】E=∠EMA,∠BQM=∠BMQ,∠EMA=∠BMQ,∠∠E=∠BQM,∠EF∠BC;(2)证明:∠FP∠AC,∠∠PGC=90°,∠EF∠BC,∠∠EAC+∠C=180°,∠∠2+∠C=90°,∠∠BAC=∠PGC=90°,∠AB∠FP,∠∠1=∠B;(3)解:∠∠3+∠4=180°,∠4=∠MNF,∠∠3+∠MNF=180°,∠AB∠FP,∠∠F+∠BAF=180°,∠∠BAF=3∠F﹣20°,∠∠F+3∠F﹣20°=180°,解得∠F=50°,∠AB∠FP,EF∠BC,∠∠B=∠1,∠1=∠F,∠∠B=∠F=50°.1.(2021•鞍山一模)如图,∠1=∠2=∠3=56°,则∠4的度数是()A.56°B.114°C.124°D.146°【思路点拨】根据对顶角相等得到∠2=∠5,结合∠1=∠2,得到∠1=∠5,即可判定l1∠l2,根据平行线的性质得出∠6=56°,再根据邻补角的定义求解即可.【解题过程】解:如图,∠∠1=∠2,∠2=∠5,∠∠1=∠5,∠l1∠l2,∠∠3=∠6,∠∠3=56°,∠∠6=56°,∠∠4+∠6=180°,∠∠4=180°﹣56°=124°,故选:C.2.(2021•雁塔区校级模拟)如图,在三角形ABC中,CD平分∠ACB,∠1=∠2=36°,则∠3=()A.36°B.52°C.72°D.80°【思路点拨】由平行线的判定定理可得AC∠DE,由平行线的性质可得∠ACB=∠3,由平分线的定义可得∠ACB=2∠1=72°,即得∠3的度数.【解题过程】解:∠∠1=∠2=36°,∠AC∠DE,∠∠ACB=∠3,∠CD平分∠ACB,∠∠ACB=2∠1=72°,∠∠3=72°.故选:C.3.(2021春•单县期末)如图,AB∠BC于点B,DC∠BC于点C,DE平分∠ADC交BC于点E,点F为线段CD延长线上一点,∠BAF=∠EDF,则下列结论正确的有()∠∠BAD+∠ADC=180°;∠AF∠DE;∠∠DAF=∠F.A.3个B.2个C.1个D.0个【思路点拨】∠证明AB∠CD,可做判断;∠根据平行线的判定和性质可做判断;∠根据AF∠ED得内错角相等和同位角相等,再由角平分线的定义得∠ADE=∠CDE,从而可做判断.【解题过程】解:∠∠AB∠BC,DC∠BC,∠AB∠CD,∠∠BAD+∠ADC=180°,故∠正确;∠∠AB∠CD,∠∠AFD+∠BAF=180°,∠∠BAF=∠EDF,∠∠AFD+∠EDF=180°,∠AF∠DE,故∠正确;∠∠AF∠ED,∠∠DAF=∠ADE,∠F=∠CDE,∠DE平分∠ADC,∠∠ADE=∠CDE,∠∠DAF=∠F,故∠正确;故选:A.4.(2021春•德宏州期末)如图所示,AC∠BC,DC∠EC,则下列结论:∠∠1=∠3;∠∠ACE+∠2=180°;∠若∠A=∠2,则有AB∠CE;∠若∠2=∠E,则有∠4=∠A.其中正确的有()A.∠∠∠B.∠∠∠C.∠∠D.∠∠∠∠【思路点拨】由已知可得∠1+∠2=90°,∠3+∠2=90°,等量代换即可得出∠结论;延长EC,如图1,由已知条件可得∠1+∠5=90°,∠1+∠2=90°,可得∠2=∠5,根据平角的性质可得∠ACE+∠5=180°,等量代换即可得出∠结论;由已知条件可得∠A=∠2,∠ACE+∠2=180°,等量代换可得∠A+∠ACE=180°,根据平行线的判定即可得出∠结论;由平行线的性质可得∠E=∠4,由已知条件∠2=∠E,∠2=∠A,等量代换可得∠4=∠A.即可得出∠结论.【解题过程】证明:∠AC∠BC,DC∠EC,∠∠1+∠2=90°,∠3+∠2=90°,∠∠1=∠3.故结论∠正确;延长EC,如图1,∠DC∠CE,AC∠BC,∠∠1+∠5=90°,∠1+∠2=90°,∠∠2=∠5,∠∠ACE+∠5=180°,∠∠ACE+∠2=180°.故结论∠正确;∠∠A=∠2,∠ACE+∠2=180°,∠∠A+∠ACE=180°,∠AB∠CE.故结论∠正确;∠AB∠CE,∠∠E=∠4,∠∠2=∠E,∠2=∠A,∠∠4=∠A.故结论∠正确.所以结论正确的有∠∠∠∠.故选:D.5.(2021春•汉川市期末)如图,AD∠BC,∠B=∠D,延长BA至点E,连接CE,∠EAD∠EAD+∠ECD;∠若和∠ECD的角平分线交于点P.下列三个结论:∠AB∠CD;∠∠AOC=12∠E=60°,∠APC=70°,则∠D=80°.其中结论正确的个数有()A.0B.1C.2D.3【思路点拨】∠EAD,∠E=∠根据平行线的性质与判定即可判断;∠∠AOC=∠EAP+∠E,而∠EAP==12∠ECD,即可判断;∠利用平行线的性质和角平分线定义即可判断.【解题过程】解:∠AD∠BC,∠∠BAD+∠B=180o,∠∠B=∠D,∠∠BAD+∠D=180o,∠AB∠CD,故∠正确;∠AB∠CD,∠∠ECD=∠E,∠AP平分∠EAD,∠EAD∠∠EAP=12∠∠AOC=∠EAP+∠E,∠∠AOC=1∠EAD+∠ECD,故∠正确;2∠∠ECD=∠E=60o,∠CP平分∠ECD,∠ECD=30°,∠∠ECP=12∠∠APC=70°,∠AOE=∠COP,∠∠EAP=40°,∠AP平分∠EAD,∠∠EAD=2∠EAP=80°,∠AB∠CD,∠∠D=∠EAD=80°,故∠正确;故选:D.6.(2021春•夏津县期末)如图,CB平分∠ACD,∠2=∠3,若∠4=60°,则∠5的度数是.【思路点拨】由∠2与∠3间关系,可得到AB与CD的位置关系,利用角平分线的性质和平行线的性质可求得∠5度数.【解题过程】解:∠CB平分∠ACD,∠ACD..∠∠1=∠2=12∠∠2=∠3,∠AB∠CD.∠∠5=∠2,∠4=∠ACD=60°.∠∠5=∠2=30°.故答案为:30°.7.(2021秋•嵩县期末)如图,AE∠CF,∠ACF的平分线交AE于点B,G是CF上的一点,∠GBE的平分线交CF于点D,且BD∠BC,下列结论:∠BC平分∠ABG;∠AC∠BG;∠与∠DBE互余的角有2个;∠若∠A=α,则∠BDF=180°−α.其中正确的是.(请把正确结论的序号都填上)8【思路点拨】根据平行线的性质得出∠A和∠ACB的关系,再根据角平分线的性质找出图中相等的角,由等角的余角相等即可得出结论.【解题过程】解:∠CBD=90°,∠∠ABC+∠EBD=90°,又∠∠DBG=∠EBD,∠∠ABC=∠CBG,∠BC平分∠ABG,∠∠正确,∠∠GBC=∠ABC=∠ACB,∠AC∠BG,∠∠正确,∠∠DBE=∠DBG,∠与∠DBE互余的角有∠ABC,∠GBC,∠ACB,∠GCB,有4个,∠∠错误,∠∠BDF=180°﹣∠BDG,∠BDG=90°﹣∠CBG=90°﹣∠ACB,又∠∠ACB=12×(180°﹣α)=90°−α2,∠∠BDF=180°﹣[90°﹣(90°−α2)]=180°−α2,∠∠错误,故答案为:∠∠.8.(2021春•凤山县期末)如图,已知∠1=∠2,∠C=∠F.请指出∠A与∠D的数量关系,并说明理由.【思路点拨】根据∠1=∠2,∠3=∠2,可得∠1=∠3,得BF∠CE,根据平行线的性质得∠ABF=∠C,由∠C =∠F,得∠ABF=∠F,即可得出AC∠DF,得∠A和∠D的数量关系是相等.【解题过程】解:∠A和∠D的数量关系是相等.理由是:如图,∠∠1=∠2,∠3=∠2,∠∠1=∠3,∠BF∠CE,∠∠ABF=∠C,∠∠C=∠F,∠∠ABF=∠F,∠AC∠DF,∠∠A=∠D.9.(2021春•陇县期末)如图,∠AEM+∠CDN=180°,EC平分∠AEF.若∠EFC=62°,求∠C的度数.【思路点拨】根据同角的补角相等可得出∠AEM=∠CDM,利用“同位角相等,两直线平行”可得出AB∠CD,由“两直线平行,同旁内角互补”及∠EFC=62°可求出∠AEF=118°,结合角平分线的定义可求出∠AEC的度数,再利用“两直线平行,内错角相等”即可求出∠C的度数.【解题过程】解:∠∠CDM+∠CDN=180°,又∠∠AEM+∠CDN=180°,∠∠AEM=∠CDM,∠AB∠CD,∠∠AEF+∠EFC=180°,∠∠EFC=62°,∠∠AEF=118°,∠EC平分∠AEF,∠∠AEC=59°,∠AB∠CD,∠∠C=∠AEC=59°.10.(2021春•江都区校级期中)已知:如图,CD∠AB,FG∠AB,垂足分别为D、G,点E 在AC上,且∠1=∠2.(1)那么DE与BC平行吗?为什么?(2)如果∠B=40°,且∠A比∠ACB小10°,求∠DEC的度数.【思路点拨】(1)根据CD∠AB,FG∠AB,可判定CD∠FG,利用平行线的性质可知∠2=∠BCD,已知∠1=∠2,等量代换得∠1=∠BCD,故可证DE与BC平行;(2)根据三角形内角和求出∠ACB=75°,再根据平行线的性质即可求解.【解题过程】解:(1)DE∠BC,理由如下:∠CD∠AB,FG∠AB,∠CD∠FG.∠∠2=∠BCD,又∠∠1=∠2,∠∠1=∠BCD,∠DE∠BC;(2)∠∠B=40°,∠ACB﹣10°=∠A,∠∠ACB+(∠ACB﹣10°)+40°=180°,∠∠ACB=75°,由(1)知,DE∠BC,∠∠DEC+∠ACB=180°,∠∠DEC=105°.11.(2021春•老河口市期末)如图,已知∠1=∠BDC,∠2+∠3=180°.(1)求证:AD∠CE;(2)若DA平分∠BDC,CE∠AE于E,∠F AB=55°,求∠1的度数.【思路点拨】(1)根据同位角相等,两直线平行可判定AB∠CD,得到∠2=∠ADC,等量代换得出∠ADC+∠3=180°,即可根据同旁内角互补,两直线平行得解;(2)由CE∠AE,AD∠CE得出∠DAF=∠CEF=90°,再根据平行线的性质即可求出∠ADC =∠2=35°,再根据角平分线的定义即可得解.【解题过程】(1)证明:∠∠1=∠BDC,∠AB∠CD,∠∠2=∠ADC,∠∠2+∠3=180°,∠∠ADC+∠3=180°,∠AD∠CE;(2)解:∠CE∠AE于E,∠∠CEF=90°,由(1)知AD∠CE,∠∠DAF=∠CEF=90°,∠∠ADC=∠2=∠DAF﹣∠F AB,∠∠F AB=55°,∠∠ADC=35°,∠DA平分∠BDC,∠1=∠BDC,∠∠1=∠BDC=2∠ADC=70°.12.(2021春•镇江期中)已知:如图所示,∠BAC和∠ACD的平分线交于E,AE交CD于点F,∠1+∠2=90°.(1)求证:AB∠CD;(2)试探究∠2与∠3的数量关系,并说明理由.【思路点拨】(1)根据角平分线定义得出∠BAC=2∠1,∠ACD=2∠2,根据∠1+∠2=90°得出∠BAC+∠ACD =180°,根据平行线的判定得出即可;(2)根据平行线的性质和角平分线定义得出∠1=∠3,即可求出答案.【解题过程】(1)证明:∠∠BAC和∠ACD的平分线交于E,∠∠BAC=2∠1,∠ACD=2∠2,∠∠1+∠2=90°,∠∠BAC+∠ACD=180°,∠AB∠CD;(2)解:∠2+∠3=90°,理由如下:∠AF平分∠BAC,∠∠BAF=∠1,∠AB∠CD,∠∠BAF=∠3,∠∠1=∠3,∠∠1+∠2=90°,∠∠2+∠3=90°.13.(2021秋•禅城区期末)已知:如图,点B、C在线段AD的异侧,点E、F分别是线段AB、CD上的点,∠AEG=∠AGE,∠C=∠DGC.(1)求证:AB∠CD;(2)若∠AGE+∠AHF=180°,求证:∠B=∠C;(3)在(2)的条件下,若∠BFC=4∠C,求∠D的度数.【思路点拨】(1)由对顶角相等可得∠AGE=∠DGC,从而可得∠AEG=∠C,则可判定AB∠CD;(2)由平角的定义可得∠AGE+∠EGH=180°,从而可求得∠EGH=∠AHF,则可判定EC∠BF,则有∠B=∠AEG,从而可求证;(3)由(2)得BF∠EC,则有∠C+∠BFC=180°,从而可求∠C的度数,利用三角形的内角和即可求∠D的度数.【解题过程】(1)证明:∠∠AEG=∠AGE,∠C=∠DGC,∠AGE=∠DGC,∠∠AEG=∠C,∠AB∠CD;(2)证明:∠∠AGE+∠EGH=180°,∠AGE+∠AHF=180°,∠∠EGH=∠AHF,∠EC∠BF,∠∠B=∠AEG,∠AB∠CD,∠∠C=∠AEG,∠∠B=∠C;(3)解:∠BF∠EC,∠∠C+∠BFC=180°,∠∠BFC=4∠C,∠∠C+4∠C=180°,解得∠C=36°,∠∠C=∠DGC,∠∠DGC=36°,∠∠D=180°﹣∠C﹣∠DGC=108°.14.(2021秋•南岗区期末)已知:在四边形ABCD中,∠B=∠D,点E在边BC的延长线上,连接AE交CD于点F,若∠BAF+∠AFC=180°.(1)如图1,求证:AD∠BC;(2)如图2,过点D作DG∠AE交BE的延长线于点C,若∠G=∠B,在不添加任何辅助线的情况下,请直接写出图2中除∠B以外的四个与∠G相等的角.【思路点拨】(1)由已知条件可得AB∠CD,从而有∠B=∠ECD,则可求得∠D=∠ECD,即可得AD∠BC;(2)利用平行线的性质进行求解即可.【解题过程】(1)证明:∠∠BAF+∠AFC=180°,∠AB∠CD,∠∠B=∠ECD,∠∠D=∠ECD,∠AD∠BC;(2)∠DG∠AE,∠∠G=∠AEB,由(1)得AD∠BC,∠∠AEB=∠DAE,∠ADC=∠DCG,∠∠G=∠DAE,∠∠B=∠ADC,∠G=∠B,∠∠G=∠ADC=∠DCG,综上所述,所∠G相等的角有:∠AEB,∠DAE,∠ADC,∠DCG.15.(2021秋•安居区期末)如图,∠ADE+∠BCF=180°,AF平分∠BAD,∠BAD=2∠F.(1)AD与BC平行吗?请说明理由.(2)AB与EF的位置关系如何?为什么?(3)若BE平分∠ABC.试说明:∠∠ABC=2∠E;∠∠E+∠F=90°.【思路点拨】(1)由∠ADE+∠BCF=180°结合邻补角互补,可得出∠BCF=∠ADC,再利用“同位角相等,两直线平行”可得出AD∠BC;(2)根据角平分线的定义及∠BAD=2∠F,可得出∠BAF=∠F,再利用“内错角相等,两直线平行”可得出AB∠EF;(3)∠由AB∠EF,利用“两直线平行,内错角相等”可得出∠ABE=∠E,结合角平分线的定义可得出∠ABC=2∠E;∠由AD∠BC,利用“两直线平行,同旁内角互补”可得出∠BAD+∠ABC=180°,再结合∠BAD =2∠F,∠ABC=2∠E可得出∠E+∠F=90°.【解题过程】解:(1)AD∠BC,理由如下:∠∠ADE+∠BCF=180°,∠ADE+∠ADC=180°,∠∠BCF=∠ADC,(2)AB∠EF,理由如下:∠AF平分∠BAD,∠BAD=2∠F,∠BAD=∠F,∠∠BAF=12∠AB∠EF.(3)∠∠ABC=2∠E,理由如下:∠AB∠EF,∠∠ABE=∠E.∠BE平分∠ABC,∠∠ABC=2∠ABE=2∠E.∠∠E+∠F=90°,理由如下:∠AD∠BC,∠∠BAD+∠ABC=180°.∠∠BAD=2∠F,∠ABC=2∠E,∠2∠E+2∠F=180°,∠∠E+∠F=90°.16.(2021春•铁西区期末)如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF 的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.(1)请直接写出直线AC与DG的位置关系;(2)求证:BE∠CF;(3)若∠C=35°,求∠BED的度数.【思路点拨】(1)由对顶角相等可得∠ABF=∠1,从而有∠ABF=∠2,即可得AC∠DG;(2)求出∠1=∠BFG,根据平行线的判定得出AC∠DG,求出∠EBF=∠BFC,根据平行线的判定得出即可;(3)根据平行线的性质得出∠C=∠CFG=∠BEF=35°,再求出答案即可.【解题过程】解:(1)AC∠DG,理由如下:∠∠ABF=∠1,∠1=∠2,∠∠ABF=∠2,∠AC∠DG;(2)由(1)知AC∠DG,∠∠ABF=∠BFG,∠∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C,∠∠EBF=12∠ABF,∠CFB=12∠BFG,∠∠EBF=∠CFB,∠BE∠CF.(3)∠AC∠DG,∠C=35°,∠∠C=∠CFG=35°,∠BE∠CF,∠∠CFG=∠BEG=35°,∠∠BED=180°﹣∠BEG=145°.17.(2021春•广陵区校级期中)如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.(1)试判断直线AB与直线CD的位置关系,并说明理由;(2)如图2,∠AEF与∠EFC的角平分线交于点P,EP延长线与CD交于点G,点H是MN 上一点,且PF∠GH,试判断直GH与EG的位置关系,并说明理由.【思路点拨】(1)利用邻补角的定义及已知得出∠1=∠CFE,即可判定AB∠CD;(2)利用(1)中平行线的性质推知∠AEF+∠EFC=180°,然后根据角平分线的性质、三角形内角和定理证得∠EPF=90°,即EG∠PF,故结合已知条件PF∠GH,易证GH∠EG;【解题过程】解:(1)AB∠CD,理由如下:∠∠1与∠2互补,∠∠1+∠2=180°,又∠∠2+∠CFE=180°,∠∠1=∠CFE,∠AB∠CD;(2)GH∠EG,理由如下:由(1)知,AB∠CD,∠∠AEF+∠EFC=180°.又∠∠AEF与∠EFC的角平分线交于点P,∠∠FEP+∠EFP=1(∠BEF+∠EFD)=90°,2∠∠EPF=90°,即EG∠PF,∠PF∠GH,∠GH∠EG.18.(2021秋•嵩县期末)图1展示了光线反射定律:EF是镜面AB的垂线,一束光线m射到平面镜AB上,被AB反射后的光线为n,则入射光线m,反射光线n与垂线EF所夹的锐角θ1=θ2.(1)在图1中,证明:∠1=∠2.(2)图2中,AB,BC是平面镜,入射光线m经过两次反射后得到反射光线n,已知∠1=30°,∠4=60°,判断直线m与直线n的位置关系,并说明理由.(3)图3是潜望镜工作原理示意图,AB,CD是平行放置的两面平面镜.请解释进入潜望镜的光线m为什么和离开潜望镜的光线n是平行的?【思路点拨】(1)根据角的关系解答即可;(2)求出∠5+∠6=180°,根据平行线的判定得出即可;(3)根据平行线的性质和平均的定义得到∠5=∠6,根据平行线的判定得出即可.【解题过程】(1)证明:∠∠AFE=∠BFE=90°,∠θ1=θ2.(2)解:直线m∠直线n,理由:如图2,∠∠1=∠2=30°,∠3=∠4=60°,∠∠5=180°﹣∠1﹣∠2=120°,∠6=180°﹣∠3﹣∠4=60°,∠∠5+∠6=180°,∠直线m∠直线n;(3)解:∠AB∠CD,∠∠2=∠3,∠∠1=∠2,∠3=∠4,∠∠1=∠2=∠3=∠4,∠180°﹣∠1﹣∠2=180°﹣∠3﹣∠4,即:∠5=∠6,∠m∠n.19.(2021秋•上蔡县期末)已知:如图,AB∠CD∠GH,GH过点P.(1)如图1,若∠BAP=40°,∠DCP=30°,则∠APC=(直接写出结果);(2)如图2,直线MN分别交AB于点E,交CD于点F,点P在线段EF上,点Q在射线FC上.若∠MEB=110°,∠PQF=50°,求∠EPQ的度数;(3)如图3,点P在射线FN上,点Q在射线FD上,∠AEF的平分线交CD于点O.若∠PQF= 1∠MEB,试判断OE与PQ是否平行?并说明理由.2(1)依据平行线的性质,即可得到∠APG =∠BAP =40°,∠CPG =∠DCP =30,再根据∠APC =∠APG +∠CPG 进行计算即可;(2)利用邻补角的定义可得∠BEP =180°﹣110°=70°,利用(1)的结论即可得∠EPQ 的度数; (3)根据对顶角相等以及角平分线的定义可得∠PQF =12∠MEB =12∠AEF =∠AEO ,再根据平行线的性质∠AEO =∠EOF ,可得∠PQF =∠EOF ,根据内错角相等两直线平行即可得OE ∠PQ .【解题过程】解:(1)∠AB ∠CD ∠GH ,∠∠APG =∠BAP =40°,∠CPG =∠DCP =30,∠∠APC =∠APG +∠CPG =40°+30°=70°,故答案为:70°;(2)∠∠MEB =110°,∠∠BEP =180°﹣110°=70°,由(1)可得:∠EPQ =∠EPG +∠QPG =∠BEP +∠PQF =70°+50°=120°;(3)OE ∠PQ .理由:∠∠PQF =12∠MEB ,∠MEB =∠AEF ,∠∠PQF =12∠MEB =12∠AEF ,∠EO 平分∠AEF .∠∠PQF =12∠AEF =∠AEO , ∠AB ∠CD ,∠∠AEO =∠EOF ,∠∠PQF =∠EOF ,∠OE ∠PQ .20.(2021春•汉阳区期中)如图1,已知两条直线AB ,CD 被直线EF 所截,分别交于点E ,F ,EM 平分∠AEF 交CD 于点M ,且∠FEM =∠FME .(1)直线AB 与直线CD 的位置关系是 ;(2)如图2,点G 是射线FD 上一动点(不与点F 重合),EH 平分∠FEG 交CD 于点H ,过点H 作HN ∠EM 于点N ,设∠EHN =α,∠EGF =β.∠当点G 在运动过程中,若β=56°,求α的度数;∠当点G 在运动过程中,α和β之间有怎样的数量关系?请写出你的猜想,并加以证明.【思路点拨】(1)根据角平分线的性质可得∠AEM=∠FEM,由已知条件∠FEM=∠FME,等量代换可得∠AEM=∠FME,由平行线的判定即可得出答案;(2)由平行线的性质可得β=∠GEB,由平角的性质可得∠AED=180°﹣∠GEB,根据角平分线的性质可得∠CEF=12∠AEF,∠FEH=12∠FEG,由∠CEH=∠CEF+∠FEH可计算出度数,根据垂线的性质可得α+∠CEH=90°,代入计算即可得出答案;(3)证明方法同(2).【解题过程】证明:(1)∠EM平分∠AEF,∠∠AEM=∠FEM,∠∠FEM=∠FME,∠∠AEM=∠FME,∠AB∠CD.故答案为:AB∠CD;(2)∠∠AB∠CD,∠β=∠GEB=56°,∠∠AEG=180°﹣∠GEB=180°﹣56°=124°,∠EH平分∠FEG,EM平分∠AEF,∠∠CEF=12∠AEF,∠FEH=12∠FEG,∠∠CEH=∠CEF+∠FEH=12∠AEF+12∠FEG=12(∠AEF+∠FEG)=12∠AED=12×124°=62°,∠HN∠EM,∠α+∠CEH=90°,∠α=90°﹣∠CEH=90°﹣62°=28°;∠a=12β.理由如下:∠AB∠CD,∠β=∠GEB,∠∠AED=180°﹣∠GEB=180°﹣β,∠EH平分∠FEG,EM平分∠AEF,∠∠CEF=12∠AEF,∠FEH=12∠FEG,∠∠CEH=∠CEF+∠FEH=12∠AEF+12∠FEG=12(∠AEF+∠FEG)=12∠AEG=12(180°−β),∠HN∠EM,∠α+∠CEH=90°,∠α+12(180°−β)=90°,即a=12β.21.(2021秋•南岗区校级期中)已知,直线EF分别与直线AB、CD相交于点G、H,并且∠AGE+∠DHE=180°.(1)如图1,求证:AB∠CD.(2)如图2,点M在直线AB、CD之间,连接MG、HM,当∠AGM=32°,∠MHC=68°时,求∠GMH的度数.(3)只保持(2)中所求∠GMH的度数不变,如图3,GP是∠AGM的平分线,HQ是∠MHD 的平分线,作HN∠PG,则∠QHN的度数是否改变?若不发生改变,请求出它的度数.若发生改变,请说明理由.(本题中的角均为大于0°且小于180°的角)【思路点拨】(1)先由邻补角得到∠AGE+∠BGE=180°,然后结合∠AGE+∠DHE=180°得到∠BGE=∠DHE,最后得证AB∠CD;(2)先由AB∠CD得到∠AGH+∠CHG=180°,即∠AGM+∠MGH+∠MHG+∠MHC=180°,再结合∠MGH+∠MHG+∠GMH=180°得到∠GMH=∠AGM+∠MHC,最后结合已知条件得到∠GMH的大小;(3)先由(2)得到∠AGM+∠MHC=∠GMH=100°,∠MGH+∠MHG=80°,然后结合角平分线的定义得到∠MGP和∠MHQ,再结合HN∠PG得到∠GHN=∠PGH,最后由∠QHN=∠GHN﹣∠GHQ求得∠QHN的大小.【解题过程】(1)证明:∠∠AGE +∠BGE =180°,∠AGE +∠DHE =180°,∠∠BGE =∠DHE ,∠AB ∠CD .(2)解:∠AB ∠CD ,∠∠AGH +∠CHG =180°,即∠AGM +∠MGH +∠MHG +∠MHC =180°,∠∠MGH +∠MHG +∠GMH =180°,∠∠GMH =∠AGM +∠MHC ,∠∠AGM =32°,∠MHC =68°,∠∠GMH =100°.(3)解:∠QHN 的度数不发生改变,理由如下,由(2)得,∠AGM +∠MHC =∠GMH =100°,∠∠MGH +∠MHG =80°,∠GP 、HQ 分别平分∠MGA 和∠MHD ,∠∠MGP =12∠MGA ,∠MHQ =12∠MHD =12(180°﹣∠MHC )=90°−12∠MHC , ∠∠PGH =∠MGP +∠MGH =12∠MGA +∠MGH , ∠HN ∠PG , ∠∠GHN =∠PGH =12∠MGA +∠MGH ,∠∠QHN =∠GHN ﹣∠GHQ =(12∠MGA +∠MGH )﹣(∠MHQ ﹣∠MHG )=12∠MGA +∠MGH ﹣∠MHQ +∠MHG =12∠MGA +80°﹣∠MHQ ,∠∠QHN =12∠MGA +80°﹣(90°−12∠MHC )=﹣10°+12(∠MGA +∠MHC )=﹣10°+12×100°=40°.22.(2021秋•香坊区校级期中)点E 在射线DA 上,点F 、G 为射线BC 上两个动点,满足∠DBF =∠DEF ,∠BDG =∠BGD ,DG 平分∠BDE .(1)如图1,当点G 在F 右侧时,求证:BD ∠EF ;(2)如图2,当点G 在BF 左侧时,求证:∠DGE =∠BDG +∠FEG ;(3)如图3,在(2)的条件下,P 为BD 延长线上一点,DM 平分∠BDG ,交BC 于点M ,DN 平分∠PDM ,交EF 于点N ,连接NG ,若DG ∠NG ,∠B ﹣∠DNG =∠EDN ,求∠B 的度数.【思路点拨】(1)通过证明∠DBF=∠EFG,利用同位角相等,两直线平行即可得出结论;(2)过点E作GH∠BD,交AD于点H,利用(1)的结论和平行线的性质即可得出结论;(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α,∠PDM =180°﹣α;利用已知条件用含α的式子表示∠PDN,∠EDN,∠GDN,∠DNG,再利用∠B ﹣∠DNG=∠EDN,得到关于α的方程,解方程求得α的值,则∠B=180°﹣4α,结论可求.【解题过程】证明:(1)∠DG平分∠BDE,∠∠BDG=∠ADG.又∠∠BDG=∠BGD,∠∠ADG=∠DGB.∠AD∠BC.∠∠DEF=∠EFG.∠∠DBF=∠DEF,∠∠DBF=∠EFG.∠BD∠EF.(2)过点G作GH∠BD,交AD于点H,如图,∠BD∠EF,∠GH∠EF.∠∠BDG=∠DGH,∠GEF=∠HGE,∠∠DGE=∠DGH+∠HGE,∠∠DGE=∠BDG+∠FEG.(3)设∠BDM=∠MDG=α,则∠BDG=∠EDG=∠DGB=2α,∠PDE=180°﹣4α.∠∠PDM=180°﹣α.∠DN平分∠PDM∠∠PDN=∠MDN=90°−α2.∠∠EDN=∠PDN−∠PDE=90°−α2−(180°−4α)=72α−90°.∠∠GDN=∠MDN﹣∠MDG=90°−α2−α=90°−32α.∠DG∠ON,∠∠DNG=90°.∠∠DNG=90°−(90°−32α)=32α.∠DE∠BF,∠∠B=∠PDE=180°﹣4α.∠∠B﹣∠DNG=∠EDN,∠180°−4α−32α=72α−90°,解得:α=30°.∠∠B=180°﹣4α=60°.。
完整版)平行线的判定和性质经典题

完整版)平行线的判定和性质经典题平行线的判定和性质经典题一、选择题(共18小题)1.同位角共有()。
A。
6对B。
8对C。
1对D。
12对2.将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是()。
A。
平行B。
垂直C。
平行或垂直D。
无法确定3.下列说法中正确的个数为()。
①不相交的两条直线叫做平行线②平面内,过一点有且只有一条直线与已知直线垂直③平行于同一条直线的两条直线互相平行④在同一平面内,两条直线不是平行就是相交A。
1个B。
2个C。
3个D。
4个4.在同一平面内,有8条互不重合的直线,l1,l2,l3 (8)若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是()。
A。
平行B。
垂直C。
平行或垂直D。
无法确定5.若两个角的两边分别平行,且这两个角的差为40°,则这两角的度数分别是()。
A。
150°和110°B。
140°和100°C。
110°和70°D。
7°和30°6.XXX所示,AC⊥BC,DE⊥BC,CD⊥AB,∠ACD=40°,则∠XXX等于()。
A。
4°B。
5°C。
6°D。
不能确定7.如图,AB∥CD,且∠BAP=60°-α,∠APC=45°+α,∠PCD=30°-α,则α=()。
A。
1°B。
2°C。
3°D。
15°8.下列所示的四个图形中,∠1和∠2是同位角的是()。
①②③④A。
②③B。
①②C。
①④D。
②④9.已知∠AOB=40°,∠XXX的边CD⊥OA于点C,边DE∥OB,那么∠CDE等于()。
A。
5°B。
130°C。
5°或130°D。
100°10.如图,AB∥CD∥EF,AF∥CG,则图中与∠A(不包括∠A)相等的角有()。
七年级数学平行线的判定和性质(二)(北师版)(含答案)

学生做题前请先回答以下问题问题1:在同一平面内,__________的两条直线叫做平行线.问题2:平行线的判定定理:①____________________,两直线平行;②____________________,两直线平行;③____________________,两直线平行.问题3:平行线的性质定理:①两直线平行,____________________;②两直线平行,____________________;③两直线平行,____________________.问题4:平行线的判定定理是用来判定两条直线平行的定理,即已知角的关系证明平行,用平行线的判定定理.平行线的性质定理是由直线平行,可以得到的结论,即已知平行求角的关系,用平行线的性质定理.请根据下面推理,填写推理的依据.①已知:如图,直线a和直线b被直线c所截,∠1=∠2.求证:a∥b.证明:∵∠1=∠2(已知)∴a∥b(_______________________________)①已知:如图,直线a和直线b被直线c所截,a∥b.求证:∠1=∠2.证明:∵a∥b(已知)∴∠1=∠2(_______________________________)平行线的判定和性质(二)(北师版)一、单选题(共10道,每道10分)1.如图,直线DE经过点A,若∠B=∠DAB,则DE∥BC,其依据是( )A.两直线平行,内错角相等B.内错角相等,两直线平行C.同旁内角互补,两直线平行D.内错角相等答案:B解题思路:条件是∠B=∠DAB,结论是DE∥BC,且∠B和∠DAB是直线DE和直线BC被直线AB所截得到的内错角,由内错角相等得到两直线平行,依据是内错角相等,两直线平行,故选B.试题难度:三颗星知识点:平行线的判定2.如图,已知D,E在△ABC的边上,DE∥BC,可得∠ADE=∠B,依据是( )A.两直线平行,同位角相等B.两直线平行,内错角相等C.同位角相等D.同位角相等,两直线平行答案:A解题思路:条件是DE∥BC,结论是∠ADE=∠B.∠ADE和∠B是直线DE和直线BC被直线AB所截得到的同位角,由两直线平行得到同位角相等,依据是两直线平行,同位角相等,故选A.试题难度:三颗星知识点:平行线的性质3.如图,直线,分别与直线,相交,若∥,则∠1=_________,依据是_____________.( )A.∠2;两直线平行,内错角相等B.∠3;两直线平行,内错角相等C.∠2;内错角相等,两直线平行D.∠3;内错角相等,两直线平行答案:B解题思路:由平行得角的关系,先找截线,观察图形,与∠1有关的截线是直线,∠1和∠3是由直线和直线被直线所截得到的内错角,由∥,可以得到∠1=∠3,依据是两直线平行,内错角相等,故选B.试题难度:三颗星知识点:平行线的性质4.如图,若AB∥EF,则∠ADE=_________,依据是_____________.( )A.∠B;两直线平行,同位角相等B.∠DEF;内错角相等,两直线平行C.∠DEF;两直线平行,内错角相等D.∠CEF;两直线平行,同位角相等答案:C解题思路:由平行得角的关系,先找截线,观察图形,与∠ADE有关的截线是直线DE,∠ADE和∠DEF是由直线AB和EF被直线DE所截得到的内错角,若AB∥EF,则∠ADE=∠DEF,理由是两直线平行,内错角相等,故选C.试题难度:三颗星知识点:平行线的性质5.如图,两直线a,b被直线c所截形成八个角,若a∥b,则下列结论错误的是( )A.∠1=∠2B.∠3+∠8=180°C.∠5=∠6D.∠7+∠8=180°答案:D解题思路:A选项:∵a∥b(已知)∴∠1=∠2(两直线平行,内错角相等)故A选项结论正确;B选项:∵a∥b(已知)∴∠3+∠2=180°(两直线平行,同旁内角互补)∵∠8=∠2(对顶角相等)∴∠3+∠8=180°(等量代换)故B选项结论正确;C选项:∵a∥b(已知)∴∠3=∠6(两直线平行,同位角相等)∵∠3=∠5(对顶角相等)∴∠5=∠6(等量代换)故C选项结论正确;D选项:∵a∥b(已知)∴∠1=∠8(两直线平行,同位角相等)∵∠1=∠7(对顶角相等)∴∠7=∠8(等量代换)故D选项结论错误.故选D.试题难度:三颗星知识点:平行线的性质6.如图,若AD∥BC,则一定正确的是( )A.∠1=∠2B.∠3=∠4C.∠1=∠2,∠3=∠4D.∠2=∠3答案:B解题思路:根据平行线的性质,由AD∥BC,要找角之间的关系,需要找两条平行直线AD和BC被第三条直线所截得到的角,四个选项中,只有∠3和∠4是两条平行直线AD和BC被直线BD所截得到的内错角,根据两直线平行,内错角相等,得∠3=∠4,故选B.试题难度:三颗星知识点:平行线的性质7.如图,能判定EB∥AC的条件是( )A.∠C=∠ABEB.∠A=∠EBDC.∠C=∠ABCD.∠A=∠ABE答案:D解题思路:要证平行,考虑找同位角,内错角,同旁内角,分析可得只有选项D中,∠A与∠ABE是直线EB和直线AC被直线AB所截的内错角,根据内错角相等,两直线平行,可以判定EB∥AC,故选D.试题难度:三颗星知识点:平行线的判定8.如图,若BE∥CF,则一定正确的是( )A.∠1=∠2B.∠3=∠4C.AB∥CDD.∠ABC=∠BCD答案:B解题思路:根据平行线的性质,由BE∥CF,可以得到角之间的关系,需要找两条平行直线BE和CF被第三条直线所截得到的角,只有∠3和∠4是两条平行直线BE和CF被直线BC所截得到的内错角,根据两直线平行,内错角相等,得∠3=∠4,故选B.试题难度:三颗星知识点:平行线的性质9.如图,DE∥BC,则下列结论正确的( )A.∠1=∠3B.∠2=∠3C.∠4=∠CD.∠2=∠C答案:B解题思路:根据平行线的性质,由DE∥BC,可以得到角之间的关系,需要找两条平行直线DE和BC被第三条直线所截得到的角,分析可得只有∠2和∠3是两条平行线DE和BC被直线BE所截得到的内错角,根据两直线平行,内错角相等,得∠2=∠3,故选B.试题难度:三颗星知识点:平行线的性质10.如图,AB∥CD,AD平分∠BAC,若∠BAD=70°,则∠1的度数为( )A.35°B.40°C.45°D.50°答案:B解题思路:解:如图,∵AD平分∠BAC(已知)∴∠BAC=2∠BAD(角平分线的定义)∵∠BAD=70°(已知)∴∠BAC=2×70°=140°(等量代换)∵AB∥CD(已知)∴∠1+∠BAC=180°(两直线平行,同旁内角互补)∴∠1=40°(等式的性质)故选B.试题难度:三颗星知识点:平行线的性质。
平行线的判定和性质专项练习题

[一]、平行线的性质一、填空1.如图1,已知∠1 = 100°,AB∥CD,则∠2 = ,∠3= ,∠4 = .2所截,若∠1 =∠2,则∠AEF 3(1)若EF∥AC,则∠A +∠ = 180°,∠F + ∠ = 180°( ).(2)若∠2 =∠ ,则AE∥BF.(3)若∠A +∠ = 180°,则AE∥BF.4.如图4,AB∥CD,∠2 = 2∠1,则∠2 = .5.如图5,AB∥CD,EG⊥AB 于G ,∠1 = 50°,则∠E= .6.如图6,直线l 1∥l 2,AB⊥l 1于O ,BC 与l 2交于E ,∠1 = 43°,则∠2 = . 7.如图7,AB∥CD ,AC⊥BC ,图中与∠CAB 互余的角有 .8.如图8,AB∥EF∥CD,EG∥BD,则图中与∠1相等的角(不图 B 图1 2 3 4 5 A B C D F E 图1 2 A B C D E F 图图1 A B C D E F G H 图1 2 D A C B l l 图1 A B F C D E G 图C D F E B A包括∠1)共有 个.二、解答下列各题9.已知:如图,BC ∥DE .BE 平分∠ABC ,.求证:∠1=∠210、如图:已知,AB ∥ON ∠BOA=∠BAO ,求证:OP 平分∠MON 。
11、已知,如图B 、D 、A 在一直线上,DE ∥BC ,BC 是∠ABE 的平分线,求证:∠D=∠E .12、如图,已知AB ∥CD ,试说明:.∠AEC=∠A+∠C.13、如图,已知,DB ∥EC .AC ∥DF ,那么∠C=∠D 吗?试说明你的理由.14.如图,DE∥BC,∠D∶∠DBC = 2∶1,∠1 =∠2,求∠DEB 的度数.11.如图,已知AB∥CD,试再添上一个条件,使∠1 =∠2成立.(要求给出两个以上答案,并选择其中一个加以证明) 12.如图12,∠ABD 与∠BDC 的平分线交于E ,BE 交CD 于点F ,∠1 +∠2 = 90°. 求证:(1)AB∥CD; (2)∠2 +∠3 = 90°.[二]、平行线的判定 图2 1 B C ED 图1 2 A BEF D C 1 AB一、填空1.如图1,若∠A=∠3,则 ∥ ; 若∠2=∠E ,则 ∥ ;若∠ +∠ = 180°,则 ∥ .2.若a⊥c,b⊥c,则. 3.如图2个能判定直线l 1∥l 2的条件: .4.在四边形ABCD 中,∠A +∠B = 180°,则 ∥ ( ).5.如图3,若∠1 +∠2 = 180°,则 ∥ 。
5.平行线的判定与性质

1. (2011 江苏省徐州市) 如图,AB CD AB ∥,与DE 交于点F ,4070B D ∠=︒∠=︒,,则E ∠=__________.答案:302. (2011 江苏省扬州市) 如图,C 岛在A 岛的北偏东60°方向,在B 岛的北偏西45°方向,则从C 岛看A B 、两岛的视角ACB ∠=__________°.答案:1053. (2011 辽宁省本溪市) 如图,AB CD ∥,直线MN 分别交AB 、CD 于点E 、F ,EG 平分AEF ∠,EG FG ⊥于点G .若50BEM ∠=°,则CFG ∠=_____________度.北答案:654. (2011 辽宁省大连市) 如图,直线1115a b ∠=︒∥,,则2∠=_________︒.答案:65;5. (2011 内蒙古鄂尔多斯市) 如图,直线12l l ∥,365∠=°,2130∠=°,则1∠为()A .50°B .55°C .60°D .65°答案:D6. (2011 青海省西宁市) 如图,将三角形的直角顶点放在直尺的一边上,130∠=︒,320∠=︒,则2∠=___________.答案:50︒7. (2011 山东省德州市) 如图,直线12l l ∥,1=402=75∠,∠,则3∠等于( )(A )55 (B )60(C )65 (D )70答案:C8. (2011 山东省菏泽市) 一次数学活动课上,小聪将一副三角板按图中方式叠放,则∠α等于( )A.30°B.45°C.60°D.75° l 1l 21 2 3答案:D9. (2011 山东省济南市) 如图,直线l 与直线a 、b 分别交于点A 、B ,a b ∥,若170∠=°,则2∠____________度.答案:11010. (2011 山东省济宁市) 如图,AE BD ∥,1120240∠=∠=°,°,则C ∠的度数是( )A.10° B.20° C.30° D.40°30°45°α答案:B11. (2011 山东省聊城市) 如图,已知a b ∥,150∠=°,则2∠的度数是( )A .40°B .50°C .120°D .130°答案:D12. (2011 山东省临沂市) 如图,已知AB CD ∥,170∠=°,则2∠的度数是( )A .60° B.70° C .80° D .110°A BDC 1 2 cab1 2答案:D13. (2011 山东省枣庄市) 如图,直线AB ∥CD ,∠A =70︒,∠C =40︒,则∠E 等于( )A .30° B.40°C .60° D.70°答案:A14. (2011 山东省淄博市) 如图,直线AB ,CD 分别与直线AC 相交于点A ,C ,与直线BD 相交于点B ,D .若12∠=∠,375∠=°,求4∠的度数.A C BDE答案:解:12∠=∠AB CD ∴∥34∴∠=∠375∠=°475∴∠=°15. (2011 山西省) 如图所示,AOB ∠的两边OA 、OB 均为平面反光镜,35AOB =∠,在OB 上有一点E ,从E 点射出一束光线经OA 上的点D 反射后,反射光线DC 恰好与OB 平行,则DEB ∠的度数是( )A .35B .70C .110D .120答案:B16. (2011 陕西省) 如图,AC BD AE ∥,平分BAC ∠交BD 于点E .若164∠=°,则2∠=_________.答案:122°17. (2011 广东省肇庆市) 如图,已知直线a ∥b ∥c ,直线m 、n 与a 、b 、c 分别交于点A 、C 、E 、B 、D 、F ,AC = 4,CE = 6,BD = 3,则BF =( )A. 7B. 7.5C. 8D. 8.5答案:B18. (2011 四川省泸州市) 如图,1∠与2∠互补,3135∠=︒,则4∠的度数是( )(A )45︒ (B )55︒ (C )65︒ (D )75︒abcA B C D E F m n答案:A19. (2011 四川省绵阳市) 如图,AB CD CP ∥,交AB 于O ,AO PO =,若50C ∠=°,则A ∠=_____度.答案:25°20. (2011 新疆建设兵团) 如图,AB ∥CD ,AD 和BC 相交于O 点,∠A =40°,∠AOB =75°.则∠C 等于( )A .40°B .65°C .75°D .115°答案:B21. (2011 新疆乌鲁木齐) 如图,AD 与BC 相交于点O ,AB CD ∥,若3060B D ∠=∠=°,°,则BOD ∠= ______度.答案:9022. (2011 云南省大理市) 如图,l 1∥l 2,∠1=120°,则∠2= .答案:60︒23. (2011 浙江省湖州市) 如图,已知CD 平分130ACBDE AC ∠∠=︒,∥,,则2∠= 度.l 1l 2 l 312答案:6024. (2011 浙江省丽水市) 如图,把一块含有45°角的直角三角板的两个顶点放在直尺的对边上.如果120∠=°,那么2∠的度数是( )A .30°B .25°C .20°D .15°答案:B25. (2011 浙江省宁波市) 如图所示,3720AB CD E C ∠=∠=∥,°,°,则EAB ∠的度数为( )D2 1ABE CA .57° B.60° C.63° D.123°答案:A26. (2011 浙江省绍兴市) 如图,已知AB ∥CD ,BC 平分∠ABE ,∠C =34°,则∠BED 的 度数是( )A .17°B .34°C .56°D .68°答案:D27. (2011 浙江省温州市) 如图,1402803a b ∠=∠=∠=∥,°,°, 度.A DB CE答案:12028. (2011 重庆市) 如图,8060AB CD C CAD ∠=∠=∥,°,°,则BAD ∠的度数等于() A .60° B.50° C.45° D.40°A BD C答案:D29. (2011 山东省日照市) 如图,已知直线AB CD ∥,125C ∠=°,45A ∠=°,那么E ∠的大小为( )A .70°B .80°C .90°D .100°答案:B30. (2011 山东省泰安市) 如图,l ∥m ,等腰直角三角形ABC 的直角顶点C 在直线m 上,若∠β=20°,则∠α的度数为( )A .25°B .30°C .20°D .35°答案:A。
第二章第02讲 平行线的判定和性质(10类热点题型讲练)(解析版)
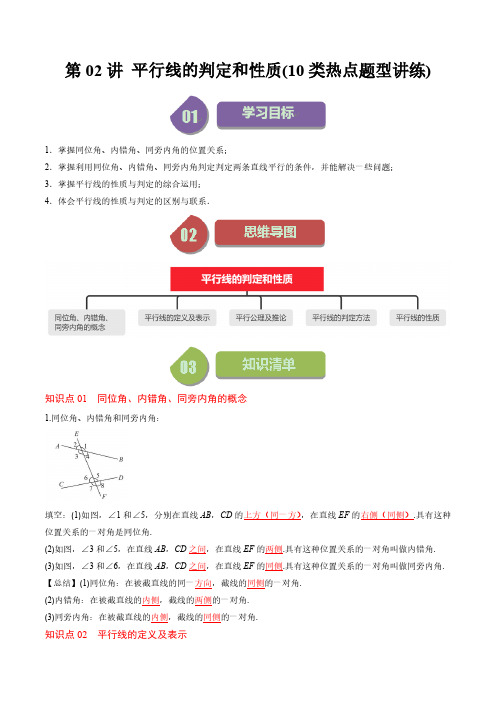
第02讲平行线的判定和性质(10类热点题型讲练)1.掌握同位角、内错角、同旁内角的位置关系;2.掌握利用同位角、内错角、同旁内角判定判定两条直线平行的条件,并能解决一些问题;3.掌握平行线的性质与判定的综合运用;4.体会平行线的性质与判定的区别与联系.知识点01 同位角、内错角、同旁内角的概念1.同位角、内错角和同旁内角:填空:(1)如图,∠1和∠5,分别在直线AB,CD的上方(同一方),在直线EF的右侧(同侧).具有这种位置关系的一对角是同位角.(2)如图,∠3和∠5,在直线AB,CD之间,在直线EF的两侧.具有这种位置关系的一对角叫做内错角.(3)如图,∠3和∠6,在直线AB,CD之间,在直线EF的同侧.具有这种位置关系的一对角叫做同旁内角.【总结】(1)同位角:在被截直线的同一方向,截线的同侧的一对角.(2)内错角:在被截直线的内侧,截线的两侧的一对角.(3)同旁内角:在被截直线的内侧,截线的同侧的一对角.知识点02 平行线的定义及表示(1)定义:在同一平面内内,不相交的两条直线.(2)表示:平行用“∥”符号表示,读作“平行于”.1.同一平面内,两条直线的位置关系:(1)平行 (2)相交2.利用直尺和三角尺画平行线:一“落”、二“靠”、三“移”、四“画”.【注意】平行线的画法四字诀1.“落”:三角板的一边落在已知直线上;2.“靠”:用直尺紧靠三角板的另一边;3.“移”:沿直尺移动三角板,直至落在已知直线上的三角板的一边经过已知点;4.“画”:沿三角板过已知点的边画直线.知识点03 平行公理及推论(1)平行公理:经过直线外一点,有且只有一条直线与这条直线平行.(2)推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.即如果b∥a,c∥a,那么b∥c.【注意】平行公理(1)“有且只有”强调直线的存在性和唯一性.(2)前提条件“经过直线外一点”,若点在直线上,不可能有平行线.知识点04 平行线的判定方法平行线的判定方法1:(1)文字表述:两条直线被第三条直线所截,如果同位角相等,那么这两条直线平行.简单说成:同位角相等,两直线平行.(2)几何语言:∵∠1=∠5(或者∠2=∠6,∠4=∠8,∠3=∠7),∴AB∥CD.平行线的判定方法2:(1)文字表述:两条直线被第三条直线所截,如果内错角相等,那么这两条直线平行.简单说成:内错角相等,两直线平行.(2)几何语言:∵∠2=∠8(或者∠3=∠5),∴AB∥CD.平行线的判定方法3:(1)文字表述:两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行.简单说成:同旁内角互补,两直线平行.(2)几何语言:∵∠2+∠5=180°(或者∠3+∠8=180°),∴AB∥CD.平行线的其他判定方法:(1)在同一平面内,平行于同一条直线的两条直线平行.(2)在同一平面内,垂直于同一条直线的两条直线平行.【总结】判定两直线平行的方法方法一:平行线的定义:在同一平面内,不相交的两条直线就是平行线.方法二:平行公理的推论:如果两条直线都与第三条直线平行,那么这两条直线也互相平行.方法三:同位角相等,两直线平行.方法四:内错角相等,两直线平行.方法五:同旁内角互补,两直线平行.方法六:同一平面内,垂直于同一条直线的两条直线平行.知识点05 平行线的性质(1)文字表达:①两条平行线被第三条直线所截,同位角相等,内错角相等,同旁内角互补;②简单说成:两直线平行,同位角相等;两直线平行,内错家相等;两直线平行,同旁内角互补;(2)几何语言表述:已知,如图所示,若AB∥CD,则①同位角:∠1=∠5(或∠2=∠6,∠4=∠8,∠3=∠7);②内错角:∠2=∠8(或∠3=∠5);③同旁内角:∠2+∠5=180°(或∠3+∠8=180°).题型01 同位角、内错角、同旁内角的辨别【例题】(2023上·黑龙江哈尔滨·七年级校考期中)如图,下列结论正确的是( )A .5Ð与4Ð是对顶角B .1Ð与3Ð是同位角C .2Ð与3Ð是同旁内角D .1Ð与2Ð是同旁内角【答案】D【分析】本题考查同位角同旁内角、对顶角,根据同位角、同旁内角、对顶角的定义进行判断,熟练掌握各角的定义是解题的关键.【详解】A 、5Ð与23Ð+Ð是对顶角,故本选项错误,不符合题意;B 、1Ð与34Ð+Ð是同位角,故本选项错误,不符合题意;C 、2Ð与3Ð没有处在两条被截线之间,故本选项错误,不符合题意;D 、1Ð与2Ð是同旁内角;故本选项正确,符合题意;故选:D .【变式训练】1.(2023上·四川巴中·七年级四川省巴中中学校考阶段练习)如图所示,有下列五种说法:①1Ð和4Ð是同位角;②3Ð和5Ð是内错角;③2Ð和6Ð是同旁内角;④5Ð和2Ð是同位角;⑤1Ð和3Ð是同旁内角;其中正确的是( )A .①②③⑤B .①②③④C .①②③④⑤D .①②④⑤【答案】D 【分析】本题考查了同位角、 内错角以及同旁内角的定义,根据内错角、 同位角以及同旁内角的定义寻找出各角之间的关系, 再比照五种说法判断对错, 即可得出结论 .【详解】解: 根据内错角、 同位角以及同旁内角的定义分析五种说法 .①1Ð和4Ð是同位角, 即①正确;②3Ð和5Ð是内错角, 即②正确;③2Ð和6Ð是内错角, 即③不正确;④5Ð和2Ð是同位角, 即④正确;⑤1Ð和3Ð是同旁内角, 即⑤正确 .2.(2023下·广东河源·七年级期中)如图,a ,b ,c 三条直线两两相交,下列说法错误的是( )A .1Ð与2Ð是同位角B .2Ð与4Ð是内错角C .3Ð与4Ð是对顶角D .1Ð与3Ð是同旁内角【答案】B 【分析】本题考查相交直线所成相关角的概念,解答关键是熟知同位角、内错角、同旁内角、对顶角的相关概念和判断方法.【详解】解:A .1Ð与2Ð是直线a 、直线b 被直线c 所截,所得到的同位角,因此选项A 不符合题意;B .2Ð与4Ð是直线a 、直线c 被直线b 所截,所得到的同位角,因此选项B 符合题意;C .3Ð与4Ð是对顶角,因此选项C 不符合题意;D .1Ð与3Ð是直线b 、直线c 被直线a 所截,所得到的同旁内角,因此选项D 不符合题意;故选:B .题型02 同位角相等,两直线平行【例题】根据要求完成下面的填空:如图,直线AB ,CD 被EF 所截,若已知12Ð=Ð.23Ð=ÐQ (______),又12Ð=ÐQ (已知),\Ð______=Ð______,∴______∥______(______).【详解】23Ð=ÐQ (对顶角相等),又12Ð=ÐQ (已知),AB CD \∥(同位角相等,两直线平行),故答案为:对顶角相等,1,3,AB ,CD ,同位角相等,两直线平行.【变式训练】1.请完成下面的推理过程并在括号里填写推理依据:如图,129023,,AB BC ^=°Ð+ÐÐ=Ð,BE 与DF 平行吗?为什么?解:BE DF ∥.理由如下:∵AB BC ^(已知),∴ABC Ð=________°即34Ð+Ð=________°( )又∵1290Ð+Ð=°( ),且23ÐÐ=(已知)∴14Ð=Ð( )∴BE DF ∥( )【详解】解:BE DF ∥.理由如下:∵AB BC ^(已知),∴90ABC Ð=°,即3490Ð+Ð=°(等量代换)又∵1290Ð+Ð=°(已知),且23ÐÐ=(已知)∴14Ð=Ð(等角的补角相等)∴BE DF ∥(同位角相等,两直线平行).故答案为:90,90,等量代换,已知,等角的补角相等,同位角相等,两直线平行.2.如图,已知AC AE ^,BD BF ^,135Ð=°,235Ð=°.AC 与BD 平行吗?AE 与BF 平行吗?阅读下面的解答过程,并填空或填写理由.解:AC 与BD 平行;AE 与BF 平行,理由如下:Q 135Ð=°,235Ð=°\12Ð=Ð\(________)∥(________)(________________________);又Q AC AE^\EAC 90Ð=o\1EAB EAC Ð=Ð+Ð=(________)o同理可得2FBG FBD Ð=Ð+Ð=(________)o∴(________)∥(________)(_____________________________).【详解】解:AC 与BD 平行;AE 与BF 平行,理由如下:Q 135Ð=°,235Ð=°\12Ð=Ð\AC ∥BD (同位角相等,两直线平行);又Q AC AE^\90EAC Ð=°\1125EAB EAC Ð=Ð+Ð=°同理可得2125FBG FBD Ð=Ð+Ð=°\AE ∥BF (同位角相等,两直线平行).题型03 内错角相等,两直线平行【例题】如图,EF 交AD 于O ,AB 交AD 于A ,CD 交AD 于D ,12Ð=Ð,34ÐÐ=,试判断AB 和CD 的位置关系,并说明为什么.【详解】解:AB CD P .理由:12Ð=ÐQ ,34ÐÐ=,23ÐÐ=,14\Ð=Ð,∴AB CD P .【变式训练】1.推理填空:已知:如图AB BC ^于B ,CD BC ^于C ,12Ð=Ð,求证:BE CF ∥.证明:∵AB BC ^于B ,CO ∴139024Ð+Ð=°Ð+Ð=,∴1Ð与3Ð互余,2Ð与4Ð又∵12Ð=Ð( ),(1)求BOF Ð的度数;(2)试说明AB CD ∥的理由.【详解】(1)∵OA OB ,分别平分∴12AOE AOC COE ÐÐÐÐ==,∵180COE DOE Ð+Ð=°,题型04 同旁内角互补,两直线平行【例题】如图,已知直线AB CD 、被直线EF 所截,GE 平分AEF Ð,GF 平分EFC Ð,1290Ð+Ð=°,AB CD ∥吗?为什么?解:∵GE 平分AEF Ð,GF 平分EFC Ð(已知),∴2AEF ÐÐ=___________,2EFC ÐÐ=___________,∴AEF EFC ÐÐ+=___________( ),∵1290Ð+Ð=°( ),∴AEF EFC ÐÐ+=___________°,∴AB CD ∥.【详解】解:GE Q 平分AEF Ð,GF 平分EFC Ð(已知),21AEF \Ð=Ð,22EFC Ð=Ð,2(12)AEF EFC \Ð+Ð=Ð+Ð(等量代换)1290Ð+Ð=°Q (已知),180AEF EFC \Ð+Ð=°,AB CD \∥.【变式训练】1.如图,160,260,3120°°°Ð=Ð=Ð=.试说明,DE BC DF ∥∵160260,°°Ð=Ð=∴12Ð=Ð(等量代换)证明:∵12180Ð+Ð=°,∴a ∥______(______).∵13Ð=Ð,∴a ∥______(______).∴b c ∥(______).【详解】证明:∵12180Ð+Ð=°,∴a ∥b (同旁内角互补,两直线平行).∵13Ð=Ð,∴a ∥ c (同位角相等,两直线平行).∴b c ∥(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).题型05 平行线及平行公理【详解】解:因为Ð13Ð=Ð(对顶角相等)所以Ð2=Ð3(等量代换)所以a ∥c (同位角相等,两直线平行)又因为a b ∥(已知)1.如图所示,直线AB CD ,相交于点O ,OD 平分EOB Ð,OF 平分AOE Ð,GH CD ^,垂足为点H ,GH 与FO 平行吗?说明理由.(1)判断CD与AB的位置关系;(2)求证:DF BE∥.^【详解】(1)解:∵AB MN∥.∴CD AB题型06添加一条件使两条直线平行Ð=Ð【答案】EAB【分析】本题主要考查了平行线的判定.要判断的位置关系,根据平行线的判定定理解答即可.∵180CDB B Ð+Ð=°,∴AB CD ∥(同旁内角互补,两直线平行);故答案为:EAB C Ð=Ð(答案不唯一).【变式训练】【答案】①②④【分析】根据平行线的判定条件,逐一判断即可解答.【详解】解:①12Ð=Ð,能判断【答案】250Ð=°.(答案不唯一)【分析】根据平行线的判定和性质进行解答即可.【详解】解:可以添加条件Ð∵EF MN ^,∴90EFM Ð=°【点睛】本题主要考查了平行线的判定和性质,解题的关键是熟练掌握平行线的判定,内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.题型07 根据平行线的性质求角度【例题】(2023下·新疆阿克苏·七年级校考期末)如图,AB CD ∥,直线EF 分别交AB 、CD 于点E 、F ,EG 平分AEF Ð,135Ð=°,求2Ð的度数.【答案】110°【分析】根据平行线的性质、角平分线的定义结合平角的定义即可求解.【详解】解:如图所示,∵AB CD ∥,135Ð=°∴3135Ð=Ð=°∵EG 平分AEFÐ∴3435Ð=Ð=°∴21803535110Ð=°-°-°=°.【点睛】本题主要考查了平行线的性质、角平分线的定义,熟练掌握平行线的性质、求出3135Ð=Ð=°是关键.【变式训练】1.(2023下·浙江金华·七年级校联考期末)如图,点E 在BC 的延长线上,连接DE ,作CED Ð的角平分线分别交线段AD ,DC 于点F ,点G ,已知AB CD ∥,AD BC ∥.(1)试说明2BED DFE Ð=Ð;(2)若105B Ð=°,28DFE Ð=°,求CDE Ð的度数.【答案】(1)见解析(2)19CDE Ð=°【分析】(1)根据角平分线的性质得出2BED BEF Ð=Ð,根据平行线的性质可得DFE BEF Ð=Ð;(2)根据平行线的性质可得105DCE B Ð=Ð=°,根据平行线的性质得出105ADC DCE Ð=Ð=°,180ADE BED Ð+Ð=°,根据(1)的结论得出256BED DFE Ð=Ð=°,180124ADE BED Ð=°-Ð=°,进而根据CDE ADE ADC Ð=Ð-Ð,即可求解.【详解】(1)解:∵EF 平分CED Ð,∴2BED BEF Ð=Ð,∵AD BC∥∴DFE BEF Ð=Ð,(2)解:∵AB CD ∥,105B Ð=°,∴105DCE B Ð=Ð=°,∵AD BC ∥,∴105ADC DCE Ð=Ð=°,180ADE BED Ð+Ð=°.∵28DFE Ð=°,∴256BED DFE Ð=Ð=°,∴180124ADE BED Ð=°-Ð=°,∴12410519CDE ADE ADC Ð=Ð-Ð=°-°=°.【点睛】本题考查了平行线的性质,角平分线的定义,熟练掌握平行线的性质是解题的关键.2.(2023下·贵州黔南·七年级统考期末)如图,已知AB CD ∥,AD BC ∥,90DCE Ð=°,点E 在线段AB 上,90FCG Ð=°,点F 在直线AD 上,90AHG Ð=°.(1)图中与D Ð相等的角有__________;(2)若25ECF Ð=°,求BCD Ð的度数;(3)在(2)的条件下,点C (点C 不与B ,H 两点重合)从点B 出发,沿射线BG 的方向运动,其他条件不变,求BAF Ð的度数.【答案】(1)DCG Ð,ECF Ð,BÐ(2)155°(3)25°或155°【分析】(1)根据同角的余角相等以及平行线的性质,即可得到与D Ð相等的角;(2)根据25ECF Ð=°,90DCE Ð=°,可得65FCD Ð=°,再根据90BCF Ð=°,即可得到6590155BCD Ð=°+°=°;(3)分两种情况讨论:当点C 在线段BH 上;点C 在BH 延长线上,根据平行线的性质,即可得到BAF Ð的度数为25°或155°.【详解】(1)解:AD BC ∥Q ,D DCG \Ð=Ð,90FCG Ð=°Q ,90DCE Ð=°,ECF DCG \Ð=Ð,D ECF \Ð=Ð,AB DC Q ∥,DCG B \Ð=Ð,D B \Ð=Ð;\与D Ð相等的角为DCG Ð,ECF Ð,B Ð;(2)解:25ECF Ð=°Q ,90DCE Ð=°,65FCD \Ð=°,90BCF Ð=°Q ,6590155BCD \Ð=°+°=°;(3)解:分两种情况进行讨论:①如图a ,当点C 在线段BH 上时,点F 在DA 的延长线上,此时25ECF DCG B Ð=Ð=Ð=°,AD BC ∥Q ,25BAF B \Ð=Ð=°;②如图b ,当点C 在BH 的延长线上时,点F 在线段AD 上.25B Ð=°Q ,AD BC ∥,18025155BAF \Ð=°-°=°,综上所述,BAF Ð的度数为25°或155°.【点睛】本题考查了平行线的性质,熟练掌握平行线的性质定理是解题关键.题型08平行线的性质在生活中的应用【答案】120°/120度【分析】首先过B作BF AE∥,根据100Ð=°Q,A\Ð=Ð=°,100ABF A又160ABC Ð=°Q ,16010060FBC \Ð=°-°=°,AE CD ∥Q ,FB CD \∥,180********C FBC \Ð=°-Ð=°-°=°,故答案为:120°.【点睛】此题主要考查了平行线性质,关键是掌握两直线平行,同旁内角互补;两直线平行,内错角相等.【变式训练】【答案】17°/17度【分析】由平行线的性质可知D B C M B C M B D Ð=Ð-Ð求解即可.【详解】解:∵MN EF ∥,∴160M B C Ð=Ð=°.【答案】30°/30度【分析】过点B 作BF CE ∥.先利用平行线的性质和垂直的定义、角的和差关系求出CBF Ð,再利用平行线的性质和角的和差关系求得结论.【详解】解:过点B 作BF CE ∥.CE l ∥Q ,BF l \∥.190ABF \Ð=Ð=°.140ABC Ð=°Q ,1409050CBF \Ð=°-°=°.BF CE ∥Q ,50ECB CBF \Ð=Ð=°.DCE DCB BCE\Ð=Ð-Ð8050=°-°30=°.故答案为:30°.【点睛】本题主要考查了平行线的性质,掌握平行线的性质和角的和差关系是解决本题的关键.题型09 平行线的性质与判定综合应用【答案】(1)见解析;(2)F BMF DNFÐ=Ð-Ð;(3)20【分析】本题主要考查平行线的判定和性质,作辅助线是解题的关键.(1)过点E作EF AB∥,根据平行线的性质可求解;(2)如图②,过F作FH AB∥,根据平行线的性质即可得到结论;∥,根据平行线的性质即可得到结论.(3)如图③,过C作CG AB【详解】(1)证明:如图①,过点E作EF AB∥,则MEF BMEÐ=Ð,∥,又∵AB CD∥,∴EF CD\Ð=Ð,NEF DNEMEN MEF NEF\Ð=Ð+Ð,Ð=Ð+Ð;即MEN BME DNE(2)解:BMF MFN FNDÐ=Ð+Ð.P,证明:如图②,过F作FK AB\Ð=Ð,BMF MFK∥,∵AB CDP,∴FK CD\Ð=Ð,FND KFN\Ð=Ð-Ð=Ð-Ð,MFN MFK KFN BMF FND即:BMF MFN FND Ð=Ð+Ð.故答案为:BMF MFN FND Ð=Ð+Ð;(3)如图③,过C 作CG AB ∥,18060GCA BAC \Ð=°-Ð=°,∵AB DE ∥,∴CG DE ∥,80GCD CDE \Ð=Ð=°,20ACD \Ð=°,故答案为:20.【变式训练】1.(2023上·湖南岳阳·八年级校考开学考试)如图,12Ð=Ð,BAE BDE Ð=Ð,点F 在DE 的延长线上,点C 在AB 的延长线上,且EA 平分BEF Ð.(1)求证:AB DE ∥;(2)若40BAE Ð=°,求EBD Ð.【答案】(1)见解析(2)40°【分析】(1)根据对顶角相等结合题意推出1ABE Ð=Ð,根据“同位角相等,两直线平行”即可判定AB DE ∥;(2)根据平行线的性质结合题意推出AEF BDE Ð=Ð,即可判定AE BD P ,根据平行线的性质及角平分线的定义求解即可.【详解】(1)证明:∵2ABE Ð=Ð(对顶角相等),又12Ð=Ð(已知),∴1ABE Ð=Ð(等量代换),∴AB DE ∥(同位角相等,两直线平行);(2)解:由(1)已证AB DE ∥可得:40BAE AEF Ð=Ð=°(两直线平行,内错角相等),又∵BAE BDE Ð=Ð,∴AEF BDE Ð=Ð(等量代换),∴AE BD P (同位角相等,两直线平行),∴AEB EBD Ð=Ð(两直线平行,内错角相等),又∵EA 平分BEF Ð,∴AEB AEF Ð=Ð,∴40EBD AEB AEF BAE Ð=Ð=Ð=Ð=°,∴40Ð=°EBD .【点评】此题考查了平行线的判定与性质,熟记平行线的判定定理与性质定理是解题的关键.2.(2023下·江苏泰州·七年级校考期中)如图,在ABC V 中,点D 、F 在BC 边上,点E 在AB 边上,点G 在AC 边上,EF 与GD 的延长线交于点H ,BDH B Ð=Ð,AEH ADH Ð=Ð.(1)EH 与AD 平行吗?为什么?(2)若40H Ð=°,求BAD Ð的度数.【答案】(1)平行,见解析(2)40°【分析】(1)EH AD ∥,理由如下:由已知条件,BDH B Ð=Ð,根据平行线的判定可得AB GH ∥,根据平行线的性质得180BAD ADH Ð+Ð=°,等量代换得到180BAD AEH Ð+Ð=°,即可得出答案;(2)结合(1)根据平行线的性质即可得解.【详解】(1)EH AD ∥,理由如下:BDH B Ð=ÐQ ,AB GH \∥,180BAD ADH \Ð+Ð=°,AEH ADH Ð=ÐQ ,180BAD AEH \Ð+Ð=°,EH AD \∥;(2)180BAD ADH Ð+Ð=°Q ,又EH AD Q ∥,180H ADH \Ð+Ð=°,H BAD \Ð=Ð,40H Ð=°Q ,40BAD \Ð=°.【点睛】此题考查了平行线的判定与性质,熟记平行线的判定与性质定理是解题的关键.题型10 根据平行线的性质与判定探究角的关系(1)123ÐÐÐ、、之间的关系为(2)如果点P 在A 、B 两点之间运动时,(3)如果点P (点P 和A 、【答案】(1)123Ð+Ð=Ð(2)123Ð+Ð=Ð(3)123Ð-Ð=Ð或2Ð-Ð∴52Ð=Ð(两直线平行,内错角相等),∵345Ð=Ð+Ð,∴123Ð+Ð=Ð(等量代换);故答案为:123Ð+Ð=Ð;(2)解:由(1)的证明过程知,123ÐÐÐ、、之间的关系不发生变化;故答案为:123Ð+Ð=Ð;(3)解:过点P 作1PQ l ∥,∵12l l ∥,∴21PQ l l ∥∥;当点P 在AB 延长线上时,如左图,则24ÐÐ=,134CPQ Ð=Ð=Ð+Ð,∴132Ð=Ð+Ð,即123Ð-Ð=Ð;当点P 在BA 延长线上时,如右图,∵21PQ l l ∥∥,∴14Ð=Ð,234DPQ Ð=Ð=Ð+Ð,∴231Ð=Ð+Ð,即213Ð-Ð=Ð;综上,123Ð-Ð=Ð或213Ð-Ð=Ð.故答案为:123Ð-Ð=Ð或213Ð-Ð=Ð.【变式训练】(1)图中CBD Ð= °;(2)当ACB ABD Ð=Ð时,ABC Ð=(3)随点P 位置的变化,图中APB Ð【答案】(1)60P;(1)求证:AB CD(2)点G是射线MD上的一个动点∥交直线AB于点N,设HN EMβ=°①点G在点F右侧,且70∵EH 平分FEG Ð,∴HEF HEG Ð=Ð,∵HN EM ∥,∴EHN HEM HEF FEM Ð=Ð=Ð+Ð,∵FEM FME Ð=Ð,∴EHN HEF FME αÐ=Ð+Ð=,∵()180********EGF FME GEM FME FEM HEF FME HEF Ð=°-Ð-Ð=°-Ð-Ð-Ð=°-Ð+Ð,∴1802βα=°-,∵70β=°,∴701802α°=°-,解得55α=°.②α和β之间的数量关系为2βα=或1802βα=°-.理由如下:当点G 在点F 的右侧,由(2)得1802αβ=°-,当点G 在点F 的左侧时,如图2,∵EH 平分FEG Ð,∴HEF HEG Ð=Ð,∵HN EM ∥,∴EHN HEM Ð=Ð,∵FEM FME Ð=Ð,∴()222EGF FME GEM FEM GEM GEM HEG GEM GEM HEG HEM Ð=Ð+Ð=Ð+Ð=Ð+Ð+Ð=Ð+Ð=Ð,∴2EGF EHN Ð=Ð,即2βα=,综上所述,α和β之间的数量关系为2βα=或1802βα=°-.【点睛】本题考查角平分线的定义,平行线的性质,利用数形结合和分类讨论的思想是解题关键.一、单选题1.(2023下·云南昭通·七年级统考阶段练习)如图,下列条件不能判定AB CD P 的是( )A .13Ð=ÐB .35Ð=ÐC .12180Ð+Ð=°D .15Ð=Ð【答案】B 【分析】根据平行线的判定定理,对各项逐一进行判断即可.【详解】解:A 、13Ð=Ð,根据同位角相等,两直线平行可判定AB CD P ,故此选项不符合题意;B 、35Ð=Ð,对顶角相等,不能判定AB CD P ,故此选项符合题意;C 、12180Ð+Ð=°,根据同旁内角互补,两直线平行可判定AB CD P ,此选项不符合题意;D 、15Ð=Ð,根据内错角相等,两直线平行可判定AB CD P ,故此选项不符合题意;故选:B .【点睛】本题考查了平行线的判定定理,解题的关键是正确识别“三线八角”中的同位角、内错角、同旁内角,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.2.(2023下·广东江门·七年级统考期末)如图所示,以下说法错误的是( )A .1Ð与2Ð是同位角B .4Ð与3Ð是同位角C .5Ð与3Ð是内错角D .4Ð与5Ð是同旁内角【答案】C 【分析】根据同位角、内错角、同旁内角的定义逐项判断即可.【详解】解:A 、1Ð与2Ð是同位角,正确,不符合题意;B 、4Ð与3Ð是同位角,正确,不符合题意;C 、5Ð与3Ð不是内错角,错误,符合题意;D 、4Ð与5Ð是同旁内角,正确,不符合题意,故选:C .【点睛】本题考查同位角、内错角、同旁内角,解答的关键是理解定义:如果两条直线被第三条直线所截所形成的的角,在两条被截直线之间且在截线两侧的两个角互为内错角;在两条被截直线同一方且在截线同侧的两个角互为同位角;在两条被截线之间且在截线同侧的两个角互为同旁内角.3.(2023上·陕西铜川·八年级统考期末)如图,下列推理及括号中所注明的推理依据错误的是( )A .∵AD BC ∥,180BAD D \Ð+Ð=°(两直线平行,同旁内角互补)B .∥Q AB CD ,180BCD ABC \Ð+Ð=°(两直线平行,同旁内角互补)C .13Ð=ÐQ ,AB CD \∥(内错角相等,两直线平行)D .DAM CBM Ð=ÐQ ,AD BC \∥(同位角相等,两直线平行)【答案】A【分析】本题考查的是平行线的判定与性质,利用平行线的判定方法与性质逐一分析即可得到答案,熟记平行线的判定方法与平行线的性质是解本题的关键.【详解】解:∵AD BC ∥,180BAD ABC \Ð+Ð=°(两直线平行,同旁内角互补),故A 符合题意;∥Q AB CD ,180BCD ABC \Ð+Ð=°(两直线平行,同旁内角互补),故B 不符合题意;13Ð=ÐQ ,AB CD \∥(内错角相等,两直线平行),故C 不符合题意;DAM CBM Ð=ÐQ ,AD BC \∥(同位角相等,两直线平行),故D 不符合题意;故选A4.(2023上·陕西榆林·八年级校考期末)如图,直线a b P ,直线l 与直线a 相交于点P ,与直线b 相交于点Q ,PM l ^于点P ,若155Ð=°,则2Ð的度数为( )A .35°B .55°C .125°D .145°【答案】A 【分析】本题考查了平行线性质,根据两直线平行,同位角相等,平角的定义计算即可.【详解】如图,∵a b P ,155Ð=°,∵34180,2+Ð=°ÐÐ+Ð∴180324а--Ð==Ð故选A .5.(2023上·四川宜宾·七年级四川省宜宾市第二中学校校考阶段练习)平分BAC Ð,A C CE ^A .1个【答案】D 【分析】①根据平行线的传递性可以判断出来内角互补可得2BAC Ð+Ð212180Ð+Ð=°,可求得结果;二、填空题【答案】①②④【分析】根据同位角的定义,逐一判断选项,即可得到答案.【详解】解:①∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角;②∠1和∠2在两条直线的同侧,也在第三条直线的同侧,故它们是同位角;【答案】B DAB Ð=Ð【分析】根据“内错角相等,两直线平行【详解】解:由“内错角相等,两直线平行【答案】36°/36度【分析】由对顶角相等可得Ð件可求得B Ð,即可求解.【详解】解:如图,1108Ð=°Q ,31108\Ð=Ð=°,∵l AB ∥,3180A \Ð+Ð=°,2B Ð=Ð,【答案】3或7.5或12【分析】本题考查了平行线的性质.分类讨论Ð的大小即可求解.性质确定旋转角AFE∥时,如图所示:【详解】解:①当DE BC30AFE Ð=°∴30310t ==秒②当DE AB ∥时,如图所示:∵45FHD A Ð=Ð=°,∴45HFD Ð=°45AFE HFD EFD Ð=Ð+Ð=°+∴757.510t ==秒180120AFE E Ð=°-Ð=°∴1201210t ==秒综上所述:t 的值为3或7.5或12三、解答题11.(2023上·新疆克孜勒苏·七年级统考期末)如图,已知12180Ð+Ð=°,3B Ð=Ð,试判断C Ð与AED Ð的大小关系,请补全证明过程,即在横线处填上结论或理由.解:AED C Ð=Ð.理由如下:∵12180Ð+Ð=°(已知),1180DFE Ð+Ð=°(_______),∴2DFE Ð=Ð(_______),∴AB ∥ _______(_______),∴3ADE Ð=Ð(_______),∵3B Ð=Ð(已知),∴∠_______=Ð_______(_______),∴_______∥_______(_______),C AED Ð=Ð(_______).【答案】平角的定义;等量代换;EF ;内错角相等,两直线平行;两直线平行,内错角相等:ADE ;B ;等量代换;DE ;BC ,同位角相等,两直线平行;两直线平行,同位角相等【分析】本题考查了平行线的判定与性质,根据证明的思路,把证明过程填写完整即可.【详解】AED C Ð=Ð.理由如下:∵12180Ð+Ð=°(已知),1180DFE Ð+Ð=°(平角的定义),∴2DFE Ð=Ð(等量代换),∴AB EF ∥(内错角相等,两直线平行),∴3ADE Ð=Ð(两直线平行,内错角相等),∵3B Ð=Ð(已知),∴ADE B Ð=Ð(等量代换),∴DE BC ∥(同位角相等,两直线平行),∴C AED Ð=Ð(两直线平行,同位角相等).故答案为:平角的定义;等量代换;EF ;内错角相等,两直线平行;两直线平行,内错角相等:ADE ;B ;等量代换;DE ;BC ,同位角相等,两直线平行;两直线平行,同位角相等.12.(2023上·吉林长春·七年级统考期末)在下列解答中,填空(理由或数学式).如图,已知直线b c ∥,1116Ð=°,3=4ÐÐ.(1)求AOB Ð的度数;(2)求证:直线a c ∥.解:(1)∵1116Ð=° (已知)∴2116Ð=°( ).∵b c ∥(已知),∴2AOB Ð=Ð( ).故答案为:已知;内错角相等,两直线平行;如果两条直线都和第三条直线平行,那么这两条直线也互相平行.13.(2023上·吉林长春·七年级校考期末)如图,已知AB CD P ,AC 与BD 相交于点E ,从点E 引一条射线EF 交线段AB 于点F ,若180AFE DCB Ð+Ð=°,A AEF Ð=Ð,求证:DCA ACB Ð=Ð.证明:∵AB CD P (已知),∴180ABC DCB Ð+Ð=°(两直线平行,同旁内角互补),又∵180AFE DCB Ð+Ð=°(已知),∴AFE ABC Ð=Ð(____________________),∴EF ∥__________(____________________),∴Ð=AEF __________(____________________),∵AB CD P (已知),∴A DCA Ð=Ð(____________________),∵A AEF Ð=Ð(已知),∴DCA ACB Ð=Ð(____________________).【答案】见解析【分析】本题考查平行线的性质与判定,根据题目已知条件及现有步骤结合平行线的判定和性质定理,即可得到答案.【详解】证明:AB CD P (已知),∴180ABC DCB Ð+Ð=°(两直线平行同旁内角互补),又∵180AFE DCB Ð+Ð=°(已知),∴AFE ABC Ð=Ð(同角的补角相等);∴ EF BC ∥(同位角相等,两直线平行),∴AEF ACB Ð=Ð(两直线平行,同位角相等),∵AB CD P (已知),∴A DCA Ð=Ð(两直线平行,内错角相等),∴A AEF Ð=Ð(已知),∴DCA ACB Ð=Ð(等量代换),故答案为:同角的补角相等;BC ;同位角相等,两直线平行;ACB Ð;两直线平行,同位角相等;两直线平行,内错角相等;等量代换.14.(2023上·重庆沙坪坝·八年级统考期中)已知:如图,在ABC V 中,点D 在BC 边上,EF AD ∥分别交AB ,CB 于点E ,F ,DG 平分ADC Ð,12180Ð+Ð=°,(1)求证:AB DG ∥;(2)若40B Ð=°,60DAC Ð=°,求DGC Ð的度数.【答案】(1)见解析(2)100°【分析】本题考查了平行线的性质与判定、角平分线的定义、三角形的外角性质,熟练掌握平行线的性质和判定,是解决本题的关键.平行线的性质:两直线平行,内错角相等;两直线平行,同位角相等;两直线平行,同旁内角互补;平行线的判定:内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.三角形的外角性质:三角形的外角等于与它不相邻的两个内角的和.【详解】(1)证明:∵EF AD ∥,∴1180BAD Ð+Ð=°.∵12180Ð+Ð=°.∴2BAD Ð=Ð.∴AB DG ∥;(2)解:∵AB DG ∥,40B Ð=°,∴40GDC B Ð=Ð=°,∵DG 平分ADC Ð,∴240GDC Ð=Ð=°,又∵60DAC Ð=°,∴2100DGC DAC Ð=Ð+Ð=°.15.(2023上·四川遂宁·七年级射洪中学校联考阶段练习)如图1,直线AD EF P ,点B C ,分别在EF 和AD 上,A ABC Ð=Ð,BD 平分CBF Ð.【探索】如图②,AM 平分BAC Ð,CAM CMA Ð=Ð,点E 在射线AB 上,点F 在线段CM 上,若AEF C Ð=Ð,求证:EF AC ∥.【拓展】如图③,将【探索】中的点F 移动到线段CM 的延长线上,其他条件不变,若357CAM MEF Ð=Ð=°,请直接写出AME Ð的度数.【答案】感知:BAM Ð;BAM Ð;探索:见解析;拓展:76AME =°∠【分析】感知:根据角平分线定义和平行线的性质进行解答即可;探索:先证明AB CD P ,得出AEF EFD Ð=Ð,在证明EFD C Ð=Ð,根据平行线的判定得出结论即可;拓展:根据角平分线定义得出57BAM CAM ==°∠∠, 257114BAC =´°=°∠,根据平行线的性质求出18066C BAC =°-=°∠∠,求出661947AEM =°-°=°∠,最后根据平行线的性质求出结果即可.【详解】解:感知:∵AM 平分BAC Ð,(已知),∴CAM BAM Ð=Ð(角平分线的定义),∵AB CD P (已知),∴CMA BAM Ð=Ð(两直线平行,内错角相等)∴CAM CMA Ð=Ð(等量代换).故答案为:BAM Ð;BAM Ð.探索:∵AM 平分BAC Ð,∴CAM BAM Ð=Ð,∵CAM CMA Ð=Ð,∴A BAM CM =Ð∠,∴AB CD P ,∴AEF EFD Ð=Ð,∵AEF C Ð=Ð,∴EFD C Ð=Ð,∴EF AC ∥.拓展:∵357CAM MEF Ð=Ð=°,∴根据探索可知:57BAM CAM ==°∠∠,19MEF =°∠,∴257114BAC =´°=°∠,根据探索可知:AB CD P ,∴18066C BAC =°-=°∠∠,∴66AEF C ==°∠∠,∴661947AEM =°-°=°∠,∵AB CD P ,∴57AMC BAM ==°∠∠,47DME AEM ==°∠∠,∴18076AME AMC DME =°--=°∠∠∠.【点睛】本题主要考查了平行线的判定和性质,角平分线的定义,几何图形中的角度计算,解题的关键是熟练掌握平行线的判定方法,内错角相等,两直线平行;同位角相等,两直线平行;同旁内角互补,两直线平行.平行线的性质,两直线平行,同位角相等;两直线平行,内错角相等;两直线平行,同旁内角互补.17.(2023上·内蒙古乌海·八年级统考期末)综合与实践:问题:如图1,直线AB 、BC 、AC 两两相交,交点分别为点A 、B 、C ,点D 在线段AB 上,过点D 作DE BC ∥交AC 于点E ,过点E 作EF AB ∥交BC 于点F .(1)若65ABC Ð=°,求DEF Ð的度数.请将下面的解答过程补充完整,并填空(理由或数学式)解:∵DE BC ∥,∴DEF Ð= ______(______),∵EF AB ∥,∴______ ABC =Ð(______),∴DEF ABC Ð=Ð(______),∵65ABC Ð=°,∴65DEF Ð=°.探究:如图2,直线AB 、BC 、AC 两两相交,交点分别为点A 、B 、C ,点D 在线段AB 的延长线上,过点D 作DE BC ∥交AC 于点E ,过点E 作EF AB ∥交BC 于点F .(2)在图2中,若65ABC Ð=°,求DEF Ð的度数并说明理由.(3)猜想:如果ABC Ð的两边分别平行于DEF Ð的两边,直接写出ABC Ð与DEF Ð这两个角之间有怎样的数量关系?【答案】(1)EFC Ð;两直线平行,内错角相等;EFC Ð;两直线平行,同位角相等;等量代换;(2)115DEF Ð=°,理由见解析;(3)ABC DEF Ð=Ð或180ABC DEF Ð+Ð=°【分析】本题主要考查平行线的性质,解答的关键是熟记平行线的性质并灵活运用.(1)由平行线的性质可得DEF EFC Ð=Ð,EFC ABC Ð=Ð,则有DEF ABC Ð=Ð,即可得解;(2)由平行线的性质得65ABC ADE Ð=Ð=°,180ADE DEF Ð+Ð=°,则可求DEF Ð得度数.(3)根据平行线的性质分析,即可获得答案.【详解】解:(1)∵DE BC ∥,∴DEF EFC Ð=Ð(两直线平行,内错角相等),∵EF AB ∥,∴EFC ABC Ð=Ð(两直线平行,同位角相等),∴DEF ABC Ð=Ð(等量代换),∵65ABC Ð=°,∴65DEF Ð=°.故答案为:EFC Ð;两直线平行,内错角相等;EFC Ð;两直线平行,同位角相等;等量代换;(2)115DEF Ð=°,理由如下:∵DE BC ∥,∴65ABC ADE Ð=Ð=°(两直线平行,同位角相等),∵EF AB ∥,∴180ADE DEF Ð+Ð=°(两直线平行,同旁内角互补),∴180115DEF ADE Ð=°-Ð=°;(3)ABC DEF Ð=Ð或180ABC DEF Ð+Ð=°,理由如下:如图1,ABC Ð的两边分别平行于DEF Ð的两边时,ABC DEF Ð=Ð;如图2,ABC Ð的两边分别平行于DEF Ð的两边时,180ABC DEF Ð+Ð=°.18.(2023上·全国·八年级专题练习)如图,线段AB 与线段CD 平行,P 是平面内一点,连接PA PD ,,射线AM DN ,分别平分BAP CDP ÐÐ,.(1)当点P 在线段DA 的延长线上时:①在图1中,依题意补全图形;②请直接写出直线AM 与直线DN 的位置关系:___________;(2)如图2,当点P 在直线AB 与直线CD 之间时,射线AM ,DN 交于点Q ,探究P Ð与AQD Ð的数量关系,。
2022年人教版平行线的判定性质练习知识点考点典型例题

5.2平行线及其鉴定【知识要点】平行线旳鉴定(1)同位角相等,两直线平行(2)内错角相等,两直线平行(3)同旁内角互补,两直线平行(4)在同一平面内,垂直于同一条直线旳两条直线互相平行(5)平行公理旳推论:假如两条直线都与第三条直线互相平行,那么这两条直线也互相平行。
【配套练习】一.判断题:1.两条直线被第三条直线所截,只要同旁内角相等,则两条直线一定平行。
()2.如图②,∵∠GMB=∠HND(已知)∴AB∥CD(同位角相等,两直线平行)()二.填空题:1.∵a∥b,b∥c(已知)∴______ ∥______()2.如图:1234ab c(1)∵______=∠3,∴a∥b ()。
(2)∵∠2=∠4,∴______∥________()(3)∵∠2+∠3=180°,∴______∥________()3.如图③∵∠1=∠2,∴______∥________()∵∠2=∠3,∴______∥_______()4.如图④∵∠1=∠2,∴______∥________()∵∠3=∠4,∴______∥________()5.如图⑤∠B=∠D=∠E,那么图形中旳平行线有________________________________。
6.如图⑥∵AB⊥BD,CD⊥BD(已知)∴∠B=∠D=90°()∴∠B+∠D=180°∴AB∥CD ( )又∵∠1+∠2 =180°(已知)∴AB∥EF ( )∴CD∥EF ( )三.选择题:1.如图⑦,∠D=∠EFC,那么()A.AD∥BC B.AB∥CDC.EF∥BC D.AD∥EF2.如图⑧,鉴定AB∥CE旳理由是()A.∠B=∠ACE B.∠A=∠ECD C.∠B=∠ACB D.∠A=∠ACE3.如图⑨,下列推理错误旳是()A.∵∠1=∠3,∴a∥b B.∵∠1=∠2,∴a∥bC.∵∠1=∠2,∴c∥d D.∵∠1=∠2,∴c∥d4.如图,直线a、b被直线c所截,给出下列条件,①∠1=∠2,②∠3=∠6,③∠4+∠7=180°,④∠5+∠8=180°其中能判断a∥b旳是()A.①③B.②④C.①③④D.①②③④四.完毕推理,填写推理根据:1.如图⑩∵∠B=∠______,∴AB∥CD()∵∠BGC=∠____,∴CD∥EF()∵AB∥CD ,CD∥EF,∴AB∥_______()2.如图⑾填空:(1)∵∠2=∠3(已知)∴AB__________()(2)∵∠1=∠A(已知)∴__________()(3)∵∠1=∠D(已知)∴__________()(4)∵_______=∠F(已知)∴AC∥DF()3.填空。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
平行线的判定和性质经典题一.选择题(共18小题)1.如图所示,同位角共有( )第1题第2题A. 6对B.8对C.10对D.12对2.如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是( )A.平行 B. 垂直 C. 平行或垂直D.无法确定3.下列说法中正确的个数为( )①不相交的两条直线叫做平行线②平面内,过一点有且只有一条直线与已知直线垂直③平行于同一条直线的两条直线互相平行④在同一平面内,两条直线不是平行就是相交A.1个 B. 2个C.3个 D. 4个4.在同一平面内,有8条互不重合的直线,l1,l2,l3…l8,若l1⊥l2,l2∥l3,l3⊥l4,l4∥l5…以此类推,则l1和l8的位置关系是( )A.平行B.垂直 C. 平行或垂直D.无法确定5.若两个角的两边分别平行,且这两个角的差为40°,则这两角的度数分别是()A.150°和110° B. 140°和100°C.110°和70° D. 70°和30°6.如图所示,AC⊥BC,DE⊥BC,CD⊥AB,∠ACD=40°,则∠BDE等于()第6题第7题A.40°B. 50°C. 60°D. 不能确定7.如图,AB∥CD,且∠BAP=60°﹣α,∠APC=45°+α,∠PCD=30°﹣α,则α=( ) A. 10°B.15°C.20°D.30°8.下列所示的四个图形中,∠1和∠2是同位角的是( )A. ②③B. ①②③ C. ①②④D.①④9.已知∠AOB=40°,∠CDE的边CD⊥OA于点C,边DE∥OB,那么∠CDE等于( )A. 50°B. 130°C.50°或130°D. 100°10.如图,AB∥CD∥EF,AF∥CG,则图中与∠A(不包括∠A)相等的角有()第10题第11题A.5个B.4个 C. 3个D.2个11.如图所示,BE∥DF,DE∥BC,图中相等的角共有( )A.5对 B. 6对C.7对 D. 8对12.已知∠A=50°,∠A的两边分别平行于∠B的两边,则∠B=( )A. 50°B.130°C.100° D. 50°或130°( )13.如图所示,DE∥BC,DC∥FG,则图中相等的同位角共有14.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有( )A. 2个B. 3个C.4个D.5个15.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是( )A.42°、138°B. 都是10°C. 42°、138°或42°、10°D.以上都不对16.把直线a沿水平方向平移4cm,平移后的像为直线b,则直线a与直线b之间的距离为( )A.等于4cm B.小于4cm C. 大于4cm D. 小于或等于4cm 17.(2009•宁德)在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是()A. B. C. D.18.(2004•烟台)4根火柴棒摆成如图所示的象形“口”字,平移火柴棒后,原图形变成 )的象形文字是(A. B. C. D.二.填空题(共12小题)19.已知∠α和∠β的两边互相平行,且∠α=60°,则∠β= _________ .20.(2004•西宁)如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)有 _________ 个;若∠1=50°,则∠AHG=_________度.第20题第21题第22题21.(2009•永州)如图,直线a、b分别被直线c、b所截,如果∠1=∠2,那么∠3+∠4=_________ 度.直线a、b分别被直线c、b所截.22.(2010•抚顺)如图所示,已知a∥b,∠1=28°,∠2=25°,则∠3= _________ 度.23.如图,已知BO平分∠CBA,CO平分∠ACB,MN∥BC,且过点O,若AB=12,AC=14,则△AMN的周长是 _________.第23题第24题24.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为_________ cm;(2)如图2,若∠_________ =∠ _________ ,则AD∥BC;(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC=_________度;25.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为 _________ .26.如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠AGE相等的角有_________ 个.第26题第27题27.如图所示,AD∥EF∥BC,AC∥EN,则图中与∠1相等的角有 _________ 个.28.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为_________ .第28题第29题第30题29.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动_________ 格.30.如图,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积是_________ cm2.平行线的判定和性质经典题参考答案与试题解析一.选择题(共18小题)1.如图所示,同位角共有( )A.6对B.8对 C. 10对D.12对考点:同位角、内错角、同旁内角.分析:在基本图形“三线八角”中有四对同位角,再看增加射线GM、HN后,增加了多少对同位角,求总和.解答:解:如图,由AB、CD、EF组成的“三线八角”中同位角有四对,射线GM和直线CD被直线EF所截,形成2对同位角;射线GM和直线HN被直线EF所截,形成2对同位角;射线HN和直线AB被直线EF所截,形成2对同位角.则总共10对.故选C.点评:本题主要考查同位角的概念.即两个都在截线的同旁,又分别处在被截的两条直线同侧的位置的角叫做同位角.2.如图所示,将一张长方形纸对折三次,则产生的折痕与折痕间的位置关系是()A. 平行 B . 垂直 C. 平行或垂直 D. 无法确定 考点:平行线;垂线.分析:根据平行公理和垂直的定义解答.解答: 解:∵长方形对边平行,∴根据平行公理,前两次折痕互相平行,∵第三次折叠,是把平角折成两个相等的角,∴是90°,与前两次折痕垂直.∴折痕与折痕之间平行或垂直.故选C.点评:本题利用平行公理和垂直定义求解,需要熟练掌握.3.下列说法中正确的个数为( )①不相交的两条直线叫做平行线②平面内,过一点有且只有一条直线与已知直线垂直③平行于同一条直线的两条直线互相平行④在同一平面内,两条直线不是平行就是相交A. 1个B. 2个 C. 3个 D. 4个考点:平行线;垂线.分析:本题从平行线的定义及平行公理入手,对选项逐一分析即可.解答: 解:①不相交的两条直线叫做平行线必须是在同一个平面内才能成立,故错误. ②平面内,过一点有且只有一条直线与已知直线垂直是正确的.③平行于同一条直线的两条直线互相平行,故正确.④在同一平面内,两条直线不是平行就是相交是正确的.故答案为C.点评:本题考查平行线的定义及平行公理,需熟练掌握.4.在同一平面内,有8条互不重合的直线,l 1,l2,l 3…l 8,若l1⊥l 2,l2∥l 3,l 3⊥l 4,l4∥l5…以此类推,则l 1和l 8的位置关系是( )A. 平行 B . 垂直 C. 平行或垂直 D. 无法确定 考点:平行线的判定.分析: 如果一条直线垂直于两平行线中的一条,那么它与另一条一定也垂直.再根据“垂直于同一条直线的两直线平行”,可知L 1与L 8的位置关系是平行.解答: 解:∵l2∥l3,l 3⊥l 4,l4∥l5,l 5⊥l6,l 6∥l7,l 7⊥l 8,∴l 2⊥l 4,l 4⊥l 6,l 6⊥l 8,∴l 2⊥l 8.∵l1⊥l 2,∴l1∥l 8.故选A点灵活运用“垂直于同一条直线的两直线平行”是解决此类问题的关键.5.若两个角的两边分别平行,且这两个角的差为40°,则这两角的度数分别是( )A. 150°和110° B . 140°和100° C . 110°和70° D. 70°和30° 考点:平行线的性质.专题:计算题.分析: 若两个角的两边分别平行,可运用平行线的性质得出两角相等或互补,根据题意,两角不相等,只有互补,逐一排除.解答: 解:根据两个角的两边分别平行,则两角相等或互补.又这两个角的差为40°,则只有互补的情况,则这两角的度数分别是110°和70度.故选C.点评:此题要特别注意两种情况的考虑,以及互补情况的排除.6.如图所示,AC⊥BC,DE⊥BC,CD⊥AB,∠ACD =40°,则∠BDE 等于( )A. 40° B. 50° C. 60° D. 不能确定 考点:平行线的性质;垂线.专题:计算题.分析: 先根据垂直得到D E与AC 平行,然后可知其内错角∠EDC的度数,再利用CD 与A B垂直就可以求出.解答: 解:∵AC⊥BC,D E⊥BC,∴DE∥AC,∴∠EDC=∠AC D=40°又CD⊥AB,∴∠BDE=90°﹣∠EDC=90°﹣40°=50°;故选B.点评: 首先根据平面内垂直于同一条直线的两条直线平行得到两条平行线,再根据平行线的性质得到两个内错角相等,最后根据垂直的定义进行求解.7.如图,AB∥CD,且∠BAP=60°﹣α,∠APC=45°+α,∠PCD=30°﹣α,则α=( )A. 10°B. 15° C. 20° D. 30°考平行线的性质.专题:计算题.分析:过点P作一条直线平行于AB,根据两直线平行内错角相等得:∠APC=∠BAP+∠PCD,得到关于α的方程,解即可.解答:解:过点P作PM∥AB,∴AB∥PM∥CD,∴∠BAP=∠APM,∠DCP=∠MPC,∴∠APC=∠APM+∠CPM=∠BAP+∠DCP, ∴45°+α=(60°﹣α)+(30°﹣α),解得α=15°.故选B.点评:注意此类题要常作的辅助线,充分运用平行线的性质探求角之间的关系. 8.下列所示的四个图形中,∠1和∠2是同位角的是( )A.②③ B. ①②③ C. ①②④ D. ①④考点:同位角、内错角、同旁内角.分析:此题在于考查同位角的概念,在截线的同侧,并且在被截线的同一方的两个角是同位角,所以①②④符合要求.解答:解:图①、②、④中,∠1与∠2在截线的同侧,并且在被截线的同一方,是同位角;图③中,∠1与∠2的两条边都不在同一条直线上,不是同位角.故选C.点评:判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两个角是同位角.9.已知∠AOB=40°,∠CDE的边CD⊥OA于点C,边DE∥OB,那么∠CDE等于( ) A. 50° B. 130° C. 50°或130° D. 100°考点:平行线的性质;垂线.专题:计算题;分类讨论.分析:作出草图,根据平行,先求出∠AED的度数,再利用垂直,即可得到∠CDE的度数.解答:解:如图,∵DE∥OB, ∴∠AED=∠AOB=40°,∵CD⊥OA,∴∠1=50°,∴∠2=130°∵∠CDE可能是∠1也可能是∠2,∴∠CDE等于50°或130°.故选C.点评:正确根据题目的叙述作出满足条件的图形,是解决这类题的有效方法;会有些同学只求出一个解,而忽视了另一个的情况导致出错.10.如图,AB∥CD∥EF,AF∥CG,则图中与∠A(不包括∠A)相等的角有( )A.5个 B. 4个 C. 3个 D. 2个考点:平行线的性质.分析:由平行线的性质,可知与∠A相等的角有∠ADC、∠AFE、∠EGC、∠GCD.解答:解:∵AB∥CD,∴∠A=∠ADC;∵AB∥EF,∴∠A=∠AFE;∵AF∥CG,∴∠EGC=∠AFE=∠A;∵CD∥EF,∴∠EGC=∠DCG=∠A;所以与∠A相等的角有∠ADC、∠AFE、∠EGC、∠GCD四个,故选B.点评:本题考查了平行线的性质,找到相等关系的角是解题的关键.11.如图所示,BE∥DF,DE∥BC,图中相等的角共有( )A.5对 B. 6对 C. 7对D.8对考平行线的性质.点:分析:分别找出两组平行得到的内错角和同位角.解答:解:∵DE∥BC,∴∠EBC=∠DEB、∠AED=∠ACB、∠ADE=∠A BC;∵BE∥DF,∴∠DFE=∠BEC、∠FDE=∠DEB、∠ADF=∠ABE、∠AFD=∠AEB;∴∠FDE=∠EBC;共8对,故选D.点评:本题主要考查两直线平行时,内错角与同位角相等,另外本题对图象的识别要求较高,需要同学们仔细,做到不重不漏.12.已知∠A=50°,∠A的两边分别平行于∠B的两边,则∠B=( )A. 50°B. 130°C.100°D.50°或130°考点:平行线的性质.专题:分类讨论.分析:根据平行线的性质,若两个角的两边互相平行,则这两个角相等或互补.解答:解:如图:∠B=50°或130°;故选D.点评:注意此题要分两种情况进行讨论,互补的情况学生可能考虑不到.13.如图所示,DE∥BC,DC∥FG,则图中相等的同位角共有( )A. 6对B. 5对C. 4对D.3对考点:平行线的性质;同位角、内错角、同旁内角.分析:根据同位角的定义,在截线的同侧,并且在被截线的同一方的两个角是同位角.解答:解:根据两直线平行,同位角相等,DE∥BC时有2对同位角:∠ADE与∠ABC,∠AED与∠ACB;DC∥FG时有3对同位角:∠ADC与∠AFG,∠BFG与∠BDC,∠BGF与∠BCD;所以在图中共有5对同位角相等.故选B.点判断是否是同位角,必须符合三线八角中,在截线的同侧,并且在被截线的同一方的两评:个角是同位角.根据两直线平行,同位角相等,来判断相等同位角的个数.14.如图所示,AD∥EF∥BC,AC平分∠BCD,图中和α相等的角有( )A.2个 B. 3个C.4个 D. 5个考点:平行线的性质;对顶角、邻补角.分析:根据平行线的性质:两直线平行同位角相等,内错角相等,以及对顶角相等,得到与α相等的角有:∠FGC=∠FCA=∠BCA=∠DAC,共4个.解答:解:∵AD∥EF∥BC,∴∠α=∠BCA=∠DAC;∵AC平分∠BCD,∴∠BCA=∠DAC;∵∠α=∠FGC,∴图中和α相等的角有4个,分别是:∠FGC=∠FCA=∠BCA=∠DAC.故选C.点评:平行线有三个性质,其基本图形都是两条平行线被第三条直线所截.解答此类题关键是在复杂图形之中辨认出应用性质的基本图形,从而利用性质和已知条件计算.15.如果两个角的两边分别平行,而其中一个角比另一个角的4倍少30°,那么这两个角是()A. 42°、138°B. 都是10°C. 42°、138°或42°、10°D. 以上都不对考点: 平行线的性质.分析:根据两边分别平行的两个角相等或互补列方程求解.解答:解:设另一个角为x,则这一个角为4x﹣30°,(1)两个角相等,则x=4x﹣30°,解得x=10°,4x﹣30°=4×10°﹣30°=10°;(2)两个角互补,则x+(4x﹣30°)=180°,解得x=42°,4x﹣30°=4×42°﹣30°=138°.所以这两个角是42°、138°或10°、10°.以上答案都不对.故选D.点评:本题主要运用两边分别平行的两个角相等或互补,学生容易忽视互补的情况而导致出错.16.把直线a沿水平方向平移4cm,平移后的像为直线b,则直线a与直线b之间的距离为()A. 等于4cmB. 小于4cm C.大于4cm D. 小于或等于4cm 考平行线之间的距离.点:专题:分类讨论.分析:分两种情况:如图(1)、如果直线与水平方向垂直,则直线a与直线b之间的距离为4cm;如图(2)、如果直线a与水平方向不垂直时,直线a与直线b之间的距离小于4cm.解答:解:根据两平行线间的距离的定义,4cm可以是直线a与直线b距离,也可以不是;故选D.点评:本题考查了直线的平移与平行线的距离,注意要分类讨论.17.(2009•宁德)在下列四个汽车标志图案中,能用平移变换来分析其形成过程的图案是( )A.B.C.D.考点:生活中的平移现象.分析:根据平移不改变图形的形状和大小,将题中所示的图案通过平移后可以得到的图案是D.解答:解:观察图形可知图案D通过平移后可以得到. 故选D.点评:本题考查了图形的平移,图形的平移只改变图形的位置,而不改变图形的形状和大小,学生易混淆图形的平移与旋转或翻转,而误选A、B、C.18.(2004•烟台)4根火柴棒摆成如图所示的象形“口”字,平移火柴棒后,原图形变成的象形文字是()A.B. C.D.考点:生活中的平移现象.分析:由平移的性质,结合图形,采用排除法判断正确结果.解答:解:原图形平移后,水平的火柴头应在左边,竖直的火柴头应是一上一下.只有B符合. 故选B.点评:本题利用了平移的基本性质:平移不改变图形的形状、大小和方向,只改变图形的位置.二.填空题(共12小题)19.已知∠α和∠β的两边互相平行,且∠α=60°,则∠β=60°或120° .考点:平行线的性质.专题:计算题;分类讨论.分析:根据两边互相平行的两个角相等或互补解答.解答:解:∵a∥b,∴∠1=∠α,∠2+∠α=180°,∵c∥d,∴∠1=∠3,∠2=∠4,∴∠3=∠α,∠4+∠α=180°,即若两角的两边互相平行,则这两个角相等或互补.∴∠β与∠α相等或互补,∵∠α=60°,∴∠β=60°或120°.故答案为:60°或120°.点评:本题从两直线平行,同位角和同旁内角两种情况考虑比较简单.20.(2004•西宁)如图,AD∥EG∥BC,AC∥EF,则图中与∠1相等的角(不含∠1)有 5 个;若∠1=50°,则∠AHG= 130 度.考点:平行线的性质;对顶角、邻补角.专题:计算题.分析:此题主要是能够结合平行线正确找到同位角、内错角以及同旁内角.解答:解:∵AD∥EG∥BC,AC∥EF,∴∠1=∠3,∠3=∠4,∠4=∠5,∠5=∠6,∠5=∠2.故∠1相等的角(不含∠1)有∠3,∠4,∠2,∠5,∠6共5个.∵∠1=50°,∴∠4=50°.则∠AHG=180°﹣50°=130°.点评:本题很简单,考查的是平行线的性质,即两直线平行内错角相等,同位角相等,及两角互补的性质.21.(2009•永州)如图,直线a、b分别被直线c、b所截,如果∠1=∠2,那么∠3+∠4=180度.直线a、b分别被直线c、b所截.考点:平行线的性质.专题: 计算题.分析:先根据∠1=∠2,判断出a∥b,再根据平线的性质便可解答.解答:解:∵直线a、b分别被直线c、b所截,∠1=∠2,∴a∥b,∴∠3+∠4=180°.点评:本题考查的是平行线的性质及平行线的判定定理,比较简单.22.(2010•抚顺)如图所示,已知a∥b,∠1=28°,∠2=25°,则∠3= 53 度.考点: 平行线的性质.专题:计算题.分析:过∠3作a的平行线,则∠1=∠4,∠2=∠5,所以∠3=∠4+∠5=53°.解答:解:过∠3的顶点作a的平行线,则也平行于b,则∠1=∠4,∠2=∠5(内错角相等),∵∠3=∠4+∠5,∴∠3=∠4+∠5=53°.所以答案是53°.点评:解答此类题,若平行线无截线,可适当构造截线转化角的关系.两直线平行时,应该想到它们的性质,由两直线平行的关系得到角之间的数量关系,从而达到解决问题的目的.23.如图,已知BO平分∠CBA,CO平分∠ACB,MN∥BC,且过点O,若AB=12,AC=14,则△AMN的周长是26 .考点:平行线的性质;角平分线的定义.专题:计算题.分析:利用角平分线的性质和平行线的性质求得MN的长就是BM+CN的长,所以三角形的周长就是AB+AC的长.解答:解:BO平分∠CBA,CO平分∠ACB,∴∠MBO=∠CBO,∠OCB=∠OCN;∵MN∥BC,∴∠MOB=∠CBO,∠NOC=∠OCB,∴∠MBO=∠MOB,∠NOC=∠NCO;∴OM=BM,CN=ON,∴△AMN的周长=12+14=26.点评:本题主要考查角平分线的性质和平行线的性质以及三角形的周长求法,合理利用图中线段的相等关系是关键.24.(1)如图1,在长方形ABCD中,AB=3cm,BC=2cm,则AB与CD之间的距离为 2 cm;(2)如图2,若∠ 1 =∠2,则AD∥BC;(3)如图3,DE∥BC,CD是∠ACB的平分线,∠ACB=50°,则∠EDC= 25 度;考点:平行线之间的距离;角平分线的定义;平行线的判定与性质.专题:计算题.分析:(1)夹在两条平行线间的垂线段的长度即为两平行线的距离.(2)运用的是平行线判定定理.(3)运用的是角平分线的定义和平行线的性质.解答:解:(1)已知四边形ABCD为长方形,则AB∥CD,∠C=90°,∠B=90°.又BC=2cm,故AB与CD之间的距离为2cm.故填2.(2)要使AD∥BC,根据平行线的判定定理可得∠1=∠2.故填∠1;∠2.(3)已知DE∥BC,根据平行线判定定理可得∠EDC=∠DCB,又CD是∠ACB的平分线,∴∠ECD=∠DCB,∵∠ACB=50°,∴∠EDC=25°.故填25.点评:此类题考查的是平行线的性质以及平行线的判定定理,考生一定要熟记.25.已知直线a∥b,点M到直线a的距离是5cm,到直线b的距离是3cm,那么直线a和直线b之间的距离为 2cm或8cm.考点:平行线之间的距离;点到直线的距离.专题:分类讨论.分析:点M的位置不确定,可分情况讨论.(1)点M在直线b的下方,直线a和直线b之间的距离为5cm﹣3cm=2cm(2)点M在直线a、b的之间,直线a和直线b之间的距离为5cm+3cm=8cm.解答:解:当M在b下方时,距离为5﹣3=2cm;当M在a、b之间时,距离为5+3=8cm.点评:本题需注意点M的位置不确定,需分情况讨论.26.如图,已知AB∥CD∥EF,BC∥AD,AC平分∠BAD,那么图中与∠AGE相等的角有 5 个.考点:平行线的性质;角平分线的定义;对顶角、邻补角.分析:由AB∥CD∥EF,可得∠AGE=∠GAB=∠DCA;由BC∥AD,可得∠GAE=∠GCF;又因为AC平分∠BAD,可得∠GAB=∠GAE;根据对顶角相等可得∠AGE=∠CGF.所以图中与∠AGE相等的角有5个.解答:解:∵AB∥CD∥EF,∴∠AGE=∠GAB=∠DCA;∵BC∥AD,∴∠GAE=∠GCF;又∵AC平分∠BAD,∴∠GAB=∠GAE;∵∠AGE=∠CGF.∴∠AGE=∠GAB=∠DCA=∠CGF=∠GAE=∠GCF.∴图中与∠AGE相等的角有5个.点评:此题考查了平行线的性质、角平分线的定义以及对顶角的性质.注意数形结合思想的应用.27.如图所示,AD∥EF∥BC,AC∥EN,则图中与∠1相等的角有5个.考点:平行线的性质.专题:计算题.分析:两直线平行,同位角、内错角相等,找到图中和∠1成这两种关系的角即可.解答:解:根据两直线平行,同位角、内错角相等可知∠1=∠ENB=∠FMC=∠AME=∠DAC=∠F EN.所以共有5个.点评:考查了平行线性质,找角时一定要找全,不重不漏.28.如图:直角△ABC中,AC=5,BC=12,AB=13,则内部五个小直角三角形的周长为30 .考点: 平移的性质.分析:由图形可知,内部小三角形直角边是大三角形直角边平移得到的,故内部五个小直角三角形的周长为大直角三角形的周长.解答:解:由图形可以看出:内部小三角形直角边是大三角形直角边平移得到的, 故内部五个小直角三角形的周长为AC+BC+AB=30.点评:主要考查了平移的性质,需要注意的是:平移前后图形的大小、形状都不改变.29.如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形,至少需要移动9格.考点:平移的性质.专题: 网格型.分析:要使平移的个数最少,可将它们朝同一方向共同移动,此时需要平移的格数最少.解答:解:如图,将网格中的三条线段沿网格线平移后组成一个首尾相接的三角形, 根据平移的基本性质知:左边的线段向右平移3格,中间的线段向下平移2格,最右边的线段先向左平移2格,再向上平移2格,此时平移的格数最少为:3+2+2+2=9,其它平移方法都超过9格,∴至少需要移动9格.点评:本题考查平移的基本概念及平移规律,是比较简单的几何图形变换.关键是要观察比较平移前后物体的位置.30.如图,面积为12cm2的△ABC沿BC方向平移至△DEF位置,平移的距离是边BC长的两倍,则图中的四边形ACED的面积是 36 cm2.考点:平移的性质.分析:根据平移的性质可以知道四边形ACED的面积是三个△ABC的面积,依此计算即可. 解答:解:∵平移的距离是边BC长的两倍,∴BC=CE=EF,∴四边形ACED的面积是三个△ABC的面积;∴四边形ACED的面积=12×3=36cm2.点评:本题的关键是得出四边形ACED的面积是三个△ABC的面积.然后根据已知条件计算.。
