1.1.2 空间向量的数量积运算(基础知识+基本题型)(含解析)(人教A版2019选择性必修第一册)
数学人教A版选择性必修第一册1.1.2空间向量的数量积运算

若 a ,b 是锐角,则 a b >0 若 a ,b 是钝角,则 a b <0
2
2
a a 即a a
2
问题2.空间向量数量积的运算律有哪些?
平面向量数量积的运算律
数乘向量与向量
数量积的结合律
ab a b
交换律
a b b a
分配律
a b c a b a c
2
2
[针对训练]已知在长方体 − 中, = = ,
= , 为侧面的中心,为的中点.求下列向量的数
量积. →
→
→
→
(1)· ;
(2)· .
例2 如图1.1 12, 在平行六面体ABCD A BC D中, AB 5, AD 3,
存在唯一的有序实数对( x , y ), 使 g xm yn,
将上式两边分别与向量l作数量积运算 ,
l
得 l g xl m yl n.
因为l m 0, l n 0, 所以l g 0. 所以l g
g
n
m
m
l
n
g
这就证明了直线l垂直于平面内的任意一条直线, 所以l .
[解析]
―→ ―→ ―→
―→ ―→
在正四面体 OABC 中,| OA |=| OB |=| OC |=1,〈 OA , OB 〉
―→ ―→
―→ ―→
=〈 OA , OC 〉=〈 OB , OC 〉=60°.
―→ ―→ ―→ ―→
(1) OA ·OB =| OA || OB |·
cos∠AOB
1
=1×1×cos 60°= .
判断或证明垂直问题
人教A版选择性必修第一册高中数学1.1.2空间向量的数量积运算精品课件

2×4×cos 135°+16λ
例题解析
例 9.在正方体 ABCD-A1B1C1D1 中,有下列说法:
→1+AD
→ +AB
→ )2=3|AB
→ |2;②A→
→
→
→
→
①(AA
1C·(A1B1-A1A)=0;③AD1与A1B的夹角为 60°.
其中说法正确的有( B )
A.1 个
B.2 个
C.3 个
D.0 个
知识梳理
三、数量积的运算规律:
注意:等式 (a b)c a (b c ) 是否成立?
不成立
练习:判断下列说法的真假.
(1)若a b 0, 则a 0或b 0;
( × )
(2)若a b b c(b 0),则a c;
( × )
2
2
(3) p q ( p q ) ;
A
知识梳理
投影向量
(1)投影向量
在空间,向量 a 向向量 b 投影,可以先将它们平移到同一个平面内,
进而利用平面上向量的投影,得到与向量 b 共线的向量 c,
b
c=|a|cos〈a,b〉|b|,则向量 c 称为向量 a 在向量 b 上的投影向量,
a
同理向量 b 在向量 a 上的投影向量是|b|cos〈a,b〉
A.0
B.-2
C.2
D.-3
1
1
→
→
→
→
如图所示.在棱长为 2 的正四面体 ABCD 中,因为 E,F 分别是棱 BC,AD 的中点,所以AE·CF= (AB+AC)·
2
2
1
1
→
→
→
→
空间向量的数量积运算- (人教A版2019选择性必修第一册)

【题型归纳】
题型一:空间向量的数量积的运算
1.已知空间中非零向量 , ,且 , , ,则 的值为().
15.已知平行六面体 中, , , , , .则 的长为()
A. B. C. D.
16.如图在长方体 中,设 , ,则 等于()
A.1B.2C.3D.
【高分突破】
一:单选题
17.已知空间向量 ,0, , ,2, ,则向量 在向量 上的投影向量是()
A. ,2, B. ,2, C. ,0, D. ,0,
D:由图知: ,正方体 的体积不为 ,错误;
故选:AB.
26.BC
如下图所示:
对于A选项, ,A选项错误;
对于B选项, ,B选项正确;
对于C选项, ,C选项正确;
对于D选项, ,D选项错误.
故选:BC.
27.AB
【详解】
由向量的加法得到: ,∵ ,∴ ,所以A正确;
∵ ,AB1⊥A1C,∴ ,故B正确;
对于④,由空间向量数量积的运算性质可得 ,④正确.
故选:B.
21.D
【详解】
解:在平行六面体 中,因为 ,所以 .
所以 .
22.A
【详解】
记 , , ,
因为 , ,
所以 , .
又因为 , ,
所以 , .
易得 ,
所以 ,
所以 .
故选:A
23.B
解:因为底面 是边长为1的正方形,侧棱 且 ,
则 , , , , , ,
数学人教A版(2019)选择性必修第一册 空间向量的数量积运算

向量来分析,看条件可以转化为向量的什么条件?要证
的目标可以转化为向量的什么目标?怎样建立向量的
条件与向量的目标的联系?
证明: 在 内作任一直线, 分别在, , , 上
取非零向量,Ԧ , , .
Ԧ
因为与相交, 故向量, 不平行, 由向量共
m
gl
面的充要条件知, 存在惟一的有序实数对
以上命题中的真命题是
)
D (
A.(1)(2)
C.(3)(4)
B.(2)(3)
D.(2)(4)
՜
՜
՜
՜
2、已知向量 , 满足 = 1,
՜1
՜
= 2, − = 3, 则
՜
՜
+ =___________
课堂小结
通过学习,体会到我们可以利用向量
数量积解决立体几何中的以下问题:
m
, ), 使Ԧ = + ,
g
n
n
将上式两边与向量l作数量பைடு நூலகம்,得
Ԧ × Ԧ = Ԧ × + Ԧ × .
因为Ԧ × = 0, Ԧ × = 0,
所以Ԧ × Ԧ = 0, 即Ԧ ⊥ .
Ԧ 所以 ⊥ ,
即垂直于平面内任一直线. 所以 ⊥ .
阶段检测(二)
b=
|a|·
|b| ______;若反向,则
-|a|·|b|
向量 a·b = ________.
|a|2
·
数量 特别地,a·a =____或 |a|a·
b
=
|a||b|
积的
③若θ为a,b的夹角,则cos θ=_______
性质
④|a·b| ≤ |a|·|b|
1.1.2空间向量的数量积运算2024-2025学年高二上学期数学人教A版(2019)选择性必修一

a
a
c
b
称为向
投影向量
向量a向直线l投影
a
a
c
l
投影向量
在空间,向量向平面β投影,分别由向量的起点和终点作平面的垂
线,得到向量’ ’ ,向量’ ’ 称为向量在平面上的投影向量. 向量,’ ’
的夹角就是向量所在直线与平面β所成的角.
A
a
a
A
c
B
B
例 题
如图,在平行六面体ABCD-A'B'C'D'中,AB=5,AD=3,AA'=7,
数量积运算求模长,是立体几何
中求线段长度的常用向量方法.
A
B
(1) AA ' AB
(2) AB的长
(3) AC '的长
总结归纳
✓ 空间向量数量积运算的定义;
✓ 空间向量数量积运算的运算律;
✓ 空间向量数量积运算的应用.
例 题
l
如图,,是平面内的两条相交直线.如果
⊥ , ⊥ ,求证: ⊥ .
不能,没有定义向量的除法运算.
(或
=
(或
=
).对
)的形式?
思 考
3.对于三个均不为0的数,,,有() = (). 对于向量
,,,( ∙ ) = ( ∙ )成立吗?为什么?
不成立,向量的数量积不满足结合律.
例如,任意取三个不共面的向量,,,( ∙ )是一个数与向
∠AOB
OB =b,则_______=θ
范围:________
0≤θ≤π
B
b
bห้องสมุดไป่ตู้
第02讲 1.1.2空间向量的数量积运算(教师版)
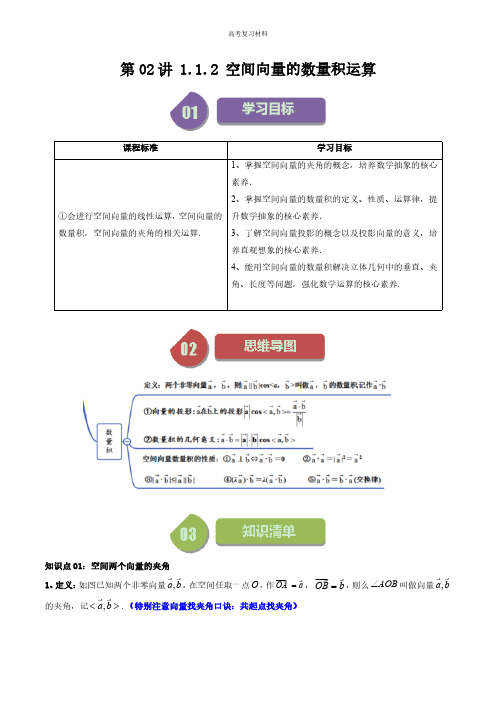
r r的投影.所成的角.量积的几何意义:向量a r ,b r 的数量积等于a r 的长度||a r 与b r 在的乘积或等于br 的长度||b r 与a r 在b r方向上的投影||cos ,a a b <>r r r 的乘积、数量积的运算:()a b ×r r,R λÎ.A .1-B .1【答案】B【详解】由题意得1BD BA =uuuu r uuu r 则11(BD AC AD AB AA ×=-+uuuu r uuu r uuu r uuu r uuur 1111cos6011cos60=-+´´+´´o B故12EF DC BD DC ×=×=uuu r uuu r uuu r uuu r 故答案为:14-【变式1】(2024秋·浙江绍兴AB AM ×=uuu r uuuu r( )【答案】2,22éùêúëû【详解】由已知E 为棱1B C 因为111AE AB B E AB =+=u u u r u u u r u u u r u u u r 所以(AE AC AB BB ×=++u u u r u u u r u u u r u u u r 【答案】18-/-0.125因PA^平面ABC,BC 则BC^平面PAB,又【答案】66.【详解】记AB a uuu r r=,AD b =uuu r r ,1AA =uuur 12a b b c a c \×=×=×=r r r r r r ,BD b c a =+-uuuu r r r r Q ,AC a b =+uuu r r r ,(1)求EF uuu r的模长;(2)求EF uuu r ,GH uuur的夹角【答案】(1)22;(1)1AC 的长;【答案】22【详解】棱长为1的正方体ABCD 所以1111AB A C A C =×uuu r uuuu ruuuu r 11cos ,AB A C AB ×uuu r uuuu r uuu 向量 AB uuu r在向量 11AC uuuu r 方向上的投影向量是uuu r uuuu r uuuu r uuuu r【答案】32 BC uuu r【详解】PA^Q平面ABC,则PA BC^,()PC BC PA AB BC BC ×=++×= uuu r uuu r uuu r uuu r uuu r uuu r向量uuu r在uuu r上的投影向量为【典例2】(2024春·,,60a c b c ==°r r r r,则A .5B 【答案】D【详解】因为a b ^r r ,(1)用,,OA OB OC uuu r uuu r uuu r 表示OM uuuu r,并求出(2)求证:OM BC ^.【答案】(1)1126OM OA OB =+uuuu r uuu r uuu r (2)证明见解析【详解】(1)因为点G 是OBC △(1)EF ^平面11BB D D ;(2)平面1EFB ^平面11C D M 【答案】(1)证明见解析(2)证明见解析【详解】(1)正方体ABCD(1)求线段1CA 的长;(2)求证:111CA B D ^.【答案】(1)11(2)证明见解析【详解】(1)设,CD a CB =uuu r r uuu r (1)求A B '和B C '的夹角;(2)求证:A A B C ''^.【答案】(1)60°(2)证明见解析【详解】(1)AB a uuu r r=,AD uuu r则(1PA PC PO ×=+uuu r uuuu r uuu r uuu Q 当P 为侧面1ABB 又11122OA AC ==uuu r uuuu r【详解】如图所示,在边长为1的正四面体CDEF 内切球半径为r ,取EF 中点为G ,13142-=,12333DO DG ==0DEF O CDE O CDF CEF V V V V ---=+++11143DEF DEF CO S OO ´=´´△△,所以设外接球球心为O,则uuuu r uuu r uuuu22=-=|||||MO OE MO由于点M在正方体的棱上运动即为正方体面对角线的一半,为uuur uuur的最小值为由题知,22216,9,AB AD AA '===uuu r uuu r uuur 43cos900AB AD ×=´´°=uuu r uuu r,AB AA ×uuu r uuur 1535cos 602AD AA '×=´´°=uuu r uuur .AC AB AD AA ''=++uuuu r uuu r uuu r uuur Q ,A .14-【答案】D【详解】如图,因为D 为棱AB 的中点,所以()(1122P P C P A PB PA =××+=uuur uuu r uuu r uuu r uuuA.4B.5【详解】AM ,由棱柱性质,侧棱1AA ^2211415AA A M +=+=,又()()(1122AN AM AN AM =+×-=uuu r uuuu r uuu r uuuu rA .112333MN a b c=++uuuu r r r r C .111A B A C ^uuur uuuu r【答案】BD【详解】因为12BM A M =,1C N =11uuuur uuur uuu r uuurA. 由向量的加法运算得1A A uuur 确;B. 正方体的性质易知1A C ^C. 因为11A BC V 是等边三角形,且D. 由正方体的性质得过1,A D【答案】9【详解】因为1BB ^平面ABC 所以,(1EF BB EA AA ×=+uuu r uuur uuu r uuur 211111122BA BB BB A C =×++uuur uuur uuur uuuu r 故答案为:9.12.(2024秋·山东菏泽·高二统考期末)如图所示,在平行六面体【答案】12+/21+【详解】向量的拆分,11112D E AE AD AA =-=+u u u u r u u u r u u u u r u u u r 122cos 23AA AB AD p =×=´´=u r u u u r u u u r ,22211124AB AA AD AB AA ++-×-u u r u u u r u u u r u u u r u u u r【答案】AB uuu r,2a 【详解】因为PC AB ×uuu r uuu 又||AB a =uuu r,所以PC uuu r 在AB uuu r上的投影向量为:uuu r uuu r uuu r 【答案】证明见解析【详解】因为CD OA ^,所以因为AB α^,CD αÌ,所以又OA AB OB +=uuu r uuu r uuu r,所以CD OB ×uuu r uuuA .1B .2C .3D .【答案】C【详解】解:过B 和D 分别作BE AC ^,DF AC ^,Q 在矩形,1,3ABCD AB BC ==,\Q ABC ADC S S =△△,1122AB BC AC \×=32BE DF \==,则1AE CF ==,即211EF =-=,(1)试用向量,,a b c r r r 表示向量OE uuu r;(2)若4,3,OA OC OB AOC Ð===【答案】(1)111236OE a b c =++uuu r r r r;(2)83-.【详解】(1)因为点E 为AD 的中点,所以(1)确定PC uuu r在平面ABC (2)确定PC uuu r 在AB uuu r上的投影向量,并求【答案】(1)PC uuu r在平面(2)PC uuu r 在AB uuu r 上的投影向量为【详解】(1)因为A .1111AB AC AD D B ´=´uuur uuu r uuuu r uuuur C .111A C A D ´uuuu r uuuu r 与1BD uuuu r 共线【答案】ACD【详解】设正方体棱长为1,3.(2024春·上海杨浦·高二上海市控江中学校考期中)在空间中,不共面的向量,且它们两两之间的夹角都是锐角uuu r uuu r uuu r【答案】10【详解】作母线CEAF CE,所以因为//EC^平面ABC,又由已知得AC^所以BC^平面ACEF5.(2024春·江苏常州Ð=Ð形,且1C CB【答案】1【详解】解:如图所示:设1,0CD x x CC =>,11CC =,则因为1A C ^平面1C BD ,11,C B C D Ì平面1C BD ,所以11C D C C CD =+u u u u r u u u u r u u u r ,11A C A =u u u r u u 由110A C C D ×=u u u r u u u u r ,得(AD +u u u r。
1.1.2空间向量的数量积运算2024-2025学年高二上学期数学人教A版(2019)选择性必修一

6. 如图,已知E,F,G,H 分别为四面体ABCD 的棱AB,BC,CD,DA
的
中点,求证: E,F,G,H
四点共面 .
证明:E,H 分别为AB,AD 的中点,
又F,G 分别为BC,CD 的中点,
∴EH=FG,∴E,F,G,H 四点共面
(第6题)
7.如图,正方体ABCD-A'B'C'D '的棱长为a.
(1)AA'·AB; (2)AB '的长;
(3)AC'的长.
(1)AA·AB=AA
(2)∵AB'=AB+AA',
= √16+2×10+25= √61, 即AB'的长为√61;
(第3题)
3.如图,在平行六面体ABCD-A'B'C'D '中,AB=4,AD=3,AA'=5,
∠BAD=90°,∠BAA'=∠DAA'=60°. 求:
环节四辨析理解深化概念 例2如图1.1-12,在平行六面体ABCD-A'B'CD '中,AB=5,AD=3,
AA'=7,∠BAD=60°,∠BAA'=∠DAA'=45°.
求(1)AB·AD;(2)AC '的长(精确到0.1).
(1)AB·AD=AB AD cos(AB,AD) =5×3×cos60°=7.5,
设a是非零向量,且b≠c,求证:a·b=a·c ⇔b-c)⊥a B
a.b=a·c ⇔a.b-a·c=0
⇔a.(b-c)=0 →(b-c)⊥a
思考
2.对于三个均不为0的数a,b,c,若ab=c, 则 (或
人教A版选择性必修第一册1.1.2空间向量的数量积运算课件

2
探究二:空间向量的数量积
已知两个非零向量 a,b,则 | a || b | cosa, b 叫做 a,b 的数量积, 记作 a b .即 a b | a || b | cosa,b . 特别地,零向量与任意向量的数量积为 0. 由向量的数量积定义,可以得到: a b a b 0 ; a a | a || a | cosa,a | a |2 .
B.45° D.以上都不对
解析
设 a 与 b 的夹角为 .由 a b c 0 ,得 a b c , 两边平方,得 a2 2a b b2 c2 ,所以 4 2 23cos 9 16 , 解得 cos 1 ,故选 D.
4
练一练
3.已知 a (1,2, y) , b (x,1,2) ,且 (a 2b)//(2a b) ,则( B )
A. x 1 , y 1 3
C. x 2 , y 1 4
B. x 1 , y 4 2
D. x 1, y 1
解析
由题意可得, a 2b (1 2x,4,4 y) , 2a b (2 x,3,2y 2) .
(a 2b)//(2a b) ,
R ,使 a 2b (2a b) ,
1 2x (2 x),
4 3
,
得
4 4
3, y
(2
y
2),
解得
x y
1, 2 4,
故选
B.
练一练
4.已知 a (cos,1,sin),b (sin,1,cos) ,若 a b ,
1.1.2 空间向量的数量积运算课件高二上学期数学人教A版(2019)选择性必修第一册

∴异面直线 BA1 与 AC 成 60°角.
利用数量积证明垂直关系
例 如右图,m,n是平面α内的两条相交直线.如果l⊥m, l⊥n,求证: l⊥平面α;
追问(1) 直线和平面垂直的定义是什么?
如果直线l和平面α内的任意一条直线都垂直, 则直线l垂直于平面α .
l
g n
• 向量a向直线l投影:
• 向量a向平面β投影:
B a A
A1 c B1
注:向量a与投影向量c的夹角 就是向量a所在的直线与平面β 所成的角
空间向量的投影向量
空间向量的投影向量
将空间向量a,b ,平移到 同一个平面α内,利用平面上 向量的投影得到与向量b共线 的向量c,即:
c =|a|cos〈a,b〉b ,
• 分配律a·(b+c)=a·b+a·c的证明
B
c
C
b
O B’
C’ A
a
左边= | OA || OC ' |
OB向OA投影,投影向量为OB ' 记OB与OA的夹角为1 同理,BC向OA投影,投影向量为B 'C ' 记BC与OA的夹角为2
右边 OAOB OA BC
= | OA || OB | cos1 | OA || BC | cos2 = | OA || OB ' | | OA || B 'C ' |
g n
m
α
l
lm gn
练习 在三棱锥S-ABC中,SA⊥BC,SB⊥AC,求证:SC⊥AB.
解:
S
A
C
B
课堂小结
回顾本节课的学习过程,你学到了什么?
1 数量积运算解决立体几何问题 (1) 求空间中两点间的距离或线段长度:求对应的向量的模 (2) 求空间中两条异面直线所成的角:求对应的两个向量的夹角 (3) 证明线线垂直问题:对应的两向量的数量积为零
1.1.2空间向量的数量积运算课件(人教版)

空间向量的数量积
8.已知空间四边形ABCD中,AB⊥CD,AC⊥BD,求证:AD⊥BC.
∵AB⊥CD,AC⊥BD,
∴ AB ·CD =0, AC ·BD =0.
∴ AD ·BC =( AB + BD )·( AC - AB )
= AB ·AC + BD ·AC - AB 2 - AB ·BD
= AB ·AC - AB 2 - AB ·BD
人教A版2019选修第一册
第 1 章空间向
量与立体几何
1.1.2 空间向量的数量积运算
学习目标
1.掌握空间向量的夹角的概念.
2.掌握空间向量的数量积的定义、性质、运算律.
3.了解空间向量投影的概念以及投影向量的意义.
4.能用空间向量的数量积解决立体几何中的垂直、夹角、长度等问题,
强化数学运算的核心素养.
其次利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积;
最后利用数量积的定义求解即可.
空间向量的数量积
5.已知正四面体OABC的棱长为1.求:
(1)OA·
OB;(2)(OA+OB)·
(CA+CB).
空间向量的数量积
6.如图,在直三棱柱ABCA1B1C1中,∠BCA=90°,CA=CB=1,棱AA1=2,点N为AA1的中点.
∴(2e1+3e2)·
(ke1-4e2)=0,
∴2k-12=0,∴k=6.
空间向量的数量积
4.如图,已知空间四边形ABCD的每条边和对角线长都等于1,点E,F分别是AB,AD的中点,计算:
(1)EF·
BA;(2)EF ∙ BD;(3) EF·
DC.
空间向量的数量积
在几何体中求空间向量的数量积:
高二上学期数学人教A版选择性必修第一册1.1.2空间向量的数量积运算课件

1B→(DA→B=+A→DA→D-)A→=Bc+=1b-a+a,1 b,
→2 OG
=O→C
+C→G
=12
→ (AB
2
2+A→D
)+12
→ CC1
=1 2
a+12
b-12
c,
因为A1O =A1A +AO =A1A +
所12以(A→A→B1O+·AB→D
=)=( c+12
a+1 2
b),·(b-a)
=c·b-c·a+1 a·b-1 a2+1 b2-1 b·a
数乘向量与向量数量积的结 合律
交换律
(λa)·b=_λ_(_a_·b_)__,λ∈R a·b=_b_·_a_
分配律
(a+b)·c=_a_·_c_+__b_·c__
(3). 空间向量的数量积的性质
①若a,b是非零向量,则a⊥b⇔_a_·_b_=__0_ 两个 向量 ②若a与b同向,则a·b=_|_a_|·_|b_|_;若反向,则a·b=_-__|a_|·_|b_|__. 数量 ③特别地,a·a=_|_a_|2_ 积的
2
222
=1 (b2-a2)=1 (|b|2-|a|2)=0.
2
2
于是A→1O ⊥B→D ,即 A1O⊥BD.
同理可证A→1O ⊥O→G ,即 A1O⊥OG.
又因为OG∩BD=O,OG⊂平面GBD,BD⊂平面GBD, 所以A1O⊥平面GBD.
已知在空间四边形OABC中,∠AOB=∠BOC=∠AOC,且OA=OB
→→
→→
→→
→→
(1)EF ·BA ;(2)EF ·BD ;(3)EF ·DC ;(4)AB ·CD .
A E B
C
→ (1)EF
2022-2023人教A版高二数学上学期同步讲义1-1-2空间向量的数量积运算

1.1.2 空间向量的数量积运算课程标准课标解读1.会进行空间向量的线性运算,空间向量的数量积,空间向量的夹角的相关运算. 1.理解空间向量的相关概念的基础上进行与向量的加、减运算、数量积的运算、夹角的相关运算及空间距离的求解.知识点1 空间向量的夹角定义如图,已知两个非零向量a,b,在空间任取一点O,作OA→=a,OB→=b,则∠AOB叫做向量a,b的夹角,记作〈a,b〉范围0≤〈a,b〉≤π向量垂直如果〈a,b〉=π2,那么向量a,b互相垂直,记作a∠b拓展提升:(1)当两个非零向量同向时,它们的夹角为多少度?反向时,它们的夹角为多少度?只有两个非零空间向量才有夹角,当两个非零空间向量共线同向时,夹角为0,共线反向时,夹角为π.(2)〈a,b〉,〈-a,b〉,〈a,-b〉,〈-a,-b〉,它们有什么关系?对空间任意两个非零向量a,b有:∠〈a,b〉=〈b,a〉;∠〈-a,b〉=〈a,-b〉;∠〈-a,-b〉=〈a,b〉.【即学即练1】在正四面体ABCD 中,BC →与CD →的夹角等于( ) A .30° B .60° C .150° D .120°【解析】〈BC →,CD →〉=180°-〈CB →,CD →〉=180°-60°=120°.故选D知识点2 空间向量的数量积运算1.(1)空间向量的数量积已知两个非零向量a ,b ,则|a ||b |cos 〈a ,b 〉叫做a ,b 的数量积,记作a ·b ,即a ·b =|a ||b |·cos 〈a ,b 〉.零向量与任意向量的数量积为0,即0·a =0. (2)运算律2.投影向量及直线与平面所成的角(1)如图∠,在空间,向量a 向向量b 投影,由于它们是自由向量,因此可以先将它们平移到同一个平面α内,进而利用平面上向量的投影,得到与向量b 共线的向量c ,c =|a |cos 〈a ,b 〉b|b |,向量c 称为向量a 在向量b 上的投影向量.类似地,可以将向量a 向直线l 投影(如图∠).(2)如图∠,向量a 向平面β投影,就是分别由向量a 的起点A 和终点B 作平面β的垂线,垂足分别为A ′,B ′,得到向量A ′B ′——→,向量A ′B ′——→称为向量a 在平面β上的投影向量.这时,向量a ,A ′B ′——→的夹角就是向量a 所在直线与平面β所成的角.注意点:(1)向量a ,b 的数量积记为a ·b ,而不能表示为a ×b 或者ab .(2)向量的数量积的结果为实数,而不是向量,它可以是正数、负数或零,其符号由夹角θ的范围决定.∠当θ为锐角时,a ·b >0;但当a ·b >0时,θ不一定为锐角,因为θ也可能为0. ∠当θ为钝角时,a ·b <0;但当a ·b <0时,θ不一定为钝角,因为θ也可能为π. (3)空间向量的数量积运算不满足消去律和结合律.【即学即练2】在棱长为1的正方体1111ABCD A B C D -中,设AB a =,AD b =,1AA c =,则()a b c ⋅+的值为( ) A .1B .0C .1-D .2-【解析】()0a b c a b a c ⋅+=⋅+⋅=.故选B .【即学即练3】如图,正方体ABCD A B C D ''''-的棱长为1,设AB a =,AD b =,AA c '=,求:(1)()a b c ⋅+;(2)()a a b c ⋅++;(3)()()a b b c ⋅++.【解析】(1)在正方体中,AB AA ⊥',AB AD ⊥ 故()0a b c a b a c →→→→→→→⋅+=⋅+⋅=(2)由(1)知,()()1a a b c a a a b c →→→→→→→→→⋅++=⋅+⋅+= (3)由(1)及AD AA '⊥知,2()()()1a b b c a b c b b c →→→→→→→→→→++=⋅+++⋅=【即学即练4】如图,在三棱锥P ABC -中,,,AP AB AC 两两垂直,2,1,AP AB AC M ===为PC 的中点,则AC BM ⋅的值为( )A .1B .13C .14D .12【解析】由题意得()111222BM BA AM BA AP AC BA AP AC =+=++=++,故1122AC BM AC BA AP AC ⎛⎫⋅=⋅++ ⎪⎝⎭211112222AC BA AC AP AC AC AC =⋅+⋅+⋅==.故选:D.知识点3 空间向量数量积的性质(1)若a ,b 为非零向量,则a ∠b ∠a ·b =0; (2)a ·a =|a |2或|a |=a ·a =a 2;(3)若a ,b 为非零向量,则cos 〈a ,b 〉=a ·b|a ||b |;(4)|a ·b |≤|a ||b |(当且仅当a ,b 共线时等号成立).【即学即练5】已知在平行六面体ABCD -A 1B 1C 1D 1中,AA 1=AB =AD =1,且这三条棱彼此之间的夹角都是60°,则AC 1的长为( ) A .6 B. 6 C .3 D.3【解析】设AB →=a ,AD →=b ,AA 1→=c , 则|a|=|b |=|c |=1,且〈a ,b 〉=〈b ,c 〉=〈c ,a 〉=60°, 因此a·b =b ·c =c ·a =12.由AC 1→=a +b +c ,得|AC 1→|2=AC 1→2=a 2+b 2+c 2+2a ·b +2b ·c +2c ·a =6.所以|AC 1→|= 6.故选B【即学即练6】已知12,e e 是夹角为60°的两个单位向量,则a =1e +2e 与b=1e -22e 的夹角是( )A .60°B .120°C .30°D .90°【解析】由题意得a b =(1e +2e )·(1e -22e )=21e 12·2--e e 22e 111122=-⨯⨯-=32-,|a |=2222121122()21113a e e e e e e =+=+⋅+=++=,|b |=2222121122(2)441243b e e e e e e ==++---⋅==.cos ,a b ∴=323||||a b a b -⋅==12-. ,120a b ∴=°.故选:B.【即学即练7】在空间四边形OABC 中,连接AC ,OB ,OA =8,AB =6,AC =4,BC =5,∠OAC =45°,∠OAB =60°,求向量OA 与BC 所成角的余弦值.【解析】BC AC AB =-,cos ,cos ,OA BC OA AC OA AB OA AC OA AC OA AB OA AB ∴⋅=⋅-⋅=⋅⋅<>-⋅⋅<>=8×4×cos 135°-8×6×cos120°=24-162, ∠24162cos ,85OA BC OA BC OA BC⋅-<>===⨯⋅3225- 故答案为:3225- 考点一 空间向量数量积的概念辨析解题方略:注意空间向量的夹角的定义及熟练掌握数量积的运算律【例1-1】对于空间任意两个非零向量a ,b ,“a ∠b ”是“〈a ,b 〉=0”的( ) A .充分不必要条件 B .必要不充分条件 C .充要条件D .既不充分也不必要条件【解析】显然〈a ,b 〉=0∠a ∠b ,但a ∠b 包括向量a ,b 同向共线和反向共线两种情况,即当a ∠b 时,〈a ,b 〉=0或π,因此a ∠b ∠〈a ,b 〉=0.故“a ∠b ”是“〈a ,b 〉=0”的必要不充分条件.故选B【例1-2】如图,在正方体ABCD -A ′B ′C ′D ′中,求向量AC →分别与向量A ′B ′——→,B ′A ′——→,AD ′—→,CD ′—→,B ′D ′——→的夹角.【解析】连接BD (图略),则在正方体ABCD -A ′B ′C ′D ′中,AC ∠BD ,∠BAC =45°,AC =AD ′=CD ′,所以〈AC →,A ′B ′——→〉=〈AC →,AB →〉=45°,〈AC →,B ′A ′——→〉=180°-〈AC →,AB →〉=135°,〈AC →,AD ′→〉=∠D ′AC =60°,〈AC →,CD ′—→〉=180°-〈CA →,CD ′—→〉=180°-60°=120°,〈AC →,B ′D ′——→〉=〈AC →,BD →〉=90°. 【例1-3】设a 、b 为空间中的任意两个非零向量,有下列各式: ∠22a a =;∠2a b b aa⋅=;∠()222a ba b ⋅=⋅;∠()2222a ba ab b -=-⋅+.其中正确的个数为( ) A .1B .2C .3D .4【解析】对于∠,222cos 0a a a ==,∠正确;对于∠,向量不能作比值,即ba错误,∠错误;对于∠,设a 、b 的夹角为θ,则()()2222222cos cos a ba b a b a b θθ⋅=⋅=⋅≤⋅,∠错误;对于∠,由空间向量数量积的运算性质可得()2222a b a a b b -=-⋅+,∠正确.故选:B.考点二 空间向量数量积的运算解题方略:求空间向量数量积的步骤(1)将待求数量积的两向量的模长及它们的夹角理清;(2)利用向量的运算律将数量积展开,转化为已知模和夹角余弦值的乘积; (3)代入a ·b =|a ||b |cos 〈a ,b 〉求解.注:在几何体中求空间向量的数量积,首先要充分利用向量所在的图形,将各向量分解成已知模和夹角的向量的组合形式;其次利用向量的运算律将数量积展开,转化为已知模和夹角的向量的数量积;最后利用数量积的定义求解即可.注意挖掘几何体中的垂直关系或特殊角.【例2-1】已知a =3p -2q ,b =p +q ,p 和q 是相互垂直的单位向量,则a·b =( ) A .1 B .2 C .3D .4【解析】∠p ∠q 且|p |=|q |=1,∠a ·b =(3p -2q )·(p +q )=3p 2+p ·q -2q 2=3+0-2=1.故选A 【例2-2】已知四面体A -BCD 的所有棱长都是2,点E,F 分别是AD,DC 的中点,则EF BA ⋅=( ) A .1B .-1C .3D .3-【解析】由题意可得12EF AC =,所以1122cos120122EF BA AC BA ⋅=⋅=⨯⨯⨯︒=-.故选B .变式1:已知正四面体OABC 的棱长为1,如图所示.求: (1)OA ―→·OB ―→;(2)(OA ―→+OB ―→)·(CA ―→+CB ―→).【解析】在正四面体OABC 中,|OA ―→|=|OB ―→|=|OC ―→|=1. 〈OA ―→,OB ―→〉=〈OA ―→,OC ―→〉=〈OB ―→,OC ―→〉=60°. (1)OA ―→·OB ―→=|OA ―→||OB ―→|cos∠AOB =1×1×cos 60°=12.(2)(OA ―→+OB ―→)·(CA ―→+CB ―→)=(OA ―→+OB ―→)·(OA ―→-OC ―→+OB ―→-OC ―→) =(OA ―→+OB ―→)·(OA ―→+OB ―→-2OC ―→)=OA ―→2+2OA ―→·OB ―→-2OA ―→·OC ―→+OB ―→2-2OB ―→·OC ―→ =12+2×1×1×cos 60°-2×1×1×cos 60°+12-2×1×1×cos 60° =1+1-1+1-1 =1.变式2:已知正四面体OABC 的棱长为1,若E ,F 分别是OA ,OC 的中点,求值: (1)EF ―→·AO ―→;(2)EF ―→·AC ―→;(3)EF ―→·CB ―→. 【解析】(1)EF ―→·AO ―→=12AC ―→·AO ―→=12|AC ―→||AO ―→|cos 〈AC ―→,AO ―→〉 =12cos 60°=14. (2)EF ―→·AC ―→=12AC ―→·AC ―→=12|AC ―→|2=12.(3)EF ―→·CB ―→=12AC ―→·CB ―→=12|AC ―→||CB ―→|cos 〈AC ―→,CB ―→〉=12cos 120°=-14.变式3:已知棱长为1的正方体ABCD A 1B 1C 1D 1的上底面A 1B 1C 1D 1的中心为O 1,则AO 1―→·AC ―→的值为( ) A .-1 B .0 C .1D .2【解析】AO 1―→=AA 1―→+A 1O 1――→=AA 1―→+12(A 1B 1―→+A 1D 1―→)=AA 1―→+12(AB ―→+AD ―→),AC ―→=AB ―→+AD ―→,则AO 1―→·AC―→=12(|AB ―→|2+|AD ―→|2)=1,故选C. 【例2-3】已知空间向量a ,b ,c 满足a +b +c =0,|a |=3,|b |=1,|c |=4,则a ·b +b ·c +c ·a 的值为________. 【解析】∠a +b +c =0,∠(a +b +c )2=0, ∠a 2+b 2+c 2+2(a ·b +b ·c +c ·a )=0, ∠a ·b +b ·c +c ·a =-32+12+422=-13.考点三 利用空间向量的数量积求夹角解题方略:1、求两个向量的夹角有两种方法:①结合图形,平移向量,利用空间向量夹角的定义来求,但要注意向量夹角的范围;②先求a ·b ,再利用公式cos 〈a ,b 〉=a ba b求出cos 〈a ,b 〉的值,最后确定〈a ,b 〉的值.2、利用数量积求夹角或其余弦值的步骤注:求两向量夹角,必须特别关注两向量方向,应用向量夹角定义确定夹角是锐角、直角还是钝角.【例3-1】如图,在正方体ABCD A 1B 1C 1D 1中,求BC 1―→与AC ―→夹角的大小.【解析】不妨设正方体的棱长为1,则BC 1―→·AC ―→=(BC ―→+CC 1―→)·(AB ―→+BC ―→)=(AD ―→+AA 1―→)·(AB ―→+AD ―→) =AD ―→·AB ―→+AD ―→2+AA 1―→·AB ―→+AA 1―→·AD ―→ =0+AD ―→2+0+0=AD ―→2=1, 又∠|BC 1―→|=2,|AC ―→|=2,∠cos 〈BC 1―→,AC ―→〉=BC 1―→·AC ―→|BC 1―→||AC ―→|=12×2=12.∠〈BC 1―→,AC ―→〉∠[0,π],∠〈BC 1―→,AC ―→〉=π3.即BC 1―→与AC ―→夹角的大小为π3.变式1:已知空间四边形OABC 中,OB =OC ,∠AOB =∠AOC =π3,则cos 〈OA →,BC →〉的值为( )A.12B.22 C .-12D .0 【解析】OA →·BC →=OA →·(OC →-OB →)=OA →·OC →-OA →·OB →=|OA →||OC →|cos∠AOC -|OA →||OB →|cos∠AOB =12|OA →||OC →|-12|OA →||OB →|=0, 所以OA →∠BC →.所以cos 〈OA →,BC →〉=0. 故选D变式2:在边长及对角线都为1的空间四边形ABCD 中,E ,F 分别是BC ,AD 的中点,则直线AE 和CF夹角的余弦值为( ) A .23-B .23C .34D .12【解析】如图,连接对角线BC ,AD ,则可构成棱长均为1的正四面体A BCD - 由E ,F 分别是BC ,AD 的中点,()12AE AB AC ∴=+,()12CF CA CD =+()()()1144AE CF AB AC CA CD AB CA AC CA AB CD AC CD ∴⋅=++=⋅+⋅+⋅+⋅()11111112422424AB CD AB CD AB CD ⎛⎫=--+⋅-=-+⋅=-+⋅ ⎪⎝⎭又()11022AB CD AB AD AC AB AD AB AC ⋅=⋅-=⋅-⋅=-=,12AE CF ∴⋅=- 则12cos ,33AE CF AE CF AE CF⋅===⋅ 所以直线AE 和CF 夹角的余弦值为23. 故选:B变式3:如图,在平行六面体1111ABCD A B C D -中,以顶点A 为端点的三条棱长度都为1,且两两夹角为60.求:(1)1AC 的长;(2)1BD 与AC 夹角的余弦值.【解析】(1)记AB a =,AD b =,1AA c =,则1a b c ===,,,,60a b b c a c <>=<>=<>=,12a b b c a c ∴⋅=⋅=⋅=, ()()222221323262AC a b ca b c a b b c a c ∴=++=+++⋅+⋅+⋅=+⨯=,16AC ∴=1AC ; (2)1BD b c a =+-,AC a b =+,()222212312BD b c a b c a b a c ∴=+++⋅-⋅-⋅=-=,22223AC a b a b =++⋅=,12BD ∴=,3AC =()()2211BD AC b c a a b b a b c a c ⋅=+-⋅+=-+⋅+⋅=, 111cos ,2BD AC BD AC BD AC⋅∴<>===⋅1BD 与AC 【例3-2】已知a ,b 是空间两向量,若3,2,7a b a b ==-=,则a 与b 的夹角为______. 【解析】设a 与b 的夹角为θ,所以根据2222cos a b a b a b θ-=+-⋅⋅,794232cos θ=+-⨯⨯⨯,即1cos 2θ=, 又0πθ≤≤,π3θ∴=. 故答案为:π3变式1:已知m →,n →是两个空间单位向量,它们的夹角为60,设向量2a m n →→→=+,32b m n →→→=-+.求: (1)a b →→⋅;(2)向量a →与b →的夹角.【解析】(1)因为m →,n →是两个空间单位向量,它们的夹角为60, 所以1cos 602m n n m →→→→⋅==, 所以2217232626222a b m n m n m m n n →→→→→→→→→→⎛⎫⎛⎫⋅=+⋅-+=-+⋅+=-++=- ⎪ ⎪⎝⎭⎝⎭;(2)因为2222124444172a m n m m n n →→→→→→→⎛⎫=+=+⋅+=+⨯+= ⎪⎝⎭,22221329124912472b m nm m n n →→→→→→→⎛⎫=-+=-⋅+=-⨯+= ⎪⎝⎭所以a →=,b →=又因为72a b →→⋅=-所以71cos ,2a b a b a b→→→→→→-⋅===-,因为[],0,a b π→→∈,所以23,a b π→→=,即向量a →与b →的夹角为23π. 【例3-3】已知空间向量a 、b 满足2=a ,1=b ,,60a b =︒,若向量a b λ+与2a b λ-的夹角为钝角,求实数λ的取值范围.【解析】因为向量a b λ+与2a b λ-的夹角为钝角, 所以()()20,λλ+⋅-<a b a b 且a b λ+与2λ-b a 不共线, 因为1a b ⋅=,所以()222220a a b b λλλ+-⋅-<,即2220λλ+-<,解得11λ-<<-+;当a b λ+与2a b λ-平行时,则存在实数k ,使得()2a b k a b λλ+=-, 即()()12k a k b λλ-=+, 因为a 、b 不平行,所以10,20,k k λλ-=⎧⎨+=⎩即22λ=-,则λ∈∅∠.由∠∠得,实数λ的取值范围是(11--+.【例3-4】如图,三棱柱111ABC A B C -中,底面边长和侧棱长都相等,1160BAA CAA ︒∠=∠=,则异面直线1AB 与1BC 所成角的余弦值为_____________【解析】三棱柱111ABC A B C -中,底面边长和侧棱长都相等,1160BAA CAA ︒∠=∠=,设棱长为1,则111cos602AB AC ︒⋅=⨯⨯=,1111cos602AB AA ︒⋅=⨯⨯=, 1111cos602AC AA ︒⋅=⨯⨯=. 又11AB AB AA =+,11BC AA AC AB =+-,所以()()1111AB BC AB AA AA AC AB ⋅=+⋅+-22111111111112222AB AA AB AC AB AA AA AC AA AB =⋅+⋅-++⋅-⋅=+-++-=而()222111123AB ABAA AB AB AA AA =+=+⋅+=,()2111BC AA AC AB =+-==所以111111cos 2AB BC AB BC AB BC ⋅<⋅>===⋅. 故答案为:6. 考点四 利用空间向量的数量积证明垂直解题方略:利用空间向量解决垂直问题的方法(1)证明线线垂直的方法:证明线线垂直的关键是确定直线的方向向量,看方向向量的数量积是否为0来判断两直线是否垂直.(2)证明与空间向量a ,b ,c 有关的向量m ,n 垂直的方法:先用向量a ,b ,c 表示向量m ,n ,再求解向量m ,n 的数量积并判断是否为0.【例4-1】已知空间四边形ABCD 中,AB ∠CD ,AC ∠BD ,求证:AD ∠BC . 【证明】∠AB ∠CD ,AC ∠BD ,∠AB ―→·CD ―→=0,AC ―→·BD ―→=0. ∠AD ―→·BC ―→=(AB ―→+BD ―→)·(AC ―→-AB ―→)=AB ―→·AC ―→+BD ―→·AC ―→-AB ―→2-AB ―→·BD ―→=AB ―→·AC ―→-AB ―→2-AB ―→·BD ―→ =AB ―→·(AC ―→-AB ―→-BD ―→)=AB ―→·DC ―→=0. ∠AD ―→∠BC ―→,从而AD ∠BC .变式1:如图,四面体OABC 各棱的棱长都是1,D ,E 分别是OC ,AB 的中点,记OA a →→=,OB b →→=,OC c →→=.(1)用向量,,a b c →→→表示向量DE →;(2)求证DE AB ⊥.【解析】(1)根据题意,11112222DE DO OA AE OC OA AB OC OA OB OA →→→→→→→→→→→⎛⎫=++=-++=-++- ⎪⎝⎭1122OA OB OC a b c →→→→→→⎛⎫⎛⎫=+-=+- ⎪ ⎪⎝⎭⎝⎭. (2)根据题意,,,a b c →→→相互之间的夹角为π3,且模均为1,由(1)2211=22DE AB a b c b a a b b c a c →→→→→→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+-⋅-=-+-⋅+⋅ ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭1111111110222⎛⎫=-+-⨯⨯+⨯⨯= ⎪⎝⎭, 所以DE AB ⊥.变式2:如图所示,三棱柱111ABC A B C -中,CA a =,CB b =,1CC c =,11CA CB CC ===,2π,,3a b a c ==,π,2b c =,N 是AB 中点.(1)用a ,b ,c 表示向量1A N ;(2)在线段11C B 上是否存在点M ,使1AM A N ⊥?若存在,求出M 的位置,若不存在,说明理由. 【解析】(1)11111111()2222A N A A AN C C AB CC CB CA a b c =+=+=-+-=-+-; (2)假设存在点M ,使1AM A N ⊥,设111,([0,1])C M C B λλ∈=, 显然1C M CB b λλ==,1111AM AA AC C M c a b λ=++=-+,因为1AM A N ⊥,所以110AM A N AM A N ⊥⇒⋅=,即()c a b λ-+⋅11()022a b c -+-=,2221111110222222c a c b c a a b c a a b b b c λλλ-⋅+⋅-+-⋅+⋅-⋅+-⋅=, 因为11CA CB CC ===,2π,,3a b a c ==,π,2b c =,所以有:22211111()022222c a c a a b b λλ⋅-+-+⋅+=,即222111111111()11()11()102222222λλ⨯⨯⨯--+⨯-+⨯⨯⨯-+⋅=, 解得13λ=,所以当11113C M C B =时, 1AM A N ⊥.【例4-2】如图所示,在正方体ABCD A 1B 1C 1D 1中,O 为AC 与BD 的交点,G 为CC 1的中点,求证:A 1O ∠平面GBD .证明:设A 1B 1―→=a ,A 1D 1―→=b ,A 1A ―→=c ,则a ·b =0,b ·c =0,a ·c =0,|a |=|b |=|c |. ∠A 1O ―→=A 1A ―→+AO ―→=A 1A ―→+12(AB ―→+AD ―→)=c +12a +12b ,BD ―→=AD ―→-AB ―→=b -a ,OG ―→=OC ―→+CG ―→=12(AB ―→+AD ―→)+12CC 1―→=12a +12b -12c . ∠A 1O ―→·BD ―→=⎝⎛⎭⎫c +12a +12b ·(b -a ) =c ·b -c ·a +12a ·b -12a 2+12b 2-12b ·a=12(b 2-a 2)=12(|b |2-|a |2)=0. 于是A 1O ―→∠BD ―→,即A 1O ∠BD . 同理可证A 1O ―→∠OG ―→, 即A 1O ∠OG .又BD ∩OG =O , 于是有A 1O ∠平面GBD .考点五 利用空间向量的数量积求距离(即线段长度)解题方略:求两点间的距离或线段长的方法(1)将相应线段用向量表示,通过向量运算来求对应向量的模. (2)用其他已知夹角和模的向量表示该向量;(3)因为a ·a =|a |2,所以|a |=a a ⋅,这是利用向量解决距离问题的基本公式.另外,该公式还可以推广为|a ±b |=()2222a b a a b b ±=±⋅+.(4)可用|a ·e |=|a ||cos θ|(e 为单位向量,θ为a ,e 的夹角)来求一个向量在另一个向量所在直线上的投影. 【例5-1】已知空间向量,,a b c 两两夹角均为60,其模均为1,则2a b c +-=( )AB C .2D 【解析】2a b c +-=2(2)a b c +-2224244a b c a b a c b c +++⋅-⋅-⋅=故选:B【例5-2】如图所示,在∠ABCD 中,AD =4,CD =3,∠ADC =60°,PA ∠平面ABCD ,PA =6,求线段PC 的长.【解析】∠PC ―→=PA ―→+AD ―→+DC ―→,∠|PC ―→|2=(PA ―→+AD ―→+DC ―→)2=|PA ―→|2+|AD ―→|2+|DC ―→|2+2PA ―→·AD ―→+2AD ―→·DC ―→+2DC ―→·PA ―→=62+42+32+2|AD ―→||DC ―→|cos 120°=61-12=49.∠|PC ―→|=7,即PC =7.变式1:如图,平行六面体1111ABCD A B C D -中,11AB AD AA ===,1120BAD BAA ∠=∠=︒,160DAA ∠=︒,则1AC =( )A .1B .2C .3D .2【解析】11AC AB AD AA =++,2221111222AC AB AD AA AB AD AB AA AD AA ∴=+++⋅+⋅+⋅1111112112112112222⎛⎫⎛⎫=+++⨯⨯⨯-+⨯⨯⨯-+⨯⨯⨯= ⎪ ⎪⎝⎭⎝⎭,1AC ∴=故选:D变式2:如图,已知一个60°的二面角的棱上有两点A ,B ,AC ,BD 分别是在这两个面内且垂直于AB 的线段.又知AB =4,AC =6,BD =8,求CD 的长.【解析】∠CA ∠AB ,BD ∠AB ,∠〈CA →,BD →〉=120°.∠CD →=CA →+AB →+BD →,且CA →·AB →=0,BD →·AB →=0,∠|CD →|2=CD →·CD →=(CA →+AB →+BD →)·(CA →+AB →+BD →)=|CA →|2+|AB →|2+|BD →|2+2CA →·BD →+2CA →·AB →+2AB →·BD → =|CA →|2+|AB →|2+|BD →|2+2|CA →||BD →|cos 〈CA →,BD →〉 =62+42+82+2×6×8×⎝⎛⎭⎫-12=68, ∠|CD →|=217,故CD 的长为217.变式3:如图,在平行四边形ABCD 中,AD =4,CD =3,∠BAD =120°,PA ∠平面ABCD ,且PA =6.求PC 的长.【解析】因为PC PA AD DC =++,所以22222()222PC PA AD DC PA AD DC PA AD PA DC AD DC =++=+++⋅+⋅+⋅222643243cos12049=+++⨯⨯⨯︒=,所以7PC =. 故PC 的长为7.变式4:如图,三棱锥O ABC -各棱的棱长都是1,点D 是棱AB 的中点,点E 在棱OC 上,且OE =OC λ,记OA a =,OB b =,OC c =.(1)用向量a ,b ,c 表示向量DE ;(2)求||DE 的最小值.【解析】(1)根据题意,连接OD ,CD ,点D 是棱AB 的中点,点E 在棱OC 上,如下图:由题意可得,OE =OC λ,记OA a =,OB b =,OC c =,∠DE OE OD =-=12OC λ-(OA OB +)=λ1122c a b --.(2)根据题意,点D 是棱AB 的中点,三棱锥O ABC -的各个面是边长为1,易得,||||OD CD ==在DOC △中,由余弦定理可得,222||||||cos cos 2||||OD OC CD DOC DOE OD OC +-∠=∠==222222311||||221()422DE OE OD OE OE OD OD DOE λλλ→→→→→→→=-=-+=-⨯⨯∠+=-+, 当12λ=时,2||DE →取得最小值12,则||DE →变式5:已知正方形ABCD ,ABEF 的边长均为1,且平面ABCD ∠平面ABEF ,点M 在AC 上移动,点N 在BF 上移动,若|CM |=|BN |=a (0<a <2).(1)求线段MN 的长;(2)当a 为何值时,线段MN 最短?【解析】(1)由已知得|AC ―→|=2,|BF ―→|=2,∠AM ―→=⎝⎛⎭⎫1-a 2AC ―→,NF ―→=⎝⎛⎭⎫1-a 2BF ―→,∠NM ―→=NF ―→+FA ―→+AM ―→=⎝⎛⎭⎫1-a 2BF ―→+FA ―→+⎝⎛⎭⎫1-a 2AC ―→=⎝⎛⎭⎫1-a 2(BE ―→+BA ―→)-BE ―→+⎝⎛⎭⎫1-a 2(-BA ―→+BC ―→) =⎝⎛⎭⎫1-a 2BC ―→+⎝⎛⎭⎫-a 2BE ―→,∠|NM ―→|=NM ―→·NM ―→=⎣⎢⎡⎦⎥⎤⎝⎛⎭⎫1-a 2BC ―→-a 2 BE ―→2 =⎝⎛⎭⎫1-a 22-2a 2⎝⎛⎭⎫1-a 2BC ―→·BE ―→+12a 2=⎝⎛⎭⎫a -222+12(0<a <2).即MN 的长度为 ⎝⎛⎭⎫a -222+12(0<a <2).(2)由(1)知当a =22,即M ,N 分别是AC ,BF 的中点时,MN 的长度最小,最小值为22. 考点六 利用空间向量的数量积求投影解题方略:向量a 在向量b 上的投影数量|a |cos 〈a ,b 〉||⋅=a bb 向量a 在向量b 上的投影向量|a |cos 〈a ,b 〉b |b |2||⋅=a bb b 【例6-1】如图,在长方体ABCD A B C D ''''-中,已知1AB =,2AD =,3AA '=,分别求向量AC '在AB 、AD 、AA '方向上的投影数量.【解析】非零向量a 在非零向量b 方向上的投影数量为cos ,a b a b a a b a a bb⋅⋅<>=⋅=⋅,由空间向量的平行六面体法则可得A AB AD A C A =+'+', 在长方体ABCD A B C D ''''-中,0AB AD AB AA AD AA ''⋅=⋅=⋅=, 因此,向量AC '在AB 方向上的投影数量为()1AB AD AA AB AC AB AB ABAB'++⋅'⋅===,向量AC '在AD 方向上的投影数量为()2AB AD AA AD AC AD AD ADAD'++⋅'⋅===,向量AC '在AA '方向上的投影数量为()3AB AD AA AA AC AA AA AA AA''++⋅''⋅'===''. 变式1:如图,已知正方体1111ABCD A B C D -的棱长为1,E 为11B C 的中点.(1)求1,DD BC ,11,D C CA 的大小; (2)求向量AE 在向量DC 方向上的投影的数量. 【解析】(1)在正方体1111ABCD A B C D -中, 因为1DD BC ⊥, 所以1,90DD BC =︒, 因为11//D C DC ,所以11,,135D C CA DC CA ==︒; (2)连接EC , 因为DC ⊥平面11BCC B , 所以DC CE ⊥, 又因为AD DC ⊥,所以AE 在向量DC 方向上的投影为DC , 因为1DC =,所以向量AE 在向量DC 方向上的投影的数量为1【例6-2】已知正方体1111ABCD A B C D -的棱长为1,E 为棱11B C 上的动点.求向量AE 在向量AC 方向上投影的数量的取值范围.【解析】由已知E 为棱11B C 上的动点,设111(01).B E B C λλ=≤≤因为11111111AE AB B E AB B C AB BB B C λλ=+=+=++所以111111()AE AC AB BB B C AC AB AC BB AC B C AC λλ⋅=++⋅=⋅+⋅+⋅1cos 451cos 451λλ︒︒=+⨯=+所以向量AE 在向量AC又01λ≤≤,112λ∴≤+≤,≤≤所以向量AE 在向量AC 方向上投影的数量的取值范围为.⎣ 题组A 基础过关练1.在正方体1111ABCD A B C D -中,有下列命题:∠221()3||AA AD AB AB ++=;∠1111()0AC A B A A ⋅-=;∠1AD 与1A B 的夹角为60︒.其中正确的命题有( ). A .1个B .2个C .3个D .0个【解析】对于∠,222221111()()()()2223,AA AD AB AA AD AB AA AD AA AB AD AB AB ++=+++⋅+⋅+⋅=所以∠正确;对于∠,111111()()()AC A B A A AB AD AA AB A A ⋅-=+-⋅-2210AB A A =-=,所以∠正确; 对于∠,因为1A B ∠1D C ,11,,AD AC D C 分别为面的对角线, 所以160AD C ∠=︒,所以1AD 与1A B 的夹角为120︒,所以∠错误 故选:B2.四边形ABCD 为矩形,SA ∠平面ABCD ,连接AC ,BD ,SB ,SC ,SD ,下列各组运算中,不一定为零的是( ) A .SC BD ⋅B .DA SB ⋅C .SD AB ⋅D .SA CD ⋅【解析】根据题意,依次分析选项:对于A :若SC 与BD 垂直,又SA 与BD 垂直,则平面SAC 与BD 垂直,则AC 与BD 垂直,与AC 与BD 不一定垂直矛盾,所以SC 与BD 不一定垂直,即向量SC 、BD 不一定垂直,则向量SC 、BD 的数量积不一定为0;对于B :根据题意,有SA ⊥平面ABCD ,则SA AD ⊥,又由AD AB ⊥,则有AD ⊥平面SAB ,进而有AD SB ⊥,即向量DA 、SB 一定垂直,则向量DA 、SB 的数量积一定为0;对于C :根据题意,有SA ⊥平面ABCD ,则SA AB ⊥,又由AD AB ⊥,则有AB ⊥平面SAD ,进而有AB SD ⊥,即向量SD 、AB 一定垂直,则向量SD 、AB 的数量积一定为0;对于D :根据题意,有SA ⊥平面ABCD ,则SA CD ⊥,即向量SA 、CD 一定垂直,则向量SA 、CD 的数量积一定为0.故选:A .3.已知正三棱锥P ABC -的底面ABC 的边长为2,M 是空间中任意一点,则()MA MB MC ⋅+的最小值为( )A .32-B .1-C .D .12-【解析】设BC 中点为O ,连接MO ,设MO 中点为H ,则HA ==()()()()22?MA MB MC MA MO MH HA MH HO ⋅+=⋅=++()()()22232?224MH HA MH HA MH HAMH⎛⎫+-=-=- ⎪⎝⎭,当M 与H 重合时,2MH 取最小值0.此时()MA MB MC ⋅+有最小值32-,故选:A4.棱长为1的正四面体ABCD 中,点E ,F 分别是线段BC ,AD 上的点,且满足13BE BC =,12AF AD =,则AE CF ⋅=( ) A .1324B .12-C .12D .512-【解析】由已知111cos602AB AC AB AD AC AD ⋅=⋅=⋅=⨯⨯︒=, 因为13BE BC =,12AF AD =,所以1121()3333AE AB BE AB BC AB AC AB AB AC =+=+=+-=+,12CF AF AC AD AC =-=-, 211()()332AE CF AB AC AD AC ⋅=+⋅-212113363AB AD AB AC AC AD AC=⋅-⋅+⋅-2121115()13362312=-+⨯-⨯=-. 故选:D .5.如图,P 为圆锥的顶点,O 是圆锥底面的圆心,圆锥PO 的轴截面PAE 是边长为2的等边三角形,ABC 是底面圆的内接正三角形.则PB PC →→⋅=( )A .32 B .52C .72D .92【解析】由题得PO 120BOC ∠=,21531122PB PC PO OB PO OC PO OB OC →→→→→→→→→⎛⎫⎛⎫⎛⎫⋅=+⋅+=+⋅=+⨯⨯-= ⎪ ⎪ ⎪⎝⎭⎝⎭⎝⎭.故选:B6.我国古代数学名著《九章算术》商功中记载“斜解立方,得两堑堵”,堑堵是底面为直角三角形的直三棱柱.在堑堵111ABC A B C -中,12AB AC AA ===,P 为11B C 的中点,则1AC BP ⋅=( ). A .6B .6-C .2D .2-【解析】根据堑堵的几何性质知:AB AC ⊥,1AA AB ⊥,1AA AC ⊥.因为11AC AC AA =+,()11111122BP BB B C AA AC AB =+=+-,所以()()11112AC BP AC AA AA AC AB ⎡⎤⋅=+⋅+-⎢⎥⎣⎦22111111112222AC AA AC AC AB AA AC AA AA AB=⋅+-⋅++⋅-⋅246=+=. 故选:A .7.已知平行六面体ABCD A B C D ''''-中,4AB =,3AD =,5AA '=,90BAD ∠=︒,60BAA DAA ''∠=∠=︒.则AC '的长为( )A B C .12D .【解析】216AB =,29AD =,225AA '=,43cos900AB AD ⋅=⨯⨯︒=,45cos6010AB AA ⋅'=⨯⨯︒=,1535cos602AD AA ⋅'=⨯⨯︒=.AC AB AD AA '=++',∴2222222AC AB AD AA AB AD AB AA AD AA '=++'+⋅+⋅'+⋅'1516925202102852=+++⨯+⨯+⨯=,∴||85AC '=即AC ' 故选:A .8.已知正方体ABCD A B C D ''''-的棱长为a ,对角线 AC '与BD '相交于点O ,则有( ).A .2AB A C a ''⋅=B .22AB AC a '⋅=C .12AB AO a ⋅=D .2BC DA a '⋅= 【解析】A ://AB A B ''且AB A B ''=,则2|||o |c s AB AC A B A C A B A C B A C a ''''''='''''''⋅=⋅∠=,正确; B :2||||cos AB AC AB AC BAC a '''⋅=∠=,错误;C :21||||cos 2AB AO AB AO BAO a ⋅=∠=,错误;D ://BC AD 且BC AD =,则2||cos ||()BC DA AD DA AD DA ADA a π'=-=-'''⋅=⋅∠,错误. 故选:A.9.空间四边形ABCD 中若,,2,1,AB BD CD BD AC BD ⊥⊥==则AC BD ⋅=( ) A .12B .1CD .0【解析】因为AC BD ⋅=()AB BC BD +()AB BD DC BD =++⋅ 2AB BD BD DC BD =⋅++⋅,因为AB BD ⊥,DC BD ⊥,所以0,0AB BD DC BD ⋅=⋅=, 所以AC BD ⋅=20101++=, 故选:B10.已知,a b 均为空间单位向量,它们的夹角为60°,那么3a b +等于( )AB C D .4【解析】222(3)93613a b a a b b a b =+=++⋅=+.故选:C.11.若OA 、OB 、OC 为空间三个单位向量,OA OB ⊥,且OC 与OA 、OB 所成的角均为60,则OA OB OC ++=( )A .5BC D【解析】()22222OA OB OC OA OB OC OA OB OB OC OA OC ++=+++⋅+⋅+⋅11320522⎛⎫=+++= ⎪⎝⎭,故5OA OB OC =++ 故选:C12.已知向量1e ,2e ,3e 是两两垂直的单位向量,且12332a e e e =+-,132b e e =+则()162a b ⎛⎫= ⎝⋅⎪⎭( ).A .15B .3C .3-D .5【解析】向量1e ,2e ,3e 是两两垂直的单位向量,且12332a e e e =+-,132b e e =+,∴()()()12313212332163396223e e e e e e e a b a b →→⎛⎫=⋅=⨯=-= ⎪⎝⋅+-+⎭.故选:B13.如图所示,在平行六面体ABCD A B C D ''''-中,各棱长均为2,90BAD ∠=︒,60BAA DAA ''∠=∠=︒,则向量D O '的长度为( )A .6B .22CD .【解析】''''111()222D D DO D D DA AO D D DA AD AB AA AD AB D O =+=++=++'+=--+,D O '11||22AA AD AB =--+211)22AA AD AB --+=222111442AA AD AB AA AD AA AB AD AB +++⋅-⋅-⋅==A14.如图,在平行六面体1111ABCD A B C D -中,M 为AC 与BD 的交点,若111111===A B A D A A ,1190AA D ∠=,1111160AA B B A D ∠∠==,则1B M 的值为( )A .12B .3C .1D .32【解析】因为四边形ABCD 为平行四边形,且AC BD M =,则M 为BD 的中点,()11111111111112222B M B B BM B B BD B B AD AB A A A B A D =+=+=+-=-+,则()2111111122B M A A A B A D =-+2221111111111111114442A A A B A D A A A B A A A D A B A D ++-⋅+⋅-⋅236021cos 602=-⨯⨯=. 故选:D.题组B 能力提升练15.如图,空间四边形ABCD 的每条边和对角线长都等于1,点E ,F ,G 分别是AB ,AD ,DC 的中点,则FG AB ⋅=( )A .34B .14C .12D .32【解析】依题意,,,E F G 分别是,,AB AD DC 的中点, 所以,2//1FG AC FG AC =,三角形ABC 是等边三角形,且边长为1. 所以111cos60224FG AB AC AB AC AB ⋅=⋅=⋅⋅︒=. 故选:B16.若非零向量a ,b 满足a b =,(2)0a b b -⋅= ,则a 与b 的夹角为( ) A .30°B .60°C .120°D .150°【解析】设a 与b 的夹角为θ, 因为(2)0a b b -⋅=,所以22a b b ⋅=, 所以22cos a b b θ=,因为非零向量a ,b 满足a b =, 所以1cos 2θ=, 因为[0,]θπ∈,所以3πθ=,即60θ=︒,故选:B17.已知4a =,空间向量e 为单位向量,23,a e π=,则空间向量a 在向量e 方向上的投影的数量为( ) A .2B .2-C .12-D .12【解析】由题意,4a =,1e =,23,a e π=, 则空间向量a 在向量e 方向上的投影为2cos13242e e a ea e π⋅⋅==⎛⎫-=- ⎪⎝⨯⎭.故选:B.18.在平行六面体1111ABCD A B C D -中,其中11AB BC BB ===,113ABB ABC B BC π∠=∠=∠=,12AE BD =,则1B E =( ) A .25B .5C .14D 【解析】()11111232B E B B BA AE B B BA BA BB BC BA BB BC =++=++++=++, 所以()22222221111132364122B E BA BB BCBA BB BC BA BB BB BC BA BC =++=+++⋅++⋅⋅222111312611411121125222=+++⨯⨯⨯+⨯⨯⨯+⨯⨯⨯=,所以15B E =,故选:B.19.在正方体1111ABCD A B C D -中,P 为11A B 上任意一点,则DP 与1BC 的位置关系是______.【解析】由题意,得()()111111111110DP C B DA A P C B CB A P C B C B C B A P C B ⋅=+⋅=+⋅=⋅+⋅=,所以1DP C B ⊥,即1DPBC .故答案为:垂直.20.如图,已知线段AB ⊥平面α,,,BC CD BC DF α⊂⊥⊥平面α,且30DCF ︒∠=,D 与A 在α的同侧,若2AB BC CD ===,求A ,D 两点间的距离.【解析】因为AB ⊥平面α,DF ⊥平面α,所以//AB DF ,30DCF ︒∠=,所以AB 与CD 的夹角为120︒,因为2AB BC CD ===,AD AB BC CD , 所以22||()AD AB BC CD =++222||||||222AB BC CD AB BC AB CD BC CD=+++⋅+⋅+⋅()12222cos9022cos12022cos908︒︒︒=+⨯⨯⨯+⨯⨯+⨯⨯=,所以||22AD =,即A ,D 两点间的距离为22. 21.如图所示,在四棱锥P ABCD -中,PA ⊥底面ABCD ,,,60,AB AD AC CD ABC PA AB BC ︒⊥⊥∠===,E 是PC 的中点.证明:(1)CD AE ⊥;(2)PD ⊥平面ABE .【解析】证明:(1)因为PA ⊥底面ABCD ,所以PA CD ⊥,所以0AP CD ⋅=,又AC CD ⊥,所以0AC CD ⋅=,又1()2AE AP AC =+,所以111()0222AE CD AP AC CD AP CD AC CD ⋅=+⋅=⋅+⋅=,所以CD AE ⊥.(2)设1PA AB BC ===,因为60ABC ︒∠=,1AB BC ==,所以1AC =.又AC CD ⊥,所以()0CD AC AD AC AC ⋅=-⋅=,得1AC AD ⋅=.因为()211()()22PD AE AD AP AP AC AD AP AD AC AP AP AC ⋅=-⋅+=⋅+⋅--⋅1(0110)02=⨯+--=,()0PD AB AD AP AB ⋅=-⋅=,所以,PD AE PD AB ⊥⊥,又AE AB A =,所以PD ⊥平面ABE .题组C 培优拔尖练22.如图,已知平行六面体1111ABCD A B C D -中,底面ABCD 是边长为1的菱形,12CC =,1160C CB BCD C CD ∠=∠=∠=︒.(1)求线段1CA 的长;(2)求异面直线1CA 与11B D 所成角的大小. 【解析】(1)设CD a →→=,CB b →→=,1CC c →→=, 则1a →=,1b →=,2c →=,111cos 602a b →→⋅=⨯⨯︒=,21cos601a cbc →→→→⋅=⋅=⨯⨯︒=,∠111CA CA AA CD CB CC a b c →→→→→→→→→=+=++=++,∠1CA a b c →→→→=++=∠线段1CA(2)∠1CA a b c →→→→=++,11B D BD a b →→→→==-,∠2211111110CA B D a b c a b a b a c b c →→→→→→→→→→→→→⎛⎫⎛⎫⋅=++⋅-=-+⋅-⋅=-+-= ⎪ ⎪⎝⎭⎝⎭,∠111CA B D →→⊥,故异面直线1CA 与11B D 所成的角为90°.23.如图,在三棱锥P ABC -中,PA ⊥平面ABC ,CB AB ⊥,AB BC a ==,PA b =.(1)确定PC 在平面ABC 上的投影向量,并求⋅PC AB ;(2)确定PC 在AB 上的投影向量,并求⋅PC AB .【解析】(1)因为PA ⊥平面ABC ,所以PC 在平面ABC 上的投影向量为AC , 因为PA ⊥平面ABC ,AB面ABC ,可得PA AB ⊥,所以0PA AB ⋅=,因为CB AB ⊥,所以0BC AB ⋅=,所以()PC AB PA AB PA AB AB BC AB BC AB AB =++=+⋅⋅⋅⋅+⋅ 2200a a =++=.(2)由(1)知:2PC AB a ⋅=,AB a =, 所以PC 在AB 上的投影向量为:2cos ,ABPC ABABPC AB AB a ABPC PC AB PC AB a a AB PC AB AB AB AB⋅⋅⋅⋅=⋅⋅=⋅=⋅=⋅,由数量积的几何意义可得:2PC AB AB a AB ⋅=⋅=.24.如图,在平行六面体1111ABCD A B C D -中,底面ABCD 是边长为2的正方形,侧棱1AA 的长度为4,且11120A AB A AD ︒∠=∠=.用向量法求:(1)1BD 的长;(2)直线1BD 与AC 所成角的余弦值.【解析】(1)111111BD BB B A A D =++,()22222111111111111111111111222BD BB B A A D BB B A A D BB B A BB A D B A A D =++=+++⋅+⋅+⋅1644242cos60242cos120024=+++⨯⨯︒+⨯⨯︒+=,故126BD =1BD的长为(2)()()111111AC BD AB BC BB B A A D ⋅=+⋅++1111111111AB BB AB B A AB A D BC BB BC B A BC A D =⋅+⋅+⋅+⋅+⋅+⋅ 24cos1204024cos120048=⨯︒-++⨯︒++=-()22222AC AB BC AB AB BC BC =+=+⋅+=,由(1)知:126BD =设直线1BD 与AC 所成角为θ ∠111cos cos ,2AC BD ACBD BD AC θ====⋅⋅ ∠直线1BD 与AC 25.如图所示的平行六面体1111ABCD A B C D -中,已知1AB AA AD ==,160DAB A AD ∠=∠=︒,130BAA ∠=︒,N 为11A D 上一点,且111A N A D λ=,点M 棱11D C 上,且11112D M D C =.(1)用1AA ,AD ,AB 表示BM ;(2)若BD AN ⊥,求λ;(3)若23λ=,求证://BM 平面1ANB . 【解析】(1)11BM BA AD DD D M =+++ 112AB AD AA AB =-+++112AB AD AA =-++即112BM AB AD AA =-++ (2)因为BD AN ⊥,不妨取11AB AA AD ===, ∴111()()BD AN AD AB AA A D λ⋅=-⋅+1()()AD AB AA AD λ=-⋅+1111cos60cos30cos60022AD AA AD AD AB AA AD AB λλλλλ=⋅+⋅-⋅-⋅=︒+-︒-︒==.1λ∴=. (3)过点N 作11//NG A B ,交11B C 于点G ,连接,BG MG ,则//BG AN , BG ⊄平面1ANB ,AN ⊂平面1ANB ,所以//BG 平面1ANB , 因为11123A N A D =,令113A D =,则12A N =,132MC =,11GC =,所以11111A N GC A B MC =,所以111A NB GM C ∽,所以111C MG A B N ∠=∠,又1C MG MGN ∠=∠,111B NG A B N ∠=∠,所以1B NG MGN ∠=∠,所以1//MG B N,MG ⊄平面1ANB ,1NB ⊂平面1ANB ,所以//MG 平面1ANB ,因为BG MG G =,,BG MG ⊂平面BMG ,所以平面//BMG 平面1ANB ,BM ⊂平面BMG ,所以//BM 平面1ANB ;。
1.1.2空间向量的数量积运算-【新教材】2020-2021学年人教A版

通过预习你发现空间向量的数量积和平面向量的数量积
有什么区别?
没有本质区别
新课探究
思考1:如何定义两个非零空间向量的夹角呢?
如图,已知两个非零向量, , 在空间任取一点O,作 =,
= ,则∠AOB叫做向量, 夹角,记作<, >.
A
a
a
b
o
b
B
关键是起点
相同!
向量a向平面β的投影呢?
(1)如图,在空间,向量a向向量b投影,可以先将它们平移到同一个
平面内,进而利用平面上向量的投影,得到与向量b共线的向量c,
c= |a|cos<a,b> ,
则向量c称为向量a在向量b上的投影向量.
||
(2)如图,在空间,向量a向直线l投影,若设直线l的
(1)向量, 同向
a
<, >=0
b
a
b
O
A
B
(2)向量, 反向
(3)<, >=
a
<, >=π
⊥
a
b
b
a
b
B
A
a
O
(4)非零向量, 的夹角的范围: 0 ≤ <, > ≤
(5)<, >=<, >
O
A
b
|a|cos<a,b> 称为向量a向直线l的投影.
||
a
a
a
c
b
a
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1.1.2 空间向量的数量积运算
(基础知识+基本题型)
知识点一 空间向量的夹角 1.概念
如图3.1-26,已知两个非零向量,a b ,在空间任取一点O ,作 OA a =,OB b =,则么AOB ∠叫做向量,a b 的夹角,记,a b <>.
2.范围
[],0,a b π<>∈. 3.特别地,如果,2
a b π
<>=
,那么向量,a b 互相垂直,记作a b ⊥.
对空间两个向量的夹角的理解,应注意以下几点:
(1)由概念,知两个非零向量才有夹角,当两非零向量同向时,夹角为0;反向时,夹角为π,故,0a b <>=(或π)//a b ⇔(,a b 为非零向量).
(2)零向量与其他向量之间不定义夹角,并约定0与任何向量a 都是共线的,即0∥a .两非零向量的夹角是唯一确定的.
(3)对空间任意两个向量,a b ,有;
①,,,a b a b b a <>=<-->=<-->;②,,,a b a b a b π<->=<->=-<>;③AB AC BACA AB AC π<>=<>=-<>....
拓展
若两个向量,a b 所在直线为异面直线,两异面直线所成的角为θ, (1)向量夹角的范围是0<<,a b ><π,异面直线的夹角θ的范围是0<θ<
2
π
,
(2)当两向量的夹角为锐角时,,a b θ=<>;当两向量的夹角为2
π
时,两异面直线垂直;当两向量的夹角为钝角时,,a b θπ=-<>. 知识点二 空间向量的数量积
定义
已知两个非零向量,a b ,则||||cos ,a b a b <>叫做向量,a b 的数量积,记作a b ⋅,
即||||cos ,a b a b a b ⋅=<>.
零向量与任意向量的数量积为0,即00a ⋅=.
几何意义
向量,a b 的数量积等于a 的长度||a 与b 在a 的方向上的投影||cos ,b a b <>的乘
积或等于b 的长度||b 与a 在b 的方向上的投影||cos ,a a b <>的乘积.
运算律
()()a b a b λλ⋅=⋅
a b b a ⋅=⋅(交换律)
()a b c a b a c ⋅+=⋅+⋅(分配律)
1. 对于空间向量的数量积,我们可以从以下几个方面理解:
(1)向量,a b 的数量积记为a b ⋅.而不能表示为a b ⨯或ab ;
(2)向量的数量积的结果为实数,而不是向量,其符号由夹角θ的余弦值的符号决定:当θ为锐角时,
a b ⋅>0,但当a b ⋅>0时, θ也可能为0;当θ为钝角时.a b ⋅<0,但当a b ⋅<0时,θ也可能为π:
(3)当θ≠0时, a b ⋅=0不能推出b 一定是零向量,这是因为对于任一个与a 垂直的非零向量b .都有a b ⋅=0.
2. 在考向量数量积的运算律时,要准确区分两向量的数量积与向量的数乘 、实数与实数的乘积之问的差
异.
(1)向量的数量积的运算不满足消去律,即a b ⋅=b c ⋅推不出a c =, (2)向量数量积的运算不满足结合律,即()a b c ⋅⋅不一定等于()
a b c ⋅ . (3)向量数量积的运算不满足除法,即对于向量a b ⋅,若a b ⋅=k ,不能得到k a b =
(或k
b a
=).例如,当非零向量a b ⋅垂直时,a b ⋅=0,但0
a b
=
显然是不正确的.
知识点三 空间向量数量积的性质
若,a b 是非零向量,e 是与b 方向相同的单位向量,θ为a 与e 夹角,则: (l) cos e a a e a θ⋅=⋅=. (2) 0a b a b ⊥⇔⋅=
(3)若a 与b 同向,则a b a b ⋅=;若a 与b 反向,则a b a b ⋅=-.特别地,2
=a a a a a a ⋅=⋅或. (4)若θ为a 与b 的夹角.则cos =
a b a b
θ⋅.
(5)a b a b ⋅≤. 拓展
空间向量数量积的性质可以看作数量积的定义的.引申和拓展,空间向量数量积与向量的模和夹角有关,更多的是以它为工具解决立体几何中与夹角和距离有关的问题.例如.
(1)求空间中两点间的距离或线段的长度,可以理解为求解为求相应线段所对应的向量的模. (2)求空间中两条直线的夹角(特别是两条异面直线所成的角),即求这两条直线所对应的两个向量的夹角或其补角.
(3)证明线线垂直问题时,可以通过计算两条直线所对应的两向量的数量积为零来说明这两条直线垂直.
考点一 空间向量数量积的运算问题
例1 已知向量,a b 之间的夹角为30,且a =3,b =4,求22
,,,(2)()a b a b a b a b ⋅+⋅-.
解:0cos ,34cos3063a b a b a b ⋅==⨯⨯=,2
2
9a a a a =⋅==,2
2
16b b b b =⋅==
22
(2)()2963326323a b a b a a b b +⋅-=+⋅-=+-=-
总结:有关向量数量积的运算应注意的问题:
⑴要与数乘运算区分开,数乘运算的结果仍是向量,向量的数量积为实数. ⑵书写规范:不能写成a b ⨯,也不能写成ab . ⑶向量数量积运算不满足结合律,也不满足消去律.
(4)向量数量积与实数运算有很多是相同的,如平方差公式、完全平方公式、多项式展开法则等,但也有很多区别,要注意总结.
考点二 利用向量的数量积求角
例2如图3.1—30.在正方体1111ABCD A B C D -中,求向量1BC 与AC 的夹角的大小.
解:方法1:因为11AD BC =,所以1CAD ∠的大小就等于1,BC AC
因为△1CAD 为等边三角形,所以0160CAD ∠=,所以1BC 与AC 的夹角的大小为60︒. 方法2.设正方体的棱长为1,()()()()
111BC
AC BC
CC AB BC AD AA AB AD ⋅=+⋅+=+⋅+ 2
2
2
110001AD AB AD AA AB AA AD AD AD =⋅++⋅+⋅=+++==
又因为12,2BC AC ==,所以cos 11111,2
22
BC AC BC AC BC AC
⋅=
=
=
⨯⋅, 因为[]1,0,BC AC π∈,所以1BC 与AC 的夹角的大小为60︒.
求两个向量的夹角有两种方法:⑴结合图形,平移向量,利用空间向量的夹角定义来求,但要注意向量夹角的范围;⑵先求a b ⋅,再利用公式cos ,a b a b a b
⋅<>=
,求cos ,a b <>,最后确定,a b <>.
考点三 利用向量的数量积求距离
例 3 已知线段AB 在平面α内,线段AC α⊥,线段BD AB ⊥,且与α所成的角是30︒,如果
,AB a AC BD b ===,求C ,D 间的距离.
解:如图,由AC α⊥,知AC AB ⊥,过点D 作'DD α⊥于点'D ,连接'BD ,
则
'30,,120DBD CA BD ∠=︒=︒,所以22||()CD CD CD CA AB BD ==++2||CA =+
22222222||||2222cos120AB BD CA AB CA BD AB BD b a b b a b ++++=+++︒=+
故22CD a b =+.
总结:(1)线段长度的计算通常有两种方法:一是构建三角形,解三角形;二是向量法,计算相应向量的模,此时常需将待求向量转化为关系明确的向量(一般向几何体的棱上转化).
(2)应牢记并能熟练地考公式
2222||()||||||222a b c a b c a b c a c a b b c ++=++=+++++.
考点四 利用向量的数量积证明垂直
例4 如图,在四面体O ABC -中,M,N,P,Q 分别为BC ,AC ,OA ,OB 的中点,若AB OC =,求证:
PM QN ⊥.
分析:欲证PM QN ⊥,只要证明0PM QN =,需将PM QN 用其他向量表示后再进行计算. 证明:如图3.1-34,连接OM ,设,,OA a OB b OC c ===.
因为P ,M 分别为OA ,BC 的中点,所以111
()[()]222PM OM OP b c a b a c =-=+-=-+.
同理,连接ON ,所以111
()[()]222QN a c b b a c =+-=--+.
所以22111
[()]{[()]}(||||)224PM QN b a c b a c b a c =-+⋅--+=---.
又因为AB OC =,所以||||b a c -=
所以0PM QN =,所以PM QN ⊥,即PM QN ⊥.。
