mit课程
mit离散数学笔记

mit离散数学笔记离散数学是一门重要的数学学科,它研究离散对象和离散结构,如集合、图论、逻辑等。
MIT(麻省理工学院)是世界知名的学府,其离散数学课程给予了很多学生深刻的学习体验。
本篇文章将对MIT离散数学课程的内容进行笔记总结。
一、集合论集合论是离散数学的基础。
在MIT的离散数学课程中,集合论位于开篇的位置,主要包括集合的定义与运算、集合的基数、无穷集合、基本逻辑等内容。
集合论不仅在数学领域有着广泛的应用,还在计算机科学、人工智能等领域中扮演着重要的角色。
二、图论图论是离散数学中最重要的分支之一。
MIT的离散数学课程中,图论部分包含了图的基本概念、图的表示方法、图的连通性、最短路径算法、最小生成树算法等内容。
图论在计算机科学、社交网络分析、电路设计等领域中有着广泛的应用。
三、逻辑与证明逻辑是离散数学的核心内容之一。
MIT的离散数学课程中,逻辑与证明部分包括命题逻辑、谓词逻辑、命题等价性、谓词等价性、证明方法等内容。
通过学习逻辑与证明,学生不仅可以提高思维的严密性,还可以培养解决问题的能力。
四、数论数论是离散数学中的重要分支,研究整数的性质与结构。
MIT的离散数学课程中,数论部分主要包括整除性、素数、模运算等内容。
数论在密码学、编码理论等领域有着广泛的应用。
五、关系与函数关系与函数是离散数学中的重要概念。
MIT的离散数学课程中,关系与函数部分主要包括关系的性质、函数的性质、逆关系、复合函数等内容。
关系与函数不仅在数学中有着重要的应用,还在数据库设计、计算机网络等领域中起着重要作用。
六、排列与组合排列与组合是离散数学中的经典话题。
MIT的离散数学课程中,排列与组合部分主要包括排列、组合、二项式定理等内容。
排列与组合在概率论、统计学等领域中有着重要的应用。
总结:通过学习MIT离散数学课程,我们不仅可以掌握离散数学的基础概念和重要理论,还可以培养严密的逻辑思维和解决问题的能力。
离散数学在计算机科学、人工智能、密码学等领域都发挥着重要的作用。
学生MIT创意课程总结

学生MIT创意课程总结在MIT的创意课程中,我度过了一段充满挑战和创造力的学习时光。
这门课程给我提供了一个多元化的平台,让我从不同的角度思考和解决问题。
在这篇文章中,我将回顾我的学习经历并总结我从这门课程中学到的重要教训和技能。
第一节:认识创意课程开始时,我对创意课程的概念和目标有了一个初步的了解。
这门课程的主要目的是培养学生的创新思维和解决问题的能力。
在这个过程中,学生们将有机会参与到各种创意项目中,并与来自不同学科领域的同学合作。
这种多学科的合作有助于拓宽我们的思维边界,并提供了更多的创意和解决问题的方法。
第二节:培养创新思维通过创意课程,我学会了如何培养创新思维。
在这个过程中,我们被鼓励提出不同的观点和想法,并从不同的角度思考问题。
课程设有许多创意激发活动,例如头脑风暴、设计思维和故事讲述,这些活动不仅有助于激活我们的思维,还可以帮助我们更好地表达和沟通我们的想法。
第三节:解决问题的方法在创意课程中,我们不仅学会了提出创新思路,还学会了应用不同的问题解决方法。
这包括系统思维、设计思维和批判性思维等。
通过学习这些方法,我们可以更好地分析和理解问题,并提出更加有效的解决方案。
第四节:合作与团队合作合作是创意课程中的重要组成部分。
在学习过程中,我们经常需要与来自不同专业的同学合作完成项目。
这种跨学科合作有助于拓宽我们的视野,让我们能够从不同的角度思考问题。
同时,合作也培养了我们的团队精神和领导能力。
第五节:创意项目在创意课程中,我们有机会参与各种创意项目。
这些项目要求我们将理论知识应用到实际问题中,并提出创新的解决方案。
通过这些项目,我们获得了宝贵的实践经验,并提高了我们的创意和解决问题的能力。
第六节:实践应用创意课程强调实践应用。
不仅仅是理论学习,课程还鼓励我们将所学知识和技能应用到实际生活中。
我们有机会与行业专业人士交流,并访问一些创新企业和实验室,以了解实践中的创意和解决问题的方法。
第七节:创意思维的重要性通过创意课程,我意识到创意思维在现代社会中的重要性。
mit 线性代数

mit 线性代数
mit性代数是一门在理工科专业中很重要的课程,它包含许多数学理论及应用,主要研究线性方程、高阶代数及微积分等内容,通过学习可以增强学生的数学基础。
mit的线性代数课程容易学习,但又非常有挑战性,它涵盖很多数学理论和概念,有助于学生更好地理解对线性变换、矩阵分析和线性系统有关的内容。
MIT的线性代数课程分为大纲和提纲型,提纲型课程提供了一些更具体的示例,以便帮助学生更深入地理解课程内容。
线性代数在各个工程专业中都有着非常重要的地位,它可以帮助工程师、科学家以及数学家更好地分析和解决复杂的数学问题。
学习mit的线性代数不仅可以提高学生的数学能力,而且还可以帮助他们更好地理解实际问题,解决工程问题,这对于学生的发展有着非常大的帮助。
mit的线性代数课程主要分为5个模块:矩阵、线性变换、直线和平面、线性系统和矩阵分析。
每一个模块都有许多详尽的例子,涉及到不同的应用及相关的理论和技术。
学习mit的线性代数可以帮助学生了解矩阵的表示与操作,以及如何用矩阵来分析线性系统、处理相关问题。
mit的线性代数课程也可以帮助学生更好地理解诸如统计学、偏微分方程以及数值解析等专业的内容。
学习线性代数的学生可以更轻松地理解这些新的科学领域,同时也能够更有效地学习和应用这些科学理论及技术。
总之,学习mit的线性代数是一个有趣而又具有挑战性的过程,它可以帮助学生了解矩阵及其应用,从而加强他们的学习能力,有助于他们找到理想的工作。
只有经过一定的学习,才能真正掌握mit的线性代数课程所涉及的内容,并在实践中发挥出价值。
MIT和UM核工程相关课程目录
本科: SH2701: Thermal-Hydraulic in Nuclear Energy Engineering, 6 ECTS credits SH2702: Nuclear Reactor Technology, 8 ECTS credits SH2703: Reactor Dynamics and Stability, 6 ECTS credits Project Course in Nuclear Energy Technology, as a part of course 4A1609 Undergraduate courses in previous years 研究生 Advanced Course in Thermal Hyቤተ መጻሕፍቲ ባይዱraulics, 9 ECTS credits
Nuclear Power Reactors(核电站反应堆) Thermal-hydraulics for Nuclear Systems(热工水力) Reactor Safety Analysis(反应堆安全分析) Introduction to Plasmas(等离子体导论) Fusion Reactor Technology(聚变反应堆技术) Engineering Principles of Radiation Imaging(辐射成像工程原理) Radiological Health Engineering Fundamentals(放射卫生工程基础) Special Topics in Nuclear Engineering and Radiological Sciences(核工程与放射科学专 题) Research in Nuclear Engineering and Radiological Sciences(核工程与放射科学研究) 500level Quantum Mechanics in Neutron-Nuclear Reactions(中子核反应中的量子力学) Interaction of Radiation and Matter(射线与材料相互做用) Nuclear Measurements Laboratory(核测量实验室) Advanced Radiation Measurements and Imaging(先进辐射测量和成像) Radiation Materials Science I/II/III(辐射材料科学) Nuclear Fuels(核燃料) Nuclear Waste Management(核废料管理) Detection Techniques of Nuclear Non-proliferation(防扩散探测技术) Nuclear Reactor Theory II(核反应堆理论) Monte Carlo Methods(蒙特卡罗方法) Thermal Fluids for Nuclear Reactor Safety Analysis(反应堆安全中的热工流体) Nuclear Reactor Kinetics(反应堆动力学) Radiation Shielding Design(辐射屏蔽设计) Nuclear Core Design and Analysis I/II(堆芯设计分析) Intermediate Plasma Physics I/II(中间等离子体物理) Plasma Engineering(等离子体工程) Plasma Generation and Diagnostics Laboratory(等离子体产生和诊断实验室) Charged Particle Accelerators and Beams(带点粒子加速器和束流) Plasma Spectroscopy(等离子体光谱学) Physical Processes in Plasmas(等离子体中的物理过程)
mit公共核心课程计划

mit公共核心课程计划麻省理工学院(MlT)作为全球顶尖的科技学府,一直以来都在为社会培养出大量的优秀人才。
为了适应不断变化的社会需求,Mrr 在20世纪70年代开始实施公共核心课程计划,旨在为学生提供全面的教育,培养他们成为具有创新精神和领导能力的复合型人才。
本文将对MIT公共核心课程计划进行详细介绍,以期对我国高等教育改革提供借鉴。
一、Mrr公共核心课程计划的背景随着科技的快速发展和社会的进步,人们对高等教育的需求也在不断变化。
为了更好地满足这些需求,MIT在20世纪70年代开始实施公共核心课程计划,以期为学生提供更加全面、系统的教育。
这一计划的核心理念是:培养学生的创新精神、团队协作能力、跨学科知识体系和领导能力,使他们能够在未来的职业生涯中取得成功。
二、Mrr公共核心课程计划的内容MIT公共核心课程计划包括以下几个方面的内容:1.人文学科人文学科课程旨在培养学生的人文素养,提高他们的文化修养和审美能力。
这些课程涵盖了文学、历史、哲学、艺术等领域,使学生能够更好地理解人类社会的发展和变迁,以及不同文化之间的差异和联系。
2.社会科学社会科学课程主要关注人类社会的组织、行为和发展规律。
这些课程包括政治学、经济学、社会学、心理学等,使学生能够更好地理解社会现象,分析社会问题,提出解决方案。
3.自然科学自然科学课程旨在培养学生的科学素养,提高他们的科学思维和实验能力。
这些课程涵盖了物理、化学、生物、地球科学等领域,使学生能够掌握科学研究的基本方法和技能,为未来的科研工作打下坚实基础。
4.工程与应用科学工程与应用科学课程主要关注科学技术在实际应用中的问题和挑战。
这些课程包括计算机科学、电子工程、机械工程、材料科学等,使学生能够将理论知识与实际问题相结合,提高解决实际问题的能力。
5.写作与沟通写作与沟通课程旨在提高学生的书面和口头表达能力,培养他们的沟通技巧和团队协作能力。
这些课程包括写作、演讲、辩论等,使学生能够更好地表达自己的观点,有效地与他人沟通交流。
mit高等数学教材

mit高等数学教材高等数学是一门在大学或者研究生阶段必修的重要学科。
它建立在微积分、线性代数和数理方程等基础上,通过推导和证明来研究数学的更高层次的概念和理论。
这篇文章将介绍MIT高等数学教材,探讨其内容和特点。
一、概述MIT高等数学教材是由麻省理工学院的数学系编写的,它是由一系列教授讲授的课程结集而成。
该教材不仅是理论性强的教科书,同时也是一个严格思考和探索数学问题的指导工具。
它包含了大量的例题和习题,能够帮助学生巩固知识和提高解题能力。
二、内容介绍MIT高等数学教材的内容非常全面和深入。
它涵盖了微积分、线性代数、常微分方程、概率统计和数理方程等多个方面的知识。
每个主题都以清晰的章节和子章节展开,让学生能够有条理地理解和掌握数学的各个领域。
该教材特别注重数学的应用和实例分析。
在每个章节中,都有大量的实际问题和案例,以帮助学生将理论知识应用到实际中去。
这种实践性的学习方式对于学生培养数学建模和解决实际问题的能力非常有帮助。
三、特点与优势1. 高度严谨:MIT高等数学教材采用了严密的推导和证明过程,确保学生在学习过程中能够深入理解数学的基本概念和原理。
通过反复练习和思考,学生可以逐步培养出自己的证明能力和逻辑思维。
2. 广泛的应用领域:该教材不仅覆盖了数学专业的核心知识,还涉及到物理学、工程学、经济学等多个学科。
它能够满足不同专业学生对数学的需求,帮助他们理解其他学科中的数学模型和方法。
3. 系统性和完整性:MIT高等数学教材将各个数学领域的知识有机地串联在一起,形成了一个完整的理论体系。
学生可以从基础开始,逐步深入学习,建立坚实的数学基础。
4. 注重实践和应用:该教材通过大量的例题和习题,鼓励学生动手实践和解决实际问题。
这种实用性的教学方法可以培养学生的问题解决能力和创新思维。
四、总结MIT高等数学教材是一本内容丰富、深入浅出的数学教材。
它不仅适合数学专业的学生,也适用于其他专业对数学有需求的学生。
mit 线性代数

mit 线性代数《MIT线性代数》是麻省理工学院提出的一门非常重要的数学课程。
它主要涉及线性代数的概念,目的是让学生意识到它的基本原理和应用。
为了让学生理解MIT线性代数的概念,本课程将研究两个重要的方面:线性方程组和矩阵代数。
MIT线性代数将介绍线性方程组、矩阵和向量空间的概念,并分析线性空间的性质,学习在实际应用中运用线性空间的技术。
1.性方程组及其解的概念线性方程组是线性关系的变量集,用来描述一些实际情况或现象。
线性方程组具有两个基本特点:其一,它的基本形式由n个变量的n 个等式组成,其二,在这个等式组中,各项的幂小于等于一。
MIT线性代数将介绍线性方程组和其解的概念。
它教授了不同类型的线性方程组解的方法,如通解、增量法以及最小二乘法,并且提供了其理论证明及实际应用。
2.阵代数的概念MIT线性代数还将介绍矩阵代数的概念和方法。
矩阵代数是一种把一组数据可视化的手段,可以在矩阵里进行更多的有效运算,从而深入到数据细节。
它也可以用来构造各种数学模型,如线性方程组,用于分析实际问题。
内容包括矩阵的表示、性质及运算、行列式、逆矩阵、秩与范数、线性变换及应用等等。
3.性空间的性质及实际应用MIT线性代数也会介绍线性空间的性质,以及它们在实际应用中的技术。
它介绍的知识包括空间的维度和基,及如何用线性变换和矩阵来描述空间变换,以及投影、对角化、对称和正交运算等技术。
实际应用方面,MIT线性代数主要介绍机器学习、向量图像处理和数据挖掘等应用等,以及这些技术能够分析的实际问题,如和矩阵的最小二乘求解,基于线性模型的多元统计分析、绘制矩阵图像、多元线性决策边界等。
MIT线性代数的深入学习,不仅能帮助学生深刻理解数学概念,更重要的是,可以让学生在实践中使用线性代数的技术,用数学模型分析实际问题,帮助他们解决实际问题,以期获得最优结果。
mit课程设计

mit 课程设计一、课程目标知识目标:1. 让学生掌握/mit/课程中关键的科学原理和概念,如基础的物理定律、编程思维等;2. 使学生理解并能够描述/mit/课程中涉及的复杂科学现象和工程问题;3. 引导学生了解科学、技术、工程和数学(STEM)的交叉应用,以及它们在现代问题解决中的作用。
技能目标:1. 培养学生运用/mit/课程知识进行问题分析、数据解读和实验设计的能力;2. 通过项目式的学习活动,提升学生的团队合作、批判性思考和创新能力;3. 培养学生使用适当的技术工具和资源,进行信息搜索、数据处理和报告编制的能力。
情感态度价值观目标:1. 激发学生对科学探究的热情,培养好奇心和探究欲;2. 引导学生形成尊重事实、注重证据的科学态度,并认识到科学在解决实际问题时的重要性;3. 通过对实际问题的探讨,增强学生的社会责任感和环保意识;4. 鼓励学生面对挑战时保持积极心态,培养坚持和克服困难的意志。
本课程设计旨在结合学生的年级特点,注重理论与实践的结合,通过具体可衡量的学习成果,使学生在知识掌握、技能提升和情感态度价值观培养方面取得全面发展。
二、教学内容本章节教学内容紧密围绕课程目标,选择以下核心内容进行科学性和系统性的组织:1. 科学原理与概念:- 物理定律:牛顿运动定律、能量守恒定律等;- 计算机编程:基础编程语法、算法思维、模拟与仿真。
2. 实践与应用:- 项目一:基于物理引擎的小游戏设计;- 项目二:数据采集与分析,如传感器应用。
3. 教学内容的安排与进度:- 第一周:科学原理与概念导入,物理定律学习;- 第二周:计算机编程基础,算法思维培养;- 第三周:项目一实践,团队合作进行小游戏设计;- 第四周:项目二实践,数据采集与分析。
4. 教材章节及内容列举:- 教材第一章:科学探究方法与实验设计;- 教材第二章:物理定律及其应用;- 教材第三章:计算机编程基础;- 教材第四章:项目实践与问题解决。
MIT公开课ppt

虚拟现实和增强 现实技术,提供 更真实的互动体 验
形式:虚拟现实、 增强现实等技术 将进一步丰富在 线教育体验
内容:更加注重 实践和应用,更 加关注跨学科和 交叉领域的知识 传授
互动:借助智能 教学平台,加强 教师与学生的在 线互动与交流
个性化:基于大 数据和人工智能 技术,实现个性 化教学和推荐学 习资源
,a click to unlimited possibilities
01 m i t 公 开 课 简 介 02 m i t 公 开 课 对 个 人 的 好 处 03 m i t 公 开 课 对 社 会 的 贡 献 04 m i t 公 开 课 的 使 用 方 法 05 m i t 公 开 课 的 未 来 发 展
为学术界和教育 界提供有益的参 考和借鉴
提高学术研究的 开放性和共享性 ,推动知识创新 和发展
mit公开课提高 公众的科学素
养
mit公开课促进 科技与人文的
融合
mit公开课激发 年轻人的创新
精神
mit公开课为全 球教育资源共
享提供平台
创新思维的重要性
MIT公开课如何培养创新思维
Hale Waihona Puke 创新思维对社会的推动作用接触到前沿的知识和研究成果 了解不同的学术观点和思想 学习到严谨的学术方法和思维方式 增强自己的学术背景和竞争力
培养自主思考和解决问题的能力
拓展视野,了解不同领域的知识
添加标题
添加标题
掌握学科知识,提高综合素质
添加标题
添加标题
提高自我学习和自我发展的能力
增加学科知识储备
拓宽视野,了解不同领域 的知识
增加互动性:通过 在线讨论、问答、 测验等方式增强学 生与教师之间的互 动,提高学习效果。
美国麻省理工学院 MIT 学生的作息时间表

美国麻省理工学院MIT 学生的作息时间表你的大学生活是不是这样度过的:上午睡到10点,去食堂吃个饭,回来跟室友聊天唠嗑,下午心情好去上课,心情不好去打球/购物,吃了晚饭后就窝在宿舍看视频/打游戏?Loser 的做法!来看看美国顶尖大学,麻省理工学院MIT的学霸们是如何安排自己的一天的!Rose Robb,女,MIT 数学专业周一到周五我的作息时间表通常是这样的:8点:起床,吃早饭,喂猫,准备去上课。
如果前一天晚上熬夜了,起床时间会推迟到上课前的45分钟。
9点到下午4点:上课,学习,写作业。
下图是我上个学期的课程表。
我会利用每天两堂课的间隙去吃饭,做psets。
周五只有一节课,下课后我会去逛超市补充下一周的食粮,然后继续做psets。
下午4点到晚上12点:这一段时间主要用来写作业、打工、参加课外活动。
上学期我打了三份工,每周工作10小时左右。
周二和周四的下午3点到5点,我会去辅导班当老师。
周一的晚上6点到8点去图书馆工作,有时候可能会加班。
周二晚上我会参加数学小组的会议。
我还会参加莎士比亚戏剧社的排练,排练时间通常是工作日的下午6点到10点,或者周末的下午1点到5点。
周五晚上是自由活动的时间,我会去波士顿逛逛,或者去观摩其他戏剧社的排练,有时也会和男朋友一起看电影。
24点到早晨8点:睡觉!如果睡不够8小时,我的精力会受到很大的影响。
当然睡眠时间因人而异,我的睡眠质量不怎么好,所以时间一定要保证。
周末的安排比较自由,通常我会在周末完成一些比较简单的学习任务,例如阅读参考书籍。
不过周末大部分时间都是跟学习无关的~Thom Lu:MIT计算机专业学生,男周一到周五:1.在第一堂课开始前半个小时起床,一般在10:30AM-12:30PM。
我喜欢熬夜做作业,所以早晨起的总是很晚。
对我来说,30分钟足够我穿衣洗漱到达教室了。
和身边很多同学一样,我很少吃早饭。
2.上课。
当然到学期末的时候我也经常翘课。
3.一般下午4点半到家。
mit 线性代数

mit 线性代数
线性代数是一门计算机科学、统计学、信号处理等其他数学领域中所使用的基本数学工具。
线性代数是一门涉及向量、矩阵、空间、几何体和多重变换等内容的数学学科。
线性代数背后的基本概念是空间的抽象,它们用于描述实现空间中的向量、矩阵和几何体的结构关系和变换。
MIT的线性代数课程涉及空间的抽象,描述空间中向量、矩阵和几何体的结构关系和变换。
课程将研究从最基本的向量和矩阵开始,教授向量空间,到矩阵分解、范数、特征值等。
它们将被用来说明这些空间、矩阵和几何体之间的变换以及这些变换的性质。
MIT的线性代数课程的主要内容包括几何课中的矢量分析、代数方面的矩阵论和线性变换、以及线性代数应用。
该课程将会介绍矩阵的性质,例如初等矩阵的性质、秩的概念、行列式的特性以及如何通过LU变换来求解线性方程组。
此外,也会讨论矩阵乘法中几何变换的性质,以及如何计算向量空间中的内积和距离。
此外,该课程还会讨论常见的线性代数应用,例如线性拟合线性方程组的求解、最小二乘方法的应用、最优解的求解、极大似然估计的应用等。
有关统计和信号处理等数学应用,也会详细讨论。
最后,课程还会介绍线性代数在空间变换、游戏开发、照片处理等方面的应用。
MIT线性代数课程旨在让学生了解线性代数的基本概念,学会如何运用数学理论推导出结果,并学会一些线性代数在实际应用中的技
能。
该课程的目标是为学生们提供一个系统的学习环境,完全了解线性代数的基本概念,以及如何运用线性代数理论解决实际问题。
学完该课程,学生们将掌握高效运用线性代数理论和技能,更好地掌握和应用线性代数在实际应用中的重要性。
MIT公开课程介绍

MIT公开课程介绍(MIT OCW)网址://ocwweb/MIT网上免费公开课程项目于2001年4月宣布,计划在今后十年内把MIT 所有的课程内容放到网上,称之为“MIT OpenCourseWare”(MIT OCW)。
此项目2001年秋季正式启动,计划在此后两年内进行大规模的OCW试验项目,两年半内使500门以上的课程上网,到2007年总量将达到1800门课程。
目的是通过这个项目推动MIT本身的教育教学,提升MIT在全世界的形象、同时供全世界所有的人免费使用,但OCW提供的并不是网上的MIT学历教育。
到目前为止,MIT已免费公开500 门课程,涉及MIT的33个学科和全部5个学院。
我校相关课程的教师备课及课件制作、学生自学、尤其是使用双语教学的教师都可以将其作为很好的学习和参考资料,使我们能够站在一个更高的起点上进行课程建设,提高教学水平。
网址为/MIT网上所有课程都有教程大纲、课程的日期安排(教学日历)和讲课记录。
许多课程还有作业、试卷、问题(包括解答)、实验室、项目、超文本的课本、模拟、演示、辅导和讲课的视频实况及网络资源链接等。
下面对公开课程的有关内容举例介绍,希望广大教师有一个更直观的感受,以便更好的利用和借鉴。
一、33个学科1.Aeronautics and Astronautics2.Anthropology3.Architecture4.Biological Engineering Division5.Biology6.Brain and Cognitive Sciences7.Chemical Engineering8.Chemistry9.Civil and Environmental Engineering10.Comparative Media Studies11.Earth,Atmospheric,and Planetary Sciences12.Economics13.Electrical Engineering and Computer Science14.Engineering Systems Division15.Foreign Languages and Literatures16.Health Science and Technology17.History18.Linguistics and Philosophy19.Literature20.Material Science and Technology21.Mathematics22.Mechanical Engineering23.Media Arts and Sciences24.Music and Theater Arts25.Nuclear Engineering26.Ocean Engineering27.Physics28.Political Science29.Science ,Technology and Society30.Sloan School of Management31.Urban Studies and Planning32.Women’s Studies33.Writing and Humanistic Studies二、课程大纲我们以建筑学系为例。
mit高等数学教材pdf

mit高等数学教材pdfMIT高等数学教材是一本经典的数学教材,被广泛应用于全球各个知名大学的数学课程中。
本文将探讨MIT高等数学教材的特点、使用方法以及对学生学习数学的重要性。
一、MIT高等数学教材的特点MIT高等数学教材的特点主要体现在以下几个方面:1.内容全面:该教材涵盖了高等数学的各个分支,包括微积分、线性代数、微分方程等内容。
无论是初学者还是深入学习数学的高级学生,都能从中获取到所需的知识。
2.严谨性强:MIT高等数学教材以其严谨的数学推导和证明而闻名,每个定理和公式都有详细的证明过程,让学生能够更好地理解其中的数学原理。
3.注重实践应用:教材中不仅包含了理论知识,还结合了大量的实例和应用案例,帮助学生将抽象的数学理论应用到实际问题中,增强了学习的实用性。
二、使用MIT高等数学教材的方法使用MIT高等数学教材有多种方法,下面介绍几种常见的途径:1.课堂教学:教师可以根据教材的章节内容,结合自己的教学风格和学生的实际情况,进行系统的课堂授课。
通过讲解和示范,帮助学生掌握数学知识。
2.学习小组:学生可以组建学习小组,每个小组选择一到两个章节进行深入学习,并和其他小组进行讨论和交流。
这种合作学习的方式可以加深对知识的理解,提高解决问题的能力。
3.个人研究:有些学生习惯独立研究,他们可以按照自己的进度,选择教材中感兴趣的章节进行学习。
通过阅读教材上的内容,做一些相关的习题和探究性的实践,提高数学思维能力。
三、学习高等数学的重要性高等数学作为大学数学课程的一部分,对学生们的数学素养和综合能力的培养具有重要作用:1.发展逻辑思维:高等数学是一门逻辑严密的学科,通过学习高等数学,可以培养学生的逻辑思维能力,提高解决问题的能力,并培养良好的数学推理习惯。
2.提高抽象思维能力:高等数学中包含了大量的抽象概念和符号,学生需要通过学习数学公式和定理,并将其运用到实际问题中进行分析和解决。
这样的过程可以培养学生的抽象思维和数学建模能力。
麻省理工学院核心课程介绍

麻省理工学院核心课程介绍---1. 课程概述麻省理工学院(Massachusetts Institute of Technology, MIT)作为全球顶尖的科技研究与教育机构之一,致力于培养拥有广泛知识背景和深度专业能力的学生。
为了实现这一目标,MIT设立了一系列核心课程,旨在为学生提供全面深入的教育。
这些核心课程涵盖了数理基础、人文社会科学、工程技术等多个领域,帮助学生培养扎实的学科基础、综合分析能力、创新思维以及解决复杂问题的能力。
以下将详细介绍MIT的核心课程。
2. 数理基础课程麻省理工学院的数理基础课程涵盖了数学、物理和计算机科学等领域。
其中,数学课程包括微积分、线性代数、概率与统计等,为学生提供了数学分析和推理的基础。
物理课程深入浅出地教授了经典力学、电磁学、量子力学等内容,培养了学生的物理思维和实验技能。
计算机科学课程则帮助学生掌握编程基础、算法设计和计算机系统等知识,为学生提供了解决实际问题的工具。
3. 人文社会科学课程人文社会科学课程旨在培养学生的社会意识、文化素养和人际交往能力。
这些课程包括哲学、历史、经济学、社会学等。
通过研究哲学,学生能够思考存在、知识和伦理等基本问题。
历史课程帮助学生深入了解人类文明的演进过程,促使他们对社会变迁有更深入的理解。
经济学和社会学课程则让学生了解社会运行的规律和经济现象的原因,培养他们的经济分析和社会研究能力。
4. 工程技术课程工程技术课程是麻省理工学院的一大特色。
该类课程主要包括电子工程、机械工程、材料科学和化学工程等领域。
学生将通过实验和项目实践研究工程设计和创新的过程,培养他们解决实际工程问题的能力。
这些课程还涉及到机器人技术、人工智能、能源工程等前沿领域,使学生能够跟上科技发展的最新趋势。
5. 课程特点MIT的核心课程具有以下特点:首先,注重理论与实践相结合。
学生在课堂研究理论知识的同时,还需要进行实验、项目和研究等实践活动,将所学知识应用于实际问题。
麻省理工学院有哪些本科和研究生课程?

麻省理工学院有哪些本科和研究生课程?麻省理工学院的本质是我们对问题的兴趣,特别是那些大而棘手,复杂的问题,这些问题的解决方案会产生永久性的影响,那么这所大学是否有你感兴趣的专业呢?跟着来了解一下详情吧。
一、重要信息英文名:麻省理工大学(MIT)区域:北美洲国家:美国找到年份:1861年地址:77 Massachusetts Avenue网站:入学总人数:10264国际学生:2726(27%)本科入学人数:4199国际学生:383(9%)研究生入学人数:6065国际学生:2343(39%)二、本科课程介绍航空航天工程、航空航天工程与信息技术、人类学、考古与材料、艺术与设计、生物工程、生物学、脑与认知科学、化学工程、化学,生物工程、化学、土木与环境工程、土木工程、比较媒体研究、计算机科学与工程、地球,大气和行星科学、经济学、电气工程与计算机科学、电气科学与工程、工程、环境工程科学、外国语言与文学、历史、人文、科学人文与工程、人文与科学、语言学与哲学、文献、管理科学、材料科学与工程、数学、数学与计算机科学、机械与海洋工程、机械工程、机械工程、音乐、核科学与工程、哲学、物理、规划、治学、科学技术与社会、写作。
三、研究生课程航空航天、航空航天计算工程、航空运输系统、空气呼吸推进、飞机系统工程、应用生物科学、考古材料、建筑研究、建筑:建筑技术、架构:设计与计算、架构:建筑历史与理论、架构:历史与艺术理论、大气化学、大气科学、自主系统、生物与高分子材料、生物化学、生物工程、生物化学、生物工程、生物海洋学(与WHOI共同提供)、生物海洋学、生物学、生物医学工程、生物物理化学和分子结构、建筑技术、细胞生物学、化学工程、化学工程实践、化学海洋学(与伍兹霍尔海洋研究所共同提供)、化学海洋学(与伍兹霍尔海洋研究所联合)、城市规划、土木与环境工程、土木与环境系统、土木工程、气候物理与化学、海岸工程、认知科学、通讯和网络、比较媒体研究、设计和优化、计算计算和系统生物学、计算和系统生物学(与工程学院联合)、计算和系统生物学(与科学学院联合)、计算机科学、计算机科学与工程、建筑工程和管理、控制、发展生物学、地球和行星科学、经济学、电气工程师、电子工程和计算机科学、电子,光子和磁性材料、新兴,基本和计算研究的材料科学、工程和管理、工程与管理,共同通过系统设计和管理方案与斯隆管理学院提供、工程系统、工程系统、技术/管理,双学位与领导的全球运营计划、、全球运营的领导者、环境生物学、环境化学、环境工程、环境流体力学、遗传学、地球化学、地质学、地球物理学、岩土工程和地球环境工程、历史、人类航空航天、水文学、免疫学、信息技术、无机化学、语言学、物流、管理、管理、技术、管理研究管理、制造、海洋地质和地球物理学(与WHOI共同提供)、金融硕士、材料与结构、材料科学与工程、数学、机械工程、媒体艺术与科学、媒体技术、微生物学、微生物学微生物学、分子生物学、海军建筑与海洋工程、神经生物学神经、科学、核科学与工程、海洋工程、海洋学工程(与WHOI合作)、运筹学、有机化学、哲学、物理化学、物理海洋学(与WHOI联合)、物理学、行星科学、政治科学、高分子科学与技术、房地产开发、科学写作、空间推进、空间系统、结构与环境材料、结构与材料、技术与政策、技术,管理与政策、毒理学、交通、城市与区域规划、城市与区域研究、城市研究与规划、视觉研究。
国际贸易学硕士

国际贸易学硕士简介国际贸易学硕士(Master of International Trade,MIT)是研究国际贸易规则和政策以及国际贸易实务理论与方法的学位。
该学位旨在培养具备国际贸易理论和实践能力的高级专业人才,为他们在国际贸易和跨国公司等领域工作提供专业知识和技能支持。
课程设置国际贸易学硕士的课程设置包含了贸易理论、国际贸易政策、国际商务、跨境电子商务、国际金融、货物流通以及国际采购等方面的内容。
学生将通过深入学习这些课程,掌握国际贸易的基本原理和方法,并了解当今世界贸易的发展趋势。
以下是国际贸易学硕士的一些典型课程:1.国际贸易理论与实务2.国际贸易政策与法规3.国际商务战略与管理4.国际市场开拓与营销5.国际采购与供应链管理6.跨境电子商务7.国际金融与贸易融资8.货物运输与物流管理就业前景国际贸易学硕士的毕业生通常有着广阔的就业前景。
他们可以在政府、跨国公司、国际组织以及国际贸易咨询公司等机构工作。
以下是一些国际贸易学硕士毕业生的常见职业方向:1.贸易政策分析师2.国际贸易顾问3.跨国公司国际贸易经理4.国际商务部经理5.跨境电子商务专员6.货物物流与运输经理学习要求想要申请国际贸易学硕士,通常需要满足以下条件:1.本科学位:通常要求本科学位为相关领域,如国际贸易、国际商务、经济学等。
2.学术背景:申请者需要有一定的学术基础,如经济学、统计学等。
3.英语水平:考虑到国际贸易学硕士的课程通常使用英语进行教学,申请者需具备良好的英语听说读写能力。
通常需要提供英语考试成绩,如TOEFL或IELTS。
申请流程申请国际贸易学硕士的具体流程可能因学校而异,以下是一般的申请流程:1.确定学校和专业:选择感兴趣的学校和国际贸易学硕士专业,并了解学校的申请要求和截止日期。
2.准备申请材料:准备个人简历、推荐信、个人陈述以及英语考试成绩等申请材料。
3.申请表填写:填写所选择学校的申请表格,并附上所需的申请材料。
mit教材高等数学

mit教材高等数学高等数学是一门限制学位课程的学科,对于数学专业的学生而言,它是必不可少的一门课程。
麻省理工学院(MIT)作为世界一流的科技学府,教材自然也是非常经典和权威的。
本文将介绍MIT教材中关于高等数学的内容,帮助读者了解该课程的知识点和学习路径。
第一部分:微积分微积分是高等数学的重要组成部分,是分析数学的基础。
MIT教材中的微积分章节,从导数和极限开始,逐步引入积分和微分方程等概念。
通过理论分析和实际问题求解,帮助学生掌握微积分的基本原理和应用方法。
第二部分:线性代数线性代数是数学中的另一门重要学科,涉及向量空间、线性方程组、矩阵理论等内容。
在MIT教材中,线性代数章节详细介绍了向量和矩阵的运算规则,线性变换和特征值等概念,同时强调了线性代数在科学和工程问题中的应用。
第三部分:概率论与数理统计概率论与数理统计是应用数学中的重要学科,也是MIT教材中的一部分。
该章节从概率的基本概念出发,介绍了随机变量、概率分布、统计参数估计等内容,帮助学生理解随机事件和统计规律,并学会运用概率论和数理统计解决实际问题。
第四部分:常微分方程常微分方程是微积分和线性代数的应用领域,也是MIT教材中的重要内容。
该章节系统地介绍了常微分方程的基本理论、解法和应用,帮助学生掌握常微分方程建模和求解的思路,培养解决实际问题的能力。
第五部分:多元函数微积分多元函数微积分是高等数学的深入学习内容,也是MIT教材中的重点章节之一。
通过引入多元函数的概念,讨论偏导数、多元积分和梯度等概念和应用,帮助学生理解高维空间中的微积分原理和方法,并应用于实际问题的求解。
总结:MIT教材中的高等数学内容十分丰富和系统,覆盖了微积分、线性代数、概率论与数理统计、常微分方程和多元函数微积分等重要学科。
通过学习这些内容,学生能够培养数学建模和问题求解的能力,为进一步学习和研究数学打下坚实基础。
无论是对于数学专业的学生,还是其他理工科的学生,高等数学都是不可或缺的一门学科。
mit6.828课程笔记

mit6.828课程笔记
MIT 6.828是一门由麻省理工学院提供的操作系统工程课程。
这门课程涵盖了操作系统的设计与实现的基本原理和技术。
学生将
通过实验来深入了解操作系统的内部工作原理,并且掌握操作系统
的设计和实现方法。
以下是一些关于MIT 6.828课程的笔记:
1. 课程简介,MIT 6.828课程主要围绕操作系统的设计和实现
展开。
学生将学习操作系统的各个组成部分,包括内核、文件系统、进程管理、内存管理等,并通过实验来加深对这些概念的理解。
2. 课程内容,课程内容包括但不限于,操作系统引导启动、内
存管理、进程调度、系统调用、文件系统、网络等方面的内容。
学
生将通过实验来实际操作和实践这些概念。
3. 实验项目,MIT 6.828课程的重点是实验项目。
学生将完成
一系列的实验项目,这些项目涵盖了操作系统的各个方面,通过实
验来加深对操作系统原理的理解,并掌握实际操作系统的设计和实
现技能。
4. 教学方法,课程采用了讲授理论知识和实验相结合的教学方
法。
学生将在课堂上学习相关理论知识,并通过实验项目来加深理
解和掌握操作系统的设计与实现技术。
5. 学习收获,通过学习MIT
6.828课程,学生将能够深入了解操作系统的内部原理和技术,并且掌握操作系统的设计和实现方法,为日后的系统开发和研究打下坚实的基础。
总的来说,MIT 6.828课程是一门涵盖了操作系统设计与实现
基本原理和技术的课程,通过理论教学和实验项目的方式,帮助学
生深入理解操作系统的工作原理,并掌握操作系统的设计与实现技能。
mit软件工程课程设计

mit软件工程课程设计一、课程目标知识目标:1. 学生能理解软件工程的基本概念,掌握软件开发的生命周期及其各个阶段的关键任务。
2. 学生能掌握软件需求分析、软件设计、编码、测试等基本方法和技能。
3. 学生了解软件项目管理的基本原理,掌握进度控制、风险管理等实践方法。
技能目标:1. 学生具备运用结构化分析方法进行软件需求分析的能力。
2. 学生能够根据需求设计合理的软件架构,并使用适当的设计模式进行软件设计。
3. 学生掌握至少一种编程语言,能够进行软件编码和单元测试。
4. 学生能够参与团队协作,共同完成软件项目的开发与管理工作。
情感态度价值观目标:1. 培养学生严谨、细致的工作态度,养成良好编程习惯,提高代码质量。
2. 培养学生团队协作精神,增强沟通与表达能力,提升解决问题的能力。
3. 培养学生对软件工程的兴趣,激发创新精神,提高自主学习能力。
4. 培养学生关注软件行业发展趋势,树立正确的职业道德观念。
本课程旨在帮助学生在理解软件工程基本理论的基础上,掌握软件开发过程中的关键技术和方法,培养实际项目开发与管理能力。
针对学生的年级特点,课程内容注重理论与实践相结合,强调动手实践和团队协作。
通过本课程的学习,使学生能够适应未来软件行业的发展需求,为从事软件开发和管理工作打下坚实基础。
二、教学内容1. 软件工程概述:介绍软件工程的基本概念、目标、原则,分析软件开发的生命周期。
教材章节:第1章 软件工程概述2. 软件需求分析:讲解需求分析的方法、工具,实践需求文档的编写。
教材章节:第2章 软件需求分析3. 软件设计:介绍软件设计的基本概念、方法,学习设计模式,进行软件架构设计。
教材章节:第3章 软件设计4. 编码与单元测试:学习编程语言,实践编码规范,开展单元测试。
教材章节:第4章 编码与单元测试5. 软件测试:讲解软件测试的基本理论,实践黑盒测试和白盒测试。
教材章节:第5章 软件测试6. 软件项目管理:介绍项目管理的基本概念、方法,实践进度控制、风险管理。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
converge to something?
2 3
• Does the limit depend on the initial state?
1
2
3
4
Recurrent and Transient States
• State is recurrent if:
– Starting from , and from wherever you can go, there is a way of returning to . 3 5 1 2 8 4 6 7
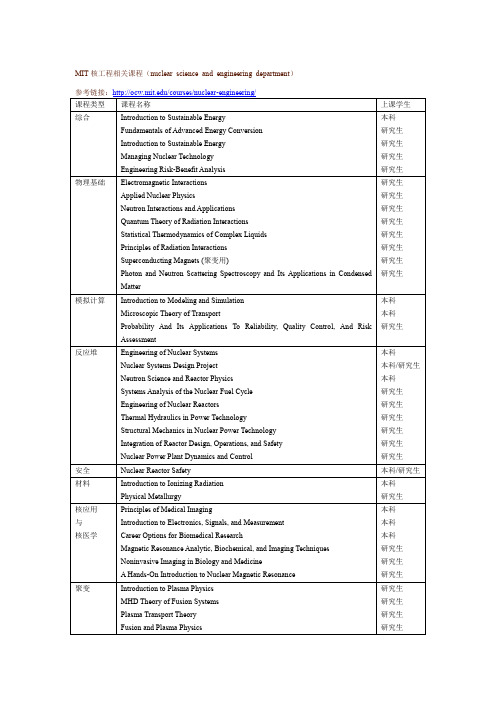
Example: Checkout Counter
• Discrete time • Customer arrivals: Bernoulli( ) – Geometric interarrival times. • Customer service times: Geometric( ) • “State” : number of customers at time .
0
1
2
3
9
10
Finite State Markov Models
•
–
: state after
transitions
– Belongs to a finite set, e.g. is either given or random.
• Markov Property / Assumption:
– Given the current state, the past does not matter.
Periodic States
• The states in a recurrent class are periodic if:
– They can be grouped into groups so that all transitions from one group lead to the next group.
• State occupancy probabilities, given initial state :
Time 0
Time n-1
Time n
i
l k m j
• Key recursion: • Random initial state:
Example
1
2
Generic Question
• Does
• Modeling steps:
– Identify the possible states. – Mark the possible transitions. – Record the transition probabilities.
-step Transition Probabilities
3 4 se,
cannot converge.
• If not recurrent, a state is called transient.
– If is transient then as . – State is visited only a finite number of times.
• Recurrent Class:
– Collection of recurrent states that “communicate” to each other, and to no other state.
LECTURE 19
• Readings: Finish Section 5.2 Lecture outline
• Markov Processes – I
– Checkout counter example. – Markov process: definition. – -step transition probabilities. – Classification of states.
