高中数学必修一1.1集合人教版
新人教版高中数学必修第一册集合与常用逻辑用语课件

数学 必修 第一册 A
返回导航
第一章 集合与常用逻辑用语
2.元素a与集合A之间只有两种关系:a∈A,a∉A. 3.在用列举法表示集合时应注意 (1)元素间用分隔号“,”;(2)元素不重复;(3)元素无顺序;(4)列举法可表示 有限集,也可以表示无限集.若集合中的元素个数比较少,则用列举法比较简单; 若集合中的元素较多或无限,但出现一定的规律性,在不发生误解的情况下,也可 以用列举法表示. 4.在用描述法表示集合时应注意 (1)弄清元素所具有的形式(即代表元素是什么),是数、还是有序实数对(点)、 还是集合或其他形式; (2)当题目中用了其他字母来描述元素所具有的属性时,要去伪存真(元素具有 怎样的属性),而不能被表面的字母形式所迷惑.
数学 必修 第一册 A
返回导航
第一章 集合与常用逻辑用语
解 (1)对任意一个实数能判断出是不是“不超过 20 的非负数”,所以能构成集 合;
(2)能构成集合; (3)“高个子”无明确的标准,对于某个人算不算高个子无法客观地判断,因此 不能构成一个集合; (4)“ 3的近似值”不明确精确到什么程度,因此很难判断一个数,如“2”,是不 是它的近似值,所以不能构成集合.
数学 必修 第一册 A
返回导航
第一章 集合与常用逻辑用语
解 (1)不大于 10 的非负偶数有 0,2,4,6,8,10,所以 A={0,2,4,6,8,10}. (2)小于 8 的质数有 2,3,5,7,所以 B={2,3,5,7}. (3)方程 2x2-x-3=0 的实数根为-1,32,所以 C=-1,32. (4)由yy==-x+23x+,6, 得yx==41., 所以一次函数 y=x+3 与 y=-2x+6 的交点为(1,4), 所以 D={(1,4)}.
人教版高中数学必修一知识点与重难点

人教版高中数学必修一————各章节知识点与重难点第一章集合与函数概念1.1 集合1.1.1集合的含义与表示【知识要点】1、集合的含义一般地,我们把研究对象统称为元素,把一些元素组成的总体叫做集合。
2、集合的中元素的三个特性〔1〕元素确实定性;〔2〕元素的互异性;〔3〕元素的无序性2、“属于〞的概念我们通常用大写的拉丁字母A,B,C, ……表示集合,用小写拉丁字母a,b,c, ……表示元素如:如果a是集合A的元素,就说a属于集合A 记作 a∈A,如果a不属于集合A 记作 a A3、常用数集及其记法非负整数集〔即自然数集〕记作:N;正整数集记作:N*或 N+ ;整数集记作:Z;有理数集记作:Q;实数集记作:R4、集合的表示法〔1〕列举法:把集合中的元素一一列举出来,然后用一个大括号括上。
〔2〕描述法:用集合所含元素的公共特征表示集合的方法称为描述法。
①语言描述法:例:{不是直角三角形的三角形}②数学式子描述法:例:不等式x-3>2的解集是{x∈R| x-3>2}或{x| x-3>2}〔3〕图示法〔Venn图〕【重点】集合的根本概念和表示方法【难点】运用集合的三种常用表示方法正确表示一些简单的集合【知识要点】1、“包含〞关系——子集一般地,对于两个集合A与B,如果集合A的任何一个元素都是集合B的元素,我们就说这两个集合有包含关系,称集合A为集合B的子集,记作A⊆B2、“相等〞关系如果集合A的任何一个元素都是集合B的元素,同时,集合B的任何一个元素都是集合A的元素,我们就说集合A等于集合B,即:A=B A B B A且⇔⊆⊆3、真子集如果A⊆B,且A≠B那就说集合A是集合B的真子集,记作A⊂B(或B⊃A)4、空集不含任何元素的集合叫做空集,记为Φ规定: 空集是任何集合的子集,空集是任何非空集合的真子集.【重点】子集与空集的概念;用Venn图表达集合间的关系【难点】弄清元素与子集、属于与包含之间的区别【知识要点】1、交集的定义一般地,由所有属于A且属于B的元素所组成的集合,叫做A,B的交集.记作A∩B(读作“A交B〞),即A∩B={x| x∈A,且x∈B}.2、并集的定义一般地,由所有属于集合A或属于集合B的元素所组成的集合,叫做A,B的并集。
人教版高中数学必修一第一章知识点
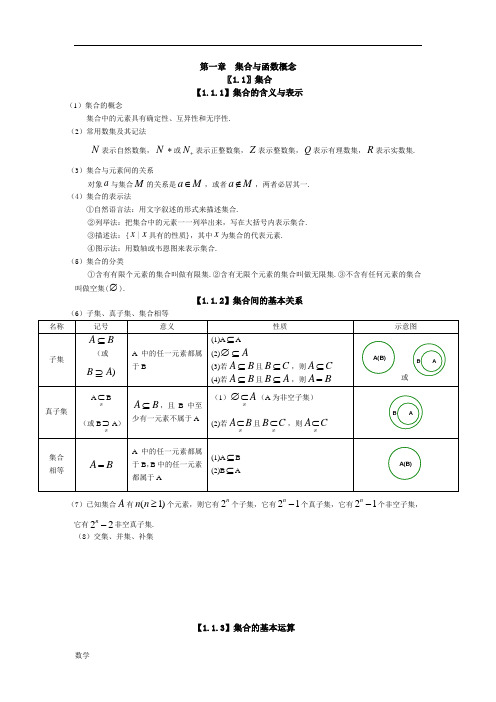
第一章 集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示(1)集合的概念集合中的元素具有确定性、互异性和无序性. (2)常用数集及其记法N 表示自然数集,N *或N +表示正整数集,Z 表示整数集,Q 表示有理数集,R 表示实数集.(3)集合与元素间的关系对象a 与集合M 的关系是a M ∈,或者a M ∉,两者必居其一. (4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合. ③描述法:{x |x 具有的性质},其中x 为集合的代表元素. ④图示法:用数轴或韦恩图来表示集合. (5)集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集(∅).【1.1.2】集合间的基本关系(6)子集、真子集、集合相等(7)已知集合A 有(1)n n ≥个元素,则它有2n 个子集,它有21n -个真子集,它有21n -个非空子集,它有22n-非空真子集.(8)交集、并集、补集【1.1.3】集合的基本运算名称记号意义性质示意图交集A B{|,x x A∈且}x B∈(1)A A A=(2)A∅=∅(3)A B A⊆A B B⊆BA并集A B{|,x x A∈或}x B∈(1)A A A=(2)A A∅=(3)A B A⊇A B B⊇BA补集U A{|,}x x U x A∈∉且1()UA A=∅2()UA A U=【补充知识】含绝对值的不等式与一元二次不等式的解法(1)含绝对值的不等式的解法不等式解集||(0)x a a<>{|}x a x a-<<||(0)x a a>>|x x a<-或}x a>||,||(0)ax b c ax b c c+<+>>把ax b+看成一个整体,化成||x a<,||(0)x a a>>型不等式来求解(2)一元二次不等式的解法判别式24b ac∆=-∆>0∆=0∆<二次函数2(0)y ax bx c a=++>的图象O 一元二次方程20(0)ax bx c a++=>的根21,242b b acxa-±-=(其中12)x x<122bx xa==-无实根20(0)ax bx c a++>>的解集1{|x x x<或2}x x>{|x}2bxa≠-R()()()U U UA B A B=()()()U U UA B A B=〖1.2〗函数及其表示 【1.2.1】函数的概念(1)函数的概念①设A 、B 是两个非空的数集,如果按照某种对应法则f,对于集合A 中任何一个数x ,在集合B中都有唯一确定的数()f x 和它对应,那么这样的对应(包括集合A ,B 以及A 到B 的对应法则f )叫做集合A 到B 的一个函数,记作:f A B →.②函数的三要素:定义域、值域和对应法则.③只有定义域相同,且对应法则也相同的两个函数才是同一函数. (2)区间的概念及表示法①设,a b 是两个实数,且a b <,满足a x b ≤≤的实数x 的集合叫做闭区间,记做[,]a b ;满足a xb <<的实数x 的集合叫做开区间,记做(,)a b ;满足a x b ≤<,或a x b <≤的实数x 的集合叫做半开半闭区间,分别记做[,)a b ,(,]a b ;满足,,,x a x a x b x b ≥>≤<的实数x 的集合分别记做[,),(,),(,],(,)a a b b +∞+∞-∞-∞. 注意:对于集合{|}x a x b <<与区间(,)a b ,前者a 可以大于或等于b ,而后者必须a b <.(3)求函数的定义域时,一般遵循以下原则:①()f x 是整式时,定义域是全体实数.②()f x 是分式函数时,定义域是使分母不为零的一切实数.③()f x 是偶次根式时,定义域是使被开方式为非负值时的实数的集合.④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1. ⑤tan y x =中,()2x k k Z ππ≠+∈.⑥零(负)指数幂的底数不能为零. ⑦若()f x 是由有限个基本初等函数的四则运算而合成的函数时,则其定义域一般是各基本初等函数的定义域的交集.⑧对于求复合函数定义域问题,一般步骤是:若已知()f x 的定义域为[,]a b ,其复合函数[()]f g x 的定义域应由不等式()a g x b ≤≤解出.⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论. ⑩由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义. (4)求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,只是提问的角度不同.求函数值域与最值的常用方法:①观察法:对于比较简单的函数,我们可以通过观察直接得到值域或最值.②配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的值域或最值. ③判别式法:若函数()y f x =可以化成一个系数含有y 的关于x 的二次方程2()()()0a y x b y x c y ++=,则在()0a y ≠时,由于,x y 为实数,故必须有2()4()()0b y a y c y ∆=-⋅≥,从而确定函数的值域或最值.④不等式法:利用基本不等式确定函数的值域或最值.⑤换元法:通过变量代换达到化繁为简、化难为易的目的,三角代换可将代数函数的最值问题转化为三角函数的最值问题.⑥反函数法:利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值. ⑦数形结合法:利用函数图象或几何方法确定函数的值域或最值. ⑧函数的单调性法.【1.2.2】函数的表示法(5)函数的表示方法表示函数的方法,常用的有解析法、列表法、图象法三种.解析法:就是用数学表达式表示两个变量之间的对应关系.列表法:就是列出表格来表示两个变量之间的对应关系.图象法:就是用图象表示两个变量之间的对应关系. (6)映射的概念①设A 、B 是两个集合,如果按照某种对应法则f,对于集合A 中任何一个元素,在集合B 中都有唯一的元素和它对应,那么这样的对应(包括集合A ,B 以及A 到B 的对应法则f )叫做集合A 到B 的映射,记作:f A B →.②给定一个集合A 到集合B 的映射,且,a A b B ∈∈.如果元素a 和元素b 对应,那么我们把元素b 叫做元素a 的象,元素a 叫做元素b 的原象.yxo〖1.3〗函数的基本性质 【1.3.1】单调性与最大(小)值(1)函数的单调性①定义及判定方法 函数的 性 质定义图象判定方法 函数的 单调性如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x .1.< x ..2.时,都有f(x ...1.)<f(x .....2.).,那么就说f(x)在这个区间上是增函数.... x 1x 2y=f(X)xy f(x )1f(x )2o(1)利用定义(2)利用已知函数的单调性(3)利用函数图象(在某个区间图象上升为增) (4)利用复合函数 如果对于属于定义域I 内某个区间上的任意两个自变量的值x 1、x 2,当x .1.< x ..2.时,都有f(x ...1.)>f(x .....2.).,那么就说f(x)在这个区间上是减函数.... y=f(X)yxox x 2f(x )f(x )211(1)利用定义(2)利用已知函数的单调性(3)利用函数图象(在某个区间图象下降为减) (4)利用复合函数②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为增函数,减函数减去一个增函数为减函数. ③对于复合函数[()]y f g x =,令()u g x =,若()y f u =为增,()u g x =为增,则[()]y f g x =为增;若()y f u =为减,()u g x =为减,则[()]y f g x =为增;若()y f u =为增,()ug x =为减,则[()]y f g x =为减;若()y f u =为减,()u g x =为增,则[()]y f g x =为减.(2)打“√”函数()(0)af x x a x=+>的图象与性质()f x 分别在(,]a -∞-、,)a +∞上为增函数,分别在[,0)a 、]a 上为减函数.(3)最大(小)值定义 ①一般地,设函数()y f x =的定义域为I,如果存在实数M 满足:(1)对于任意的x I ∈,都有()f x M≤;(2)存在0x I ∈,使得0()f x M=.那么,我们称M 是函数()f x 的最大值,记作max ()f x M=.②一般地,设函数()y f x =的定义域为I ,如果存在实数m 满足:(1)对于任意的x I ∈,都有()f x m ≥;(2)存在0x I ∈,使得0()f x m =.那么,我们称m 是函数()f x 的最小值,记作max ()f x m =.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法 函数的 性 质定义图象判定方法 函数的 奇偶性如果对于函数f(x)定义域内任意一个x ,都有f(..-.x)=...-.f(x)....,那么函数f(x)叫做奇函..数..(1)利用定义(要先判断定义域是否关于原点对称)(2)利用图象(图象关于原点对称)如果对于函数f(x)定义域内任意一个x ,都有f(..-.x)=...f(x)....,那么函数f(x)叫做偶函数....(1)利用定义(要先判断定义域是否关于原点对称)(2)利用图象(图象关于y 轴对称) ②若函数()f x 为奇函数,且在0x =处有定义,则(0)0f =.③奇函数在y 轴两侧相对称的区间增减性相同,偶函数在y 轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.〖补充知识〗函数的图象(1)作图利用描点法作图:①确定函数的定义域; ②化解函数解析式; ③讨论函数的性质(奇偶性、单调性); ④画出函数的图象. 利用基本函数图象的变换作图:要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象. ①平移变换0,0,|()()h h h h y f x y f x h ><=−−−−−−−→=+左移个单位右移|个单位0,0,|()()k k k k y f x y f x k ><=−−−−−−−→=+上移个单位下移|个单位②伸缩变换01,1,()()y f x y f x ωωω<<>=−−−−→=伸缩01,1,()()A A y f x y Af x <<>=−−−−→=缩伸③对称变换()()x y f x y f x =−−−→=-轴()()y y f x y f x =−−−→=-轴 ()()y f x y f x =−−−→=--原点1()()y x y f x y f x -==−−−−→=直线 ()(||)y y y y f x y f x =−−−−−−−−−−−−−−−→=去掉轴左边图象保留轴右边图象,并作其关于轴对称图象()|()|x x y f x y f x =−−−−−−−−−→=保留轴上方图象将轴下方图象翻折上去(2)识图对于给定函数的图象,要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性,注意图象与函数解析式中参数的关系. (3)用图函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,获得问题结果的重要工具.要重视数形结合解题的思想方法.。
人教版高中数学必修1《集合的概念》PPT课件

• 题型二 元素与集合的关系 • 【学透用活】
• 元素与集合的关系解读
a∈A与a∉A取决于a是不是集合A中的元素,只 唯一性
有属于和不属于两种关系 符号“∈”“∉”具有方向性,左边是元素, 方向性 右边是集合
[典例 2] (1)满足“a∈A 且 4-a∈A,a∈N 且 4-a∈N ”,有且只有 2
名称 自然数集 正整数集 整数集 有理数集 实数集
记法
N _________
_N_*_或N_+_
_Z__
_Q__
_R__
• [微思考] N与N*有何区别?
• 提示:N*是所有正整数组成的集合,而N是由0和所有的 正整数组成的集合,所以N比N*多一个元素0.
(二)基本知能小试
1.给出下列关系:①13∈R ;② 5∈Q ;③-3∉Z ;④- 3∉N ,其中正确的个
数为
()
A.1
B.2
C.3
D.4
解析:13是实数,①正确; 5是无理数,②错误;-3 是整数,③错误;- 3
是无理数,④正确.故选 B. 答案:B
2.已知集合 M 有两个元素 3 和 a+1,且 4∈M,则实数 a=________.
解析:由题意可知 a+1=4,即 a=3. 答案:3
• 知识点三 集合的表示方法
• [方法技巧] • 用列举法表示集合的3个步骤
• (1)求出集合的元素.
• (2)把元素一一列举出来,且相同元素只能列举一次.
• (3)用花括号括起来.
• 提醒:二元方程组的所有实数解组成的集合、函数图象 上的所有点构成的集合都是点的集合,一定要写成实数对 的形式,元素与元素之间用“,”隔开,如{(2,3),(5,- 1)}.
人教版(新教材)高中数学第一册(必修1)精品课件4:1.1 第1课时 集合的概念

名称 自然数集 正整数集 整数集 有理数集 实数集
符号 _N__ __N__+_或__N_*_ _Z__
_Q__
_R__
[题型探究] 题型一 集合的基本概念 例1 下列每组对象能否构成一个集合: (1)我们班的所有高个子同学; 解 “高个子”没有明确的标准,因此不能构成集合. (2)不超过20的非负数; 解 任给一个实数x,可以明确地判断是不是“不超过20的非负数”, 即“0≤x≤20”与“x>20或x<0”,两者必居其一,且仅居其一,故 “不超过20的非负数”能构成集合;
[预习导引]
1.元素与集合的概念 (1)集合:把一些能够 确定的不同的对象看成一个整体,就说这个 整体是由这些对象的全体 构成的集合(或集). (2)元素:构成集合的 每个对象 叫做这个集合的元素. (3)集合元素的特性: 确定性、 互异性 .
2.元素与集合的关系
关系
概念
记法
如果 a是集合A 的元素, 属于
[即时达标]
1.下列能构成集合的是( C ) A.中央电视台著名节目主持人 C.上海市所有的中学生
B.我市跑得快的汽车 D.香港的高楼
【解析】A、B、D中研究的对象不确定,因此不能构成集合.
2.已知1∈{a2,a},则a=__-_1___.
【解析】当a2=1时,a=±1,但a=1时,a2=a,由元素的互异性 知a=-1.
【解析】深圳不是省会城市,而广州是广东省的省会.
4.已知① 5∈R;②13∈Q;③0∈N;④π∈Q;⑤-3∉Z.
【解析】序号 Biblioteka 否构成集合理由(1)
能
其中的元素是“三条边相等的三角形”
“难题”的标准是模糊的、不确定的,所以
(2)
不能
广东省惠州市人教版高中数学必修一1.1.1集合的含义与表示

第一章 集合与函数概念1.1.1集合的含义与表示【知识要点】1.元素:一般地,把研究对象统称为元素,小写字母a,b,c 表示.2.集合:一些元素集合组成的总体,简称集,大写字母A,B,C 表示.3.集合的元素的性质:确定性、互异性和无序性.4.元素与集合的关系:①a A ∈↔a 属于集合A ;②a A ∉↔a 不属于集合A .5.常用数集6.集合的表示与分类方法{}{}⎪⎩⎪⎨⎧>↔↔1:,,,:x x d c b a 描述法无限集列举法有限集考点一:集合的概念与特征1.已知集合S 中的三个元素a,b,c 是△ABC 的三边长,那么△ABC 一定不是( )A.锐角三角形B.直角三角形C.钝角三角形D.等腰三角形2.下列集合表示正确的是( )A.(1,2,3)B.{2,4,4}C.{2,4}D.{高个子男生}3.已知集合A={(x,y)丨x+y ≤2,x,y ∈N},则A 中元素的个数为( )A.1B.5C.6D.无数个4.设集合A={0,1,2},则集合B={x-y 丨x ∈A,y ∈A}中元素的个数是( )A.1B.3C.5D.95.若1∈{x+2,2x },则实数x 的值为( )A.-1B.1C.1或-1D.1或36.如果一个集合含有三个元素:1,x,x x -2,则实数x 的取值范围是______________. 考点二:元素与集合的关系1.下列元素与集合的关系表示正确的是( )①-1∈*N ;②Q Q Z ∈∈⊄π;④;③232 A.①② B.②③ C.①③ D.③④2.下列表示正确的是( )A.0∈NB.N ∈72 C.-3∈N D.π∈Q 3.设集合A 只含有一个元素a,则下列各式正确的是( )A.0∈AB.a AC.a ∈AD.a=A4.下列四个关系式中,正确的是( )A.a ∈{a,b}B.{a}∈{(a,b)}C.a {a}D.a {a,b}5.已知集合A 中含有三个元素:2,4,6,且当a ∈A 时,6-a ∈A,那么a 为____________.6.已知A 中元素满足x=3k-1,k ∈Z,则下列表示正确的是( )A.-1A B.-11∈A C.-34 A D.1k 32-∈A7.已知x,y 都是非零实数,xy xy y y x x z ++=可能的取值组合成集合A,则下列判断正确的是( )A.3∈A,-1∉AB.3∈A,-1∈AC.3∉A,-1∈AD.3∉A,-1∉A8.由a,1ab ,组合成的集合与由0,,a 2b a +组成的集合是同一个集合,求20202020a b +.考点三:集合的表示方法1.集合{1,3,5,7}用描述法表示出来为( )A.{x|x 是不大于7的非负奇数}B.{x|1≤x ≤7}C.{x|x ∈N 且x ≤7}D.{x|x ∈Z 且1≤x ≤7}2.集合{x ∈N|x-3|<2}用列举法表示( )A.{1,2,3,4}B.{1,2,3,4,5}C.{0,1,2,3,4,5}D.{0,1,2,3,4}3.下列集合中,不同于另外三个集合的是( )A.{x|x=1}B.{x|2x =1}C.{1}D.{y|0)1(2=-y }4.方程组⎩⎨⎧=-=+02y x y x 的解构成的集合是( ) A.{1} B.(1,1) C.{(1,1)} D.{1,1}5.把集合{x|0542=--x x }用列举法表示为( )A.{x=-1,x=5}B.{x|x=-1或x=5}C.{0542=--x x }D.{-1,5}6.下列选项中,集合{2,1,12--x x } 中的实数x 不能取的值为是( )A.2B.3C.4D.57.下列四个命题正确的是( )A.某校高一一班所有聪明的学生可以构成一个集合B.集合{a,b,c }与集合{c,b,a }是相等的集合C.方程0122=+-x x 的解构成的集合是{1,1}D.0与{0}表示同一个集合8.下列命题中正确的为( )A.很小的实数可以构成集合B.集合{y|12-=x y }与集合{(x,y )丨12-=x y }是同一的集合C.1,23,46,21-,0.5这些数组成的集合有5个元素 D.集合{(x,y )丨R y R x xy ∈∈<,,0}是指第二和第四象限内的点集9.已知集合A={x 丨N x N x∈∈-,512},用列举法可表示为______________.10.已知集合A={x 丨a x x +-22,x ∈R }中只有一个元素,则a 为______________.11.设集合B={N x ∈丨N x∈+26}. (1)试判断元素1和元素2与集合B 的关系;(2)用列举法表示集合B.12.用适当的方法表示下列集合:(1)所有能被3整除的整数;(2)图中阴影部分的点(含边界)的坐标的集合;(3)满足方程x=丨x 丨,x ∈Z 的所有x 的值构成的集合B.。
人教版高中数学必修一课件:1.1《集合》 (共23张PPT)

一个给定集合中的元素是互不相同的.即集合 中的元素是不重复出现的。
(3)无序性:
元素完全相同的两个集合相等,而与列举顺序 无关。
【注】两个集合相等当且仅当构成
这两个集合的元素是完全一样的.
三、元素与集合的关系
常见数集:
1. 自然数集(非负整数集): N 2. 正整数集: N*或N+ 3. 整数集: Z 4. 有理数集: Q 5. 实数集: R
(2) 描述法:
{ x I | P( x)}
元素符号 范围 元素的特征
【例2】试分别用列举法和描述法表示下列 集合 (1)方程x2-2=0的所有实数根组成的集合; (2)由大于10小于20的所有整数组成的集合.
【思考题】用列举法表示集合:
ab 1) A { x | x ,
a, b为非零实数}
3.
方程组
x x
y9 y3
的解集用列举
法或描述法表示为
。
4、已知x2∈ {1, x, 0}, 求实数x的值.
52、) 补充 : 含有三个实数的集合可
表示为{ a, b , 1 }, 也可表示为 a
{a 2 , aabb,,00},}求, 求a 2a0120006 b b . 20120006.
6、已知集合A={x∈R|mx2-2x+3=0, m∈R}且A中只有一个元素,求m的值.
课堂练习 P5 练习1、2
小结
1. 集合的概念; 2. 元素与集合的关系; 3. 集合的元素特征; 4. 集合的表示方法;
ab
2) B {k N | 6 Z} 3k
思考:B { 6 Z | k N }呢? 3k
1. 已知集合S中有三个元素 a, b, c
第一章-1.1-集合的概念高中数学必修第一册人教A版

A
1到20内的质数有:2,3,5,7,11,13,17,19,是确定的.
√
B
如何才算著名?标准不明确.
×
C
我国古代四大发明为造纸术、指南针、火药、印刷术,是确定的.
√
D
集合中元素明确,能构成集合.
√
例1-2 [教材改编P5习题1.1 T1]用符号“∈ ”和“∉ ”填空:
∉
∉
(1)设集合是正整数的集合,则0___,
设另一元素为,由集合中元素的互异性可得 ≠ 1且 ≠ 2,假设 ≠ 3,此时 = {1,
2,}, + 1 ∉ , − 1 ∉ ,是B的一个“孤立元”,不合题意,故 = 3.
据此分析满足条件的集合为{1,2,3},{2,3,4},{3,4,5},{4,5,6},{5,
6,7},{6,7,8},共有6个.
第一章 集合与常用逻辑用语
1.1 集合的概念
必备知识解读
知识点1 集合与元素的含义
例1-1 [教材改编P2引例][多选题]下列各对象可以组成集合的是( ACD
A.1到20内的所有质数
B.中国著名的数学家
C.我国古代四大发明
D.某学校2023~2024学年度第一学期全体高一学生
)
【解析】
选项
分析
结果
∈ ,对任意 ∈ ,都有 ⊕ = ⊕ = ,则称关于运算⊕ 为“融洽集”.现给出下
列集合和运算:
① = {|是非负整数},⊕ 为整数的加法;
② = {|是偶数},⊕ 为整数的乘法;
③ = {|是二次三项式},⊕ 为多项式的加法.
①
其中关于运算⊕ 为“融洽集”的是____.(写出所有满足条件的序号)
【解析】① = {|是非负整数},⊕ 为整数的加法,满足对任意, ∈ ,都有
高中数学人教版必修1课件1.1.1集合的含义(系列一)

)
A.0 B.1
C.-1 D.1或-1
解析:由x2∈A,得x2=0或x2=1或x2=x.
当x2=0时,解得x=0,不符合集合中元素的互异性,舍去.
当x2=1时,解得x=±1.
若x=1,不符合集合中元素的互异性,舍去.
若x=-1,符合集合中元素的互异性.
当x2=x时,解得x=0或x=1,由上可知,都舍去.
性进行检验.
3
2
解:因为-3∈A,所以a-2=-3或2a +5a=-3,解得a=-1或a=- .
2
2
当a=-1时,a-2=-3,2a +5a=-3,集合A不满足元素的互异性,所以舍
去a=-1.
3
3
当a=- 时,经检验,符合题意.故a=- .
2
2
变式训练3 已知集合A含有3个元素0,1,x,且x2∈A,则实数x的值
)
A.2
B.3
C.0或3
D.0,2,3均可
解析:因为2∈A,所以m=2或m2-3m+2=2.
当m=2时,m2-3m+2=0,不满足集合中元素的互异性,舍去.
当m2-3m+2=2时,m=0或m=3,由集合中元素的互异性知,m=3.故
选B.
答案:B
1.下列各组对象能构成集合的是(
)
A.所有漂亮的工艺品
解析:因为a2=5,所以a=± 5 .
答案:∈ ∉
5.已知集合 M 中含有 3 个元素 0,x2,-x,求 x 满足的条件.
2 ≠ 0,
≠ 0,
解:根据集合中元素的互异性知 - ≠ 0, 解得
≠ -1.
2
≠ -,
故 x 满足的条件为 x≠0,且 x≠-1.
人教A版高中数学必修第一册1.1集合的概念课件

集合的表示方法——描述法
把一般地,设A为一个集合,我们把A中所具有的
共同特征P(x)的元素中的x所组成的集合表示为
x A|P ( x )
这种表示集合的方法称为描述法.
有时也用冒号或分号代替竖
线,写成:{ ∈ : ()}
或{ ∈ ;()}
例如:实数集中,有限小数和无限循环小数都具有
(2)由大于10小于20的所有整数组成的集合.
达标检测
1.下列对象不能构成集合的是( D )
①我国近代著名的数学家;②所有的欧盟成员国;③空气中密度大的气体.
A.①②
B.②③
C.①②③
D.①③
1
2.下列三个关系式:① 5∈R;② ∉Q;③0∈Z.其中正确的个数是( B )
4
A.1 B.2 C.3 D.0
元素组成的总体叫做集合(简称为集).
字母表示:
通常用大写字母A.B.C…表示集合;用小写字母
a.b.c…表示集合中的元素。
探究2 集合中元素的性质
1、所有“帅哥”能否构成一个集合?
不能,因为这个集合不确定
确定性
2、由1、3、0、5、|-3|组成的集合有5个元素,对吗?
互异性
不对,只有4个元素
3、5班同学组成一个集合,调整座位后集合变了吗?
没变,因为元素没变
无序性
补充:两个集合中,元素完全一样,则两集合相等
小试牛刀
判断以下元素的全体是否组成集合,并说明理由:
(1) 大于3小于11的偶数; √
×
(2) 我国的小河流.
探究3 元素和集合的关系
思考:用A表示高一(3)班全体学生组成的集合,用a表示高一(3)班的
一位同学,b表示高一(4)班的一位同学.
高中数学人教A必修一课件-1.1.1集合的含义与表示

集合的表示方法
3、描述法:
将集合的所有元素都具有的性质(共同特征) 表示出来的方法叫做描述法,可写成{x︱p(x)} 的情势。其中x为元素符号及取值范围。
共同特征性质
Venn图:形象 直观
(1)中国的直辖市 (2)中国的高个子 (3)所有的直角三角形 (4)x,3x+2,5y-x,x+y (5)本的元素必须是确定 的.
(2)互异性:集合中的元素必须是互不相同 的。
(3)无序性:集合中的元素是无先后顺序的. 集合中的任何两个元素都可以交换位置.
集合的有关概念
元素(element)---我们把研究的对象 统称为元素
集合(set)---把一些元素组成的总体叫 做集合, 简称集.
一般用大括号”{ }”表示集合,也常用 大写的拉丁字母A、B、C…表示集合. 用小写的拉丁字母a,b,c…表示元素
注:组成集合的元素可以是物,数,图,点等
下列对象能不能构成集合?元素 是什么?有多少个?
注意:只要构成两个集合的元素是一 样的,我们就称这两个集合是相等的。
思考:
判断以下元素的全体是否组成集合,并 说明理由; (1) 大于3小于11的偶数; (2) 我国的小河流。
判断下列例子能否构成集合
地球的四大洋
√
身材较肥的人
×
著名的数学家
×
高一(17)班眼睛很近视的同学 ×
注:像”很”,”非常”,”比较”这些不确定的词 都不能构成集合。
a,b,c…
• 例2试分别用列举法和描述法表示下 列集合:
• (1)方程x2-2=0的所有实数根组成的集 合;
人教 高中数学必修第一册第一章《1.1集合的概念》课件(共17张ppt)

(4). Venn图
我们常常画一条封闭的曲线,用 它的内部表示一个集合.
例如,图1-1表示一个集合AA 图1-1
元素,称为空集,记为;
(4) 两个集合的元素若一样,则称它们相等。
4.几个常用数集:
(1) N: 自然数集(含0) 即非负整数集
(2) N+* : 正整数集(不含0) (3) Z:整数集 (4) Q:有理数集 (5) R:实数集
5.集合的几种表示法
(1).自然语言法
(2).列举法:适用对象:有限、有规律
取值范围.a≠-2 (互异性应用)
知识点2 元素与集合的关系
1. 用符号“∈”或“ ”填空
(1) 3.14 Q (2)
Q
(3) 0 N+ (4) (-2)0 N+ (5) 2 3 Q (6) 2 3 R
书本P5:1
温馨提示:分类讨论+检验
3.已知x2∈{1, 0,x},求实数x的值.
(3)无序性:集合中的元素是无
先后顺序的.
3.集合与元素的关系:
(1) 如果a是集合A的元素,就说a属于集 合A,记作a ∈ A;
如果a不是集合A的元素,就说a不属
于集合A,记作a A.
(2) 集合中的元素可以是数,点,式, 图,人,物……;
(3) 集合中的元素个数如果有限,称为有 限集;如果个数无限,称为无限集;如果没有
(5)小于10的所有自然数组成的集合; (6)1~20以内的所有素数组成的集合;
2、用描述法表示下列集合: (1)正偶数集; (2)被3除余2的正整数集合; (3)直角坐标平面内坐标轴上的点集.
高中数学 第一章 集合与函数概念 1.1.1 集合的含义与表示 第2课时 集合的表示课件 新人教版必修1

举法表示为{(1,2)},也可用描述法表示为{(x,y)|xy= =12, }.
易错警示
解析答案
跟踪训练4 用列举法表示下列集合. (1)A={y|y=-x2+6,x∈N,y∈N}; 解 因为y=-x2+6≤6,且x∈N,y∈N, 所以x=0,1,2时,y=6,5,2,符合题意, 所以A={2,5,6}. (2)B={(x,y)|y=-x2+6,x∈N,y∈N}. 解 (x,y)满足条件y=-x2+6,x∈N,y∈N,
{0,1,2,3,4,5,6,7,8,9}.
(2)方程x2=x的所有实数根组成的集合;
解 设方程x2=x的所有实数根组成的集合为B,那么B={0,1}.
(3)由1~20以内的所有质数组成的集合.
解 设 由 1 ~ 2 0 以 内 的 所 有 质 数 组 成 的 集 合 为 C , 那 么 C=
反思与感悟
第一章 1.1.1 集合的含义与表示
第2课时 集合的表示
学习 目标
1.掌握集合的两种表示方法(列举法、描述法). 2.能够运用集合的两种表示方法表示一些简单集合.
栏目 索引
知识梳理 题型探究 当堂检测
自主学习 重点突破 自查自纠
知识梳理
自主学习
知识点 集合的表示方法 1.列举法:把集合的元素 一一列举 出来,并用花括号“{ }”括起来表 示集合的方法叫做列举法. 2.描述法:(1)定义:用集合所含元素的 共同特征 表示集合的方法称为描 述法. (2)写法:在花括号内先写上表示这个集合元素的_一__般__符__号__及__取__值__(_或__变__ 化)范围 ,再画一条竖线,在竖线后写出这个集合中元素所具有的_共__同__ 特征 .
则Δ=64-64k=0,即k=1.
人教A版高中数学必修1第一章1.1集合的概念与运算课件

人教A版高中数学必修1第一章1.1集合 的概念 与运算 课件
5.集合分类:
按集合中元素个数的多少可分为:有限集和无限集. 含有有限个元素的集合叫做有限集. 含有无限个元素的集合叫做无限集. 若按集合中元素属性来分:数集,点集 高中数学主要研究数集和点集.
人教A版高中数学必修1第一章1.1集合 的概念 与运算 课件
列举法:把集合中的元素一一列举出来,并用 花括号{ }括起来表示集合的方法叫做列举法.
注意:对含有较多元素的集合,如果构成该集 合的元素具有明显的规律,可用列举法表 示,但是必须把元素间的规律显示清楚后, 才能用省略号表示.
x2 x
人教A版高中数学必修1第一章1.1集合 的概念 与运算 课件
人教A版高中数学必修1第一章1.1集合 的概念 与运算 课件
P4 思考?
人教A版高中数学必修1第一章1.1集合 的概念 与运算 课件
人教A版高中数学必修1第一章1.1集合 的概念 与运算 课件
描述法:用集合所含元素的共同特征
表示集合的方法称为描述法.
可分为:
(1)文字描述法——用文字把元素所具有的属性 描述出来,如﹛自然数﹜
(2)符号描述法——用符号把元素所具有 的属性 描述出来,即{x| P(x)} 或{x∈A| P(x)},{(x,y)|f(x,y)=0}等。
其中能构成集合的有: (1) 不能构成集合的有: (2)(3)(4)
人教A版高中数学必修1第一章1.1集合 的概念 与运算 课件
人教A版高中数学必修1第一章1.1集合 的概念 与运算 课件
在我们要了解集合的特征前,先看看这 些具有代表性的问题。 (1)A={1,3},问3,5哪个是A的元素? (2)A={素质好的人}能否表示成集合? (3)A={2,2,4 }表示是否正确? (4)A={太平洋,大西洋},
高中数学集合的概念课件人教版必修一.ppt1.1.1

如果a是集A的元素,记作: a ∈ A 如果a不是集A的元素,记作: a ∉A
例如,用A表示“ 1~20以内所有的整数”组成的集合,则有
4.常见的数集有哪些?分别要怎样来表示?
数集 自然数集(非负整数集) 正整数集 符号
N N* 或N+ Z Q R
整数集
有理数集 实数集
知识探究(一)集合的表示方法 问题1:通过我们对课本的预习,我们知道,课本为我们提供了 哪几种集合表示方法?
B={ x Z 10 x 20 }
用列举法表示为 B= { 11,12,13,14,15,16,17,18,19}
课堂练习 用适当的方法表示下列集合: (1)绝对值小于3的所有整数组成的集合;
(2)在平面直角坐标系中以原点为圆心,横坐标上的点 组成的集合;
(3)所有奇数组成的集合; (4)由数字1,2,3组成的所有三位数构成的集合.
知识探究(三)
思考1:a 与{a }的含义是否相同? 思考2:集合{1,2}与集合{(1,2)}相同吗? 思考3:集合{ y | y x 2 , x R} 与集合 { y x 2 } 相同吗? 思考4:集合 {( x, y) | y x 2 , x R}11,13,17,19}.
2.互异性
3.无序性
问题4:考察下列集合: (1)不等式2 x 7 3 的解组成的集合; (2)绝对值小于2的实数组成的集合.
思考1:这两个集合能不能用列举法表示? 思考2:如何用数学式子描述上述两个集合的元素特征? 思考3:上述两个集合还可以怎么表示? 思考4:这种表示集合的方法叫什么? 描述法 思考5:描述法表示集合的基本模式是什么? 用集合所含元素的共同特征表示集合的方法.
他的著作有:《G.康托尔全集》1卷及《康托尔-戴德金通信集》等。 康托尔是德国数学家,集合论的创始者。1845年3月3日生于圣彼得堡,1918年1 月6日病逝于哈雷。 康托尔11岁时移居德国,在德国读中学。1862年17岁时入瑞士苏黎世大学,翌年 入柏林大学,主修数学,1866年曾去格丁根学习一学期。1867年以数论方面的论文获 博士学位。1869年在哈雷大学通过讲师资格考试,后在该大学任讲师,1872年任副教 授,1879年任教授。 集合论是现代数学的基础,康托尔在研究函数论时产生了探索无穷集和超穷数的 兴趣。康托尔肯定了无穷数的存在,并对无穷问题进行了哲学的讨论,最终建立了较 完善的集合理论,为现代数学的发展打下了坚实的基础。
人教版高中数学必修一第一章知识点
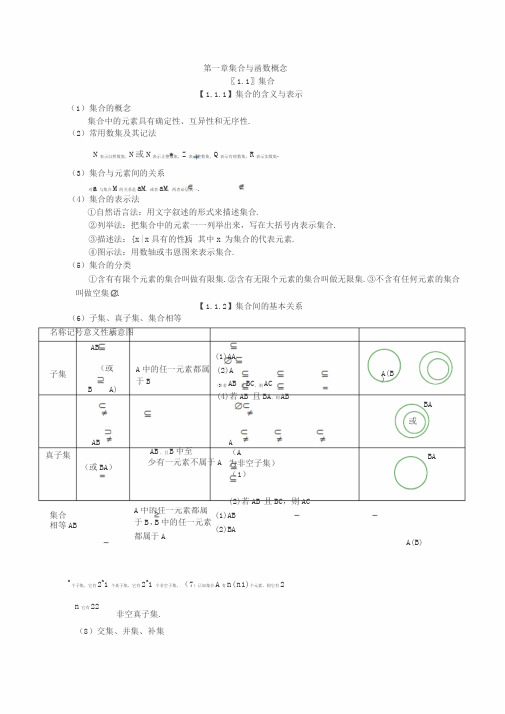
第一章集合与函数概念〖1.1〗集合【1.1.1】集合的含义与表示(1)集合的概念集合中的元素具有确定性、互异性和无序性.(2)常用数集及其记法N表示自然数集,N或N表示正整数集,Z表示整数集,Q表示有理数集,R表示实数集.(3)集合与元素间的关系对象a与集合M的关系是aM,或者aM,两者必居其一.(4)集合的表示法①自然语言法:用文字叙述的形式来描述集合.②列举法:把集合中的元素一一列举出来,写在大括号内表示集合.③描述法:{x|x具有的性质},其中x为集合的代表元素.④图示法:用数轴或韦恩图来表示集合.(5)集合的分类①含有有限个元素的集合叫做有限集.②含有无限个元素的集合叫做无限集.③不含有任何元素的集合叫做空集().【1.1.2】集合间的基本关系(6)子集、真子集、集合相等名称记号意义性质示意图AB(1)AA子集B (或A)A中的任一元素都属于B(2)A(3)若AB且BC,则AC(4)若AB且BA,则ABA(B)BA或真子集AB(或BA)AB,且B中至少有一元素不属于AA(A为非空子集)(1)(2)若AB且BC,则ACBA集合相等AB A中的任一元素都属于B,B中的任一元素都属于A(1)AB(2)BAA(B)n个子集,它有2n1个真子集,它有2n1个非空子集,(7)已知集合A有n(n1)个元素,则它有2n它有22非空真子集. (8)交集、并集、补集1【1.1.3】集合的基本运算名称记号意义性质示意图AB 交集{x|x A,且(1)AAA(2)AAB(3)ABAxB}ABBAB 并集{x|x A,或(1)AAA(2)AAAB(3)ABAxB}ABB1A(e U A)2()AeAUU补集e U A{x|xU,且xA} 痧U(A B)(U A)(?U B)痧U(AB)(U A)(?U B)【补充知识】含绝对值的不等式与一元二次不等式的解法(1)含绝对值的不等式的解法不等式解集|x|a(a0){x|axa}|x|a(a0)x|xa或xa}把axb看成一个整体,化成|x|a,|axb|c,|axb|c(c0)|x|a(a0)型不等式来求解(2)一元二次不等式的解法判别式24bac000二次函数2(0)yaxbxcaO的图象一元二次方程20(0)axbxcax1,22bb4ac2abxx122a无实根(其中x1x2)的根20(0) axbxca的解集b{x|xx或xx2}{x|x}12aR 220(0)axbxca的解集{x|xxx}12〖1.2〗函数及其表示【1.2.1】函数的概念(1)函数的概念①设A、B是两个非空的数集,如果按照某种对应法则f,对于集合A中任何一个数x,在集合B中都有唯一确定的数f(x)和它对应,那么这样的对应(包括集合A,B以及A到B的对应法则f)叫做集合A到B的一个函数,记作f:AB.②函数的三要素:定义域、值域和对应法则.③只有定义域相同,且对应法则也相同的两个函数才是同一函数.(2)区间的概念及表示法①设a,b是两个实数,且ab,满足a xb的实数x的集合叫做闭区间,记做[a,b];满足axb的实数x的集合叫做开区间,记做(a,b);满足a xb,或axb的实数x的集合叫做半开半闭区间,分别记做[a,b),(a,b];满足x a,xa,xb,xb的实数x的集合分别记做[a,),(a,),(,b],(,b).注意:对于集合{x|axb}与区间(a,b),前者a可以大于或等于b,而后者必须ab.(3)求函数的定义域时,一般遵循以下原则:①f(x)是整式时,定义域是全体实数.②f(x)是分式函数时,定义域是使分母不为零的一切实数.③f(x)是偶次根式时,定义域是使被开方式为非负值时的实数的集合.④对数函数的真数大于零,当对数或指数函数的底数中含变量时,底数须大于零且不等于1.⑤ytanx中,()xkkZ.2⑥零(负)指数幂的底数不能为零.⑦若f(x)是由有限个基本初等函数的四则运算而合成的函数时,则其定义域一般是各基本初等函数的定义域的交集.⑧对于求复合函数定义域问题,一般步骤是:若已知f(x)的定义域为[a,b],其复合函数f[g(x)]的定义域应由不等式ag(x)b解出.⑨对于含字母参数的函数,求其定义域,根据问题具体情况需对字母参数进行分类讨论.⑩由实际问题确定的函数,其定义域除使函数有意义外,还要符合问题的实际意义.(4)求函数的值域或最值求函数最值的常用方法和求函数值域的方法基本上是相同的.事实上,如果在函数的值域中存在一个最小(大)数,这个数就是函数的最小(大)值.因此求函数的最值与值域,其实质是相同的,只是提问的角度不同.求函数值域与最值的常用方法:①观察法:对于比较简单的函数,我们可以通过观察直接得到值域或最值.②配方法:将函数解析式化成含有自变量的平方式与常数的和,然后根据变量的取值范围确定函数的值域或最值.③判别式法:若函数yf(x)可以化成一个系数含有y的关于x的二次方程2a(y)xb(y)xc(y)0,则在a(y)0时,由于x,y为实数,故必须有byaycy,从而确定函数的值域或最值.2()4()()0④不等式法:利用基本不等式确定函数的值域或最值.⑤换元法:通过变量代换达到化繁为简、化难为易的目的,三角代换可将代数函数的最值问题转化为三角函数的最值问题.⑥反函数法:利用函数和它的反函数的定义域与值域的互逆关系确定函数的值域或最值.⑦数形结合法:利用函数图象或几何方法确定函数的值域或最值.⑧函数的单调性法.【1.2.2】函数的表示法(5)函数的表示方法表示函数的方法,常用的有解析法、列表法、图象法三种.解析法:就是用数学表达式表示两个变量之间的对应关系.列表法:就是列出表格来表示两个变量之间的对应关系.图象法:就是用图象表示两个变量之间的对应关系.(6)映射的概念①设A、B是两个集合,如果按照某种对应法则f,对于集合A中任何一个元素,在集合B中都有唯一的元素和它对应,那么这样的对应(包括集合A,B以及A到B的对应法则f)叫做集合A到B的映射,记作f:AB.②给定一个集合A到集合B的映射,且aA,bB.如果元素a和元素b对应,那么我们把元素b叫做元素a的象,元素a叫做元素b的原象.〖1.3〗函数的基本性质 【1.3.1】单调性与最大(小)值(1)函数的单调性①定义及判定方法 函数的定义图象判定方法性质 如果对于属于定义域I 内某(1)利用定义个区间上的任意两个自变量 的值x2,当x . 1、x 1.<.x .2.时,都y y=f(X) f(x)2(2)利用已知函数的 单调性有f .(x ...).<.f(.x ...).,那么就说 12 f(x)在这个区间上是增函数. ...f(x)1(3)利用函数图象(在 某个区间图o x 1x 2x 象上升为增)函数的(4)利用复合函数 单调性(1)利用定义如果对于属于定义域I 内某yy=f(X)(2)利用已知函数的个区间上的任意两个自变量 11、x .<.x .的值x2,当x .2.时,都 有f .(x ..12.).,那么就说f(x) 1f(x) 2单调性 (3)利用函数图象(在 某个区间图f(x)在这个区间上是减函数. ...o xx 12x象下降为减)(4)利用复合函数②在公共定义域内,两个增函数的和是增函数,两个减函数的和是减函数,增函数减去一个减函数为 增函数,减函数减去一个增函数为减函数.③对于复合函数yf[g(x)],令ug(x),若yf(u)为增,ug(x)为增,则yf[g(x)]为增;若yf(u)为减,ug(x)为减,则y f[g(x)]为增;若yf(u)为 增,ug(x)为减,则y f[g(x)]为减;若yf(u)为减,ug(x)为增,则yyf[g(x)]为减.a(2)打“√”函数()(0)fxxax的图象与性质 f(x)分别在(,a ]、[a ,)上为增函数,分别在ox[a,0)、(0,a]上为减函数.(3)最大(小)值定义①一般地,设函数yf(x)的定义域为I,如果存在实数M满足:(1)对于任意的xI,都有f(x)M;(2)存在x I,使得f(x0)M.那么,我们称M是函数f(x)的最大值,记作0f max(x)M.5②一般地,设函数yf(x)的定义域为I,如果存在实数m满足:(1)对于任意的xI,都有f(x)m;(2)存在x0I,使得f(x0)m.那么,我们称m是函数f(x)的最小值,记作f max(x)m.【1.3.2】奇偶性(4)函数的奇偶性①定义及判定方法函数的定义图象判定方法性质如果对于函数f(x)定义域内(1)利用定义(要先任意一个x,都有.f(.-.x..)=.-.判断定义域是否关于f(x)....,那么函数f(x)叫做奇.函.原点对称)数..(2)利用图象(图象关于原点对称)函数的奇偶性如果对于函数f(x)定义域内(1)利用定义(要先任意一个x,都有f(-.x..)=.f.(x.)..,..判断定义域是否关于那么函数f(x)叫做偶.函.数..原点对称)(2)利用图象(图象关于y轴对称)②若函数f(x)为奇函数,且在x0处有定义,则f(0)0.③奇函数在y轴两侧相对称的区间增减性相同,偶函数在y轴两侧相对称的区间增减性相反.④在公共定义域内,两个偶函数(或奇函数)的和(或差)仍是偶函数(或奇函数),两个偶函数(或奇函数)的积(或商)是偶函数,一个偶函数与一个奇函数的积(或商)是奇函数.〖补充知识〗函数的图象(1)作图利用描点法作图:①确定函数的定义域;②化解函数解析式;③讨论函数的性质(奇偶性、单调性);④画出函数的图象.利用基本函数图象的变换作图:要准确记忆一次函数、二次函数、反比例函数、指数函数、对数函数、幂函数、三角函数等各种基本初等函数的图象.①平移变换yfxyfxh()h0,h()左移个单位右移|个单位h0,h|yfxyfxk()kk()0,上移个单位下移|个单位k0,k|变换②伸缩01,伸yf(x)yf(x)1,缩6yfxyAfx()0A1,缩()A1,伸③对称变换x轴yf(x)y轴yf(x)yf(x)yf(x)原点直线1yxyf(x)yf(x)yf(x)yf(x)去掉轴左边图象yyf(x)yf(|x|)保留y轴右边图象,并作其关于y轴对称图象保留轴上方图象yfxyfx()x|()|将轴下方图象翻折上去x(2)识图对于给定函数的图象,要能从图象的左右、上下分别范围、变化趋势、对称性等方面研究函数的定义域、值域、单调性、奇偶性,注意图象与函数解析式中参数的关系.(3)用图函数图象形象地显示了函数的性质,为研究数量关系问题提供了“形”的直观性,它是探求解题途径,获得问题结果的重要工具.要重视数形结合解题的思想方法.7。
集合的概念课件-人教A版高中数学必修第一册

解题方法 (根据集合中元素的特性求解字母取值(范围)的3个步骤)
求解
根据集合中元素的确定性,解出字母的所有取值
检验 作答
根据集合中元素的互异性,对解出的值进行检验 写出所有符合题意的字母的取值
自主预习,回答问题
阅读课本3-5页,思考并完成以下问题
1.集合有哪两种表示方法?它们如何定义? 2.它们各自有什么特点? 3.它们使用什么符号表示?
(3)不能出现未被说明的字母.
[小试身手]
1.判断(正确的打“ √ ”,错误的打“×”)
(1)由1,1,2,3组成的集合可用列举法表示为{1,1,2,3}. ( × )
(2)集合{(1,2)}中的元素是1和2.
(×)
(3)集合A={xlx—1=0} 与集合B={1} 表示同一个集合.( √ )
答案: C
_个元素.
答案:2
所有解组成的集合中共有
题型分析 举一反三
题型一集合的含义
[例1] 考查下列每组对象,能构成一个集合的是(B ) ①某校高一年级成绩优秀的学生;
②直角坐标系中横、纵坐标相等的点;
③不小于3的自然数;
④202X年第23届冬季奥运会金牌获得者.
A.③④
B.②③④
C.②③
D.②④
解 题 方 法(判断一组对象能否组成集合的标准)
· 解题方法(描述法表示集合的2个步骤)
写代表元素
明确元素 的特征
分清楚集合中的元素是点还是数或是其 他的元素
将集合中元素所具有的公共特征,写在竖 线的后面
[跟踪训练二]
3. 用符号“∈”或“中”填空:
(1)A={xlx²—x=0}, 则1
A,—1
A;
(2)(1,2)
人教版高中数学必修一1.1.1_集合的含义与表示ppt课件

A,记作属于 . A,记不作属于
高一(1)班的学生组成集合A,a是高一(1)班的学生,b不是高一(1)班的学生 a与A,b与A之间有何关系? 提示:a∈A b∉A
Hale Waihona Puke 3.几种常用的数集及记法N
N*或N+
Z
Q
用“∈”或“∉”填空. 2________N; 2________Q;12________R; -3________Z;0________N*;5________Z. 提示:∈ ∉ ∈ ∈ ∉ ∈
[解] ∵1∈A,∴a+2,(a+1)2,a2+3a+3都可能等于1. ①若a+2=1,则a=-1,此时A中的元素为1,0,1与集合中元素的互异性矛盾 故舍去; ②若(a+1)2=1,则a=0或a=-2, 当a=0时,A={2,1,3}适合题意, 当a=-2时,A中的元素为0,1,1与集合中元素的互异性矛盾,舍去, ③若a2+3a+3=1,则a=-1或a=-2,由①②知都不合题意,舍去. 综上所述,a=0.
的、 确定 的.互不相同
(1)“高一(2)班1.78米以上的同学”、“16岁的少年”、 “大于1的数”能构成一个集合吗? 提示:能构成集合.
(2)“高一(2)班的高个子同学”、“年轻人”、“帅哥”、 “接近0的数”能构成集合吗? 提示:不能构成集合.
2.元素与集合的关系 (1)如果a是集合A中的元素,就说a (2)如果a不是集合A中的元素,就说a
• 一、释疑难 • 对课堂上老师讲到的内容自己想不通卡壳的问题,应该在课堂上标出来,下课时,在老师还未离开教室的时候,要主动请老师讲解清楚。如果老师已
经离开教室,也可以向同学请教,及时消除疑难问题。做到当堂知识,当堂解决。 • 二、补笔记 • 上课时,如果有些东西没有记下来,不要因为惦记着漏了的笔记而影响记下面的内容,可以在笔记本上留下一定的空间。下课后,再从头到尾阅读一
【人教版】高中数学必修一:《集合》PPT课件

(3) A={x|2x>1},B={x|2x1},C=R
你发现集合A,B,C之间有什么关系吗?
并集:
一般地,由所有属于集合A或属于B的 元素所组成的集合,称为集合A与B的 并集(union set),记作AB,即
AB={x|xA,或xB}
Venn图:
A AB
B
例6. 实验中学开运动会,设 A={x|x是实验中学高一年级参加百米赛跑的同学}, B={x|x是实验中学高一年级参加跳高比赛的同学}, 求AB.
例7.设平面内直线l1上点的集合为L1,直线l2上点 的集合为L2,试用集合的运算表示l1、l2的位置关 系.
补集: 引入:U={高一(13)班全体同学}, A={高一(13)班 全体男同学}, B={高一(13)班全体女同学},则集 合U, A, B的关系如何?
Venn图:
A
B
AB
例4.设A={4,5,6,8},B={3,5,7,8},求AB.
例5.设集合A={x|-1<x<2},集合B={x|1<x<3}, 求AB.
交集: 考察下面例子:
(1) A={2,4,6,8,10},B={3,5,8,12},C={8}; (2) A={x|x实验中学2004年9月在校的女
你能说出它们所包含的内容吗?
2.有关概念与性质: 元素: 把研究对象统称为元素(element).
集合: 把一些元素组成的总体叫做集合(set) . 确定性
性质:
互异性
无序性
相等: 构成两个集合的元素是一样的,则称 两个集合是相等的.
3.表示方法:
集合的表示: 用大写拉丁字母A,B,C,表示.
