固体物理学第三章第一节

合集下载

固体物理-第三章金属自由电子论讲解

N=I0G(EF)+ I1G’(EF)+ I2G’’(EF)+….. 其中, I0=- (-f/E) dE, I1=-(E-EF)(-f/E)dE,
3.1.量子自由电子理论
I2=(1/2!)-(E-EF)2(-f/E) dE 不难算出, I0=1(d-函数积分), I1=0 (根据d-函数的性质）为了计算I2, 而令h=(E-EF)/kBT,于是, I2=[(kBT)2/2]-{h2/[(eh+1)(e-h+1)] }dh=(pkBT)2/6
波长)，可见k为电子的波矢, 是3 维空间矢量. r:电子的位置矢量。
由波函数的归一化性质:vy*(r) y(r)d(r)=1, v:金属体积, 假设为立方体,边长为L，把3.1.1.3式代入归一化式子, 得: A=L-3/2=V-1/2, 所以
y(r)= V-1/2eik•r 3.1.1.4，此即自由电子的本征态。由周期性边界条件, y(x,y,z)= y(x+L,y,z) = y(x,y+L,z) = y(x,y,z+L)
一状态的电子具有确定的动量ħk和能量ħ2k2/(2m)，因而具有确定的速度,v=ħk/m,故一个k全面反映了自由电子的一个状态，简称态。
2. k-空间
以kx, ky , kz 为坐标轴建立的波矢空间叫k-空间。电子的本征态可以用该空间的一点
来代表。点的坐标由3.1.1.5 式确定。
3.1.量子自由电子理论
T>0K的费米能EF 把3.1.2.2和3.1.3.1代入3.1.3.2, 分步积分, 得:
N= (-2C/3) 0 E3/2(f/E) dE 3.1.3.3 令G(E)= 2C E3/2/3, 3.1.3.3.式化简为 N= 0G(E) (-f/E) dE 3.1.3.4 (-f/E)函数具有类似d函数的特性,仅仅在EF附近kBT范围内才有显著的值，且为E-EF偶函数. 由于(-f/E)函数具有这些性质,把G(E)在EF附近展开为泰勒级数, 且积分下限写成 -,不会影响积分值. 3.1.3.4化为:

固体物理第三章1

A
B A

2 2
cos(qa)
m2A

0
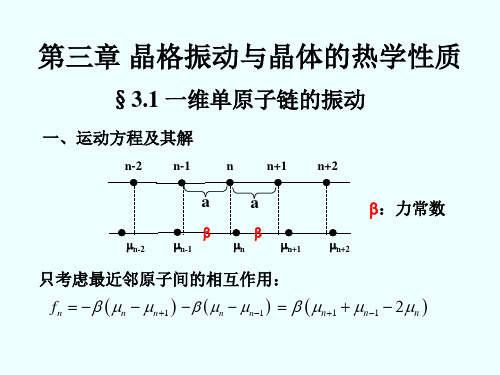
质量为m的原子静止，质量为M的原子振动。
本章主要讨论晶格的动力学
晶体中离子实或原子围绕其平衡位置的振动振动对固体性质的影响。
晶格动力学理论又叫晶格谐振理论，1912年由玻恩和卡门建立，其基本假设：
假设晶体中每个原子的中心平衡位置在对应的晶格格点上；这个原子离开平衡位置的位移与原子间距比是小量，可以用谐振近似，也就是说原子间的弹性势能可以表达成位移的二次项。
周期性边界条件（玻恩－卡门边界条件）：
un un N Ae iqna t Ae iq( N n)at
Ae iqna ωt eiqNa
eiqNa 1 qNa 2l q 2 l
Na
上式表明，周期性边界条件限制了晶格振动。即描写晶格振动状态的波矢q只能取一些分立的值。

(2)
A与B分别表示质量为m与M的原子的振幅。将试解代入运动方程可得：
(2 m 2 )A 2 cosqaB 0

2
co s qaA

(2

M 2 )B

0

(3)
这是振幅A与B的线性齐次方程，A与B不能同时为零，要求
2 m 2 2 cosqa
因为q的取值范围限制在第一布里渊区，即
q
a
a
π 2π l π L Na a Na a
N l N
2
2
q只能取相隔 2 L 的分立值
在波矢空间中，每一个可能的q所占据的线度为 2
L
波矢代表点的密度即为

固体物理第三章1-2

小振动，U(r)与U(a) 差别不大，在平衡位置泰勒级数展开：
3 1 d 2U 1 d U dU 2 3 U ( r ) U a r a 2 r a 3 r a ...... 2 dr a 6 dr a dr a
A 2 1 2 2 Mm 2 1 2 O 2 Mm
1 2 16 Mm qa 2 2 1 2 ( M m ) ( M m ) sin 2 ( ) 2 1 2 1 2 16 Mm qa 2 2 1 2 ( M m ) ( M m ) sin 2 ( ) 2 1 2
与单原子一维晶格类似：上述方程具有下述格波形式解
2n i q a t 2
u2 n Ae
Ae
i ( qnat )
u2 n1 B' e
2n i q( )a qbt 2
Be
i ( qnat )
U2n / u2n+1表示同一原胞中两种不等价原子的位移
相互作用力：
r = un+1 + a －un
2 1 d 3U dU d U 2 r a r a ...... f ( r ) 2 3 2 dr a dr a dr a
= 0
(d2U/dr2)a =
玻恩—卡门边界条件下平衡位置运动方程组的通解：
un Ae
i ( qnat )
A为振幅，是圆频率，qna是第n个原子在t＝0时刻的振动相位

固体物理第三章_ 晶体中的缺陷

4
由以上讨论可知：刃位错：外加切应力的方向、原子的滑移方向和位错线的运动方向是相互平行的。螺位错：外加切应力的方向与原子的滑移方向平行，原子的滑移方向与螺位错的运动方向垂直。在左右两部分受到向上和向下的切应力的作用时，位错线向前移动，直到位错线移动到尽头表面，这时左右两部分整个相对滑移b 的距离，晶体产生形变。
固体物理第三章
1. 热缺陷：由热起伏的原因所产生的空位和填隙原子，又叫热缺陷，它们的产生与温度直接有关
(a) 肖脱基缺陷
(b)弗伦克耳缺陷
(c) 间隙原子
固体物理第三章
（ a ）肖特基缺陷 (vacancy) ：原子脱离正常格点移动到晶体表面的正常位置，在原子格点位置留下空位，称为肖特基缺陷。（b）弗伦克尔缺陷(Frenkel defect)，原子脱离格点后，形成一个间隙原子和一个空位。称为弗伦克尔缺陷。（c）间隙原子(interstitial)：如果一个原子从正常表面位置挤进完整晶格中的间隙位置则称为间隙原子，由于原子已经排列在各个格点上，为了容纳间隙原子，其周围的原子必定受到相当大的挤压。
固体物理第三章固体物理第三章
产生位错的外力: 机械应力：挤压、拉伸、切割、研磨热应力：温度梯度、热胀冷缩晶格失配：晶体内部已经存在位错，只用较小的外力就可推动这些位错移动，原来的位错成为了位错源，位错源引起位错的增殖，有位错源的晶体屈服强度降低。晶体的屈服强度强烈地依赖于温度的变化。 T升高，原子热运动加剧，晶体的屈服强度下降，容易产生范性形变。
固体物理第三章
在实际晶体中，由于存在某种缺陷，所以晶面的滑移过程，可能是晶面的一部分原子先发生滑移，然后推动同晶面的另一部分原子滑移。按照这样的循序渐移，最后使上方的晶面相对于下方的晶面有了滑移。 1934 年， Taylor( 泰勒 ), orowan( 奥罗万 ) 和 Polanyi( 波拉尼）彼此独立提出滑移是借助于位错在晶体中运动实现的，成功解释了理论切应力比实验值低得多的矛盾。

第三章固体物理ppt课件

§2
三维晶格的振动
设实际三维晶体沿基矢a1、a2、a3方向的初基原胞数分别为N1、N2、N3，即晶体由N＝N1·N2·N3个初基原胞组成，每个初基原胞内含s个原子。一维情况下，波矢q和原子振动方向相同，所以只有纵波。三维情况下，有纵波也有横波。
原则上讲，每支格波都描述了晶格中原子振动的一类运动形式。初基原胞有多少个自由度，晶格原子振动就有多少种可能的运动形式，就需要多少支格波来描述。
一个波矢为K的第S支模式处在第N个激发态，我们就说在晶体中存在着N个波矢为K的第S支声子（因为给定了K与第S支模式则ω可由色散关系唯一确定），在晶体中波矢为K的纵声学支模式处于N激发态，我们就说晶体中有N个波矢为K的纵声学支声子。
声子这个名词是模仿光子而来（因为电磁波也是一种简谐振动）。声子与光子都代表简谐振动能量的量子。所不同的是光子可存在于介质或真空中，而声子只能存在于晶体之中，只有当晶体中的晶格由于热激发而振动时才会有声子，在绝对零度下，即在0K时，所有的简正模式都没有被激发，这时晶体中没有声子，称之为声子真空。声子与光子存在的范围不同，即寄居区不同。
每一组整数（L1,L2,L3 ）对应一个波矢量q。将这些波矢在倒空间逐点表示出来，它们仍是均匀分布的。每个点所占的“体积” 等于“边长”为(b1/N1)、（b2/N2）、(b3/N3)的平行六面体的 “体积”，它等于： b b b 3 1 2 N N N 1 N 2 3 式中Ω*是倒格子初原胞的“体积”，也就是第一布里渊区的“体积”，而Ω*＝（2π）3/Ω ，所以每个波矢q在倒空间所占的“体积”为：
子的位移构成了波，这个波称之为格波，把寻求到的
运动方程的解带入运动方程就能找出ω 与q的关系即

固体物理第三章

LOGO
Click to edit Master text styles
qa qa sin m sin 或者： 2 m 2 2
m 2
m
2 a

——色散关系
为截止频率
2 i a
由上可见，ω与q的关系具有明显的周期性， ω是q的周
期函数，周期为，q与 q q （i为整数）对应于，q与 q 相应同样的角频率ω，而且由
相邻原子的位相差：
格波2（绿色标示）的波矢：相邻原子的位相差：
—— 两种波矢下，格波描述的原子振动是完全相同。
所以，为了保证 un 的单值性，只须将q限制在 , a a （a为晶格常数），这恰好是一维布拉菲格子的第一布里渊区。
LOGO
Click to edit Master text styles

m
2
2
q
弹q
在长波极限下，一维单原子晶格格波的色散关系和连续介质中弹性波的色散关系一致。

LOGO
Click to edit Master text styles
下面再比较一下长波近似下，格波与弹性波的相速度
弹性波的相速度：弹 C

C——弹性模量 ρ——连续介质密度
晶格振动与格波的传播是不可分割的物理现象。
LOGO
Click to edit Master text styles
模型：一维无限长的单原子链，原子间距(晶格常量)为a，
原子质量为m.
u n 代表第n个原子离开平衡位置的位移。
第n个原子和第n+1个原子间的相对位移是
un 1 un
LOGO
Click to edit Master text styles

固体物理(第3章)解析

1 3N ( 2V
2 i, j1 i j
)0 i j
—— 含有坐标的交叉项
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
引入简正坐标
—— 原子的坐标和简正坐标通过正交变换联系起来
假设存在线性变换系统的哈密顿量
拉格朗日函数
T
1 2
3N i 1
Qi 2
V
1 2
3N
Q 2 2
ii
i 1
正则动量
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
系统的哈密顿量
正则方程
pi
H Qi
正则动量
pi
L Q i
Qi
Qi i2Qi 0, i 1, 2, 3, 3N —— 3N个独立无关的方程简正坐标方程解 Qi Asin(it )
简正振动 —— 所有原子参与的振动，振动频率相同振动模 —— 简正坐标代表所有原子共同参与的一个振动
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
只考察某一个振动模
系统能量本征值计算
i
aij mi
Qj
aij mi
Asin( jt )
正则动量算符
系统薛定谔方程
(1
2
3N i 1
pi2
1 2
3N
i2Qi2 ) (Q1, Q3N )
i 1
E (Q1,
Q3N )
§3-1 简谐近似和简正坐标 —— 晶格振动与晶体的热学性质
E
3N
i
i 1
3N i 1
(ni
1 2
)
i
3N
系统本征态函数 (Q1, Q2, Q3,Q3N ) ni (Qi )

固体物理第三章相图

相图分析（相图三要素）（1）点：纯组元熔点；共晶点等。（2）线：结晶开始、结束线；溶解度曲线；共晶线等。（3）区：3个单相区；3个两相区；1个三相区。
（1）Sn<2％的合金凝固过程（冷却曲线、相变、组织示意图）。
(c)2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.
共晶合金
%
de cd 100%; % 100% ce ce
合金的平衡结晶及其组织（以Pb-Sn相图为例）
（4）亚共晶合金 ① 凝固过程（冷却曲线、相变、组织示意图）。 ② 共晶线上两相的相对量计算。 ③ 室温组织（α＋βⅡ＋（α＋β））及其相对量计算。
(c)2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license. (c)2003 Brooks/Cole, a division of Thomson Learning, Inc. Thomson Learning™ is a trademark used herein under license.
+ Ld c
+ e
共晶转变：由一定成分的液相同时结晶出两个一定成分固相的转变。共晶相图：具有共晶转变特征的相图。（液态无限互溶、固态有限互溶或完全不溶，且发生共晶反应）。共晶组织：共晶转变产物。（是两相混合物）
特征：三相点的温度低于A 和B的纯组元的凝固点

(完整版)固体物理课件ppt完全版

布拉伐格子 + 基元 = 晶体结构
③ 格矢量：若在布拉伐格子中取格点为原点，它至其

他格点的矢量 Rl 称为格矢量。可表示为
Rl

l1a1

l2a2

l3a3
，
a1,
a2 ,
a3为
一组基矢
注意事项：
1）一个布拉伐格子基矢的取法不是唯一的
2
4x
·
1
3
二维布拉伐格子几种可能的基矢和原胞取法 2）不同的基矢一般形成不同的布拉伐格子
2·堆积方式：AB AB AB……，上、下两个底面为A
层，中间的三个原子为 B 层
3·原胞：
a, 1
a 2
在密排面内，互成1200角，a3
沿垂直
密排面的方向构成的菱形柱体 → 原胞
B A
六角密排晶格的堆积方式
A
a
B c
六角密排晶格结构的典型单元
a3
a1
a2
六角密排晶格结构的原胞
4·注意: A 层中的原子≠ B 层中的原子 → 复式晶格
bγ a
b a
b a
b a
简六体心底正简单三面心正单方底心单心交立斜交斜方简单立方体心正交面立方简四体心四方简单正交简单菱方简单单斜单方
二、原胞
所有晶格的共同特点 — 具有周期性（平移对称性）
描
用原胞和基矢来描述
述
方
位置坐标描述
式
1、定义：
原胞：一个晶格最小的周期性单元，也称为固体物理学原胞
a1, a2 , a3 为晶格基矢
复式晶格：
l1, l2 , l3 为一组整数
每个原子的位置坐标：r l1a1 l2a2 l3a3

固体物理教学课件：Chapt3-1

§3.1 简正模和格波
一、微振动理论——简正模
主要内容：
从原子之间的相互作用出发，在简谐近似下去讨论晶体的本征振动，即简正模。
利用晶格周期性证明晶体中的一个简正模对应一个振幅调制的平面波，即格波。
晶体中，与原子振动相关的任意激发，只是这些本征振动的线性叠加。
设晶体包含N个原子，有3N个自由度
( Pj2
+
ω
2j Q
2 j
)
j
微振动系统的Schrödinger方程为
∑ 1
2
j
(−2
∂2
∂Q
2 j
+
ω
Q 2 2
jj
)ψ
(Q1
,
Q2
,
,
Q3N
)
= Eψ (Q1, Q2 ,, Q3N )
由于没有交叉项，分离变量得：
1 [−2 2
∂2 ∂Q2j
+
ω
2j Q
2 j
]ϕ
(Q
j
)
= ε jϕ(Qj )
谐振子方程，解为：
第三章
晶格动力学和晶体的热学性质
第一章: 晶体的结构、分类及其测量方法
第二章: 晶体的结合
T=0
负电性、成键类型、结合能
有限温度下，晶体中的原子都在平衡位置附近作微振动。
晶格动力学：
从晶体中原子的振动出发讨论晶体的宏观物性 19世纪：杜隆-帕蒂定律的统计解释 (高温下适用，解释不了低温) 1907：爱因斯坦开辟固体比热容的量子理论 1912：德拜 “关于比热容理论”（连续介质） 1913：波恩-卡曼 “关于比热容理论”（格波解释）
M
d 2un dt 2

固体物理学第三章固体的结合

原子呈现出瞬时偶极矩
性元素具有球对称，性元素具有球对称，结合时排列最紧密以使势能最低 :Ne、Ar、Kr、Xe的晶体都是面心立方、、、的晶体都是面心立方
明的绝缘体，熔点特低分别为24K、84K、117K和161K 明的绝缘体，熔点特低, 分别为、、和
惰性原子之间的相互作用势能两个相距为r的原子，两个相距为的原子，原子中电子是对称分布的原子
U
i
=
∑ jU
'
ij
i≠j
U
ij
−r = λ exp( n
b
ij
r
ij ρ
q )± r
2
ij
1)正负号的选取同号为正, 正负号的选取: 意: 1)正负号的选取:同号为正,异号取负 2)排斥项中排斥项中, 2)排斥项中,每个离子都倾向于拒绝和其近原子的电子云发生交迭. 原子的电子云发生交迭. 2)国际单位制中,4πε 国际单位制中,4 2)国际单位制中,4πε0rij
r) 和u(r)分别表示相互分别表示相互用力和相互作用势 :
U
排斥
∂u (r ) f (r ) = − ∂r
(r ) =
B rn
f (r ) = r
u (r ) = −
A
r
+ m
B
r
n
U
吸引
(r ) =
−
A rm
求解 r0
dU (r ) dr
内聚能U 内聚能Uc
r =r0
=0
r0 =
n−m
Bn Am
—— A12和A6: 与晶格结构有关的求和项
注意:引入新的参量所对应的物理意义注意引入新的参量所对应的物理意义: 引入新的参量所对应的物理意义

固体物理(第3章)讲解

2
—— 每一个原子运动方程类似 —— 方程的数目和原子数相同
§ 3-2简谐近似和简正坐标一维单原子链 —— —— 晶格振动与晶体的热学性质 § 3-1 晶格振动与晶体的热学性质
方程解和振动频率设方程组的解 naq — 第n个原子振动相位因子
得到应用三角公式
4 2 aq sin ( ) m 2
—— 常数
—— 平衡条件
§ 3-2简谐近似和简正坐标一维单原子链 —— —— 晶格振动与晶体的热学性质 § 3-1 晶格振动与晶体的热学性质
dv 1 d v v (a ) v (a ) ( )a ( 2 )a 2 High items dr 2 dr
简谐近似 —— 振动很微弱，势能展式中只保留到二阶项
2 1 2 2 任意一个简正坐标 [ 2 i Qi ] (Qi ) i (Qi ) 2 2 Qi
1 能量本征值 i ( ni ) i 2
本征态函数
—— 谐振子方程
n (Qi )
i
i

exp(

2
2
) H ni ( )
— 厄密多项式
§3-1 简谐近似和简正坐标 ——
格波波矢的取值和布里渊区相邻原子相位差格波1的波矢
—— 原子的振动状态相同
相邻原子相位差
§ 3-2简谐近似和简正坐标一维单原子链 —— —— 晶格振动与晶体的热学性质 § 3-1 晶格振动与晶体的热学性质
格波格波2的波矢
aq1 / 2
相邻原子的位相差
—— 两种波矢q1和q2的格波中，原子的振动完全相同
原子位移宗量
N个原子的位移矢量 —— 体系的势能函数在平衡位置按泰勒级数展开

固体物理第三章晶体衍射

Chapter 3晶体衍射§3.1 倒格子 Reciprocal lattice倒格子的概念及其应用在固体物理学中是十分重要的。

在前面，我们在坐标空间里讨论晶体结构的周期性，由此引入了坐标空间的布拉菲格子概念。

实际上，晶体结构的周期性，也可以在波矢空间里进行描述。

如果前者称为正格子，后者就称为这个正格子的倒格子。

这样以来，描述一种晶体结构的周期性可以利用两种类型的格子：一种是正格子，它是晶体结构在坐标空间的数学表现形式；一种是倒格子，它是晶体结构在波矢空间的数学表现形式。

由坐标空间变换到波矢空间，对处理周期性结构中的波动过程、X 射线衍射等问题是非常方便的。

3.1.1波矢空间前面我们研究晶体结构的周期性，无论是采用直角坐标系还是晶胞坐标系，都是在坐标空间里进行的。

格点的位置或某点的位置都是用位矢→l R 或→r 来表示，其量值单位是“米”。

晶体结构的周期性在坐标空间里的数学形式用布拉菲格子来表示，如果把坐标空间称为“实空间”或“正空间”，那么坐标空间里的布拉菲格子就可以称为正格子。

在固体物理学的研究中，还需要另外一种空间形式。

例如，在晶体的X 射线衍射过程中，晶体作为衍射光栅，X 射线通过晶体在照相底片形成一些斑点。

这些斑点和晶体中的晶面族有着一一对应的关系。

对这些斑点的分布情况进行分析，就可以了解作为衍射光栅的那个晶体的结构情况。

从衍射斑点并不能直接看出晶体的结构，需要进行傅里叶变换，这里就需要引入波矢空间的概念。

另外，计算固体的能带结构和电子状态也要用到波矢空间。

（李商隐：庄生晓梦迷蝴蝶。

《庄子·齐物论》说，庄子曾梦化为蝴蝶，醒后弄不清楚是自己变成蝴蝶了，还是蝴蝶变成庄周了。

庄周先生在两个空间－－真实空间和梦幻空间－－里转化。

蝴蝶成为庄周先生在梦幻空间里的化身。

）波矢空间又称状态空间，在波矢空间中同样可以建立直角坐标系，三个方向的单位矢量分别记为→x k 、→y k 、→z k 。

固体物理学课件第三章

10
3.1 一维单原子链的晶格振动
将：
un1 Aei[t(n1)aq] un1 Aei[t(n1)aq] un Aei[tnaq]
代入到运动方程：
m
d 2un dt 2

(un1 un1 2un )
消去共同因子，得到：
m 2 (eiap eiaq 2)
《固体物理学》微电子与固体电子学院
14
3.1 一维单原子链的晶格振动
格波的波长： 2
q
格波的波矢：q 2 n
n 代表沿格波传播方向的单位
矢量。
格波的相速度：v p

q
不同原子间的位相差：
n’aq-naq = (n’-n)aq
《固体物理学》微电子与固体电子学院
15
3.1 一维单原子链的晶格振动

a
2

f
U

U R
a

2U R2

a

第一项与振动无关，为常数项，第二项中因为平衡位置处，
势能为极小值，互作用力为零。
《固体物理学》微电子与固体电子学院
4
3.1 一维单原子链的晶格振动
引入弹性系数

2U R 2
(un1 un1 2un )
《固体物理学》微电子与固体电子学院
5
3.1 一维单原子链的晶格振动
最近邻近似下一维单原子振动可简化为质量为m的小球被用弹性系
数为的弹簧连起来的弹性链。处
理微小振动一般都采取这种简谐近似。在有些物理问题需要考虑高阶项的效应，称为非简谐效应。

固体物理课件3.1

引言在第一章介绍晶体的微观结构中在第一章介绍晶体的微观结构中，，为了便于显示出晶体微观结构的内禀特征显示出晶体微观结构的内禀特征，，将组成晶体的各原子集团各用一个位置固定的几何点来代替构成Ｂravais 格子或将组成晶体的各个原子各用一个位置固定的小球来代替构成晶格个位置固定的小球来代替构成晶格，，这里显然忽略了原子的运动略了原子的运动。

实际上实际上，，大量的实验现象表明，组成晶体的原子并不是静止在晶格格点上固定不动的定不动的，，各原子是在围绕其晶格格点这一平衡位置永不停息地振动着位置永不停息地振动着。

第三章晶格振动与晶体热学性质晶格振动的研究——晶体的热学性质固体热容量——热运动是晶体宏观性质的表现晶格振动——研究固体宏观性质和微观过程的重要基础晶格振动——晶体的热学性质晶体的热学性质、、电学性质电学性质、、光学性质光学性质、、超导电性导电性、、磁性磁性、、结构相变有密切关系原子的振动——晶格振动在晶体中形成了各种模式的波——简谐近似下简谐近似下，，系统哈密顿量是相互独立简谐振动哈密顿量之和——这些谐振子的能量量子这些谐振子的能量量子，，称为声子——晶格振动的总体可看作是声子的系综——用一系列独立的简谐振子来描述这些独立而又分立的振动模式——这些模式是相互独立的这些模式是相互独立的，，模式所取的能量值是分立的§3.1 一维晶格的振动由于晶体中原子数目巨大由于晶体中原子数目巨大，，原子与原子之间存在相互关系原子与原子之间存在相互关系，，任一原子的位移至少与相邻原子任一原子的位移至少与相邻原子、、次近邻原子的位移有关次近邻原子的位移有关，，所以严格求解晶格振动是极其困难的所以严格求解晶格振动是极其困难的。

为了探讨晶格振动的基本特征基本特征，，需要采用一些近似的方法需要采用一些近似的方法。

晶格具有周期性晶格具有周期性，，晶格的振动具有波的形式——格波格波的研究——先计算原子之间的相互作用力——根据牛顿定律写出原子运动方程根据牛顿定律写出原子运动方程，，最后求解方程一维晶格——每个相同原子的质量m ，平衡时原子间距a 个原子和第n ＋1个原子间的相对位移nx ＋1个原子间的距离1n na x x ++−nn n x x a x −++−111、一维简单格子——原子之间的作用力du f dx =−平衡位置时平衡位置时，，两个原子间的互作用势能()u a ()u a δ+发生相对位移后，相互作用势能1n n x x δ+=−2221()()()()2a a du d u u a u a High itemsdr drδδδ+=+++常数——平衡条件nn n x x a x −++−112221()()()2a d u u a u a High itemsdrδδ+=++简谐近似——振动很微弱振动很微弱，，势能展式中只保留到二阶项βδ——恢复力系数nn n x x a x −++−11原子的运动方程——只考虑相邻原子的作用只考虑相邻原子的作用，，第n 个原子受到的作用力1111()()(2)n n n n n n n x x x x x x x βββ+−+−−−−=+−第n 个原子的运动方程1,2,3,)N ⋯每一个原子运动方程类似方程的数目和原子数相同nn n x x a x −++−11最近邻近似方程解和振动频率2112(2)nn n n d x m x x x dtβ+−=+−设方程组的解()i qna t n x Aeω−=qna —第n 个原子振动相位因子1)]1)]1aq t aq t n x Aeωω−−+−+=)2(2−+=−−iaqiaqeem βω得到224sin ()2aq m βω=应用三角公式)2sin(2aq m βω=)2sin(2aqm βω=1）波矢q 增加倒格矢的整数倍的整数倍，，频率不变不变，，即格波的频率在波矢空间内是以倒格矢为波矢的取值范围波矢的取值范围：：aa2a π2a πωω换成-q ，频率不变不变，，即格波的频率在波矢空间内具有反演对称性在波矢空间内具有反演对称性。

固体物理基础教学课件-第3章

边界条件限制波数在简约布里渊区内取均匀分布的N个分立值
3-1 格波的色散关系
2 4sin2(aq)
(q)
m2
ω取正值，则有
2 sin(aq)
m2
频率是波数的偶函数
q
色散关系曲线具有周期性，
- -2 0 2
aa
aa
仅取简约布里渊区的结果即可
由正弦函数的性质可知，只有满足 02 /m的格波
所以发生在晶格中的中子散射的变换规则不如动量守恒严格，允许相差，h其G 中n Gn为某一倒格子矢量。慢中子的能量：0.02~0.04 eV，与声子的能量同数量级；中子的德布罗意波长：2~3×10-10 m（2~3 Å），与晶格常数同数量级；可直接准确地给出晶格振动谱的信息局限性：不适用于原子核对中子有强俘获能力的情况
第2n+1个M原子的方程 M d2 dt2 2n1(22n12n22n)
第2n个m原子的方程 mdd 2t22n(22n2n12n1)
解也具有平面波的形式
两种原子振动的振幅（m取A， M取B）一般来说是不同的
3-2 声学波与光学波
色散关系有不同的两种
2(m m M M ) 11(m 4 m M M )2sin2aq12 2(m m M M ) 11(m 4 m M M )2sin2aq12
缺点：一个典型X光光子的能量约为104 eV，一个典型声子的能量约为10-2 eV。一个X光光子吸收（或发射）一个声子而发生非弹性散射时，X光光子能量的相对变化为10-6，在实验上要分辨这么小的能量改变是非常困难的。相比较而言，可见光的能量约为1eV，采用拉曼散射能量的相对变化为10-2，有利于降低误差。
以下只讨论单声子过程。

固体物理--第三章晶格振动

三、周期性边界条件周期性边界条件：
N n n
e
iNaq
1
2 q h Na
q的分布密度：
h =整数， N：晶体链的原胞数
Na L q const. 2 2
{
简约区中q的取值总数＝ q
2 N ＝晶体的原胞数 a 晶格振动的格波总数＝2N＝晶体的自由度数
2 1
两个色散关系即有两支格波：（＋：光学波；－：声学波）

简约区：

a
q

a

π a
π a
对于不在简约区中的波数q’ ，一定可在简约区中找到唯一一个q，使之满足：
2 q q G a
G 为倒格矢
二、光学波和声学波的物理图象第n个原胞中P、Q两种原子的位移之比
n m M n q0
离子晶体在某种光波的照射下，光波的电场可以激发这种晶格振动，因此，我们称这种振动为光学波或光学支。
对于单声子过程（一级近似），电磁波只与波数相同的格
(q)
=c0q +
+(0)
波相互作用。如果它们具有相同
的形式在整个晶体中传播，称为格波。
q取不同的值，相邻两原子间的振动位相差不同，则晶格振动状态不同。 2 则 q 与 q描述同一晶格振动状态若 q q a
1 4a
例：
q1
q2
2
1

2 a
5
4
2
2a 5
2a
2
2 q2 q1 a
三、周期性边界条件（Born－Karman边界条件）
N+1