二重积分的几种换元法
二重积分换元法
y D
定(积3)分变换换元T法: D D是一一对应的 , O
x
则
D
f
b
(xa, fy()xd)xddxy
f [f (tx)(]u,v(t)), dy(tu,(vx))J(u(t,)v))
D
dudv
证: 根据定理条件可知变换 T 可逆.
在uOv坐标面上 , 用平行于坐标轴的
直线分割区域D, 任取其中一个小矩
D : r 1, 0 2 π
J
(x, y)
( r, )
a cos b sin
a r sin b r cos
abr
2 abc 2π d 1
0
0
1
r2
r
d
r
4 3
π
abc
形, 其顶点为
v
vk v
M 4 M3
D
M1 M 2
O u u h u
M1 (u, v) ,
M 2 (u h,v),
T
M3 (u h,v k), M 4 (u,v k).
通过变换T, 在 xOy 面上得到一个四边
形, 其对应顶点为Mi (xi , yi ) (i 1, 2,3, 4)
y
M3
二重积分换元法
v
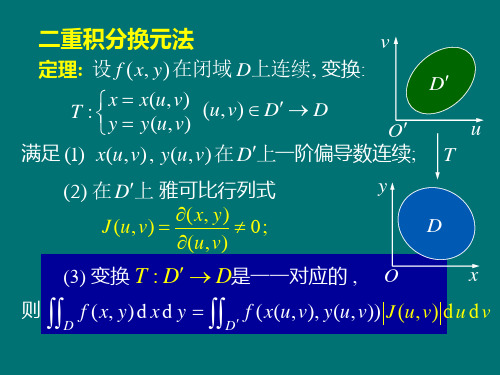
定理: 设 f (x, y) 在闭域 D上连续, 变换:
D
T
:
x y
x(u, v) y(u, v)
(u,v) D D
O
u
满足 (1) x(u,v), y(u,v) 在 D上一阶偏导数连续; T
(2) 在 D上 雅可比行列式 J (u, v) (x, y) 0; (u, v)
v
Ou
D
二重积分的换元法

0
0
(在积分中注意使用对称性)
1.作什么变换主要取决于积分区域 D 的形状, 同时也兼顾被积函数 f (x, y)的形式.
基本要求:变换后定限简便,求积容易.
2.
J
(x, y) (u, v )
1 (u, v )
.
(x, y)
思考题
计算
D
x
y
e( x y)2 d
y
,其中
dxdy
,
其中
D
为
椭圆 x2 a2
y2 b2
1 所围成的闭区域.
解
作广义极坐标变换
x y
ar br
cos , sin ,
其中a 0, b 0, r 0, 0 2.
在这变换下 D D {(r, ) 0 r 1 , 0 2},
(1)极点 O 在区域 D 的外部
D
:
r1
(
)
r
r2
(
)
r r1( )
D
o
f (r cos ,r sin ) r dr d
D
d
r2 ( )
r1 ( )
f (r cos ,r sin )
r dr
r r2( )
(2)极点 O 在区域 D 的边界上
x2 y2 2y
3x 0
x 3y 0
x2 y2 4 y r 4sin o
x
( x2 y2 )dxdy
3 d
r 4sin 2 rdr 15(
10.2 二重积分的计算

∫∫D
b a d
f (x, y) dx dy
ϕ2 ( x)
1
= ∫ d x ∫ (x) f (x, y) dy ϕ = ∫ d y∫
c
ψ 2 ( y)
ψ 1( y) y)
f (x, y) dx
y y = ϕ (x) 2 d x =ψ2 ( y) x =ψ1( y) D y y = ϕ1(x) c o a x bx
§10.2 二重积分的计算
一、利用直角坐标计算二重积分 二、利用极坐标计算二重积分 三、二重积分的换元法
1
一、利用直角坐标计算二重积分
由曲顶柱体体积的计算可知, 被 函 由曲顶柱体体积的计算可知 当 积 数 f (x, y) ≥ 0 且在D上连续时 且在 上连续时, 若D为 X – 型区域 上连续时 为 ϕ1(x) ≤ y ≤ ϕ2 (x) D: a ≤ x ≤b
I = ∫∫ f (x, y) d x d y = ∫ dy ∫
D
2
8− y2 2y
0
f (x, y)dx
8
例5. 计算 所围成. y = 4 − x2, y = −3x, x =1 所围成. 解: 令f (x, y) = x ln(y + 1+ y )
2
其中D 由
4
y = −3x
y
y = 4 − x2
令ρ = ∆u + ∆v , 则
2 2
T
y
M4
M3
D
M1
M2
o
x
∂x x2 − x1= x(u + ∆u, v) − x(u, v)= ∆u + o(ρ) ∂u (u, v)
18
∂x x4 − x1= x(u, v + ∆v) − x(u, v) = ∆v + o(ρ) ∂v (u, v) 同理得 y2 − y1 = ∂ y ∆u + o(ρ) ∂u (u, v) ∂y y4 − y1 = ∆v + o(ρ) ∂v (u, v) 充分小时, 当∆u, ∆v充分小时 曲边四边形 M1M2M3M4 近似于平行四 充分小时
二重积分的换元法

f ( x , y )dxdy f [ x(u, v ), y( u, v )] J ( u, v ) dudv.
D D
二重积分化为二次积分时,根据积分区域 D
的特征,可分为以下三种情况:
(1)极点 O 在区域 D 的外部
r1 ( ) r r2 ( ) D:
x
练习
计算
e
D
x2 y2
dxdy
y a
其中积分区域 D为x 2 y 2 a 2 . 由直角坐标化 x r cos 解 极坐标公式 y r sin
圆的极坐标方程为 r a
D o
a x
0 r a 故 D: 0 2
e
D
f ( x , y )dxdy f [ x(u, v ), y( u, v )] J ( u, v ) dudv.
D D
r r
将区域 D 用从O出发的射线和 以O为圆心的圆弧进行划分 .
D
则 r r 于是面积微元 d r drd
f ( r cos , r sin ) r dr d D
r r1 ( )
D
r r2 ( )
o
d
r1 ( )
r2 ( )
f ( r cos , r sin ) r dr
(2)极点 O 在区域 D 的边界上
r r ( )
D
0 r r ( ) D: f (r cos , r sin ) r dr d
2
r ( )
f ( r cos , r sin ) r dr
二重积分的换元法
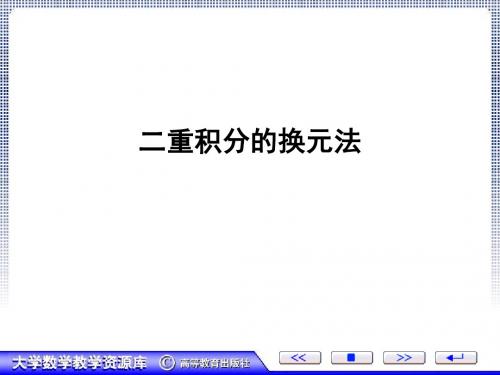
Dxy {( x , y ) | ( x x0 )2 ( y y0 )2 1}.
于是所求立体体积为
V
Dxy
2 2 2 2 [ 2 x x 2 y y x y 1 ( x y )]d 0 0 0 0
[1 ( x x0 ) D
( x, y) 1 1 J 1, ( u, v ) 0 1
D : x y 1 u 1, x 0 u v 0, y 0 v 0.
O
x uv D
v
O
u
原式 f ( u, v ) | J | dudv
D
du
0
1
即 z 2 x0 x 2 y0 y x y 1,
2 0 2 0
该切平面与曲面 z x 2 y 2交线为
2 2 z 2 x0 x 2 y0 y x0 y0 1 2 2 z x y
消去z得 : ( x x0 )2 ( y y0 )2 1,
y x y x
vu vu x ,y . 2 2
1 1 1 ( x, y) 2 2 , J 1 1 2 ( u, v ) 2 2
v v2 D u v u v
2
O
2 u
故
e D
y x y x
1 dxdy e dudv 2 D
b
O
x a cos , y b sin ,
a
x
D D {( , ) 0 1 , 0 2π},
( x , y ) a cos J ( , ) b sin
a sin b cos
第七章 第二节 二重积分的换元法

x2 y2 解: 取 D : 2 2 1, 由对称性 a b 2 2 y 2 c 1 x 2 2 d x d y
D a b
D : r 1 , 0 2 ( x, y ) a cos a r sin J abr b sin b r cos ( r , )
0 k 1
n
即
D f ( x, y) d D f (r cos , r sin ) r d r d
r d d dr d r
机动 目录 上页 下页 返回 结束
( ) r ( ) 1 2 设D : ,则
r ( ) 2 D
x
充分利用对称性
应用换元公式
机动 目录 上页 下页 返回 结束
1. 交换积分顺序
提示: 积分域如图
o
r a cos r arccos r a
r
r arccos a
a
x
I dr r f ( r, ) d 0 arccos a
机动 目录 上页 下页 返回 结束
a
x y 4 y 及直线 x 3 y 0, y 3x 0 所围成的 y 平面闭区域. 4 2 2 解: x y 2 y r 2 sin x 2 y 2 4 y r 4 sin y 3x 0 2 3 x 3 y 0 1 6
x2 e 0
dx
事实上, 当D 为 R2 时,
2
①
利用例6的结果, 得
故①式成立 .
机动 目录 上页 下页 返回 结束
例2. 求球体
被圆柱面 x 2 y 2 2 a x
14-7.二重积分的换元法PPT

D
D2
u
J =2 J:部-Vvevdu = -£‘(2e - eT)vdv = e — e_1
例2计算JJ
1 -亳2-^22dxdy,其中D为 a b
D
22
椭圆Xr + % = 1所围成的闭区域.
ab
解作广义极坐标变
x = ar cos 0,
y = br sin
其中 a > 0, b > 0, r > 0, 0 < 0 0<, 2冗.
1,二重积分换元公式
__________ ______平_:面__上__同__一_■个_点.—,直角坐标与极坐标之
x = pcos^, 间的关系为 y = psin^.
上式可看成是从直角坐标平面po(P到直角
坐标平面 xoy 的一种变换,即对于皆湃
面上的一点M3,饥,通过上式变换,变 成
xoy 平面上的一点M(x, y),且这种变 换 是一对一的.
\x + y = =2
则 x = ,y= . 22
没
o
x
D — D,艮卩 x = 0 T u = —
v;
v
v=2
y = 0 T u = v;
u = —v
u=v
x + y = 2 T v = 2.
o
u
11
J = a (X, y) 2 2 1 d (u, v) 1 1 2,
22
y-x
u
故 JJ ey+Xdxdy = JJ ev -dudv
(3) 变换T : D'T D是一对一的,则有 JJ f ( x,
y )dxdy = JJ f [ x ( u, v ), y ( u, v )]| J ( u, v )
二重积分的所有变换

ax
.
y 5x
例4 计算二重积分 (x6,y其)d中xdy
D
D是由三条线 yx,y所5x围,x成1 的区域.
yx
x 1
解 易知积分区域可表为
D :0x 1 ,xy 5 x
于是
1 5x
(x6y)dxdy dx (x6y)dy
D
0x
1(xy3y2)
0
5x x
dx
176x2dx 76.
0
3
y
D1:00yx122x2, D2:02yx822x2 将 D D 1D 2视为Y–型区域 , 则
x2 y2 8
2
y
1 2
x2
D1
D2
o 22 2 x
D :
2yx 8y2 0y2
2
8y2
ID f(x,y)dxdy 0 d y 2y f (x,y)dx
.
机动 目录 上页 下页 返回 结束
例8. 计算I xln y ( 1y2)dxdy,其中D 由 D
exydxdy( 1exdx)( 2eydy)ex1ey2
0
1
01
D
(e1)(e2e)e(e1)2
或先积 y再积 x
exydxdy
1
dx
2exydy
01
e1 xy
0
2 1
dx
D
1(ex2
0
ex1)dx
(ex2
ex1)
1 0
(e3 e2)(e2 e) e(e1)2
.
例3 计算二重积分 x y.d其x d中y 积分区域 分 D
k
k
r rk x
域的面积
k 1 2(rk rk)2 k12rk2k
8_3重积分的换元法

αβD)(θϕ=r (2θϕ=r注: 利用例3可得到一个在概率论与数理统计及工程上 非常有用的反常积分公式+∞ − x2 e dx 0 当D 为 R2 时,∫=π2+∞ − x2 e −∞①事实上,∫∫D e− x2 − y2d xd y = ∫d x∫+∞ − y 2 e −∞dy利用例3的结果, 得= 4⎛ ⎜∫ ⎝2+∞ − x 2 e 0d x⎞ ⎟ ⎠24⎛ ⎜∫ ⎝ 故①式成立 .+∞ − x2 e 0−a 2 ⎞ d x ⎟ = lim π (1 − e ) = π ⎠ a → +∞112 2 x + y = 2 ax 例4. 求球体 x + y + z ≤ 4 a 被圆柱面 (a > 0) 所截得的(含在柱面内的)立体的体积. 2 2 2 2解: 设 D : 0 ≤ r ≤ 2 a cosθ , 0 ≤ θ ≤ 由对称性可知π2zV = 4 ∫∫ = 4∫π0D 24 a 2 − r 2 r d r dθ dθo2y∫02 acosθ4a − r r dr22ax32 3 π 2 32 3 π 2 3 = a ∫ (1 − sin θ ) d θ = a ( − ) 0 3 2 3 312x2 y2 z 2 例5. 试计算椭球体 2 + 2 + 2 ≤ 1 的体积V. a b c 2 2 x y 解: 取 D : 2 + 2 ≤ 1, 由对称性 a b令 x = a r cosθ , y = b r sin θ , 则D 的原象为 D′ : r ≤ 1 , 0 ≤ θ ≤ 2π ∂( x, y ) a cosθ − a r sin θ J= = = abr b sin θ b r cos θ ∂( r ,θ )V = 2 ∫∫ z d x d y = 2 c ∫∫DD1−x2 a2−y2 2 d xd by∴ V = 2 c ∫∫D1 − r 2 a b r d r dθ2π 0= 2 abc ∫dθ∫104 1 − r r d r = π abc 3213内容小结(1) 二重积分的换元法x = x(u , v) 下 ⎧ 在变换 ⎨ ⎩ y = y (u , v) ∂ ( x, y ) (u , v) ∈ D′, 且 J = ≠0 ( x, y ) ∈ D ∂ (u , v) 则 ∫∫ f ( x, y ) d σ = ∫∫ f [ x(u , v), y (u , v)] J d u d vD D′14极坐标系情形: 若积分区域为 D = { (r ,θ ) α ≤ θ ≤ β , ϕ1 (θ ) ≤ r ≤ ϕ 2 (θ ) } 则∫∫D f ( x, y) d σ = ∫∫D f (r cosθ , r sin θ ) rd r dθ= ∫ dθ ∫α β ϕ 2 (θ ) ϕ 1 (θ )f (r cosθ , r sin θ ) rd rβD r = ϕ 2 (θ ) oαr = ϕ1 (θ )15二、三重积分换元法定理: 设f (x, y, z)在有界闭区域Ω上连续变换: ⎧ x = x(u , v, w) ⎪ T : ⎨ y = y (u , v, w) (u , v, w) ∈ Ω′ → Ω ⎪ z = z (u , v, w) ⎩ 满足 (1) x, y , z在 Ω′上 有一阶连续偏导数;(2) 在 Ω′上 雅可比行列式 ∂ ( x, y , z ) ≠ 0; 注 J (u , v, w) = ∂ (u , v, w) (3) 变换 T : Ω′ → Ω 是一一对应的 ,则∫∫∫ = ∫∫∫Ωf ( x, y, z )d x d y d zf ( x(u , v), y (u , v), z (u , v)) J (u , v, w) d u d v d w 16 Ω′常用的变换 1. 柱面坐标变换设 M ( x, y, z ) ∈ R 3 , 将x, y用相应的极坐标 ρ ,θ 代替,则称 (ρ ,θ , z ) 为点M 的柱坐标. 直角坐标与柱面坐标的关系:x = ρ cosθ y = ρ sin θ z=z坐标面分别为⎛ 0 ≤ ρ < +∞ ⎞ ⎜ 0 ≤ θ ≤ 2π ⎟ ⎜ ⎟ ⎝ − ∞ < z < +∞ ⎠圆柱面 半平面 平面zzM ( x, y , z )ρ = 常数 θ = 常数z = 常数ox ρy θ ( x, y,0)17如图所示, 在柱面坐标系中体积元素为 d v = ρ d ρ dθ d z 因此zρ dθ∫∫∫Ω f ( x, y, z )d xd yd z = ∫∫∫ F ( ρ ,θ , z )ρ d ρ d θ d z Ωxzρodρ dzy其中 F ( ρ ,θ , z ) = f ( ρ cosθ , ρ sin θ , z ) 适用范围:θρdθdρ1) 积分域表面用柱面坐标表示时方程简单 ; 2) 被积函数用柱面坐标表示时变量互相分离. 积分次序通常为 z → ρ → θ .18柱面 x 2 + y 2 = 2 x 及平面 z = 0, z = a (a > 0), y = 0 所围 成半圆柱体.例6. 计算三重积分 ∫∫∫ z x 2 + y 2 d xd yd z 其中Ω为由Ω0 ≤ ρ ≤ 2 cosθ 解: 在柱面坐标系下 Ω : 0 ≤ θ ≤ π 2 0≤ z≤a原式 = ∫∫∫ z ρ 2 d ρ dθ d zΩz ao= ∫ zd z ∫0aπ02 dθ∫02 cosθρ2 d ρ2 ρ = 2 cos θ xy=2 π 4a3∫02 cos 3θ8 2 dθ = a 9dv = ρ d ρ d θ d z19d xd yd z , 其中Ω由抛物面 例7. 计算三重积分 ∫∫∫ 2 2 Ω1 + x + y z x 2 + y 2 = 4 z 与平面 z = h (h > 0) 所围成 .hxoy20ox h d d θρρ),,(ϕθr Myo4πRr =o x y2 4πo xy24πvd )作业P163 1(2)(4), 2(2)(4), 3(4),6(1)(3)(6), 7(3), 12, 13, 1531。
【精品】第一章2重积分计算的换元法分析

绥化学院本科毕业设计(论文)重积分计算的换元法分析学生姓名:李婷婷学号:200854100专业:应用数学年级:2008级一班指导教师:齐秀丽副教授Suihua UniversityGraduationPaperStudentnameLiTingtingStudentnumber200854100MajorAppliedchemistry SupervisingteacherQiXiuliSuihuaUniversit摘要换元法是数学中求重积分时用到的一种非常重要的计算方法,它不仅是重点,也是难点。
本文共分为两章,第一章介绍的就是与二重积分和三重积分在换元法上的一些相关概念、定理及其公式推导过程,而第二章则是结合第一章的相关内容进一步运用到实例中进行分析研究及其说明。
关键词:二重积分;三重积分;换元法目录SuihuaUniversityGraduationPaper ......................... 错误!未指定书签。
SuihuaUniversit ............................................ 错误!未指定书签。
摘要 ....................................................... 错误!未指定书签。
目录 ..................................................................... 前言 ....................................................... 错误!未指定书签。
第1章重积分计算的换元法理论 ............................... 错误!未指定书签。
第1节二重积分换元法的理论分析.......................... 错误!未指定书签。
第2节三重积分换元法的理论分析.......................... 错误!未指定书签。
重积分的换元法

1. 在直D角坐标系下二重积分
f ( x, y) 复习:二重积 分在直角坐标 系下的计算
D
f (x, y)
D
2.二重积分在直角坐标系下的计算:
f(x, y)dxdy
D
1 WORKREVIEW
2 UNDERWORK
添加标题2(x)
f(x,
添加标题
y)dy
1(x)
2(y) f(x,y)dx
(1) x (u, v ), y(u, v ) 在 D 上具有一阶连续偏导数 ;
(2) 在 D 上雅可比式 J (u,v ) ( x, y) 0; (u,v)
(3) 变换 T : D D 是一对一的,则有
f ( x , y )dxdy f [ x ( u , v ), y ( u , v )] J ( u , v ) dudv .
小结
一般地,当积分区域为圆形、扇形、环形区域, 而被积函数中含有 x2 y2 的项时,采用极坐标 计算往往比较方便.
二重积分在极坐标下的计算公式
f(rco,srsin)rdrd
D dr2()f(rco ,rsi)n rdr
r1()
d 0 r()f(rc o,rsi)n rdr 0 2 d 0 r()f(rc o,rs si)n rdr
思考题解答
衬底1
雅 可 比 行 列 式 J (x ,y ) 1 ,
x u (u ,v )v
yv
,
令 u vx yy
单击添加副标题
感谢您
的 欣 赏 y
Dx
ye(xy)2dDf(u,v)|J|dudv
1
u
du
v
eu2
dv
1 u eu2du
二重积分的计算方法资料

二重积分的计算方法资料二重积分是微积分中的重要内容,在物理、工程、统计学等领域都有广泛应用。
本文将介绍二重积分的计算方法,包括定积分计算与几何应用两个方面。
一、定积分计算方法(一)极坐标下的二重积分计算:在极坐标下,平面上的一个点可以用极径和极角来表示。
设区域D由曲线r=f(θ)和两直线θ=a,θ=b(0≤a≤b≤2π)所围成。
要计算D上的二重积分,可以通过极坐标转换来简化计算。
1.若函数f为连续函数,则有二重积分I = ∬D f(x,y) dA = ∫ab ∫f(r,θ) r dθ dr2.计算时,先按θ积分,再按r积分。
3.需要注意的是,r的取值范围是由f(θ)和直线θ=a,θ=b所围成的区域。
(二)直角坐标下的二重积分计算:在直角坐标系下,可以利用定积分的性质计算二重积分。
设区域D的上下界分别为y=g1(x)和y=g2(x)(a≤x≤b),则有二重积分I = ∬D f(x,y) dA = ∫ab ∫g2(x) g1(x) f(x,y) dy dx1.计算时,先按y积分,再按x积分。
2.需要注意的是,y的取值范围是由g1(x)和g2(x)所围成的区域。
对于一些复杂的积分,可以通过换元法来简化计算。
一般来说,选择适当的变量替换可以使原积分转化为更简单的形式。
1.平面区域变换:设变换为x = φ(u,v),y = ψ(u,v),则有 dA = ,J, du dv,其中J为变换的雅可比行列式,可利用行列式的性质计算。
2.极坐标变换:设变换为x = r cos(θ),y = r sin(θ),则有dA = r dr dθ。
3.球坐标变换:设变换为x = ρ sinφ cosθ,y = ρ sinφ sinθ,z = ρcosφ,则有dV = ρ^2 sinφ dρ dφ dθ。
(四)离散型二重积分与曲边梯形面积:如果函数f(x,y)是有界函数,并且在区域D上有无穷多个不连续点,则可以通过计算曲边梯形面积来近似计算二重积分:I ≈ ∑f(xi,yi) ΔA = ∑f(xi,yi) Δx Δy其中(Δx,Δy)为曲边梯形的底边与两侧边长,(xi,yi)为底边上的任意点。
