基于巴特沃斯低通滤波器的图像增强
【完整版毕业论文】巴特沃斯有源低通滤波器的设计

巴特沃斯有源低通滤波器的设计摘要随着社会科学技术的飞速发展,各种科技产品在人类社会中随处可见,极大的丰富了人们的日常生活。
物联设备、可穿戴设备以及虚拟仪器产品在各种应用和消费场合变得极为普遍。
就目前而言,在几乎所有的电子产品中,各种增益、带宽以及高性能的滤波器都发挥着至关重要的作用,例如可穿戴设备的语音信号输入系统中,运用高性能的低通滤波器进行语音信号的降噪、滤波、回声消除,来提高系统的音质和语音识别精准度等。
本论文通过对各种低通滤波器的通频带、增益和截止频率的分析,采用通频带最大扁平度技术(巴特沃斯技术)来设计实现四阶高性能低通滤波器,通过Multisum仿真软件,验证了设计的正确性。
在这基础上,本文还对如何提高该滤波器的响应速度进行了研究,提出了一种有效的提高响应速度的方案,并通过仿真软件得以验证。
这在低通滤波器的理论以及实际工程应用中,都具有非常重要的意义。
关键词:有源低通滤波器,巴特沃斯,运算放大器Design of Butterworth Active Low Pass FilterABSTRACTWith the rapid development of social science and technology, various technological products can be seen everywhere in human society, which greatly enriches people's daily lives. IoT devices, wearable devices, and virtual instrument products have become extremely common in various applications and consumer occasions. For now, in almost all electronic products, various gains, bandwidths, and high-performance filters play a vital role. For example, in the voice signal input system of wearable devices, the use of high-performance low-pass The filter performs noise reduction, filtering, and echo cancellation of the speech signal to improve the sound quality of the system and the accuracy of speech recognition.In this paper, through the analysis of the passband, gain and cutoff frequency of various low-pass filters, the maximum flatness of the passband technology (Butterworth technology) is used to design and implement a fourth-order high-performance low-pass filter, through Multisum simulation software To verify the correctness of the design. On this basis, this paper also studies how to improve the response speed of the filter, and puts forward an effective scheme to improve the response speed, which is verified by simulation software. This is of great significance in the theory of low-pass filters and in practical engineering applications.KEYWORDS:active low-pass filter,butterworth,amplifier1绪论1.1 引言在近现代的科技发展中,滤波器作为一种必不可少的组成成分,在仪器仪表、智能控制、计算机科学、通信技术、电子应用技术和现代信号处理等领域有着十分重要的作用。
医学图像处理实验报告

d、分别对其进行10*10、5*5、2*2的均值滤波;
e、显示原图像和选用不同大小模版处理后的图像。
(3)高斯滤波
a、读入图像;
b、对数字图像进行直方图均衡化处理;
c、选择高斯滤波参数(标准差)sigma为1.6;
d、选择滤波器尺寸为5*5;
i、显示原图像和处理后的图像。
(2)四八领域均值滤波
a、读入图像;
b、转换图像矩阵为双精度型;
c、创建4邻域平均滤波模版[0 1 0; 1 0 1; 0 1 0];
创建8邻域平均滤波模版[1 1 1; 1 0 1; 1 1 1];
d、进行滤波;
e、显示原图像和处理后图像。
(3)巴特沃斯高通滤波
a、读取图像;
e、创建高斯滤波器进行滤波;
f、显示原图像和处理后的图像。
3
(1)同态滤波
a、读入图像;
b、对数字图像进行直方图均衡化处理;
c、转换图像矩阵为双精度型;
d、取对数;
e、对其做傅里叶变换;
f、选择参数,截止频率为10,锐化系数为2, =1.5, =2.0;
g、进行高斯同态滤波;
h、滤波之后进行傅里叶逆变换;
c、显示原图像和经过均衡化处理过的图像;
d、记录和整理实验报告。
(2)中值滤波加直方图均衡化
a、将模板在图中漫游,并将模板中心与图中某个像素位置重合;
b、读取模板下各对应像素的灰度值;
c、将这些灰度值从小到大排成1列;
d、找出这些值中排在中间的1个;
e、将这个中间值赋给对应模板中心位置的像素;
f、中值滤波之后的像素值进行直方图均衡化处理;
用 MATLAB 设计巴特沃斯低通滤波器
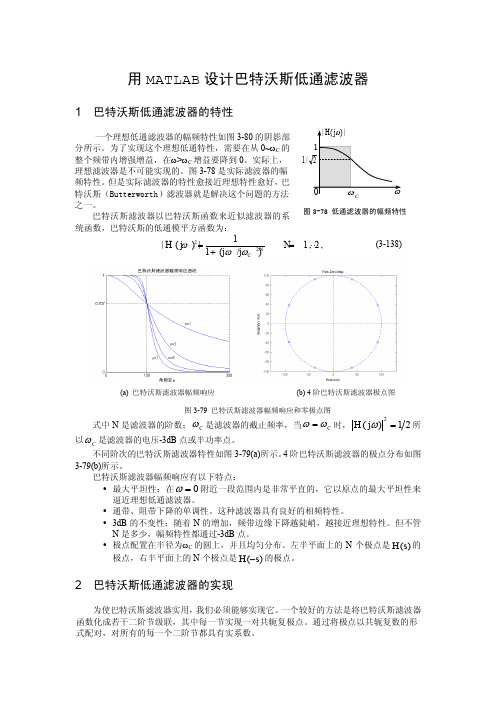
用MATLAB 设计巴特沃斯低通滤波器1 巴特沃斯低通滤波器的特性一个理想低通滤波器的幅频特性如图3-80的阴影部分所示。
为了实现这个理想低通特性,需要在从0~ωC 的整个频带内增强增益,在ω>ωC 增益要降到0。
实际上,理想滤波器是不可能实现的。
图3-78是实际滤波器的幅频特性。
但是实际滤波器的特性愈接近理想特性愈好,巴特沃斯(Butterworth )滤波器就是解决这个问题的方法之一。
巴特沃斯滤波器以巴特沃斯函数来近似滤波器的系统函数,巴特沃斯的低通模平方函数为:221|()|1,2,,1(/)NC H j N j j ωωω==+ (3-138)式中以C ω是滤波器的电压-3dB 点或半功率点。
不同阶次的巴特沃斯滤波器特性如图3-79(a)所示。
4阶巴特沃斯滤波器的极点分布如图3-79(b)所示。
巴特沃斯滤波器幅频响应有以下特点:• 最大平坦性:在0=ω附近一段范围内是非常平直的,它以原点的最大平坦性来逼近理想低通滤波器。
• 通带、阻带下降的单调性。
这种滤波器具有良好的相频特性。
• 3dB 的不变性:随着N 的增加,频带边缘下降越陡峭,越接近理想特性。
但不管N 是多少,幅频特性都通过-3dB 点。
• 极点配置在半径为ωC 的圆上,并且均匀分布。
左半平面上的N 个极点是)(s H 的极点,右半平面上的N 个极点是)(s H -的极点。
2 巴特沃斯低通滤波器的实现为使巴特沃斯滤波器实用,我们必须能够实现它。
一个较好的方法是将巴特沃斯滤波器函数化成若干二阶节级联,其中每一节实现一对共轭复极点。
通过将极点以共轭复数的形式配对,对所有的每一个二阶节都具有实系数。
1图3-78 低通滤波器的幅频特性图3-80所示运算放大器电路为实现一对共轭极点提供了很好的方法。
电路的系统函数为202202121121122121)(1)11(1)(ωωω++=+++=s Qs C C R R s C R C R s C C R R s H (3-139)式中,ω0是S 平面原点与极点之间的距离,Q 被称为电路的“品质因数”,它提供了对响应峰值尖锐程度的一种度量。
实验四 图像增强

信息工程学院实验报告课程名称:数字图像处理Array实验项目名称:实验四图像增强实验时间:班级:姓名:学号:一、实验目的1.了解图像增强的目的及意义,加深对图像增强的感性认识,巩固所学理论知识。
2. 掌握图像空域增强算法的基本原理。
3. 掌握图像空域增强的实际应用及MATLAB实现。
4. 掌握频域滤波的概念及方法。
5. 熟练掌握频域空间的各类滤波器。
6.掌握怎样利用傅立叶变换进行频域滤波。
7. 掌握图像频域增强增强的实际应用及MATLAB实现。
二、实验步骤及结果分析1. 基于幂次变换的图像增强程序代码:clear all;close all;I{1}=double(imread('fig534b.tif'));I{1}=I{1}/255;figure,subplot(2,4,1);imshow(I{1},[]);hold onI{2}=double(imread('room.tif'));I{2}=I{2}/255;subplot(2,4,5);imshow(I{2},[]);hold onfor m=1:2Index=0;for lemta=[0.5 5]Index=Index+1;F{m}{Index}=I{m}.^lemta;subplot(2,4,(m-1)*4+Index+1),imshow(F{m}{Index},[])endend执行结果:图1 幂次变换增强结果实验结果分析:由实验结果可知,当r<1时,黑色区域被扩展,变的清晰;当r>1时,黑色区域被压缩,变的几乎不可见。
2.直方图规定化处理程序代码:clear allclcclose all%0.读图像I=double(imread('lena.tiff'));subplot(2,4,1);imshow(I,[]);title('原图')N=32;Hist_image=hist(I(:),N);Hist_image=Hist_image/sum(Hist_image);Hist_image_cumulation=cumsum(Hist_image);%累计直方图subplot(245);stem(0:N-1,Hist_image);title('原直方图');%1.设计目标直方图Index=0:N-1;%正态分布直方图Hist{1}=exp(-(Index-N/2).^2/N);Hist{1}=Hist{1}/sum(Hist{1});Hist_cumulation{1}=cumsum(Hist{1});subplot(242);stem([0:N-1],Hist{1});title('规定化直方图1');%倒三角形状直方图Hist{2}=abs(2*N-1-2*Index);Hist{2}=Hist{2}/sum(Hist{2});Hist_cumulation{2}=cumsum(Hist{2});subplot(246);stem(0:N-1,Hist{2});title('规定化直方图2');%2. 规定化处理Project{1}=zeros(N);Project{2}=zeros(N);Hist_result{1}=zeros(N);Hist_result{2}=zeros(N);for m=1:2Image=I;%SML处理(SML,Single Mapping Law单映射规则for k=1:NTemp=abs(Hist_image_cumulation(k)-Hist_cumulation{m});[Temp1,Project{m}(k)]=min(Temp);end%2.2 变换后直方图for k=1:NTemp=find(Project{m}==k);if isempty(Temp)Hist_result{m}(k)=0;elseHist_result{m}(k)=sum(Hist_image(T emp));endendsubplot(2,4,(m-1)*4+3);stem(0:N-1,Hist_result{m}); title(['变换后的直方图',num2str(m)]);%2.3结果图Step=256/N;for K=1:NIndex=find(I>=Step*(k-1)&I<Step*k) ;Image(Index)=Project{m}(k);endsubplot(2,4,(m-1)*4+4),imshow(Imag e,[]);title(['变换后的结果图',num2str(m)]);end执行结果:原图规定化直方图2变换后的直方图1变换后的结果图1变换后的直方图2变换后的结果图2图2 直方图规定化实验结果分析:由实验结果可知,采用直方图规定化技术后,原图的直方图逼近规定化的直方图,从而有相应的变换后的结果图1和变换后的结果图2。
实验报告六频域图像增强的方法

实验报告六频域图像增强的方法实验报告六姓名:学号:班级:实验日期: 2016.5.13 实验成绩:实验题目:频域图像增强的方法一.实验目的(1)熟练掌握频域滤波增强的各类滤波器的原理及实现。
(2)分析不同用途的滤波器对频域滤波增强效果的影响,并分析不同的滤波器截止频率对频域滤波增强效果的影响。
二.实验原理变换最慢的频率分量与图像的平均灰度成正比,当远离变换的原点时,低频对应于图像中变换缓慢的灰度分量,当从原点离开得更远时,较高的频率开始对应图像中越来越快的灰度变换,频率域滤波是通过傅里叶变换在频域上对频谱进行修改后再回到空间域的一种方法,在频域中直流项决定了图像的平均灰度,衰减高频通过低频的低通滤波器会模糊一副图像,而衰减低频通过高频的高通滤波器则会增加尖锐的细节,但会导致图像对比度的降低。
三.实验内容及结果(1)选择图像fig620.jpg,对其进行傅里叶变换,在频率域中实现五种不同半径(截止频率)的butterworth低通滤波器的平滑作用。
显示原始图像和滤波图像。
图 1 不同半径巴特沃斯低通滤波图(2)选择图像fig620.jpg,对其进行傅里叶变换,在频率域中实现五种不同半径(截止频率)的butterworth高通滤波的锐化效果,显示原始图像和滤波图像。
图2 不同半径巴特沃斯高通滤波图四.结果分析(1)观察图1,可以发现巴特沃斯低通滤波器半径越小,图像越模糊,但图像的背景亮度大小和原图像别无二致,这是因为低通滤波器实现的是滤除高频分量,保留低频分量的功能,所以半径越小,通过的低频分量越少,所以越模糊,但不论半径多小,它的整体亮度不变,这是由于决定图像平均灰度的直流分量处于图像中点(经过fftshift平移后),它一直是通过的,同时观察变量区的原图像傅里叶变换后的数据矩阵发现,最大数据小于并接近100,所以第五个滤波器设定为100半径,但是发现,滤波后图像的小a还是有一定的模糊,这是因为巴特沃斯滤波器不是理想滤波器,在截止频率处存在一定的过度带,所以小尺寸的物体可能会有模糊。
二维巴特沃斯滤波器c语言

二维巴特沃斯滤波器1. 简介二维巴特沃斯滤波器是一种常用的图像处理方法,用于对图像进行频域滤波。
它基于巴特沃斯滤波器的原理,在频域中对图像进行平滑或增强。
本文将详细介绍二维巴特沃斯滤波器的原理、实现步骤以及应用案例。
2. 巴特沃斯滤波器原理巴特沃斯滤波器是一种频率域滤波器,通过调整截止频率和阶数来控制信号的频率响应。
其传输函数可以表示为:H (u,v )=11+(D (u,v )D 0)2n其中,D (u,v ) 是图像中每个点到中心点的距离,D 0 是截止频率,n 是阶数。
当 n 取不同值时,巴特沃斯滤波器可以实现不同程度的平滑或增强效果。
当 n >1 时,增加了阶数可以使得低频信号更加平坦;当 n <1 时,减小了阶数可以使得低频信号更加突出。
3. 实现步骤二维巴特沃斯滤波器的实现步骤如下:步骤 1:读取图像首先,需要从文件中读取待处理的图像。
可以使用 C 语言中的图像处理库,如 OpenCV ,来实现图像读取功能。
#include <opencv2/opencv.hpp>int main() {// 读取图像cv::Mat image = cv::imread("input.jpg", cv::IMREAD_GRAYSCALE);// 其他处理步骤...return 0;}步骤 2:进行傅里叶变换将读取的图像进行傅里叶变换,得到频域表示。
可以使用 OpenCV 提供的函数dft 来实现傅里叶变换。
#include <opencv2/opencv.hpp>int main() {// 读取图像cv::Mat image = cv::imread("input.jpg", cv::IMREAD_GRAYSCALE);// 进行傅里叶变换cv::Mat frequencyDomain;cv::dft(image, frequencyDomain, cv::DFT_COMPLEX_OUTPUT);// 其他处理步骤...return 0;}步骤 3:生成巴特沃斯滤波器根据巴特沃斯滤波器的传输函数公式,可以生成巴特沃斯滤波器的频域表示。
图像增强

1/5
1/5
0
1/5
1/9
1/9
1/9
1/5
1/5
1/9
1/9
1/9
1/9
1/9
1/9
0
0
邻区平均
1/10 1/10 1/10 1/10 1/10 1/10 1/10 1/16
1/8 1/4 1/8
1/16
1/5
1/10
1/8
1/16
1/8
1/16
加权平均
3.2 中值滤波
虽然均值滤波器对噪声有抑制作用,但同时会使图像变 得模糊。为了改善这一状况,必须寻找新的滤波器。中值 滤波就是一种有效的方法。 中值滤波的原理 1. 用一个大小为 N 的窗口(N=3, 5, 7, …)在图像上滑动; 2. 把窗口中像素的灰度值按升(或降)次序排列; 3. 取排列在正中间的灰度值作为窗口中心所在像素的灰度值。 中值滤波是一种非线性滤波,它对消除脉冲噪声十分有用。 中值滤波优点 1. 抑制噪声 2. 较好地保护边缘轮廓信息
s T (r )
r
p ( r ) dr
r
0
( 2r 2) dr
2 r r
0
r |0 2r |0 r 2r
2
r
2
数字图像的直方图均衡化:
计算公式: sk
P(r)
p
i 0
k
r
( ri )
2
r
2.2 直方图修正
均衡化效果实例:
2.2 直方图修正
均衡化效果实例(续):
3.2 中值滤波 1. 中值滤波的设计思想: 因为噪声的出现,使该点像素比周围的像 素亮(暗)许多, 给出滤波用的模板,如下 图所示是一个一维的模板,对模板中的像素 值由小到大排列,最终待处理像素的灰度取 这个模板中的灰度的中值。
巴特沃斯算法

巴特沃斯算法
巴特沃斯滤波器是一种经典的频域滤波器,由英国工程师斯蒂芬·巴特沃斯于1930年提出。
它通过调整滤波器的截止频率和阶数,可以实现对不同频率信号的增强或抑制。
在信号处理领域,巴特沃斯低通滤波算法是一种常用的数字滤波算法,能够有效地去除信号中高频成分,保留低频成分,常用于音频处理、图像处理等领域。
此外,根据具体的使用场景和需求,可以在巴特沃斯滤波器算法的基础上进行一些延伸和改进,例如自适应巴特沃斯滤波可以根据信号或图像的局部特征自动调整截止频率或阶数,以提高滤波效果;多尺度巴特沃斯滤波使用不同尺度的巴特沃斯滤波器来处理具有多个频率成分的信号或图像;巴特沃斯带通/带阻滤波设计滤波器以在指定频率范围内增强或抑制信号或图像的频率成分等。
使用巴特沃斯滤波器算法通常包括以下步骤:确定滤波类型,根据需求选择巴特沃斯滤波器的类型,如低通、高通、带通或带阻等;设计滤波器,确定滤波器的截止频率和阶数,并使用相应的库函数或工具进行滤波器设计;滤波操作,将待处理的信号或图像与设计好的巴特沃斯滤波器进行卷积或滤波操作;可选的后处理,根据需要,可以对滤波结果进行后处理,如调整对比度、增强细节等。
c++ 3阶巴特沃斯低通滤波算法

C++ 3阶巴特沃斯低通滤波算法在信号处理领域,巴特沃斯低通滤波算法是一种常用的数字滤波算法,它能够有效地去除信号中高频成分,保留低频成分,常用于音频处理、图像处理等领域。
C++作为一种高效的编程语言,能够很好地支持这一算法的实现。
本文将结合C++语言,深入探讨3阶巴特沃斯低通滤波算法的原理、实现和应用。
1. 巴特沃斯低通滤波算法概述巴特沃斯低通滤波器是一种能够通过滤波器将信号中高频成分抑制、低频成分保留的数字滤波器。
其传输函数具有一定的特点,采用巴特沃斯低通滤波器可以实现对信号的平滑处理,去除高频噪声,保留低频信号。
3阶巴特沃斯低通滤波器具有更加优化的特性,能够更好地滤除高频噪声,保留低频信号,因此在实际应用中具有广泛的价值。
2. 3阶巴特沃斯低通滤波算法原理3阶巴特沃斯低通滤波算法是建立在巴特沃斯低通滤波器基础上的改进版本,其核心原理是通过多级滤波器级联的方式,增强滤波效果,同时减少不必要的波纹和相位失真。
其数学模型和传输函数较为复杂,需要通过C++编程语言实现。
3. C++实现3阶巴特沃斯低通滤波算法在C++中实现3阶巴特沃斯低通滤波算法,需要充分利用C++语言的面向对象特性、模板编程等特点。
可以采用模块化的设计思路,将滤波器的设计、参数设置、滤波处理等功能进行封装,从而提高代码的可复用性和可维护性。
C++的性能优势也能够保证算法的高效性。
4. 应用案例分析3阶巴特沃斯低通滤波算法在信号处理领域具有广泛的应用,比如在音频去噪、图像平滑处理、信号恢复等方面均有重要作用。
通过具体的应用案例分析,可以更好地展现算法的效果和实用性,也有助于读者深入理解算法的具体应用场景。
5. 个人观点和总结作为一种经典的数字滤波算法,3阶巴特沃斯低通滤波算法在实际应用中能够发挥重要作用。
在C++语言中实现该算法,既能够充分发挥C++语言的优势,也能够更好地与实际应用结合,为信号处理领域的工程实践提供技术支持。
在未来的发展中,可以进一步优化算法的性能、扩展算法的适用范围,从而更好地满足不同领域的需求。
数字图像处理图像变换实验报告

实验报告实验名称:图像处理姓名:刘强班级:电信1102学号:1404110128实验一图像变换实验——图像点运算、几何变换及正交变换一、实验条件PC机数字图像处理实验教学软件大量样图二、实验目的1、学习使用“数字图像处理实验教学软件系统”,能够进行图像处理方面的简单操作;2、熟悉图像点运算、几何变换及正交变换的基本原理,了解编程实现的具体步骤;3、观察图像的灰度直方图,明确直方图的作用与意义;4、观察图像点运算与几何变换的结果,比较不同参数条件下的变换效果;5、观察图像正交变换的结果,明确图像的空间频率分布情况。
三、实验原理1、图像灰度直方图、点运算与几何变换的基本原理及编程实现步骤图像灰度直方图就是数字图像处理中一个最简单、最有用的工具,它描述了一幅图像的灰度分布情况,为图像的相关处理操作提供了基本信息。
图像点运算就是一种简单而重要的处理技术,它能让用户改变图像数据占据的灰度范围。
点运算可以瞧作就是“从象素到象素”的复制操作,而这种复制操作就是通过灰度变换函数实现的。
如果输入图像为A(x,y),输出图像为B(x,y),则点运算可以表示为:B(x,y)=f[A(x,y)]其中f(x)被称为灰度变换(Gray Scale Transformation,GST)函数,它描述了输入灰度值与输出灰度值之间的转换关系。
一旦灰度变换函数确定,该点运算就完全确定下来了。
另外,点运算处理将改变图像的灰度直方图分布。
点运算又被称为对比度增强、对比度拉伸或灰度变换。
点运算一般包括灰度的线性变换、阈值变换、窗口变换、灰度拉伸与均衡等。
图像几何变换就是图像的一种基本变换,通常包括图像镜像变换、图像转置、图像平移、图像缩放与图像旋转等,其理论基础主要就是一些矩阵运算,详细原理可以参考有关书籍。
实验系统提供了图像灰度直方图、点运算与几何变换相关内容的文字说明,用户在操作过程中可以参考。
下面以图像点运算中的阈值变换为例给出编程实现的程序流程图,如下:2、图像正交变换的基本原理及编程实现步骤数字图像的处理方法主要有空域法与频域法,点运算与几何变换属于空域法。
最新医学图像处理实验报告

(1)直方图均衡化
直方图是图像的最基本的统计特征,它反映的是图像的灰度值的分布情况。直方图均衡化的目的是使图像在整个灰度值动态变化范围内的分布均匀化,改善图像的亮度分布状态,增强图像的视觉效果。灰度直方图是图像预处理中涉及最广泛的基本概念之一。
图像的直方图事实上就是图像的亮度分布的概率密度函数,是一幅图像的所有象素集合的最基本的统计规律。直方图反映了图像的明暗分布规律,可以通过图像变换进行直方图调整,获得较好的视觉效果。
(3)高斯滤波
高斯滤波器的二维形式为: ,D(u,v)是距频率矩形中心的距离。 是关于中心的扩展度的度量。通过令 ,该滤波器可表示为:
其中, 是截止频率。当 时,H下降到其最大值的0.607处。
3
(1)同态滤波
同态滤波是把频率过滤和灰度变换结合起来的一种图像处理方法,它依靠图像的照度/反射率模型作为频域处理的基础,利用压缩亮度范围和增强对比度来改善图像的质量。使用这种方法可以使图像处理符合人眼对于亮度响应的非线性特性,避免了直接对图像进行傅立叶变换处理的失真。
医学图像处理实验报告
班级专业姓名学号
实验
一、实验目的
1:理解并掌握常用的图像的增强技术。
2:熟悉并掌握MATLAB图像处理工具箱的使用。
3:实践几种常用数字图像增强的方法,增强自主动手能力。
二、实验任务
对于每张图像(共三张图片),实现3种图像增强方法。根据图像的特点,分别选用不用的图像增强算法。
三、实验内容(设计思路)
直方图均衡化是指:采用累积分布函数(CDF)变化生成一幅图像,该图像的灰度级较为均衡化,且覆盖了整个范围[0,1],均衡化处理的结果是一幅扩展了动态范围的图像。直方图均衡化就是通过灰度变换将一幅图像转换为另一幅具有均衡直方图,即在每个灰度级上都具有相同的象素点数的过程。主要用途是:将一幅灰度分布集中在较窄区间,细节不够清晰的图像,修正后使图像的灰度间距增大或灰度分布均匀,令图像的细节清晰,达到图像增强的目的。
遥感数字图像处理:遥感图像处理-图像滤波

Mean 11x11
1.2 中值滤波器
在邻域平均法中,是将n×n局部区域中的灰度的平
均值作为区域中央象元的灰度值。而在中值滤波中,是 把局部区域中灰度的中央值作为区域中央象元的值。
g(x, y) median(of (x, y))
如,在3×3区域内进行中值滤波,是将区域内9个 灰度值按由小到大排列,从小的一方开始的第5个值即 为中央象元的值。
矢量微分----梯度
二元函数f(x,y)在坐标点(x,y)处的梯度向量的定义:
f
G[
f
( x,
y)]
x f
y
梯度的幅度:
G[ f (x, y)] ( f )2 ( f ) 2
x
y
梯度的幅角:
M
tg 1[ f / f ] y x
连续域的微分----离散域的差分
x f (i, j) f (i 1, j) f (i, j) y f (i, j) f (i, j 1) f (i, j)
MN
r(i, j) (m, n)t(m, n) m1 n1
将计算结果r(i,j) 放在窗口中心的像 元位置,成为新像 元的灰度值。然后 活动窗口向右移动 一个像元,再按公 式做同样的运算, 仍旧把计算结果放 在移动后的窗口中 心位置上,依次进 行,逐行扫描,直 到全幅图像扫描一 遍结束,则新图像 生成。
数字图像处理matlab代码

一、编写程序完成不同滤波器的图像频域降噪和边缘增强的算法并进行比较,得出结论。
1、不同滤波器的频域降噪1.1 理想低通滤波器(ILPF)和二阶巴特沃斯低通滤波器(BLPF)clc;clear all;close all;I1=imread('me.jpg');I1=rgb2gray(I1);subplot(2,2,1),imshow(I1),title('原始图像');I2=imnoise(I1,'salt & pepper');subplot(2,2,2),imshow(I2),title('噪声图像');F=double(I2);g = fft2(F);g = fftshift(g);[M, N]=size(g);result1=zeros(M,N);result2=zeros(M,N);nn = 2;d0 =50;m = fix(M/2);n = fix(N/2);for i = 1:Mfor j = 2:Nd = sqrt((i-m)^2+(j-n)^2);h = 1/(1+0.414*(d/d0)^(2*nn));result1(i,j) = h*g(i,j);if(g(i,j)< 50)result2(i,j) = 0;elseresult2(i,j) =g(i,j);endendendresult1 = ifftshift(result1);result2 = ifftshift(result2);J2 = ifft2(result1);J3 = uint8(real(J2));subplot(2, 2, 3),imshow(J3,[]),title('巴特沃斯低通滤波结果'); J4 = ifft2(result2);J5 = uint8(real(J4));subplot(2, 2, 4),imshow(J5,[]),title('理想低通滤波结果');实验结果:原始图像噪声图像巴特沃斯低通滤波结果理想低通滤波结果1.2 指数型低通滤波器(ELPF)clc;clear all;close all;I1=imread('me.jpg');I1=rgb2gray(I1);I2=im2double(I1);I3=imnoise(I2,'gaussian',0.01);I4=imnoise(I3,'salt & pepper',0.01);subplot(1,3,1),imshow(I2), title('原始图像'); %显示原始图像subplot(1,3,2),imshow(I4),title('加入混合躁声后图像 ');s=fftshift(fft2(I4));%将灰度图像的二维不连续Fourier 变换的零频率成分移到频谱的中心[M,N]=size(s); %分别返回s的行数到M中,列数到N中n1=floor(M/2); %对M/2进行取整n2=floor(N/2); %对N/2进行取整d0=40;for i=1:Mfor j=1:Nd=sqrt((i-n1)^2+(j-n2)^2); %点(i,j)到傅立叶变换中心的距离 h=exp(log(1/sqrt(2))*(d/d0)^2);s(i,j)=h*s(i,j); %ILPF滤波后的频域表示endends=ifftshift(s); %对s进行反FFT移动s=im2uint8(real(ifft2(s)));subplot(1,3,3),imshow(s),title('ELPF滤波后的图像(d=40)');运行结果:1.3 梯形低通滤波器(TLPF)clc;clear all;close all;I1=imread('me.jpg');I1=rgb2gray(I1); %读取图像I2=im2double(I1);I3=imnoise(I2,'gaussian',0.01);I4=imnoise(I3,'salt & pepper',0.01);subplot(1,3,1),imshow(I2),title('原始图像'); %显示原始图像subplot(1,3,2),imshow(I4),title('加噪后的图像');s=fftshift(fft2(I4));%将灰度图像的二维不连续Fourier 变换的零频率成分移到频谱的中心[M,N]=size(s); %分别返回s的行数到M中,列数到N中n1=floor(M/2); %对M/2进行取整n2=floor(N/2); %对N/2进行取整d0=10;d1=160;for i=1:Mfor j=1:Nd=sqrt((i-n1)^2+(j-n2)^2); %点(i,j)到傅立叶变换中心的距离 if (d<=d0)h=1;else if (d0<=d1)h=(d-d1)/(d0-d1);else h=0;endends(i,j)=h*s(i,j); %ILPF滤波后的频域表示endends=ifftshift(s); %对s进行反FFT移动s=im2uint8(real(ifft2(s))); %对s进行二维反离散的Fourier变换后,取复数的实部转化为无符号8位整数subplot(1,3,3),imshow(s),title('TLPF滤波后的图像');运行结果:1.4 高斯低通滤波器(GLPF)clear all;clc;close all;I1=imread('me.jpg');I1=rgb2gray(I1);I2=im2double(I1);I3=imnoise(I2,'gaussian',0.01);I4=imnoise(I3,'salt & pepper',0.01);subplot(1,3,1),imshow(I2),title('原始图像');subplot(1,3,2),imshow(I4),title('加噪后的图像');s=fftshift(fft2(I4));%将灰度图像的二维不连续Fourier 变换的零频率成分移到频谱的中心[M,N]=size(s); %分别返回s的行数到M中,列数到N中n1=floor(M/2); %对M/2进行取整n2=floor(N/2); %对N/2进行取整d0=40;for i=1:Mfor j=1:Nd=sqrt((i-n1)^2+(j-n2)^2); %点(i,j)到傅立叶变换中心的距离 h=1*exp(-1/2*(d^2/d0^2)); %GLPF滤波函数s(i,j)=h*s(i,j); %ILPF滤波后的频域表示endends=ifftshift(s); %对s进行反FFT移动s=im2uint8(real(ifft2(s))); %对s进行二维反离散的Fourier变换后,取复数的实部转化为无符号8位整数subplot(1,3,3),imshow(s),title('GLPF滤波后的图像(d=40)');运行结果:1.5 维纳滤波器clc;clear all;close all;I=imread('me.jpg'); %读取图像I=rgb2gray(I);I1=im2double(I);I2=imnoise(I1,'gaussian',0.01);I3=imnoise(I2,'salt & pepper',0.01);I4=wiener2(I3);subplot(1,3,1),imshow(I1),title('原始图像'); %显示原始图像subplot(1,3,2),imshow(I3),title('加入混合躁声后图像');I4=wiener2(I3);subplot(1,3,3),imshow(I4),title('wiener滤波后的图像');运行结果:结论:理想低通滤波器,虽然有陡峭的截止频率,却不能产生良好的效果,图像由于高频分量的滤除而变得模糊,同时还产生振铃效应。
图像增强ppt课件

编辑课件
38
均值降噪
编辑课件
39
补充1 图像的γ校正
• 我们知道,数字图像信息的获取通常都
是通过光电传感器(如:CCD)来完成的。 但是,由于传感器的输入输出特性不是 线性的。所以,如果不进行校正处理的 话,将无法得到好的图像效果。
(同理,加洗照片不对颜色进行校正配准,所以效果 都会略差一些)
编辑课件
一维窗口
编辑课件
28
除上述窗口外,常用的窗口还有方形、 十字形、圆形和环形等等,如下图所示。
图 中值滤波的常用窗口
编辑课件
29
中值滤波是一种非线性运算。它对于 消除孤立点和线段的干扰十分有用。特别是 对于二进噪声尤为有效,对于消除高斯噪声 的影响效果不佳。对于一些细节较多的复杂 图像,还可以多次使用不同的中值滤波,然 后通过适当的方式综合所得的结果作为输出, 这样可以获得更好的平滑和保护边缘的效果。
2)典型低通滤波器
理想的低通滤波器 梯形滤波器 指数滤波器
巴特沃兹滤波器
振铃程度 图像模糊 噪声平 程度 滑效果
严重
严重
最好
较轻
轻
好
无
较轻
一般
无
很轻
一般
编辑课件
17
图6.21 指纹图像的频率域增强
(a)指纹原图
(b)频率域增强后的指纹图像
编辑课件
18
频率域图像增强
编辑课件
19
理想低通滤波器举例
原始信息
• 校正后的误差为计算误差,是不得已的,可忽略的误差
编辑课件
47
• 值得注意的是:所得到的 γ 值不一定 准确,那么我们来看一下, γ 值不准确 时,进行校正后的图像效果。
巴特沃斯数字低通滤波器的设计课题论文

电子技术课程设计----巴特沃斯数字低通滤波器的设计专业年级:姓名:学号:指导教师:日期:巴特沃斯数字低通滤波器的设计一、选题依据滤波器是能够过滤波动信号的电路, 它可以从具有各种不同频率成分的信号中, 取出具有特定频率成分的信号。
滤波器在信号处理、数据采集和传输、干扰抑制方面应用非常广泛, 其性能优劣直接影响整个系统的性能, 所以滤波器的设计在很多领域必不可少, 而且至关重要。
由于理想滤波器的特性难以实现, 在设计滤波器时关键是选择一个合适的逼近函数, 使其频率特性满足所需滤波器的所有要求。
目前比较成熟的逼近函数有巴特沃斯、切比雪夫、椭圆函数和贝塞尔滤等。
但是无论用哪种逼近函数设计滤波器都要经过繁琐的计算, 而且通过综合设计确定实现这个传递函数的电路及其元器件的方法也很复杂。
本文介绍了一种利用归一化表经过简单的计算就可以快速设计滤波器的方法。
模拟滤波器可以分为有源滤波和无源滤波两大类, 其中有源滤波器是由R、C 元件和OP 放大器构成。
与无源滤波器相比, 它具有易集成、易标准化、易制造、输出电阻低且不受负载影响, 体积小等优点。
因此得到了更加广泛的应用。
目前可实现的滤波器中巴特沃斯滤波器具有通带内响应平坦, 衰减特性和相位特性好, 对构成滤波器的器件的要求不甚严格, 易于得到符合设计值的特性, 适应性强, 在不知道使用哪种函数合适的情况下, 可以选择巴特沃斯型滤波器, 本文设计的就是巴特沃斯低通滤波器。
滤波器从广义上来说对特定的频点或频点以外的频率进行有效滤波的电路,这种电路保留输入信号中的有用信息,滤除不需要的信息,从而达到信号的检测、提取、识别等不同的目的。
如果处理的信号是时域离散信号,那么相应的处理系统就称为数字滤波器,由于在实际工作中被处理的信号都是幅度量化的数字信号,因此,数字滤波器实际上是用有限精度的算法实现一个线性时不变的时域离散系统。
目前,数字滤波器的应用越来越广泛,它已深入到很多领域,如图象处理、医学生物信息处理、地质信号处理和模式识别处理等。
图像平滑

第一章概述1.1图像锐化图像在传输和变换过程中会受到各种干扰而退化,比较典型的就是图像模糊。
图像锐化的目的就是使边缘和轮廓线模糊的图像变得清晰,并使其细节清晰。
锐化技术可以在空间域进行,常用的方法是对图像进行微分处理,也可以在频域中运用高通滤波技术处理。
1.1.1 图像模糊机理及处理方法图像模糊是常见的图像降质问题。
在图像提取、传输及处理过程中有许多因素可以使图像变模糊。
如光的衍射、聚焦不良、景物和取像装置的相对运动都会使图像变模糊,电子系统高频性能不好也会损失图像高频分量,而使图像不清晰。
在对图像进行数字化时,实际取样点总是有一定的面积,所得的样本是这个具有一定面积的区域的亮度平均值,若取样点正好在边界上,则使样本值降低,从而使数字图像的边界变得不清楚。
大量的研究表明,图像的模糊实质上就是受到了平均或积分运算,因此对其进行逆运算如微分运算、梯度运算,就可以使图像清晰。
从频谱角度来分析,图像模糊的实质是其高频分量被衰减,因而可以用高频加重来使图像清晰。
但要注意,能够进行锐化处理的图像必须要求有较高的信噪比,否则,图像锐化后,信噪比更低。
因为锐化将使噪声受到比信号还强的增强,故必须小心处理。
一般是先去除或减轻干扰噪声后,才能进行锐化处理。
1.1.2 常用的锐化处理方法常用的锐化处理方法有微分法和高通滤波法。
微分法:从数学上看,图像模糊的实质就是图像受到平均或者积分运算,因此对其进行逆运算就可以使图像清晰,因为微分运算是求信号的变化率,有加强高频分量的作用,从而使图像轮廓清晰。
由于图像模糊的特征(如边缘的走向等)各不相同,为了把图像中间任何方向伸展的边缘和轮廓的模糊变清晰,那么要采用各向同性的、具有旋转不变的线性微分算子来锐化它们,梯度算子和拉普拉斯算子就是满足要求的线性微分算子,它们是常用的图像锐化运算方法。
高通滤波:图像中的边缘或线条等细节部分与图像频谱中的高频成分相对应,因此采用高通滤波的方法让高频分量顺利通过,使低频分量受到抑制,就可以增强高频的成分,是图像的边缘或线条变得清晰,实现图像的锐化。
基于巴特沃斯低通滤波器的图像增强

基于巴特沃斯低通滤波器的图像增强陈传峰,朱长仁,宋洪芹(国防科技大学电子科学与工程学院湖南长沙410073)l 引言在进行图像处理的过程中,获取原始图像后,首先需要对图像进行图像预处理,因为在获取图像的过程中,往往会发生图像失真,使所得图像与原图像有某种程度上的差别。
在许多情况下,人们难以确切了解引起图像降质的具体物理过程及其数学模型,但却能估计出使图像降质的一些可能原因,针对这些原因采取简单易行的方法,改善图像质量。
由于噪声、光照等原因,使图像质量不高,为了改善视觉效果或便于人、机器对图像的分析理解,一般都需要对图像进行增强处理,但这个过程并没有统一的标准。
图像增强一般不能增加原图像信息,只能针对一些成像条件,把弱信号突出出来,使一些信息更容易分辨。
图像增强的方法比较多,可以大概分为对比度增强,直方图增强、平滑和锐化[1]4大类,其中,直方图均衡是图像增强的经典方法,因为其有效性和简单易用性已成为图像增强最常用的方法,他又分为全局均衡和局部均衡2种。
全局的直方图均衡[2.3]是对整幅图像进行均衡,使其灰度分布均匀,让每一个灰度等级上的象素个数基本相等,算法简单、计算量小、容易实现,但对图像细节部分增强不够;局部直方图均衡[4.5]则可以增强图像内部细节信息,得到很好的增强效果。
Yin[6]通过对小波分解各个分量进行直方图均衡,然后重构得到处理后图像,S.M.Pi-zer[2]提出自适应直方图均衡算法,这也是一种局部均衡算法。
在对全局直方图均衡和局部直方图均衡详细分析的基础上,本文提出了一种基于Buterworth低通滤波的图像增强方法。
由于Buterworth低通滤波器在抑制噪声的同时,图像边缘模糊程度大大减小,且没有振铃效应。
基于以上特点,用Buterworth低通滤波器将低频分量和高频分量分离,低频分量进行均衡后,再将两部分融合,实现图像的增强。
2直方图均衡化直方图均衡化[8]是灰度变换的一个重要应用,他是以累计分布函数变换为基础的直方图修正法。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于巴特沃斯低通滤波器的图像增强
陈传峰,朱长仁,宋洪芹
(国防科技大学电子科学与工程学院湖南长沙410073)
l 引言
在进行图像处理的过程中,获取原始图像后,首先需要对图像进行图像预处理,因为在获取图像的过程中,往往会发生图像失真,使所得图像与原图像有某种程度上的差别。
在许多情况下,人们难以确切了解引起图像降质的具体物理过程及其数学模型,但却能估计出使图像降质的一些可能原因,针对这些原因采取简单易行的方法,改善图像质量。
由于噪声、光照等原因,使图像质量不高,为了改善视觉效果或便于人、机器对图像的分析理解,一般都需要对图像进行增强处理,但这个过程并没有统一的标准。
图像增强一般不能增加原图像信息,只能针对一些成像条件,把弱信号突出出来,使一些信息更容易分辨。
图像增强的方法比较多,可以大概分为对比度增强,直方图增强、平滑和锐化[1]4大类,其中,直方图均衡是图像增强的经典方法,因为其有效性和简单易用性已成为图像增强最常用的方法,他又分为全局均衡和局部均衡2种。
全局的直方图均衡[2.3]是对整幅图像进行均衡,使其灰度分布均匀,让每一个灰度等级上的象素个数基本相等,算法简单、计算量小、容易实现,但对图像细节部分增强不够;局部直方图均衡[4.5]则可以增强图像内部细节信息,得到很好的增强效果。
Yin[6]通过对小波分解各个分量进行直方图均衡,然后重构得到处理后图像,S.M.Pi-zer[2]提出自适应直方图均衡算法,这也是一种局部均衡算法。
在对全局直方图均衡和局部直方图均衡详细分析的基础上,本文提出了一种基于Buterworth低通滤波的图像增强方法。
由于Buterworth低通滤波器在抑制噪声的同时,图像边缘模糊程度大大减小,且没有振铃效应。
基于以上特点,用Buterworth低通滤波器将低频分量和高频分量分离,低频分量进行均衡后,再将两部分融合,实现图像的增强。
2直方图均衡化
直方图均衡化[8]是灰度变换的一个重要应用,他是以累计分布函数变换为基础的直方图修正法。
一幅均匀量化的自然图像的灰度直方图通常在低值灰度区间上频率较大,这样的图像的较暗区域中的细节常常看不清楚。
为使图像变清晰,一个自然的想法是使图像的灰度动态范围变大,并且让灰度频率较小的灰度级经变换后其频率变的大一些,从而使象素个数增多,即应使变换后的图像灰度直方图在较大的动态范围内趋于均衡,产生一幅灰度级分布具有均匀概率密度的图像,扩展象素的取值动态范围。
传统的直方图均衡算法(HE)是利用全局图像信息,对给定的数字图像进行对比度增强处理,其处理过程如下:
(1)计算原图像的灰度级直方图;
(2)求原图像各灰度级的累积概率分布函数,并由此构造灰度转换函数;
(3)根据灰度转换函数将原图像所有象素灰度值映射到输出图像,得到增强图像。
这种直方图均衡方法限制了图像中某些局部区域的对比度拉伸力度,使某些细节与背景之间的对比度难以得
到有效增强,甚至出现蜕化。
3局部直方图均衡化算法
全局的直方图均衡使直方图在整个灰度级上的分布趋于均匀,取得一定的增强效果,但忽略了细节的信息甚至出现细节信息的丢失,局部直方图均衡则可以较好地解决这一问题,突出细节信息。
在一幅图像中,图像高频分量对应于图像的细节信息,而低频分量对图像的整体视觉效果有着决定性的影响。
对一幅图像进行分频[9],得到高频分量和低频分量,然后对低频分量用传统算法进行直方图均衡,高频分量乘以一个加权系数,再将处理得到的结果进行融合,得到最终的处理结果,实现对原图像的增强。
通过实验,证明了其有效性。
整个处理过程分为以下几步:
3.1 分频
对一幅图像来说,能量主要集中在低频分量中,而噪声和图像细节信息主要集中在高频分量中。
在图像处理过程中,将两种分量分离开,进行不同的操作与处理,可以取得更佳的处理效果。
分频的目的就是将输入图像的高频分量和低频分量分开。
进行分频时,既可以选择高通滤波器又可以选择低通滤波器,都能达到分频的目的。
本文实验的过程中使用的是低通滤波器。
在诸多低通滤波器中,Buterworth低通滤波器没有"振铃"现象,而且能够提高图像的细节清晰度,所以,本文算法采用的是Buter-worth低通滤波器,文献[9]采用的是高斯低通滤波器。
Buterworth低通滤波器(BLPF)传递函数:
式中D。
为截止频率,,在D(u,V)=D。
处,;"为阶数,取正整数,用来控制衰减速度。
本文Buterworth低通滤波器截止频率D。
,一50,阶数n一2。
该2阶Buterworth低通滤波器如图1所示。
对一幅输入图像f(r,y),可将其分解为高频分量fh(x,y)和低频分量f1(x,y),如下式所示:
将图像f(x,y)通过2阶Buterworth低通滤波器g(x,y),即f(x,y)与g(x,y)进行卷积,可得到图像的低频分量f(x,y),如下:
其中(D。
为截止频率)在图像f(x,y)中减去低频分量f1(x,y)就得到高频分量:
3.2低频分量均衡化
图像的能量主要集中在低频分量f1(x,y)中,对图像的整体视觉效果起着决定性的作用,必然要对该分量进行直方图均衡。
对低频分量f(x,y)利用传统算法进行直方图均衡,得到t1(r,y):
3.3 线性组合得输出图像
噪声存在于高频分量中,如果直接进行直方图均衡,必将使噪声得到增强,影响图像质量。
因此,将fh(x,y)乘上一个加权系数a得到th(x,y):
a的取值因具体情况而定:若图像受噪声影响比较严重严重,a的取值应小于1,以免放大噪声;若图豫受噪声影响比较小,a的取值应大于l。
输出图像t(T,y)为高频分量fh(x,y)和低频分量f1(T,y)之和:
所以,输出图像f(x,y)为fh(x,y)和HE(f1(x,y))的线性组合,即:
t(x,y)就是希望得到的图像。
通过分频,输人图像被分解为高频分量和低频分量,对两分量进行不同的操作,再经过线性组合得到最终的增强图像,图像清晰度高,细节信息丰富,增强效果明显。
本文算法如下:
(1)对输入图像,f(x,y)进行快速傅里叶变换得F(u,v);
(2)将F(u,v)作为Buterworth低通滤波器的输入,输出得到低频分量Fl(u,v),用F(u,v)减去F1(u,v)的高频分量Fh(u,v),并进行傅里叶反变换,得到fh(x,y)和f1(x,y);
(3)利用HE算法对低频分量f1(x,y)进行直方图均衡;
(4)高频分量fh(x,y)乘以一个加权系数,再对两分量进行线性组合,融合得到输出图像。
4实验及结果分析本文以lena,flower,frog图像为例进行了实验。
图2中(a)为原始图像;(b)为灰度级较低的退化图像,图像的细节信息和整体的视觉效果都比较差(实验中以退化图像作为输入图像,检验算法的增强效果);(c)为使用传统HE算法得到的处理结果;(d)为利用本文算法对原图进行增强得到的结果。
4.1 实验结果
实验结果如图2所示:
4.2 结果分析
(1)主观评价
图1(c)中,图像的细节信息并未得到有效增强。
这是因为全局直方图均衡利用的是全局信息,限制了对图像局部区域对比度的拉伸力度,本文算法则利用了局部图像信息,充分再现了图像细节,使细节信息更加突出,
并且视觉效果更好。
(2)客观评价
为了从数据上显示出本文算法的效果,采用了一个评价参量一灰度标准差Sd,定义式如下:
其中,I'表示增强后图像,I表示原图,N为图像象素数。
计算Sd时,首先计算I'中每一象素与I中对应象素的灰度值的差平方;然后求平均;最后再求算术平方根。
分别计算传统算法、本文算法增强后图像与原图间的灰度标准差,数据统计结果如表1所示:
从表1的统计数据来看,对退化图像进行图像增强,本文算法的处理结果较传统算法与原图更为接近,通过增强,更好地将退化图像恢复出原始图像的信息,并且还有了更为丰富的信息。
因而,灰度标准差的值比较大,但数据依然很好地表明了本文算法的有效性。
无论直观地从处理结果上还是从统计数据上来看,与传统图像增强算法相比,本文算法都取得了较好的实验效果,是一种有效的图像增强算法。
5 结语
为使图像处理后的效果得到进一步的提高,文献[10]采用将对比度增强算法与直方图均衡算法级联,使得图中的局部信息和全局信息在增强时都能被利用。
国外文献[2,ll,12]介绍采用多尺度自适应的直方图均衡(Multi-scale Adaptive Histogram Equali-zation)对图像进行处理以增强图像的对比度。
本文采用Buterworth低通滤波器将图像分为高频分量和低频分量,低频分量进行HE算法直方图均衡,然后再将高频分量和低频分量进行融合得到最终处理结果,这样可以突出图像的细节信息,使图像整体视觉效果得到改善,有利于后续图像处理工作的进行。
实验结果证明了本文算法的有效性。
