1.2 30°、45°、60°角的三角函数值课件(北师大版九下)

合集下载

2019春九年级下册北师大版数学课件：1.2.30°,45°,60°角的三角函数值(共15张PPT)

如右图，根据题意可知，解： 1 AOD 60 30; OD 2.5m, 2 AC = 2.5 －2.165≈0.34(m).
所以,最高位置与最低位置的高度差约为0.34m.
0
1 2
B
C
3 1 2 3 1 ( 3 1 ) 3 解：原式＝＝＝＝2 3. 3 3 1 2 2 1 2 3
观察一副三角板：它们其中有几个锐角？分别是多少度？ (1)sin30°,sin45°,sin60°等于多少？ (2)cos30°,cos45°,cos60°等于多少？ (3)tan30°,tan45°,tan60°等于多少？你能对一直伴随我们学三角 1 余弦习的这副三角尺所具有的功函数正弦正切 2 cos 能来个重新认识和评价？ tan α 锐角 sin α 3 3 α 根据上面的计算,完成右表: α 2 3 〈特殊角的三角函数值表〉 2 2 30 1 2 2 ° 1 3 3 45 2 2
1 3 2 2 解：原式＝ 3 ( ) 1 2 ( 1) 2 3 2 2 2 2 2 ＝ 1 1 2(1 ) ＝2
(1) tan 2 cos30 0 解： 3 tan 2 0 2 tan 3
1 3 (1 3)2 4 3 1 3 ( 3 1) (2)方程的根为： x 2 2 1. x 3或 1. tan A的值是 3或
阅读课本内容，了解本节主要内容.
1 2
60°
2 2
45°
3 2
30°
3 3
<45°3直角来自角形中边与角的关系：锐角三角函数.
在直角三角形中,若一个锐角确定,那么这个角的对边、邻边和斜边之间的比值也随之确定.

北师大版九年级下册数学：1. 2 30°,45°,60°角的三角函数值 (共14张PPT)

1
3
1
2
2
3
认真观察一下特殊角三角函数值表格中的
数据,你能发现什么规律？
快速抢答：（看谁又快又准！）
tan600 3
sin450 2 2
cos600 1 2
sin600 3 2
cos450 2 2
sin300 1 2
tan300
3 3
tan450 1
cos300
3 2
快速抢答：（已知特殊值求角的度数）
B
c
a
┌
b
C
300
450
450 ┌ 600 ┌
布置作业习题1.3 5,6题;
结束寄语
数学是思维的体操，只有认真学习数学，并努力学好数学的人，才会使自己的思维更敏锐，更科学，更完美，才能使自己的思维品质更优秀！
当一个人用工作去迎接光明，光明很快就会来照耀着他。人在身处逆境时，适应环境的能力实在惊人。人可以忍受不幸，也可以战胜不幸，因为人有着惊人的挥它，就一定能渡过难关。倘若你想达成目标，便得在心中描绘出目标达成后的景象；那么，梦想必会成真。心等待,就可以每一个人都具有特殊能力的电路，知道，所以无法充分利用，就好像怀重宝而不知其在；只要能发掘出这项秘藏的能力，人类的能力将会完全大改观，也能展现出超乎常人的能力我这一生不曾和伟大的著作都来自于求助潜意识心智无穷尽的宝藏。那些最能干的人，往往是那些即使在最绝望的环境里，仍不断传送成功意念的人。他们不但鼓舞自己，成功，誓不休止。灵感并不是在逻辑思考的延长线上产生，而是在破除逻辑或常识的地方才有灵感。真正的强者，善于从顺境中找到阴影，从逆境中找到光亮进的目标。每一种挫折或不利的突变，是带着同样或较大的有利的种子。什么叫做失败？失败是到达较佳境地的第一步。失败是坚忍的最后考验。对于不屈不失败这回事。一次失败，只是证明我们成功的决心还够坚强。失败也是我需要的，它和成功对我一样有价值。我们关心的，不是你是否失败了，而是你对失败失败？失败是到达较佳境地的第一步。没有人事先了解自己到底有多大的力量，直到他试过以后才知道。对于不屈不挠的人来说，没有失败这回事。要成功不能，只要把你能做的小事做得好就行了。成功的唯一秘诀——坚持最后一分钟。只有胜利才能生存，只有成功才有代价，只有耕耘才有收获。只有把抱怨环境的力量，才是成功的保证。不要为已消尽之年华叹息，必须正视匆匆溜走的时光。当许多人在一条路上徘徊不前时，他们不得不让开一条大路，让那珍惜时间面去。敢于浪费哪怕一个钟头时间的人，说明他还不懂得珍惜生命的全部价值。成功＝艰苦劳动＋正确的方法＋少说空话。合理安排时间，就等于节约时间。

度北师大版九年级数学下册30°,45°,60°角的三角函数值课件

D.
【解析】由三角函数的定义知cos30°=
课堂小测
B
sin
课堂小测
A
【解析】作AE∥DC，
30° B
ห้องสมุดไป่ตู้
可得∠AEB=30°，∠BAE=90°, EC=AD=4，
D
60° C
利用AB的长和∠B=30°这一条件，再利用勾股定理，即可解题.
课堂小测
4．计算：
cos
sin
【解析】原原式式 2 (2 2 3 ) 2 6 22 4
九年级数学北师版·下册
第一章直角三角形的边角关系
1.2 30°，45°，60°角的三角函数值
授课人：X
教学目标
1.经历探索30°,45°,60°角的三角函数值的过程，能够进行有关的推理，进一步体会三角函数的意义. 2.能够进行30°,45°,60°角的三角函数值的计算. 3.能够根据30°,45°,60°角的三角函数值说明相应的锐角的大小.
所以，最高位置与最低位置的高度差约为0.34m.
新知探究
【跟踪训练】 1.计算:
(1)sin 60°- cos 45°. (2)cos 60°+ tan 60°.
sin
sin
cos
新知探究
【解析】（1）
，
（2）
，
（3）
，
新知探究
2.某商场有一自动扶梯,其倾斜角为30°,高为7m,扶梯的长度是多少?
【解析】如图所示,BC=7m，
∠A=30° sinA= ∴AB=14 m，
B
C
A
即扶梯的长度为14 m.
新知探究
3.如图,在Rt△ABC中,∠C=90°,∠A,∠B ,∠C的对边分别是a,b,c. 求证 : sin2A+cos2A=1.

1.2 30°,45°,60°角的三角函数值北师大版数学九年级下册课件

2a
60°
sin 30°表示在直角三角形
a
中，30°角的对边与斜边的比
30°
值，与直角三角形的大小无关.
3a
不妨设30°角所对的边为a（如图所示），根据
“直角三角形中30°角所对的边等于斜边的一半”的性
质，知斜边等于2a.根据勾股定理，可知30°角的邻边
为
3a
，所以 sin 30° = a
2a
= 1. 2
第1章直角三角形的边角关系
1.2 30°，45°，60°角的三角函数值
创设问题情境，引入新课
如图，为了测量一棵大树的高度，准备了如下测量工具：①含30°和60°两个锐角的三角尺；②皮尺.
请你设计一个测量方案，测出这棵大树的高度.
创设问题情境，引入新课
如图，让一位同学拿着三角尺站在一个适当的位置
三角函数值
角α
三角函数
30°
sin α
1 2
45°
2
2
60°
3
2
探究：（3）第三列呢？
cos α
3 2 2 2 1 2
tan α
3 3 1
3
显然第三列是30°，45°，60°角的正切值，首先 45°角是等腰直角三角形中的一个锐角，所以tan 45°=1 比较特殊.但通过比较可以得出，正切值随角度的增大而增大.
30°
1
2
45°
2
2
3
3
2
3
2
2
1
60°
3
2
1 2
3
讲授新课
三角函数值
角α
三角函数
30°
sin α
1 2

1.2 30°,45°,60°角的三角函数值课件北师大版数学九年级下册

-4-
第一章直角三角形的边角关系
1.2 30°，45°，60°角的三角函数值
1. A 提示：由题意得∠A=90°-60°=30°，∴sinA=sin30°= ．
2. B 提示：sin45°=cos45°=
．
3. C 提示：sin60°+cos30°=
．
4.
提示：原式=
.
5. 1 提示：∵∠A 为锐角，且 sinA= ，∴∠A=45°，∴tanA=tan45°=1．
sin60 ° -2sin45 °
=6 ×
．
错因：记混特殊角的三角函数值.
易错警示：记错特殊角的三角函数值是常犯的错误，要结合规律牢记特殊
角的三角函数值.
-9-
1.2 30°，45°，60°角的三角函数值
[题型探究]
■题型一特殊角的三角函数值的计算
例 1 计算：4sin45°+cos230°-
.
-7-
1.2 30°，45°，60°角的三角函数值
解析：在 Rt△AMD 中，∠MAD=45°，∴DM=AM·tan45°=2×1=2（m），在 Rt△BMC 中，∠MBC=30°，∴CM=BM·tan30°， ∵BM=AM+AB=2+4=6（m），
∴CM=6×
=2 ≈3.46（m），
∴CD=CM-DM=3.46-2≈1.5（m）.
，cosB= ，则∠C= _____．
8.（教材 P10，T1 高仿）计算：（1）
；
（2）
.
-2-
1.2 30°，45°，60°角的三角函数值
■考点 2 30°，45°，60°AC 是电杆的一根拉线，测得 BC=4 米，∠ACB= 60°，则 AB 的

北师大九年级数学下课件：1.2 30°_45°_60°角的三角函数值(公开课)

30米
150
知识应用
3.一个小孩荡秋千,秋千链子的长度为 2.5m,当秋千向两边摆动时,摆角恰为60°, 且两边的摆动角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差
3 2 sin 450 sin 600 2 cos 450.
2
4 2 sin 2 300 cos2 600 2 cos2 450.
2
直击中考
(1+ 2 )0-｜1-sin30°｜+ ( 1 ) -1；
2
知识应用
1.某商场有一自动扶梯,其倾斜角为30°,高为7m.扶梯的长度是多少?
B
1
┌
A
2C
新课导入
若∠A=300 ，
B
sin300=
cos300=
a ┌
tan300=
A
C
∠B的三角函数值呢？
若∠A=450 呢？
sin450 = cos450 = tan450 =
A
B
a
┌
a
C
这张表还可以看出哪些知
特殊三角函数值识之间的内在联系?
sinα 三角函数值三角函数
角α
30°
1
2
45°
2
2
60°
3
2
cosα ቤተ መጻሕፍቲ ባይዱanα
3
3
2
3
21
2
1 2
3
想一想:
如果已知某一锐角的某种三角函数值,你能求出这一锐角吗?比如tanA＝1,锐角A 是多少度?
例题示范
[例1]计算： (1)sin30°+cos45°；
(2)sin260°+cos260°.

北师大版九年级数学下册课件 1.2 30°,45°,60°角的三角函数值

典型例题
例3：已知α为锐角，且tanα是方程x2+2x-3=0的一个根，求
2sin2α+cos2α- tan（α+15°）的值．
解：解方程x2+2x-3=0，得x1=1，x2=-3，
∵tanα＞0，∴tanα=1，∴α=45°.
∴2sin2α+cos2α- 3 tan（α+15°）
=2sin245°+cos245°- 3 tan60°
2
2
2 2
3
2

3
2
2 2
3
(1 3).
2
三、即学即练，应用知识
1.在Rt△ABC中，∠C＝90°，sin A＝
)A．30°
B．45°

，则∠A的度数是(

C．60°
D．90°
2.计算 2cos 30°－tan 45°－（1－tan 60°） 2的结果是(
北师大版数学九年级下册
第一章直角三角形的边角关系
2
30°,45°,60°角的三角函数值
学习目标
1.经历探索 30°， 45°，60°角的三角函数值的过程，能够进
行有关推理，进一步体会三角函数的意义，并熟记特殊角的三
角函数值。（重点）
2.能够进行含有30°， 45°，60°角的三角函数值的计算。
二、自主合作，探究新知
典型例题
例2：如图，在Rt△ABC中，∠C＝90°，AB 6 , BC 3 ，求∠A的
度数．
B
解：如图，∵ AB 6, BC 3
BC
sin A

AB
3
2

北师大版九年级下册课件 1.2 30°、45°、60°角的三角函数值

例题欣赏P151
行家看“门道”
例1 计算: (1)sin300+cos450; (2) sin2600+cos2600+tan450.
友情提示:
?怎样
解答
Sin2600表示(sin600)2, cos2600表示(cos600)2,其余类推.
随堂练习P162 计算: (1)sin600-cos450;
3.如图,Rt△ABC中,∠C=90°
B
∠A,∠B ,∠C的对边分别是 c
a,b,c.求证:sin2A+cos2A=1
友情提示:
A
a
┌
b
C
sin2A+cos2A=1它反映了同角之间的三角函数
的关系,且它更具有灵活变换的特点,若能予以
掌握,则将有益于智力开发.
随堂练习P128
同角之间的三角函数的关系
2.5
OB
B ┌C D
?咋办
A
OC OB cos 300 2.5 3 2.165(m). 2
∴AC=OA-OC=2.5-2.165≈0.34(m).
∴最高位置与最低位置的高度
差约为0.34m.
随堂练习P128
八仙过海,尽显才能
2.某商场有一自动扶梯,其倾斜角为 300,高为7m,扶梯的长度是多少?
c
c
b
a
sin B b , cos B a , tan B b , cot B a .
c
c
a
b
A
B
c
a
┌
b
C
互余两角之间的三角函数关系
sinA=cosB tanA=cotB
cosA=sinB. cotA=tanB.

30°、45°、60°角的三角函数值-九年级数学下册课件(北师大版)

难点
计算含有特殊角的三角函数值的式子。
探索与思考
问题一指出下列三角板中的角度？
90°
30°
90°
60°
45°
45°
本节课我们尝试根据所学知识，求出图中各锐角三角函数值。
探索与思考
问题二探索含30°角的直角板中，30°的正弦、余弦、正切值？
假设30°角所对的边AC = a，
则AB = 2a，由勾股定理得BC=
2
=1
课堂基础练
求满足下列条件的锐角 α
(1) 2sinα － = 0；
解：(1) sinα =

(2) tanα－1 = 0.
，∠α = 60°
(2) tanα =1， ∠α = 45°
探索与思考
由特殊三角函数值确定锐角度数
300
60 0
450
60 0
450
300
300
60 0
450
课堂基础练
6. 如图，河岸AD，BC互相平行，桥AB垂直于两岸。桥长12m，在C处看桥两端A,B，夹角
∠BCA=600。求B,C间的距离(结果精确到1m).
在Rt△ABC中， tan ∠ BCA =
AB
, 即 tan 6 00
BC
=
12
,
BC
∴BC≈7m.
随堂测试-提高
7 已知：| tanB－ 3 | ＋ (2sinA－ 3)2 ＝0，求∠A，∠B的度数.
一个小孩荡秋千,秋千链子的长度为2.5m,当秋千向两边摆动时,摆角恰好为60°,
且两边的摆动角度相同，求它摆至最高位置时与其摆至最低位置时的高度之差（结
果精确到0.01m）.

数学：1.2《30°,45°,60°角的三角函数值》课件(北师大版九年级下)

300
┌
600
┌
三角函数正弦sinα 余弦cosα 锐角α
300 450 600
1 2
2 2
正切 tanα
3 3
3 2
2 2
1
3
3 2
1 2
老师提示:
例1 计算: (1)sin300+cos450; (2) sin2600+cos2600+tan450.
解: (1)sin300+cos450 1 2 1 2 . 2 2 2 (2) sin2600+cos2600-tan450
●
3 OC OD cos30 2.5 2.165(m). B 2
0
OC 0 cos 30 , OD
2.5
┌
C A
D
∴AC=2.5-2.165≈0.34(m).
∴最高位置与最低位置的高度差约为0.34m.
计算:
(1)sin600-cos450; (2)cos600+tan600; 怎样做？
3 1 1 2 2
2 2
Sin2600表示 (sin600)2,
cos2600表示 (cos600)2, 其余类推.
怎样解答
?
0.
3 1 1 4 4
例2 如图:一个小孩荡秋千,秋千链子的长度为 2.5m,当秋千向两边摆动时,摆角恰好为600,且两边摆动的角度相同,求它摆至最高位置时与其摆至最低位置时的高度之差(结果精确到0.01m).
则CD=a· tan30°
你能求出30°角的三个三角函数值吗?
探索30°角的三角函数值 ①观察一副三角尺，其中有几个锐角?它们分别等于多少度? ② sin30°等于多少呢?你是怎样得到的?与同伴交流. ③cos30°等于多少?tan30°呢? 2．我们求出了30°角的三个三角函数值，还有两个特殊角——45°、60°，它们的三角函数值分别是多少?你是如何得到的? 450 450

1.2 30°45°60°角的三角函数值 (北师大版)优秀课件

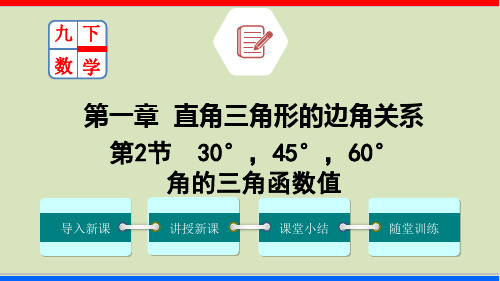
1
22 3
3.
随堂训练
1.cos60°的值等于( )
A. 3
B. 1
C. 2
D. 1
2
2
2.在Rt△ABC中，∠C＝90°，sin
B＝
12 13
,
则cos A
的值为( )
A. 5 12
B. 12 5
C. 12 13
D. 13 12
3.在△ABC中，∠A，∠B都是锐角，且sin A＝ 1 ，
知识点二已知特殊三角函数值求角
通过该表可以方便地知道30°，45°，60°角的三角函数值．它的另一个应用：如果已知一个锐角的三角函数值，就可以求出这个锐角的度数．例如：若sin θ＝ 2 ，则锐
2
角θ＝45°.
典例赏析
例2 一个小孩荡秋千,秋千链子的长度为2.5m,当秋
千向两边摆动时,摆角恰好为60°,且两边摆动的角
九下
数
2020
学
第一章直角三角形的边角关系
第2节 30°，45°，60° 角的三角函数值
导入新课
讲授新课
课堂小结
随堂训练
学习目标
1、经历探索30°，45°，60°角的三角函数值的过程，能够进行有关的推理，进一步体会三角函数的意义。 2、能够进行30°，45°，60°角的三角函数值的计算。 3、能够根据30°，45°，60°的三角函数值说明相应的锐角的大小。
求 cos 的值． 1 sin
解：由sin2α＋cos2α＝1，sin α＞0，得sin α＝ 1－cos2 ,
而cosα＝ 1 ,
3
所以sin α＝
1
1 3
2
22 3
.