高二选修(2--33.1 回归分析
人教版高中选修2-33.1回归分析的基本思想及其初步应用课程设计 (2)

人教版高中选修2-33.1 回归分析的基本思想及其初步应用课程设计一、课程设计背景和目的《人教版高中选修2》是高中阶段的一门重要课程,涉及到较为复杂的数学知识和方法,需要学生们认真学习和掌握。
其中第33章“统计学基础(一)”中的第1节“回归分析的基本思想及其初步应用”是课程内容中比较重要的一部分。
通过本节课程的学习,可以帮助学生掌握回归分析这一重要的统计学方法,建立相关的模型,进行数据预测和分析以及决策制定。
本次课程设计的目的是通过教学手段,让学生掌握回归分析的基本思想,熟悉如何建立回归模型,并能在实际问题中应用回归分析方法解决问题。
在课堂上通过实例演示,引导学生独立思考和合作探究,提高学生的实际分析问题能力,拓宽学生的视野和思维方式。
二、课程设计内容和步骤1.课程设计内容:•回归分析的基本思想•如何进行回归分析•回归分析的应用实例2.课程设计步骤:Step 1:回归分析的基本思想在本节课程中,我们将首先介绍回归分析的基本思想。
通过给出一个实例,让学生能够了解回归分析的实际应用,引导学生思考问题产生的背景和根源。
通过精心设计的问题引导,让学生自主探索回归分析的基本思想,理解回归分析的本质和研究方法。
Step 2:如何进行回归分析通过讲解回归分析的计算步骤及实例演示,让学生掌握如何建立回归模型,如何计算回归系数、残差等。
同时,要求学生能够运用回归模型进行数据分析和预测,并感受回归分析在实际问题解决中的重要作用。
Step 3:回归分析的应用实例通过实际案例演示让学生了解回归分析在社会、企业等领域的实际应用。
并引导学生思考在其它领域中,如何将回归分析方法应用到实际问题中解决。
三、教学方法和手段为了使课程更具标志性和互动性,本次课程设计采用了多种教学方法和手段:•组织以小组为单位的讨论活动,让学生通过探究问题和交流思路,提高团队协作意识和解决问题能力。
•通过多媒体、黑板演示、幻灯片等方式展示引导学生理解和掌握回归分析的基本思想和应用方法。
人教版高中选修(B版)2-33.2回归分析课程设计 (2)

人教版高中选修(B版)2-33.2回归分析课程设计一、课程设计背景回归分析作为数学分析的重要分支之一,旨在建立有效的数学模型来预测变量间的关系。
在现代经济学、社会学、医学等领域中,回归分析被广泛应用。
在高中数学教学中,学生需要掌握回归分析的基础知识,在将来的学习和实践中能够更好地应用。
二、课程设计目标本课程设计旨在达到以下目标:1.学习回归分析的基本概念和理论知识;2.掌握回归方程的建立和应用方法;3.能够使用软件进行回归分析;4.学会如何对回归方程进行解释和分析;5.能够将回归方程应用于实际问题中。
三、课程设计内容1. 回归分析的概念•回归分析的定义;•单变量回归分析和多变量回归分析;•回归分析的应用领域。
2. 回归方程的建立和应用•距离最小法与普通最小二乘法;•线性回归和非线性回归;•连续变量和分类变量的处理。
3. 软件的使用•Excel 中的回归分析;•STATA 软件的使用;•SPSS 软件的使用。
4. 解释和分析回归方程•判定系数的含义;• F 统计量和 t 统计量;•残差分析和异常值诊断;•回归模型的预测与验证。
5. 应用实例选取实际数据进行回归分析,并对回归方程进行解释和分析。
四、课程设计教学方法本课程设计采用以下教学方法:1.前置讲解。
通过教师的讲解,让学生了解回归分析的概念、建立回归方程的方法和软件的使用等;2.上机实践。
让学生在计算机上学习 Excel、STATA、SPSS 等软件的使用,把理论知识转化为实际操作能力;3.课堂练习。
针对学生的理解程度,布置一些练习题,帮助学生深入理解知识点,提高能力;4.课程项目。
让学生根据现实问题进行数据收集,并用回归分析技术进行处理,培养学生的实际问题解决能力。
五、课程设计评估方法本课程设计采用以下评估方法:1.课堂测验。
通过课堂检查了解学生对理论知识的掌握情况;2.实验报告。
要求学生针对课堂实验进行报告,评估学生对实验操作的掌握情况;3.课程项目报告。
人教版高中选修2-3数学3.1回归分析的基本思想及其初步应用教案(2)
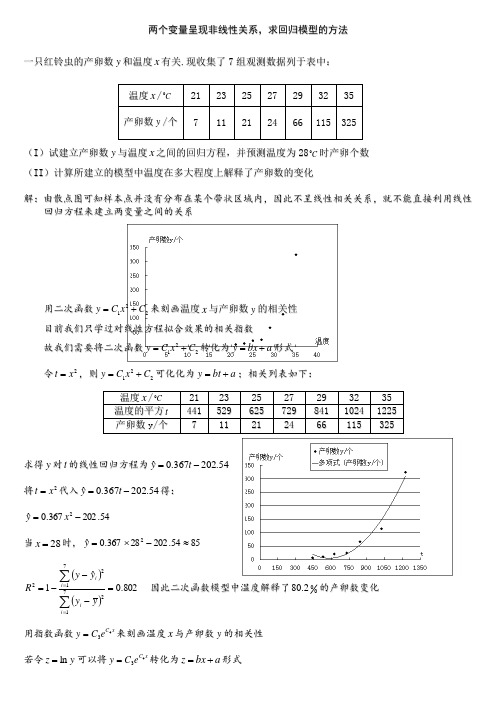
两个变量呈现非线性关系,求回归模型的方法一只红铃虫的产卵数y 和温度x 有关.现收集了7组观测数据列于表中:(I )试建立产卵数y 与温度x 之间的回归方程,并预测温度为28C 0时产卵个数(I I )计算所建立的模型中温度在多大程度上解释了产卵数的变化解:由散点图可知样本点并没有分布在某个带状区域内,因此不呈线性相关关系,就不能直接利用线性 回归方程来建立两变量之间的关系用二次函数221C x C y +=来刻画温度x 与产卵数y 的相关性 目前我们只学过对线性方程拟合效果的相关指数故我们需要将二次函数221C x C y +=转化为a bx y +=形式 令2x t =,则221C x C y +=可化化为a bt y +=;相关列表如下:求得y 对t 的线性回归方程为54.202367.0ˆ-=t y 将2x t =代入54.202367.0ˆ-=t y得: 54.202367.0ˆ2-=x y当28=x 时,8554.20228367.0ˆ2≈-⨯=y()()802.0ˆ17127122=---=∑∑==i i i i y y y y R 因此二次函数模型中温度解释了002.80的产卵数变化用指数函数x C e C y 43=来刻画温度x 与产卵数y 的相关性 若令y z ln =可以将x C e C y 43=转化为a bx z +=形式温度x /C 02123 25 27 293235产卵数y /个 7 11212466 115 325温度x /C 0 21 23 2527 29 32 35 温度的平方t 441 529 625 729 841 1024 1225 产卵数y /个7 11212466 115 325对x C e C y 43=两边取对数343ln ln ln ln 4C x C e C y x C +=+=令y z ln =,b C =4,a C =3ln 则有a bx z +=;相关列表如下:求得z 对x 的线性回归方程为849.3272.0ˆ-=x z将272.04=C ,849.3-3e C =代入x C e C y 43=得:849.3272.0ˆ-=x e y当28=x 时,44ˆ849.328272.0≈=-⨯e y利用计算器求得98.02=R因此二次函数模型中温度解释了0098的产卵数变化综上可得用指数模型拟合效果较好,也就是说刻画产卵数与温度的关系更接近实际情况1.在回归分析中,代表了数据点和它在回归直线上相应位置的差异的是( ) A .总偏差平方和 B .残差平方和 C .回归平方和 D .相关指数R 22.回归分析中,相关指数R 2的值越大,说明残差平方和( )A .越小B .越大C .可能大也可能小D .以上都不对3.若对于变量y 与x 的10组统计数据的回归模型中,相关指数95.02=R ,又知残差平方和为53.120,那么∑=-1012)(i i y y 的值为( ) (A ) 06.241 (B )6.2410 (C )08.253 (D )8.25304.在一次抽样调查中测得样本的5个样本点,数据如下: (1)画出散点图;(2)通过作出的散点图发现,y 与x 之间的关系可用函数a xby +=拟合,试确定a b ,的值 温度x /C 021232527293235y z ln = 1.946 2.398 3.405 3.178 4.19 4.745 5.784 产卵数y /个 7 11 21 24 66 115 325 x 0.25 0.5 1 2 4 y 16 125 2 1。
人教版高中数学选修(2-3)-3.1要点解析:回归分析

回归分析1.回归直线:如果散点图中点的分布从整体上看大致在一条直线附近,我们就称这两个变量之间具有线性相关关系,这条直线叫作回归直线.求回归直线方程的一般步骤:作出散点图(由样本点是否呈条状分布来判断两个量是否具有线性相关关系),若存在线性相关关系→②求回归系数→③写出回归直线方程,并利用回归直线方程进行预测说明.2.回归分析:对具有相关关系的两个变量进行统计分析的一种常用方法.建立回归模型的基本步骤是:①确定研究对象,明确哪个变量是解释变量,哪个变量是预报变量;②画好确定好的解释变量和预报变量的散点图,观察它们之间的关系(线性关系).③由经验确定回归方程的类型.④按一定规则估计回归方程中的参数(最小二乘法);⑤得出结论后在分析残差图是否异常,若存在异常,则检验数据是否有误,后模型是否合适等.3.利用统计方法解决实际问题的基本步骤:①提出问题;②收集数据;③分析整理数据;④进行预测或决策.4.残差变量e 的主要来源:①用线性回归模型近似真实模型(真实模型是客观存在的,通常我们并不知道真实模型到底是什么)所引起的误差.可能存在非线性的函数能够更好地描述y 与x 之间的关系,但是现在却用线性函数来表述这种关系,结果就会产生误差.这种由于模型近似所引起的误差包含在e 中.②忽略了某些因素的影响.影响变量y 的因素不只变量x 一个,可能还包含其他许多因素(例如在描述身高和体重关系的模型中,体重不仅受身高的影响,还会受遗传基因、饮食习惯、生长环境等其他因素的影响),但通常它们每一个因素的影响可能都是比较小的,它们的影响都体现在e 中.③观测误差.由于测量工具等原因,得到的y 的观测值一般是有误差的(比如一个人的体重是确定的数,不同的秤可能会得到不同的观测值,它们与真实值之间存在误差),这样的误差也包含在e 中.上面三项误差越小,说明我们的回归模型的拟合效果越好.名师要点解析例1研究某灌溉渠道水的流速与水深之间的关系,测得一组数据如下:(1)求y对x的回归直线方程;(2)预测水深为1.95m时水的流速是多少?【分析】本题考查如何求回归直线的方程,可先把有关数据用散点图表示出来,若这些点大致分布在通过散点图中心的一条直线附近,说明这两个变量线性相关,从而可利用我们学过的最小二乘估计思想及计算公式求得线性回归直线方程.【解】(1)由于问题中要求根据水深预报水的流速,因此选取水深为解释变量,流速为预报变量,作散点图:由图容易看出,x与y之间有近似的线性关系,或者说,可以用一个回归直线方程来反映这种关系.由计算器求得.对x的回归直线方程为.(2)由(1)中求出的回归直线方程,把x=1.95代入,易得。
人教版高中选修2-33.1回归分析的基本思想及其初步应用课程设计

人教版高中选修2-33.1回归分析的基本思想及其初步应用课程设计课程背景随着社会的不断发展,数据在我们的生活中扮演着越来越重要的角色。
而回归分析作为一种统计量分析方法,在数据分析和决策制定中具有广泛的应用。
在人教版高中选修2中,33.1回归分析作为一章内容深度的分析,是培养学生数据分析和决策制定能力的重要内容。
本文主要介绍33.1回归分析的基本思想及其初步应用,帮助学生正确认识回归分析,加深其对数据科学的理解与掌握。
课程目标1.正确理解回归分析的基本思想,掌握回归分析的基本工具和方法;2.在实际问题中运用所学回归分析的方法,对数据进行处理和分析,从而得出相关结论;3.培养学生的数据分析和决策制定能力。
课程设计课程内容第一部分:回归分析的基本思想1.回归分析的概念和基本概率模型;2.构建简单线性回归模型,理解残差和回归系数的含义;3.多元线性回归模型,理解多个自变量对因变量的影响;4.假设检验、置信区间及相关系数等统计指标的解读。
第二部分:回归分析的初步应用5.利用Excel等工具进行简单线性回归分析,并从模型中得出结论;6.运用多元线性回归模型对实际问题进行分析,并得出相应结论;7.学习和应用回归分析的实践方法。
课程形式1.由老师讲授回归分析的基础理论;2.在课程中穿插实际案例的讲解和演示;3.带领学生利用Excel等工具进行数据的回归分析,小组讨论分析结果,并总结结论。
学习建议1.独立学习课程的核心基础理论知识,理解每个概念的含义;2.建议同时进行课堂学习和课后练习,加深对于每个概念的掌握;3.在理论学习和数学公式掌握的基础上,运用实际案例进行数据分析练习。
课程评价该课程结合了回归分析的基础理论和实际应用案例,既有基础的概念和理论知识的讲解,又能够让学生在实际操作中深入了解回归分析的实际运用。
通过该课程的学习,学生能够有效地掌握回归分析的基础知识及实际应用,为今后的学习和实践打下良好的基础。
人教版数学高二选修2-3讲义3.1回归分析的基本思想及其初步应用

3.1 回归分析的基本思想及其初步应用1.通过对典型案例的探究,了解回归分析的基本思想、方法及其初步应用. 2.会求回归直线方程,并用回归直线方程进行预报.(重点)3.了解最小二乘法的思想方法,理解回归方程与一般函数的区别与联系.了解判断模型拟合效果的方法(相关指数和残差分析).(难点)[基础·初探]教材整理1 回归直线方程阅读教材P 80~P 82探究上面倒数第一行,完成下列问题. 1.回归分析回归分析是对具有相关关系的两个变量进行统计分析的一种常用方法. 2.回归直线方程方程y ^=b ^x +a ^是两个具有线性相关关系的变量的一组数据(x 1,y 1),(x 2,y 2),…,(x n ,y n )的回归方程,其中a^,b ^是待定参数,其最小二乘估计分别为: ⎩⎪⎨⎪⎧b ^=∑i =1n (x i -x -)(y i -y -)∑i =1n(x i -x -)2=∑i =1nx i y i -n x -y -∑i =1nx 2i -n x -2,a ^=y --b ^x -,其中x -=1n ∑i =1n x i ,y -=1n ∑i =1n y i ,(x -,y -)称为样本点的中心.1.在对两个变量x,y进行线性回归分析时,有下列步骤:①对所求出的回归直线方程作出解释;②收集数据(x i,y i),i=1,2,…,n;③求线性回归方程;④求相关系数;⑤根据所搜集的数据绘制散点图.如果根据可行性要求能够作出变量x,y具有线性相关的结论,则在下列操作顺序中正确的是()A.①②⑤③④B.③②④⑤①C.②④③①⑤D.②⑤④③①【解析】对两个变量进行回归分析时,首先收集数据(x i,y i),i=1,2,…,n;根据所搜集的数据绘制散点图.观察散点图的形状,判断线性相关关系的强弱,求相关系数,写出线性回归方程,最后依据所求出的回归直线方程作出解释.故正确顺序是②⑤④③①.【答案】 D2.如图3-1-1四个散点图中,适合用线性回归模型拟合的两个变量的是________(填序号).图3-1-1【解析】由题图易知,①③两个图中的样本点在一条直线附近,因此适合用线性回归模型拟合.【答案】①③3.若y与x之间的一组数据为x 0123 4y 1355 6则y对x【解析】由表中数据得x=0+1+2+3+45=2,y=1+3+5+5+65=4.因回归直线必过样本中心点(x,y),所以y与x的回归直线一定经过的点是(2,4).【答案】(2,4)教材整理2线性回归分析阅读教材P82探究~P89,完成下列问题.1.线性回归模型(1)表达式y=bx+a+e.(2)基本概念:①a和b为模型的未知参数.②e是y与bx+a之间的误差.通常e为随机变量,称为随机误差.③x称为解释变量,y称为预报变量.2.衡量回归方程的预报精度的方法(1)残差平方和法:①e i^称为相应于点(x i,y i)的残差.②残差平方和∑i=1n(y i-y i^)2越小,模型的拟合效果越好.(2)残差图法:残差点比较均匀地落在水平的带状区域内,说明选用的模型比较合适.这样的带状区域的宽度越窄,说明模型的拟合精度越高.(3)利用相关指数R2刻画回归效果:其计算公式为:R2=1-∑i=1n(y i-y i^)2∑i=1n(y i-y)2;其几何意义:R2越接近于1,表示回归的效果越好.1.判断(正确的打“√”,错误的打“×”)(1)求线性回归方程前可以不进行相关性检验.()(2)在残差图中,纵坐标为残差,横坐标可以选为样本编号.()(3)利用线性回归方程求出的值是准确值.()(4)变量x与y之间的回归直线方程表示x与y之间的真实关系形式.()(5)随机误差也就是残差.()【解析】(1)×因为如果两个变量之间不具有线性相关关系,就不用求线性回归方程了,求出的回归直线方程当然也不能很好的反映两变量间的关系.(2)√因为由残差图的方法步骤可知,该说法正确.(3)×因为利用线性回归方程求出的值为估计值,而不是真实值.(4)×因为变量x与y之间的线性回归直线方程仅表示x与y之间近似的线性关系,x与y之间满足y=bx+a+e,其中e为随机误差.(5)×因为随机误差e是真实值y与bx之间的误差,而残差e^=y-y^是随机误差e的估计量.【答案】(1)×(2)√(3)×(4)×(5)×2.在判断两个变量y与x是否相关时,选择了4个不同的模型,它们的R2分别为:模型1的R2为0.98,模型2的R2为0.80,模型3的R2为0.50,模型4的R2为0.25.其中拟合效果最好的模型是()【导学号:29472081】A.模型1 B.模型2C.模型3 D.模型4【解析】R2能够刻画用回归模型拟合数据的效果,R2的值越接近于1,说明回归模型拟合数据的效果越好.【答案】 A[小组合作型]求线性回归方程下表提供了某厂节能降耗技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产能耗y(吨标准煤)的几组对照数据:x 345 6y 2.534 4.5(1)(2)请根据上表提供的数据,用最小二乘法求出y关于x的回归直线方程y^=b^ x+a^;(3)已知该厂技改前100吨甲产品的生产能耗为90吨标准煤.试根据(2)求出的回归直线方程,预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤?(参考数值:3×2.5+4×3+5×4+6×4.5=66.5)【精彩点拨】(1)按表中的数据在平面直角坐标系中描点即得散点图;(2)由公式求出a^,b^,写出回归直线方程;(3)利用回归方程分析.【自主解答】(1)由题设所给数据,可得散点图如图.(2)由数据,计算得:∑i=14x2i=86,x=3+4+5+64=4.5,y=2.5+3+4+4.54=3.5,又已知∑i=14x i y i=66.5.所以,由最小二乘法确定的回归方程的系数为:b^=∑i=14x i y i-4x y∑i=14x2i-4 x2=66.5-4×4.5×3.586-4×4.52=0.7,a ^=y --b ^x -=3.5-0.7×4.5=0.35,因此,所求的回归直线方程为y ^=0.7x +0.35.(3)由(2)的回归方程及技改前生产100吨甲产品的生产能耗,得降低的生产能耗为90-(0.7×100+0.35)=19.65吨标准煤.求回归直线方程的三个步骤1.画散点图:由样本点是否呈条状分布来判断两个量是否具有线性相关关系.2.求回归系数:若存在线性相关关系,则求回归系数.3.写方程:写出回归直线方程,并利用回归直线方程进行预测说明.[再练一题]1.已知x ,y 的取值如表所示:x 0 1 3 4 y2.24.34.86.7若从散点图分析,y 与x 线性相关,且y ^=0.95x +a^,则a ^的值等于( ) 【导学号:29472082】A .2.6B .6.3C .2D .4.5【解析】 x -=14(0+1+3+4)=2,y -=2.2+4.3+4.8+6.74=4.5,而回归直线方程过样本点的中心(2,4.5),所以a ^=y --0.95x -=4.5-0.95×2=2.6. 【答案】 A线性回归分析已知某种商品的价格x (元)与需求量y (件)之间的关系有如下一组数据:x (元) 14 16 18 20 22 y (件)1210753求y 对【精彩点拨】 先利用求线性回归直线方程的方法步骤求出回归直线方程,再利用相关指数R 2说明拟合效果.【自主解答】 x -=15×(14+16+18+20+22)=18, y -=15×(12+10+7+5+3)=7.4, ∑5i =1x 2i =142+162+182+202+222=1 660, ∑5 i =1y 2i =122+102+72+52+32=327,∑5 i =1x i y i =14×12+16×10+18×7+20×5+22×3=620, ∴b ^=∑5i =1x i y i -5x - y -∑5 i =1x 2i -5x -2=620-5×18×7.41 660-5×182=-1.15. a ^=y --b ^x -=7.4+1.15×18=28.1, ∴所求回归直线方程为y ^=-1.15x +28.1. 列出残差表: y i -y ^i 0 0.3 -0.4 -0.1 0.2 y i -y -4.62.6-0.4-2.4-4.4∴∑5i =1 (y i -y i )2=0.3,∑5i =1 (y i -y )2=53.2,R 2=1-∑5i =1 (y i -y ^i )2∑5 i =1 (y i -y -)2≈0.994,故回归模型的拟合效果很好.1.该类题属于线性回归问题,解答本题应先通过散点图来分析两变量间的关系是否线性相关,然后再利用求回归方程的公式求解回归方程,并利用残差图或相关指数R2来分析函数模型的拟合效果,在此基础上,借助回归方程对实际问题进行分析.2.刻画回归效果的三个方式(1)残差图法:残差点比较均匀地落在水平的带状区域内说明选用的模型比较合适.(2)残差平方和法:残差平方和∑ni=1(y i-y^i)2越小,模型的拟合效果越好.(3)相关指数法:R2=1-∑ni=1(y i-y^i)2∑ni=1(y i-y)2越接近1,表明回归的效果越好.[再练一题]2.假设关于某设备的使用年限x和所支出的维修费用y(万元),有如下表的统计资料:使用年限x 2345 6维修费用y 2.2 3.8 5.5 6.57.0(1)求线性回归方程y^=b^x+a^;(2)求残差平方和;(3)求相关指数R2.【解】(1)由已知条件可得:x=4,y=5,∑i=1nx2i=90,∑i=1nx i y i=112.3.于是有b^=112.3-5×4×590-5×42=12.310=1.23,a^=y-b^x=5-1.23×4=0.08.所以y^=1.23x+0.08.(2)由公式y^i=1.23x i+0.08和e^i=y i-y^i,得下表1234 5 y^i 2.54 3.775 6.237.46e^i-0.340.030.50.27-0.4622222(3)R2=1-0.651∑i=15(y i-y)2≈0.958 7.[探究共研型]非线性回归分析探究1如果两个相关变量x,y满足回归方程y=c1x2+c2,那么x,y具有线性相关关系吗?如何把它化归为线性回归方程问题?【提示】x,y不具有线性相关关系,但是若令z=x2,则y=c1x2+c2可变换为y=c1z+c2,即化归为线性回归方程问题.探究2如果两个相关变量x,y满足非线性回归方程y=c1ec2x,如何转化为线性回归方程问题?如果两个变量呈非线性相关关系,怎样求回归方程?【提示】令z=ln y,则原回归方程可变换为z=bx+a(a=ln c1,b=c2).若两个变量呈非线性相关关系可以通过对解释变量进行变换,如对数变换或平方变换,先得到另外两个变量间的回归方程,再得到所求两个变量的回归方程.探究3若对同一个问题建立的两种不同回归模型,怎样比较它们的拟合效果?【提示】有两种比较方法:(1)计算残差平方和,残差平方和小的模型拟合效果好;(2)计算相关指数R2,R2越接近于1的模型拟合效果越好.下表为收集到的一组数据:x 21232527293235y 711212466115325(2)建立x与y的关系,预报回归模型并计算残差;(3)利用所得模型,预报x=40时y的值.【精彩点拨】画出散点图→确定是否线性相关→确定函数模型→转化为线性模型→求回归方程→进行拟合→进行预报【自主解答】(1)作出散点图如图,从散点图可以看出x与y不具有线性相关关系,根据已有知识可以发现样本点分布在某一条指数型函数曲线y=c1e c2x 的周围,其中c1,c2为待定的参数.(2)对两边取对数把指数关系变为线性关系,令z=ln y,则变换后的样本点应分布在直线z=bx+a,a=ln c1,b=c2的周围,这样就可以利用线性回归模型来建立y与x之间的非线性回归方程了,数据可以转化为:x 21232527293235z 1.946 2.398 3.045 3.178 4.190 4.745 5.784 求得回归直线方程为z=0.272x-3.849,^=e0.272x-3.849.∴y残差列表如下:y i711212466115325y^i 6.44311.10119.12532.95056.770128.381290.325 e^i0.557-0.101 1.875-8.9509.23-13.38134.6750.272×40-3.849非线性回归问题的处理方法1.指数函数型y=e bx+a(1)函数y=e bx+a的图象:(2)处理方法:两边取对数得ln y=ln e bx+a,即ln y=bx+a.令z=ln y,把原始数据(x,y)转化为(x,z),再根据线性回归模型的方法求出a,b.2.对数函数型y=b ln x+a(1)函数y=b ln x+a的图象:(2)处理方法:设x′=ln x,原方程可化为y=bx′+a,再根据线性回归模型的方法求出a,b.3.y=bx2+a型处理方法:设x′=x2,原方程可化为y=bx′+a,再根据线性回归模型的方法求出a,b.[再练一题]3.在一次抽样调查中测得样本的5个样本点,数值如下表:x 0.250.512 4y 161252 1试建立y与【解】画出散点图如图所示.根据散点图可知y与x近似地呈反比例函数关系,设y=kx,令t=1x,则y=kt,原数据变为:t 4210.50.25y 161252 1由散点图可以看出y与t呈近似的线性相关关系.列表如下:序号t i y i t i y i t2i y2i141664162562212244144315512540.5210.25 450.2510.250.0625 1∑7.753694.2521.312 5430所以t=1.55,y=7.2.所以b^=∑i=15t i y i-5t y∑i=15t2i-5t2≈4.134 4,a^=y--b^t-≈0.8.所以y^=4.134 4t+0.8.所以y 与x 的回归方程是y ^=4.134 4x +0.8.1.关于回归分析,下列说法错误的是( ) A .回归分析是研究两个具有相关关系的变量的方法 B .散点图中,解释变量在x 轴,预报变量在y 轴 C .回归模型中一定存在随机误差 D .散点图能明确反映变量间的关系【解析】 用散点图反映两个变量间的关系时,存在误差. 【答案】 D2.甲、乙、丙、丁四位同学在建立变量x ,y 的回归模型时,分别选择了4种不同模型,计算可得它们的相关指数R 2分别如下表:甲 乙 丙 丁 R 20.980.780.500.85A .甲B .乙C .丙D .丁【解析】 相关指数R 2越大,表示回归模型的拟合效果越好. 【答案】 A3.在研究气温和热茶销售杯数的关系时,若求得相关指数R 2≈0.85,则表明气温解释了________的热茶销售杯数变化,而随机误差贡献了剩余的________,所以气温对热茶销售杯数的效应比随机误差的效应大得多.【解析】 由相关指数R 2的意义可知,R 2≈0.85表明气温解释了85%,而随机误差贡献了剩余的15%.【答案】 85% 15%4.已知某车间加工零件的个数x 与花费时间y (h)之间的线性回归直线方程为y ^=0.01x +0.5,则加工600个零件大约需要________h.【解析】 y ^=0.01×600+0.5=6.5,所以加工600个零件大约需要6.5 h.【答案】 6.55.在一段时间内,分5次测得某种商品的价格x (万元)和需求量y (t)之间的一组数据为:已知∑i =15x i y i =62,∑i =15x 2i =16.6,且y 与x 呈线性相关.(1)求出y 对x 的回归方程;(2)如价格定为1.9万元,预测需求量大约是多少?(精确到0.01 t).【导学号:29472083】【解】 (1)因为x -=15×9=1.8,y -=15×37=7.4,∑i =15x i y i =62,∑i =15x 2i =16.6,所以b^=∑i =15x i y i -5x -y -∑i =15x 2i -5x-2=62-5×1.8×7.416.6-5×1.82=-11.5,a ^=y --b ^x -=7.4+11.5×1.8=28.1,故y 对x 的回归方程为b ^=28.1-11.5x .(2)y ^=28.1-11.5×1.9=6.25(t).。
人教A版数学选修2-3全册课件:第三章 3.1 回归分析的基本思想及其初步应用

回归
第 三
分析 的基 本思
章 想及
其初
步应
用
1 理解教 材新知
2 突破常 考题型
3 跨越高 分障碍
4 应用落 实体验
知识点一 知识点二
题型一 题型二 题型三
随堂即时演练 课时达标检测
3.1 回归分析的基本思想及其初步应用
回归直线方程 [提出问题] 《必修 3》中,求出回归直线方程^y=^bx+^a. 问题 1:回归直线方程准确的反映了 x,y 之间的关系吗? 提示:不是. 问题2:所有的两个相关变量都可以求回归方程吗?
∴
(yi-^y i)2=(-0.5)2+(-3.5)2+102+(-6.5)2+0.52=155,
i=1
5
(yi--y )2=(-20)2+(-10)2+102+02+202=1 000.
i=1
5
yi-^y i2
i=1
∴R12=1- 5
=1-1105050=0.845. yi--y 2
i=1
由(2)可得 yi-^yi 与 yi--y 的关系如下表:
n
n
xi- x yi- y xiyi-n x y
^b=i=1
n
xi- x 2
i=1
=
,
n
x2i -n x 2
i=1
i=1
^a= y -^b x ,
其中 x =n1i=n1xi, y =n1i=n1yi,( x , y ) 称为样本点的中心.
[化解疑难] 线性回归方程中系数^b的含义
(1)^b是回归直线的斜率的估计值,表示 x 每增加一个 单位,y 的平均增加单位数,而不是增加单位数.
[导入新知]
1.残差平方和法
人教版高中选修2-3数学3.1回归分析的基本思想及其初步应用课件(8)

相关指数
ˆ=e y
R2=0.98
当x=28oC 时,y ≈44 ,R2=0.98 指数回归模型中温度解释了98.5%的产卵数的变化
R2分析
400 300
哪个模型最好?
400 300 200 100 0
产卵数
200 100 0 -100 0 5 10 15 20 25 30 35 40
-40
-30
c2 x
令:z = lny, a = lnc1 , b = c 2 则y = c1e 就转换为:z = bx + a
温度xoC z=lny 产卵数y/个 21
1.946
c2 x
23
2.398
25
3.045
27
3.178
29
4.190
32
4.745
35
5.784
7
11
21
24
66
115
325
方案3解答
数学选修2-3[人教版]
3.1 回归分析的基本思想 及其初步应用(二)
复习回顾
1、线性回归模型: y=bx+a+e, (3)
y=bx+a+e,
E(e)=0,D(e)=
.
2
(4)
其中a和b为模型的未知参数,e称为随机误差。 2、数据点和它在回归直线上相应位置的差异(y y ) i i 是随机误差的效应,称 ei =y y 为残差。 i i 在残差图中残差点比较均匀地落在水平的带状区域中, 说明选用的模型比较合适,这样的带状区域的宽度越 窄,说明模型拟合精度越高,回归方程的预报精度越 高。
温度xoC z=lny 产卵数y/个 21
北师大版高中数学选修2-3课件:3.1.1 回归分析

由散点图可以看出,两个变量之间呈现出 近似的线性关系,所以可以建立弹簧长度y 对拉力x的线性回归方程.
备课素材
[例] 弹簧长度y(cm)随拉力x(N)不同而 变化的情况如下:
x 5 10 15 20 25 30 y 7.25 8.12 8.95 9.90 10.90 11.80
(1)求出弹簧长度y对拉力x的线性回归 方程; (2)预测当拉力为18N时,弹簧的长度 是多少.
考点类析
【变式】下表是某种产品销售收入与销售量 之间的一组数据:
销售量x(吨) 2 3 5 6 销售收入y(万元) 7 8 9 12
(3)当x=9时,y=1.1×9+4.6=14.5.
故当销售量为9吨时,估计销售收入约 为14.5万元.
(1)画出散点图; (2)求出线性回归方程; (3)根据线性回归方程估计销售量为9吨时的销 售收入.
(1)请判断y与x是否具有线性相关关系;
解:(1)画出数据的散点图如图所示, 直观判断散点分布在一条直线附近, 故具有线性相关关系.
考点类析
例3 一家保险公司为了研究营业部加班对签发 新保单的影响,做了10次试验,得数据如下:
每月 加班时 10 20 30 40 50 60 70 80 90 100 间x(h) 签发的 新保单 62 68 75 81 89 95 102 108 115 122 数y(单)
考点类析
考点类析
x
5
6
7
8
y 10 8
7
3
[答案] 6.8
考点类析
备课素材
回归分析的应用 回归分析的应用主要体现在两个方面: (1)对两个变量关系的判断,通过分析两个变量的变化关系,利用最小二乘法 可以求出对应的线性回归方程; (2)对变量值的预测,即由给定的变量值预测与其有相关关系的变量值.
人教A版高中数学选修2-3课件3.1.1回归分析的基本思想及其初步应用(1)

i=1 n
=
( xi - x)2
xi
- nx y
i
i=1
n
xi2
-
2
nx
,
i=1
i=1
aˆ = y - bˆ x
2.相应的直线叫做回归直线.
3.对两个变量进行的线性分析叫做线性
回归分析.
相关系数
• 1.计算公式
n
( xi - x )( yi - y )
r=
i=1
n
n
( xi - x )2 ( yi - y )2
n
Q( , ) ( yi xi )2 i 1
随机误差ei yi bxi a(i 1, 2,....n)
其估计值为: eˆi yi yˆi yi bˆxi aˆ eˆi称为相应点(xi,yi )的残差.
类比样本方差估计总体方差的思想,
ˆ 2
yˆ
yˆ
160 170 180
体重 线性 (体重) 线性 (体重) 线性 (体重)
线性回归模型
y = b x + a + e E(e)= 0, D(e)=σ2
y = b x + a + e 其中a 和b 为模型的未知参数, e是
y与 yˆ 之间的误差, 通常 e 称为随机误差.
为了衡量预报的精度,需要估计的σ2值?
函数 y=b x +a 来描述它们之间的关系。这时我们用
下面的线性回归模型来描述身高和体重的关系:
y=b x+ a + e 其中a 和b 为模型的未知参数,e 是 y
与 yˆ 之间的误差,通常e 称为随机误差.
图表标题
高中数学新课标人教A版选修2-3 3.1.1回归分析课件

教学目标 (1)通过实例引入线性回归模型,感受产生 随机误差的原因; ( 2 )通过对回归模型的合理性等问题的研 究,渗透线性回归分析的思想和方法; (3)能求出简单实际问题的线性回归方程. 教学重点,难点 线性回归模型的建立和线性回归系数的最佳 估计值的探求方法. 教学过程 一.问题情境
1. 情境:对一作直线运动的质点的运动过程观 测了 8 次, 得到如下表所示的数据,试估计当 x=9时的位置 y 的值.
时刻 x /s 位置观测值
5.54
y /cm
1
2
3
4
5
6
7
8
7.52
10.02
11.73
15.69 16.12
16.98
21.06
根据《数学 3 (必修)》中的有关内容,解决 这个问题的方法是: 先作散点图,如下图所示:
从散点图中可以看出,样本点呈直线趋势,时 间 x 与位置观测值 y 之间有着较好的线性关系.因 此可以用线性回归方程来刻画它们之间的关
n xi yi nx y i 1 b n xi2 n( x)2 系.根据线性回归的系数公式, i 1 a y bx
说明: (1)产生随机误差的主要原因有: ①所用的确定性函数不恰当引起的误差; ②忽略了某些因素的影响; ③存在观测误差. ( 2 )对于线性回归模型,我们应该考虑下面两 个问题: ①模型是否合理; ②在模型合理的情况下, 如何估计 a ,b ?
2.探求线性回归系数的最佳估计值: 对于问题②,设有 n 对观测数据
(1) y a b ,令 y ' y , x ' 1 ,则有 y ' a bx ' .
人教版数学高二A版选修2-3课堂探究 3.1 回归分析的基本思想及其初步应用

课堂探究探究一 求线性回归直线方程(1)散点图是定义在具有相关关系的两个变量基础上的,对于性质不明确的两组数据,可先作散点图,在图上看它们有无关系,关系的密切程度,然后再进行相关回归分析.(2)求回归直线方程,首先应注意到,只有在散点图大致呈线性时,求出的回归直线方程才有实际意义,否则,求出的回归直线方程毫无意义.【典型例题1】某商场经营一批进价是30元/件的小商品,在市场试验中发现,此商品的销售单价x (x 取整数)元与日销售量y 台之间有如下关系(1)y 与x (方程的斜率保留一个有效数字)(2)设经营此商品的日销售利润为P 元,根据(1)写出P 关于x 的函数关系式,并预测当销售单价x 为多少元时,才能获得最大日销售利润.解:(1)散点图如图所示,从图中可以看出这些点大致分布在一条直线附近,因此两个变量线性相关.设回归直线为y ^=b ^x +a ^,由题知x =42.5,y =34, 则求得b ^=∑i =14(x i -x )(y i -y )∑i =14(x i -x )2=-370125≈-3.a ^=y -b ^x =34-(-3)×42.5=161.5. ∴y ^=-3x +161.5. (2)依题意有P =(-3x +161.5)(x -30) =-3x 2+251.5x -4 845=-3⎝⎛⎭⎫x -251.562+251.5212-4 845. ∴当x =251.56≈42时,P 有最大值,约为426.即预测当销售单价为42元时,才能获得最大日销售利润.规律总结 先根据所给数据画出散点图,判断y 与x 是否具有线性相关关系,在此基础上利用回归方程系数的有关公式,求出相应的系数,然后结合函数知识求出日销售利润最大时的销售单价.探究二 线性回归分析解答本类题目应先通过散点图来分析两变量间的关系是否线性相关,然后再利用求回归方程的公式求解回归方程,并利用残差图或相关指数R 2来分析函数模型的拟合效果,在此基础上,借助回归方程对实际问题进行分析.【典型例题2】在一段时间内,某种商品的价格x 元和需求量y 件之间的一组数据为:且知x 与y 解:x =15×(14+16+18+20+22)=18,y =15×(12+10+7+5+3)=7.4,∑i =15x 2i =142+162+182+202+222=1 660,∑i =15y 2i =122+102+72+52+32=327,∑i =15x i y i =14×12+16×10+18×7+20×5+22×3=620,∴b ^=∑i =15x i y i -5x y∑i =15x 2i -5x 2=620-5×18×7.41 660-5×182=-4640=-1.15.∴a ^=7.4+1.15×18=28.1, ∴回归直线方程为y ^=-1.15x +28.1. 列出残差表为∴∑i =15(y i -y i ^)2=0.3,∑i =15 (y i -y )2=53.2,R 2=1-∑i =15(y i -y i ^)2∑i =15(y i -y )2≈0.994.故R 2≈0.994,说明拟合效果较好.规律总结 “相关指数R 2、残差图”在回归分析中的作用:(1)相关指数R 2是用来刻画回归效果的,由R 2=1-∑i =1n(y i -y i ^)2∑i =1n(y i -y )2可知R 2越大,意味着残差平方和越小,也就是说模型的拟合效果就越好.(2)残差图也是用来刻画回归效果的,判断依据是:残差点比较均匀地分布在水平带状区域中,带状区域越窄,说明模型拟合精度越高, 回归方程预报精度越高.探究三 求非线性回归方程非线性回归问题有时并不给出经验公式,这时我们可以画出已知数据的散点图.把它与必修模块数学1中学过的各种函数(幂函数、指数函数、对数函数等)图象作比较,挑选一种跟这些散点拟合得最好的函数,然后采用适当的变量置换,把问题化为线性回归分析问题,使之得到解决.【典型例题3】假设关于某设备的使用年限x 和支出的维修费用y (万元),有如下表的统计资料:若由资料知y (1)线性回归方程y ^=b ^x +a ^.(2)估计使用年限为10年时,维修费用是多少? (3)计算总偏差平方和、残差平方和及回归平方和. (4)求R 2并说明模型的拟合效果. 解:(1)将已知条件制成下表设回归方程为y =b x +a ,于是有b ^=∑i =15x i y i -5x y∑i =15x 2i -5x 2=112.3-5×4×590-5×42=1.23,a ^=y -b ^ x =5-1.23×4=0.08,所以线性回归方程是y ^=1.23x +0.08. (2)当x =10时,y ^=1.23×10+0.08=12.38, 即估计使用10年时维修费用是12.38万元. (3)总偏差平方和:∑i =15 (y i -y )2=15.78,残差平方和:y 1^=2.46+0.08=2.54,y 2^=3.77,y 3^=5,y 4^=6.23,y 5^=7.46,∑i =15 (y i -y i ^)2=0.651,回归平方和:15.78-0.651=15.129.(4)R 2=1-∑i =15(y i -y i ^)2∑i =15(y i -y )2=1-0.65115.78≈0.958 7,模型的拟合效果较好,使用年限解释了95.87%的维修费用支出. 规律总结 把非线性回归问题转化为线性回归问题,拓展了解题思路. 探究四 易错辨析易错点 残差平方和与相关指数的理解不清致误【典型例题4】对两个变量y 和x 进行回归分析,得到一组样本数据:(x 1,y 1),(x 2,y 2),…,(x n ,y n ),则下列说法中不正确的是( )A .由样本数据得到的回归方程y ^=b ^x +a ^必过样本点的中心(x ,y ) B .残差平方和越小的模型,拟合的效果越好C .用相关指数R 2来刻画回归效果,R 2的值越小,说明模型的拟合效果越好D .若变量y 和x 之间的相关系数r =-0.936 2,则变量y 和x 之间具有线性相关关系 错解:B错因分析:对残差平方和和相关指数R 2理解错误.正解:R 2的值越大,说明残差平方和越小,也就是说模型的拟合效果越好. 答案:C。
高中数学人教A版选修2-3第三章:3.1回归分析的基本思想及其初步应用 课件

从散点图可以看到,样本点散布在某一条直线的 附近,而不是一条直线上,所以不能用一次函数 y=bx+a来描述它们之间的关系。
这时我们用下面的线性回归模型来描述身高和体
重的关系:y=bx+a+e
其中a和b为模型的未知参数,
e是y与 yˆ 之间的误差,通常e称为随机误差。
产生随机误差e的原因是什么?
(1)所用确定性函数模拟不恰当; (2)忽略了某些因素的影响; (3)观测误差,如使用的测量工具不同等。
4.线性回归模型y=bx+a+e中, 把自变量x称为解释变量, 把因变量y称为预报变量。
^
^
5.残差: ei yi yi
n
^
6.残差平方和:
( yi yi )2
i 1
n
7.总偏差平方和: ( yi y)2
i 1
n
^
( yi y)2
8.相关指数:R2
1
i 1 n
( yi y)2
新课讲解
例 从某大学中随机选出8名女大学生,其 身高和体重数据如下表:
编号 1 2 3 4 5 6 7 8 身高 165 165 157 170 175 165 155 170 体重 48 57 50 54 64 61 43 59
求根据一名女大学生的身高预报她的体重的 回归方程,并预报一名身高为172cm的女 大学生的体重。
三、回归直线方程:最小二乘法
1、所求回归直线方程为 yˆ = bˆ x + aˆ ,其中:
n
n
y bˆ =
(xi - x)(yi - y)
i=1 n
=
(xi - x)2
xi
- nxy
i
i=1
人教高中数学选修2-3第三章3.1回归分析的基本思想及其初步应用课件

xiyi 9 14 15 12 5 5 15 12 14 9
所求回归直线方程为
70 65 60 55 50 45 40
150 155 160 165 170 175 180
图1.1 2
假设随机误差对体重没有影响,也就是说,体重仅受身高的影响,那么散 点图中所有的点将完全落在回归直线上。但是,在图中,数据点并没有完全落 在回归直线上。这些点散布在回归直线附近。
有如下的两个线性模型:
(1) yˆ 6.5x 17.5 ;(2) yˆ 7x 17.
试比较哪一个拟合效果更好。
7、一般地,建立回归模型的基本步骤为:
(1)确定研究对象,明确哪个变量是解析变量,哪个变量是 预报变量。
(2)画出确定好的解析变量和预报变量的散点图,视察它们 之间的关系(如是否存在线性关系等)。
探索2:在这些点附近可画直线不止一条,哪条直 线最能代表x与y之间的关系呢?
探究
对于一组具有线性相关关系的数据 (x1, y1), (x2 , y2 ),..., (xn , yn ),
我们知道其回归方程的截距和斜率的最小二乘估计公式分别为:
其中x
1 n
n i 1
xi ,
y
1 n
n i 1
yi .
aˆ y bˆx
2、求回归直线方程的步骤:
(1)求x
1 n
n i 1
xi , y
1 n
n i 1
yi
n
n
(2)求 xi2 , xi yi. n
n
i 1
i 1
y (xi x)(yi y)
xi
nxy
人教A版高中数学选修2-3课件《3.1回归分析(二)》.pptx

Q(aˆ, bˆ) 例如,编号为6的女大学生,计算随机误差的效应(残差)为:即, 61 (0.849165 85.712) 6.627
对每名女大学生计算这个差异,然后分别将所得的值平方后加起来,用数学符号
n
表示为: ( yi yi )2 称为残差平方和,它代表了随机误差的效应。 i 1
首先根据理论和对问题的分析判断,将变量分为自变量和因变 量; 其次,设法找出合适的数学方程式(即回归模型)描述变量间 的关系;
由于涉及到的变量具有不确定性,接着还要对回归模型进行 统计检验;
统计检验通过后,最后是利用回归模型,根据自变量去估计、 预测因变量。
•
案例1:女大学生的身高与体重
例1从某大学中随机选取8名女大学生,其身高和体重数据如表1-1所示。
•
分析:由于问题中 要求根据身高预报 体重,因此选取身 高为自变量,体重 为因变量.
1.散点图;
2.回归方程: yˆ 0.849x 85.172 身高172cm女大学生体重 yˆ = 0.849×172 - 85.712 = 60.316(kg)
本例中,r=0.798>0.75.这表明体重与身高有很强的线性相关关 系,从而也表明我们建立的回归模型是有意义的。
解:1、选取身高为自变量x,体重为因变量y,作散点图: 2、由散点图知道身高和体重有比较 好的线性相关关系,因此可以用线性 回归方程刻画它们之间的关系。
3、从散点图还看到,样本点散布在 某一条直线的附近,而不是在一条 直线上,所以不能用一次函数 y=bx+a描述它们关系。
•
我们可以用下面的线性回归模型来表示:
假中设所随有机的误点作差将n为对完的体全2估重落i2计1没在量有回,影归越响直n 小,线,2也上2预就。报是但精说是度,,越体在高重图。仅中受,身数高据的点影并响没,有那完么全散落点在图回归
人教版数学高二新人教A版选修2-3 3.1《回归分析的基本思想及其应用研析》文字素材3

回归分析的基本思想及其应用研析回归分析是研究如何从样本的统计性质去推测相应总体的统计性质,即如何根据样本去探求有关总体的规律性,是统计学中一种重要的方法,体现了统计的基本思想。
回归分析,从所收集数据的特点,找出一条最接近的直线方程,即线性回归方程,而把其他一些不具有线性回归关系的数据用一种线性回归方程进行拟合,给出数据之间类似函数的一种关系,体现了从特殊到一般的基本思路,使对不确定关系的预报成为一种可能。
回归分析不仅体现了统计的基本思想,还提供了建立数学模型的一种基本方法,回归分析可以总结很多数学或者生产、生活中的规律,比如人的身高与体重的关系、水稻的产量与施肥量的关系等。
例1.高一·一班学生每周用于数学学习的时间x (单位:h)与数学成绩y (单位:分)之间有如下对应数据:如果y 与x 之间具有线性相关关系,求回归直线方程.分析:本题考查求回归直线方程的方法及回归直线的应用.可以直接代入相关公式得出回归直线方程。
解析:本题数据表中,自变量x 的取值没有按从小到大排列,这更接近实际,对结论没有任何影响。
从表中看出:同样是每周用16 h 学数学,一位同学成绩是64分,另一位却是68分,这反映了y 与x 只有相关关系,没有函数关系。
列出下表,并用科学计算器进行有关计算.设回归直线方程为yˆ=bx +a , 则b =53.34.1544.545101022101101≈=-∑-∑==xx yx y x i i i i i , a =5.134.1753.39.74≈⨯-=-x b y ,因此所求的回归直线方程是yˆ=3.53x +13.5. 评注:最小二乘估计是求回归直线方程的常用方法,通过本题的解答可以体会最小二乘估计的优越性。
为了计算方便,通常将有关数据列成表格,然后借助于计算器算出各个量,进而求得回归直线方程。
(备选例 1 )一个车间为了规定工时定额,需要确定加工零件所花费的时间。
为此进行了10次试验,测得数据如下:请判断y 与x 是否具有线性相关关系,如果y 与x 具有线性相关关系,求线性回归方程。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
由于涉及到的变量具有不确定性,接着还要对回归模型进行 统计检验;
统计检验通过后,最后是利用回归模型,根据自变量去估计、 预测因变量。
2021/3/11
郑平正 制作
3
案例1:女大学生的身高与体重
例1 从某大学中随机选取8名女大学生,其身高和体重数据如表1-1所示。
思考:
如何刻画预报变量(体重)的变化?这个变化在多大程度上
与解释变量(身高)有关?在多大程度上与随机误差有关?
2021/3/11
郑平正 制作
11
编号 身高/cm 体重/kg
1
2
3
4
5
6
7
8
165 165 157 170 175 165 155 170
48 57 50 54 64 61 43 59
例如,编号为6的女大学生的体重并没有落在水平直线上,她的体重为61kg。解释 变量(身高)和随机误差共同把这名学生的体重从54.5kg“推”到了61kg,相差6.5kg, 所以6.5kg是解释变量和随机误差的组合效应。
本例中, r=0.798>0.75.这表明体重与身高有很强的线性相关关系,
从而也表明我们建立的回归模型是有意义的。
2021/3/11
郑平正 制作
5
探究:
身高为172cm的女大学生的体重一定是60.316kg吗? 如果不是,你能解释一下原因吗?
答:身高为172cm的女大学生的体重不一定是 60.316kg,但一般可以认为她的体重接近于 60.316kg。
7. 了解相关指数 R2 和模型拟 合的效果之间的关系
8. 了解残差图的作用
9. 利用线性回归模型解决一类 非线性回归问题
2021/3/11
10. 正确理解分析方法与结果
郑平正 制作
2
回归分析的内容与步骤:
回归分析通过一个变量或一些变量的变化解释另 一变量的变化。
其主要内容和步骤是:
首先根据理论和对问题的分析判断,将变量分为自变量和因变 量;
2021/3/11
郑平正 制作
7
思考: 产生随机误差项e的原因是什么?
随机误差e的来源(可以推广到一般):
1、忽略了其它因素的影响:影响身高 y 的因素不只 是体重 x,可能还包括遗传基因、饮食习惯、生 长环境等因素;
2、用线性回归模型近似真实模型所引起的误差;
3、身高 y 的观测误差。
以上三项误差越小,说明我们的回归模型的拟合 效果越好。
可以提供 选择模型的准则
2021/3/11
郑平正 制作
9
函数模型与回归模型之间的差别
函数模型: y bx a 回归模型: y bx a e
线性回归模型y=bx+a+e增加了随机误差项e,因变量y的值由自变量x和 随机误差项e共同确定,即自变量x只能解释部分y的变化。
在统计中,我们也把自变量x称为解释变量,因变量y称为预报变量。
2021/3/11
郑平正 制作
8
函数模型与回归模型之间的差别
120000
中国GDP散点图
100000
80000
GDP
60000
40000
20000
0 1992
1993
1994
1995
1996
1997
1998
年
1999
2000
2001
2002
2003
函数模型: y bx a 回归模型: y bx a e
4 170 54
-4.618
5 175 64
1.137
6 165 61
6.627
7 155 43
-2.883
8 170 59
0.382
我们可以利用图形来分析残差特性,作图时纵坐标为残差,横坐标可以选为样本 编号,或身高数据,或体重估计值等,这样作出的图形称为残差图。
编号为3的女大学生的体重并也没有落在水平直线上,她的体重为50kg。解释 变量(身高)和随机误差共同把这名学生的体重从50kg“推”到了54.5kg,相差-4.5kg, 这时解释变量和随机误差的组合效应为-4.5kg。
用这种方法可以对所有预报变量计算组合效应。
数学上,把每个效应(观测值减去总的平均值)的平方加起来,即用
在线性回归模型中,R2表示解释变量对预报变量变化的贡献率。
R2越接近1,表示回归的效果越好(因为R2越接近1,表示解释变量和预报变量的 线性相关性越强)。
如果某组数据可能采取几种不同回归方程进行回归分析,则可以通过比较R2的值 来做出选择,即选取R2较大的模型作为这组数据的模型。
总的来说:
相关指数R2是度量模型拟合效果的一种指标。
对每名女大学生计算这个差异,然后分别将所得的值平方后加起来,用数学符号
n
表示为: ( yi yi )2 称为残差平方和,它代表了随机误差的效应。 i 1
202在1/例3/111中,残差平方和约为128.36郑1。平正 制作
13
皮肌炎图片——皮肌炎的症状表现
皮肌炎是一种引起皮肤、肌肉、 心、肺、肾等多脏器严重损害的, 全身性疾病,而且不少患者同时 伴有恶性肿瘤。它的1症状表现如 下:
直线上。这些点散布在回归直线附近,所以一定是随机误差把这些点从回归直线上
“推”开了。
因此,数据点和它在回归直线上相应位置的差异(yi yi ) 是随机误差的效应, 称 ei =yi yi 为残差。
Q(aˆ, bˆ) 例如,编号为6的女大学生,计算随机误差的效应(残差)为:即, 61 (0.849165 85.712) 6.627
3. 残差平方和(SSE)
反映除 x 以外的其他因素对 y 取值的影响,也称 为不可解释的平方和或剩余平方和
2021/3/11
郑平正 制作
16
样本决定系数
(判定系数 R2 )
1.回归平方和占总离差平方和的比例
2. 反映回归直线的拟合程度 3. 取值范围在 [ 0 , 1 ] 之间 4. R2 1,说明回归方程拟合的越好;R20
2021/3/11
3、从散点图还看到,样本点散布在 某一条直线的附近,而不是在一条 直线上,所以不能用一次函数 y=bx+a描述它们关系。
4
分析:由于问题中 要求根据身高预报 体重,因此选取身 高为自变量,体重 为因变量.
1. 散点图;
2.回归方程:
yˆ 0.849x 85.172 身高172cm女大学生体重 yˆ = 0.849×172 - 85.712 = 60.316(kg)
在线性模型中,它代表自变量刻画预报变量的能力。
2021/3/11
郑平正 制作
18
我们可以用相关指数R2来刻画回归的效果,其计算公式是
n
R2
1
i 1 n
( yi yi )2 ( yi y)2
1
残差平方和 。 总偏差平方和
i 1
表1-3
来源 随机误差 残差变量
总计
平方和 225.639 128.361
即,用这个回归方程不能给出每个身高为172cm 的女大学生的体重的预测值,只能给出她们平均 体重的值。
2021/3/11
郑平正 制作
6
我们可以用下面的线性回归模型来表示:
y=bx+a+e, (3)
y=bx+a+e, E(e)=0,D(e)= 2.
(4)
其中a和b为模型的未知参数,e称为随机误差。
3.1回归分析的基 本思想及其初步
应用(二)
2021/3/11
郑平正 制作
1
比《数学3》中“回归”增加的内
数学3——统计
容选修1-2——统计案例
5. 引入线性回归模型
1. 画散点图
2. 了解最小二乘法 的思想
y=bx+a+e
6. 了解模型中随机误差项e产 生的原因
3. 求回归直线方程
y=bx+a
4. 用回归直线方程 解决应用问题
,说明回归方程拟合的越差
5. 判定系数等于相关系数的平方,即R2=(r)2
2021/3/11
郑平正 制作
17
我们可以用相关指数R2来刻画回归的效果,其计算公式是
n
R2
1
( yi yi )2
i 1
n
( yi y)2
1
残差平方和 。 总偏差平方和
i 1
显然,R2的值越大,说明残差平方和越小,也就是说模型拟合效果越好。
1、早期皮肌炎患者,还往往伴 有全身不适症状,如-全身肌肉酸 痛,软弱无力,上楼梯时感觉两 腿费力;举手梳理头发时,举高 手臂很吃力;抬头转头缓慢而费 力。
由于解释变量和随机误差的总效应(总偏差平方和)为354,而随机误差的效应为 128.361,所以解释变量的效应为
354-128.361=225.639 这个值称为回归平方和。
解释变量和随机误差的总效应(总偏差平方和) =解释变量的效应(回归平方和)+随机误差的效应(残差平方和)
我们可以用相关指数R2来刻画回归的效果,其计算公式是
n
R2
1
i 1 n
( yi yi )2 ( yi y)2
1
残差平方和 总偏差平方和
。
i 1
n
n
R2
( yi
i 1
y)2 ( yi
编号 1 2 3 4 5 6 7 8
身高/cm 165 165 157 170 175 165 155 170
体重/kg 48 57 50 54 64 61 43 59
求根据一名女大学生的身高预报她的体重的回归方程,并预报一名身高为 172cm的女大学生的体重。
