节点导纳矩阵程序代码
最优潮流编程 节点导纳矩阵编程

则电力系统最优潮流的数学模型可表示为
min f (u, x) ⎫
u
s .t .
g(u, x) = 0⎪⎪⎬
h(u, x ) ≤ 0⎪⎪⎭
五、实验数据及处理结果
简化梯度法的迭代计算步骤: 1)令迭代计数 k=0;
2)假定一组控制变量 u(0) ;
3)由式 ∂L = g(u, x) = 0 ,通过潮流计算由已知的 u 求得相应的 x(k) ; ∂λ
等。
部分用不等式表示如下
PGi ≤ PGi ≤ PGi ( i ∈ SG )
QRi ≤ QRi ≤ QRi ( i ∈ SR )
Vi ≤ Vi ≤ Vi
( i ∈ SB )
Pl = Pij = ViVj (Gij cosθij + Bij sin θij ) − Vi2Gij ≤ Pl ( l ∈ Sl )
+
⎛ ⎜
⎝
∂g
T
⎞
∂u
⎟ ⎠
λ
=
0
,则有
∂L ∂u
=
∂f ∂u
−
⎛ ⎜⎝
∂g ∂u
T
⎞ ⎟⎠
⎡⎛ ⎢⎢⎣⎜⎝
∂g ∂x
T
⎞ ⎟⎠
−1
⎤ ⎥ ⎥⎦
∂f ∂x
6) 若 ∂L = 0 ,说明这组解是最优解,计算结束。否则,转第 7)步。 ∂u
7) 若 ∂L ≠ 0 ,必须按照能使目标函数下降的方向对 u 进行修正, ∂u
f=f(u,x)
(四)最优潮流的约束条件及其数学模型
(1)等式约束条件: 最优潮流分布必须满足基本潮流方程,即
∑ PGi − PDi −Vi
电力网节点导纳矩阵计算例题与程序

电力网节点导纳矩阵计算例题与程序例图1-1对于具有n 个节点b 条支路的有向图,它的关联矩阵为一个N ×B 的矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i ,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0, 图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m :% M FUNCTION ffm.m% Np is number of node point,Nb is number of braches% nstart--the start point of branches ,nend -- the end point, % A -- network incidence matrix function [A]=ffm(nstart,nend) global Np Nb n=length(nstart); A=zeros(Np,Nb); for i=1:nA(nstart(i),i)=1; A(nend(i),i)=-1; end②③①YYY④⑤1:1 1.042315Z21=0.04+J0.25Z23=0.08+J0.30Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。
1.2生成节点导纳矩阵程序:⑴由网络原始矩阵计算节点导纳矩阵公式Y=AYs0A t (1-1)Y ----节点导纳矩阵A------网络关联矩阵A t-----A的转置矩阵YS0----网络原始导纳矩阵若网络各支路阻抗为Zb =[zb1,zb2,……,zbn]则ZS0=Y s0=Z s0-1 (1-2)Y=A Zs0-1A t (1-3)⑵节点导纳计算程序以例1-1网络为例,在不计对地电容和变压器变比假定为1条件下,节点导纳矩阵计算程序如下:clearglobal Np Nb% Np is number of node point,Nb is number of braches,Np=5;Nb=5;% nstart--the start point of branches ,nend -- the end point,% mm -- network incidence matrixnstart=[2,2,1,4,5];nend=[1,3,3,2,3];mm=ffm(nstart,nend);% zb1,the series impedances of transmission line% yb1,the series admittances of transmission linezb1r=[0.04,0.08,0.1,0.0,0.0];zb1i=[0.25,0.30,0.35,0.015,0.03];zb1=zb1r+zb1i*j;yb1=zb1.^(-1);yb=diag(conj(yb1'));y=mm*yb*(mm)';运算程序后可得节点导纳矩阵y=1.3787 - 6.5417i -0.6240 + 3.9002i-0.7547 + 2.6415i 0 0 -0.6240 + 3.9002i 1.4539 -73.6789i-0.8299 + 3.1120i 0 +66.6667i 0 -0.7547 +2.6415i -0.8299+ 3.1120i1.5846 -39.0869i 0 0+33.3333i0 0 +66.6667i 0 0 -66.6667i 00 0 0+33.3333i 0 0-33.3333i⑶线路对地并联电容的处理例图1-1网络中,线路①,②两端对地电容导纳均为j0.25,节点1,2,3自导纳相应增加j0.25,j0.5,j0.25。
MATLAB节点导纳矩阵计算.

第一章导纳矩阵的计算简介
1.1变压器的∏型等值电路
在电力系统潮流计算中,往往要计算节点导纳矩阵,而我们计算节点导纳矩阵采用节点电压法来实现, 如在变压器构成的电力系统中, 需要将变压器模型转变成变压器∏型等值电路 (见图 1-1 ,在利用电路知识列节点电压方程,从而导
图 1-1双绕组变压器的∏型等值电路(i , j 为节点
而在电力系统潮流计算中一般采用标幺值进行计算,标幺值公式如下:
标幺值 ? 有名值(任意单位基准值(与有名值同单位
如果采用标么值计算,元件参数都应归算到同一基准值时得标么值,才能在同一个等值电路上分析和计算。
所以,变压器转变成∏型等值电路时,我们采用标幺值计算,使所求参数为变压器变比 k 的函数。
而在一个已经归算好的电力系统网中,若改变变压器的分接头来进行调压,这时变压器的等值电路参数也会相应得改变,此时采用∏型等值电路进行折算就显得较为方便。
下面是变压器的∏型等值电路分析过程:
如不计励磁支路的影响,双绕组变压器可用其阻抗与一个理想变压器串联的电路表示,如图所示。
理想变压器只有一个参数,那就是变比 k=U1。
现以变压 U2
器阻抗按实际变比归算到低压侧的情况为例,推导出双绕组变压器的∏型等值电路。
流入和流出理想变压器的功率相等:
1。
节点导纳矩阵与节点阻抗矩阵

节点导纳矩阵与节点阻抗矩阵### Node Conductance Matrix vs. Node Impedance Matrix.Node Conductance Matrix.The node conductance matrix is a square matrix that represents the electrical conductance between each pair of nodes in an electrical circuit. It is a symmetric matrix, meaning that the conductance between node i and node j is the same as the conductance between node j and node i. The node conductance matrix is used to solve for the node voltages in a circuit.To derive the node conductance matrix, we start by writing the current law equations for each node in the circuit. The current law states that the sum of the currents entering a node is equal to the sum of the currents leaving the node. For node i, this equation can be written as:\sum_{j=1}^n G_{ij}V_j = I_i.where:G_{ij} is the conductance between node i and node j. V_j is the voltage at node j.I_i is the current entering node i.This equation can be written in matrix form as:GV = I.where:G is the node conductance matrix.V is a column vector of the node voltages.I is a column vector of the node currents.The node conductance matrix can be solved for using a variety of techniques, such as Gaussian elimination or LU decomposition. Once the node conductance matrix has been solved for, the node voltages can be determined by multiplying the node conductance matrix by the column vector of the node currents.Node Impedance Matrix.The node impedance matrix is a square matrix that represents the electrical impedance between each pair of nodes in an electrical circuit. It is a symmetric matrix, meaning that the impedance between node i and node j is the same as the impedance between node j and node i. The node impedance matrix is used to solve for the node currents in a circuit.To derive the node impedance matrix, we start bywriting the voltage law equations for each loop in the circuit. The voltage law states that the sum of the voltages around a loop is equal to zero. For loop k, this equation can be written as:\sum_{j=1}^n Z_{kj}I_j = 0。
节点导纳矩阵潮流计算matlab

《节点导纳矩阵潮流计算matlab分析与应用》在电力系统领域中,潮流计算是一项非常重要的任务,它用于分析和评估电网的稳定性和可靠性。
而在潮流计算中,节点导纳矩阵则是一个关键的数学工具,它能够有效地描述电力系统中各个节点之间的电压和功率之间的关系。
本文将以"节点导纳矩阵潮流计算matlab"为主题,深入探讨节点导纳矩阵的原理、matlab实现以及潮流计算的应用。
一、节点导纳矩阵的原理1.1 节点导纳矩阵的概念节点导纳矩阵是描述电力系统中节点之间电压和电流关系的重要工具。
它通过描述节点之间的导纳关系,能够有效地表达电力系统的复杂结构和参数。
1.2 节点导纳矩阵的构建在电力系统中,节点导纳矩阵可以通过对系统进行潮流分析来建立。
通过建立节点导纳矩阵,我们可以清晰地了解系统中各个节点之间的电压和功率关系,为潮流计算提供了重要的基础。
二、matlab中节点导纳矩阵的实现2.1 matlab在电力系统分析中的优势matlab作为一款强大的数学工具软件,具有丰富的数学库和可视化功能,非常适合用于电力系统的建模和分析。
在节点导纳矩阵潮流计算中,matlab能够提供高效的数学运算和直观的结果展示。
2.2 节点导纳矩阵的matlab实现通过matlab的编程能力,我们可以编写程序来实现节点导纳矩阵的计算和应用。
通过调用matlab的数学库和矩阵运算功能,我们可以快速、准确地建立节点导纳矩阵,并进行潮流计算和分析。
三、潮流计算的应用与案例分析3.1 节点导纳矩阵在潮流计算中的应用通过节点导纳矩阵,我们可以进行系统的潮流计算和分析,从而评估电力系统的稳定性和可靠性。
节点导纳矩阵能够提供系统中各个节点的电压和功率的关系,为系统运行和维护提供重要的参考依据。
3.2 实际案例分析通过一个实际的案例分析,我们可以更好地理解节点导纳矩阵潮流计算在实际电力系统中的应用。
通过matlab的编程和分析能力,我们可以对系统中的电压、功率、损耗等进行全面评估,为系统的优化和改进提供重要的参考依据。
含四种受控源电路的节点导纳矩阵系统列写法

一、概述在电力系统分析中,受控源是一种被广泛使用的模型,在各种电路和系统的分析中都有重要的应用。
受控源电路的节点导纳矩阵系统列写法是一种用来表示受控源电路的方法,能够方便地进行分析和计算。
本文将重点介绍含四种受控源电路的节点导纳矩阵系统列写法,包括其原理、方法和应用。
二、含四种受控源电路的节点导纳矩阵1. 受控电压源受控电压源是一个电压源,其输出电压由电路中的某个变量控制。
在节点导纳矩阵系统列写法中,受控电压源可以表示为:$I_k = -G_{NK}V_k + H_{NK}V_m$其中,$I_k$为电流,$V_k$为电压,$G_{NK}$为导纳矩阵的元素,$H_{NK}$表示受控源的系数。
2. 受控电流源受控电流源是一个电流源,其输出电流由电路中的某个变量控制。
在节点导纳矩阵系统列写法中,受控电流源可以表示为:$V_k = -B_{NK}I_k + E_{NK}I_m$其中,$V_k$为电压,$I_k$为电流,$B_{NK}$为导纳矩阵的元素,$E_{NK}$表示受控源的系数。
3. 受控电压源的双向连接受控电压源的双向连接是一种复杂的受控源模型,其输出电压由电路中的两个变量控制。
在节点导纳矩阵系统列写法中,受控电压源的双向连接可以表示为:$I_k = -G_{NK}V_k + H_{NK}V_m$$I_m = -G_{NM}V_m + H_{NM}V_k$其中,$I_k$和$I_m$分别为电流,$V_k$和$V_m$分别为电压,$G_{NK}$、$H_{NK}$、$G_{NM}$、$H_{NM}$为导纳矩阵的元素。
4. 受控电流源的双向连接受控电流源的双向连接是一种更为复杂的受控源模型,其输出电流由电路中的两个变量控制。
在节点导纳矩阵系统列写法中,受控电流源的双向连接可以表示为:$V_k = -B_{NK}I_k + E_{NK}I_m$$V_m = -B_{NM}I_m + E_{NM}I_k$其中,$V_k$和$V_m$分别为电压,$I_k$和$I_m$分别为电流,$B_{NK}$、$E_{NK}$、$B_{NM}$、$E_{NM}$为导纳矩阵的元素。
Matlab节点导纳矩阵计算
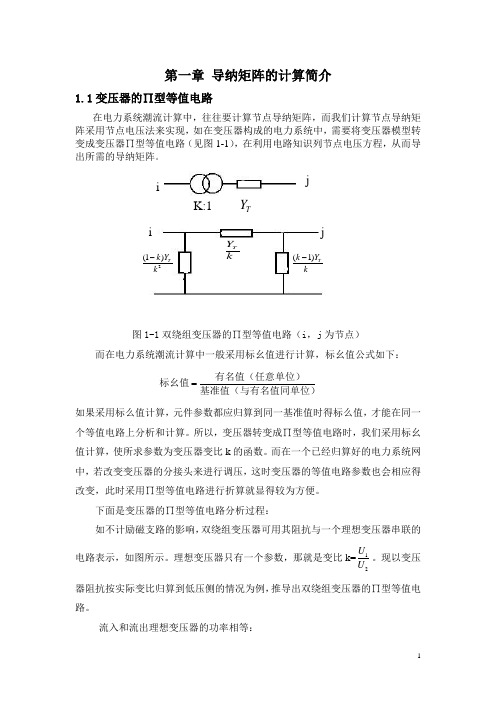
第一章 导纳矩阵的计算简介1.1变压器的∏型等值电路在电力系统潮流计算中,往往要计算节点导纳矩阵,而我们计算节点导纳矩阵采用节点电压法来实现,如在变压器构成的电力系统中,需要将变压器模型转变成变压器∏型等值电路(见图1-1),在利用电路知识列节点电压方程,从而导出所需的导纳矩阵。
图1-1双绕组变压器的∏型等值电路(i ,j 为节点)而在电力系统潮流计算中一般采用标幺值进行计算,标幺值公式如下:=有名值(任意单位)标幺值基准值(与有名值同单位)如果采用标么值计算,元件参数都应归算到同一基准值时得标么值,才能在同一个等值电路上分析和计算。
所以,变压器转变成∏型等值电路时,我们采用标幺值计算,使所求参数为变压器变比k 的函数。
而在一个已经归算好的电力系统网中,若改变变压器的分接头来进行调压,这时变压器的等值电路参数也会相应得改变,此时采用∏型等值电路进行折算就显得较为方便。
下面是变压器的∏型等值电路分析过程:如不计励磁支路的影响,双绕组变压器可用其阻抗与一个理想变压器串联的电路表示,如图所示。
理想变压器只有一个参数,那就是变比k=12U U 。
现以变压器阻抗按实际变比归算到低压侧的情况为例,推导出双绕组变压器的∏型等值电路。
流入和流出理想变压器的功率相等:K:1 T Y ij ij2(1)T k Y k - (1)T k Y k- T Y k....1212/k U I U I = (1U 、2U 分别为变压器高、低绕组的实际电压) (1-1)..12/k I I = (1-2)联立(1-1)、(1-2)两个公式解得:.....1212122T k kZ k kT T T Y U Y U U U I Z =-=- (1-3) ....11222T k Z kT T T Y U U U I Y U Z ∙=-=- (1-4)根据《电路原理》节点1、2的节点电流方程具有如下形式:...1121112...2122122I Y U Y U I Y U Y U ⎫=+⎪⎬⎪-=+⎭ (1-5) 将式(1-3)、(1-4)与式(1-5)比较得(1-6):211T 12T 21T 12T Y Y /k Y Y /k Y Y /k Y Y ⎫=⎪=-⎪⎬=-⎪⎪=⎭ (1-6)因此可以的得到各支路导纳为1212T 2121T 2101112T T T 2202221T T T Y y Y /kY y Y /k 1k y Y y Y /k Y /k Y k k 1y Y y Y Y /k Y k =-=-⎫⎪=-=-⎪⎪-⎬=-=-=⎪⎪-=-=-=⎪⎭(1-7)1.2 节点电压方程在电路中我们已经学过利用节点电压方程来求解某几条支路的电流,现以下图1-2-1与图1-2-2为例推导节点电压方程组。
高等电力网络(张伯明)课后习题5_1,习题5_2程序

程序1(W ARD等值法):function [] = e_ward( )%本段程序实现ward静态等值clc;%形成节点导纳矩阵E=input('请输入外部系统节点集E=');B=input('请输入边界系统节点集B=');I=input('请输入内部系统节点集I=');%priMatrix=load('grid.txt');priMatrix=load('grid5_1.txt');[rows cols]=size(priMatrix);Y=zeros(rows);for m=1:rowsfor n=1:rowsif m==nY(m,n)=sum(priMatrix(m,1:rows));elseY(m,n)=-1*priMatrix(m,n);endendendY=Y*1i;%形成注入电流矩阵current=zeros(rows,1);for m=1:rowscurrent(m)=priMatrix(m,cols);end%按照外部系统节点集E、边界系统节点集B,以及内部系统节点集分配节点导纳矩阵nodeMatrix=zeros(rows,1);a=length(E);b=length(B);c=length(I);for m=1:anodeMatrix(m)=E(m);endfor m=1+a:b+anodeMatrix(m)=B(m-a);endfor m=a+b+1:a+b+cnodeMatrix(m)=I(m-b-a);end%按照EBI节点顺序更新导纳矩阵Y1=zeros(rows);for m=1:rowsfor n=1:rowsd=nodeMatrix(m);e=nodeMatrix(n);Y1(m,n)=Y(d,e);endend%抽出Ybb、Yee、Ybe、Yeb,用于计算Ybb1 Ybb=zeros(b);Yee=zeros(a);Yeb=zeros(a,b);Ybe=Yeb';for m=1:afor n=1:aYee(m,n)=Y1(m,n);endendfor m=1:afor n=a+1:a+bYeb(m,n-a)=Y1(m,n);endendYbe=Yeb.';for m=a+1:a+bfor n=a+1:a+bYbb(m-a,n-a)=Y1(m,n);endendYbb1=Ybb-Ybe*inv(Yee)*Yeb;Y2=zeros(rows-a);for m=1:bfor n=1:bY2(m,n)=Ybb1(m,n);endend%Y2为变换后的导纳矩阵for m=a+1:rowsfor n=a+1:rowsif m<=a+b&&n>a+bY2(m-a,n-a)=Y1(m,n);elseif m>a+bY2(m-a,n-a)=Y1(m,n);endendend%变换后的电流矩阵currentB=zeros(b,1);currentE=zeros(a,1);for m=a+1:a+bcurrentB(m-a)=current(m);endfor m=1:acurrentE(m)=current(m);endcurrentB1=currentB-Ybe*inv(Yee)*currentE; current1=zeros(rows-a,1);for m=1:bcurrent1(m)=currentB1(m);endfor m=b+1:b+ccurrent1(m)=current(m+a);enddisp('变换前的导纳矩阵');disp(Y);disp('变换后的导纳矩阵');disp(Y2);disp('变换前的电流矩阵');disp(current);disp('变换后的电流矩阵');disp(current1);end该程序可以实现习题5.1,还有例5.2的结果priMatrix=load('grid.txt');priMatrix=load('grid5_1.txt');与这两个程序有关下面先实现习题5.1载入的支路导纳矩阵为0.05 -1 -1 -1 0 0 1-1 -0.1 0 -1 0 0 -2-1 0 0 -1 -1 -1 2-1 -1 -1 0 0 -1 10 0 -1 0 -0.1 -1 -10 0 -1 -1 -1 -0.2 0运行过程以及结果为:请输入外部系统节点集E=[1 2]请输入边界系统节点集B=[3 4]请输入内部系统节点集I=[5 6]变换前的导纳矩阵变换后的导纳矩阵0 - 3.5958i 0 + 1.5967i 0 + 1.0000i 0 + 1.0000i0 + 1.5967i 0 - 2.6429i 0 0 + 1.0000i0 + 1.0000i 0 0 - 2.1000i 0 + 1.0000i0 + 1.0000i 0 + 1.0000i 0 + 1.0000i 0 - 3.2000i 变换前的电流矩阵1-221-1变换后的电流矩阵2.01920.0760-1.0000下面实现例题5.20.1 -1 -1 0 0 1-1 0.1 -1 -1 0 -1-1 -1 0.1 -1 -1 20 -1 -1 0.1 -1 -1.50 0 -1 -1 -0.5 -1运行过程及其结果如下:请输入外部系统节点集E=[1 2]请输入边界系统节点集B=[3 4]请输入内部系统节点集I=[5]变换前的导纳矩阵Columns 1 through 30 - 1.9000i 0 + 1.0000i 0 + 1.0000i0 + 1.0000i 0 - 2.9000i 0 + 1.0000i0 + 1.0000i 0 + 1.0000i 0 - 3.9000i0 0 + 1.0000i 0 + 1.0000i0 0 0 + 1.0000iColumns 4 through 50 00 + 1.0000i 00 + 1.0000i 0 + 1.0000i0 - 2.9000i 0 + 1.0000i0 + 1.0000i 0 - 2.5000i变换后的导纳矩阵0 - 2.3922i 0 + 1.6430i 0 + 1.0000i0 + 1.6430i 0 - 2.4787i 0 + 1.0000i0 + 1.0000i 0 + 1.0000i 0 - 2.5000i变换前的电流矩阵1.0000-1.00002.0000-1.5000-1.0000变换后的电流矩阵2.2217-1.6996-1.0000程序2(REI等值):function [] =REI()%本程序实现REI等值参数的计算clc;nodeNum=input('请输入外部网络需要归并到一起的节点数目nodeNum=');S=input('请输入外部网络节点的注入功率矩阵S=');U=input('请输入外部网络节点的电压U=');%S=[2+1*i 3+2*i 1+0.5*i]%U=[1.0*exp(i*5*pi/180) 1.01*exp(i*10*pi/180) 0.98*exp(i*2*pi/180)] %%确定SmSm=sum(S);%求虚拟节点m的电压UmsumI=zeros(1);for m=1:nodeNumsumI(1)=sumI(1)+S(m)/U(m);endUm=Sm/sumI(1);%求Um的模值相角Um_magnitude=abs(Um);Um_angle_radian=angle(Um);Um_angle_degree=angle(Um)*180/pi;%求虚拟节点m的支路导纳ymym=conj(Sm)/Um_magnitude.^2;%求与节点对应的支路导纳矩阵yy=zeros(nodeNum,1);for m=1:nodeNumy(m)=(-1)*conj(S(m))/abs(U(m)).^2;enddisp('虚拟节点的注入功率为:');disp(Sm);fprintf('虚拟节点m的电压的模值为%d\n',Um_magnitude);fprintf('虚拟节点m的电压的相角为%d\n',Um_angle_degree);disp('虚拟节点m的支路导纳为:');disp(ym);disp('归并支路的导纳为:');disp(y);end对于书上的例题运行过程及其结果如下:请输入外部网络需要归并到一起的节点数目nodeNum=3请输入外部网络节点的注入功率矩阵S=[2+1*i 3+2*i 1+0.5*i]请输入外部网络节点的电压U=[1.0*exp(i*5*pi/180) 1.01*exp(i*10*pi/180) 0.98*exp(i*2*pi/180)]虚拟节点的注入功率为:6.0000 + 3.5000i虚拟节点m的电压的模值为1.000117e+000虚拟节点m的电压的相角为7.106649e+000虚拟节点m的支路导纳为:5.9986 - 3.4992i归并支路的导纳为:-2.0000 + 1.0000i-2.9409 + 1.9606i-1.0412 + 0.5206i结果与书上一致程序3(戴维南等值与诺顿等值)该段程序也能实现课后习题5.2以及例题5.3priMatrix=load('daiweinan5_2.txt');%priMatrix=load('daiweinan.txt');由这两段程序分开function [ ] = daiweinanNuodun( )%实现戴维南诺顿等值的程序clc;port=input('请输入端口对矩阵,格式为一对端口为一行,0代表地节点port=');%输入支路导纳矩阵priMatrix=load('daiweinan5_2.txt');%priMatrix=load('daiweinan.txt');[rows cols]=size(priMatrix);%形成节点导纳矩阵Y=zeros(rows);for m=1:rowsfor n=1:rowsif m==nY(m,n)=sum(priMatrix(m,1:rows));elseY(m,n)=-1*priMatrix(m,n);endendendY=Y*1i;%形成注入电流矩阵I0=zeros(rows,1);for m=1:rowsI0(m)=priMatrix(m,cols);end%先形成节点端口关联矢量,然后形成节点端口关联矩阵[a,b]=size(port);Ml=[];for m=1:aMa=zeros(rows,1);c=port(m,1);d=port(m,2);for n=1:rowsif n==cMa(n)=1;elseif n==dMa(n)=-1;endendMl=[Ml Ma];end%求出系统戴维南等值的等值阻抗Zeq=Ml'*inv(Y)*Ml;%由节点电流求出节点电压V0=inv(Y)*I0;%戴维南等值的等值电压Veq=Ml'*V0;%根据戴维南等值的等值阻抗喝等值电压转换成诺顿等值的等值导纳和等值电流Yeq=inv(Zeq);Ieq=Yeq*Veq;disp('戴维南等值的等值阻抗');disp(Zeq);disp('戴维南等值的等值电压');disp(Veq);disp('诺顿等值的等值导纳');disp(Yeq);disp('诺顿等值的等值电流');disp(Ieq);end实现课后习题5.2运行过程以及结果如下:输入支路导纳矩阵0.1 -1 -1 -1 2-1 0.1 0 -1 -2-1 0 0 -1 3-1 -1 -1 -0.2 -1请输入端口对矩阵,格式为一对端口为一行,0代表地节点port=[3 0;4 0] 戴维南等值的等值阻抗0 -60.5714i 0 -58.8095i0 -58.8095i 0 -56.5079i戴维南等值的等值电压1.0e+002 *0 - 1.2100i0 - 1.1833i诺顿等值的等值导纳0 - 1.5787i 0 + 1.6430i0 + 1.6430i 0 - 1.6922i诺顿等值的等值电流3.3991-1.4435例题5.3的实现过程:Txt文件中包含的题目信息(支路导纳矩阵)-0.5 -5 -10 1-5 -0.5 -5 0.5-10 -5 -0.5 -1.2运行过程以及结果:请输入端口对矩阵,格式为一对端口为一行,0代表地节点port=[1 2;3 0] 戴维南等值的等值阻抗0 + 0.1164i 0 + 0.0127i0 + 0.0127i 0 + 0.6970i戴维南等值的等值电压0 + 0.0044i0 + 0.1440i诺顿等值的等值导纳0 - 8.6094i 0 + 0.1563i0 + 0.1563i 0 - 1.4375i诺顿等值的等值电流0.01560.2063结果与书上的结论一致。
电力网节点导纳矩阵计算例题与程序
电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序,程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
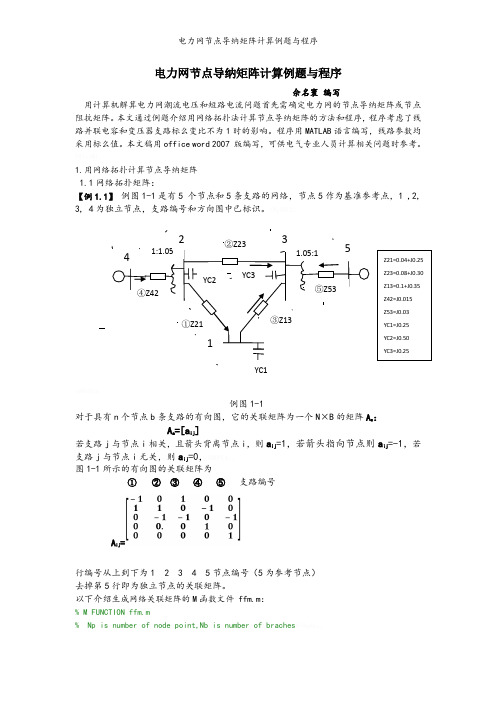
1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵:【例1.1】 例图1-1是有5 个节点和5条支路的网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号和方向图中已标识。
例图1-1对于具有n 个节点b 条支路的有向图,它的关联矩阵为一个N ×B 的矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i ,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0,图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m :% M FUNCTION ffm.m% Np is number of node point,Nb is number of braches ②Z23③Z13①Z21YC2YC3YC1④Z42⑤Z531:1.051.05:142315Z21=0.04+J0.25 Z23=0.08+J0.30 Z13=0.1+J0.35 Z42=J0.015 Z53=J0.03 YC1=J0.25 YC2=J0.50 YC3=J0.25% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm.m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij是相同的。
牛顿-拉夫逊法潮流计算matlab程序

end
fprintf(myf,'n线路计算结果:n节点I 节点J 线路功率S(I,J) 线路功率S(J,I) 线路损耗dS(I,J)n');
[bus,line] = ReNum_(bus,line,nodenum); % 对节点恢复编号的子程序
YtYm = YtYm_(line); % 计算线路的等效Yt和Ym的子程序,以计算线路潮流
bus_res = bus_res_(bus); % 计算节点数据结果的子程序
J = Jac_(bus,Y,nPQ); % 计算雅克比矩阵的子程序
UD = zeros(nPQ,nPQ);
for i = 1:nPQ
UD(i,i) = bus(i,2); % 生成电压对角矩阵
fclose(myf); % 在当前目录下生成“Result.m”文件,写入节点导纳矩阵
format long
EPS = 1.0e-10; % 设定误差精度
for t = 1:100 % 开始迭代计算,设定最大迭代次数为100,以便不收敛情况下及时跳出
[dP,dQ] = dPQ_(Y,bus,nPQ,nPV); % 计算功率偏差dP和dQ的子程序
for i = 1:nb
fprintf(myf,'%2.0f ',bus_res(i,1));
fprintf(myf,'%10.6f ',bus_res(i,2));
fprintf(myf,'%10.6f ',bus_res(i,3));
导纳矩阵计算课程设计

南昌工程学院本科课程设计第一章引言导纳矩阵计算是电力系统分析最基本的计算。
除它自身的重要作用之外,在《电力系统分析综合程序》(PSASP)中,还是网损计算、静态安全分析、暂态稳定计算、小干扰静态稳定计算、短路计算、静态和动态等值计算的基础。
对规划中的电力系统,通过计算可以检验所提出的电力系统规划方案能否满足各种运行方式的要求;对运行中的电力系统,通过计算可以预知各种负荷变化和网络结构的改变会不会危及系统的安全,系统中所有母线的电压是否在允许的范围以内,系统中各种元件(线路、变压器等)是否会出现过负荷,以及可能出现过负荷时应事先采取哪些预防措施等。
1.1课程设计目的与要求1.1.1设计目的1.掌握电力系统潮流计算导纳矩阵的基本原理;2.掌握并能熟练运用一门计算机语言(MA TLAB语言或C语言或C++语言);3.采用计算机语言对潮流计算导纳矩阵进行计算机编程。
1.1.2 设计要求1.程序源代码;2.给定题目的输入,输出文件;3. 程序说明;4. 给定系统的程序计算过程;5. 给定系统的手算过程(至少迭代2次)。
1.2设计内容1.根据电力系统网络推导电力网络数学模型,写出节点导纳矩阵;2.赋予各节点电压变量(直角坐标系形式)初值后,求解不平衡量;3.形成雅可比矩阵;4.求解修正量后,重新修改初值,从2开始重新循环计算;5.求解的电压变量达到所要求的精度时,再计算各支路功率分布、功率损耗和平衡节点功率;6.上机编程调试;7. 计算分析给定系统导纳矩阵分析并与手工计算结果做比较分析;8.书写课程设计说明书,准备答辩。
第二章导纳矩阵计算概述第二章导纳矩阵计算概述2.1导纳矩阵计算简介电力系统潮流导纳矩阵计算是研究电力系统稳态运行情况的一种计算,它根据给定的运行条件及系统接线情况确定整个电力系统各部分的运行状态:各母线的电压。
各元件中流过的功率,系统的功率损耗等等。
在电力系统规划的设计和现有电力系统运行方式的研究中,都需要利用潮流计算来定量的分析比较供电方案或运行方式的合理性。
电力网节点导纳矩阵计算例题与程序
电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压与短路电流问题首先需确定电力网得节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵得方法与程序,程序考虑了线路并联电容与变压器支路标么变比不为1时得影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
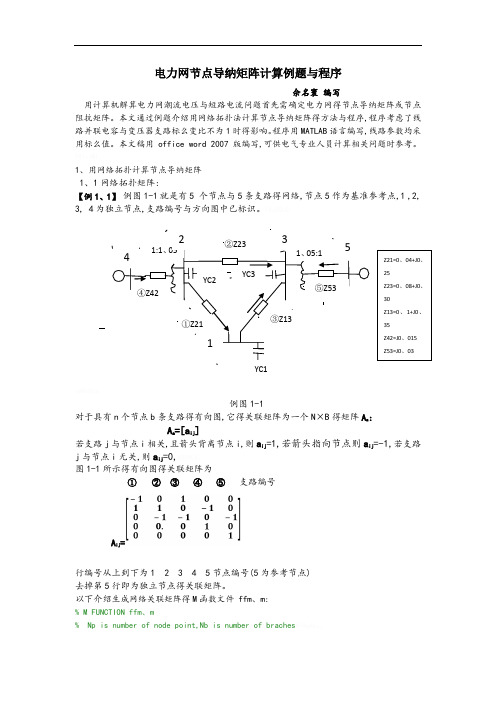
1、用网络拓扑计算节点导纳矩阵 1、1网络拓扑矩阵:【例1、1】 例图1-1就是有5 个节点与5条支路得网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号与方向图中已标识。
例图1-1对于具有n 个节点b 条支路得有向图,它得关联矩阵为一个N ×B 得矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0,图1-1所示得有向图得关联矩阵为① ② ③ ④ ⑤ 支路编号A ij =行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点得关联矩阵。
以下介绍生成网络关联矩阵得M 函数文件 ffm 、m:% M FUNCTION ffm 、m% Np is number of node point,Nb is number of braches ②Z23③Z13①Z21YC2YC3YC1④Z42⑤Z531:1、051、05:142315Z21=0、04+J0、25Z23=0、08+J0、30Z13=0、1+J0、35Z42=J0、015 Z53=J0、03% nstart--the start point of branches ,nend -- the end point,% A -- network incidence matrixfunction[A]=ffm(nstart,nend)global Np Nbn=length(nstart);A=zeros(Np,Nb);for i=1:nA(nstart(i),i)=1;A(nend(i),i)=-1;end以例图1-1网络为例调用ffm、m文件求其关联矩阵运算以上程序可得关联矩阵 mm ij如下:mm =-1 0 1 0 01 1 0 -1 00 -1 -1 0 -10 0 0 1 00 0 0 0 1Mm ij明显与A ij就是相同得。
电力网节点导纳矩阵计算例题与程序文件
电力网节点导纳矩阵计算例题与程序佘名寰 编写用计算机解算电力网潮流电压和短路电流问题首先需确定电力网的节点导纳矩阵或节点阻抗矩阵。
本文通过例题介绍用网络拓扑法计算节点导纳矩阵的方法和程序,程序考虑了线路并联电容和变压器支路标么变比不为1时的影响。
程序用MATLAB 语言编写,线路参数均采用标么值。
本文稿用office word 2007 版编写,可供电气专业人员计算相关问题时参考。
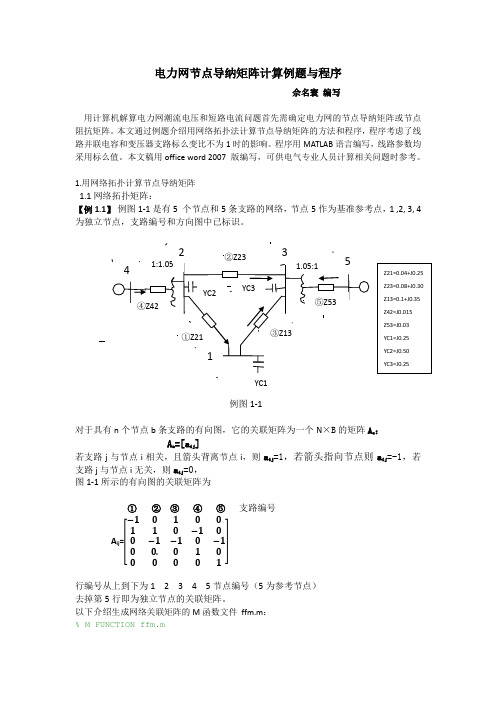
1.用网络拓扑计算节点导纳矩阵 1.1网络拓扑矩阵:【例1.1】 例图1-1是有5 个节点和5条支路的网络,节点5作为基准参考点,1 ,2, 3, 4为独立节点,支路编号和方向图中已标识。
例图1-1对于具有n 个节点b 条支路的有向图,它的关联矩阵为一个N ×B 的矩阵A a :A a =[a ij ]若支路j 与节点i 相关,且箭头背离节点i ,则a ij =1,若箭头指向节点则a ij =-1,若支路j 与节点i 无关,则a ij =0, 图1-1所示的有向图的关联矩阵为① ② ③ ④ ⑤ 支路编号 A ij =[ −10100110−100−1−10−100.01000001]行编号从上到下为1 2 3 4 5节点编号(5为参考节点) 去掉第5行即为独立节点的关联矩阵。
以下介绍生成网络关联矩阵的M 函数文件 ffm.m :% M FUNCTION ffm.m% Np is number of node point,Nb is number of braches% nstart--the start point of branches ,nend -- the end point, % A -- network incidence matrix function [A]=ffm(nstart,nend) global Np Nb n=length(nstart); A=zeros(Np,Nb); for i=1:nA(nstart(i),i)=1; A(nend(i),i)=-1; end以例图1-1网络为例调用ffm.m 文件求其关联矩阵运算以上程序可得关联矩阵 mm ij 如下:mm =-1 0 1 0 0 1 1 0 -1 0 0 -1 -1 0 -1 0 0 0 1 0 0 0 0 0 1 Mm ij 明显与A ij 是相同的。
Matlab节点导纳矩阵计算

第一章 导纳矩阵的计算简介1.1变压器的∏型等值电路在电力系统潮流计算中,往往要计算节点导纳矩阵,而我们计算节点导纳矩阵采用节点电压法来实现,如在变压器构成的电力系统中,需要将变压器模型转变成变压器∏型等值电路(见图1-1),在利用电路知识列节点电压方程,从而导出所需的导纳矩阵。
图1-1双绕组变压器的∏型等值电路(i ,j 为节点)而在电力系统潮流计算中一般采用标幺值进行计算,标幺值公式如下:=有名值(任意单位)标幺值基准值(与有名值同单位)如果采用标么值计算,元件参数都应归算到同一基准值时得标么值,才能在同一个等值电路上分析和计算。
所以,变压器转变成∏型等值电路时,我们采用标幺值计算,使所求参数为变压器变比k 的函数。
而在一个已经归算好的电力系统网中,若改变变压器的分接头来进行调压,这时变压器的等值电路参数也会相应得改变,此时采用∏型等值电路进行折算就显得较为方便。
下面是变压器的∏型等值电路分析过程:如不计励磁支路的影响,双绕组变压器可用其阻抗与一个理想变压器串联的电路表示,如图所示。
理想变压器只有一个参数,那就是变比k=12U U 。
现以变压器阻抗按实际变比归算到低压侧的情况为例,推导出双绕组变压器的∏型等值电路。
流入和流出理想变压器的功率相等:K:1 T Y ij ij2(1)T k Y k - (1)T k Y k- T Y k....1212/k U I U I = (1U 、2U 分别为变压器高、低绕组的实际电压) (1-1)..12/k I I = (1-2)联立(1-1)、(1-2)两个公式解得:.....1212122T k kZ k kT T T Y U Y U U U I Z =-=- (1-3) ....11222T k Z kT T T Y U U U I Y U Z ∙=-=- (1-4)根据《电路原理》节点1、2的节点电流方程具有如下形式:...1121112...2122122I Y U Y U I Y U Y U ⎫=+⎪⎬⎪-=+⎭ (1-5) 将式(1-3)、(1-4)与式(1-5)比较得(1-6):211T 12T 21T 12T Y Y /k Y Y /k Y Y /k Y Y ⎫=⎪=-⎪⎬=-⎪⎪=⎭ (1-6)因此可以的得到各支路导纳为1212T 2121T 2101112T T T 2202221T T T Y y Y /kY y Y /k 1k y Y y Y /k Y /k Y k k 1y Y y Y Y /k Y k =-=-⎫⎪=-=-⎪⎪-⎬=-=-=⎪⎪-=-=-=⎪⎭(1-7)1.2 节点电压方程在电路中我们已经学过利用节点电压方程来求解某几条支路的电流,现以下图1-2-1与图1-2-2为例推导节点电压方程组。
计算导纳矩阵

//****************计算导纳矩阵*******************G[1][1]=z12r/(z12r*z12r+z12m*z12m)+k*k*z13r/(z13r*z13r+z13m*z13m)+z14r/(z14r*z14r+z1 4m*z14m);B[1][1]=-z12m/(z12r*z12r+z12m*z12m)-k*k*z13m/(z13r*z13r+z13m*z13m)-z14m/(z14r*z14r+z14m*z14m)+y140+y120;G[2][2]=z12r/(z12r*z12r+z12m*z12m)+z24r/(z24r*z24r+z24m*z24m);B[2][2]=-z12m/(z12r*z12r+z12m*z12m)-z24m/(z24r*z24r+z24m*z24m)+y240+y120;G[3][3]=z13r/(z13r*z13r+z13m*z13m);B[3][3]=-z13m/(z13r*z13r+z13m*z13m);G[4][4]=z14r/(z14r*z14r+z14m*z14m)+z24r/(z24r*z24r+z24m*z24m;B[4][4]=-z14m/(z14r*z14r+z14m*z14m)-z24m/(z24r*z24r+z24m*z24m)+y240+y140;G[1][2]=G[2][1]=-z12r/(z12r*z12r+z12m*z12m);B[1][2]=B[2][1]=z12m/(z12r*z12r+z12m*z12m);G[1][3]=G[3][1]=-k*z13r/(z13r*z13r+z13m*z13m);B[1][3]=B[3][1]=k*z13m/(z13r*z13r+z13m*z13m);G[1][4]=G[4][1]=-z14r/(z14r*z14r+z14m*z14m);B[1][4]=B[4][1]=z14m/(z14r*z14r+z14m*z14m);G[2][3]=G[3][2]=0.0;B[2][3]=B[3][2]=0.0;G[2][4]=G[4][2]=-z24r/(z24r*z24r+z24m*z24m);B[2][4]=B[4][2]=z24m/(z24r*z24r+z24m*z24m);G[3][4]=G[4][3]=0.0;B[3][4]=B[4][3]=0.0;for(i=1;i<5;i++){for(j=1;j<5;j++){printf("%f+%fj",G[i][j],B[i][j]); printf(" ");}printf("\n");//形成节点导纳矩阵//计算各节点不平衡量loop1:printf("迭代次数k1=%d\n",k1); for (i=1;i<5;i++){float a=0,b=0;for(j=1;j<5;j++){a+=G[i][j]*e[j]-B[i][j]*f[j];b+=G[i][j]*f[j]+B[i][j]*e[j];}P[i]=Ps[i]-(e[i]*a+f[i]*b);//计算有功功率的增量Q[i]=Qs[i]-(f[i]*a-e[i]*b);//计算无功功率的增量V32=V3s*V3s-e[3]*e[3];}printf("有功功率增量P[1]=%f",P[1]);printf(" ,");printf("有功功率增量P[2]=%f",P[2]);printf(" ,");printf("有功功率增量P[3]=%f",P[3]);printf("无功功率增量Q[1]=%f",Q[1]);printf(" ,");printf("无功功率增量Q[2]=%f",Q[2]);printf(" ,");printf("电压增量V32=%f",V32);printf("\n");//****形成雅克比矩阵********************** for(j=1;j<4;j++){if(1==j){float c=0,d=0;int m;for(m=1;m<5;m++){c+=G[1][m]*e[m]-B[1][m]*f[m];d+=G[1][m]*f[m]+B[1][m]*e[m];}J[1*N-1][j*N-1]=-c-G[1][j]*e[1]-B[1][j]*f[1];J[1*N-1][j*N]=-d+B[1][j]*e[1]-G[1][j]*f[1];J[1*N][j*N-1]=d+B[1][j]*e[1]-G[1][j]*f[1];J[1*N][j*N]=-c+G[1][j]*e[1]+B[1][j]*f[1];}else{J[1*N-1][j*N-1]=-G[1][j]*e[1]-B[1][j]*f[1];J[1*N][j*N]=G[1][j]*e[1]-B[1][j]*f[1];J[1*N-1][j*N]=B[1][j]*e[1]-G[1][j]*f[1];J[1*N][j*N-1]=B[1][j]*e[1]-G[1][j]*f[1];}}//********计算修正方程************* for(i=1;i<M;i++){L[i][i]=1;}L[i][1]=J[i][1]/U[1][1];}for(n=2;n<M;n++){for(j=n;j<M;j++){sigma1=0;for(s=0;s<=n-1;s++)sigma1+=L[n][s]*U[s][j];U[n][j]=J[n][j]-sigma1;}for(i=n;i<M;i++){sigma2=0;for(s=0;s<=n-1;s++)sigma2+=L[i][s]*U[s][n];L[i][n]=(J[i][n]-sigma2)/U[n][n]; }}b[1]=P[1];b[2]=Q[1];b[3]=P[2];b[4]=Q[2];b[5]=P[3];b[6]=V32;for(i=1;i<M;i++){sigma1=0;for(n=1;n<=i-1;n++)for(i=1;i<M;i++){U[1][i]=J[1][i];sigma1+=L[i][n]*y[n];y[i]=b[i]-sigma1;}for(i=M-1;i>=1;i--){sigma2=0;for(n=i+1;n<M;n++)sigma2+=U[i][n]*x[n];x[i]=(y[i]-sigma2)/U[i][i];}xe[1]=-x[1];xe[2]=-x[3];xe[3]=-x[5]; xf[1]=-x[2];xf[2]=-x[4];xf[3]=-x[6]; printf("节点电压:\n");for(i=1;i<4;i++){e[i]+=xe[i];f[i]+=xf[i];}for(i=1;i<4;i++){printf("e[%d]=",i);printf("%f",e[i]);printf(" ,");}for(i=1;i<4;i++){printf("f[%d]=",i);printf("%f",f[i]);printf(" ,");}%给定节点电压初值e = [1 1 1.1 1.05];f = [0 0 0 0 ];%给定PQ节点有用和无功功率,以及PV节点有功和电压P1 = -0.3;Q1 = -0.18;P2 = -0.55;Q2 = -0.13;P3 = 0.5;V3 = 1.1;%手动输入节点导纳矩阵G=[ 1.042093, -0.588235, 0, -0.453858;-0.588235, 1.069005, 0, -0.480769;0 , 0 , 0, 0;-0.453858, -0.480769, 0, 0.934627];B=[ -8.242876, 2.352941, 3.666667, 1.891074;2.352941, -4.727377, 0, 2.403846;3.666667, 0 ,-3.333333, 0;1.891074,2.403846, 0, -4.261590];maxP = 0;maxQ = 0;maxV = 0;I = [ 0,0;0,0;0,0;0,0];for v=1:15 %迭代次数for n=1:4I(1,1)=I(1,1)+G(1,n)*e(n)-B(1,n)*f(n);I(1,2)=I(1,2)+G(1,n)*f(n)+B(1,n)*e(n);endfor n=1:4I(2,1)=I(2,1)+G(2,n)*e(n)-B(2,n)*f(n);I(2,2)=I(2,2)+G(2,n)*f(n)+B(2,n)*e(n);endfor n=1:4I(3,1)=I(3,1)+G(3,n)*e(n)-B(3,n)*f(n);I(3,2)=I(3,2)+G(3,n)*f(n)+B(3,n)*e(n);endfor n=1:4I(4,1)=I(4,1)+e(n)*e(n)+f(n)*f(n);I(4,2)=0;endH =[];N =[];M =[];L =[];R =[];S =[];J =[];%求不平衡量P1 = -0.30-e(1)*I(1,1)-f(1)*I(1,2);Q1 = -0.18-f(1)*I(1,1)+e(1)*I(1,2);P2 = -0.55-e(2)*I(2,1)-f(2)*I(2,2);Q2 = -0.13-f(2)*I(2,1)+e(2)*I(2,2);P3 = 0.50-e(3)*I(3,1)-f(3)*I(3,2);V3 = 1.10^2-I(4,1);%分块计算雅各比矩阵元素for m=1:3for n=1:3if(m==n)H(m,m) = B(m,m)*e(m)-G(m,m)*f(m)-I(m,2); N(m,m) = -G(m,m)*e(m)-B(m,m)*f(m)-I(m,1); M(m,m) = G(m,m)*e(m)+B(m,m)*f(m)-I(m,1); L(m,m) = B(m,m)*e(m)-G(m,m)*f(m)+I(m,2); R(m,m) = -2*f(m);S(m,m )= -2*e(m);elseH(m,n) = B(m,n)*e(m)-G(m,n)*f(m);N(m,n) = -G(m,n)*e(m)-B(m,n)*f(m);M(m,n) = -N(m,n);L(m,n) = H(m,n);R(m,m) = 0;S(m,m )= 0;endendend%确定雅克比矩阵各元素J=[ H(1,1),N(1,1),H(1,2),N(1,2),H(1,3),N(1,3);M(1,1),L(1,1),M(1,2),L(1,2),M(1,3),L(1,3);H(2,1),N(2,1),H(2,2),N(2,2),H(2,3),N(2,3);M(2,1),L(2,1),M(2,2),L(2,2),M(2,3),L(2,3);H(3,1),N(3,1),H(3,2),N(3,2),H(3,3),N(3,3);R(3,1),S(3,1),R(3,2),S(3,2),R(3,3),S(3,3)];%求解节点电压的修正量A =[];C =[ P1;Q1;P2;Q2;P3;V3]A = -inv(J)*C;%排序找出最大误差maxP=C(1);maxQ=C(2);maxV=C(6); %V3直接赋给电压误差最大值maxVfor d = 1:2:5 %在P1/P3/P5中找出最大值赋给maxP if(C(d)>maxP)maxP=C(d);endendfor t = 2:2:4 %在Q2/Q4中找出最大值赋给maxQif(C(t)>maxQ)maxQ=C(t);endend%修正节点电压值if((maxP>0.00001)&&(maxQ>0.00001)&&(maxV>0.00001)) e(1)= e(1)+A(2)e(2)= e(2)+A(4)e(3)= e(3)+A(6)f(1)= f(1)+A(1)f(2)= f(2)+A(3)f(3)= f(3)+A(5)endend%计算平衡节点功率和网络中的功率分布S4 = (1.05+0*i)*[(G(4,1)-i*B(4,1))*(e(1)-i*f(1))+(G(4,2)-i*B(4,2))*(e(2)-i*f(2))+(G(4,3)-i*B(4,3))*(e(3)-i*f(3))+(G(4,4)-i*B(4,4))*(1.05-0*i)] %平衡节点功率S12 = (e(1)+i*f(1))*[e(1)+i*f(1)-e(2)-f(2)*i]*(G(1,2)+i*B(1,2)) S13 = (e(1)+i*f(1))*[e(1)+i*f(1)-e(3)-f(3)*i]*(G(1,3)+i*B(1,3)) S14 = (e(1)+i*f(1))*[e(1)+i*f(1)-1.05-0*i]*(G(1,4)+i*B(1,4))S21 = (e(2)+i*f(2))*[e(2)+i*f(2)-e(1)-i*f(1)]*(G(2,1)+i*B(2,1)) S24 = (e(2)+i*f(2))*[e(2)+i*f(2)-1.05-0*i]*(G(2,4)+i*B(2,4))S31 = (e(3)+i*f(3))*[e(3)+i*f(3)-e(1)-f(1)*i]*(G(3,1)+i*B(3,1)) S41 = (1.05+0*i)*[1.05+0*i-e(1)-f(1)*i]*(G(4,3)+i*B(4,3))S42 = (1.05+0*i)*[1.05+0*i-e(2)-f(2)*i]*(G(4,2)+i*B(4,2))课程设计任务书学生姓名: 专业班级: 指导教师: 工作单位:题 目: 直角坐标下牛顿法潮流计算 初始条件:下图所示的简单电力系统中,网络各元件参数的标幺值如下:z12=0.10+j0.40; y120=y210=j0.01528;z13=j0.3; k=1.1; z14=0.12+j0.50; y140=y410=j0.01920; z24=0.08+j0.40; y240=y420=j0.01413。
